Optimum Sensor Placement Method for Cable-Stayed Bridges Based on Damage Identifiability
-
摘要: 为使布置在斜拉桥上的传感器识别出的模态参数对结构损伤足够敏感,从传感器优化布置的损伤可识别性要求出发,应用参数试验法和参数相关性理论,提出并得到一种包含所有单元损伤信息的节点自由度损伤信息指标,对该指标排序可获得节点自由度包含损伤信息多少的次序,即每个自由度的损伤敏感性排名,此过程无需优化迭代.在此基础上利用传感器优化布置的第1类方法继续分析,避免了迭代或优化效率低下等缺陷,可得到既满足损伤可识别性,也满足模态可观测性的传感器布置位置.在单塔双索面斜拉桥上,展示了本文方法的实现过程,与EI(effective independence)法相比,损伤信息总量:3阶时高出589;4阶时高出582;5阶时高出591.Abstract: In order to make the modal parameters identified by the sensors on cable-stayed bridges that are sufficiently sensitive to structural damage, a damage information index of the node degree of freedom containing the damage information of all elements was proposed and obtained, considering the damage identifiability requirements for optimum sensor placement, and using the method of parameter study and parameter correlation theory. The damage information regarding the degrees of freedom of the nodes could be ordered by ranking the index, i.e. by ranking the damage sensitivity of each degree of freedom. This process did not require the use of any optimization iterative algorithm. Based on this proposal, the first such method for optimum sensor placement, which can avoid defects such as inefficient iterations and optimization, could be analysed. Finally, the location of the sensor, which could provide satisfactory damage identifiability and modal observability, was obtained. The feasibility of the proposed method was demonstrated using a single-tower double-cable-plane cable-stayed bridge. A comparison of the results with those obtained using the EI method (effective independence method) revealed that the total damage information obtained using the proposed method is greater by factors of 589, 582, and 591 for the 3rd, 4th, and 5th orders, respectively.
-
表 1 基准有限元模型与实测频率对比
Table 1. Comparison between calculated and measured frequencies
阶数 实测频率/Hz 基准有限元模型频率/Hz 误差/% 1 0.469 951 0.464 782 1.1 2 0.781 907 0.791 290 -1.2 3 0.903 752 0.891 099 1.4 4 1.114 995 1.100 500 1.3 5 1.136 485 1.147 850 -1.0 表 2 提取不同模态数时较大的损伤信息指标及对应节点
Table 2. Partial data of the design matrix obtained using the parameter study method
编号 D0_1 D1_1y D1_1z D10_1y D10_1z D11_1y D11_1z D12_1y D12_1z D13_1y 1 1 1 1 1 1 1 1 1 1 1 2 0 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 4 2 1 1 1 1 1 1 1 1 1 5 1 1 1 0 1 1 1 1 1 1 6 1 1 1 1 1 1 1 1 1 1 7 1 1 1 2 1 1 1 1 1 1 8 1 1 1 1 0 1 1 1 1 1 9 1 1 1 1 1 1 1 1 1 1 10 1 1 1 1 2 1 1 1 1 1 115 1 1 1 1 1 1 1 1 1 1 116 1 1 1 1 1 1 1 1 1 1 117 1 1 1 1 1 1 1 1 1 1 118 1 1 1 1 1 1 1 1 1 1 119 1 1 1 1 1 1 1 1 1 1 120 1 1 1 1 1 1 1 1 1 1 121 1 1 1 1 1 1 1 1 1 1 122 1 1 1 1 1 1 1 1 1 1 123 1 1 1 1 1 1 1 1 1 1 124 1 1 1 1 1 1 1 1 1 1 表 3 仿真试验部分节点的前5阶归一化振型值
Table 3. Normalized mode shape values of the first five orders of the partial nodes obtained via simulation
m 编号 n1_10 n1_11 n1_12 n1_13 n1_14 n1_15 1 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 2 -0.378 650 13 -0.325 432 84 0.381 763 70 0.327 884 42 -0.483 275 11 -0.431 511 80 3 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 4 -0.378 711 20 -0.325 486 55 0.381 850 31 0.327 959 68 -0.483 347 22 -0.431 579 04 5 -0.378 649 96 -0.325 436 72 0.381 794 24 0.327 910 07 -0.483 258 80 -0.431 504 99 6 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 7 -0.378 711 35 -0.325 482 57 0.381 819 17 0.327 933 54 -0.483 363 83 -0.431 585 96 8 -0.378 659 60 -0.325 440 35 0.381 756 87 0.327 883 06 -0.483 287 81 -0.431 523 01 9 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 10 -0.378 701 53 -0.325 478 88 0.381 857 27 0.327 961 07 -0.483 334 27 -0.431 567 60 115 -0.378 757 57 -0.325 521 09 0.381 843 80 0.327 955 16 -0.483 426 98 -0.431 640 48 116 -0.378 638 92 -0.325 422 16 0.381 717 47 0.327 850 20 -0.483 262 92 -0.431 500 08 117 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 118 -0.378 722 62 -0.325 497 43 0.381 897 46 0.327 994 58 -0.483 359 65 -0.431 590 98 119 -0.378 625 12 -0.325 416 08 0.381 781 03 0.327 898 45 -0.483 224 64 -0.431 475 60 120 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 121 -0.378 736 68 -0.325 503 63 0.381 832 65 0.327 945 38 -0.483 398 66 -0.431 615 93 122 -0.378 647 64 -0.325 429 82 0.381 733 81 0.327 863 89 -0.483 273 47 -0.431 509 78 123 -0.378 680 36 -0.325 459 43 0.381 806 59 0.327 921 69 -0.483 310 82 -0.431 545 09 124 -0.378 713 72 -0.325 489 62 0.381 880 80 0.327 980 62 -0.483 348 89 -0.431 581 09 表 4 不同模态阶数时传感器布点位置
Table 4. Sensor locations for different mode shape orders
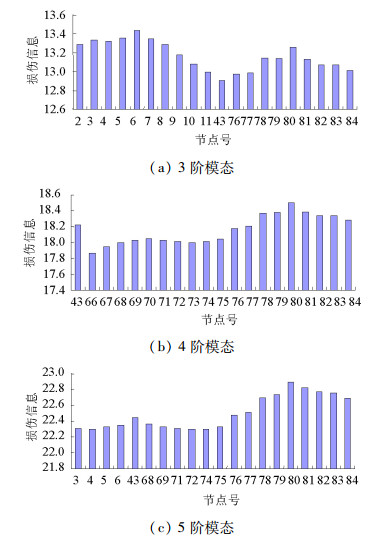
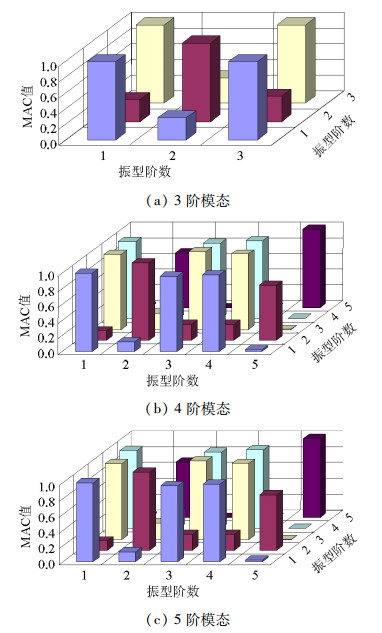
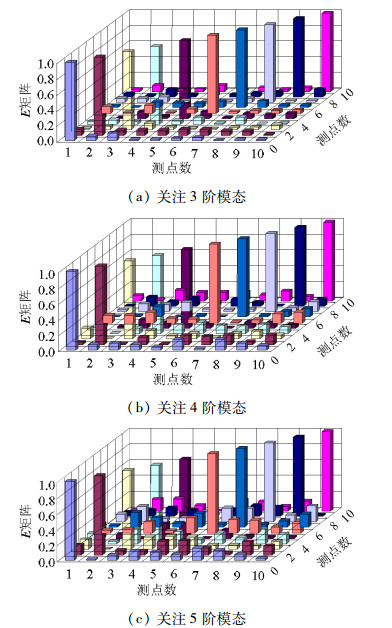
提取模态数/个 传感器布点位置 3 2 3 4 5 6 7 8 9 10 11 43 76 77 78 79 80 81 82 83 84 4 43 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 5 3 4 5 6 43 68 69 71 72 74 75 76 77 78 79 80 81 82 83 84 表 5 最终的传感器布点位置
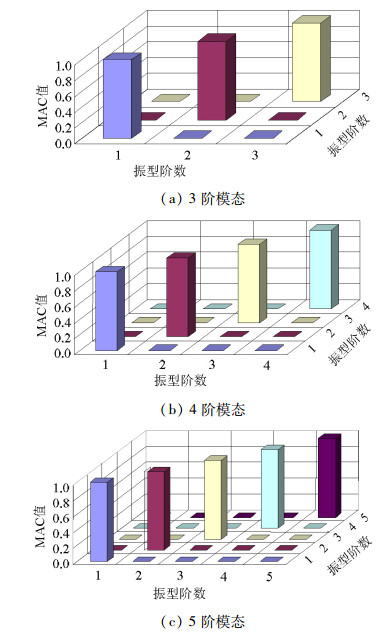
Table 5. Final sensor locations
提取模态数/个 传感器布点位置 3 2 4 6 8 10 43 77 79 81 84 4 43 66 68 70 72 74 76 78 80 84 5 3 5 43 68 71 75 77 80 82 84 表 6 EI法的传感器布点位置
Table 6. Sensor locations using the EI method
提取模态数/个 传感器布点位置 3 4 8 20 22 42 43 64 66 78 82 4 6 18 20 22 42 43 64 66 68 80 5 5 15 18 20 22 64 66 68 71 81 -
张明金, 李永乐, 余显全, 等.桥塔上风传感器安装位置对测量结果的影响[J].西南交通大学学报, 2015, 50(4):617-662. doi: 10.3969/j.issn.0258-2724.2015.04.007ZHANG Mingjin, LI Yongle, YU Xianquan, et al. Influence of wind sensor location on bridge tower on measurement result[J]. Journal of Southwest Jiaotong University, 2015, 50(4):617-662. doi: 10.3969/j.issn.0258-2724.2015.04.007 蒲黔辉, 秦世强, 施洲, 等.环境激励下钢筋混凝土拱桥模态参数识别[J].西南交通大学学报, 2012, 47(4):539-545. doi: 10.3969/j.issn.0258-2724.2012.04.001PU Qianhui, QIN Shiqiang, SHI Zhou, et al. Modal parameter identification of reinforced concrete arch bridge under ambient excitation[J]. Journal of Southwest Jiaotong University, 2012, 47(4):539-545. doi: 10.3969/j.issn.0258-2724.2012.04.001 吴向男, 徐岳, 梁鹏, 等.桥梁结构损伤识别研究现状与展望[J].长安大学学报:自然科学版, 2013, 33(6):49-58. http://d.old.wanfangdata.com.cn/Periodical/xagljtdx201306008WU Xiangnan, XU Yue, LIANG Peng, et al. Research status and prospect of bridge structure damage identification[J]. Journal of Chang'an University:Natural Science Edition, 2013, 33(6):49-58. http://d.old.wanfangdata.com.cn/Periodical/xagljtdx201306008 孙小猛, 冯新, 周晶.基于损伤可识别性的传感器优化布置方法[J].大连理工大学学报, 2010, 50(2):264-270. http://d.old.wanfangdata.com.cn/Periodical/dllgdxxb201002020SUN Xiaomeng, FENG Xin, ZHOU Jing. A method for optimum sensor placement based on damage identifiability[J]. Journal of Dalian University of Technology, 2010, 50(2):264-270. http://d.old.wanfangdata.com.cn/Periodical/dllgdxxb201002020 刘国华, 吴志根.引入信息熵理论的砼结构损伤动力识别新思路[J].振动与冲击, 2011, 30(6):162-171. doi: 10.3969/j.issn.1000-3835.2011.06.034LIU Guohua, WU Zhigen. New thought on dynamic identification technology for damage detection of RC structures by introducing information entropytheory[J]. Journal of Vibration and Shock, 2011, 30(6):162-171. doi: 10.3969/j.issn.1000-3835.2011.06.034 单德山, 王振华, 李乔.大跨度铁路钢桁斜拉桥传感器优化布置[J].土木建筑与环境工程, 2011, 33(增刊1):156-160. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201102765953SHAN Deshan, WANG Zhenhua, LI Qiao. Optimal sensors placement for long-span railway steel truss cable-stayed bridge[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(S1):156-160. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201102765953 杨伟, 孙利民.针对结构易损场景监测的传感器优化布置方法[J].同济大学学报:自然科学版, 2015, 43(11):1670-1676. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201511009YANG Wei, SUN Limin. Optimal sensor placement for monitoring structural vulnerable scenarios[J]. Journal of Tongji University:Natural Science, 2015, 43(11):1670-1676. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201511009 伊廷华, 张旭东, 李宏男.基于分布式猴群算法的传感器优化布置方法研究[J].工程力学, 2014, 31(3):93-100. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013201248.htmYIN Tinghua, ZHANG Xudong, Li Hongnan. Distributed monkey algorithm for optimal sensor placement[J]. Engineering Mechanics, 2014, 31(3):93-100. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013201248.htm 赵建华, 张陵, 孙清.利用粒子群算法的传感器优化布置及结构损伤识别研究[J].西安交通大学学报, 2015, 49(1):79-85. http://d.old.wanfangdata.com.cn/Periodical/xajtdxxb201501013ZHAO Jianhua, ZHANG Ling, SUN Qing. Optimal placement of sensors for structural damage identification using improved particle swarm optimization[J]. Journal of Xi'an Jiaotong University, 2015, 49(1):79-85. http://d.old.wanfangdata.com.cn/Periodical/xajtdxxb201501013 相阳, 罗永峰, 廖冰, 等.球面网壳地震动输入与振型响应的相关性[J].浙江大学学报:工学版, 2016, 50(6):1040-1047. http://d.old.wanfangdata.com.cn/Periodical/zjdxxb-gx201606005XIANG Yang, LUO Yongfeng, LIAO Bing, et al. Correlation between seismic input and modal response of spherical latticed shell[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(6):1040-1047. http://d.old.wanfangdata.com.cn/Periodical/zjdxxb-gx201606005 刘江南, 洪义海.三轴数控平面磨床几何精度分析与稳健设计[J].湖南大学学报:自然科学版, 2016, 43(4):1-8. http://d.old.wanfangdata.com.cn/Periodical/hndxxb201604001LIU Jiangnan, HONG Yiha. Analysis and robust design of geometric accuracy of a three-axis CNC surface grinding machine[J]. Journal of Hunan University:Natural Sciences, 2016, 43(4):1-8. http://d.old.wanfangdata.com.cn/Periodical/hndxxb201604001 单德山, 孙松松, 黄珍, 等.基于试验数据的吊拉组合模型桥梁有限元模型修正[J].土木工程学报, 2014, 47(10):88-95. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201410013.htmSHAN Deshan, SUN Songsong, HUANG Zhen, et al. Finite element model updating of combined cable-stayed suspension model bridge based on experimental data[J]. China Civil Engineering Journal, 2014, 47(10):88-95. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201410013.htm 马建, 孙守增, 杨琦, 等.中国桥梁工程学术研究综述·2014[J].中国公路学报, 2014, 27(5):1-96. doi: 10.3969/j.issn.1001-7372.2014.05.001MA Jian, SUN Shouzeng, YANG Qi, et al. Review on China's bridge engineering research:2014[J]. China Journal of Highway and Transport, 2014, 27(5):1-9. doi: 10.3969/j.issn.1001-7372.2014.05.001 江祥林, 程高.基于EfI法的桥梁模态测试中传感器优化布置[J].桥梁建设, 2012, 42(2):59-65. http://d.old.wanfangdata.com.cn/Periodical/qljs201202010JIANG Xianglin, CHENG Gao. Optimal sensor placement for bridge modal testing based on efi method[J]. Bridge Construction, 2012, 42(2):59-65. http://d.old.wanfangdata.com.cn/Periodical/qljs201202010 唐勇, 陈志坚.大型群桩基础安全监测传感器选型优化[J].西南交通大学学报, 2011, 42(2):247-251. doi: 10.3969/j.issn.0258-2724.2011.02.012TANG Yong, CHEN Zhijian. Sensor selection optimizaion for monitoring system of large-scale group-pile foundation[J]. Journal of Southwest Jiaotong University, 2011, 42(2):247-251. doi: 10.3969/j.issn.0258-2724.2011.02.012 LI B B, LI D S, ZHAO X F, et al. Optimal sensor placement in health monitoring of suspension bridge[J]. Science China:Technology Sciences, 2012, 55(7):2039-2047. doi: 10.1007/s11431-012-4815-8 MOORE E Z, MURPHY K D, NICHOLS J M. Optimized sensor placement for damage parameter estimation:experimental results for a cracked plate[J]. Structural Health Monitoring, 2013, 12(3):197-206. doi: 10.1177/1475921713476330 LIU W, GAO W C, SUN Y, et al. Optimal sensor placement for spatial lattice structure based on genetic algorithms[J]. Journal of Sound and Vibration, 2008, 317:175-189. doi: 10.1016/j.jsv.2008.03.026 王海龙, 刘杰, 王新敏, 等.建立斜拉桥基准有限元模型的新方法与实现[J].振动·测试与诊断, 2014, 34(3):458-462. http://d.old.wanfangdata.com.cn/Periodical/zdcsyzd201403009WANG Hailong, LIU Jie, WANG Xinmin, et al. A new method and it's implementation of building baseline FE model of cable-stayed bridge[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3):458-462. http://d.old.wanfangdata.com.cn/Periodical/zdcsyzd201403009 -




 下载:
下载: