Seismic Vulnerabilitu Models and Simplified Calculation Method for Regular Highway Girder Bridges
-
摘要: 为了快速评估桥梁结构达到特定损伤状态的概率，基于非线性动力时程分析结果，建立了公路规则梁桥地震易损性模型并提出了简化计算方法.依据不同上部结构支承形式、墩柱形式和设计规范，将公路规则梁桥细化为8种桥型，针对每种桥型分别建构了80个基准桥梁样本作为各类桥型代表.选择墩柱和支座作为桥梁的易损构件，确定桥梁墩柱和支座在不同损伤状态下对应的参数能力范围.用OpenSees建立桥梁样本的有限元模型，采用增量动力分析方法，分析得到各类桥梁的全桥系统地震易损性模型.以计算得到的易损性模型参数为样本，提出适用于我国公路规则梁桥的中位值简化计算公式，同时给出对数标准差的建议值.研究结果表明：对于规则梁桥中位值，双柱式梁桥相对单柱式梁桥增大17%、新规范相对旧规范增长7%、连续梁桥相对简支梁桥增大8%；简化公式计算结果与分类易损性模型吻合较好，均方误差和均方根误差分别为5.26%和5.95%，最大绝对误差10.58%.Abstract: In order to swiftly assess the probability of a bridge structure reaching a specific damage state, seismic vulnerability models for regular highway girder bridges and a simplified method for their calculation are established, based on the results of a nonlinear dynamic time history analysis. Depending on the type of bridge, column, and design specification, regular highway girder bridges are divided into eight categories, with 80 benchmark bridge samples constructed for each category. Columns and bearings are considered vulnerable components, in which the component limits for different bridge damage states are determined. A finite element model of bridge samples is established using the OpenSees database. By employing an incremental dynamic analysis approach, seismic vulnerability models for regular highway girder bridges are obtained. Based on the analysis results, a new simplified formula for the calculation of median values was fitted and proposed for application to the existing regular highway girder bridge situation in China, along with the recommended values of logarithmic standard deviation. The results indicate that the median value for a double-pier bridge increased by 17% compared to a single-pier type and that of a continuous type increased by 8% compared to a simply supported bridge. Also, the efficiency of the latest design code increase by 7% compared to its former version. The results computed using the proposed simplified formula showed a good correlation with the categorical vulnerability models, with a mean square error and root mean square error of 5.26% and 5.95%, respectively, and a maximum absolute error of 10.58%.
-
图 2 地震易损伤参数简化计算流程
Figure 2. Flow chart of simplified calculation for Seismic vulnerability parameters
图 3 不同场地类别下地震易损性函数中位值间的关系
Figure 3. Correspondence of Seismic vulnerability median under the various sites
表 1 公路规则梁桥桥型分类
Table 1. Category of regular highway girder bridges
墩柱形式 上部结构 设计规范 代号 双柱式 简支梁 旧 TYPE1T 新 TYPE1N 双柱式 连续梁 旧 TYPE2T 新 TYPE2N 单柱式 简支梁 旧 TYPE3T 新 TYPE3N 单柱式 连续梁 旧 TYPE4T 新 TYPE4N 
下载: 导出CSV
表 2 新旧规范对墩柱配筋率、配箍率的规定
Table 2. Provisionsfor reinforcement ratio and stirrupratio by old & newly specification
% 设计规范 配筋率 配箍率 《89抗震规范》 ≥0.4 ≥0.3 《08抗震细则》 ≥0.6且≤4.0 ≥0.4
下载: 导出CSV
表 3 公路规则梁桥墩柱和支座极限状态
Table 3. Limit states of pier and bearing for regular highway girder bridges
损伤状态 位移延性比μΔ 容许剪切应变γa 完好无损 μΔ＜1.00 γa＜100% 轻微破坏 1.00≤μΔ＜1.20 100%≤γa＜150% 中等破坏 1.20≤μΔ＜1.76 150%≤γa＜200% 严重破坏 1.76≤μΔ＜4.76(3.00) 200%≤γa＜250% 完全破坏 μΔ≥4.76(3.00) γa≥250% 注:括号中的取值适用于《08抗震细则》之前设计的公路规则梁桥
下载: 导出CSV
表 4 公路规则梁桥各类场地下的地震易损性参数
Table 4. Seismic vulnerability parameters of regular highway girder bridges under the various fields
桥型 损伤状态 Ⅰ类场地 Ⅱ类场地 Ⅲ类场地 场地汇总 msys/(×g) βsys msys/(×g) βsys msys/(×g) βsys msys/(×g) βsys 单柱连续(旧) 轻微破坏 0.179 0.818 0.155 0.665 0.108 0.422 0.141 0.750 中等破坏 0.246 0.706 0.216 0.610 0.143 0.582 0.194 0.700 严重破坏 0.351 0.487 0.321 0.451 0.203 0.538 0.273 0.663 完全破坏 0.516 0.556 0.470 0.553 0.304 0.416 0.425 0.545 单柱连续(新) 轻微破坏 0.211 0.666 0.183 0.540 0.131 0.379 0.170 0.576 中等破坏 0.300 0.425 0.260 0.523 0.188 0.317 0.240 0.509 严重破坏 0.395 0.486 0.357 0.470 0.241 0.321 0.328 0.446 完全破坏 0.561 0.521 0.542 0.460 0.368 0.323 0.480 0.494 单柱简支(旧) 轻微破坏 0.181 0.837 0.147 0.688 0.105 0.391 0.139 0.625 中等破坏 0.241 0.720 0.217 0.516 0.143 0.455 0.191 0.554 严重破坏 0.335 0.670 0.323 0.450 0.204 0.427 0.276 0.578 完全破坏 0.486 0.528 0.483 0.556 0.321 0.435 0.423 0.508 单柱简支(新) 轻微破坏 0.192 0.650 0.167 0.643 0.110 0.389 0.150 0.649 中等破坏 0.291 0.417 0.255 0.554 0.166 0.353 0.225 0.563 严重破坏 0.392 0.516 0.368 0.480 0.236 0.308 0.327 0.451 完全破坏 0.674 0.638 0.617 0.623 0.412 0.510 0.553 0.614 双柱连续(旧) 轻微破坏 0.281 0.395 0.253 0.340 0.176 0.322 0.226 0.460 中等破坏 0.329 0.458 0.302 0.398 0.205 0.248 0.275 0.380 严重破坏 0.453 0.507 0.426 0.407 0.291 0.317 0.382 0.462 完全破坏 0.688 0.320 0.666 0.309 0.465 0.297 0.588 0.385 双柱连续(新) 轻微破坏 0.303 0.421 0.283 0.377 0.209 0.259 0.262 0.358 中等破坏 0.377 0.479 0.353 0.410 0.252 0.306 0.324 0.423 严重破坏 0.548 0.388 0.508 0.350 0.360 0.307 0.455 0.435 完全破坏 0.837 0.423 0.823 0.442 0.566 0.285 0.720 0.415 双柱简支(旧) 轻微破坏 0.216 0.645 0.200 0.600 0.148 0.420 0.185 0.598 中等破坏 0.320 0.443 0.288 0.571 0.190 0.356 0.257 0.561 严重破坏 0.424 0.530 0.407 0.512 0.275 0.338 0.353 0.556 完全破坏 0.630 0.429 0.627 0.556 0.418 0.402 0.543 0.521 双柱简支(新) 轻微破坏 0.221 0.668 0.197 0.591 0.146 0.440 0.185 0.613 中等破坏 0.342 0.470 0.299 0.599 0.209 0.437 0.274 0.591 严重破坏 0.473 0.551 0.450 0.554 0.310 0.411 0.395 0.589 完全破坏 0.884 0.579 0.861 0.757 0.554 0.603 0.742 0.716 桥型汇总 轻微破坏 0.219 0.696 0.196 0.610 0.139 0.474 0.180 0.654 中等破坏 0.298 0.628 0.274 0.565 0.187 0.436 0.245 0.599 严重破坏 0.423 0.591 0.400 0.507 0.269 0.448 0.353 0.573 完全破坏 0.734 0.603 0.699 0.580 0.474 0.507 0.617 0.629
下载: 导出CSV
表 5 定性参数取值
Table 5. Value of qualitative parameters
属性参数 桥梁参数 取值 新旧规范 新规范 1 旧规范 -1 墩柱形式 双柱 1 单柱 -1 上部结构形式 连续 1 简支 -1
下载: 导出CSV
表 6 不同参数下各中位值的误差估计
Table 6. Error estimation of median under various parameters
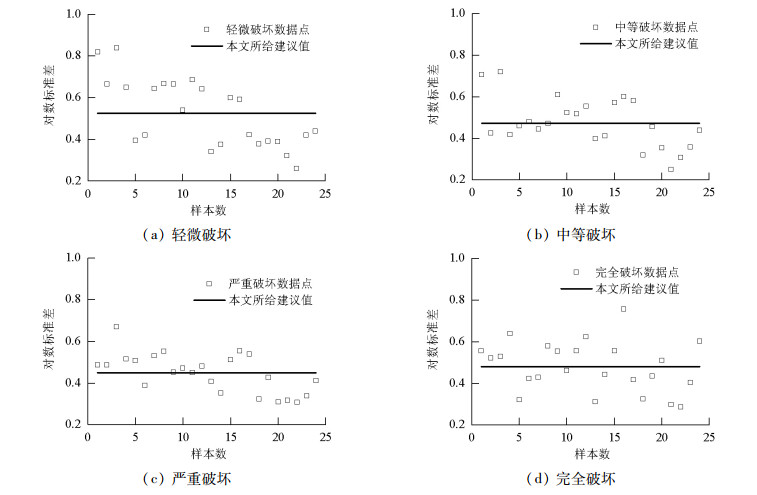
损伤状态 场地类型 EAug/% Emax/% ERms/% 轻微损伤 Ⅰ类 3.79 8.98 4.67 Ⅱ类 4.13 10.20 5.18 Ⅲ类 4.68 10.58 5.78 中等损伤 Ⅰ类 4.16 8.55 4.98 Ⅱ类 3.15 7.65 3.90 Ⅲ类 2.30 3.37 2.49 严重损伤 Ⅰ类 2.51 6.15 3.08 Ⅱ类 2.62 4.05 2.94 Ⅲ类 3.55 6.95 4.02 完全破坏 Ⅰ类 5.26 8.91 5.95 Ⅱ类 3.66 9.78 4.83 Ⅲ类 3.36 6.40 3.82
下载: 导出CSV
表 7 对数标准差建议值
Table 7. Proposed values of logarithmic standard deviation
轻微破坏 中等破坏 严重破坏 完全破坏 0.52 0.47 0.44 0.48
下载: 导出CSV
-
SHINOZUKA M, FENG M Q, LEE J, et al. Statistical analysis of fragility curves[J]. Journal of Engineering Mechanics, 2003, 126(12):1224-1231. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=51e26465861e3f8e3a9eb1f5a45113a7 SINGHAL A, KIREMIDJIAN A S. Method for probabilistic evaluation of seismic structural damage[J]. Structural Engineering, 1996, 122(12):1459-1467. doi: 10.1061/(ASCE)0733-9445(1996)122:12(1459) DUTTA A, MANDER J B. Seismic fragility analysis of highway bridges[C]//Proceedings of the INCEDE-MCEER Center-to-Center Project Workshop on Earthquake Engineering Frontiers in Transportation Systems. Blacksburg: State University of New York, 1998: 22-23. 陈力波.汶川地区公路桥梁地震易损性分析研究[D].成都: 西南交通大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014251544.htm HWANG H, JERNIGAN J B, LIN Y W. Evaluation of seismic damage to Memphis bridges and highway systems[J]. Journal of Bridge Engineering, 2000, 5(4):322-330. doi: 10.1061/(ASCE)1084-0702(2000)5:4(322) CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones[J]. Engineering Structures, 2004, 26(2):187-199. doi: 10.1016/j.engstruct.2003.09.006 GHOSH J, PADGETT J E. Aging considerations in the development of time-dependent seismic fragility curves[J]. Journal of Structural Engineering, 2010, 136(12):1497-1511. doi: 10.1061/(ASCE)ST.1943-541X.0000260 张菊辉, 管仲国.规则连续梁桥地震易损性研究[J].振动与冲击, 2014, 33(20):140-145. http://d.old.wanfangdata.com.cn/Periodical/zdycj201420028ZHANG Juhui, GUAN Zhongguo. Seismic vulnerability analysis of regular continuous girder bridges[J]. Journal of Vibration and shock, 2014, 33(20):140-145. http://d.old.wanfangdata.com.cn/Periodical/zdycj201420028 BUCKLE I G, FRIEDLAND I, MANDER J, et al. Seismic retrofitting manual for highway structures: part 1-bridges[R]. Washington D.C.: Federal Highway Administration, 2006. JAPAN Road Association. Specifications for highway bridges: part Ⅴ. seismic design[S]. Tokyo: Maruzen, 2002. 张国镇, 蔡益超, 宋裕祺, 等.公路桥梁耐震能力评估及不强准则之研究[R].台北: 地震工程研究中心, 2009. 重庆交通科研设计院. JTG/TB02-01-2008公路桥梁抗震设计细则[S].北京: 人民交通出版社, 2008. 中华人民共和国交通部. JTJ 004-1989公路工程抗震设计规范[S].北京: 人民交通出版社, 1989. 中华人民共和国交通部. JT/T663-2006公路桥梁板式橡胶支座规格系列[S].北京: 人民交通出版社, 2006. MAZZONI S, MCKENNA F, FENVES G L. OpenSees command language manual[EB].[2008-01-25] http://opensees.berkeley.edu/OpenSees/manuals/usermanual. SPACONE E, CIAMPI V, FILIPPOU F C. Mixed formulation of nonlinear beam finite element[J]. Computers & Structures, 1996, 58(1):71-83. http://www.sciencedirect.com/science/article/pii/004579499500103N TRIFUNAC M D, BRADY A G. A study on the duration of strong earthquake ground motion[J]. Bulletin of the Seismological Society of America, 1975, 65(3):581-626. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=954aacfd06f585487542ce832a2bf632 BERTERO V V. Strength and deformation capacities of buildings under extreme environments[J]. Structural engineering and mechanics, 1977, 53(1):211-215. VAMVATSIKOS D. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3):491-514. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201002006 Federal Emergency Management Agency. HAZUS-MH MR4 earthquake model technical manual[M]. Washington D.C.:Springer, 2003:1-93. HWANG H, LIU J B, CHIU Y H. Seismic fragility analysis of highway bridges[R]. Memphis: The University of Memphi, 2001. https://www.ideals.illinois.edu/handle/2142/9267 ZHANG J, HUO Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method[J]. Engineering Structures, 2009, 31(8):1648-1660. doi: 10.1016/j.engstruct.2009.02.017 JAMES G, WITTEN D, HASTIE T, et al. An introduction to statistical Learning with Applications in R[M]. Berlin:Springer, 2013:41-72. -
下载:
点击查看大图
图(4) / 表(7)
计量
- 文章访问数: 438
- HTML全文浏览量: 212
- PDF下载量: 98
- 被引次数: 0