Dynamic Reliability Analysis on Pounding of High-Pier Bridges Subjected to Stochastic Seismic Excitations
-
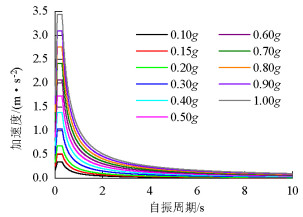
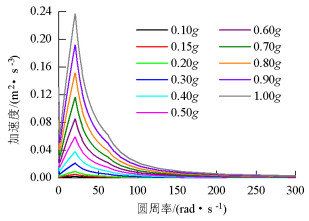
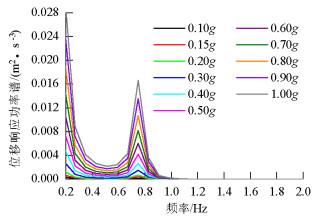
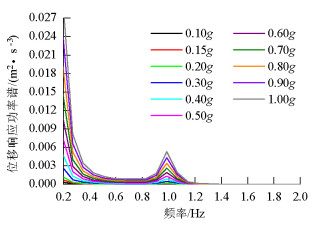
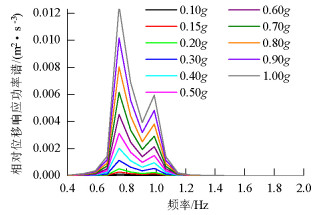
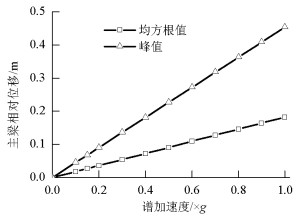
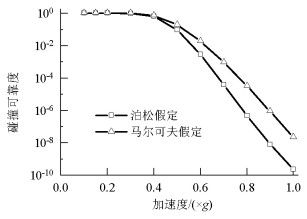
摘要: 为了研究不同地震动强度作用下高墩桥梁的碰撞可靠度的不同,在频域范围内提出了一种以虚拟激励法为基础的动力可靠度计算方法,依托某高墩大跨度桥梁为工程背景,分析了高墩桥梁在不同地震强度下的碰撞可靠度.选择反应谱的水平加速度作为地震强度衡量指标,且将不同强度指标的反应谱转化为相应的功率谱;利用虚拟激励法求解随机振动方程,得到结构响应的均值与均方差值,再基于Davenport理论获得结构峰值响应的期望和标准差;根据首次超越理论计算梁体碰撞可靠度.研究表明:地震动加速度小于0.22g时,梁体之间不发生碰撞,动力可靠度为1.0;加速度大于0.22g时,梁体碰撞动力可靠度下降明显,即在强震作用下,梁体发生碰撞.Abstract: A dynamic reliability analysis based on the pseudo-excitation method in the frequency domain was proposed to investigate the pounding reliability of high-pier bridges subjected to seismic excitations with different ground motion intensity levels. A high-pier bridge was selected as the numerical example and the pounding reliability of the high-pier bridge was computed for each ground motion intensity level. The horizontal acceleration response spectrum was chosen as the seismic intensity measure and the response spectra for different intensity measures were converted into the corresponding power spectra. Next, the stochastic vibration equation was solved using the pseudo-excitation method to determine the mean and mean square deviation of the structural dynamic responses. The expected values and standard deviation of the structural peak responses were obtained using Davenport's theory. Finally, the pounding reliability between the adjacent beams of the high-pier bridge was determined using the first passage theory. The results indicate that pounding will not occur between the adjacent decks and the pounding reliability is 1.0 when the ground acceleration is less than 0.22g. In addition, there is an obvious decrease in the pounding reliability such that the structure collides under the strong ground motions when the ground acceleration is more than 0.22g.
-
表 1 动力特性
Table 1. Dynamic characteristics
阶数 频率/Hz 振型 1 0.71 主桥纵向振动 2 0.92 主桥横向振动 3 1.02 引桥纵向振动 4 1.35 全桥对称横向振动 5 1.38 主桥横向振动 -
JANKOWSKI R, MAHMOUD S. Earthquake-induced structural pounding[M]. New York:Springer, 2015:73-74. HAO Hong. A parametric study of the required seating length for bridge decks during earthquake[J]. Earthquake Engineering & Structural Dynamics, 1998, 27(1):91-103. doi: 10.1002-(SICI)1096-9845(199801)27-1-91--AID-EQE722-3.0.CO%3b2-I/ 林家浩, 张亚辉.随机振动的虚拟激励法[M].北京:科学出版社, 2006:1-25. 李桂青, 曹宏.结构动力可靠性理论及其应用[M].北京:地震出版社, 1993:13-35. LIN J H. Separation distance to avoid seismic pounding of adjacent buildings[J]. Earthquake Engineering & Structural Dynamics, 1997, 26(3):395-403. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=47b2de499a0ddc5115e33253e2253a7d LIN J H, WENG C C. Probability analysis of seismic pounding of adjacent buildings[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(10):1539-1557. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0e364149039000e54980e4bb29772e77 CHOUW N, HAO H. Study of SSI and non-uniform ground motion effect on pounding between bridge girders[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(7-10):717-728. doi: 10.1016/j.soildyn.2004.11.015 LI B, BI K, CHOUW N, et al. Experimental investigation of spatially varying effect of ground motions on bridge pounding[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(14):1959-1976. doi: 10.1002/eqe.2168/full HAO H, ZHANG S R. Spatial ground motion effect on relative displacement of adjacent building structures[J]. Earthquake Engineering & Structural Dynamics. 1999, 28(4):333-349. doi: 10.1002/(SICI)1096-9845(199904)28:4<333::AID-EQE820>3.0.CO;2-R/pdf ZHANG D Y, JIA Hong, ZHENG S, et al. A highly efficient and accurate stochastic seismic analysis approach for structures under tridirectional nonstationary multiple excitations[J]. Computers & Structures, 2014, 145(C):23-35. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=278980d6a499c14664ea70825d15b27a 李忠献, 周莉, 岳福青.地震动空间效应与土-基础相互作用效应对隔震桥梁临界碰撞间隙的影响[J].土木工程学报, 2010, 43(7):85-90. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001629757LI Zhongxian, ZHOU Li, YUE Fuqing. Effects of spatial variation of ground motion and soil foundation interaction on critical pounding gap length of seismic isolated bridges[J]. Journal of Civil Engineering, 2010, 43(7):85-90. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001629757 李忠献, 岳福青, 周莉, 等.基于随机振动理论确定桥梁地震碰撞的临界间隙[J].地震工程与工程振动, 2006, 26(4):156-161. doi: 10.3969/j.issn.1000-1301.2006.04.027LI Zhongxian, YUE Fuqing, ZHOU Li, et al. Determination of critical gap length of seismic pounding for bridges based on random vibration theory[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(4):156-161. doi: 10.3969/j.issn.1000-1301.2006.04.027 BI K, HAO H, CHOUW N. Required separation distance between decks and at abutments of a bridge crossing a canyon site to avoid seismic pounding[J]. Earthquake Engineering & Structural Dynamics, 2010, 39(3):303-323. doi: 10.1002/eqe.943/full CHOUW N, HAO H. Significance of SSI and non-uniform near-fault ground motions in bridge response Ⅱ:effect on response with modular expansion joint[J]. Engineering Structures, 2008, 30(1):154-162. doi: 10.1016/j.engstruct.2007.02.020 CHOUW N, HAO H. Significance of SSI and nonuniform near-fault ground motions in bridge response Ⅰ:effect on response with conventional expansion joint[J]. Engineering Structures, 2008, 30(1):141-153. doi: 10.1016/j.engstruct.2007.03.002 BI K, HAO H, NAWAWI C. Influence of ground motion spatial variation, site condition and SSI on the required separation distances of bridge structures to avoid seismic pounding[J]. 2011: 40(9), 1027-1043. 贾宏宇, 杜修力, 李晰, 等.地震作用下高墩铁路桥梁梁体碰撞间隙宽度需求机理分析[J].工程力学, 2017, 34(2):207-215. http://www.cnki.com.cn/Article/CJFDTotal-GCLX201702026.htmJIA Hongyu, DU Xiuli, LI Xi, et al. Demand mechanism analysis on pounding separation distance of high pier railway bridges subjected to earthquake excitations[J]. Engineering Mechanics, 2011, 34(2):207-215. http://www.cnki.com.cn/Article/CJFDTotal-GCLX201702026.htm KAUL M K. Stochastic characterization of earthquakes through their response spectrum[J]. Earthquake Engineering & Structural Dynamics, 2010, 6(5):497-509. doi: 10.1002/eqe.4290060506/full 李永华, 桂国庆, 廖宇.绝对位移直接求解虚拟激励法采用附加振型求解的理论研究[J].振动与冲击, 2015, 34(8):12-19. http://d.old.wanfangdata.com.cn/Periodical/zdycj201508004LI Yonghua, GUI Guoqing, LIAO Yu. Pseudo excitation method based on directly solving absolute displacements with additional modes[J]. Vibration and Shock, 2015, 34(8):12-19. http://d.old.wanfangdata.com.cn/Periodical/zdycj201508004 -





 下载:
下载: