Failure Mode of Isolated Beam Bridge by Weighted Rank Sum Ratio Method
-
摘要: 为了综合评价桥梁在地震作用下失效模式的信息，考虑地震动中存在的不确定性影响，对实际工程中的某6跨隔震连续梁桥的失效模式进行了分析.基于IDA法，选用16条足够反映地震动中存在的不确定性且PDA分布在一个较宽强度范围内的地震动，对桥梁中支座、桥墩墩底这两个最容易失效的部位分别基于位移和修正的Park-Ang损伤理论判断其失效，引用加权秩和比法综合了16条地震动作用下的桥梁失效模式的评价信息，分析给出具有统计意义的失效模式，并找出了桥梁的最弱失效模式.研究结果表明：该隔震连续梁桥的失效模式为该桥梁中墩的隔震支座先失效，然后是桥梁过渡墩支座失效，最后是边墩底部和边墩的支座失效；桥梁的最弱失效模式为桥梁所有隔震支座先失效，其次是边墩底部失效，然后是中墩失效，最后是过渡墩失效.Abstract: To estimate the failure modes of seismically isolated continuous girder bridges, a practical engineering with six spans was analyzed considering the uncertainty of seismic ground motions. Sixteen ground motion records were selected to be used in IDA method, which could provide sufficient accuracy of seismic analysis demands, and the PGA of these records were distributed in a wide range. Bearings and the bottom of piers were the most vulnerable parts of the bridge, of which failure criteria were estimated by displacement and modified Park-Ang damage theory, respectively. And weighted rank sum ratio method was adopted to analyze evaluation information of the bridge under sixteen ground motion records, then the statistically significant failure modes and the weakest failure mode of the bridge were identified. The results show that the final failure mode of the isolation continuous girder bridge arises at the isolation bearings of the middle piers, at the isolation bearings of the transition piers, and at the bottom of side piers and bearings. The weakest failure mode of this bridge happens with all isolation bearings cease to be effective first, then it comes to the bottom of the side piers and the middle piers, and finally the transitional piers.
-
Key words:
- isolation /
- failure mode /
- IDA method /
- continuous girder bridge
-
表 1 LRB支座的参数
Table 1. Details of LRB
支座类型 布置位置 竖向承载力/kN 横向刚度
/(kN·mm-1)竖向刚度Kv
/(kN·mm-1)屈服力
Qy/kN屈服前刚度K1
/(kN·mm-1)屈服后刚度K2
/(kN·mm-1)LRB1250 1#、7#(边墩) 12 500 4.4 2 000 848 18.2 2.8 LRB2750 2#、6#(过渡墩) 27 500 10.0 4 922 965 50.9 7.9 LRB2500 3#、4#、5#(中墩) 25 000 9.2 4 357 877 46.5 7.2 
下载: 导出CSV
表 2 选取的地震动参数
Table 2. Details of ground movements
序号 地震动 PGA/(×g) 年份 GM-1 El Centro 0.357 1940 GM-2 Northridge 0.416 1994 GM-3 人工波1 0.150 — GM-4 Loma Prieta 0.220 1989 GM-5 Taft Lincoln 0.156 1952 GM-6 James RD 0.550 1979 GM-7 Hollywood Storage 0.059 1952 GM-8 kobe 0.370 1995 GM-9 MIYAGI-Coast 0.325 1978 GM-10 HOKKAIDO-SW_Coast 0.330 1993 GM-11 HYUGANADA-Coast 0.392 1968 GM-12 NIHONKAI-Central 0.432 1983 GM-13 HOKKAIDO-EastCoast 0.447 1994 GM-14 HYOUGOKEN_South 0.828 1995 GM-15 San Fernando 0.315 1971 GM-16 人工波2 0.319 —
下载: 导出CSV
表 3 修正Park-Ang构件损伤分级及参数
Table 3. Structural member classification and parameters of amendatory Park-Ang
序号 损伤等级 损伤描述 量化指标 1 无损伤 无损伤或仅在局部产生微细裂缝 Ds＜0.1 2 可修复损坏 裂缝扩展明显并伴有局部表层混凝土剥落, 刚度依旧保持 Ds=0.1＜0.4 3 不可修复损坏 虽然维持有一定的竖向承载力, 但遗留下永久损伤 Ds=0.4＜0.77 4 倒塌 Ds=0.77 注:本文Ds=0.75时, 认为构件失效.
下载: 导出CSV
表 4 桥墩的能力参数
Table 4. Capacity parameters of the pier
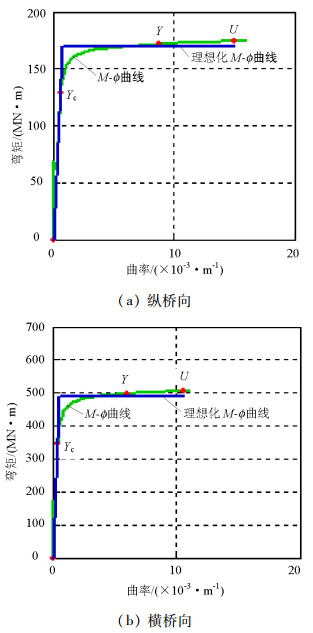
状态 弯矩/
(MN·m)曲率/
(1·m-1)屈服(纵桥向) 186 0.008 8 极限(纵桥向) 191 0.015 0 屈服(横桥向) 498 0.003 0 极限(横桥向) 505 0.005 3
下载: 导出CSV
表 5 各地震动作用下桥梁各单元的失效次序
Table 5. Failure sequence of bridge element in every ground movement
序号 地震动 失效秩序 1 2 3 4 5 6 7 8 9 GM-1 El Centro ⑤ ④ ③ ② ⑥ ⑦ ① ⑧ ⑭ GM-2 Northridge ⑤ ④ ③ ② ⑥ ⑦ ① ⑧ ⑭ GM-3 人工波1 ⑧ ⑤ ④ ③ ② ⑥ ⑦ ① ⑭ GM-4 Loma Prieta ④ ③ ⑤ ⑥ ② ① ⑦ ⑧ ⑭ GM-5 Taft Lincoln ⑧ ④ ③ ⑤ ⑥ ② ① ⑦ ⑭ GM-6 James RD ③ ⑤ ④ ⑥ ② ① ⑦ ⑧ ⑭ GM-7 Hollywood Storage ④ ③ ⑤ ⑥ ② ① ⑦ ⑧ ⑭ GM-8 kobe ⑧ ③ ④ ⑤ ⑥ ② ① ⑦ ⑭ GM-9 MIYAGI-Coast ③ ④ ⑤ ⑥ ② ① ⑦ ⑧ ⑭ GM-10 Hokkaido-SW Coast ⑤ ④ ③ ② ⑥ ⑦ ① ⑧ ⑭ GM-11 Hyuganada-Coast ⑧ ⑭ ⑤ ④ ③ ② ⑥ ⑦ ① GM-12 Nihonkai-Centrall ⑤ ③ ④ ② ⑥ ⑦ ① ⑧ ⑭ GM-13 Hokkaido-East Coast ③ ④ ⑤ ⑥ ② ① ⑦ ⑧ ⑭ GM-14 Hyougoken South ⑤ ③ ④ ② ⑥ ⑦ ① ⑧ ⑭ GM-15 San Fernando ④ ⑤ ③ ② ⑥ ⑦ ① ⑧ ⑭ GM-16 人工波2 ③ ⑤ ④ ⑥ ② ① ⑦ ⑧ ⑭
下载: 导出CSV
表 6 失效单元的加权秩和比
Table 6. Rank-sum ratio of failure element
秩R 单元 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑭ 1 7 4 3 2 1 5 6 8 9 2 7 4 3 2 1 5 6 8 9 3 8 5 4 3 2 6 7 1 9 4 6 5 2 1 3 4 7 8 9 5 7 6 3 2 4 5 8 1 9 6 6 5 1 3 2 4 8 7 9 7 6 5 2 1 3 4 7 8 9 8 7 6 2 3 4 5 8 1 9 9 6 5 1 2 3 4 7 8 9 10 7 4 3 2 1 5 6 8 9 11 9 6 5 4 3 7 8 1 2 12 7 4 2 3 1 5 6 8 9 13 6 5 1 2 3 4 7 8 9 14 7 4 2 3 1 5 6 8 9 15 7 4 2 1 3 5 6 8 9 16 6 5 1 2 3 4 7 8 9 WRSR 0.748 7 0.551 2 0.254 2 0.250 7 0.277 3 0.524 9 0.790 1 0.695 7 0.990 2 失效顺序 7 5 2 1 3 4 8 6 9
下载: 导出CSV
-
郑史雄, 张金, 贾宏宇, 等.大跨度斜拉桥多维多点随机地震激励响应分析[J].西南交通大学学报, 2014, 49(5):747-753. doi: 10.3969/j.issn.0258-2724.2014.05.001ZHENG Shixiong, ZHANG Jin, JIA Hongyu, et al. Stochastic seismic response analysis of large-span cable-stayed bridge subjected to multi-dimensional and multi-support excitations[J]. Journal of Southwest Jiaotong University, 2014, 49(5):747-753. doi: 10.3969/j.issn.0258-2724.2014.05.001 聂建国, 周萌, 姬同庚, 等.基于多尺度模型的自锚式钢箱梁悬索桥主缆锚固区受力性能研究[J].土木工程学报, 2014(6):57-69. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201406011.htmNIE Jianguo, ZHOU Meng, JI Tonggeng, et al. Study on behaviors of cable anchorage zone of self-anchored suspension bridges with steel box girders based on multi-scale modeling method[J]. China Civil Engineering Journal, 2014(6):57-69. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201406011.htm 徐小龙.基于ABAQUS纤维梁元的静力弹塑性分析[D].成都: 西南交通大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1012390756.htm 强斌, 李亚东, 顾颖, 等.钢板喷丸处理残余应力场和表面粗糙度数值模拟[J].西南交通大学学报, 2015, 50(4):691-697. doi: 10.3969/j.issn.0258-2724.2015.04.018QIANG Bin, LI Yadong, GU Ying, et al. Numerical simulation of residual stress field and surface roughness for steel plate subjected to shot peening[J]. Journal of Southwest Jiaotong University, 2015, 50(4):691-697. doi: 10.3969/j.issn.0258-2724.2015.04.018 彭建新, 胡守旺, 张建仁.考虑空间变量的氯盐环境下RC简支梁桥失效概率分析[J].土木工程学报, 2014(12):115-121. http://d.old.wanfangdata.com.cn/Conference/8608658PENG Jianxin, HU Shouwang, ZHANG jianren. Analysis on failure probabilities of RC simply-supported beam under Chloride environment with spatial variables considered[J]. China Civil Engineering Journal, 2014(12):115-121. http://d.old.wanfangdata.com.cn/Conference/8608658 石雪飞, 王晓明, 阮欣, 等.考虑空间变异性的在役钢筋混凝土梁桥失效概率评估[J].土木工程学报, 2011(6):74-79. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201106013.htmSHI Xuefei, WANG Xiaoming, RUAN Xin, et al.Failure probability assessment of existing RC beam bridges considering spatial variability[J]. China Civil Engineering Journal, 2011(6):74-79. http://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201106013.htm 刘梦莹, 徐岳.基于失效树的连续刚构桥体系可靠度研究[J].合肥工业大学学报:自然科学版, 2014(11):1341-1345. http://d.old.wanfangdata.com.cn/Periodical/hfgydxxb201411015LIU Mengying, XU Yue. Research on the reliability of continuous rigid frame bridge system based on failure tree[J]. Journal of Hefei University of Technology:Natural Science, 2014(11):1341-1345. http://d.old.wanfangdata.com.cn/Periodical/hfgydxxb201411015 MANDER J B, DHAKAL R P, MASHIKO N, et al. Incremental dynamic analysis applied to seismic financial risk assessment of bridges[J]. Engineering Structures, 2007, 29(10):2662-2672. doi: 10.1016/j.engstruct.2006.12.015 BILLAH A H M M, ALAM M S. Seismic performance evaluation of multi-column bridge bents retrofitted with different alternatives using incremental dynamic analysis[J]. Engineering Structures, 2014, 62:105-117. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3495f6a31c75c51a78ff904ce75eee05 WANG G, WANG Y, LU W, et al. XFEM based seismic potential failure mode analysis of concrete gravity dam-water-foundation systems through incremental dynamic analysis[J]. Engineering Structures, 2015, 98:81-94. doi: 10.1016/j.engstruct.2015.04.023 周颖, 苏宁粉, 吕西林.高层建筑结构增量动力分析的地震动强度参数研究[J].建筑结构学报, 2013, 34(2):53-60. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201302006ZHOU Ying, SU Ningfen, LU Xilin. Study on intensity measure of incremental dynamic analysis for high-rise structures[J]. Journal of Building Structures, 2013, 34(2):53-60. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201302006 VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3):491-514. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201002006 于晓辉.钢筋混凝土框架结构的概率地震易损性与风险分析[D].哈尔滨: 哈尔滨工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013035280.htm STONE W C, TAYLOR A W. Seismic Performance of circular bridge columns designed in accordance with AASHTO/CALTRANS standards[R]. Gaithersburg: National Institute of Standards and Technology, 1993. 郭进, 王君杰.基于累积损伤的弯矩-曲率强度退化滞回模型[J].同济大学学报:自然科学版, 2013, 41(12):1767-1774. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201312001GUO Jin, WANG Junjie. Reinforced concrete strength degradation hystertic moment-curvature mode based on cumulative damage[J]. Journal of Tongji University:Natural Science, 2013, 41(12):1767-1774. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201312001 李伟伟, 李洪兴, 王卫, 等.基于加权秩和比法的农村水厂风险评估[J].环境与健康杂志, 2014, 31(10):934-937. http://d.old.wanfangdata.com.cn/Periodical/hjyjkzz201410021LI Weiwei, LI Hongxing, WANG Wei, et al. Risk assessment of rural waterworks by weighted rank sum ratio method[J]. Journal of Environment and Health, 2014, 31(10):934-937. http://d.old.wanfangdata.com.cn/Periodical/hjyjkzz201410021 刘耀龙.强震作用下结构连续倒塌过程中的失效模式研究[D].大连: 大连理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013201015.htm 期刊类型引用(15)
1. 陆粤，王铭，陈嵘，李小珍，王平. 基于行车平稳性的大跨度铁路桥梁成桥线形评价方法研究. 铁道标准设计. 2024(06): 44-51 . 
百度学术2. 张明金，周远洲，沈孔健，苑仁安，郑清刚. 常泰长江大桥主航道桥桥塔横向偏位及其控制方案研究. 桥梁建设. 2023(01): 1-8 . 百度学术3. 黄春阳. 基于监测数据的独塔斜拉桥施工过程受力性能分析. 安徽建筑. 2023(04): 137-138+185 . 百度学术4. 苑仁安，张明金，郑清刚，傅战工，喻济昇. 超大跨斜拉桥横桥向恒载非对称力学行为. 西南交通大学学报. 2023(03): 527-534 . 
本站查看5. 黄学漾. 双塔双索面异形塔柱斜拉桥施工控制关键技术探讨. 福建交通科技. 2023(06): 51-57 . 百度学术6. 汪劲丰，杨松伟，亢阳阳，向华伟. 分阶段施工中钢箱梁制造参数的通用计算方法. 浙江大学学报(工学版). 2022(03): 550-557 . 百度学术7. 李江刚，石建华，张巨生. 鳊鱼洲长江大桥南汊航道桥施工控制关键技术. 桥梁建设. 2022(04): 8-15 . 百度学术8. 李鹏飞，王石磊，魏思聪，李毅，罗吉庆. 大型空间异形钢塔斜拉桥拉索张拉控制. 公路交通科技. 2022(10): 49-58 . 百度学术9. 周仁忠，黄灿，郑建新. 福厦高铁泉州湾跨海大桥主桥施工控制关键技术. 桥梁建设. 2022(06): 131-139 . 百度学术10. 黄继荣，马牛静，王荣辉，陈广韬. 叠合梁斜拉桥快速施工过程中主梁线形及索力调控精细化分析. 交通世界. 2022(36): 145-148 . 百度学术11. 张飞，黄福云，王燕. V型墩刚构桥悬浇施工中应变修正与应力监测. 山东建筑大学学报. 2020(03): 36-41 . 百度学术12. 廖贵星，严汝辉，胡辉跃，张燕飞，徐恭义. 武汉青山长江公路大桥中跨钢箱梁施工控制关键技术. 桥梁建设. 2020(S1): 126-132 . 百度学术13. 高玉峰，杨永清，蒲黔辉，李晓斌. 桥梁施工监测控制理论及工程应用2019年度研究进展. 土木与环境工程学报(中英文). 2020(05): 98-105 . 百度学术14. 董晓兵，余友江. 青海哇加滩黄河特大桥施工控制. 桥梁建设. 2019(04): 96-101 . 百度学术15. 梅秀道，卢亦焱. 基于索长的大跨径斜拉桥施工控制计算方法及应用. 桥梁建设. 2019(06): 42-47 . 百度学术其他类型引用(12)
-
下载:
百度学术
点击查看大图
图(5) / 表(6)
计量
- 文章访问数: 548
- HTML全文浏览量: 254
- PDF下载量: 69
- 被引次数: 27