Application Study on Grillage Method for Multiple-Cells Box Girder with Transverse Slope
-
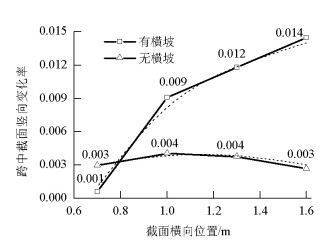
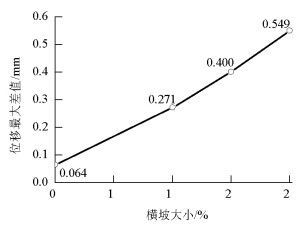
摘要: 为了研究多箱室箱梁基于梁格法计算的影响因素，考虑了横坡构造对多箱室箱梁的受力特性进行了分析.对梁格法理论的应用进行拓展，推导了适用于具有横坡构造的多箱室箱梁梁格截面特性值计算公式，并讨论考虑横坡的合理性；采用数值模拟的方法进行参数分析，通过改变加载位置、箱梁宽跨比、横坡大小等参数，对研究对象的受力特性进行了对比分析.研究结果表明：考虑横坡时，梁格截面刚度特征值更加接近实际，减小了12.12%的误差；具有横坡构造的多箱室箱梁的梁格模型与实体有限元模型计算结果吻合程度好，但仍无法反映箱梁在承受荷载时产生的畸变；考虑横坡构造的梁格法计算精度的提高主要体现在截面横向位移计算结果上；当箱梁宽跨比大于0.8时，采用梁格法计算时需要考虑横坡的影响；随着横坡大小从0增加到2%时，截面的竖向位移最大差值增加了758%，呈线性递增.Abstract: Mechanical properties of multiple-cells box girder with the transverse slope were analyzed in order to study the factors when using the grillage method. Based on the grillage method, formulas for multiple-cells box girder with tte transverse slope were derived while rationality of considering the transverse slope was discussed. Parameter analysis was done by adopting numerical simulation. Contrastive analysis on mechanical characteristic were done by changing the parameters such as loading positions, width-span ratios of box girder, cross slope angles. The results show that the error in computing characteristic value of grillage section rigidity is decreased up to 12.12% when the transverse slope is considered. The calculated results of grillage model fit the results of solid model, however, distortion cannot be reflect in the grillage model of multiple-cells box girder. The improvement of calculation precision is mainly appear on lateral displacement. Transverse slope would be considered in the grillage model if width-span ratio is greater than 0.8. Vertical displacement of cross section is increased linearly up to 758% when the transverse slope is change from 0 to 2%.
-
图 3 跨中荷载作用下1/2跨与1/4跨截面位移
Figure 3. Displacement of 1/2 span and 1/4 span section under effect of loadings in 1/2 span
图 4 1/4跨荷载作用下跨中截面位移
Figure 4. Displacement of mid-span section under the effect of loadings in 1/4 span.
图 5 1/2荷载作用下1/2跨与1/4跨截面顶、底板应力
Figure 5. Stress at the top and bottom of 1/2 span and 1/4 span section under the effect of loadings in 1/2 span
图 6 1/4跨中心荷载作用下跨中截面顶、底板应力对比图
Figure 6. Stress value contrast at the top and bottom of 1/2 span section under the effect of centric load in 1/4 span
图 7 9箱室梁在自重作用下跨中截面位移
Figure 7. Displacement in 1/2 span section of 9 cells box girder under the effect of self-weight
图 9 1/2跨截面位移最大差值与横坡的关系
Figure 9. Relationship between displacement of 1/2 span section and transverse slope
表 1 纵、横向梁格截面特征值
Table 1. Characteristic value of the longitudinal and transverse girder section
梁格 0横坡, 1.5%横坡(纵向梁格) 0横坡, 1.5%横坡(横向梁格) Iy/m4 Jx/m4 As/m2 Ix/m4 Jy/m4 Ash/m2 ① 3.84, 3.43 5.21, 4.77 1.12, 1.07 2.87, 2.71 5.74, 5.42 0.01, 0.01 ② 4.81, 4.67 7.34, 7.14 1.12, 1.10 2.87, 2.87 5.74, 5.74 0.01, 0.01 ③ 4.81, 4.95 7.34, 7.55 1.12, 1.13 2.87, 3.03 5.74, 6.06 0.01, 0.01 ④ 4.81, 5.24 7.34, 7.98 1.12, 1.16 2.87, 3.12 5.74, 6.23 0.01, 0.01 
下载: 导出CSV
表 2 参数要素
Table 2. Specification of parameter factor
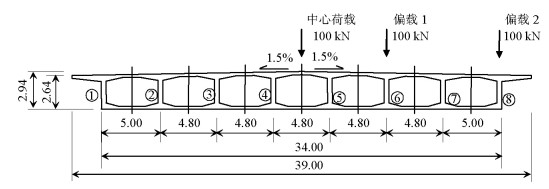
参数 箱梁宽跨比 横坡大小/% 加载位置 1 1.6(9箱室) 0 自重 2 1.3(7箱室) 1.0 中心荷载 3 1.0(5箱室) 1.5 偏载1 4 0.7(3箱室) 2.0 偏载2
下载: 导出CSV
表 3 位移误差分析
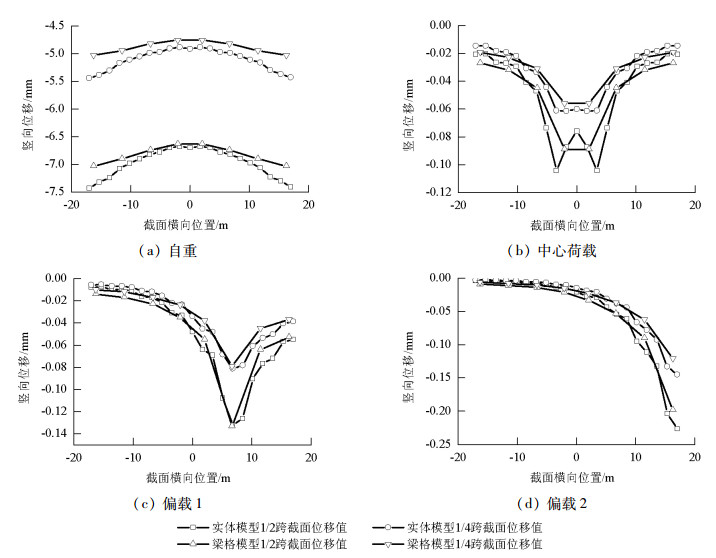
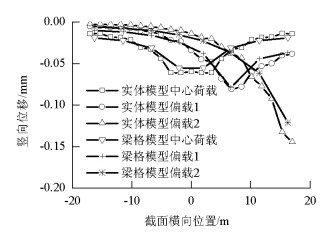
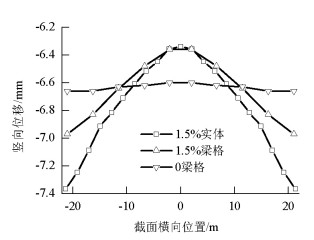
Table 3. Tolerance analysis of displacement
因素 自重 中心荷载 偏载1 偏载2 无横坡 有横坡 无横坡 有横坡 无横坡 有横坡 无横坡 有横坡 均差/mm 0.244 0.174 0.004 0.005 0.006 0.006 0.012 0.010 方差 1.0×10-1 4.5×10-2 2.1×10-5 2.8×10-5 4.5×10-5 4.4×10-5 2.8×10-4 1.8×10-4 相关系数 0.958 0.991 0.999 0.999 0.987 0.987 0.998 0.998
下载: 导出CSV
表 4 应力误差分析
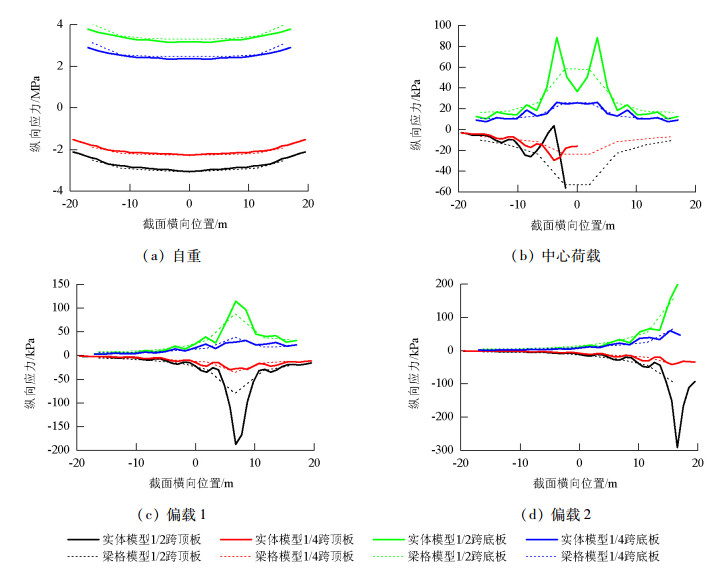
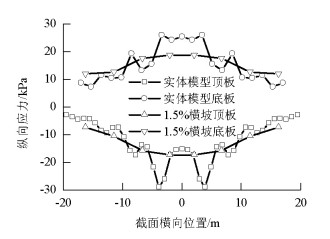
Table 4. Tolerance analysis of stress
位置 因素 自重 中心荷载 偏载1 偏载2 无横坡 有横坡 无横坡 有横坡 无横坡 有横坡 无横坡 有横坡 顶板 均差/kPa 108.21 88.49 7.71 7.06 1.70 1.59 1.62 1.65 方差 1.7×104 9.4×104 1.2×102 1.1×102 3.4 3.5 3.1 3.5 相关系数 0.988 0.995 0.938 0.941 0.998 0.999 0.999 0.999 底板 均差/kPa 128.27 81.38 5.82 5.86 6.63 6.64 10.69 9.92 方差 4.6×104 1.8×104 4.8×101 5.3×101 9.1×101 1.2×102 3.6×102 3.0×102 相关系数 0.977 0.974 0.998 0.997 0.988 0.993 0.999 0.999
下载: 导出CSV
-
张凯, 张俊平.梁格法在变宽多室梁桥结构分析中的应用[J].广东土木与建筑, 2009, 9:41-43. http://www.cqvip.com/Main/Detail.aspx?id=32261099ZHANG Kai, ZHANG Junping. Application of grillage method in structure analysis for broadens multi-chamber box girder bridge[J]. Guangdong Architecture Civil Engineering, 2009, 9:41-43. http://www.cqvip.com/Main/Detail.aspx?id=32261099 YI L Y. The application of grillage method in analyzing box girder structure[J]. Applied Mechanics & Materials, 2011, 55/56/57:1034-1039. http://www.scientific.net/AMM.55-57.1034 SHREEDHAR R, KHARDE R. Comparative study of grillage method and finite element method of RCC bridge deck[J]. International Journal of Scientific & Engineering Research, 2013, 4(2):1-10. SADEGHI J, FATHALI M. Grillage analogy applications in analysis of bridge decks[J]. Australian Journal of Civil Engineering, 2012, 10(1):23-36. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=98834109695f3038a7836259bf08759d 虞谨菲.剪力柔性梁格法在异形箱梁桥分析中的应用[D].西安: 长安大学, 2009. 刘瑶.梁格法在分析梁梁结构中的应用[D].哈尔滨: 东北林业大学, 2007. 张稳.梁格法在多室宽箱梁桥中的研究与应用[D].武汉: 武汉理工大学, 2014. 张发春, 杨昌正.梁格法在弯箱梁桥上的分析及应用[J].重庆交通大学学报, 2008, 27(1):13-16. doi: 10.3969/j.issn.1674-0297.2008.01.004ZHANG Fachun, YANG Changzheng. Analysis and application of grillage method to curved girder bridge[J]. Journal of Chongqing Jiaotong University, 2008, 27(1):13-16. doi: 10.3969/j.issn.1674-0297.2008.01.004 陈晶, 消文杰.基于梁格法的异型箱梁有限元计算分析[J].河南科技, 2015, 46(3):105-107. http://d.old.wanfangdata.com.cn/Periodical/hnkj201506037CHEN Jing, XIAO Wenjie. The finite element calculation and analysis of irregular box girder beam based on grillage method[J]. Journal of Henan Science and Technology, 2015, 46(3):105-107. http://d.old.wanfangdata.com.cn/Periodical/hnkj201506037 宋明曦.多室宽箱梁实用计算方法研究[D].重庆: 重庆交通大学, 2013. 陆光闾, 曹中银, 徐科英, 等.城市高架弧形底宽箱梁桥横向效应分析[J].中国市政工程, 2004(4):17-20. doi: 10.3969/j.issn.1004-4655.2004.04.007LU Guanglv, CAO Zhongyin, XU Keying, et al. Analysis on transverse effect of urban elevated bridge with broad box girders of arc bottom[J]. China Municipal Engineering, 2004(4):17-20. doi: 10.3969/j.issn.1004-4655.2004.04.007 苏巨峰.多室连续梁桥横向受力分析研究[D].西安: 长安大学, 2013. 姜军, 蒲黔辉, 勾红叶.连续刚构拱组合桥锚固区局部应力模型试验[J].西南交通大学学报, 2011, 46(5):726-731. doi: 10.3969/j.issn.0258-2724.2011.05.003JIANG Jun, PU Qianhui, GOU Hongye. Model test for local stress distribution in anchorage zones of continuous rigid frame compostie arch bridge[J]. Journal of Southwest Jiaotong University, 2011, 46(5):726-731. doi: 10.3969/j.issn.0258-2724.2011.05.003 HAMBLY E C. Bridge deck behaviour[M].London:Chapman and Hall, 1976:145-150. HAMBLY E C, PENNELLS E. Grillage analysis applied to cellular bridge decks[J]. Structural Engineer, 1975, 53(7):267-274. http://trid.trb.org/view.aspx?id=35563 戴公连, 李德建.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社, 2001:15-37. 肖汝诚.桥梁结构分析及程序系统[M].北京:人民交通出版社, 2002:28-31. 李小珍, 肖军, 刘德军, 等.局部应力差异对压杆弹性稳定的影响[J].西南交通大学学报, 2015, 50(6):971-976. doi: 10.3969/j.issn.0258-2724.2015.06.001LI Xiaozhen, XIAO Jun, LIU Dejun, et al. Influence of local stress variance on elastic stability of compression bar[J]. Journal of Southwest Jiaotong University, 2015, 50(6):971-976. doi: 10.3969/j.issn.0258-2724.2015.06.001 -
下载:
点击查看大图
计量
- 文章访问数: 591
- HTML全文浏览量: 241
- PDF下载量: 86
- 被引次数: 0