Mechanical Performance of Novel Prefabricated Composite Girder with Top Flange of Ultra Hight Performance Concrete Waffle Deck Panel
-
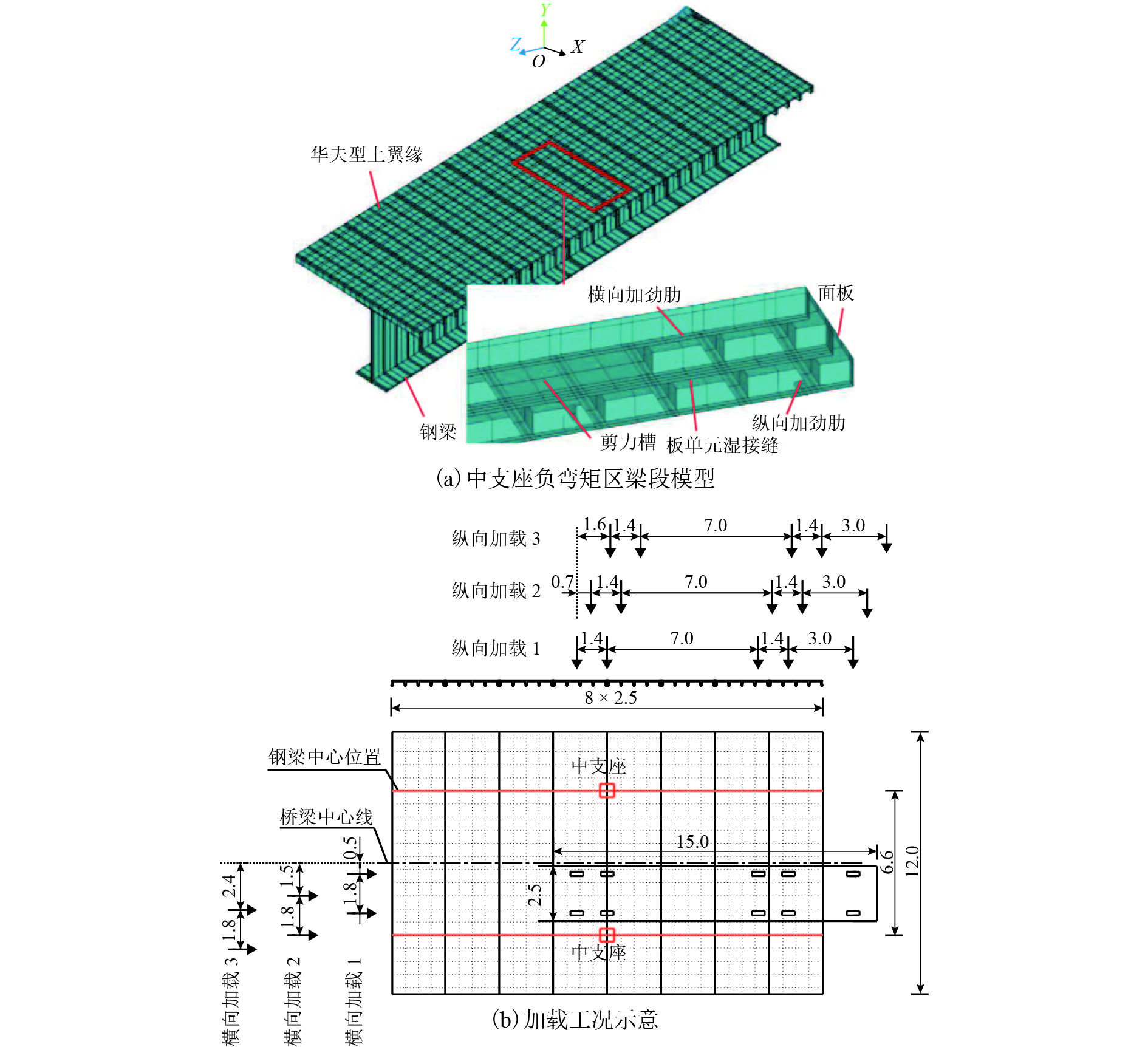
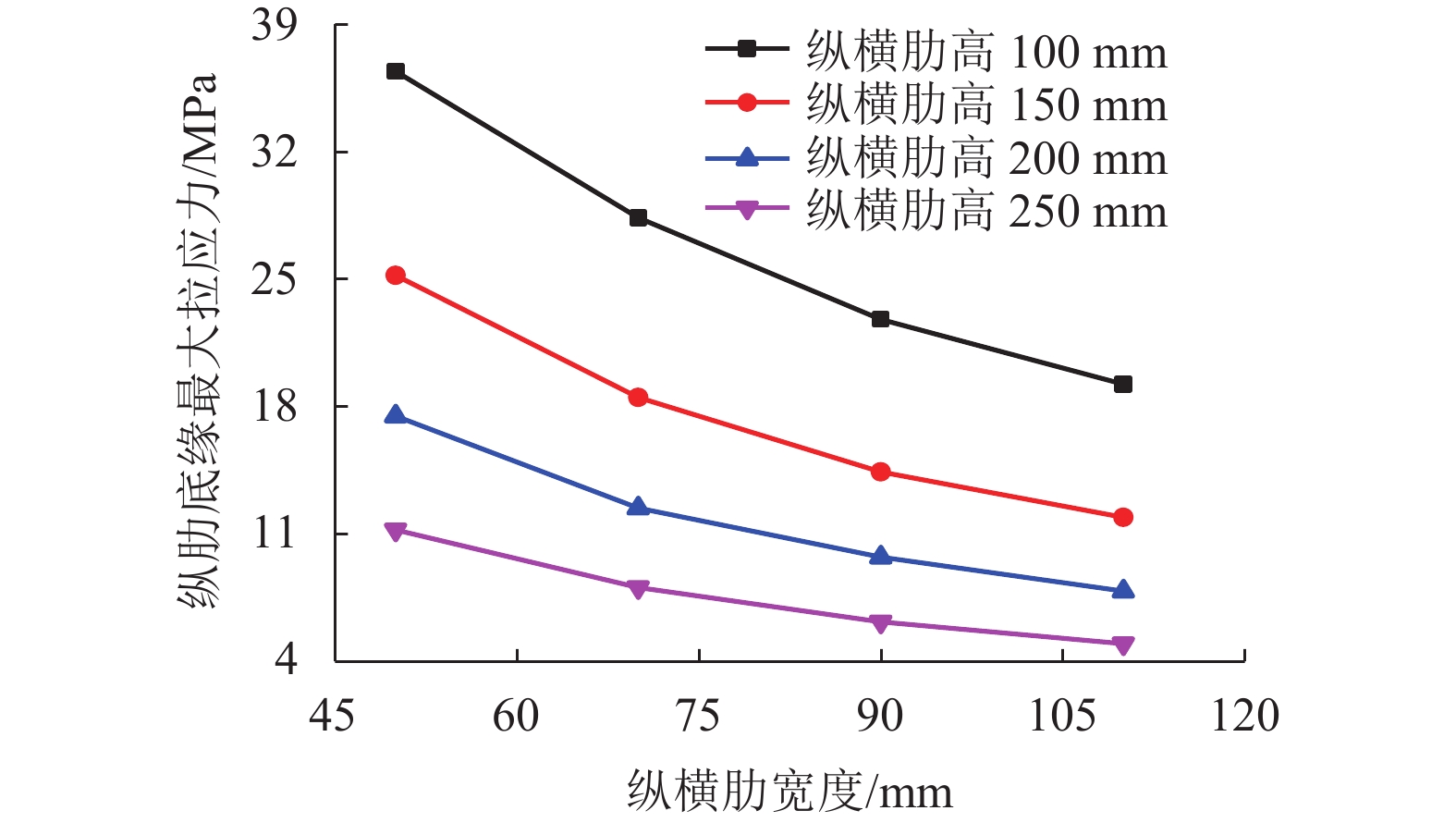
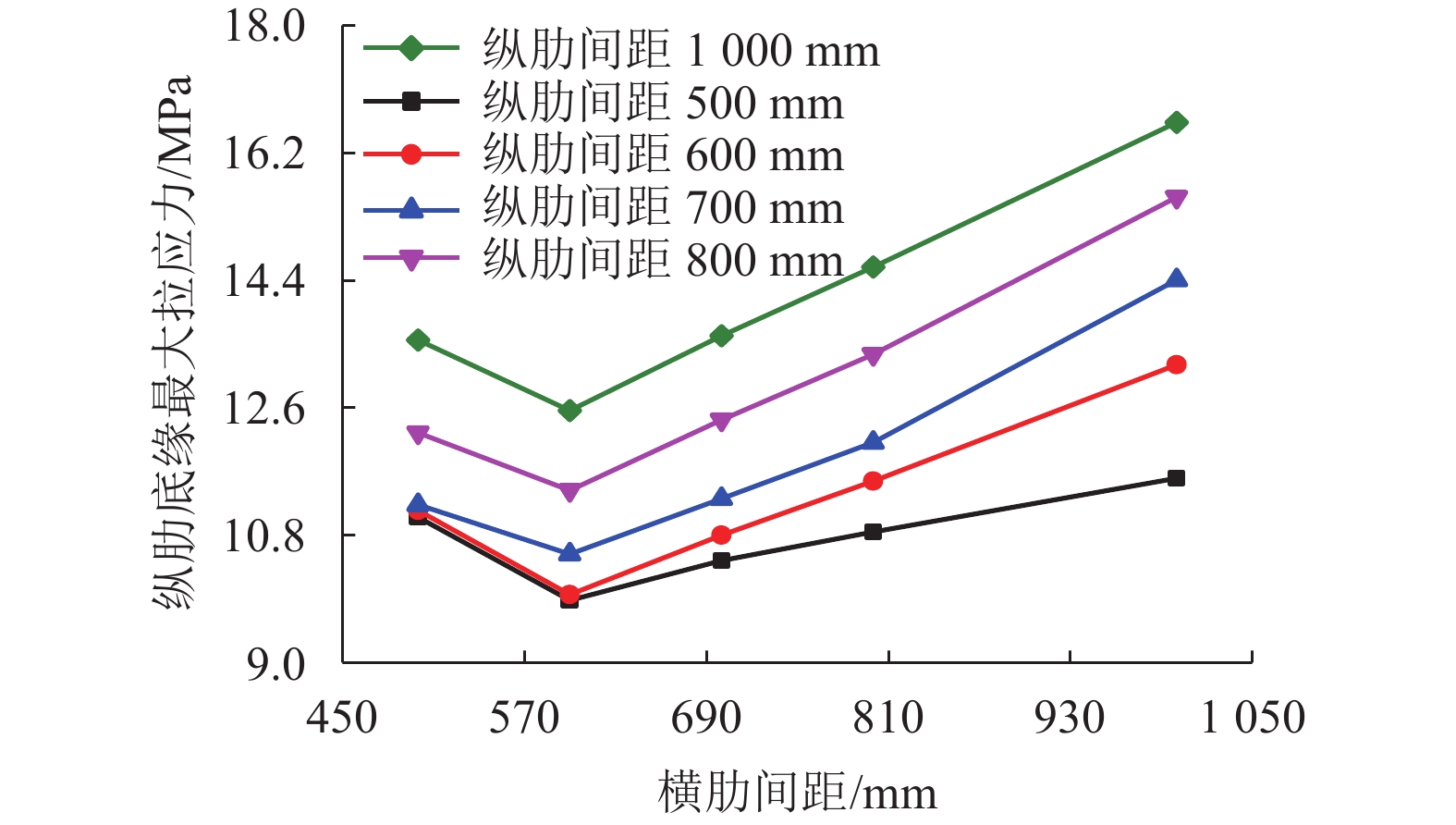
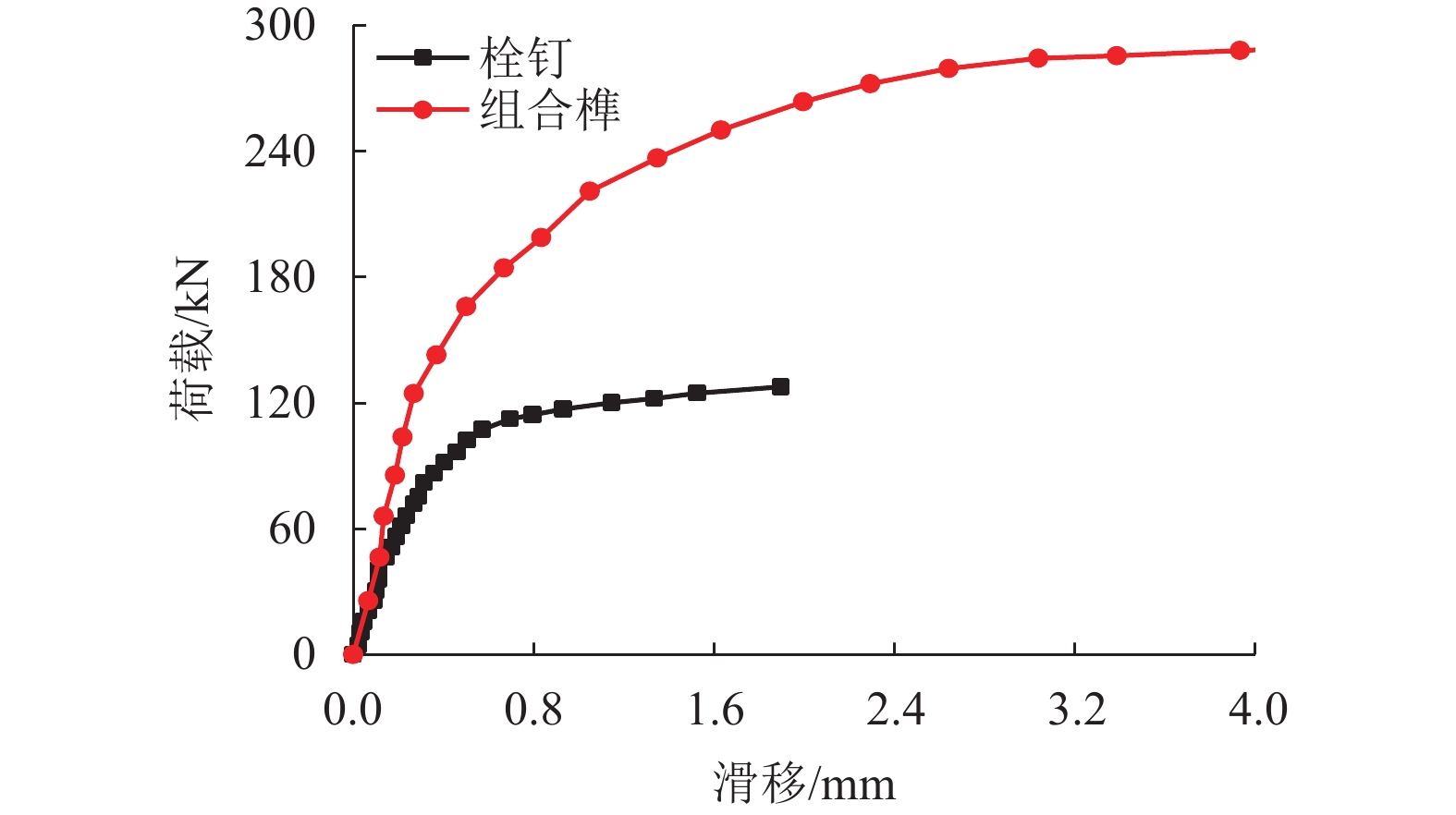
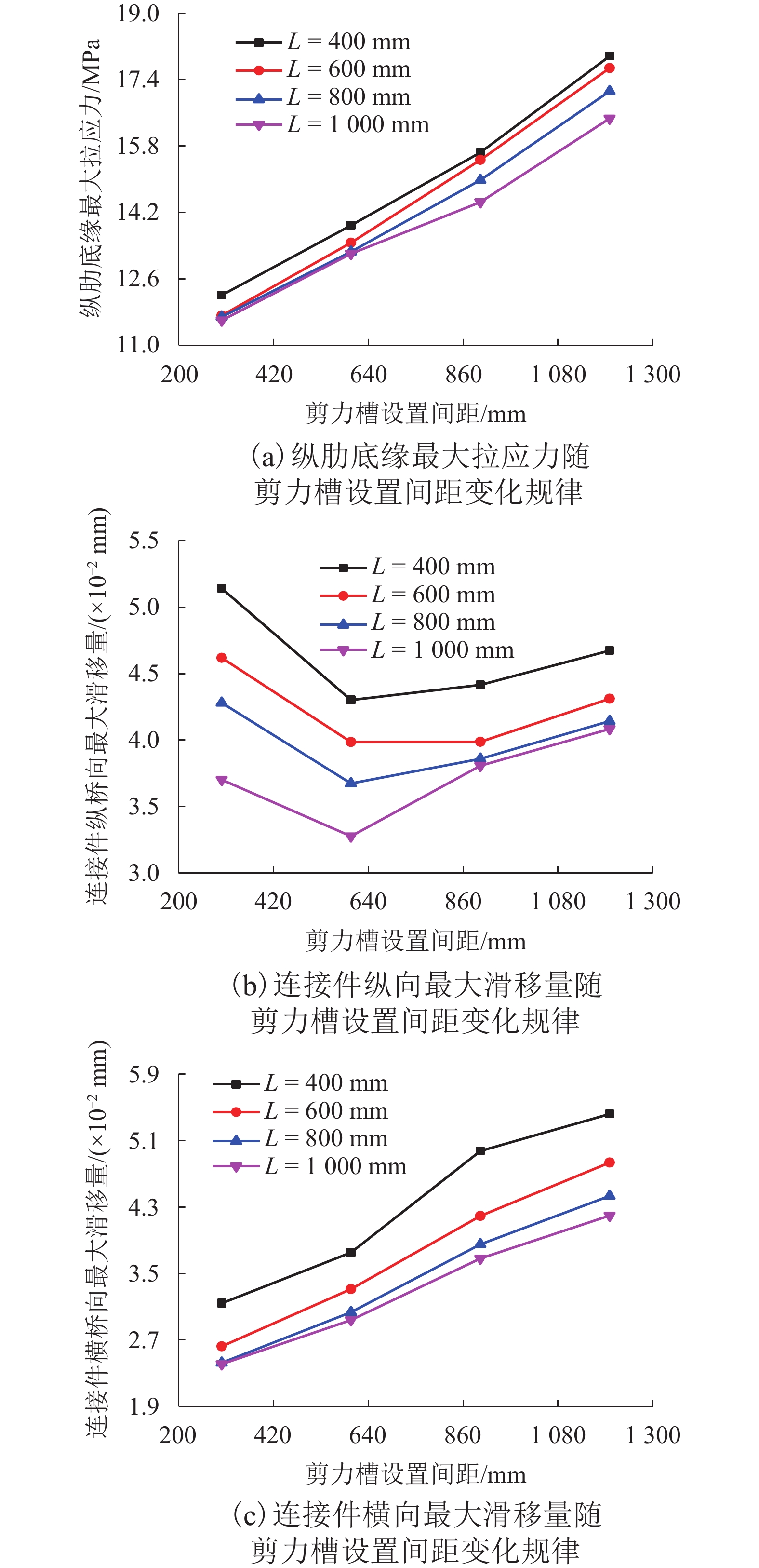
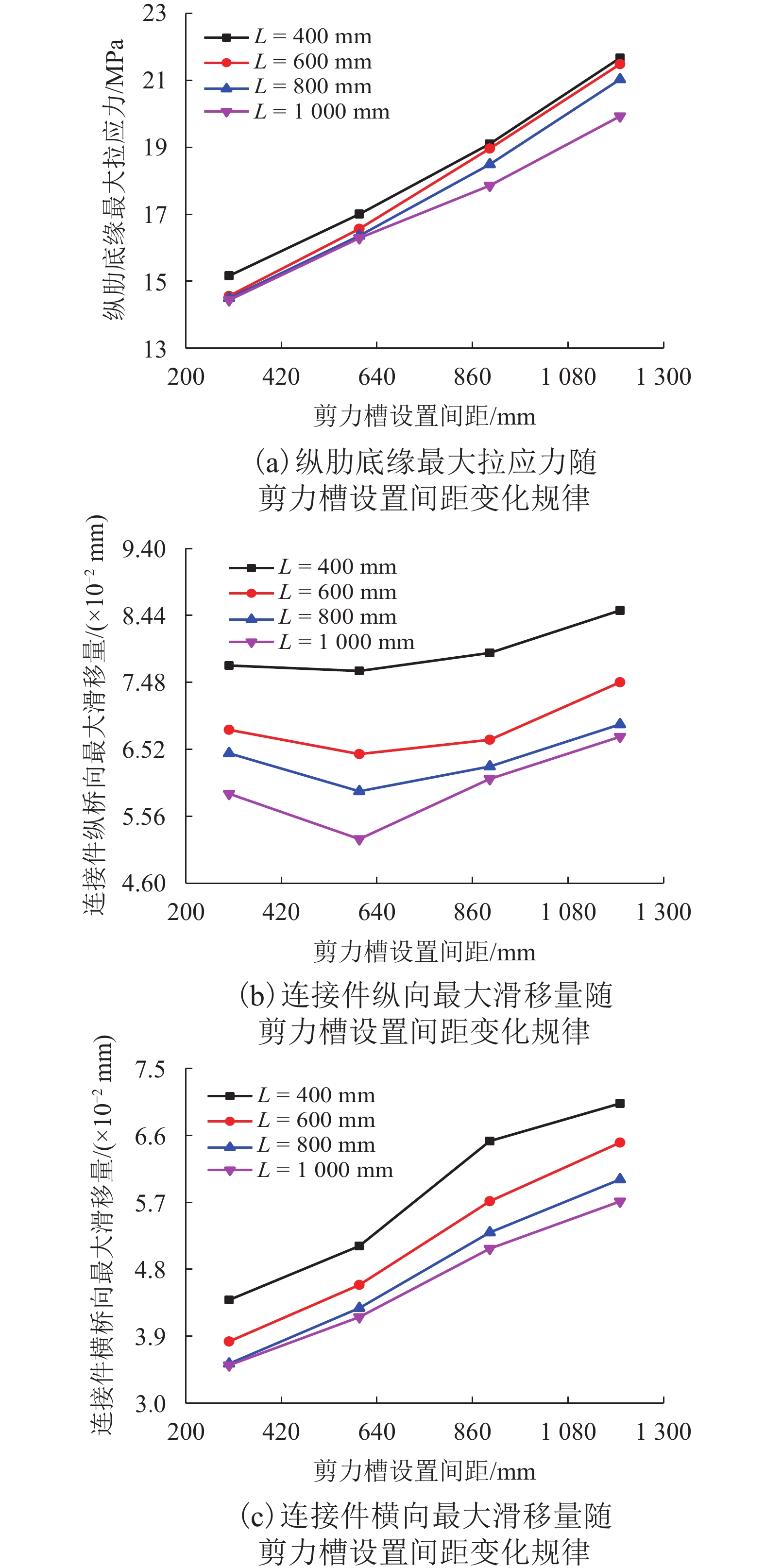
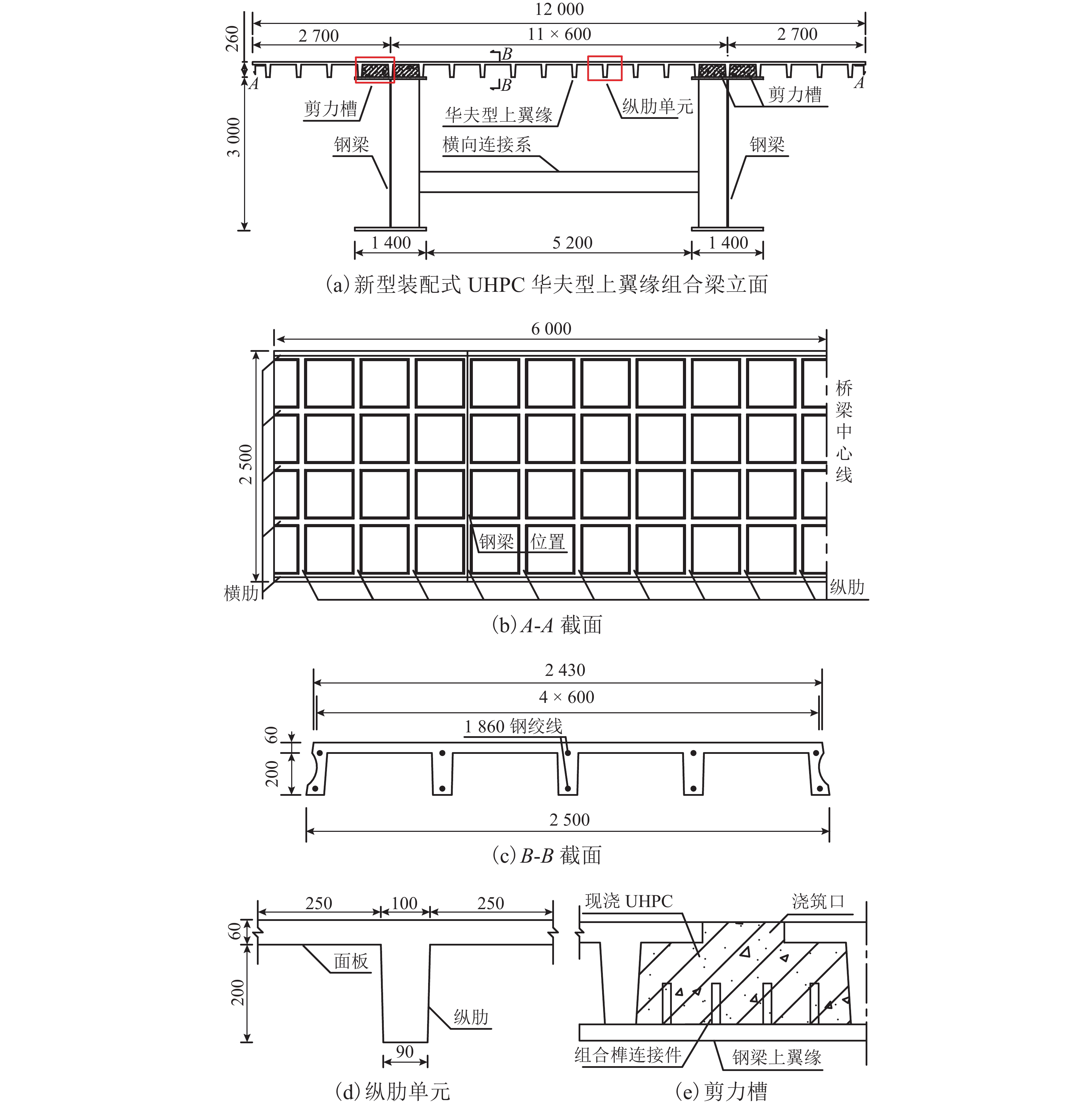
摘要: 为综合解决传统钢-混凝土组合结构中混凝土桥面板自重偏大和负弯矩区易开裂的问题，引入超高性能混凝土（ultra high performance concrete，UHPC）华夫板代替普通混凝土桥面板，提出一种新型组合梁—装配式UHPC华夫型上翼缘组合梁. 以某典型3跨连续梁桥为研究对象，分别建立3跨连续梁整体和中支座区域梁段的有限元模型，研究了不同荷载工况下新型装配式UHPC华夫型上翼缘组合梁的受力性能，分析了UHPC华夫型上翼缘关键设计参数对该新型组合梁力学性能的影响规律，对比研究了组合榫型剪力槽与栓钉型剪力槽对该新型组合梁受力性能的影响. 研究结果表明：在恒 + 活组合作用下，中支座负弯矩段华夫型上翼缘纵肋底缘和面板最大拉应力均小于配筋UHPC的抗拉强度设计值；当UHPC华夫型上翼缘纵、横肋宽90 mm、高200 mm，纵肋间距700 mm，横肋间距600 mm，面板厚60 mm时，UHPC华夫型上翼缘受力较为合理；组合榫型剪力槽更适用于新型装配式UHPC华夫型上翼缘组合梁.Abstract: A novel prefabricated composite girder with the top flange of an ultra-high-performance concrete (UHPC) waffle deck panel in place of a normal concrete deck panel was proposed, to resolve problems associated with the high self-weight and high probability of cracking in conventional steel-concrete composite structures. To investigate the mechanical behaviour and application of the structure in continuous bridges, a whole bridge model and mid-support region girder model of a typical three-span continuous bridge were established by finite element analysis (FEA). The mechanical behaviour of the novel composite girder under various load modes was studied, and the influence of the key design parameters for the UHPC waffle deck panel on the mechanical behaviour of the novel composite girder was analysed. In addition, the influences of the composite dowel-type shear pocket and stud-type shear pocket on the mechanical performance of the novel composite girder were compared. The maximum tensile stress at the bottom of the longitudinal ribs and the top deck of the UHPC waffle deck panel meets the tensile strength limit of reinforced UHPC under the composite action of dead loads and live loads; when the longitudinal ribs and transverse ribs are 90 mm in width, 200 mm in height, 700 mm in the space of the longitudinal ribs, 600 mm in the space of the transverse ribs, and 60 mm in the thickness of the top deck, the UHPC waffle deck panels exhibit better mechanical performance than before. The composite dowel-type shear pocket is more applicable to the novel prefabricated composite girder than the stud-type shear pocket.
-
波形钢腹板箱梁因为能减轻结构自重、减小预应力损失、避免腹板斜裂缝而成为具有广阔应用前景和吸引力的新型桥梁结构[1-2]. 不同于混凝土箱梁，波形钢腹板箱梁用波形钢腹板替换混凝土腹板后，箱梁的抗扭刚度被显著削弱[2-3]，因此其扭转和畸变效应也更加突出.
国内外学者对波形钢腹板箱梁的约束扭转效应开展了不少研究工作. 杨丙文等[4]分析了单箱单室波形钢腹板箱梁的约束扭转效应，但在悬臂板自由端出现了剪应力，与实际不符. 马磊等[5]推导了单箱双室波形钢腹板箱梁扭转控制微分方程，但仅分析了翘曲正应力. 邓文琴等[6]推导了单箱三室波形钢腹板悬臂梁扭转控制微分方程，并给出了翘曲正应力和剪应力计算式. Nie等[7-8]等在波形钢腹板箱梁的试验研究结果中靠近顶底板局部区域内出现了可观的正应变. 张元海等[9]指出分析波形钢腹板箱梁的约束扭转时应考虑顶底板对波形钢腹板的约束作用. 以上都是基于乌曼斯基第二理论（下文简称乌-Ⅱ理论）建立约束扭转控制微分方程并开展的理论分析，而乌-Ⅱ理论应用了剪应力的两种算式，出现了两种不一致的纵向翘曲位移[10]. 张元海等[11]指出约束扭转剪应力应按微元体平衡条件或根据自由扭矩和二次扭矩计算，不能直接按胡克定律计算. 此外，Kato等[12]采用矩阵法提出了波形钢腹板箱梁扭转效应计算理论. 李运生等[13]采用能量变分法推导了波形钢腹板曲线梁弯扭控制微分方程，并采用伽辽金法求得其解析解. 徐勋等[14]在广义坐标法的基础上基于混合变分原理建立了薄壁箱梁约束扭转分析新理论，与Reissner原理的结果是统一的，均考虑了全部次生剪应力对中面剪切变形的影响，计算精度更高. 鲍永方等[15]对适用于刚性扭转的乌曼斯基理论和Reissner原理进行比较，指出Reissner原理的计算精度高于乌曼斯基理论.
为了更加合理地分析波形钢腹板箱梁约束扭转效应，本文将位移和应力同时作为变分参量，应用Reissner原理推导出约束扭转控制微分方程，给出了不同于乌-Ⅱ理论的翘曲系数. 同时考虑波形钢腹板的褶皱效应，合理计算截面几何特性，推演出翘曲正应力和剪应力的计算公式. 结合波形钢腹板简支箱梁数值算例，研究了应力分布特征及截面几何参数变化对应力的影响规律.
1. 波形钢腹板的等效
1.1 等效剪切模量及等效厚度
图1为波形钢腹板的形状简图. 图中：a、c、d分别为直板段长、斜板段投影长、斜板段长；hw、tw分别为波高和板厚.
因组成波形钢腹板箱梁的各板件材料不同，约束扭转分析时需通过等效原则将材料统一. 本文根据波形钢腹板的力学性能先将其等效为正交异性平钢板，再等效为混凝土腹板. 将波形钢腹板等效为正交异性平钢板后的等效剪切模量[16]为
Gse=(a+c)/(a+d)Gs=ηGs, (1) 式中：Gs为钢板剪切模量；
$\eta = (a + c)/(a + d)$ .波形钢腹板在箱梁的受力中主要承受剪力，由式（1）采用剪切模量比可计算波形钢腹板等效为混凝土腹板的厚度，波形钢腹板的等效厚度为
twe=Gse/Gctw=ηnGtw, (2) 式中：Gc为混凝土剪切模量；
${n_{\text{G}}}$ 为钢板与混凝土的剪切模量比，${n_{\text{G}}} = {G_{\text{s}}}/{G_{\text{c}}}$ .1.2 纵向等效弹性模量
在一个波长的波形钢腹板两端施加一对等值、反向的轴向力，采用卡氏第二定理计算出弯矩和轴力下的轴向位移，根据位移等效原则可求得波形钢腹板等效为平钢板的纵向弹性模量为
Ese=κEs, (3) 式中：Es为钢板弹性模量；
$\kappa $ 为系数，κ=a+c(a+c2/d)(tw/hw)2+(3a+d)(twhw)2. 根据
${E_{{\text{ce}}}}{t_{{\text{we}}}} = {E_{{\text{se}}}}{t_{\text{w}}}$ 及式（2）、（3）求出波形钢腹板等效为混凝土腹板的纵向等效弹性模量为Ece=κnE/(ηnG)Ec = λEc, (4) 式中：Ec为混凝土弹性模量；
${n_{\text{E}}}$ 为钢板与混凝土的弹性模量比，${n_{\text{E}}} = {E_{\text{s}}}/{E_{\text{c}}}$ ；系数$\lambda = \kappa {n_{\text{E}}}/(\eta {n_{\text{G}}})$ .由于tw/hw一般很小，κ、λ则更小，波形钢腹板表现出明显的褶皱效应.
1.3 基本假定
根据薄壁箱梁的约束扭转分析理论，结合波形钢腹板的力学性能，对波形钢腹板箱梁约束扭转分析时作以下基本假定：
1） 刚性周边假设，横截面周边不变形；
2） 横截面上的翘曲正应力和剪应力沿壁厚均匀分布；
3） 混凝土顶底板与波形钢腹板间不产生界面滑移，波形钢腹板不发生剪切屈曲；
4） 波形钢腹板箱梁处于线性弹性工作状态.
2. 约束扭转应力
2.1 约束扭转翘曲正应力
分析波形钢腹板箱梁的约束扭转效应时需考虑二次剪切变形的影响，引入广义翘曲位移
$ \beta '(x) $ . 壁厚中面上任一点的纵向翘曲位移u(x,s)和切向位移v(x,s)分别为u(x,s)=−β′(x)ˉω(s), v(x,s)=φ(x)ρ(s), 式中：
$ \beta '(x) $ 为广义翘曲位移，x为纵向坐标；$\bar \omega (s)$ 为广义主扇性坐标，s为沿箱壁的曲线坐标，本文s原点取在竖向对称轴与顶板中面的交点处；$ \rho (s) $ 为扭心至各板壁厚中面的垂直距离；$\varphi $ (x) 为横截面扭转角.由式（5）可得壁厚中面任一点的翘曲正应变和剪应变分别为
ε(x,s)=∂u/∂x=−β″ˉω， γ(x,s)=∂u/∂s+∂v/∂x=φ′ρ−β′ˉω′. 根据刚性周边假设得各板件横向正应变
${\varepsilon _{\rm{s}}} = 0$ ，将式（6a）代入平面问题的物理方程求得翘曲正应力为σ={−Eoβ″ˉω, 顶底板,−λEoβ″ˉω,等效腹板, (7) 式中：
$E_{\rm{o}} = {E_{\text{c}}}/(1 - \mu _{\text{c}}^2)$ ，μc为混凝土泊松比.引起翘曲正应力的内力定义为扭转双力矩
$ {B_{\bar \omega }} $ ，借助式（7），可得Bˉω=∫s1σˉωtds=−EoIˉωβ″， (8) 式中：
$ {I_{\bar \omega }} $ 为波形钢腹板箱梁的广义主扇性惯性矩，${I_{\bar \omega }} \;= \displaystyle \int_{b_{\rm{t}}\;+\;2b_{\rm{f}}} {{{\bar \omega }^2}{t_{\rm{t}}}{\text{d}}s} + \int_{b_{\rm{b}}} {{{\bar \omega }^2}{t_{\rm{b}}}{\text{d}}s} \;+\; 2\lambda \int_{b_{\rm{w}}} {{{\bar \omega }^2}{t_{{\rm{we}}}}{\text{d}}s}，$ $ \displaystyle \int_{s_1} {{\text{d}}s}、$ $\displaystyle \int_{b_{\rm{t}}+2b_{\rm{f}}} {{\text{d}}s}、$ $\displaystyle \int_{b_{\rm{b}}} {{\text{d}}s} 、$ $ \displaystyle \int_{b_{\rm{w}}} {{\text{d}}s} $ 分别为在全截面（s1）、顶板宽度（bt）（含2倍悬臂板宽bf）、底板宽度（bb）、腹板宽度（bw）的积分；tt、tb分别为顶、底板的厚度.联立式（7）和式（8）可得翘曲正应力与扭转双力矩的关系式为
σ={Bˉωˉω/Iˉω, 顶底板,λBˉωˉω/Iˉω,等效腹板. (9) 2.2 约束扭转剪应力
约束扭转剪应力应按微元体平衡条件或根据自由扭矩和二次扭矩计算. 约束扭转总扭矩Mz分解为自由扭转扭矩M1和二次扭矩
$ {M_2} $ ，对应总剪应力τz包含自由扭转剪应力τ1和二次剪应力$ {\tau _{2 }} $ . 在闭口箱壁和悬臂板内同时存在τ1和$ {\tau _{2}} $ ，但是在悬臂板内的τ1沿壁厚呈线性分布且在壁厚中面上为0，故悬臂板承担的自由扭转扭矩和提供的抗扭刚度较小.闭口箱壁中面上任一点的自由扭转剪应力为
τ1=Msc/(Ωt)=M1ψ/(Idt), (10) 式中：Msc为闭口箱壁承担的自由扭矩；
$\psi = \varOmega / \displaystyle \oint 1/t{\text{d}}s $ ，Ω为箱梁横截面闭口箱壁中面所围面积的2倍；${I_{\rm{d}}} = {{{\varOmega}} ^2}/ \displaystyle \oint \;1/t{{\text{d}}s} + 2{b_{\rm{f}}}t_{\text{t}}^3/3$ ，为全截面抗扭惯性矩；t为壁厚.根据波形钢腹板箱梁的抗扭特性需对抗扭惯性矩进行修正，考虑悬臂板的贡献，抗扭惯性矩[17]为
Id=Ω2/Ω2[bttt(1−ζ)+bbtb(1−ζ)+2bwtwe(1+ζ)][bttt(1−ζ)+bbtb(1−ζ)+2bwtwe(1+ζ)]+2bft3t3, 式中：ζ为修正系数，对矩形波形钢腹板箱梁，
$\zeta = 0.400{b_{\text{w}}}/{b_{\text{t}}} - 0.060 \geqslant 0$ .将式（9）代入各板件微元体平衡方程
${{\partial}} {{q_{\bar \omega }}}/{{\partial}} s +$ $({\partial} {\sigma}/{\partial} x)t = 0 $ ，根据截面翘曲位移连续性条件$\displaystyle \oint {({{q_{\bar \omega }}}/t)} {\text{d}}s = 0$ ，求得各板件的二次剪力流$ {q_{\bar \omega }} $ ，进而可得壁厚中面上任一点的二次剪应力$ {\tau _{2 }} $ 为τ2=qˉω/t=−(M2ˉSˉω)/(Iˉωt), (11) 式中：
$ {M_{2}} = {B' _{\bar \omega }}$ ；$ {\bar S_{\bar \omega }} $ 为广义扇性静面矩.各板壁厚中面上任一点的
$ {\bar S_{\bar \omega }} $ 为ˉSˉω={Sˉω，悬臂板，Sˉω−∮(Sˉω/t)ds/∮1/tds，闭口箱壁， 式中：
$ {S_{\bar \omega }} $ 为壁厚中面上任一点的广义主扇性静面矩，${S_{\bar \omega }} = $ ${\bar \lambda} \displaystyle \int_0^s {\bar \omega t} {\text{d}}s$ ，对于顶底板，$\bar \lambda = 1$ ，对于等效腹板，$\bar \lambda = \lambda$ ；由式（10）、（11）可得各板壁厚中面上任一点的总剪应力为
τz={−M2ˉSˉω/(Iˉωt), 悬臂板,M1ψ/(Idt)−M2ˉSˉω/（Iˉωt),闭口箱壁. (12) 3. 基于Reissner原理建立控制微分方程
基于Reissner原理建立波形钢腹板箱梁的约束扭转控制微分方程时，将位移和应力同时作为了变分参量，建立的能量泛函[18]为
ΠR(σ,u)=∫V(σTε(u)−V(σ)−Fu)dV−∫lPudx, (13) 式中：
${\boldsymbol{\sigma}}$ 为应力向量；${\boldsymbol{u}}$ 为位移向量；${\boldsymbol{\varepsilon}} ({\boldsymbol{u}})$ 为应变向量；${\boldsymbol{V}}({\boldsymbol{\sigma}} )$ 为余能密度；${\boldsymbol{F}}$ 为体力向量，本文中为0；${\boldsymbol{P}}$ 为面力向量；V为体积；l为计算跨径.能量泛函中的应变能为
∫VσTε(u)dV=∫V(σε+τzγ)dV. (14) 将式（6）、（9）和式（12）代入式（14），得
∫VσTε(u)dV=∫l0(−Bˉωβ″+Mzφ′−M2β′)dx. (15) 余能函数为
∫VV(σ)dV=∫V(σ22Eo+τ2z2Gc)dV. (16) 将式（9）和式（12）代入式（16），得
∫VV(σ)dV=∫l0(B2ˉω2EoIˉω+M212GcId+χM222GcId)dx, (17) 式中：
$\chi = \dfrac{{{I_{\rm{d}}}}}{{I_{\bar \omega }^2}}\displaystyle \int_{s_{1}} {\left(\bar S_{\bar \omega }^2/t\right)} {\text{d}}s$ .当箱梁上仅作用分布扭矩mt时，外力势能为
−∫l0Pudx=−∫l0mtφdx. (18) 将式（15）、（17）和式（18）代入式（13），并对能量泛函数
${\varPi _R}$ 进行一阶变分运算，可得δΠR=∫l0[(−β″−BˉωEoIˉω)δBˉω+(φ′−MsGcId)δM1+(φ′−β′−χM2GcId)δM2 + (B′ˉω−M2)δβ′−(M′1+M′2+mt)δφ]dx. (19) 由
$\delta {\varPi _R} = 0$ 可得能量泛函的约束条件：1） 力与位移的关系条件
{−β″=BˉωEoIˉω,φ′=M1GcId,φ′−β′=χM2GcId. (20) 2） 力的平衡条件
{B′ˉω=M2,M′1+M′2=−mt. (21) 借助式（20）和式（21），并忽略mt的高阶微分，可得波形钢腹板箱梁约束扭转控制微分方程为
φ(4)−k2Rφ″=ξRmt/(EoIˉω), (22) 式中：
${k_{\text{R}}} = \sqrt {({\xi _{\text{R}}}{G_{\rm{c}}}{I_{\rm{d}}})/(E_{\rm{o}}{I_{\bar \omega }})}$ ；$ {\xi _{\text{R}}} $ 为按Reissner原理计算的翘曲系数，$ {\xi _{\text{R}}} = 1/(1 + \chi ) $ .不同于Reissner原理，采用乌Ⅱ-理论推导波形钢腹板箱梁约束扭转控制微分方程时，首先要确定广义翘曲位移
$\beta '$ 与扭率$\varphi '$ 之间的关系. 由剪切胡克定律及式（6b）可得总剪力流qz为qz=τzt=Gct(φ′ρ−β′ˉω′). (23) 将式（23）代入静力平衡方程
${M_{\text{z}}} =\displaystyle \int_{s_1} {{q_{\textit{z}}}\rho } {\text{d}}s$ ，可得φ′−ξwβ=Mz/(GcIρ). (24) 式中：
${\xi _{\text{w}}}$ 为按乌-Ⅱ理论计算的翘曲系数，${\xi _{\text{w}}} = $ $1 - {I_{\text{d}}}/{I_\rho }$ ；$ {I_\rho } $ 为极惯性矩，${I_\rho } =\displaystyle \int_{s_1} {{\rho ^2}t{\text{d}}s}$ .由微元体平衡方程
$\partial{{q_{\bar \omega }}} / {\partial}s + ({\partial} {\sigma}/{\partial} x)t = 0$ 及截面翘曲位移连续性条件$\displaystyle \oint {({{q_{\bar \omega }}}/t)} {\text{d}}s = 0$ ，可求得二次剪力流$ {{q_{\bar \omega }}} $ . 将其代入静力平衡方程${M_{2}} = \displaystyle \int _{s_1}{{q_{\bar \omega }}}\rho {\text{d}}s$ ，得$ {M_{2}} = - E_{\rm{o}}{I_{\bar \omega }}\beta ''' $ .由功能原理及自由扭转剪力流qs满足的静力平衡方程
${M_1} = \displaystyle \oint {{q_{\rm{s}}}\rho {\text{d}}s}$ 得$ {M_1} = {G_{\rm{c}}}{I_{\text{d}}}\varphi ' $ .M1和M2叠加得Mz，即
Mz=GcIdφ′−EoIˉωβ‴. (25) 将式（24）及
${\text{d}}{M_{\text{z}}} = - {m_{\rm{t}}}{\text{d}}\textit{z}$ 代入式（25），忽略mt的高阶微分，可得约束扭转控制微分方程为φ(4)−k2wφ″=ξwmt/(EoIˉω), (26) 式中：
${k_{\text{w}}} = \sqrt {({\xi _{\text{w}}}{G_{\rm{c}}}{I_{\rm{d}}})/(E_{\rm{o}}{I_{\bar \omega }})}$ .两种方法推导的约束扭转控制微分方程表达式相同，且均可采用初参数法求解[19]，但翘曲系数公式不同. 采用乌-Ⅱ理论推导约束扭转控制微分方程时应用了由胡克定律和微元体平衡条件得到的剪力流的两种算式及两种不一致的纵向翘曲位移[10]，且未考虑全部次生剪应力对中面剪切变形的影响. 应用Reissner原理建立扭转控制微分方程时将位移和应力同时作为变分参量，并考虑了全部次生剪应力对中面剪切变形的影响，通过建立能量泛函并对其变分，得出力与位移的关系条件及力的平衡条件，与刚性周边假设下的力与位移的关系条件及力的平衡条件是相符的，因此该理论更准确.
4. 算例分析
4.1 算例概况
算例采用计算跨径为40 m的简支波形钢腹板箱梁，梁端设置1.5 m厚混凝土横隔板，跨中作用集中扭矩荷载
$\bar M = 1\;000 \;{\text{kN}}{\text{•}} {\text{m}}$ ，箱梁横截面尺寸见图2. 图2中还示出了计算点Ⅰ ~ Ⅵ 的位置. 波形钢腹板采用1600型，其几何尺寸：a=d=430 mm，c=370 mm，hw=220 mm，tw=16 mm. 混凝土的材料特性：Ec=34.5 GPa，Gc=13.8 GPa，μc=0.2；钢板的材料特性：Es=206 GPa，Gs=79 GPa，μs=0.31. 求得扭心至顶板中面的距离为0.595 0 m，极惯性矩Iρ=4.8236 m4，抗扭惯性矩${I_{\rm{d}}} = 4.059\;8\;{{\text{m}}^4}$ ，广义主扇性惯性矩${I_{\bar \omega }} $ =0.7555 m6，按乌-Ⅱ理论和本文方法计算的翘曲系数分别为ξw=0.1583，ξR=0.069 3.4.2 理论验证
图3为按本文方法和乌-Ⅱ理论计算的扭转内力分布曲线. 由图3可以看出：按不同方法计算的双力矩和二次扭矩在跨中截面有明显差异，按乌-Ⅱ理论计算的双力矩和二次扭矩分别比本文方法计算的约增大了51%和128%. 由于两种方法计算的翘曲系数差异较大导致扭转内力的差异较大，也说明不同方法计算的翘曲系数对扭转内力有显著影响.
为验证本文方法合理性，按本文方法、乌-Ⅱ理论计算横截面翘曲正应力和总剪应力，并与有限元解对比. 有限元解是采用ANSYS软件建立空间有限元模型求得，有限元模型如图4所示. 混凝土板和波形钢腹板分别采用SOLID45实体单元和SHELL63壳单元模拟，由于分析时假设波形钢腹板与混凝土顶底板之间无界面滑移[20]，故在模型中壳单元和实体单元间用主从约束法作刚性连接处理；每侧梁端底板上设置2个支座，左侧梁端约束为3个坐标轴方向的平动位移Ux 、Uy和Uz，右侧梁端约束为横向和竖向平动位移Uy和Uz；集中扭矩荷载等效成刚性扭转荷载的力流形式，均匀施加于跨中截面闭合箱壁各单元的节点上，顶底板施加反向水平荷载
$\bar M/(2h)$ ，其中，h为梁高，波形钢腹板施加反向竖直荷载$\bar M/(2{b_{\text{t}}})$ . 刚性扭转荷载下的箱梁有限元模型在纵向仅产生扭转翘曲正应力.为避免有限元模型中集中扭矩施加位置的局部应力影响，根据扭转内力分布及有限元模型的应力分布，选取距跨中1.6 m的左截面正面（外法线方向与x轴一致的横截面为正面）为分析截面. 以该截面上的Ⅰ、Ⅱ、Ⅴ 3个计算点进行翘曲正应力对比，Ⅲ、Ⅳ、Ⅵ 3个计算点进行总剪应力对比，各计算点的应力结果见表1. 表1中的相对误差为本文方法解或乌-Ⅱ理论解与有限元解的差除以有限元解求得. 由表1可以看出，本文方法计算的应力与有限元解吻合更好. 但是由于刚性周边等假设，理论解与有限元解之间还是存在一定的误差.
表 1 距跨中1.6 m左截面应力比较Table 1. Comparison of stresses at left section 1.6 m from mid-span名称 计算点 有限元
解/kPa本文方
法/kPa乌-Ⅱ
理论/kPa相对误差/% 本文
方法乌-Ⅱ
理论${\sigma}$ Ⅰ 54.06 57.35 63.61 6.09 17.67 Ⅱ −27.83 −25.42 −28.18 −8.66 1.28 Ⅴ −75.83 −81.24 −90.10 7.13 18.82 $ {\tau _{\text{z}}} $ Ⅲ 82.37 84.59 77.37 2.70 −6.07 Ⅳ 1670.20 1480.32 1354.03 −11.37 −18.93 Ⅵ 154.55 154.50 176.98 −0.03 15.51 4.3 应力分布
为了解波形钢腹板箱梁的应力在横截面上的分布规律，图5为跨中左截面翘曲正应力、二次剪应力、总剪应力的分布图，其中箭头方向为剪应力的方向. 由图5可以看出：点Ⅰ和点Ⅴ的翘曲正应力绝对值较大，而波形钢腹板几乎不产生翘曲正应力；点Ⅴ和点Ⅵ的二次剪应力绝对值较大，腹板的二次剪应力与自由扭转剪应力叠加后使得总剪应力减小且沿梁高呈均匀分布，而底板的二次剪应力与自由扭转剪应力叠加后使得总剪应力增大，悬臂板壁厚中面上不产生自由扭转剪应力，但存在二次剪应力.
图 5 跨中左截面应力分布（单位：kPa）Figure 5. Stress distribution at left section from mid-span （unit： kPa）4.4 参数影响分析
为进一步探索截面几何参数变化对波形钢腹板箱梁约束扭转效应的影响，选取不同高宽比的梁为分析对象. 梁高h分别取值为2.15、4.30 m，即高宽比h/bt分别为0.5、1.0. 根据图2分别改变tw、bf，腹板厚度tw以2 mm为步长从8 mm增大至22 mm，悬臂板单侧宽度bf从0开始以0.215 m为步长增大至4.300 m，即悬臂板宽度与闭合箱壁宽度的比值（简称悬臂板宽度比，bf /bt）从0开始以0.05为步长增大至1.00.
为比较乌-Ⅱ理论与本文方法计算的翘曲系数的差异，图6绘制了乌-Ⅱ理论与本文方法计算的翘曲系数比值
${\xi _{\text{w}}}/{\xi _{\rm{R}}}$ 随tw、bf /bt的变化曲线. 由图6可以看出：翘曲系数比值受腹板厚度和悬臂板宽度比的影响显著，且随腹板厚度和悬臂板宽度比的增大呈增长趋势，不同高宽比梁的翘曲系数比值增长趋势有差异；当tw＞10 mm和bf /bt＞0.20时，翘曲系数比值大于1；翘曲系数比值偏离1越远，则两种方法的计算结果差异越大；当腹板厚度为22 mm时，高宽比较小的梁的翘曲系数比值达到了4.70；当悬臂板宽度比为1.00时，高宽比较大的梁的翘曲系数比值达到了3.10.
图 6 翘曲系数比值随腹板厚度和悬臂板宽度比的变化曲线Figure 6. Variation of warping coefficient ratio with web thickness and cantilever slab width ratio由于点Ⅰ和点Ⅴ的翘曲正应力绝对值较大，图7绘制了跨中左截面点Ⅰ和点Ⅴ翘曲正应力随tw、bf /bt的变化曲线. 由图7可以看出：点Ⅰ和点Ⅴ的翘曲正应力绝对值均随腹板厚度的增大而减少，随悬臂板宽度比的增大先增大后减少，bf /bt=0.10时开始减小；当bf /bt＞0.10时，悬臂板宽度增大可以减少翘曲正应力.
图 7 翘曲正应力随腹板厚度和悬臂板宽度比的变化曲线Figure 7. Variation of warping normal stress with web thickness and cantilever slab width ratio图8绘制了跨中左截面点 Ⅳ 和点 Ⅵ 的总剪应力随tw、bf/bt的变化曲线. 由图8可以看出：高宽比较小的梁的总剪应力明显大于高宽比较大的梁；对高宽比较大的梁，当tw=8 mm和bf/bt=0.30时，点Ⅵ总剪应力分别达到点 Ⅳ总剪应力的34.4%、30.2%，而混凝土与钢板的剪切模量比为0.17，底板总剪应力显然不容忽视，经分析，悬臂板根部的总剪应力同样不容忽视. 因此，在波形钢腹板箱梁设计时，应对顶底板进行精细化设计，防止斜裂缝的产生；随着悬臂板宽度的增大，当bf /bt＞0.30时，总剪应力几乎不变；对高宽比较小的梁的总剪应力随腹板厚度增大而减小，而对高宽比较大的梁，腹板厚度对总剪应力的影响不显著.
图 8 总剪应力随腹板厚度和悬臂板宽度比的变化曲线Figure 8. Variation of total shear stress with web thickness and cantilever slab width ratio5. 结 论
1） Reissner原理将位移和应力同时作为变分参量，考虑约束扭转全部次生剪应力对中面剪切变形的影响来推导波形钢腹板箱梁约束扭转控制微分方程，理论更准确. 本文推导的约束扭转控制微分方程表达式与乌-Ⅱ理论的相同，但翘曲系数公式不同. 数值算例的结果表明，相对于乌-Ⅱ理论，本文方法的计算结果与有限元解吻合更好，验证了本文方法的合理性.
2） 按乌-Ⅱ理论与本文方法计算的翘曲系数的比值表征了两种理论计算结果的差异，翘曲系数比值偏离1越远，则计算结果的差异越大. 两种方法计算的翘曲系数受腹板厚度和悬臂板宽度的影响显著，翘曲系数比值最大可达到4.70.
3） 波形钢腹板箱梁发生约束扭转时，波形钢腹板几乎不承担翘曲正应力，主要承担剪应力，混凝土顶底板既承担翘曲正应力又承担剪应力. 底板总剪应力可达到腹板总剪应力的34.4%，而混凝土相对钢板的抗剪性能较差，应对顶底板予以重视，并对其精细化设计，防止主拉应力超限引起斜裂缝.
4） 波形钢腹板厚度增大可以减小约束扭转翘曲正应力；随着悬臂板宽度的增大，悬臂板宽度比大于0.10时，翘曲正应力减小，而当悬臂板宽度比大于0.30时，总剪应力几乎无变化.
-
图 1 新型装配式UHPC华夫型上翼缘组合梁
Figure 1. Novel prefabricated composite girder with the top flange of UHPC waffle deck panel
图 2 典型三跨连续梁桥整体计算模型
Figure 2. Whole bridge model of the typical three-span continuous bridge
图 3 中支座负弯矩区梁段模型及其加载工况示意（单位：m）
Figure 3. The local model and load modes of the mid-support region girder (unit: m)
图 4 纵横肋尺寸对纵肋底缘应力影响
Figure 4. Influence of sizes of longitudinal and transverse ribs on the stress at the bottom of longitudinal ribs
图 5 纵横肋间距对纵肋底缘应力影响
Figure 5. Influence of space of longitudinal and transverse ribs on the stress at the bottom of longitudinal ribs
图 6 面板厚度对纵肋底缘及面板应力影响
Figure 6. Influence of thickness of top deck on the stress at the bottom of longitudinal ribs and top deck
图 7 典型组合榫连接件和栓钉连接件荷载滑移曲线
Figure 7. Typical load-slide curves of composite dowels and shear studs
图 9 组合榫型剪力槽参数变化对新型组合梁影响
Figure 9. Parameter influence of the dowel-type shear pocket on the novel composite girder
图 10 栓钉型剪力槽参数变化对新型组合梁影响
Figure 10. Parameter influence of the stud-type shear pocket on the novel composite girder
表 1 材料特性
Table 1. Material property
材料 弹性模量/GPa 泊松比 密度/（kg•m–3） UHPC 60 0.20 2 650 Q345钢 206 0.31 7 850 1860钢绞线 195 0.31 7 850 
下载: 导出CSV
表 2 华夫型上翼缘各部位应力计算结果
Table 2. The calculated stress at parts of the waffle deck panel
位置 最大应力/MPa 加载工况 纵肋底缘 9.9 纵向加载3、横向加载1 横肋底缘 – 4.3 纵向加载2、横向加载1 面板 8.0 纵向加载3、横向加载1
下载: 导出CSV
-
聂建国,陶慕轩,吴丽丽,等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报,2012,45(6): 110-122.NIE Jianguo, TAO Muxuan, WU Lili, et al. Advances of research on steel-concrete composite bridges[J]. China Civil Engineering Journal, 2012, 45(6): 110-122. 陈宝春, 牟廷敏, 陈宜言, 等. 我国钢-混凝土组合结构桥梁研究进展及工程应用[J]. 建筑结构学报, 2013, 34（增刊1）: 1-10CHEN Baochun, MU Tingmin, CHEN Yiyan, et al. State-of-the-art of research and engineering application of steel-concrete composite bridges in China[J]. Journal of Building Structures, 2013, 34（S1）: 1-10 聂建国. 钢-混凝土组合结构桥梁[M]. 北京: 人民交通出版社, 2011: 1-18 樊健生,聂建国,张彦玲. 钢-混凝土组合梁抗裂性能的试验研究[J]. 土木工程学报,2011,44(2): 1-7.FAN Jiansheng, NIE Jianguo, ZHANG Yanling. Experimental study of crack resistance of steel concrete composite beams[J]. China Civil Engineering Journal, 2011, 44(2): 1-7. 邵旭东, 胡建华. 钢-超高性能混凝土轻型组合桥梁结构[M]. 北京: 人民交通出版社, 2015: 20-21 樊健生,聂建国. 钢-混凝土组合桥梁研究及应用新进展[J]. 建筑钢结构进展,2006,8(5): 35-39. doi: 10.3969/j.issn.1671-9379.2006.05.005FAN Jiansheng, NIE Jianguo. Progress in research and application of composite steel concrete bridges[J]. Progress in Steel Building Structures, 2006, 8(5): 35-39. doi: 10.3969/j.issn.1671-9379.2006.05.005 聂建国,陶慕轩,聂鑫,等. 抗拔不抗剪连接新技术及其应用[J]. 土木工程学报,2015,48(4): 7-14.NIE Jianguo, TAO Muxuan, NIE Xin, et al. New technique and application of uplift-restricted and slip-permitted connection[J]. China Civil Engineering Journal, 2015, 48(4): 7-14. 聂建国,李一昕,陶慕轩,等. 新型抗拔不抗剪连接件抗拔性能试验[J]. 中国公路学报,2014,27(4): 38-45. doi: 10.3969/j.issn.1001-7372.2014.04.006NIE Jianguo, LI Yixin, TAO Muxuan, et al. Experiment research on uplift performance of a new type of uplift restricted-slip free connector[J]. China Journal of Highway and Transport, 2014, 27(4): 38-45. doi: 10.3969/j.issn.1001-7372.2014.04.006 聂建国. 我国结构工程的未来——高性能结构工程[J]. 土木工程学报,2016,49(9): 1-8.NIE Jianguo. The future of structural engineering in China—high-performance structural engineering[J]. China Civil Engineering Journal, 2016, 49(9): 1-8. 刘永健,高诣民,周绪红,等. 中小跨径钢-混凝土组合梁桥技术经济性分析[J]. 中国公路学报,2017,30(3): 1-13. doi: 10.3969/j.issn.1001-7372.2017.03.001LIU Yongjian, GAO Yimin, ZHOU Xuhong, et al. Technical and economic analysis in steel-concrete composite girder bridges with small and medium span[J]. China Journal of Highway and Transport, 2017, 30(3): 1-13. doi: 10.3969/j.issn.1001-7372.2017.03.001 HABEL K, VIVIANI M, DENARIÉ E, et al. Development of the mechanical properties of an ultra-high performance fiber reinforced concrete (UHPFRC)[J]. Cement & Concrete Research, 2006, 36(7): 1362-1370. GRAYBEAL B A. Material property characterization of Ultra-high performance concrete[R]. Washington D. C.: Federal Highway Administration, 2006 RUSSELL H G, GRAYBEAL B A. Ultra-high performance concrete: a state-of-the-art report for the bridge community[R]. McLean: High Performance Concrete, 2013 BABY F, GRAYBEAL B A, MARCHAND P, et al. UHPFRC tensile behavior characterization:inverse analysis of four-point bending test results[J]. Materials & Structures, 2013, 46(8): 1337-1354. 陈宝春,季韬,黄卿维,等. 超高性能混凝土研究综述[J]. 建筑科学与工程学报,2014,31(3): 1-24. doi: 10.3969/j.issn.1673-2049.2014.03.002CHEN Baochun, JI Tao, HUANG Qingwei, et al. Review of research on ultra-high performance concrete[J]. Journal of Architecture and Civil Engineering, 2014, 31(3): 1-24. doi: 10.3969/j.issn.1673-2049.2014.03.002 李成君,周志祥,黄雅意,等. 装配式组合梁剪力钉抗剪承载力研究[J]. 中国公路学报,2017,30(3): 264-270. doi: 10.3969/j.issn.1001-7372.2017.03.029LI Chengjun, ZHOU Zhixiang, HUANG Yayi, et al. Research on shear resistance of shear studs in prefabricated composite beam[J]. China Journal of Highway and Transport, 2017, 30(3): 264-270. doi: 10.3969/j.issn.1001-7372.2017.03.029 贾俊峰,赵建瑜,张强,等. 后张预应力节段拼装CFST桥墩抗侧力学行为试验[J]. 中国公路学报,2017,30(3): 236-245. doi: 10.3969/j.issn.1001-7372.2017.03.026JIA Junfeng, ZHAO Jianyu, ZHANG Qiang, et al. Experiment on lateral bearing behavior of post-tensioned segmental CFST bridge pier columns[J]. China Journal of Highway and Transport, 2017, 30(3): 236-245. doi: 10.3969/j.issn.1001-7372.2017.03.026 TOUTLEMODE F, RESPLENDINO J, SORRELLI L, et al. Innovative design of Ultra high-performance fiber reinforced concrete ribbed slab: experimental validation and preliminary detailed analysis[C]//Proc. 7th Int. Symp. on Utilization of High Strength/High Performance Concrete. Washington D. C.: [s.n.], 2005: 1187-1206 GARCIA HECTOR M. Analysis of an Ultra-high performance concrete two-way ribbed bridge deck slab[R]. Washington D. C.: Federal Highway Administration, 2007 AALETI S, PETERSEN B, SRITHARAN S. Design guide for precast UHPC waffle deck panel system, including connections[R]. Washington D. C.: Federal Highway Administration, 2013 兰枢灵. 薄壁钢箱梁计算方法研究[D]. 西安: 长安大学, 2011 CLAßEN M, GALLWOSZUS J. Concrete fatigue in composite dowels[J]. Structural Concrete, 2016, 17(1): 63-73. doi: 10.1002/suco.v17.1 罗应章. 钢-混凝土组合梁栓钉剪力连接件的研究[D]. 长沙: 中南大学, 2008 马增. 新型装配式钢——混组合箱梁桥结构设计与试验研究[D]. 南京: 东南大学, 2015 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 575
- HTML全文浏览量: 427
- PDF下载量: 109
- 被引次数: 0