Vehicle-Guideway Coupling Vibration Comparative Analysis for Maglev Vehicles While Standing Still
-
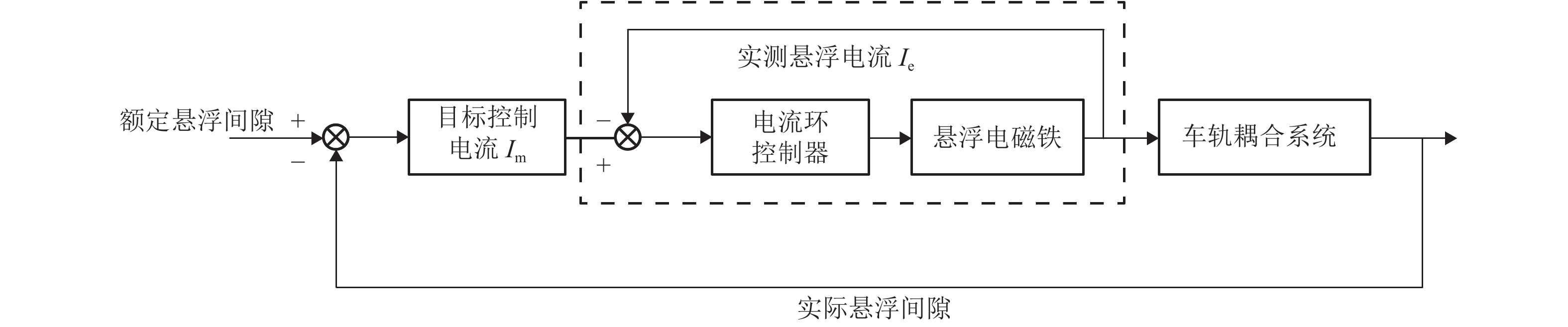
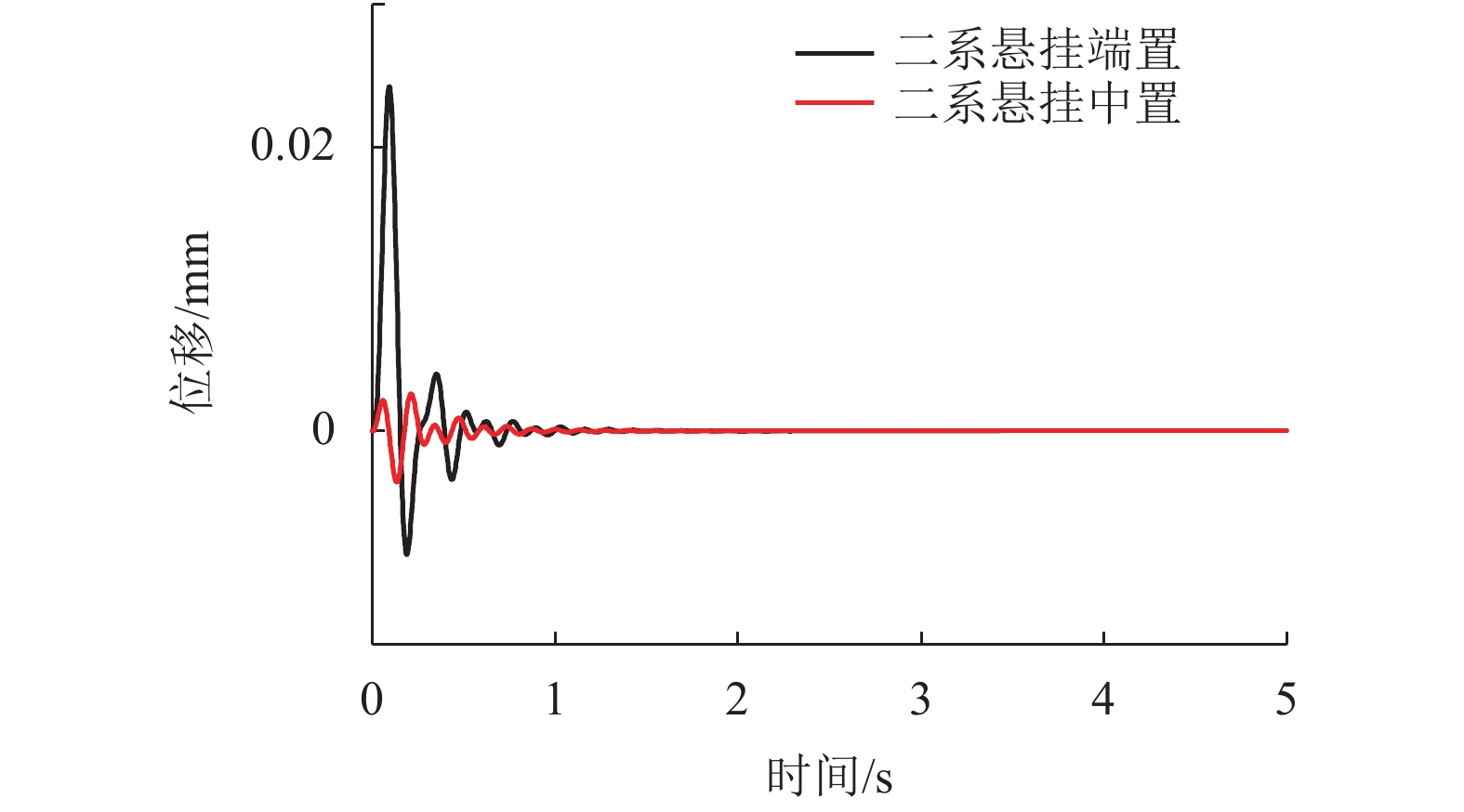
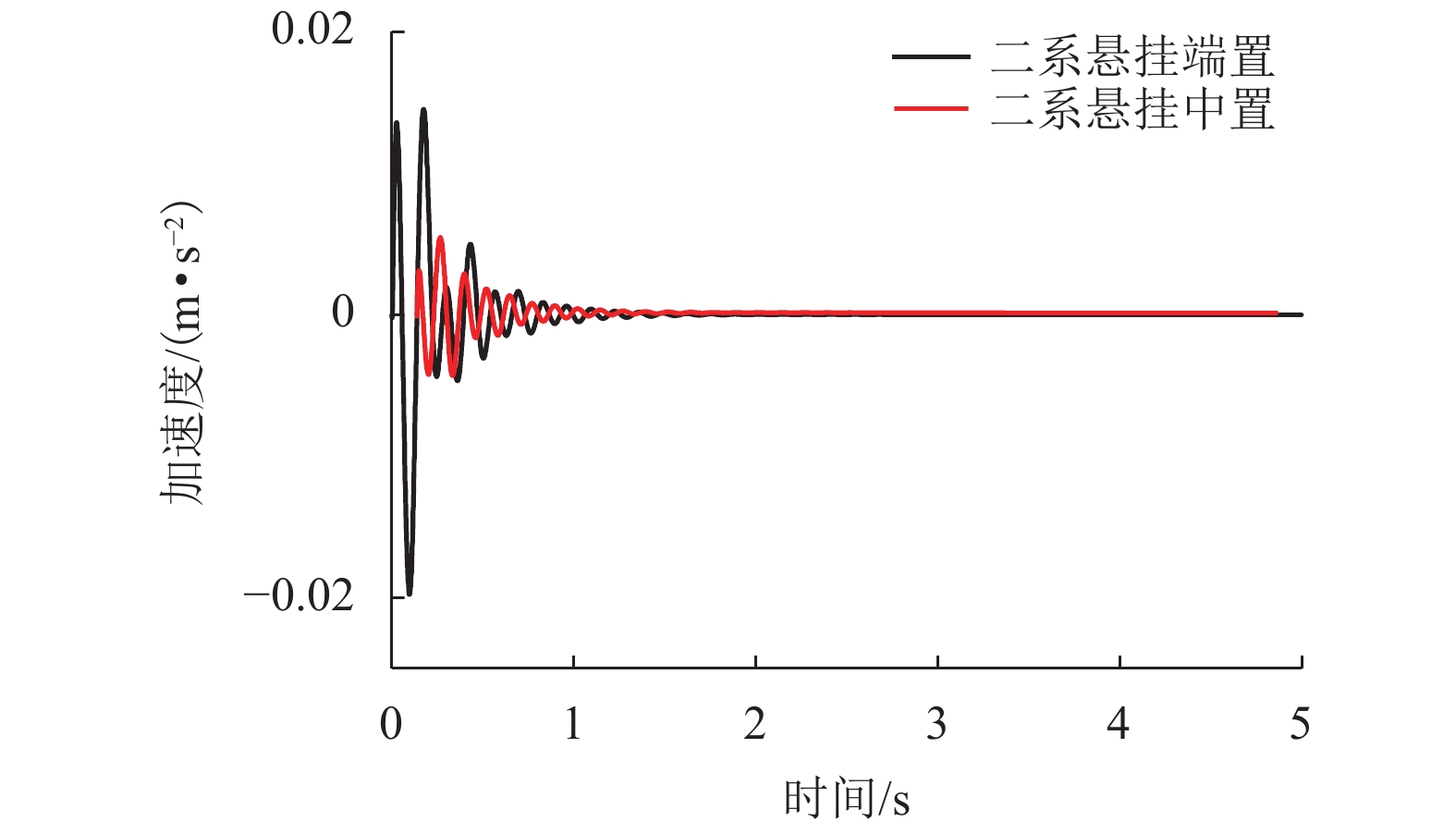
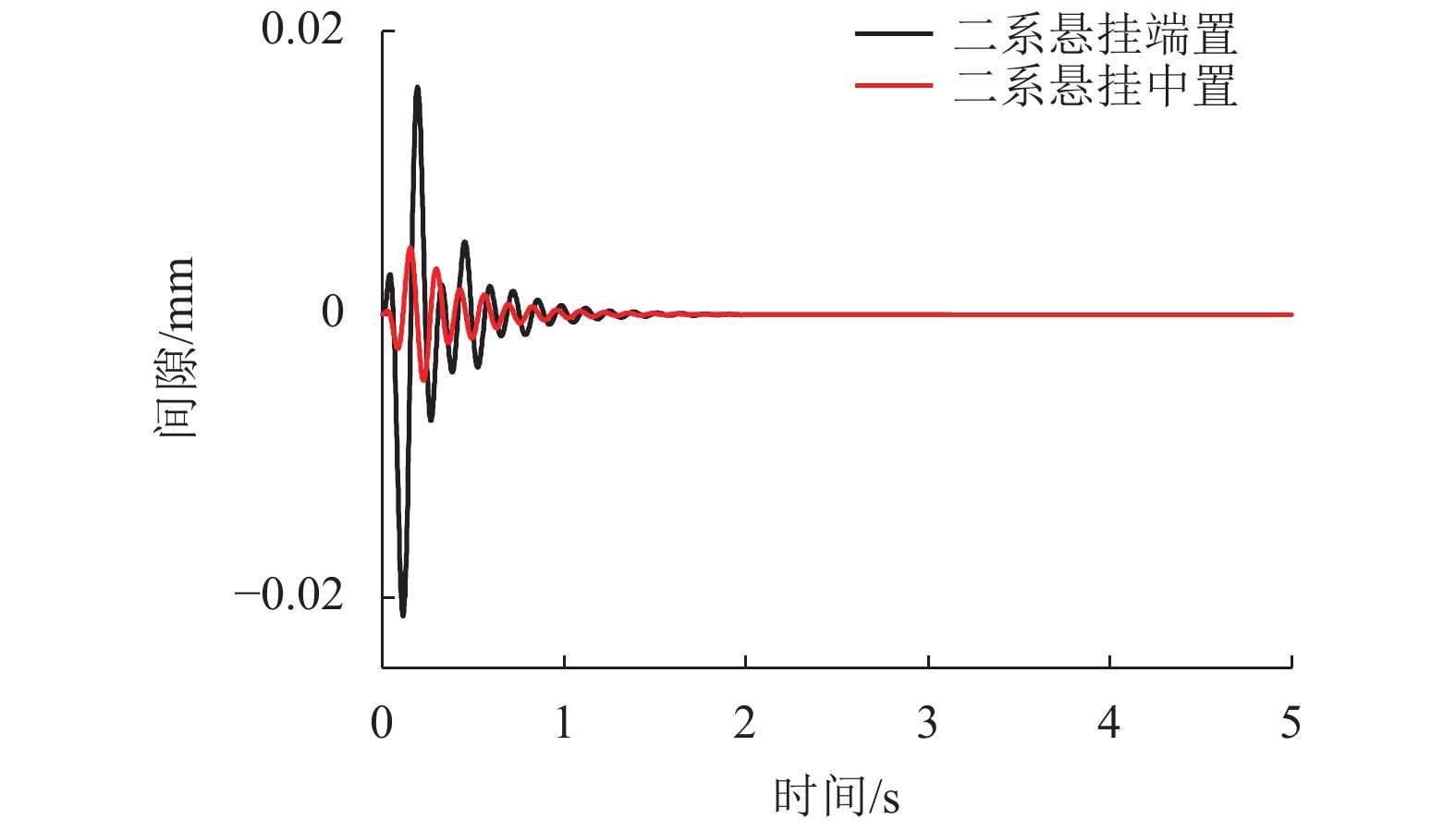
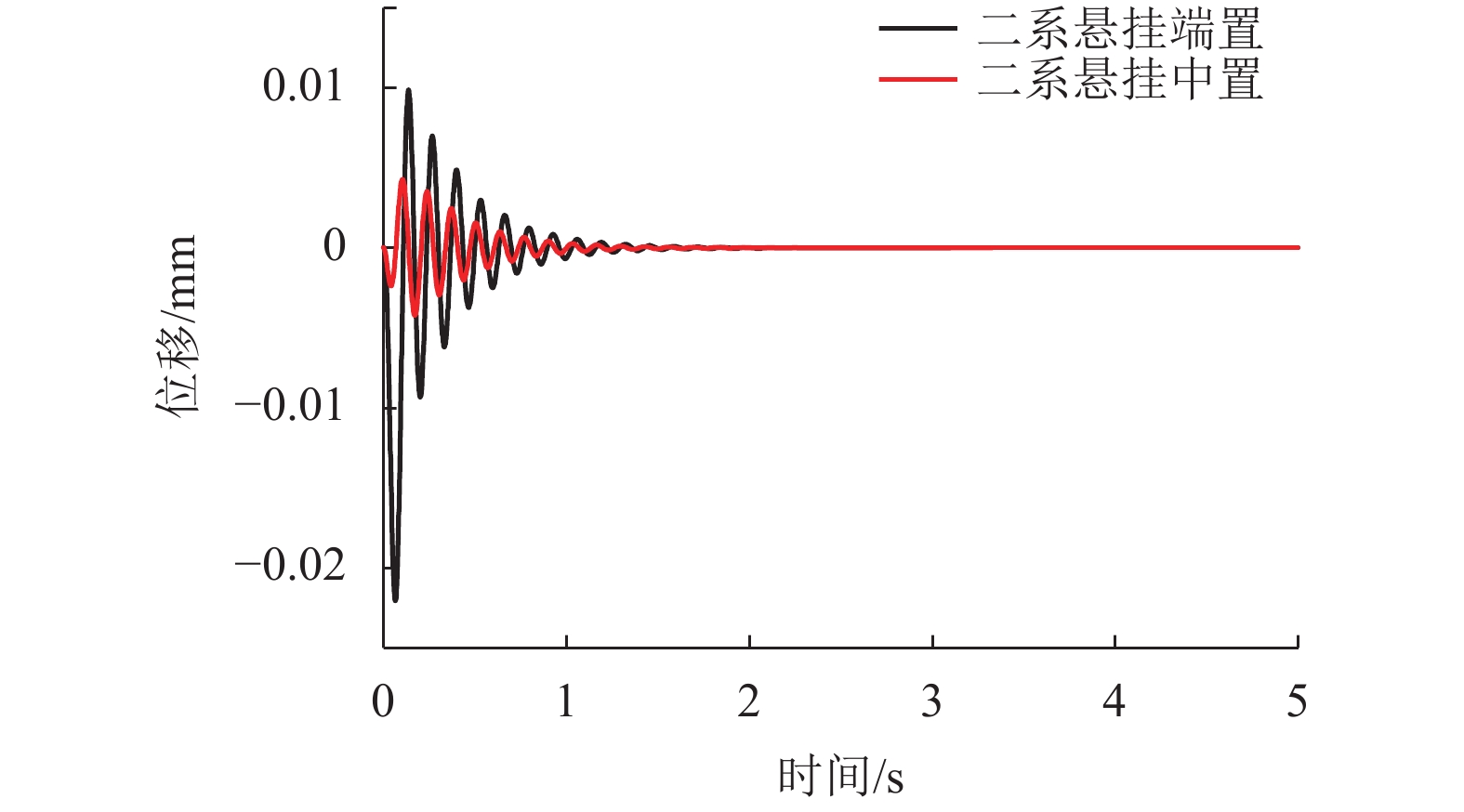
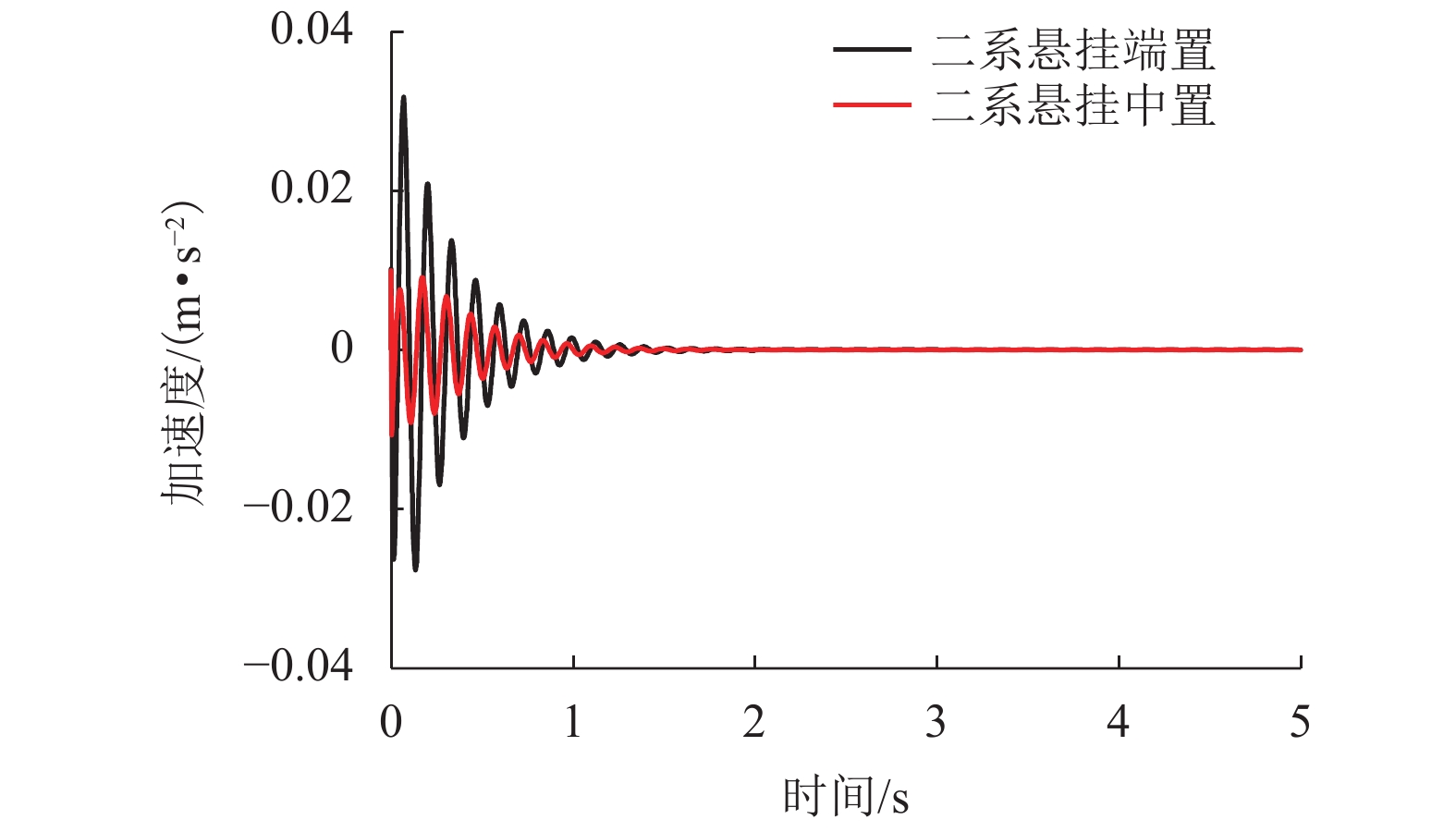
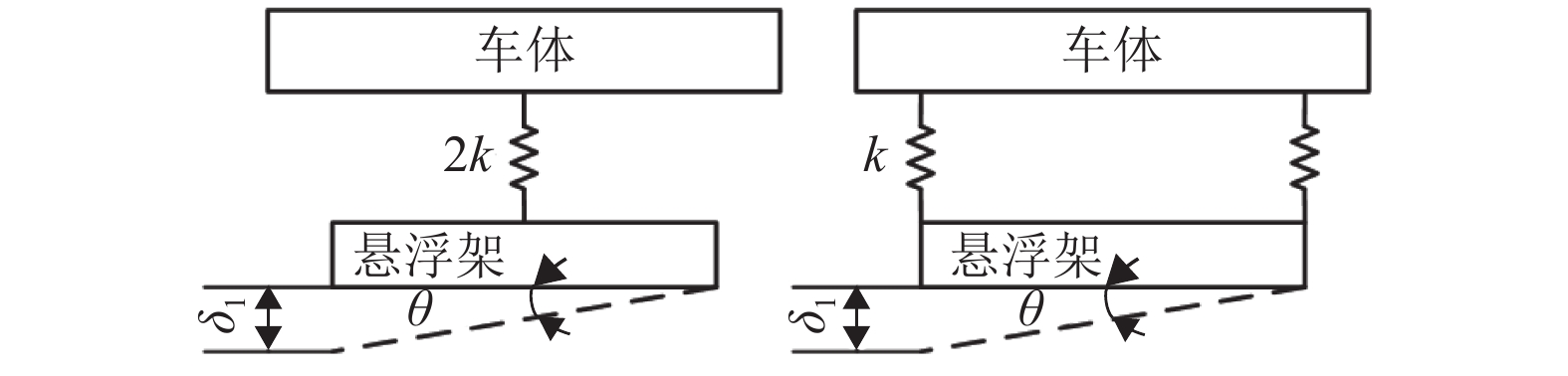
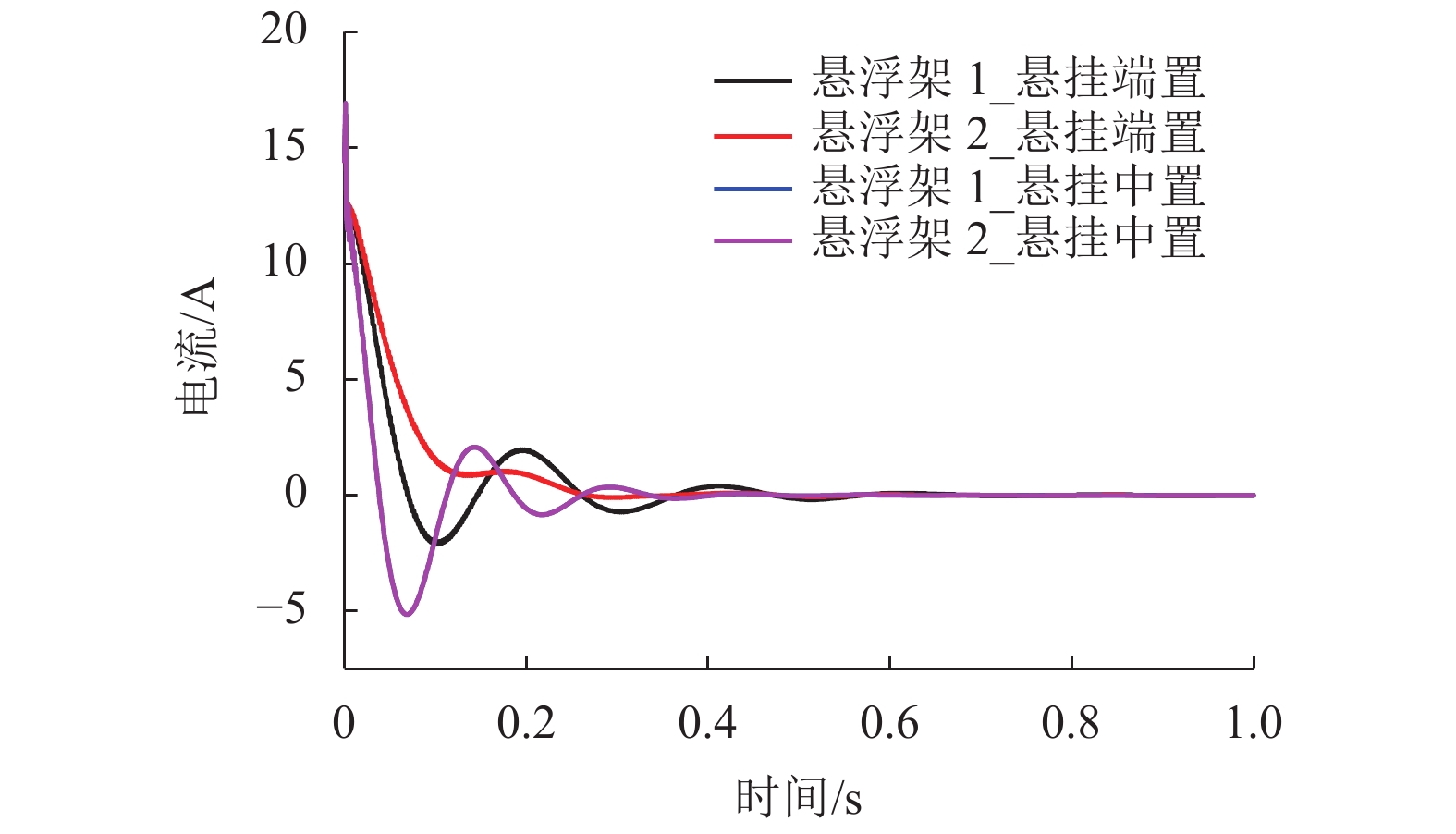
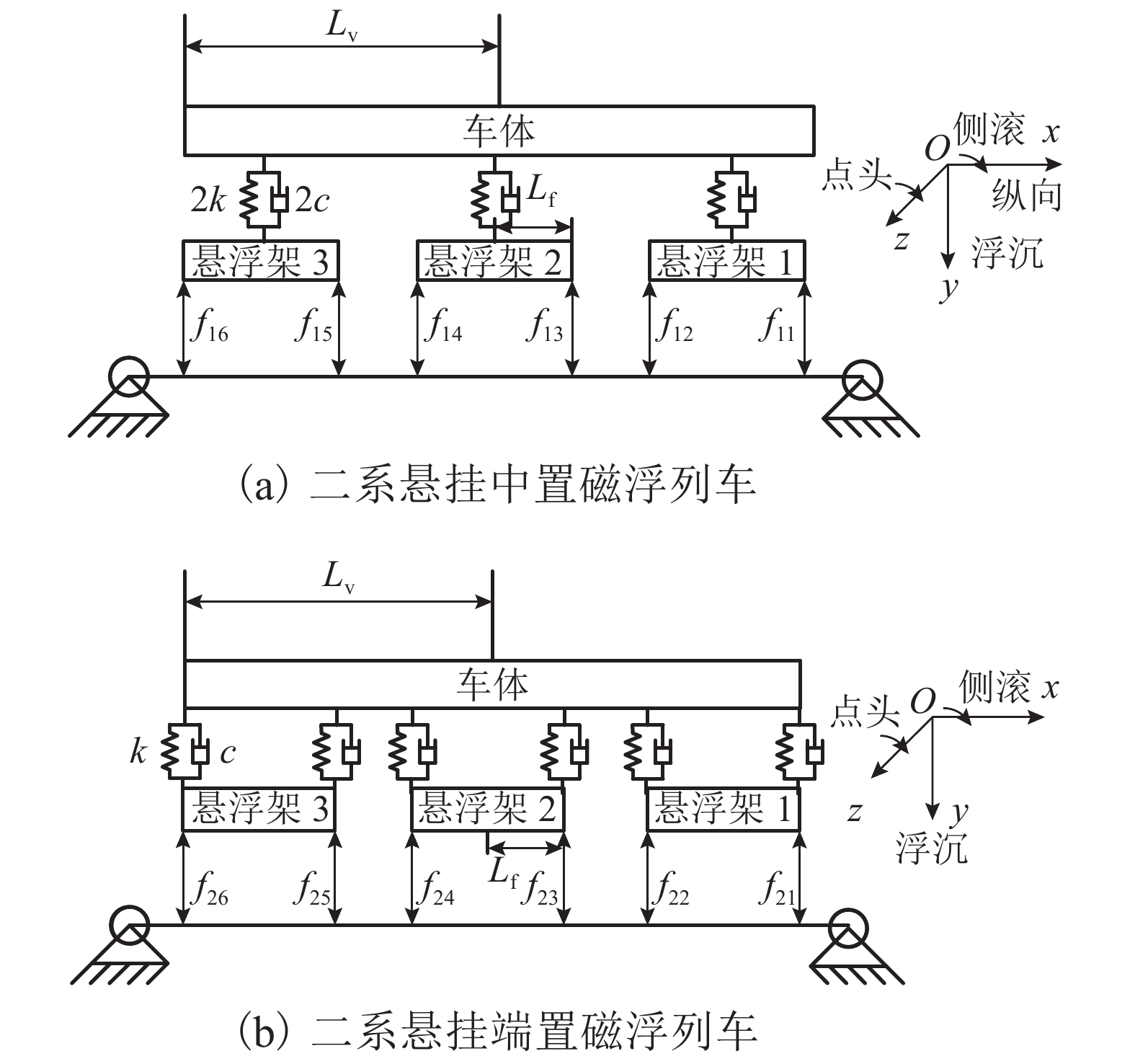
摘要: 为研究二系悬挂中置与端置的两种三悬浮架低速磁浮列车的车轨耦合振动特性,依据牛顿第二定律建立了其垂向车轨耦合动力学模型. 首先通过动力学方程分别分析了两种磁浮列车车体和悬浮架之间的耦合关系,然后研究了两种磁浮列车悬浮架均存在0.09° 的初始角位移时的动力学特性,最后研究了两种磁浮列车中二系悬挂对悬浮架作功的差异. 研究结果表明:与二系悬挂端置的磁浮列车相比,二系悬挂中置的磁浮列车,车体与悬浮架之间的耦合关系更少;当两种磁浮列车悬浮架均存在0.09° 的初始角位移时,采用二系悬挂中置的磁浮列车与采用二系悬挂端置的磁浮列车相比,前者具有更小的车体位移、车体垂向振动加速度、轨道梁振动位移和悬浮间隙波动;以上4个参数前者最大值分别为0.005 mm、0.004 m/s2、0.004 mm和0.005 mm;而后者最大值分别为0.023 mm、0.02 m/s2、0.021 mm和0.02 mm;与二系悬挂端置的磁浮列车相比,二系悬挂中置的磁浮列车,其二系空气弹簧对悬浮架作功更小,仅为前者的50%.Abstract: In order to study the vehicle-guideway coupling vibration characteristics of the two kinds of low-speed maglev trains with three suspension frame and the second suspension installed in the end and middle of the suspension frame respectively, the vertical vehicle-guideway coupling vibration dynamic model was established according to Newton’s second law. Firstly, the coupling relationship between the vehicle body and the suspension frame of the two kinds of maglev trains was analyzed through the dynamic equation, then the dynamic characteristics of the two kinds of maglev trains were studied respectively when the initial angular displacement of 0.09 degrees was existed, and finally the difference of the work of the second suspension on the suspension frame of the two kinds of maglev trains was studied, respectively. The results show that compared with the maglev train with the secondary suspension installed at the end of the suspension frame, the maglev train with the secondary suspension installed at the middle of the suspension frame has less coupling between the vehicle body and the suspension frame. When there is an initial angular displacement of 0.09 degree in the suspension frames of the two kinds of maglev trains, the maglev train with the secondary suspension installed at the middle of the suspension frame has smaller vehicle body displacement, vertical vibration acceleration of the vehicle body, vibration displacement of the track beam and suspension gap fluctuation compared with the maglev train with the secondary suspension installed at the end of the suspension frame. The maximum value of vehicle body displacement, vertical vibration acceleration of the vehicle body, vibration displacement of the track beam and suspension gap fluctuation of the maglev train with the secondary suspension installed at the middle of the suspension frame is about 0.005 mm, 0.004 m/s2, 0.004 mm and 0.005 mm respectively, and the maglev train with the secondary suspension installed at the end of the suspension frame is about 0.023 mm, 0.02 m/s2, 0.021 mm and 0.02 mm respectively. Compared with the maglev train with the secondary suspension installed at the end of the suspension frame, the maglev train with the secondary suspension installed at the middle of the suspension frame has less work of the secondary air spring on the suspension frame, only 50% of the former.
-
表 1 系统参数
Table 1. System parameters
物理量 数值 物理量 数值 M/kg 11 800 k/(kN•m−1) 50 m1~m3/kg 1 800 l/m 24 Am/m2 0.021 c/(kN•s•m−1) 100 N 365 u0 1.256 × 10−6 EI(/N•m−1) 19.39 × 109 ρ/(kg•m−1) 2 200 -
THORNTON R D. Efficient and affordable maglev opportunities in the United States[J]. Proceedings of the IEEE, 2009, 97(11): 1901-1921. doi: 10.1109/JPROC.2009.2030251 刘耀宗,邓文熙,李杰. 磁浮列车悬浮架吊杆型防滚解耦机构研究[J]. 铁道学报,2014,36(3): 38-41.LIU Yaozong, DENG Wenxi, LI Jie. Study on anti-rolling and decoupling mechanism of maglev bogies[J]. Journal of the China Railway Society, 2014, 36(3): 38-41. 张耿,李杰,李金辉. 低速磁浮列车防侧滚吊杆运动学研究[J]. 铁道学报,2012,34(4): 28-33. doi: 10.3969/j.issn.1001-8360.2012.04.005ZHANG Geng, LI Jie, LI Jinhui. Kinematics study on anti-roll boom of low-speed maglev train[J]. Journal of the China Railway Society, 2012, 34(4): 28-33. doi: 10.3969/j.issn.1001-8360.2012.04.005 叶学艳,赵春发,翟婉明. 低速磁浮车辆动力学建模与导向机构仿真分析[J]. 交通运输工程学报,2007,7(3): 7-10.YE Xueyan, ZHAO Chunfa, ZHAI Wanming. Dynamics modeling of low-speed maglev vehicle system and simulation of its guidance mechanisms[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 7-10. LEE J S, KWO S D, KIM M Y, et al. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guide-way bridges[J]. Journal of Sound and Vibration, 2009, 3(28): 301-317. YAU J D. Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration, 2009, 3(21): 184-200. KONG E H, SONG J S, KANG B B. Dynamic response and robust control of coupled maglev vehicle and guideway system[J]. Journal of Sound and Vibration, 2011, 3(30): 6237-6253. 李金辉. EMS型磁浮列车-桥梁耦合振动控制技术研究[D]. 合肥: 国防科技大学, 2015. REN S, ROMEIGN A, KLAP K. Dynamic simulation of the maglev vehicle/guideway system[J]. Journal of Bridge Engineering, 2009, 15(3): 269-278. 赵春发. 磁悬浮车辆系统动力学研究[D]. 成都: 西南交通大学, 2004. ALBERT T E, OLESECZUK G. On the influence of structural flexible on feedback control system stability for EMS maglev vehicle[J]. Journal of Dynamic Systems Measurement and Control Transactions of the ASME, 2011, 133(5): 1-6. 陶兴. 中低速磁悬浮轨道梁关键设计参数研究[D]. 上海: 同济大学, 2008. 翟婉明,赵春发. 现代轨道交通工程科技前言与挑战[J]. 西南交通大学学报,2016,51(2): 210-226.ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 210-226. 刘耀宗,邓文熙,龚朴. 低速磁浮列车单悬浮架机电控制建模及动力学特性研究[J]. 铁道学报,2014,36(9): 39-43. doi: 10.3969/j.issn.1001-8360.2014.09.08LIU Yaozong, DENG Wenxi, GONG Pu. Dynamics-control modeling and analysis for bogie of low-speed maglev train[J]. Journal of the China Railway Society, 2014, 36(9): 39-43. doi: 10.3969/j.issn.1001-8360.2014.09.08 黎松奇,张昆仑. 基于悬浮控制算法的磁浮列车动力学仿真研究[J]. 系统仿真学报,2015,27(1): 179-184.LI Songqi, ZHANG Kunlun. Research of maglev train dynamics simulation based on levitation control algorithm[J]. Journal of System Simulation, 2015, 27(1): 179-184. WANG H, SHEN G, LI L. Study on the maglev vehicle-guideway coupling vibration system[J]. Journal of Rail and Rapid Transit, 2013, 229(5): 507-517. ZHOU D F, HANSEN C H. Review of coupled vibration problems in EMS maglev vehicle[J]. international Journal of Acoustics and Vibration, 2010, 15(1): 10-23. -




 下载:
下载: