Site Selection Method of Booster Substations by Integrating Fuzzy Analytic Hierarchy Process with 3D Geographic Information System
-
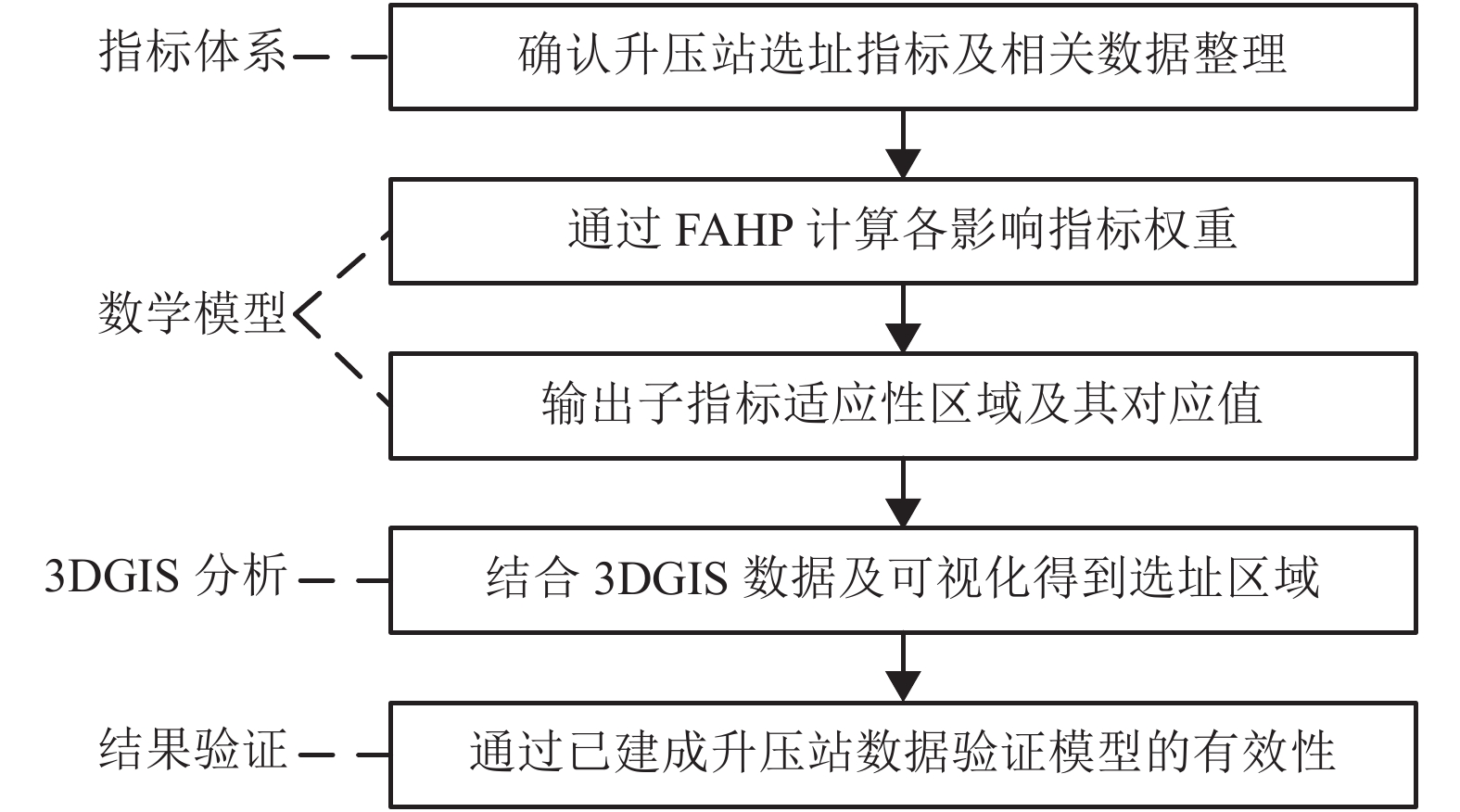
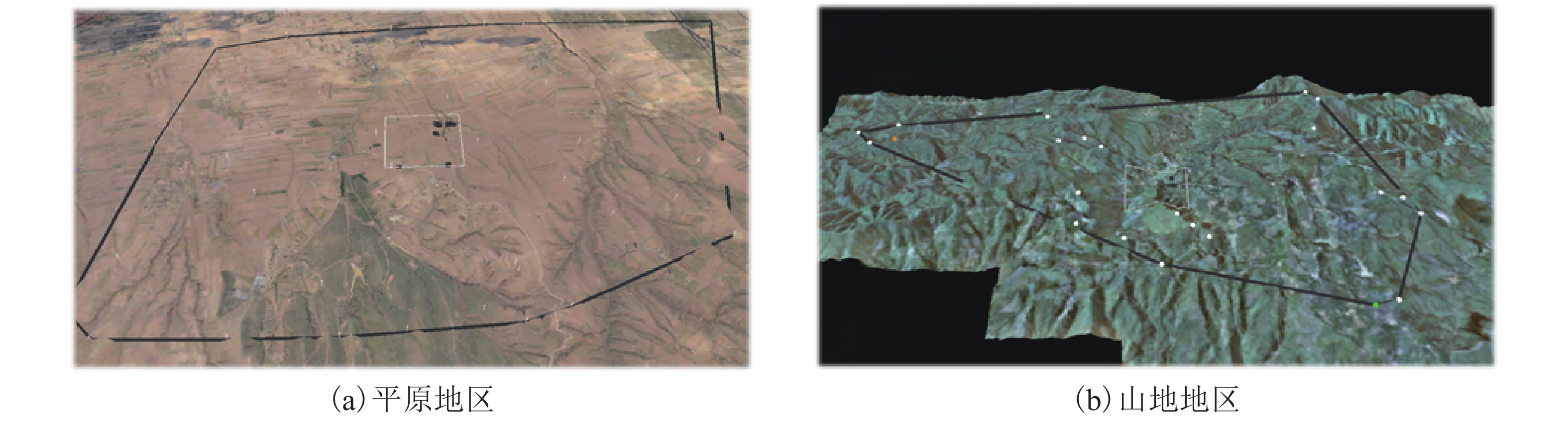
摘要: 为了克服传统风电场升压站选址方法的局限性，基于模糊层次分析选址综合评价方法，在三维GIS中对升压站的选址进行了可行性比对分析. 首先从施工成本、选址地形因子、灾害指标、临近资源及障碍区域五个类别的准则建立风电场升压站选址递阶层次结构；其次集成三维地理信息系统与模糊层次分析法构建一种新的选址评估模型；通过预设几何初选规则获取模型输入参数，最终解算模糊评价矩阵实现升压变电站自动选址. 通过对不同地形的已建成风电场升压变电站选址结果进行比对研究实验表明：以风机分布区域范围内的2 m分辨率的数字高程模型作为实验数据，系统解算时间均在10 min内. 平原最佳选址的站址评分为0.957 8优于已建成站址评分0.941 2；山地最佳选址的站址评分为0.743 5优于已建成站址0.706 8. 该方法有效地提升了选址的时间效率且具备较高的精准性及较好的适用性.Abstract: In order to overcome the limitations of the traditional selection method of booster substations on wind farms and realize an efficient and low-cost site selection of booster substations, feasibility analyses of candidate sites selected for booster substations are conducted in 3D geographic information system (GIS) based on fuzzy analytic hierarchy process. First, a hierarchical structure of the site selection of booster substations is defined from five aspects: construction cost, disaster index, location factor, obstacle area and adjacent resources. Then, a new siting evaluation model is established by integrating the fuzzy analytic hierarchy process with 3D GIS to realize the evaluation. The model input parameter are obtained by presetting the geometric primary selection rules, and finally the fuzzy evaluation matrix is solved to realize the automatic location selection of the boost substation. Comparing the experimental results of site selection of booster substations on wind farms built in different terrains shows that the calculation time is within 10 min using digital elevation model with 2 m resolution in the fan area. The optimal site score of plain is 0.957 8, which is better than that of the actual built site (0.941 2); the optimal site score of mountain is 0.743 5, which is also better than that of the actual built site (0.706 8). The results show that the method has high accuracy and universal applicability.
-
Key words:
- booster site selection /
- fuzzy analytic hierarchy process /
- GIS /
- onshore wind farms
-
近年来，区块链技术开始应用于金融[1]、运输[2]、能源[3-4]等领域. 2019年习近平总书记提出“要把区块链作为核心技术自主创新的主要突破口”之后，区块链平台建设速度加快. 但是，区块链平台也面临着链上交易事件的风险评价机制不成熟的问题，给区块链的应用推广带来了不便. 以金融领域为例，根据银行的2019年度报告，工行、农行、中行、建行、交行的不良贷款规模接近万亿元. 同时，中小企业融资难的问题仍然存在，很多优质项目难以获得资金支持. 例如，中欧班列中，很多企业要承担昂贵的运输成本和通关费用，却难以获得足够的资金支持. 区块链用纯数字方法构建信任关系，可以增强供应链金融的透明度、自动化和信任水平，提升企业融资的效率[5-6]. 然而，区块链无法确保源头信息的真实准确性，所以金融机构仍需进行融资前的风险评价. 而区块链平台公开透明的特点使得隐私数据存在着被泄露的风险，不利于金融机构获取多方信息，获得更加客观的评价结果[7-8]. 因此，建立一种更完善的风险评价机制，降低融资难度，为对外经贸合作提供支撑，具有重要意义.
通常情况下，金融机构需耗费时间和精力调研融资企业的经营情况，且该过程存在评价结果失真的风险. 除融资之外，在人事任用、社会管理等领域也存在着相似的情况. 因此，若能融合区块链上多个节点的评价结果，对风险进行综合评价，既能降低评价成本，也能使决策评价结果更客观. 然而，节点之间信息共享的过程存在数据泄露的风险，因此，风险评价方法还需考虑数据安全问题. 学者们对数据安全进行了长期的研究，同态加密算法是其中一项重要成果. 1978年，Rivest等[9]提出同态加密的思想和支持乘法计算的RSA （Rivest，Shamir and Adleman）方案. 随后，支持加法计算的同态加密方案[10]和全同态加密方案陆续被提出[11-12]. 2017年，Cheon等[13-14]提出了CKKS （Cheon-Kim-Kim-Song）加密方案，支持对浮点数的近似计算，在全同态加密算法中，效率较高，是最重要、最具前景的同态加密算法之一. 部分学者[15-18]已将同态加密算法应用到区块链系统中，以保障链上用户的数据隐私安全.
目前，风险评价方法已较成熟，广泛应用于公司经营[19-20]、企业融资[21-22]、社会管理[23]、工程管理[24-25]、事故预防[26-27]等领域. 但是，既有评价方法对区块链平台去中心化、去信任的特点考虑不足，并不适用. 为此，本文提出了一种结合多种评价方法与CKKS加密方案的集成风险评价模型. 区块链上各节点采用合适的模型进行风险评价；随后，利用公钥对各节点评价结果进行加密；之后，对密文评价结果进行同态运算，获得综合多方意见的评价结果；最后，利用私钥进行解密，获得明文综合评价结果. 该模型考虑了单节点评价结果的片面性和数据隐私问题，能为链上交易事件提供更加客观的风险评价结果.
1. 问题描述与模型构建思路
本文研究的是区块链平台建立之后，链上节点对交易事件风险评价过程中的数据失真和信息安全问题. 对于传统的风险评价模型，数据对象垂直分布的情况下，各节点需花费人力和时间调研交易对象的背景情况及交易历史等. 同时在沟通机制缺失的情况下，仅凭自身掌握的数据信息，也容易造成评价结果的失真. 本文研究在数据对象垂直分布情况下考虑信息安全问题，并且集成模型指标固定达到水平分布已知条件，将多节点对交易事件的风险评价结果在加密状态下融合，对交易事件的风险进行客观的综合评价，实现评价结果的安全共享. 现有评价模型与基于CKKS加密方案的区块链平台的集成风险评价模型运作模式如图1所示.
如图1所示，银行A从分布式数据库中获取与融资企业的交易记录信息，并提取评价指标数据，利用风险评价模型对提取出的评价指标数据进行计算，得到风险评价结果A. 之后，通过CKKS加密计算，得到综合评价结果，风险评价流程如图2所示.
2. 模型构建
2.1 单节点风险评价
区块链上各节点可以采用不同评价方法对交易事件的风险进行评价，假设各节点通过三角模糊函数对指标赋权后，利用不同评价模型进行风险评价. 设某一节点的专家数量为
K ，第k 个专家的权重为pk ，依据专家的履历确定. 专家k 给出评价指标i 相对于评价指标j 的重要度三角模糊数为skij=(lkij,Mkij,ukij)， (1) 式中：
k=1,2,⋯,K ；i,j=1,2,⋯,a ；ukij 、Mkij 、lkij 分别为评价指标i 相对于评价指标j 的重要度的上界、中指和下界.根据0.1～0.9标度[28]（如表1所示），确定
skij 的值. 则评价指标i 相对于评价指标j 的重要度三角模糊数为表 1 0.1～0.9标度的含义Table 1. Meaning of scale 0.1～0.9标度 对应的三角模糊数 含义 0.1 （0.1，0.1，0.2） 指标 i 相对于指标 j 极端不重要 0.3 （0.2，0.3，0.4） 指标 i 相对于指标 j 明显不重要 0.5 （0.4，0.5，0.6） 指标 i 与指标 j 同样重要 0.7 （0.6，0.7，0.8） 指标 i 相对于指标 j 明显重要 0.9 （0.8，0.9，0.9） 指标 i 相对于指标 j 极端重要 sij=(lij,Mij,uij)=(K∑k=1pklkij,K∑k=1pkMkij,K∑k=1pkukij). (2) 利用三角模糊数的期望值公式将三角模糊数转化为清晰值，期望值为
E(sij)=[(1−μ)lij+Mij+μuij]/2， (3) 式中：
μ 为上界倾向系数，取决于专家对指标i、j 的态度，μ∈(0,1) ，μ 值越大，表明专家更倾向于sij 取上界，以提高指标i 相对于指标j 的重要性，反之，则表明专家更倾向于sij 取下界，以降低指标i 相对于指标j 的重要性，假设专家对sij 取上、下界保持中立，取μ=0.5 .通过转化，将三角模糊评价指标矩阵
S=(sij)a×a 转化为模糊互补判断矩阵SE=(E(sij))a×a .计算评价指标三角模糊权重向量为
W=(w1,w2,⋯,wi,⋯,wa)， (4) wi=(a∑j=1lija∑i=1a∑j=1lij,a∑j=1Mija∑i=1a∑j=1Mij,a∑j=1uija∑i=1a∑j=1uij). (5) 利用三角模糊数期望值公式计算评价指标的最终权重向量为
V=(v1,v2,⋯,vi,⋯,va), (6) 式中：
vi=a∑j=1lij2a∑i=1a∑j=1lij+a∑j=1Mija∑i=1a∑j=1Mij+a∑j=1uij2a∑i=1a∑j=1uij .对结果进行一致性检验，若不满足一致性条件，需要重新建立评价矩阵. 若符合一致性检验要求，即根据指标权重，对交易事件的风险进行评价.
设该节点从分布式数据库中获取样本集T，假设有
n 个交易事件需要进行评价，则该节点评价结果向量为C=X(T,W)=（c1,c2,⋯,cf,⋯,cn）， (7) 式中：
X 为采用的评价方法，可以是决策树、SVM （support vector machine）模型、KNN （K-nearest neighbor）模型等；X(T,W) 表示该节点利用评价方法X ，结合样本集T和模糊权重向量W 对一系列交易事件进行风险评价；cf 为节点对交易事件f 的风险评价结果，f=1,2,⋯,n .假设链上有
d 个相关节点能够对交易事件进行评价，则交易事件f 的风险评级结果向量为Cf=(cf1,cf2,⋯,cft,⋯,cfd)， (8) 式中：
cft 为节点t对交易事件f的评价结果，t=1,2,⋯,d .2.2 评价结果加密
基于LWE （learning with error）问题生成公私钥对
(pk,sk) 和计算密钥ek ，将各节点的评价节点结果转化为密文，公式为H=(h1,h2,⋯,hd)， (9) ht=(cft,0)+pTkr， (10) 式中：
r 为随机均匀选取的τ 维向量，τ 为生成公私钥对和计算密钥的过程中选取的整数参数，r=(r1,r2,⋯,ro⋯,rτ) ，ro∈{0,1} .对获得的密文进行同态运算，假设所有节点评价结果的权重相同，则
h=h1+d∑t=2ht(mod (11) 式中：
p 、l1、q0均为生成密钥LWE （learning with error）问题中的整数参数，其中，p 为质数.对获得的加密结果进行重缩放，缩放之后的密文为
{{\boldsymbol{h}}_{\rm{z}}} = \left[ {\frac{{{p^{{l_2}}}}}{{{p^{{l_1}}}}}{\boldsymbol{h}}} \right] \text{，} (12) 式中：
\left[ x \right] 为距离x 最近的整数；l2为生成密钥的LWE问题中的整数参数.2.3 密文解码
利用密文向量hz与私钥
{\boldsymbol{s}_{\rm{k}}} 进行解密，输出解密后的明文评价结果为c = {\boldsymbol{h}}_{\rm{z}}{\boldsymbol{s}}_{\rm{k}}\bmod {q_l}. (13) 3. 案例分析
本文选取5 000条2019年11月份的中欧班列企业的海关运单数据，提取出企业规模、销售利润率、速动比率、存货周转率、资产负债率、以往履约情况、核心企业对外担保情况、供应链关系强度、赊销周期、产品可替代性、权益乘数、质押物变现能力、总资产周转率等15个评价指标数据[29]. 通过随机抽样，得到45 00条样本数据，采用回归算法训练得到风险评价水平分布刻画模型. 利用回归得到的模型对剩余的500条数据进行计算，得到单模型融资风险评价结果. 随后，对各模型的评价结果分别运用CKKS方案进行同态加密计算，得到密文综合评价结果，经过解密后得到的综合评价结果分别与组合条件下明文计算结果进行对比，计算误差率. 最后，选取KNN （K-nearest neighbor）模型、随机森林模型的评价结果，分别利用CKKS和BFV （Brakerski-Fan-vercauteren）两种经典的全同态加密方案进行同态加密计算，对比综合评价结果的误差率.
3.1 定性指标赋值
梳理企业融资风险评价指标体系中的定性指标，包括交易履约情况、核心企业对外担保情况、供应链关系强度，并对其进行了赋值，所有指标的评分取值为0～10分，定性指标的评分标准见表2.
表 2 定性指标量化评分表Table 2. Quantitative scoring of qualitative indices定性指标 评价指标分档/分 [8, 10] [4, 8) [0, 4) 交易履约情况（X8） 好 中 差 核心企业的对外担保状况（X9） 几乎无 少量 较多 供应链关系的强度（X10） 高 中 低 3.2 指标赋权
分别请5组专家对指标进行打分，每组专家5人，专家的权重三角模糊数如表3所示. 表中：
{B_m} 为第m 个专家组，m = 1,2, \cdots ,5 ；{w_m} 为通过计算得到的每个专家组的权重三角模糊数.表 3 三角模糊打分表Table 3. Triangular fuzzy scoring resultsk B1 B2 B3 B4 B5 1 （0.1，0.2，0.3） （0，0.1，0.3） （0.1，0.3，0.5） （0.5，0.2，0.3） （0.6，0.8，0.9） 2 （0.2，0.3，0.3） （0.4，0.7，0.8） （0.3，0.2，0.2） （0.7，0.8，0.9） （0.1，0.2，0.4） 3 （0.4，0.5，0.3） （0.1，0.3，0.5） （04，0.5，0.7） （0.1，0.4，0.6） （0.1，0.6，0.7） 4 （0.5，0.7，0.3） （0.3，0.6，0.9） （0.4，0.6，0.8） （0.3，0.5，0.7） （0.1，0.3，0.4） 5 （0.6，0.4，0.3） （0.2，0.4，0.5） （0.5，0.8，0.9） （0.5，0.6，0.8） （0.2，0.4，0.5） wm （0.15， 0.21，0.32） （0.13，0.22，0.35） （0.11，0.18，0.28） （0.18，0.25，0.39） （0.09，0.14，0.24） 将三角模糊数转化为清晰值，通过量纲归一化处理，构造加权判断矩阵计算相对贴近度，排序后得到最终权重如表4所示.
表 4 指标赋权结果Table 4. Index weighting results指标名称 变量 权重 指标名称 变量 权重 企业规模 X1 0.0246 核心企业对外担保情况 X9 0.1512 销售利润率 X2 0.0833 供应链关系强度 X10 0.0014 速动比率 X3 0.0255 赊销周期 X11 0.1146 存货周转率 X4 0.0117 产品可替代性 X12 0.0884 资产负债率 X5 0.0140 权益乘数 X13 0.0176 交易量 X6 0.0748 质押物变现能力 X14 0.0799 交易金额 X7 0.0363 总资产周转率 X15 0.1329 交易履约情况 X8 0.1437 由表可知：核心企业对外担保情况、总资产周转率、以往履约情况等3个指标的权重较大，说明这3个指标对企业融资风险的影响较大，从财务理论角度是合适的，核心企业对外担保情况、以往履约情况的权重较大，与实际情况契合.
3.3 企业融资风险评价模型
分别选取目前最为常见的决策树模型、Adaboost模型、Bagging模型、ExtraTree极端随机数模型、GBDT （gradient boosting regression trees）模型、KNN模型、随机森林模型、SVM （support vector machine）模型等评价模型对企业融资风险进行评价，调用python sklearn库中算法执行该过程. 从5 000个样本中随机抽取4 500个训练样本集和500个测试样本集，用于回归模型的训练和测试，测试结果如图3所示.
从图中可以看出：不同模型的预测效果良好，预测分类结果基本与真实情况一致，所有模型预测准确率均超过95%，能够对企业的融资风险进行准确的评价.
3.4 同态加密结果
利用CKKS全同态加密方案对基于不同模型评价后的结果进行不同组合后进行加密，采用pyseal基于微软的seal修改的python版本执行该过程，并将评价结果和直接进行明文加权平均的综合评价结果进行了对比，误差率分布如图4和图5所示.
图 4 CKKS加密机制基于不同评价模型结果的误差率结果Figure 4. Comparison of error rates of encrypted results by CKKS scheme based on different assessment models从图4可知：所有评价结果之间误差率均小于1.00 × 10−9，仅有个别异常数据的加密误差率大于3.00 × 10−10，结合图5中的加密结果的误差率箱线图结果可知，所有组合方案得到的结果的正态分布均呈现偏左分布，均值均小于1 × 10−10. 图4和图5显示，CKKS全同态加密算法的组合方案适用于目前常用的评价模型，对企业融资风险评价结果影响较小. 因而，基于CKKS全同态加密方案的融资风险评价机制普适性高，可以用于实际的评价中.
分别利用CKKS全同态加密方案和BFV全同态加密方案对KNN模型、随机森林模型的评价结果进行加密计算，调用pyseal基于微软的seal修改的python版本执行该过程，并将两种经过同态加密后的评价结果和直接进行明文加权平均的综合评价结果进行了对比，结果如表5和图6、7所示.
表 5 CKKS方案和BFV方案同态加密结果及误差率Table 5. Homomorphic encryption results and error rates of CKKS and BFV schemes编号 KNN 模型 +
随机森林模型CKKS 全同态加密
评价结果CKKS 方案
误差率BFV 全同态加密
评价结果BFV 方案
误差率1 48.6117737805 48.6117737789 3.34 × 10−11 48.6094744655 4.73 × 10−5 2 38.4173642857 38.4173642916 1.53 × 10−10 38.3934853887 6.22 × 10−4 3 66.6095043478 66.6095043506 4.09 × 10−11 66.6003539367 1.37 × 10−4 4 40.7277690992 40.7277690999 1.66 × 10−11 40.7098999864 4.39 × 10−4 5 36.0318162194 36.0318162184 2.58 × 10−11 36.0170565909 4.10 × 10−4 6 39.2235467290 39.2235467305 3.98 × 10−11 39.1413627605 2.10 × 10−3 7 45.2551751634 45.2551751619 3.20 × 10−11 45.2384881180 3.69 × 10−4 8 85.5722701987 85.5722701993 7.54 × 10−12 85.5655826327 7.82 × 10−5 9 59.7378161329 59.7378161324 8.14 × 10−12 59.7254652272 2.07 × 10−4 10 49.4582034252 49.4582034281 5.74 × 10−11 49.4489389677 1.87 × 10−4 11 50.6262683040 50.6262683016 4.62 × 10−11 50.6237741777 4.93 × 10−5 12 59.0855247219 59.0855247221 4.30 × 10−12 59.0248410817 1.03 × 10−3 13 50.8218075188 50.8218075195 1.39 × 10−11 50.8154754434 1.25 × 10−4 14 51.5208750000 51.5208750014 2.77 × 10−11 51.5204698244 7.86 × 10−6 15 40.6476813842 40.6476813860 4.43 × 10−11 40.6440481786 8.94 × 10−5 16 41.8885428177 41.8885428182 1.16 × 10−11 41.8792671831 2.21 × 10−4 17 37.0070685441 37.0070685404 1.01 × 10−10 36.9933666065 3.70 × 10−4 18 66.6304171240 66.6304171283 6.33 × 10−11 66.6209557226 1.42 × 10−4 19 14.8742302481 14.8742302472 6.03 × 10−11 14.8490706101 1.69 × 10−3 20 38.9383642857 38.9383642857 3.34 × 10−11 38.8372207385 2.60 × 10−5 
图 6 CKKS方案评价结果误差率分布Figure 6. Error rate distribution of evaluation results by CKKS scheme
图 7 BFV方案评价结果误差率分布Figure 7. Error rate distribution of evaluation results by BFV scheme从表5和图7可以看出，基于BFV方案的评价结果的误差率几乎都大于1.00 × 10−6；而从表5和图6可以看出，基于CKKS方案的评价结果的误差率均小于3.00 × 10−10，仅有个别异常数据的加密误差率大于1.50 × 10−11，误差率更小. 因此，基于CKKS方案的融资风险评价机制对企业融资风险评价结果影响较小，评价结果更为准确.
4. 结 论
本文提出了一种结合评价方法与CKKS加密方案的集成风险评价模型，用于解决评价过程中存在的隐私数据泄露的问题. 研究了在数据对象垂直分布情况下，区块链各节点如何在保证信息安全的前提下，结合其他节点所掌握的信息，实现对区块链上单个交易事件的风险进行相对客观的评价. 考虑信息安全问题，集成评价模型将区块链中多节点对交易事件的风险评价结果在加密状态下融合，对交易事件的风险进行客观的综合评价，能有效解决评价资源共享和信息泄露问题. 通过对中欧班列企业的案例研究，验证了模型的准确性、有效性和普适性. 随着中欧班列区块链基础设施的逐步建成，利用该模型可以更好地对企业的融资风险进行评估，从而推动中欧班列的高质量发展.
-
表 1 风电场升压站选址评价指标体系
Table 1. System of site evaluation indexes for booster station
一级准则层（F层） 次级指标层（S层） 施工工程量成本准则（F1） 升压站填挖工程量（S1） 集电线路成本（S2） 进站道路工程量（S3） 灾害指标准则（F2） 百年一遇洪水水位（S4） 地震基本烈度（S5） 选址地质沉降（S6） 选址地形因子准则（F3） 局部皱褶度（S7） 局部凹凸性质（S8） 局部高差极值（S9） 障碍区域准则（F4） 农田用地范围（S10） 特殊用地范围（S11） 生活用地范围（S12） 极端地形区域范围（S13） 临近资源准则（F5） 送电距离（S14） 出线方向距离（S15） 水资源区域（S16） 
下载: 导出CSV
表 2 0.1～0.9标度法及说明
Table 2. The 0.1 – 0.9 scale method and its specifications
标度值 定义 说明 0.5 同等权重 指标相比同等重要 0.6 权重稍高 该指标稍加重要于另一指标 0.7 权重较高 该指标明显重要于另一指标 0.8 权重特高 该指标较另一指标重要的多 0.9 权重极高 该指标较另一指标极端重要 0.1，0.2 反比较 若该指标 si 与指标 sj 对比得到
标度值 rij，0.3，0.4 则指标 sj 与指标 si 对比得到的
标度值 1 – rij
下载: 导出CSV
表 3 实验粗选参数
Table 3. Parameters of rough site selection
项目 升压站规格 集电出电规划 区域性质 施工工程量 障碍区域 性质 50 m × 50 m 最短距离 筛除谷底地形 减少挖方规避填方 与障碍区域交集为空
下载: 导出CSV
表 4 备选站址次级指标评价矩阵因素
Table 4. Evaluation matrix of candidate sites
站址 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 S14 S15 S16 A 0.0 0.0 0.0 1.0 0.0 1.0 0.5 1.0 0.7 1.0 1.0 1.0 1.0 0.7 0.7 0.7 B 0.6 0.7 0.5 1.0 0.9 0.9 0.5 0.0 0.6 1.0 1.0 1.0 1.0 0.5 0.3 0.4 C 0.4 0.5 0.5 1.0 0.9 1.0 0.6 1.0 0.7 1.0 1.0 1.0 1.0 0.0 0.0 0.0 D 1.0 0.6 0.5 0.0 0.9 0.0 0.0 1.0 0.0 1.0 1.0 1.0 1.0 1.0 0.9 0.8 E 0.8 1.0 1.0 1.0 1.0 0.9 1.0 0.5 1.0 1.0 1.0 1.0 1.0 0.9 1.0 1.0
下载: 导出CSV
表 5 评分值
Table 5. Score value
地形
种类站址 已有
站址A B C D E 平原 0.551 8 0.837 1 0.600 5 0.612 3 0.957 8 0.941 2 山地 0.625 4 0.743 8 0.743 5 0.711 1 0.693 9 0.706 8
下载: 导出CSV
-
游欣佩,马平. 基于模糊层次分析法的风电场优化选址方法研究[J]. 电力科学与工程,2012,28(12): 45-49.YOU Xinpei, MA Ping. Wind farm optimal location based on fuzzy analytic hierarchy process[J]. Electric Power Science & Engineering, 2012, 28(12): 45-49. 刘海燕,庞小平. 利用GIS和模糊层次分析法的南极考察站选址研究[J]. 武汉大学学报(信息科学版),2015,40(2): 249-252.LIU Haiyan, PANG Xiaoping. Selection of antarctic research stations based on GIS and fuzzy AHP[J]. Geomatics & Information Science of Wuhan University, 2015, 40(2): 249-252. 王倩. 寒冷山区风电场升压站选址[J]. 科技创新导报,2017(35): 17-18. Helimax Energy Inc. Analysis of wind power potential in Ontario[R]. Ontario: Technical Report/OPA, 2005 SUSAN K. WILLIAMS, T AC, GRANT B, et al. Arizona wind energy assesment[R]. [S.L.]: Arizona Technical Report/Northern Arizona University, 2007 KLINE D, HEIMILLER D, COWLIN S. GIS method for developing wind supply curves[R]. Office of Scientific & Technical Information Technical Report, 2008 BEATA S S, JOACHIM V. GIS-based approach for the evaluation of wind energy potential:a case study for the Kujawsko-Pomorskie Voivodeship[J]. Renewable and Sustainable Energy Reviews, 2011(15): 1696-1707. JASON R J. Multicriteria GIS modeling of wind and olar farms in Colorado[J]. Renewable Energy, 2010, 35(10): 2228-2234. doi: 10.1016/j.renene.2010.03.014 ROB V H, VASILIS F. GIS-based wind farm site selection using spatial multi-criteria analysis (SMCA):evaluating the case for New York State[J]. Renewable and Sustainable Energy Reviews, 2011, 15(7): 3332-3340. doi: 10.1016/j.rser.2011.04.010 MARI R, BOTTAI L, BUSILLO C, et al. A GIS-based interactive web decision support system for planning wind farms in Tuscany (Italy)[J]. Renewable Energy, 2011, 36(2): 754-763. doi: 10.1016/j.renene.2010.07.005 NAZLI Y A, ELCIN K, SEBNEM D. GIS-based environmental assessment of wind energy systems for spatial planning:a case study from western turkey[J]. Renewable and Sustainable Energy Reviews, 2010, 14(1): 364-373. doi: 10.1016/j.rser.2009.07.023 PILAR C, TOMÁS A. Wind farms:GIS-based visual impact assessment and visualization tools[J]. Cartography and Geographic Information Science, 2013, 40(3): 229-237. doi: 10.1080/15230406.2013.809231 CAVAZZI S, DUTTON A G. An offshore wind energy geographic information system (OWE-GIS) for assessment of the UK’s offshore wind energy potential[J]. Renewable Energy, 2016, 87: 212-228. doi: 10.1016/j.renene.2015.09.021 ADDISU D M, PECE V G. A web-based participatory GIS (PGIS) for offshore wind farm suitability within Lake Erie,Ohio[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 162-177. doi: 10.1016/j.rser.2014.08.030 刘学峰,王健. 试议陆上风电场升压站选址[J]. 中国勘察设计,2016(3): 92-95. doi: 10.3969/j.issn.1006-9607.2016.03.001 岑晋峰. 浅析风力发电场升压站站址选择[J]. 中国勘察设计,2013(1): 80-82. doi: 10.3969/j.issn.1006-9607.2013.01.004 乔兵. 风电场升压站选址应注意的问题[J]. 内蒙古石油化工,2009(10): 89-89. 卢华兴,刘学军,汤国安. 地形复杂度的多因子综合评价方法[J]. 山地学报,2012,30(5): 616-621.LU Huaxing, LIU Xuejun, TANG Guoan. Terrain complexity assessment based on multivariate analysis[J]. Journal of Mountain Science, 2012, 30(5): 616-621. 朱庆. 三维GIS及其在智慧城市中的应用[J]. 地球信息科学学报,2014,16(2): 151-157.ZHU Qing. Full three-dimensional GIS and its key roles in smart city[J]. Journal of Geo-Information Science, 2014, 16(2): 151-157. 朱庆. 3维GIS技术进展[J]. 地理信息世界,2011,9(2): 25-27. doi: 10.3969/j.issn.1672-1586.2011.02.006ZHU Qing. Technical progress of three dimensional GIS[J]. Geomatics World, 2011, 9(2): 25-27. doi: 10.3969/j.issn.1672-1586.2011.02.006 郭金玉,张忠彬,孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报,2008,47(1): 148-153.GUO Jinyu, ZHANG Zhongbin, SUN Qingyun, et al. Study and applications of analytic hierarchy process[J]. China Safety Science Journal, 2008, 47(1): 148-153. CHAO K, DANG F, JIA Y. Application of AHP in the selection of our country wind farm’s location[C]//International Conference on Management and Service Science. Wuhan: IEEE, 2011: 1-4 ZHAO Z, HUANG W. Multi-objective decision-making on wind power projects based on AHP method[C]//International Conference on Computer Distributed Control & Intelligent Environmental Monitoring. Changsha: IEEE, 2011: 242-245 姬东朝,宋笔锋,喻天翔. 模糊层次分析法及其在设计方案选优中的应用[J]. 系统工程与电子技术,2006,28(11): 1692-1552. doi: 10.3321/j.issn:1001-506X.2006.11.022JI Dongchao, SONG Bifeng, YU Tianxiang. FAHP and its application in the selection of design scheme[J]. Systems Engineering & Electronics, 2006, 28(11): 1692-1552. doi: 10.3321/j.issn:1001-506X.2006.11.022 张吉军. 模糊层次分析法(FAHP)[J]. 模糊系统与数学,2000,14(2): 80-88. doi: 10.3969/j.issn.1001-7402.2000.02.016ZHANG Jijun. Fuzzy analytical hierarchy process[J]. Fuzzy Systems & Mathematics, 2000, 14(2): 80-88. doi: 10.3969/j.issn.1001-7402.2000.02.016 陶余会,刘家才,张吉军. 如何构造模糊层次分析法中模糊一致判断矩阵[J]. 四川师范学院学报,2002,23(3): 282-285. doi: 10.3969/j.issn.1673-5072.2002.03.017TAO Yuhui, LIU Jiacai, ZHANG Jijun. How to make fuzzy consistent judgement matrix of the fAHP[J]. Journal of Sichuan Teachers College, 2002, 23(3): 282-285. doi: 10.3969/j.issn.1673-5072.2002.03.017 中华人民共和国建设部. 岩土工程勘察规范: GB50021—2001[S]. 北京: 中国建筑工业出版社, 2002 中国电力企业联合会. 风力发电场设计技术规范: DL/T5383—2007[S]. 北京: 中国电力出版社, 2007 中国电力企业联合会标准化中心. 变电站总布置设计技术规程: DL/T5056—2007[S]. 北京: 中国电力出版社, 2008 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 771
- HTML全文浏览量: 558
- PDF下载量: 32
- 被引次数: 0