考虑二阶效应的空间刚架结构布局优化

李银启; 程文明; 刘华森

doi:10.3969/j.issn.0258-2724.20170863

考虑二阶效应的空间刚架结构布局优化

doi: 10.3969/j.issn.0258-2724.20170863

基金项目: 国家自然科学基金资助项目（51175442）

详细信息

作者简介:
李银启（1990—），男，博士研究生，研究方向为金属结构优化，E-mail：bk20090920@my.swjtu.edu.cn

通讯作者:
程文明（1963—），男，教授，研究方向为起重机轻量化与智能化控制研究，E-mail：wmcheng@home.swjtu.edu.cn

中图分类号: TH213.3；TU312+.1；TU328
计量
- 文章访问数: 468
- HTML全文浏览量: 275
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2017-12-07
- 修回日期: 2018-09-06
- 网络出版日期: 2018-09-14
- 刊出日期: 2019-10-01

Layout Optimization of Spatial Rigid Frame by Second-Order Effect Analysis

摘要

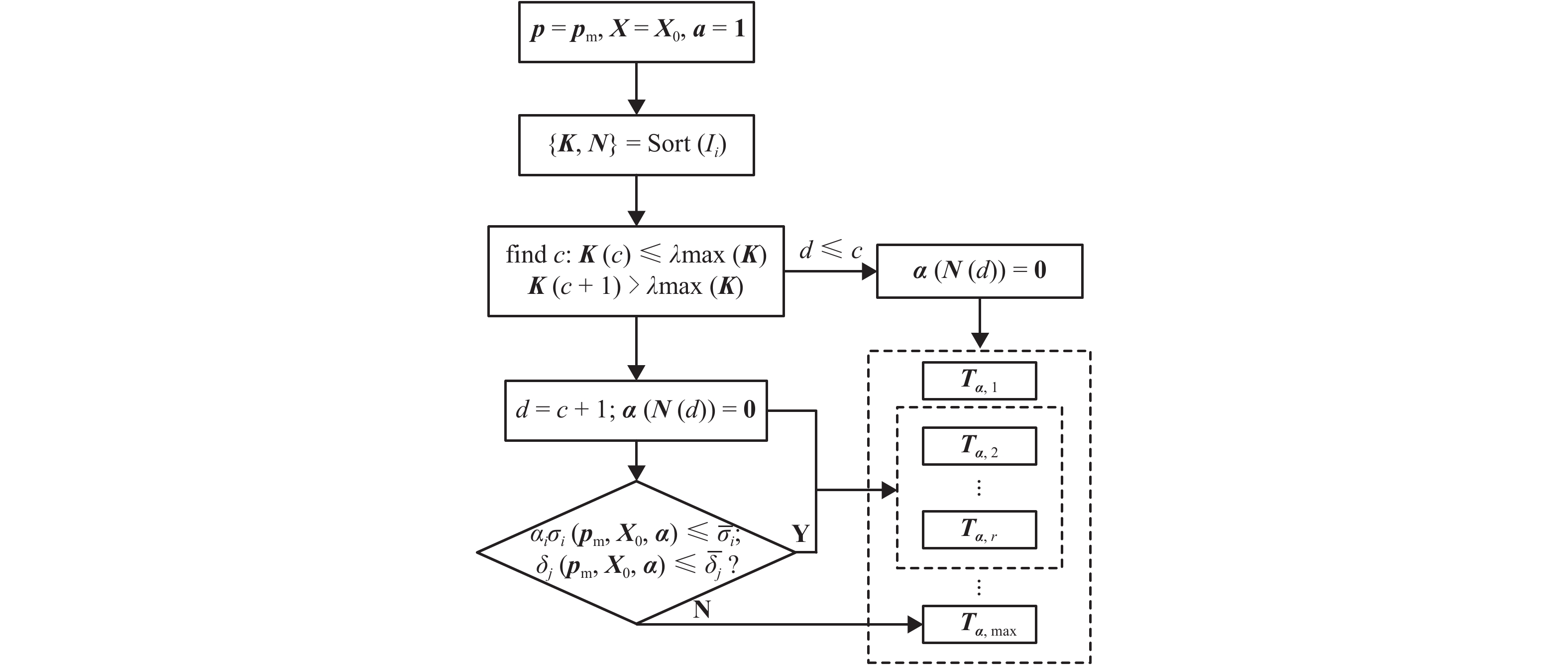
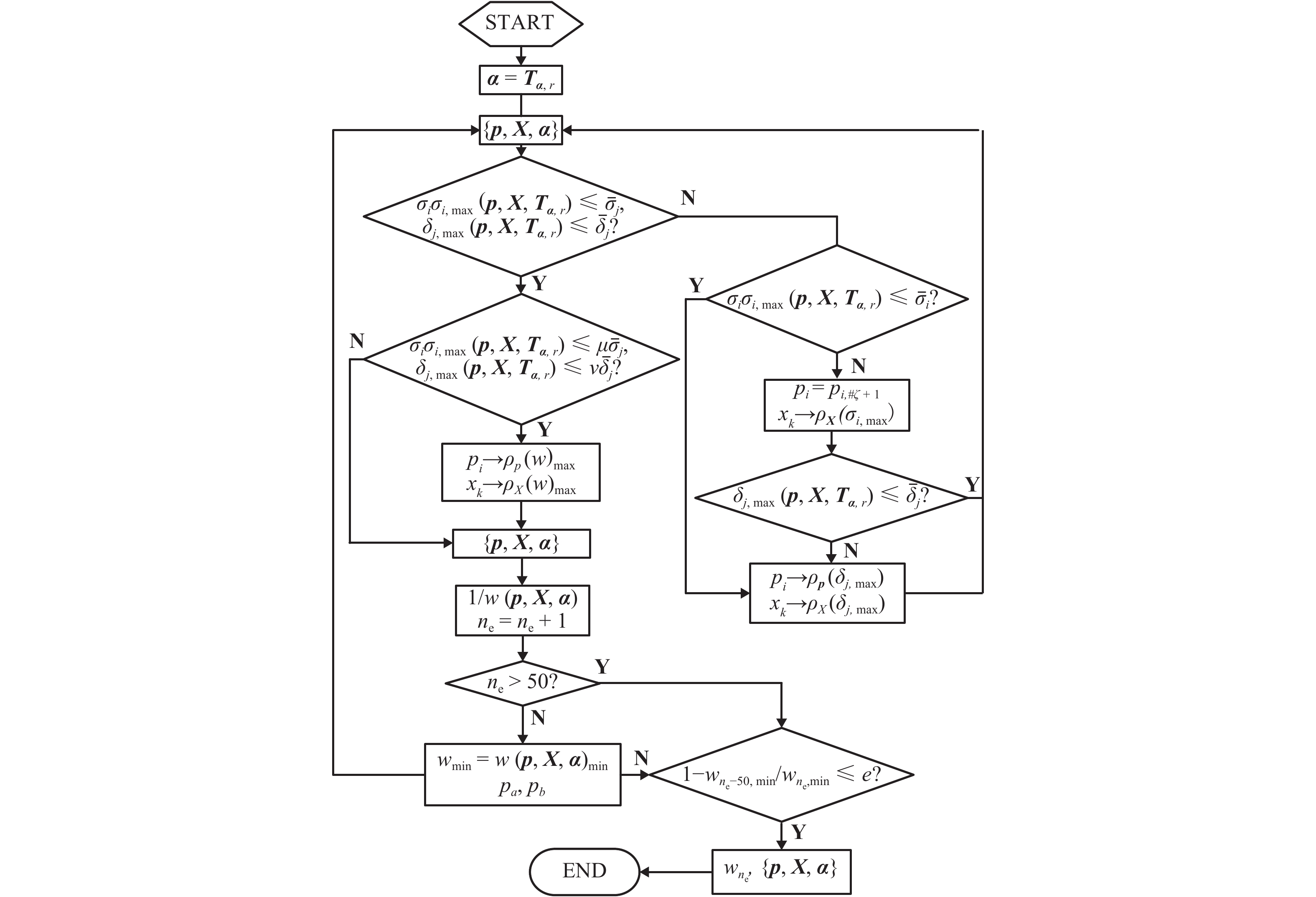
摘要: 针对三维空间刚架布局优化问题，以七自由度节点梁柱单元二阶弹性理论推导考虑构件几何非线性和截面翘曲变形的非线性刚度矩阵，通过整合梁柱单元非线性刚度矩阵对刚架结构进行整体的二阶弹性分析，建立满足刚架结构强度、刚度和稳定性要求的布局优化数值模型；并针对复杂刚架结构布局优化数值求解问题，改进遗传搜索算法（GA），提出可靠拓扑和引导型遗传算法双向控制方法（KLGA）. 该方法一方面将拓扑变量从布局设计变量中分离，以构件重要度评定结构可靠拓扑变量组合，再与设计变量整合；另一方面将结构特有的引导信息加入算法中，为GA提供全局最优解的指引路径. 通过两种典型的刚架算例表明二阶效应模型和KLGA算法的可行性和有效性，例如算例2中基于二阶效应模型的KLGA得到的最优结构质量比GA减轻了24.5%，波动幅度从9.61%提升到1.39%，算法更加稳定.
- 空间刚架结构 /
- 二阶效应 /
- 布局优化 /
- 可靠拓扑 /
- 引导型遗传算法
Abstract: In order to handle three-dimensional spatial frame layout optimization, nonlinear rigidity matrix of the beam-column element with seven degrees of freedom was deduced by second-order elastic theory, while the geometric nonlinearity and restrained torsional warping were considered. An overall second-order analysis for rigid-frame structure was conducted by integrating the nonlinear rigidity matrices of all beam-column elements. A numerical layout optimization model of spatial rigid frame was built, which was able to satisfy the requirements for structural strength, stiffness and stability. In order to solve the numerical model, a two-way control method of reliable topology and guided genetic algorithm (KLGA) was proposed based on the improvement of the genetic algorithm (GA). In one respect, this method enables the separation of the topological variables from the layout design variables, and then integrates them after evaluating the reliable topological variable combinations based on component importance. In addition, the guidance information of structure was added in the algorithm to guide the path of global optimal solution for GA. Finally, two typical examples of rigid frame structure are presented to validate the feasibility and effectiveness of the second-order effect model and optimization method KLGA. For example, in the second-order effect model of example 2, the optimal structural mass acquired by KLGA is 24.5% less than that of GA, and its range of fluctuation promotes from 9.61% to 1.39%, indicating the stability of KLGA.
- spatial rigid frame /
- second-order effect /
- layout optimization /
- reliable topology /
- guided genetic algorithm

HTML全文

图 1 构件载荷二阶效应

Figure 1. Second-order effect of loaded frame component

下载: 全尺寸图片幻灯片

图 2 KLGA可靠拓扑控制程序框图

Figure 2. Block diagram of KLGA reliable topology control

下载: 全尺寸图片幻灯片

图 3 KLGA引导型遗传算法控制程序框图

Figure 3. Block diagram of KLGA guided genetic algorithm program

下载: 全尺寸图片幻灯片

图 4 槽钢框架优化前后模型

Figure 4. Original and optimized frame models

下载: 全尺寸图片幻灯片

图 5 刚架优化前后模型

Figure 5. Original and optimized models of latticed rigid-frame structure

下载: 全尺寸图片幻灯片

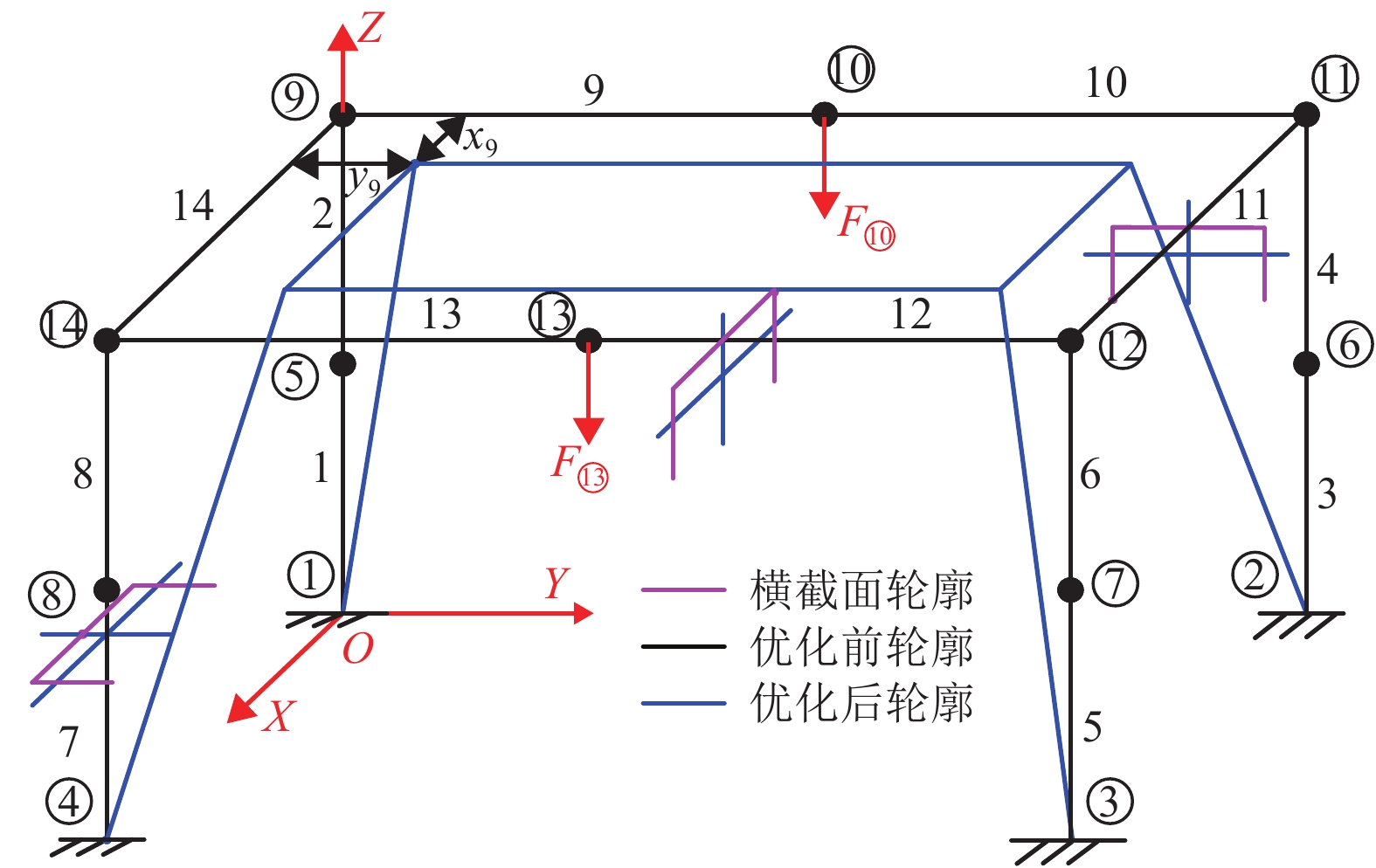
表 1 槽钢框架布局优化变量信息

Table 1. Layout optimization variables of channel frame

项目	描述
单元分组	e₁ = {1，3，5，7，2，4，6，8}； e₂ = {9，10，12，13}；e₃ = {11，14}
截面型号	a类槽钢：5^#，6.3^#，8^#，10^#，12^#，14^#，16^#， 18^#，20^#，22^#，25^#，28^#，30^#，32^#，36^#，40^#
设计变量	型号拓扑变量：p_①~p_⑭；α_①~α_⑭；位置设计变量：x_⑨∈[0，400]； x_⑭ = x_⑨；y_⑨∈[0，600]；y_⑪ = y_⑨

下载: 导出CSV

表 2 槽钢框架布局优化结果

Table 2. Layout optimization results of channel frame

分组号	单元号	初始模型		优化结果GA/KLGA
分组号	单元号	线弹性约束	二阶效应约束	线弹性约束	二阶效应约束
1	e₁	40^#（42.337）	40^#（45.593）	14^#	14^#
2	e₂	40^#（12.271）	40^#（13.214）	22^#	22^#
3	e₃	40^#（6.076）	40^#（6.543）	5^#	5^#
4	x_⑨/mm	0	0	212.50	212.50
5	y_⑨/mm	0	0	318.75	318.75
下挠位移/mm		8.221	8.854	9.808	10.788
最大应力/MPa		42.337	45.593	150.652	158.501
结构重量/kg		1 131.072	1 131.072	308.103	308.103

下载: 导出CSV

表 3 格构式刚架优化变量信息

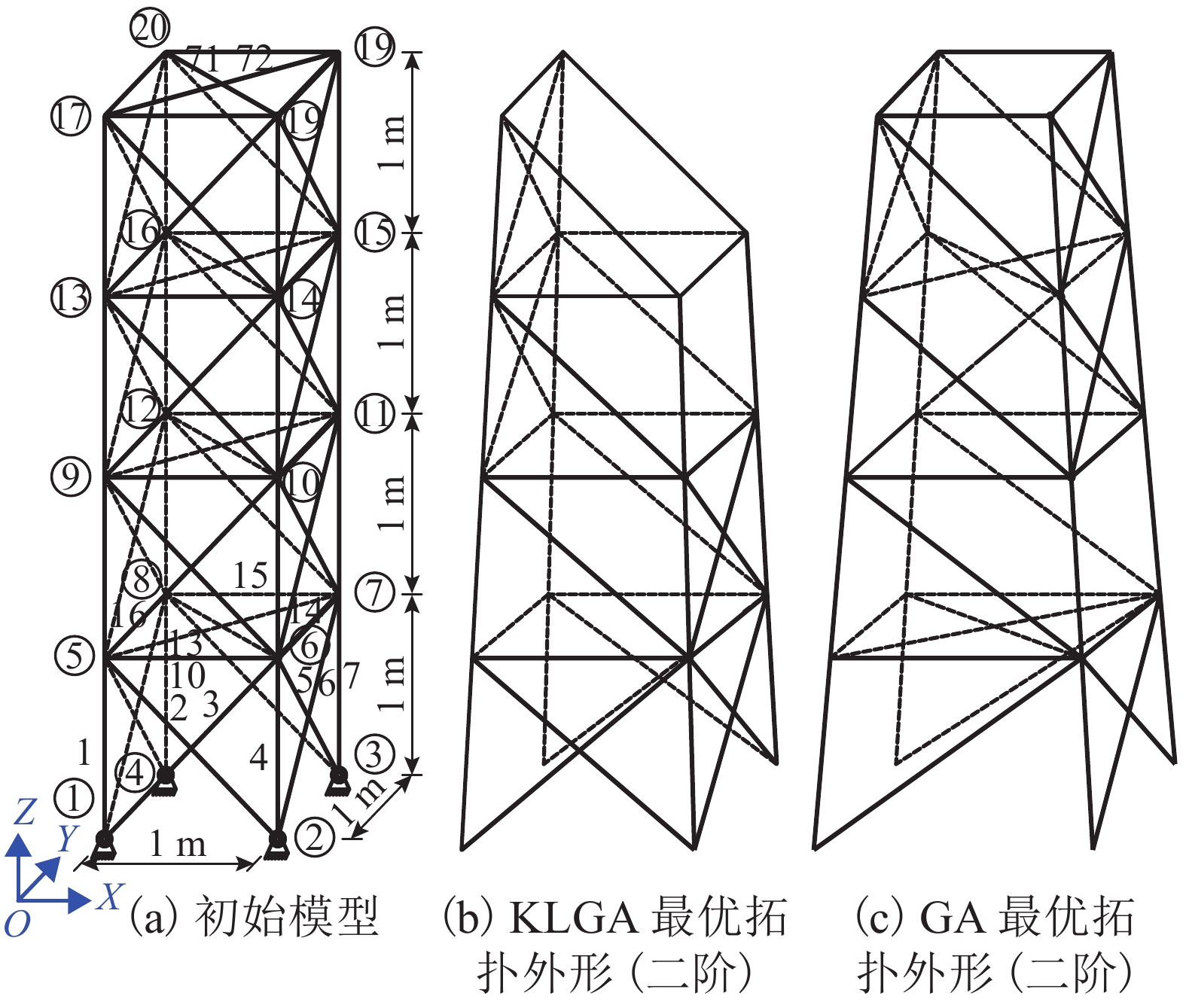
Table 3. Layout optimization variables of latticed column

项目	描述
对称单元	{1,10},···,{55,64}；{2,8},···,{56,62}； {3,9},···,{57,63}；{4,7},···,{58,61}； {5,6},···,{59,60}；{11,12},···,{65,66}； {13,15},···,{67,69}；{17,18},···,{71,72}
截面型号	缀条：{20,25,30,36,40,45,50,56}3；肢脚：{63,70,75,80,90,100,110,125}8
设计变量	型号拓扑变量：p_①~p；α_①~α；节点位置/mm：1 000 ≤ x_③，y_③ ≤ 1 600
注：截面型号表示为等边角钢宽度厚度，如563表示　　角钢宽度56 mm、厚度3 mm.

下载: 导出CSV

表 4 格构式刚架结构布局优化结果

Table 4. Layout optimization results of latticed rigid structure

分组号	单元号	初始模型		优化结果（GA）		优化结果（KLGA）
分组号	单元号	线弹性约束	二阶效应约束	线弹性约束	二阶效应约束	线弹性约束	二阶效应约束
1	1，10	125*8（11.70）	125*8（12.20）	75*8	63*8	63*8	70*8
2	2，8	56*3（22.19）	56*3（23.71）	25*3	—	—	—

下载: 导出CSV

续　表 4　 Continue　Tab. 4
分组号	单元号	初始模型		优化结果（GA）		优化结果（KLGA）
分组号	单元号	线弹性约束	二阶效应约束	线弹性约束	二阶效应约束	线弹性约束	二阶效应约束
3	3，9	56*3（12.77）	56*3（14.16）	—	30*3	20*3	25*3
4	4，7	125*8（21.57）	125*8（22.49）	70*8	63*8	90*8	70*8
5	5，6	56*3（7.85）	56*3（8.51）	—	40*3	45*3	50*3
6	11，12	56*3（3.62）	56*3（3.91）	30*3	—	—	—
7	13，15	56*3（8.16）	56*3（8.58）	45*3	20*3	20*3	30*3
8	14	56*3（4.56）	56*3（5.08）	30*3	40*3	45*3	25*3
9	16	56*3（1.71）	56*3（2.19）	50*3	20*3	30*3	25*3
10	17，18	56*3（5.76）	56*3（5.98）	—	30*3	—	—
11	19，28	125*8（10.41）	125*8（11.52）	63*8	63*8	63*8	110*8
12	20，26	56*3（23.41）	56*3（24.99）	—	36*3	25*3	45*3
13	21，27	56*3（14.64）	56*3（16.17）	40*3	—	—	—
14	22，25	125*8（11.63）	125*8（12.53）	63*8	90*8	63*8	90*8
15	23，24	56*3（4.42）	56*3（4.76）	25*3	—	40*3	36*3
16	29，30	56*3（4.16）	56*3（4.44）	20*3	—	—	—
17	31，33	56*3（6.87）	56*3（7.20）	36*3	40*3	20*3	25*3
18	32	56*3（2.35）	56*3（2.66）	30*3	30*3	30*3	30*3
19	34	56*3（3.91）	56*3（4.16）	30*3	36*3	40*3	25*3
20	35，36	56*3（4.91）	56*3（5.08）	40*3	—	—	—
21	37，46	125*8（15.46）	125*8（15.92）	70*8	63*8	63*8	63*8
22	38，44	56*3（22.62）	56*3（24.14）	—	20*3	—	—
23	39，45	56*3（14.13）	56*3（15.61）	20*3	30*3	25*3	30*3
24	40，43	125*8（7.98）	125*8（8.55）	75*8	75*8	75*8	63*8
25	41，42	56*3（3.04）	56*3（3.24）	25*3	36*3	36*3	—
26	47，48	56*3（5.89）	56*3（6.02）	—	50*3	20*3	40*3
27	49，51	56*3（8.03）	56*3（8.47）	45*3	—	40*3	25*3
28	50	56*3（0.18）	56*3（0.23）	50*3	—	50*3	30*3
29	52	56*3（5.80）	56*3（5.93）	30*3	20*3	36*3	40*3
30	53，54	56*3（5.40）	56*3（5.61）	20*3	30*3	—	—
31	55，64	125*8（20.11）	125*8（20.13）	70*8	75*8	100*8	75*8
32	56，62	56*3（25.25）	56*3（25.95）	45*3	—	20*3	36*3
33	57，63	56*3（12.65）	56*3（14.01）	—	36*3	—	—
34	58，61	125*8（2.80）	125*8（2.96）	70*8	70*8	—	—
35	59，60	56*3（0.72）	56*3（0.73）	40*3	36*3	—	—
36	65，66	56*3（7.75）	56*3（7.79）	36*3	30*3	36*3	30*3
37	67，69	56*3（11.71）	56*3（12.75）	20*3	25*3	—	—
38	68	56*3（1.45）	56*3（1.64）	45*3	45*3	—	—
39	70	56*3（6.04）	56*3（6.21）	50*3	45*3	36*3	45*3
40	71，72	56*3（4.00）	56*3（4.43）	20*3	—	—	—
43	x_③/mm	0	0	243.75	337.5	468.75	56.25
44	y_③/mm	0	0	262.5	75	18.75	56.25
最大约束位移/mm		1.72	1.85	3.96	3.15	2.18	3.93
最大约束应力/MPa		25.25	25.95	113.54	106.03	151.52	156.59
w/kg		427.34	427.34	216.32	228.46	184.67	179.90
迭代次数		—	—	65	86	122	109
注：“—”代表优化中被删除的项目（节点或构件）；初始模型目录下括号内为构件上的最大应力；截面型号表示为等　　　边角钢宽度厚度，如563表示角钢宽度56 mm、厚度3 mm.

下载: 导出CSV

参考文献(16)

王毅,姚卫星. 桁架结构布局优化的并行子空间方法[J]. 工程设计学报,2015,22(3): 256-261. doi: 10.3785/j.issn.1006-754X.2015.03.009

WANG Yi, YAO Weixing. Concurrent subspace optimization for layout design of trusses[J]. Chinese Journal of Engineering Design, 2015, 22(3): 256-261. doi: 10.3785/j.issn.1006-754X.2015.03.009

SHI Lianshuan, WANG Yuefang, SUN Huanchun. Approach for layout optimization of truss structures with discrete variables under dynamic stress,displacement and stability constraints[J]. Applied Mathematics and Mechanics, 2006, 27(5): 593-599. doi: 10.1007/s10483-006-0504-y

GHOLIZADEH S. Layout optimization of truss structures by hybridizing cellular automata and particle swarm optimization[J]. Computers and Structures, 2013, 125: 86-99. doi: 10.1016/j.compstruc.2013.04.024

HOOSHMAND A, CAMPBELL M I. Truss layout design and optimization using a generative synthesis approach[J]. Computers and Structures, 2016, 163: 1-28. doi: 10.1016/j.compstruc.2015.09.010

AHRARI A, DEB K. An improved fully stressed design evolution strategy for layout optimization of truss structures[J]. Computers and Structures, 2016, 164: 127-144. doi: 10.1016/j.compstruc.2015.11.009

AHRARI A, ATAI A. Fully stressed design evolution strategy for shape and size optimization of truss structures[J]. Computers and Structures, 2013, 123: 58-67. doi: 10.1016/j.compstruc.2013.04.013

GAO Ge, LIU Zhenyu, LI Yaobin, et al. A new method to generate the ground structure in truss topology optimization[J]. Engineering Optimization, 2017, 49(2): 235-251. doi: 10.1080/0305215X.2016.1169050

STOLPE M. Truss topology optimization with discrete design variables by outer approximation[J]. Global Optimization, 2015, 61: 139-163. doi: 10.1007/s10898-014-0142-x

肖阿阳. 基于演化算法的杆系结构拓扑与布局优化设计研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.

童根树. 钢结构的平面外稳定性[M]. 修订版. 北京: 中国建筑工业出版社, 2012: 107-108.

中华人民共和国住房与城乡建设部. 钢结构设计规范: GB 50017—2003[S]. 北京: 中国计划出版社, 2003.

AISC Committee. Specification for structural steel buildings: ANSI/AISC360—05[S]. Chicago: AISC B. D, 2005.

CEN. Eurocode 3: Design of Steel Structures: BS EN 1993-1-1[S]. Brussels: BSI, 2003.

ALWIS W A M, WANG C M. Wangner term in flexural-torsional buckling of thin-walled open-profile columns[J]. Engineering Structures, 1996, 18(2): 125-132. doi: 10.1016/0141-0296(95)00112-3

刘坚. 钢结构高等分析的二阶非弹性理论与应用[M]. 北京: 科学出版社, 2011: 147–158.

朱朝艳,刘斌,张延年,等. 复合形遗传算法在离散变量桁架结构拓扑优化中的应用[J]. 四川大学学报(工程科学版),2004,36(5): 6-10. doi: 10.3969/j.issn.1009-3087.2004.05.002

ZHU Chaoyan, LIU Bin, ZHANG Yannian, et al. Application of complex genetic algorithm to discrete topology optimization of truss structure[J]. Journal of Sichuan University (Engineering Science Edition), 2004, 36(5): 6-10. doi: 10.3969/j.issn.1009-3087.2004.05.002

施引文献

附加材料(0)

访问统计