Verification of Theoretical Model and Vibration Effect Caused by Blasting in Shallow Buried Tunnel on Mountain Slope
-
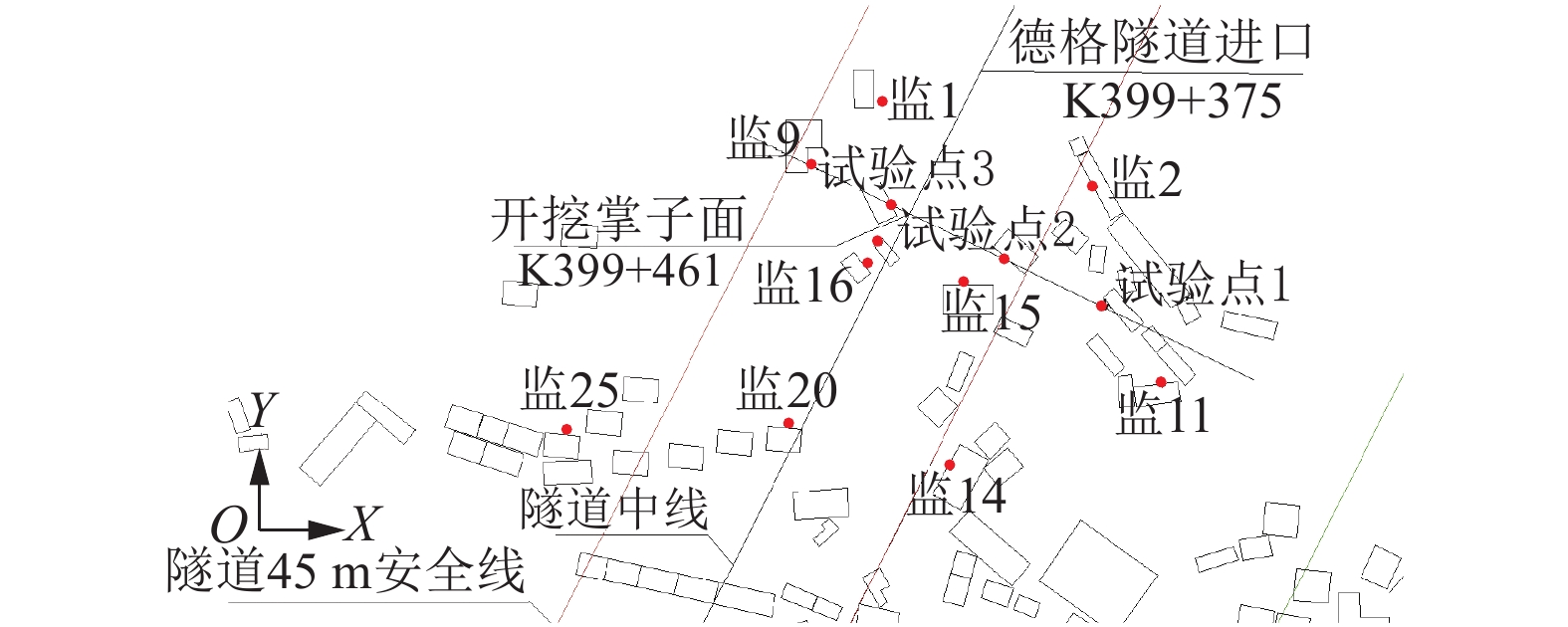
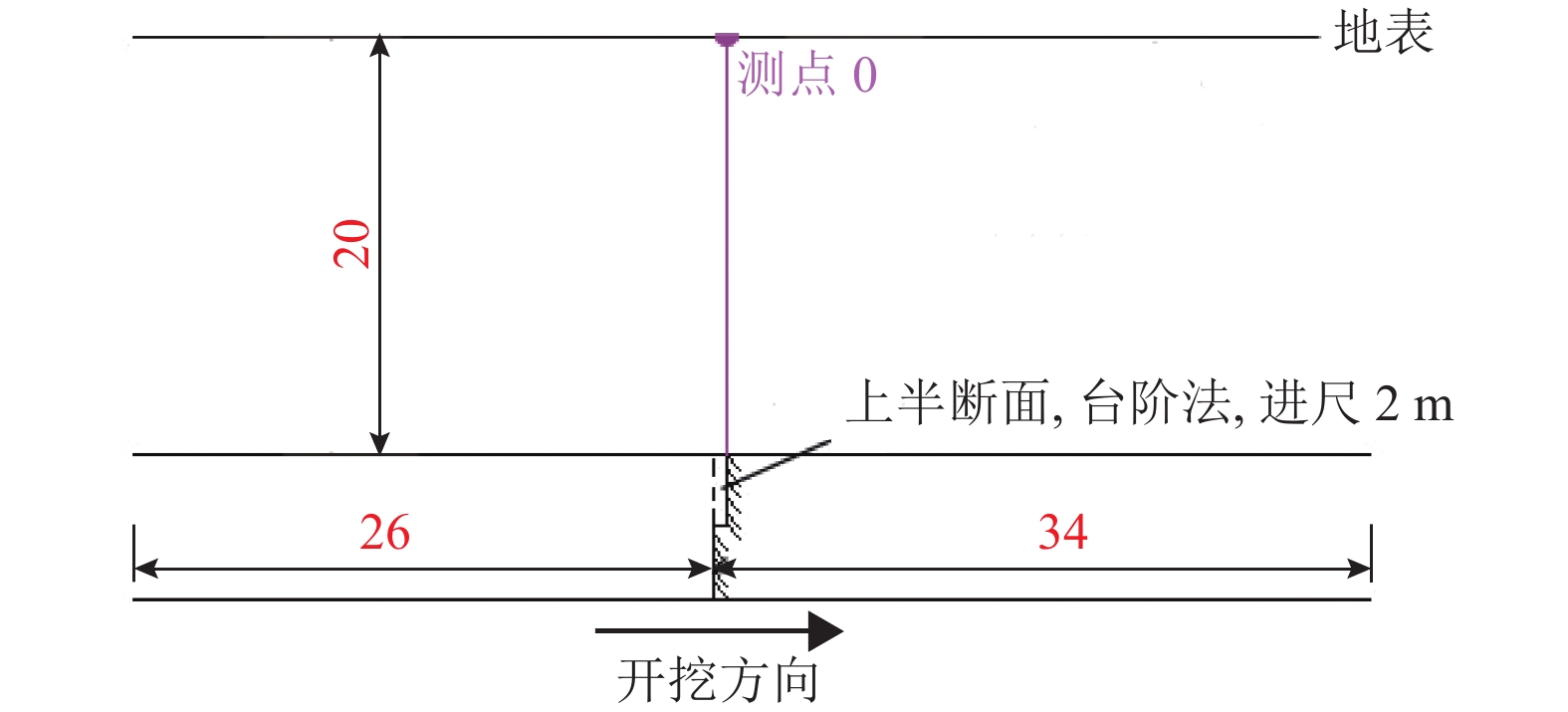
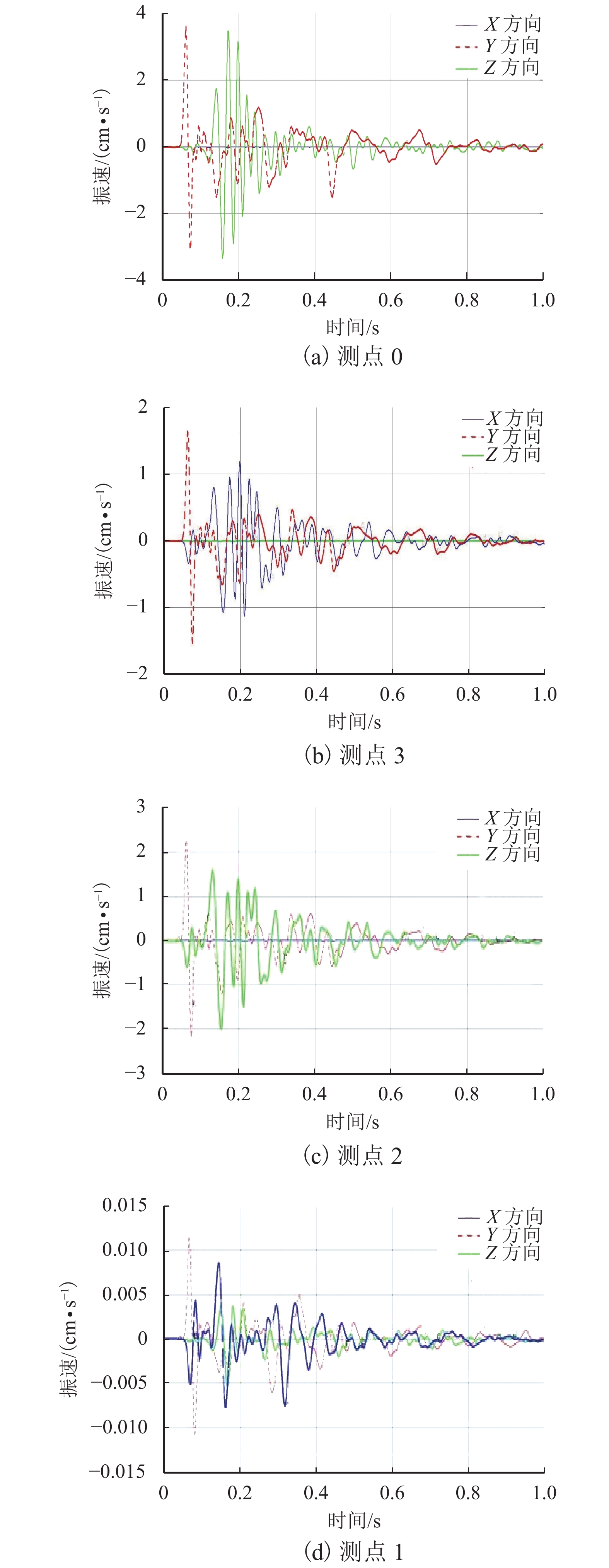
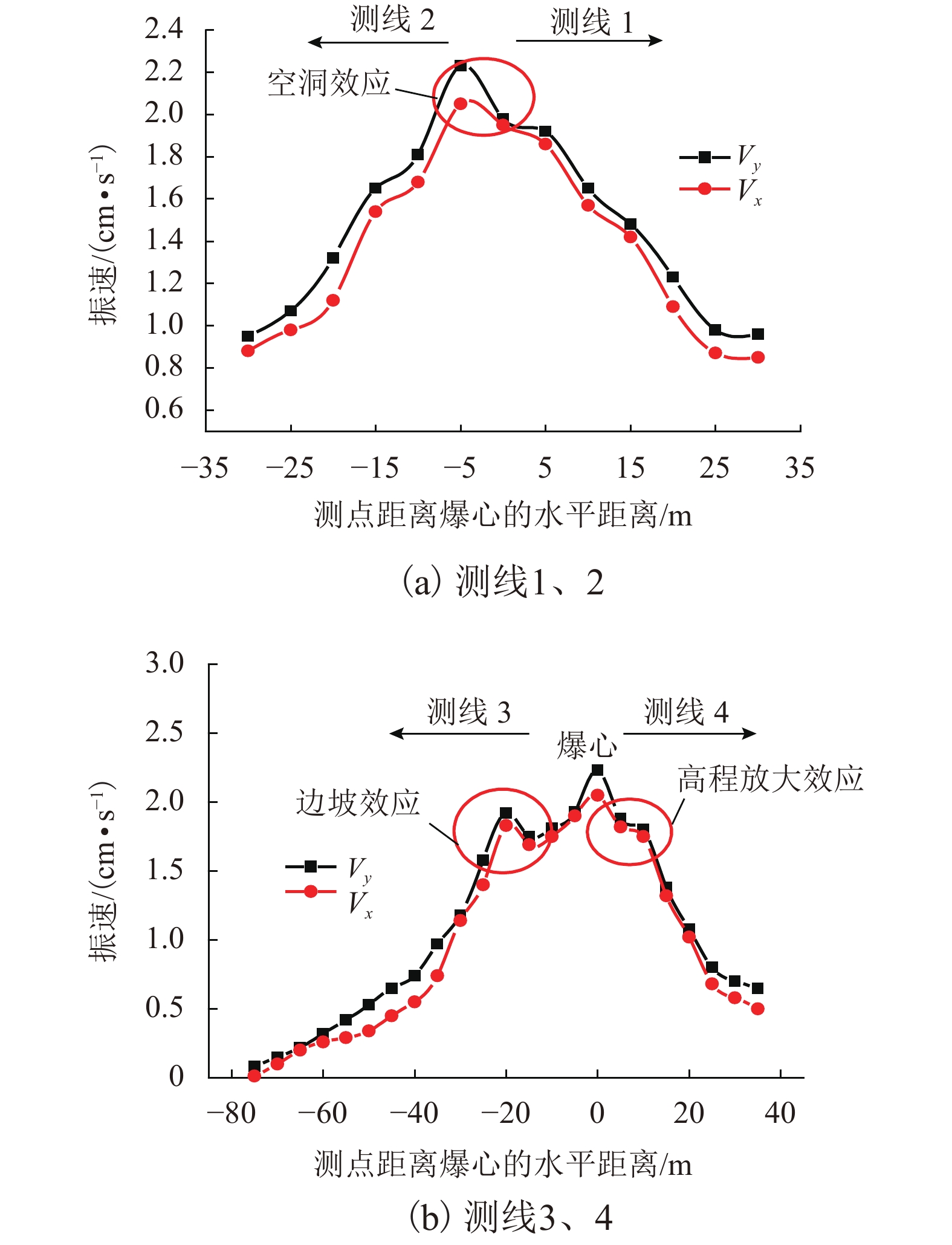
摘要: 为研究位于边坡地形和浅埋土岩复合地层条件下的山岭隧道施工爆破振动效应和振动影响范围，验证并获得准确适用的振速理论模型，以国道317线下穿县城密集区的德格隧道为依托，利用现场爆破振动监测和回归分析对4组常用理论模型进行验证，同时，通过三维数值模拟及与理论模型计算、现场实测结果的比较，围绕爆破振速、振动影响范围以及存在的爆破振动效应进行分析. 研究结果表明：4组常见理论模型计算拟合度在0.15～0.86之间，其中，唐海、朱传统和周同龄理论模型公式对应不同爆心水平距离、高程差时各有优势；理论模型计算得到的爆破振动影响范围比数值计算结果更接近现场实测结果；在隧道成洞区28 m范围内爆破施工引起的“空洞效应”明显，地表垂向最大振速由起爆点处的1.98 cm/s增大到了2.23 cm/s；爆心所在横切面内顺坡向一侧距离开挖中线10～20 m范围坡面上“边坡效应”显著，最大垂向振速达1.83 cm/s之后随爆心距增大而线性减小；在逆坡向一侧5～10 m范围内随高程增加将出现“高程放大效应”，因此，上述范围内的地表建筑应作为现场监测重点并做好防震措施.Abstract: Results on the blasting vibration effect and influence range of a mountain tunnel under a slope terrain and shallow buried soil in rock composite stratum conditions are presented. The objective was to verify and obtain an accurate and applicable theoretical model of vibration velocity based on a case study by taking the De-ge tunnel in the project of No.317 national highway that passes below a densely populated county. The 4 usual theoretical models were verified by on-site blasting vibration monitoring and regression analysis. Simultaneously, the vibration velocity, the influence range of vibration and the blasting vibration effect were analyzed through 3-D numerical simulation and comparison with theoretical calculations and field measurement results. The results show that: the degree of fitting of the 4 usual theoretical models is 0.15−0.86, and the theoretical model formulas by Tang, Zhu, and Zhou can complement each other with respective advantages in terms of different blasting horizontal distance and elevation difference. The influence range of blasting vibration obtained by the theoretical model is closer to field measurements than the numerical results. The " hole effect” located on the surface within 28 m of the completed tunnel is clear and the maximum vertical vibration velocity increased from 1.98 cm/s at the initiation point up to 2.23 cm/s at the surface. The " slope effect” is remarkable in 10−20 m from the middle line on the downslope surface. The vertical velocity decreases linearly with the increase of the detonation distance when it reaches 1.83 cm/s. The " elevation amplification effect” on the adverse slope will occur within 5−10 m on the other side of the center line as the elevation increases. In the above range on the ground surface, the protected buildings should be the key points of field monitoring, and the earthquake precautions should be strengthened.
-
石材幕墙面板背栓式连接是石材幕墙的一种常见施工方法，采用背栓式连接的石材幕墙抗震性能力强[1-3]，稳定性能高[4-6]，施工强度低，机械化施工程度高，安装方便灵活. 石材幕墙连接节点的破坏占很大比例[7-8]，另外高温、湿度的变化都会导致石材强度下降[9]. 石材经风化后，承载力下降明显，石材幕墙面板常有断裂情况出现[10-11]，因此保证石材幕墙面板断裂后的整体性是提高面板安全性的重要措施. 目前，国内外关于石材幕墙面板加固和高空防坠措施的研究相对较少.
本文对33块背栓式石材面板进行了抗弯试验，并对其抗弯承载力进行了分析，研究了石材面板的加固和防高空坠落措施，为背栓式石材幕墙面板工程应用提供参考.
1. 试验概况
1.1 试件设计
石材面板为尺寸600 mm × 400 mm × 30 mm的花岗岩. 背栓采用慧鱼敲击式背栓，节点加固用不锈钢金属圆环，金属圆环厚度2 mm，金属圆环半径40 mm. 石材面板尺寸及加工方案见图1，试件的参数变化见表1. 试件编号中，BS、J、F、B分别表示背栓式石材面板、节点加固、迎风面加载、背风面加载，1、2、3、4分别代表GFRP （glass fiber reinforced plastics）布采用十字、对角、纵向全贴和横向全贴的加固方式. 所用石材均为同一批次黄金麻花岗岩.
考虑正负风压的作用，对石材面板进行了迎风面和背风面加载方向的试验，加载速度为0.5 mm/min，当荷载降至峰值荷载85%时停止加载，加载装置及测量方案如图2所示.
表 1 试件设计参数Table 1. Details of specimens试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 BS-F 3 30 BS-B 3 30 BS-J-F 3 30 加固 BS-J-B 3 30 加固 BS-J-F-1 3 30 加固 十字 BS-J-B-1 3 30 加固 十字 BS-J-F-2 3 30 加固 对角 BS-J-B-2 3 30 加固 对角 BS-J-F-3 3 30 加固 纵向全贴 BS-J-B-3 3 30 加固 纵向全贴 BS-J-F-4 3 30 加固 横向全贴 1.2 材料性能
黄金麻花岗岩的实测弯曲强度为4.14 MPa. GFRP的实测性能如表2所示.
表 2 GFRP实测性能Table 2. Measured performance of GFRP试样 抗拉强度/MPa 厚度/mm 弹性模量/MPa GFRP 1 444.4 0.167 1.33 × 105 2. 试验结果
2.1 试验现象及破坏形态
在迎风面荷载作用下，石材面板标准件和节点加固的面板破坏时发出轻微的断裂声，面板断裂严重，承载力迅速下降，破坏非常突然. 背面采用GFRP十字粘贴和对角粘贴的石材幕墙面板，石材面板主要产生纵向贯通裂缝，加载过程中有GFRP的撕裂声，石材面板开裂后承载力缓慢下降，GFRP与断裂石材表面逐渐出现滑脱，破坏过程缓慢. 背面采用GFRP纵向和横向全贴的石材幕墙面板，破坏过程相似，分别出现纵向和横向贯通裂纹，承载力下降缓慢. 其破坏形态如图3（a）~（f）所示.
在背风面荷载的作用下，未进行加固的石材面板在背栓处产生了拉拔破坏现象，节点加固后的石材面板背栓孔处未发生破坏，说明采用金属圆环对石材面板连接节点进行加固是有效的. 背面采用GFRP加固的石材面板断裂后无碎块掉落，断裂石材与GFRP粘接完好，能保证一定的整体性. 其破坏形态如图3（g）~（k）所示.
2.2 试验结果与分析
不同试件极限荷载的柱状图如图4所示. 石材幕墙面板在不同荷载下的试验结果见表3所示，其中(1)、(2)、(3)表示在3次不同荷载下的试验.
表 3 不同荷载下试验结果Table 3. Test results under different loadings试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 BS-F (1) 20.530 1.12 节点破坏 BS-B (1) 9.423 1.29 节点破坏 (2) 21.873 0.91 (2) 9.603 1.22 (3) 20.794 1.05 (3) 9.279 1.19 平均荷载 21.065 1.03 平均荷载 9.435 1.23 BS-J-F (1) 23.676 1.18 板断裂 BS-J-B (1) 14.051 1.91 板断裂 (2) 23.245 1.26 (2) 13.946 1.94 (3) 24.152 1.22 (3) 14.513 2.08 平均荷载 23.691 1.22 平均荷载 14.170 1.98 BS-J-F-1 (1) 69.533 5.03 板断裂 BS-J-B-1 (1) 14.867 1.63 板断裂 (2) 70.463 4.97 (2) 14.513 1.45 (3) 68.987 4.85 (3) 14.725 1.53 平均荷载 69.661 4.95 平均荷载 14.702 1.54 BS-J-F-2 (1) 58.765 4.22 板断裂 BS-J-B-2 (1) 16.478 1.32 板断裂 (2) 57.360 4.13 (2) 16.344 1.51 (3) 57.553 4.24 (3) 15.681 1.45 平均荷载 57.893 4.20 平均荷载 16.168 1.43 BS-J-F-3 (1) 31.113 1.43 板断裂 BS-J-B-3 (1) 14.862 1.29 板断裂 (2) 38.031 1.52 (2) 15.577 1.36 (3) 36.145 1.48 (3) 15.245 1.45 平均荷载 35.096 1.48 平均荷载 15.227 1.37 BS-J-F-4 (1) 56.975 2.71 板断裂 (2) 60.895 2.77 平均荷载 58.935 2.74 由表3可以看出：在迎风面加载作用下，背面采用十字、对角、纵向全贴和横向全贴GFRP进行加固石材面板，极限承载力分别是未加固石材面板的3.30倍、2.75倍、1.74倍和2.80倍. 试验采用的GFRP是单向编制的，GFRP粘贴方向对加固石材面板的极限承载力和破坏形态有一定影响. 两种全贴GFRP的加固方式下，石材断裂裂纹都出现在与纤维平行的方向，都没能充分发挥GFRP的强度.
在背风面加载条件下，节点加固石材面板的承载力是未加固试件的1.50倍，均为脆性破坏. 石材面板背面粘贴GFRP后，虽然承载力无明显提高，但是石材面板破坏后能保持整体性.
3. 有限元分析
3.1 有限元模拟校核
为了分析GFRP加固背栓式石材面板的受力过程，采用Abacus有限元软件对极限荷载进行了模拟. 将石材定为线弹性材料，采用最大主拉应力破坏准模拟开裂. 石材性能取实测性能，参考高强混凝土开裂应变经验值为1 × 10−4 [12]，石材的开裂应变取相同值. 石材实体单元用C3D8R减缩积分进行模拟，为了限制“沙漏”的扩展，直接选用enhanced方式控制沙漏.
假定纤维方向GFRP应力-应变关系为线弹性，用S4R壳单元来模拟. 材料本构关系和有限元本构模型分别如图5和图6所示. 图5中：σ和ε分别为石材的应力和应变；σu和εu分别为石材的极限压应力和极限压应变；σfe和εfe分别为GFRP的有效拉应力和有效拉应变. 石材面板与钢垫板设置表面与表面接触，接触属性定义为默认属性. 背栓与背栓孔的相互作用采用铰接约束.
模拟的结果与试验值进行对比如表4所示. 由表4可以看出，所建立的有限元模型基本正确，极限强度的误差在15.00%以内，可以用来分析GFRP加固石材幕墙面板的抗弯性能.
表 4 荷载模拟值与试验值对比Table 4. Comparison of simulated and experimental values试件编号 试验值/N 模拟值/N 误差/% BS-B 9 435.45 9 965.11 5.61 BS-J-B 14 170.55 15 383.55 8.56 BS-J-B-1 14 702.06 15 957.79 8.54 BS-J-B-2 16 168.12 17 680.88 9.36 BS-J-B-3 15 227.31 13 246.92 13.01 BS-F 21 065.81 23 706.66 12.54 BS-J-F-1 69 661.34 78 417.77 12.57 BS-J-F-2 57 893.21 64 527.76 11.46 BS-J-F-3 35 096.88 38 880.32 10.78 3.2 初始安装缺陷分析
背栓成孔质量对石材面板的受力有很大影响. 采用有限元模型可以分析背栓的初始安装缺陷对承载力的影响. 当背栓安装不合格时，认为该背栓不参与石材面板受力，其分析结果如表5所示.
表 5 初始安装缺陷分析Table 5. Initial installation defect analysis石材
编号缺陷数/个 极限荷载/N 试验荷载/N 降低率/% BS-B 1 6 382.3 9 435.0 32.36 BS-B 2 （对角） 4 229.7 9 435.0 55.17 由表5可以看出，背栓质量出现问题后，对背栓承载力影响很大，一个背栓开孔质量不合格，承载力下降约32.36%，出现两个不合格，则承载力下降达55.17%.
4. 结 论
1） 采用金属圆环对连接节点进行加固，对石材面板连接节点的承载力有明显的提高作用，相对于未加固的石材面板，承载力提高0.50倍.
2） 石材面板背面粘贴GFRP的3种加固方式，都能较好地保证石材面板破坏后的整体性，并能提高石材面板迎风面加载方向的抗弯承载力，十字粘贴效果较好，承载力提高2.30倍. 考虑到承载力的提高率以及材料用量的经济性，十字粘贴效果最好.
3） 有限元模型可以用来计算石材面板的承载力抗弯强度，计算误差在15.00%以内.
-
图 2 爆破振动监测试验点
Figure 2. Schematic diagram of the plane layout of monitoring points for the blasting vibration
图 5 开挖及监测点（单位：m）
Figure 5. Schematic diagram of the excavationand monitoring (unit: m)
表 1 现场监测结果
Table 1. Results of monitoring in conducted experiment
最大段
装药量/kg监测点
编号直线距离
$R$/m水平距离
$S$/m高程差
$H$/m实测垂向
速度${V_{y{\rm{1}}}}$/（cm•s–1）实测水平
速度${V_{x1}}$/（cm•s–1）${V_0}$/（cm•s–1） 1.5 监16 25.11 2.4 25 1.462 0.825 0.740 监14 41.73 30 29 0.474 0.352 0.309 监 2 49.37 49 6 0.331 0.282 0.231 监15 43.83 39 20 0.475 0.220 0.284 1.5 监 1 66.22 64 17 0.299 0.122 0.140 监11 83.01 83 1 0.162 0.025 0.095 监 2 70.66 63 32 0.263 0.142 0.125 2.0 监14 67.19 65 17 0.248 0.123 0.136 监15 39.45 34 20 0.222 0.175 0.340 监15 49.24 45 20 0.491 0.350 0.340 监14 62.36 60 17 0.100 0.080 0.155 监 1 62.39 58 23 0.183 0.240 0.155 
下载: 导出CSV
表 2 拟合结果及试验点振速计算
Table 2. Fitting results and vibration velocity calculation of test points
名称 回归方程 拟合度 试验点1 试验点2 试验点3 Vy2 Vy1 Vy2 Vy1 Vy2 Vy1 周同龄 ${{V_y} = 150{\left( {\displaystyle\frac{{{Q^{1/3}}}}{R}} \right)^{{\rm{1}}{\rm{.72}}}}{H^{0.275}}}$ 0.62 0.141 0.163 2.900 1.462 1.785 1.475 唐海 ${{V_y} = 150 \times 1.45 \times {\left( {\displaystyle\frac{{{Q^{1/3}}}}{R}} \right)^{1.72}}{\left( {\displaystyle\frac{H}{R}} \right)^{0.80}}}$ 0.86 0.008 0.163 1.503 1.462 1.062 1.475 朱传统 ${{V_y} = 150{\left( {\displaystyle\frac{{{Q^{1/3}}}}{R}} \right)^{1.72}}{\left( {\displaystyle\frac{{{Q^{1/3}}}}{H}} \right)^{{\rm{ - 0}}{\rm{.12}}}}}$ 0.75 0.130 0.163 1.997 1.462 1.066 1.475 水工技规 ${{V_y} = 150{\left( {\displaystyle\frac{{{Q^{1/3}}}}{S}} \right)^{1.72}}{\left( {\displaystyle\frac{{{Q^{1/3}}}}{H}} \right)^{{\rm{ - }}0.18}}}$ 0.15 0.133 0.163 3.392 1.462 49.817 1.475
下载: 导出CSV
表 3 模型物理力学计算参数
Table 3. Physical and mechanical calculation parameters of the model
名称 Ed/GPa 泊松比 粘聚力/kPa 内摩擦角/（°） 密度/（kg•m–3） 坡洪积松散堆积体（V） 0.40 0.45 20 28 1 950 裂隙发育灰岩、片岩（Ⅳ） 15.00 0.28 80 38 2 500 混凝土 35.00 0.20 – – 2 500
下载: 导出CSV
表 4 最大振速比较
Table 4. Comparison of the maximum vibration
试验点编号 式（2） 式（3） 式（4） 数值计算结果 实测结果 1 0.141 0.008 0.130 0.155 0.163 2 2.900 1.503 1.997 1.750 1.462 3 1.785 1.062 1.066 1.880 1.475
下载: 导出CSV
-
李铮,汪波,何川,等. 城市浅埋隧道穿越饱和砂土复合地层时适宜的施工法[J]. 中国铁道科学,2015,36(1): 75-82. doi: 10.3969/j.issn.1001-4632.2015.01.11LI Zheng, WANG Bo, HE Chuan, et al. Suitable constitution method for urban shallow tunnel crossing through complex stratum in satcnated sandy soil[J]. China Railway Science, 2015, 36(1): 75-82. doi: 10.3969/j.issn.1001-4632.2015.01.11 HE Chuan, WANG Bo. Research progress and development trends of highway tunnels in China[J]. Journal of Modern Transportation, 2013, 21(4): 209-223. doi: 10.1007/s40534-013-0029-4 NAKANO K I, OKADA S, FURUKAWA K, et al. Vibration and cracking of tunnel lining due to adjacent blasting[J]. Doboku Gakkai Rombun-Hokokushu/Proceedings of the Japan Society of Civil Engineers, 1993, 462(6): 53-62. 李铮,汪波,骆耀文. 城市隧道下穿密集建筑区静、动力响应特征分析[J]. 铁道科学与工程学报,2015,12(2): 384-392. doi: 10.3969/j.issn.1672-7029.2015.02.025LI Zheng, WANG Bo, LUO Yaowen. Analysis of static and dynamic response characteristics of urban tunnels passing underneath dense-constructed areas[J]. Journal of Railway Science and Engineering, 2015, 12(2): 384-392. doi: 10.3969/j.issn.1672-7029.2015.02.025 阳军生,杨元洪,晏莉,等. 大断面隧道下穿既有高压输电铁塔施工方案比选及其应用[J]. 岩石力学与工程学报,2012,31(6): 1184-1191. doi: 10.3969/j.issn.1000-6915.2012.06.013YANG Junsheng, YANG Yuanhong, YAN li, et al. Construction scheme choice of large span tunnels under-passing high voltage transmission tower and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1184-1191. doi: 10.3969/j.issn.1000-6915.2012.06.013 汪波,何川,夏炜洋. 爆破施工新建地铁隧道与既有运营地铁的相互动力响应研究[J]. 中国铁道科学,2011,32(5): 64-70.WANG Bo, HE Chuan, XIA Weiyang. Study on the dynamic esponses between the New-Built subway tunnel y blasting construction and the existing operation subway unnel[J]. China Railway Science, 2011, 32(5): 64-70. 赵东平. 小净距平行隧道下穿施工对多层建筑的影响研究[J]. 现代隧道技术,2011,48(5): 30-38. doi: 10.3969/j.issn.1009-6582.2011.05.006ZHAO Dongping. The effects of parallel tunnel construction with a small clear distance on a multistory building[J]. Modern Tunnelling Technology, 2011, 48(5): 30-38. doi: 10.3969/j.issn.1009-6582.2011.05.006 LIAO Tao, PU ChuanJin, YANG Xin, et al. Special effects of vibration caused by pile-well blasting in adjacent slope[J]. Rock and Soil Mechanics, 2015, 36(10): 623-628. 唐海. 地形地貌对爆破振动波影响的试验和理论研究[D]. 武汉: 中国科学院研究生院（武汉岩土力学研究所）, 2007 中国工程爆破协会. 爆破安全规程: GB6722—2014[S].北京: 中国标准出版社, 2015 萨道夫斯基. 地震预报[M]. 北京: 地震出版社, 1986: 45-58 周同龄,李玉寿. 反映高程的爆破震动公式及其应用[J]. 江苏煤炭,1997(4): 21-22.ZHOU Tongling, LI Yushou. Application of blasting vibration formula related to highness[J]. Jiangsu Coal, 1997(4): 21-22. 唐海,李海波. 反映高程放大效应的爆破振动公式研究[J]. 岩土力学,2011,32(3): 820-824. doi: 10.3969/j.issn.1000-7598.2011.03.030TANG Hai, LI Haibo. Study of blasting vibration formula of reflecting amplification effect on elevation[J]. Rock and Soil Mechanics, 2011, 32(3): 820-824. doi: 10.3969/j.issn.1000-7598.2011.03.030 朱传统,刘宏根. 地震波参数沿边坡坡面传播规律公式选择[J]. 爆破,1988(2): 30-34.ZHU Chuantong, LIU Honggen. Selection of formula on propagation of the parameters of explosive seismic wave along slope[J]. Blasting, 1988(2): 30-34. 长江水利委员会长江科学院等. 水工建筑物岩石基础开挖工程施工技术规范: T5389—2007[S]. 北京: 中国电力出版社, 2007 沈明荣. 岩体力学[M]. 上海: 同济大学出版社, 1999: 45-48 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 499
- HTML全文浏览量: 238
- PDF下载量: 16
- 被引次数: 0