Optimal Sensor Placement of EMU Frame Based on Frequency Response Function
-
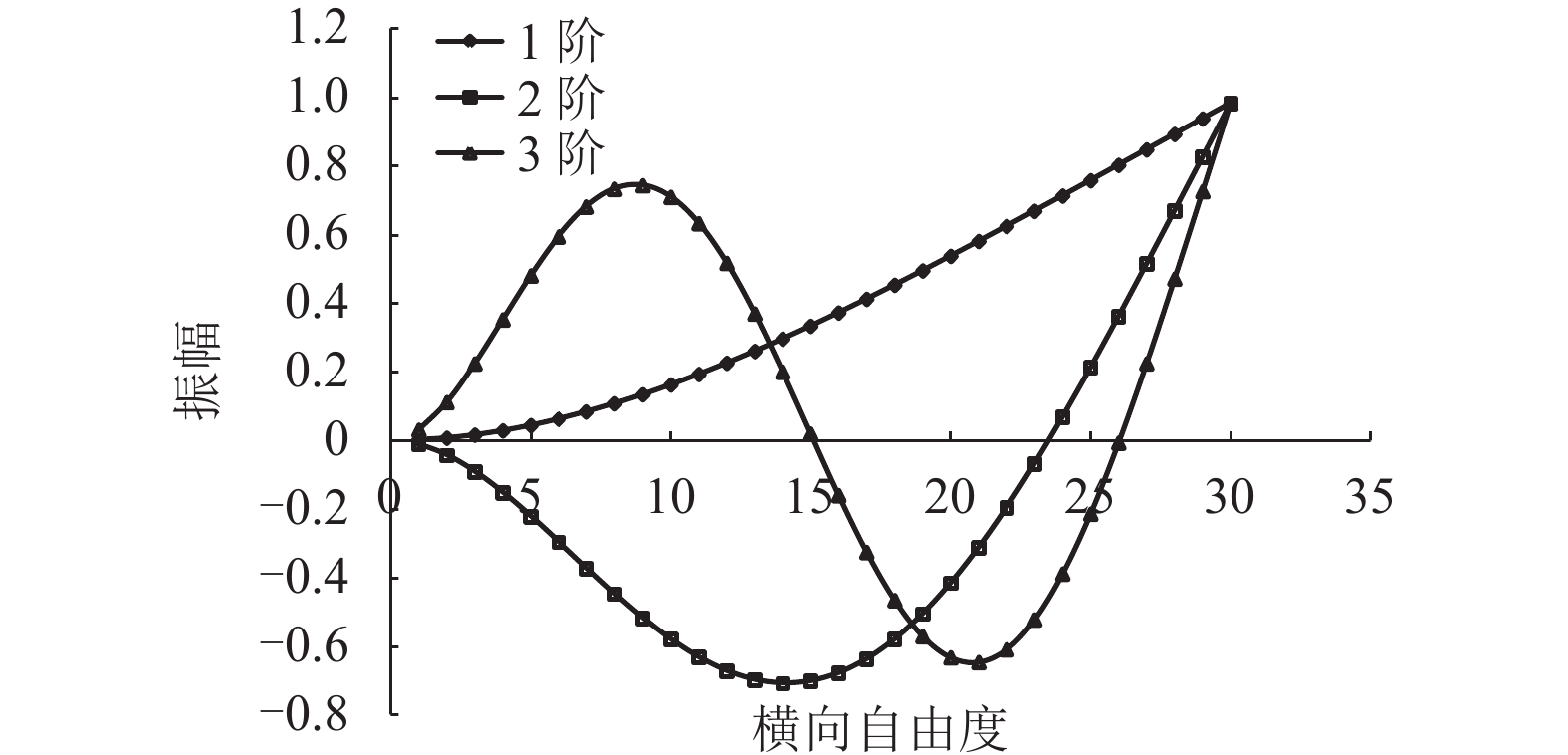
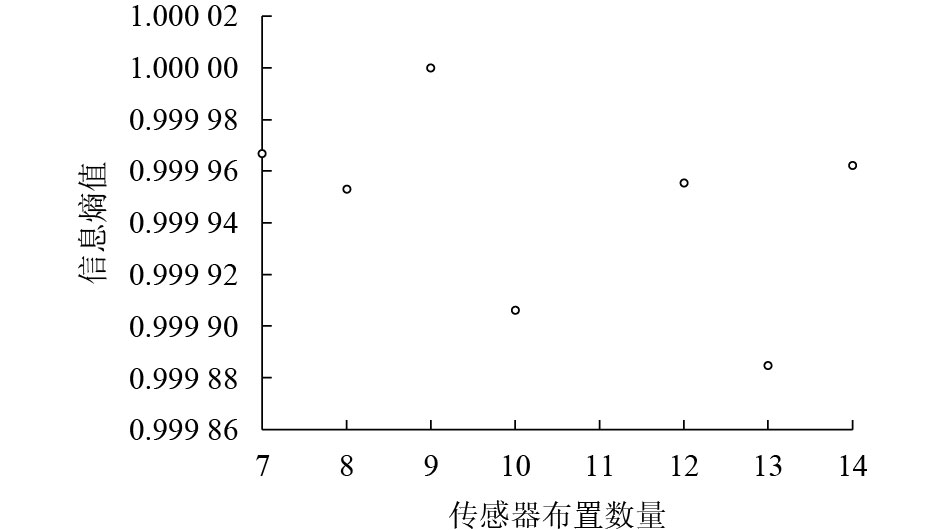
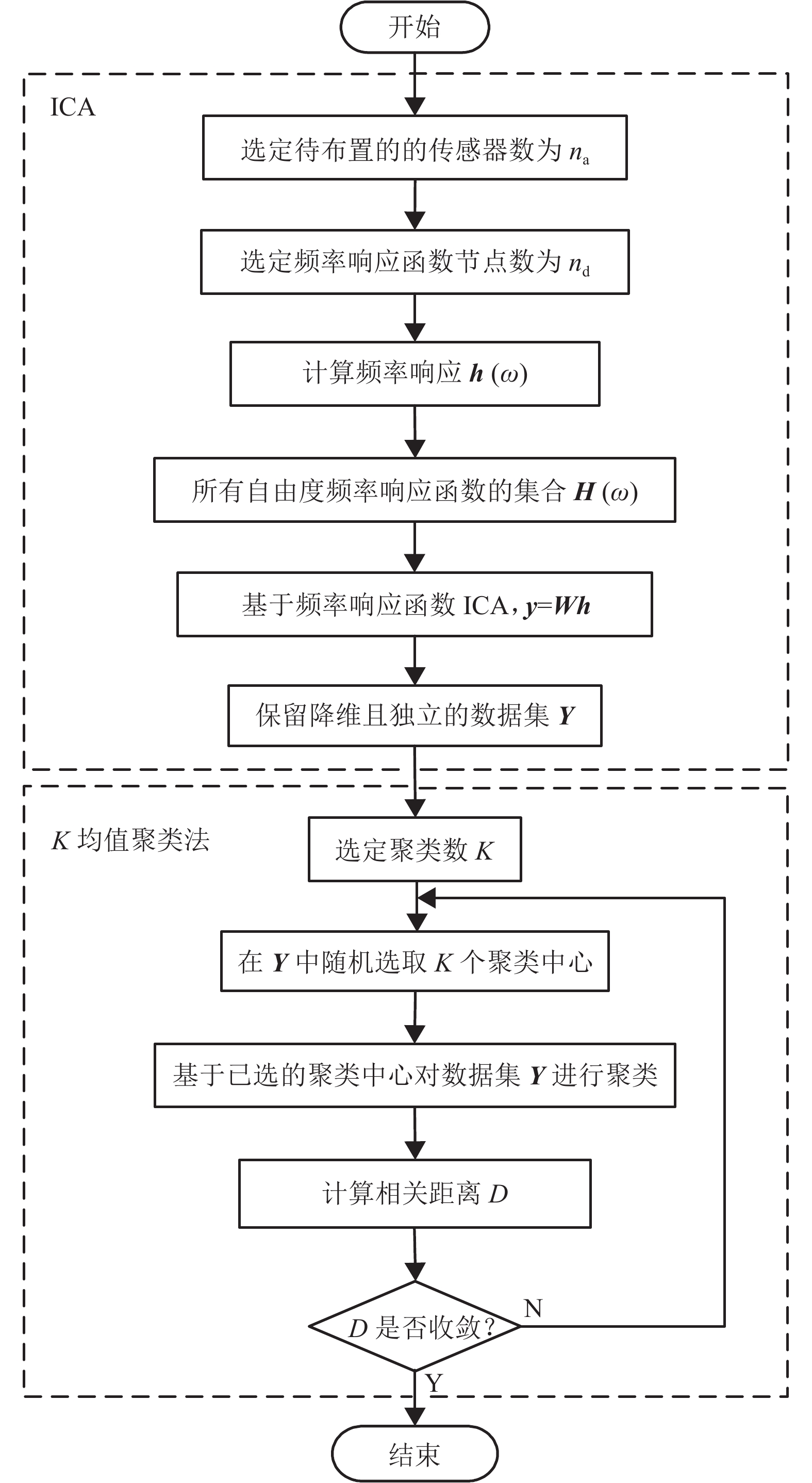
摘要: 为了实现传感器布置的位置和数量双重优化，提出了一种基于频率响应函数的传感器优化布置方法. 首先，对结构进行模态分析并提取模态振型，计算结构的频率响应函数；然后，基于独立分量分析和K-均值聚类法优化传感器布置位置；最后，计算不同传感器数量对应的布置结果的Fisher信息矩阵及其熵，信息熵的极小值对应的传感器数量即为传感器布置最优的数量. CRH3型动车组构架传感器优化布置结果表明，传感器均布置在符合国际铁路联盟标准UIC615-4规定的所有工况下构架产生最大应力位置附近，并且布置结果可以使数量有限的传感器获得的信息量最大化.Abstract: To realize both location and quantity optimization, a method of optimal sensor placement based on a frequency response function is proposed. First, the structure modal analysis was conducted and mode shapes were extracted, and the frequency response function of the structure was calculated. Then, based on independent component analysis and the K-means clustering method, the sensors’ positions were optimized. Finally, the Fisher information matrices and their entropies corresponding to the placement results with different numbers of sensors were calculated. The number of sensors corresponding to minimum information entropy is the optimal number. The simulation results of the CRH3 frame show that all sensors are placed near the maximum stress positions, meeting the UIC615-4 standard, and also show that the result of sensor placement can maximize the information with limited sensors.
-
图 3 悬臂梁Fisher信息矩阵信息熵值
Figure 3. Entropy of Fisher information matrix of cantilever beam
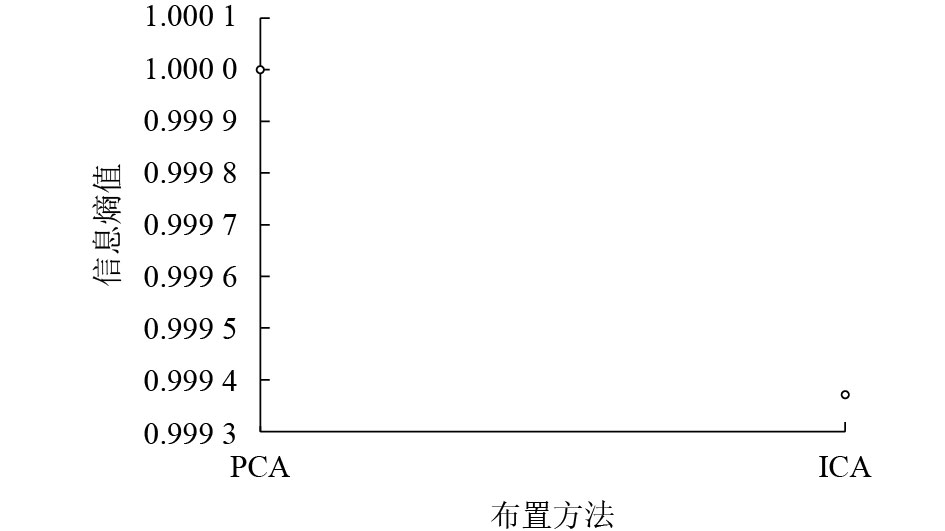
表 1 PCA与ICA特性简要比较
Table 1. Brief comparison of the characteristics between PCA and ICA
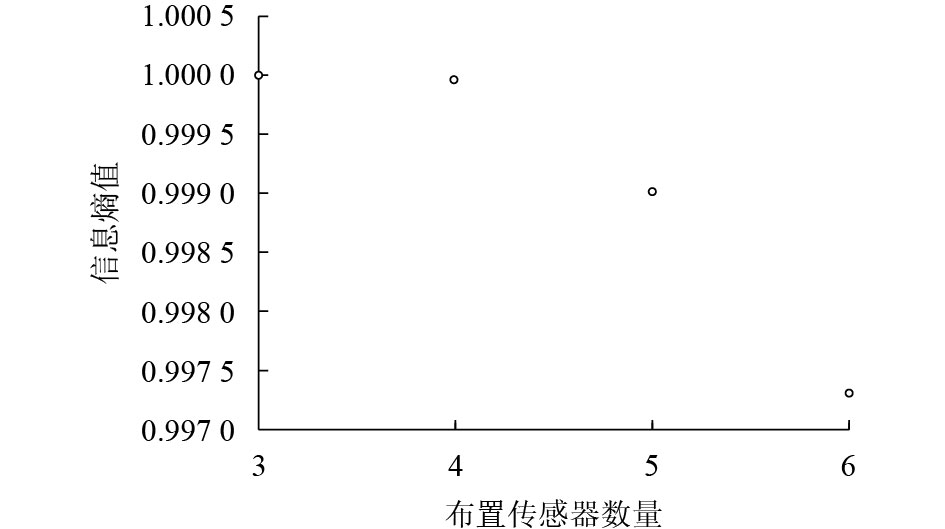
项目 PCA ICA 处理信号类型 高斯信号 非高斯信号 统计特性 二阶 高阶 处理效果 得到非相关分量 得到独立分量 
下载: 导出CSV
表 2 悬臂梁布置结果
Table 2. Results of sensor placement of cantilever beam
传感器数目 布置位置 3 1、19、25 4 1、17、19、24 5 1、11、14、17、30 6 1、5、11、14、17、25
下载: 导出CSV
-
WANG J, LAW S S, YANG Q S. Sensor placement method for dynamic response reconstruction[J]. Journal of Sound & Vibration, 2014, 333(9): 2469-2482. YI T, LI H, SONG G, et al. Optimal sensor placement for health monitoring of high-rise structure using adaptive monkey algorithm[J]. Structural Control & Health Monitoring, 2015, 22(4): 667-681. 詹杰子,余岭. 传感器优化布置的有效独立-改进模态应变能方法[J]. 振动与冲击,2017,36(1): 82-87.ZHAN Jiezi, YU Ling. An effective independence-improved modal strain energy method for optimal sensor placement[J]. Journal of Vibration And Shock, 2017, 36(1): 82-87. 陈春强,陈前. 电流变夹层板控制系统的传感器优化布置[J]. 振动与冲击,2017,36(4): 132-138.CHEN Chunqiang, CHEN Qian. Optimal sensor placement in the control system of a sandwich plate with electro-rheological fluid[J]. Journal of Vibration and Shock, 2017, 36(4): 132-138. 王伟,游鹏辉,钟万里,等. 薄壁小直径管道导波探伤的传感器布置方案优化[J]. 中南大学学报(自然科学版),2016,47(7): 2254-2259.WANG Wei, YOU Penghui, ZHONG Wanli, et al. Optimization of guided wave sensors distribution along thin-walled small-diameter pipe[J]. Journal of Central South University (Science and Technology), 2016, 47(7): 2254-2259. LI S, ZHANG H, LIU S, et al. Optimal sensor placement using FRFs-based clustering method[J]. Journal of Sound & Vibration, 2016, 385(12): 69-80. 许昕,潘宏侠,潘铭志. 独立分量分析在自动机振动信号处理中的应用[J]. 振动、测试与诊断,2016,36(1): 120-125.XU Xin, PAN Hongxia, PAN Mingzhi. Estimation of the unbalance of rotor system based on robust regression analysis[J]. Journal of Vibration,Measurement & Diagnosis, 2016, 36(1): 120-125. 曾生根,王小敏,范瑞彬,等. 基于独立分量分析的遥感图像分类技术[J]. 遥感学报,2004,8(2): 150-157.ZENG Shenggen, WANG Xiaomin, FAN Ruibin, et al. Remote image classification based on independent component analysis[J]. Journal of Remote Sensing, 2004, 8(2): 150-157. 陈法法,杨勇,马婧华,等. 信息熵与优化LS-SVM的轴承性能退化模糊粒化预测[J]. 仪器仪表学报,2016,37(4): 779-787. doi: 10.3969/j.issn.0254-3087.2016.04.009CHEN Fafa, YANG Yong, MA Jinghua, et al. Fuzzy granulation prediction for bearing performance degradation based on information entropy and optimized LS-SVM[J]. Chinese Journal of Scientific Instrument, 2016, 37(4): 779-787. doi: 10.3969/j.issn.0254-3087.2016.04.009 KAMMER D C. Sensor placement for on orbit modal identification of large space structures[J]. Journal of Guidance,Control,and Dynamics, 1991, 14(2): 252-259. 何浩祥,闫维明,张爱林. 面向结构健康监测的传感器数量及位置优化研究[J]. 振动与冲击,2008,27(9): 131-134. doi: 10.3969/j.issn.1000-3835.2008.09.031HE Haoxiang, YAN Weiming, ZHANG Ailin. Dynamic characteristic analysis of fluid-structure interaction in steam generator tubes[J]. Journal of Vibration and Shock, 2008, 27(9): 131-134. doi: 10.3969/j.issn.1000-3835.2008.09.031 International Union of Railways. Motive power units-bogies and running gear-bogie frame structure strength tests: CodeUIC615-4[S]. Paris: International Union of Railways, 2003 李德春,何龙军,陈媛媛,等. 基于改进粒子群算法的应变传感器优化布置[J]. 振动、测试与诊断,2014,34(4): 610-615. doi: 10.3969/j.issn.1004-6801.2014.04.002LI Dechun, HE Longjun, CHEN Yuanyuan, et al. Optimal strain sensor placement based on an improved particle swarm optimization algorithm[J]. Journal of Vibration,Measurement & Diagnosis, 2014, 34(4): 610-615. doi: 10.3969/j.issn.1004-6801.2014.04.002 张楠,彭珍瑞,殷红,等. 基于熵值法的目标模态最优数目确定新方法[J]. 铁道科学与工程学报,2018,15(2): 483-488. doi: 10.3969/j.issn.1672-7029.2018.02.028ZHANG Nan, PENG Zhenrui, YIN Hong, et al. Entropy-based approach for determining the optimal number of target modes[J]. Journal of Railway Science and Engineering, 2018, 15(2): 483-488. doi: 10.3969/j.issn.1672-7029.2018.02.028 期刊类型引用(15)
1. 徐秀丽，钱思博，李洪涛，吴冲，王仁贵，李琦，丁兴国，李枝军，李雪红. 新型开口肋正交异性钢桥面板疲劳性能对比试验研究. 土木工程学报. 2025(03): 50-67 . 
百度学术2. 鲁乃唯，刘静，王凯，王鸿浩. 随机轮载下钢桥面顶板与纵肋焊缝疲劳裂纹扩展特性研究. 振动与冲击. 2024(01): 193-201 . 百度学术3. 宋旭明，罗祥威，季苏瑶，唐冕. 基于断裂力学的横隔板弧形切口CFRP加固参数研究. 中南大学学报(自然科学版). 2024(03): 1046-1055 . 百度学术4. 邹晓琴. 正交异性钢桥面板U肋顶板全熔透焊缝制造工艺与疲劳性能研究. 公路. 2024(09): 72-78 . 百度学术5. 彭振楠，宋神友，陈焕勇. 正交异性钢桥面顶板U肋全熔透焊接接头研发及疲劳性能研究. 广东公路交通. 2024(06): 6-11 . 百度学术6. 袁毅，彭最. 武汉汉江湾桥主桥设计关键技术. 桥梁建设. 2023(01): 9-15 . 百度学术7. 宋松科，张翔，杜桃明，侯宇博，权新蕊. 焊接微裂纹缺陷对顶板与纵肋构造疲劳性能影响研究. 桥梁建设. 2023(01): 24-32 . 百度学术8. 雷丙超. 焊接缝疲劳开裂对斜拉桥钢桥面板的影响及加固方式. 现代机械. 2023(02): 98-102 . 百度学术9. 王晓，郭亚文，梁爱霞，张莹，张雪松. 基于断裂力学的钢桥面板纵肋顶板焊缝疲劳效应分析. 公路交通科技. 2023(03): 105-114 . 百度学术10. 赵秋，唐琨，黄冠铭，林铮哲. 对接焊缝初始缺陷对疲劳寿命影响规律研究. 合肥工业大学学报(自然科学版). 2023(04): 473-480 . 百度学术11. 王大鹏，王景春，张先萌，张振波，徐强. 考虑列车荷载的隧道衬砌裂缝疲劳扩展可靠性分析. 中国铁道科学. 2023(06): 95-102 . 百度学术12. 张亚海，郭宝圣，张卫国，陈方怀. 钢桥面板-纵肋双面焊缝疲劳裂纹应力强度因子. 土木与环境工程学报(中英文). 2022(03): 62-70 . 百度学术13. 张清华，李俊，袁道云，朱金柱，崔闯. 高疲劳抗力钢桥面板的疲劳问题Ⅰ:模型试验. 中国公路学报. 2021(03): 124-135 . 百度学术14. 李丹，张启伟，姜旭. 钢桥面板纵肋-顶板焊缝细节疲劳裂纹的应力强度因子分析. 城市道桥与防洪. 2021(07): 249-252+257+25 . 百度学术15. 张清华，李俊，袁道云，朱金柱，崔闯. 深圳至中山跨江通道钢桥面板结构疲劳试验研究. 土木工程学报. 2020(11): 102-115 . 百度学术其他类型引用(16)
-
下载:
百度学术
点击查看大图
图(7) / 表(3)
计量
- 文章访问数: 441
- HTML全文浏览量: 209
- PDF下载量: 3
- 被引次数: 31