Application of Digital One-Cycle Control for Current in Electromagnetic Suspension System
-
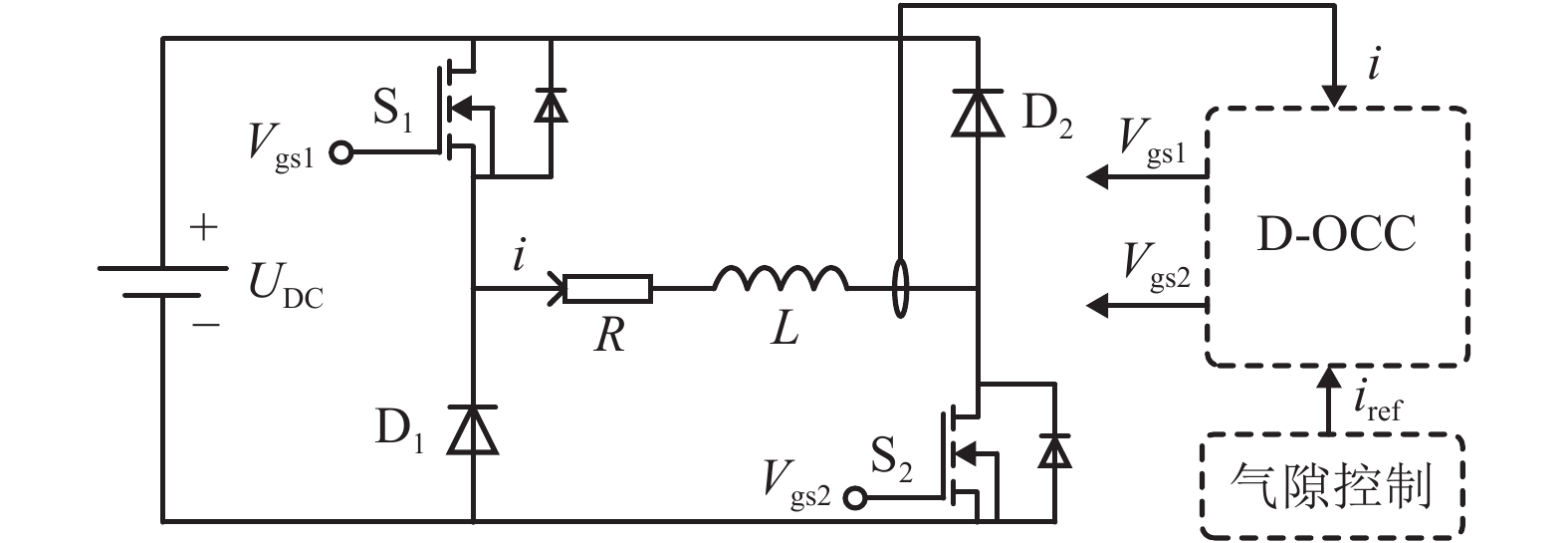
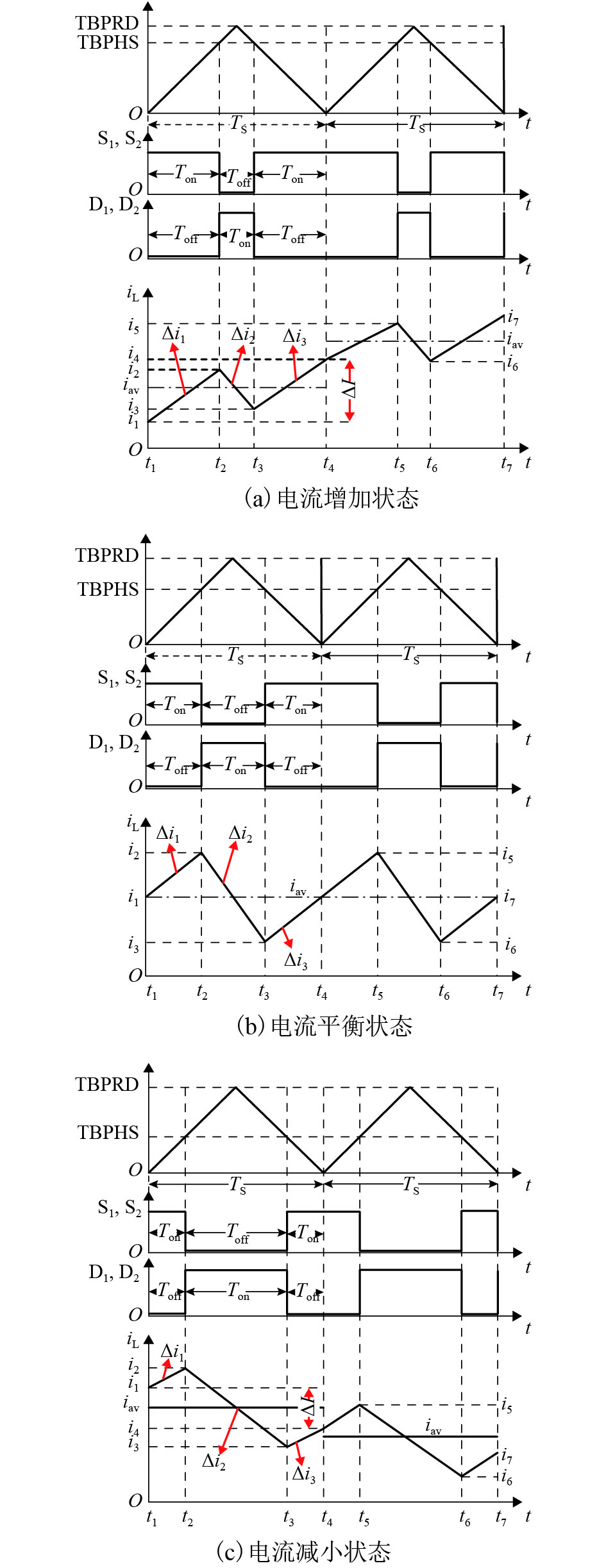
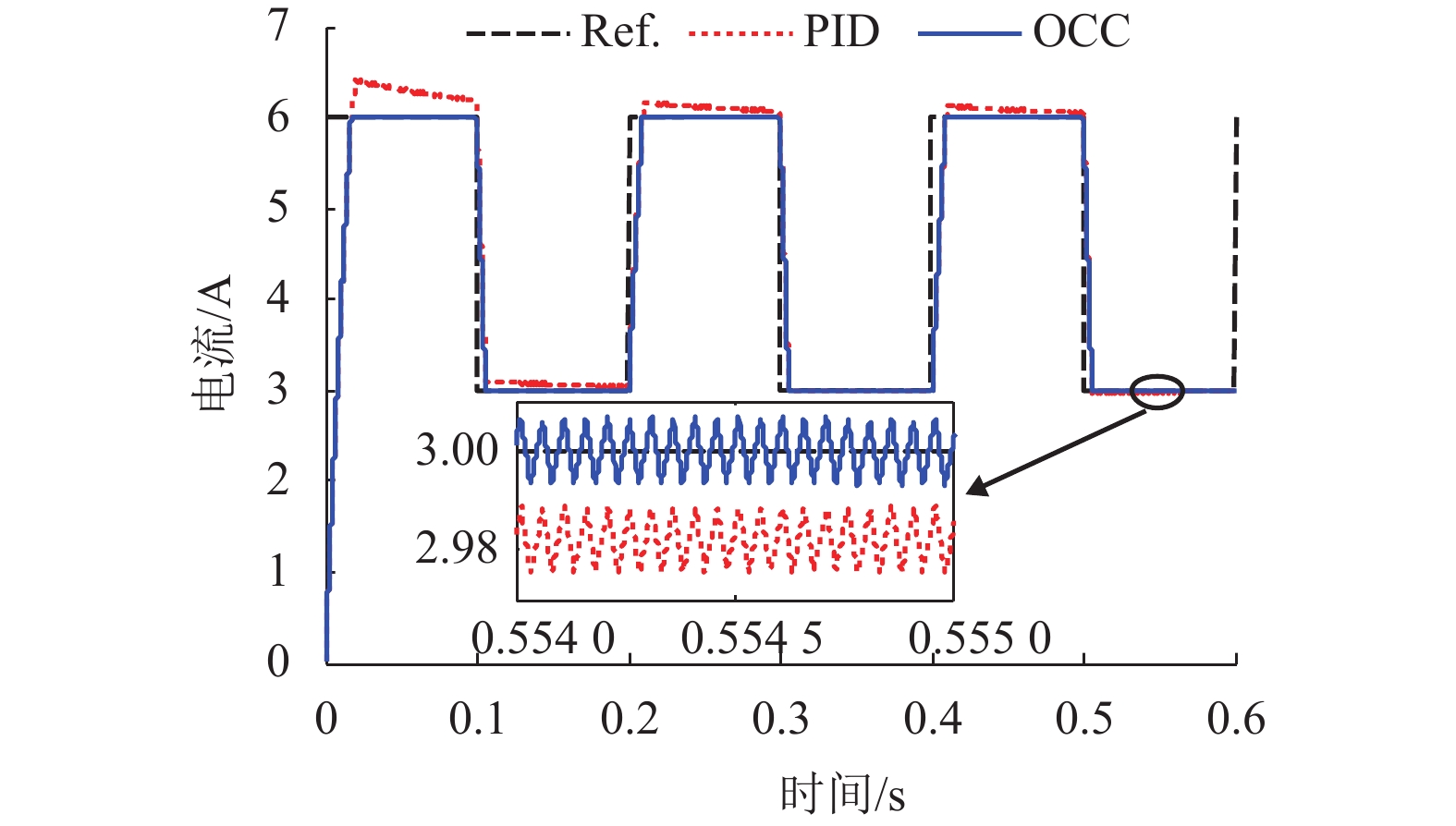
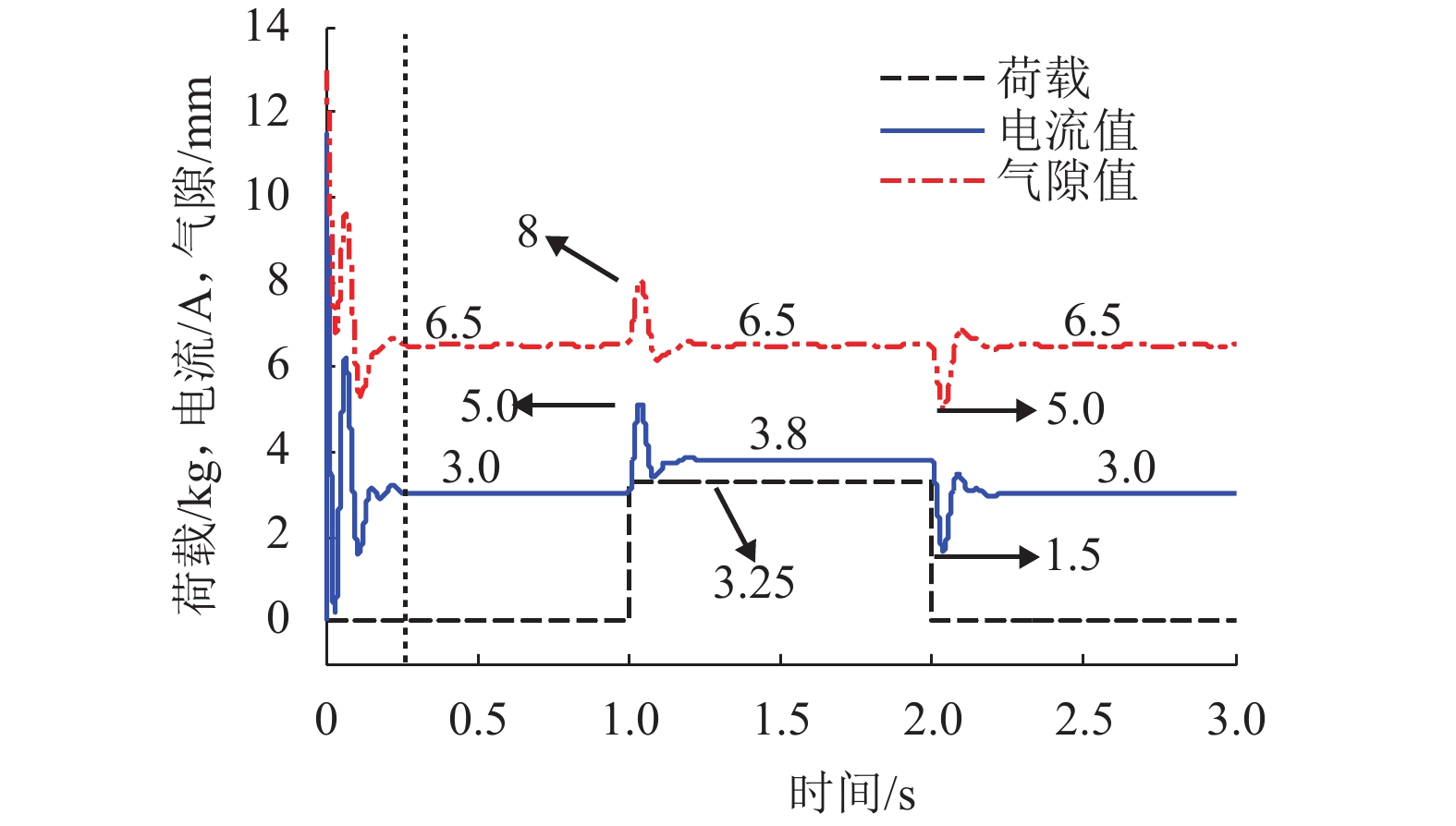
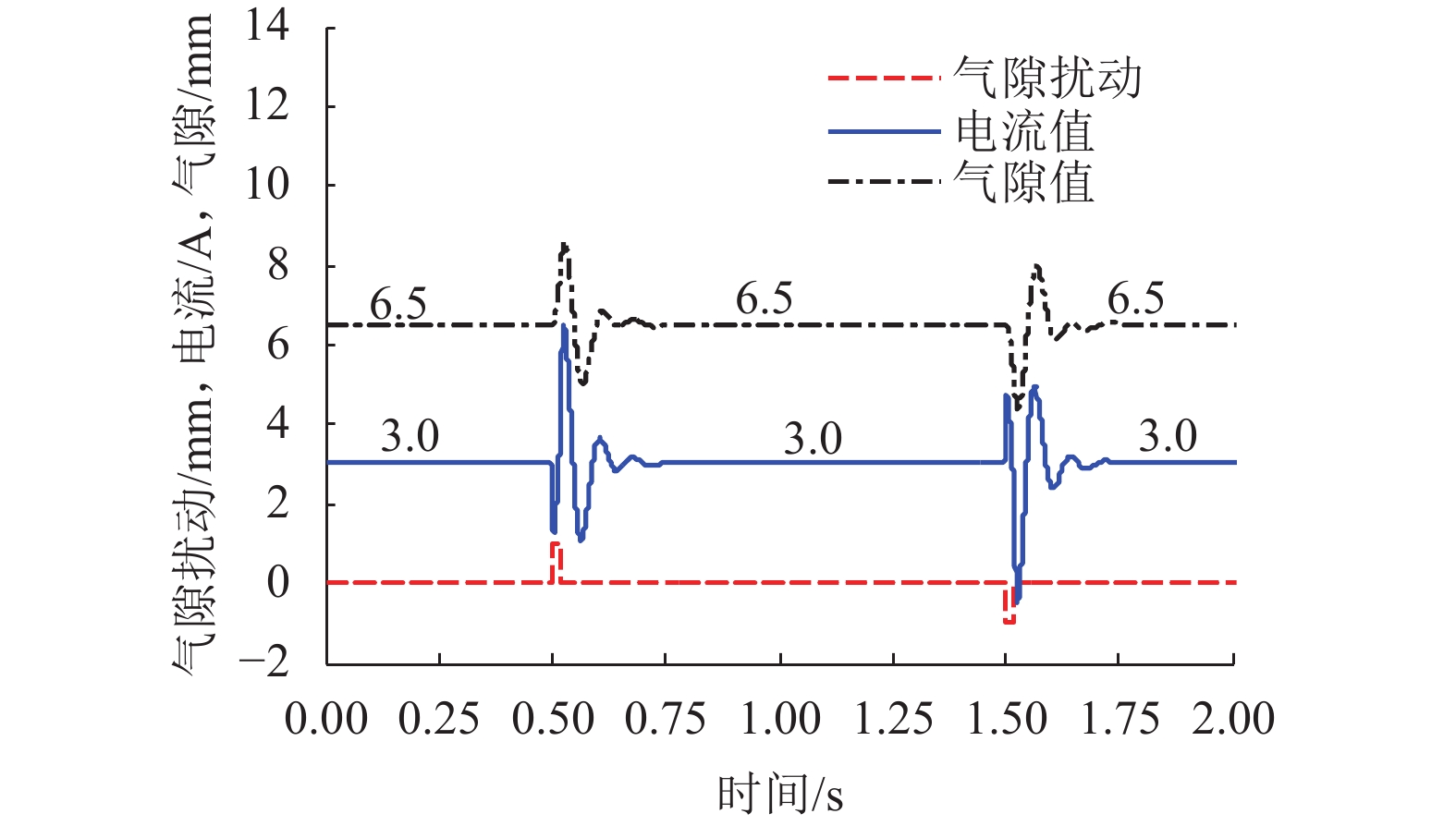
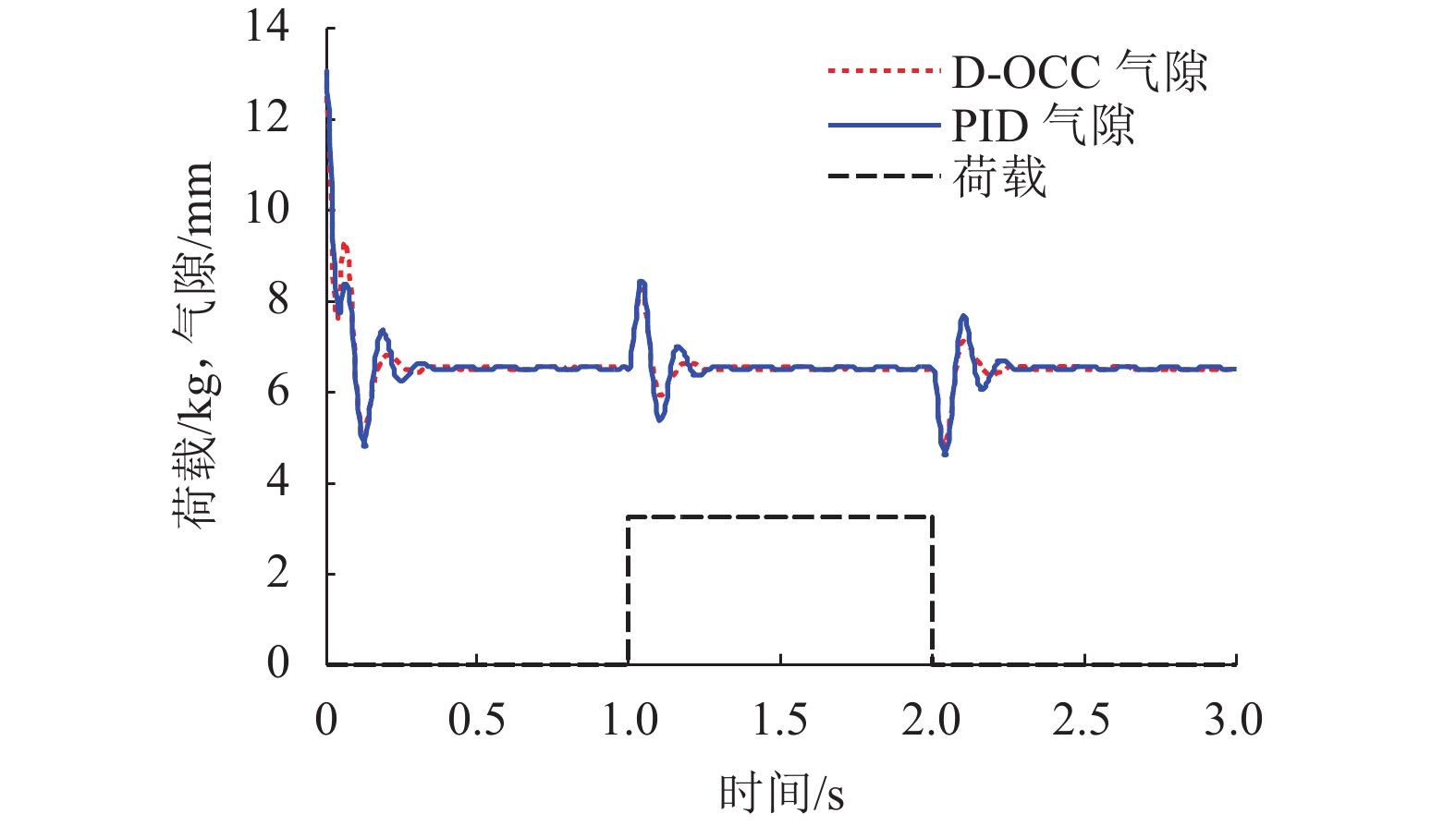
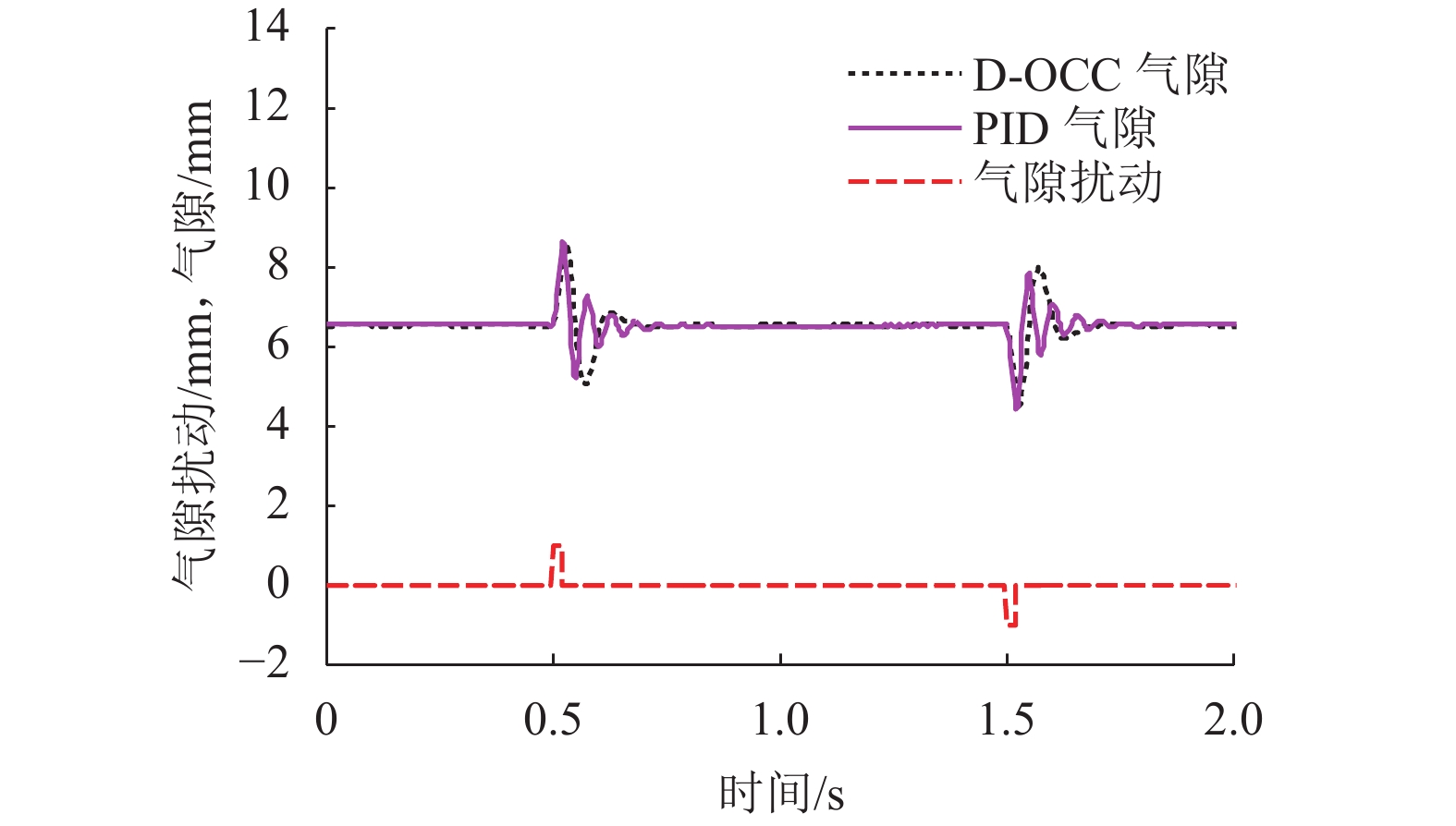
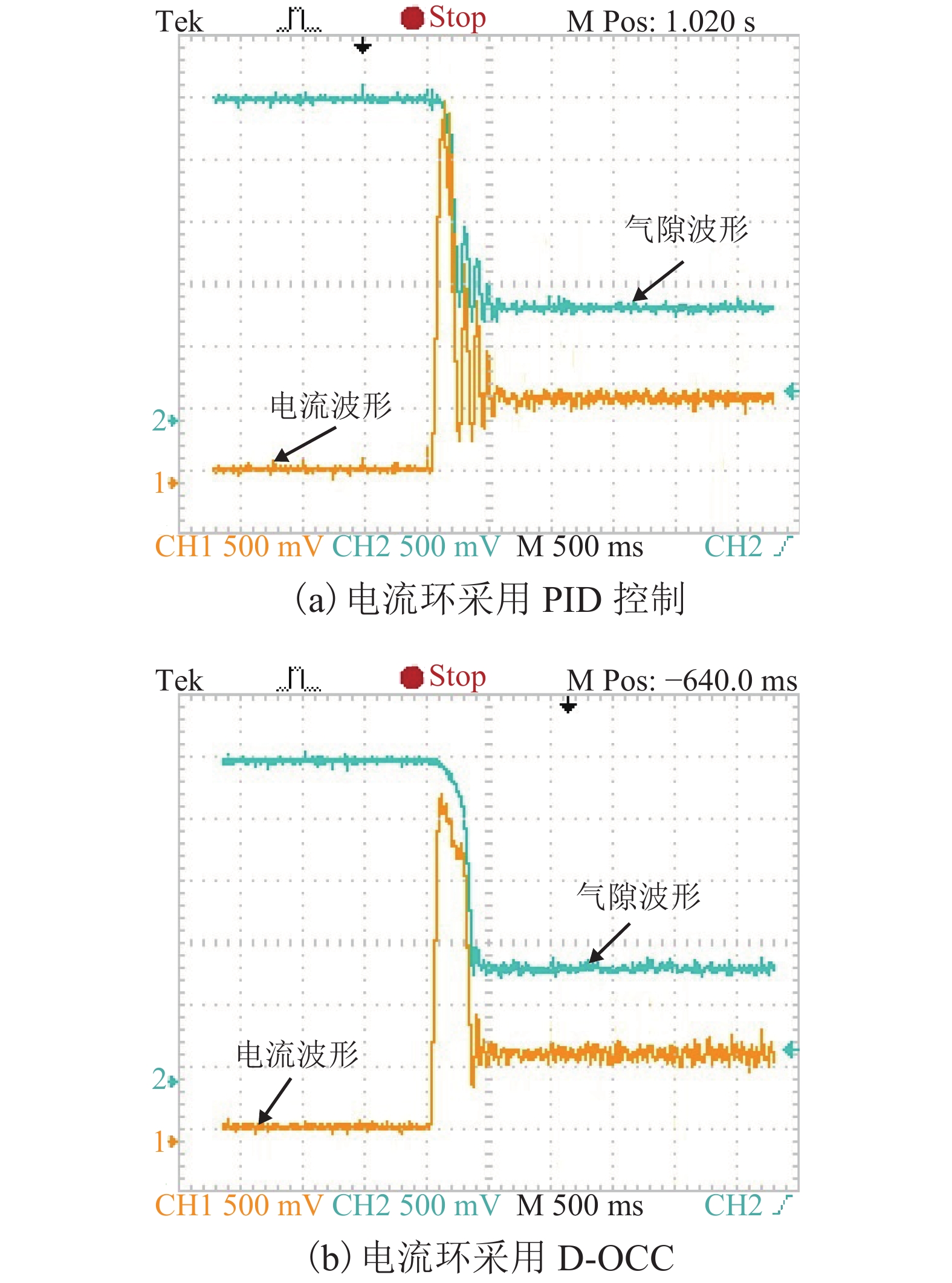
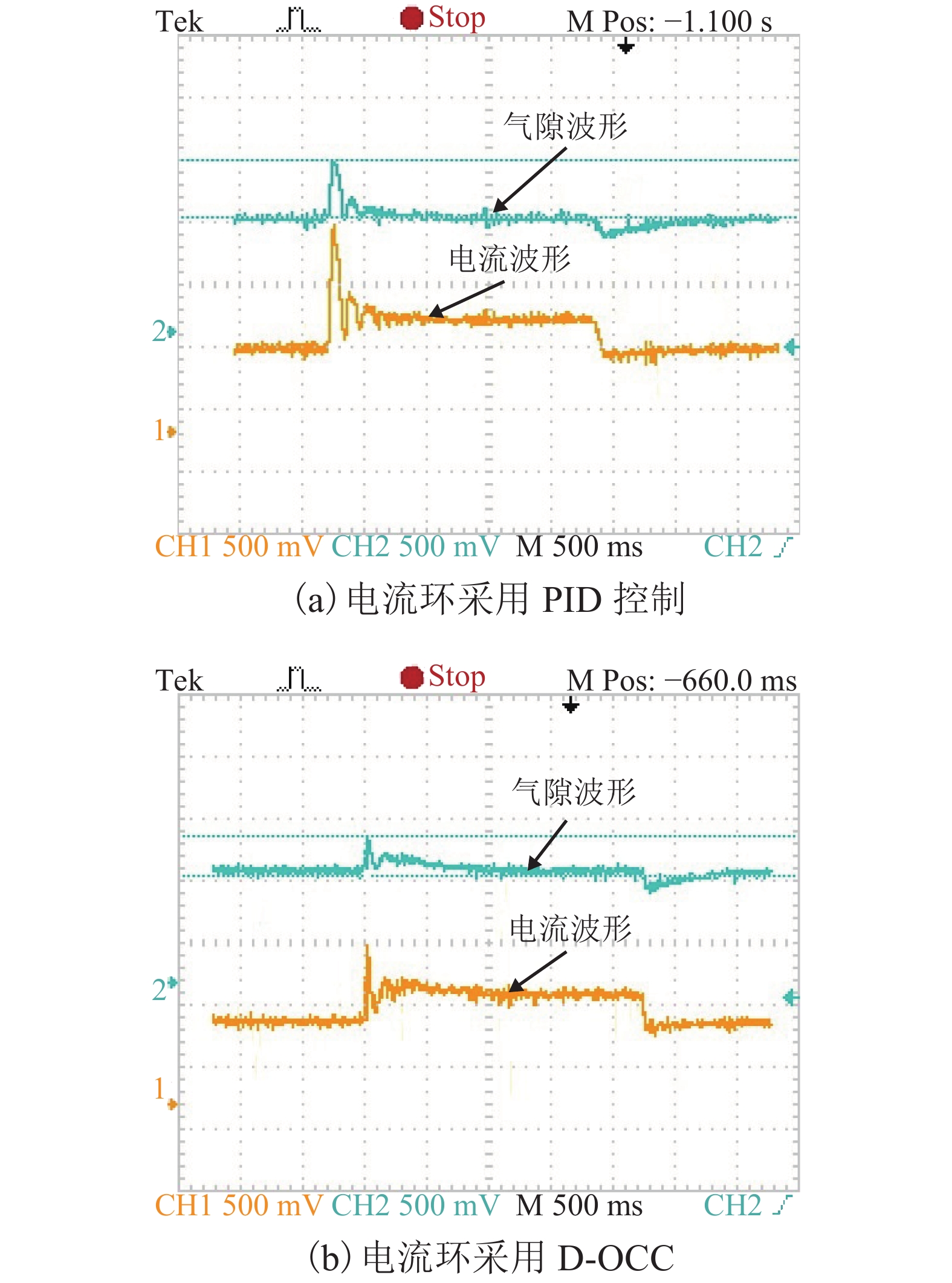
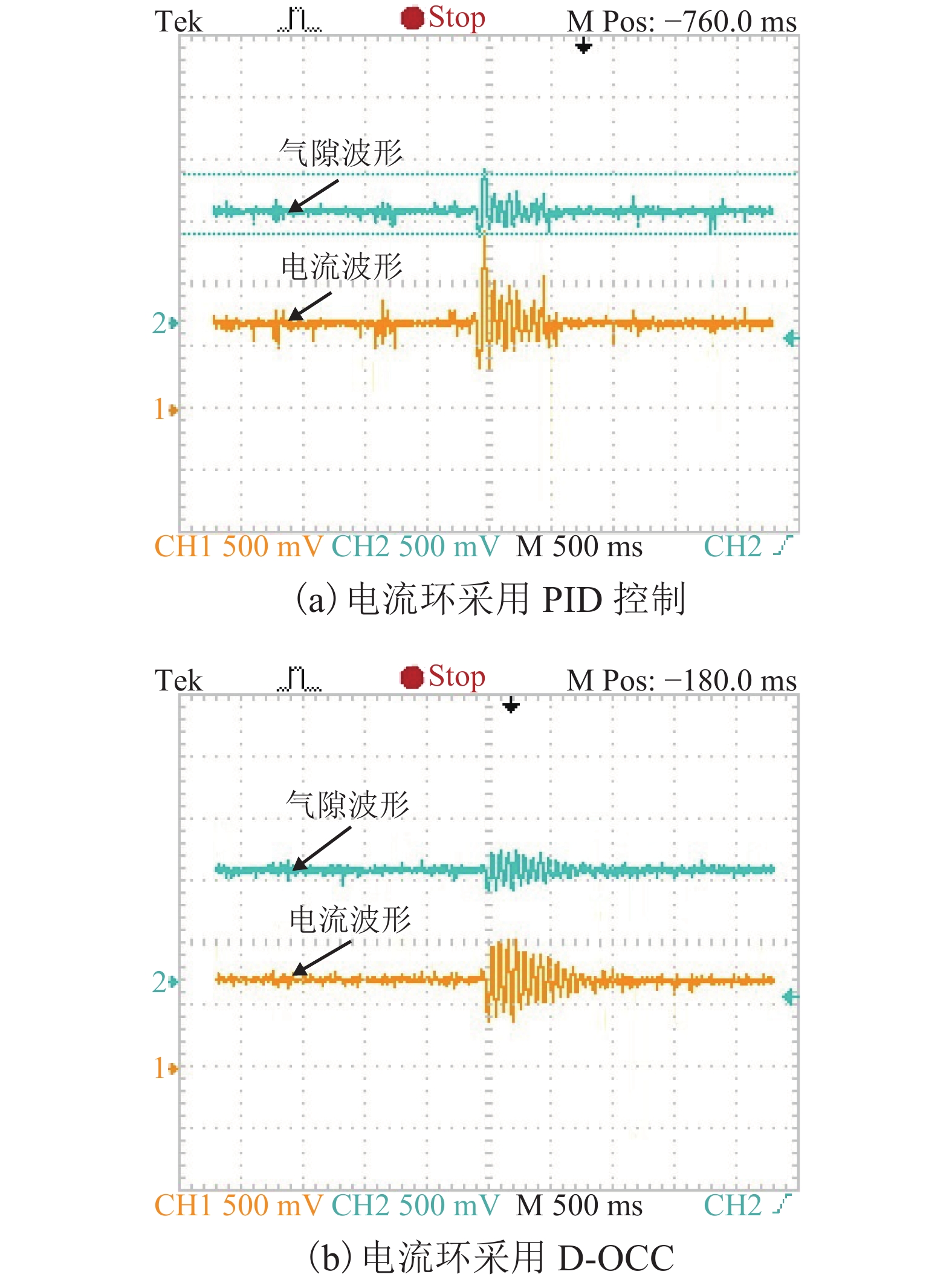
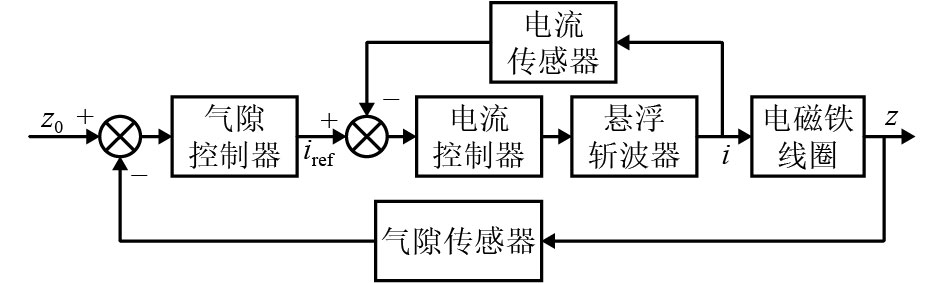
摘要: 在串级控制的电磁悬浮系统中，电流环的响应速度和精度对整个悬浮控制起着至关重要的作用. 为了加快悬浮系统电流环的响应速度以及减小跟随误差，基于TMS320F28335设计了EMS （electromagnetic suspension system）的数字单周期控制（digital one-cycle control，D-OCC）电流控制器. 以悬浮斩波器为研究对象，建立起D-OCC的数学模型，对额定悬浮工作点处斩波器电流的D-OCC算法进行了详细推导；通过Simulink平台对算法进行仿真验证，并将D-OCC的电流环投入到实际悬浮系统中进行悬浮实验. 实验结果表明：对频率为5 Hz，幅值为3 A的方波信号进行跟随时，传统PID控制在方波上升沿和下降沿均存在一定的超调，且稳定后存在不小于20 mA的跟随误差，D-OCC在调节过程中不存在超调，且稳定后没有跟随误差，说明D-OCC算法能够实现对指令电流快速、准确跟随；采用电流环D-OCC的悬浮系统起浮过程需要约0.4 s的调整时间，并且悬浮稳定后可以克服50%荷载扰动和1.5 mm气隙扰动，说明该方法可以实现系统稳定悬浮，且具有较强的鲁棒性能.Abstract: In an electromagnetic suspension system （EMS） with cascade control, the response speed and accuracy of the current loop play a vital role in the overall suspension control. A current controller was designed for digital one-cycle control （D-OCC） based on TMS320F28335 for the suspension system, in order to improve the response speed of the current loop and reduce the following error. Taking a chopper circuit as the research object, the D-OCC’s mathematical model was established and the control algorithm of rated suspension point was derived in detail. The algorithm was validated through Simulink, and the current loop controlled by D-OCC was incorporated into the actual EMS. Experimental results show that the conventional PID control has a certain overshoot at the wave’s rising and falling edges when a square wave signal with frequency of 5 Hz and amplitude of 3 A is followed. Moreover, there is a following error of not less than 20 mA after the stabilization. However, there is no overshoot in the adjustment process and no following error after stabilization, when following the same wave with the method of D-OCC. This means that the D-OCC algorithm can follow the instruction current quickly and accurately. The floating process of the suspension system using the D-OCC current loop requires an adjustment time of about 0.4 s, and the system can overcome the 50% load disturbance and the 1.5 mm air gap disturbance; this shows that the method can achieve the system stable levitation and has strong robust performance.
-
Key words:
- electromagnetic suspension system /
- cascade control /
- current loop /
- chopper /
- digital one-cycle control
-
图 3 不同电流状态增-减计数PWM模式D-OCC波形
Figure 3. Waveform of D-OCC based on up-down count PWM mode in different current states
图 5 数字单周期电流控制悬浮系统起浮及加减载仿真波形
Figure 5. Simulation waveforms of levitation system using current D-OCC with conditions of no-load floating，50% loading and load shedding
图 6 数字单周期电流控制悬浮系统气隙扰动仿真波形
Figure 6. Simulation waveform of air gap disturbance condition in levitation system using current D-OCC
图 7 两种控制方式空载起浮及50%加减载气隙波形比较
Figure 7. Comparison of air gap waveforms in two control modes with conditions of no-load floating，50% loading and load shedding
图 8 两种控制方式1 mm气隙扰动时气隙波形比较
Figure 8. Comparison of air gap waveforms in two control modes with 1 mm air gap disturbance
图 10 单周期电流控制悬浮系统起浮实验波形
Figure 10. Experimental waveform of floating condition in EMS using current D-OCC
图 11 单周期电流控制悬浮系统加减载实验波形
Figure 11. Experimental waveform of loading and load shedding condition in EMS using current D-OCC
图 12 单周期电流控制悬浮系统气隙扰动实验波形
Figure 12. Experimental waveform of air gap disturbance condition in EMS using current D-OCC
表 1 单电磁铁模型参数
Table 1. Single electromagnet model parameters
参数 符号 取值 电磁铁等效荷载/kg m 6.5 电磁铁磁极面积/m2 A 0.003 75 电磁铁线圈数/匝 N 500 真空磁导率/（H•m–1） μ 4 ${\text{π}}$ × 10–7 初始悬浮气隙/m z0 0.006 5 
下载: 导出CSV
表 2 仿真参数
Table 2. Simulation parameters
参数 符号 取值 直流母线电压/V UDC 48 开关频率/kHz f 20 线圈等效电阻/Ω R0 2 线圈等效电感/mH L0 90.62
下载: 导出CSV
-
朱开锋,董金文,雷学国,等. 电流最小方差控制在电磁吸力悬浮系统中的应用[J]. 电气开关,2010,48(1): 58-60 doi: 10.3969/j.issn.1004-289X.2010.01.020ZHU Kaifeng, DONG Jinwen, LEI Xueguo, et al. Application of the current minimum variance control in EMS system[J]. Electric Switchgear, 2010, 48(1): 58-60 doi: 10.3969/j.issn.1004-289X.2010.01.020 张德魁,赵雷,赵鸿宾. 电流响应速度及力响应速度对磁轴承系统性能的影响[J]. 清华大学学报(自然科学版),2001,41(6): 23-26 doi: 10.3321/j.issn:1000-0054.2001.06.007ZHANG Dekui, ZHAO Lei, ZHAO Hongbin. Effect of current response rate and force response rate on performance of magnetic bearing systems[J]. Jourrnal of Tsinghua University (Science and Technology), 2001, 41(6): 23-26 doi: 10.3321/j.issn:1000-0054.2001.06.007 蒋启龙,胡基士. 磁浮列车斩波器研究[J]. 电力电子技术,1997(2): 60-62JIANG Qilong, HU Jishi. Study of the maglev chopper[J]. Power Electronics, 1997(2): 60-62 李云钢,常文森. 磁浮列车悬浮系统的串级控制[J]. 自动化学报,1999,25(2): 247-251LI Yungang, CHANG Wensen. Cascade control of an EMS maglev vehicle’s levitation control system[J]. Acta Automatic Sinica, 1999, 25(2): 247-251 周媛. 三电平悬浮斩波器性能研究[J]. 电气传动,2011,41(12): 12-15 doi: 10.3969/j.issn.1001-2095.2011.12.003ZHOU Yuan. Performance analysis of a maglev chopper based on three-level control[J]. Electric Drive, 2011, 41(12): 12-15 doi: 10.3969/j.issn.1001-2095.2011.12.003 李云钢,柯朝雄,程虎. 磁浮列车悬浮控制器的电流环分析与优化设计[J]. 国防科技大学学报,2006,28(1): 94-97 doi: 10.3969/j.issn.1001-2486.2006.01.021LI Yungang, HE Chaoxiong, CHENG Hu. Analyzing and optimizing design of current-loop in the magnetic levitation controller on maglev vehicle[J]. Journal of National University of Defense Technology, 2006, 28(1): 94-97 doi: 10.3969/j.issn.1001-2486.2006.01.021 程金路,张承进. 自适应有限拍感应电机电流控制器设计[J]. 控制与决策,2005,20(10): 1097-1102 doi: 10.3321/j.issn:1001-0920.2005.10.003CHENG Jinlu, ZHANG Chenjin. Adaptive deadbeat current controller for induction machine drives[J]. Control and Decision, 2005, 20(10): 1097-1102 doi: 10.3321/j.issn:1001-0920.2005.10.003 张东升,梅雪松,郝晓红,等. 磁悬浮系统的电流控制方法[J]. 西安交通大学学报,2007,41(9): 1096-1100 doi: 10.3321/j.issn:0253-987x.2007.09.021ZHANG Dongshen, MEI Xuesong, HAO Xiaohong, et al. Current control method for magnetic suspension system[J]. Journal of Xi’an Jiaotong University, 2007, 41(9): 1096-1100 doi: 10.3321/j.issn:0253-987x.2007.09.021 SMEDLEY K M, CUK S. One-cycle control of switching converters[J]. IEEE Transactions on Power Electronics, 1995, 10(6): 625-633 doi: 10.1109/63.471281 万蕴杰,周林,张海,等. 单周控制的发展及其应用[J]. 高电压技术,2007,33(4): 163-169 doi: 10.3969/j.issn.1003-6520.2007.04.040WAN YunJie, ZHOU Lin, ZHANG Hai, et al. Development and application of one-cycle control[J]. High Voltage Engineering, 2007, 33(4): 163-169 doi: 10.3969/j.issn.1003-6520.2007.04.040 韦徵,陈新,陈杰,等. 基于D-OCC的三相PFC整流器输入电流相位滞后及闭环补偿[J]. 中国电机工程学报,2013,33(33): 42-49WEI Zheng, CHEN Xin, CHEN Jie, et al. Input current phase lag and closed loop compensation for three-phase PFC rectifiers based on one-cycle control strategy[J]. Proceedings of the CSEE, 2013, 33(33): 42-49 BARBATI M, CALUISI C, CECATI C. One-cycle controlled active rectifier for full digital implementation[C]//36th Annual Conference on IEEE Industrial Electronics Society. Glendale: [s.n.], 2010: 625-630 LOCK A S, FERNANDES D A, SILVA E R C, et al. A current based OCC technique implemented by DSP for a three-phase OCC rectifier[C]//40th Annual Conference of the IEEE Industrial Electronics Society. Dallas: IEEE, 2014: 5136-5142 凌雁波. D-OCC技术的研究和应用[D]. 南京: 南京航空航天大学, 2009 蒋真. 单相/三相逆变器的D-OCC研究[D]. 南京: 南京航空航天大学, 2011 刘程子. 适用于高速电机的混合型磁悬浮轴承设计及控制策略的研究[D]. 南京: 南京航空航天大学, 2015 PETRONE G, VITELLI M, SPAGNULOL G. Digital implementation of one cycle control in back to back converters[C]//IEEE International Symposium on Power Electronics for Distributed Generation Systems. Aalborg: IEEE, 2012: 344-348 Ul-HAQ A, CECATI C, KHALID H A. FPGA based one-cycle control of multilevel cascaded H-bridge inverter[C]//Fortieth Annual Conference of IEEE Industrial Electronics Society. Dallas: IEEE, 2015: 4628-4634 BAGAWADE S, JAIN P. Digital implementation of one-cycle controller （OCC） for AC-DC converters[C]// IEEE International Conference on Power Electronics, Drives and Energy Systems. Trivandrum: IEEE, 2017: 1-6 刘程子,邓智泉,曹鑫,等. 混合型磁悬浮轴承开关功放的单周期数字控制[J]. 中国电机工程学报,2015,35(22): 5899-5907LIU Chengzi, DENG Zhiquan, CAO Xin, et al. An one-cycle control digital control strategy for switching power amplifiers in hybrid magnetic levitation bearing systems[J]. Proceedings of the CSEE, 2015, 35(22): 5899-5907 HAO A, SHE L, LIU H, et al. Research of force feedback controlling on high speed maglev train guidance system[C]//IEEE International Conference on Control and Automation. Guangzhou: IEEE, 2007: 1381-1384 钟毅. 磁悬浮嵌入式控制系统基础理论和关键技术研究[D]. 武汉: 武汉理工大学, 2007 -
下载:
点击查看大图
计量
- 文章访问数: 509
- HTML全文浏览量: 297
- PDF下载量: 20
- 被引次数: 0