Seismic Response Analysis of High-Pier Bridge under Near-Fault Multiple Pulse Record Excitation
-
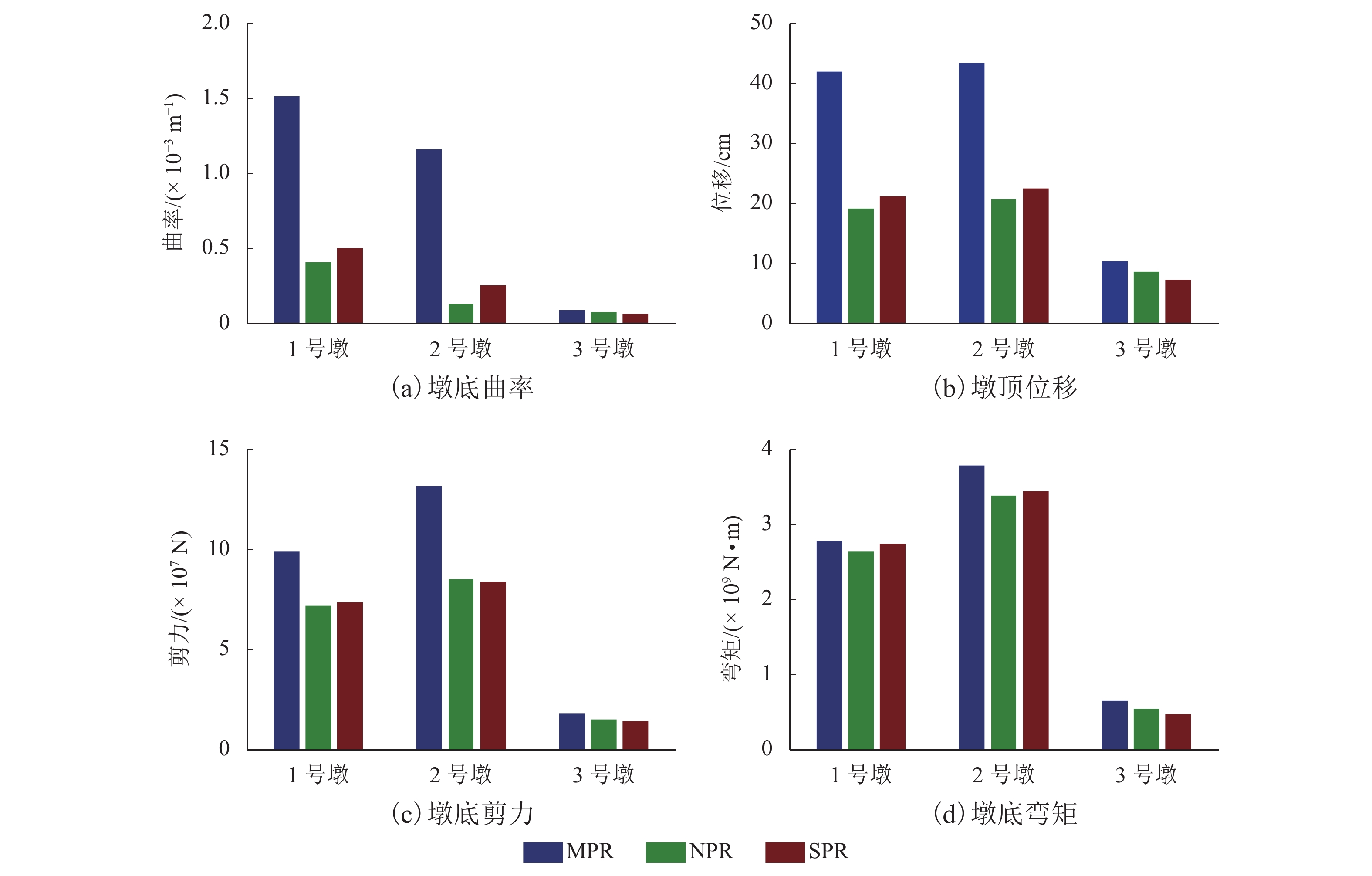
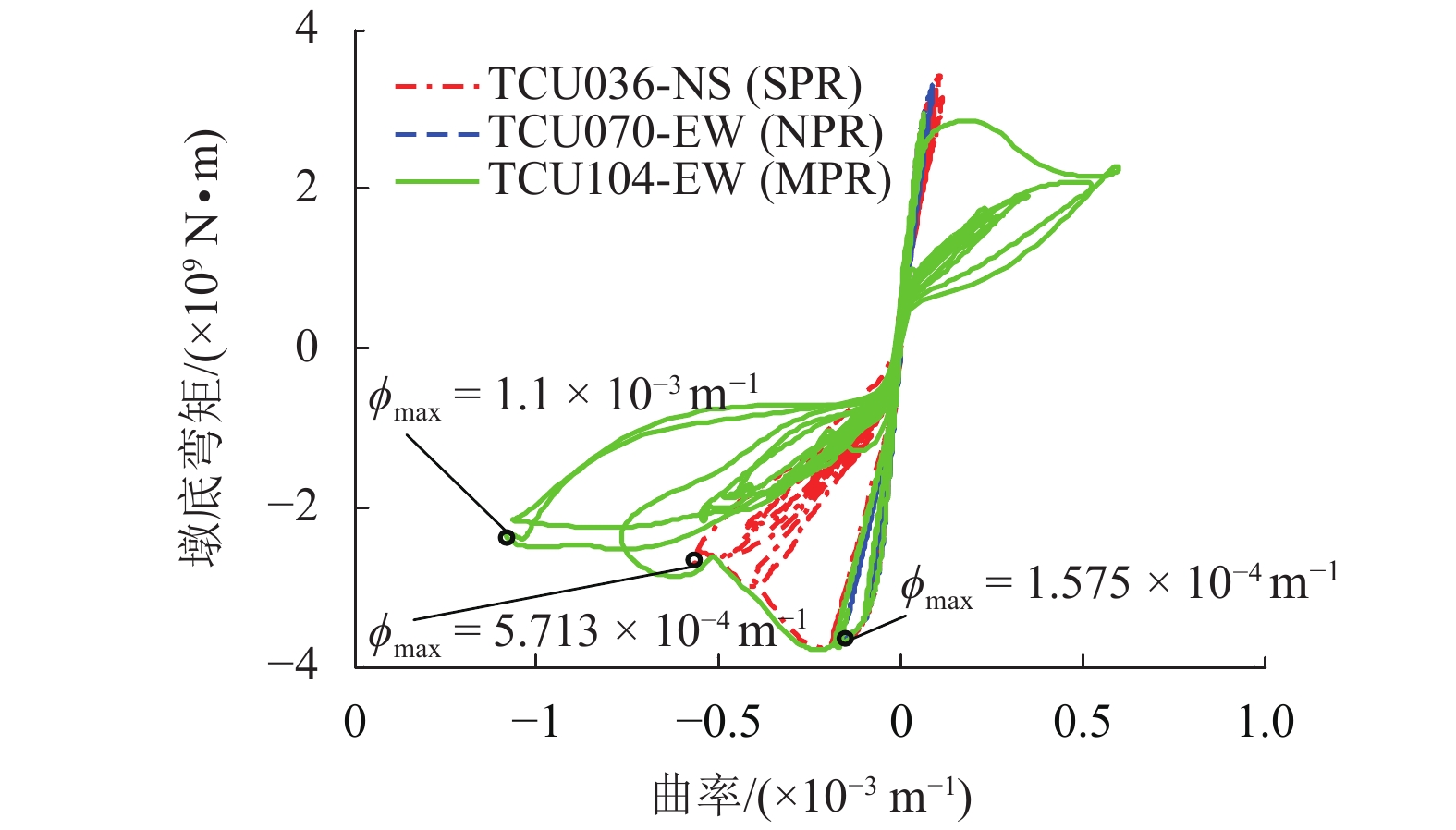
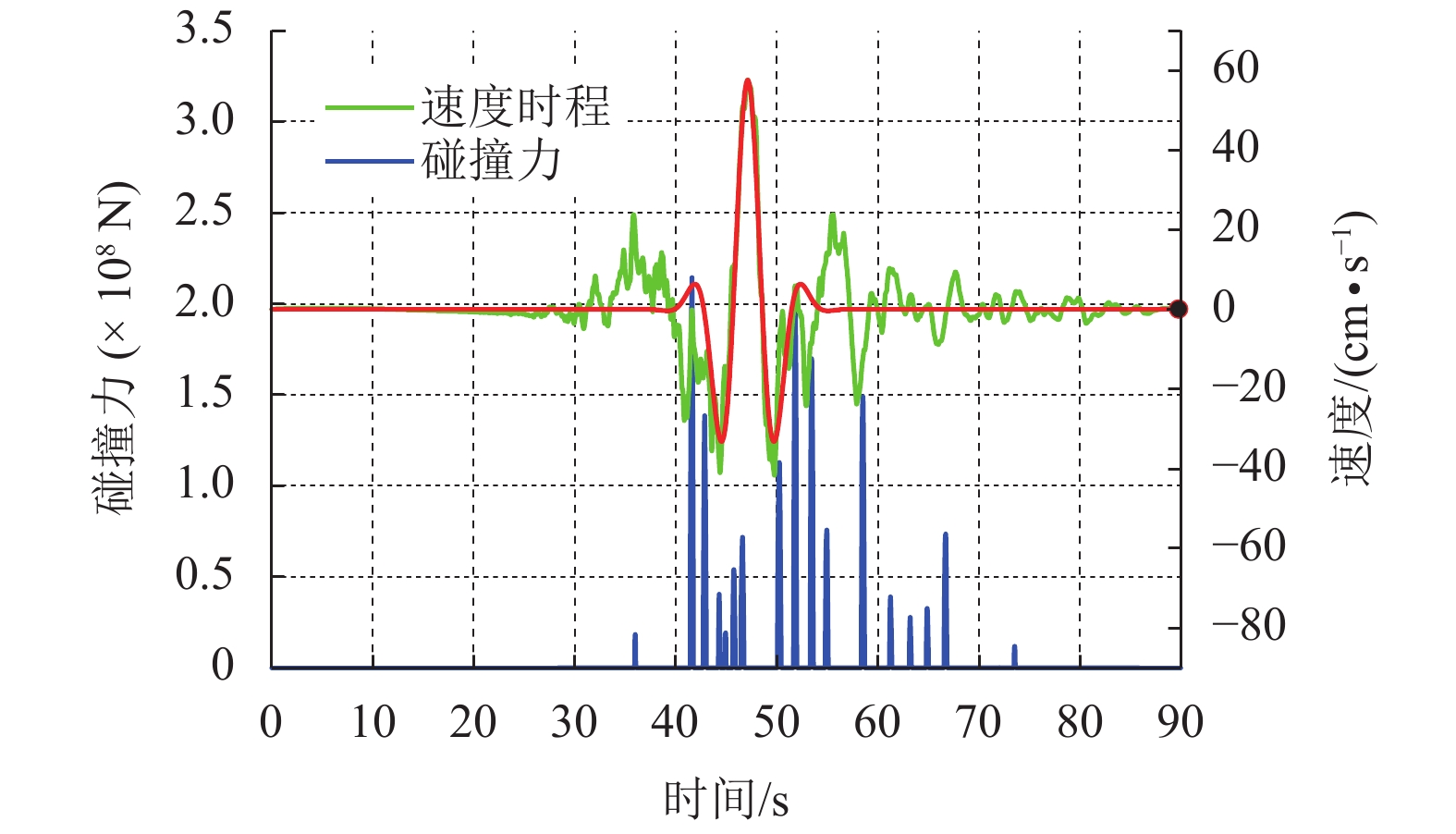
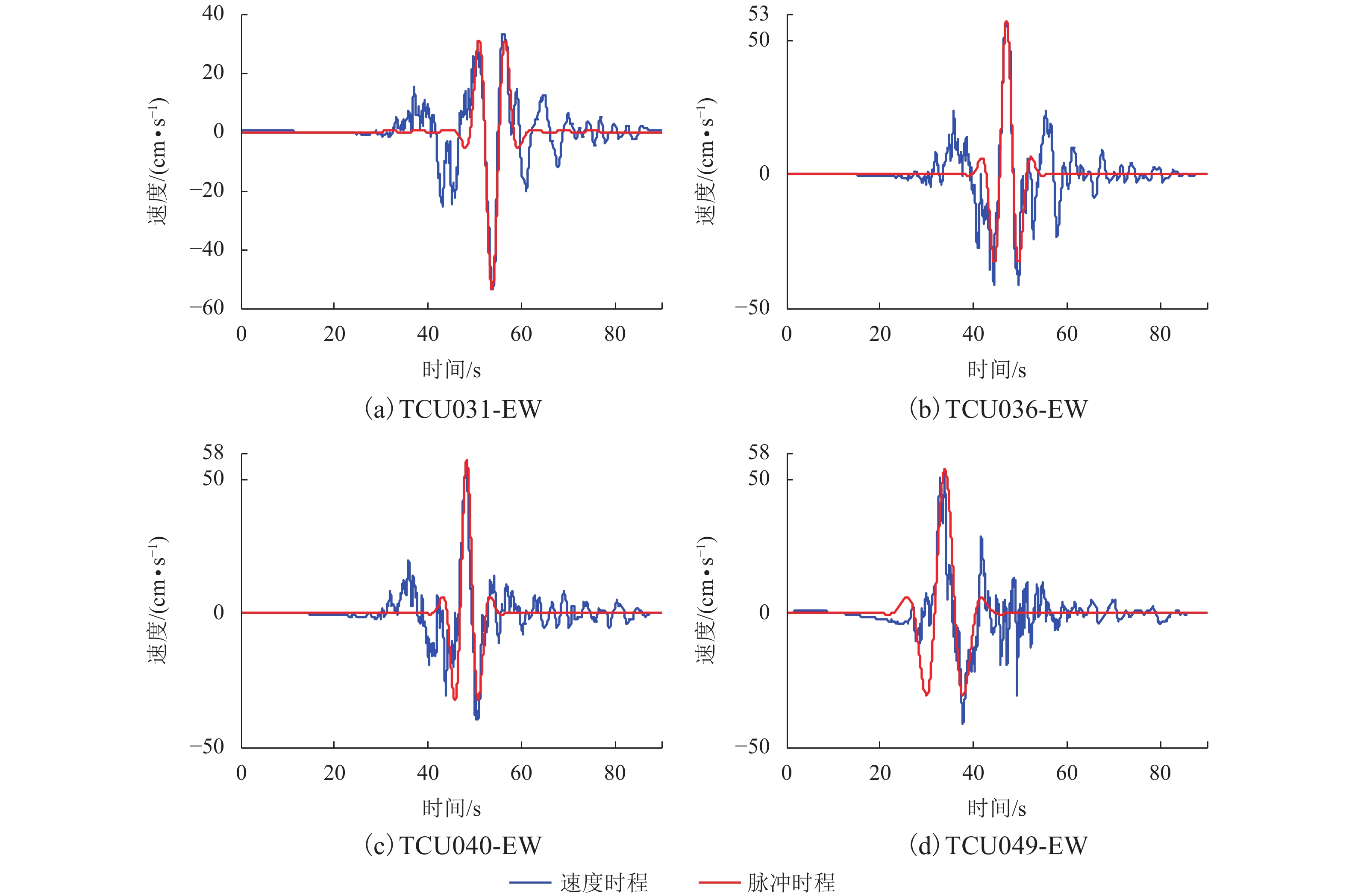
摘要: 为了研究近断层地震的多脉冲效应对不规则高墩大跨桥梁非线性地震响应的影响，首先，采用眼观识别的方法选取了典型的多脉冲、单脉冲和非脉冲3组地震动；然后，采用小波变换识别方法和能量识别方法对其脉冲性进行识别，研究了脉冲地震动识别方法对多脉冲地震动的适用性；最后，以某大跨度高墩桥梁为例，基于OpenSees建立了其非线性有限元模型，对其进行了非线性地震响应分析，对比研究了近断层多脉冲地震动及单脉冲地震动对不规则高墩桥梁非线性地震响应的影响. 研究结果表明：现有的近断层脉冲识别方法只适用于速度时程中只含有一个主脉冲的地震动，对于多脉冲地震动，其失效的可能性非常大；近断层脉冲地震动对不规则高墩桥梁具有更强的破坏性，特别是在多脉冲地震作用下，1号、2号两个高墩的墩顶位移需求分别增加了118.9%和109.6%，墩底弯矩和墩底曲率也有明显的增大；近场多脉冲地震作用下主梁的碰撞次数增大了3～5倍，碰撞力也会增大2～3倍，主梁更容易发生严重的碰撞破坏，在抗震设计时应采取适当防撞措施.Abstract: The multiple pulse effect of near-fault seismic records on the nonlinear seismic response of high pier railway bridges (HPRB) was investigated. First, three representative groups of seismic records, namely, single pulse record (SPR), multiple pulse record (MPR) and none pulse record (NPR) were selected by visual inspection. Second, pulse characteristics were quantitatively identified using wavelet analysis method (WAM) and energy-based approach (EBA) to investigate if impulse ground motion identification method was applicable to MPR. Finally, a typical HPRB, located in the southern region of China, was adopted as the research object, the non-linear finite element model was established in OpenSees platform, and the non-linear seismic response analysis of the HPRB was carried out. The effects of MPR and SPR on the nonlinear seismic response of the HPRB were compared. The results obtained from the analyses indicate that the WAM and EBA are applicable to ground motions with only one dominant pulse in the velocity history, and are not applicable to multiple pulse ground motions. Near-fault MPRs and SPRs pose the risk of stronger damage to irregular high pier bridges than NPRs. Under MPR excitation, the top displacement of pier 1 and pier 2 is, respectively, 118.9% and 109.6% larger than under NPR excitation. The bending moment and the curvature at the bottom of the pier also increase. Near-fault MPR is found to produce pounding force and pounding times that are, respectively, 3−5 times and 2−3 times greater than those by NPR excitation. In the near field multiple pulse earthquake, the main beam is more likely to cause severe impact damage, and thus, the appropriate anti-collision measures should be adopted in seismic design.
-
青藏铁路的开通对促进青藏高原的交通与经济建设发挥了重要作用. 为进一步提高其运输能力和效益，青藏铁路格拉段电气化工程提上日程. 青藏铁路格拉段穿越青藏高原多年冻土地段546.43 km，地质条件复杂，路基的冻胀融沉病害严重[1-2]. 由于接触网支柱桩基础承担的上部荷载较小且桩长较短，在长期冻融循环约束冻胀作用下易产生冻拔失稳或破坏[3]. 如何保证接触网支柱桩基础的冻拔稳定性是青藏铁路格拉段电气化改造工程中的关键问题[4-5].
目前，在冻土地基中桩基冻拔方面，国内外学者已通过现场试验、模型试验与数值模拟的方法取得了一定的研究成果：Lu等[6]通过引入关于层状饱和土的状态向量、静态波向量和反射-透射矩阵（RTM）的基本解，建立层状冻土与单桩相互作用的第二类Fredholm积分方程，并对其进行了数值求解；Zhou等[7]采用现场试验与数值模拟的方法研究了热管对青藏高原多年冻土区输电塔基热力学特性的影响；王腾飞等[8-10]研究了季节冻土区光伏支架螺旋桩基础在单向冻结条件下的冻拔响应及半螺旋桩的抗冻拔理论计算方法；为减小桩基冻拔量，锥形桩与扩底桩逐渐被应用于工程实践中，许健等[11-16]采用模型试验、理论分析及数值模拟的方法对冻土区锥形桩与扩底桩的抗冻拔性能及其影响因素进行深入研究，并对扩底桩的优化选型进行总结分析. 上述研究中，桩周土体都产生水平方向的对称冻胀. 然而，铁路接触网支柱桩基是设置于既有路基中的柱型构件，其稳定性受路基与边坡2个方向冷（热）量的共同影响，桩周土体产生水平方向的非对称冻胀. 关于多年冻土区既有路基活动层在二维冻融过程中桩基受力变形方面的研究成果较少.
鉴于此，本文通过大比例模型试验，对多年冻土区不同桩型的接触网支柱桩基在冻融作用下的相关热力学特性开展研究. 探讨在冻拔作用下等截面圆形桩、直锥柱形桩及曲锥柱形桩的抗冻拔效果，得到接触网支柱桩基础的地温、冻拔位移、切向冻胀力的分布规律，揭示接触网支柱桩基在冻融循环作用下的受力变形机理.
1. 试验设计
1.1 试验土样与试验装置
为更好地体现青藏铁路路基土体对接触网桩基础的影响，试验用土取自青藏铁路沱沱河车站，接触网下部基础钻孔施工试验的现场. 试验土体的最大干密度为1.92 g/cm3，其中，小于0.075 mm粒径的颗粒占5.6%，根据土工试验方法标准（GB/T 50123—2019）[17]，该土样定义为含细粒土砂（SF）. 试验所用低温环境箱的内尺寸为3.2 m （长） × 1.7 m （宽） × 1.9 m （高）. 制作1.6 m （长） × 1.0 m （宽） × 1.0 m （高）的模型箱，置于低温环境箱，模型箱四周均覆盖保温隔热材料. 为模拟多年冻土，采用2个冷浴系统分别模拟控制环境温度与多年冻土层的温度.
1.2 模型桩与测试元件布设
为降低接触网支柱桩基的冻拔力，改变普通等截面圆形桩在活动层的桩基截面形状，本次试验中共设置3种截面形式的模型桩，分别为等截面圆形桩Z1、圆锥柱形桩Z2及曲锥柱形桩Z3. 根据模型试验相似原理，土质、含水量及环境温度与现场实际情况一致，现场接触网支柱桩基预设计桩长8 m，桩径0.55 m. 模型桩采用有机玻璃加工制作，桩身材料的密度、弹性模量与导热系数分别为1.18 g/cm3、2.56 GP和0.19 W/（m·℃）. 结合现有的试验条件，将模型试验的几何相似比取为1∶10. 模型桩的具体尺寸及应变片布设见图1所示. 沿桩身同一深度处对称布设BE120-3AA-P300型号应变片，利用同一深度处相同的温度变化来消除温度对应变片的影响，其中一片沿桩身轴向贴在外表面（测量片），另一片沿桩身环向贴于相应的位置（温度补偿片）. 在应变采集仪中采用半桥接线法.
图 1 模型桩几何尺寸及应变片布设示意Figure 1. Geometric dimension of model pile and layout of strain gauge试验采用PT100温度传感器测试土体温度，精度为 ± 0.1 ℃. 图2为模型桩及测试元件布设图，温度传感器共布设3个断面，从左到右依次为断面A、断面B与断面C，每个断面有2个测温孔，分别位于路基与边坡上. 环境箱内布设3个环境温度测点. 在桩顶布设2个位移传感器实时测试桩顶的竖向与水平位移，在Z1与Z2桩之间、Z2与Z3桩之间分别布设3个位移计，测试路基、路肩及边坡土体的位移. 根据文献[7]的研究成果，距桩3.4 倍桩径处土体的冻胀位移基本不受桩体影响，故本试验中模型桩之间的相互影响忽略不计.
2. 试验方法步骤
选取青藏高原沱沱河地区一年内正弦气温变化函数为
Ta(t)=−2.5+12.0sin(2πt/8640+π/2)， (1) 式中：－2.5为年平均气温，12.0为气温振幅，t为时间，h.
模型试验共设计3个冻融循环，正式试验前通过多次预试验可得：若时间相似比取1∶10，即模型试验中3.6 d模拟现场的1年，土体的冻融深度达不到30 cm；当时间相似比取1∶6时，冻融深度约为30 cm. 因此，将模型试验的时间相似比取为1∶6，即模型试验中10.0 d模拟现场的1年. 模型试验中环境箱温度按式（2）控制.
T(t)=−2.5+12.0sin(2πt/240+π/2). (2) 试验步骤主要包含：
步骤1 准备试验. 按试验设计加工制作试验模型箱，模型箱四周均粘贴保温隔热材料，底部设计冷浴管路；按各模型桩的设计尺寸加工有机玻璃模型桩，桩周粘贴布设BE120-3AA-P300型号应变片；将现场取回的土样配备足量含水量为15%的试验用土，将其搅拌充分均匀后用塑料布包裹并静置72 h.
步骤2 土样分层填筑压实及测设元件布设. 在模型箱内壁涂抹凡士林，以此来消除模型箱边界对土体的约束作用. 试验填土初始含水量15%，分10层填筑，压实度按0.93控制，模型箱内壁粘贴软皮尺以控制土层的填筑厚度，桩身附近的土体采用橡皮锤击实. 填筑过程中，温度及位移传感器按图2进行布设.
步骤3 模型箱底板与顶板温度的控制. 将底板温度调为−2 ℃恒温控制，顶板调制为10 ℃， 静置30 d，形成初始温度场.
步骤4 开始试验. 按T(t) 调节环境温度实现土体的冻融变化.
步骤5 试验数据的自动采集. 自动实时采集冻融循环过程中应变、温度传感器与位移传感器的读数.
3. 试验结果分析
3.1 温度场分布
试验中断面A、B、C的温度场分布基本一致，以断面B桩Z2附近路基与边坡上2个测温孔的温度场进行分析. 图3为断面B路基与边坡测温孔不同深度土层温度随时间的变化曲线，其中第17天的数据缺失. 由图3可以看出：整个试验共进行30.0 d，为3个冻融循环，随着T(t)的变化，不同深度土层温度随时间也呈正弦状分布，能较好地模拟现场实际地温的变化情况；各土层温度的变化相对于环境温度出现滞后现象，且随深度的增加，滞后效应越明显；下冷板能较好地控制模型下部土层的地温，路基与边坡2个测温孔深90 cm处的平均地温约为−1.5 ℃ .
图 3 断面B不同深度土体温度随时间的变化曲线Figure 3. Changes of soil temperature at different depths of section B with time通过试验进程中所得的各测点温度，绘制冻融过程中断面B路基与边坡处的等温线分布，如图4所示. 由图可得：试验开始阶段，模型箱底部20 cm 厚的土层处于冻结状态，其他土层都为未冻土，随着环境温度的降低，基础与土体的热量向环境中扩散，冻结锋面下移，土层主要发生自上而下的冻结. 经过一个冻结期后，整个基础完全处于冻结状态. 随着环境温度的升高，模型上部土层融化，路基测温孔第2、3个周期的最大融化深度分别为31.5 cm和28.0 cm，边坡测温孔第2、3个周期的最大融化深度分别为17.0、14.0 cm.
图 4 冻融过程中断面B的等温线分布（单位：℃）Figure 4. Isotherm distribution of section B during freezing and thawing (unit: ℃)图5为路基与边坡2个测温孔地温沿深度变化的对比曲线. 由图可以看出：冻土上限以上活动层地温正负温变化较剧烈，其中第11、12、19、20 天活动层地温为正值，呈融化状态，第16天活动层地表地温最低，达到 −8.1 ℃. 通过比较2个测温孔的地温数值，发现相同时间同一深度处2个测温孔的数据存在较大的差异，在暖季阶段，边坡测温孔的地温比相同条件下路基测温孔的地温较高；在寒季阶段，边坡测温孔的地温比相同条件下路基测温孔的地温较低，且在活动层内这种现象愈剧烈. 以上说明路基体的冻结（融化）受路基顶面与边坡的2个方向冷（热）量的共同影响，是一个二维冻结（融化）问题，接触网支柱基础路基与边坡两侧的温度场是非对称分布的.
图 5 断面B 2个测温孔地温沿深度变化的对比Figure 5. Comparison of ground temperature variation along depth between two temperature measuring holes at section B第1个周期，由于土层的填筑与环境箱内初始温度等因素的影响，试验数据的变化规律相对杂乱，在下面的分析中以第10天为起点. 图6（a）为路基、路肩及边坡处土体表层的位移随时间的变化曲线. 由图可知：路基、路肩及边坡处位移变化趋势基本一致，都与环境温度的变化密切相关. 当环境温度为正温阶段，路基、路肩及边坡土体位移基本不变，环境温度降为负温时，土体的冻结速率较快，土层位移迅速发生冻胀，路基、路肩及边坡处土体最大冻胀量分别为2.2、4.3、3.1 mm，其中，路肩处的位移最大. 产生以上现象的原因是环境温度降低时，冷量从路基顶面与边坡2个方向进入路基体，路基土体在2个方向上产生二维冻结，导致路肩处的冻胀位移最大. 当环境温度为正温并升高时，路基、路肩及边坡处土体位移均产生融沉，基本回到冻胀起始前的位移.
图 6 土体与桩顶位移随时间的变化曲线Figure 6. Variation curves of displacement of soil and pile top with time图6（b）、（c）为桩顶竖向与水平位移随时间的变化曲线. 由图可知：桩顶位移的变化与土体位移的变化规律基本一致，亦与环境温度的变化密切相关；在第2个冻融周期内桩Z1、Z2、Z3的竖向冻拔量分别为0.26、0.12、0.15 mm，桩Z2、Z3的竖向冻拔量分别为桩Z1的46%、58%，说明直锥柱形桩与曲锥柱形桩在整个冻结过程中有较好的抗冻拔效果；路基土体冻结过程中桩Z1、Z2、Z3的桩顶都会产生较小的水平冻胀位移，分别为0.10、0.13、0.14 mm.
3.2 桩身应力
图7为第2个冻融周期内桩身轴力沿深度的分布曲线. 由图可以看出：活动层土体在冻结融化过程中，桩长范围内的轴力都为拉力，随桩长增加0～0.3 m范围内轴力先增大，随后轴力逐渐减小，即桩长0.3 m断面处是桩身的一个中性点；轴力在整个桩长范围内呈非均匀变化，活动层内（0.3 m以上）桩身各截面的轴力差变化较大，多年冻土层内桩身各截面的轴力差变化较小. 将桩长30.0 cm处的轴力进行比较，结果如图8所示. 由图可以看出：桩身轴力与环境温度有密切的关系，随环境温度逐渐降低，桩身各截面的轴力均逐渐增大，当环境温度升高，桩身各截面的轴力均逐渐降低，其中，第16 天的桩身轴力最大，桩Z1、Z2、Z3在第16 天的轴力分别为5.66、4.56、4.01 kN；与桩Z1相比，桩Z2及桩Z3的轴力分别降低19.4%与27.5%.
图9为温度与桩侧切向应力沿深度的变化曲线. 由图可以看出：与桩身轴力的变化规律相似，活动层内的切向应力为方向向上的冻胀应力，且变化较剧烈，在冻深附近由正值转变为负值，永冻层内的切向应力为方向向下的冻结应力. 是由于随环境温度的降低，活动层内的土体冻结后产生向上的冻胀变形，桩基的存在对土体的自由冻胀产生约束作用，从而在桩侧产生向上的切向冻胀力，永冻层的土体对桩的向上运动或运动趋势有抑制作用，导致桩土之间的冻结应力发挥作用；切向冻胀力的最大值出现在地表附近，桩Z1、Z2、Z3在第16 天的最大切向冻胀应力分别为157.2、153.5、159.4 kPa；活动层内的平均切向冻胀应力为109.3、106.4、97.7 kPa.
图 9 温度与桩侧切向应力沿深度的变化曲线Figure 9. Variation curves of temperature and pile-side tangential stress along depth3.3 桩型对切向冻胀力的影响分析与讨论
由冻结过程桩基的受力特点可知，桩基冻深处的轴力为切向冻胀总力. 3种桩基础的冻深Zn均约为0.3 m，表1为不同桩型模型桩的受力情况对比. 表中： S 为冻深范围内桩和冻土的接触面积，F为桩基的切向冻胀总力， τ为冻深范围内各桩平均切向冻胀应力. 由表可以看出：桩型的改变可明显降低F，桩Z3的切向冻胀总力最小，桩Z2次之. 桩Z1、Z2、Z3切向冻胀总力之比为1.00∶0.81∶0.71，与S之比呈正相关，且比值接近，τ 之比约等于1∶1∶1.
表 1 不同桩型模型桩的受力对比Table 1. Stress comparison of model piles in different shapes桩 Zn/m S/cm2 F/kN τ/kPa Z1 0.3 518 5.66 109.3 Z2 0.3 447 4.56 106.4 Z3 0.3 427 4.01 97.7 环境温度降低时，桩周土体逐层自上而下低发生冻结. 以第1层土冻结时对桩基的作用力进行分析：当土体冻结时，产生竖向冻胀力V1和水平冻胀力H1，每层土的厚度为ΔH，桩基锥角为 β，如图10所示.
图 10 直锥（曲锥）桩侧土体冻胀力的分解图示Figure 10. Decomposition of frost-heave force of the side of straight-cone (curved-cone) pile将V1和H1沿桩侧与垂直桩侧分解，则第1层土体作用于桩基础的切向应力和法向应力分别为
{τ1=V1cosβΔH+H1sinβΔH,σ1=H1cosβΔH−V1sinβΔH. (3) 结合式（3）与表1，直（曲）锥柱形桩比等截面圆形桩的抗冻拔效果好的主要原因可归纳为以下2点：
1） 由于锥形桩桩侧斜面的存在，改变了桩基的受力状态，式（3）中V1sin β 表现为拉应力，导致桩侧水平应力减小. 冻土桩基接触面的抗剪强度与法向应力的大小呈正相关. 因此，锥形桩桩土界面的极限抗剪强度相比于等截面桩较低，更易达到极限抗剪强度.
2） 随着桩周土体冻胀变形的发展，若桩土界面达到极限强度，则桩土界面产生滑移. 冻深范围内各桩平均切向冻胀应力的差异较小，但曲锥柱形桩与冻土的接触面积最小，从而导致曲锥柱形桩的切向冻胀总力最小，抗冻拔效果最好.
4. 结 论
1） 路基体的冻结（融化）受路基顶面与边坡 的2个方向冷（热）量的共同影响，是一个二维冻结（融化）问题，接触网支柱桩基础路基与边坡两侧的温度场是非对称分布的，桩基附近的最大融深约为 30.0 cm，边坡测温孔的最大融深约为15.0 cm.
2） 土体与桩顶的位移均与环境温度的变化密切相关. 路基土体的二维冻结现象导致路肩处的冻胀位移最大，路基、路肩及边坡处土体最大冻胀量分别为2.2、4.3、3.1 mm. 等截面圆形桩的竖向冻拔量为0.26 mm，直锥柱形桩与曲锥柱形桩的竖向冻拔量仅为Z1的46%、58%，3根桩的桩顶均产生约为0.10 mm的水平冻胀量.
3） 活动层土体在冻结过程中桩基础整体受拉，冻深处的轴力最大. 等截面圆形桩的最大切向冻胀总力为5.66 kN，与等截面圆形桩相比，直锥柱形桩与曲锥柱形桩分别降低19.4%与27.5%. 切向应力在活动层内为方向向上的切向冻胀应力，永冻层内为方向向下的冻结应力，切向冻胀应力的最大值出现在地表附近.
4） 桩周土体冻融作用下，曲锥柱形桩具有竖向冻拔位移小、切向冻胀总力小的特点，即曲锥柱形桩具有较好的抗冻拔效果. 研究成果可为多年冻土区铁路电气化接触网支柱基础的抗冻拔设计提供参考.
-
图 10 碰撞响应与速度脉冲的对应关系
Figure 10. Relationship between pounding response and velocity pulse
表 1 3类地震动详细信息
Table 1. Detail of selected three type ground motions
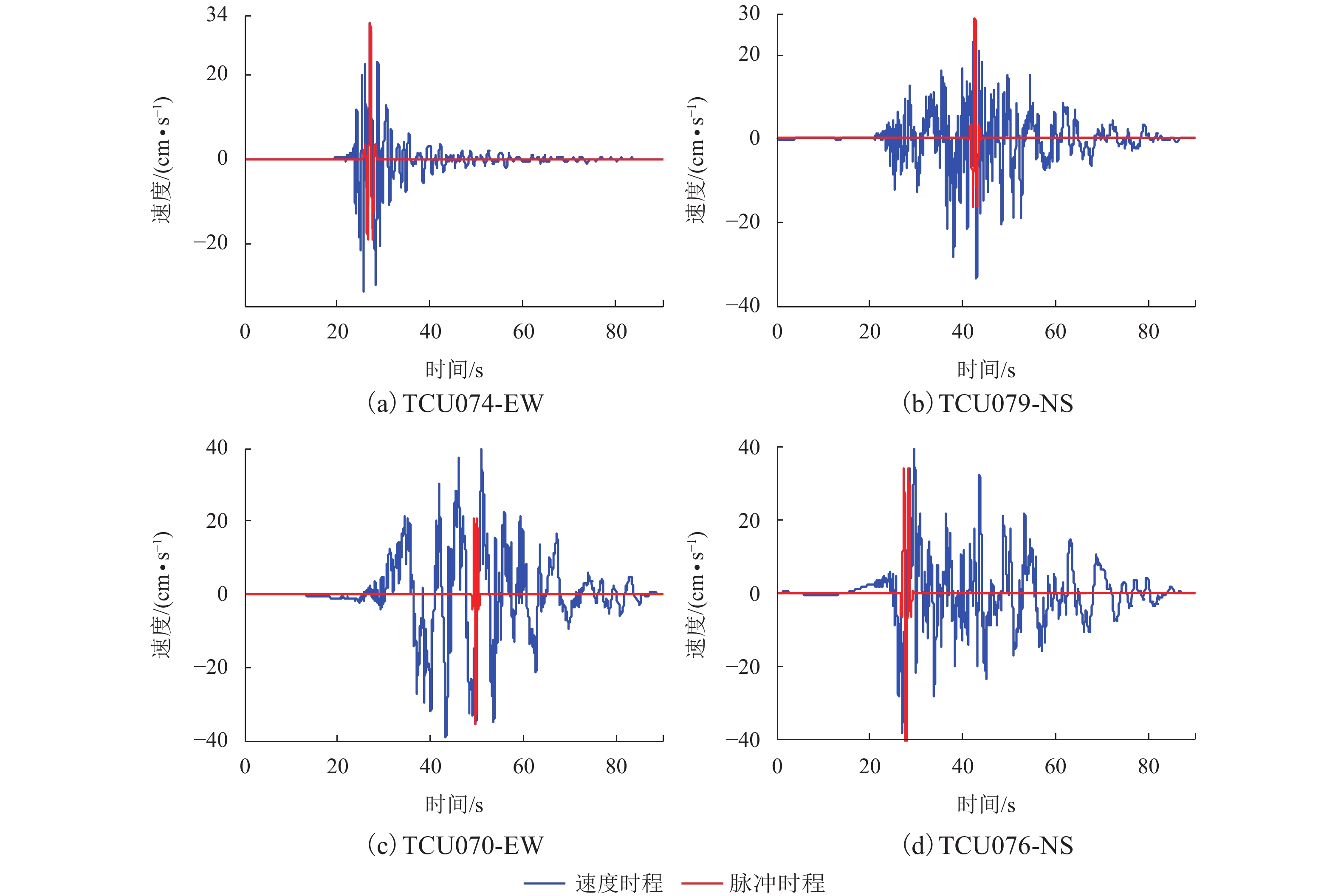
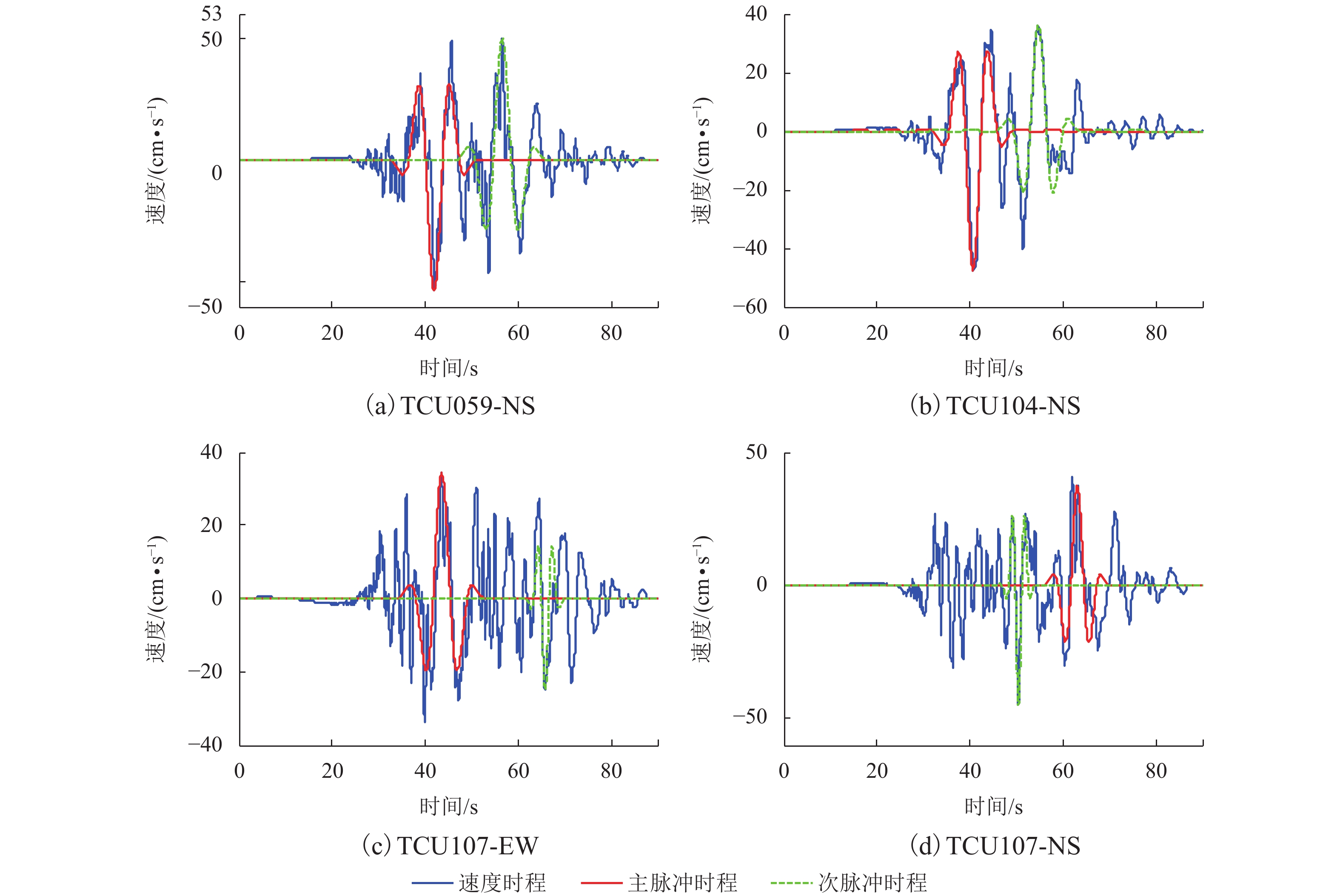
地震动类型 地震记录 Rrup/km PGA/（× g） SF Tp/s PI Ep 多脉冲 TCU059-NS 17.11 0.165 2.542 7.3 0.218 1 0.300 TCU104-NS 12.87 0.089 4.737 6.9 0.826 5 0.379 TCU107-EW 15.99 0.130 3.232 7.4 0.129 7 0.236 TCU107-NS 15.99 0.147 2.862 5.6 0.000 4 0.091 单脉冲 TCU031-EW 30.17 0.115 3.656 6.2 1.000 0 0.557 TCU036-EW 19.83 0.137 3.071 5.8 0.999 9 0.562 TCU040-EW 22.06 0.162 2.592 5.6 1.000 0 0.621 TCU049-EW 3.76 0.279 1.507 8.8 0.999 8 0.596 非脉冲 CHY074-EW 6.20 0.322 1.303 0.044 9 0.237 TCU079-NS 10.97 0.424 0.990 0.003 4 0.172 TCU070-EW 19.00 0.254 1.654 0.162 0 0.049 TCU076-NS 2.74 0.428 0.980 0.102 8 0.194 
下载: 导出CSV
表 2 Hertz-Damp模型特征参数
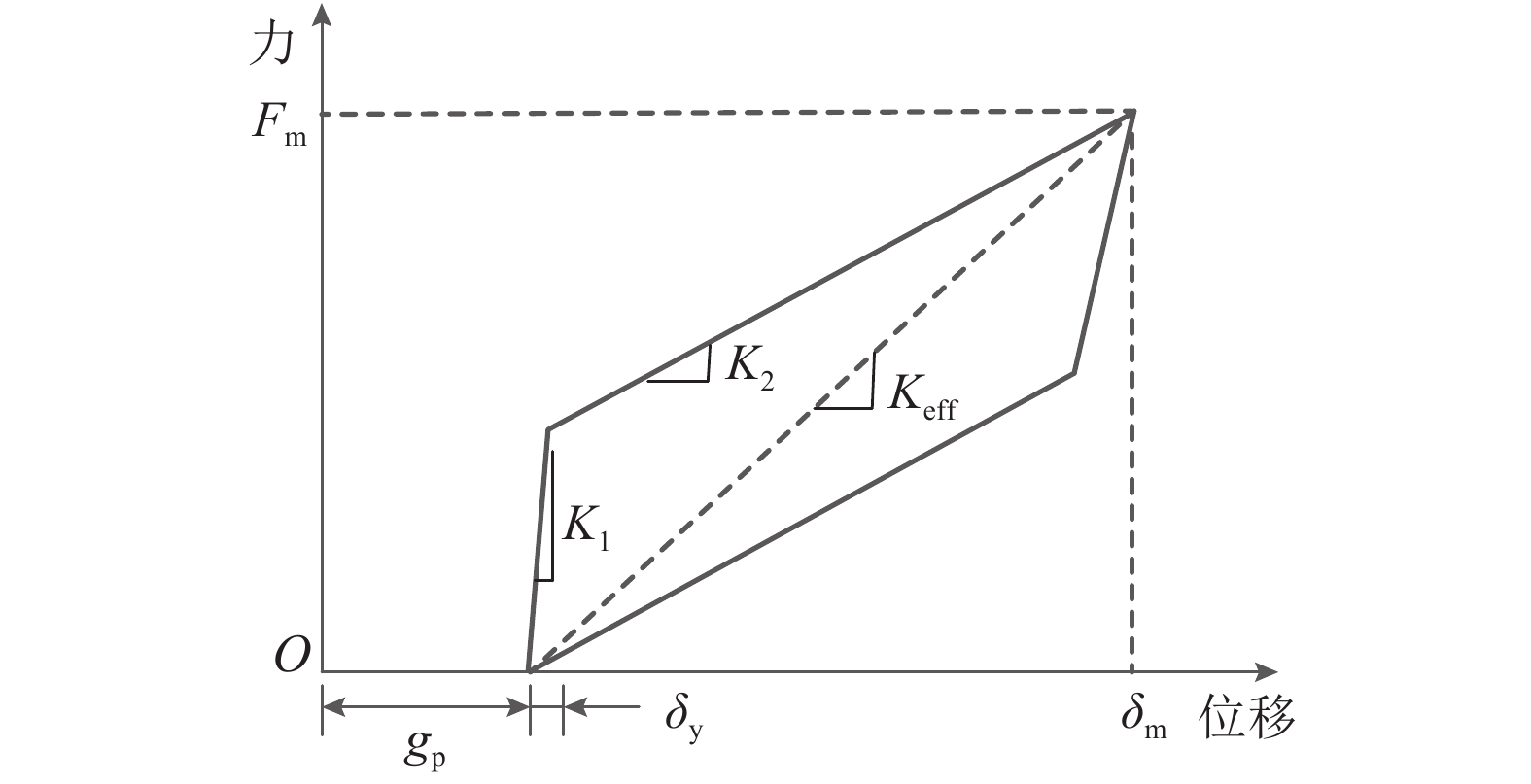
Table 2. Properties of Hertz-Damp model
特征参数 取值 初始间隙gp/mm 100 屈服位移δy/mm 1.6 初始刚度K1/（kN•mm–1） 8 472 应变硬化刚度K1/（kN•mm–1） 2 916 等效刚度Keff/（kN•mm–1） 3 472 最大入侵位移δm/mm 16
下载: 导出CSV
表 3 桥梁动力特性
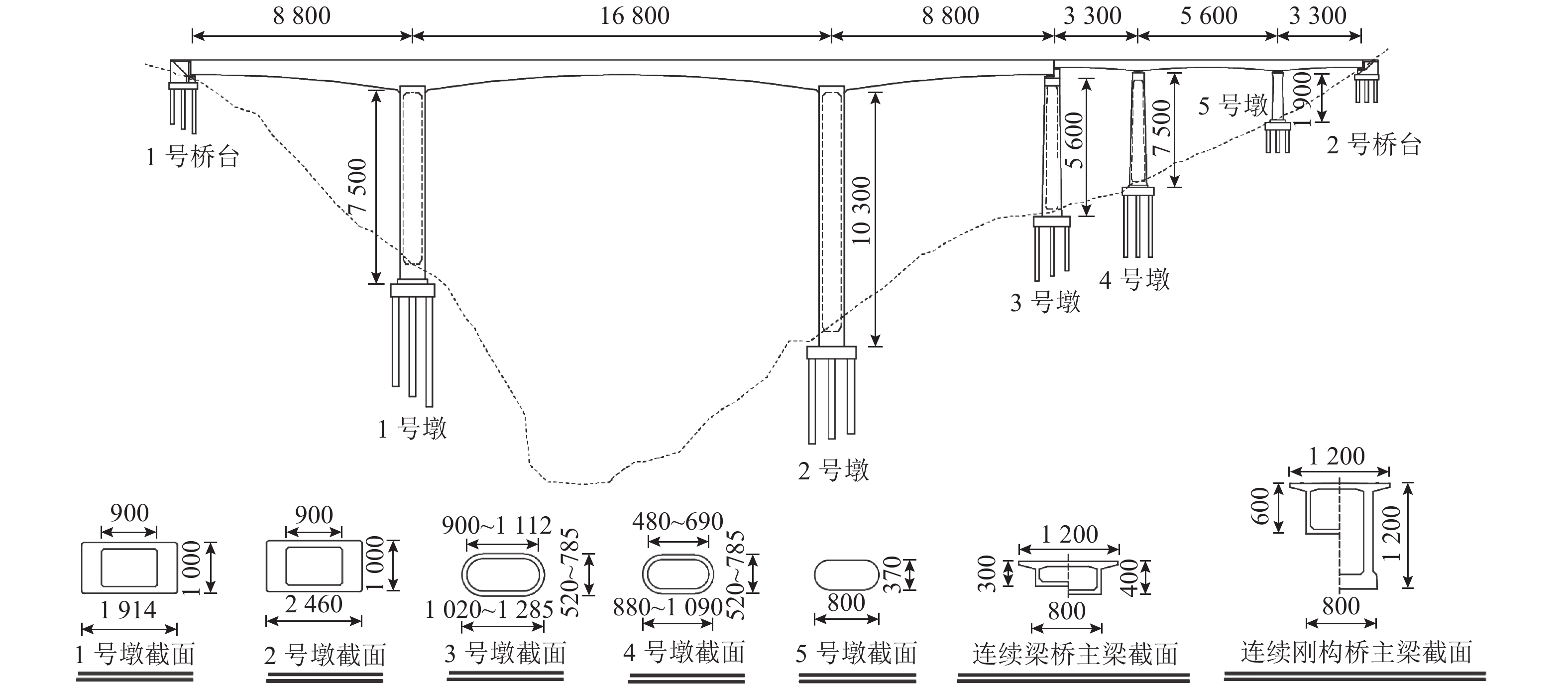
Table 3. Dynamic characteristics of the selected bridge
振型阶数 周期/s 频率/Hz 质量参与系数/% 纵桥向 横桥向 第 1 阶 1.323 0.756 61.15 0 第 2 阶 1.278 0.783 0 40.92 第 3 阶 0.953 1.049 6.33 0 第 4 阶 0.902 1.108 0 0.56 第 5 阶 0.696 1.436 0.11 0 第 6 阶 0.688 1.454 0 15.65
下载: 导出CSV
表 4 近断层脉冲效应对桥墩地震响应的放大系数
Table 4. Amplification factor of near-fault impulse effect on seismic response of pier
墩号 单一脉冲 多脉冲 曲率放大
系数位移放大
系数弯矩放大
系数剪力放大
系数曲率放大
系数放大系数
位移弯矩放大
系数剪力放大
系数1号 1.221 1.103 1.043 1.029 3.707 2.189 1.053 1.385 2号 1.926 1.085 1.019 0.983 8.924 2.096 1.119 1.543 3号 0.864 0.852 0.866 0.918 1.193 1.211 1.192 1.181
下载: 导出CSV
表 5 近断层脉冲效应对主梁碰撞响应的影响
Table 5. Details of maximum pounding force and average pounding frequency
脉冲类型 梁-台碰撞 梁-梁碰撞 梁-台碰撞 碰撞力/(× 107 N) 碰撞次数/次 碰撞力/(× 108 N) 碰撞次数/次 碰撞力/(× 108 N) 碰撞次数/次 多脉冲 29.70 32.50 3.67 23.00 32.50 27.75 单脉冲 8.73 9.95 1.41 9.00 8.56 7.25 非脉冲 9.67 5.50 1.15 5.25 10.60 5.00
下载: 导出CSV
-
梁智垚. 非规则高墩桥梁抗震设计理论研究[D]. 上海: 同济大学, 2007 JIA H Y, ZHANG D Y, ZHENG S X, et al. Local site effects on a high-pier railway bridge under tridirectional spatial excitations:nonstationary stochastic analysis[J]. Soil Dynamics & Earthquake Engineering, 2013, 52(6): 55-69. 陈旭,李建中,刘笑显. 墩身高阶振型对高墩地震反应影响[J]. 同济大学学报,2017,45(2): 159-166.CHEN Xu, LI Jianzhong, LIU Xiaoxian. Seismic performance of tall piers influenced by higher mode effects of piers[J]. Journal of Tongji University, 2017, 45(2): 159-166. 陈志伟,蒲黔辉,李晰,等. 行波效应对大跨连续刚构桥易损性影响分析[J]. 西南交通大学学报,2017,52(1): 23-29. doi: 10.3969/j.issn.0258-2724.2017.01.004CHEN Zhiwei, PU Qianhui, LI Xi, et al. Fragility analysis of large span continuous rigid bridge considering wave passage effect[J]. Journal of Southwest Jiao-tong University, 2017, 52(1): 23-29. doi: 10.3969/j.issn.0258-2724.2017.01.004 李立峰,吴文朋,胡思聪,等. 考虑氯离子侵蚀的高墩桥梁时变地震易损性分析[J]. 工程力学,2016,33(1): 163-170.LI Lifeng, WU Wenpeng, HU Sicong, et al. Time-dependent seismic fragility analysis of high pier bridge based on chlorideion induced corrosion[J]. Engineering Mechanics, 2016, 33(1): 163-170. 董俊,单德山,张二华,等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报,2016,48(3): 159-165.DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 159-165. 董俊,单德山,张二华,等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报,2015,50(5): 845-851. doi: 10.3969/j.issn.0258-2724.2015.05.012DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic fragility of irregular continuous rigid Frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 845-851. doi: 10.3969/j.issn.0258-2724.2015.05.012 MAVROEIDIS G P, DONG G, PAPAGEORGIOU A S. Near-fault ground motions,and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems[J]. Earthquake Engineering & Structural Dynamics, 2004, 33(9): 1023-1049. YANG D, PAN J, LI G. Interstory drift ratio of building structures subjected to near-fault ground motions based on generalized drift spectral analysis[J]. Soil Dynamics & Earthquake Engineering, 2010, 30(11): 1182-1197. 潘毅,王晓玥,许浒,等. 脉冲型地震动作用下尼泊尔砖木遗产建筑易损性分析[J]. 西南交通大学学报,2017,52(6): 1156-1163.PAN Yi, WANG Xiaoyue, XU Hu, et al. Seismic fragility analysis of Nepalese brick-timber heritage structures under near-fault pulse-like ground motions[J]. Journal of Southwest Jiaotong University, 2017, 52(6): 1156-1163. BAKER J W. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486-1501. doi: 10.1785/0120060255 ZHAI C, CHANG Z, LI S, et al. Quantitative identification of near-fault pulse-like ground motions based on energy[J]. Bulletin of the Seismological Society of America, 2013, 103(5): 2591-2603. doi: 10.1785/0120120320 常志旺. 近场脉冲型地震动的量化识别及特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2014 MAVROEIDIS G P. A mathematical representation of near-fault ground motions[J]. Bulletin of the Seismological Society of America, 2003, 93(3): 1099-1131. doi: 10.1785/0120020100 BRAY J D, RODRIGUEZ-MAREK A. Characterization of forward-directivity ground motions in the near-fault region[J]. Soil Dynamics & Earthquake Engineering, 2004, 24(11): 815-828. STEWART J P, CHIOU S J, BRAY J D, et al. Ground motion evaluation procedures for performance based design[J]. Soil Dynamics & Earthquake Engineering, 2002, 22(9): 765-772. IERVOLINO I, CORNELL C A. Probability of occurrence of velocity pulses in near-source ground motions[J]. Bulletin of the Seismological Society of America, 2008, 98(5): 2262-2277. doi: 10.1785/0120080033 CHANG Z, SUN X, ZHAI C, et al. An improved energy-based approach for selecting pulse-like ground motions[J]. Earthquake Engineering & Structural Dynamics, 2016, 45(14): 2405-2411. DICKINSON B W, GAVIN H P. Parametric statistical generalization of uniform-hazard earthquake ground motions[J]. Journal of Structural Engineering, 2011, 137(3): 410-422. doi: 10.1061/(ASCE)ST.1943-541X.0000330 MENEGOTTO M. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]// Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads. Lisbon: IABSE, 1973: 15-22 KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969-1990. MUTHUKUMAR S. A contact element approach with hysteresis damping for the analysis and design of pounding in bridges[D]. Atlanta: Georgia Institute of Technology, 2003 李建中,宋晓东,范立础. 桥梁高墩位移延性能力的探讨[J]. 地震工程与工程振动,2005(1): 43-48. doi: 10.3969/j.issn.1000-1301.2005.01.008LI Jianzhong, SONG Xiaodong, FAN Lichu. Investigation for displacement ductility capacity of tall piers[J]. Journal of Earthquake Engineering and Engineering Vibration, 2005(1): 43-48. doi: 10.3969/j.issn.1000-1301.2005.01.008 李立峰,黄佳梅,吴文朋,等. 基于IDA的高墩大跨桥梁抗震性能评估[J]. 地震工程与工程振动,2012,32(1): 68-77.LI Lifeng, HUANG Jiamei, WU Wenpeng, et al. Research on the seismic performance of bridge with heath piers and long spans using increment dynamic analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(1): 68-77. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 671
- HTML全文浏览量: 269
- PDF下载量: 42
- 被引次数: 0