Parallel Genetic Algorithm for SAT Problems Based on OpenMP
-
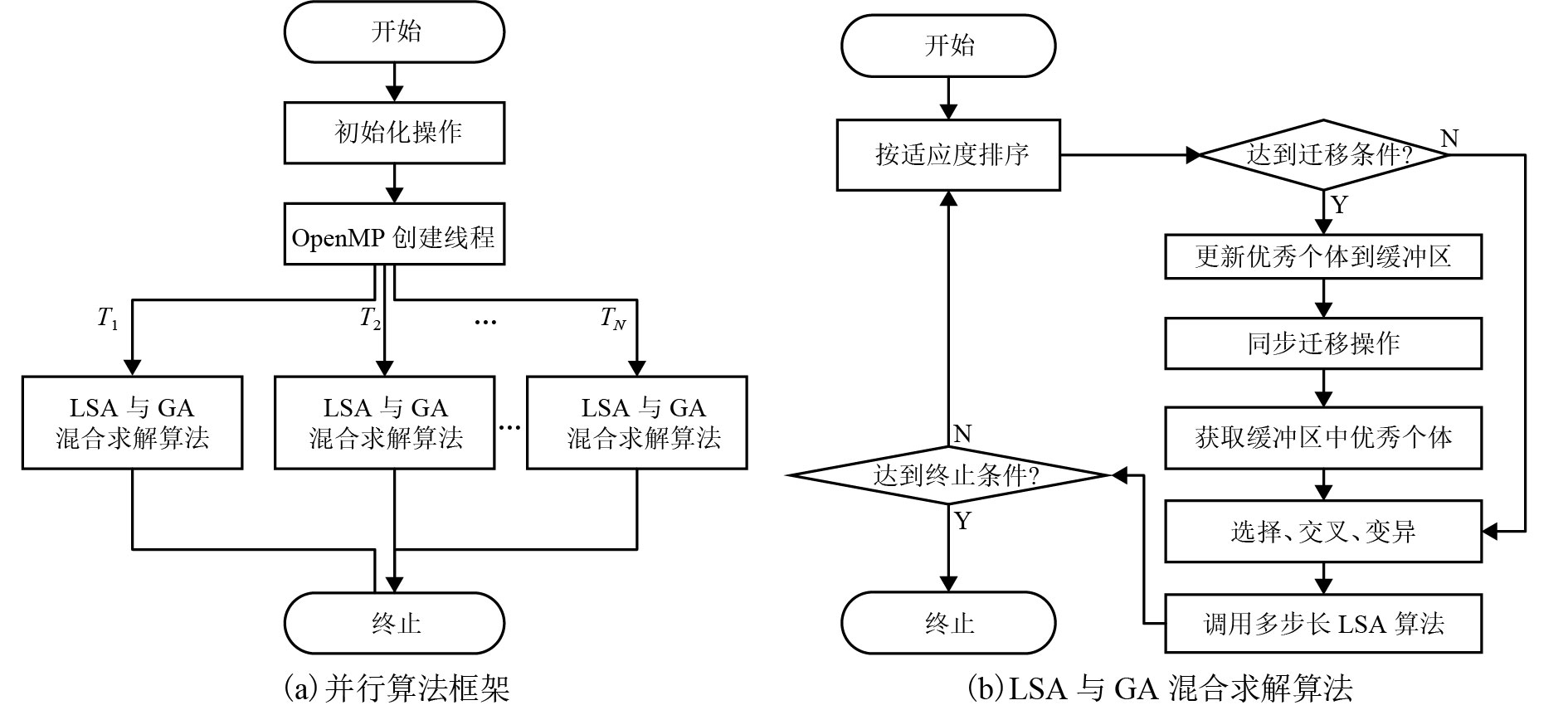
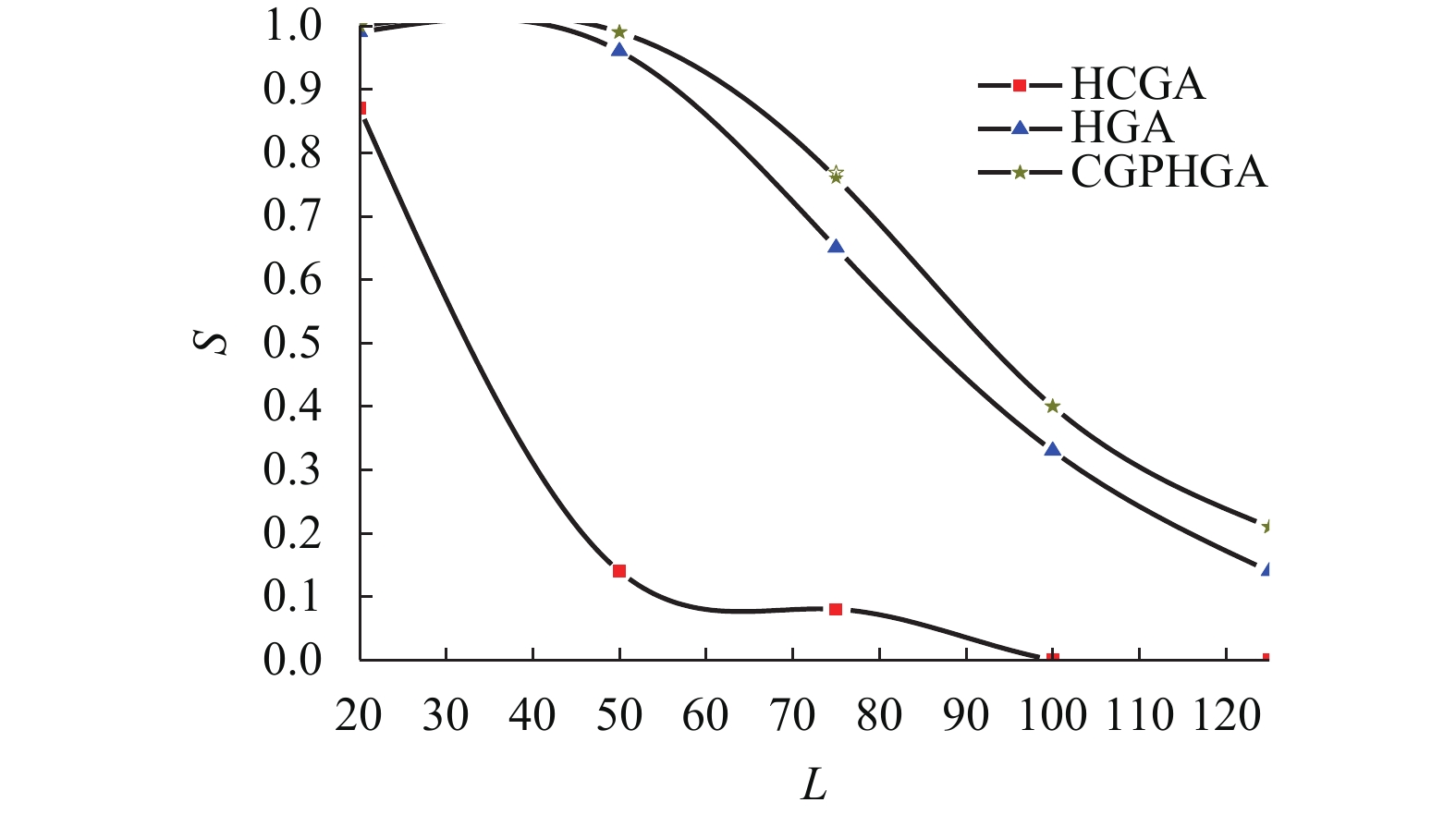
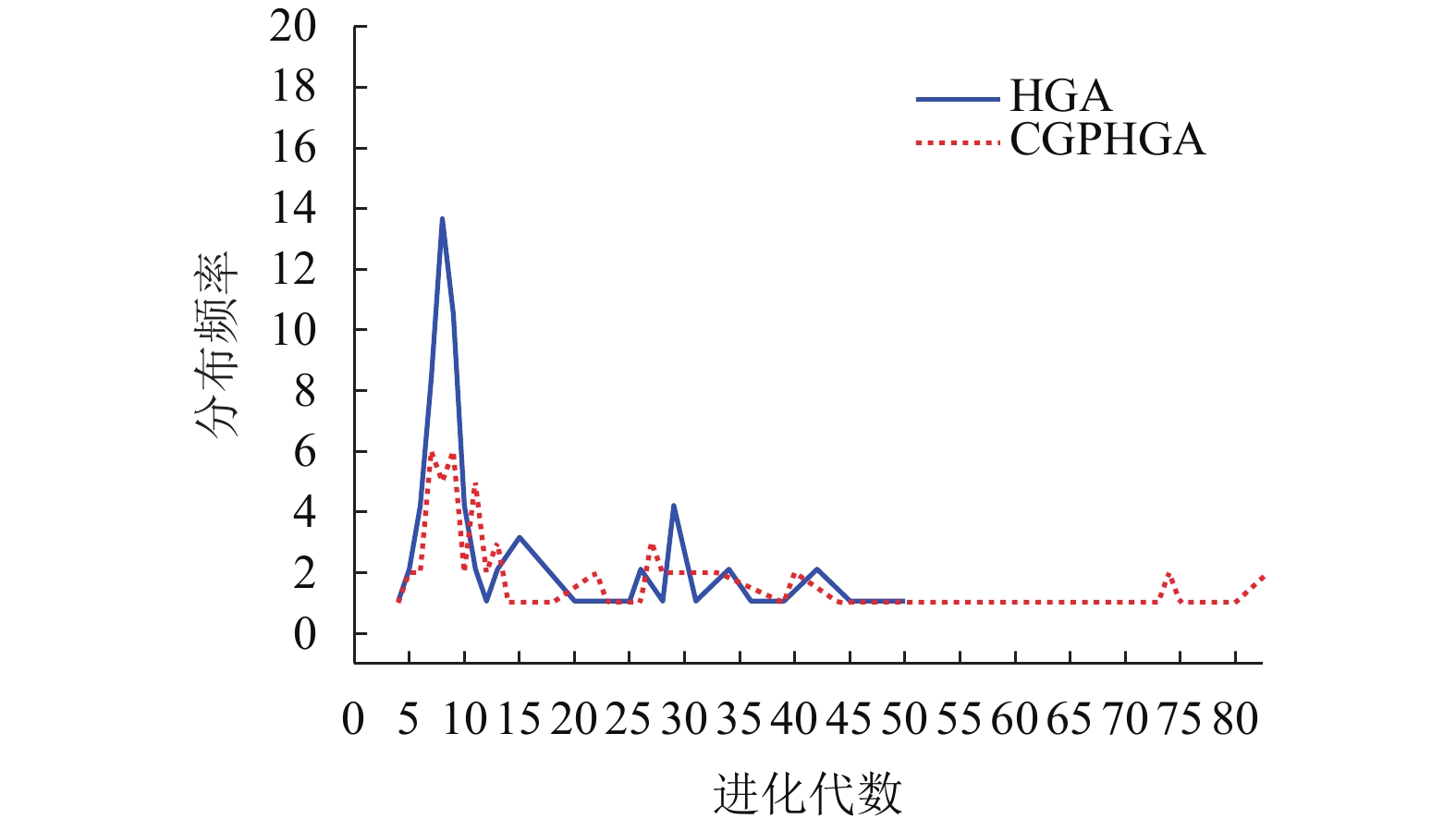
摘要: 为了提高SAT (boolean satisfiability) 问题求解效率,在OpenMP (open multi-processing) 编程框架下,将遗传算法与局部搜索算法结合,改进了混合遗传算法中的选择算法,将原有选择操作的时间复杂度降低到O(N)级别. 算法采用OpenMP中的编译制导语句#pragma omp parallel粗粒度并行化驱动混合遗传算法,采用#pragma omp single语句块实现了子种群间个体的同步迁移操作. 与同类算法HCGA (hybrid cloud genetic algorithm)比较分析表明:改进算法HGA (hybrid genetic algorithm)以及并行后的混合遗传算法CGPHGA (coarse-grained parallel hybrid genetic algorithm)在求解成功率和求解效率上都有显著提高,部分问题求解成功率提高达5倍.Abstract: To improve solving efficiency for SAT (boolean satisfiability) problems, a combination of genetic algorithm (GA) with local search algorithm (LSA) on the OpenMP (open multi-processing) framework was proposed. This combination improved the selection algorithm in the hybrid genetic algorithm (HGA) and reduced the time complexity of the original selection operation to O(N). The compiler guide statement #pragma omp parallel in OpenMP was applied to coarse-grained parallelization driven HGA, and the #pragma omp single statement block was used to implement the synchronization migration operation of the individuals in different sub-groups. Compared with the similar algorithm, HCGA (hybrid cloud genetic algorithm), both the improved algorithm (HGA) and the coarse-grained parallel hybrid genetic algorithm (CGPHGA) significantly improved solution success rate and problem solving efficiency. Solution success rate for some problems was increased by 5 times.
-
Key words:
- SAT problem /
- OpenMP /
- parallel hybrid genetic algorithm /
- coarse-grained model
-
表 1 实验环境对比
Table 1. Experimental conditions
环境 操作系统 CPU 内存/GB 限时 本文 Win10 x64 i3-3240 4 200 s 对比 Win7 x64 i5-3470 4 23 h 表 2 改进混合遗传算法和并行遗传算法运行参数信息
Table 2. Parameters of HGA and CGPHGA
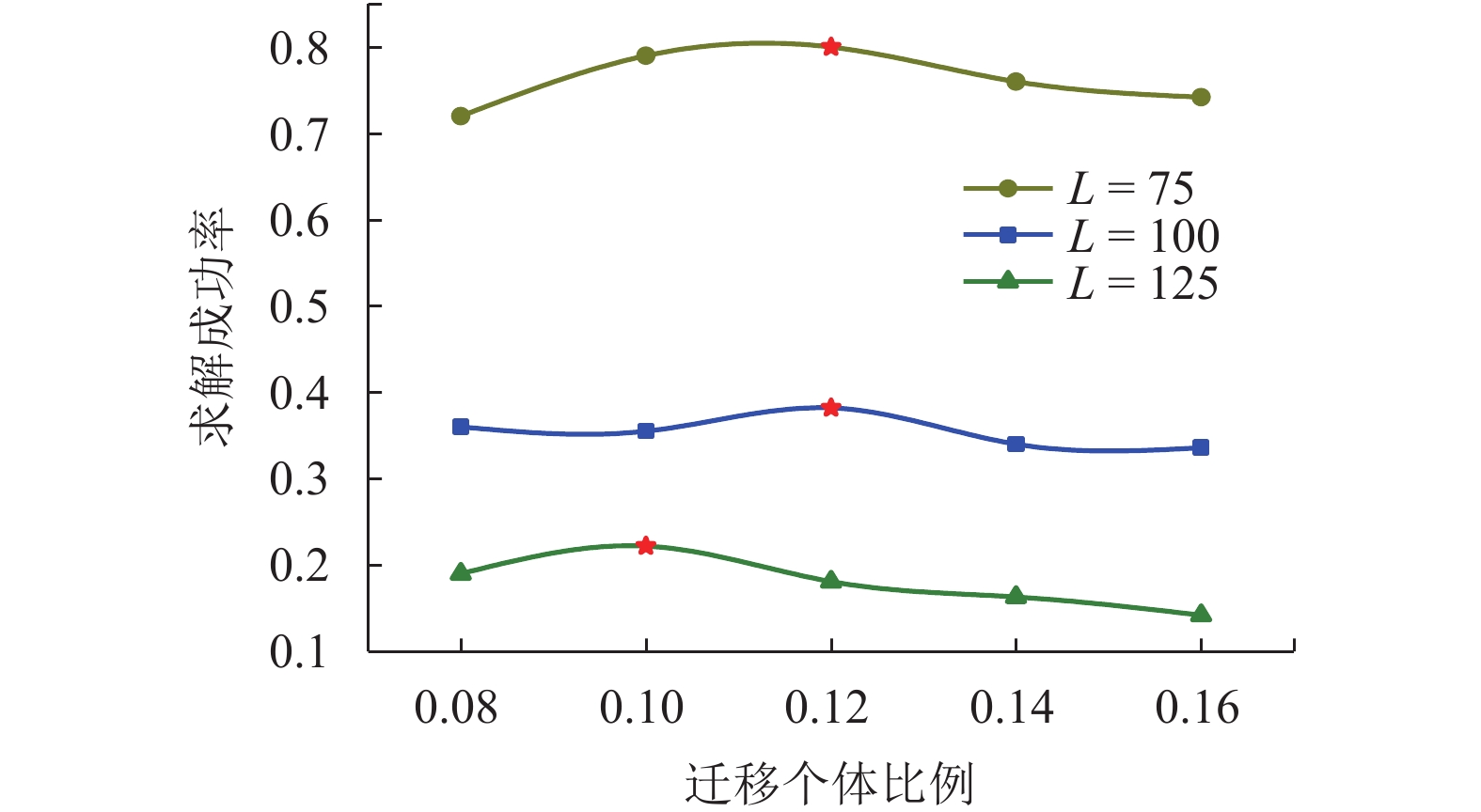
变元 子句 算法 种群大小 LSA步长 并行数 迁移间隔 迁移率 50 218 HGA 100 10 CGPHGA 25 10 4 8 0.10 75 325 HGA 100 10 CGPHGA 25 10 4 10 0.08 100 430 HGA 100 10 CGPHGA 50 10 4 8 0.10 125 538 HGA 150 15 CGPHGA 40 15 4 10 0.10 表 3 HCGA、HGA和CGPHGA平均时间对比
Table 3. Average time required by HCGA,HGA and CGPHGA
变元 子句 HCGA HGA平均
时间/sCGPHGA
平均时间/s50 218 38.089 23.451 22.779 75 325 128.754 65.064 61.132 100 430 85 714.200 93.930 93.492 125 538 0 158.960 122.740 表 4 CGPHGA与其他并行算法对比情况
Table 4. Comparison of CGPHGA with the other parallel algorithms
变元 子句 PGSAT PDPLL CGPHGA S 平均时间/s S 平均时间/s S 平均时间/s 125 538 0.10 186.400 0.41 101.206 0.21 122.541 150 645 0.14 152.957 0.10 173.612 175 753 0.02 199.298 0.05 196.793 225 960 0.01 198.570 -
黄拙,张健. 由一阶逻辑公式得到命题逻辑可满足性问题实例[J]. 软件学报,2005,16(3): 329-325.HUANG Zhuo, ZHANG Jian. Generating SAT instances from first-order formulas[J]. Journal of Software, 2005, 16(3): 329-325. LI Bingfen, ZHANG Y A. A hybrid genetic algorithm to solve 3-SAT problem.[C]//2016 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery. Changsha: IEEE Press, 2016: 476-480 潘晓英,焦李成,刘芳. 求解SAT问题的多智能体社会进化算法[J]. 计算机学报,2014,37(9): 2011-2020.PAN Xiaoying, JIAO Licheng, LIU Fang. A multi-agent social evolutionary algorithm for SAT problem[J]. Chinese Journal of Computers, 2014, 37(9): 2011-2020. LUO Chuan, CAI Shaowei, WU Wei, et al. Double configuration checking in stochastic local search for satisfiability[C]//Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence. Québec City: AAAI, 2014: 2703-2709 郭莹,张长胜,张斌. 求解SAT问题的算法的研究进展[J]. 计算机科学,2016,43(3): 8-17.GUO Ying, ZHANG Changsheng, ZHANG Bin. Research advance of SAT solving algorithm[J]. Computer Science, 2016, 43(3): 8-17. HOLLAND J H. Adaptation in natural and artificial systems[M]. Cambridge: MIT press, 1992: 159-171 DE JONG K A. The analysis of the behavior of a class of genetic adaptive systems[D]. Ann Arbor: University of Michigan, 1975 GOLDBERG D E. Genetic algorithms in search optimization and machine learning[J]. Machine Learning, 1988, 3(2): 95-99. 张琛,詹志辉. 遗传算法选择策略比较[J]. 计算机工程与设计,2009,30(23): 5471-5474,5478.ZHANG Chen, ZHAN Zhihui. Comparisons of selection strategy in genetic algorithm[J]. Computer Engineering and Design, 2009, 30(23): 5471-5474,5478. 高家全,何桂霞. 并行遗传算法研究综述[J]. 浙江工业大学学报,2007(1): 56-59,72. doi: 10.3969/j.issn.1006-4303.2007.01.013GAO Jiaquan, HE Guixia. A review of parallel genetic algorithms[J]. Journal of Zhejiang University of Technology, 2007(1): 56-59,72. doi: 10.3969/j.issn.1006-4303.2007.01.013 ROBERGE V, TARBOUCHI M, LABONTE G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning[J]. IEEE Trans. Industrial Informatics, 2013, 9(1): 132-141. doi: 10.1109/TII.2012.2198665 CALEGARI P, GUIDEC F, KUONEN P, et al. Parallel island-based genetic algorithm for radio network design[J]. J. Parallel Distrib. Comput, 1997, 47(1): 86-90. doi: 10.1006/jpdc.1997.1397 YANG Hongtai, YANG Paichuan, HUANG Chinglien. A parallel genetic algorithm approach to solving the unit commitment problem:Implementation on the transputer networks[J]. IEEE Transactions on Power Systems, 1997, 12(2): 661-668. doi: 10.1109/59.589638 TIMOTHY G. MATTSON B S, BERNA M. Patterns for parallel programming[M]. [S.l.]: Pearson Education, 2004: 76-78 ASGHAR S, AUBANEL E, BREMNER D. A dynamic moldable job scheduling based parallel SAT solver[C]//2013 42nd International Conference on Parallel Processing (ICPP). [S.l.]: IEEE, 2013: 110-119 HAMADI Y, JABBOUR S, SAIS L. ManySAT:a parallel SAT solver[J]. Journal on Satisfiability,Boolean Modeling and Computation, 2008, 1(6): 245-262. WU Guanfeng, XU Yang, CHANG Wenjing, et al. Parallel genetic algorithm for SAT problems based on the coarse-grained model[C]//Uncertainty Modelling in Knowledge Engineering and Decision Making: Proceedings of the 12th International FLINS Conference. Roubaix: Springer, 2016: 489-495 MASTSUMURA T, NAKAMURA M, OKENCH J, et al. A parallel and distributed genetic algorithm on loosely-coupled multiprocessor systems[J]. IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences, 1998, 81(4): 540-546. BECKERSM L M, DERKS EPPA, MELSSEN W J, et al. Using genetic algorithms for conformational analysis of biomacromolecules[J]. Computers & Chemistry, 1996, 20(4): 449-457. 岳嵚. 粗粒度并行遗传算法的计算性能及其应用研究[D]. 武汉: 华中科技大学, 2008 MENOUER T, BAARIR S. Parallel satisfiability solver based on hybrid partitioning method[C]//2017 25th Euromicro International Conference on Parallel, Distributed and Network-based Processing. [S.l.]: IEEE, 2017: 54-60 LAYEB A, SAIDOUNI D E. A hybrid quantum genetic algorithm and local search based DPLL for max 3-SAT problems[J]. Applied Mathematics & Information Sciences, 2014, 8(1): 77-87. ROLI, A. Criticality and parallelism in structured SAT instances[C]//International Conference on Principles and Practice of Constraint Programming. Berlin: Springer, 2002, 714-719 ZHANG Wenhui, HUANG Zhuo, ZHANG Jian. Parallel execution of stochastic search procedures on reduced SAT instances[C]//Pacific Rim International Conference on Artificial Intelligence. Berlin: Springer, 2002: 108-117 -




 下载:
下载: