Buffeting Response and Equivalent Wind Load of Single Cantilever Corridor Bridge in Mountainous Areas
-
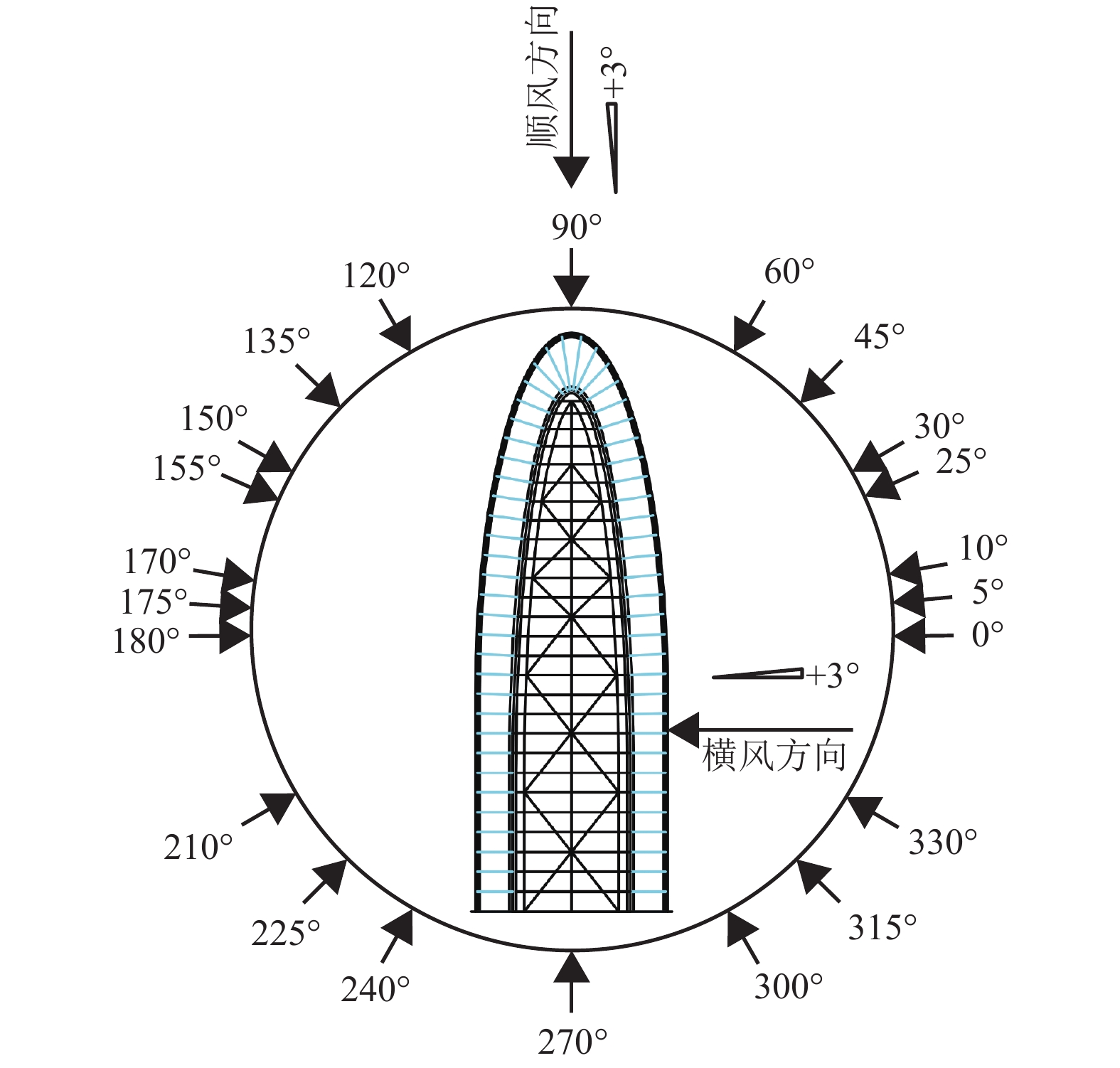
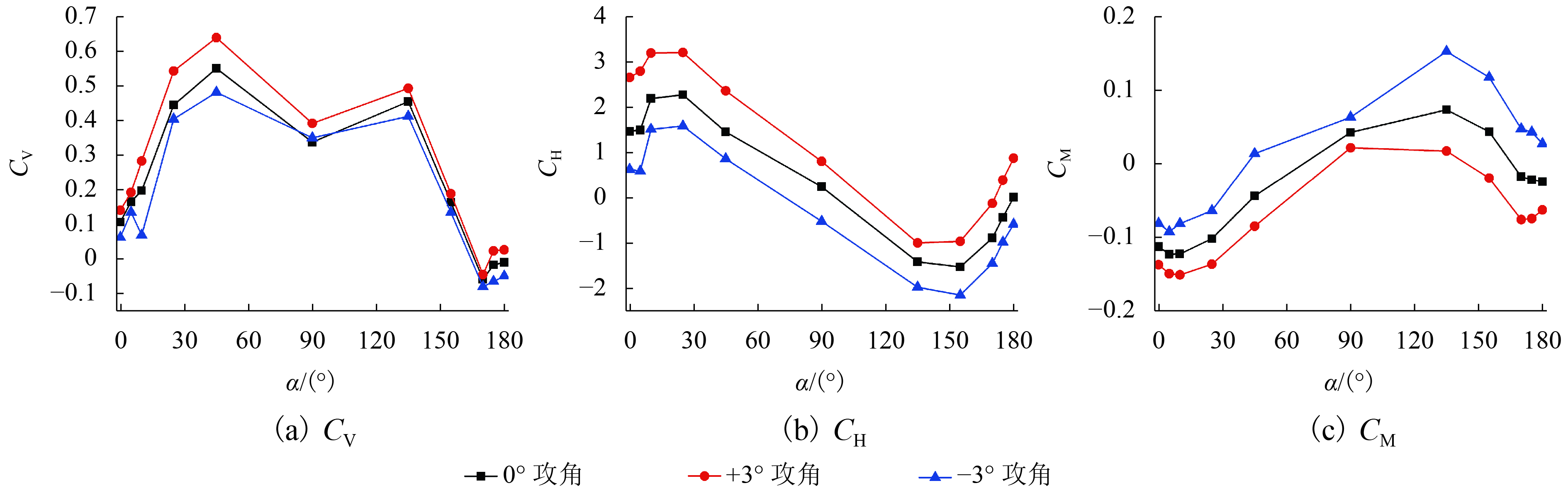
摘要: 为研究山区风环境下悬挑式人行桥梁抖振响应及风荷载，以某单悬臂观景廊桥为背景，通过风洞试验对结构的静力三分力系数以及不同风参数下的抖振响应进行了测量，并将结构横桥向最大等效风荷载规范计算值与试验值进行比较. 结果表明：山体地形对结构三分力系数及抖振响应影响较大，二者最大值均未出现在常规风向角；结构抖振响应随风速的增大而增大，受小幅风攻角的影响较小；横向抖振响应受一定程度紊流度变化的影响不敏感，但竖向及扭转响应整体随紊流度的增加呈明显增大趋势，在紊流度增大约40%的情况下二者均增大15%左右；竖向抖振响应随紊流积分尺度的增大（增幅约20%）而增大，增幅在9%左右，但积分尺度对横向抖振响应几乎无影响，对扭转响应的影响随风攻角的不同有较大差异，随着积分尺度的增大，3° 攻角下扭转响应增幅约为8%，0° 攻角其受积分尺度的变化影响较小；相比横桥向最大等效风荷载试验值，利用桥梁规范计算的结果偏于保守，静阵风系数的取值有待修正.Abstract: In order to study the buffeting response and the wind loading of a cantilevered pedestrian bridge in windy mountainous, a corridor bridge model was put in a wind tunnel to obtain its aerostatic force coefficients and buffeting responses. The maximum equivalent wind load in the transverse direction was calculated according to the bridges structural code and compared to the experimental results. The complex mountainous terrain has a significant influence on the structural aerostatic force coefficients and the buffeting responses, although neither of their maximums arises due to the general wind yaw. The structural buffeting responses increase with higher wind speeds, while are affected little by the wind attack angles in a small range. The lateral buffeting response is neither sensitive to turbulence intensity nor the turbulence integral scale. The vertical and torsional responses show an uptrend with increasing turbulence intensity, and both increase by around 15% when the turbulence intensity increases by around 40%. The vertical responses increase by about 9% if the turbulence integral scale increases by about 20%, while the lateral responses are affected little by a change in integral scale. In spite of the small influence of the turbulence integral scales on the lateral responses, the torsional responses vary greatly at different wind attack angles. At an attack angle of 3°, the torsional responses increase by around 8% with the increased integral scale, but they are influenced little by the change in integral scale at a 0° attack angle. Compared with the lateral wind loading found in the wind tunnel, the maximum equivalent calculated from the bridges structural code seems too conservative, and hence the code’s static gust factor should be further investigated.
-
图 5 各抖振响应随紊流度改变的增幅
Figure 5. Increments of buffeting responses with the variation of turbulence intensity
图 6 各抖振响应随紊流积分尺度改变的增幅
Figure 6. Increments of buffeting responses with the variation of turbulence integral scale
表 1 各类风场特性参数
Table 1. Characteristic parameters of wind fields
风场类别 ${U_{\rm{m}}}$/（m•s–1） ${U_{\rm{f}}}$/（m•s–1） ${I_u}$ ${I_w}$ ${L_u}$/m ${L_w}$/m 风场I 6.87 48.58 0.117 7 0.098 4 1.023 2 0.431 3 4.65 32.88 0.108 4 0.098 5 0.850 3 0.367 8 风场II 6.87 48.58 0.069 8 0.052 7 1.082 8 0.452 4 4.68 33.09 0.068 9 0.051 1 0.939 4 0.417 4 风场III 6.85 48.44 0.065 0 0.049 9 1.300 2 0.556 5 4.68 33.09 0.063 1 0.050 1 1.096 0 0.448 8 
下载: 导出CSV
表 2 紊流度的变化对结构抖振响应的影响
Table 2. Effects of variation of turbulence intensity on the structural buffeting responses
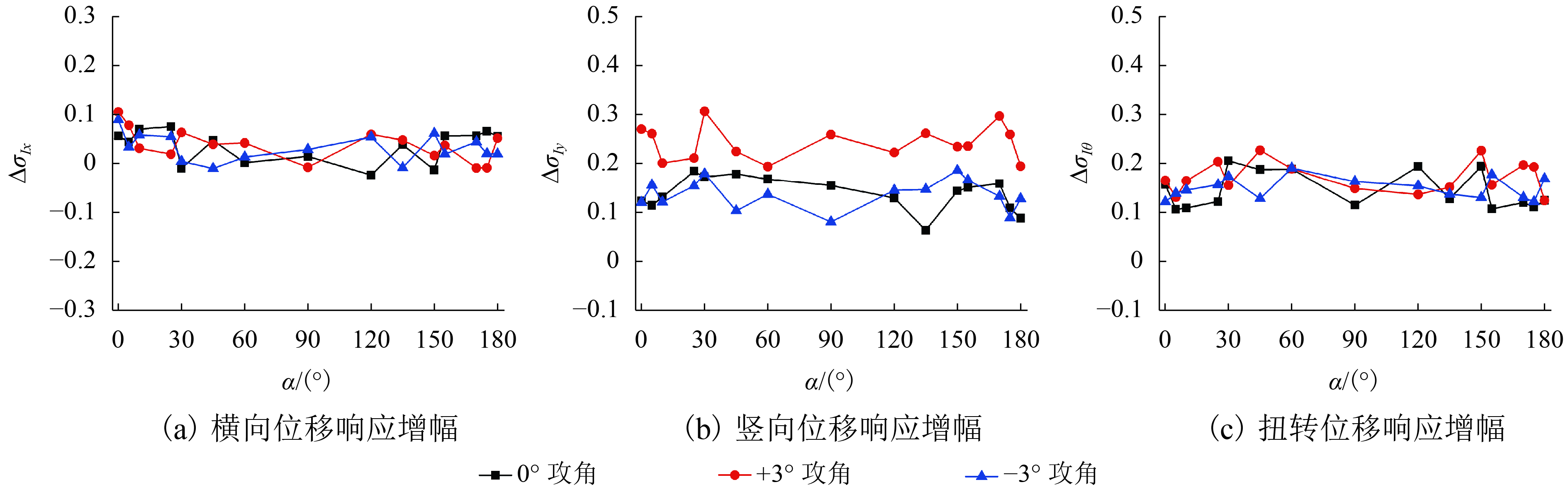
结构抖振响应 $I$对结构抖振响应的影响 ${\sigma _x}$ 随着 $I$的增大 ${\Delta \sigma_{Ix}}$较小，大体均在5%以内，甚至有些工况响应减小. $I$对 ${\sigma _x}$影响较小 ${\sigma _y}$ 随着 $I$的增大各风向角响应值均明显增大， + 3° 攻角下整体 ${\Delta \sigma_{Iy}}$最大，各风向角响应 ${\Delta \sigma_{Iy}}$平均达到24.1%左右，0° 攻角 ${\Delta \sigma_{Iy}}$平均约为13.7%，–3° 攻角约为13.6% ${\sigma _\theta }$ 随着 $I$的增大各风向角响应值均明显增大，–3° 攻角 ${\Delta \sigma_{I\theta}}$平均约为14.9%，0° 攻角约为14.4%， + 3° 攻角约为17.1%
下载: 导出CSV
表 3 紊流积分尺度的变化对结构抖振响应的影响
Table 3. Effects of variation of turbulence integral scale on the structural buffeting responses
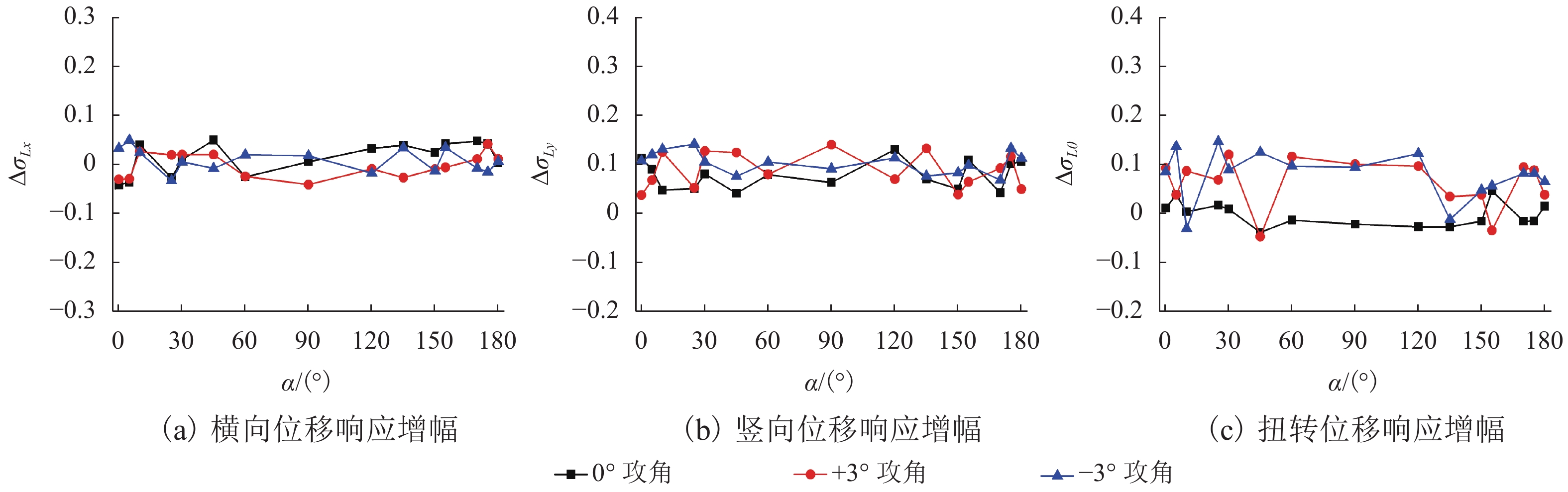
结构抖振响应 $L$对结构抖振响应的影响 ${\sigma _x}$ 所有工况各 ${\Delta \sigma_{Lx}}$不超过 $ \pm $5%， $L$的变化几乎无影响 ${\sigma _y}$ 随着 $L$的增大各风向角响应值均呈现增大趋势，–3° 攻角各风向角 ${\Delta \sigma_{Ly}}$平均约为10.4%，0° 攻角 ${\Delta \sigma_{Ly}}$平均约为7.8%， + 3° 攻角 ${\Delta \sigma_{Ly}}$平均约为8.8% ${\sigma _\theta }$ ± 3° 攻角下，随着 $L$的增大各风向角响应值大体均增大，个别风向角出现减小的情况且减幅较小，除去个别响应值随L减小的工况， + 3° 和 – 3° 攻角下各风向角响应值 ${\Delta \sigma_{L\theta}}$平均分别约为9.4%、7.8%. 在0°攻角下随着 $L$的增大响应没有统一的变化规律，增量有正有负，且 ${\Delta _{L\theta }}$较小， $L$影响较小
下载: 导出CSV
表 4 等效风荷载计算结果
Table 4. Results of equivalent wind loading
计算方法 静阵风系数 等效风荷载/N 计算误差值 《桥规》 1.325 24 361.55 38.5% 风洞试验 17 582.98
下载: 导出CSV
-
XIE J, HUNTER M, IRWIN P. Experimental and analytical approaches in wind engineering studies for bridges[R]. Budapest: Responding to Tomorrow’s Challenges in Structural Engineering, 2006 项海帆. 进入21世纪的桥梁风工程研究[J]. 同济大学学报 (自然科学版),2002,30(5): 529-532XIANG Haifan. Study on bridge wind engineering into 21st century[J]. Journal of Tongji University (Natural Science), 2002, 30(5): 529-532 叶征伟. 山区高墩大跨连续刚构桥风环境及风荷载研究[D]. 杭州: 浙江大学, 2012 KOSSMANN M, VÖGTLIN R, CORSMEIER U, et al. Aspects of the convective boundary layer structure over complex terrain[J]. Atmospheric Environment, 1998, 32(7): 1323-1348 doi: 10.1016/S1352-2310(97)00271-9 于舰涵,李明水,廖海黎. 山区地形对桥位风场影响的数值模拟[J]. 西南交通大学学报,2016,51(4): 654-662 doi: 10.3969/j.issn.0258-2724.2016.04.008YU Jianhan, LI Mingshui, LIAO Haili. Numerical simulation of effect of mountainous topography on wind field at bridge site[J]. Journal of Southwest Jiaotong University, 2016, 51(4): 654-662 doi: 10.3969/j.issn.0258-2724.2016.04.008 王凯,廖海黎,李明水,等. 山区峡谷桥梁设计基准风速的确定方法[J]. 西南交通大学学报,2013,48(1): 29-35 doi: 10.3969/j.issn.0258-2724.2013.01.005WANG Kai, LIAO Haili, LI Mingshui, et al. Determination method for basic design wind speed of mountainous-valley bridge[J]. Journal of Southwest Jiaotong University, 2013, 48(1): 29-35 doi: 10.3969/j.issn.0258-2724.2013.01.005 徐洪涛. 山区峡谷风特性参数及大跨度桁梁桥风致振动研究[D]. 成都: 西南交通大学, 2009 U.S. Department of Commerce, National Bureau of Standards. Turbulent wind effects on tension leg platform surge[S]. Washington D C: Government Printing Office, 1983 中交公路规划设计院. 公路桥梁抗风设计规范: JTG/TD60-01—2004[S]. 北京: 人民交通出版社, 2004 KIMURA K, TANAKA H. Bridge buffeting due to wind with yaw angles[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1992, 42(1/2/3): 1309-1320 ZHU L D, XU Y L. Buffeting response of long-span cable-supported bridges under skew winds, part 1:theory[J]. Journal of Sound & Vibration, 2005, 281(3/4/5): 647-673 BARNARD R H. Wind loads on cantilevered roof structures[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1981, 8(1): 21-30 王浩,李爱群,焦常科,等. 桥塔风效应对大跨度悬索桥抖振响应的影响[J]. 振动与冲击,2010,29(8): 103-106 doi: 10.3969/j.issn.1000-3835.2010.08.023WANG Hao, LI Aiqun, JIAO Changke, et al. Bridge tower wind effects on buffeting response of long-span suspension bridges[J]. Journal of Vibration and Shock, 2010, 29(8): 103-106 doi: 10.3969/j.issn.1000-3835.2010.08.023 庞加斌,葛耀君,陆烨. 大气边界层湍流积分尺度的分析方法[J]. 同济大学学报 (自然科学版),2002,30(5): 529-532PANG Jiabin, GE Yaojun, LU Ye. Methods for analysis of turbulence integral length in atmospheric boundary-layer[J]. Journal of Tongji University (Natural science), 2002, 30(5): 529-532 公路桥梁抗风设计指南编写组. 公路桥梁抗风设计指南[M]. 北京: 人民交通出版社, 1996: 24 -
下载:
点击查看大图
图(6) / 表(4)
计量
- 文章访问数: 495
- HTML全文浏览量: 230
- PDF下载量: 10
- 被引次数: 0