成层结构性软土一维非线性固结半解析分析

夏长青; 胡安峰; 付鹏; 崔军; 谢康和; 周禹杉

doi:10.3969/j.issn.0258-2724.20170612

成层结构性软土一维非线性固结半解析分析

doi: 10.3969/j.issn.0258-2724.20170612

夏长青^1,2,,
胡安峰^1,2, ,,
付鹏^1,2,
崔军^1,2,
谢康和^1,2,
周禹杉^1,2

基金项目: 国家自然科学基金资助项目（51778572，51278453）；教育部博士点基金资助项目（20120101110029）；浙江省自然科学基金资助项目（LY14E080016）

详细信息

作者简介:
夏长青（1991—），男，博士研究生，研究方向为软黏土力学和地基处理，E-mail：xiacq09@163.com

通讯作者:
胡安峰（1974—），男，副教授，研究方向为软黏土力学和地基处理、桩基工程，E-mail：anfenghu@zju.edu.cn

计量
- 文章访问数: 486
- HTML全文浏览量: 236
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2017-08-11
- 修回日期: 2018-06-26
- 网络出版日期: 2019-03-21
- 刊出日期: 2019-12-01

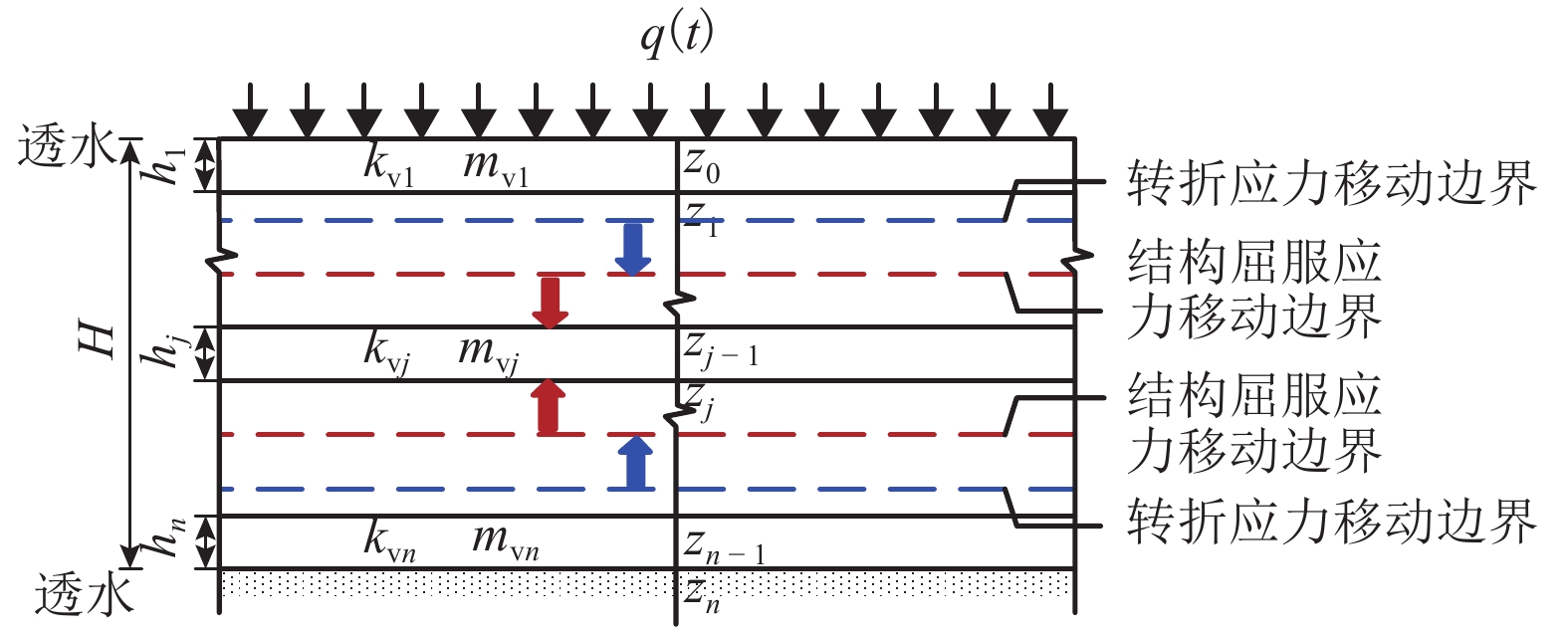
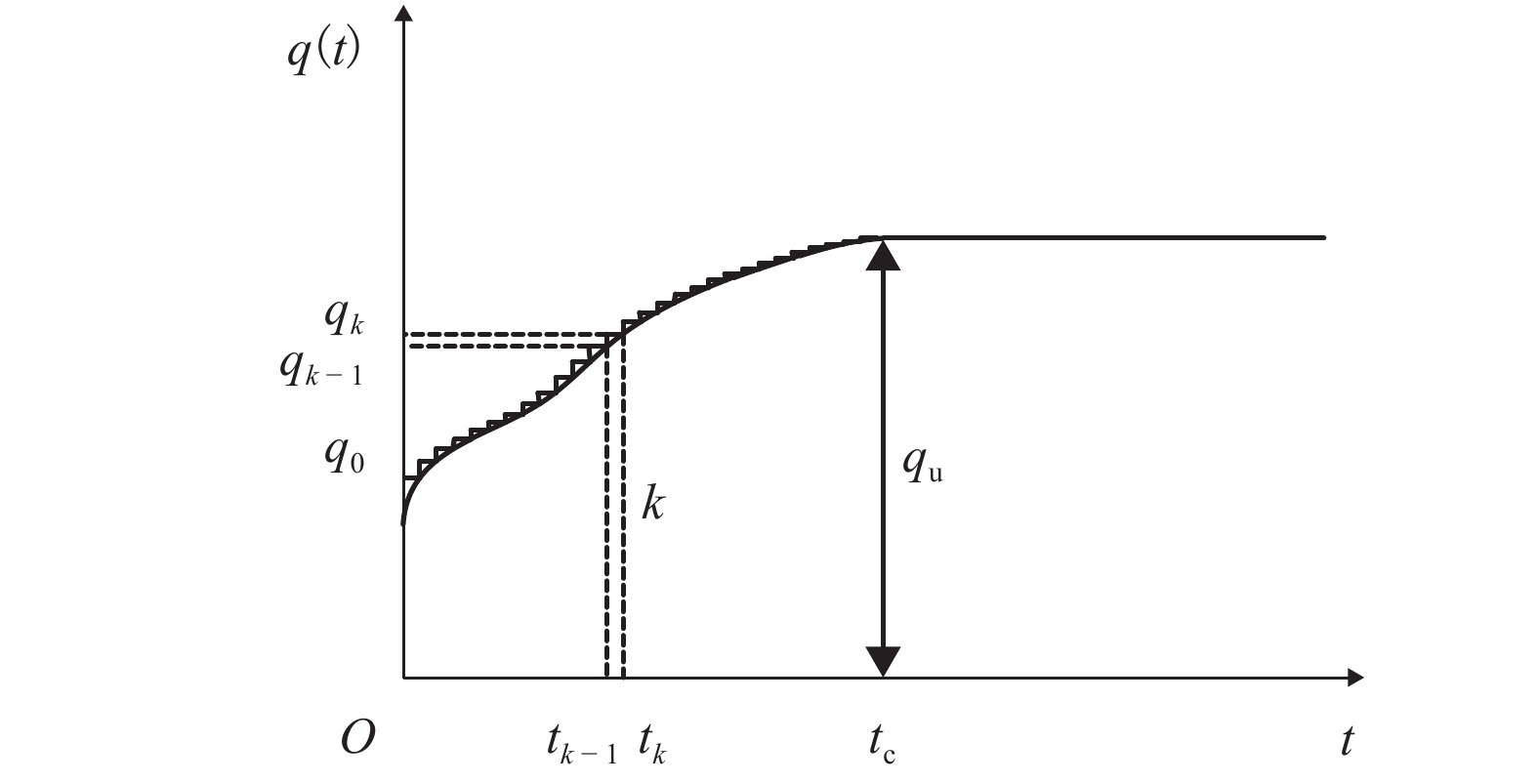
Semi-analytical Analysis of One-Dimensional Nonlinear Consolidation of Multi-layered Structured Soft Clay

XIA Changqing^{1,2
,},
HU Anfeng^{1,2
, ,},
FU Peng^1,2,
CUI Jun^1,2,
XIE Kanghe^1,2,
ZHOU Yushan^1,2

摘要

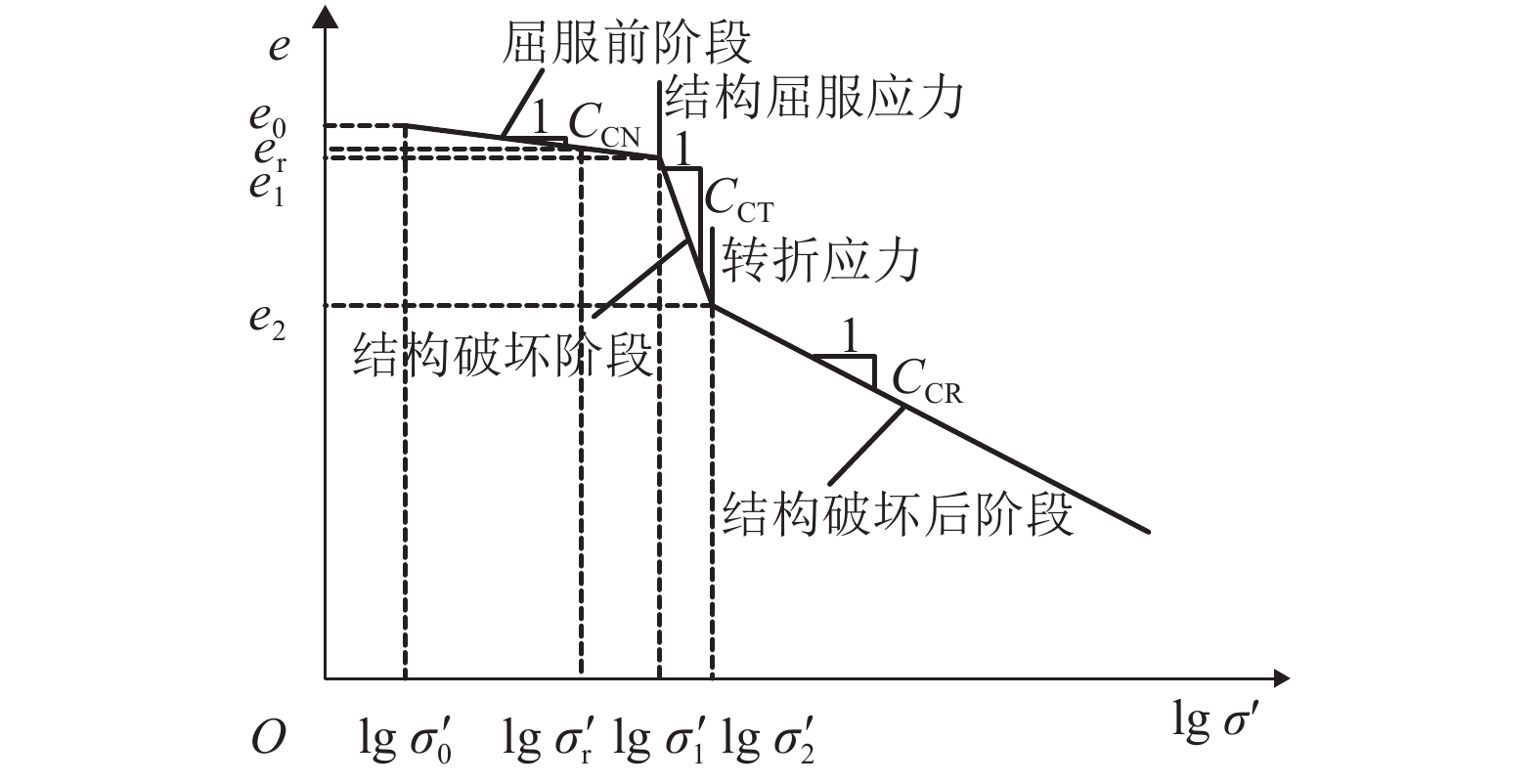
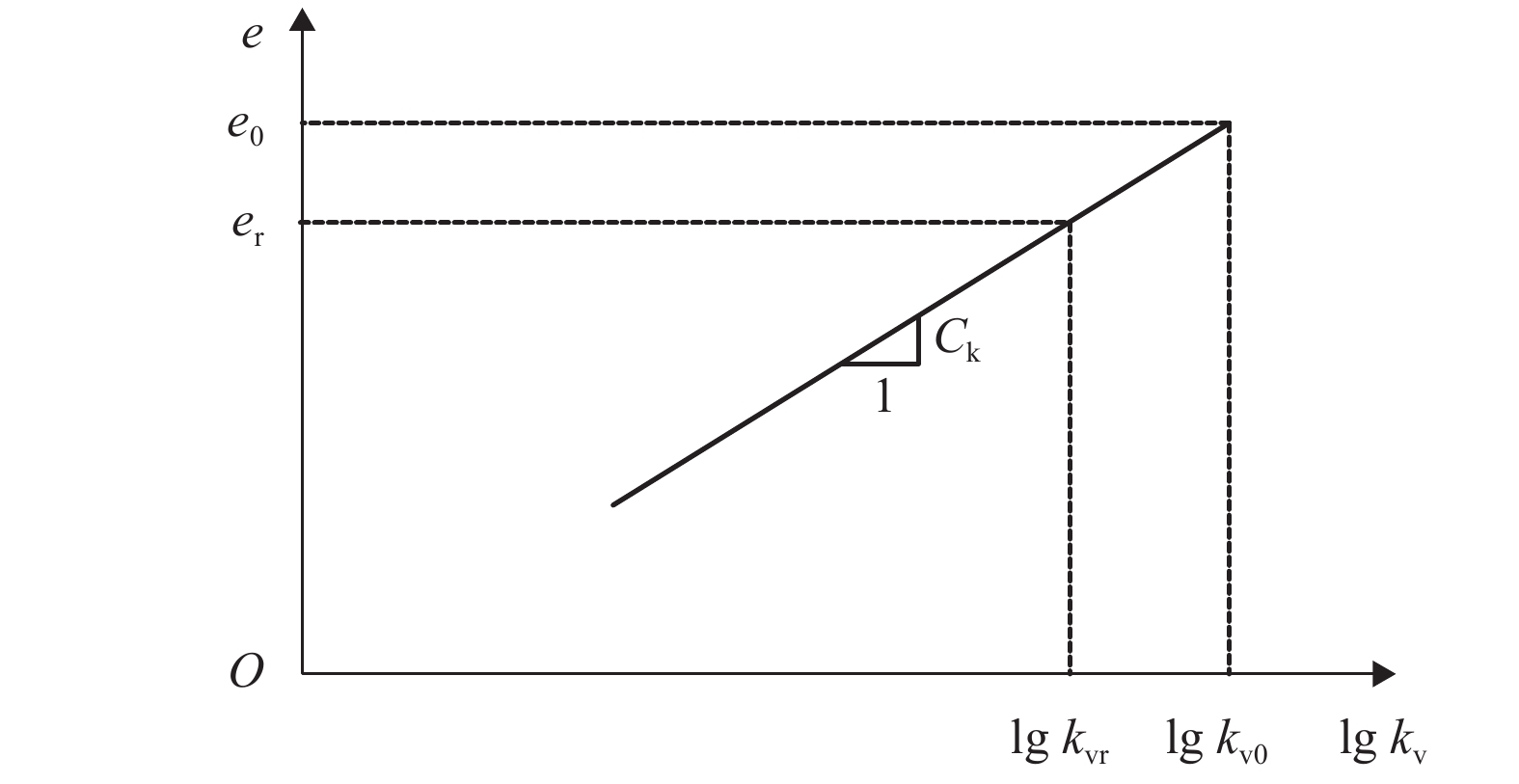
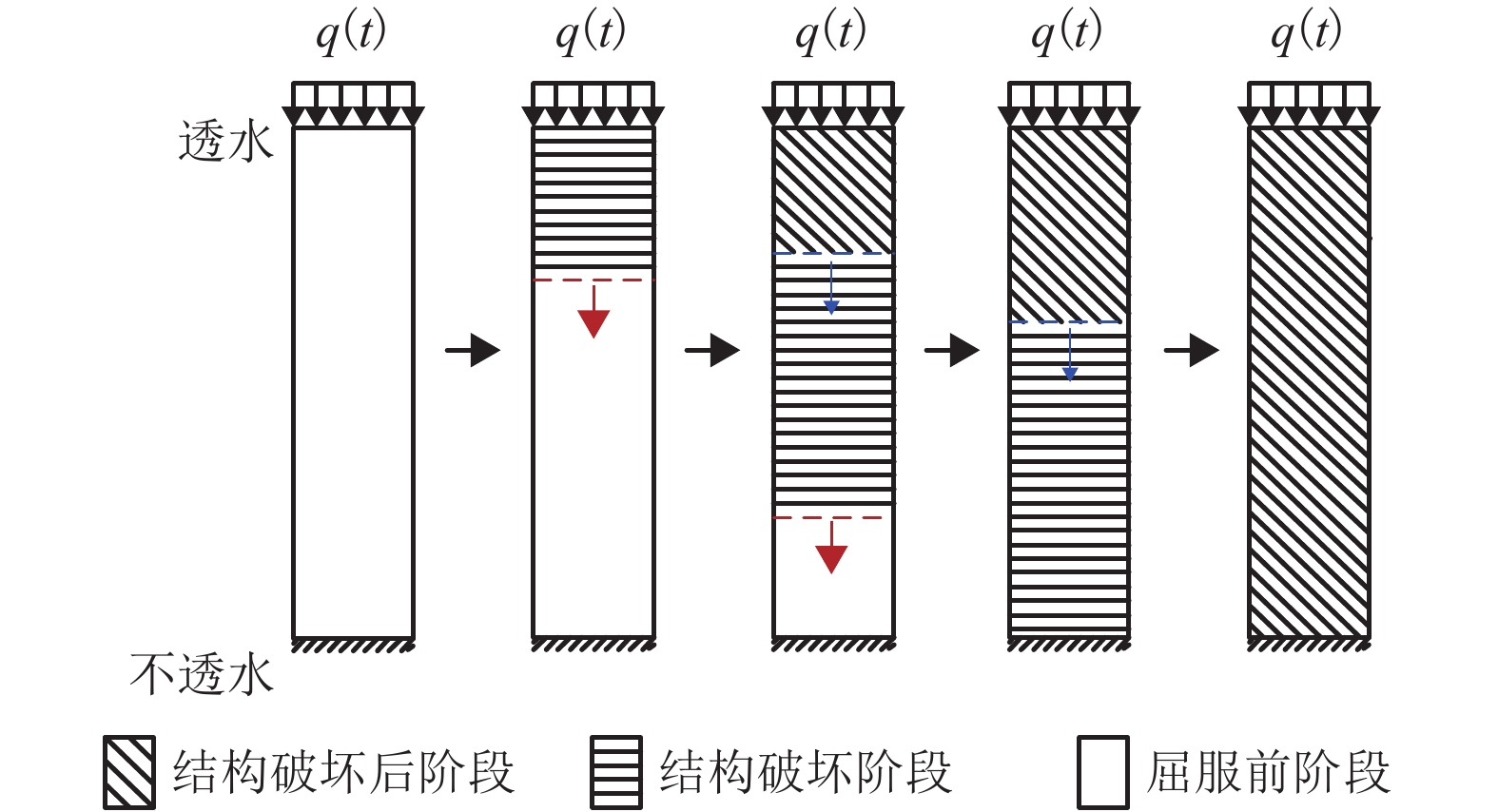
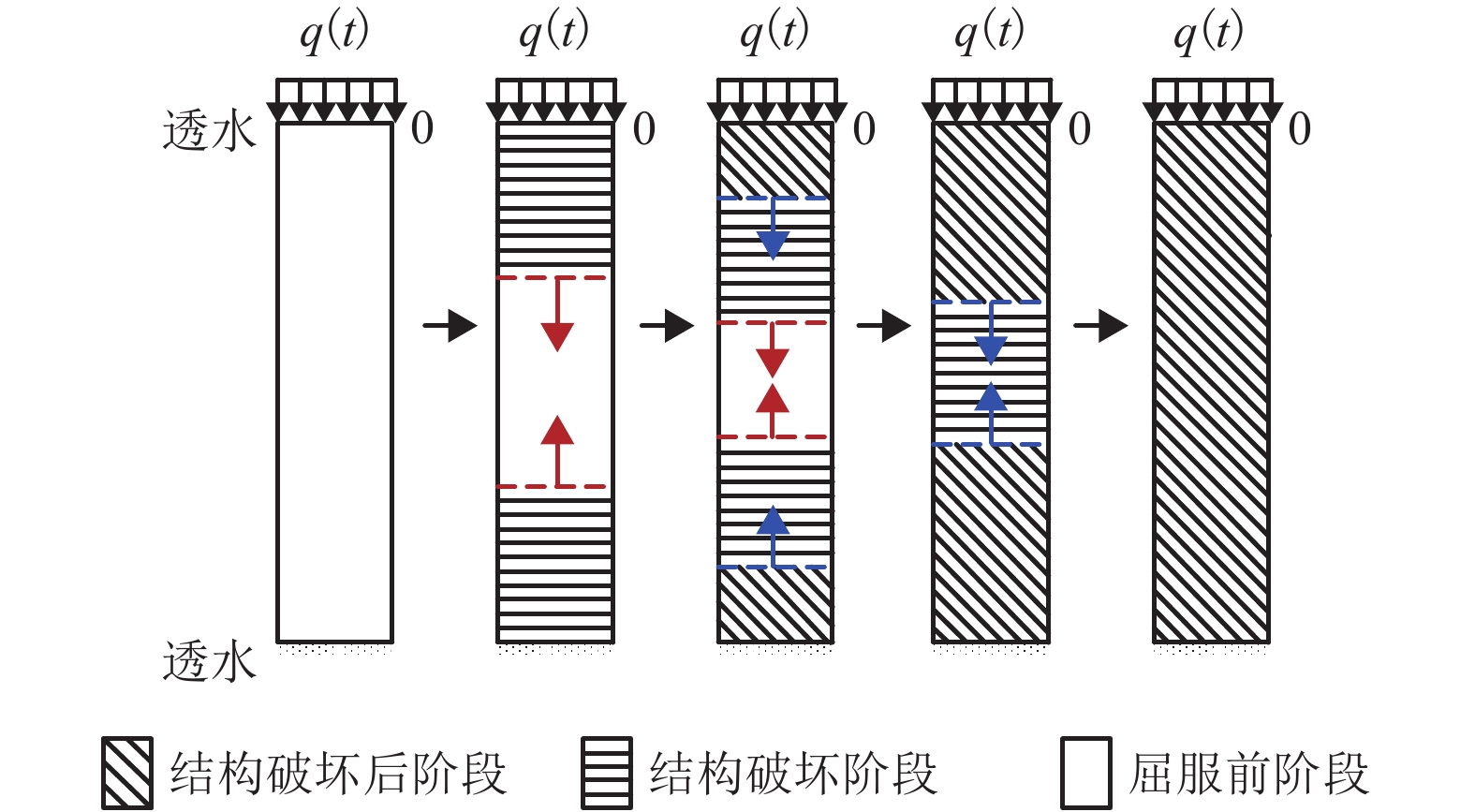
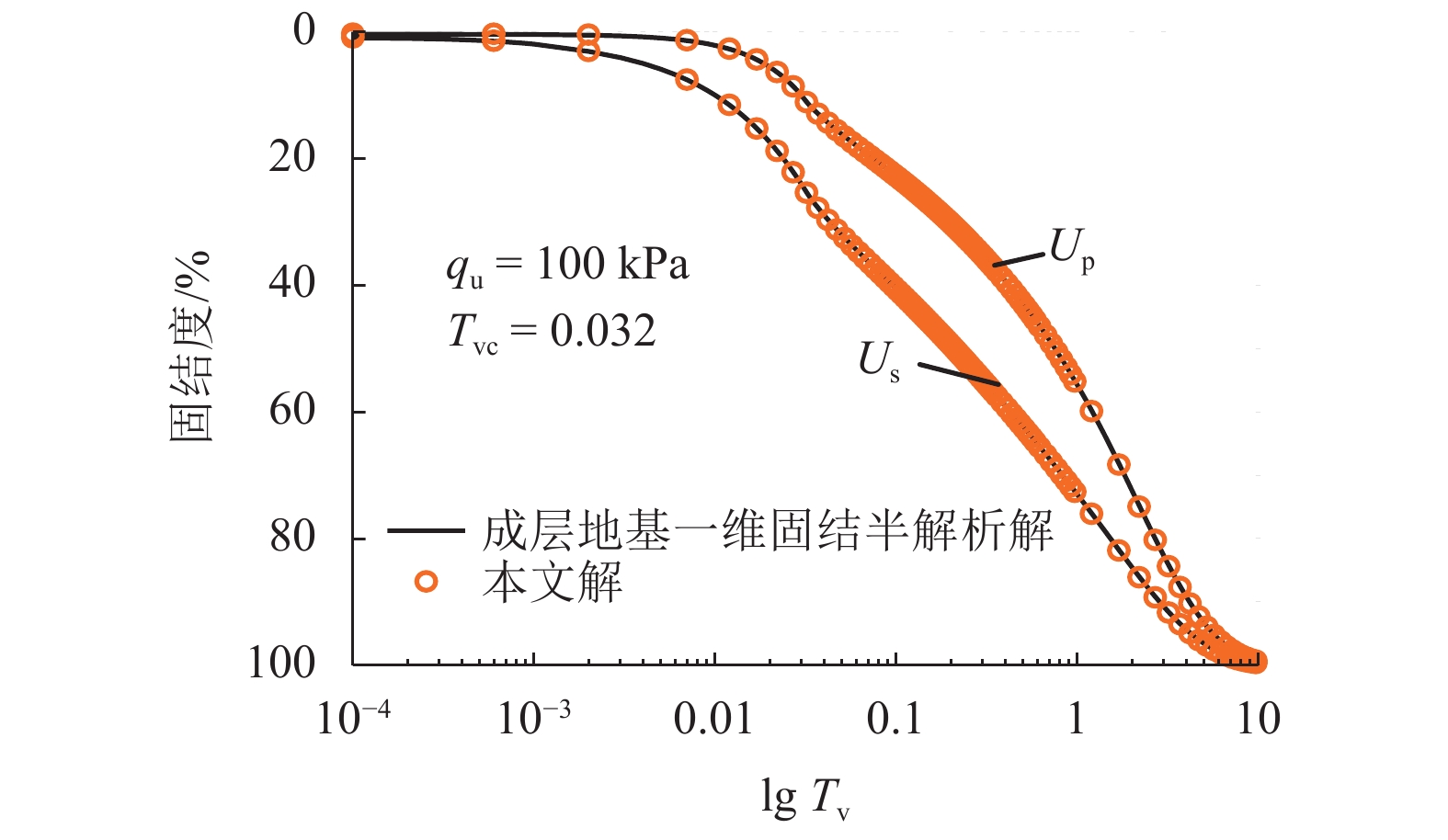
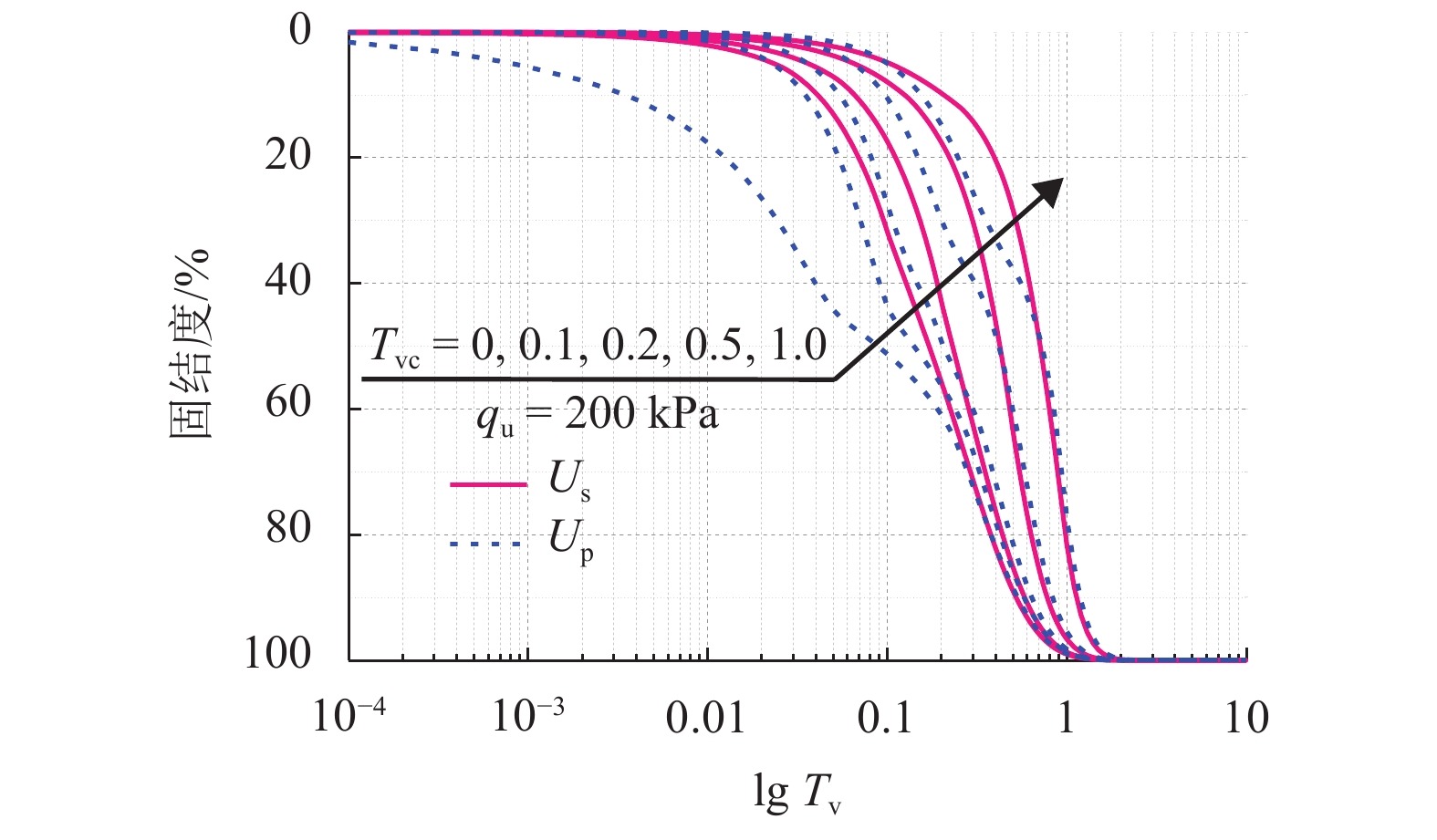
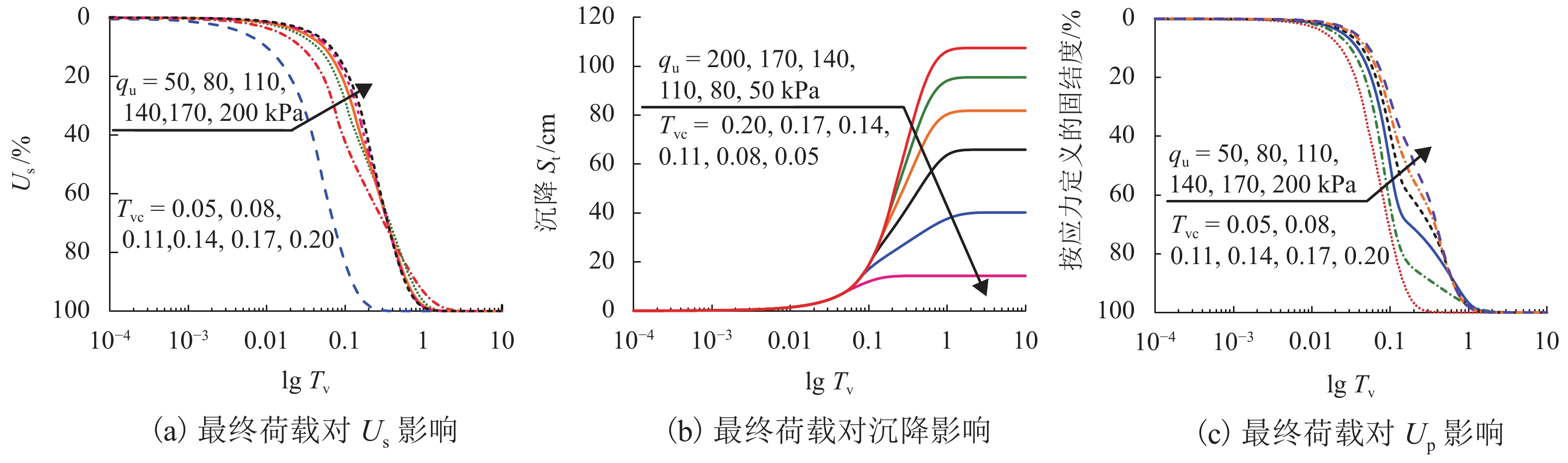
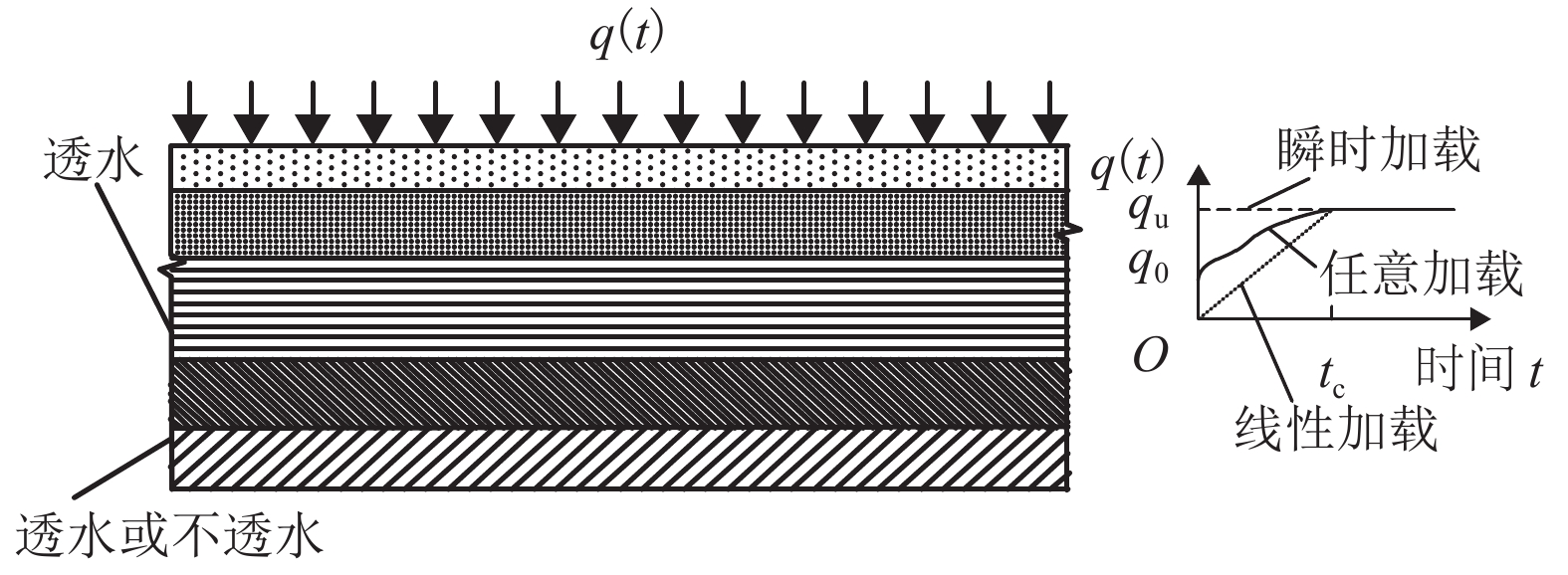
摘要: 为了研究变荷载作用下土体结构性对成层软土固结性状的影响，基于结构性软土压缩性和渗透性的非线性变化规律，以及结构屈服应力随土体深度变化等特征，对结构性软土非线性固结问题进行了分析. 首先采用三折线压缩模型、e-lg k_v渗透模型，详细分析了结构性软土在不同排水工况下的固结过程；其次，利用半解析法，建立一维固结方程，并编制程序进行求解，与目前已有的非线性固结结果进行了对比分析，验证了本文计算方法的可靠性；最后以某四层软土地基为工程背景，研究了变荷载、结构性等因素对固结性状的影响. 研究结果表明：成层结构性软土一维非线性固结过程中，当最终荷载相同，加荷速率不同时，固结前期，按应力定义的固结度大于按沉降定义的固结度，固结后期则相反；当加荷速率相同，最终荷载不同时，按应力定义和按沉降定义的固结度在固结前期均随着最终荷载的增大而减小，而在固结后期，随着最终荷载的增大而增大；考虑结构性时，按应力定义的固结度明显大于不考虑结构性的计算值，固结前期相差较大，随着固结的进行，差值逐渐减小.
- 变荷载 /
- 结构性 /
- 成层地基 /
- 非线性固结 /
- 半解析法
Abstract: To study the impact of structural properties on the consolidation behavior of multi-layered soft clay under time-dependent loading, the problem of nonlinear consolidation of structured soft clay was addressed by analyzing the nonlinear variable permeability and compressibility of structured soft clay and the variation of the yield stress with depth. First, the consolidation process in different drainage situations was analyzed in detail using the structured soft clay trilinear compression model and e-lg k_v permeability model. Then, one-dimensional consolidation equations were established by semi-analytical method. A calculation procedure was developed to solve the problem, and the effectiveness of the proposed method was verified by comparison with the existing nonlinear consolidation results. Finally, in the engineering background of a four-layer soft clay ground, influences of time-dependent loading and structural properties on the consolidation behavior of multi-layered soft clay were investigated. The results show that when the ultimate load is fixed while loading rates are varying, the degree of consolidation defined in terms of effective stress (U_p) is larger than that defined in terms of settlement (U_s) at the early stage, but the opposite will occur at the late stage. On the other hand, when the loading rate is fixed but the ultimate loads are different, with the ultimate load increasing, the values of U_s and U_p decrease at the early stage but increse at the late stage. At the early stage of cosolidation, the U_p obtained by the nonlinear consolidation analysis considering structural properties is significantly larger than that without considering structural properties, but the discrepancy decreases gradually as the consolidation proceeds.
- time-dependent loading /
- structural properties /
- multi-layered ground /
- non-linear consolidation /
- semi-analytical method

HTML全文

图 1 成层结构性软土地基模型

Figure 1. Model of multi-layered structured soft soil foundation

下载: 全尺寸图片幻灯片

图 2 三折线压缩模型

Figure 2. Trilinear compression model

下载: 全尺寸图片幻灯片

图 3 渗透模型

Figure 3. Permeability model

下载: 全尺寸图片幻灯片

图 4 单面排水固结过程

Figure 4. Consolidation process of single-drainage situation

下载: 全尺寸图片幻灯片

图 5 双面排水固结过程

Figure 5. Consolidation process of double-drainage situation

下载: 全尺寸图片幻灯片

图 6 空间离散

Figure 6. Schematic diagram of spatial discretization

下载: 全尺寸图片幻灯片

图 7 时间和荷载离散

Figure 7. Schematic diagram of temporal and loading discretization

下载: 全尺寸图片幻灯片

图 8 对比验证

Figure 8. Verification by comparison

下载: 全尺寸图片幻灯片

图 9 加荷速率对固结度影响

Figure 9. Influence of the loading rate on the degree of consolidation

下载: 全尺寸图片幻灯片

图 10 最终荷载对固结性状影响

Figure 10. Influence of the ultimate load on the consolidation behavior

下载: 全尺寸图片幻灯片

图 11 土体结构性对固结性状影响

Figure 11. Influence of structural properties on the consolidation behavior

下载: 全尺寸图片幻灯片

表 1 对比验证计算参数

Table 1. Calculation parameters for verification

i	C_c	C_k	k_vr /（×10^–9 m•s^–1）	e_r	σ'_r /kPa	γ_sat /（kN•m^–3）	h_i/ m
1	0.382	0.765	3.628	1.393	100	18.31	3
2	0.521	0.525	0.815	1.422	100	18.18	5
3	0.628	0.418	0.434	1.501	100	17.91	8
4	0.286	0.358	1.128	1.058	100	18.62	4

下载: 导出CSV

表 2 4层地基计算参数

Table 2. Calculation parameters for four layered soils

参数	土层
参数	1	2	3	4
C_CN	0.071	0.056	0.039	0.052
C_CT	0.431	0.632	0.496	0.308
C_CR	0.226	0.335	0.271	0.209
C_k	0.634	0.532	0.474	0.310
k_vr/（×10^–9 m•s^–1）	2.526	5.335	3.761	2.169
e_r	1.471	1.307	1.289	1.095
σ'_r/kPa	100	100	100	100
γ_sat/（kN•m^–3）	18.35	18.23	17.89	18.64
K₁	1.209	1.209	1.209	1.209
K₂/kPa	50	50	50	50
h_i/m	2	6	7	5

下载: 导出CSV

参考文献(19)

BURLAND J B. On the compressibility and shear strength of natural clays[J]. Geotechnique, 1990, 40(3): 329-378. doi: 10.1680/geot.1990.40.3.329

LEROUEIL S, VAUGHAN P R. The general and congruent effects of structure in natural soils and weak rocks[J]. Geotechnique, 1990, 40(3): 467-488. doi: 10.1680/geot.1990.40.3.467

沈珠江. 土体结构性的数学模型——21 世纪土力学的核心问题[J]. 岩土工程学报,1996,18(1): 95-97. doi: 10.3321/j.issn:1000-4548.1996.01.015

SHEN Zhujiang. Mathematical modelling considering soil structure: A key issue in soil mechanics in the 21^st Century[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 95-97. doi: 10.3321/j.issn:1000-4548.1996.01.015

王军,陈云敏. 均质结构性软土地基的一维固结解析解[J]. 水利学报,2003,34(3): 19-24. doi: 10.3321/j.issn:0559-9350.2003.03.004

WANG Jun, CHEN Yunmin. Analytical solution to 1-D consolidation of homogeneous structured soft foundation[J]. Journal of Hydraulic Engineering, 2003, 34(3): 19-24. doi: 10.3321/j.issn:0559-9350.2003.03.004

XIE K H, XIA C Q, AN R, et al. A study on the one-dimensional consolidation of double-layered structured soils[J]. Computers and Geotechnics, 2016, 73: 189-198. doi: 10.1016/j.compgeo.2015.12.007

XIE K H, XIA C Q, AN R, et al. A study on one-dimensional consolidation of layered structured soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(7): 1081-1098. doi: 10.1002/nag.v40.7

HU A F, XIA C Q, WU H, et al. A study on one-dimensional consolidation of layered structured aquitard soils in a leakage system[J]. Marine Georesources & Geotechnology, 2017, 35(3): 318-329.

曹宇春,陈云敏,黄茂松. 任意施工荷载作用下天然结构性软黏土的一维非线性固结分析[J]. 岩土工程学报,2006,25(8): 569-574.

CAO Yuchun, CHEN Yunmin, HUANG Maosong. One-dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading[J]. Chinese Journal of Geotechnical Engineering, 2006, 25(8): 569-574.

刘洋,宫志,王喆. 考虑结构应力的粘土一维非线性固结分析[J]. 土木建筑与环境工程,2012,34(2): 39-45. doi: 10.11835/j.issn.1674-4764.2012.02.007

LIU Yang, GONG Zhi, WANG Zhe. One-dimensional nonlinear consolidation analysis of clay considering structural stress[J]. Journal of Civil, Architectural & Environmental Engineering, 2012, 34(2): 39-45. doi: 10.11835/j.issn.1674-4764.2012.02.007

KARIM M R, OKA F, KRABBENHOFT K, et al. Simulation of long-term consolidation behavior of soft sensitive clay using an elasto-viscoplastic constitutive model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(16): 2801-2824.

OZELIM L C D S, CAMAPUM DE CARVALHO J, CAVALCANTE A L B, et al. Novel approach to consolidation theory of structured and collapsible soils[J]. International Journal of Geomechanics, 2015, 15(4): 04014064. doi: 10.1061/(ASCE)GM.1943-5622.0000409

王立忠,丁利,陈云敏,等. 结构性软土压缩特性研究[J]. 土木工程学报,2004,37(4): 46-53. doi: 10.3321/j.issn:1000-131X.2004.04.010

WANG Lizhong, DING Li, CHEN Yunmin, et al. Study on compressibility of structured soft soil[J]. China Civil Engineering Journal, 2004, 37(4): 46-53. doi: 10.3321/j.issn:1000-131X.2004.04.010

TAVENAS F, JEAN P, LEBLOND P. The permeability of natural soft clays, partⅡ:permeability characteristics[J]. Canadian Geotechnical Journal, 1983, 20(4): 645-660. doi: 10.1139/t83-073

ZENG L L, HONG Z S, CAI Y Q, et al. Change of hydraulic conductivity during compression of undisturbed and remolded clays[J]. Applied Clay Science, 2011, 51(1): 86-93.

HORPIBULSUK S, SHIBUYA S, FUENKAJORN K, et al. Assessment of engineering properties of Bangkok clay[J]. Canadian Geotechnical Journal, 2007, 44(2): 173-187. doi: 10.1139/t06-101

王立忠,李玲玲. 结构性土体的施工扰动及其对沉降的影响[J]. 岩土工程学报,2007,29(5): 697-704. doi: 10.3321/j.issn:1000-4548.2007.05.011

WANG Lizhong, LI Lingling. Field disturbance of structured clay and its effect on settlements of soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 697-704. doi: 10.3321/j.issn:1000-4548.2007.05.011

谢康和. 双层地基一维固结理论与应用[J]. 岩土工程学报,1994,16(5): 24-35. doi: 10.3321/j.issn:1000-4548.1994.05.004

XIE Kanghe. Theory of one dimensional consolidation of double-layered ground and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24-35. doi: 10.3321/j.issn:1000-4548.1994.05.004

谢康和,潘秋元. 变荷载下任意层地基一维固结理论[J]. 岩土工程学报,1995,17(5): 80-85. doi: 10.3321/j.issn:1000-4548.1995.05.013

XIE Kanghe, PAN Qiuyuan. Theory of one-dimensional consolidation of multi-layered soil under varied load[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 80-85. doi: 10.3321/j.issn:1000-4548.1995.05.013

谢康和,郑辉,李冰河,等. 变荷载下成层地基一维非线性固结分析[J]. 浙江大学学报(工学版),2003,37(4): 426-431. doi: 10.3785/j.issn.1008-973X.2003.04.011

XIE Kanghe, ZHENG Hui, LI Binghe, et al. Analysis of one dimensional nonlinear consolidation of layered soils under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(4): 426-431. doi: 10.3785/j.issn.1008-973X.2003.04.011

施引文献

附加材料(0)

访问统计