Effects of Oscillation Amplitude on Nonlinear Motion-Induced Force for 5 ∶ 1 Rectangular Cylinder
-
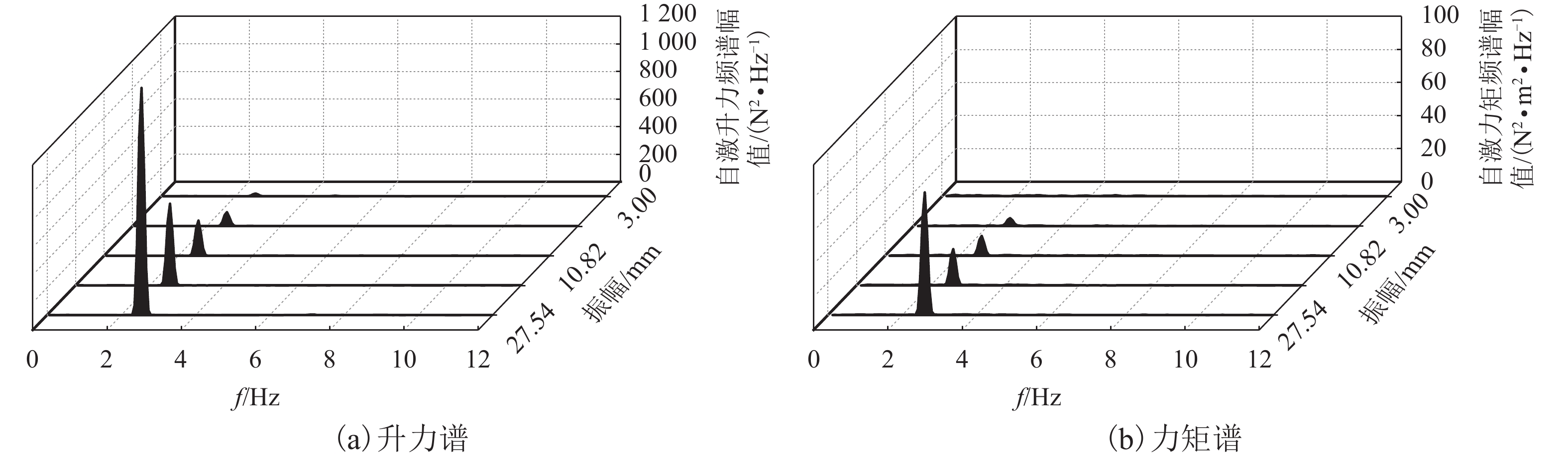
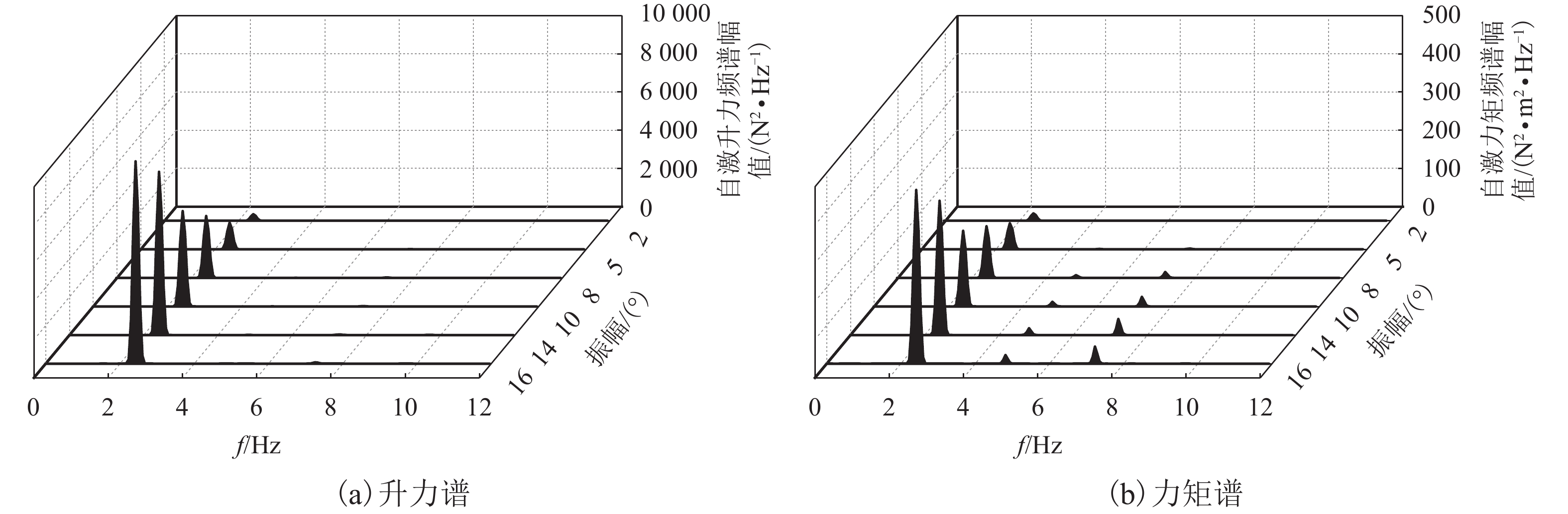
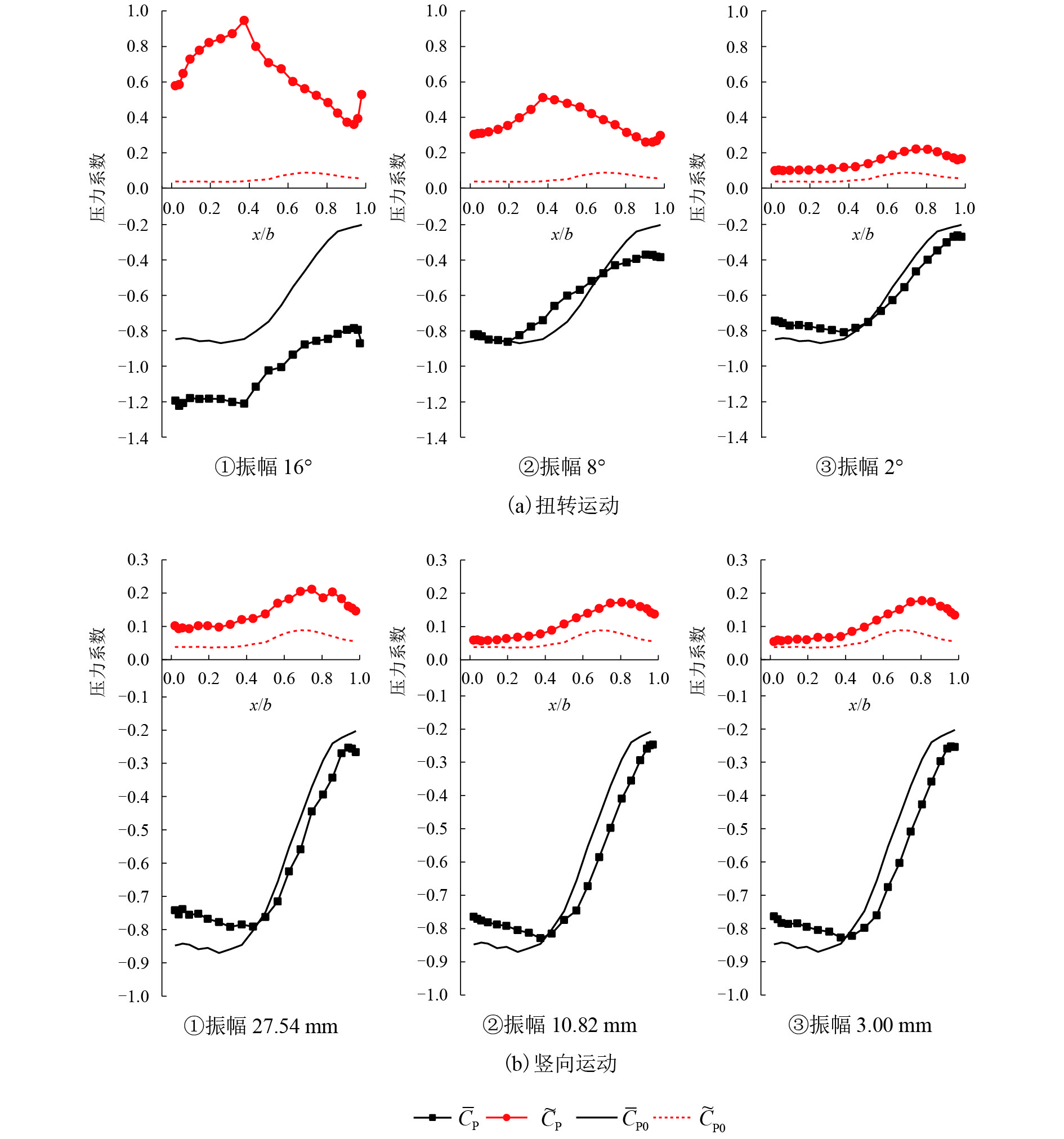
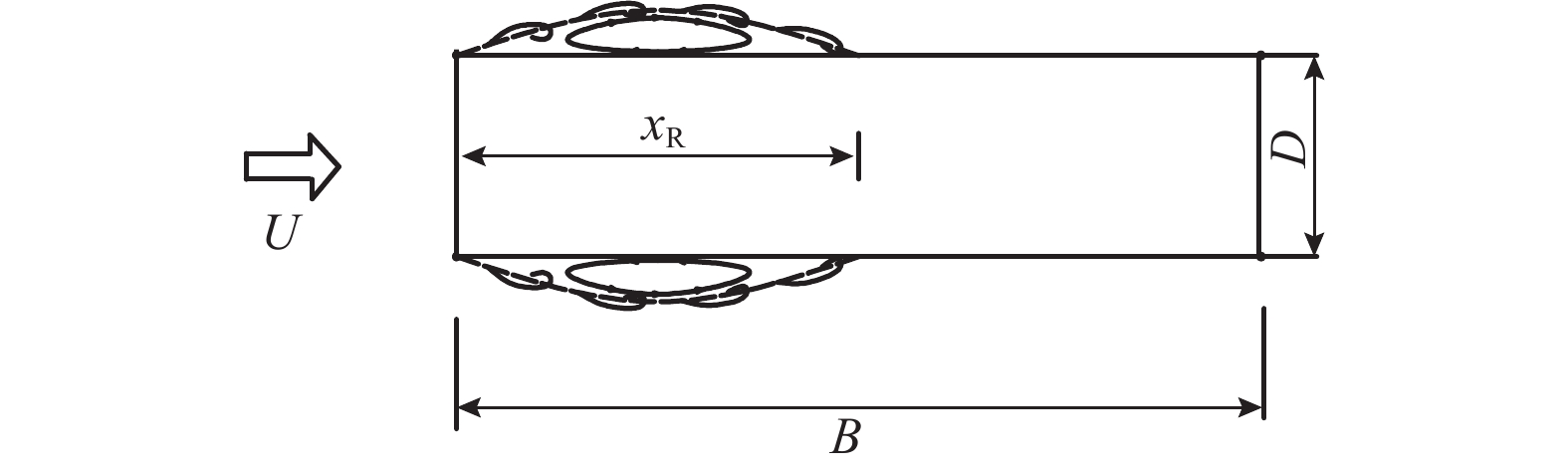
摘要: 宽高比为5∶1矩形断面的非线性自激气动力研究作为钝体空气动力学的基础性和前沿性研究，对钝体断面的非线性气动弹性行为分析有着重要的意义. 采用节段模型强迫振动风洞试验，结合模型表面同步测压技术，分析了振幅对宽高比为5∶1矩形试验断面自激气动力频谱特性和表面压力分布特性的影响，并借助本征正交分解分析了模型表面压力的模态特征函数，进而探讨了非线性气动力产生的流动机理. 试验及分析结果表明：5∶1矩形断面自激气动力的高次谐波分量仅在振幅不小于8° 的扭转运动下显著，但线性分量随着振幅增加呈非线性变化；在竖向运动或在小于8° 的扭转运动下，模型表面分离再附点位置靠近后缘且在一个周期内保持稳定，对应的压力模态为一阶对称分布，表明此时气动力仅由单一频率的主涡决定；在大于等于8° 的扭转运动下，一个周期内模型表面的分离再附点位置主要集中在前缘，对应的压力模态中也同时出现了对称分布的第1阶和反对称分布的第2和第3阶，表明此时出现了多个不同频率的主要旋涡，而频率高于运动频率的二次涡主导了高阶模态，并由此产生了气动力的高次谐波分量.Abstract: Investigations on the nonlinear motion-induced force acting on a rectangular cylinder with aspect ratio 5∶1, which is significant in the analysis of nonlinear aeroelastic behaviour for bluff sections, are part of fundamental and cutting-edge research on bluff body aerodynamics. Combined with surface synchronous pressure measurement, forced motion wind tunnel tests were carried out to investigate the influence of oscillation amplitude on the spectral characteristics of motion-induced force and pressure distribution for a 5∶1 rectangular cylinder. After analyzing the pressure distribution mode based on the proper orthogonal decomposition (POD) method, the mechanism for nonlinear motion-induced force was discussed. Experiments and analysis indicate that the higher harmonics in the motion-induced force acting on a 5∶1 rectangular cylinder only shows significant proportion when the section is under pitching motion and the amplitude exceeds 8°, while the linear components grow nonlinearly with the increase of oscillation amplitude. When the rectangular cylinder rotates with amplitude less than 8° or oscillates vertically, the reattaching point is near the trailing edge and remains stable during the period of motion. Vortices on the top surface shed directly into the wake flow and the corresponding pressure mode is symmetric, all of which suggest that the motion-induced force is determined by a main vortex with single frequency. When the rectangular cylinder rotates with amplitude greater than or equal to 8°, the first symmetric pressure mode along with the second and third anti-symmetrical pressure mode appear simultaneously. The corresponding reattaching point is concentrated at the leading edge, so that vortices continue to develop along the model surface. These suggest the existence of several vortices with different frequencies. The secondary vortex with a frequency larger than the motion frequency leads to the occurrence of higher pressure mode, and results in higher harmonics in motion-induced force.
-
Key words:
- rectangular section /
- oscillation amplitude /
- nonlinear motion-induced force /
- POD /
- secondary vortex
-
图 4 静止状态模型各个测压断面的气动力系数
Figure 4. Aerodynamic coefficients for each section of a stationary model
图 5 矩形断面的涡脱频率试验值和计算值的对比
Figure 5. Comparison of experimental and calculated values of vortex-shedding frequency for 5∶1 rectangular cylinder
图 6 升力时程和频谱（Ur = 12，模型运动频率 = 2.5 Hz）
Figure 6. Time history and PSD of lift force（Ur = 12，heaving motion frequency = 2.5 Hz）
图 11 扭转振幅对自激力矩的各阶谐波的影响（Ur = 12）
Figure 11. Effects of torsional amplitude on PSD of motion-induced moment
图 12 不同振幅下模型上表面压力系数分布
Figure 12. Pressure coefficient distribution on the top surface of the rectangular cylinder under different oscillation amplitudes
图 13 矩形断面流动分离示意
Figure 13. Schematic diagram of separation and reattachment of the flow
图 16 不同振幅下各阶次本征模态的贡献率
Figure 16. Contribution rate of POD mode at different oscillating amplitude
表 1 试验工况组合
Table 1. Summary of testing cases
振幅 Ur 扭转/（°） 竖向/mm 2、5、8、10、14、16 3.00、6.61、10.82、16.50、27.54 6、12 
下载: 导出CSV
表 2 不同扭转振幅下表面压力场前3阶本征模态和断面压力系数分布
Table 2. Pressure coefficient distribution and first three POD mode at different torsion motion amplitude
振幅/（°） POD模态 平均压力系数 脉动压力系数 第1阶 第2阶 第3阶 2 
8 
16 
下载: 导出CSV
-
BRUNO L, SALVETTI M V, RICCIARDELLI F. Benchmark on the aerodynamics of a rectangular 5∶1 cylinder:an overview after the first four years of activity[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 126(1): 87-106. MATSUMOTO M, SHIRATO H, ARAKI K, et al. Spanwise coherence characteristics of surface pressure field on 2-D bluff bodies[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 91(1): 155-63. RICCIARDELLI F, MARRA A M. Sectional aerodynamic forces and their longitudinal correlation on a vibrating 5∶1 rectangular cylinder[C]//Proceedings of the 6th International Colloquium on Bluff Body Aerodynamics and Applications. Milan: [s.n.], 2008: 1-4 LE T H, MATSUMOTO M, SHIRATO H. Spanwise coherent structure of wind turbulence and induced pressure on rectangular cylinders[J]. Wind and Structures, 2009, 12(5): 441. doi: 10.12989/was.2009.12.5.441 HAAN F L, KAREEM A. Anatomy of turbulence effects on the aerodynamics of an oscillating prism[J]. Journal of Engineering Mechanics, 2009, 135(9): 987-99. doi: 10.1061/(ASCE)EM.1943-7889.0000012 TAMURA T, ITOH Y, WADA A, et al. Numerical study of pressure fluctuations on a rectangular cylinder in aerodynamic oscillation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54(2): 39-50. 刘志文, 陈政清. H/B=1/5矩形断面气动性能研究[C]//第十三届全国结构风工程学术会议论文集（上册）. 大连: [出版者不详], 2007: 91-99 ZHU Z. LES prediction of aerodynamics and coherence analysis of fluctuating pressure on box girders of long-span bridges[J]. Computers & Fluids, 2015, 110: 169-180. 刘小兵, 张海东, 王彦彪. 宽高比为5的矩形断面梁气动力展向相关性研究[J]. 工程力学, 2015, 32（增刊1）: 50-54LIU Xiaobing, ZHANG Haidong, WANG Yanbiao. Study on spanwise correlation of aerodynamic force of rectangular cylinder with aspect ratio 5[J]. Engineering Mechanics, 2015, 32（S1）: 50-54 NODA M, UTSUNOMIYA H, NAGAO F, et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1/2): 101-11. WANG Q, LIAO H, WAN J, et al. Coupling and nonlinearity and spanwise correlation in aerodynamic force of a rectangular cylinder[C]//Proceedings of 8th International Colloquium on Bluff Body Aerodynamics and Applications（BBAA VIII）. Boston: [s.n.], 2016: 1-10 陈政清,于向东. 大跨桥梁颤振自激力的强迫振动法研究[J]. 土木工程学报,2002,35(5): 34-41. doi: 10.3321/j.issn:1000-131X.2002.05.008CHEN Zhengqing, YU Xiangdong. A new method for measuring flutter self-excited forces of long-span bridges[J]. China Civil Engineering Journal, 2002, 35(5): 34-41. doi: 10.3321/j.issn:1000-131X.2002.05.008 DIANA G, RESTA F, ROCCHI D. A new numerical approach to reproduce bridge aerodynamic non-linearities in time domain[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1871-84. 王骑. 大跨度桥梁断面非线性自激气动力与非线性气动稳定性研究[D]. 成都: 西南交通大学, 2011 唐煜. 流线型箱梁断面非线性自激力与非线性颤振响应研究[D]. 成都: 西南交通大学, 2015 HUANG L, XU Y L, LIAO H. Nonlinear aerodynamic forces on thin flat plate:numerical study[J]. Journal of Fluids & Structures, 2014, 44(7): 182-94. 马存明. 流线箱型桥梁断面三维气动导纳研究[D]. 成都: 西南交通大学, 2007 COOK N. Designers’ guide to EN 1991-1-4 eurocode 1: actions on structures, general actions part 1-4. Wind actions[M]. [S.l]: Thomas Telford Publishing, 2007: 66-67 NAKAMURA Y, OZONO S. The effects of turbulence on a separated and reattaching flow[J]. Journal of Fluid Mechanics, 1987, 178: 477-90. doi: 10.1017/S0022112087001320 MATSUMOTO M. Aerodynamic damping of prisms[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1996, 59(2/3): 159-75. 李少鹏. 矩形和流线型箱梁断面抖振力特性研究[D]. 成都: 西南交通大学, 2015 HOLMES J D. Analysis and synthesis of pressure fluctuations on bluff bodies using eigenvectors[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1990, 33(1/2): 219-30. 刘祖军,杨詠昕. H形桥梁断面颤振的流场驱动机理及气流能量分析[J]. 土木工程学报,2013,46(4): 110-116.LIU Zujun, YANG Yongxin. Flow field mechanism and air energy characteristic of H-shape section in flutter[J]. China Civil Engineering Journal, 2013, 46(4): 110-116. -
下载:
点击查看大图
计量
- 文章访问数: 534
- HTML全文浏览量: 243
- PDF下载量: 83
- 被引次数: 0