Time-History Analysis of Temperature Field of Medium-Low Maglev Guideway Girder
-
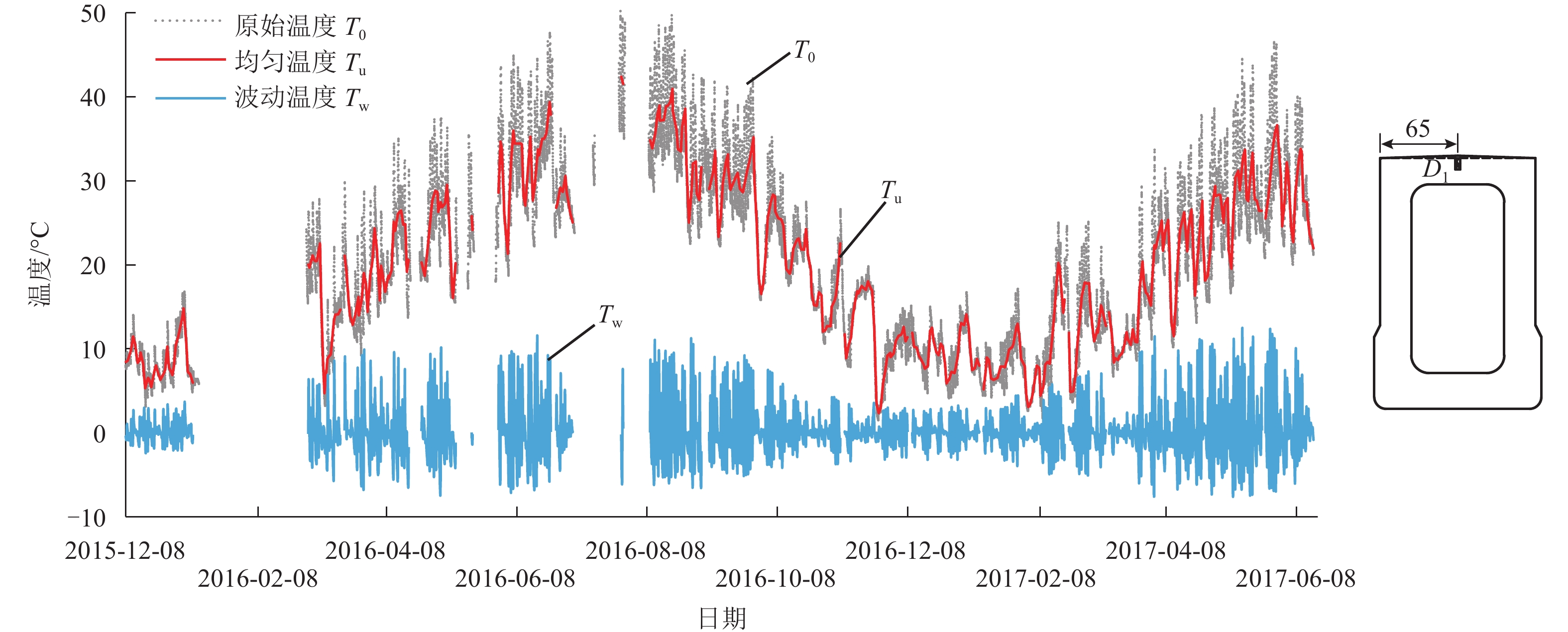
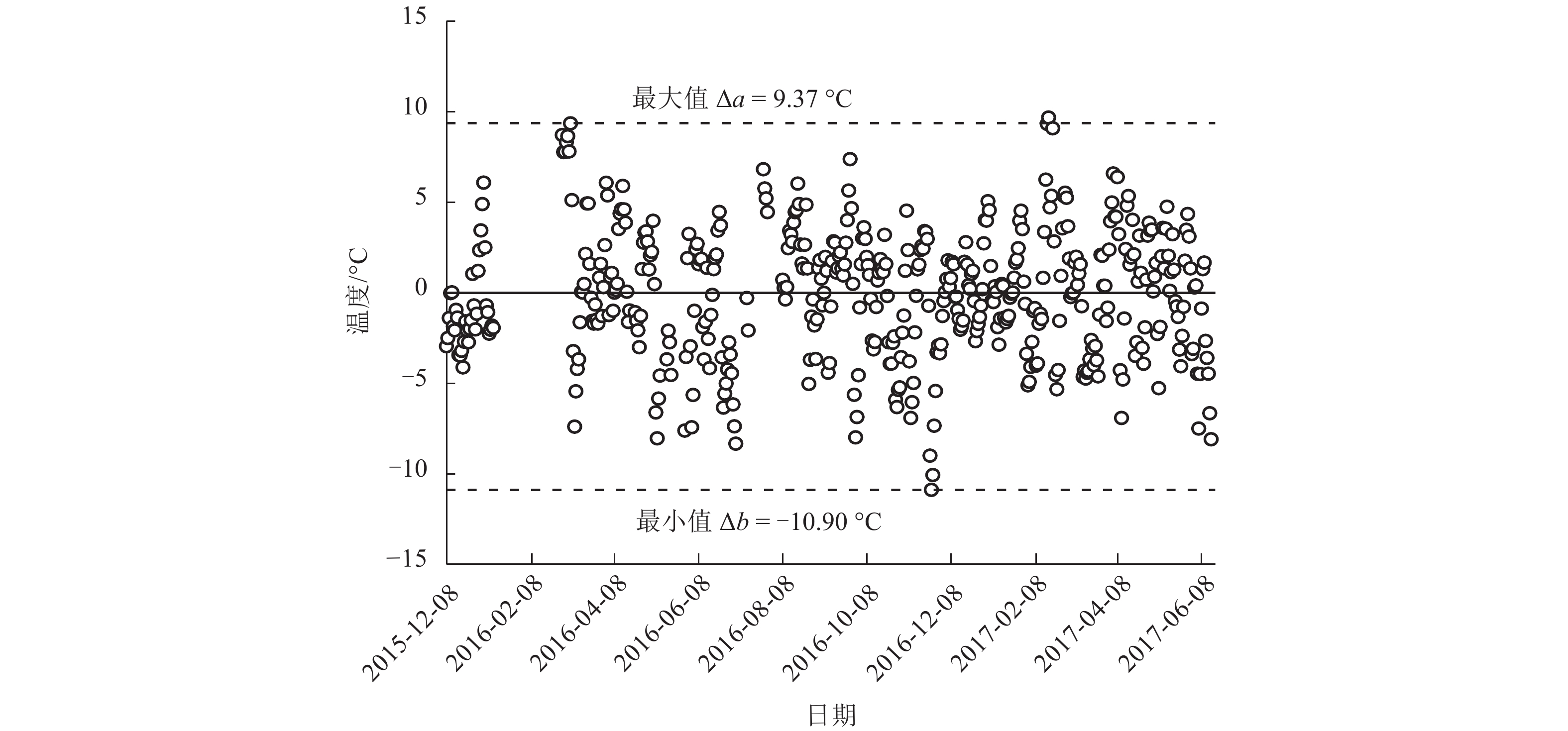
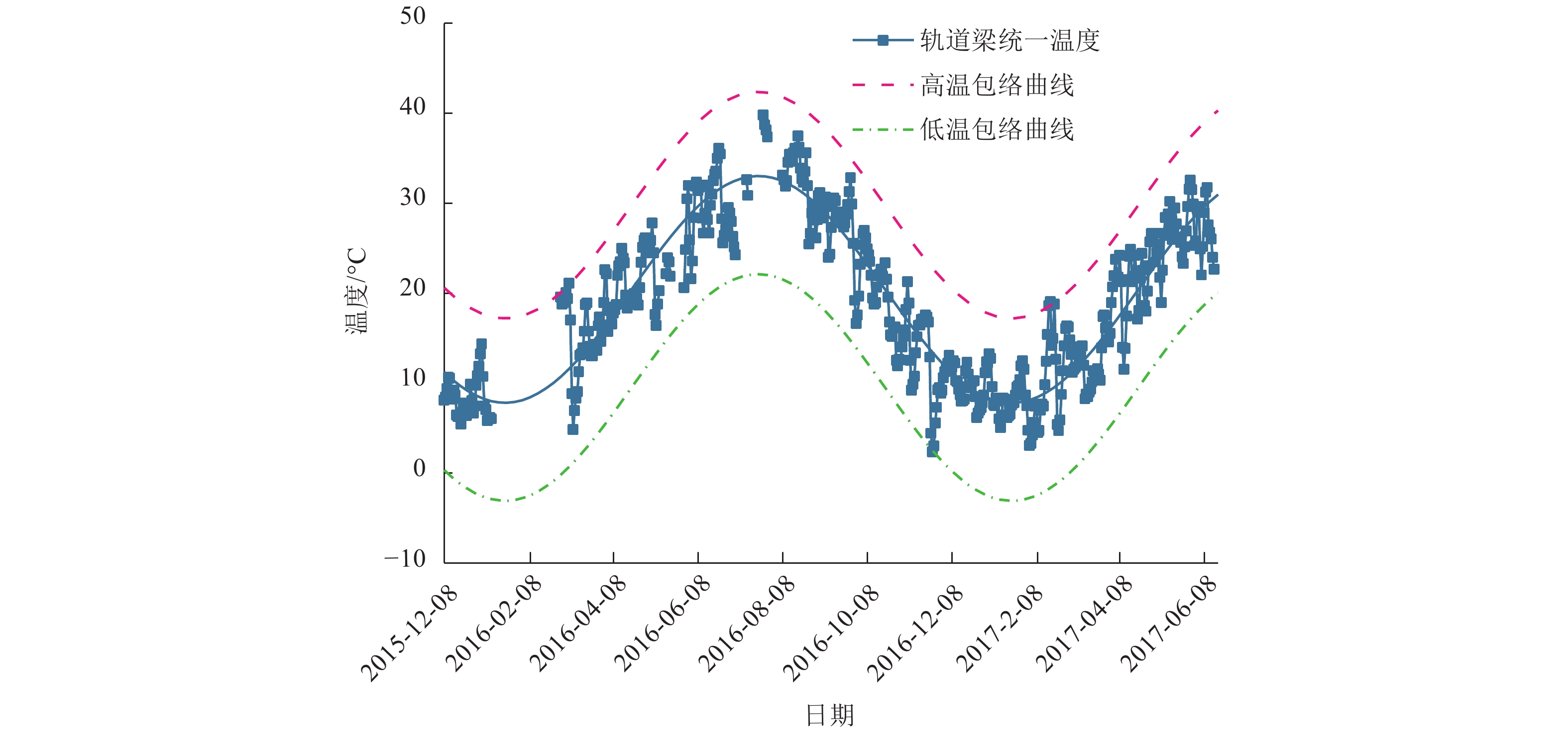
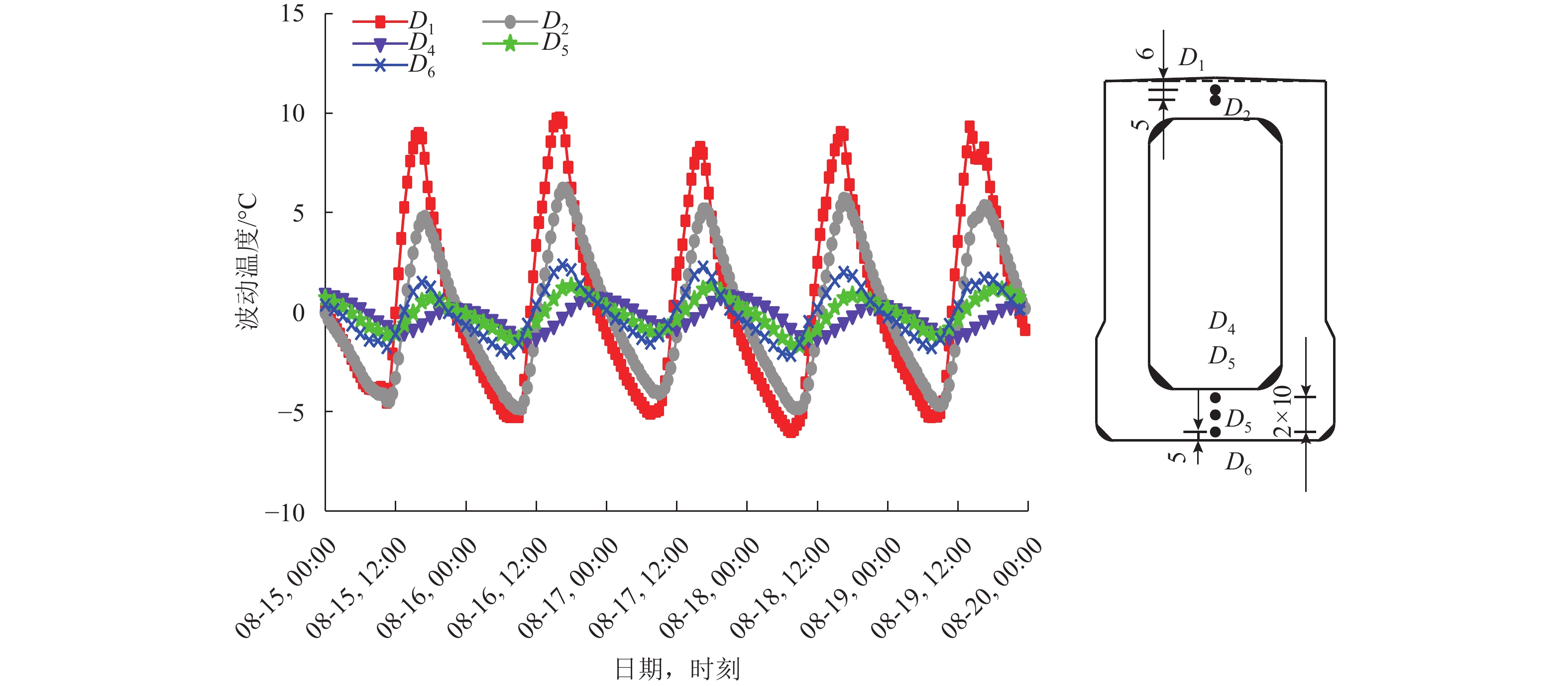
摘要: 为掌握磁浮轨道梁在长期外界环境作用下产生的复杂的温度场时变规律，在长沙磁浮运营线的轨道梁内埋设温度传感器，通过1.5 a的现场温度监测，获得测点温度时程曲线，并提出了基于时间序列加法模型求解的方法. 该方法将测点温度分解成均匀温度与波动温度，并利用傅立叶曲线拟合方法研究二者的时程曲线，得到轨道梁温度场时变规律. 研究结果表明：均匀温度与当地气候变化相关，各测点均温基本相同，结构温度时变趋势可用中位值为20.41 ℃、变化幅值为12.61 ℃、初相位为20 d、周期为365 d的余弦函数表示长沙磁浮轨道梁均温时程曲线；波动温度与日照作用相关，以日为周期在0线上下波动，可用两个正弦函数分段拟合升降温时程曲线.Abstract: To master the laws of time-varying temperature fields of maglev girders generated by long-term environmental loading, thermal sensors were installed on a concrete guideway girder in the Changsha Maglev Express. By performing up to 1.5 a of site monitoring, the time-history curve of points was obtained. A method based on the time-series addition model is presented. With this method, the original temperature is decomposed into uniform temperature and fluctuating temperature, and the time-history curves of both temperatures are analysed using the Fourier curve fitting method. Then, the time-varying temperature field of the guideway girder is determined. The results show that uniform temperature is relevant to the climate, and each point is basically the same, reflecting the trend of the original temperature. The overall time-history curve of the girder can be expressed as a cosine function with a median value of 20.41 ℃, amplitude of 12.61 ℃, initial phase of 20 d, and cycle of 365 d. The fluctuating temperature is mainly because of solar radiation, and the curves fluctuate near the zero line. Two sine functions can be used to fit the rising and falling time-history curves.
-
Key words:
- medium-low maglev transit /
- guideway girder /
- temperature field /
- time history analysis /
- site test
-
青藏铁路的开通对促进青藏高原的交通与经济建设发挥了重要作用. 为进一步提高其运输能力和效益，青藏铁路格拉段电气化工程提上日程. 青藏铁路格拉段穿越青藏高原多年冻土地段546.43 km，地质条件复杂，路基的冻胀融沉病害严重[1-2]. 由于接触网支柱桩基础承担的上部荷载较小且桩长较短，在长期冻融循环约束冻胀作用下易产生冻拔失稳或破坏[3]. 如何保证接触网支柱桩基础的冻拔稳定性是青藏铁路格拉段电气化改造工程中的关键问题[4-5].
目前，在冻土地基中桩基冻拔方面，国内外学者已通过现场试验、模型试验与数值模拟的方法取得了一定的研究成果：Lu等[6]通过引入关于层状饱和土的状态向量、静态波向量和反射-透射矩阵（RTM）的基本解，建立层状冻土与单桩相互作用的第二类Fredholm积分方程，并对其进行了数值求解；Zhou等[7]采用现场试验与数值模拟的方法研究了热管对青藏高原多年冻土区输电塔基热力学特性的影响；王腾飞等[8-10]研究了季节冻土区光伏支架螺旋桩基础在单向冻结条件下的冻拔响应及半螺旋桩的抗冻拔理论计算方法；为减小桩基冻拔量，锥形桩与扩底桩逐渐被应用于工程实践中，许健等[11-16]采用模型试验、理论分析及数值模拟的方法对冻土区锥形桩与扩底桩的抗冻拔性能及其影响因素进行深入研究，并对扩底桩的优化选型进行总结分析. 上述研究中，桩周土体都产生水平方向的对称冻胀. 然而，铁路接触网支柱桩基是设置于既有路基中的柱型构件，其稳定性受路基与边坡2个方向冷（热）量的共同影响，桩周土体产生水平方向的非对称冻胀. 关于多年冻土区既有路基活动层在二维冻融过程中桩基受力变形方面的研究成果较少.
鉴于此，本文通过大比例模型试验，对多年冻土区不同桩型的接触网支柱桩基在冻融作用下的相关热力学特性开展研究. 探讨在冻拔作用下等截面圆形桩、直锥柱形桩及曲锥柱形桩的抗冻拔效果，得到接触网支柱桩基础的地温、冻拔位移、切向冻胀力的分布规律，揭示接触网支柱桩基在冻融循环作用下的受力变形机理.
1. 试验设计
1.1 试验土样与试验装置
为更好地体现青藏铁路路基土体对接触网桩基础的影响，试验用土取自青藏铁路沱沱河车站，接触网下部基础钻孔施工试验的现场. 试验土体的最大干密度为1.92 g/cm3，其中，小于0.075 mm粒径的颗粒占5.6%，根据土工试验方法标准（GB/T 50123—2019）[17]，该土样定义为含细粒土砂（SF）. 试验所用低温环境箱的内尺寸为3.2 m （长） × 1.7 m （宽） × 1.9 m （高）. 制作1.6 m （长） × 1.0 m （宽） × 1.0 m （高）的模型箱，置于低温环境箱，模型箱四周均覆盖保温隔热材料. 为模拟多年冻土，采用2个冷浴系统分别模拟控制环境温度与多年冻土层的温度.
1.2 模型桩与测试元件布设
为降低接触网支柱桩基的冻拔力，改变普通等截面圆形桩在活动层的桩基截面形状，本次试验中共设置3种截面形式的模型桩，分别为等截面圆形桩Z1、圆锥柱形桩Z2及曲锥柱形桩Z3. 根据模型试验相似原理，土质、含水量及环境温度与现场实际情况一致，现场接触网支柱桩基预设计桩长8 m，桩径0.55 m. 模型桩采用有机玻璃加工制作，桩身材料的密度、弹性模量与导热系数分别为1.18 g/cm3、2.56 GP和0.19 W/（m·℃）. 结合现有的试验条件，将模型试验的几何相似比取为1∶10. 模型桩的具体尺寸及应变片布设见图1所示. 沿桩身同一深度处对称布设BE120-3AA-P300型号应变片，利用同一深度处相同的温度变化来消除温度对应变片的影响，其中一片沿桩身轴向贴在外表面（测量片），另一片沿桩身环向贴于相应的位置（温度补偿片）. 在应变采集仪中采用半桥接线法.
图 1 模型桩几何尺寸及应变片布设示意Figure 1. Geometric dimension of model pile and layout of strain gauge试验采用PT100温度传感器测试土体温度，精度为 ± 0.1 ℃. 图2为模型桩及测试元件布设图，温度传感器共布设3个断面，从左到右依次为断面A、断面B与断面C，每个断面有2个测温孔，分别位于路基与边坡上. 环境箱内布设3个环境温度测点. 在桩顶布设2个位移传感器实时测试桩顶的竖向与水平位移，在Z1与Z2桩之间、Z2与Z3桩之间分别布设3个位移计，测试路基、路肩及边坡土体的位移. 根据文献[7]的研究成果，距桩3.4 倍桩径处土体的冻胀位移基本不受桩体影响，故本试验中模型桩之间的相互影响忽略不计.
2. 试验方法步骤
选取青藏高原沱沱河地区一年内正弦气温变化函数为
Ta(t)=−2.5+12.0sin(2πt/8640+π/2)， (1) 式中：－2.5为年平均气温，12.0为气温振幅，t为时间，h.
模型试验共设计3个冻融循环，正式试验前通过多次预试验可得：若时间相似比取1∶10，即模型试验中3.6 d模拟现场的1年，土体的冻融深度达不到30 cm；当时间相似比取1∶6时，冻融深度约为30 cm. 因此，将模型试验的时间相似比取为1∶6，即模型试验中10.0 d模拟现场的1年. 模型试验中环境箱温度按式（2）控制.
T(t)=−2.5+12.0sin(2πt/240+π/2). (2) 试验步骤主要包含：
步骤1 准备试验. 按试验设计加工制作试验模型箱，模型箱四周均粘贴保温隔热材料，底部设计冷浴管路；按各模型桩的设计尺寸加工有机玻璃模型桩，桩周粘贴布设BE120-3AA-P300型号应变片；将现场取回的土样配备足量含水量为15%的试验用土，将其搅拌充分均匀后用塑料布包裹并静置72 h.
步骤2 土样分层填筑压实及测设元件布设. 在模型箱内壁涂抹凡士林，以此来消除模型箱边界对土体的约束作用. 试验填土初始含水量15%，分10层填筑，压实度按0.93控制，模型箱内壁粘贴软皮尺以控制土层的填筑厚度，桩身附近的土体采用橡皮锤击实. 填筑过程中，温度及位移传感器按图2进行布设.
步骤3 模型箱底板与顶板温度的控制. 将底板温度调为−2 ℃恒温控制，顶板调制为10 ℃， 静置30 d，形成初始温度场.
步骤4 开始试验. 按T(t) 调节环境温度实现土体的冻融变化.
步骤5 试验数据的自动采集. 自动实时采集冻融循环过程中应变、温度传感器与位移传感器的读数.
3. 试验结果分析
3.1 温度场分布
试验中断面A、B、C的温度场分布基本一致，以断面B桩Z2附近路基与边坡上2个测温孔的温度场进行分析. 图3为断面B路基与边坡测温孔不同深度土层温度随时间的变化曲线，其中第17天的数据缺失. 由图3可以看出：整个试验共进行30.0 d，为3个冻融循环，随着T(t)的变化，不同深度土层温度随时间也呈正弦状分布，能较好地模拟现场实际地温的变化情况；各土层温度的变化相对于环境温度出现滞后现象，且随深度的增加，滞后效应越明显；下冷板能较好地控制模型下部土层的地温，路基与边坡2个测温孔深90 cm处的平均地温约为−1.5 ℃ .
图 3 断面B不同深度土体温度随时间的变化曲线Figure 3. Changes of soil temperature at different depths of section B with time通过试验进程中所得的各测点温度，绘制冻融过程中断面B路基与边坡处的等温线分布，如图4所示. 由图可得：试验开始阶段，模型箱底部20 cm 厚的土层处于冻结状态，其他土层都为未冻土，随着环境温度的降低，基础与土体的热量向环境中扩散，冻结锋面下移，土层主要发生自上而下的冻结. 经过一个冻结期后，整个基础完全处于冻结状态. 随着环境温度的升高，模型上部土层融化，路基测温孔第2、3个周期的最大融化深度分别为31.5 cm和28.0 cm，边坡测温孔第2、3个周期的最大融化深度分别为17.0、14.0 cm.
图 4 冻融过程中断面B的等温线分布（单位：℃）Figure 4. Isotherm distribution of section B during freezing and thawing (unit: ℃)图5为路基与边坡2个测温孔地温沿深度变化的对比曲线. 由图可以看出：冻土上限以上活动层地温正负温变化较剧烈，其中第11、12、19、20 天活动层地温为正值，呈融化状态，第16天活动层地表地温最低，达到 −8.1 ℃. 通过比较2个测温孔的地温数值，发现相同时间同一深度处2个测温孔的数据存在较大的差异，在暖季阶段，边坡测温孔的地温比相同条件下路基测温孔的地温较高；在寒季阶段，边坡测温孔的地温比相同条件下路基测温孔的地温较低，且在活动层内这种现象愈剧烈. 以上说明路基体的冻结（融化）受路基顶面与边坡的2个方向冷（热）量的共同影响，是一个二维冻结（融化）问题，接触网支柱基础路基与边坡两侧的温度场是非对称分布的.
图 5 断面B 2个测温孔地温沿深度变化的对比Figure 5. Comparison of ground temperature variation along depth between two temperature measuring holes at section B第1个周期，由于土层的填筑与环境箱内初始温度等因素的影响，试验数据的变化规律相对杂乱，在下面的分析中以第10天为起点. 图6（a）为路基、路肩及边坡处土体表层的位移随时间的变化曲线. 由图可知：路基、路肩及边坡处位移变化趋势基本一致，都与环境温度的变化密切相关. 当环境温度为正温阶段，路基、路肩及边坡土体位移基本不变，环境温度降为负温时，土体的冻结速率较快，土层位移迅速发生冻胀，路基、路肩及边坡处土体最大冻胀量分别为2.2、4.3、3.1 mm，其中，路肩处的位移最大. 产生以上现象的原因是环境温度降低时，冷量从路基顶面与边坡2个方向进入路基体，路基土体在2个方向上产生二维冻结，导致路肩处的冻胀位移最大. 当环境温度为正温并升高时，路基、路肩及边坡处土体位移均产生融沉，基本回到冻胀起始前的位移.
图 6 土体与桩顶位移随时间的变化曲线Figure 6. Variation curves of displacement of soil and pile top with time图6（b）、（c）为桩顶竖向与水平位移随时间的变化曲线. 由图可知：桩顶位移的变化与土体位移的变化规律基本一致，亦与环境温度的变化密切相关；在第2个冻融周期内桩Z1、Z2、Z3的竖向冻拔量分别为0.26、0.12、0.15 mm，桩Z2、Z3的竖向冻拔量分别为桩Z1的46%、58%，说明直锥柱形桩与曲锥柱形桩在整个冻结过程中有较好的抗冻拔效果；路基土体冻结过程中桩Z1、Z2、Z3的桩顶都会产生较小的水平冻胀位移，分别为0.10、0.13、0.14 mm.
3.2 桩身应力
图7为第2个冻融周期内桩身轴力沿深度的分布曲线. 由图可以看出：活动层土体在冻结融化过程中，桩长范围内的轴力都为拉力，随桩长增加0～0.3 m范围内轴力先增大，随后轴力逐渐减小，即桩长0.3 m断面处是桩身的一个中性点；轴力在整个桩长范围内呈非均匀变化，活动层内（0.3 m以上）桩身各截面的轴力差变化较大，多年冻土层内桩身各截面的轴力差变化较小. 将桩长30.0 cm处的轴力进行比较，结果如图8所示. 由图可以看出：桩身轴力与环境温度有密切的关系，随环境温度逐渐降低，桩身各截面的轴力均逐渐增大，当环境温度升高，桩身各截面的轴力均逐渐降低，其中，第16 天的桩身轴力最大，桩Z1、Z2、Z3在第16 天的轴力分别为5.66、4.56、4.01 kN；与桩Z1相比，桩Z2及桩Z3的轴力分别降低19.4%与27.5%.
图9为温度与桩侧切向应力沿深度的变化曲线. 由图可以看出：与桩身轴力的变化规律相似，活动层内的切向应力为方向向上的冻胀应力，且变化较剧烈，在冻深附近由正值转变为负值，永冻层内的切向应力为方向向下的冻结应力. 是由于随环境温度的降低，活动层内的土体冻结后产生向上的冻胀变形，桩基的存在对土体的自由冻胀产生约束作用，从而在桩侧产生向上的切向冻胀力，永冻层的土体对桩的向上运动或运动趋势有抑制作用，导致桩土之间的冻结应力发挥作用；切向冻胀力的最大值出现在地表附近，桩Z1、Z2、Z3在第16 天的最大切向冻胀应力分别为157.2、153.5、159.4 kPa；活动层内的平均切向冻胀应力为109.3、106.4、97.7 kPa.
图 9 温度与桩侧切向应力沿深度的变化曲线Figure 9. Variation curves of temperature and pile-side tangential stress along depth3.3 桩型对切向冻胀力的影响分析与讨论
由冻结过程桩基的受力特点可知，桩基冻深处的轴力为切向冻胀总力. 3种桩基础的冻深Zn均约为0.3 m，表1为不同桩型模型桩的受力情况对比. 表中： S 为冻深范围内桩和冻土的接触面积，F为桩基的切向冻胀总力， τ为冻深范围内各桩平均切向冻胀应力. 由表可以看出：桩型的改变可明显降低F，桩Z3的切向冻胀总力最小，桩Z2次之. 桩Z1、Z2、Z3切向冻胀总力之比为1.00∶0.81∶0.71，与S之比呈正相关，且比值接近，τ 之比约等于1∶1∶1.
表 1 不同桩型模型桩的受力对比Table 1. Stress comparison of model piles in different shapes桩 Zn/m S/cm2 F/kN τ/kPa Z1 0.3 518 5.66 109.3 Z2 0.3 447 4.56 106.4 Z3 0.3 427 4.01 97.7 环境温度降低时，桩周土体逐层自上而下低发生冻结. 以第1层土冻结时对桩基的作用力进行分析：当土体冻结时，产生竖向冻胀力V1和水平冻胀力H1，每层土的厚度为ΔH，桩基锥角为 β，如图10所示.
图 10 直锥（曲锥）桩侧土体冻胀力的分解图示Figure 10. Decomposition of frost-heave force of the side of straight-cone (curved-cone) pile将V1和H1沿桩侧与垂直桩侧分解，则第1层土体作用于桩基础的切向应力和法向应力分别为
{τ1=V1cosβΔH+H1sinβΔH,σ1=H1cosβΔH−V1sinβΔH. (3) 结合式（3）与表1，直（曲）锥柱形桩比等截面圆形桩的抗冻拔效果好的主要原因可归纳为以下2点：
1） 由于锥形桩桩侧斜面的存在，改变了桩基的受力状态，式（3）中V1sin β 表现为拉应力，导致桩侧水平应力减小. 冻土桩基接触面的抗剪强度与法向应力的大小呈正相关. 因此，锥形桩桩土界面的极限抗剪强度相比于等截面桩较低，更易达到极限抗剪强度.
2） 随着桩周土体冻胀变形的发展，若桩土界面达到极限强度，则桩土界面产生滑移. 冻深范围内各桩平均切向冻胀应力的差异较小，但曲锥柱形桩与冻土的接触面积最小，从而导致曲锥柱形桩的切向冻胀总力最小，抗冻拔效果最好.
4. 结 论
1） 路基体的冻结（融化）受路基顶面与边坡 的2个方向冷（热）量的共同影响，是一个二维冻结（融化）问题，接触网支柱桩基础路基与边坡两侧的温度场是非对称分布的，桩基附近的最大融深约为 30.0 cm，边坡测温孔的最大融深约为15.0 cm.
2） 土体与桩顶的位移均与环境温度的变化密切相关. 路基土体的二维冻结现象导致路肩处的冻胀位移最大，路基、路肩及边坡处土体最大冻胀量分别为2.2、4.3、3.1 mm. 等截面圆形桩的竖向冻拔量为0.26 mm，直锥柱形桩与曲锥柱形桩的竖向冻拔量仅为Z1的46%、58%，3根桩的桩顶均产生约为0.10 mm的水平冻胀量.
3） 活动层土体在冻结过程中桩基础整体受拉，冻深处的轴力最大. 等截面圆形桩的最大切向冻胀总力为5.66 kN，与等截面圆形桩相比，直锥柱形桩与曲锥柱形桩分别降低19.4%与27.5%. 切向应力在活动层内为方向向上的切向冻胀应力，永冻层内为方向向下的冻结应力，切向冻胀应力的最大值出现在地表附近.
4） 桩周土体冻融作用下，曲锥柱形桩具有竖向冻拔位移小、切向冻胀总力小的特点，即曲锥柱形桩具有较好的抗冻拔效果. 研究成果可为多年冻土区铁路电气化接触网支柱基础的抗冻拔设计提供参考.
-
图 4 统一温度与拟合温度差值
Figure 4. Differences between overall temperature and fitting temperature
图 7 波动温度幅值竖向分布规律
Figure 7. Vertical dispersion law of amplitude of fluctuating temperature
图 8 波动温度实测与拟合曲线对比
Figure 8. Comparison between observed temperature and fitting temperature
表 1 特定测点拟合结果
Table 1. Fitting results of specific points
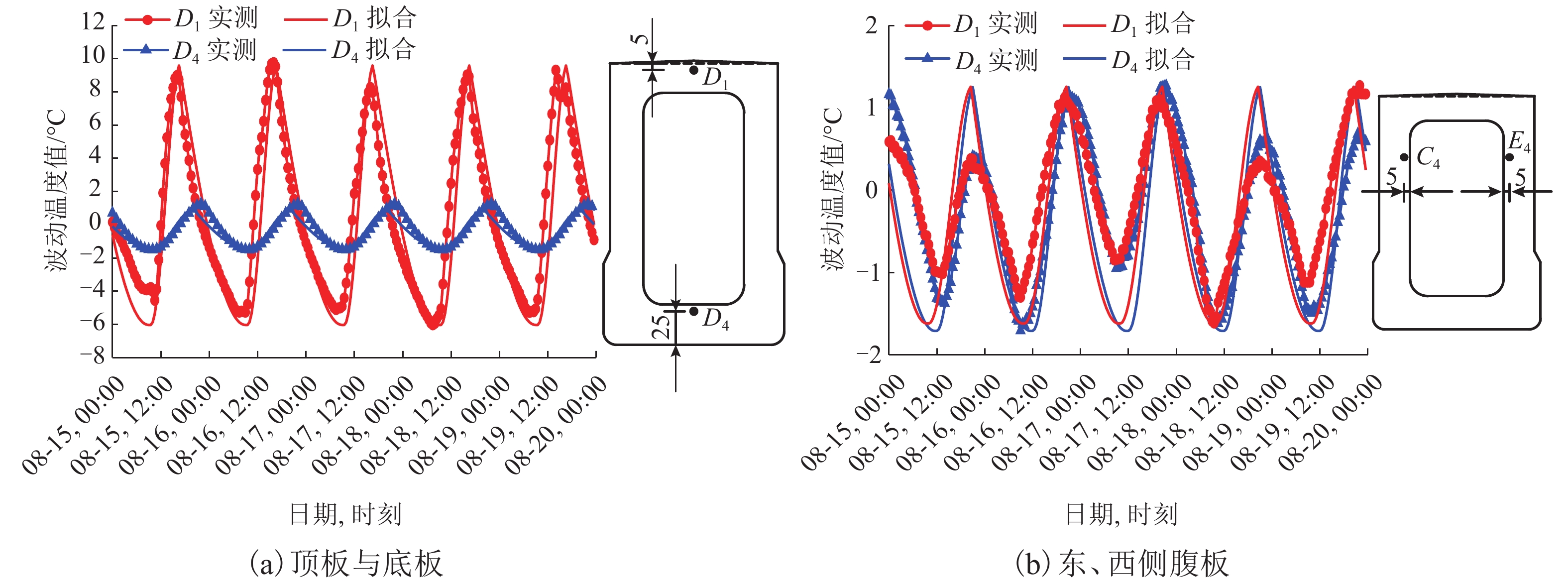
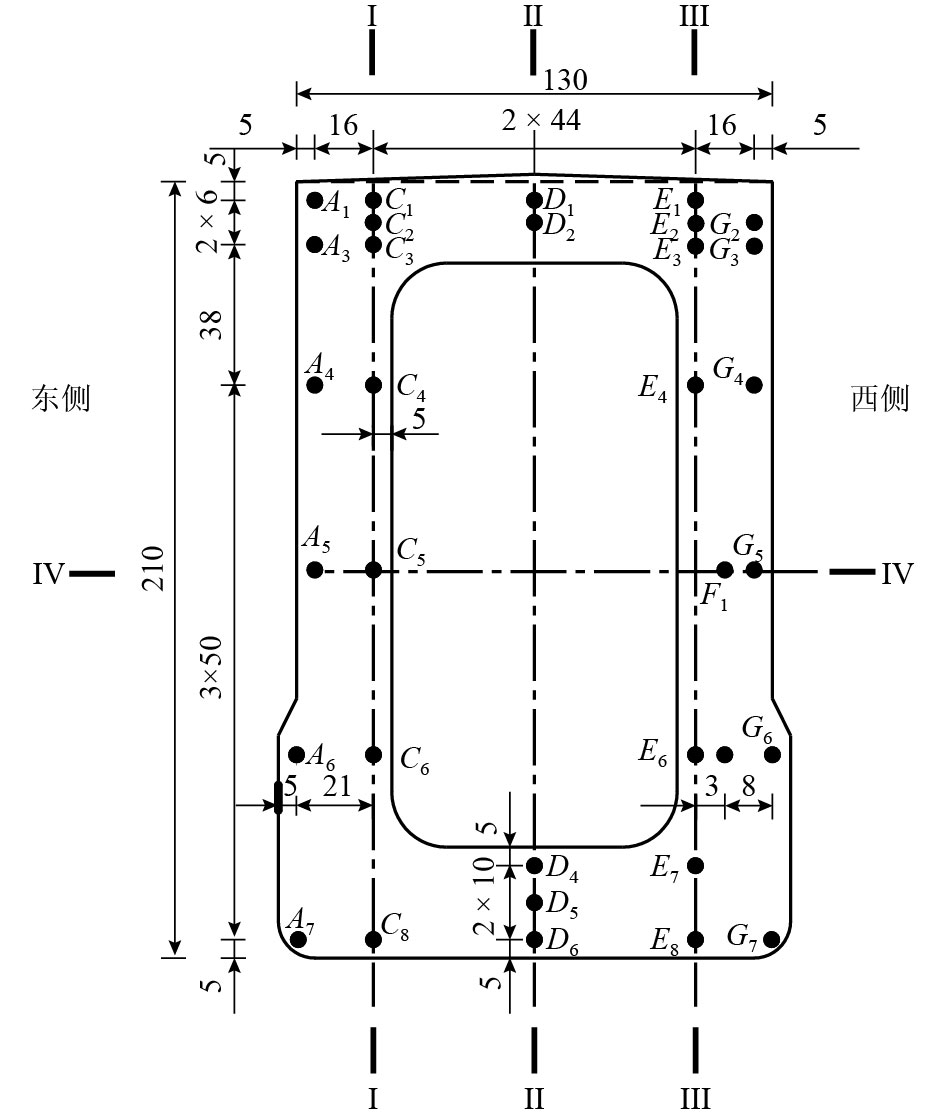
测点组 测点号 距表面距离/m Tum/℃ ΔTu/℃ φd/d R2 截面Ⅱ D1 0.05 21.55 13.21 18 0.940 1 D2 0.11 21.39 13.15 19 0.937 3 D4 1.85 20.01 11.89 21 0.950 6 D5 1.95 20.07 11.73 21 0.949 6 D6 2.05 20.02 11.74 21 0.947 0 截面IV A5 0.05 19.92 11.74 20 0.943 2 C5 0.16 20.08 11.76 21 0.946 4 F1 0.65 20.45 12.38 20 0.947 6 G5 1.09 21.34 13.59 22 0.947 8 注：截面Ⅱ，距表面距离表示测点距上表面距离；截面IV，距表面距离表示距左侧表面距离. 
下载: 导出CSV
表 2 各结构的统一温度曲线拟合结果
Table 2. Fitting results of overall temperature of structures
结构类型 Tum/℃ ΔTu/℃ φd/d R2 西侧轨道梁 20.41 12.61 20 0.944 6 东侧轨道梁 20.52 12.19 22 0.915 3 端横梁 19.51 11.95 19 0.911 3 中横梁 18.37 11.77 20 0.915 4 桥墩 18.96 11.34 21 0.901 7
下载: 导出CSV
表 3 波动温度幅值竖向分布拟合结果
Table 3. Fitting results of vertical dispersion of amplitudes
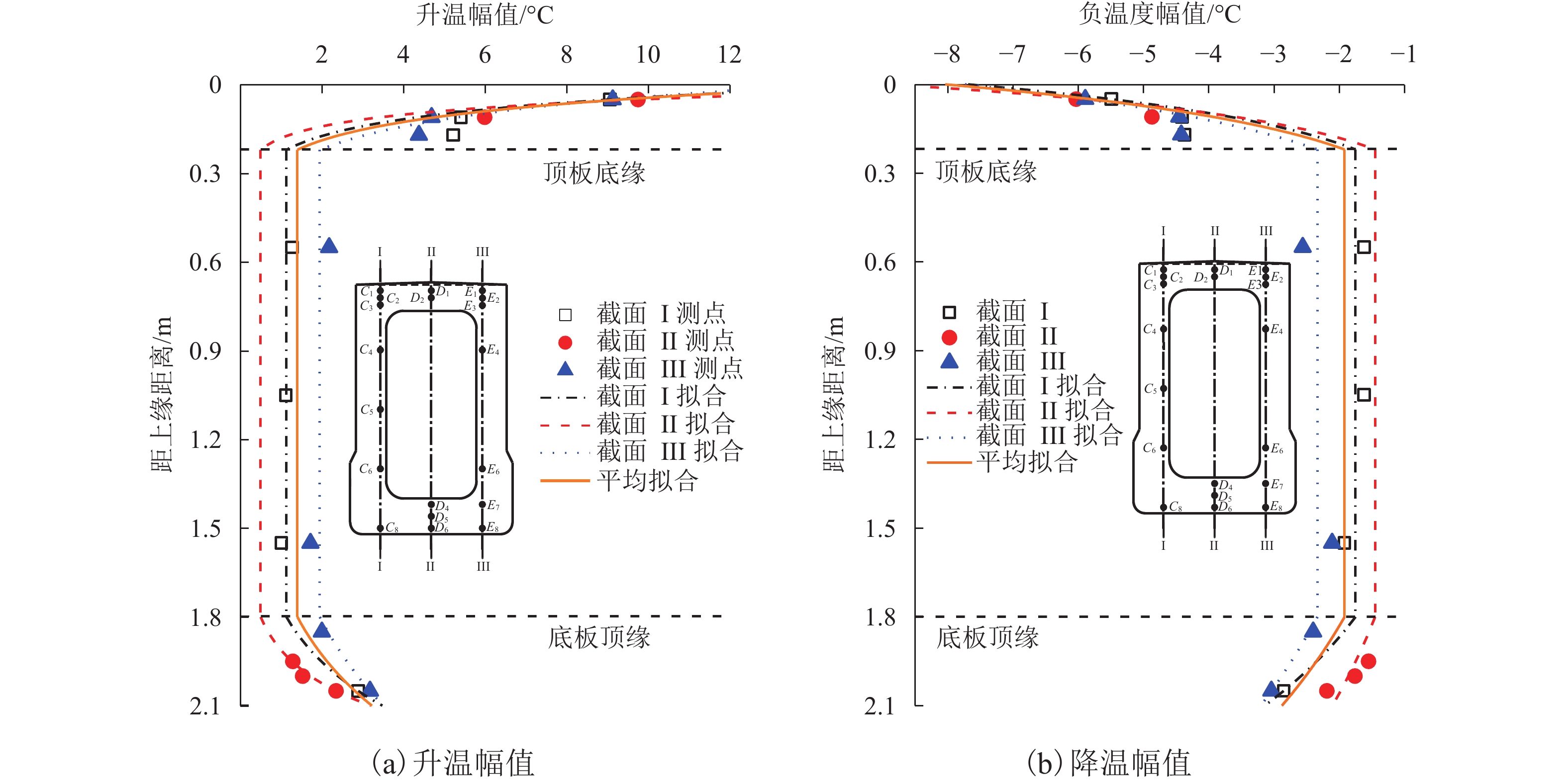
拟合参数 顶板A（y） = aeby 腹板A = T0 底板A（y） = aeby 升温 降温 升温 降温 升温 降温 a/℃ b/m–1 a/℃ b/m–1 c/℃ b/℃ a/℃ b/m–1 a/℃ b/m–1 截面I 16.71 –12.25 –7.68 –6.73 1.13 –1.75 3.49 –3.76 –3.14 –1.95 截面II 17.11 –11.25 –8.9 –8.25 0.5 –1.45 2.59 –1.96 –2.11 –1.25 截面III 14.38 –9.08 –7.73 –5.44 1.95 –2.34 3.51 –1.96 –3.21 –1.06 平均 16.26 –11.15 –7.73 –6.51 1.4 –1.92 3.23 –2.78 –2.88 –1.35 注：为表现传热随箱梁结构深度的变化，规定顶板、底板均以外表面到内表面为正方向.
下载: 导出CSV
表 4 升降温时刻及时长规律
Table 4. Moment and duration of riging and falling stage
位置 tr tf Lr Lf 顶板 9.0 16.5 7.5 16.5 底板 10.0 20.0 10.0 14.0 东侧腹板 9.5 20.5 11.0 13.0 西侧腹板 11.5 21.0 9.5 14.5
下载: 导出CSV
-
陈波,孙玉周,郭伟华. 钢筋混凝土板动力特性的时变温度效应实验研究[J]. 西南交通大学学报,2014,49(1): 66-71. doi: 10.3969/j.issn.0258-2724.2014.01.011CHEN Bo, SUN Yuzhou, GUO Weihua. Experimental investigation of temperature effects on dynamic characteristics of reinforced concrete slab[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 66-71. doi: 10.3969/j.issn.0258-2724.2014.01.011 乔柏平. 磁浮单跨轨道梁温度变形及对振动的影响[D]. 上海: 上海交通大学, 2008 张庆福. 磁浮连续轨道梁温度变形及对振动的影响[D]. 上海: 上海交通大学, 2009 中国土木工程学会. 中低速磁浮交通设计规范: CJJ/T262—2017[S]. 北京: 中国建筑工业出版社出版, 2017 刘华波. 异形截面预应力混凝土箱梁温度场及温度效应研究[D]. 上海: 同济大学, 2002 徐钢. 箱梁温度场及其效应分析[D]. 上海: 同济大学, 2008 张智晖. 预应力混凝土箱梁时变温度场及其效应研究[D]. 西安: 长安大学, 2010 LEE J H, KALKAN I. Analysis of thermal environmental effects on precast,prestressed concrete bridge girders:temperature differentials and thermal deformations[J]. Advances in Structural Engineering, 2012, 15(3): 447-459. doi: 10.1260/1369-4332.15.3.447 SALLAL R A, NILDEM T, MUSTAFA O. Experimental analysis of temperature gradients in concrete box-girders[J]. Construction and Building Materials, 2016, 106: 523-532. doi: 10.1016/j.conbuildmat.2015.12.144 徐庆元,孟亚军,李斌,等. 温度梯度作用下纵连板式无砟轨道疲劳应力谱[J]. 中南大学学报:自然科学版,2015,46(2): 736-741.XU Qingyuan, MENG Yajun, LI Bin, et al. Fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient[J]. Journal of Central South University:Science and Technology, 2015, 46(2): 736-741. PETER J B, RICHARD A D. Time series: theory and methods[M]. Second Edition. New York: Springeze-Verlag, 1991: 14-25 刘兴法. 混凝土结构的温度应力分析[M]. 北京: 人民交通出版社, 1991: 10-13 卢理. 时间序列加法模型的分解预测研究[D]. 成都: 西南交通大学, 2007 廖春花,刘甜甜,林海,等. 长沙近57年气温变化特征分析[J]. 气象与环境科学,2008,31(4): 21-24. doi: 10.3969/j.issn.1673-7148.2008.04.005LIAO Chunhua, LIU Tiantian, LIN Hai, et al. Analysis of the characteristics of temperature variation in recent 57 years in Changsha[J]. Meteorological and Environmental Sciences, 2008, 31(4): 21-24. doi: 10.3969/j.issn.1673-7148.2008.04.005 Standards Policy and Strategy Committee. Eurocode Ⅰ, actions on structures – part 1-5: general actions-thermal actions: BS EN 1991-1-5—2003[S]. London: BSI Group, 2003 戴公连,杨凌皓,朱俊樸,等. 桥上CRTS II型板式无砟轨道均匀温度研究[J]. 湖南大学学报:自然科学版,2017,44(7): 136-142.DAI Gonglian, YANG Linghao, ZHU Junpu, et al. Research on uniform temperature of CRTS II slab-type ballastless track on bridge[J]. Journal of Hunan University:Natural Sciences, 2017, 44(7): 136-142. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 585
- HTML全文浏览量: 262
- PDF下载量: 4
- 被引次数: 0