Overloaded Truck Models and Their Load Effects on Multiple-One Lane for Highway Bridges
-
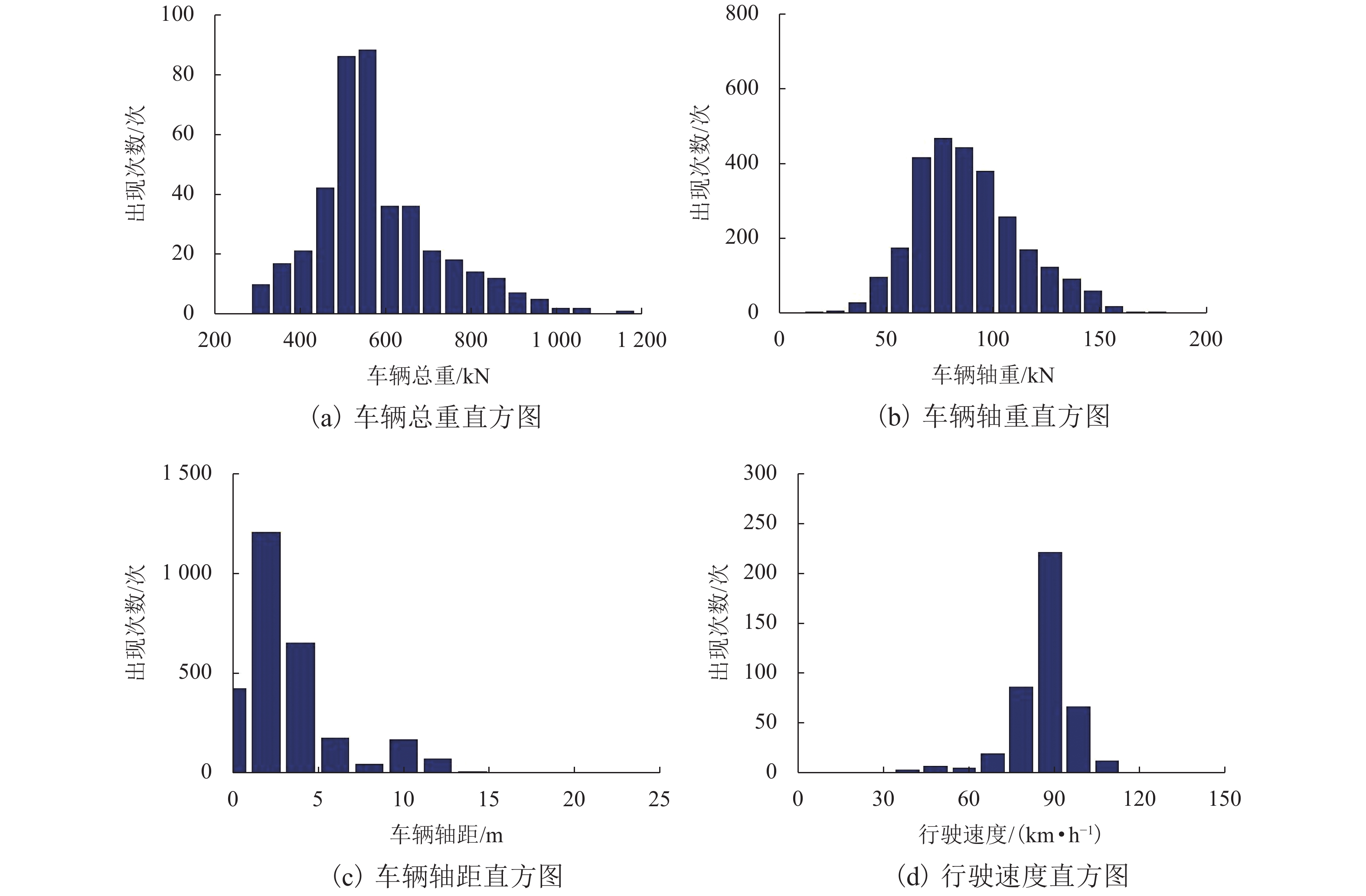
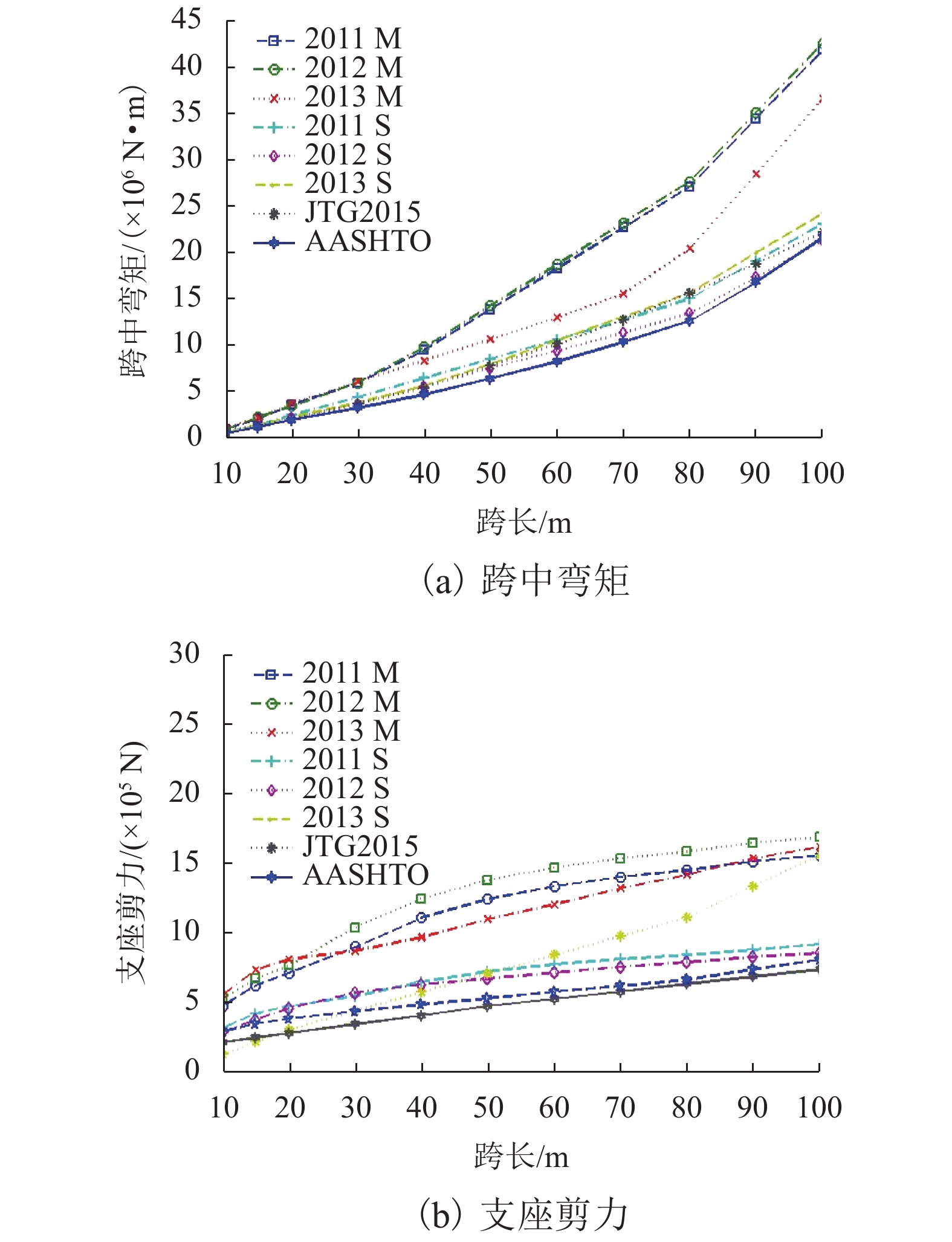
摘要: 为获取超重车主要参数特性以及典型超重车模型，计算并对比多车道和单车道上超重车纵横向并行引起的荷载效应，收集了美国加州历时3 a的动态称重（weight-in-motion，WIM）数据，以加州交通厅许可荷载车模型为参照，提取实测超重车数据，分析了超重车辆荷载构成特点，建立了典型超重车辆模型. 分别计算了多、单车道超重车荷载效应，并将两者与现行的中国JTG D60—2015规范和美国AASHTO （American Association of State Highway and Transportation Officials）规范进行了对比. 结果表明：多车道叠加荷载效应较单车道以及中美规范值都大得多，单车道荷载效应与规范值相近或略高一点；多-单车道跨中弯矩最大比值为2.05倍，平均比值为1.65倍；剪力最大为2.05倍，平均为1.70倍.Abstract: To analyze characteristics of typical parameters of overloaded trucks as well as their models, weight-in-motion (WIM) data was collected over three years from California, U.S., and the permit truck issued by California Department of Transportation (Caltrans) was selected as a reference to extract overloaded truck data, then, the characteristics and configurations of these overloaded trucks were analyzed to build typical overloaded truck models with mean and standard deviation calculated. In addition, load effects induced by trucks moving on multiple lanes and single lane were calculated respectively, and the two load effects were compared with the specifications issued by the Ministry of Transport of China (JTG D60−2015) and American Association of State Highway and Transportation Officials (AASHTO) respectively. The results show, superposed load effects on multiple lanes were significantly greater than those loading on one lane and the codified values in specifications, whereas, the load effects on one lane are close to or a little higher than the specified values. For effect ratios of multiple lanes to one lane, the largest one is 2.05 for both moment and shear, and the average value is 1.65 and 1.70 for the two, respectively.
-
图 4 预应力混凝土梁桥横截面（单位：m）
Figure 4. Cross-section of prestressed concrete girder bridge (unit：m)
图 5 多-单车道荷载效应与中美规范对比
Figure 5. Comparison of load effects of multiple-one lane and values specified in JTG and AASHTO
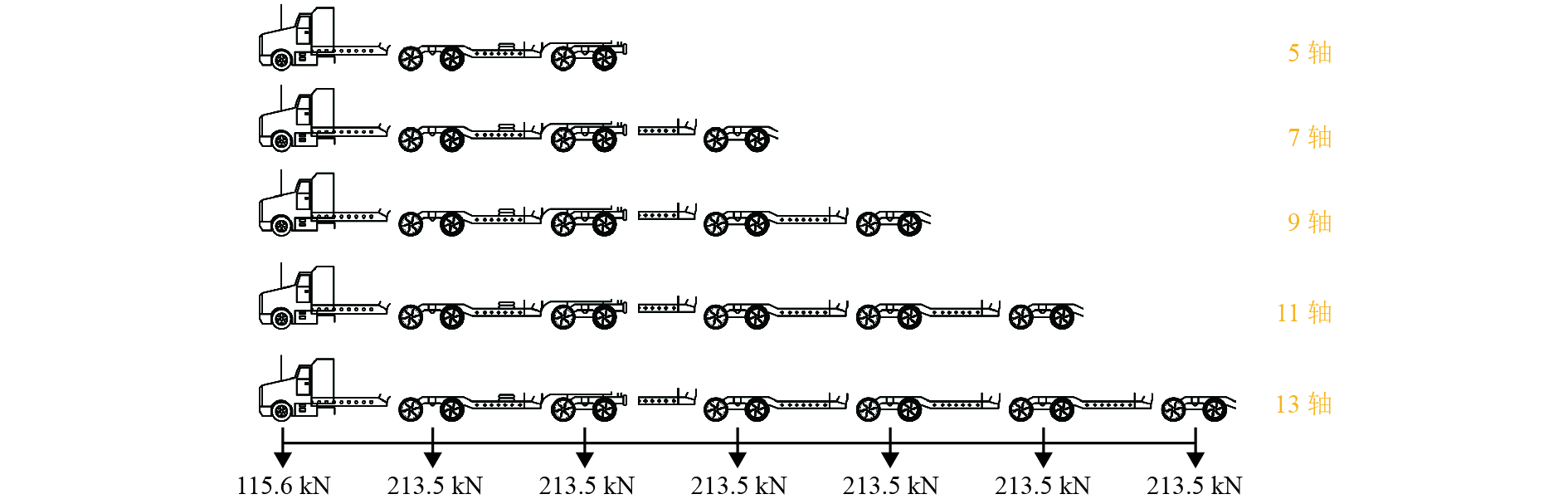
表 1 超重车模型及其特性参数统计
Table 1. Schematic overloaded truck models and their statistical parameters
序号 所占比例/% 轴数 超重车模型简图 1 17.4 4 
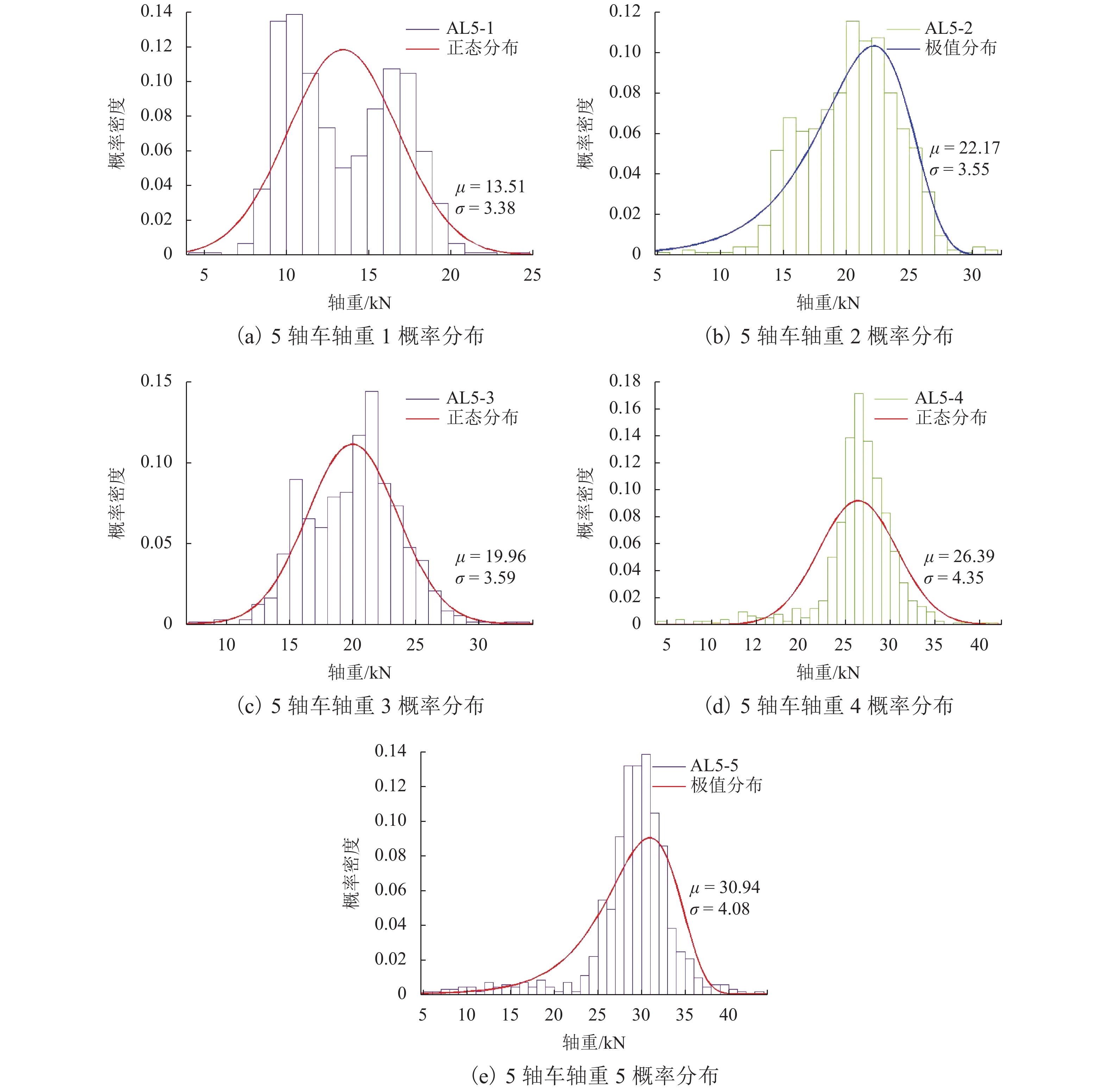
2 38.2 5 
3 8.2 6 
4 19.1 7 
5 2.1 8 
6 14.9 9 
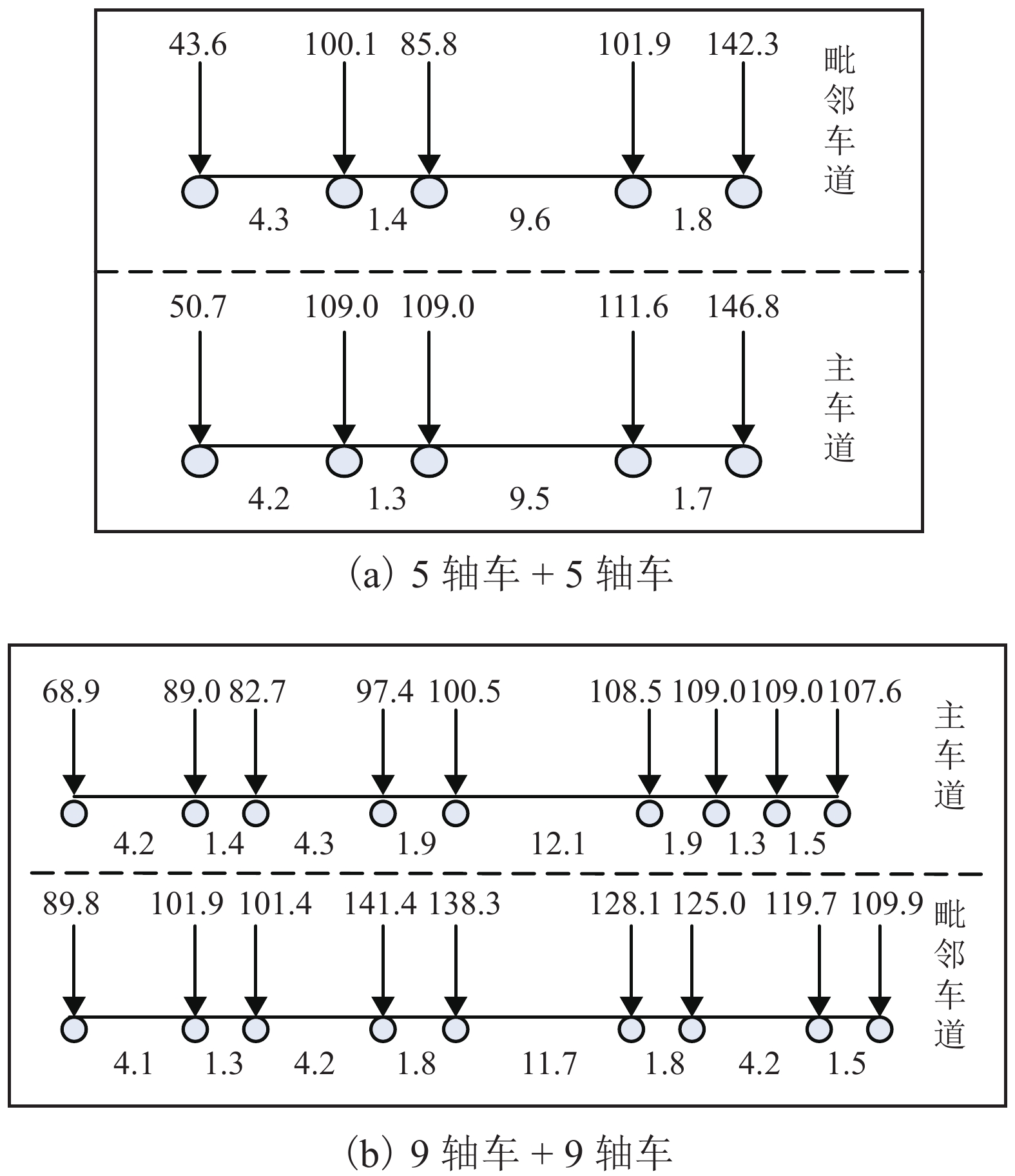
注：表中 µ 为均值；σ 为标准差；箭头上方参数为轴重，kN；车轮下方为轴距，m；后图同. 
下载: 导出CSV
表 2 多-单车道荷载效之比
Table 2. Ratios of load effects of multiple lanes to one lane
跨长/m 各年的跨中弯矩比值 各年的支座剪力比值 2011 2012 2013 2011 2012 2013 10 1.59 1.67 1.83 1.47 1.83 1.64 15 1.52 1.68 1.64 1.48 1.76 1.71 20 1.46 1.51 1.69 1.49 1.65 1.69 30 1.36 1.59 1.59 1.64 1.82 1.42 40 1.47 1.75 1.48 1.71 1.97 1.33 50 1.62 1.90 1.34 1.71 2.05 1.37 60 1.72 1.98 1.23 1.71 2.05 1.41 70 1.79 2.04 1.19 1.72 2.02 1.48 80 1.80 2.05 1.30 1.72 2.00 1.54 90 1.81 2.02 1.43 1.71 1.98 1.61 100 1.81 2.00 1.51 1.69 1.97 1.66 平均比值 1.65 1.70
下载: 导出CSV
-
FU Zhongqiu, JI Bohai, CHENG Miao, et al. Statistical analysis of the causes of bridge collapse in China[C]//Proceedings of Forensic Engineering: Gateway to a safer tomorrow. Reston: ASCE, 2012: 75-83 DIAZ E E M, MORENO F N, MOHAMMADI J. Investigation of common causes of bridge collapse in Colombia[J]. Practice Periodical on Structural Design and Construction, 2009, 14(4): 194-200. doi: 10.1061/(ASCE)SC.1943-5576.0000006 孙莉,刘钊. 2000~2008年美国桥梁倒塌案例分析与启示[J]. 世界桥梁,2009(3): 46-49. MOSES F and GHOSN M. Calibration of a Bridge rating formula for overload permits[C]//ASCE Structures Congress, Bridges and Transmission Line Structure. [S.l.]: ASCE, 1987: 1245-1251. ZHANG Jianren, PENG Hui, CAI C S. Field study of overload behavior of an existing reinforced concrete bridge under simulated vehicle loads[J]. Journal of Bridge Engineering, 2011, 16(2): 226-237. doi: 10.1061/(ASCE)BE.1943-5592.0000140 VIGH A, KOLLAR L. Routing and permitting techniques of overweight vehicles[J]. Journal of Bridge Engineering, 2007, 12(6): 774-784. doi: 10.1061/(ASCE)1084-0702(2007)12:6(774) 韩万水,闫君媛,武隽,等. 基于长期监测的特重车交通荷载特性及动态过桥分析[J]. 中国公路学报,2014,27(2): 54-61. doi: 10.3969/j.issn.1001-7372.2014.02.007HAN Wanshui, YAN Junyuan, WU Jun, et al. Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record[J]. China Journal of Highway and Transport, 2014, 27(2): 54-61. doi: 10.3969/j.issn.1001-7372.2014.02.007 HAN Wanshui, YUAN Yangguang, HUANG Pingming, et al. Dynamic impact of heavy traffic load on typical T-beam bridges based on WIM data[J]. Journal of Performance of Construction Facilities, 2017, 31(3): 1-14. doi: 10.1061/(ASCE)CF.1943-5509.0000991 HAN Wanshui, WU Jun , CAI C S, et al. Characteristics and dynamic impact of overloaded extra heavy trucks on typical highway bridges[J]. Journal of Bridge Engineering, 2015, 20(2): 1-11. 李全旺, 李春前, 孙健康. 基于结构可靠性理论的既有桥梁承载能力评估[J]. 工程力学, 2010, 27（增刊2）: 142-151LI Quanwang, LI Chunqian, SUN Jiankang. Reliability-based capacity assessment of existing bridges[J]. Engineering Mechanics, 2010, 27 (S2): 142-151 刘浪. 基于WIM的公路桥梁车辆荷载特性分析[D].上海: 同济大学, 2014 ROGER D T. Overload truck wheel load distribution on bridge decks[R]. Michigan: Michigan Department of Transportation, 2009. CALTRANS. California amendments to AASHTO LRFD bridge design specifications. 4th Edition[S]. California: California Department of Transportation, 2008. 尤吉. 基于WIM卡车数据的公路桥梁承载力评估[D].上海: 同济大学, 2009. 刘浪,唐光武,刘海明. 考虑多车道行车效应的车辆荷载外推方法研究[J]. 福州大学学报(自然科学版),2017,45(2): 222-225. doi: 10.7631/issn.1000-2243.2017.02.222LIU Lang, TANG Guangwu, LIU Haiming. A study on extrapolation method for vehicle load on highway bridges with multiple lanes[J]. Journal of Fuzhou University (Natural Science Edition), 2017, 45(2): 222-225. doi: 10.7631/issn.1000-2243.2017.02.222 FU G K, LIU L, BOWMAN M D. Multiple presence factor for truck load on highway bridges[J]. Journal of Bridge Engineering, 2013, 18(3): 240-249. doi: 10.1061/(ASCE)BE.1943-5592.0000330 AASHTO. LRFD bridge design specifications[S]. 5th ed. Washington D. C.: AASHTO, 2010. 中华人民共和国交通运输部. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015 AASHTO. Standard specifications for highway bridge design[S]. 17th ed. Washington D. C.: AASHO, 2002 -
下载:
点击查看大图
图(6) / 表(2)
计量
- 文章访问数: 509
- HTML全文浏览量: 253
- PDF下载量: 9
- 被引次数: 0