Micromechanical Analysis of Steel Fiber Corrosion in Ultra-high Performance Concrete
-
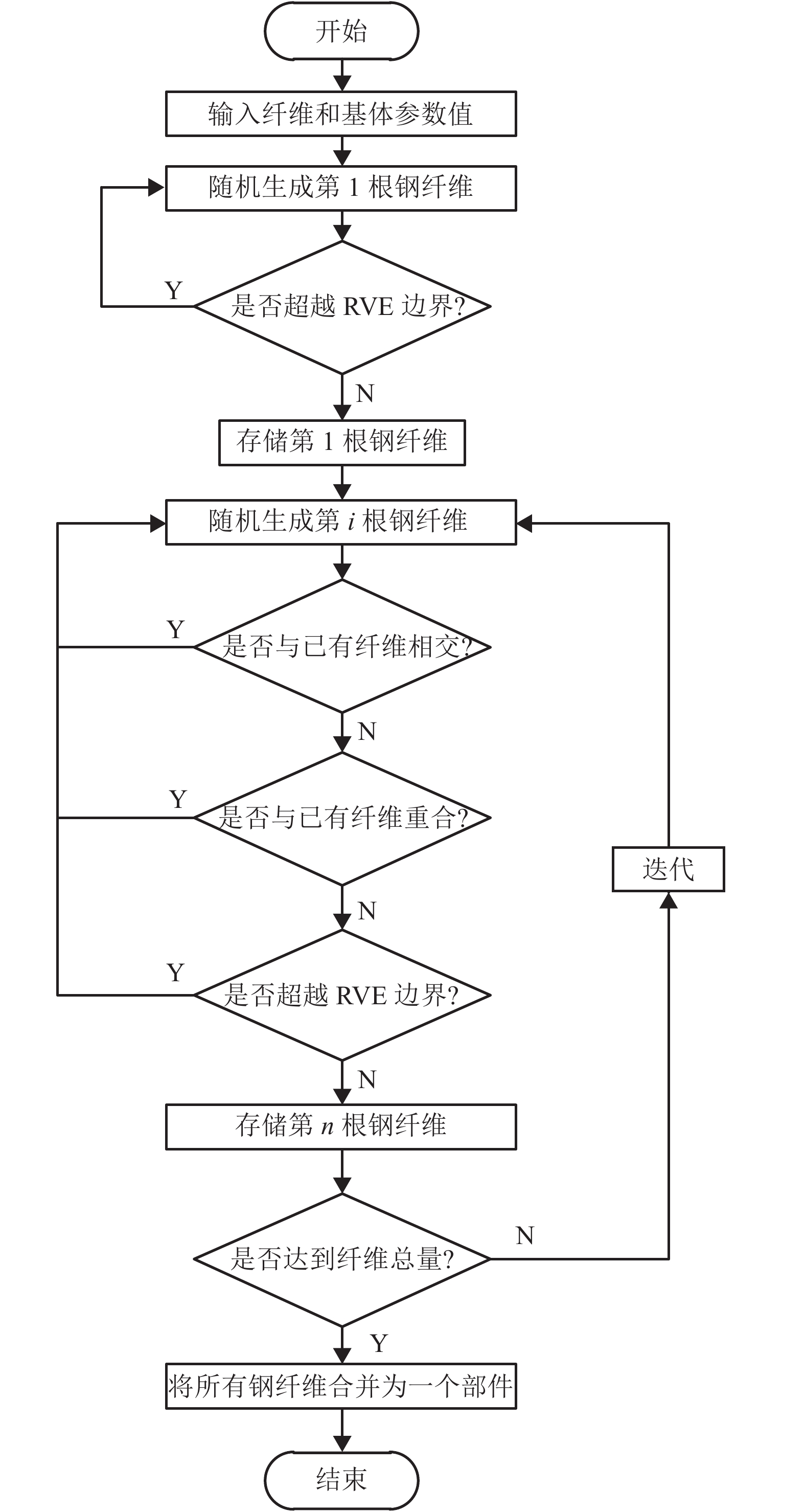
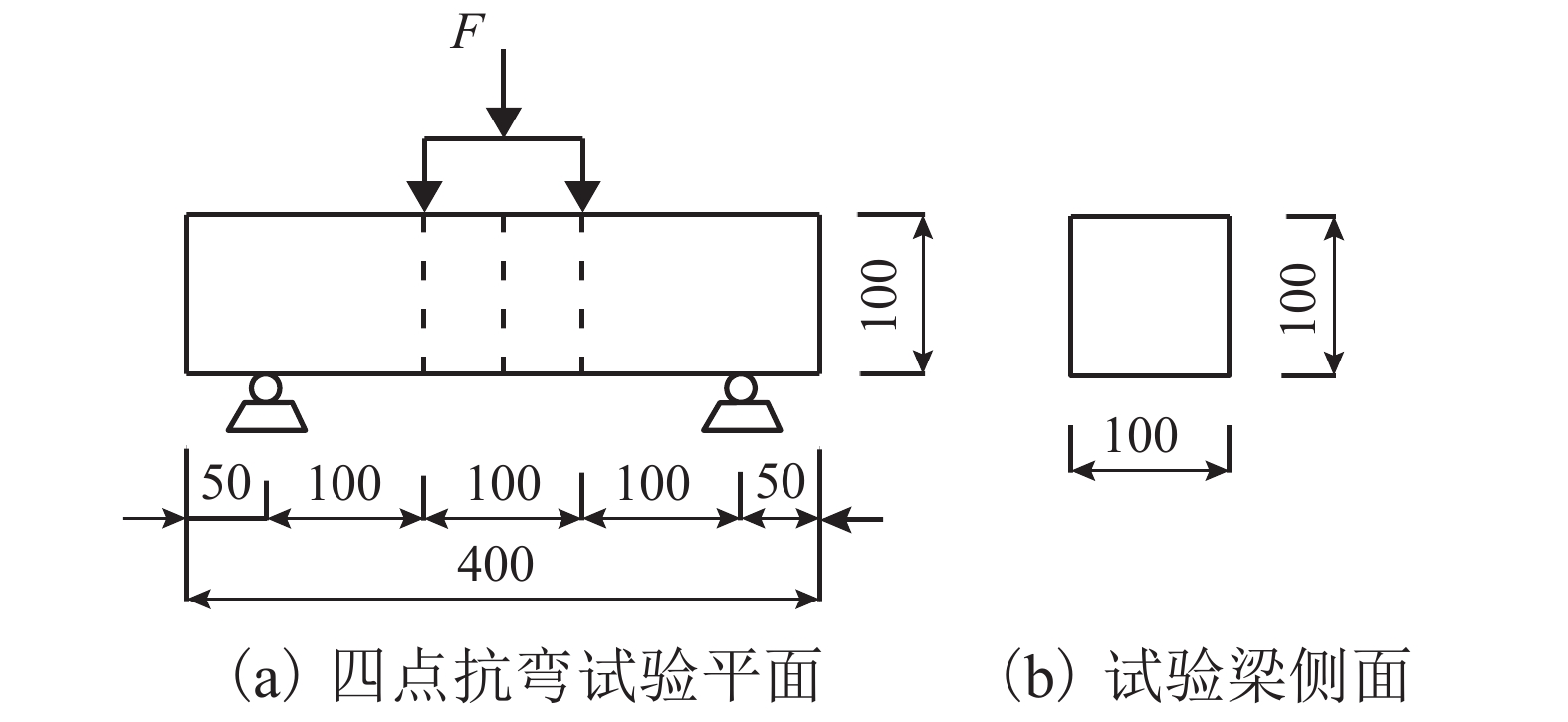
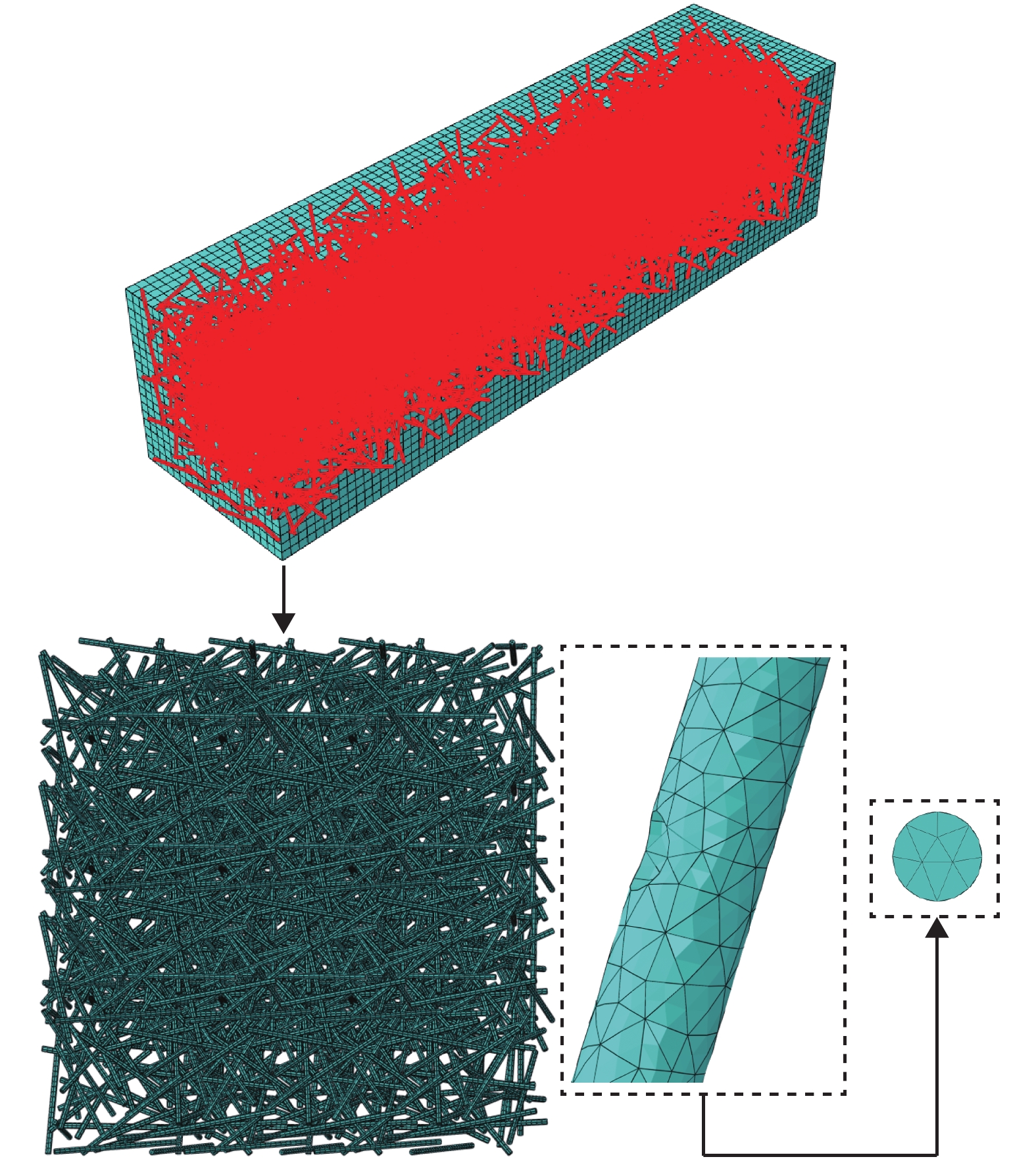
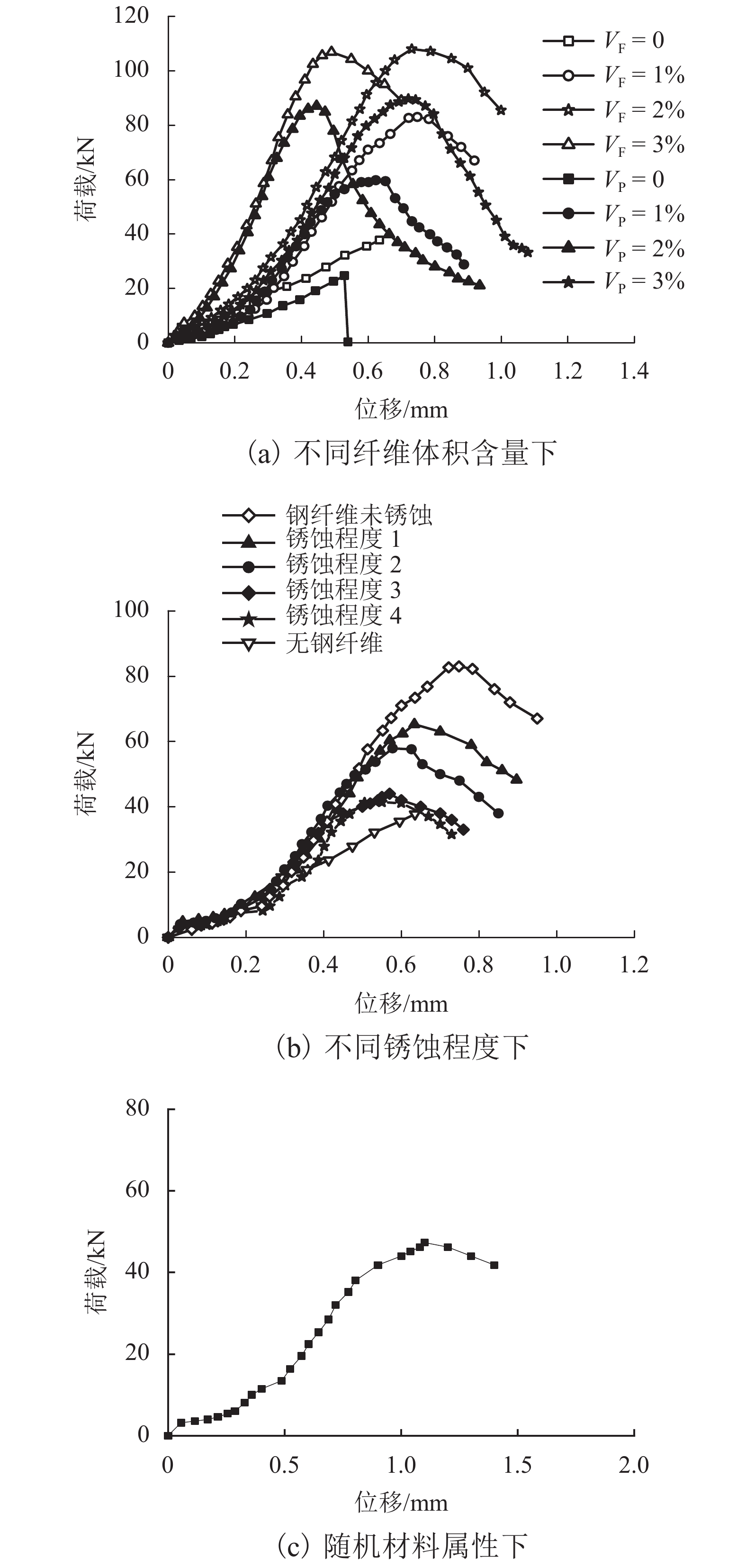
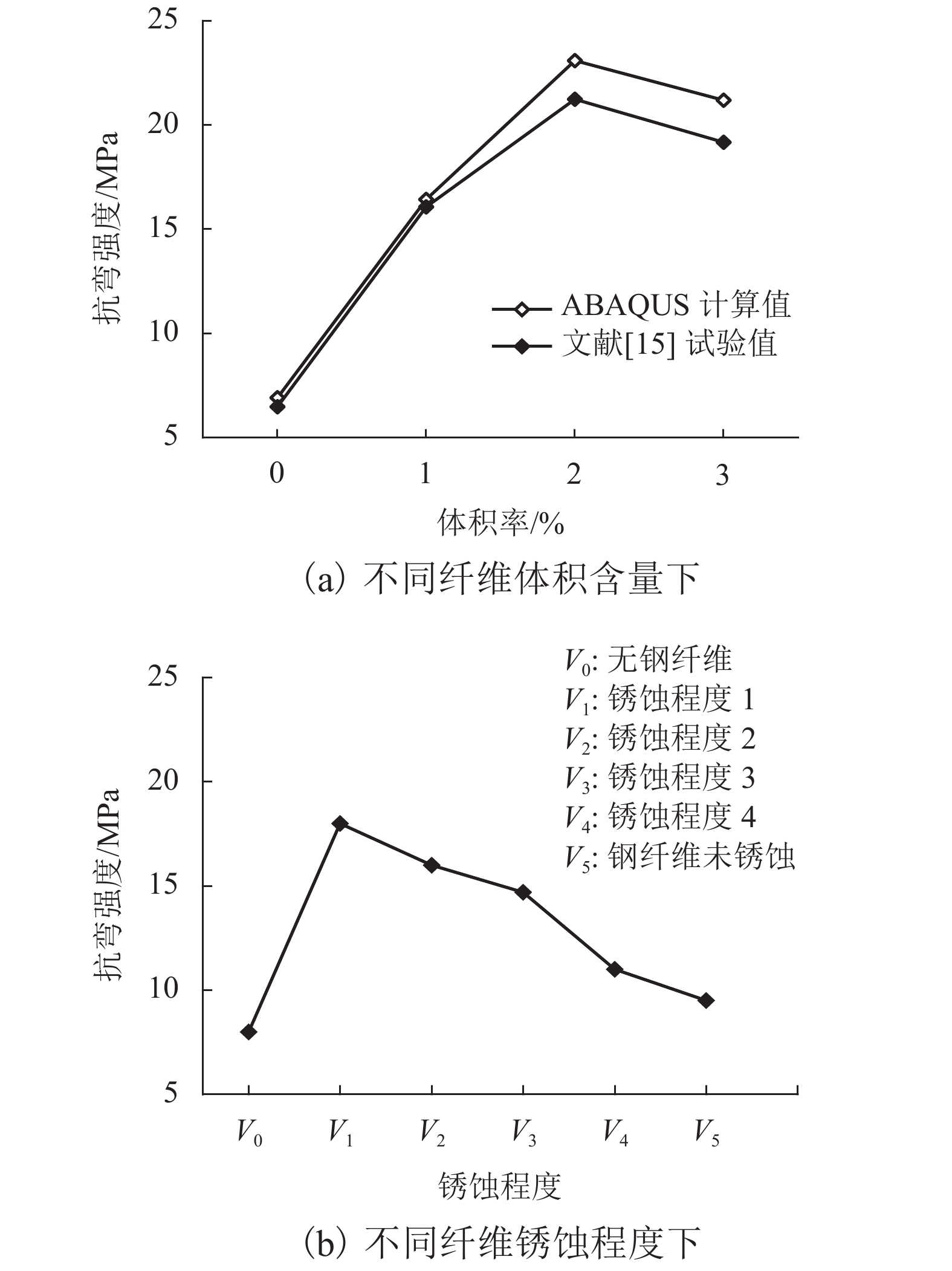
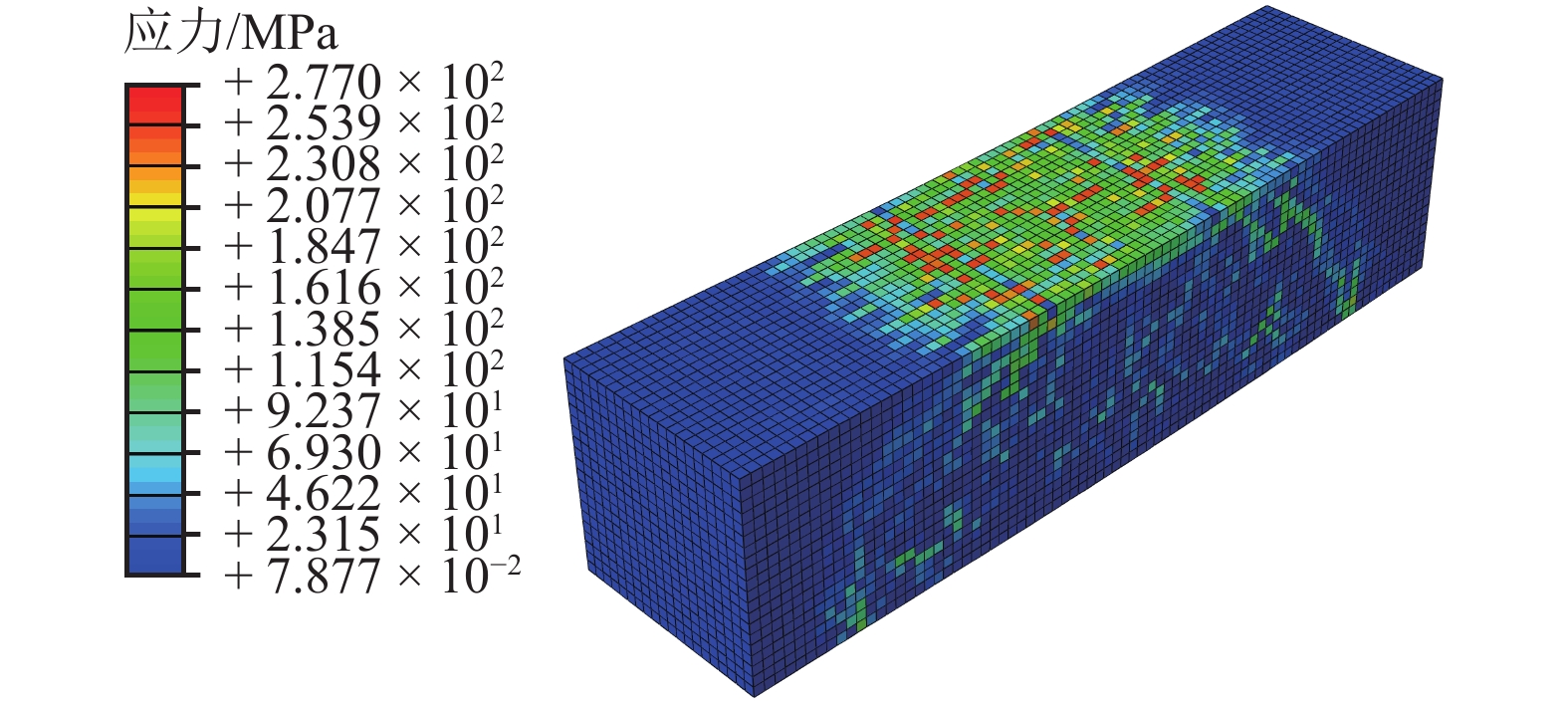
摘要: 为了研究钢纤维体积含量和锈蚀程度对结构强度和变形的影响，通过自行编写Python脚本文件，对ABAQUS软件进行二次开发，实现了钢纤维在超高性能混凝土（UHPC）基体中的大批量随机乱向均匀分布；在此基础上研究了UHPC带缺陷锈蚀模拟方法，进而探索了钢纤维锈蚀的等效方法；最后以UHPC梁四点抗弯试验为例，对UHPC细观力学分析方法、锈蚀的模拟方法和等效手段进行了验证. 研究结果表明：当纤维体积含量为2% 时，UHPC梁的抗弯曲性能最佳；影响锈蚀效应的关键因素为锈蚀造成纤维截面削弱、锈坑附近产生应力集中、界面粘结遭到破坏；采用随机材料属性分配的方式，仅局限于模拟UHPC梁的宏观变形，无法准确模拟应力场分布情况.
-
关键词:
- 超高性能混凝土（UHPC） /
- 细观力学分析 /
- 钢纤维锈蚀模拟 /
- ABAQUS二次开发 /
- PYTHON算法 /
- 模型试验
Abstract: In order to study the influence of the volume content and corrosion degree of the steel fiber on the strength and deformation of the structure, the large-volume randomization of the steel fiber in ultra-high performance concrete (UHPC) matrix was realized by the ABAQUS software redeveloped by self-compiling Python script file. Based on this, the UHPC defect corrosion simulation method was developed and the equivalent method of the steel fiber corrosion was explored. Finally, the UHPC beam four-point bending test was taked as an example to verify the UHPC micromechanics analysis method, corrosion simulation method, and equivalent means. The results show that when the fiber volume content is 2%, the UHPC beam has the best bending resistance; corrosion weakens the cross-section of fibers, stress concentration near the corrosion pits and the destroyed interfacial bonding are the key factors affecting the corrosion effect. The random material property distribution method is limited to simulate the macroscopic deformation of UHPC beams, and can’t accurately simulate the distribution of stress field. -
截至2020年底，我国铁路营业里程达14.63万公里，其中高速铁路里程为3.79万公里. 随着高速铁路的发展，设计速度为400 km/h的高速铁路已提上日程，如正在建设的“莫斯科—喀山”高铁[1]，我国成渝中线高铁[2]预留了400 km/h的提速能力. 现行《铁路桥涵设计规范》[3] 适用于350 km/h及以下速度的铁路，速度增长对铁路桥梁结构的设计提出更高要求，其中，列车荷载图式是关键的设计参数. 针对400 km/h高速铁路，研究荷载图式取值对线下结构的设计具有重要意义.
荷载图式是对各种运营列车的一种概化表达形式[4]，主要反映对桥梁的静态作用，用设计动力系数乘以荷载图式对桥梁的静力效应，可得到列车荷载图式下桥梁的动力效应. 国内外高速铁路桥梁设计活载标准有较大差异，荷载图式的制定需要结合实际运营车辆的情况进行制定. 在国外，欧盟国家普遍采用 UIC荷载[5]、英国采用RU活载和RL活载[6]、美国采用Cooper E系列荷载[7]、日本采用接近实际运营列车的N、P和H等荷载图式[8]. 我国于20世纪50年代制定了中-Z活载图式，70年代制定了中-活载图式，90年代至今制定了能反映线路运输特征的ZK、ZC、ZKH和ZH荷载图式[9]，分别用于高速铁路、城际铁路、客货共线铁路、重载铁路. 其中，在《京沪高速铁路设计暂行规定》[10]中，通过计算0.6UIC、0.7UIC、0.8UIC与国外运营高速铁路列车、我国高速运营列车活载图式、中速列车和货物列车的弯矩换算均布活载动效应比值，分析了分级 UIC荷载对运营列车活载的概括情况，确定高速铁路列车荷载图式按0.8UIC荷载（即ZK荷载）取值，目前《铁路桥涵设计规范》仍采用此规定.
此外，陈夏新等[11]通过调研和理论分析国内外铁路桥梁的发展储备，论证了铁路桥梁中-活载标准修订的必要性，总结了铁路桥梁列车活载图式的修订原则. 辛学忠等[12]指出中-活载图式不能较好与国际铁路荷载图式接轨，也不适应我国“客运高速、货运重载”的运输发展方向，在国内外相关研究成果上提出了客运专线、城际铁路、客货共线和货运专线的相应荷载图式. 戴公连等[13]指出我国中小跨度高速铁路桥梁采用现有活载设计标准指导设计，会有过大安全储备量，建议采用0.6UIC荷载作为高速铁路中小跨度桥梁的设计活载. 王丽等[14]通过荷载静力效应确定集中力间距和集中力与均布力间距并预备了10%的荷载储备，对市域铁路列车提出ZS荷载图式. 在城市轨道交通中，由于运营列车情况相对固定，桥梁设计荷载图式直接采用车辆最大轴重[15].
综上可见，已有研究均针对时速350公里及以下的铁路. 随着铁路建设里程不断增加，我国实现客、货分流的铁路运营模式，时速250公里以上的高速铁路均以客运专线为主，时速400公里的高速铁路也应是客运，采用包络货物列车活载的ZK荷载（0.8UIC荷载）会导致安全储备过大. 考虑荷载图式的制定不宜改变现有设计体系，因此在 UIC荷载图式基础上，对400 km/h高速铁路列车荷载图式进行研究非常必要.
针对400 km/h高速铁路列车荷载图式的制定及其与现行设计标准之间适应性进行研究. 通过荷载图式动效应包络各类实际运营列车动效应，提出400 km/h高速铁路列车荷载图式；基于车桥耦合振动分析方法，计算时速400公里高速列车对常用跨度简支梁桥的动力效应，对现行《铁路桥涵设计规范》与列车荷载图式相关的参数体系，如动力系数、竖向挠度限值、梁端竖向转角、轨面不平顺、离心力等指标进行适应性分析.
1. 列车荷载图式制定
参考《京沪高速铁路设计暂行规定》[10]中确定0.8UIC荷载作为高速铁路列车荷载图式的方法，不考虑货物DF4＋C62列车，以包络中国ZGS（中国拟定的高速运营列车活载图式）、德国ICE（Intercity-Express）列车和中速列车对各跨度跨中弯矩换算均布活载动效应的原则，仍采用系数乘 UIC荷载的模式制定400 km/h高速铁路的列车荷载图式. 在《京沪高速铁路设计暂行规定》相关计算结果的基础上，采用以下方法得到系数乘 UIC荷载作用下效应，具体步骤如下：
步骤1 UIC荷载对各跨度跨中弯矩换算均布活载静效应乘以系数，得到新制定列车荷载图式对各跨度跨中弯矩换算均布活载静效应.
步骤2 《京沪高速铁路设计暂行规定》[10]指出0.6UIC、0.7UIC、0.8UIC的活载效应需减小0.68倍、0.75倍、0.83倍，动力系数相应乘上0.68/0.6、0.75/0.7、0.83/0.8. 按系数与0.6、0.7、0.8的比值关系，对0.68、0.75、0.83线性插值减小活载效应，得到新制定列车荷载图式的动力系数. 将第一步的活载静效应乘以动力系数，计算新制定列车荷载图式对各跨度跨中弯矩换算均布活载动效应.
步骤3 当系数乘 UIC荷载刚好包络中国ZGS列车、德国ICE列车和中速列车的各跨度跨中弯矩换算均布活载动效应时，可确定系数大小，制定400 km/h高速铁路列车荷载图式.
经以上步骤计算，当采用0.65UIC荷载可刚好包络上述3种运营列车活载动效应. 0.65UIC荷载、0.80UIC荷载和4种运营列车活载与 UIC荷载对各种跨度桥梁跨中弯矩换算均布活载动效应比值如图1所示.
图 1 跨中弯矩换算均布活载动效应比值Figure 1. Ratio of dynamic effect of uniform live load converted from mid span bending moment由图1可见：0.8UIC荷载包络的4类运营列车活载中，以货车活载控制，最大活载动效应比为98.4%；当仅运行客运专线列车、跨度6 m以上时，最大活载动效应比为74.4%，富裕量较大；0.65UIC荷载包络的3类运营列车活载中，以中速列车活载控制，最大活载动效应比为99.3%，当仅运行客运专线列车、跨度6 m以上时，最大活载动效应比为86.4%，相对0.8UIC荷载的动活载效应比值富余量下降了12%，但仍有一定储备量. 所以，建议400 km/h高速铁路列车荷载图式按0.65UIC荷载取值，见图2. 对于跨度小于6 m的桥涵结构，可按特种荷载进行设计，参考《铁路桥涵设计规范》，特种荷载大小按荷载图式集中力1.25倍取值，间距与荷载图式集中力间距一致.
2. 车桥耦合振动模型
为进一步验证0.65UIC荷载图式的合理性，采用车桥耦合振动分析方法对结构设计的相关参数进行分析. 车桥耦合模型通常把车辆和桥梁当作两个子系统进行建模.
2.1 车辆模型
时速400公里高速列车的车辆结构应与已运营高速列车类似，车辆模型[16]简化为23自由度四轮对两系悬挂质量弹簧阻尼车，4个轮对各有2个自由度（横移、摇头），车体和前后转向架各有5个自由度，轮对和转向架间由一系悬挂系统的弹簧阻尼元件连接，车体和转向架间由二系悬挂系统的弹簧阻尼元件连接. 每节车运动相对独立，悬挂系统的弹簧按线性弹簧考虑，阻尼按黏性阻尼考虑，根据达朗贝尔原理，车辆子系统运动方程[17]为
Mv¨Xv+Cv˙Xv+KvXv=Fbv, (1) 式中：Mv、Cv、Kv分别为车辆的总体质量、阻尼和刚度矩阵；Xv为车辆子系统的位移；Fbv为车辆系统受到的轮轨作用力.
列车同一转向架固定轴距为2.5 m，车辆两转向架轴距为17.8 m，头车长28.064 m，中间车长25.650 m，列车最大轴重为17 t，车辆悬挂系统刚度与阻尼参数见表1. 同时，车辆编组考虑8车和16车两种编组，车辆载重考虑空载和满载两种情况.
表 1 车辆悬挂系统参数Table 1. Parameters of the train suspension system悬挂系统 刚度/（kN·m−1） 阻尼/（kN·s·m−1） 纵向 横向 竖向 纵向 横向 竖向 一系 14000 6000 1280 — — 10 二系 9500 220 220 4900 40 20 2.2 桥梁模型
采用空间梁单元模拟主梁和桥墩，在形成质量和刚度矩阵后，结合Rayleigh阻尼计算方法得到桥梁阻尼矩阵为
Cb=2ξω1ω2ω1+ω2Mb+2ξω1+ω2Kb, (2) 式中：ξ为桥梁结构阻尼比，为2%；ω1、ω2为桥梁的两阶自振频率；Mb、Kb分别为桥梁总体质量和刚度矩阵.
根据达朗贝尔原理，桥梁子系统的运动方程可写为
Mb¨Xb+Cb˙Xb+KbXb=Fvb， (3) 式中：Xb为车辆子系统的位移向量；Fvb为桥梁系统受到的轮轨作用力.
虽然《铁路桥涵设计规范》适用于跨度168 m以下的钢桥和跨度128 m以下的混凝土桥，但从图1可见，动力效应总体上随着跨度增大而减小. 考虑到我国高速铁路中大量采用24 m跨度和32 m跨度的简支梁桥[18]（以京沪高铁为例，简支梁占桥梁总里程的80%以上，其中跨度24 m和32 m的简支梁桥占桥梁总数85%以上[19]），近年来，40 m跨度简支梁桥也有一定应用. 因此，选择跨度为24、32 m和40 m的简支梁桥进行后续分析，桥梁的总长度均为480 m. 3种跨度简支梁桥墩高均为50 m，主梁采用C50混凝土，桥墩采用C40混凝土. 由于本研究侧重于动力参数的验证，未对截面进行静力受力分析，桥梁截面参考文献[20]取值.
分析中，空间步长取为0.2 m，采用AR（autoregressive）法[21]将德国低干扰谱转换为轨道不平顺时程样本. 借助自主研发的桥梁结构分析软件BANSYS将车辆子系统和桥梁子系统看作两个独立系统，通过分离迭代进行车桥耦合系统响应的求解.
3. 荷载图式的适应性分析
列车荷载图式需要与规范中的设计标准体系配套使用. 当400 km/h高速铁路采用0.65UIC荷载代替原ZK荷载时，不宜改变现行规范的设计体系，需将规范中与ZK荷载相关的参数体系进行适应性分析. 以下仅针对与ZK荷载直接相关的主要指标，如动力系数、竖向挠度、梁端竖向转角、轨面不平顺、离心力和制动力等进行分析.
3.1 动力系数
当列车荷载图式为0.65UIC荷载，对现行《铁路桥涵设计规范》设计动力系数计算公式进行适应性分析，可按“设计动力系数 × 列车荷载图式静效应 > 运营列车动力系数 × 运营列车静效应”的原则进行判断.
在3种跨度简支梁桥有限元模型的最不利位置施加0.65UIC荷载（图3），得到列车荷载图式对桥梁的静力效应. 设计动力系数μ按式（4）计算，得到24、32、40 m简支梁桥的设计动力系数分别为1.126、1.084、1.055.
1+μ=1+(1.44√L−0.2−0.18), (4) 式中：L为桥梁跨度.
采用车桥耦合振动分析方法得到运营荷载作用下的动力响应. 分析中，计算了车速200～440 km/h， 8编组空载、8编组满载、16编组空载、16编组满载情况下，列车对3种跨度简支梁桥的竖向动力响应，每种车速取车辆编组和载重工况中最大的竖向动力响应进行分析.
0.65UIC荷载对桥梁的静力效应乘以设计动力系数，即为荷载图式对桥梁的动力效应. 由车桥耦合振动计算得到桥梁动力响应，即为运营列车动力系数乘以运营列车静效应. 运营列车与0.65UIC荷载对3种跨度简支梁桥的动效应比值见图4.
图 4 3种跨度简支梁桥动效应比值Figure 4. Dynamic effect ratio of three kinds of span simply supported girder bridges由图4可见：列车车速为440 km/h时的荷载最大动效应与0.65UIC荷载最大动效应比值为0.816，仍具有一定富余量，说明400 km/h高速铁路列车荷载图式取为0.65UIC荷载时，现行《铁路桥涵设计规范》中的设计动力系数计算公式仍然适用. 对于简支梁桥而言，当桥梁截面发生变化时，图4中的动效应会有所变化. 以24 m跨度为例，在380 km/h附近存在共振区间，此时动效应比较大. 在设计时，从截面、跨度的选择等方面调整共振车速，尽可能在设计车速附近避开共振区间.
从图4还可看出：虽然24 m跨度简支梁桥在380 km/h附近有较大的动效应，但车速达到400 km/h及以上时，32 m简支梁桥动力响应的富余量最小，考虑到我国高速铁路建设中大量采用32 m简支梁桥，后续仅对32 m简支梁桥在0.65UIC荷载作用下的竖向变形限值、梁端转角限值和轨面不平顺限值进行适应性分析.
3.2 竖向变形和梁端转角
现行《铁路桥涵设计规范》规定，32 m简支梁桥在车速250、300、350 km/h的竖向变形限值分别为L/1400、L/1500、L/1600，车速为400 km/h时竖向变形限值应更为严格. 32 m简支梁桥梁端悬出长度为0.55 m，规范要求桥台与桥梁间转角限值θ为1.5‰ rad，相邻两孔梁每孔梁转角限值θ1/θ2为1.5‰ rad，相邻两孔梁转角限值之和为 3.0‰ rad，当车速为400 km/h时，转角的限值应不低于此要求. 偏保守地仍按规范对350 km/h的限值要求与后文车桥耦合计算所得限值进行对比.
规定桥梁竖向变形和梁端转角的限值是为满足列车运营安全性和乘坐舒适性要求. 研究中，列车的安全性和舒适性指标仍按现行《铁路桥涵设计规范》进行取值. 参考文献[22]计算城市轨道交通桥横向挠度限值的计算方法，通过调整桥梁模型竖向刚度，在其他条件均不变的情况下，基于车桥耦合振动分析方法，得到车辆动力响应，相应的桥梁模型加载0.65UIC荷载得到桥梁竖向挠度和梁端转角，当车辆响应接近限值时的竖向挠度和梁端转角可认为是桥梁的竖向挠度限值和梁端转角限值. 与《铁路桥涵设计规范》中的限值进行比较，判断列车荷载图式为0.65UIC荷载时桥梁竖向变形限值和梁端转角限值的适应性.
按上述桥梁竖向挠度和梁端转角限值计算方法，桥梁竖向惯性矩分别下降5倍、8倍、10倍、12倍、14倍、16倍、18倍、20倍，考虑车速为350 km/h和400 km/h得到两种车速下车辆编组和载重工况中最严格的车辆响应. 经计算，车辆舒适性指标较安全性指标更快达到限值，考虑到车辆舒适性指标是以人体感觉来确定的，其不应随车速的改变而改变. 所以图5、6中均以车体竖向加速度限值（1.3 m/s2）插值计算桥梁竖向挠度限值和梁端转角限值.
图 5 32 m简支梁桥竖向挠度限值Figure 5. Vertical deflection limit value of 32 m simply supported girder bridge
图 6 32 m简支梁桥梁端转角限值Figure 6. Beam end angle limit value of 32 m simply supported girder bridge由图5可见：32 m简支梁桥在车速350 km/h时竖向变形限值为L/866，车速400 km/h时竖向变形限值为L/1056，与已有《铁路桥涵设计规范》限相比仍有较大安全储备.
由图6可见：桥梁和桥台梁转角限值θ、相邻两孔梁每孔梁转角限值θ1/θ2在车速350 km/h分别为2.7‰、3.5‰ rad，车速400 km/h分别为2.2‰、2.9‰ rad；相邻两孔梁转角限值之和（θ1 + θ2）在车速350 km/h为6.2‰ rad，400 km/h为5.1‰ rad，相比现行规范限值仍有较大安全储备.
在轨道不平顺相同的条件下，车速增加，桥梁的挠度限值要求有所提高，虽然车辆响应受轨道不平顺随机性的影响较大，但车辆响应采用峰值进行评价，且有较大安全储备. 因此，荷载图式采用0.65UIC荷载时，按现行规范体系中的竖向挠度和梁端转角限值进行设计应是可行的.
3.3 轨面不平顺
现行《铁路桥涵设计规范》要求在3 m长的线路范围一线两根钢轨的竖向相对变形量限值应小于1.5 mm，当车速提高到400 km/h时，该指标要求应不会降低，本研究中仍假定为1.5 mm. 通过减小主梁截面扭转惯性矩降低桥梁抗扭刚度，在其他条件均不变的条件下进行车桥耦合振动分析，得到车辆响应，然后将对应的桥梁有限元模型按最不利位置加载0.65UIC荷载，计算轨面不平顺. 由文献[23]可知，轨面不平顺分为整体扭转和局部扭转两部分（图7），整体扭转用桥面绕轴线最大扭转角乘以轨距1.435 m计算得到，在最大扭转角位置左右相邻3 m处考虑轨面高差即为局部扭转，整体扭转和局部扭转的扭转总变形即为轨面不平顺.
按上述桥梁轨面不平顺限值计算方法，桥梁扭转惯性矩分别下降5倍、10倍、20倍、25倍、30倍、40倍、50倍，考虑车速为350 km/h和400 km/h，得到两种车速下车辆编组和载重工况中最严格的车辆响应. 经计算，横向加速度最快达到限值（1.0 m/s2），插值得到图8中加速度限值处的桥梁轨面不平顺限值.
图 8 32m简支梁桥轨面不平顺限值Figure 8. Track surface irregularity limit value of 32 m simply supported girder bridge由图8可见：32 m简支梁桥在车速350 km/h时轨面不平顺限值为2.70 mm，车速400 km/h时竖向变形限值为2.98 mm，与规范限值1.5 mm相比，规范对桥梁轨面不平顺限值要求更加严格，说明当400 km/h高速铁路将0.65UIC荷载作为列车荷载图式时，现行《铁路桥涵设计规范》对桥梁轨面不平顺限值的规定是适用的.
3.4 离心力与制动力
《铁路桥涵设计规范》中，与ZK荷载直接相关还有离心力、牵引力及制动力. 当ZK荷载替换为0.65UIC荷载时，需要考查设计荷载是否具有一定安全储备.
本文研究3种跨度简支梁桥均为直线桥，但400 km/h高速铁路中有曲线桥梁，所以对离心力限值也需进行一定分析，离心力限值[3]为
Fli=fCW， (5) 式中：f为列车竖向活载折减系数，400 km/h高速铁路桥梁曲线部分荷载长取值为150 m，计算得到f为0.439；C为离心力率，小于0.15；W为列车荷载图式的集中活荷载.
荷载图示中包含集中力和均布力，400 km/h高速铁路桥梁离心力限值分别计算如下：
集中力：
${F_{\rm{li}}} = 0.439 \times 0.15 \times 163 = 10.734{\text{ kN}}$ .均布力：
${F_{\rm{li}}} = 0.439 \times 0.15 \times 52 = 3.424{\text{ kN}}$ .当车速为400 km/h，车辆对桥梁考虑超高未被平衡的离心力计算值
${F_{\rm{lis}}}$ [3]为Flis=V2127RN−NhS， (6) 式中：V为设计速度，取值400 km/h；R为最小曲线半径，时速400公里高速列车参数要求一般情况下R为7500 m，对《高速铁路设计规范》[24]中设计速度为250、300、350 km/h的无砟轨道平曲线半径按二次项拟合，得到400 km/h无砟轨道平曲线半径为9200 m；N为列车轴重，取值167 kN；h为超高，取值150 mm；S为轨距中心距，取值1500 mm.
按式（6）计算得到车辆对桥梁R分别为7500、9200 m的离心力为11.352、6.169 kN，11.352 kN大于离心力限值，所以时速400公里高速列车最小曲线半径可按9200 m取值，此时
${{F}}_{{\rm{lis}}} < {F}_{{\rm{li}}}$ ，表明按0.65UIC荷载计算的离心力时，现行《铁路桥涵规范》对离心限值的计算公式仍旧适用，且有一定的安全储备.现行《铁路桥涵设计规范》规定制动力或牵引力限值按列车荷载图式在计算长度内的10%计算，列车荷载图式取为0.65UIC荷载，8车编组和16车编组列车的牵引力或制动力限值分别为1129 kN和2215 kN.
时速400公里高速列车牵引力在启动时最大，为256 kN，制动力通过质量和减速度进行计算[25]，如式（7）.
FD=M（1+r）β−Mω, (7) 式中：M为车体质量，按车辆满载考虑，8车编组M为503 t，16车编组M为1006 t；β为减速度，取为0.92 m/s2；r为列车回转质量系数，取为0.06；ω为列车单位运行阻力，简化处理可忽略.
由式（7）可得到8车满载的制动力为491 kN、16车满载为981 kN，大于牵引力256 kN，这表明时速400公里高速列车的制动力较牵引力更大，且牵引力和制动力不会同时作用在桥梁线路上. 将8车编组和16车编组列车的制动力与0.65UIC荷载计算限值对比可见， 400 km/h高速铁路将0.65UIC荷载作为列车荷载图式时，现行《铁路桥涵设计规范》对牵引力或制动力限值的规定仍有较大安全储备.
4. 结 论
通过包络德国ICE列车、中国ZGS列车、中速列车的各跨度弯矩换算均布活载动效应，提出将0.65UIC荷载作为400 km/h高速铁路的列车荷载图式，并对0.65UIC荷载配套参数进行适应性分析. 结果表明，列车荷载图式选取0.65UIC荷载，按现行《铁路桥涵设计规范》中的动力系数、竖向挠度、梁端竖向转角、轨道不平顺、离心力、牵引力和制动力进行计算时仍有一定安全储备，建议将0.65UIC荷载作为400 km/h高速铁路列车荷载图式.
-
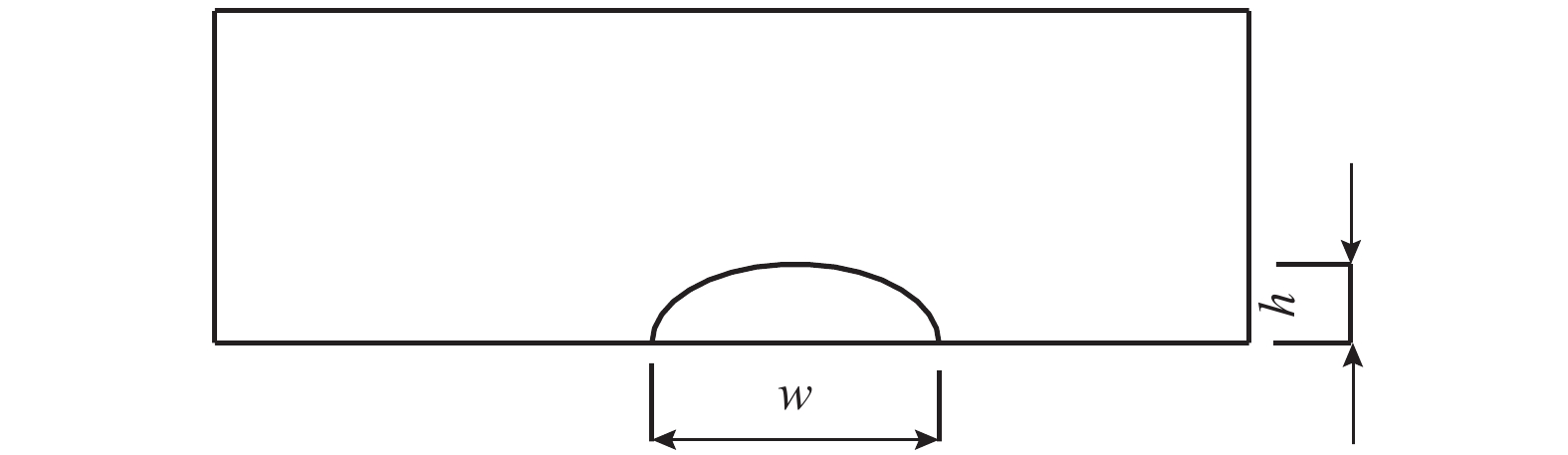
表 1 锈坑参数
Table 1. Pit parameters
锈蚀程度 锈坑深度/mm 锈坑宽度/mm $1$ 0.08 0.30 $2$ 0.08 1.10 $3$ 0.18 0.30 $4$ 0.18 1.10 
下载: 导出CSV
-
赵筠,廉慧珍,金建昌. 钢-混凝土复合的新模式——超高性能混凝土(UHPC/UHPFRC)之一:钢-混凝土复合模式的现状、问题及对策与UHPC发展历程[J]. 混凝土世界,2013,52: 56-69. doi: 10.3969/j.issn.1674-7011.2013.05.013ZHAO Jun, LIAN Huizhen, JIN Jianchang. A new model of steel concrete composite— ultra-high performance concrete (UHPC/UHPFRC):the current situation,problems and countermeasures of steel concrete composite model and the development of UHPC[J]. China Concrete, 2013, 52: 56-69. doi: 10.3969/j.issn.1674-7011.2013.05.013 AITCIN P C. High-performance concrete[M]. London: E & FN Spon, 2004: 22-30. WILLE K, NAAMAN A E, EL-TAWIL S, et al. Ultra-high performance concrete and fiber reinforced concrete:achieving strength and ductility without heat curing[J]. Materials & Structures, 2012, 45(3): 309-324. 阎培渝. 超高性能混凝土(UHPC)的发展与现状[J]. 混凝土世界,2010,15: 36-41. doi: 10.3969/j.issn.1674-7011.2010.02.010YAN Peiyu. Development and present situation of ultra-high performance concrete (UHPC)[J]. China Concrete, 2010, 15: 36-41. doi: 10.3969/j.issn.1674-7011.2010.02.010 PIMIENTA P, CHANVILLARD G. Durability of UHPFRC specimens kept in various aggressive environments[C]//10DBMC International Conference on Durability of Building Materials and Components. Paris: [s.n.], 2005: 17-20. TOUTLEMONDE F, BOUTEILLER V, PLATRET G, et al. Field demonstration of UHPFRC durability[J]. Concrete International, 2010, 10: 39-45. 赵军,李洪杰,高丹盈. 锈蚀后钢纤维和钢纤维混凝土的力学性能[J]. 建筑材料学报,2015,18(3): 409-414. doi: 10.3969/j.issn.1007-9629.2015.03.009ZHAO Jun, LI Hongjie, GAO Danying. Mechanical properties of steel fiber and steel fiber reinforced concrete after corrosion[J]. Journal of Building Materials, 2015, 18(3): 409-414. doi: 10.3969/j.issn.1007-9629.2015.03.009 高丹盈,陈刚,HADI M N S,et al. 锈蚀钢纤维力学性能及极限拉伸荷载计算方法[J]. 建筑材料学报,2016,19(3): 436-441. doi: 10.3969/j.issn.1007-9629.2016.03.004GAO Danying, CHEN Gang, HADI M N S, et al. Mechanical properties and calculation method for ultimate tensile load of corroded steel fibers[J]. Journal of Building Materials, 2016, 19(3): 436-441. doi: 10.3969/j.issn.1007-9629.2016.03.004 张研, 张子明. 材料细观力学[M]. 北京: 科学出版社, 2008: 10-15. 王娟,李庆斌,卿龙邦,等. 基于细观结构统计特征的混凝土几何代表体尺寸研究[J]. 工程力学,2012,29(12): 1-6. doi: 10.6052/j.issn.1000-4750.2011.05.0278WANG Juan, LI Qingbin, QING Longbang, et al. Studies on representative volume element size of concrete based on meso-structure statistics[J]. Engineering Mechanics, 2012, 29(12): 1-6. doi: 10.6052/j.issn.1000-4750.2011.05.0278 王文谈. 超高性能纤维增强混凝土(UHPFRC)的实验研究及低速冲击有限元模拟[D]. 成都: 西南交通大学, 2015. 徐亦冬. 混凝土中钢筋的不均匀锈蚀特征与本构关系[D]. 南京: 东南大学, 2013. 中国工程建设标准化协会标准. 纤维混凝土试验方法标准: CECS 13—2009[S]. 北京: 中国计划出版社, 2010. 杨克家, 李桅, 陈联盟. RPC损伤塑性本构模型建构及应用[C]// 第23届全国结构工程学术会议论文集(第Ⅱ册). 北京: [出版者不详], 2014: 161-167. 王文谈, 魏耀富, 蒋晗, 等.超高性能钢纤维增强混凝土力学性能的实验研究[J].应用数学和力学, 2014, 35(增刊1):295-298.WANG Wentan, WEI Yaofu, JIANG Han, et al. Mechanical properties of ultrahigh performance steel fiber reinforced concrete[J]. Experimental Study, 2014, 35 (S1): 295-298 ROSSI P. Development of new cement composite materials for construction[J]. Proceedings of the Institution of Mechanical Engineers,Part L:Journal of Materials:Design and Applications, 2005, 219(1): 67-74. doi: 10.1243/146442005X10193 王发洲,胡曙光,丁庆军,等. 高性能复合道路水泥混凝土的研究[J]. 中国公路学报,2000,13(3): 12-14. doi: 10.3321/j.issn:1001-7372.2000.03.004WANG Fazhou, HU Shuguang, DING Qingjun, et al. Research on the high performance composite road concrete[J]. China Journal of Highway and Transport, 2000, 13(3): 12-14. doi: 10.3321/j.issn:1001-7372.2000.03.004 期刊类型引用(0)
其他类型引用(4)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 844
- HTML全文浏览量: 414
- PDF下载量: 56
- 被引次数: 4