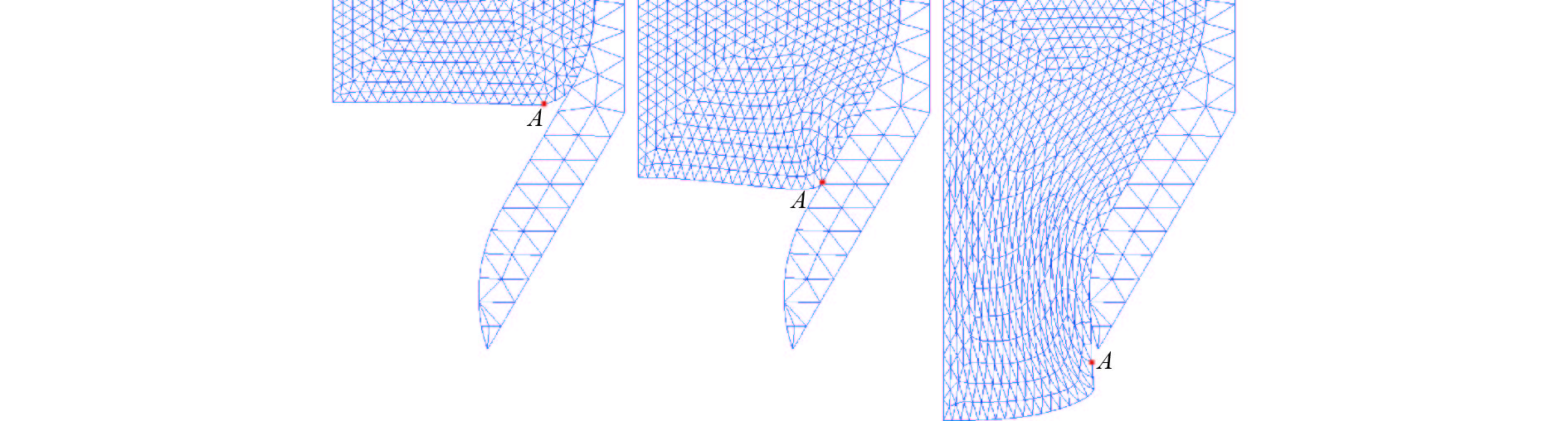
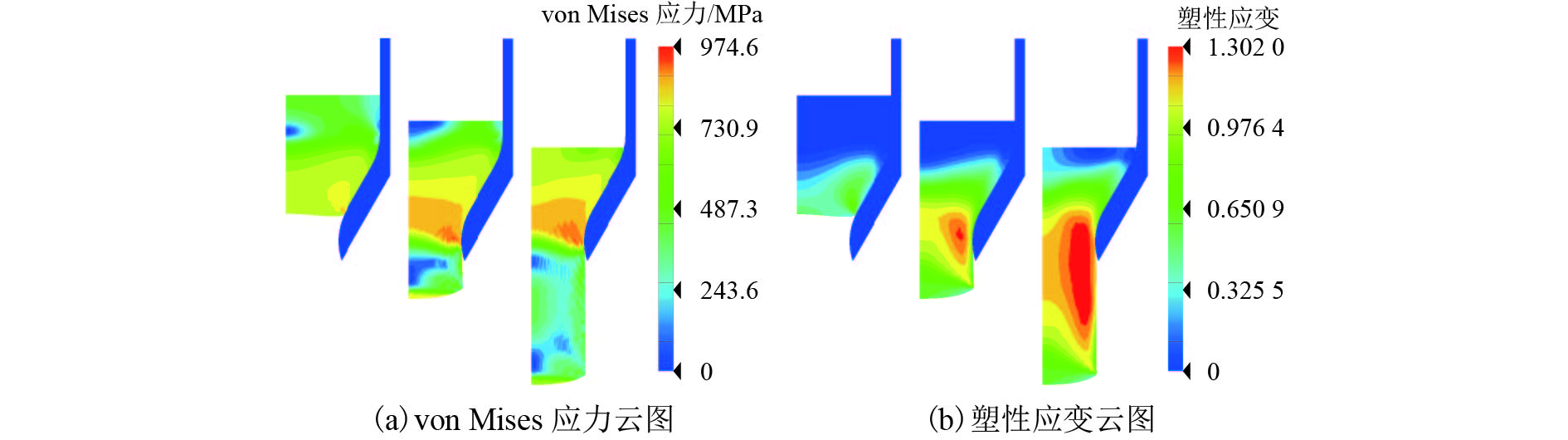
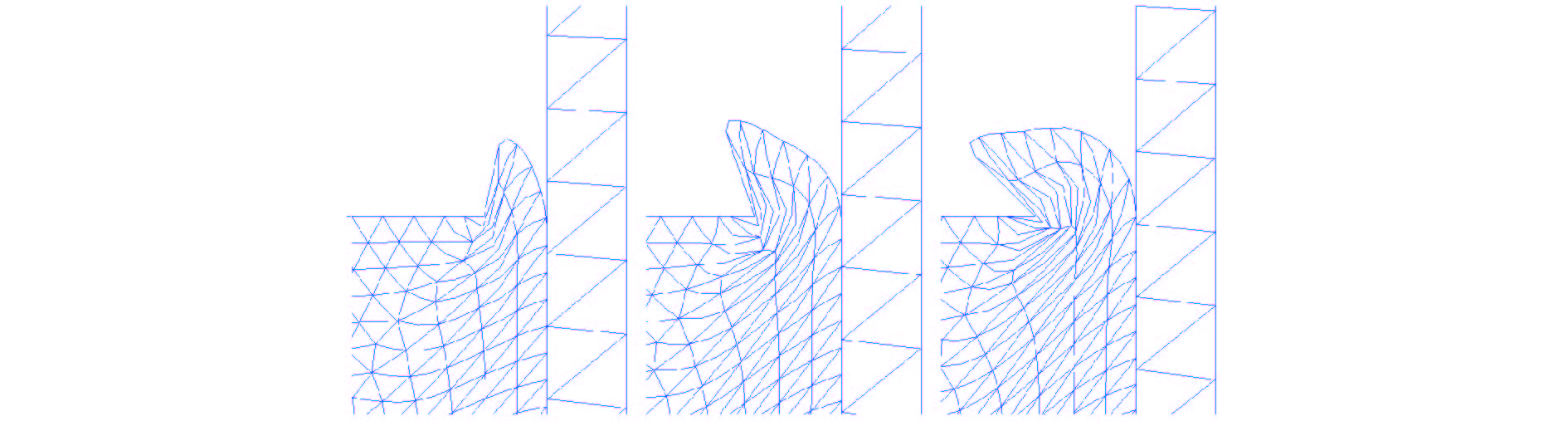
Numerical Algorithm and Software Development for Metal Forming
-
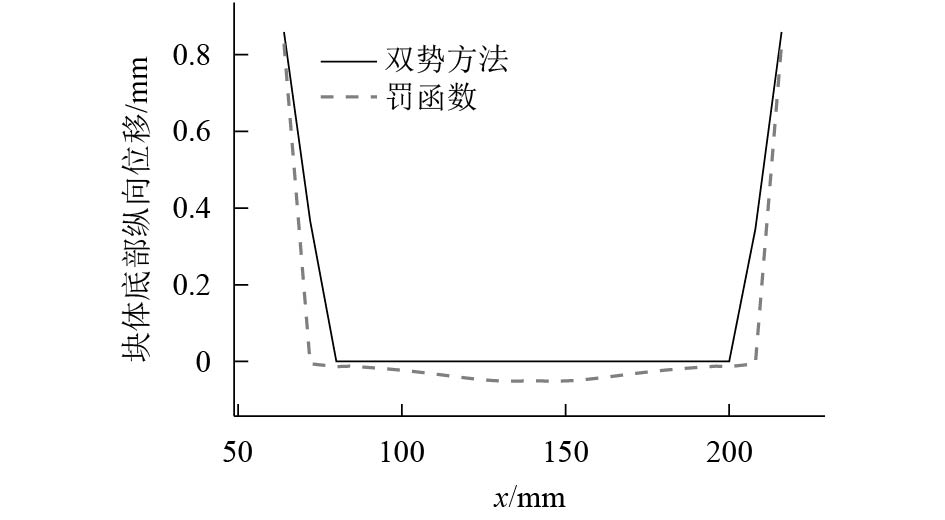
摘要: 以实现拥有部分算法特色的金属成形定制化CAE （computer-aided engineering）软件为目的，在自主开发的OmtDesk平台基础上，嵌入金属成形数值计算程序.首先，以双势理论为基础，运用Uzawa算法求解金属成形中的接触摩擦问题；其次，采用建立在更新拉格朗日框架上的返回映射算法，求解金属成形中材料非线性问题；最后，通过压缩回弹和挤压成形两个数值算例，验证了自主开发的金属成形定制化CAE软件FEM/Form的准确性与通用性，并将求解结果与ANSYS对比.在压缩回弹算例中，采用ANSYS得到10–3 mm量级的穿透量，相同算例采用FEM/Form则能将穿透量控制在10–7 mm量级,说明采用双势接触模块能更加精确地控制金属成形数值模拟中的穿透量，使金属成形过程更加准确.Abstract: To develop a customized computer-aided engineering (CAE) software with specialized features for metal forming, based on the self-developed OmtDesk platform, a numerical algorithm for mental forming calculation is proposed. On the basis of the bipotential theory, the Uzawa algorithm was applied to addressing the frictional contact. The return-mapping algorithm was then applied in the framework of the updated Lagrangian to analyze the non-linearity of metal materials. Furthermore, two numerical tests in terms of compression springback and extrusion forming were conducted for verifying the accuracy and feasibility of the developed CAE software with the aid of FEM and Form simulation software. The results are compared with those by ANSYS. In the case of the compression springback test, the penetration value calculated by ANSYS software has a magnitude of 10–3 mm, whereas those by FEM and Form software show a penetration magnitude of 10–7 mm. This demonstrates that the proposed bipotential contact module can effectively control the penetration value in the simulation of metal forming, thereby improving the precision of the metal forming process.
-
Key words:
- metal forming /
- frictional contact /
- bipotential algorithm /
- elastoplasticity /
- return-mapping algorithm
-
图 2 最大加载时网格变形与接触细部
Figure 2. Details of mesh deformation and frictional contact at the moment of maximum loading
图 3 两种接触方法渗透量比较曲线
Figure 3. Comparison between the penetration capability of two contact methods
图 4 最大卸载时网格变形与回弹细部
Figure 4. Details of mesh deformation and compression springback at the moment of maximum unloading
图 5 弹塑性块体加/卸载von Mises应力云图
Figure 5. von Mises stress nephogram of an elastoplastic block during loading and unloading
图 6 弹塑性块体加/卸载塑性应变云图
Figure 6. Plastic strain nephogram of an elastoplastic block during loading and unloading
图 8 锻件挤压过程中的网格变形
Figure 8. Grid deformation during the extrusion process of a forged piece
图 10 高摩擦系数下锻件发生卷边（μ = 0.80 ）
Figure 10. Curling selvedge of a forged piece with a high coefficient of friction (μ = 0.80)
表 1 不同材料参数对回弹量的影响
Table 1. Influence of different material parameters on resilience
$\mu $ (${\sigma _{\rm{y}}}=300$MPa) ${{{U}}_{{\rm{spb}}}}$/${\rm{mm}}$ ${\sigma _y}$/${\rm{MPa}}$ ($\mu {\rm{ = 0}}{\rm{.10}}$) ${{{U}}_{{\rm{spb}}}}$/${\rm{mm}}$ FEM/Form ANSYS FEM/Form ANSYS 0.00 0.253 560 0.108 770 200 0.122 087 0.072 006 0.05 0.202 626 0.110 240 250 0.136 296 0.087 519 0.10 0.150 369 0.101 210 300 0.150 369 0.101 210 0.15 0.117 694 0.087 472 350 0.163 935 0.114 070 0.20 0.084 306 0.078 672 400 0.179 304 0.127 840 0.25 0.022 618 0.074 449 450 0.186 924 0.141 030 
下载: 导出CSV
-
柳玉起. 计算机模拟在金属成形行业的应用和发展现状[J]. 锻造与冲压,2005(6): 16-16.LIU Yuqi. Application and development of computer simulation in metal forming industry[J]. Forging and Stamping, 2005(6): 16-16. 冯志强,刘建涛,彭磊,等. 自主 CAE 平台及计算力学软件研发新进展[J]. 西南交通大学学报,2016,51(2/3): 519-524. doi: 10.3969/j.issn.0258-2724.2016.03.010FENG Zhiqiang, LIU Jiantao, PENG Lei, et al. New development of CAE platform and computational mechanics software[J]. Journal of Southwest Jiaotong University, 2016, 51(2/3): 519-524. doi: 10.3969/j.issn.0258-2724.2016.03.010 DE SAXCÉ G, FENG Z Q. New inequality and functional for contact with friction:the implicit standard material approach[J]. Mechanics of Structures and Machines, 1991, 9(3): 301-325. doi: 10.1080/08905459108905146 DE SAXCÉ G. The bipotential method, a new variational and numerical treatment of the dissipative laws of materials[C]//10th International Conference on Mathematical and Computer Modelling and Scientific Computing. Boston: [s.n.], 1995: 5-8 RENAUD C, CROS J M, FENG Z Q, et al. The Yeoh model applied to the modeling of large deformation contact/impact problems[J]. International Journal of Impact Engineering, 2009, 36(5): 659-666. doi: 10.1016/j.ijimpeng.2008.09.008 DE SAXCÉ G, FENG Z Q. The bipotential method:a constructive approach to design the complete contact law with friction and improved numerical algorithms[J]. Mathematical and Computer Modeling, 1998, 28: 225-245. doi: 10.1016/S0895-7177(98)00119-8 ROTERS F, EISENLOHR P, HANTCHERLI L, et al. Overview of constitutive laws,kinematics,homogenization and multiscale methods in crystal plasticity finite-element modeling:theory,experiments,applications[J]. Acta Materialia, 2010, 58(4): 1152-1211. doi: 10.1016/j.actamat.2009.10.058 胡军,栗明,张锟,等. 摩擦系数对高强度钢弯曲件回弹的影响研究[J]. 热加工工艺,2015,44(21): 150-152.HU Jun, LI Ming, ZHANG Kun, et al. Impact of friction coefficient on bending springback of high strength steel[J]. Hot Working Technology, 2015, 44(21): 150-152. 王雪. 铝型材三维多点拉弯成形回弹相关问题研究[D]. 吉林: 吉林大学, 2014 SIMO J C. A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition. part Ⅱ:computational aspects[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 68(1): 1-31. doi: 10.1016/0045-7825(88)90104-1 -
下载:
点击查看大图
计量
- 文章访问数: 408
- HTML全文浏览量: 197
- PDF下载量: 10
- 被引次数: 0