Simulation and Verification of Dynamic Response of Railway Wagon on Railway Track
-
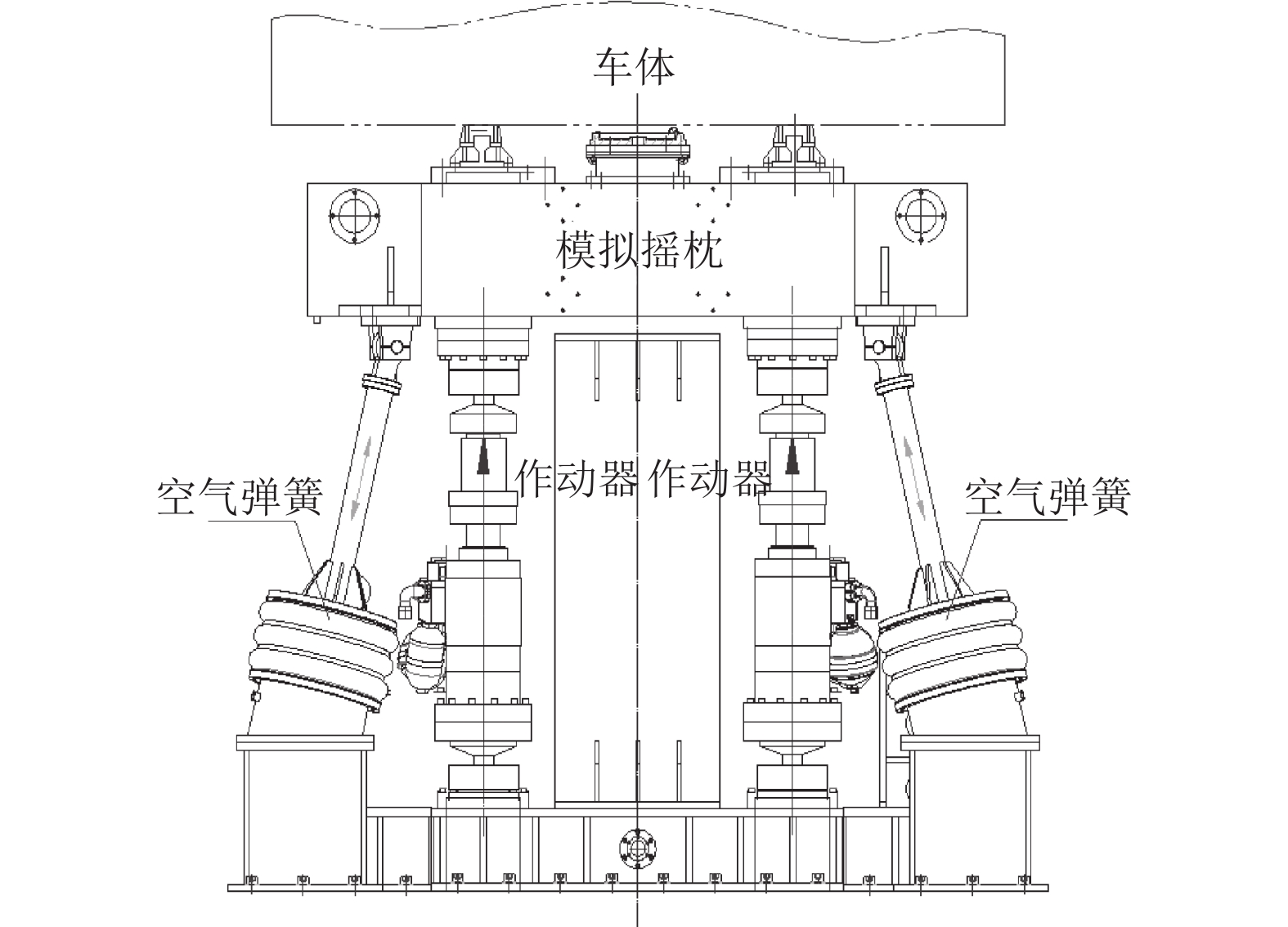
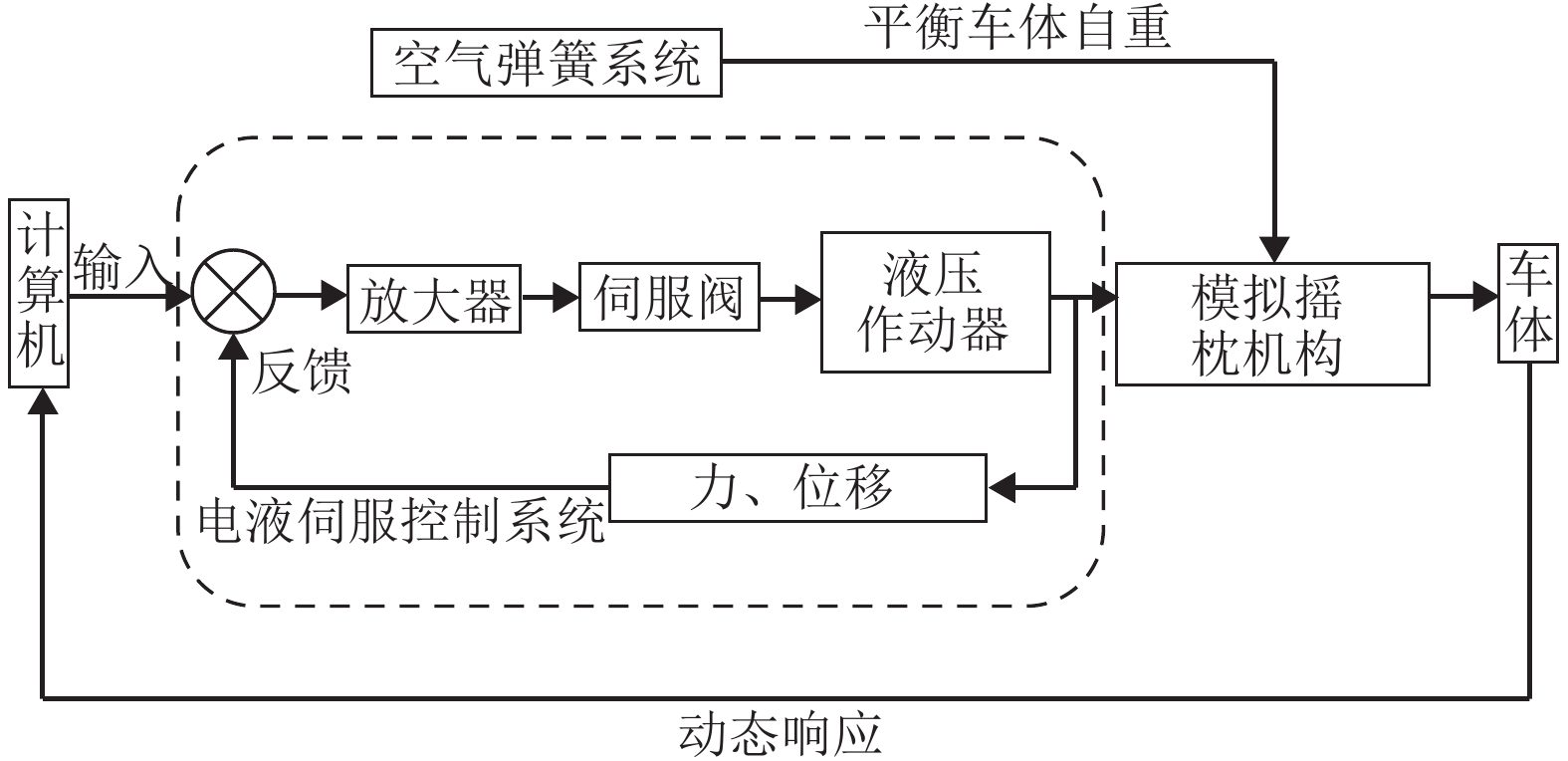
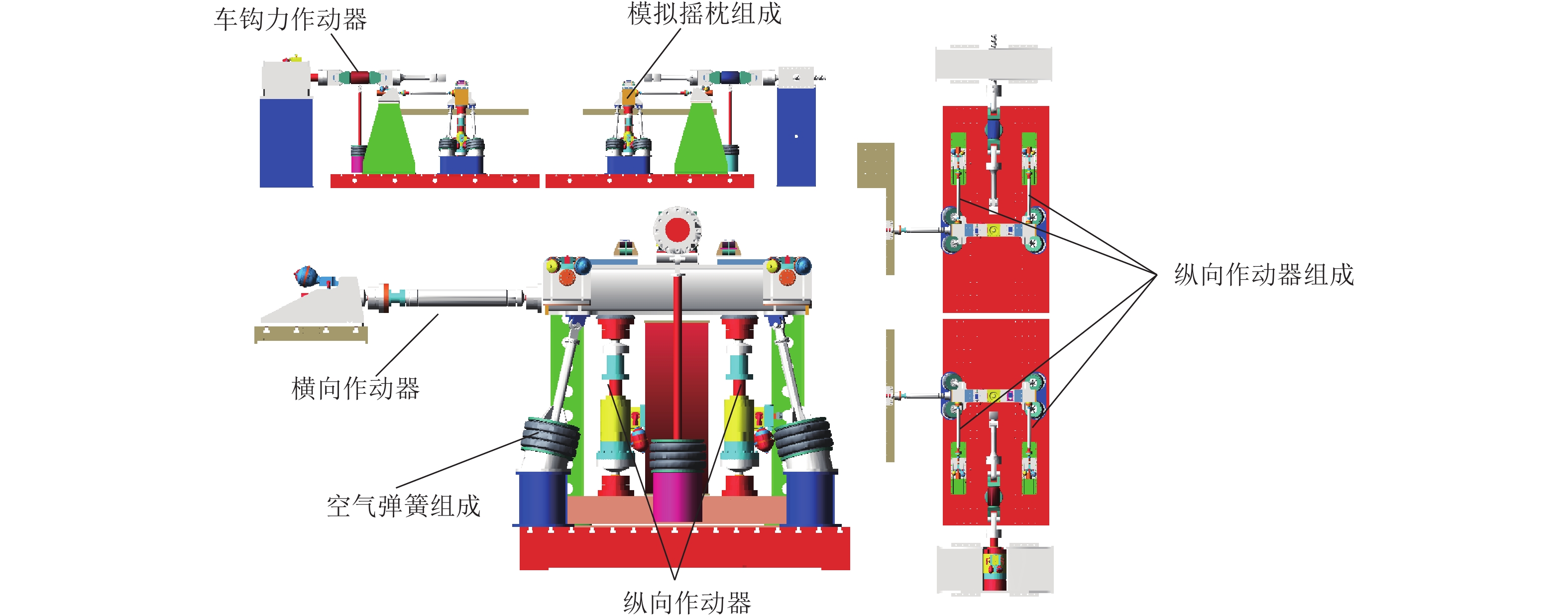
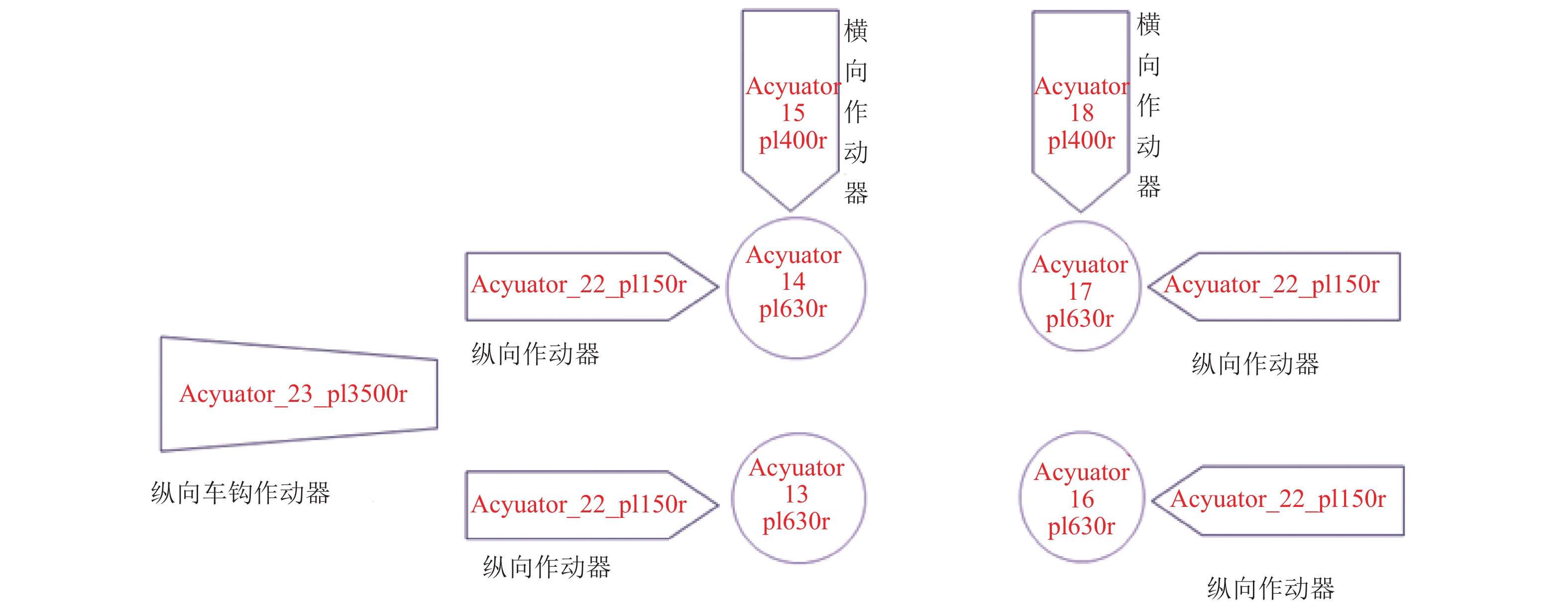
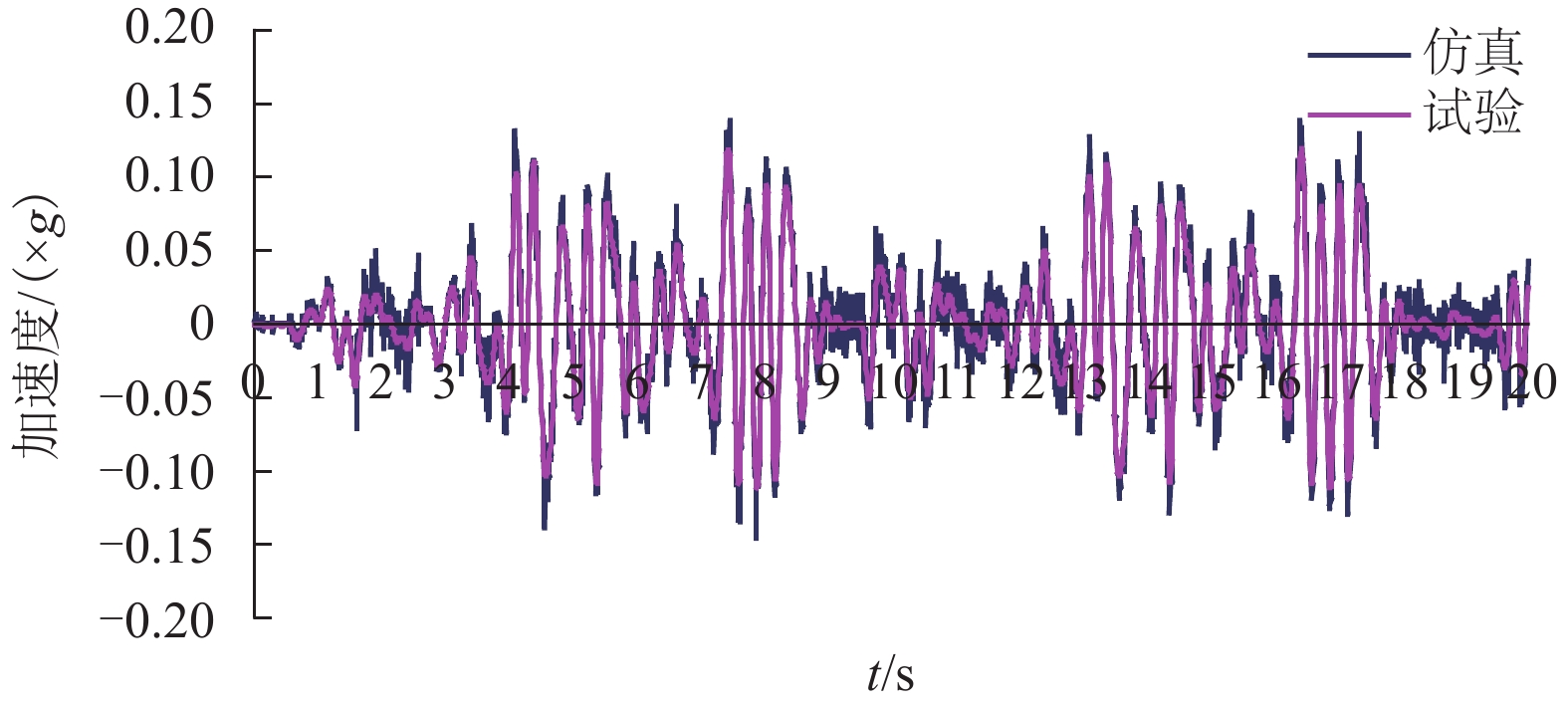
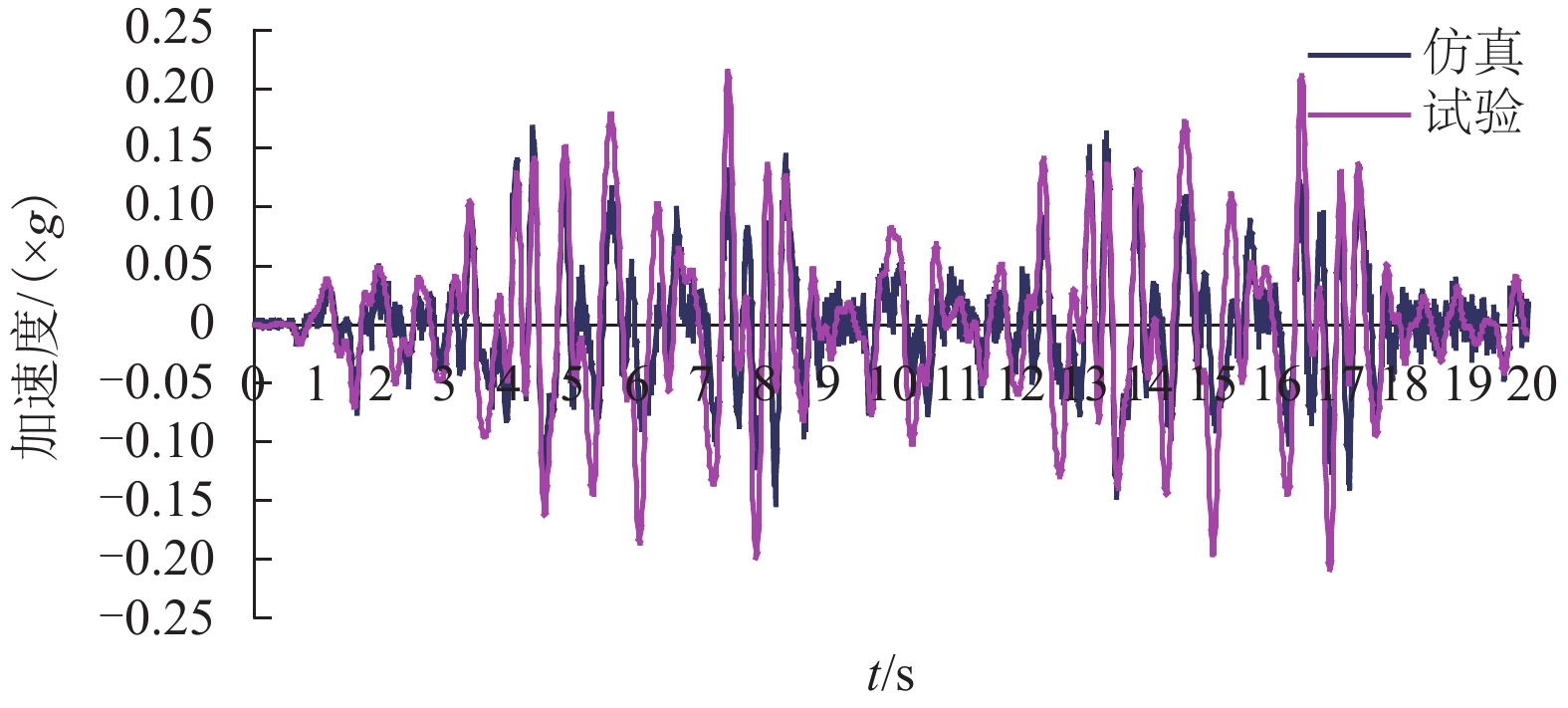
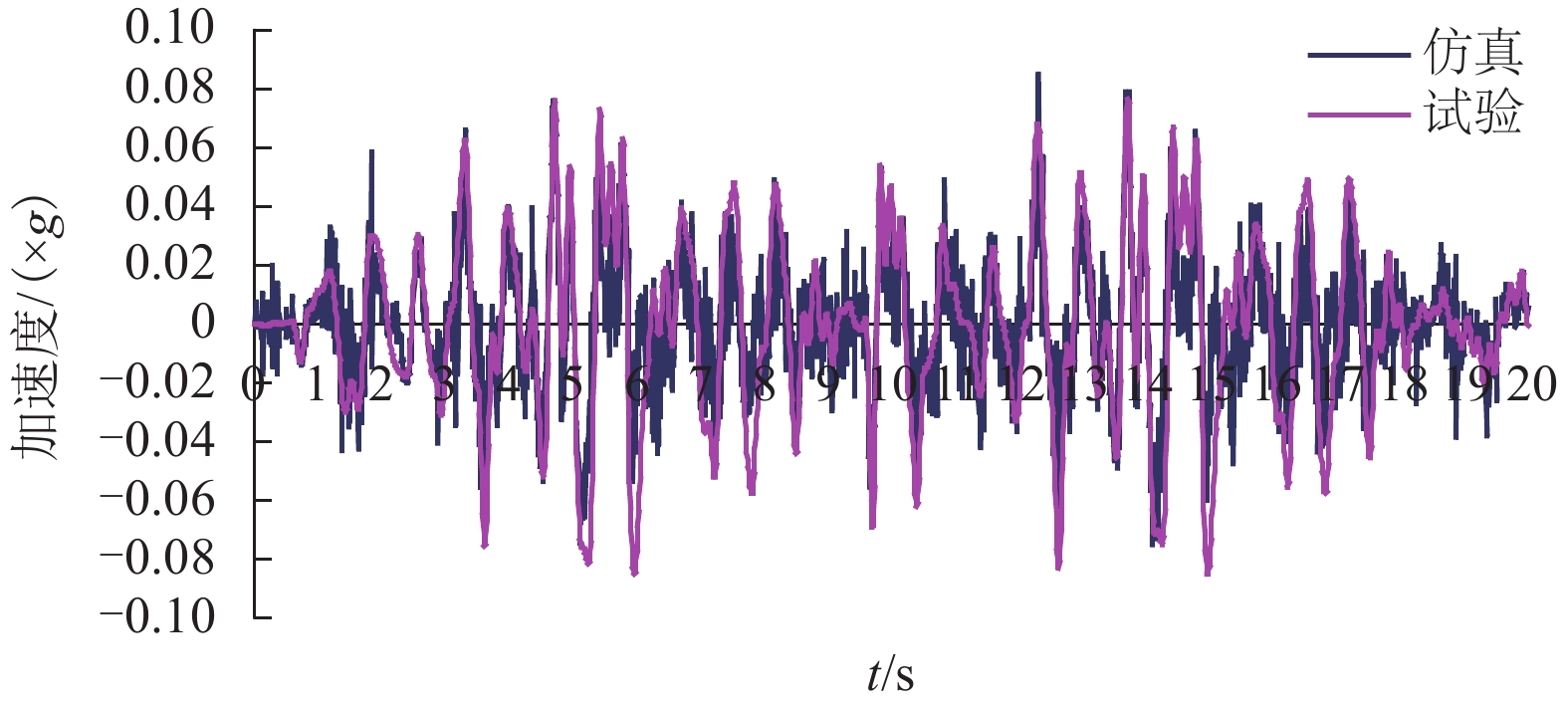
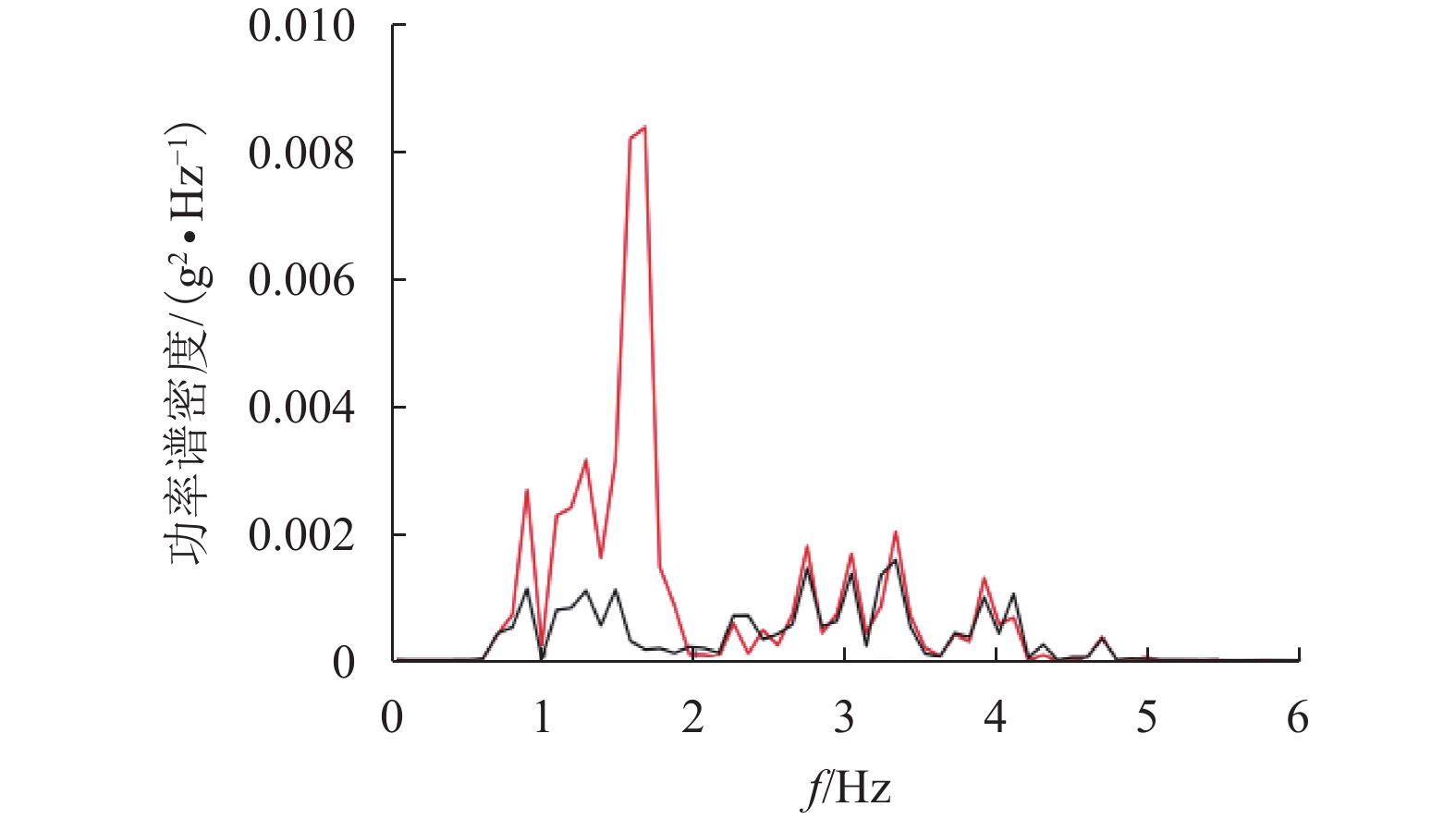
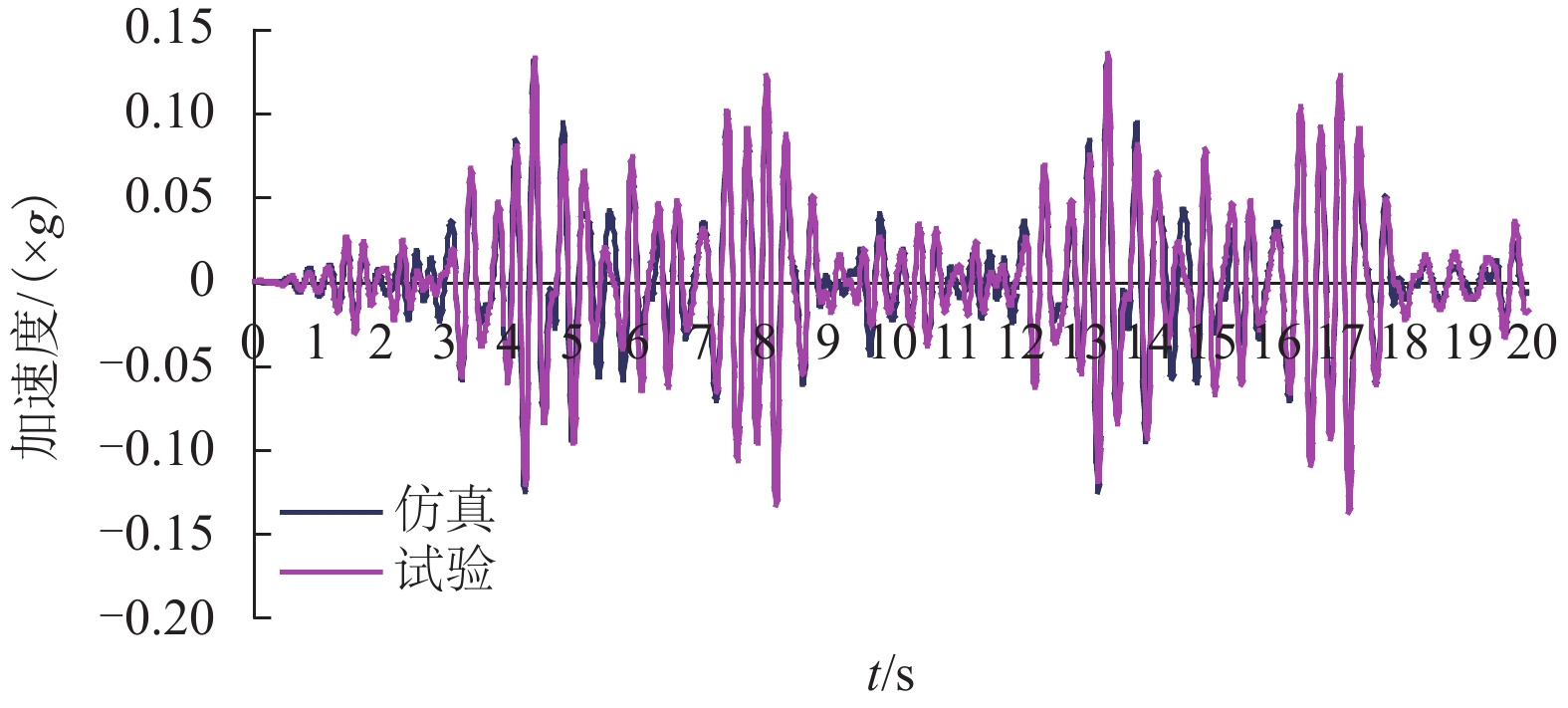
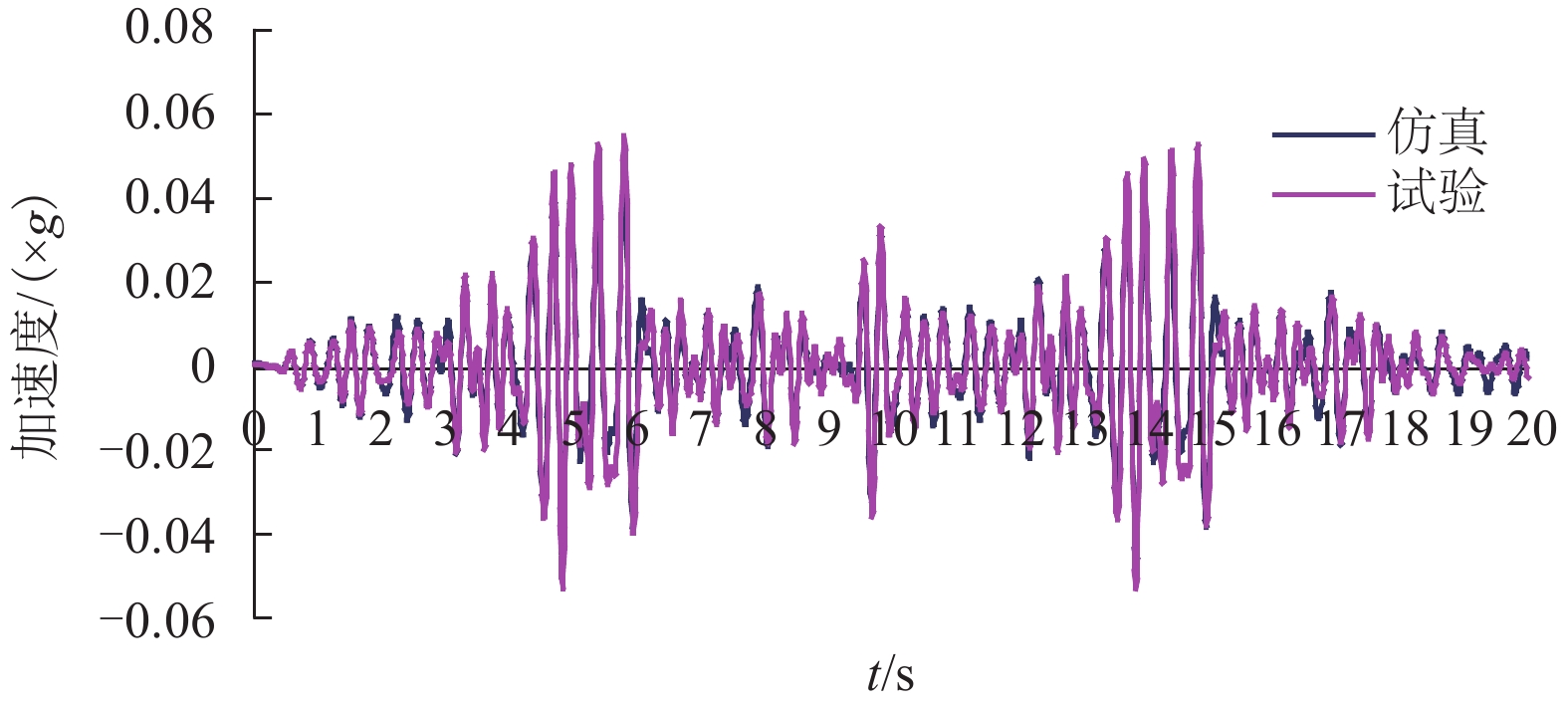
摘要: 针对大系统仿真分析方法与试验结果出现偏差问题，基于实际线路测试数据，以车体子系统为仿真对象，辅助于模拟台架的试验数据，建立了26个自由度的多体仿真模型，实现了车体线路动态响应的仿真计算. 结果表明：摇枕垂、横向加速度响应结果仿真与试验RMS （root mean square）误差最大值为9%. 在1.5～15.0 Hz主要频率段，车体枕梁垂、横向振动加速度的试验结果和仿真结果的RMS误差低于8.57%，车体关键焊缝仿真与试验的动应力响应波形基本一致. 通过与试验结果的对比验证，仿真结果基本反映了车体在实际线路运行时的动态响应情况.Abstract: For resolving errors between a simulation analysis and the test results of a large system, a multi-body simulation model of a railway wagon with 26 degrees of freedom was created using test data from a real test rig on a railway track and by incorporating the wagon body’s subsystems into the simulation object in order to realise a simulation calculation of the dynamic response of the railway wagon. The results show that the maximum RMS (root mean square) error between the simulation and the test of the wagon body bolster’s vertical and lateral vibration acceleration is 9%. Furthermore, the RMS error between the simulation and test of the wagon body bolster’s vertical and lateral vibration acceleration is less than 8.57% in the 1.5–15.0 Hz frequency range. Finally, the response signal waveforms of the dynamic stress of the simulation and that of the wagon body’s key welds are almost identical. The comparison and validation of the simulation and test results show that the simulation results substantially reproduce the dynamic response conditions of the railway wagon running along a railway track.
-
Key words:
- rails /
- dynamic simulation /
- simulation and test /
- full-scale fatigue test rig
-
无砟轨道具备高平顺性、高稳定性等诸多优势，是我国高速铁路首选的轨道型式，其中，纵连式无砟轨道占比较大，具备竖向多层、纵向连续等结构特征. 纵连板式无砟轨道的连续式轨道板和底座受温度影响很大，使得轨道结构在面临复杂气候条件时的适应性较差[1]，尤其是在路桥过渡段区域，端刺锚固结构会导致轨道结构受力及变形状况更加复杂. 据现场调研显示，CRTS Ⅱ型板式无砟轨道在路桥过渡段区域的上拱及层间离缝病害更加频繁，对线路平顺性造成较大破坏，严重影响了行车安全和稳定性. 因此，有必要针对路桥过渡段区域的结构受力及上拱特征进行研究.
目前，针对纵连板式无砟轨道纵向力及上拱问题开展了较多研究. 张鹏飞[2]研发了CRTS Ⅱ型板式无砟轨道纵向力分析系统，对桥上无砟轨道无缝线路在复杂荷载作用下的纵向受力与变形规律进行分析；戴公连等[3]通过实测获取的无砟轨道及桥梁温度数据施加荷载，分析大跨桥上无砟轨道纵向受力特征；徐庆元等[4]研究高速铁路纵连板桥上无砟轨道纵向力学特性，并与单元板进行对比. Zhang等[5]通过热流固耦合分析的方式，研究日照辐射下纵连板式无砟轨道温度场时空分布特征，以及轨道结构内力分布与结构变形特征；高亮等[6]采用有限元内聚力单元模拟的方式，研究CRTSⅡ板式无砟轨道不同层间及板间内聚力参数对无砟轨道上拱变形的影响；周凌宇等[7]通过制作的三跨无砟轨道-简支梁桥结构1/4缩尺模型，研究循环温度荷载作用下梁端位置的无砟轨道层间离缝发展规律；钟垚等[8]研究CRTSⅡ型板式无砟轨道在持续高温作用下的层间离缝发展规律；赵国堂等[9]建立了CRTSⅡ型板式无砟轨道全过程三维渐进损伤力学模型，发现层间界面离缝主要从主剪切型损伤区域开始，且损伤和离缝发展存在继承性.
综上所述，现有纵连板式无砟轨道纵向受力特征的研究主要关注桥梁基础上的钢轨及无砟轨道受力及变形规律，而针对结构及受力机理更加复杂的路桥过渡段区域的无砟轨道纵向力分布特征的研究仍存在不足. 除此之外，现有研究在分析纵连板式无砟轨道的上拱问题时，较少结合路桥过渡段锚固结构变形的影响. 因此，本文建立轨道-桥梁-端刺-路基一体化有限元模型，在纵连板式无砟轨道板间及层间建立基于双线性内聚力的黏结单元，对温度荷载作用下路桥过渡段纵连轨道板纵向力分布特征以及上拱机理进行研究.
1. 轨道-桥梁-端刺-路基空间耦合模型
1.1 有限元模型及参数
路桥过渡段纵连板式无砟轨道一体化有限元模型包括轨道结构、桥梁段、端刺锚固结构及路基等. 其中：轨道结构从上至下依次为钢轨、扣件、预制轨道板、宽窄接缝、水泥乳化沥青（CA）砂浆层、底座（路基段为支承层）；桥梁段包括 2跨32.6 m简支梁、桥台、桥墩、侧向挡块及剪力齿槽；端刺锚固结构包括摩擦板、主端刺及过渡板；路基分为2部分，过渡段端刺范围内靠近桥台侧路基采用掺水泥的级配碎石进行填筑，其后采用与普通路基段相同的AB组填料填筑. 纵连轨道结构底座与桥面之间设“两布一膜”滑动层，底座与端刺摩擦板之间设2层土工布，均采用面与面接触方式模拟，摩擦系数分别取0.35和0.70；端刺与路基土体之间同样采用面与面接触关系模拟，摩擦系数参考桩土接触分析取0.30[2]. 模型轨道结构两端以及路基一侧采用对称约束，钢轨扣件、剪力齿槽、墩台刚度采用弹簧阻尼单元模拟，其余部件均采用实体单元模拟. 钢轨弹性模量为210 GPa，泊松比为0.3，线膨胀系数为1.18 × 10−5 ℃−1. 轨道板及宽窄接缝、桥梁及墩台材料为C55混凝土，底座为C40混凝土，支承层及端刺为C30混凝土，弹性模量依次为35.5、32.5、30.0 GPa，密度、泊松比和线膨胀系数参数一致，分别取
2500 kg/m3、0.20、1.0 × 10−5 ℃−1. CA砂浆层密度为2400 kg/m3，弹性模量为8.5 GPa，泊松比为0.34，线膨胀系数为1.3 × 10−5 ℃−1. 模型总体示意如图1所示. 路基土体材料[2,10]的参数取值如表1所示.
图 1 纵连板式无砟轨道-桥梁-端刺-路基空间耦合模型Figure 1. Spatial coupling model of longitudinally connected ballastless track slab-bridge-end spine-subgrade表 1 路基模型计算参数Table 1. Calculation parameters of subgrade model部件 密度/（kg•m−3） 弹性模量/MPa 泊松比 黏聚力/（kN•m−2） 剪切角/（°） 剪切膨胀角/（°） 级配碎石 2200 200 0.20 35 30 5 AB 组填料 2100 120 0.25 15 20 8 1.2 双线性内聚力模型
为探究路桥过渡段区域纵连板式无砟轨道在温度荷载及下部锚固结构变形双重作用下的结构受力变形特征及上拱演化机理，在轨道板与宽窄接缝及CA砂浆层之间的接触界面采用双线性内聚力单元模型，以表征其损伤开裂关系.
1） 内聚力损伤判定准则
本文模型计算选取二次名义应力准则（Quads）作为层间内聚力界面损伤萌生的判断条件，如式（1）.
(⟨tn⟩tn,0)2+(tsts,0)2+(tttt,0)2=1, (1) 式中：tn,0、ts,0、tt,0分别为抗拉强度、第一剪切强度和第二抗剪强度；tn为法向牵引力，〈tn〉表示法向应力为负时内聚力黏结界面为受压状态，不发生损伤；ts、tt分别为切向的第一、第二切向牵引力.
2） 损伤演化机理
基于弹塑性断裂力学理论[11-14]，双线性内聚力模型定义黏结面之间法向和切向的牵引-分离作用关系[15]如图2所示. 图中： tτ为切向牵引力，点Aτ、Am、An分别为切向、复合模型、法向的损伤起始点，点B表示界面完全损伤失效点，点Bτ、Bm、Bn分别为切向、复合模型、法向的界面完全损伤失效点，δτ,0、δm,0、δn,0分别为切向、有效相对位移、法向的损伤起始时的相对位移，tτ,0、tm,0、tn,0为分别切向、有效相对应力、法向的极限强度，δτ,f、δm,f、δn,f分别为切向、有效相对位移、法向完全破坏时的相对位移，Gn,C、Gs,C为法向和切向2种断裂模式下的界面断裂能，GC为临界断裂能.
图2中路径OAn与OAτ分别为黏结面法向张拉与切向剪切2种牵引-分离准则的初始阶段，此阶段黏结面损伤尚未产生，界面应力与应变关系为线弹性特征，牵引力-分离位移的关系如式（2）.
[tntstt]=[KnnKnsKntKnsKssKstKntKstKtt][δnδsδt], (2) 式中：Knn、Kss、Ktt分别为法向、第一与第二切向的界面刚度，Kns、Knt、Kst均为0，δn、δs、δt分别为法向、第一与第二切向的相对位移.
图2中AnBn与AτBτ分别为黏结面法向与切向破坏的损伤演化阶段，点A表示损伤起始点，此时内聚力接触面开始萌生损伤裂纹，点B表示界面完全损伤失效. 引入损伤因子D（式（3））来评估界面损伤程度，D取值范围为0～1：当D=0时，表明界面没有伤损；当D=1时，表明界面完全伤损，层间脱黏.
D=δm,f(δm,max−δm,0)δm,max(δm,f−δm,0), (3) 式中：δm,max为加载过程中能达到的最大有效位移.
此时内聚力损伤演化阶段的牵引-相对位移关系可表示为
{ tn=(1−D)knδn,δn⩾0ts=(1−D)ksδs,tt=(1−D)ktδt. (4) 损伤演化过程伴随着能量的释放，因此，本文采用基于能量（断裂能）的BK损伤演化准则来判定伤损演化后内聚力接触面是否脱黏. 断裂能数值上等于牵引力-相对位移曲线下所围成的面积. 临界断裂能[16]为
GC=Gn,C+(Gs,C−Gn,C)(GSGn+Gs)η, (5) 式中：η为混合系数，Gn为法向断裂模式下的界面断裂能，Gs为切向断裂模式下的界面断裂能.
本文在轨道板与宽窄接缝间以及轨道板与CA砂浆层间设置了双线性内聚力单元表征板间及层间接触界面的损伤状况，内聚力单元的参数取值[17-19]如表2所示.
表 2 内聚力模型参数Table 2. Cohesive force model parameters黏结界面 法向抗拉
强度/MPa剪切强度/MPa 法向刚度/
（MPa•mm−1）切向刚度/
（MPa•mm−1）法向断裂
能/（J•m2）切向断裂
能/（J•m2）轨道板与宽窄接缝 1.700 1.600 500.0 150.0 35.00 15.20 轨道板与 CA 砂浆层 1.792 0.956 716.8 62.9 25.24 18.70 1.3 模型验证
为确保本文模型计算结果的准确性和可靠性，将本模型计算结果与文献[2]和文献[20]计算结果对比，并进行模型验证. 选取与文献[2,20]相同的工况进行加载，提取轨道板及底座的最大纵向应力值进行对比. 在荷载为轨道结构正温梯90 ℃/m、桥梁结构整体升温40 ℃工况下，本模型计算得到的轨道板最大纵向应力为−19.05 MPa，底座板最大纵向应力为−11.98 MPa，与文献计算结果对比如表3所示.
表 3 模型验证计算结果对比Table 3. Comparison of model verification and calculation resultsMPa 由表3可知：本文模型计算得到轨道板与底座最大纵向应力数值与文献计算结果较为吻合，且应力最大值位置与文献保持一致. 因此，本文建立的模型正确、可靠.
2. 路桥过渡段轨道板纵向力分布特征
本文对轨道及桥梁分别施加温度梯度及整体温度荷载，研究路桥过渡段区域的纵连轨道的纵向力分布特征. 轨道板温度梯度的取值[21-23]为95、85、75、65 ℃/m. 由于混凝土材料为不良导热材料[24]，故不考虑CA砂浆层和底座/支承层间的温度差异，上述部件的荷载取值与正温梯下轨道板底面的温度值相同. 桥梁整体升温取为造成轨道板不同正梯度时相对应的环境温度升温荷载值. 不同温度梯度条件下轨道板的纵向力分布特征如图3所示.
图 3 不同温度梯度条件下轨道板纵向应力Figure 3. Longitudinal stress of track slab under different temperature gradient conditions由图3可知：温度梯度大小对轨道板的受力有很大影响，温度梯度越大，轨道板的纵向压应力越大，正温梯为95、85、75、65 ℃/m时，轨道板的纵向压应力最大值分别为19.91、18.38、17.08、14.21 MPa，出现在过渡板末端与支承层结合位置处；根据纵向应力在路桥过渡段的分布特征可以看出，桥梁区段轨道板纵向应力水平总体最小，摩擦板区域稍大，主端刺区域最大. 轨道结构和桥面之间采用“两布一膜”滑动层，两者之间摩擦系数较小，轨道结构在纵向上变形相对自由，所以轨道板纵向应力总体水平较低. 轨道结构在过渡段端刺区域比较复杂，其传力机制如图4所示.
由图4可知：在纵向传力机制上，摩擦板与底座之间是摩擦状态，两者之间的摩擦系数较大，是桥梁与主端刺之间的过渡区域，轨道板纵向应力相比桥梁段稍大；到主端刺区域，轨道结构底座与主端刺共同浇筑，两者之间连结牢固，利用主端刺结构作为轨道结构纵向位移的主要限位装置，前部桥梁段和摩擦板段的纵向应力在此积聚，造成轨道板的纵向应力较大；4种工况下此界面轨道板的纵向力增幅都在21%左右.
由于纵向传力机制的变化，底座的纵向位移受到限制，但是轨道板、CA砂浆层、底座之间依靠黏结形成的3层结构往往会因为黏结力不足导致层间错动，产生轨道板与CA砂浆层之间的层间离缝. 在过渡板与支承层结合部位置处，轨道板的纵向应力出现了先增大后减小的状况，极端95 ℃/m温梯下从19.91 MPa减小至14.61 MPa，降幅达27.2%. 这是由于过渡板与支承层都受正温度梯度荷载的作用产生膨胀变形，两者相互挤压，同时过渡板一侧相对支承层一侧的纵向应力更大，支承层被过渡板挤压变形应力被释放了一部分，所以过渡板到支承层轨道板的纵向应力先增大后减小.
由以上分析可知，路桥过渡段区域的轨道板纵向应力分布复杂，纵向变形情况多变，尤其当路基土体劣化与端刺产生脱空状况下，土体的锚固能力大大下降，继而出现端刺纵向位移超过3 mm限值要求的情况. 端刺与路基接触部分的土体脱空劣化越严重，所导致的端刺纵向超限位移就越大. 本文选择端刺纵向位移限值3.00 mm、超限位移4.50、6.00 mm 3种工况在极端正温梯荷载作用下的轨道板纵向应力分布，与正常服役工况进行对比分析，如图5所示.
图 5 端刺超限位移下轨道板纵向应力分布Figure 5. Longitudinal stress distribution of track slab under over-limit displacement of end spine从图5中可以看出：随着主端刺纵向位移逐渐增加，轨道板在端刺区域的纵向应力水平整体呈现下降的趋势，尤其是在主端刺区域，当位移超过3 mm后，纵向压应力下降较大，这表明端刺结构的限位能力大大下降；在结合部位置处，随着端刺位移增加，轨道板的纵向压应力最大值却在增加，如图6所示.
从图6可以看出，在纵向位移达到6.0 mm时，结合部轨道板纵向压应力为24.06 MPa，相对的下部支承层纵向压应力为18.55 MPa，接近支承层混凝土抗压强度标准值20.10 MPa，表明随着限位能力的降低，结合部支承层受到的挤压状况逐渐严重，混凝土结构挤碎掉块的风险逐渐增大.
图7所示为某一纵连板式无砟轨道路桥过渡段现场工点状况，展示了结合部位状况及主端刺区域轨道层间黏结状况.
由图7（a）可以看出：结合部位在纵向力的作用下混凝土产生较大的挤压掉块；上部宽窄接缝和层间离缝都有修补痕迹，表明板间及层间都产生因上拱导致的损伤. 从图7（b）可以看出：主端刺上方的轨道板与CA砂浆层之间出现层间离缝，在摩擦板区域轨道板与CA砂浆层之间黏结良好，并无层间离缝产生.
3. 路桥过渡段轨道板上拱机理
过渡板与支承层结合部位是路桥过渡段纵向应力及位移的敏感区域，最容易出现挤压破坏及上拱变形病害，从而影响上部轨道结构层间及板间的黏结状态. 而层间及板间良好的黏结是保证纵连板式无砟轨道纵向均匀传力，防止其上拱的重要条件. 因此，本文建立过渡板-支承层区段无砟轨道层间及板间设置内聚力黏结，分析结合部位挤压上拱对上部无砟轨道板间宽窄接缝黏结及层间黏结的影响.
3.1 结合部上拱对宽窄接缝黏结影响
由前文可知，极端温度荷载作用下，端刺结构在不同纵向位移下造成的结合部上拱幅值分别为1.40、2.01、2.66、3.80 mm. 4种工况下的结合部上拱位置上方宽窄接缝的板间黏结状态如图8所示. 图中：白色表示宽窄接缝混凝土，左右两侧彩色部分为内聚力黏结单元，黏结状态采用刚度下降率（取值0～1，意义与1.2节中的损伤因子相同，脱黏失效的单元会自动删除）表示[25].
图 8 不同上拱幅值下宽窄接缝黏结损伤状况Figure 8. Bonding damage status of wide and narrow joints under different arching amplitudes由图8可以看出：上拱位置的宽窄接缝损伤情况随上拱幅值的增加而增加，当上拱位移为1.40 mm时（端刺纵向位移小于3 mm），内聚力单元损伤较小，宽窄接缝板间的黏结状态较好；当上拱位移为2.01 mm时（端刺纵向位移刚好3 mm），内聚力单元损伤开始蔓延并出现较严重的损伤单元，宽接缝两侧相比窄接缝的损伤更大，呈现从上至下损伤逐渐减小的趋势；当上拱位移在2.66 mm和3.80 mm时（端刺纵向位移大于3 mm），宽窄接缝与相邻轨道板之间已经出现了部分区域脱黏的状况；宽窄接缝与过渡板一侧轨道板的黏结区域脱黏相对严重，另外一侧相对较小；从上往下宽接缝一侧的损伤脱黏最为严重，其次为宽窄交接的位置处，窄接缝的一侧的损伤脱黏出现最晚.
3.2 结合部上拱对层间黏结影响
结合部位上拱对层间黏结破坏位置的影响示意如图9所示，不同的上拱幅值下对层间黏结破坏状况如图10所示.
图 10 不同上拱幅值下层间黏结损伤状况（变形放大100倍）Figure 10. Bonding damage status between layers under different arching amplitudes （deformation magnified 100 times）从图9可以看出，过渡板支承层结合部上拱对砂浆层层间黏结的破坏主要集中在拱起范围的末端以及结合部位拱起峰值处. 当上拱幅值为1.40 mm时，层间黏结状态良好，并无损伤出现，故并未在图10中列出. 由图10（a）可知：当上拱幅值为2.01 mm时，拱起范围的末端板边位置开始出现黏结损伤，但是损伤的范围很小；结合部位拱起峰值处并无损伤出现. 由图10（c）可知：当上拱幅值为2.66 mm时，层间黏结损伤的区域开始扩大，拱起范围的末端已经产生了较大范围的黏结损伤，板中部分区域开始出现了脱黏失效；结合部宽窄接缝下部上拱峰值区域也开始出现黏结损伤；黏结损伤区域占整块板的18.4%，脱黏区域占0.3%. 由图10（d）可知，当上拱幅值达到3.80 mm时，拱起范围末端的黏结损伤区域以及黏结失效区域进一步扩大，黏结损伤区域占整块板的30.6%，脱黏区域占1.3%.
4. 结 论
1） 轨道板纵向应力与温度呈正相关，其在主端刺区域及过渡板支承层结合部纵向应力水平最高，极端正温梯95 ℃/m下应力最大值为19.91 MPa；其次为摩擦板区域，桥梁段最小. 轨道板纵向应力分布特征与端刺锚固结构各组成的限位能力相对应.
2） 随着端刺纵向位移的增加，轨道板在端刺区的纵向应力降低，结合部支承层的纵向应力随之增加，表明端刺的限位能力降低，结合部位挤压的状况愈发严重；当纵向位移达到6 mm时，结合部支承层的纵向压应力达到18.55 MPa，结构压坏风险极高.
3） 随着端刺纵向位移增加，过渡板支承层结合部上拱逐步增大，其上方轨道结构板间及层间黏结状态不断降低，甚至出现了脱黏的状况，层间黏结损伤也在拱起范围的末端和上拱峰值处不断蔓延扩大，极大加剧了轨道上拱病害的风险.
-
图 12 模拟摇枕振动加速度响应的PSD分析结果
Figure 12. PSD analysis results of acceleration response of dummy bolster
图 13 车体枕梁垂向加速度对比的仿真结果
Figure 13. Comparison of vertical acceleration of body bolster with the simulation results
图 14 车体枕梁横向加速度对比的仿真结果
Figure 14. Comparison of lateral acceleration of body bolster with the simulation results
表 1 模态频率结果对比
Table 1. Results comparison of modal frequency
振型 系统试验模态 系统仿真模态 侧滚 1.25 1.45 扭转 4.52 4.66 
下载: 导出CSV
表 2 车体枕梁振动加速度的统计结果
Table 2. Statistical results of acceleration of body bolster
测点编号 RMS RMS误差/% 试验 仿真 AZN11 0.040 0.038 4.25 AYN11 0.014 0.013 8.57
下载: 导出CSV
-
来亚南. C_(80B)型车车体疲劳寿命分析[J]. 机械设计与制造,2015(8): 105-109. doi: 10.3969/j.issn.1001-3997.2015.08.028LAI Yanan. Fatigue analysis of C_(80B) freight train[J]. Machinery Design & Manufacture, 2015(8): 105-109. doi: 10.3969/j.issn.1001-3997.2015.08.028 徐刚,周鋐,陈栋华,等. 基于虚拟试验台的疲劳寿命预测研究[J]. 同济大学学报(自然科学版),2009,37(1): 97-100.XU Gang, ZHOU Hong, CHEN Donghua, et al. Virtual test rig based study on fatigue life prediction[J]. Journal of Tongji University (Natural Science), 2009, 37(1): 97-100. FERRY W B, FRISE P R, ANDREW G T, et al. Combining virtual simulation and physical vehicle test data to optimaze durability testing[J]. Fatigue and Fracture of Engineering Materials and Structures, 2002, 25: 1127. doi: 10.1046/j.1460-2695.2002.00605.x 陈栋华. 轿车底盘零部件耐久性虚拟试验理论与方法研究[D]. 上海: 同济大学, 2007 董明明,顾亮. 履带车辆非线性悬挂系统的ADAMS仿真[J]. 北京理工大学学报,2005,25(8): 670-673. doi: 10.3969/j.issn.1001-0645.2005.08.004DONG Mingming, GU Liang. Simulation of nonlinear tracked vehicle suspension with ADAMS[J]. Transactions of Beijing Institute of Technology, 2005, 25(8): 670-673. doi: 10.3969/j.issn.1001-0645.2005.08.004 石琴,王涛,张代胜,等. 大客车车身骨架结构动应力仿真计算[J]. 汽车工程,2011,33(5): 433-437.SHI Qin, WANG Tao, ZHANG Daisheng, et al. The simulation calculation of dynamic stress in bus body frame structure[J]. Automotive Engineering, 2011, 33(5): 433-437. 曾祥坤,田红旗. 散粒货物对铁路敞车端墙侧压力研究[J]. 铁道学报,2007,29(4): 32-37. doi: 10.3321/j.issn:1001-8360.2007.04.007ZENG Xiangkun, TIAN Hongqi. Rsearch of lateral pressure of granular cargo on end walls of open wagon[J]. Journal of the China Railway Society, 2007, 29(4): 32-37. doi: 10.3321/j.issn:1001-8360.2007.04.007 赵方伟,付秀琴,张弘,等. 散粒货物对敞车静侧压力的分布规律研究[J]. 铁道机车车辆,2016(6): 42-45,48. doi: 10.3969/j.issn.1008-7842.2016.06.11ZHAO Fangwei, FU Xiuqin, ZHANG Hong, et al. Static lateral pressure distribution study of granular cargo on gondola car[J]. Railway Locomotive & Car, 2016(6): 42-45,48. doi: 10.3969/j.issn.1008-7842.2016.06.11 刘宏友,李向伟,邓爱建等. C_(70E)型通用敞车模态试验研究[J]. 铁道车辆,2015,53(12): 32-36. doi: 10.3969/j.issn.1002-7602.2015.12.007LIU Hongyou, LI Xiangwei, DENG Aijian, et al. Research on modal test of C_(70E) general gondola car[J]. Rolling Stock, 2015, 53(12): 32-36. doi: 10.3969/j.issn.1002-7602.2015.12.007 缪炳荣. 基于多体动力学和有限元法的机车车辆结构疲劳仿真研究[D]. 成都: 西南交通大学, 2006 王勇,曾京,吕可维. 三大件转向架货车动力学建模与仿真[J]. 交通运输工程学报,2003,3(4): 30-34. doi: 10.3321/j.issn:1671-1637.2003.04.008WANG Yong, ZENG Jing, LU Kewei. Dynamic modeling and simulation of three-piece bogie freight car[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4): 30-34. doi: 10.3321/j.issn:1671-1637.2003.04.008 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 400
- HTML全文浏览量: 198
- PDF下载量: 11
- 被引次数: 0