Creep Buckling Analysis of Concrete-Filled Steel Tubular Columns
-
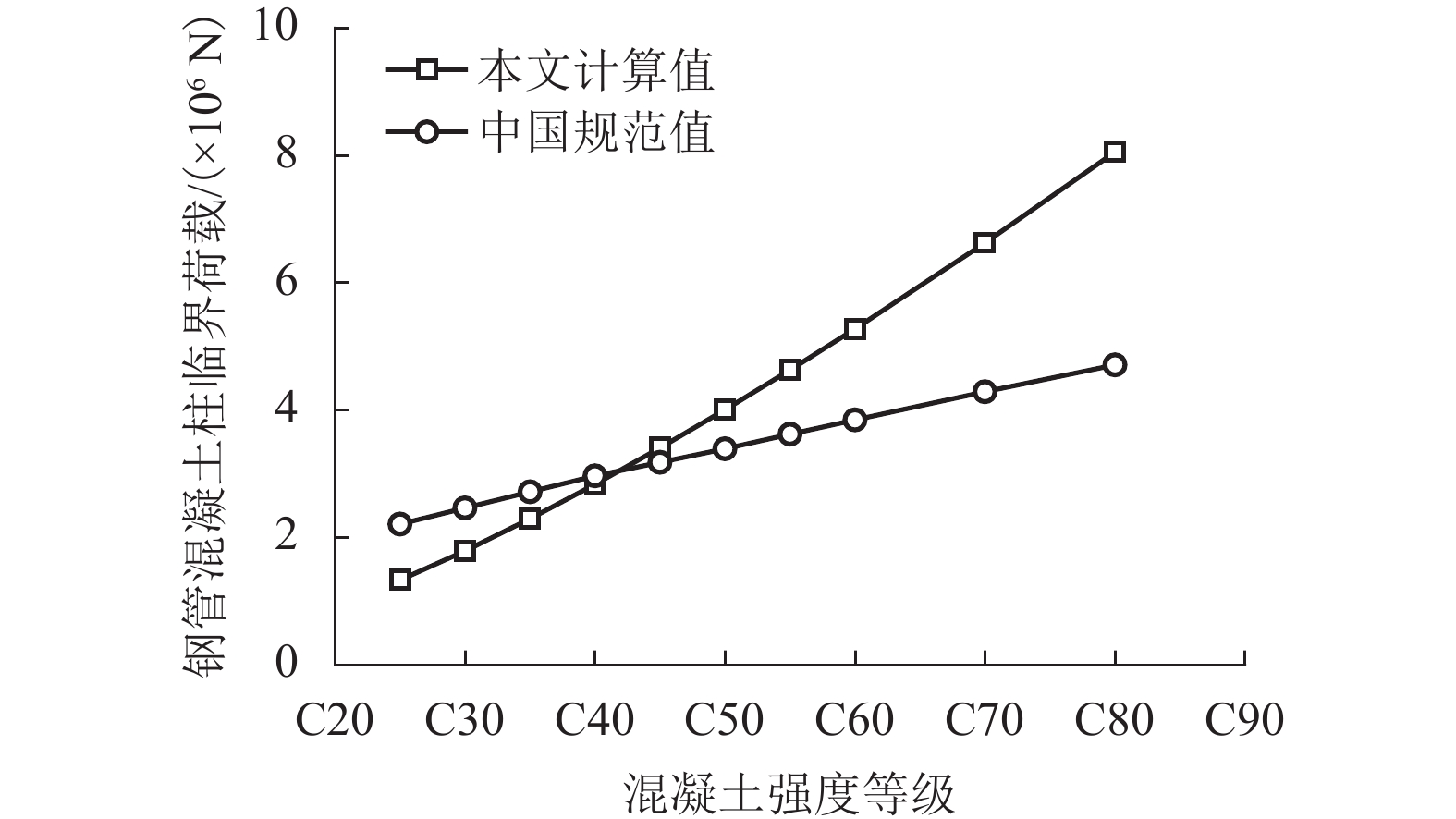
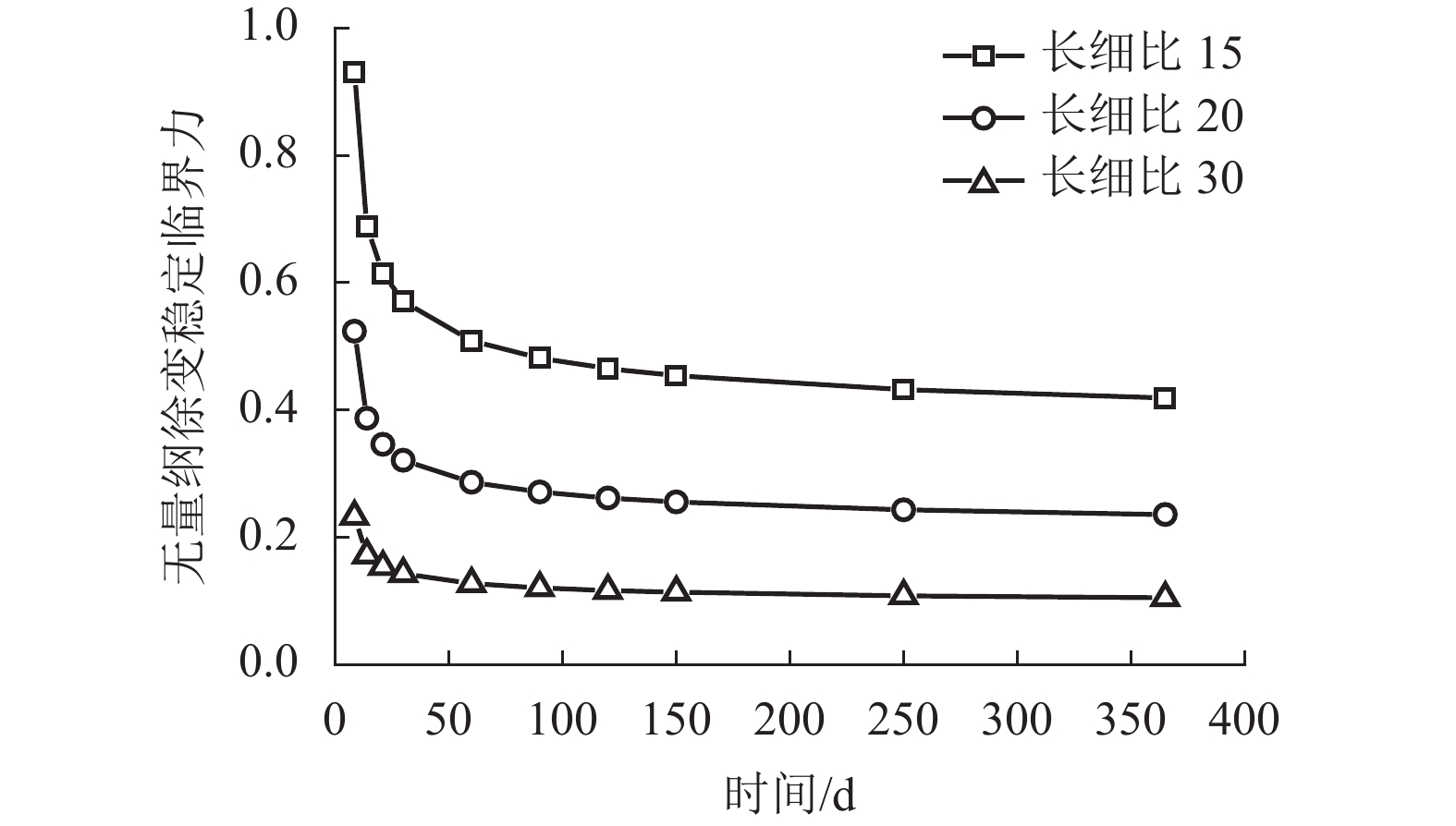
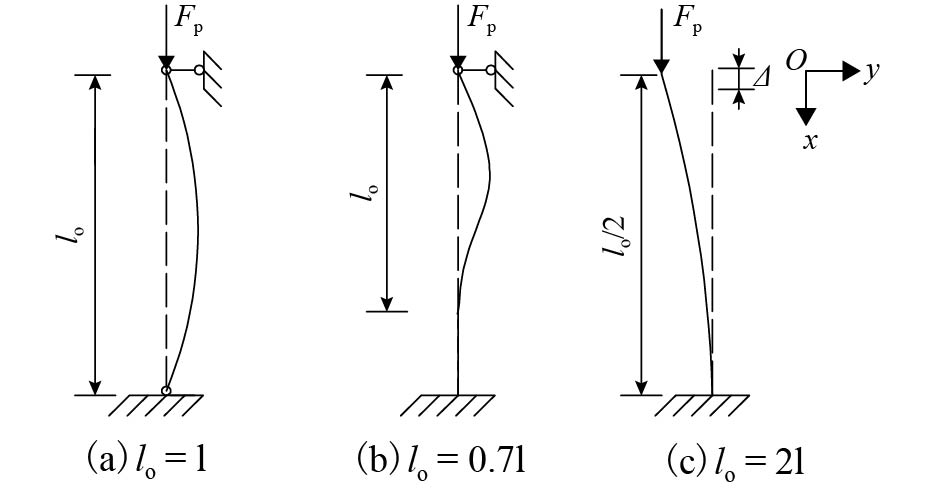
摘要: 为了探讨混凝土徐变对钢管混凝土柱轴向荷载作用下长期稳定性的影响，基于能量法和按照龄期调整的有效模量法，应用失稳准则，推导了考虑徐变和屈曲前变形的两端铰接、一端固定一端铰接和悬臂柱3种边界条件下的钢管混凝土柱长期稳定临界力计算公式，研究了该类柱徐变稳定临界力与核心混凝土强度的影响规律，并将规范取值与该临界力进行了对比. 研究结果表明：考虑徐变的钢管混凝土柱稳定临界力与徐变系数有关，相同计算长度但不同边界条件的该类柱徐变稳定临界力一致；核心混凝土强度的提高，会减小徐变对构件稳定临界力的影响；当按现行混凝土结构设计规范对核心混凝土强度等级低于C45的钢管混凝土柱进行设计时，应注意徐变失稳问题；钢管混凝土柱的徐变稳定承载力在前60 d下降明显且占总下降量约80%，在100 d后承载力逐渐趋于稳定.Abstract: In order to investigate the influence of concrete creep on the long-term stability of concrete-filled steel tubular (CFST) columns under axial load, based on the energy method and age-adjusted effective modulus method, the long-term stability equations for the critical force of CFST columns with different boundary conditions considering creep and pre-buckling deformation were deduced using an instability criterion. The influence of the critical force and strength of the core concrete were studied. In addition, the value of the current standard and critical loads were compared. The results show that the critical load for creep stability of CFST columns is related to the creep coefficient; CFST columns with the same calculated length but different boundary conditions have the same long-term critical load. The influence of creep on the stability of the column decreased with increasing core concrete strength. When designing CFST columns with low-strength concrete using the current code for the design of concrete structures, additional attention should be paid to the influence of creep buckling. The long-term stability of the critical forces of CFST column was reduced obviously reduced in the first 60 days, which accounts approximately for 80% of the total decline. The bearing capacity of the steel tube tends to be stabilize after 100 days.
-
图 1 不同边界条件的受压构件失稳示意
Figure 1. Buckling modes of compression columns with three common boundary conditions
图 2 管内混凝土强度与长期效应无量纲屈曲荷载关系
Figure 2. Relationship between dimensionless buckling load of long-term effects of creep and core concrete strength
图 4 无量纲徐变稳定临界力与时间曲线
Figure 4. Critical force time curve with different slenderness ratio
表 1 混凝土等级与徐变系数终极值的关系表（CEB10模型）
Table 1. Relationship between concrete grade and the ultimate value of creep factor （CEB10 model）
混凝土强
度等级徐变系数
终极值混凝土强
度等级徐变系数
终极值C15 4.145 C55 1.603 C20 3.525 C60 1.512 C25 3.085 C70 1.362 C30 2.775 C80 1.243 C35 2.325 C90 1.147 C40 2.133 C100 1.066 C45 1.832 C110 0.998 C50 1.708 C120 0.939 
下载: 导出CSV
-
UY B. Static long-term effects in short concrete-filled steel box columns under sustained loading[J]. ACI Structural Journal, 2001, 98(1): 96-104. HAN Linhai, LI Wei, BJORHOVDE R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures:members[J]. Journal of Constructional Steel Research, 2014, 100: 211-228. doi: 10.1016/j.jcsr.2014.04.016 孙宝俊,熊学玉. 钢筋混凝土柱的徐变稳定性[J]. 建筑结构,1994(3): 26-28. doi: 10.3321/j.issn:1000-6869.1994.03.001SUN Baojun, XIONG Xueyu. Creep stability of reinforced concrete column[J]. Building Structure, 1994(3): 26-28. doi: 10.3321/j.issn:1000-6869.1994.03.001 MORINO S, KSWANGUCHI J, CAO Z S. Creep behavior of concrete filled steel tubular members[C]//Proceeding of an Engineering Foundation Conference on Steel Concrete Composite Structures. Irsee: [s.n.], 1996: 514-524 NAKAI H, KURITA A, ICHINOSE L H. An experimental study on creep of concrete filled steel pipes[C]//Proceedings of 3rd International Conference on Japan Steel and Concrete Composite Structures. Fukuoka: [s.n.], 1991: 55-60 TERREY P J, BRADFORD M A, GILBERT R I. Creep and shrinkage of concrete in concrete-filled circular steel tubes[C]//Proceeding of 6th International Symposium on Tubular Structures. Melbourne: [s.n.], 1994: 293-298 BEHAN J E, O’CONNOR C. Creep buckling of reinforced concrete columns[J]. Journal of the Structural Division, 1982, 108(12): 2799-2818. DISTEFANO J N. Creep buckling of slender columns[J]. Journal of the Structural Division,ASCE, 1965, 91(3): 127-150. BAZANT Z P. Creep stability and buckling strength of concrete columns[J]. Magazine of Concrete Research, 1968, 20(63): 85-94. doi: 10.1680/macr.1968.20.63.85 林南薰. 混凝土和钢筋混凝土柱的徐变稳定性[J]. 土木工程学报,1987,20(3): 92-94.LIN Nanxun. Creep stability of concrete and reinforced concrete columns[J]. Journal of Civil Engineering, 1987, 20(3): 92-94. 寿楠椿,张巍,竹学叶. 钢筋混凝土压杆徐变稳定性分析的有限元法[J]. 建筑结构,1996(11): 32-37.SHOU Nanchun, ZHANG Wei, ZHU Xueye. Finite element method for analysis of creep stability of reinforced concrete compression bars[J]. Building Structure, 1996(11): 32-37. BAZANT Z P. Prediction of concrete creep effects using age-adjusted effective modulus method[J]. Journal of the American Concrete Institute, 1972, 69: 212-217. 王玉银,刘昌永,张素梅. 铰接钢管混凝土圆弧拱平面内徐变稳定[J]. 工程力学,2011,28(3): 198-204.WANG Yuying, LIU Changyong, ZHANG Sumei. In-plane creep buckling for pin-ended concrete-filled steel tubular circular arches[J]. Engineering Mechanics, 2011, 28(3): 198-204. 王振波, 乔燕, 马林. 结构力学[M]. 北京: 中国建材工业出版社, 2014: 275-280 РЖАНИЦЫН А Р. 结构力学[M]. 刘孝平, 译. 北京: 人民交通出版社, 1990: 203-210 龙驭球, 包世华, 匡文起, 等. 结构力学教程（Ⅱ）[M]. 北京: 高等教育出版社, 2001: 304-345 ACI Committee 209.2R. Prediction of creep, shrinkage and temperature effects in concrete structures: 978-0-87031-278-6[S]. Detroit: American Concrete Institute（ACI）, 2008 孙宝俊. 混凝土徐变理论的有效模量法[J]. 土木工程学报,1993,26(3): 66-68.SUN Baojun. Effective modulus method of concrete creep theory[J]. Journal of Civil Engineering, 1993, 26(3): 66-68. Comite Euro-international Du Beton. Fip model code for concrete structures 2010: Part 5, materials: 0-7277-1696-4[S]. London: Thomas Telford Services Ltd, 1993 王永宝,赵人达,徐腾飞,等. 钢管混凝土轴压构件徐变简化计算方法研究[J]. 公路交通科技,2016,33(1): 57-62. doi: 10.3969/j.issn.1002-0268.2016.01.009WANG Yongbao, ZHAO Renda, XU Tengfei, et al. Study on simplified creep calculation method of CFST members under axial loading[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 57-62. doi: 10.3969/j.issn.1002-0268.2016.01.009 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015 -
下载:
点击查看大图
图(4) / 表(1)
计量
- 文章访问数: 516
- HTML全文浏览量: 268
- PDF下载量: 11
- 被引次数: 0