Influence of Shield Construction on Pressure Fluctuation of Segment Grout
-
摘要: 为探明盾构隧道同步注浆过程中管片壁后浆液压力不稳定变化的原因，通过对珠海马骝洲隧道工程进行现场测试及施工参数统计，获得了盾构掘进过程中管片外荷载的变化规律与注浆滞后时间；将盾尾视为充满高压液体的密闭容器，盾构推进视为改变容器的边界条件，推导了盾尾体积应变与浆液压力的关系式；并用钱江隧道及Sohpia隧道的监测结果对其适用性进行了验证. 研究结果表明：造成同步注浆过程中管片壁后浆液压力不稳定变化的因素主要包括浆液注入口压力的波动变化，管片脱离盾尾过程中浆液的扩散及施工过程中同步注浆相较于盾构行程的滞后效应；马骝洲隧道注浆相较于盾构推进的平均滞后时间为86 s，当盾尾间隙体积变量为1 × 10–4时浆液压力变化值达到了0.218 MPa，盾构机从静止到掘进的短时间内滞后效应会使管片壁后浆液压力急剧降低的现象得到了验证.Abstract: In order to investigate the cause of slurry pressure instability segment tracking changes in the process of synchronous grouting segment, the variation law of external load of segments and the grouting lag time during shield tunneling were obtained, by means of the field test and construction parameter statistics of the Maliuzhou tunnel project in Zhuhai. The relationship between the volumetric strain of the shield tail and the grouting pressure was deduced by treating the clearance of the shield tail as a closed vessel filled with high pressure liquid and the shield driving as changing the boundary conditions of the vessel.The applicability of the research results was verified by the monitoring results of the Qianjiang tunnel and the Sohpia tunnel. The results show that the fluctuation of slurry injection pressure, the diffusion of serous fluid when the lining is out of the shield, the lag effect in the construction process of synchronous grouting compared with tunnel excavation are the main factors that cause the change of slurry pressure instability behind segment. The average lag time of the grouting phase compared to the shield propelling in the Maliuzhou tunnel is 86 s, when the volumetric variable is 1 × 10–4, the change of slurry pressure reaches to 0.218 MPa, which verify the phenomenon that the lag effect makes the soil pressure behind segment reduced sharply when the shield is pushed from stationary to tunneling.
-
Key words:
- shield tunnel /
- grouting pressure fluctuation /
- influence factor /
- field test /
- lag effect
-
图 4 盾尾脱环注浆水压力随时间变化关系
Figure 4. Variation of water pressure with time of shield tail ring grouting
图 5 第347环管片外侧水压力及接触压力时程曲线
Figure 5. Time history curve of water pressure and contact pressure of the 347th segment
图 6 第347环管片脱离盾尾时各浆液注入口压力时程图
Figure 6. Injection pressure of each grout when the 347th ring segments escape from the shield tail
图 7 盾构掘进第349、350环时盾构行程、注浆量与时间关系
Figure 7. Relationship between the displacement of the shield，the amount of grouting，and the time when the shield tunneling 349th and 350th segments
图 8 盾尾注浆相较于盾构行程的滞后效应
Figure 8. Hysteresis effect of shield tail grouting in shield tunnel
图 10 钱江隧道施工阶段第二实验环顶部荷载变化
Figure 10. Qianjiang tunnel top load changes in the second experimental ring during shield tunneling
-
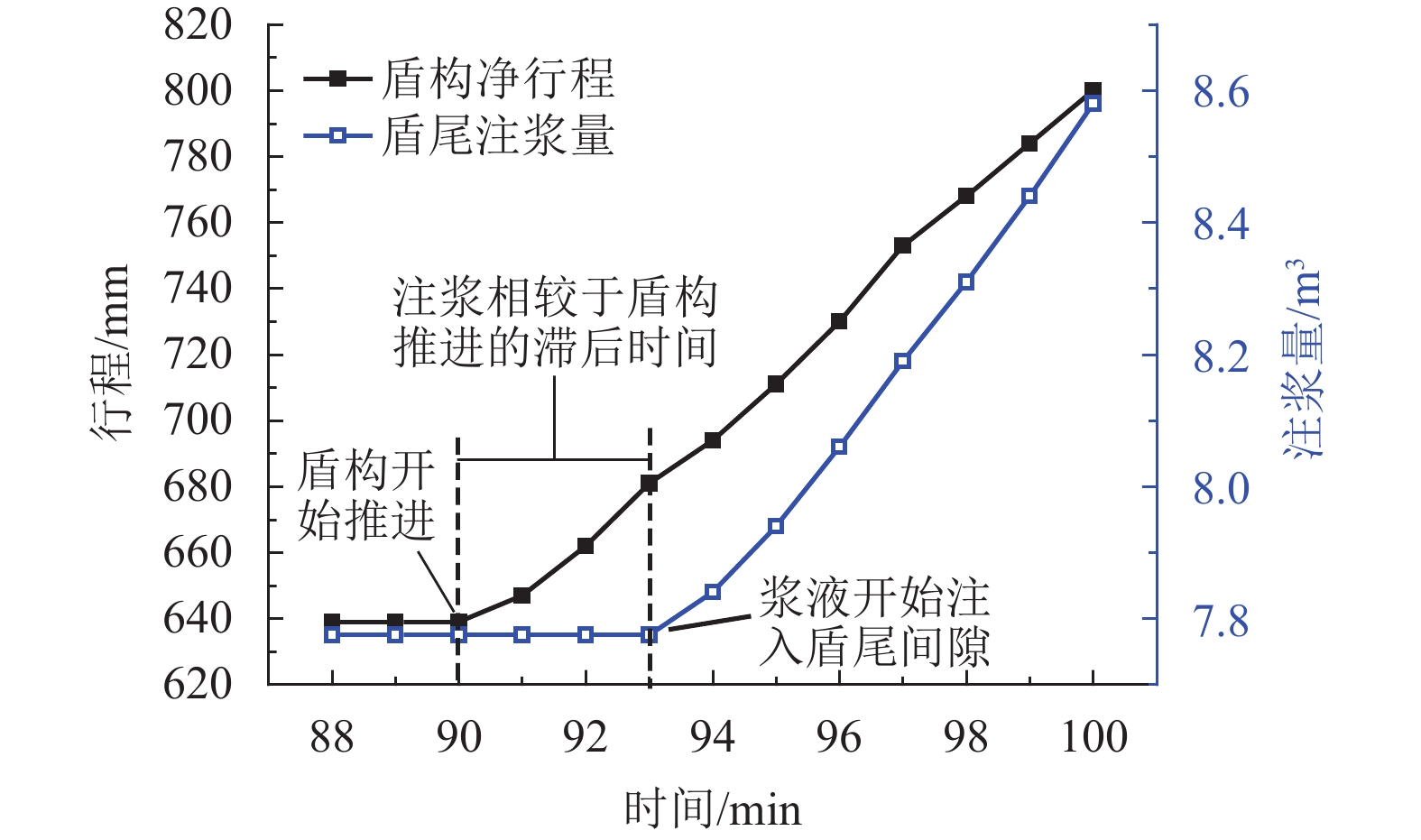
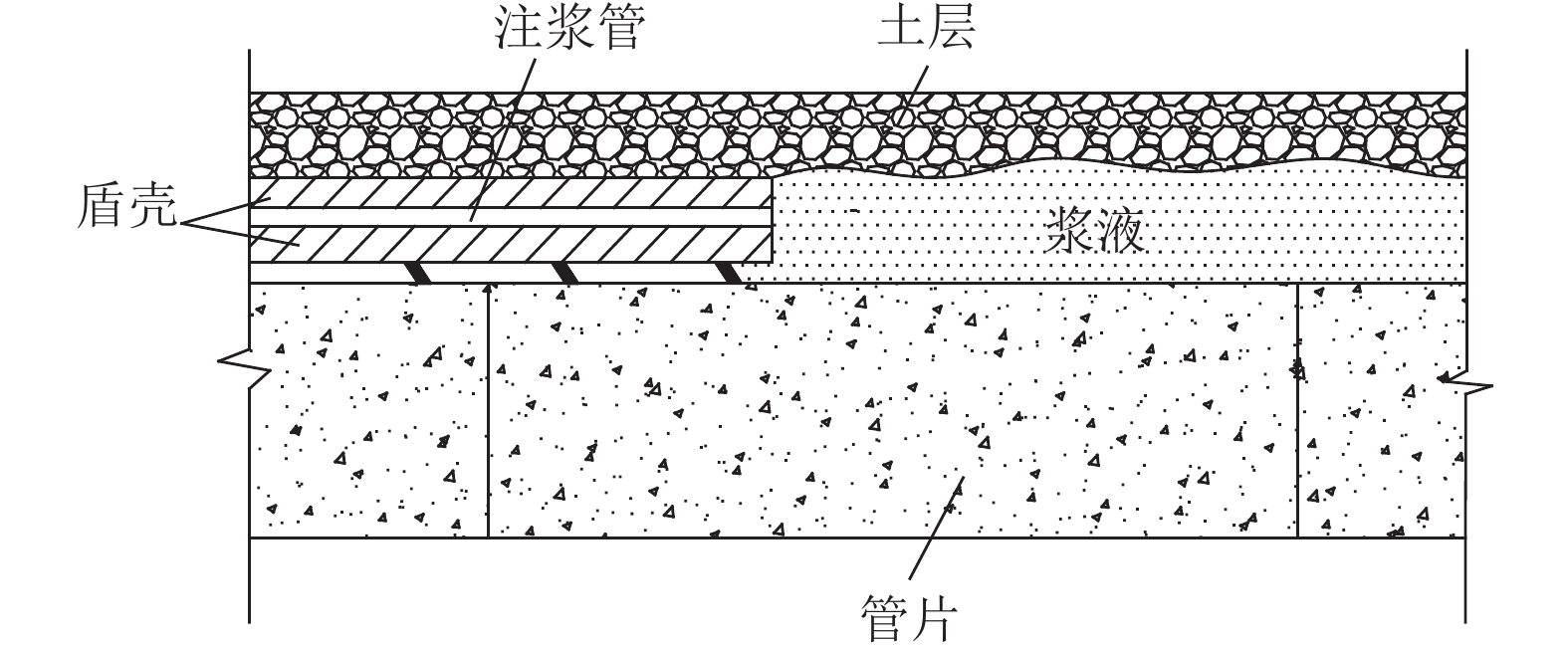
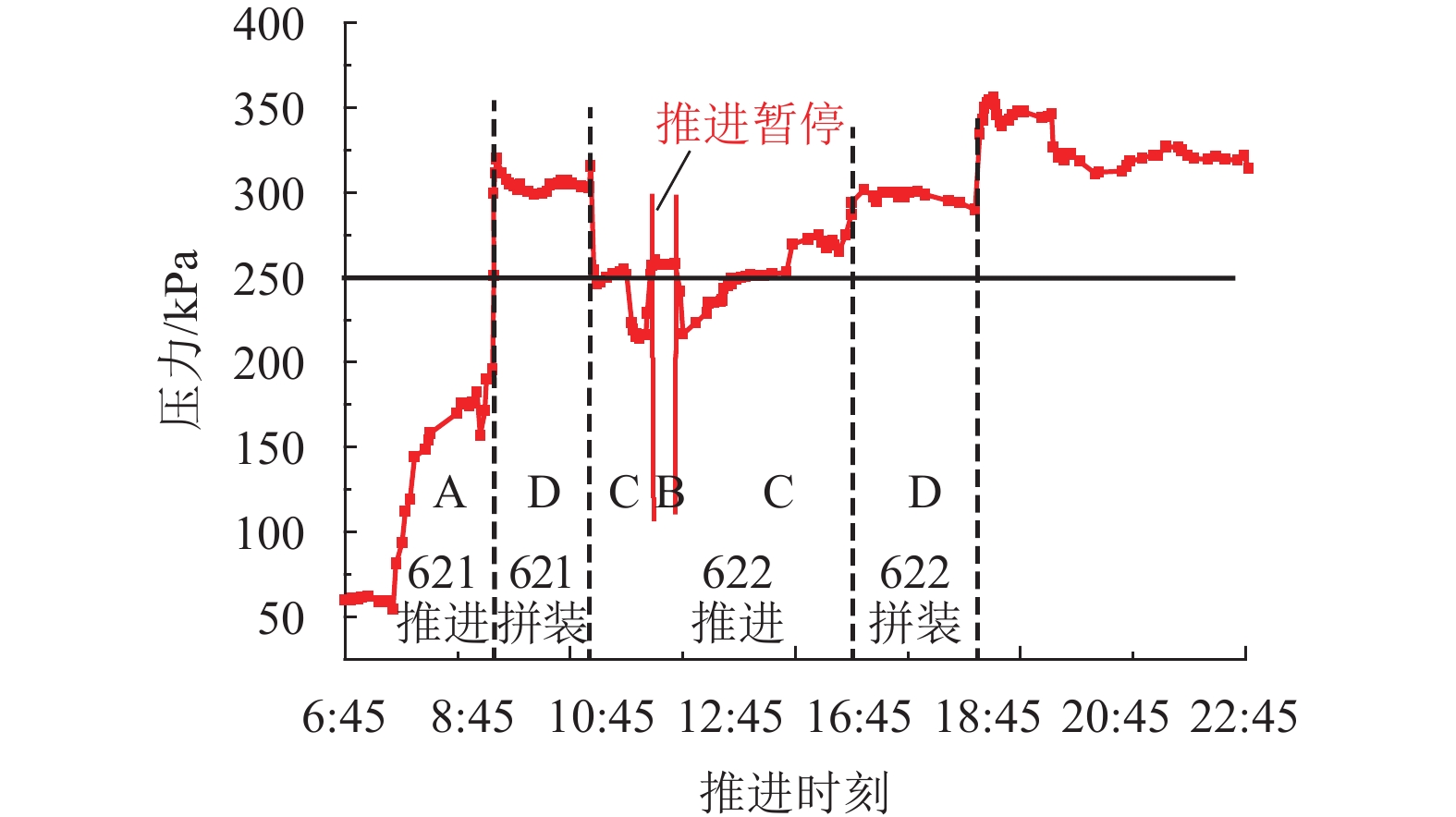
齐春,何川,封坤. 考虑流固耦合效应的水下盾构隧道受力特性[J]. 西南交通大学学报,2015,50(2): 306-311,330. doi: 10.3969/j.issn.0258-2724.2015.02.015QI Chun, HE Chuan, FENG Kun. Fluid-solid interaction-based mechanical characteristics of underwater shield tunnel[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 306-311,330. doi: 10.3969/j.issn.0258-2724.2015.02.015 何川,封坤,方勇. 盾构法修建地铁隧道的技术现状与展望[J]. 西南交通大学学报,2015,50(1): 97-109. doi: 10.3969/j.issn.0258-2724.2015.01.015HE Chuan, FENG Kun, FANG Yong. Review and prospects on constructing technologies of metro tunnels using shield tunnelling method[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 97-109. doi: 10.3969/j.issn.0258-2724.2015.01.015 叶飞,刘燕鹏,苟长飞,等. 盾构隧道壁后注浆浆液毛细管渗透扩散模型[J]. 西南交通大学学报,2013,48(3): 428-434. doi: 10.3969/j.issn.0258-2724.2013.03.006YE Fei, LIU Yanpeng, GOU Changfei, et al. Capillary penetration diffusion model for backfill grouting of shield tunnel[J]. Journal of Southwest Jiaotong University, 2013, 48(3): 428-434. doi: 10.3969/j.issn.0258-2724.2013.03.006 叶飞,朱合华,何川. 盾构隧道壁后注浆扩散模式及对管片的压力分析[J]. 岩土力学,2009,30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020YE Fei, ZHU Hehua, HE Chuan. Shield tunnel grouting diffusion model and pressure on segment analysis[J]. Rock and Soil Mechanics, 2009, 30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020 袁小会,韩月旺,钟小春. 盾构隧道壁后注浆压力分布模型[J]. 西南交通大学学报,2011,46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003YUAN Xiaohui, HAN Yuewang, ZHONG Xiaochun. Grouting pressure of shield tunnel wall after distribution model[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003 KASPER T, MESCHKE G. On the influence of face pressure,grouting pressure and TBM design in soft ground tunneling[J]. Tunnelling and Underground Space Technology, 2006, 21(2): 160-171. doi: 10.1016/j.tust.2005.06.006 BEZUIJEN A, TALMON A M, KAALBERG F J, et al. Field measurement of grout pressures during tunnelling of the Sophia rail tunnel[J]. Soils and Foundations, 2004, 44(1): 39-48. doi: 10.3208/sandf.44.39 肖明清. 水下隧道设计技术[M]. 北京: 中国铁道出版社, 2016: 245-259 刘健,张载松,韩烨,等. 考虑黏度时变性的水泥浆液盾构壁后注浆扩散规律及管片压力模型的试验研究[J]. 岩土力学,2015,36(2): 361-368.LIU Jian, ZHANG Zaisong, HAN Ye, et al. Backfilled grouting diffusion law and model of pressure on segments of shield tunnel considering viscosity variation of cement grout[J]. Rock and Soil Mechanics, 2015, 36(2): 361-368. 苟长飞,叶飞,张金龙,等. 盾构隧道同步注浆充填压力环向分布模型[J]. 岩土工程学报,2013,35(3): 590-598.GOU Changfei, YE Fei, ZHANG Jinlong, et al. Ring distribution model of filling pressure for shield tunnels under synchronous grouting[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 590-598. 孙闯,张建俊,刘家顺,等. 盾构隧道壁后注浆压力对地表沉降的影响分析[J]. 长江科学院院报,2012,29(11): 68-72. doi: 10.3969/j.issn.1001-5485.2012.11.015SUN Chuang, ZHANG Jianjun, LIU Jiashun, et al. Effect of shield tunnel backfill grouting pressure on the ground surface subsidence[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(11): 68-72. doi: 10.3969/j.issn.1001-5485.2012.11.015 李志明,廖少明,戴志仁. 盾构同步注浆填充机理及压力分布研究[J]. 岩土工程学报,2010,32(11): 1752-1757.LI Zhiming, LIAO Shaoming, DAI Zhiren. Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1752-1757. 孙斌堂,凌贤长,凌晨,等. 渗透注浆浆液扩散与注浆压力分布数值模拟[J]. 水利学报,2007,37(11): 1402-1407. doi: 10.3321/j.issn:0559-9350.2007.11.023SUN Bintang, LING Xianchang, LING Chen, et al. Numerical simulation for diffusion and pressure distribution of permeation grouting[J]. Journal of Hydraulic Engineering, 2007, 37(11): 1402-1407. doi: 10.3321/j.issn:0559-9350.2007.11.023 梁禹,阳军生,王树英,等. 考虑时变性影响的盾构壁后注浆浆液固结及消散机制研究[J]. 岩土力学,2015,36(12): 3373-3380.LIANG Yu, YANG Junsheng, WANG Shuying, et al. A study on grout consolidation and dissipation mechanism during shield backfilled grouting with considering time effect[J]. Rock and Soil Mechanics, 2015, 36(12): 3373-3380. 张莎莎,戴志仁,白云. 盾构隧道同步注浆浆液压力分布规律模型试验研究[J]. 中国铁道科学,2015,36(5): 43-53. doi: 10.3969/j.issn.1001-4632.2015.05.07ZHANG Shasha, DAI Zhiren, BAI Yun. Model test research on distribution law of grout pressure for simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2015, 36(5): 43-53. doi: 10.3969/j.issn.1001-4632.2015.05.07 张莎莎,戴志仁,白云. 盾构隧道同步注浆浆液压力消散规律研究[J]. 中国铁道科学,2012,33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07ZHANG Shasha, DAI Zhiren, BAI Yun. Research on the dissipation of grout pressure during the simultaneous grouting of shield tunnel[J]. Chinese Journal of Railway Science, 2012, 33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07 -
下载:
点击查看大图
图(11)
计量
- 文章访问数: 629
- HTML全文浏览量: 405
- PDF下载量: 16
- 被引次数: 0