Optimization of Train Timetable for Intercity Railway Based on Coordinated Operation of Multi-periodic Trains
-
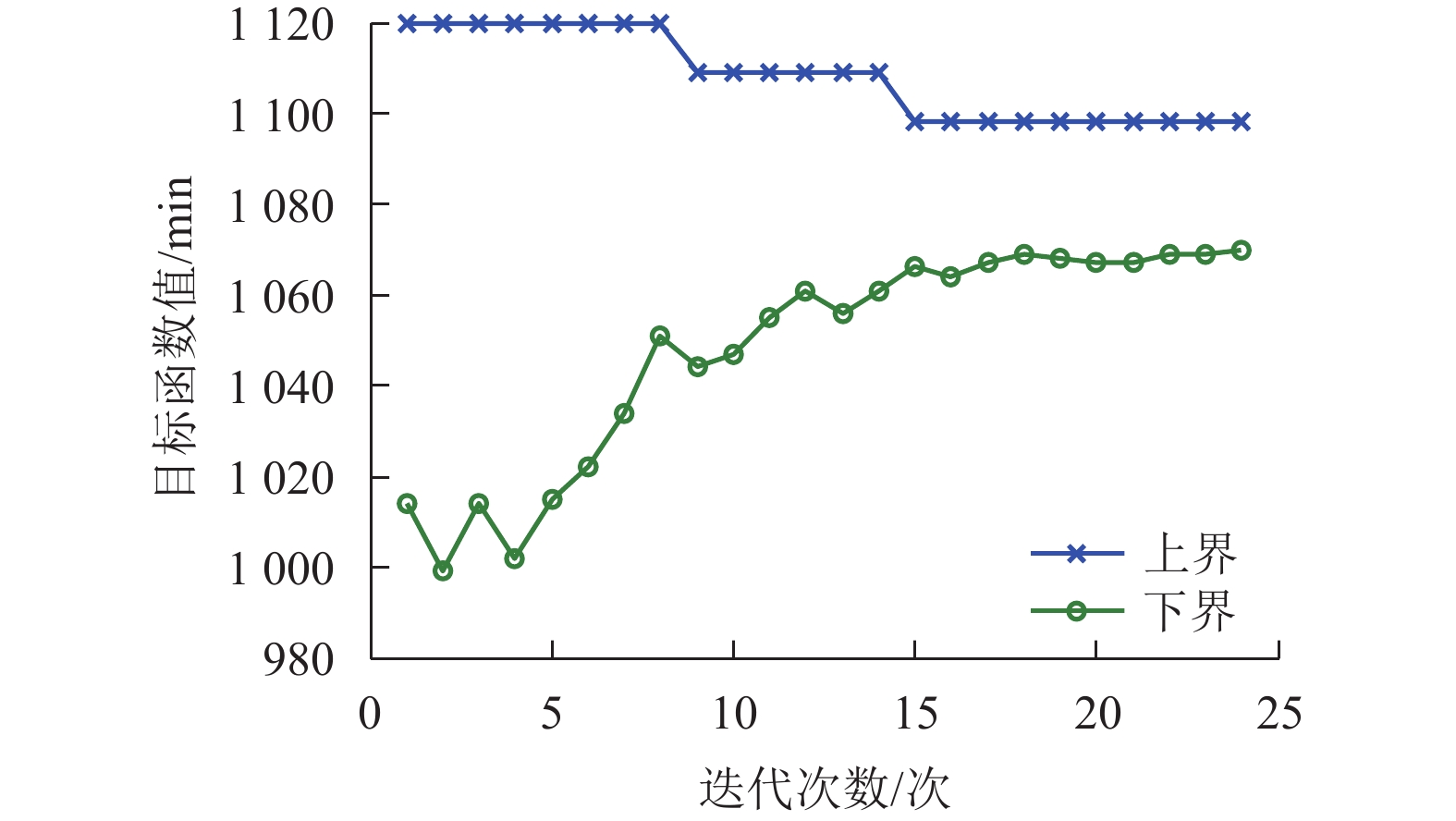
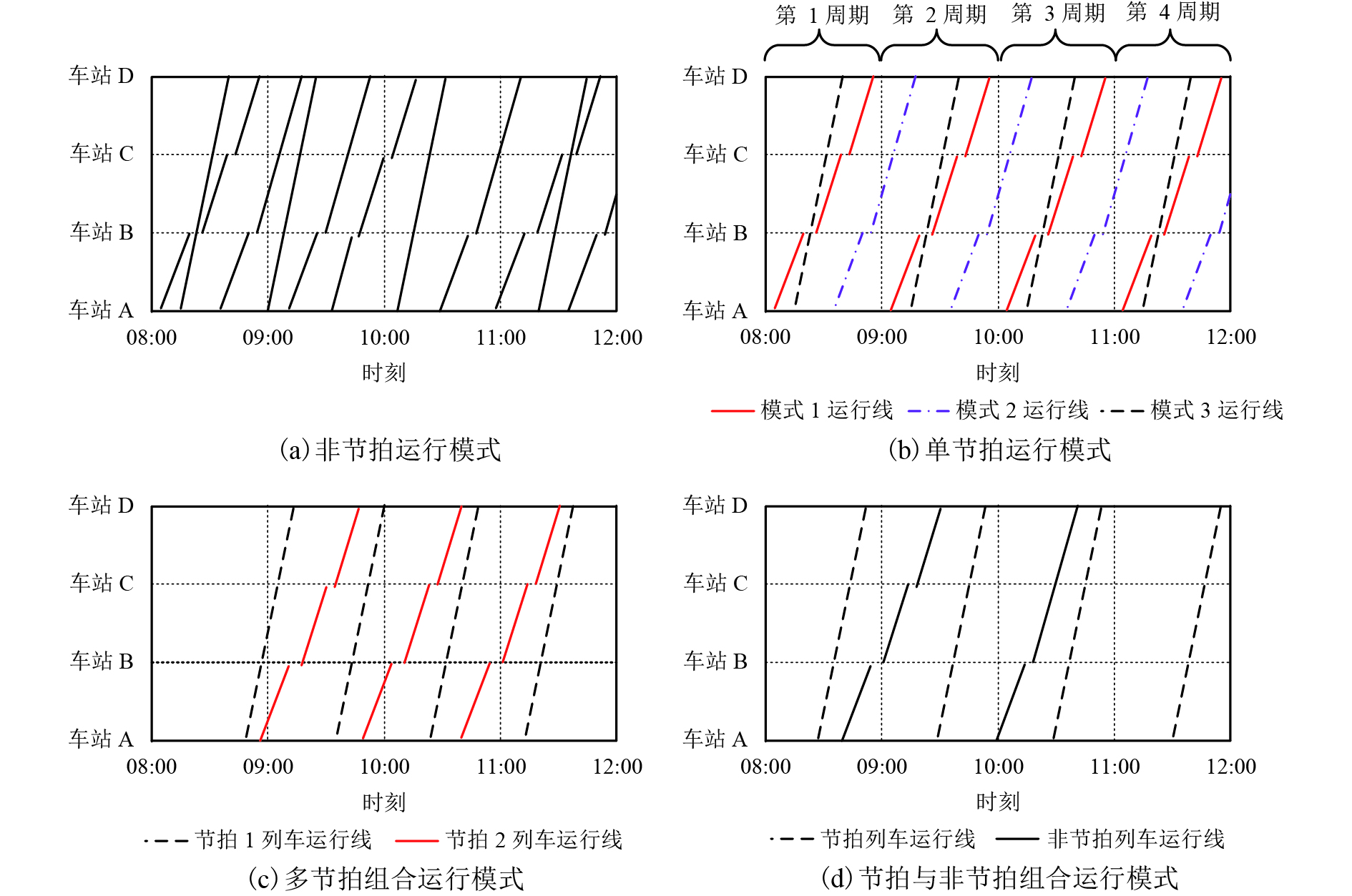
摘要: 为了使得城际铁路列车车站到发时刻既能具有严格等时间间隔的周期性规律，又能灵活适应城际铁路客流需求的时间分布，首先提出了列车多节拍组合运行组织模式，并将其与单节拍、非节拍运行组织模式进行特征对比分析. 进而基于列车多节拍组合运行模式，以最小化所有节拍单元列车总旅行时间为优化目标，以同节拍单元列车等时间间隔运行、各类作业安全时间间隔要求等为约束，构建了城际铁路列车多节拍协同运行图优化模型. 在通过确定模型中复杂约束、引入拉格朗日乘子将其松弛的基础上，结合次梯度法设计基于拉格朗日松弛的优化算法求解模型. 以京津城际为背景的算例优化获得由4个节拍列车组合的列车运行图，其中各节拍列车分别以17、34、34、35 min等时间间隔周期性运行，该方案目标函数与其最优下界的相对差距仅为2.55%.Abstract: To ensure regularity of train arrival and departure times at stations operating with strict train periodicity and timing schedules, a novel methodology for coordinated operation of multi-periodic trains is proposed. The proposed method aims to ensure a better fit for the time distribution of passenger demands in the intercity railway system and is further compared with the existing aperiodic and single periodic train operation patterns to analyze their characteristic differences. On this basis, an optimisation model aimed at minimising the total travel times of all periodical operating trains is built to solve the train scheduling problem; this involves the coordinated operation of multi-periodic trains with identical time interval constraints for each period type of trains and all safety intervals. An algorithm based on Lagrangian relaxation framework is designed and combined with the gradient method by relaxing the complex constraints via Lagrangian multiples. The proposed model is implemented numerically for Beijing-Tianjin intercity railway using its operating timetable for four periodical operating trains with intervals of 17 min, 34 min, 34 min, and 35 min. The analysis shows that their objective values differ from the optimised lower boundary by 2.55%.
-
Key words:
- intercity rail /
- train schedule /
- multi-periodici /
- coordinated operation /
- Lagrangian relaxation
-
图 2 目标函数上界与下界值随着迭代次数增加的变化关系
Figure 2. Variations of the lower and upper bounds of the objective function with the increase of iterations
表 1 各节拍单元列车运行数量与停站信息
Table 1. Number and stops of each period-type train
节拍单元序号 运行数量 起点站 终点站 中途停站 1 11 北京南 天津 武清 2 6 北京南 天津 亦庄、永乐 3 6 北京南 天津 永乐、武清 4 5 北京南 天津 亦庄、武清 
下载: 导出CSV
表 2 各节拍单元列车运行时间范围
Table 2. Operation time range of each period-type train
节拍单元
序号首班车的始发
时间范围运行时间间隔
范围/min1 [07:00，07:30] [10，30] 2 [08:00，08:30] [30，60] 3 [07:30，08:00] [30，60] 4 [07:30，08:00] [30，60]
下载: 导出CSV
表 3 各节拍单元首班车运行时刻与运行时间间隔
Table 3. Arrival and departure times of the first train and operation interval for each period-type
节拍单元序号 北京南站 亦庄站 永乐站 武清站 天津站 运行时间间隔/min 到时 发时 到时 发时 到时 发时 到时 发时 到时 发时 1 07:16 07:24 07:24 07:31 07:31 07:40 07:42 07:54 17 2 08:11 08:19 08:21 08:28 08:30 08:39 08:39 08:51 34 3 07:43 07:51 07:51 07:58 08:00 08:09 08:11 08:23 34 4 07:58 08:06 08:08 08:15 08:15 08:24 08:26 08:38 35
下载: 导出CSV
表 4 基于5、10 min等的整数倍为节拍单元列车运行时间间隔的计算指标
Table 4. Indexes of setting train operation intervals as the multiples of five or ten minutes
时间间隔的基数/min 上界值/min 下界值/min 相对差距/% 计算时间/s 5 1 098 1 075 2.09 654 10 1 098 1 073 2.27 452 15 1 108 1 071 3.34 384 20 1 114 1 071 3.86 356
下载: 导出CSV
-
ZHOU X, ZHONG M. Single-track train timetabling with guaranteed optimality:branch-and- bound algorithms with enhanced lower bounds[J]. Transportation Research Part B, 2007, 41(3): 320-341. doi: 10.1016/j.trb.2006.05.003 JONG J C, CHANG S, LAI Y C. Development of two-stage hybrid method to solve high-speed rail train scheduling problem[J]. Transportation Research Record, 2013, 11: 44-54. 许红,马建军,龙建成. 客运专线列车运行图编制模型及计算方法的研究[J]. 铁道学报,2007,29(2): 1-7. doi: 10.3321/j.issn:1001-8360.2007.02.001XU Hong, MA Jianjun, LONG Jiancheng. Research on the model and algorithm of the train working diagram of dedicated passenger line[J]. Journal of the China Railway Society, 2007, 29(2): 1-7. doi: 10.3321/j.issn:1001-8360.2007.02.001 周文梁,史峰,陈彦. 基于定序优化的客运专线列车运行图铺划方法[J]. 铁道学报,2010,32(1): 1-7. doi: 10.3969/j.issn.1001-8360.2010.01.001ZHOU Wenliang, SHI Feng, CHEN Yan. A method for drawing train diagram of dedicated passenger line based on fixed order optimization[J]. Journal of the China Railway Society, 2010, 32(1): 1-7. doi: 10.3969/j.issn.1001-8360.2010.01.001 CUCALA A P, FEMANDEZ A, SICRE C, et al. Fuzzy optimal schedule of high speed train operation to minimize energy consumption with uncertain delays and driver’s behavioral response[J]. Engineering Applications of Artificial Intelligence, 2012, 25(8): 1548-1557. doi: 10.1016/j.engappai.2012.02.006 ALBRECHT A R, PANTON D M, LEE D H. Rescheduling rail networks with maintenance disruptions using Problem Space Search[J]. Computers & Operations Research, 2013, 40(3): 703-712. CAREY M, CRAWFROD I. Scheduling trains on a network of busy complex stations[J]. Transportation Research Part B:Methodological, 2007, 41(2): 159-178. doi: 10.1016/j.trb.2006.02.002 唐金金,周磊山,冉锋,等. 基于牵引仿真的列车运行图软冲突疏解方法研究[J]. 铁道学报,2012,34(4): 1-8. doi: 10.3969/j.issn.1001-8360.2012.04.001TANG Jinjin, ZHOU Leishan, RAN Feng, et al. Research on train scheduling for high-speed railway lines based on soft conflict adjustment[J]. Journal of the China railway Society, 2012, 34(4): 1-8. doi: 10.3969/j.issn.1001-8360.2012.04.001 WILLEM L, PEETERS P. Cyclic railway timetable optimization[D]. Netherlands: Erasmus University Rotterdam, 2003 CAIMI G, FUCHSBERGER M, MARCO L, et al. Periodic railway timetabling with event flexibility[J]. Special Issue:Optimization in Scheduled Transportation Networks, 2012, 57(1): 3-18. CHRISTIAN L. Periodic timetable optimization in public transport[M]. Berlin: Winter Industries Gmbh, 2006: 102-125 汪波,杨浩,牛丰,等. 周期运行图编制模型与算法研究[J]. 铁道学报,2007,29(5): 1-7. doi: 10.3321/j.issn:1001-8360.2007.05.001WANG Bo, YANG Hao, NIU Feng, et al. Study on model and algorithm of periodic train diagram generation[J]. Journal of the China railway Society, 2007, 29(5): 1-7. doi: 10.3321/j.issn:1001-8360.2007.05.001 汪波,韩宝明,战明辉. 城市轨道交通网络周期运行图编制研究[J]. 铁道学报,2013,35(4): 9-15. doi: 10.3969/j.issn.1001-8360.2013.04.002WANG Bo, HAN Baoming, ZHAN Minghui. Study on formulation of periodic train diagram of urban rail transit network[J]. Journal of the China Railway Society, 2013, 35(4): 9-15. doi: 10.3969/j.issn.1001-8360.2013.04.002 谢美全,聂磊. 周期性列车运行图编制模型研究[J]. 铁道学报,2009,31(4): 7-13.XIE Meiquan, NIE Lei. Model of cyclic train timetable[J]. Journal of the China Railway Society, 2009, 31(4): 7-13. 贾晓秋. 客运专线旅客列车周期运行图的优化理论与方法研究[D]. 成都: 西南交通大学, 2011 李传宾. 基于矩阵表示和极大代数法的高铁周期列车运行图编制方法研究[D]. 北京: 北京交通大学, 2012 -
下载:
点击查看大图
图(2) / 表(4)
计量
- 文章访问数: 480
- HTML全文浏览量: 217
- PDF下载量: 17
- 被引次数: 0