Dynamic Displacement Response of Pavement Structure under Moving Vehicle Load
-
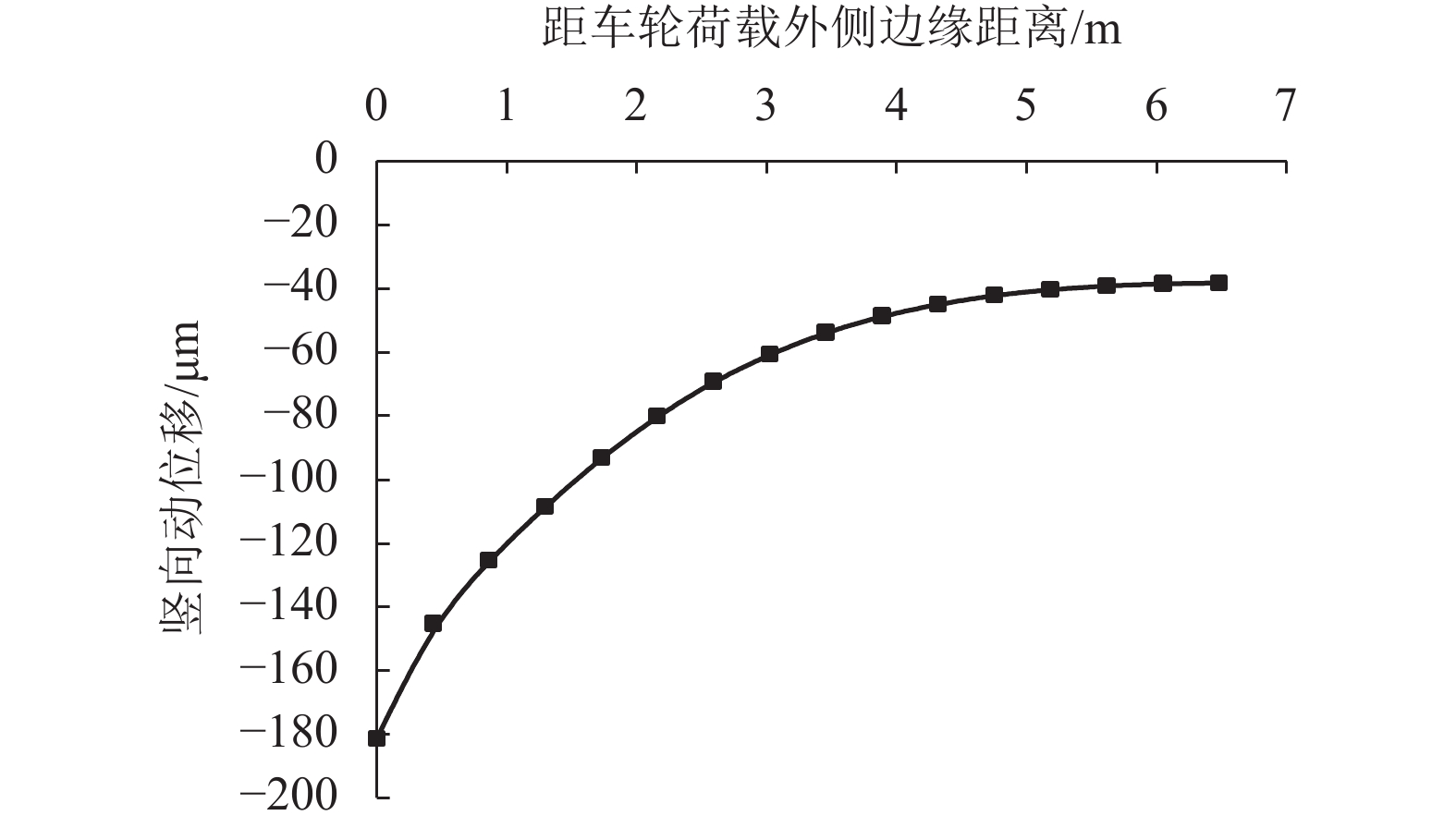
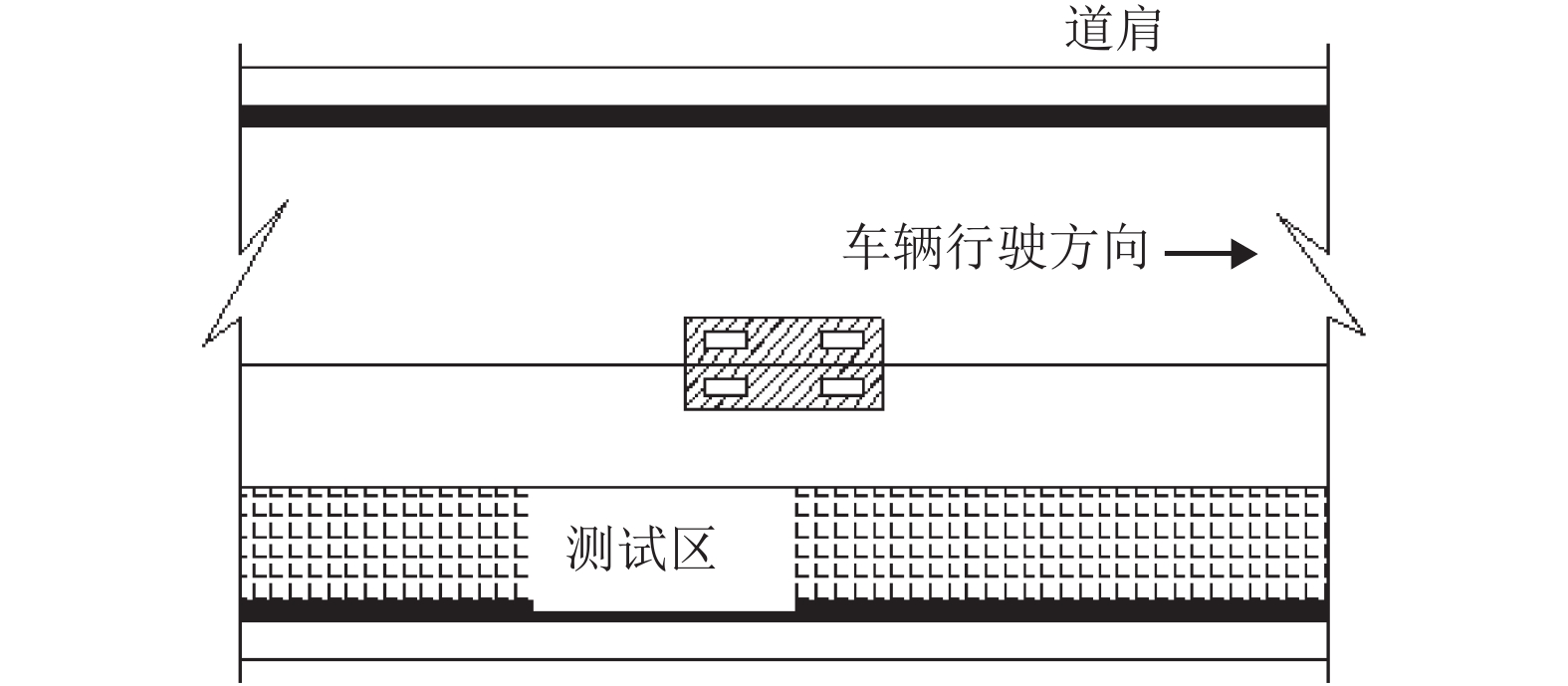
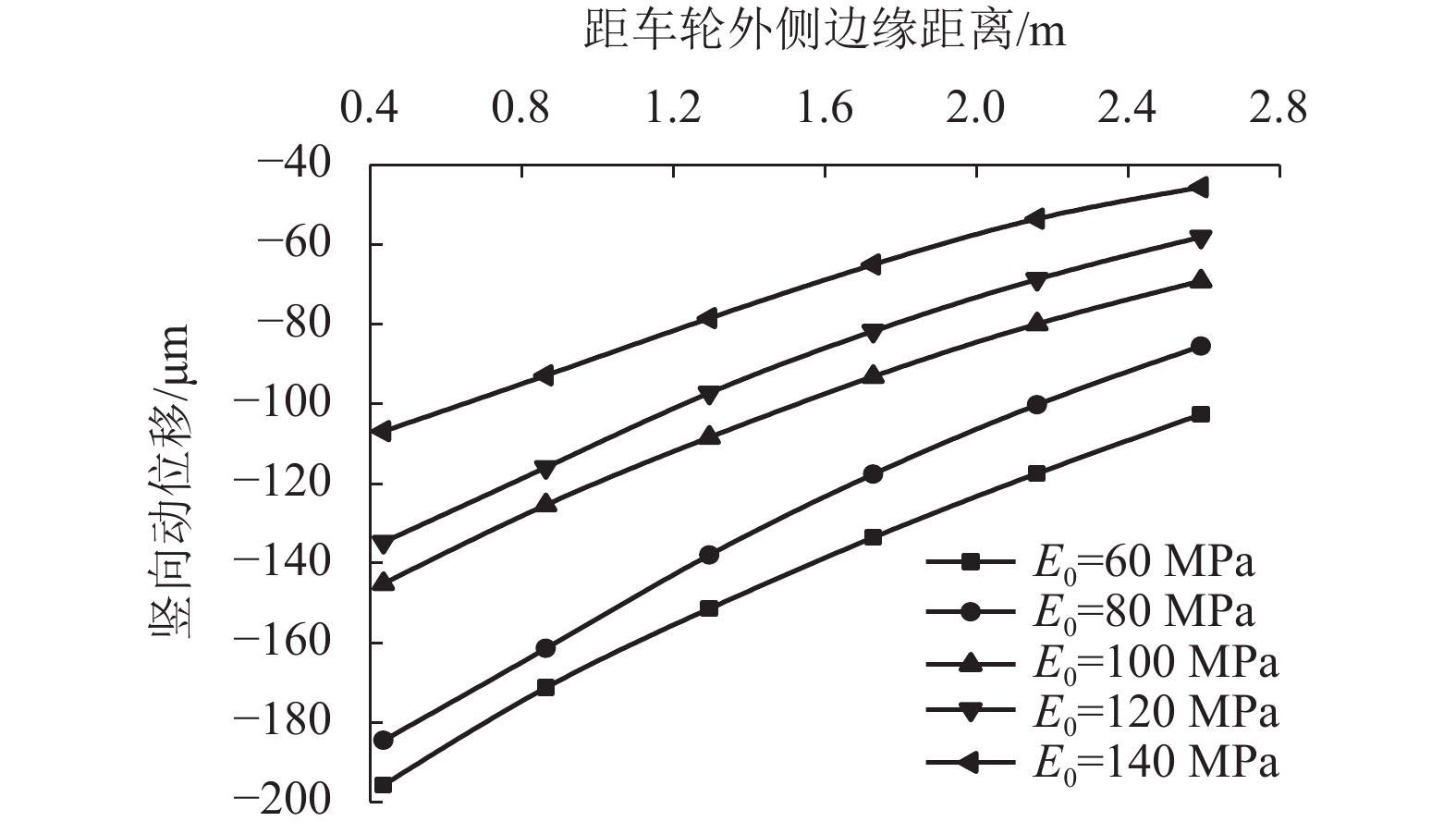
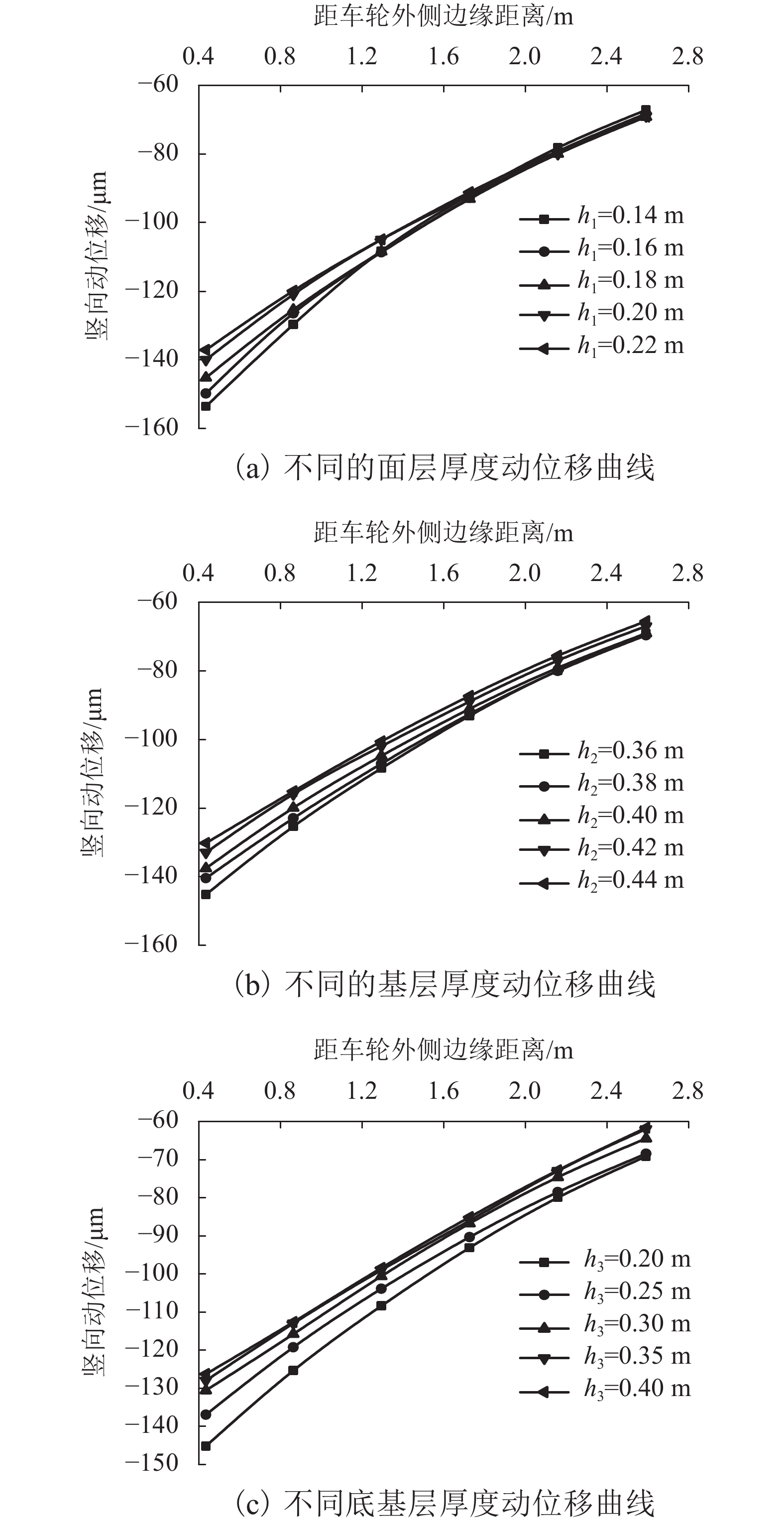
摘要: 为研究行车荷载作用下路面结构动位移响应规律，基于弹性层状体系理论建立路面结构有限元模型，将车辆随机动荷载作用在有限元模型上，通过改变路面结构层厚度与模量，研究了路面结构测试区竖向动位移变化规律，建立了测试区动位移峰值与路面结构层参数的数学模型，进一步揭示了路面结构动态响应问题. 计算结果表明：路面结构测试区动位移峰值随土基模量的增大而减少；土基模量对测试区动位移峰值影响最为敏感，两者的数学模型近似呈对数关系，测试区动位移峰与面层厚度和基层厚度近似呈线性关系，与底基层厚度近似呈对数关系；不同的面层模量、基层模量和底基层模量对应的测试区动位移曲线几乎重合，因此不是影响测试区动位移的主要影响因素. 研究结果为路面承载力检测提供了依据.Abstract: In order to study the dynamic displacement response law of pavement structure under driving load, a finite element model (FEM) of pavement structure is established by the theory of elastic layered system. Applying the random dynamic load of a vehicle to the FEM, the variation of vertical dynamic displacement in the structural test area is analyzed with changing thickness and modulus of the pavement layer, and a mathematical model of relationship between the peak dynamic displacement of the test area and parameters of the pavement structure layer is proposed to characterize the dynamic response of the pavement structure. Results of FEM calculations show that the peak dynamic displacement of the pavement test area decreases with an increase in the soil matrix modulus; what's more, the peak dynamic displacement is more sensitive to the soil matrix modulus than to other pavement layer parameters, and the mathematical relationship between them is logarithmic. Meanwhile, the peak dynamic displacement of the pavement test area is approximately linear with the thicknesses of the surface layer and the base layer, and is approximately logarithmic with the thickness of the subbase layer. However, the dynamic displacement curves of the test area with different surface layer moduli, base layer moduli and base layer moduli almost coincide, implying that they are not the main influencing factors of the dynamic displacement. The obtained results provide a basis for the detection of pavement bearing capacity.
-
图 2 B级路面激励下不同速度下的动载系数
Figure 2. Dynamic Load Coefficient at Different Speeds under B-type Pavement Excitation
图 5 有无车辆前轴动位移对比
Figure 5. Whether the vehicle front axle displacement comparison chart
图 7 路面结构动态测试区域示意
Figure 7. Schematic diagram of dynamic test area of pavement structure
图 9 不同路面结构层厚度动位移曲线
Figure 9. Dynamic displacement curve of layer thickness of different pavement structures
表 1 车辆系统参数
Table 1. Vehicle system parameters
参数 取值 悬挂质量ms/Kg 4 450 非悬挂质量mt/Kg 550 悬架刚度系数ks/（N•m−1） 106 悬架阻尼系数cs/（N•s•m−1） 15 000 轮胎刚度系数kt/（N•m−1） 1 750 000 轮胎阻尼系数ct/（N•s•m−1） 2 000 
下载: 导出CSV
表 2 路面结构层参数
Table 2. Pavement structure and material parameters
结构层 厚度/m 动模量/
MPa泊松比 密度/
（Kg•m−3）阻尼比 面层 0.18 3 000～5 000 0.30 2 400 0.05 基层 0.36 3 500～5 500 0.25 2 200 0.05 底基层 0.20 2 000～4 000 0.30 1 600 0.05 土基 10.26 60～140 0.40 1 900 0.05
下载: 导出CSV
表 3 不同速度时动位移峰值与土基模量的关系
Table 3. Relationship between the peak value of dynamic displacement and soil modulus at different speeds
速度/（m•s−1） 回归公式 相关系数R2 15 S = 147.44ln E0 − 852.01 0.976 5 20 S = 106.23ln E0 − 638.09 0.967 9 25 S = 71.69ln E0 − 478.95 0.985 4 30 S = 53.24ln E0 − 367.44 0.993 7 35 S = 37.81ln E0 − 304.65 0.993 6
下载: 导出CSV
-
陈一锴,何杰,彭佳,等. 基于动载模拟的半刚性沥青路面响应分析[J]. 东南大学学报(自然科学版),2010,40(3): 593-598.CHEN Yikai, HE Jie, PENG Jia, et al. Dynamic analysis of semi-rigid asphalt pavement subject to stimulant dynamic loads[J]. Journal of Southeast University (Natural Science Edition), 2010, 40(3): 593-598. 单景松,黄晓明,廖公云. 移动荷载下路面结构应力响应分析[J]. 公路交通科技,2007,24(1): 10-13. doi: 10.3969/j.issn.1002-0268.2007.01.003SHAN Jingsong, HUANG Xiaoming, LIAO Gongyun, et al. Dynamic response analysis of pavement structure under moving load[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 10-13. doi: 10.3969/j.issn.1002-0268.2007.01.003 卢传忠,张帅,李强,等. 半刚性基层沥青路面承载力评价指标研究[J]. 公路交通科技(应用技术版),2015(9): 91-93. 董倩. 基于飞机滑行刚性道面位移场的跑道承载力研究[D]. 天津: 中国民航大学, 2013. 张献民,董倩,吕耀志,等. 水泥混凝土跑道边缘区域力学响应[J]. 南京航空航天大学学报,2013,45(5): 693-699. doi: 10.3969/j.issn.1005-2615.2013.05.019ZHANG Xianmin, DONG Qian, LÜ Yaozhi, et al. Mechanical response of cement concrete runway edge[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(5): 693-699. doi: 10.3969/j.issn.1005-2615.2013.05.019 段虎明,石锋,马颖,等. 基于功率谱密度的路面评价与特征参数提取[J]. 振动与冲击,2013,32(4): 26-30. doi: 10.3969/j.issn.1000-3835.2013.04.006DUAN Huming, SHI Feng, MA Ying, et al. Pavement evaluation and feature parameter extraction based on power spectral density[J]. Journal of Vibration and Shock, 2013, 32(4): 26-30. doi: 10.3969/j.issn.1000-3835.2013.04.006 唐光武,贺学锋,颜永福. 路面不平度的数学模型及计算机模拟研究[J]. 中国公路学报,2000,13(1): 117-120.TANG Guangwu, HE Xuefeng, YAN Yongfu. Study on mathematical model and computer simulation of pavement roughness[J]. Journal of China Highway, 2000, 13(1): 117-120. 康忠亮. 车辆随机动载作用下柔性沥青路面的动态响应研究[D]. 青岛: 青岛大学, 2012. 吕耀志,董倩,胡春飞,等. 跑道动荷载与国际平整度指数关系研究[J]. 中外公路,2013,33(3): 74-77. doi: 10.3969/j.issn.1671-2579.2013.03.020LÜ Yaozhi, DONG Qian, HU Chunfei, et al. Study on the relationship between the dynamic load of the runway and the international flatness index[J]. China and Foreign Territories, 2013, 33(3): 74-77. doi: 10.3969/j.issn.1671-2579.2013.03.020 张献民,胡鹏. 随机荷载作用下刚性路面动态响应研究[J]. 振动与冲击,2015,34(19): 126-130,137.ZHANG Xianmin, HU Peng. Study on dynamic response of rigid pavement under random load[J]. Journal of Vibration and Shock, 2015, 34(19): 126-130,137. 李金辉,何杰,李旭宏. 车辆随机及移动荷载作用下路面动态响应[J]. 长安大学学报(自然科学版),2015,35(2): 38-45.LI Jinhui, HE Jie, LI Xuhong. Vehicle pavement dynamic response under random and mobile load[J]. Journal of Chang ’an University (Natural Science Edition), 2015, 35(2): 38-45. 黄兵,吴玉,艾长发,等. 结构参数对沥青路面动态响应的影响[J]. 公路交通科技,2013,30(9): 8-12,26. doi: 10.3969/j.issn.1002-0268.2013.09.002HUANG Bing, WU Yu, AI Changfa, et al. Influence of structural parameters on dynamic response of asphalt pavement[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 8-12,26. doi: 10.3969/j.issn.1002-0268.2013.09.002 邹会宗. 沥青混合料动态模量试验研究[D]. 西安: 长安大学, 2013. 颜利. 基于动态参数的沥青路面性能设计方法研究[D]. 长沙: 长沙理工大学, 2006. 羊明. 沥青混合料动态模量研究[D]. 长沙: 长沙理工大学, 2007. 陈团结,刘宁. 基于动态参数的新型半刚性沥青混凝土路面结构力学分析[J]. 公路,2013(6): 15-20. doi: 10.3969/j.issn.0451-0712.2013.06.003CHEN Tuanjie, LIU Ning. Mechanical analysis of new semi-rigid asphalt concrete pavement structure based on dynamic parameters[J]. Highway, 2013(6): 15-20. doi: 10.3969/j.issn.0451-0712.2013.06.003 史纪村,岳学军. 行车荷载作用下半刚性沥青路面动态弯沉数值分析[J]. 华东公路,2014(5): 74-77.SHI Jicun, YUE Xuejun. Numerical analysis of dynamic bending and sinking of semi-rigid asphalt pavement under driving load[J]. East China Highway, 2014(5): 74-77. -
下载:
点击查看大图
图(9) / 表(3)
计量
- 文章访问数: 542
- HTML全文浏览量: 408
- PDF下载量: 30
- 被引次数: 0