Structural Reliability Design of Non-Backfilling Arch Open Tunnel Structure under Rock-fall Impaction
-
摘要: 为完善拱形明洞结构可靠性设计方法,利用模型试验、数值模拟及理论分析等,结合现场实际,开展了落石冲击下无回填土拱形明洞破坏特征及失效模式、极限承载力、落石冲击荷载及极限状态表达式等的研究.首先,根据落石冲击下无回填土拱形明洞结构失效破坏特征,将结构局部失效范围部分简化为四边固支方形钢筋混凝土板结构,利用塑性极限原理按刚塑性板进行准静态极限荷载计算,得到结构极限承载力即抗力;其次,将离散元颗粒流数值模拟方法得到的落石冲击力最大峰值作为钢筋混凝土板顶部落石冲击力,通过回归分析,得到用落石重力势能的幂函数表示的落石冲击荷载表达式;再次,将得到的结构抗力与落石冲击荷载联立得到极限状态方程,利用MABLAB软件编程求得结构可靠指标,通过与目标可靠指标的比较,进行结构可靠度设计与优化;最后,利用所建立的结构可靠度设计方法,对某客专双线拱形明洞设计进行了可靠度检算.研究结果表明:当落石高度为5~15 m、落石重量为1~2 kN时,原设计明洞结构可靠指标可达到4.2;当将原设计的C35混凝土调整为C40,钢筋由HRB335调整为HRB500后,落石高度为5~20 m、落石重量为1~2 kN范围时的结构可靠指标可达到5.4以上.Abstract: A structural reliability design method for a non-backfilling arch open tunnel structure under rockfall impaction was investigated to improve the reliability of structural design. Firstly, in view of the characteristics of the failure modes of a non-backfilling arch open tunnel under rockfall impaction, a four-fixed square reinforced concrete slab was simplified to a rigid perfectly-plastic slab, and the assumed failure of the structure's ultimate load or structural resistance was calculated as a statics problem using plastic limit theory. Secondly, numerical modelling was performed using a particle flow code method, and rockfall impaction load was expressed as a power function of the gravitational potential energy of rockfall through the regression analysis of modelling results. Thirdly, the limit state equation was established by combining structural resistance and the rockfall impaction load expression. Then, the structural reliability index was obtained using a MATLAB software programming method, and structure reliability design and optimization were performed by comparing the calculated structural reliability index with the target reliability index. Finally, using the established method, the structural reliability indexes of the double-line arch open tunnel of a passenger transport line were analysed. The structural reliability index of the original structure design is up to 4.2 for a height of 5-15 m and a rockfall weight of 1-2 kN. Moreover, the structural reliability index is up to 5.4 if the concrete grade is adjusted from the original C35 to C40 and the reinforcing steel bar grade is changed from HRB335 to HRB500, for a height of 5-20 m and a rockfall weight of 1-2 kN.
-
电分相一直是既有高速铁路供电系统的供电瓶颈[1-2],西南交通大学李群湛教授等[3-4]将电力电缆和组合式同相供电技术相结合,提出一种新型电缆贯通供电系统,取消了牵引变电所出口处和分区所处电分相,从根本上解决了电分相问题,实现全线贯通供电,并且电缆波阻抗小,供电距离长,大大提升了供电性能.
新型电缆贯通供电系统自提出以来,大量文献集中于研究该系统在正常运行时的潮流计算建模[5-6]、电压电流特性分析[7-8]、谐波传递规律[9] 、再生能量利用[10]等,并取得了较大的进展,但该系统短路情况却少有研究.
为保证系统服役期间安全可靠运行,深入研究该系统短路故障的继电保护方法意义重大. 由于新型电缆贯通供电系统较既有牵引供电系统增加了牵引电缆,并且接触网也由单边供电变成了一种特殊的双边供电模式,导致短路电流与正常负荷电流流向一致[6-7],使继电保护方案的研究变得困难和复杂. 目前,新型电缆贯通供电系统接触网现有短路保护的研究均将其视为单边供电形式,提出低电压启动的纵差电流保护方案,并且高压牵引电缆的保护也是忽略分布电容电流,直接沿用现有接触网的保护方案[3,11-12],显然,接触网和牵引电缆保护的准确性和可靠性大大降低.
因此,为了使新型电缆贯通供电系统接触网和牵引电缆在发生短路故障时,保护准确可靠,并且使故障范围降到最低,本文对接触网和牵引电缆的分段保护展开研究. 首先,针对双边受电模式下负荷电流会使接触网现有保护方案误动作的问题,探讨采用故障分量电流构成接触网的短路保护,以此消除双边供电下正常负荷电流的影响;然后,针对空载时电容电流会使高压牵引电缆现有保护方案误动作的情况,拟寻求一种消除电容电流影响的方法来构成牵引电缆的短路保护;最后,仿真验证本文所提接触网和牵引电缆保护方案的准确性和可靠性,为该系统的继电保护方案提供理论指导.
1. 系统组成与分段保护结构
1.1 电缆贯通供电系统
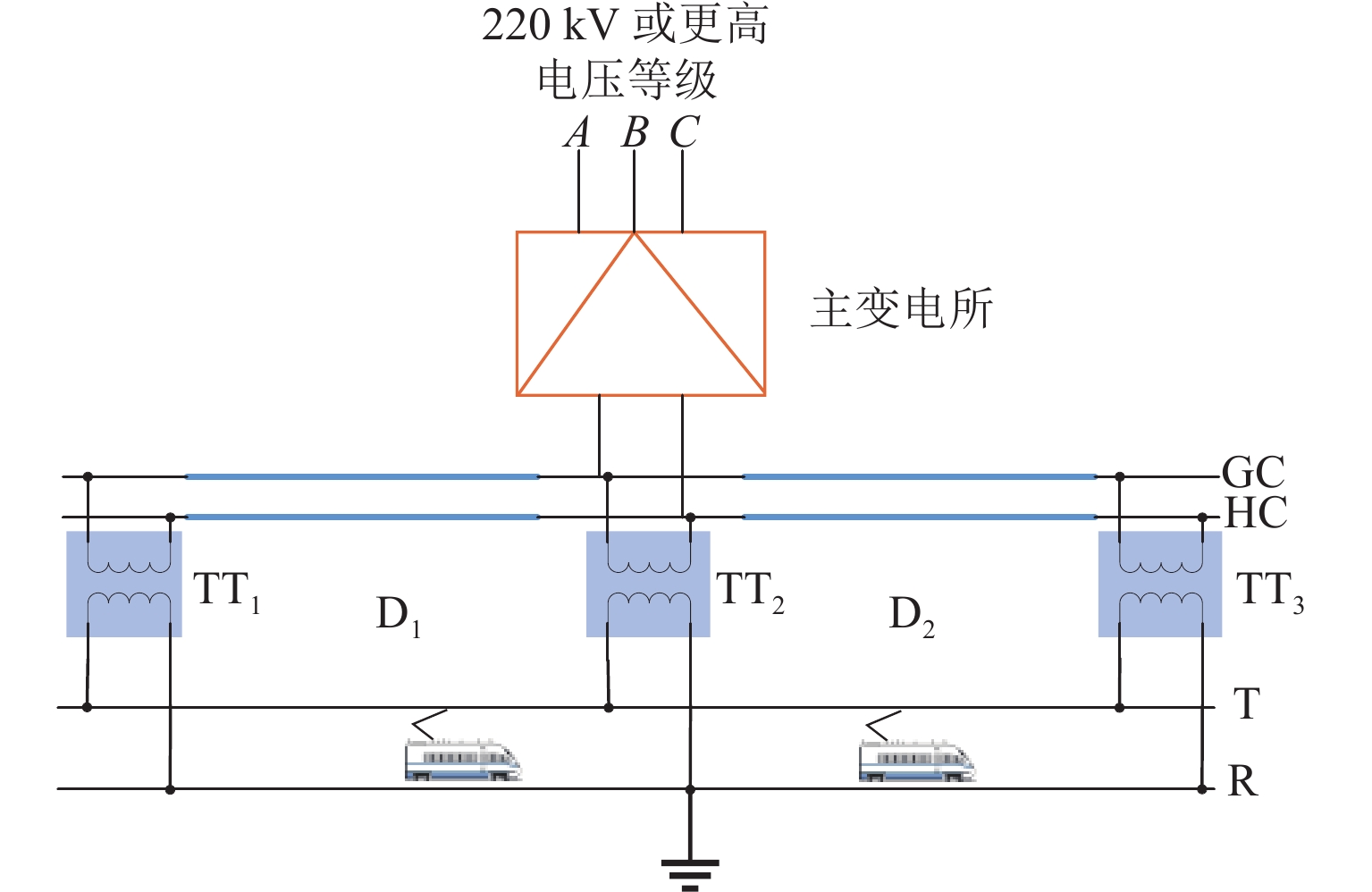
电缆贯通供电系统如图1所示. 图中:GC、HC分别为供电电缆和回流电缆;D1、D2为回路;T、R分别代表接触网和钢轨;TT1、TT2和TT3为牵引变压器. 主变电所一次侧与电力系统220 kV或者更高电压等级相连,二次侧连接110 kV牵引电缆(供电电缆和回流电缆),所内配置组合式同相供电装置[2],取消出口处电分相. 牵引电缆和27.5 kV接触网-钢轨沿电气化铁路铺设,牵引变压器一次侧和二次侧每隔一定距离连接牵引电缆和接触网-钢轨,实现全线贯通供电.
1.2 接触网和牵引电缆分段保护结构
接触网和牵引电缆采用分段保护方案,接触网和牵引电缆既可分开分段,也可集中分段[3]. 本文对接触网和牵引电缆采用集中在每个牵引变压器处进行分段,相邻的两个牵引变压器之间形成一个分段回路(简称回路). 如图1,回路D1、D2又分别包含对应回路的接触网回路和牵引电缆回路. 牵引电缆和接触网的分段保护结构一样,以接触网为例介绍分段保护结构和原理,如图2所示.
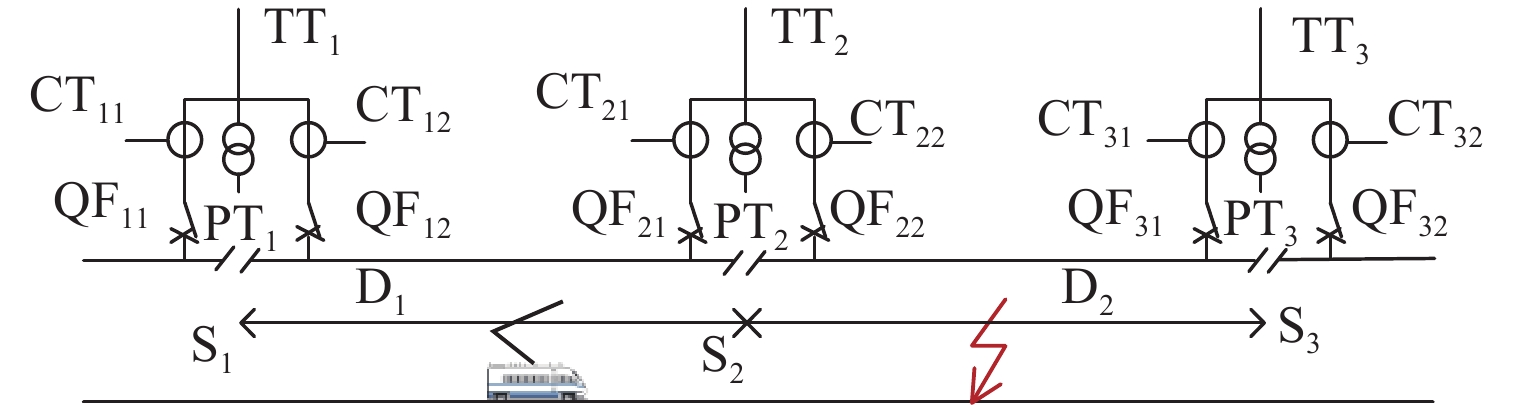
在牵引变压器处形成牵引所,每个牵引所包括牵引变压器(TT)、电流互感器(CT)、电压互感器(PT)、断路器(QF)和分段器(S). 电流互感器和断路器安装在每个分段线路左右两侧的分馈线上. 断路器正常运行时处于闭合状态,短路故障时断开用于切除故障回路. 每个牵引所的电流和电压互感器型号和变比均相同. 每个回路设置一个测控单元(CK),用于每个回路左右两侧的电流电压采集、短路故障判断和控制断路器动作. 测控单元可以借助微机保护装置实现对故障的判定. 为实现线路两端电流电压的同步采样,可以借助于GPS技术[13].
2. 接触网分段保护
2.1 现有保护方案
2.1.1 故障判据
文献[3]忽略接触网对地分布电容,提出新型系统接触网采用低电压启动的输电线路电流纵差保护,具体保护判据为
{Ux<Udz或Ux + 1<Udz,|˙Ix2+˙I(x + 1)1|>|˙Ix2−˙I(x + 1)1|, (1) 式中:Ux为第x个牵引所的接触网电压模值,$x= 1,2,\cdots$;Udz为设定的整定值;$ {\dot I_{x{2}}} $、${\dot I_{{(}x{ + 1)1}}}$分别为第x个牵引所右侧接触网电流和第x + 1个牵引所左侧接触网电流,以流入线路为正(下同),${\dot I_{x{2}}} + {\dot I_{{(}x{ + 1)1}}}$为差动电流,${\dot I_{x{2}}} - {\dot I_{{(}x{ + 1)1}}}$为制动电流.
文献[3]取制动电流为0,若满足式(1)则认定牵引所x和牵引所x + 1之间的接触网分段发生短路.
2.1.2 正常负荷对现有保护方案的影响
1) 正常负荷对本回路的影响
文献[3]指出,若Ux<Udz,但并没有发生短路时(这种情况由电压异常造成,本文称这种情况为非短路运行),${\dot I_{x{2}}} = - {\dot I_{{(}x{ + 1)1}}}$,$|{\dot I_{x{2}}} + {\dot I_{{(}x{ + 1)1}}}| = 0$,显然,这个结论是基于负荷是单边供电得出的,并没有考虑到新型系统接触网是一种特殊的双边供电形式. 文献[6]中已表明每个分段回路的机车由两侧的牵引变压器共同供电,负荷电流跟短路电流方向一样,均由两侧流入线路,所以Ux<Udz时就算没发生短路,$ |{\dot I_{x{2}}} + {\dot I_{{(}x{ + 1)1}}}| > 0 $也成立,因此,新型系统接触网如果继续采用式(1)作为短路保护判据,那么正常负荷情况下可能造成断路器误动作.
2) 正常负荷对非故障回路的影响
以图2为例,假设回路D1存在负荷,D2靠近牵引所TT2处发生接触网短路,因为D1中的机车由TT1和TT2共同供电,满足$ {U_{2}} < {U_{{\rm{d}}{\textit{z}}}}, |{{\dot I}_{12}} + {{\dot I}_{21}}| > 0 .$ 因此,当D2发生故障时,D1的断路器会误动作.
2.2 故障分量电流纵差保护
由以上分析可见,正常负荷电流成为了影响电流纵差保护方案的干扰因素,为了使接触网带负荷非短路运行时保护可靠不动作,而在发生短路故障时准确动作,就要找到一种新的保护方法,此方法需要消除负荷电流的影响,针对新型供电系统,本文提出采用故障分量电流构成纵差保护方法.
2.2.1 故障判据
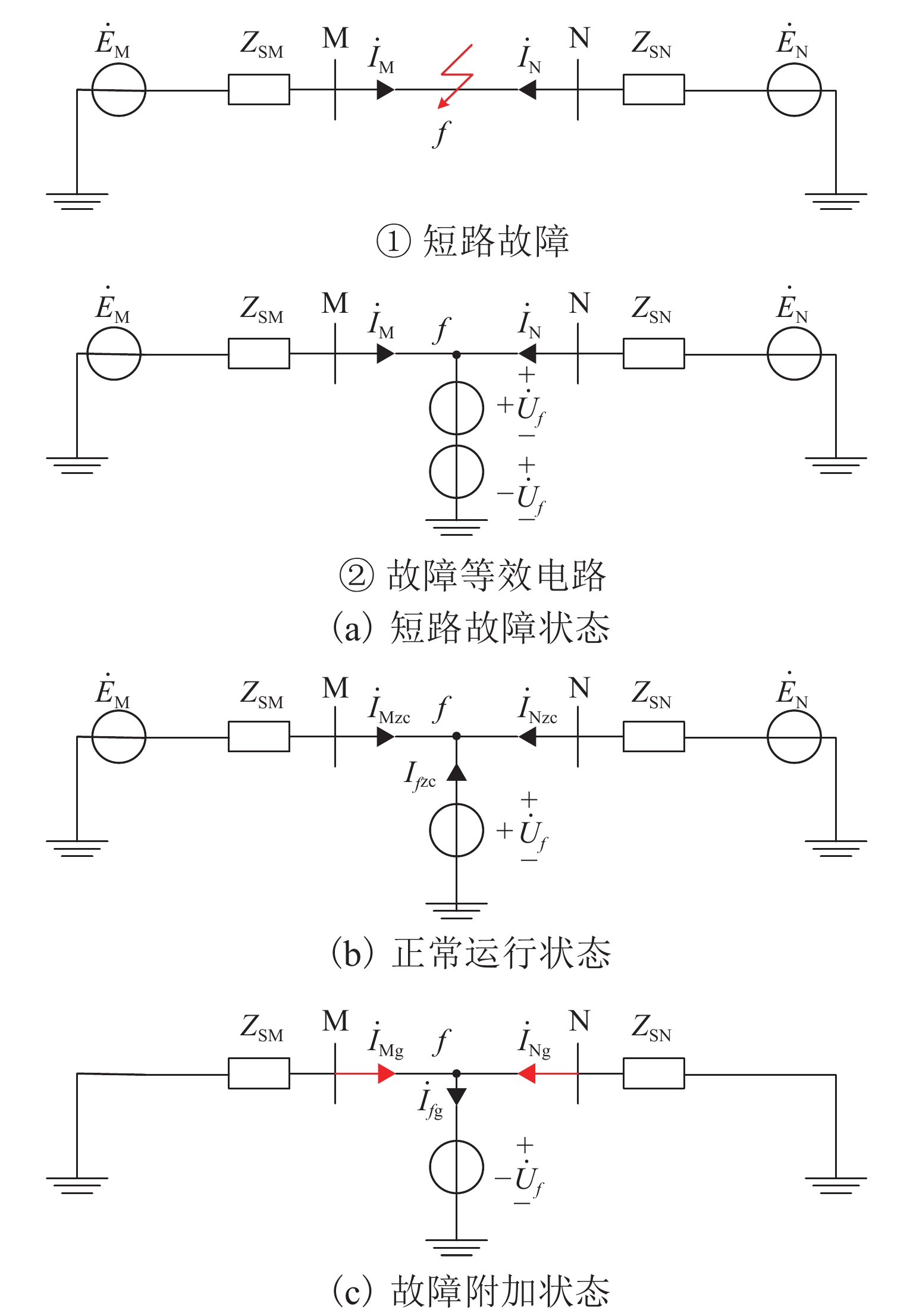
故障分量电流定义为发生故障后出现的电流,故障分量电流的原理如图3所示. 图中:${\dot E_{\rm{M}}}$、${\dot E_{\rm{N}}}$分别为线路两侧的电源;ZSM、ZSN分别为两侧等值系统阻抗;${\dot I_{\rm{M}}}$、${\dot I_{\rm{N}}}$(${\dot I_{\rm{{M}}{\textit{z}}{\rm{c}}}}$、${\dot I_{{\rm{N}}{\textit{z}}{\rm{c}}}}$)为短路故障状态(正常运行状态)时的电流;${\dot I_{f{{\textit{z}}\rm{{c}}}}} $、${\dot I_{f\rm{{g}}}} $分别为正常运行状态、故障附加状态下流经电压源的电流. 假设在点f发生短路故障,如图3(a)所示,这种状态称为短路故障状态. 在点f串联2个大小相等方向相反的电压源${\dot U_f}$等效为短路点,${\dot U_f}$是短路发生前点f的电压. 利用叠加原理可将图3(a)短路故障状态分解为图3(b)正常运行状态和图3(c)故障附加状态. 将图3(c)仅在短路故障后由${\dot U_f}$产生的电流${\dot I_{{\rm{Mg}}}}$、${\dot I_{{\rm{Ng}}}}$称为故障分量电流. 由叠加原理可知,在接触网带负荷正常运行时,${\dot I_{{\rm{Mg}}}}$、${\dot I_{{\rm{Ng}}}}$均为0,而在短路故障后不为0,因此,用故障分量电流${\dot I_{{\rm{Mg}}}}$、${\dot I_{{\rm{Ng}}}}$构成的纵差保护可以消除负荷电流的影响,使接触网在带负荷正常运行时保护可靠不动作. 但在接触网某回路发生短路后能否准确切除故障回路,而非故障回路可靠不动作还需要进一步讨论.
根据故障分量电流形式不同,可分故障分量相量电流纵差保护和故障分量瞬时值电流纵差保护2种 [14],则本文由故障分量电流构成的接触网保护判据由式(1)改写为式(2)和式(3).
{Ux<Udz或Ux + 1<Udz,|Δ˙Izg+Δ˙Iyg|>|Δ˙Izg−Δ˙Iyg|, (2) {Ux<Udz或Ux + 1<Udz,|Δizg+Δiyg|>|Δizg−Δiyg|, (3) 式中:$\Delta {\dot I_{{\textit{z}}{\rm{g}}}}$、$\Delta {\dot I_{{\rm{yg}}}}$($\Delta {i_{{\textit{z}}{\rm{g}}}}$、$\Delta {i_{\rm{yg}}}$)分别为牵引所x到牵引所x + 1分段接触网左侧和右侧故障分量相量电流(故障分量瞬时值电流).
这2个判据除了电流形式不同,保护性能并无差别[14].
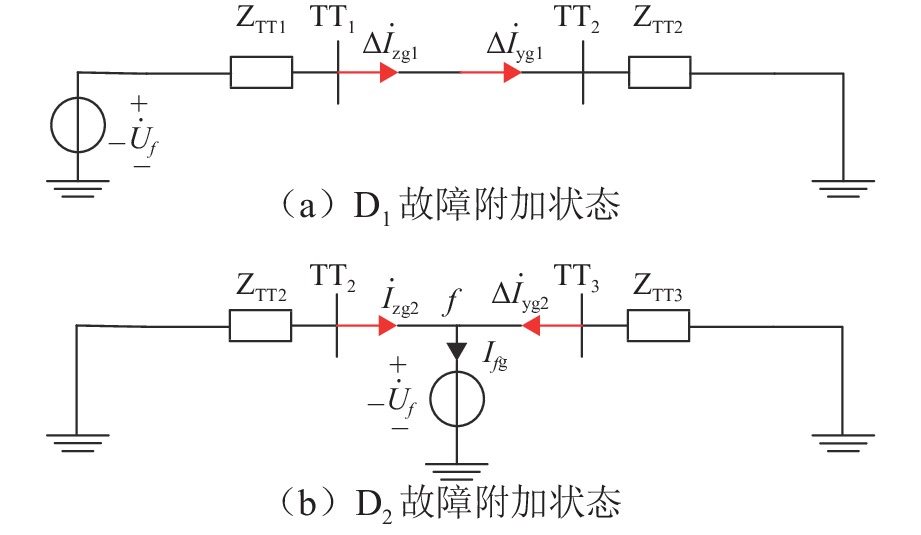
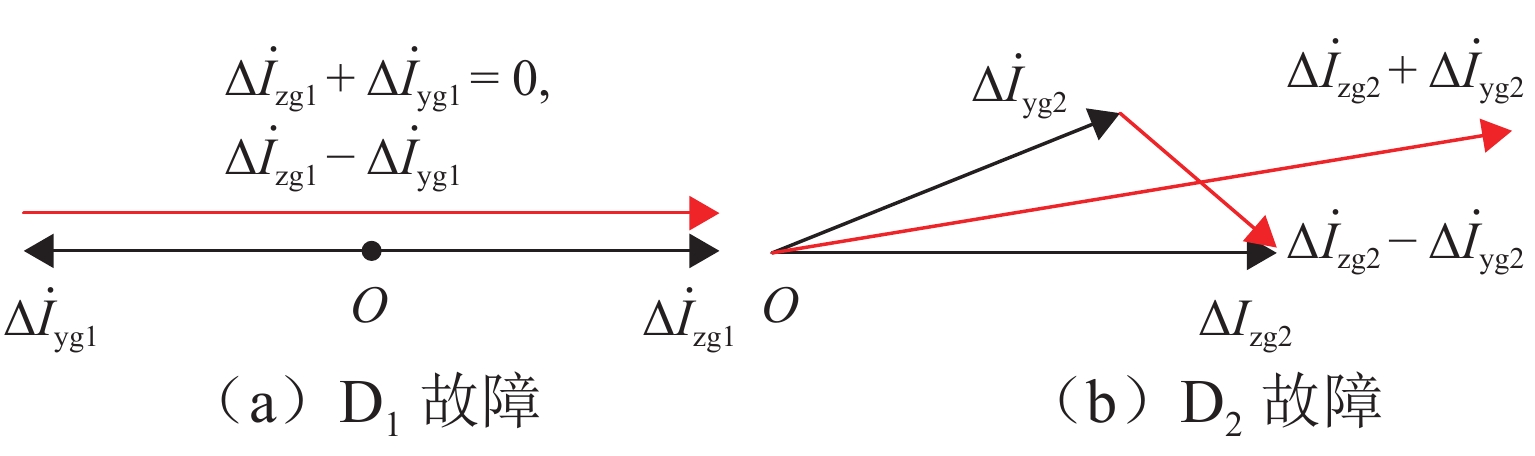
假设图1中D2分段回路接触网某位置f发生短路故障,附加电源${\dot U_f}$对于故障回路D2是区内电源,而对于非故障回路D1是区外电源,则D1、D2的故障附加状态如图4所示. 图中:${Z_{{\rm{TT}}{1}}}$、${Z_{{\rm{TT}}{2}}}$、${Z_{{\rm{TT}}{3}}}$分别为牵引变压器等效到二次侧阻抗;$\Delta {\dot I_{{{\textit{z}}{\rm{g}}1}}}$、$\Delta {\dot I_{{{\rm{yg}}1}}}$($\Delta {\dot I_{{{\textit{z}}{\rm{g}}2}}}$、$\Delta {\dot I_{{{\rm{yg}}2}}}$)分别为D1(D2)左、右两侧的故障分量电流.
由图5可知:回路D2 (D1)故障分量差动电流模值大于(小于)制动电流模值,则保护装置能够准确隔离故障回路D2,而非故障回路D1的断路器可靠不动作.
2.2.2 故障分量的提取
故障分量电流由式(4)采样提取[14].
Δi(k)=i(k)−i(k−G), (4) 式中:Δi(k)为第k次的故障分量电流采样值;i(k)为第k次的电流采样值;G为每个工频周期采样次数.
可见在接触网带负荷正常运行时,Δi(k)=0,而在接触网发生短路故障时Δi(k)≠0.
2.3 接触网保护动作流程
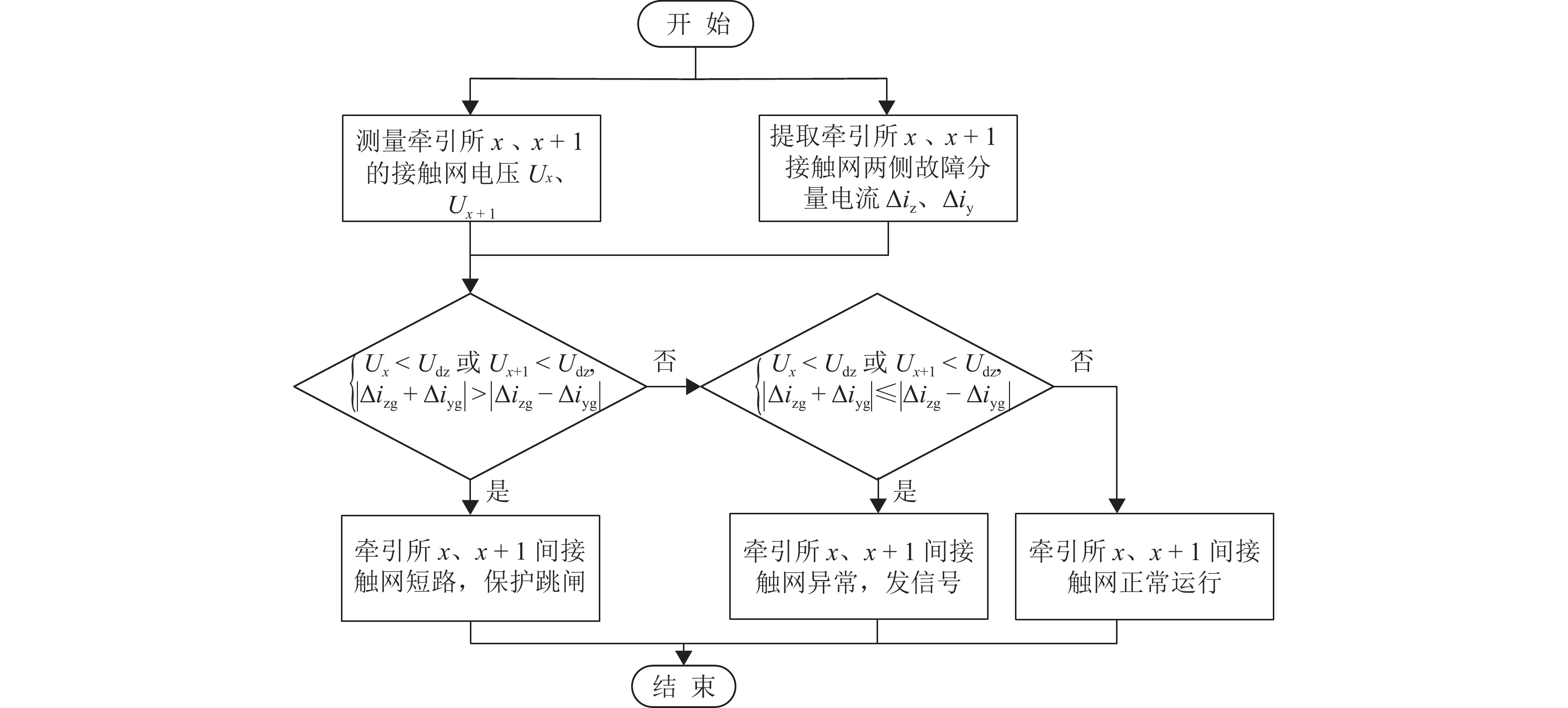
基于以上分析,本文所提的接触网保护方案的动作步骤和流程如图6所示.
3. 牵引电缆分段保护
3.1 现有保护方案
3.1.1 故障判据
文献[3]指出新型系统电缆分段保护沿用2.1.1节的接触网分段保护,此时式(1)中接触网的电压电流变为电缆的电压电流,然而,式(1)是忽略分布电容推导的,但是高压电缆的分布电容不容忽视,直接将式(1)用到电缆保护显然是不合理的.
3.1.2 分布电容对现有保护方案的影响
新型电缆贯通供电系统空载情况下电缆容性效应明显,电容电流使电缆两端电流大小和相位发生变化[15],从而影响式(1)的准确性. 而该系统在带负荷运行时电容对电流纵差保护影响不大[8],所以,本文重点研究空载情况下电缆电容对式(1)的影响. 类似于2.1.2节,分别针对Ux < Udz非短路运行和发生短路这两种情况分析电缆电容对式(1)保护的影响.
1) 空载非短路运行
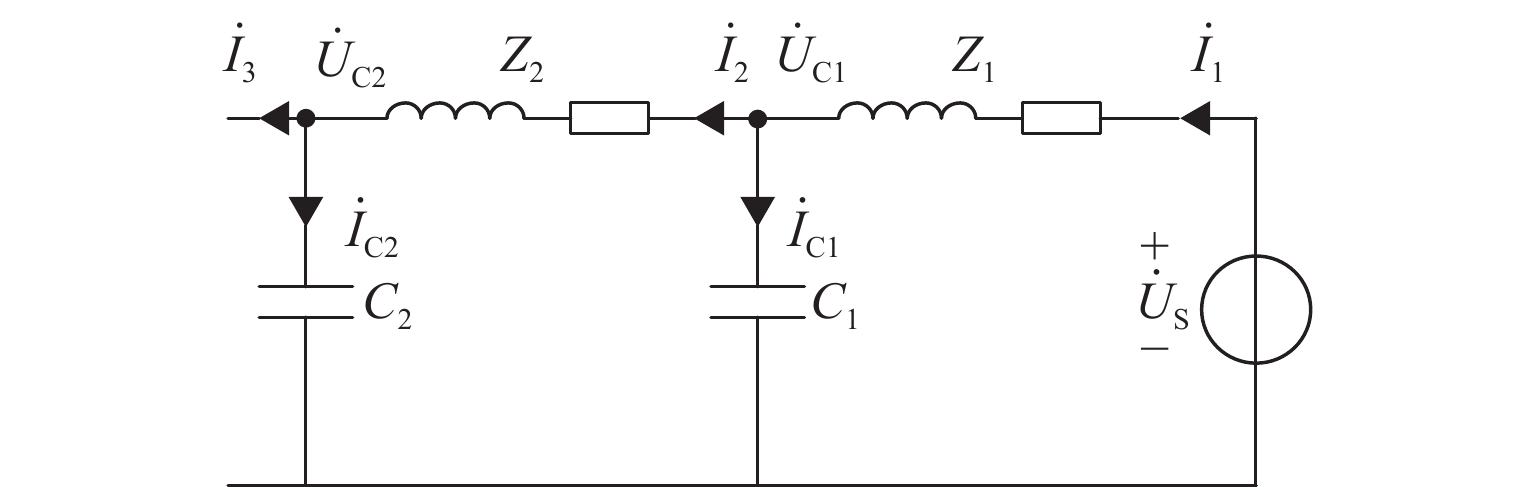
空载电缆贯通供电系统Ux < Udz非短路运行时,以图1回路D1为例分析牵引电缆断路器动作情况,回路D2电缆的动作情况同理分析. D1电缆回路等值电路如图7所示. 图中:${\dot U_{\rm{S}}}$为系统电源;${Z_1}$为系统阻抗;${Z_2}$为牵引电缆等值阻抗;${\dot I_1}$、${\dot I_2}$、${\dot I_3}$为对应支路电流;${\dot U_{{{\rm{C}}}1}}$、${\dot U_{{{\rm{C}}}2}}$为对应节点电压;${\dot I_{{\rm{C}}1}}$、${\dot I_{{\rm{C}}2}}$分别为流过电容${C_1}$、${C_2}$的电流.
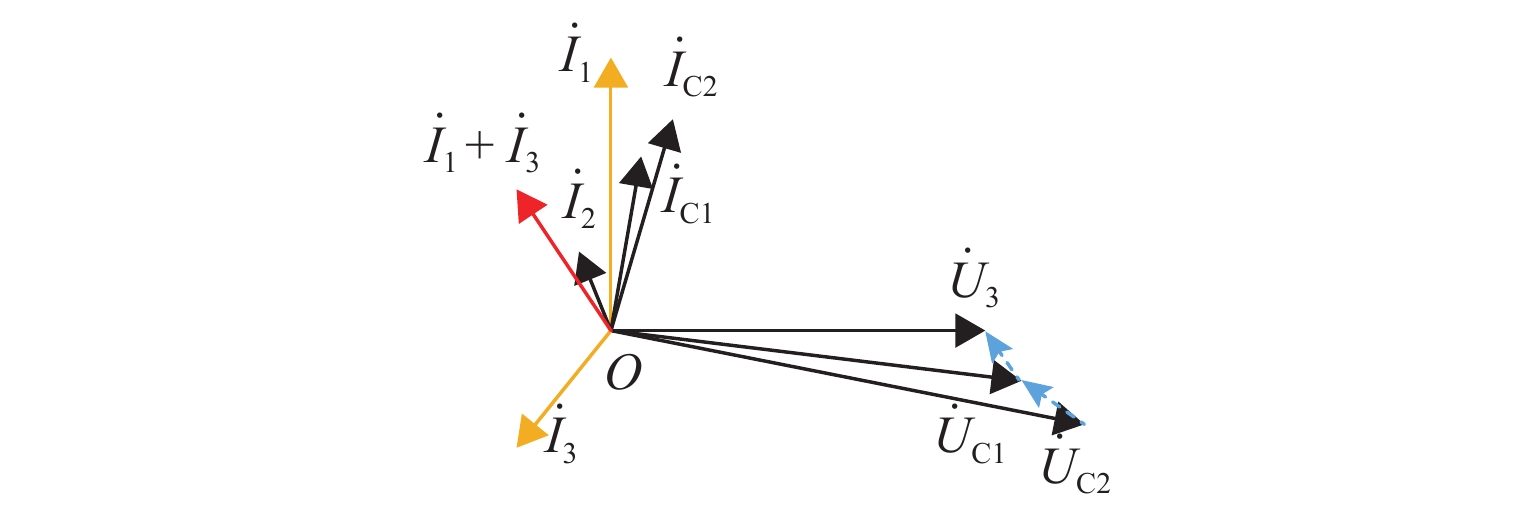
该系统空载正常运行时${\dot I_1}$几乎呈纯容性的电流[7],以${\dot U_{\rm{S}}}$为基准相量,将图7中各电流、电压的相量绘制在图8中.
由图8可知:电容电流${\dot I_{{\rm{C}}1}}$、${\dot I_{{\rm{C}}2}}$的存在使线路末端电流${\dot I_3}$较首端电流${\dot I_1}$的幅值和相位均发生变化,导致$\left| {{{\dot I}_1} + {{\dot I}_3}} \right| > 0$,可见式(1)成立,因此,该系统在空载Ux < Udz但未发生短路时,电缆电容会造成断路器误动作.
2) 空载短路运行
假设该系统空载情况下,回路D1发生牵引电缆短路故障,分析非故障回路D2牵引电缆电容对保护的影响. D2电缆回路等值电路如图9所示.
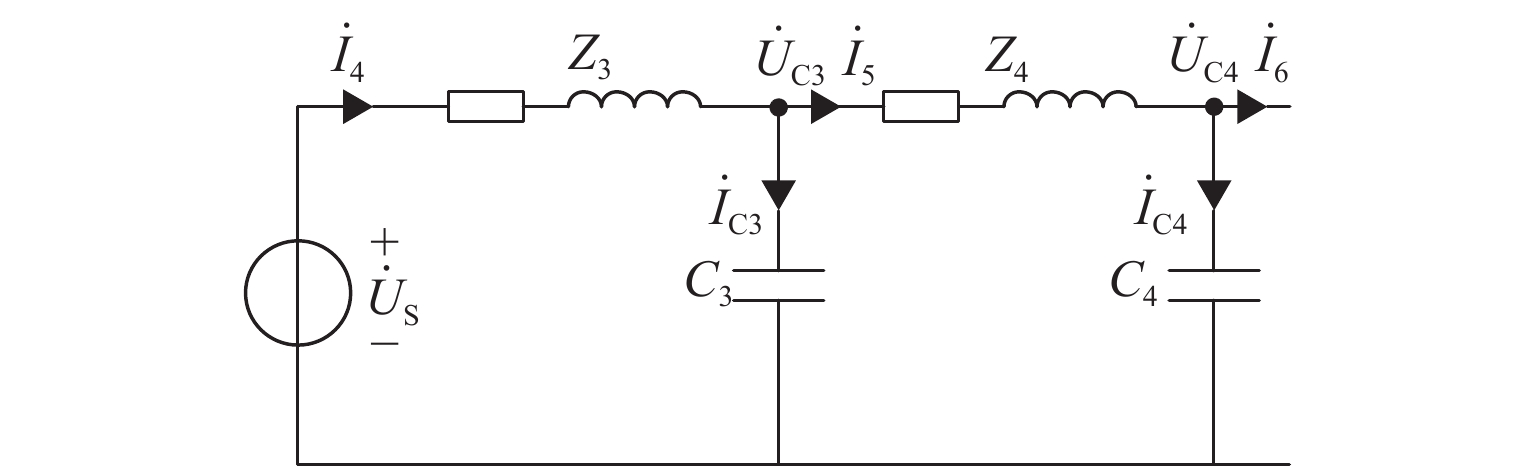
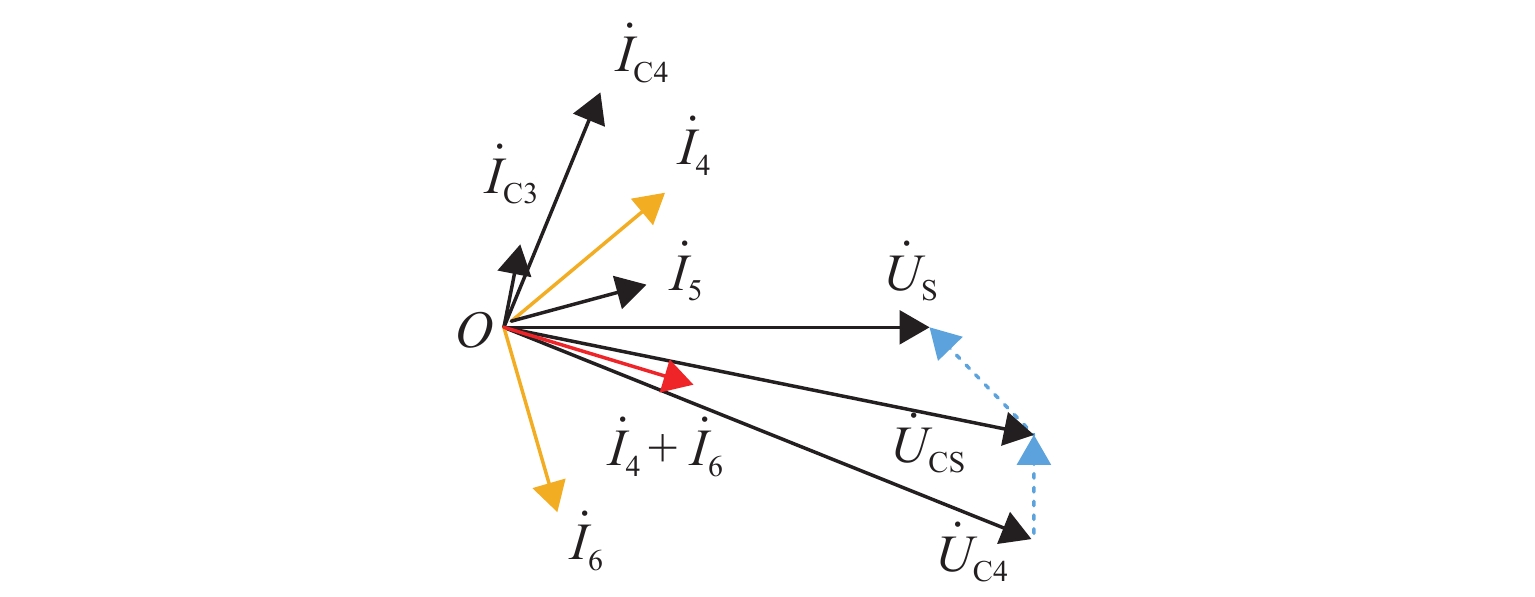
空载D1电缆短路情况下,同样以${\dot U_{\rm{S}}}$为基准相量,将图9中D2电缆回路各电流、电压的相量绘制在图10中.
图10表明,电容电流${\dot I_{{\rm{C}}3}}$、${\dot I_{{\rm{C}}4}}$的存在导致$\left| {{{\dot I}_4} + {{\dot I}_6}} \right| > 0$,满足式(1),即该系统在空载某回路发生电缆短路时,电缆电容的存在会导致非故障电缆回路断路器误动作.
3.2 空载下牵引电缆短路保护方法
分析可见,空载情况下电缆分布电容会使保护误动作,因此要采取相应措施,补偿掉空载情况下的电容电流,以此来构成牵引电缆的电流纵差分段保护,使空载情况下的断路器接收到正确的动作指令.
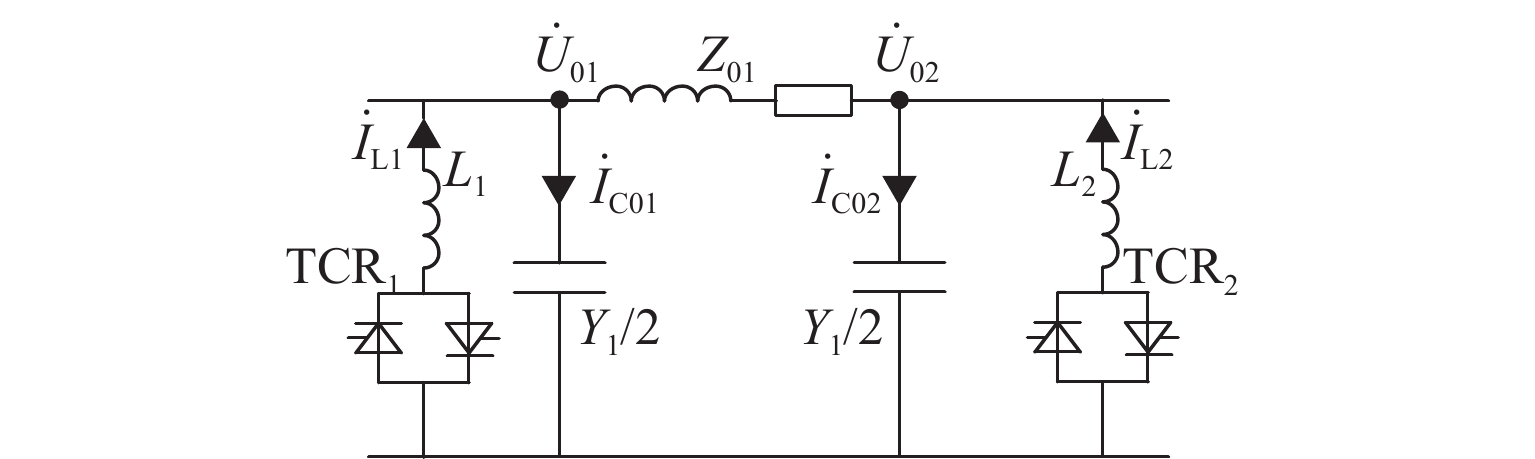
一条高压电缆输电线路可等效成一个π型等值电路[16],Z01为线路的阻抗,Y1为线路导纳,为了补偿电容电流,可以在线路首末两端分别产生一个与电容电流大小相等、方向相反的感性电流. 因此,本文采用在空载时牵引电缆首末两端并联电抗器,负载时切除电抗器的方法补偿空载下的电容电流,然后再构成电流纵差保护,电容电流补偿原理如图11所示. 图中:TCR为晶闸管控制的电抗器;L1、L2为线路首末两端并联电抗器的电感大小;${\dot I_{{{\rm{L}}}1}}$、${\dot I_{{{\rm{L}}}2}}$为电抗器提供的感性电流;${\dot I_{{{\rm{C0}}}1}}$、${\dot I_{{{\rm{C0}}}2}}$为空载时的电容电流;${\dot U_{01}}$、${\dot U_{02}}$为空载时线路首末两端的电压.
通过控制晶闸管的触发延迟角α实现电抗器的并联和退出,当α = π/2时,电抗器并联在系统中;当α = π时,电抗器退出运行.
全补偿空载电容电流时电抗器电感的大小由式(5)计算,以L1为例.
˙IC01+˙U01jωL1=0. (5) 为了避免系统发生谐振,通常对电容电流采取过补偿的方法,通常过补偿运行时的脱谐度不大于10%[17].
则本文牵引电缆保护判据由式(1)改写为
{UTx<UTdz或UT(x + 1)<UTdz,|˙Izb+˙Iyb|>|˙Izb−˙Iyb|, (6) 式中:UTx为第x个牵引所的电缆电压模值;${\dot I_{{\rm{zb}}}}$、$ {\dot I_{{\rm{yb}}}} $分别为牵引所x到牵引所x + 1分段牵引电缆左侧和右侧补偿电容电流后的电流.
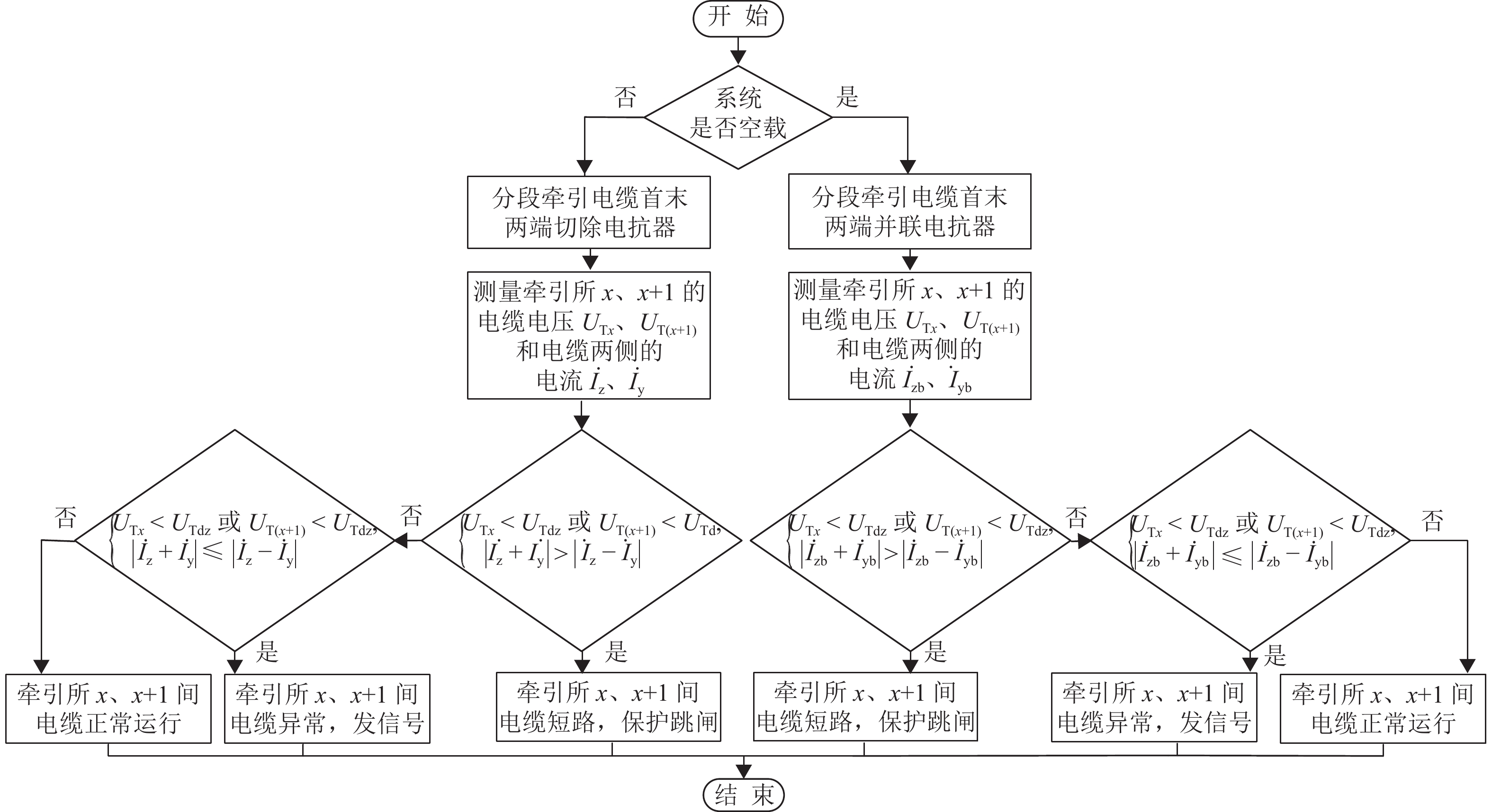
3.3 牵引电缆保护动作流程
基于本文所提的牵引电缆保护方案,其保护动作的步骤和流程如图12所示.
4. 仿真验证
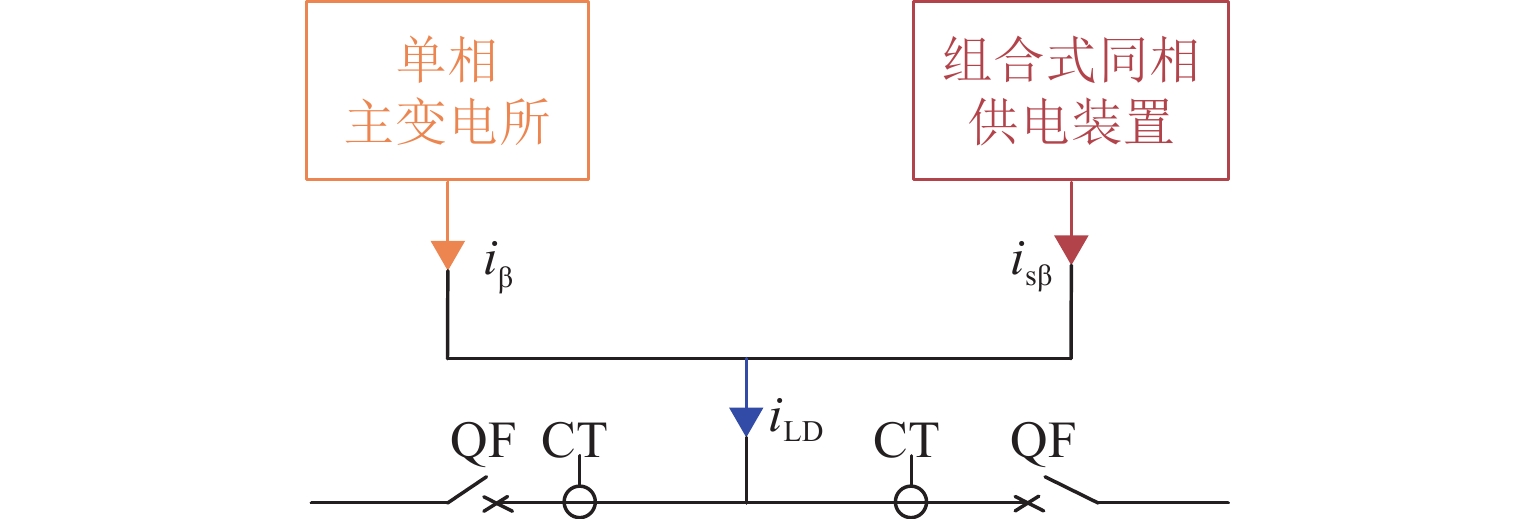
${i_{{\text{β}}}}$和${i_{{{\rm{s}}{\text{β}} }}}$分别是单相主变电所和组合式同相供电装置提供的电流. 组合式同相供电装置只是通过不同端口的电流来对负序、无功、谐波进行补偿,但是不会改变总的负荷电流${i_{{{\rm{LD}}}}}$. 由图13可知,流过牵引电缆和接触网电流互感器的电流就是${i_{{\rm{LD}}}}$的分量, 而${i_{{{\rm{LD}}}}}$只由负荷确定,跟有无组合式同相供电装置无关,所以本文为了使仿真变得简单但又不失准确性,就不考虑组合式同相供电装置模块.
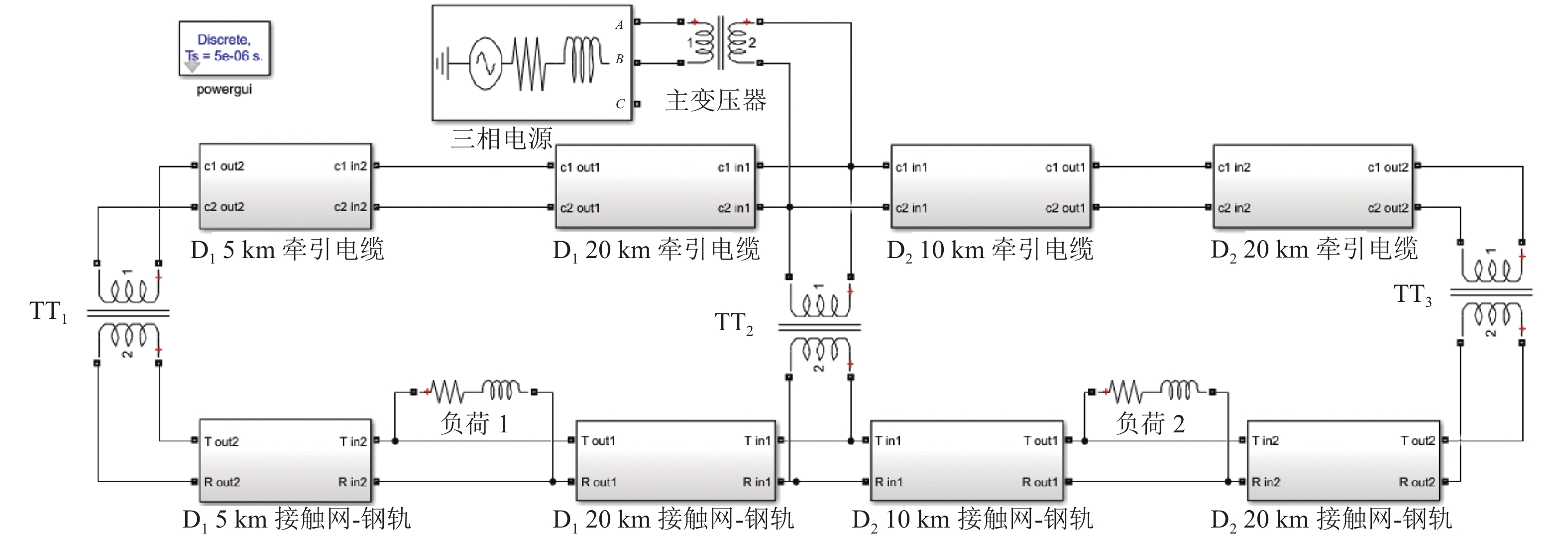
在MATLAB/Simulink中搭建图1所示的电缆贯通供电系统,牵引电缆和接触网-钢轨的线路参数引用文献[5],电力系统短路容量取18000 MV•A[18],单相主变压器容量取120 MV•A,牵引变压器容量取40 MV•A,机车功率为20 MW,功率因数0.98,回路 D1、D2长度分别取25、30 km[7], D1、D2各一辆机车,分别位于距离TT1 5 km、TT2 10 km处,仿真模型如图14所示.
4.1 接触网短路保护验证
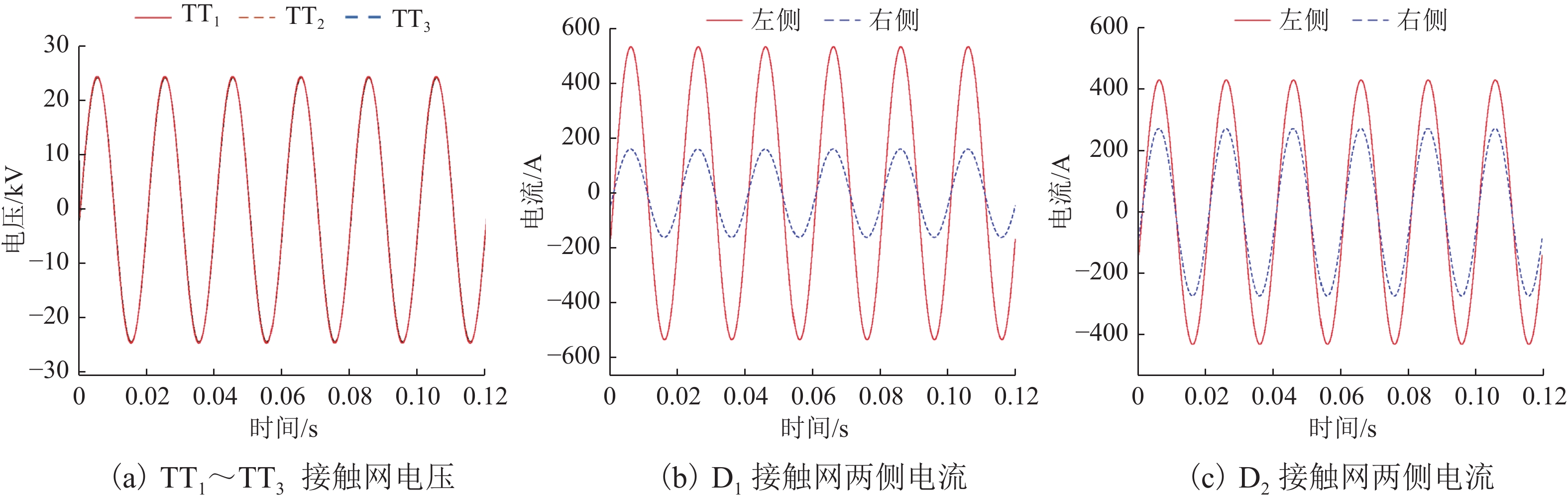
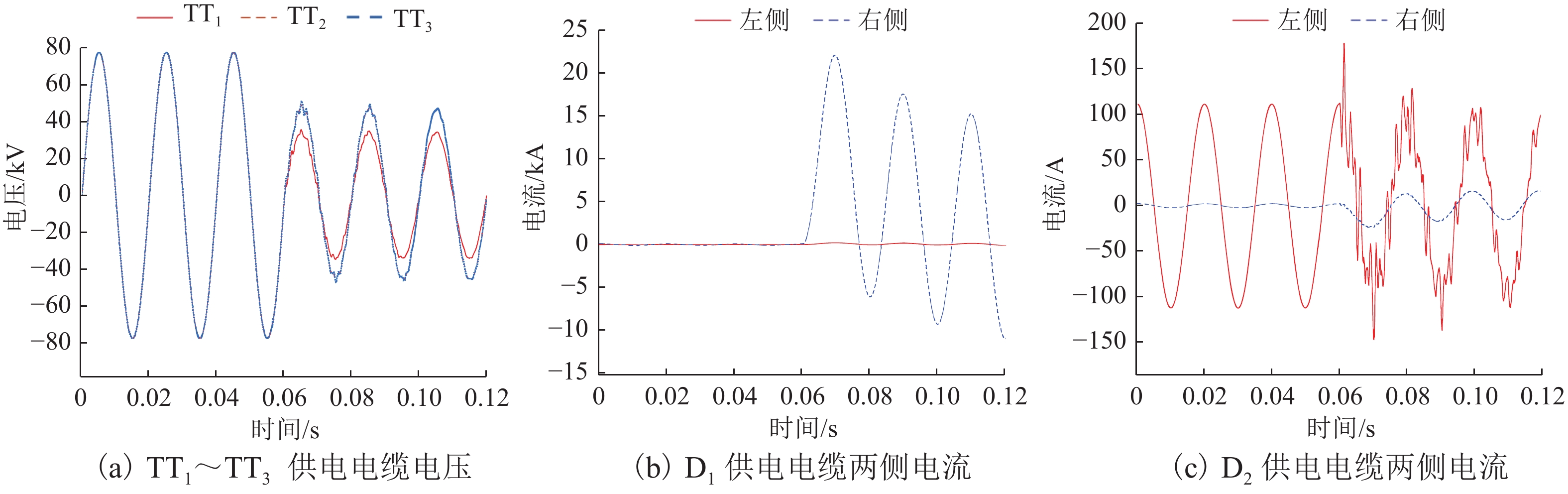
分别建立工况1 (电压异常导致Ux<Udz但接触网并没发生短路)和工况2 (0.06 s时D2距离TT35 km处接触网发生短路)2种情况. 工况1将主变电所输出电压由110 kV降为70 kV来模拟,接触网Udz取18 kV[11]. 工况1和工况2各测量点的电压电流波形分别如图15和图16所示.
考虑计算量,本文采用故障分量瞬时值电流纵差保护,将图15、16中D1、D2接触网回路左右两侧的故障分量电流瞬时值进行一周波6次采样[14]. 记录下牵引所TT1~TT3二次侧接触网电压模值U1~U3和D1、D2回路接触网的差动电流模值和制动电流模值. 工况1和工况2的数据分别如表1和表2所示,因为表1中本文方法6次采样的结果一样,所以只记录1次的数据即可.
表 1 工况1数据Table 1. Data under working condition 1方法 U1/kV U2/kV U3/kV D1 差动电流/A D1 制动电流/A D2 差动电流/A D2 制动电流/A 现有方法 17.198 17.247 17.385 491.264 0 496.225 0 本文方法 17.198 17.247 17.385 0 0 0 0 表 2 工况2数据Table 2. Data under working condition 2方法 U1/kV U2/kV U3/kV D1 差动电流/A D1 制动电流/A D2 差动电流/A D2 制动电流/A 现有方法 22.402 13.588 19.798 582.223 0 8951.995 0 本文方法采样 1 26.719 26.291 26.813 84.654 332.961 3480.336 828.158 本文方法采样 2 25.524 23.080 24.869 115.695 1049.229 11058.398 2368.965 本文方法采样 3 25.103 21.813 24.144 11.336 1161.157 13402.426 2740.661 本文方法采样 4 24.627 20.622 23.409 120.269 382.164 7222.369 1448.219 本文方法采样 5 23.018 15.829 20.827 144.321 682.623 2614.296 442.224 本文方法采样 6 22.402 13.588 19.798 36.965 1012.364 6693.269 1117.495 由表1可知:当电压Ux<Udz但并没发生短路时,现有方法回路D1和D2均满足式(1),断路器会误动作;而本文方法所提的故障分量纵差电流模值和制动电流模值均为0,不满足式(3),断路器可靠不动作,与理论分析一致.
由表2可知:当回路D2发生接触网短路故障时,现有方法非故障回路D1满足式(1),导致非故障回路的断路器误动作,而本文所提方法非故障回路D1的故障分量差动电流模值均小于制动电流模值,不满足式(3),非故障回路断路器可靠不动作,继续运行;本文方法在第5次采样时,故障回路D2满足式(3),断路器准确动作,切除故障. 结果验证了采用故障分量电流构成接触网纵差分段保护方案的正确性和可靠性.
4.2 牵引电缆短路保护验证
空载运行时回路D1、D2供电电缆左右两侧电容电流的大小如表3所示.
表 3 空载电容电流Table 3. Capacitance current without loadA D1 左侧 D1 右侧 D2 左侧 D2 右侧 33.522i 33.429i 40.123i 40.284i 由表3可知:空载下电缆会流过较大的容性电流,影响电流纵差保护的正确动作,不容忽视. 将表3数据代入式(5)便可求出完全补偿电容电流时回路D1、D2左右两侧电抗器大小分别为5.269、4.388 H,本文脱谐度取5%,则仿真时电抗器的大小分别取5.561、4.621 H.
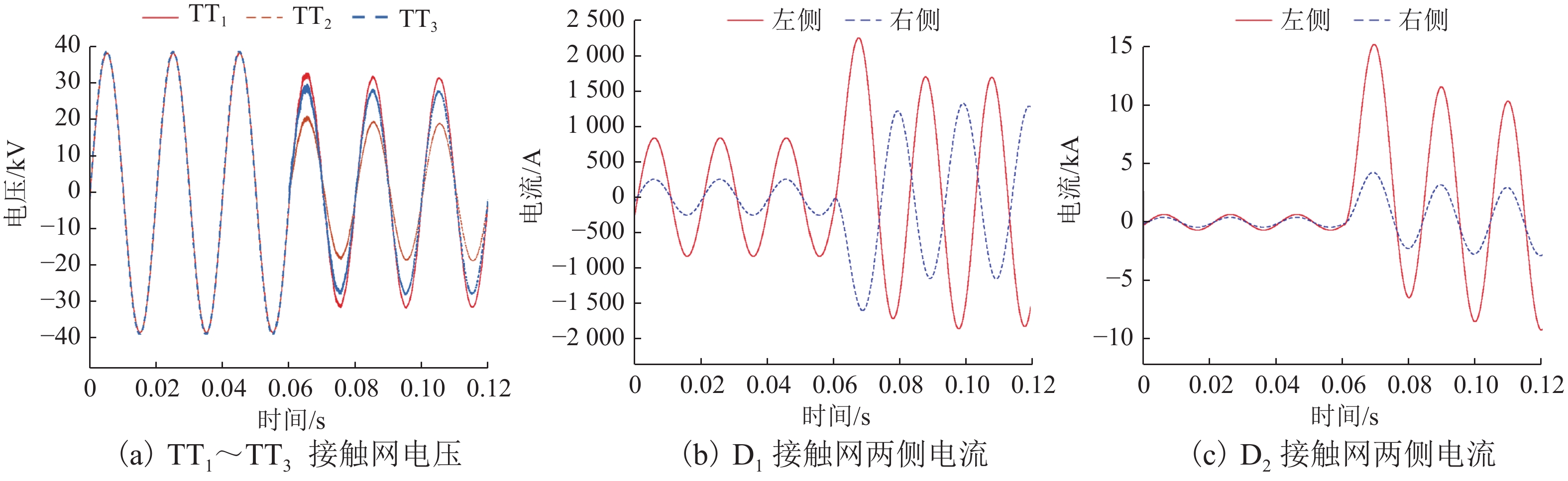
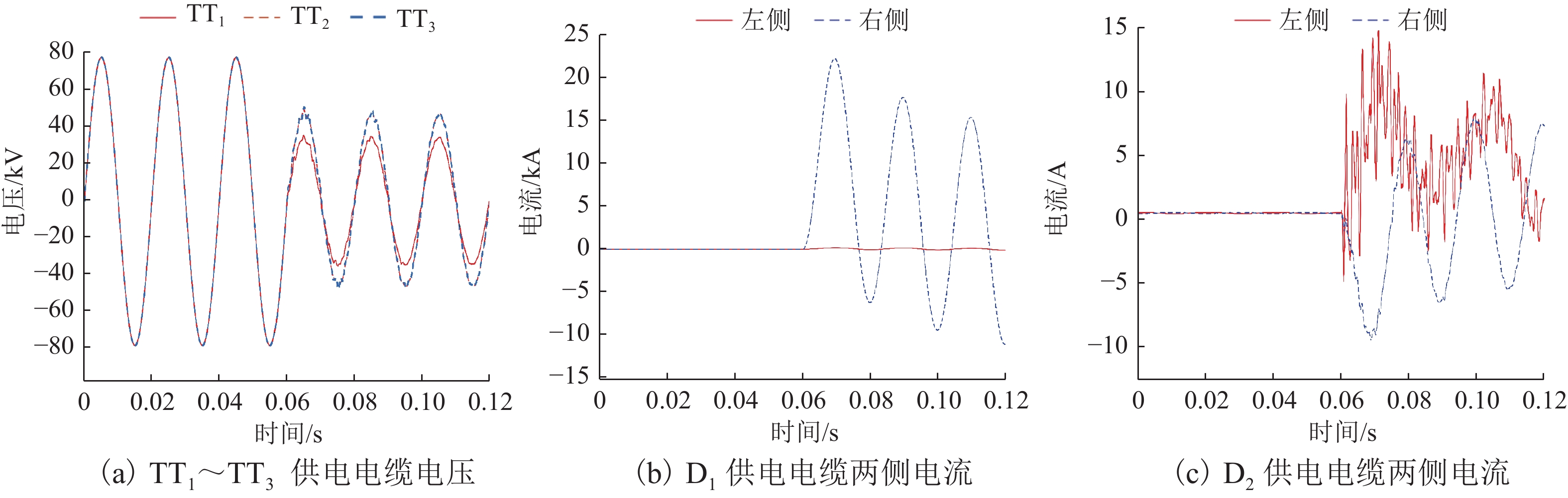
建立负载正常运行、负载运行回路D1发生供电电缆接地短路、负载运行回路D1发生电缆相间短路、空载非短路运行(将主变电所输出电压由110 kV降为70 kV来模拟)、空载回路D1发生供电电缆接地短路和空载回路D1发生电缆相间短路等各种工况,以上空载分为并联电抗器(现有方法)和并联电抗器(本文方法)2种情况,短路时刻均为0.06 s,短路点均距离主变电所10 km处. 给出上述空载未并联电抗器时回路D1供电电缆接地短路(工况3)和空载并联电抗器时回路D1供电电缆接地短路(工况4)2种情况的电压电流波形,如图17、18所示,其他情况的电压电流波形限于篇幅,不再给出.
记录上述所有情况的TT1~TT3一次侧供电电缆电压模值UT1~UT3和回路D1、D2供电电缆左右两侧的差动电流模值和制动电流模值,数据如表4所示,供电电缆UTdz取40 kV[11].
表 4 各种工况下回路D1、D2供电电缆数据Table 4. Data of power supply cables in D1 and D2 loops under various working conditions工况 UT1/kV UT2 /kV UT3/kV D1 差动电流/A D1 制动电流/A D2 差动电流/A D2 制动电流/A 负载正常运行 54.784 55.042 55.019 66.124 284.125 83.256 155.546 负载 D1 供电电缆接地 24.124 32.890 32.821 9154.159 9049.589 77.553 94.227 负载 D1 电缆相间短路 0.653 24.842 24.677 12614.594 12186.234 35.556 85.269 现有方法空载非短路运行 35.326 35.228 35.368 63.334 0 79.956 0 现有方法空载 D1 供电电缆接地 24.390 32.984 33.055 9191.226 0 154.953 0 现有方法空载 D1 电缆相间短路 0.686 24.886 24.817 12650.221 0 133.895 0 本文方法空载非短路运行 35.001 35.001 35.001 0.080 221.665 0.110 311.000 本文方法空载 D1 供电电缆接地 24.147 32.765 32.652 9203.228 9038.965 0.211 199.356 本文方法空载 D1 电缆相间短路 0.667 24.837 24.681 12633.968 12178.846 0.051 568.596 由表4可知:负载各种工况下,回路D1、D2断路器均能根据式(6)收到正确的动作指令. 现有方法空载各种工况下:电压异常但未发生短路时,回路D1、D2供电电缆电压和电流(电容电流)均满足式(1),保护误动作;回路D1发生电缆短路时,非故障回路D2供电电缆电压和电流也满足式(1),保护误动作. 本文方法空载各种工况下:电压异常但未发生短路时,回路D1、D2供电电缆电流不满足式(6),保护可靠不动作;回路D1发生电缆短路时,故障回路D1供电电缆电压和电流满足式(6),保护准确动作,非故障回路D2供电电缆电流不满足式(6),保护可靠不动作. 结果验证了空载情况下并联电抗器、负载情况下切除电抗器所构成牵引电缆电流纵差分段保护方案的准确性和可靠性.
5. 结 论
新型电缆贯通供电系统的保护方案由于接触网类似于双边供电形式和牵引电缆电容的存在较既有牵引供电系统更加复杂,因此本文对电缆贯通供电系统的接触网和牵引电缆短路保护进行研究,总结如下:
1) 接触网和牵引电缆采用分段保护方案,发生短路故障时对应回路被切除,而非故障回路继续运行,将故障范围降到最低.
2) 该系统的接触网类似于双边供电,负荷电流会引起现有保护方案误动作,采用故障分量电流构成纵差保护能有效消除负荷影响,使接触网带负荷正常运行时保护可靠不动作,当某回路发生故障时能够正确切除故障回路,而非故障回路断路器可靠不动作.
3) 牵引电缆电容会在空载情况下引起现有保护方案误动作,采用空载时电缆首末两端并联电抗器,及负载时切除电抗器构成电流差动保护可以有效解决这个问题,使空载和负载时断路器都能正确动作. 并且该方案在空载时投入电抗器可很好抑制电缆电压抬升,负载时切除电抗器也不影响系统性能.
-
史先伟. 客运专线高陡边坡洞门及缓冲结构设计[J]. 铁道建筑技术,2012(5):91-95. SHI Xianwei. Design of tunnel portal and tunnel hood with high-steep slope for passenger dedicated line[J]. Railway Construction Technology, 2012(5):91-95. 黄伦海,蒋树屏,张军. 公路隧道洞口环保型设计施工现状及展望[J]. 地下空间与工程学报,2005,1(3):455-459. HUANG Lunhai, JIANG Shuping, ZHANG Jun. Current status and prospect of environmental design and construction of road tunnel entrance[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(3):455-459. 贾玲利,赵东平. 隧道洞口景观现状及发展趋势研究[J]. 土木工程学报,2008,41(1):88-92. JIA Lingli, ZHAO Dongping. A study on the trend of development and present state of tunnel entrance landscaping[J]. China Civil Engineering Journal, 2008, 41(1):88-92. 黄亚平,陈兰兰. 陕西多地秋雨连绵, 西汉高速山石滚落堵了隧道[N]. 西安晚报,2011-9-14. WANG Yusuo, TANG Jianhui, YAN Tao, et al. Model test investigation of rock-fall impaction to cut-and-cover tunnel arch structure[J]. Applied Mechanics and Materials, 2011, 90-93:2492-2499. 王玉锁,周良,李正辉, 等. 落石冲击下单压式拱形明洞的力学响应[J]. 西南交通大学学报,2017,52(3):505-515. WANG Yusuo, ZHOU Liang, LI Zhenghui, et al. Mechanical responses of single-pressure arch-shaped open tunnel structure under rockfall impaction[J]. Journal of Southwest Jiaotong University, 2017, 52(3):505-515. 中铁二院工程集团有限责任公司. Q/CR 9129-2015铁路隧道极限状态法设计暂行规范[S]. 北京:中国铁道出版社,2015. 李乔,赵世春. 汶川大地震工程震害分析[M]. 成都:西南交通大学出版社,2008:203. 曹志远. 板壳振动理论[M]. 北京:中国铁道出版社,1989:317. 咸玉席. 弹丸撞击下钢筋混凝土结构的安全计算与评估[D]. 合肥:中国科学技术大学,2014. 余同希,邱信明. 冲击动力学[M]. 北京:清华大学出版社, 2011:41. LIU Bin, SOARES C G. Plastic response and failure of rectangular cross-section tubes subjected to transverse quasi-static and low-velocity impact loads[J]. International Journal of Mechanical Sciences, 2015, 90:213-227. FAMIYESIN O O R, HOSSAIN K M A, CHIA Y H, et al. Numerical and analytical predictions of the limit load of rectangular two way slabs[J]. Computers and Structures, 2001,79(1):43-52. 余波. 基于塑性极限分析理论的体系可靠度分析[D]. 南宁:广西大学,2007. 王玉锁,李俊杰,李正辉,等. 落石冲击力评定的离散元颗粒流数值模拟研究[J]. 西南交通大学学报,2016,51(1):22-29. WANG Yusuo, LI Junjie, LI Zhenghui, et al. Assessment of rockfall impact force by particle flow code numerical simulation based on discrete element model[J]. Journal of Southwest Jiaotong University, 2016, 51(1):22-29. 中华人民共和国铁道部. GB50216-94铁路工程结构可靠度设计统一标准[S]. 北京:中国计划出版社,1995. 赵国藩,金伟良,贡金鑫. 结构可靠度理论[M]. 北京:中国建筑工业出版社,2000:31-42. 张明. 结构可靠度分析-方法与程序[M]. 北京:科学出版社,2009:26-44. 中铁二院工程集团有限责任公司. 新建铁路长沙至昆明客运专线玉屏至昆明段变更设计施工图[R]. 贵阳:中铁二院工程集团有限责任公司沪昆铁路客运专线项目部,2014. 中华人民共和国住房和城乡建设部. GB50010-2010混凝土结构设计规范[S]. 北京:中国建筑工业出版社,2010. 赵东平,喻渝,赵万强,等. 铁路隧道衬砌目标可靠指标研究[J]. 铁道工程学报,2015,32(6):51-56. ZHAO Dongping, YU Yu, ZHAO Wanqiang, et al. Research on the target reliability index of railway tunnel lining[J]. Journal of Railway Engineering Society, 2015, 32(6):51-56. 张晓静.铁路隧道复合式衬砌目标可靠指标及分项系数研究[D]. 石家庄:石家庄铁道大学,2014. 中国铁路总公司. Q/CR9007-2014铁路工程结构可靠性设计统一标准(试行)[S]. 北京:中国铁道出版社, 2014. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 621
- HTML全文浏览量: 107
- PDF下载量: 55
- 被引次数: 0





 下载:
下载:


















 下载:
下载: