Numerical Simulation Analysis of RC Beams Strengthened with CFRP Using Viscoelasticity Constitutive
-
摘要: 为探讨胶黏剂粘弹性对碳纤维增强复合材料(CFRP)加固钢筋混凝土(RC)梁力学行为的影响,以Burger模型表征胶黏剂的应力-应变-时间关系,利用Laplace变换和逆变换推导了Burger模型Prony级数形式的松弛剪切模量;采用ABAQUS对粘贴CFRP加固RC梁进行数值模拟,分析了胶黏剂粘弹性对界面应力、CFRP轴力、RC梁弯矩和加固梁挠度的影响.研究结果表明:胶黏剂的粘弹性对加固梁的力学行为有一定的影响,随着持载时间的增加,界面峰值剪应力和峰值正应力均减小,CFRP轴力减小,RC梁弯矩增大,加固梁挠度增大;当胶层厚度为0.2 mm时,加载30 d后,界面峰值剪应力减小了40.1%,界面峰值正应力减小了33.0%,加固梁挠度增加了3.7‰,距离CFRP端部20 mm处截面上CFRP轴力减小了15.8%,RC梁弯矩增加了17.4%.Abstract: In order to investigate the mechanical behavior influence of the adhesive viscoelastic on reiforced concrete beams strengthened with the carbon fiber reinforced polymer, the Burger model was used to describe the stress-strain-time relation for the adhesive. The relaxation shear modulus with Prony series forms of Burger model was derived by the mathematical method of Laplace transform and inverse Laplace transform. The finite element software ABAQUS was used to simulate RC beams strengthened with the CFRP. The influence of the adhesive viscoelastic on the stresses of the adhesive, the axial force of the CFRP, the moment of RC beams and the deflection of the reinforced beam were analyzed. The results show that the adhesive viscoelastic affect the mechanical behavior of the reinforced beam to a certain degree. With the increasing of the loading time, the shear stresses and normal stresses peak value of the adhesive decrease, the axial force of the CFRP decrease, the bending moment of the RC beam increase and the deflection of the reinforced beam increase. When the adhesive layer thickness is 0.2 mm, and the reinforced beam has been loaded for 30 d. The peak shear stress decreases by 40.1%, the normal peak stress decreases by 33.0%, the deflection of the reinforced beam increase by 3.7 ‰. On the cross section 20 mm away from the end of the CFRP, the CFRP axial force decreases by 15.8% and the bending moment of the RC beam increases by 17.4%.
-
Key words:
- strengthen /
- mechanical behavior /
- viscoelastic /
- constitutive laws /
- simulation analysis
-
沥青混合料施工中,压实对成型路面结构的使用寿命和路用性能起到决定性作用. 摊铺机对沥青混合料进行平整与初步压实,压路机复压和终压,使最终成型路面的密实度达到沥青路面施工技术规范要求. 摊铺层初始密实度越高,后续的碾压作业越少,节约施工成本[1].
振捣机构是摊铺机压实装置的重要部件之一,振捣机构偏心轴带动振捣梁和振捣锤对沥青混合料产生周期性的强制压缩作用,沥青混合料颗粒之间的空气被排出,大小颗粒相互挤压交错重新排列,从而形成致密结构. 压路机的振动载荷使颗粒处于高频振动状态,使颗粒重新排列,进一步排出混合料颗粒之间的空气,提高混合料的密实度. 若摊铺阶段的密实度不足或产生离析,摊铺层在压路机的高频振动下受到同一压实功作用,将产生压实密度的分布不均匀. 因此,摊铺机振捣压实性能的好坏与作业参数的选择对于提高摊铺层混合料的初始密实度起关键性的作用[2].
殷超等[3]基于振捣机构和铺层材料之间的动态模型,分析了振动参数的选择对压实系统动态性能的影响. Wang等[4]指出应重点对振捣机构参数进行调节,以获得最佳摊铺效果,但是在研究摊铺机振捣机构时,只是将振捣过程简化成简谐振动,进行了粗略的计算. Plati等[5]通过不同压实作用方式对沥青混合料密实特性的影响研究,计算了冲击压实的运动参数,但计算过程较为繁琐. 孙健[6]通过建立振捣机构动力学模型,分析了振捣频率和振幅对振捣梁惯性力的影响规律,得出满足路面压实度的条件下,应尽量采用低频振捣的结论. 前期研究和工程施工表明,振捣机构工作参数的选择影响路面压实成型质量,同时摊铺层密实度越高,越易提高路面压实成型质量[7]. 金书滨等[8]指出振捣压实可以明显提高铺层的密实度,在一定仿真条件下,可以确定振捣参数的理想取值范围. 罗丹等[9]中通过建立压实装置力学模型,研究了振捣机构-介质系统的运动规律和动力学特性,基于熨平板横向振幅不均匀性,对振动器偏心质量与偏心距进行优化配置,提高了熨平板摊铺压实质量. 刘洪海等[10-11]基于共振压实理论建立了摊铺机振动参数与铺层混合料密实度之间关系,确定了最佳振动参数范围. 由谐波共振理论可知,系统存在主共振的同时,还会产生频率为基波频率倍数的谐波振动[12-13]. 在实际施工过程中,振捣参数的调节难以达到最佳振捣压实效果,需要进一步研究振捣参数对铺层密实度影响规律.
本文在已有研究成果的基础上,基于机械与材料相互作用机理,将振捣机构作用看作周期性非正弦振动波,重点研究了振捣频率的变化对铺层压实效果的影响. 建立振捣机构与铺层材料组成的振捣压实系统,通过动力学分析与试验研究,得到振捣机构的谐波振动对铺层密实度的影响规律,为摊铺作业过程参数选择和压实质量控制提供依据.
1. 振捣压实系统模型
1.1 振捣压实模型
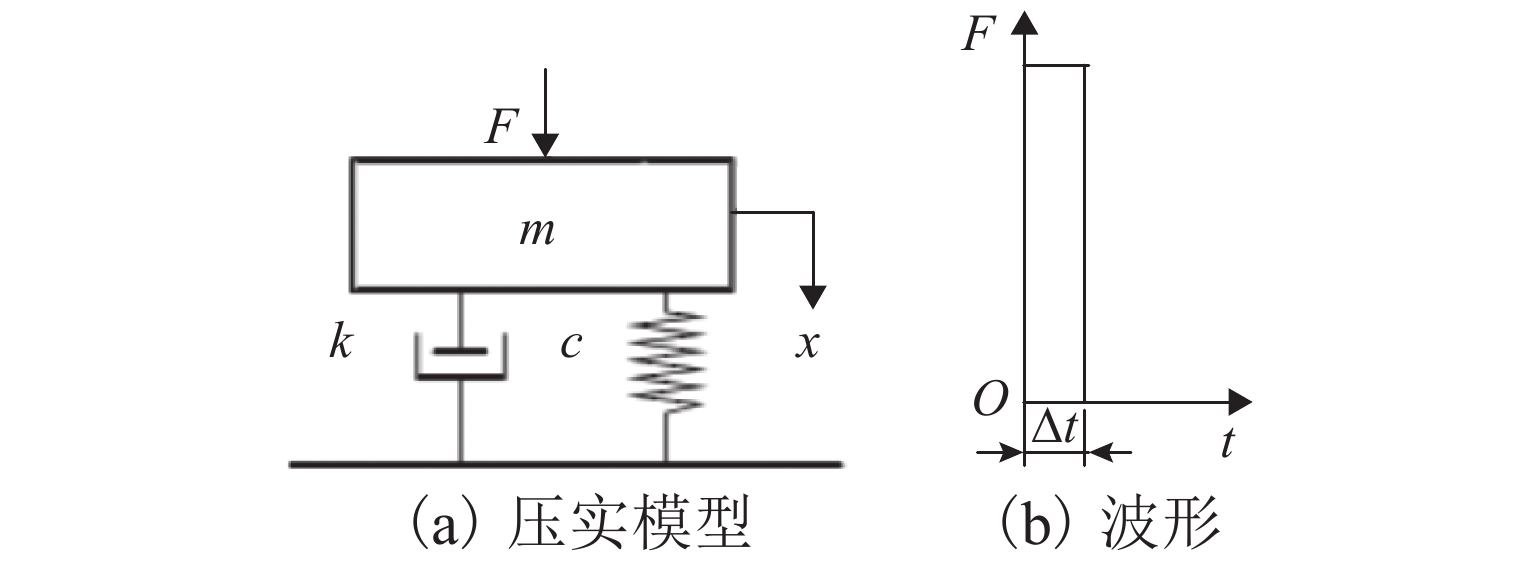
振捣开始前,沥青混合料处于松散状态,振捣机构对铺层的压实是高振幅作用下的强制压缩过程. 振捣机构频率一般在0 ~ 25 Hz可调,振捣周期为0 ~ 0.04 s,振捣激励对铺层的作用时间很短,分析单次振捣过程中振捣机构对铺层混合料的压实效果时,对于具有黏性阻尼的弹簧-质量振捣压实系统,考虑在t = 0时刻受到一个冲量为F作用的情况[14],如图1所示. 图中:k为介质的支承刚度系数;c为阻力系数;m为振捣机构质量;x为振动位移;Δt为极短的时间.
该振捣压实系统的运动微分方程见式(1),系统响应解见式(2).
m¨x+c˙x+kx=0, (1) x(t)=e−ξωnt[x0cos(ωdt)+˙x0+ξωnx0ωdsin(ωdt)], (2) 式中:
$ {x_0} $ 和$ {\dot x_0} $ 分别为系统初始位移和初始速度;$ {\omega _{\text{n}}} = \sqrt {{k \mathord{\left/ {\vphantom {k m}} \right. } m}} $ ,为系统无阻尼固有频率;$ {\omega _{\text{d}}} = {\omega _{\text{n}}}\sqrt {1 - {\xi ^2}} $ ,为有阻尼固有频率;$\xi = {c \mathord{\left/ {\vphantom {c {2m{\omega _{\text{n}}}}}} \right. } {(2m{\omega _{\text{n}}})}}$ ,为材料阻尼比.夯锤作用力施加给铺层之前,材料颗粒处于静止状态,给定时间条件,由动量定理可得
F=m˙x1|t=0+−m˙x1|t=0−=m˙x10, (3) 式中:
$ {\dot x_1} $ 为单次振捣速度响应;$ {\dot x_{10}} $ 为单次振捣初始速度.故初始条件为
x1(t=0)=x10=0, (4) ˙x1(t=0)=˙x10=Fm. (5) 系统的响应为
x1(t)=Fe−ξωntmωdsinωdt. (6) 振捣压实系统受到单位冲量时的响应,称为单位脉冲响应函数,如式(7)所示.
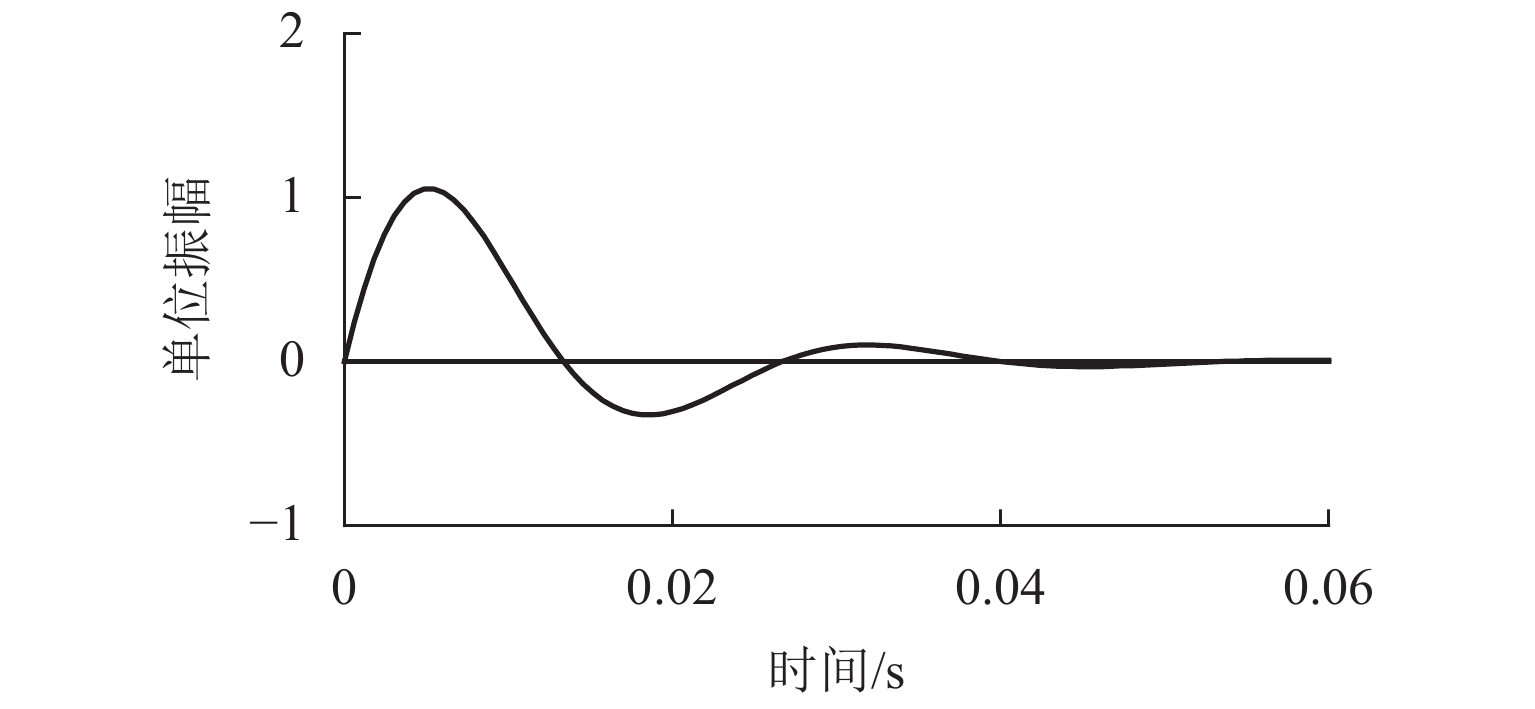
g1(t)=e−ξωntmωdsinωdt. (7) 沥青路面常用的连续级配混合料AC-20,其最佳振动频率为220 rad/s,阻尼比为0.35[10],单次冲击衰减周期为0.028,其单位脉冲响应如图2所示.
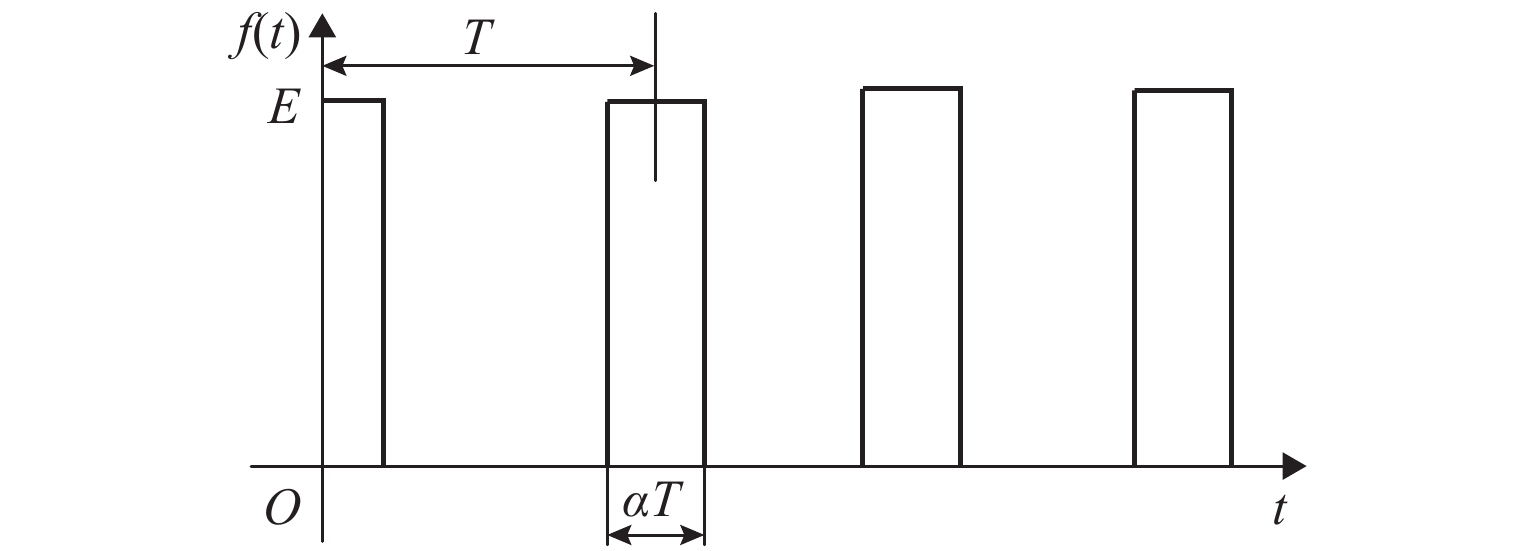
由图2可知:该响应函数为一衰减信号,衰减周期为2π/ωd. 振捣机构最小振捣周期为0.04 s,在下一次振捣发生之前,上一次的振捣能量已经衰减90%以上,在压实过程中振捣压实机构是周期性地与铺层接触和分离,振捣压实机构在运动最高点及最低点的垂直速度等于0[15]. 当夯锤开始接触铺筑材料时具有一定的速度(动量),形成起压实作用的冲击波与铺筑材料共同达到速度为0[16]. 根据冲击(夯实)原理,作用给铺层的多次振捣冲击过程如图3所示. 图中:α为冲击波宽系数;E为冲击波高度;T为振捣周期.
在分析振捣冲击作用对铺层的振动压实效果时,矩形波按傅里叶级数三角函数展开,见式(8).
f(t)=E{α+2π[sin(απ)cos(ω1t)+12sin(2απ)×cos(2ω1t)+13sin(3απ)cos(3ω1t)+⋯]}, (8) 式中:ω1 = 2π/T,为振捣冲击周期矩形波的基波角频率.
振捣机构冲击有效值为
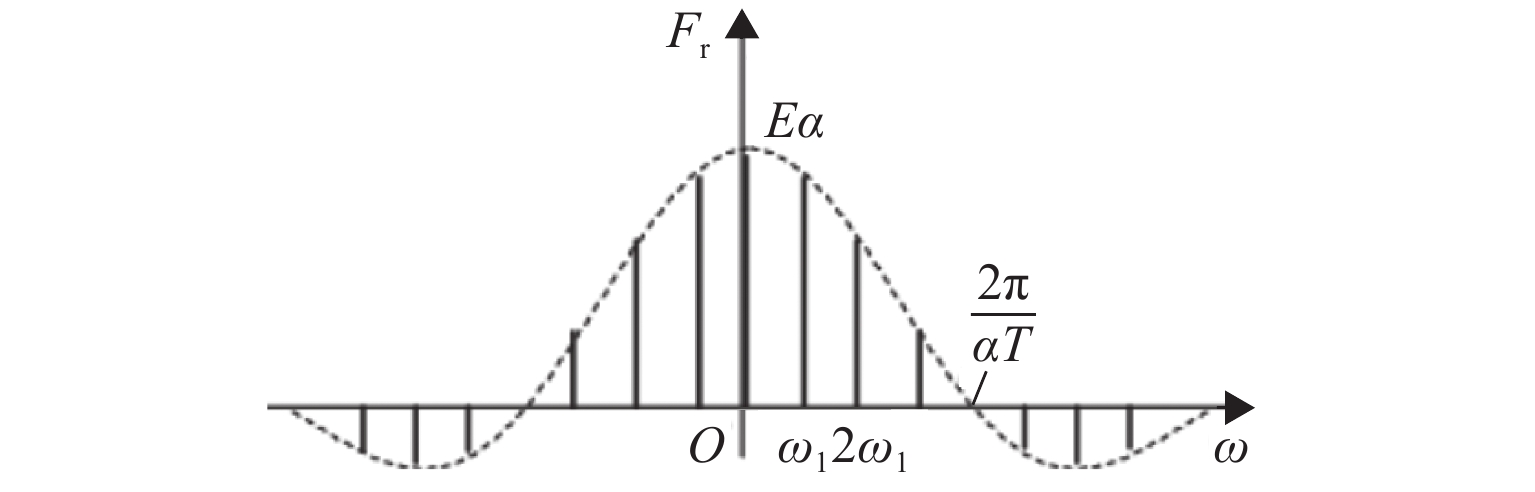
$ \sqrt \alpha E $ ,均值为αΕ. 傅里叶级数复指数函数展开,第r阶分量的激振力幅值见式(9),其频谱如图4所示.Fr=1T∫T2−T2f(t)e−irω1tdt=ET1−irω1e−irω1t|τ2−τ2=EτTSa(τ2rω1), (9) 式中:r为展开次数,r = 1, 2, …; τ为有效振捣时间周期,且τ = αT; Sa(•)为抽样函数.
由图4可知,振捣机构对混合料的冲击瞬间耗散了大部分能量,冲击波功率集中在低频段. 结合振捣机构的工作原理,取脉宽系数α为1/4,基波和前两阶谐波分量占据冲击能量的80%以上,基于振捣机构对混合料的压实作用,基波和前两阶谐波分量幅值分别如式(10) ~ (12)所示.
E0 = Eα, (10) E1 = E2πsin(απ)cos(ω1t), (11) E2 = E1πsin(2απ)cos(2ω1t). (12) 1.2 振捣机构与介质振动系统动力学模型
基于振捣机构基波和前两阶谐波分量分析混合料的压实作用,其中,基波分量看作振捣机构与混合料的初次接触压实,主要考虑混合料塑性性质,其余分量基于黏性阻尼的弹簧-质量振捣压实系统进行进一步分析. 对图1中具有黏性阻尼的弹簧-质量振捣压实系统,分别施加式(11)、(12)中各分量的激振力,建立该压实系统动力学微分方程,见式(13).
m¨x+c˙x+kx=Freirω1t. (13) 设该系统响应为
$x(t)=X_r {\rm{e}}^{{\rm{i}} r \omega_1 t}$ ,Xr为振捣机构第r阶谐波振幅,代入式(13)解得Xr=Fr[k−m(rω1)2]+icrω1=Fr[k−m(rω1)2]−i(crω1)[k−m(rω1)2]2−i(crω1)2=Fr√[k−m(rω1)2]2+(crω1)2e−iφr, (14) 式中:
$\varphi_r=\arctan \dfrac{c r \omega_1}{k-M\left(r \omega_1\right)^2}$ ,为第r阶谐波相位差角.得到系统第r阶稳态响应为
xr(t)=δ√(1−λ2r)2+(2ξλr)2ei(rω1t−φr), (15) 式中:
$\delta = {{{F_r}} \mathord{\left/ {\vphantom {{{F_r}} k}} \right. } k}$ ;$ {\lambda _r} = {{r{\omega _1}} \mathord{\left/ {\vphantom {{r{\omega _1}} {\omega _{\rm{n}}}}} \right. } {{\omega _n}}} $ ,为振捣机构第r阶谐波频率与系统无阻尼固有频率之比.由式(14)、(15)可得系统第r阶复频率响应幅值放大因子,即动态响应幅值与静作用力产生的变形之比,见式(16).
βr=|Xrδ|=1√(1−λr2)2+(2ξλr)2. (16) 2. 振捣密实度频率特性
对式(16)振捣作用下的幅值放大因子求导,得到密实度的峰值位置,如式(17)所示.
dβrdλr=2λr(1−λ2r−2ξ2)[(1−λ2r)2+(2ξλr)2]3/2=0. (17) 解得有阻尼固有频率为
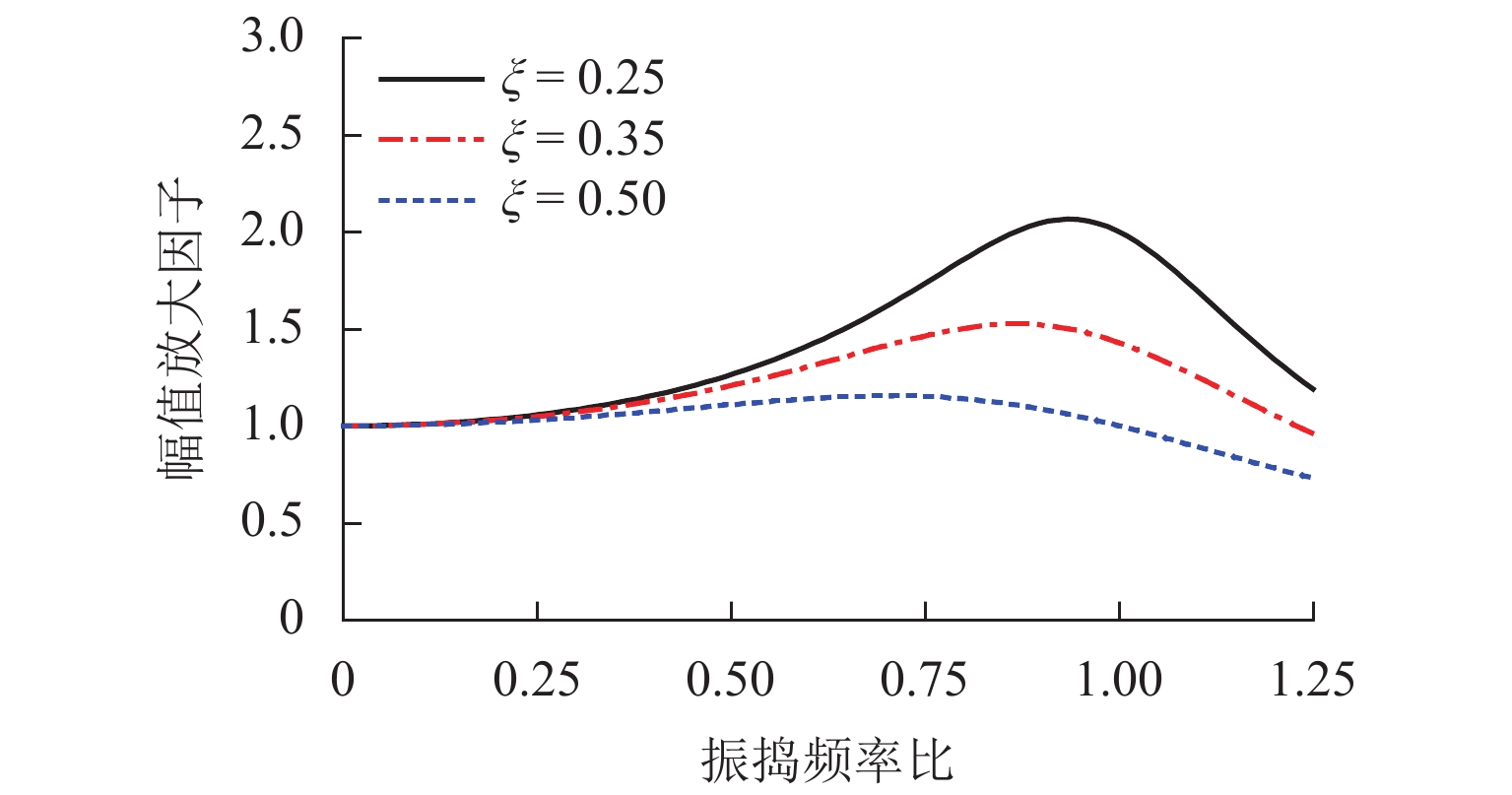
ωd=√1−2ξ2ωn. (18) 由式(18)得出了反映摊铺机振捣密实度幅频特性的振捣幅值放大因子变化曲线,如图5所示.
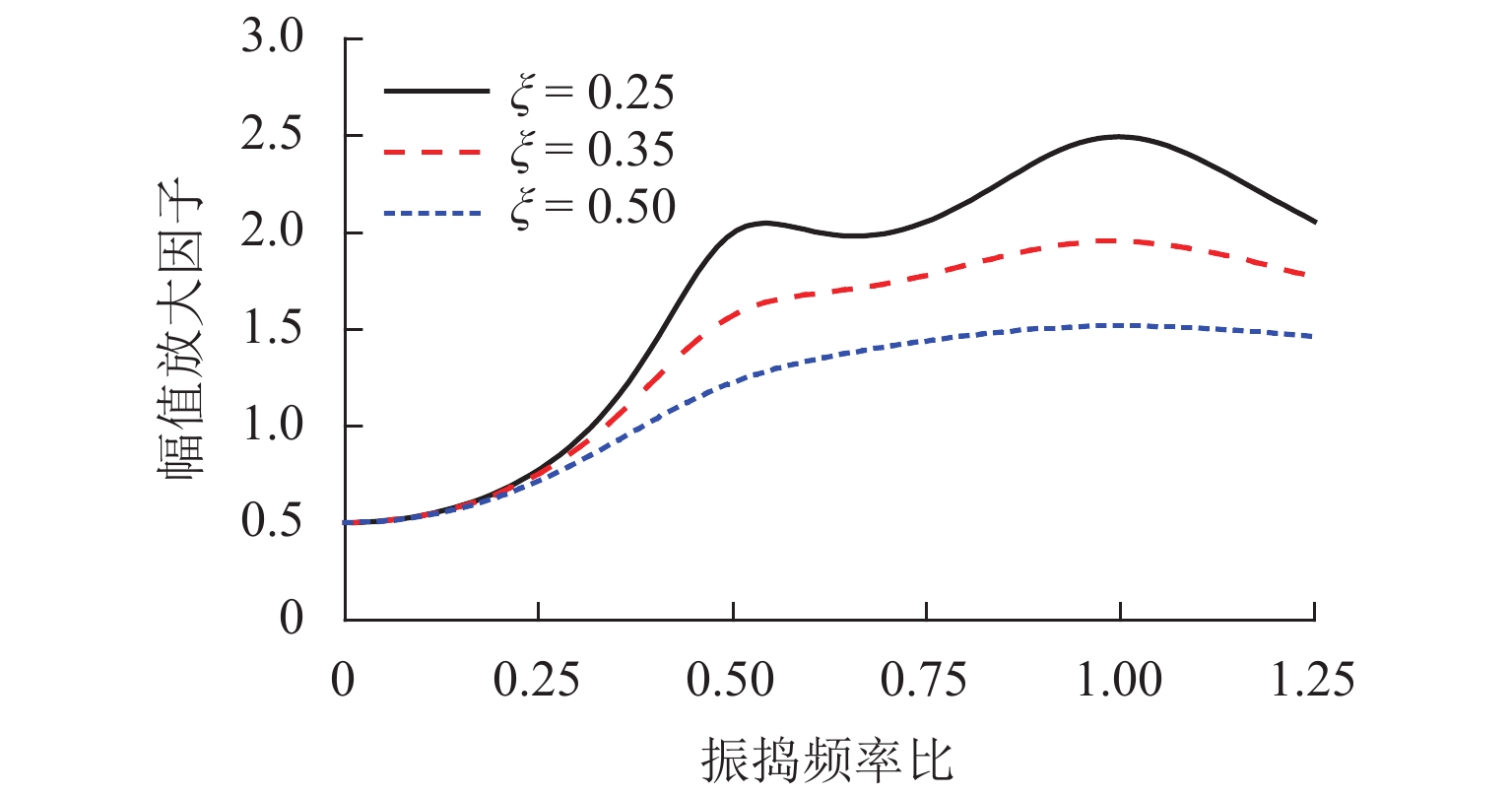
激振力幅值一定时,若振捣频率很小,振动响应幅值几乎与激振力幅值引起铺层材料的静变形相等,此后ω1增加,密实度逐渐增大,直到ω1 = ωd时,达到峰值以后,密实度与ω1呈负相关. 在密实度的峰值位置处,阻尼比越小,有阻尼固有频率越大,共振特性越明显. 对于二次振捣分量,实际的激振频率为振捣频率的2倍,共振频率范围超前一次谐波的共振区. 基于傅里叶级数系数,结合振捣压实作用机理,将各系数统一量纲,得到反映铺层混合料的振捣压实效果的多级振捣幅值放大因子变化曲线,如图6所示.
图6中,两个曲线峰值分别对应二次分量最佳频率比(0.45左右)和一次分量最佳频率比(0.90左右). 在振捣频率比所能达到的范围内,频率比小于0.45时,随着振捣频率的增大,密实度增长较快,振捣频率的变化对密实度的影响较为明显;当频率比大于0.45时,密实度增长速率逐渐趋于平缓,之后没有产生较大的波动. 在振捣压实过程中,铺层收到的振捣次数与频率及摊铺速度密切相关. 当振捣频率很小时,速度门槛值较低,在摊铺机起步、停车及速度波动较大时,振捣压实的均匀性较差,施工效率低. 根据已有研究可知[10],典型的SMA-13、AC-20混合料,其最佳振动频率在30 ~ 40 Hz.
对比不同阻尼比下的振捣幅值频率特性曲线可知,同一振捣频率下,阻尼比小的铺层比阻尼比大的铺层获得更高的振幅. 两个密实度峰值对应的振捣频率分别为最佳谐波振动频率和振捣压实系统共振频率;随着阻尼增大,密实度峰值位置逐渐弱化,这是由于存在黏性阻力的作用,振捣的高幅冲击响应来不及产生变化,铺层密实度没有出现明显的峰值点,而振捣频率在1/2有阻尼固有频率处(频率比为0.45左右)均可产生高效压实效果,称该频率为最佳振捣频率. 理论上将取振捣频率比在0.30 ~ 0.60作为二次谐波共振区,摊铺作业时振捣频率设置在该范围内可获得较高的密实度,同时振捣密实度变化均匀.
3. 振捣特性试验研究
试验选用VOLVO履带摊铺机,振捣机构工作频率可调范围在0 ~ 25 Hz,振动机构工作频率可调范围在0 ~ 60 Hz,两种机构的工作频率可分别单独调节,振捣机构为双夯锤激振. 在摊铺机作业过程中,采用LCO1系列压电型加速度传感器采集熨平板振动器振动和振捣梁振捣时的加速度信号,经过振动频率测试仪的分析处理,得到摊铺过程中的振捣频率成份. 选用磁力安装座将测试传感器探头放到靠近振捣驱动轴的位置,传感器安装位置见图7.
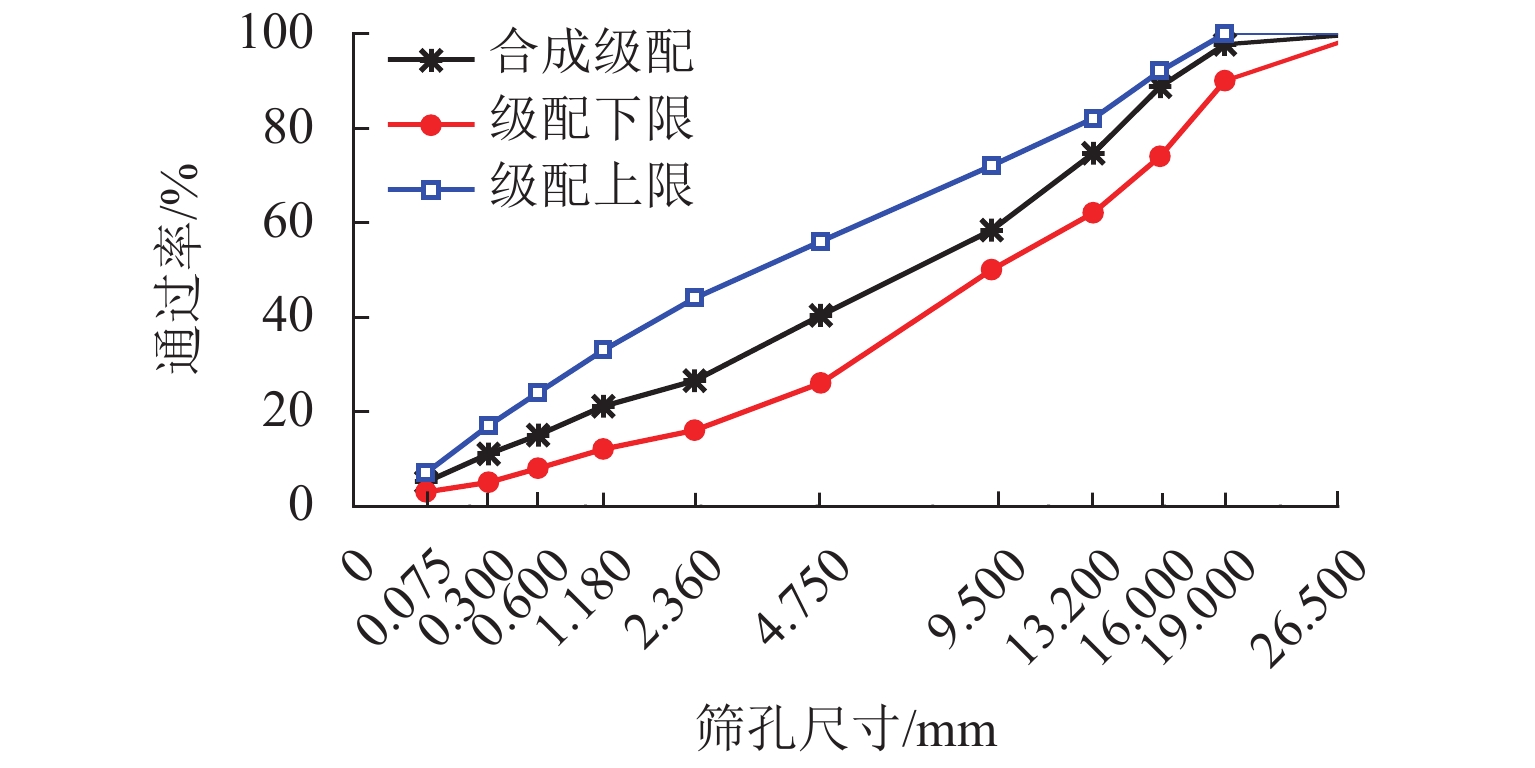
试验材料选用典型的AC-20混合料. 粗集料采用安山岩,细集料采用石灰岩机制砂,沥青采用含量为4.5%的90#A级道路沥青,该混合料的级配如图8所示.
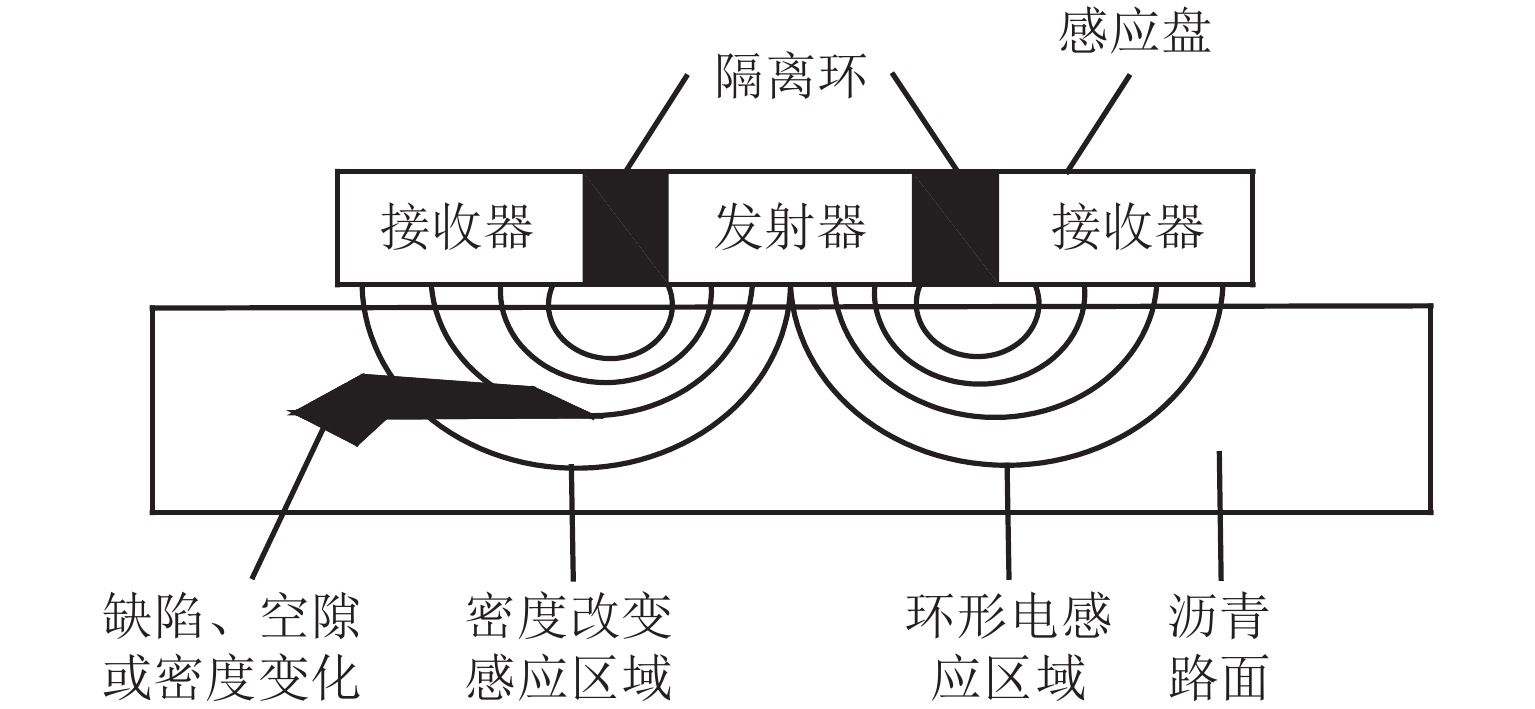
试验前,设定摊铺宽度为6.5 m,摊铺机行驶速度2 m/min,振动机构频率设置为固定值38 Hz,振捣机构设置为不同的频率进行摊铺作业,摊铺温度166 ℃左右,摊铺结束后现场检测铺层的密实度,试验振动频率固定为38 Hz,振捣频率分别为5、10、15、20 Hz. 无核密度仪采用电磁法测量沥青路面的均匀性和相对密度,现场测量过程中无需进行温度校核,用PQI301型无核密度仪检测沥青混合料铺层的密度,其工作原理如图9所示.
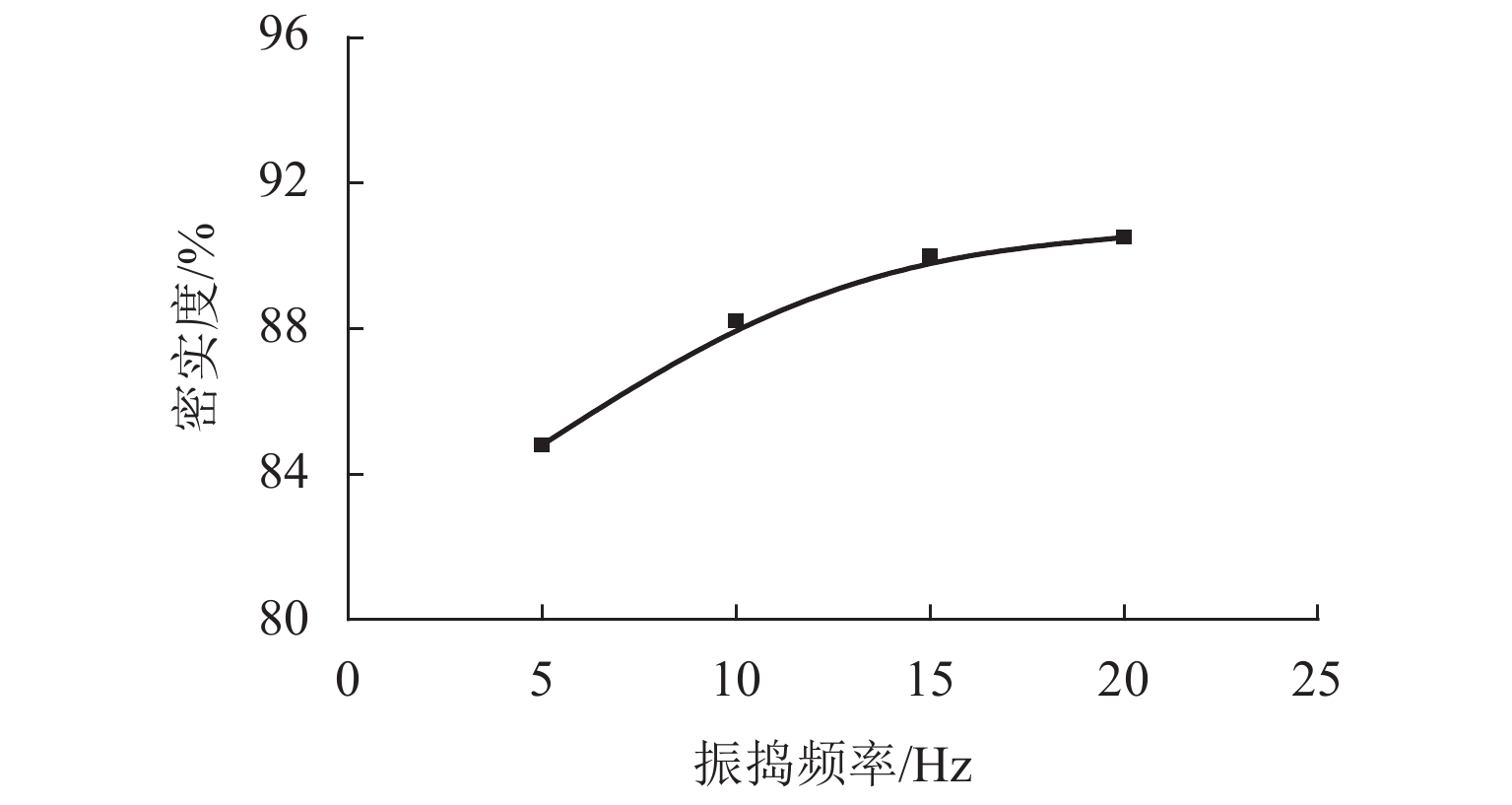
在同一位置取3点进行测量,取平均值. 为了保证无核密度仪测出的密度与压实沥青混合料的密度一致,需对无核密度仪进行标定. 在检测过程中,应避开摊铺层横向中间位置和边缘位置. 振捣频率与铺层密实度之间关系见图10.
由图10可知:振捣频率与混合料密实度正相关;在振捣初始阶段,混合料密实度增长幅值呈线性增长趋势,当振捣频率到达15 Hz时,密实度的增长逐渐趋于平缓. 这是由于冲击开始时,铺层混合料的抗压强度很小,变形率较高,受到外界冲击载荷时容易发生变形,应力水平较低,不易发生骨料破坏. 在初始压缩变形过程中,铺层可以吸收大量的冲击能量,并将其转变为混合料颗粒间的摩擦、移动等各种形式所耗散的能量. 随着冲击次数的增加,混合料越来越密实,在相同的冲击能量下,变形率逐渐降低,变形量减小,此时材料对冲击能量的吸收率降低,随着冲击次数的增加,混合料的压缩量不明显. 其原因是每种材料对于某一冲击载荷值存在一个饱和点,当达到该冲击能量的饱和点时,振捣冲击压实作用不显著.
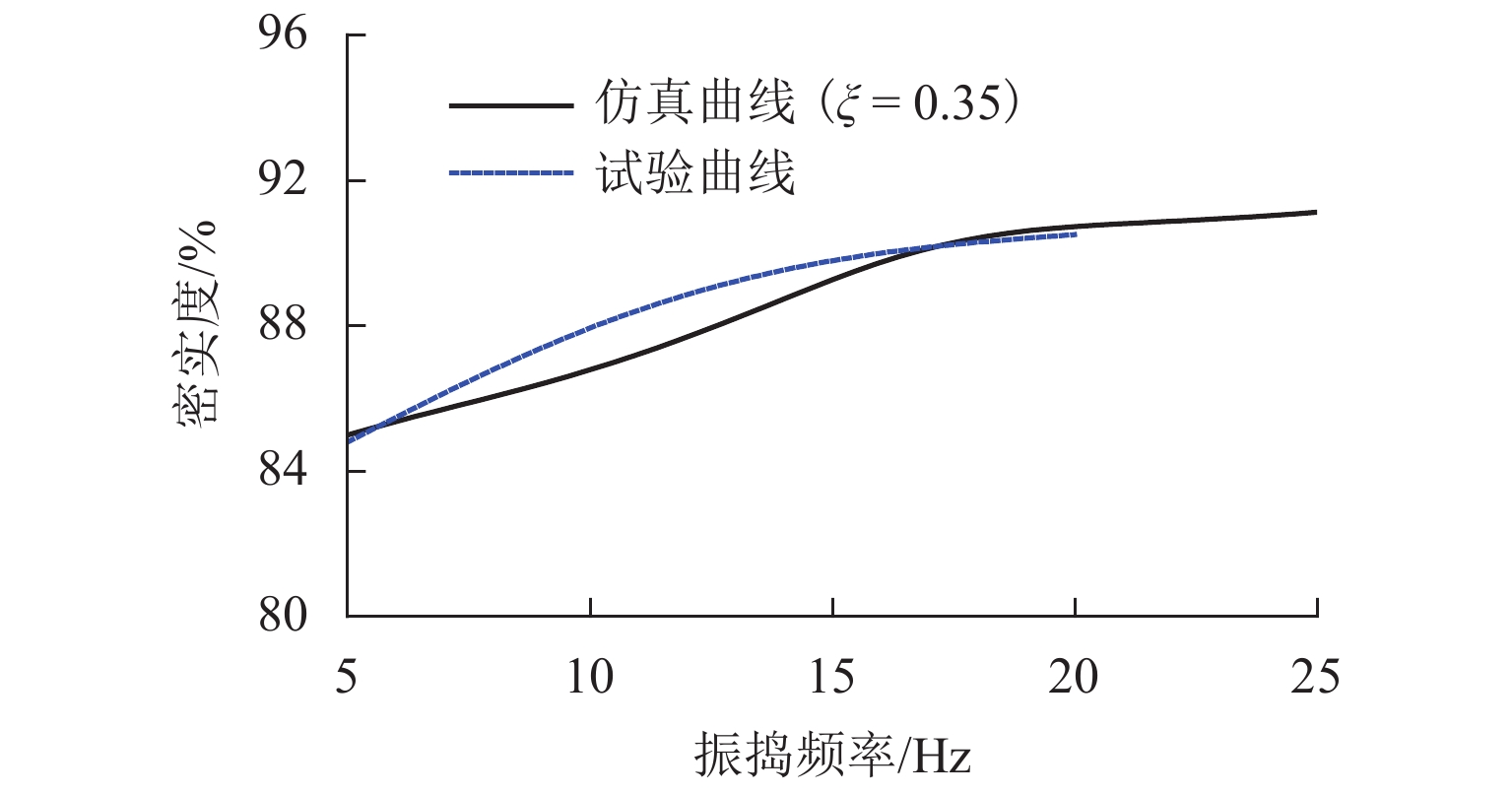
根据图10中曲线的特征点值和已有研究确定的试验铺层材料阻尼比为0.35[10],将仿真值与实测值的差值的绝对值的最小值作为目标优化问题,对图6中的曲线进行修正,得到试验与仿真对比曲线如图11所示.
对比分析图6和图11可得,在振捣压实作业过程中,随着振捣频率的增加,密实度的变化与振捣压实系统的共振频率密切相关,存在合理的振捣频率范围. 随着振捣频率的增加,试验密实度与仿真密实度最终均趋于平缓. 达到最佳振捣频率之前,仿真密实度略低于试验密实度,这是由于仿真分析时,振捣冲击波的脉宽系数α与脉冲高度E是恒定不变的,改变频率不影响作用于铺层压实力的大小. 而实际工程中,振捣频率变化影响压实力,增大压实力会增强压实效果,从而产生试验结果与仿真计算之间变化规律的误差. 根据图11中的试验和仿真结果,提取振捣频率在5、10、15、20 Hz时密实度增长量,计算密实度增量与振捣频率的比值,得到不同振捣频率下的密实度增长系数,如表1所示. 不同振捣频率下的密实度增长系数客观地反映不同频率下压实的困难程度.
表 1 密实度增长量Table 1. Density increment振捣频率/Hz 密实度/% 密实度增量/% 密实度增长系数 5 84.78 2.43 0.489 10 87.96 3.18 0.318 15 89.94 1.02 0.068 20 90.72 0.78 0.039 随着振捣频率的增加,密实度增量呈先上升后降低的趋势,振捣频率达到15 Hz,密实度仍在增加,只是增长量有所减小. 对比表1中的不同振捣频率下的密实度增长系数,当振捣频率为5 Hz时,密实度增长系数最大,此时的混合料最容易压实,因此,该振捣作用下的密实度增量增大. 随着振捣频率的增加,密实度增长系数减小,混合料越来越难压实,此时振捣作用下的密实度增量减少. 当振捣频率20 Hz,密实度增量有所降低时,密实度增长系数仍呈现减小趋势,进一步压实混合料需要更多的压实能量. 计算分析振捣密实度增量平均值与增长系数之间相关系数达到0.964,两者之间具有较高的相关程度,振捣频率的选择对混合料的进一步密实有重要的影响. 结合图11可知:随着振捣频率的增加,密实度增大,当振捣频率低于15 Hz时,铺层密实度增长量最为显著,之后密实度变化趋于平缓. 同时也说明在振捣频率大于15 Hz (频率比约为0.45)时的工作条件下,铺层可以获得较高的初始密实度. 此时谐波频率与铺层材料固有频率接近,对铺层混合料的摊铺初始密实度产生重要作用.
4. 结 论
1) 在摊铺机振捣机构间断性的冲击作用下,振捣过程会产生多个频率分量,振捣冲击对铺层产生的压实效果由振捣频率与材料特性共同决定.
2) 在摊铺作业过程中,当振捣频率小于最佳振捣频率时,密实度对振捣频率变化敏感;振捣频率大于最佳振捣频率时,随着频率的增大,铺层密实度缓慢增加,并趋于平缓;频率比在0.30 ~ 0.60属于共振区,摊铺作业时将振捣机构工作频率匹配在该范围内可获得高密实效果,为摊铺机实现高效压实的振捣机构参数的选择提供理论依据.
3) 振捣机构的谐波频率接近铺层混合料的固有频率时,对摊铺材料的密实度产生显著的影响. 摊铺作业过程中,合理利用振捣谐波分量可以产生高效压实效果.
4) 由于振捣频率的改变会影响作用于铺层混合料的振捣激励载荷,因此,需要对振捣激励载荷变化对振捣机构压实系统特性的影响做进一步研究.
-
王振领,林拥军,钱永久. 新老混凝土结合面抗剪性能试验研究[J]. 西南交通大学学报,2005,39(5):600-604. WANG Zhenling, LIN Yongjun, QIAN Yongjiu. Experimental research on shear properties of new-to-old concrete interface[J]. Journal of Southwest Jiaotong University, 2005, 39(5):600-604. 叶华文, KÖIG C, UMMENHOFER T, 等. 预应力CFRP板加固钢板受拉疲劳性能试验研究[J]. 西南交通大学学报,2009,44(6):823-829. YE Huawen, KÖIG C, UMMENHOFER T, et al. Experimental investigation of fatigue behavior of tension steel plate reinforced with prestressed CFRP laminates[J]. Journal of Southwest Jiaotong University, 2009, 44(6):823-829. 潘毅,吴晓飞,万里,等. 长期负载下CFRP约束混凝土圆柱轴压试验研究[J]. 西南交通大学学报,2016,51(5):847-854. PAN Yi, WU Xiaofei, WAN Li, et al. Experimental study on axially loaded circle-section concrete columns confined by CFRP under long-term load[J]. Journal of Southwest Jiaotong University, 2016, 51(5):847-854. HAMED E, CHANG Z T. Effect of creep on the edge debonding failure of FRP strengthened RC beams-a theoretical and experimental study[J]. Composites Science and Technology, 2013, 74:186-193. MANCUSI G, SPADEA S, BERARDI V P. Experimental analysis on the time-dependent bonding of FRP laminates under sustained loads[J]. Composites:Part B, 2013, 46:116-122. MESHGIN P, CHOI K,TAHa M. Experimental and analytical investigations of creep of epoxy adhesive at the concrete-FRP interfaces[J]. International Journal of Adhesion and Adhesives, 2009, 29(1):56-66. DIAB H, WU Z. A linear viscoelastic model for interfacial long-term behavior of FRP-concrete interface[J]. Composites:Part B, 2008, 39(4):722-730. MAJDA P, SKTODZEWICZ J. A modified creep model of epoxy adhesive at ambient temperature[J]. International Journal of Adhesion and Adhesives, 2009, 29(4):396-404. HOUHOU N, BENZARTI K, QUIERTANT M. Analysis of the nonlinear creep behavior of concrete/FRP-bonded assemblies[J]. Journal of Adhesion Science and Technology, 2014, 28(14/15):1345-1366. 杨挺青. 粘弹性力学[M]. 武汉:华中理工大学出版社,1990:8-25. 齐威. ABAQUS 6.14超级学习手册[M]. 北京:人民邮电出版社,2016:258-261. 穆霞英. 蠕变力学[M]. 西安:西安交通大学出版社,1990:46-52. 王勖成. 有限单元法[M]. 北京:清华大学出版社,2003:55-92. ROBERTS T M. Approximate analysis of shear and normal stress concentrations in the adhesive layer of plated RC beams[J]. The Structural Engineer, 1989, 67(12):229-233. SMITH S T, TENG J G. Interfacial stresses in plated RC beams[J]. Engineering Structures, 2001, 23(7):857-871. 期刊类型引用(0)
其他类型引用(5)
-

 点击查看大图
点击查看大图
计量
- 文章访问数: 581
- HTML全文浏览量: 84
- PDF下载量: 58
- 被引次数: 5





 下载:
下载:

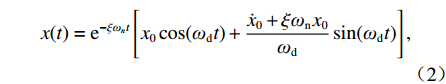
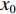
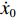
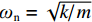
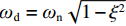
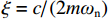
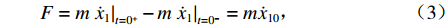
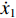
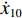


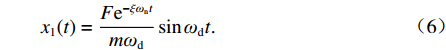
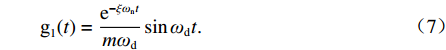


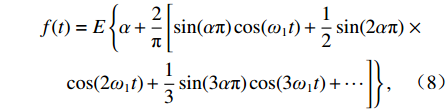
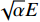

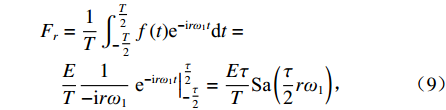

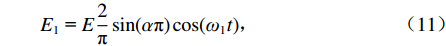
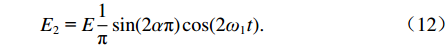
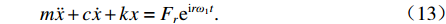
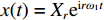
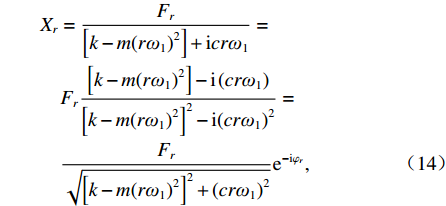
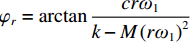
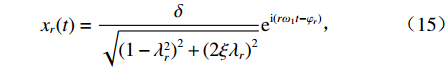
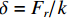
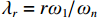
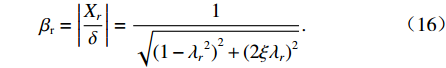
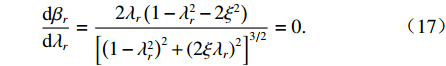









 下载:
下载: