Flexural Fatigue Performance of Concrete Prepared with Low-Heat Portland Cement
-
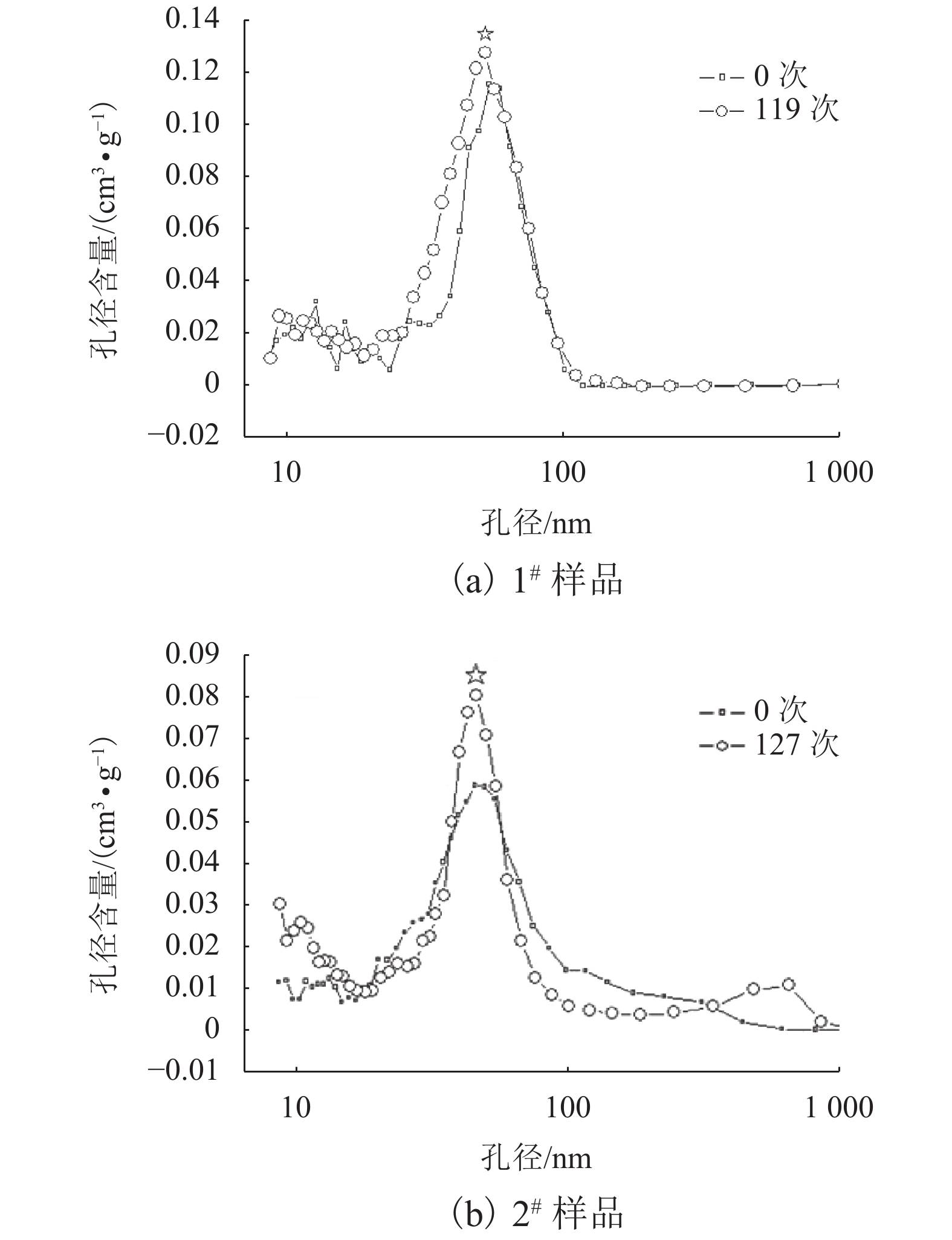
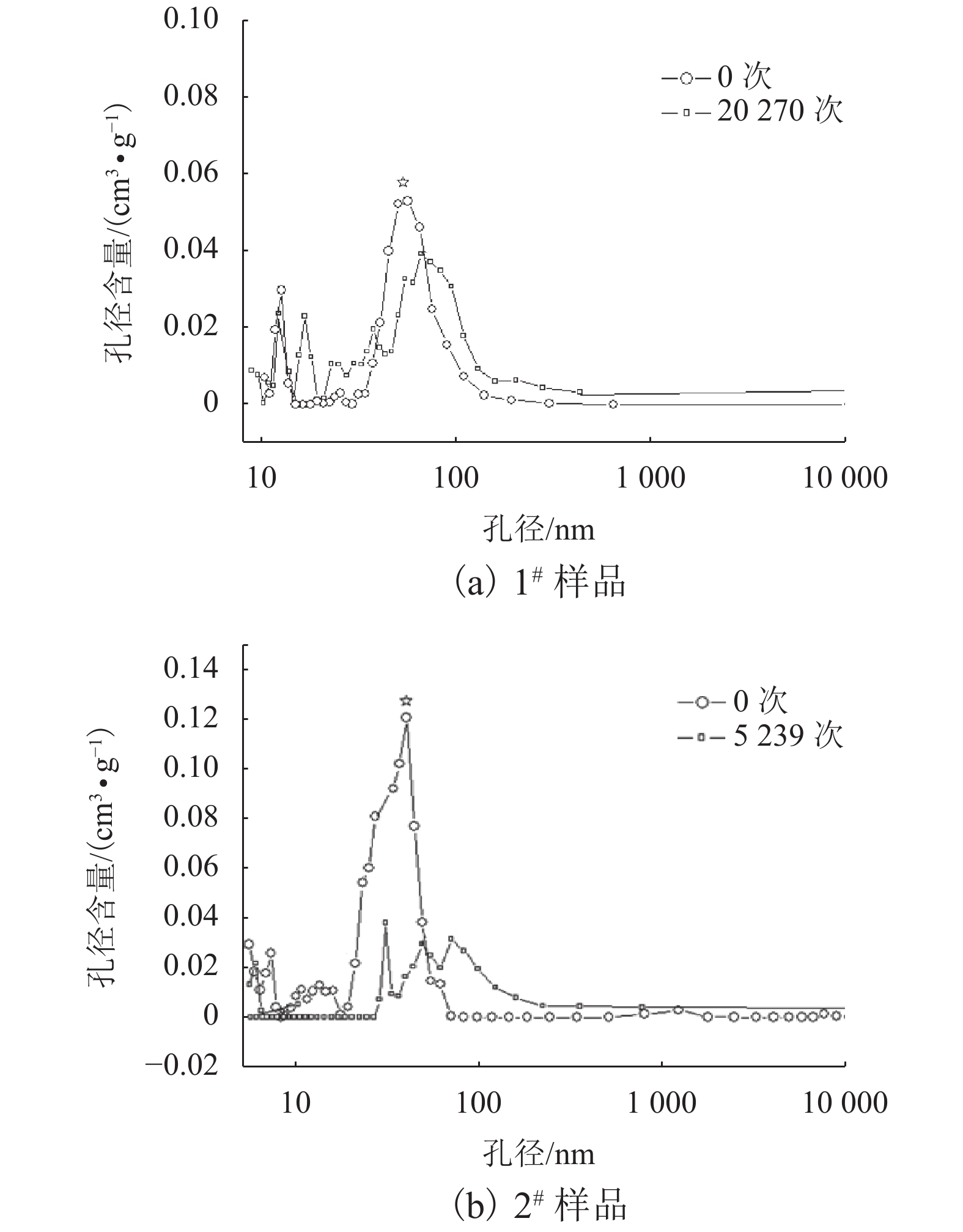
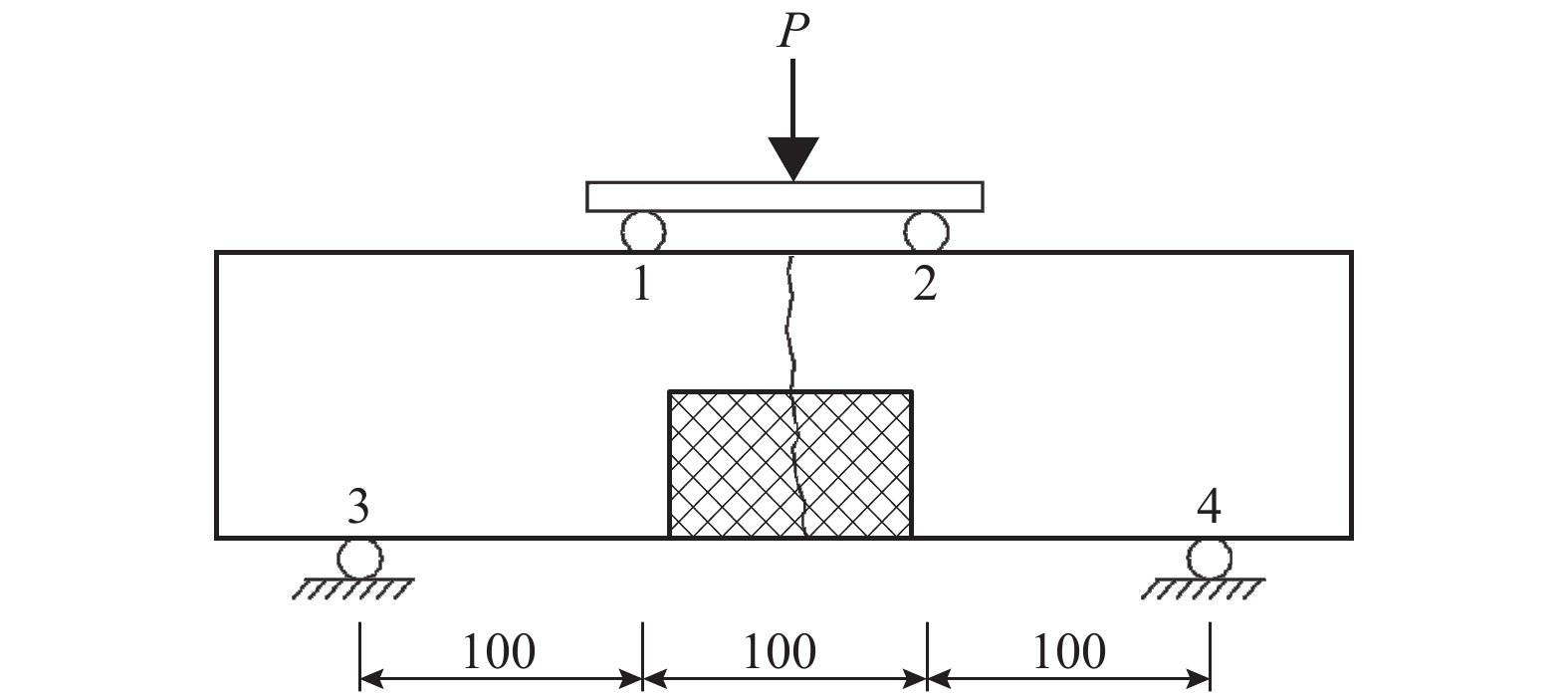
摘要: 为研究胶凝材料的差异对混凝土疲劳特性的影响，采用4点加载的弯曲疲劳实验方法，对比研究了不同应力水平下低热硅酸盐水泥和同强度等级的普通硅酸盐水泥配制混凝土的弯曲疲劳特性，利用DTA-TG、SEM和MIP探讨了两种不同水泥配制混凝土的微观组成结构差异及其对疲劳特性的影响. 实验结果表明：28、90 d和180 d标准养护条件下的低热水泥混凝土在应力水平为0.75～0.90时的弯曲疲劳寿命均高于普通硅酸盐水泥混凝土；3.49 MPa应力荷载下，养护龄期由28 d延长至180 d，两种混凝土的弯曲疲劳寿命分别提高了230 452及8 168倍，90 d与180 d养护龄期的低热硅酸盐水泥混凝土的疲劳寿命分别是普通硅酸盐水泥混凝土的4.76倍及19.88倍，养护龄期越长，低热水泥混凝土抗疲劳性能的优势越显著；低热水泥混凝土水化产物中C-S-H凝胶多，Ca（OH）2含量少，加载后最可几孔径与大孔含量的增幅较低（<10%），致使其在疲劳荷载作用下裂缝源生成的可能性减少，裂缝扩展能力降低，抗疲劳能力增强.Abstract: To investigate the influence of cementing materials on the fatigue performance of concretes, the flexural fatigue performance of concretes prepared with low-heat Portland cement and ordinary Portland cement at different stresses was studied by a four-point bending fatigue test method. Additionally, the relationship between microstructure and fatigue performance was studied by using DTA-TG, SEM, and MIP methods. It was observed that in comparison to the ordinary Portland cement, the low-heat Portland cement is favourable for the improvement of the fatigue life of the concrete under the same stress lever (0.75–0.90). As the curing age was extended from 28 days to 180 days, the flexural fatigue life of both the kinds of concrete with a loading of 3.49 MPa was increased by 230 452 times in low-heat Portland cement concrete and 8 168 times in case of ordinary Portland cement concrete. The fatigue life of low-heat Portland cement concrete on the 90th day and 180th day was 4.76 and 19.88 times higher than that of ordinary Portland cement concrete, respectively. The longer the curing age the better the anti-fatigue performance of low-heat cement concretes. The microstructure study indicated that low-heat Portland cement concrete consisted more C-S-H gel and less Ca（OH）2. Furthermore, low-heat Portland cement concrete had lower increase (less than 10%) on the most probable pore size; and the proportion of large pores after fatigue loading reduced the crack propagation and enhanced the anti-fatigue performance.
-
Key words:
- low-heat Portland cement /
- concrete /
- anti-fatigue performance /
- stress lever
-
木结构常采用榫卯节点作为构件间传递内力与耗散能量的连接形式. 地震作用下，榫卯节点的耗能可达结构总体耗能的30%左右[1]. 因此，研究榫卯节点的力学性能是研究木结构抗震性能的关键.
已有文献[2-6]介绍了多种不同地区和节点形式的榫卯节点力学性能的研究成果，但是针对传统民居木结构的研究较少. 民居木结构建筑相比古建筑木结构，其节点的建造工艺和细部构造均存在一定差异. 比如《营造法式》中记载直榫节点的榫头宽度“入柱卯减厚之半”[7]，即梁榫入柱部分截面削减一半，而根据实地考察，部分民居木结构直榫节点的榫头进入柱卯部分的截面并未削减. 在民族分布十分丰富的南方山区，存在着大量的木结构传统民居，这类民居的主要材料为杉木，其木架构的中节点以穿透榫为主，边节点以有穿销直榫为主，少数为有穿销透榫.
拔榫破坏是榫卯节点的常见破坏模式之一，南方山区民居木结构常在节点处设置穿销来锁住榫头限制其移动，防止节点拔榫. 目前，针对直榫和透榫节点已有较丰富的研究[8-11]，但针对有穿销的直榫和透榫节点的研究较少. 王展光等[12-13]变化销栓形状和偏心位置，进行了明销直榫和明销透榫的单向加载试验研究，而目前缺少针对2种带穿销节点抗震性能的研究，使得南方山区传统民居木结构的保护修缮工作缺乏理论依据.
因此，本文以梁榫截面尺寸和节点形式为变化参数，开展了4个足尺边节点试件的低周往复加载试验，获取其破坏形态以及滞回曲线、骨架曲线、强度和刚度退化曲线、等效黏滞阻尼系数等性能指标. 据此，研究梁榫截面尺寸和节点形式对节点抗震性能的影响，并提出相应的设计、加固建议. 基于试验结果推导了有穿销直榫节点的弯矩-转角理论公式，并将计算的理论承载力与试验结果进行对比. 研究成果可为南方山区地区典型木结构民居的保护和修缮工作提供一定的理论依据.
1. 试验概况
1.1 试件设计
根据田野调查的结果，有穿销直榫和透榫节点尺寸参数的取值范围为：梁高h 150～250 mm，梁宽b 30～60 mm，柱直径160～250 mm. 基于实地考察的结果，设计制作了共计4个足尺的带穿销节点试件，其中穿销尺寸均为直径30 mm，长度220 mm，与试件采用相同的木材. 试件变化参数见表1，试件标准构造详图如图1. 依据文献[14]，对试验所采用的杉木进行材性测试，其强度和弹性模量结果见表2，表2中：f为强度，E为弹性模量，下标L、R、T分别表示受力方向为纵向、径向和切向，下标t、c、m分别表示受拉、受压和受弯. 测得木材平均气干密度为0.34 g/cm3，木材平均含水率约为12.0%. 参照文献[15]的方式进行了杉木的摩擦系数试验，得到木材的滑动摩擦系数为0.24.
表 1 试件参数Table 1. Parameters of specimens试件编号 梁截面高度
/mm梁截面宽度
/mm构造形式 BS1 160 50 直榫 BS2 160 40 直榫 BS3 130 50 直榫 BS4 160 50 透榫 表 2 杉木木材力学性能Table 2. Mechanical properties of Chinese fir指标 试件个数/个 平均值/MPa 平均含水率/% fLt 12 75.27 11.7 fLc 12 31.13 11.3 fRc 12 4.33 12.4 fTc 12 4.00 12.1 fLm 12 68.12 12.2 ELt 12 11583 11.7 ELc 12 11431 11.9 ERc 12 1074 12.2 ETc 12 637 12.0 ELm 10 8687 12.2 1.2 加载方案
本次试验采用MTS液压伺服作动器进行低周往复荷载试验，试验加载布置如图2所示. 将节点试件竖向放置，柱脚与地面通过固定的单向铰支座连接，以模拟传统木结构民居柱脚直接支承在基石上的连接方式. 采用钢制夹具夹住柱顶限制其水平位移，防止试验中可能发生的平面外失稳.
为模拟节点的真实荷重状态，将实际结构的荷载折算到边节点，确定柱顶荷载为11 kN，并在加载全程使用千斤顶在柱顶施加恒定的等量竖向荷载. 加载模式采用位移控制加载，加载速率为0.8～2 mm/s，加载模式如表3所示. 当荷载下降至荷载最大值的80%或者变形过大时停止加载.
表 3 加载方案Table 3. Loading scheme控制位移/mm 每级增量/mm 循环次数/次 ≤8 2 1 16～80 8 3 >80 16 3 1.3 测量方案
具体测量布置方案见图3，在柱内侧梁榫上下端分别布置3# 和4# 位移计，测量梁榫根部与柱内侧的相对变形；5# 和7# 位移计用于测量梁长中点和加载点的竖向位移；8# 拉线式位移计用于监测节点转角的变化. 此外，为了监测柱脚和试件的平面外变形，布置了1#、2# 和6# 位移计，其中，1# 位移计用于测量柱脚的水平位移，2# 和6# 位移计分别用于测量柱脚和梁长中点处的平面外位移.
2. 试验现象及其分析
试件受力方向和梁榫部位的描述统一规定如图4所示. 加载期间梁柱夹角小于90° 时称为正向加载，大于90° 时称为反向加载；图4中柱右侧的梁榫称为柱内侧梁榫，柱左侧的梁榫称为柱外侧梁榫.
2.1 试验现象
由于木材的自然干缩变形和施工偏差，梁榫上下侧和卯口之间存在初始空隙，见图5（a）. 以试件BS1为例说明节点加载破坏过程；随着控制位移的增大，梁榫受压区开始出现塑性变形；反向加载至80 mm时，柱内侧梁榫下部的部分纤维被拉断，柱内侧梁榫的中下部产生一条较宽的水平裂缝（图5（b）），同时内侧梁榫的上部因挤压产生了明显变形（图5（c））；正向加载至96 mm时，内侧梁榫顶部纤维突然被拉断，同时梁榫上部产生了一条明显的水平裂缝，（图5（d））；随着控制位移的不断加大，柱内侧梁榫上部纤维被拉断的范围扩大、往节点域内的穿销延伸；正向加载至119 mm时，试件发出较大响动，柱内侧梁榫上端发生顺纹拉裂破坏（图5（e）），同时柱外侧梁榫下部出现了水平劈裂裂缝（图5（f））.
对于试件BS2和BS3，在加载前期的试验现象与BS1类似，最终破坏形态均为顺纹拉裂破坏，但是加载中后期的现象略有差异. 试件BS2在正向加载至128 mm时，柱内侧梁榫上部发生顺纹拉裂破坏，同时梁榫下部发生了皱折状顺纹挤压破坏（图6（a）～（b））. 试件BS3在正向加载至72 mm时柱外侧梁榫上部已出现水平劈裂裂缝（图6（c）），透榫试件BS4柱内侧梁榫的破坏现象类似于直榫节点，但柱外侧梁榫的水平劈裂仅出现在梁榫下部，且裂缝上下侧木材的错动变形更明显（图6（d））.
2.2 破坏形态及其分析
有穿销直榫节点（试件BS1～BS3）和透榫节点（BS4）均由于柱内侧梁榫受拉边缘发生顺纹拉裂导致最终破坏，同时伴随有受压边缘的挤压变形以及柱外侧梁榫的水平劈裂. 柱外侧梁榫水平劈裂裂缝是由于梁榫、卯口和穿销之间的挤压导致梁榫沿梁高产生剪应力差产生. 在加载后期，榫头嵌入柱卯口，榫卯上下接触面的竖向和水平向反力以及穿销的反作用力组成抵抗弯矩（见图7）.
图7中：FN1、FN2、FN3分别为正向加载时梁榫和柱卯口之间挤压面的竖向挤压力；Fμ1、Fμ2、Fμ3分别为正向加载时梁榫和柱卯口之间挤压面的水平摩擦力； Fs1、Fs2和fs分别为穿销与梁榫之间的水平向作用力、竖向作用力和转动摩擦力；θ为节点转角. 对有穿销直榫节点，如图7（a），接触面的一对水平反力Fμ1和Fμ2作用使得柱外侧梁榫沿梁高产生顺纹方向的剪应力，且节点域的剪应力分布与变形受到穿销与梁榫之间存在的挤压与转动摩擦作用影响. 对于有穿销透榫节点，如图7（b），梁榫与柱卯口的接触面反力为Fμ1、Fμ2和Fμ3，加上穿销与梁榫之间的反力，使得榫尾区域产生沿截面高度分布的顺纹方向剪应力. 由于杉木的顺纹抗剪强度远低于顺纹抗拉强度，较大的剪应力导致在榫尾处产生水平劈裂裂缝. 随着控制位移增加，水平劈裂裂缝不断扩张并延伸至节点域内，使梁榫出现了分层现象.
随着控制位移的持续增大，柱内侧梁榫上部或下部的木纤维应力达到木材顺纹抗拉强度而断裂，并随着位移增加不断扩展至节点域的销栓处，当柱内侧梁榫的有效面积缩小到无法承载时，节点失效.
3. 试验结果及其分析
各试件的M-θ滞回曲线如图8所示，其中，节点弯矩M定义为梁端竖向荷载与加载点到柱边水平距离的乘积，节点转角θ定义为7# 位移计（如图3所示）读数与位移计到柱边水平距离的比值.
3.1 弯矩-转角滞回曲线
1） 节点试件的滞回曲线均呈现出反Z字形，且具有明显的捏缩现象，说明有穿销直榫和透榫节点在受力过程中发生了大量摩擦滑移. 在加载和卸载阶段，由于榫卯之间存在初始空隙，当转角较小时，曲线的斜率均较小，表现为滑移为主的变形. 在每一级循环的加载阶段，滑移变形达到一定数值后，曲线斜率开始增大. 随着加载位移级数的增加，榫卯处的损伤增加，导致滑移变形量增加、曲线上升段斜率减小而下降段斜率增大、残余变形增大.
2） 对比试件BS1 （b=50 mm）与BS2 （b=40 mm）的滞回曲线（图8（a）和8（b）），可见，在同一加载级下，减小梁宽时，正向加卸载时节点抗弯承载力明显减小. 这是由于梁宽的减小降低了节点域内梁榫的截面面积，从而削弱了节点的抗弯承载力. 当减小梁宽时，反向加卸载时抗弯承载力差异不大. 试件BS2的正反向加载滞回曲线不对称，分析原因如下：1） 节点上侧的柱头和下侧的柱身长度不同导致节点上下侧刚度的不对称；2） 由于施工误差和干缩变形导致卯口上下侧的约束条件不对称；3） 榫卯之间空隙变大后梁在重力作用下松动下垂，导致反向加载时作动器记录的反力偏大；4） 由于梁宽较小，加载过程有一定的平面外弯扭变形，导致正反向加载曲线存在差异. 因此，有必要限制梁宽不过小，避免平面外失稳.
3） 对比试件BS1 （梁高h=160 mm）与BS3 （h=130 mm）的滞回曲线（图8（a）、（c））可见：在同一加载级下，当减小梁高，正向加卸载时各级循环的滞回环面积和节点抗弯承载力明显减小，这与截面削弱有关；但是，反向加卸载时的滞回环面积及节点抗弯承载力差异不大；试件BS3的滞回曲线正反向加载时不对称，源自节点上下侧的刚度差异、卯口上下侧的约束差异和松动节点受梁重力影响.
4） 对比BS1 （直榫）与BS4 （透榫）的滞回曲线（图8（a）、（d））可见：在同一加载级下，相比直榫节点，透榫节点反向加卸载时的滞回环面积和抗弯承载力下降但不明显，其峰值转角明显减小；正向加卸载时的滞回环面积、峰值转角和抗弯承载力均明显减小；透榫节点的梁榫高度在节点域内减小了一半，因此削弱了节点域内梁榫的转动刚度和承载力. 透榫节点构造上的不对称导致了滞回曲线的不对称.
3.2 节点弯矩-转角骨架曲线
连接试件各个加载级第一循环的峰值弯矩点，得到各个试件的弯矩-转角骨架曲线，各参数变化的骨架曲线对照见图9.
各试件都先后经历了滑移阶段、弹性阶段和塑性阶段. 加载位移较小时，由于榫卯之间存在空隙，曲线呈现弯矩小而位移增大的滑移段；正反向加载时的滑移量不对称，特别是试件BS3和BS4的情况；直榫节点最大滑移量对应转角为0.040 rad （试件BS3），透榫节点最大滑移量对应转角为0.039 rad（试件BS4）. 随着加载位移的增大，榫卯之间的空隙被挤紧后，曲线斜率明显增大，试件进入弹性工作阶段. 随着加载位移进一步增大，试件产生了由材料塑性应变发展以及榫卯之间接触面摩擦滑移引起的塑性变形，试件进入塑性阶段，表现为骨架曲线斜率的减小.
在试验设计参数范围内，节点的抗弯承载力随着梁截面高度和梁截面宽度增大而增大. 与BS1相比，当梁截面宽度减小20%，试件BS2的抗弯承载力比BS1最大降低约21% （正向加载段）；当梁截面高度减小18.8%，试件BS3的抗弯承载力比BS1最大减小约23% （正向加载段）. 与有穿销直榫节点相比，有穿销透榫节点在反向加卸载时抗弯承载力下降约26%，正向加卸载时抗弯承载力下降约62%，反映节点域内的梁榫截面减小对承载力不利.
直榫试件BS1在达到正、反向峰值弯矩时的转角均超过0.117 rad，而透榫试件BS4达到峰值弯矩时的转角仅0.078 rad，较直榫试件降低33%且达到峰值后荷载下降更突然，其延性比直榫节点差.
3.3 承载力和刚度退化曲线
3.3.1 承载力退化
强度退化是指在低周反复荷载作用下，试件在同一级控制位移加载中，节点强度会出现随着循环次数增加而降低的现象. 一般采用第二、第三循环强度退化系数[16]来衡量，各试件的第二循环强度退化系数λ2曲线见图10. 由图10（a）～（b）可见，在试验设计参数范围内，梁截面尺寸变化对强度退化系数的影响规律不明显. 由图10（c）可见，在加载过程中，大部分情况下直榫节点试件BS1～BS3的强度退化系数都大于0.8，仅BS1在正向加载至112 mm时，第二循环的峰值弯矩相较第一循环有较大降幅，这与BS1在往复荷载下部分梁榫边缘拉裂，截面减小导致承载力降低有关. 相较直榫节点，透榫节点的退化系数最小值低至0.73，说明透榫节点的强度退化更明显，加载过程中直榫节点的强度稳定性大于透榫节点.
3.3.2 刚度退化
刚度退化是指在低周反复荷载作用下，试件在同一级控制位移加载中，节点刚度会出现随着循环次数增加而降低的现象，一般采用割线刚度或者环线刚度来衡量. 其中用环线刚度K[17]可衡量结构在同一级控制位移幅值下的刚度退化特性，各试件的节点K-θ曲线如图11所示. 可见：除了试件BS1正向加载和BS4反向加载的情况外，其余情况下试件的环线刚度退化曲线均呈现先减小后增大再减小的形态. 这反映了BS1节点上部、BS2节点上下部、BS3节点上下部和BS4节点下部存在较大的初始空隙，引起明显的初期滑移现象. 在加载前期，节点刚度先减小后增大的过程就是节点初始空隙逐渐挤紧的过程. 待梁榫和卯口充分接触挤紧，节点刚度才逐渐增大，到达峰值后再逐渐降低. 与之不同的是，试件BS1在正向加载时，刚度持续减小，表明BS1节点下部的初始空隙较小，初始空隙的不同导致了试件BS1正反向环线刚度-转角曲线的不对称性. 有穿销透榫试件BS4也存在正反向环线刚度-转角曲线不对称的现象，主要原因是节点域的正反向受力机理不同. 由图11（a）、（b）可见，相比于对比试件BS1，随着梁宽和梁高减小，截面受到削弱，正向加载中后期试件BS2和BS3的环线刚度均降低. 从图11（c）可见，透榫节点BS4正向加载时的环线刚度低于有穿销直榫节点，但是反向加载至0.08 rad前，透榫节点环线刚度更高. 这是由于试件BS1的节点上部有更大的空隙，其在反向加载时首先经历空隙闭合的过程，导致加载初期的环线刚度较小.
3.4 耗能能力
试件的耗能能力采用等效黏滞阻尼系数ξeq[16]进行分析. 试件在正向第一加载循环的ξeq-θ曲线如图12所示. 由于木材自然的干缩变形和施工偏差，榫卯之间存在初始空隙且上下侧的空隙存在差异，使得各节点的榫卯之间开始产生挤压和摩擦作用的初始转角不同. 因此，只从ξeq-θ曲线的变化趋势讨论不同参数节点的能量耗散能力.
图 12 等效黏滞阻尼系数-转角曲线Figure 12. Curves of equivalent viscous damping coefficient versus angle从图12可见，试件BS1和BS4的等效黏滞阻尼系数随着转角增大而减小，且曲线有一个较明显的拐点，试件BS2、BS3的等效黏滞阻尼系数在转角达到约0.015 rad之后的发展趋势类似，以上反映了节点耗能能力随着转角的增大而降低. 当加载位移较小时，由于杉木的材质较软，榫卯间木材表面被频繁的滑移打磨光滑，由摩擦效应提供的耗能能力减弱；当滑移结束，榫卯间的缝隙被挤紧，节点的耗能能力降低趋势明显减缓，其后耗能能力随着纤维受挤压和拉伸损伤的积累持续降低. 在本文试验参数范围内，加载中后阶段，不同试验参数节点的等效黏滞阻尼系数比较相近.
3.5 小结与建议
本文试验中所有节点试件的破坏形态均为顺纹拉裂破坏，穿销未发生破坏. 节点的极限承载力与木纤维的抗拉强度相关，表明在往复荷载下，节点较为充分地发挥了木材的强度和延性，节点破坏形态为理想的破坏模式. 有穿销直榫节点的极限抗弯承载力和延性均高于有穿销透榫节点，在建造设计中应优先考虑有穿销的直榫节点.
本文试验所得抗震性能曲线中有较多不对称的情况，如梁宽对照组试件BS2的反向抗弯极限承载力比正向抗弯承载力低约21%，其机理均与木材干缩导致节点内部空隙较大有关. 较大的节点内部空隙不仅会导致正、反向受力状况的不同，当梁宽过小时还有可能发生弯扭变形，进而导致节点力学性能更进一步的不稳定. 对于使用历史较长、节点空隙较大的木结构民居，可通过在空隙填充木楔来增量节点的初始刚度和极限弯矩[18]，也可直接加固节点，如扒钉加固和钢板加固[19]等. 此外，还可通过增设碳纤维布、阻尼器等方式，改善节点抗震性能.
4. 穿销直榫节点的理论承载力公式
本节基于试验结果推导有穿销直榫节点在弹性和弹塑性阶段的弯矩-转角理论公式，并与试验结果进行对比验证.
4.1 基本假定
试验结果表明，节点拔榫量小，穿销作用明显，可认为梁榫与穿销不发生分离，梁榫围绕穿销发生刚体转动. 理论推导的基本假定如下：
1） 节点绕穿销中心转动，穿销为刚体且不与榫头发生分离.
2） 梁榫和卯口挤压时，柱卯口为顺纹受压，量榫为横纹受压. 由材性试验可知，木材的顺纹受压弹性模量远大于横纹受压，故假定只有榫头发生挤压变形. 同时假设木材横纹受压本构关系采用双线性强化模型，应力应变关系满足胡克定律.
3） 假设榫头发生刚体运动，忽略梁柱的弯曲效应和榫头、卯口的弯曲变形.
4） 榫头和卯口两侧面的摩擦作用力较小，为简化计算，假定侧向接触面榫卯之间的摩擦力为0.
4.2 有穿销直榫节点弯矩-转角关系推导
4.2.1 弹性阶段
1） 几何条件. 当节点枋和柱之间产生正向相对转角θ，节点变形前后的几何关系如图13所示. 设lA、lB分别为榫头底、顶面受挤压区域的长度；δA、δB分别为榫头底、顶面应挤压面的最大挤压变形；d为柱直径.
由图示几何关系可得式（1），其中L=（h2 + d2）1/2，α=arctan（h/d）. 由于穿销中心为节点几何中心，故榫头底、顶面受挤压区域的长度相等，有lA=lB. 将lA=lB，δA=lAtan θ和δB=lBtan θ代入式（1），可得式（2）.
(h+δA+δB)sin(α−θ)=Lsinα， (1) lA=lB=Lsinα/sin(α−θ)−h2tanθ. (2) 2） 平衡条件. 当节点的转角为θ，梁榫的受力状态如图14所示. 以穿销中心为原点取矩，穿销处由摩擦力产生的挤压力力矩很小，可以忽略，可得平衡方程如式（3）所示.
F(L0+d2)=(fAh2+fBh2+FAxA+FBxB)， (3) {xA=d2−lA3,xB=d2−lB3， (4) {fA=μFA,fB=μFB， (5) 式中：FA、FB分别为柱卯口对榫头底、顶面的挤压作用力；xA、xB分别为FA、FB的力臂；fA、fB分别为榫卯接触面的摩擦力；μ为木材接触面间的摩擦系数，由摩擦试验μ可取值0.24；F为作用力.
3） 物理条件. 当节点产生相对转角θ，节点在弹性阶段的弹塑性阶段各挤压面的应力分布如图15（a）所示. 设木材横纹受压弹性模量为ERc，挤压区域的宽度即为榫头宽度. 在弹性阶段，A、B挤压区的压应力还没有达到横纹屈服强度σC,R，其最大压应力分别为σA=ERcδA/h和σB=ERcδB/h. 弹性阶段应力分布为三角形分布，可求得A、B挤压区域的压应力合力分别为
FA=σAlAb2=ERcbtanθ2hl2A， (6) FB=σBlBb2=ERcbtanθ2hl2B. (7) 4） 弹性阶段理论公式. 由节点的几何条件可直接求得A、B挤压区域的挤压长度lA、lB，然后将物理条件中的各区域挤压合力FA、FB代入力矩平衡方程中可得到作用力F大小，由M=FL0可求得节点在弹性阶段的弯矩.
4.2.2 弹塑性阶段
在弹塑性阶段，节点的几何条件、平衡条件与在弹性阶段时相同，见式（1）～（7）. 在弹塑性阶段时，各挤压面应力分布如图15（b）所示. A、B挤压区域的最大压应力已达到σC,R，呈四边形分布.
各挤压区域的最大应力σA和σB可由σ=σc,R + E2（δ/h−σc,R/ERc）计算，见式（8）. 其中，E2为木材横纹受压强化段的切线模量，根据材料试验取E2=0.38ERc. 各挤压区域的应力呈四边形分布，设挤压区已屈服的区段长度为lA0和lB0，有lA0=lA−σc,Rhtan θ/ERc和lB0=lB−σc,Rhtan θ/ERc，由此可计算挤压区域的合力FA和FB，见式（9）.
各挤压区的应力呈四边形分布，求其形心后，各挤压区合力的力臂可由式（10）计算. 由节点的几何条件求得A、B挤压区域的挤压长度lA、lB，代入式（9）～（10）中，可求得各区域挤压合力FA、FB及其力臂xA、xB，最后代入力矩平衡方程中可得到作用力F大小，由M=FL0可求得节点在弹塑性阶段的弯矩.
{σA=σC,R+(δAh−σC,RERc)E2=σC,R+(lAtanθh−σC,RERc)E2，σB=σC,R+(δBh−σC,RERc)E2=σC,R+(lBtanθh−σC,RERc)E2. (8) {FA=σC,Rb2(lA+lA0)+(σA−σC,R)b2lA0，FB=σC,Rb2(lB+lB0)+(σB−σC,R)b2lB0. (9) {xA = d2−σC,R2l2A0 + σC,R(lA−lA0)(13lA+23lA0)+(σA−σC,R)l2A06FA/b，xB = d2−σC,R2l2B0 + σC,R(lB−lB0)(13lB+23lB0)+(σB−σC,R)l2B06FB/b. (10) 4.3 理论承载力与试验结果的对比
有穿销直榫节点理论承载力与试验结果的对比见表4. 由表4可见：标准试件BS1的试验结果与理论承载力分别相差3.87% （正向加载）和2.36% （反向加载），吻合较好；BS2的试验结果与理论承载力分别相差13.64% （正向加载）和4.43% （反向加载），正向加载的结果相差较大，可能与节点上下侧受力状况的不对称以及梁宽减小导致梁榫存在弯扭变形有关；BS3的试验结果与理论承载力分别相差7.10% （正向加载）和12.37% （反向加载）.
表 4 理论极限承载力与试验结果对比Table 4. Comparison of theoretical maximum capacity and test results加载方向 试件编号 试验结果/ （kN·m） 计算结果/ （kN·m） 差异/% 正向 BS1 2.867 2.978 3.87 BS2 2.257 2.565 13.64 BS3 2.196 2.352 7.10 平均 8.20 反向 BS1 −3.050 −2.978 2.36 BS2 −2.684 −2.565 4.43 BS3 −2.684 −2.352 12.37 平均 6.39 理论计算结果与试验结果的平均误差在9%以内，吻合较好. 由于理论计算模型为无空隙、接触良好的理想模型，而试验试件存在较明显的初始空隙，二者的结果存在一定误差.
5. 结 论
1） 各试件在低周往复荷载作用下，破坏形态均为柱内侧梁榫受拉边缘的顺纹拉裂破坏以及柱外侧梁榫的水平劈裂，节点较为充分地发挥了木材的强度和延性. 减小梁高的对照试件的柱内侧梁榫还发生了皱折状的挤压破坏.
2） 受榫卯之间的摩擦滑移与缝隙挤紧影响，所有试件的弯矩滞回曲线呈反Z形且捏缩效应明显. 在试验设计参数范围内，随着梁截面高度和梁截面宽度增大，有穿销直榫节点的转动刚度和抗弯承载力均增大，但是强度退化系数和等效黏滞阻尼系数变化不明显.
3） 相比于有穿销透榫节点，有穿销直榫节点的峰值转角大33%，正向抗弯承载力大62%，反向抗弯承载力大26%，且到达峰值后承载力下降更缓，强度退化系数更大，具有更好的抗震性能. 在节点形式的选择上宜优先考虑有穿销直榫节点.
4） 在木结构的设计施工过程中，木材的干缩变形对节点抗震性能有一定影响，在设计施工中应考虑木材干缩变形所导致的尺寸差异. 对既有木结构民居，可通过填充节点空隙加强节点抗震性能.
5） 所建立的有穿销直榫节点的弯矩-转角理论公式计算结果与试验结果相比，平均误差在9%以内.
-
图 3 28 d龄期混凝土疲劳加载前后的孔径分布
Figure 3. Pore size distribution of concretes before and after fatigue loading at 28 d age
图 4 90 d龄期混凝土疲劳加载前后的孔径分布
Figure 4. Pore size distribution of concretes before and after fatigue loading at 90 d age
表 1 熟料的化学成分和矿物组成（wB）
Table 1. Chemical and mineral composition of clinker
水泥编号 烧失量 SiO2 Al2O3 Fe2O3 CaO MgO SO3 C3S C2S C3A C4AF C1 0.49 24.73 4.71 4.98 62.21 1.52 0.35 21.52 54.66 4.04 15.41 C2 0.63 21.19 5.07 4.21 65.15 1.71 0.80 60.17 14.96 6.30 12.80 
下载: 导出CSV
表 2 水泥的物理性能
Table 2. Physical properties of cement
水泥编号 标准稠度/% 凝结时间/min 比表面积/（㎡•㎏–1） 抗压强度/MPa 抗折强度/MPa 水化热/（kJ•kg–1） 初凝 终凝 3 d 28 d 3 d 28 d 3 d 7 d C1 22.0 100 145 376 15.0 43.2 3.8 7.7 197.0 216.0 C2 24.2 130 180 358 28.4 52.5 5.4 8.5 304.0 333.0
下载: 导出CSV
表 3 混凝土配合比及其物理性能
Table 3. Mix propotion and physical properties of concrete
编号 水泥/
（kg•m–3）石/
（kg•m–3）砂/
（kg•m–3）水/
（kg•m–3）减水剂/
（kg•m–3）坍落度/
mm28 d强度/MPa 90 d强度/MPa 180 d强度/MPa 抗折 抗压 抗折 抗压 抗折 抗压 1# 340 1 307 666 136 3.74 35 4.1 43.0 5.0 54.1 6.0 62.4 2# 340 1 307 666 136 3.4 37 4.3 48.9 4.8 53.1 5.4 60.7
下载: 导出CSV
表 4 混凝土样品28、90 d的疲劳试验结果
Table 4. Fatigue lives of 28、90 d concrete
样品 应力水平 0.90 0.85 0.80 1#（28 d） 207.8 523.6 9 585.4 2#（28 d） 132.2 476.0 1 753.0 1#（90 d） 352.8 2 171.4 10 316.6 2#（90 d） 58.2 1 245.5 5 042.1
下载: 导出CSV
表 5 混凝土样品180 d的疲劳试验结果
Table 5. Fatigue lives of 180 d concrete
样品 应力水平 0.85 0.80 0.75 1# 398.0 2 418.6 20 226.8 2# 355.5 1 515.5 17 676.1
下载: 导出CSV
表 6 DTA-TG曲线上各样品对应吸热峰的失重比例
Table 6. Weight loss of cement pastes calculated through DTA-TG curve
样品 28 d 90 d 180 d 120℃ 450℃ 120℃ 450℃ 120℃ 450℃ PC1 8.00 2.46 10.83 2.51 11.32 2.89 PC2 9.27 3.73 10.89 3.98 11.21 4.57
下载: 导出CSV
-
郑克仁. 矿物掺合料对混凝土疲劳性能的影响及机理[D]. 南京: 东南大学, 2007 郑克仁,孙伟,赵庆新,等. 基于混凝土基体和界面过渡区性质的疲劳方程[J]. 硅酸盐学报,2007,35(2): 236-241. doi: 10.3321/j.issn:0454-5648.2007.02.022ZHENG Keren, SUN Wei, ZHAO qingxin. Fatigue equation based on properties of concrete matrix and interfacial transition zone[J]. Journal of the Chinese Ceramic Society, 2007, 35(2): 236-241. doi: 10.3321/j.issn:0454-5648.2007.02.022 LI Pingguo, WEI Sun. Study on the flexural fatigue performance and fractal mechanism of concrete with high proportions of ground granulated blast-furnace slag[J]. Cement and Concrete Research, 2007, 37(2): 242-250. SUN Wei. Fatigue performance and equations of roller compacted concrete with fly ash[J]. Cement and Concrete Research, 1998, 28(2): 309-315. doi: 10.1016/S0008-8846(97)00211-1 孙伟,严云. 高强混凝土与钢纤维高强混凝土冲击和疲劳特性机理的研究[J]. 土木工程学报,1994,27(5): 20-27. doi: 10.3321/j.issn:1000-131X.1994.05.001SUN Wei, YAN Yun. Study on the mechanism of impact and fatigue behavior of high-strength concrete and steel fiber reinforced high-strength concrete[J]. China Civil Engineering Journal, 1994, 27(5): 20-27. doi: 10.3321/j.issn:1000-131X.1994.05.001 张小辉. 钢纤维混凝土弯曲疲劳及其损伤特性和细观强度研究[D]. 昆明: 昆明理工大学, 2001 姜丽伟,肖福贵. 辅特维纤维水泥混凝土抗折疲劳性能试验研究[J]. 森林工程,2006,22(6): 47-50. doi: 10.3969/j.issn.1001-005X.2006.06.017JIANG Liwei, XIAO Fugui. Experimental studies of the flexural fatigue-resistant performance of the forta-ferro fiber cement concrete[J]. Forest Engineering, 2006, 22(6): 47-50. doi: 10.3969/j.issn.1001-005X.2006.06.017 LEE M K, BARR B I G. An overview of the fatigue behaviour of plain and fibre reinforced concrete[J]. Cement and Concrete Composites, 2004, 26(4): 299-305. doi: 10.1016/S0958-9465(02)00139-7 徐铜鑫,吴笑梅,樊粤明. 不同熟料矿物含量的水泥对混凝土部分性能的影响[J]. 水泥,2013(4): 4-8. doi: 10.3969/j.issn.1007-3922.2013.04.003XU Tongxin, WU Xiaomei, FAN Yueming. Influence of different mineral composition of clinker on partial performance of concrete[J]. Cement, 2013(4): 4-8. doi: 10.3969/j.issn.1007-3922.2013.04.003 王可良,隋同波,许尚杰,等. 高贝利特水泥混凝土的断裂韧性[J]. 硅酸盐学报,2012,40(8): 1139-1142.WANG Keliang, SUI Tongbo, XU Shangjie, et al. Fracture toughness of high belite cement concrete[J]. Journal of the Chinese Ceramic Society, 2012, 40(8): 1139-1142. 王可良,隋同波,刘玲,等. 高贝利特水泥混凝土的抗拉性能[J]. 硅酸盐学报,2012,40(8): 1139-1142.WANG Keliang, SUI Tongbo, LIU Ling, et al. Tensile properties of high belite cement concrete[J]. Journal of the Chinese Ceramic Society, 2012, 40(8): 1139-1142. 中国建筑科学研究院. JGJ63—89混凝土拌和用水标准[S]. 北京: 中国建筑工业出版社, 2002 付智, 罗翥, 王大鹏,等. 公路水泥混凝土路面施工技术细则: JTG F30—2014[S]. 北京: 人民交通出版社, 2014 中华人民共和国住房和城乡建设部. 普通混凝土拌合物性能试验方法标准: GB/T 50080—2016[S]. 北京: 中国建筑工业出版社, 2016 沈威, 黄文熙, 闵盘荣. 水泥工艺学[M]. 武汉: 武汉工业大学出版社. 1999: 291-323 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 567
- HTML全文浏览量: 236
- PDF下载量: 5
- 被引次数: 0