基于无监督学习的部分-整体关系获取
doi: 10.3969/j.issn.0258-2724.2014.04.005
Acquisition of Part-Whole Relations Based on Unsupervised Learning
-
摘要: 针对面向中文自由文本的部分-整体关系抽取问题,提出一种基于无监督学习的方法. 首先提出子模式提取算法,从领域文本集中获取概念对和概念对所在上下文模式,利用概念对和概念对上下文模式建立分布式语义模型;然后采用协同聚类算法将具有相同语义关系的概念对聚合成簇,通过训练L1正则化逻辑回归模型提取簇的特征并得到代表每个簇语义关系的概念对上下文模式;最后根据模式识别表达部分-整体关系的簇,从而获取部分-整体关系概念对. 实验结果表明,该方法取得较好的性能,F度量达到68.97%,优于传统聚类方法(55.77%)和模式匹配方法(61.95%).Abstract: An unsupervised learning method was proposed to solve the problem of part-whole relation extraction from Chinese free texts. A subsequence extraction algorithm was firstly introduced that can acquire concept pairs and their context patterns from domain texts, and a distributional semantic model was constructed according to concept pairs and context patterns of concept pairs. Then a co-clustering algorithm was applied to group the concept pairs with the same semantic relations together. L1 regularized logistic regression model was trained to select clustering feature and obtain the context pattern which represents semantic relation of each cluster. At last, according to the patterns, the clusters expressing part-whole relation were identified and part-whole relation concept pairs were acquired. The experimental results indicate the proposed method is effective and its F measure is up to 68.97% which is superior to the traditional clustering (55.77%) and pattern matching methods(61.95%).
-
Key words:
- ontology /
- unsupervised learning /
- part-whole relation /
- distributional semantic model /
- co-clustering
-
单箱双室箱梁在城市桥梁和公路桥梁中应用广泛. 采用该截面形式桥梁的箱体和桥面宽度较大,在竖向荷载作用有偏心时,其畸变效应不同于单箱单室箱梁. 箱梁的畸变效应研究文献较多,一般采用能量变分法或板元分析法都可得到一个四阶控制微分方程,方程未知量为畸变角或箱梁梁肋挠度w,都能很好地揭示单箱单室箱梁的畸变效应.
张元海等[1]采用能量变分原理对单箱单室箱梁的畸变效应进行了研究,分析了双层悬臂板对畸变的影响;徐勋等[2-3]采用广义坐标法研究了单箱单室箱梁的畸变;王兆南等[4]采用板元分析法研究了单箱单室箱梁的畸变效应;Pezeshky等[5]研究了宽翼缘钢梁的畸变. 单箱单室简支直线箱梁畸变的研究文献较多,成果较多. 曲线箱梁因扭转、弯曲和畸变相互耦合,畸变研究较为复杂[6-8]. 畸变的试验研究可对畸变理论分析结果进行验证:刘保东等[9]对连续刚构桥的扭转和畸变进行了试验研究;狄瑾等[10]对波形钢腹板组合箱梁的扭转和畸变进行了试验研究,分析了扭转、畸变和弯曲正应力的占比. 波形钢腹板组合箱梁由于结构自重轻,适合大跨度桥梁的设计,其畸变也比混凝土箱梁明显[11],畸变研究也较深入. Li等[12-14]研究了变截面箱梁的畸变,不同于求解常截面箱梁畸变控制微分方程常采用的初参解法,而采用纽马克法求解变截面箱梁的畸变控制微分方程. 双室箱梁桥的畸变不同于单室箱梁桥,蔺鹏臻等[15]研究了单箱双室箱梁对称弯曲时的局部扭转效应;Chidolue等[16]研究了多室箱梁的扭转和畸变,多数文献在研究双室箱梁的畸变效应时,只考虑反对称畸变,而忽略了正对称畸变.
单箱双室箱梁相比单箱单室箱梁增加了一道腹板,这使得在偏心竖向荷载作用下,箱梁畸变不仅有反对称畸变,还存在正对称畸变. 若忽略正对称畸变,在理论上将不完善,计算结果误差也较大,且双室箱梁在得出畸变翘曲惯性矩,框架横向抗弯惯性矩时也不同于单箱单室箱梁. 由于有两种畸变模式,因此无法采用一个微分方程来描述畸变效应,需采用两个未知量,对应两个微分方程才能完整描述单箱双室箱梁的畸变效应. 本文从单箱双室箱梁的畸变荷载分析出发,以箱梁的畸变角γd为未知量,定义正、反对称畸变对应的畸变角,建立正、反对称畸变的四阶控制微分方程,以揭示单箱双室箱梁的畸变效应,为单箱双室箱梁桥的设计计算提供参考.
1. 基本假定和畸变荷载
在薄壁箱梁畸变基本理论假定[1]的基础上,结合单箱双室箱梁在偏心荷载作用下的位移变形和实际设计需考虑的因素等,补充矩形截面单箱双室箱梁畸变分析的假定:单箱双室箱梁的边腹板厚度相同,箱梁横向变形时角点的转角位移可忽略.
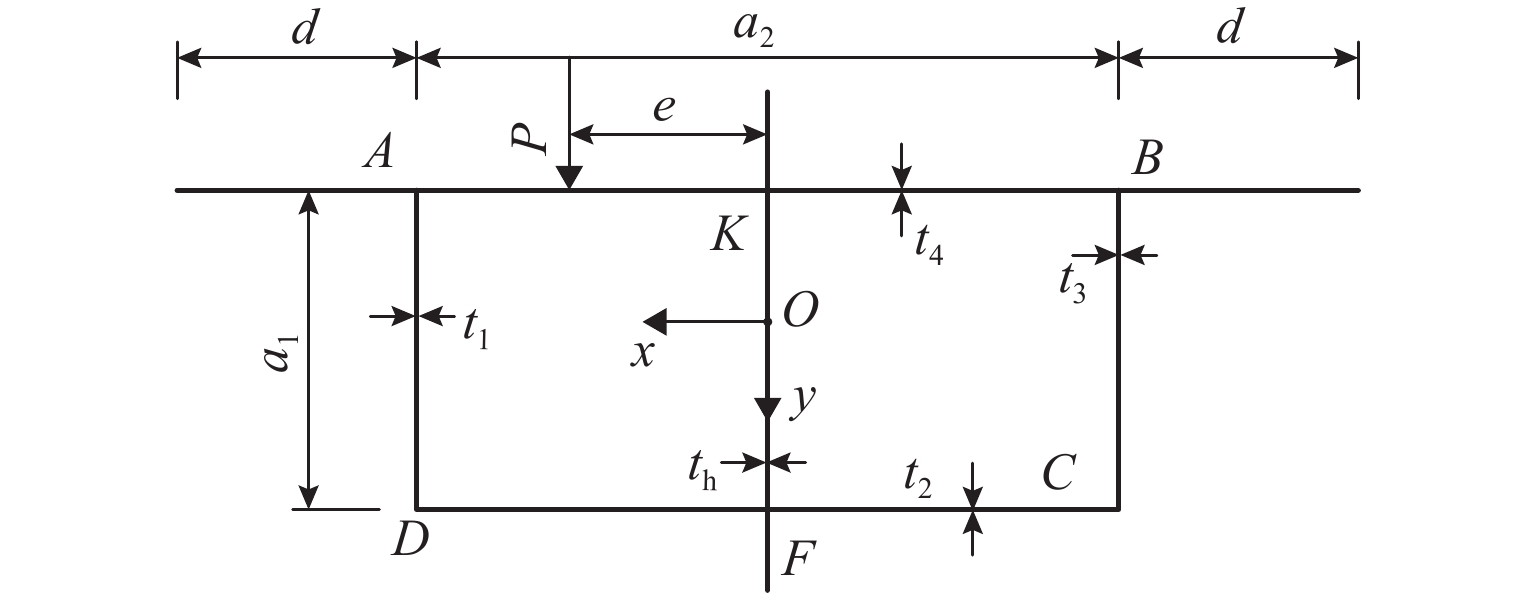
单箱双室箱梁一般都会存在一个对称轴y,箱梁截面尺寸如图1所示. 图1中:d、a1、a2分别为悬臂板、腹板、顶板(底板)的宽度;t1、t2、t3、t4、th分别为腹板AD、底板、腹板BC、顶板、腹板KF的厚度;e为荷载偏心距;P为单箱双室箱梁顶板上线性分布的偏心竖向荷载 . 采用右手坐标系,O为原点. 箱梁截面各角点分别采用A、B、C、D、K、F表示.
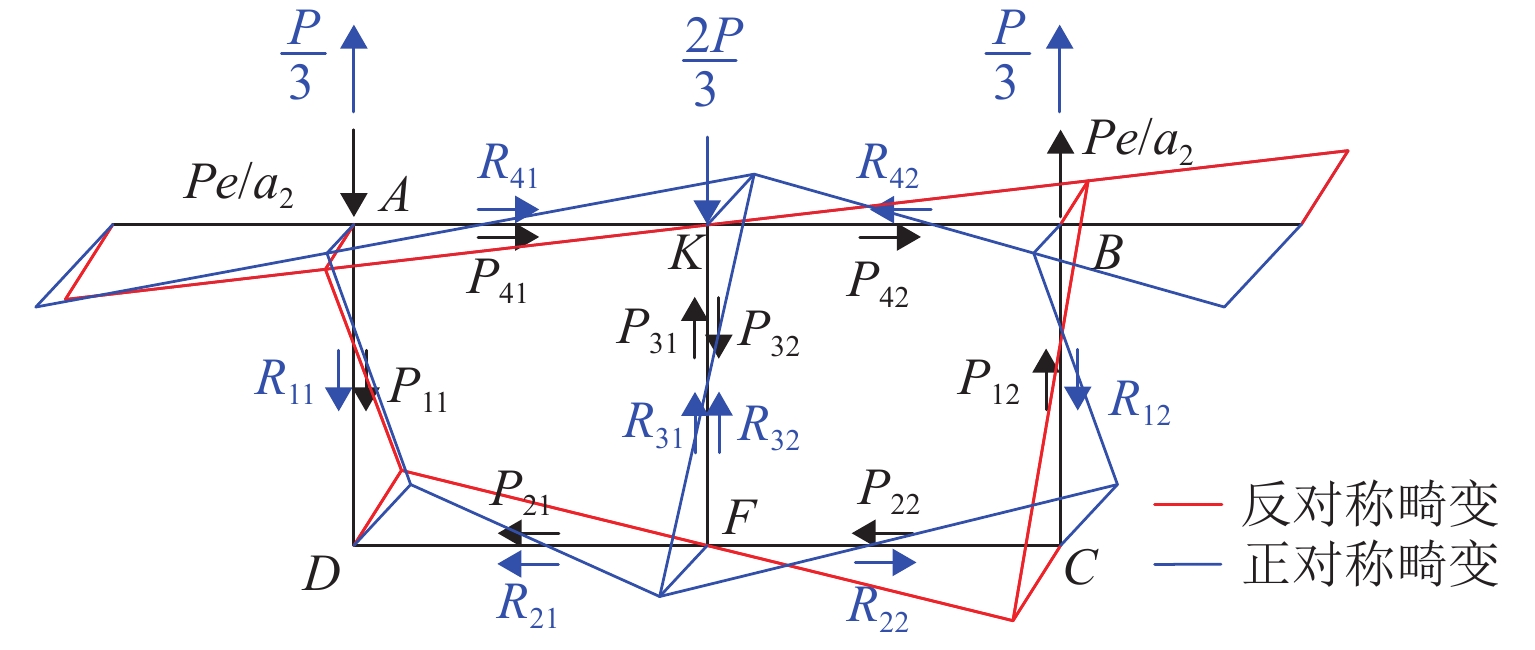
如图1所示,沿梁纵向取单位长框架后,P可等效成一力矩Pe和一作用于K点的竖向力P. 力矩可分解出使箱梁发生反对称畸变的荷载
$P_{}e/{a_2}$ ,竖向力P可分解出使箱梁发生正对称畸变的荷载$ P/3 $ 和$ 2P/3 $ ,如图2所示. 畸变正应力可对应叠加,继续分解的畸变荷载如式(1)所示.{P41=P42=P21=P22=Pe/(8a1),P11=P12=P31=P32=Pe/(4a2),R41=R42=R21=R22=Pa2/(6a1),R11=R12=R31=R32=P/3, (1) 式中:
$ {P_{41}} $ 、$ {P_{42}} $ 、$ {P_{12}} $ 、$ {P_{22}} $ 、$ {P_{21}} $ 、$ {P_{11}} $ 、$ {P_{31}} $ 和$ {P_{32}} $ 为反对称畸变荷载;$ {R_{41}} $ 、$ {R_{42}} $ 、$ {R_{12}} $ 、$ {R_{22}} $ 、$ {R_{21}} $ 、$ {R_{11}} $ 、$ {R_{31}} $ 和$ {R_{32}} $ 为正对称畸变荷载.2. 单箱双室箱梁反对称畸变
采用板元分析法研究单箱双室箱梁的反对称畸变,可得出箱梁的畸变翘曲刚度、框架横向抗弯刚度和畸变荷载之间的关系. 箱梁发生反对称畸变时,σdA和σdD为箱梁角点A、D的畸变正应力,令β1 = σdA/σdD,畸变正应力在各板件上的分布如图2所示. β1可由各板件上的畸变正应力合成的对坐标轴力矩之和为0的条件求得.
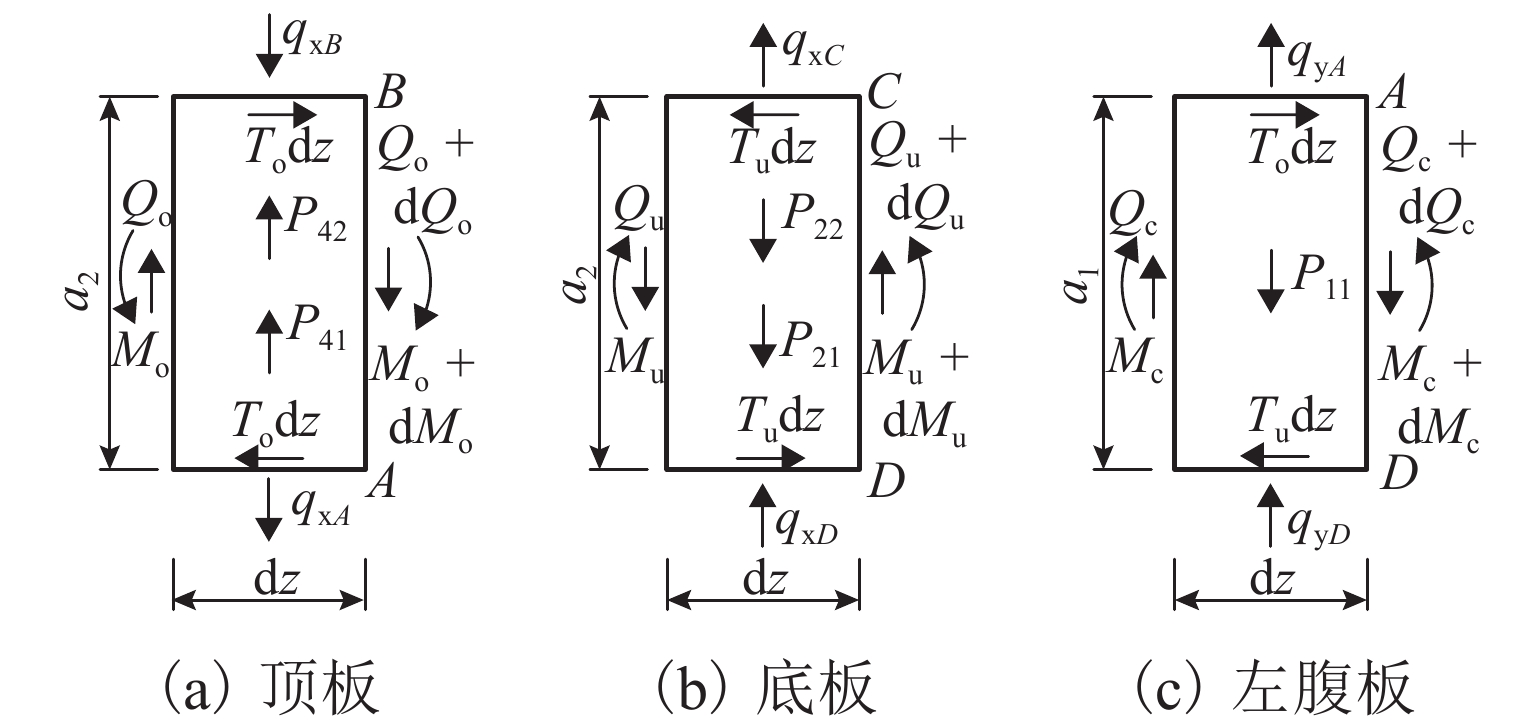
2.1 各板元面内力系分析
沿梁纵向取一微段,离散各板件,如图3所示. 图中:qxB、qxA、qxK为箱梁腹板对顶板的横向约束反力;Todz为微段上腹板对顶板的纵向约束反力;Qo、Mo分别为顶板上产生的面内剪力和力矩;qxC、qxD、qxF为腹板对底板的横向约束反力;Tudz为腹板对底板的纵向约束反力;Qu、Mu分别为底板上产生的面内剪力和力矩;qyA、qyD分别
为箱梁顶板和底板对左腹板的横向约束反力;Qc、Mc分别为左腹板面内剪力和力矩. 由顶板、底板和腹板的面内力矩平衡,顶板和底板面内沿x轴,腹板面内沿y轴方向列取力系平衡方程. 考虑到各板件之间在畸变荷载作用下维持力系平衡状态,略去高阶微量后得出:
d2Mcdz2+a12a2(d2Modz2+d2Mudz2)+a1(P41+P21)a2+P11−[a1(qx1+qx2)2a2+qy]=0, (2) 式中:
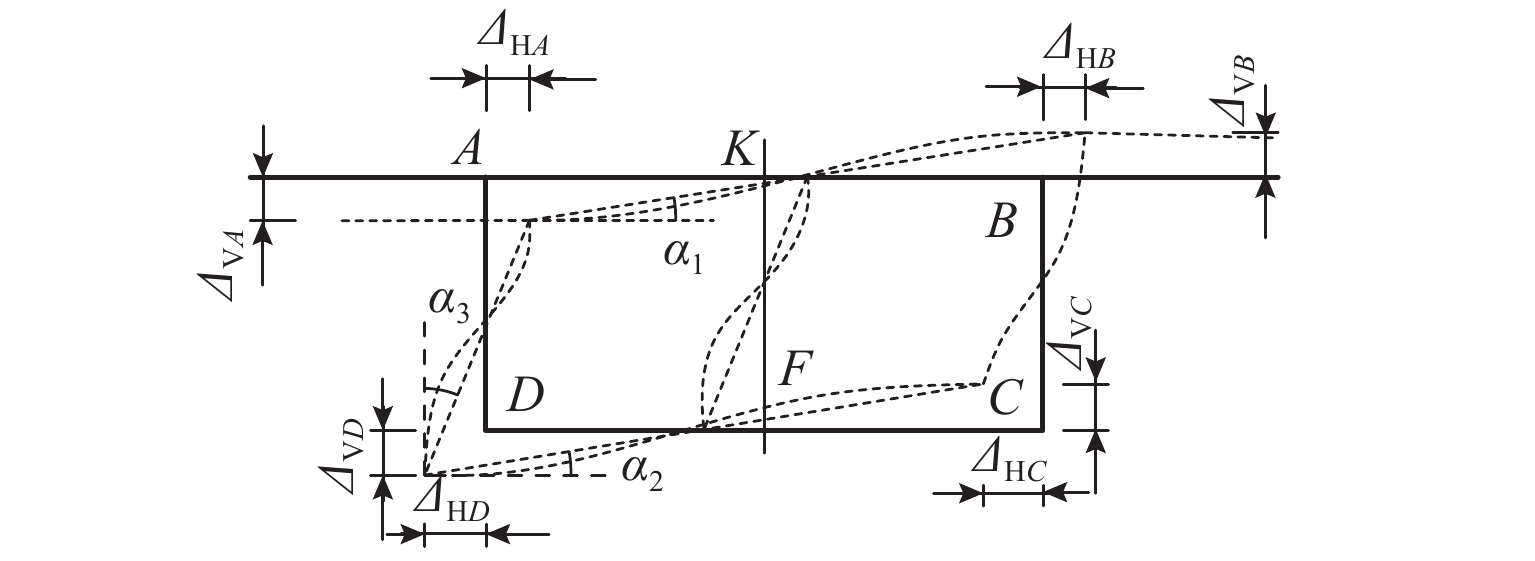
$q_{\mathrm{x} 1}=q_{\mathrm{x}A} + q_{\mathrm{x}B} + q_{\mathrm{x}K}$ ,$q_{\mathrm{x}K}$ 作用在板件AB的跨中,方向和$q_{\mathrm{x}A}$ 相同;$q_{\mathrm{x} 2}=q_{\mathrm{x}C} + q_{\mathrm{x}D} + q_{\mathrm{x}F}$ ,$q_{\mathrm{x}F}$ 作用在板件CD的跨中,方向和$q_{\mathrm{x}C}$ 相同;$q_{\mathrm{y}}=q_{\mathrm{y}A} + q_{\mathrm{y}D}$ .箱梁在反对称畸变时各角点的位移如图4所示,图中:ΔHA、ΔHB、ΔHC、ΔHD为对应各角点水平位移;ΔVA、ΔVB、ΔVC、ΔVD为对应各角点竖向位移;α1、α2、α3为对应各板件畸变后的角度改变.
定义单箱双室箱梁反对称畸变的畸变角γd1为
γd1=α1+α22+α3 = ΔVA+ΔVDa2+ΔHD+ΔHAa1. (3) 各板件上的力矩Mo、Mu、Mc之间存在对应关系[4]. 对γd1关于z轴求二次微分后,考虑到箱梁各角点位移和面内力矩的关系[1],得到
γ″d1=−4Mca2EJ1, (4) 式中:E为材料弹性模量;J 1为腹板 AD (腹板 BC )的面内惯性矩.
对式(4)再求二次微分后,可将式(2)化简为
−Ea22J1(1+β1)+a21(β1J4+J2)4a2(1+β1)γ(4)d1+a1a2(P41+P21)+P11−[a1(qx1+qx2)2a2+qy]=0, (5) 式中:Jn=tn
$ a_n^3 $ /12 (n=1,2),J4=t4 (a2 + 2d)3/12,J2、J4分别为底板、顶板的面内惯性矩.2.2 各板元面外力系分析
采用箱梁各板件的面外力系分析化简式(5)中的
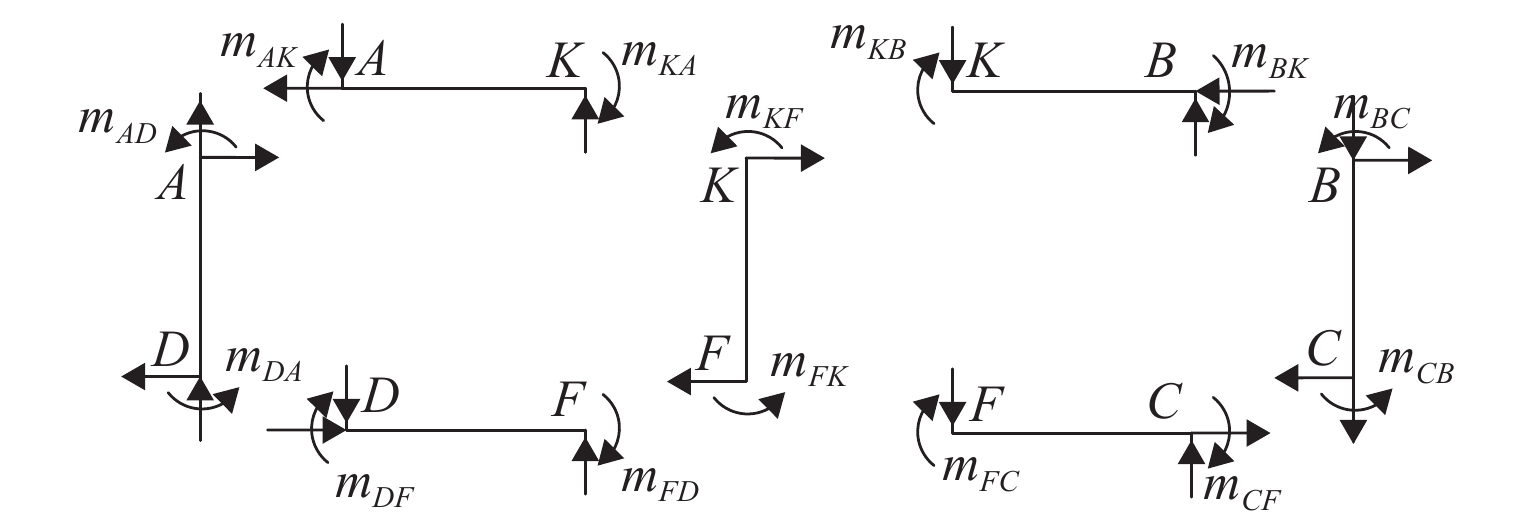
${a_1}({q_{{\rm{x}}1}} + {q_{{\rm{x}}2}})/(2{a_2}) + {q_{\rm{y}}}$ 项. 在分析过程中考虑箱梁腹板KF对框架横向抗弯惯性矩的贡献,单箱双室箱梁在反对称荷载作用下发生畸变后,离散箱梁各板件,各板件的面外受力如图5所示,图中变量mAK、mAD等为各板件板端的畸变横向弯矩.反对称畸变时,取出板件AK和DF分析面外受力可得:
${q_{{\rm{y}}A}}{a_2} = 2({m_{AK}} + {m_{KA}})$ ,${q_{{\rm{y}}D}}{a_2} = 2({m_{DF}} + {m_{FD}})$ . 取出板件AD和BC分析面外受力可得:${q_{{\rm{x}}A}}{a_1} = {m_{AD}} + {m_{DA}}$ ,${q_{{\rm{x}}B}}{a_1} = {m_{BC}} + {m_{CB}}$ ,${q_{{\rm{x}}A}} = {q_{{\rm{x}}D}}$ ,${q_{{\rm{x}}B}} = {q_{{\rm{x}}C}}$ . 取出板件KF分析面外受力可得:${q_{{\rm{x}}K}}{a_1} = {m_{KF}} + {m_{FK}} - {m_{KA}} - {m_{KB}} - {m_{FC}} - {m_{FD}}$ .板件KB和FC的面外力系分析和板件AK等相同. 为得出各板件的板端畸变横向弯矩和板端位移的关系,可采用力矩分配法进行分析,见式(6).
{mAK=24EI4i1a22(i1+i4)ΔV+12EI1i4a21(i1+i4)Δh,mAD=−12EI1i4a21(i1+i4)Δh−24EI4i1a22(i1+i4)ΔV,mDF=24EI2i1a22(i1+i2)ΔV+12EI1i2a21(i1+i2)Δh,mDA=−12EI1i2a21(i1+i2)Δh−24EI2i1a22(i1+i2)ΔV,mKA=24EI4iha22(2i4+ih)ΔV+12EIhi4a21(2i4+ih)Δh,mFD=24EI2iha22(2i2+ih)ΔV+12EIhi2a21(2i2+ih)Δh, (6) 式中:i1、i2、i4、ih分别为箱梁边腹板、底板、顶板和中腹板的线刚度;I1、I2、I4、Ih分别为箱梁边腹板、底板、顶板和中腹板的面外惯性矩;ΔV、Δh分别为板件板端竖向位移和水平位移.
在
${a_1}({q_{{\rm{x}}1}} + {q_{x2}})/(2{a_2}) + {q_{\rm{y}}}$ 中代入qx1、 qx2、 qy的表达式,结合式(6),考虑到式(3)中有ΔV = ΔVA =ΔVD,Δh = ΔHD = ΔHA,得到a1(qx1+qx2)2a2+qy=48Ea2(IhI44I4a1+Iha2+IhI2Iha2+4I2a1+I1I4I1a2+2I4a1+I1I2I1a2+2I2a1)γd1. (7) 将
$ {P_{41}} $ 、$ {P_{21}} $ 、$ {P_{11}} $ 代入式(5)中的$\dfrac{{{a_1}}}{{{a_2}}}({P_{41}} + {P_{21}}) \;+ {P_{11}}$ 项,化简得到$P_{}e/(2{a_2})$ .2.3 反对称畸变控制微分方程
根据以上分析可将式(5)化简为单箱双室箱梁在偏心竖向荷载作用下,以反对称畸变角γd1为未知量的四阶畸变控制微分方程,如式(8).
EIωd1γ(4)d1+EIR1γd1=Pe/2, (8) 式中:Iωd1为单箱双室箱梁反对称畸变的翘曲惯性矩,单位m6,如式(9);IR1为单箱双室箱梁反对称畸变的横向抗弯惯性矩,单位m2,如式(10).
Iωd1=a22(1+β1)J1+a21(β1J4+J2)4(1+β1), (9) IR1=48(IhI44I4a1+Iha2+IhI2Iha2+4I2a1+I1I4I1a2+2I4a1+I1I2I1a2+2I2a1). (10) 3. 单箱双室箱梁正对称畸变
3.1 正对称畸变时箱梁畸变翘曲惯性矩
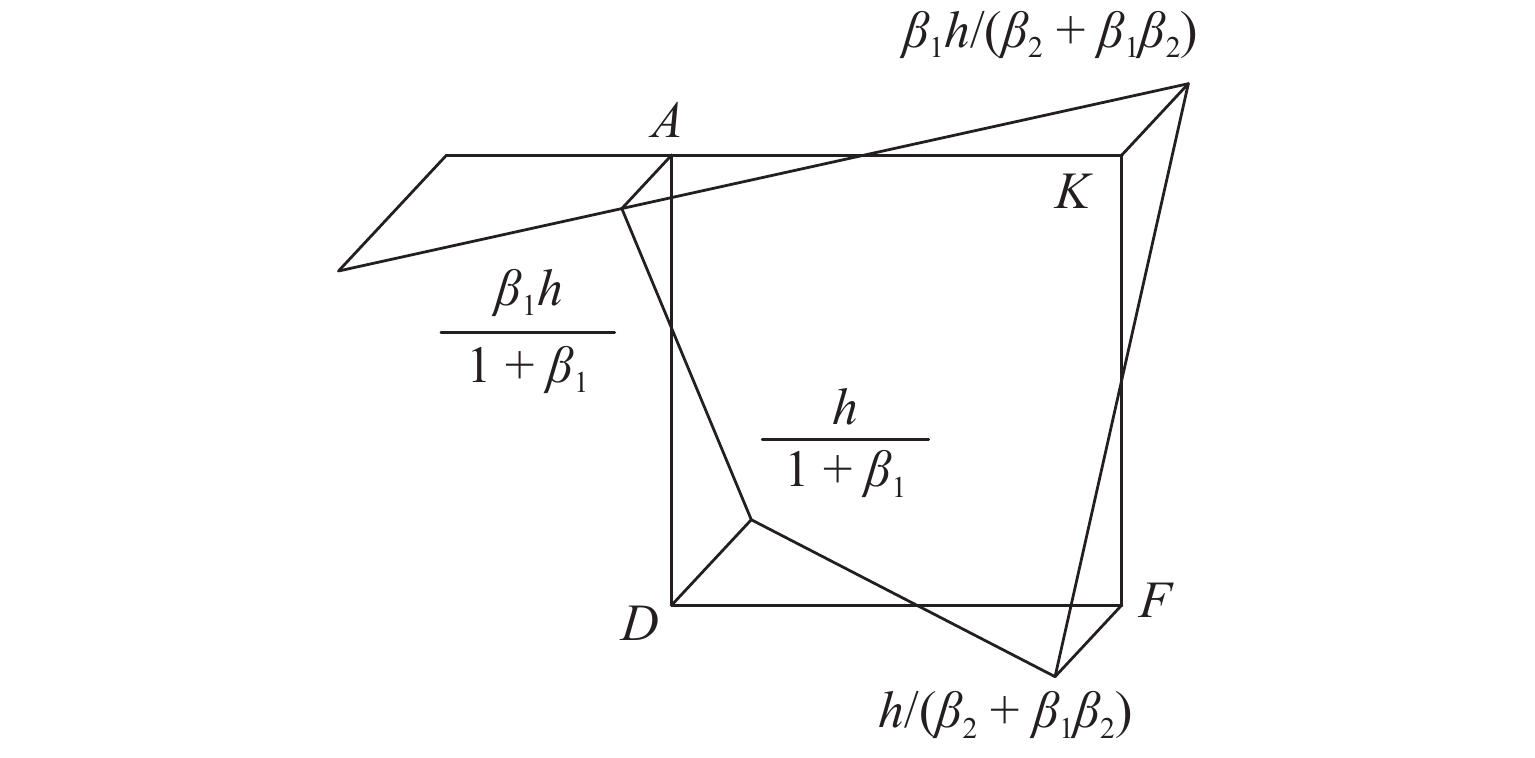
如图2所示,单箱双室箱梁在正对称畸变荷载作用下,产生正对称畸变翘曲变形. 按假定,畸变正应力在各板件上呈线性分布,关于y轴正对称. 考虑到变形亦呈正对称,顶板和底板有竖向位移,而水平位移很小几乎可以忽略,因此可采用一半结构AKFD进行分析,如图6所示,图中:h为箱梁高度. 考虑结构AKFD各角点角位移不相等的情况,当箱梁各板件厚度各不相等时,现有单箱单室箱梁畸变微分方程将不再适用,因按照假定和分析过程,其都建立在箱梁截面至少关于一个坐标轴对称的基础上.
采用一个参数β1描述畸变正应力在各板件上分布的模式不再满足箱梁各板件厚度都不同的情形. 现采用两个参数β1和β2分别描述畸变正应力在腹板、顶板(底板)上的分布. 对各板件厚度都不同的箱梁结构,令β2=σdA/σdK (σdK为箱梁角点 K 的畸变正应力),认为由畸变正应力引起的面内力矩分布在顶、底板上的反弯点位置相同,但不再二等分. 在求出β1和β2后,可确定各板件厚度都不同的箱梁的畸变翘曲位移模式.
β1和β2可由各板件面内畸变正应力对x、y轴形成的力矩之和为0的条件,且联立式(11)、(12)求得.
β1 = 2t2a3(β22+1−β2)+3a2h(t1β22+th)Γ1+Γ2, (11) β2=3t4β21(a2−d2)+3t2a2+2ahth(β21+1−β1)3t4β21(a+d)2+3t2a2+2aht1(β21+1−β1), (12) 式中:a为分割后单箱的顶板或底板宽度;
${\varGamma _1} = 2{t_4}(a + d)[(\beta _2^2 - {\beta _2} + 1){a^2} + {d^2}{({\beta _2} + 1)^2}]$ ;${\varGamma _2} = 2{t_4}(a + d)\times ad(2\beta _2^2 + {\beta _2} - 1) + 3{a^2}h({t_1}\beta _2^2 + {t_{\rm{h}}})$ .求得β1、β2后,根据
${I_{\text{ω}{\rm{ d}}}} = \displaystyle\int_S {\omega _{\rm{d}}^2{\rm{d}}S}$ 可求得结构AKFD的畸变翘曲惯性矩Iωd2,如式(13)所示,S为板件截面积.Iωd2=h2t4β21[(β2a+β2d+d)3+a3]48β22(1+β2)(1+β1)2+h2t2a3(β32+1)48β22(1+β2)(1+β1)2+(th+β22t1)(β31+1)a2h348β22(1+β1)3. (13) 3.2 正对称畸变时框架横向抗弯惯性矩
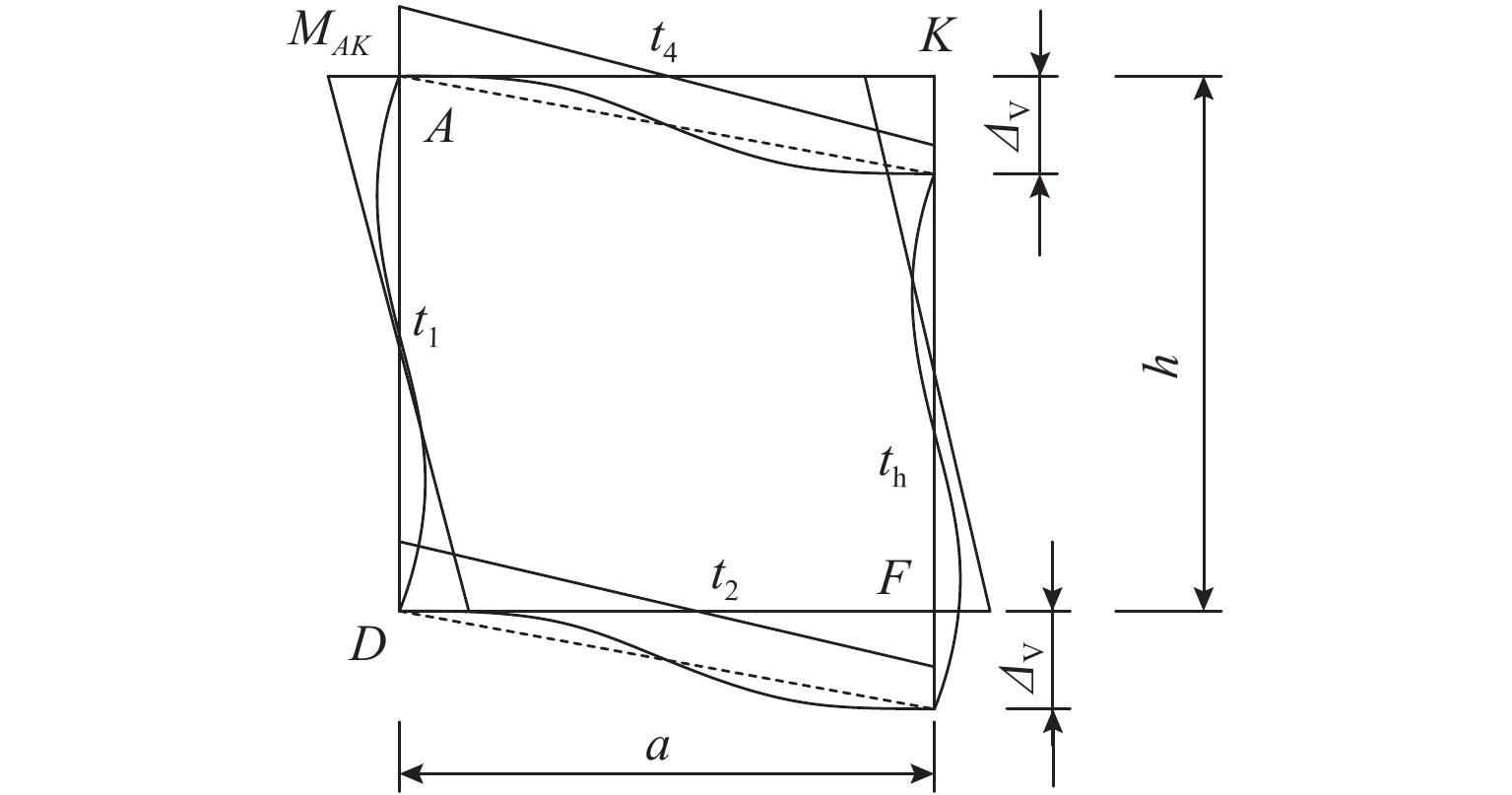
结构AKFD在正对称畸变荷载作用下发生如图7所示的变形. 在图7中:设定杆件AK和DF杆端的弯矩、转角以逆时针为正;杆件AK和DF皆沿y轴有相同的竖向位移;MAK、MKA分别
为AK杆件杆端A、K的横向弯矩;γd2 = ΔV/a,为单箱双室发生正对称畸变时的畸变角. 根据分析,可忽略杆件AD和KF水平x向位移,采用杆件的转角位移公式,可用畸变角γd2将角点D的畸变横向弯矩表示出来,有MDF = IDγd2. 同理可得其他板件的板端弯矩:MKA = IKγd2、 MAK = IAγd2、 MFD = IFγd2. ID、IK、IA和IF见式(14),同时可方便地确定结构的横向弯曲应变能.
{ID=[(4Θ1+Θ3)i2ih−3Θ1i22](Θ2+3Θ1)i1i4+[(6Θ1−Θ2)i2ih−3Θ1i22][3Θ1i21−(4Θ1+Θ3)i1i4]Γ3,IK=[(4Θ3+Θ1)i1i4−3Θ3i24](Θ2+3Θ3)i2ih+[(6Θ3−Θ2)i1i4−3Θ3i24][3Θ3i2h−(4Θ3+Θ1)i2ih]Γ4,IA=2(Θ2+3Θ1)i1i4Θ3i4+Θ1i1,IF=2(Θ2+3Θ3)i2ihΘ1i2+Θ3ih, (14) 式中:参数Θ1、Θ2、Θ3与箱梁各板件线刚度有关;
${\varGamma _3}$ =$[3{\varTheta _1}i_1^2 - (4{\varTheta _1} + {\varTheta _3}){i_1}{i_4}]{\varTheta _1}({i_{\rm{h}}} - {i_2}) +[(4{\varTheta _1} + {\varTheta _3}){i_2}{i_{\rm{h}}} - 3{\varTheta _1}i_2^2] {\varTheta _1} ({i_1} - {i_4})$ ;${\varGamma _4}$ =$[3{\varTheta _3}i_{\rm{h}}^2 - (4{\varTheta _3} + {\varTheta _1}){i_2}{i_{\rm{h}}}]{\varTheta _3}({i_1} - {i_4}) + [(4{\varTheta _3} + {\varTheta _1}){i_1}{i_4} - 3{\varTheta _3}i_4^2]{\varTheta _3}({i_{\rm{h}}} - {i_2})$ .3.3 正对称畸变控制微分方程
箱梁的总横向弯曲应变能可表示为
${u_{\rm{e}}} = \dfrac{1}{2}\displaystyle\int_L {\displaystyle\int_s {\dfrac{{M^2{{(s)}}}}{{EI}}{\rm{d}}s} {\rm{d}}L}$ ,其中:M(s)为箱室各板件周向s处的横向弯矩;I为各板件的面外惯性矩;L为梁长.沿梁轴z向取单位长框架,可得箱梁各板件的横向弯曲应变能之和,如式(15)所示.
 也可写为
也可写为$\dfrac{1}{2}E{I_{{\rm{R}}2}}\gamma _{{\rm{d}}2}^2$ ,IR2为箱室各板件厚度均不相等时的框架横向抗弯惯性矩,如式(16).ue=γ2d26E[a(I2A+I2K−IAIK)I4+h(I2K+I2F−IKIF)Ih+a(I2D+I2F−IDIF)I2+h(I2A+I2D−IAID)I1], (15) IR2=13E2[a(I2A+I2K−IAIK)I4+h(I2K+I2F−IKIF)Ih+a(I2D+I2F−IDIF)I2+h(I2A+I2D−IAID)I1]. (16) 通过以上分析可得,单箱双室箱梁发生正对称畸变时,取一半结构得出的畸变微分方程如式(17). IR2单位为m2,
${I_{{\text{ω}}{\rm{d}}2}}$ 单位为m6.EIωd2γ(4)d2+EIR2γd2=Pa/3. (17) 采用畸变角γd1、γd2分别描述箱梁的反对称和正对称畸变,得出两个畸变微分方程,方程可采用初参数法或弹性地基梁比拟法进行求解[1, 4].
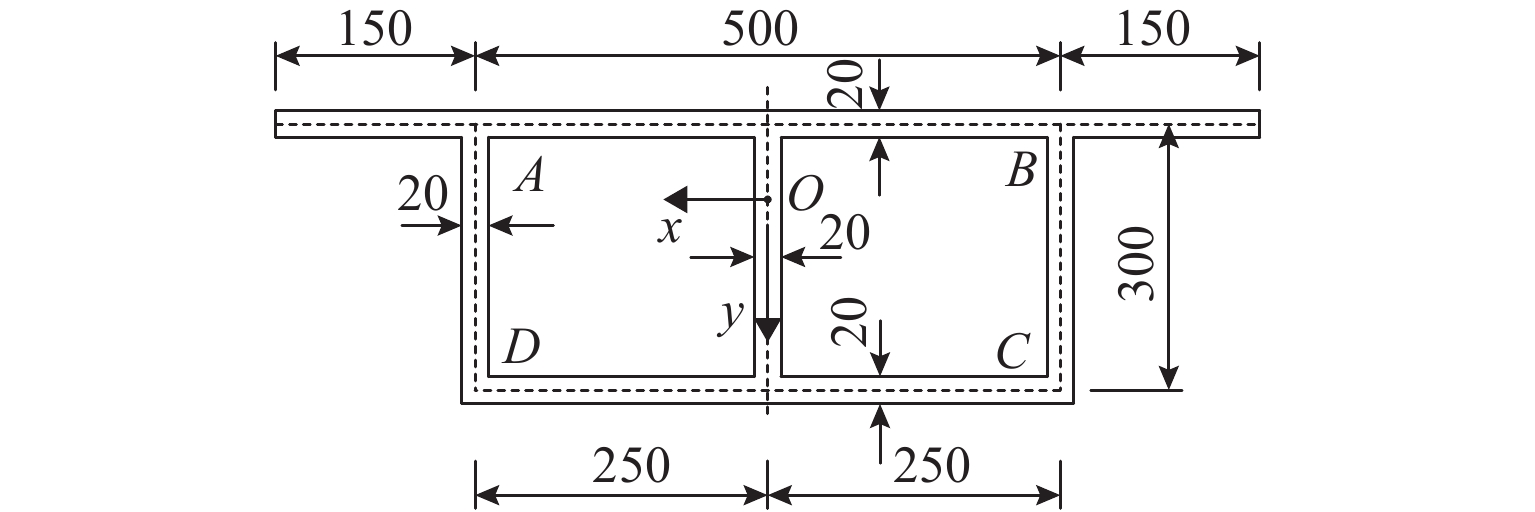
4. 数值算例及参数分析
在等高度矩形截面简支箱梁上设置端横隔板,计算跨径L=80 m,截面如图8所示. E=35 GPa,泊松比μ=0. 在箱梁顶板上作用偏心竖向分布力矩1 kN · m/m,箱梁截面关于y轴对称. 采用本文单箱双室箱梁畸变理论进行计算分析,同时去掉中腹板按照单箱单室箱梁计算对比,得到的各畸变数值见表1,表中:Bd为畸变双力矩;ωdA、ωdD为角点A、D的畸变扇性坐标. Bd、γd的值为弹性地基梁比拟法中单位荷载作用下的计算值,σd为实际荷载作用下的值.
表 1 箱梁反对称畸变计算值Table 1. Antisymmetrical distortional values方法 Iωd1/m6 IR1/m2 ωdD/m2 ωdA/m2 β1 γd1/( × 10−10 rad) Bd/(N·m2) σdA/kPa σdD/kPa 单箱单室箱梁畸变 12.1728 0.0040 2.5426 1.2075 0.4749 3.3961 2.6279 0.5213 1.0978 单箱双室箱梁反对称畸变 12.1728 0.0096 2.5426 1.2075 0.4749 1.7660 2.1110 0.2094 0.4409 单箱单室箱梁增加一道腹板成为单箱双室箱梁后,σdA由0.5213 kPa变为0.2094 kPa,应力减小率为:(0.5213−0.2094)/ 0.5213 × 100%=59.83%,σdD的减小率也为59.83%. 因单室和双室箱梁反对称畸变的假定相同,角点应力比β1数值不变,各角点的畸变扇性坐标数值不变. 由于中腹板增强了截面的横向抗弯刚度,箱梁的框架横向抗弯惯性矩从单室的0.0040增大到双室的0.0096.
算例箱梁正对称畸变计算值如表2所列. 单箱双室箱梁角点A的正对称畸变正应力为反对称畸变值的28.08%,角点D为26.76%. 若取的一半结构按照传统的单箱单室箱梁畸变方法计算角点畸变正应力,角点D的值为单箱双室箱梁反对称畸变值的1.97倍,为按照本文正对称畸变计算值的7.37倍.
表 2 箱梁正对称畸变计算值Table 2. Positive-symmetrical distortional values方法 角点应力比 γd/( × 10−10 rad) σdA/kPa σdD/kPa 单箱双室箱梁正对称畸变 β1 = 0.5000, β2 = 0.6241 0.0160 0.05897 0.11795 单箱单室箱梁畸变 0.3229 3.7516 0.28055 0.86898 最终单箱双室箱梁角点A、D的畸变正应力为箱梁正、反对称畸变计算结果的叠加,如表3. 并与有限元结果进行对比,有限元计算采用Shell-63单元建模分析. 从角点A、D的畸变正应力误差来看,本文方法解析解和有限元解最大误差的绝对值不超过8.71%,角点A的畸变正应力误差仅为1.73%,有限元解和解析解吻合良好.
表 3 箱梁角点畸变正应力Table 3. Corner distortion normal stress of box girder畸变正应力 单箱双室箱梁畸变解析解/kPa 有限元解 ②/kPa 误差((①−②)/② × 100) /% 反对称畸变 正对称畸变 最终结果 ① σdA 0.20940 0.05897 0.26837 0.26380 1.73 σdD 0.44090 0.11795 0.55885 0.61220 −8.71 本文方法得到的双室箱梁和按单箱单室箱梁计算的角点A、D的应力值如表3和表1所示. 考虑箱梁的正对称畸变后,箱梁由单箱单室变成单箱双室时,角点A畸变正应力的减小率由59.83%变为48.52%,角点D畸变正应力的减小率由59.83%变为49.09%,如忽略正对称畸变的影响,畸变效应和有限元结果的误差将会增大. 双室箱梁的畸变正应力比单室箱梁的要小. 当箱梁横向宽度较大时,增设中腹板可有效减小箱梁的畸变效应.
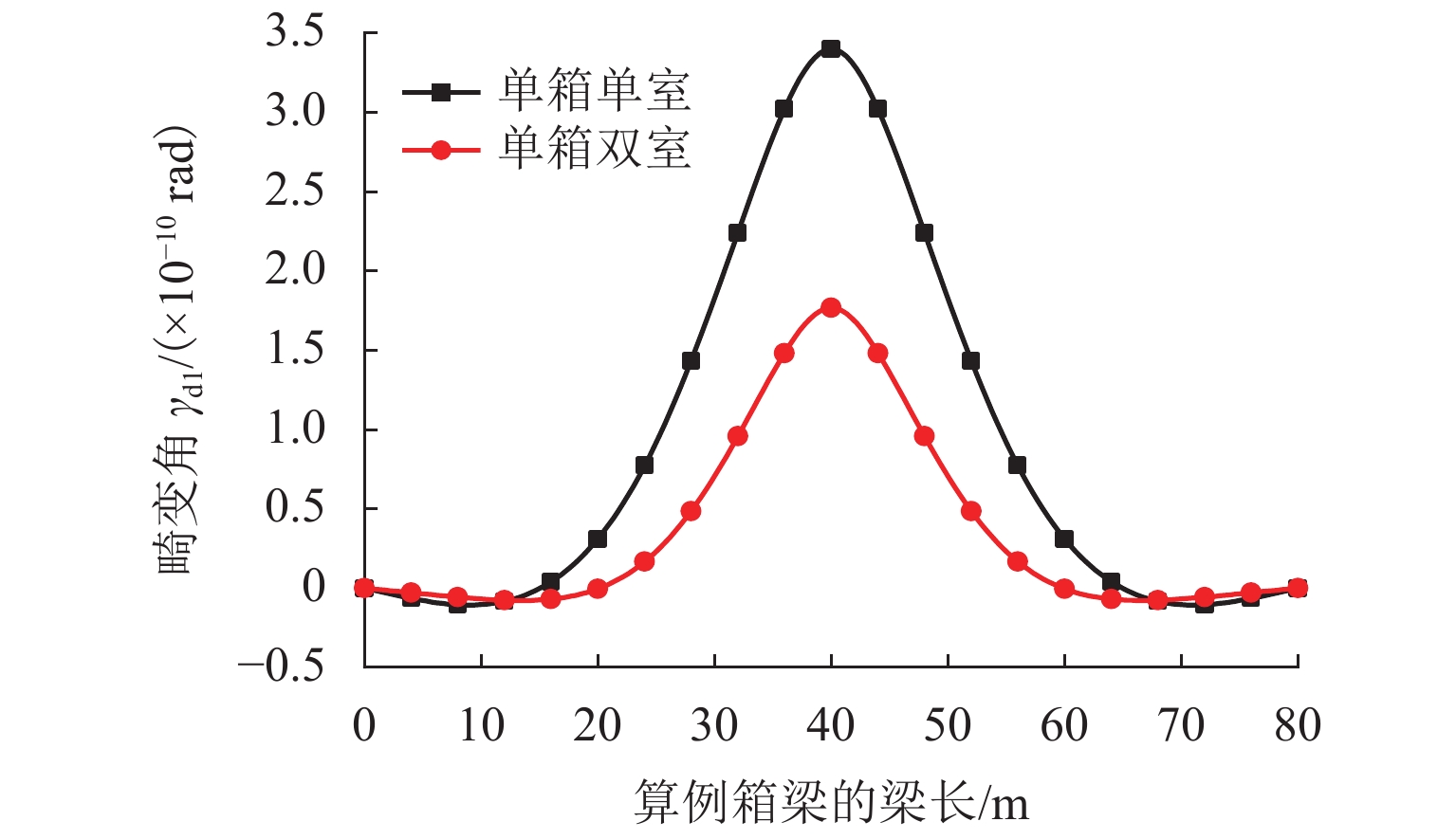
为更好地比较两种截面形式箱梁的畸变效应差别. 单箱单室和单箱双室简支箱梁跨中截面的畸变角、角点畸变正应力的对比如图9、10所示. 由图9可知:单箱双室箱梁的反对称畸变角沿梁长的分布在畸变角数值的绝对值上小于单箱单室箱梁;中腹板对箱梁畸变的削弱非常明显,跨中截面畸变角迅速变小;在梁端一定区域内,双室箱梁的畸变角变化比单室的平稳,双室箱梁在此区域的反向变形小于单室箱梁,畸变角较早地衰减趋向于0,偏心竖向荷载引起的畸变较单箱单室箱梁的小,较好地反映了增加的箱室腹板对畸变的限制作用,与增加梁跨内横隔板效果相同.
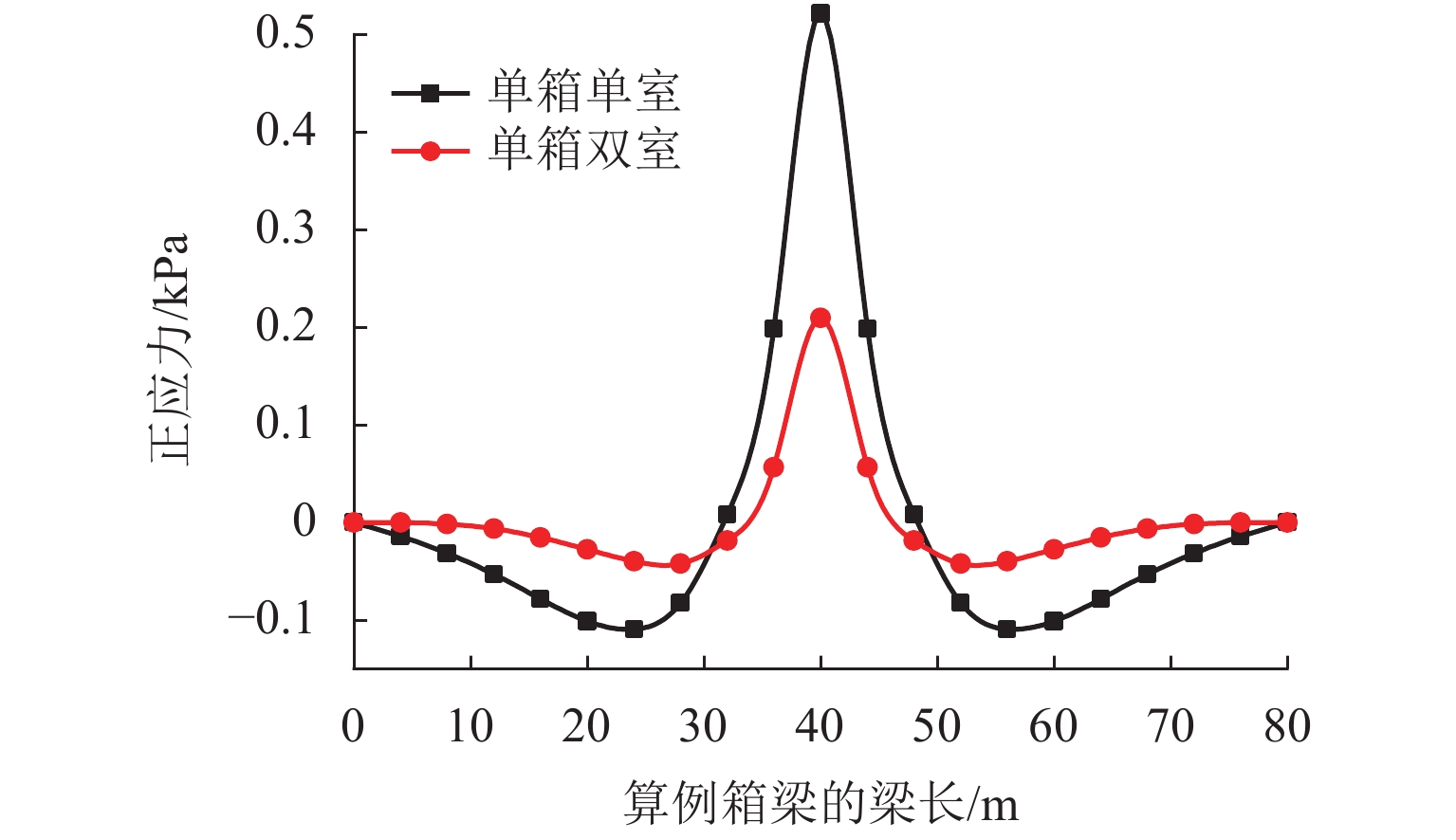
由图10可知:对箱梁畸变正应力沿梁长的分布进行分析,单室箱梁和双室箱梁角点A的畸变正应力沿梁长的分布有着明显的区别;双室箱梁角点A畸变正应力在数值的绝对值上明显小于单室箱梁,在跨中截面有最大值;双室箱梁角点A的畸变正应力向梁端衰减很快,而单室箱梁则衰减较慢. 从以上分析可以看出,双室箱梁畸变角、畸变正应力计算值都小于单室箱梁,中腹板对箱梁畸变的限制是非常明显的.
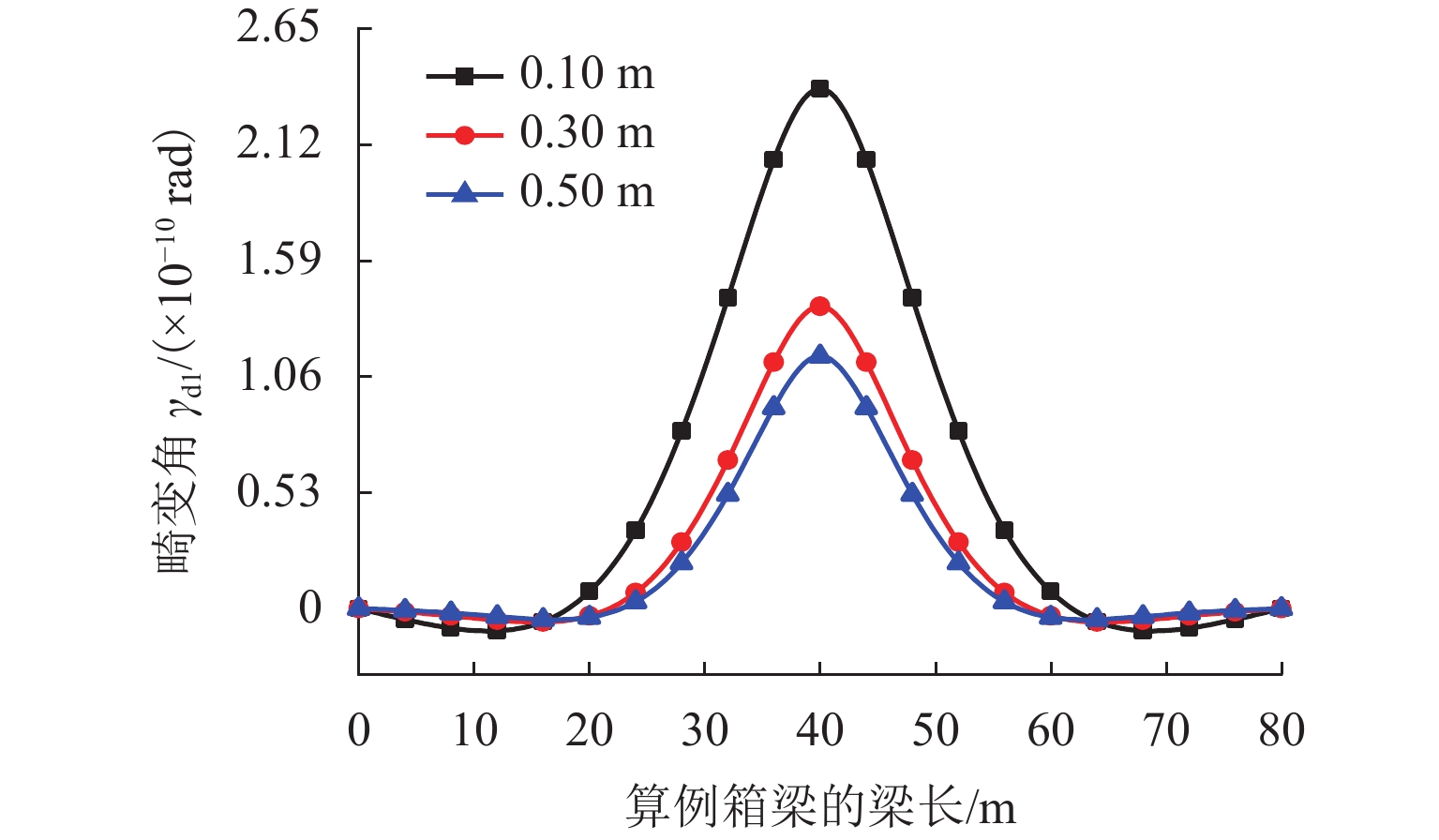
取中腹板厚度为0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50 m,其他条件皆不变,分析箱梁跨中截面反对称畸变角随中腹板厚度变化的规律. 中腹板厚度变化时,双室箱梁反对称畸变的畸变角沿梁长的变化情况如图11所示. 选取中腹板厚度为0.10、0.30、0.50 m的数据列出,0.10 m厚的板为薄板,0.30 m厚的板为薄板和厚板的界限,0.50 m厚的板为厚板.
从图11可以看出:不同中腹板厚度的双室箱梁反对称畸变角沿梁长的变化趋势在箱梁跨中截面区域内基本相同,在箱梁梁端附近变化趋势有所不同;随着中腹板厚度的增加,在梁端附近,畸变角的变化逐渐平稳,双室箱梁在梁端附近畸变翘曲的程度较小;中腹板厚度为0.10 m的双室箱梁畸变角在梁端附近的反向变形比0.50 m板厚的要突出,薄壁箱梁的畸变翘曲程度比厚壁的要明显;随着板厚的增加,双室箱梁的畸变逐渐减小,仅在跨中一定长度范围内畸变较为明显,梁两端逐渐减弱,梁端变形程度较小的区域逐渐向跨内延伸;0.50 m板厚的双室箱梁梁端畸变较小的区域较0.10 m板厚的区域要长.
5. 结 论
1) 在偏心竖向荷载作用下,单箱双室箱梁不仅存在反对称畸变,还存在正对称畸变. 正对称畸变正应力较小,本文算例中,最大只占到反对称畸变正应力的28.08%.
2) 考虑了正对称畸变效应后,双室箱梁的畸变分析在理论上将更加完善. 通过数值计算显示,畸变正应力解析解和有限元解的误差减小,误差绝对值最大为8.71%,相互吻合更好.
3) 当箱体较宽的单箱单室箱梁增设中间腹板成为单箱双室箱梁后,箱梁角点处的畸变正应力可减少到单室箱梁的49.09%. 为减小宽箱梁在偏心竖向荷载作用下的畸变,设置中腹板效果明显.
4) 单箱双室简支箱梁的畸变比单箱单室简支箱梁的要小,变形主要在跨中一定的区域内,梁端附近的区域反向变形不如单箱单室的明显. 中腹板厚度的变化可使双室箱梁的畸变发生较明显的改变,厚度较小时畸变较为明显,厚度增大时畸变逐渐减弱.
5) 采用两个参数β1、β2描述正对称畸变时,单箱双室箱梁各板件上的畸变正应力分布比一个参数的合理. 采用一个参数的箱梁畸变理论计算的正对称畸变效应,箱梁角点畸变正应力最大可为本文方法的7.37倍.
-
WINSTON M E, CHAFFIN R, HERRMANN D. A taxonomy of part-whole relations[J]. Cognitive Sciences, 1987, 11(4): 417- 444. GERSTL P, PRIBBENOW S. Midwinters, end games, and body parts: A classification of part-whole relations[J]. International Journal of Human Computer Studies, 1995, 43(5/6): 865-890. ODELL J. Six different kinds of composition[J]. Journal of Object-Oriented Programming, 1994, 5(8): 10-15. KEET C M, ARTALE A. Representing and reasoning over a taxonomy of part whole relations[J]. Applied Ontology, 2008, 3(1): 91-110. IRIS M, LUTOWITZ B, EVENS M. Relational models of the lexicon[M]. Cambridge: Cambridge University Press, 1989: 261-288. GIRJU R, BADULESCU A, MOLDOVAN D. Automatic discovery of part whole relations[J]. Computational Linguistics, 2006, 32(1): 83-135. WILLEM R H, KOLB H, SCHREIBER G. A method for learning part whole relations[C]//Proc. of the 5th International Semantic Web Conference. Athens: Springer's, 2006: 723-735. PANTEL P, PENNACCHIOTTI M. Espresso: leveraging generic patterns for automatically harvesting semantic relations[C]//Proc. of COLING/ACL-06 Joint Conference. Sydney:[s.n], 2006: 113-120. ITTOO A, BOUMA G. Minimally-supervised extraction of domain-specific part-whole relations using Wikipedia as knowledge-base[J]. Data & Knowledge Engineering, 2013, 85(5): 57-79. 曹馨宇,曹存根. 从Web获取部分整体关系语料的方法[J]. 中文信息学报,2011,25(5): 17-23. CAO Xinyu, CAO Cungen. A method for acquiring corpus rich in part-whole relation from the Web[J]. Journal of Chinese Information Processing, 2011, 25(5): 17-23. 曹馨宇,曹存根,吴昱明. 从Web中获取部分整体关系[J]. 中文信息学报,2013,27(2): 26-33. CAO Xinyu, CAO Cungen, WU Yuming. Acquiring part-whole relation from the Web[J]. Journal of Chinese Information Processing, 2013, 27(2): 26-33. LIN Dekang. Automatic retrieval and clustering of similar words[C]//Proc. of COLING/ACL-98 Joint Conference. Quebec:[s.n], 1998: 768-774. WEEDS J, WEIR D, MCCARTHY D. Characterising measures of lexical distributional similarity[C]//Proc. of COLING-04 Conference. Geneva:[s.n], 2004: 1015. YU L C, CHAN C L, LIN Chaocheng, et al. Mining association language patterns using a distributional semantic model for negative life event classification[J]. Journal of Biomedical Informatics, 2011, 44(4): 509-518. HARRIS Z. Distributional structure[J]. Word, 1954, 10(2/3): 146-162. GU Quanquan, ZHOU Jie. Co-clustering on manifolds[C]//Proc. of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris:[s.n], 2009: 359-367. BOLLEGALA D, MATSUO Y, ISHIZUKA M. Relational Duality: unsupervised extraction of semantic relations between entities on the Web[C]//Proc. of WWW'10. Raleigh:[s.n], 2010: 151-160. HEARST M A. Automatic acquisition of hyponyms from large text corpora[C]//Proc. of COLING-92. Nantes:[s.n], 1992: 539-545. GALEN A, GAO Jianfeng. Scalable training of L1-regularized log-linear models[C]//Proc. of ICML-07. Corvallis:[s.n], 2007: 33-40. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 998
- HTML全文浏览量: 97
- PDF下载量: 597
- 被引次数: 0





 下载:
下载:
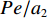
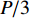
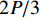

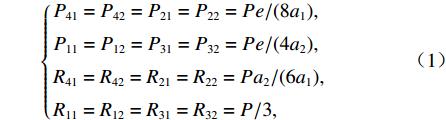
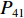
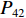
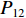
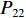
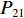
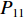
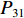
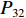
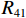
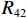
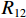
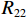
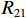
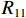
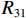
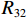

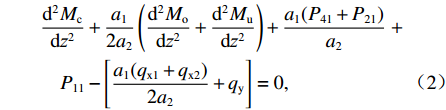

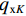
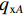

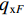
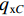
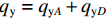

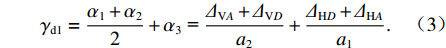

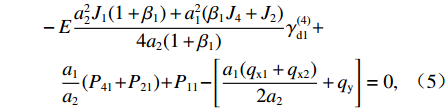
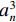
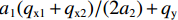

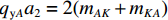
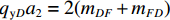

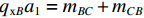
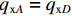

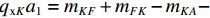
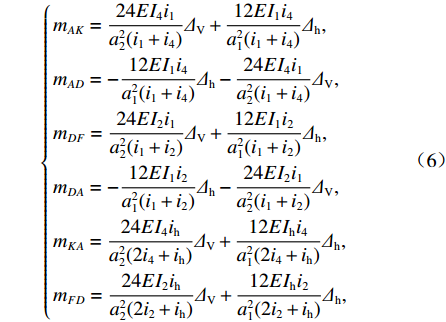
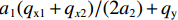
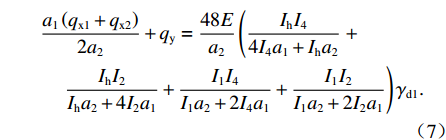
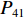
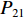
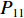
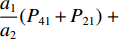
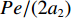
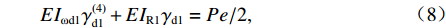
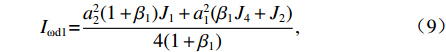
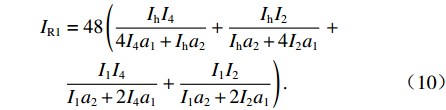



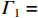
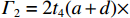

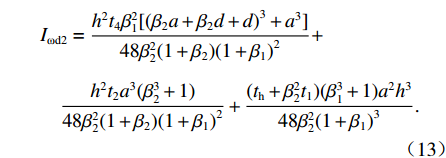

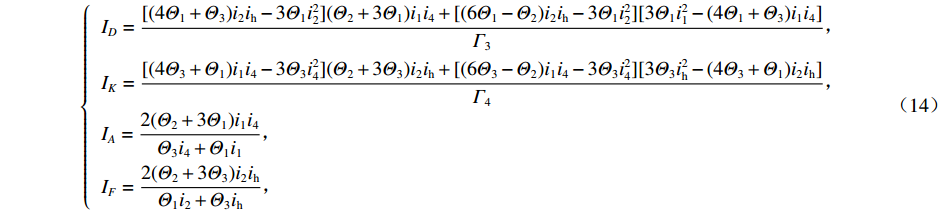
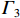
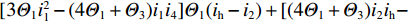
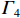
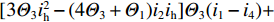
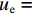
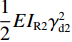
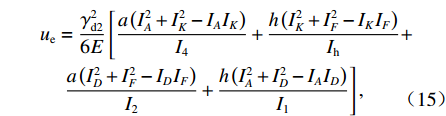
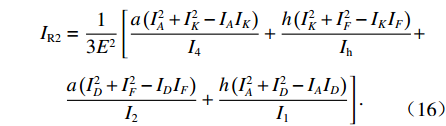

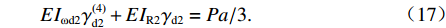





 下载:
下载: