Vortex-Induced Vibration Response of Bridges Considering Both Spanwise Variation of Vibration Amplitude and Correlation of Aerodynamic Forces
-
摘要:
为研究非线性气动力跨向振幅依存性和跨向相关性对桥梁涡振响应的影响,首先,引入由振幅多项式表达的桥梁非线性气动力模型;其次,在二维涡振分析方法的基础上,通过理论分析提出同时考虑气动力的跨向振幅依存性和跨向相关性的三维涡振振幅响应分析方法;最后,以主跨
1700 m的大跨度悬索桥为例,通过风洞实验识别其主梁在不同风攻角下的竖向涡振非线性气动力参数,进而分析不同风攻角下一阶正对称竖弯模态下的涡振振幅响应. 研究结果表明:当气动力沿跨向完全相关时,在气动力跨向振幅依存性的影响下,三维分析方法得到的各风速涡振响应明显大于二维分析,约大19%;当气动力沿跨向不完全相关时,三维分析的涡振振幅响应比不考虑相关性时降低明显,其中大部分风速下的降低范围为16%~30%,个别风速下约降低70%;证明了考虑气动力跨向不完全相关性和跨向振幅依存性对准确预测大跨度桥梁涡振响应的重要性;本文提出的分析方法对于扭转涡振及高阶模态下涡振分析同样适用.Abstract:This paper aims to study the effect of spanwise variation of vibration amplitude and spanwise correlation of the nonlinear aerodynamic forces on the vortex-induced vibration (VIV) response of bridges. Firstly, a nonlinear aerodynamic force model of the bridge represented by polynomial functions of vibration amplitude was introduced. Secondly, on the basis of the two-dimensional VIV (2D VIV) analysis method, an approach for predicting the three-dimensional VIV (3D VIV) amplitude response with consideration of both spanwise variation of vibration amplitude and spanwise correlation of aerodynamic forces was proposed through theoretical analysis. Finally, by taking a 1 700 m long-span suspension bridge as an example, the nonlinear aerodynamic force parameters of vertical VIV of the bridge girder at different angles of wind attack were extracted through a wind tunnel test. Then, the VIV amplitude response of the suspension bridge under a first-order positive symmetrical vertical mode at different angles of wind attack was analyzed. The results prove that when the aerodynamic forces are assumed to be fully correlated along the span, the 3D analysis under different wind speeds leads to a significantly higher VIV amplitude response (about 19%) as compared with the 2D analysis method due to the effect of spanwise variation of vibration amplitude of the aerodynamic forces. However, when the aerodynamic forces are assumed to be partially correlated along the span, the VIV amplitude response by 3D analysis is reduced significantly, and the reduction range is about 16%–30% under most wind speeds and about 70% under certain wind speeds. It is proved that it is important to accurately predict the VIV amplitude response of long-span bridges by considering the spanwise variation of vibration amplitude and spanwise partial correlation of aerodynamic forces. The approach proposed in this paper is also applicable to the analysis of torsional VIV or VIV at higher-order modes.
-
桥梁跨度的不断增加导致其自振频率和结构阻尼明显降低,使得其对风的作用愈加敏感,风荷载逐渐成为控制大跨度桥梁安全设计的最关键外荷载,而涡激振动是大跨度桥梁风致振动研究的重要内容之一[1-3]. 涡振一般是在较低风速下发生的,具有自激限幅特征的非线性风致振动现象. 在“漩涡锁定”风速下,气动自激力为结构系统引入了具有振幅依存性特征的非线性气动负阻尼,在气动负阻尼作用下结构总阻尼小于0,涡激振动开始发展,随着涡振振幅的增大,气动负阻尼逐渐减小,当气动负阻尼等于结构阻尼时系统总阻尼等于0,此时涡振达到稳定振幅状态[4]. 国内外多座大跨度桥梁在运营过程中均发生过明显的涡振现象,例如日本的东京湾跨海大桥、丹麦的大贝尔特跨海大桥,国内的西堠门大桥、虎门大桥等[5]. 由于涡振的发生风速一般较低,若频繁发生会造成桥梁构件疲劳损伤和行人不适,从而直接影响桥梁的使用性能[6]. 因而,对桥梁涡激振动进行深入的理论和实验研究,对大跨度桥梁的抗风抑振设计非常重要[7-9].
一般利用理论分析和风洞实验结合的手段对涡振进行研究,建立合理的涡振气动力非线性数学模型,利用节段模型风洞实验识别出气动力模型参数,并使模型能够正确地反映结构的涡振响应特性[10-11]. 关于涡振气动力模型已有广泛的研究,如国外的Scanlan经验非线性模型[7]、Larsen模型[12]以及国内Zhu等[13]建立的时域非线性气动力模型. 相关研究已经表明涡振气动力具有较强的振幅依存性特征,Chen[4]将非线性气动阻尼模型表达为速度或位移的多项式函数,并基于谐波平衡法建立了具有振幅依存性的气动力多项式模型. 由于大跨度桥梁在某阶振型下发生涡振响应时,涡振的振幅沿桥梁跨向是变化的,而非线性气动力则具有明显的振幅依存性特征,因而在涡振发生时,沿主梁跨向各点处的气动力大小也是不同的. 因此,对于大跨度桥梁的三维涡振响应分析,需要将风洞实验识别的非线性气动力模型推广到三维实桥,考虑空间模态效应的影响[13]. 此外,大量风洞实验研究表明,涡振气动力沿跨向是不完全相关的,为准确预测实际大跨度桥梁的涡振响应,考虑气动力跨向相关性的影响至关重要,目前气动力的跨向相关性研究仍缺乏现场实测研究,主要是基于二维节段风洞实验模型的研究[14-16].
目前,大跨度桥梁三维涡振响应分析方法大多是基于时域非线性气动力模型的时域分析方法,在考虑三维效应及气动力沿跨向的不完全相关性时计算比较复杂,也不容易同时考虑气动力沿跨向的振幅依存性,且无法直接求解所关心的涡振振幅响应,不便于工程应用. 本文基于Chen所建立的气动力非线性振幅依存性模型[4],提出了可以方便地同时考虑非线性气动力的跨向振幅依存性和跨向不完全相关性的大跨度桥梁三维涡振振幅响应分析方法. 通过对主跨
1700 m大跨度悬索桥不同风攻角下的三维涡振响应研究,分析了考虑气动力跨向相关性时的三维涡振响应,证明了所建立的分析方法可以为三维涡振分析带来极大的方便,同时明确了考虑气动力跨向不完全相关性和跨向振幅依存性对准确预测大跨度桥梁涡振响应的重要性. 相关研究可为大跨度桥梁涡振响应预测及控制提供理论依据.1. 大跨度桥梁涡振响应分析框架
1.1 二维涡振分析方法
Chen[4] 在研究高层横风向随机振动问题时,提出了2种非线性气动阻尼模型:模型表达为时变位移y的多项式函数(式(1))、模型表达为时变振幅Ay的多项式函数(式(2)).
ξa(y)=B1+B2|y|+B3y2, (1) ξaeq(Ay)=b1+b2Ay+b3A2y, (2) 式中:ξa 和 ξaeq分别为时变非线性气动阻尼和等效非线性气动阻尼;B1、B2、B3 和 b1、b2、b3分别为2个非线性阻尼模型的参数.
基于谐波平衡法建立了2种非线性气动阻尼模型参数之间的关系,如式(3).
{B1=b1,B2=3π4b2,B3=4b3. (3) Scanlan[17]提出的基于颤振导数表达的桥梁断面自激气动力模型是桥梁风工程领域中应用最广泛的形式,并且一直沿用至今. 本文在涡振分析中采用相似的表达式,关于单自由度竖向涡振,桥梁断面的运动方程可以表示为
m(¨h+2ξhsωhs˙h+ω2hsh)=12ρU2B(kH∗1˙hU+k2H∗4hb), (4) 式中:m为桥梁二维模型单位长度质量;ξhs为系统结构竖向阻尼比;h为模型竖向位移;ρ为空气密度;b=B/2,为桥梁断面宽B的一半;U为风速;ωhs为结构竖向自振圆频率;k=ωhb/U,为折减频率,ωh为竖向振动圆频率;H∗1和H∗4分别为与气动阻尼和气动刚度相关的气动导数,是折减频率和振幅的函数.
对于竖向涡振,气动刚度项H∗4对结构频率的影响很微弱,可以忽略不计,即ωh≈ωhs. 观察式(4)可以发现,竖向气动阻尼比ξha和气动导数H∗1之间存在如式(5)的关系.
ξha=−12μH∗1, (5) 式中:μ=ρb2/m,为质量比.
结合Chen非线性气动阻尼模型[4],可将气动导数H∗1表达为无量振幅的多项式函数,如式(6).
H∗1=B1+43πB2Ahb+14B3(Ahb)2, (6) 式中:Ah为时变振幅.
并且等价于用振动位移表达的模型,如式(7).
H∗1=B1+B2|hb|+B3(hb)2. (7) 气动导数H∗1是只跟桥梁断面外观有关的气动参数. 实际应用时,可先通过风洞实验识别模型随涡振振幅变化的气动阻尼,进而由式(5)求得式(6)所示的振幅非线性气动导数H∗1,并可转化为位移非线性气动导数(式(7)). 同时,利用得到的非线性气动导数H∗1,不但可以直接计算出振幅非线性气动阻尼,并根据气动阻尼的振幅依存性和结构阻尼求解二维涡振振幅响应(总阻尼比等于0时的振幅,即 ξhs+ξha=0);而且,还可以方便地利用时变非线性模型(式(7)),通过数值方法(如Runge-Kutta法)求解二维单自由度竖向涡振的位移时程响应.
1.2 三维涡振分析方法
同时考虑气动力跨向相关性和跨向振幅依存性的大跨度桥梁三维涡振响应分析方法如下:
大跨度桥梁在第j阶竖弯模态下的涡振位移响应[18]可以表示为
h(x,t)=hj(x)qj(t), (8) 式中:qj(t)为第j阶广义模态位移,t为时间;hj(x)为第j阶竖弯模态振型函数.
将式(8)代入式(4),两边乘以hj(x)并沿桥跨L积分,经简化可得,大跨度桥梁第j阶竖向广义模态运动方程为
¨qj(t)+2ξhsjωhsj˙qj(t)+ω2hsjqj(t)=μjGhjhj(ωhsjGH∗1hjhj˙qj(t)+ω2hsjGH∗4hjhjqj(t)), (9) {μj=ρb2/mj,Ghjhj=∫L0h2j(x)dx,GH∗1hjhj=∫L0h2j(x)H∗1(x)dx,GH∗4hjhj=∫L0h2j(x)H∗4(x)dx, (10) 式中:mj为与第j阶振型对应单位长度的等效质量;ξhsj和ωhsj分别为第j阶竖弯模态下的结构竖弯阻尼比和自振圆频率;H∗1和H∗4为桥梁跨向两空间位置处具有振幅依存性的非线性气动导数,随跨向位置的不同而变化,在进行三维涡振分析时,跨向不同位置处气动导数H∗1和H∗4的变化可以通过积分算子GH∗1hjhj和GH∗4hjhj来考虑;Ghjhj为桥梁第j阶竖弯模态的积分算子.
沿桥梁跨向不同位置的涡振气动力是不完全相关的,气动导数H∗1的跨向相关性函数可以假定为[18-19]
χH∗1(xA,xB)=exp(−cH∗1|xA−xB|/L), (11) 式中:cH∗1为衰减系数,xA和xB为沿桥梁跨向的2个空间位置.
当考虑气动力的跨向不完全相关性时,对广义模态运动方程(10)中的积分算子GH∗1hjhj引入一个相关性折减因子λH∗1(式(12))来考虑气动力的跨向不完全相关性.
λH∗1=GcH∗1hjhj/GH∗1hjhj, (12) GcH∗1hjhj=[∫L0∫L0H∗1(xA)H∗1(xB)h2j(xA)h2j(xB)χH∗1(xA,xB)dxAdxB]12, (13) 式中:GcH∗1hjhj为考虑气动力沿跨向位置不完全相关性的模态积分算子,当气动力沿跨向相关时,λH∗1=1.
同样地,对气动导数H∗4也有类似的相关性表达方法,对于涡振,气动刚度项H∗4的影响非常小,可以忽略. 当考虑涡激力跨向相关性时,大跨度桥梁具有振幅依存性的第j阶竖弯模态下桥梁的非线性气动阻尼比为
ξhaj=−12μλH∗1GH∗1hjhj/Ghjhj. (14) 对比式(14)、(5)可知,桥梁的三维涡振分析相当于将二维分析中的气动导数H∗1替换为考虑实桥三维效应的等效气动导数ˆH∗1j(aj)=λH∗1GH∗1hjhj/Ghjhj,从而实现考虑实桥的三维效应、气动力的跨向振幅依存性和跨向不完全相关性. 根据系统总阻尼比等于0,即ξhsj+ξhaj=0,可确定涡振的稳态振幅响应. 需要说明的是,以上方法同样适用于扭转涡振分析.
2. 气动力参数风洞实验识别及实桥三维涡振响应分析
2.1 风洞实验获取非线性气动参数
以一典型流线型箱梁为例,首先,通过涡振风洞实验识别获取其非线性气动参数;然后,利用第1节提出的方法对主跨
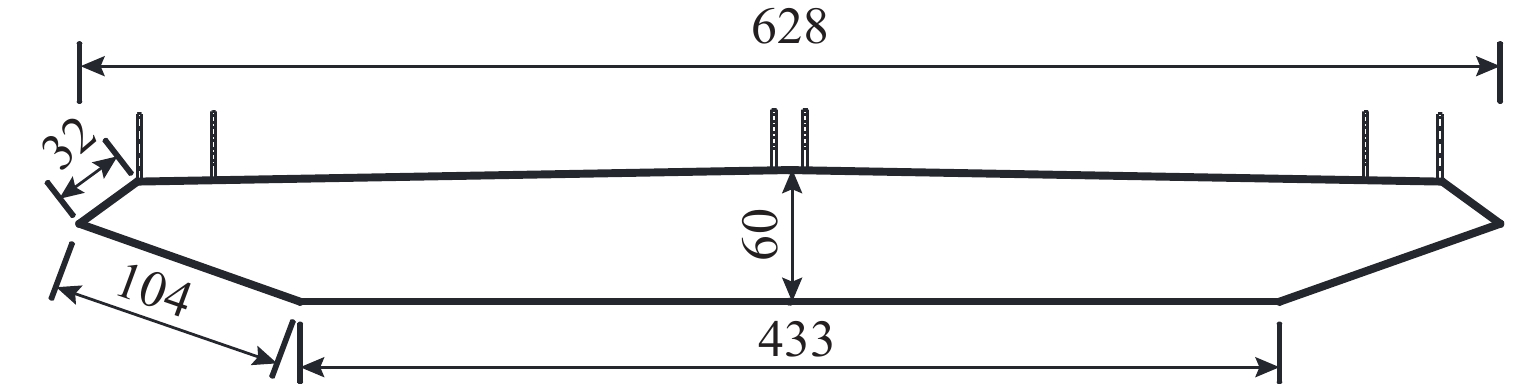
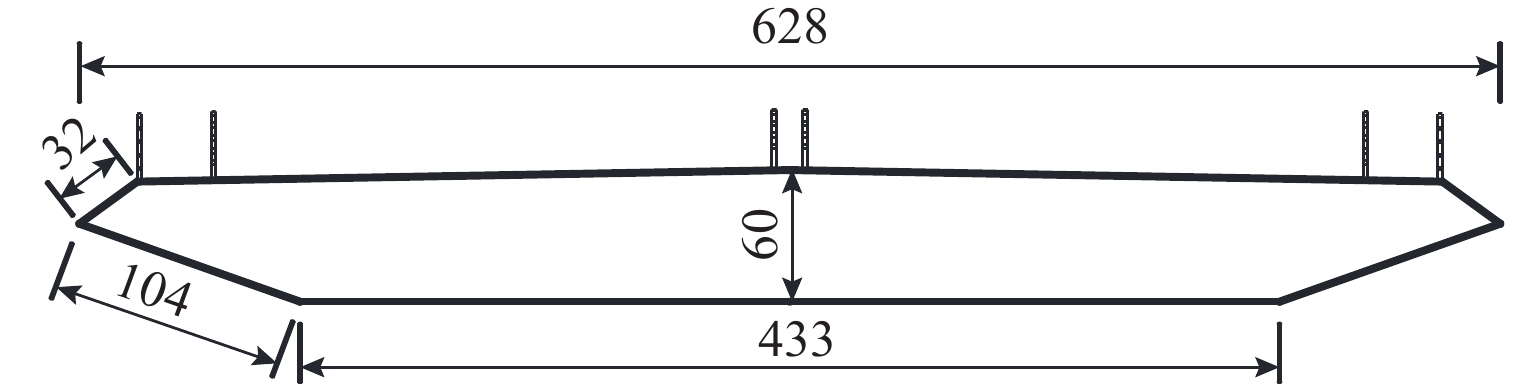
1700 m的悬索桥进行三维涡振响应分析.图1所示为采用的风洞节段模型的断面布置,为大跨度桥梁典型的流线型箱梁断面,模型缩尺比1/50,宽B = 2b = 628 mm,高D = 60 mm,长度l =
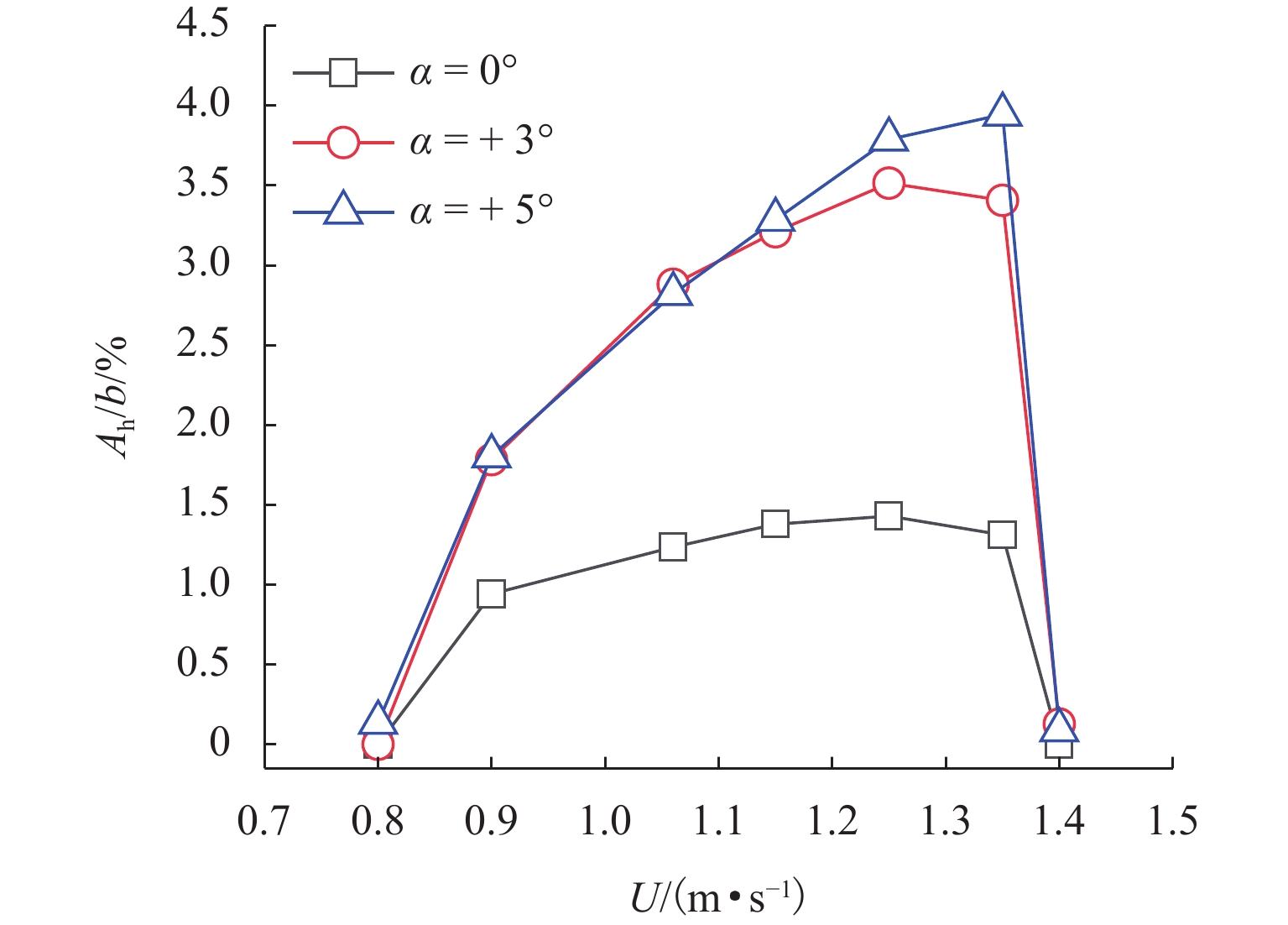
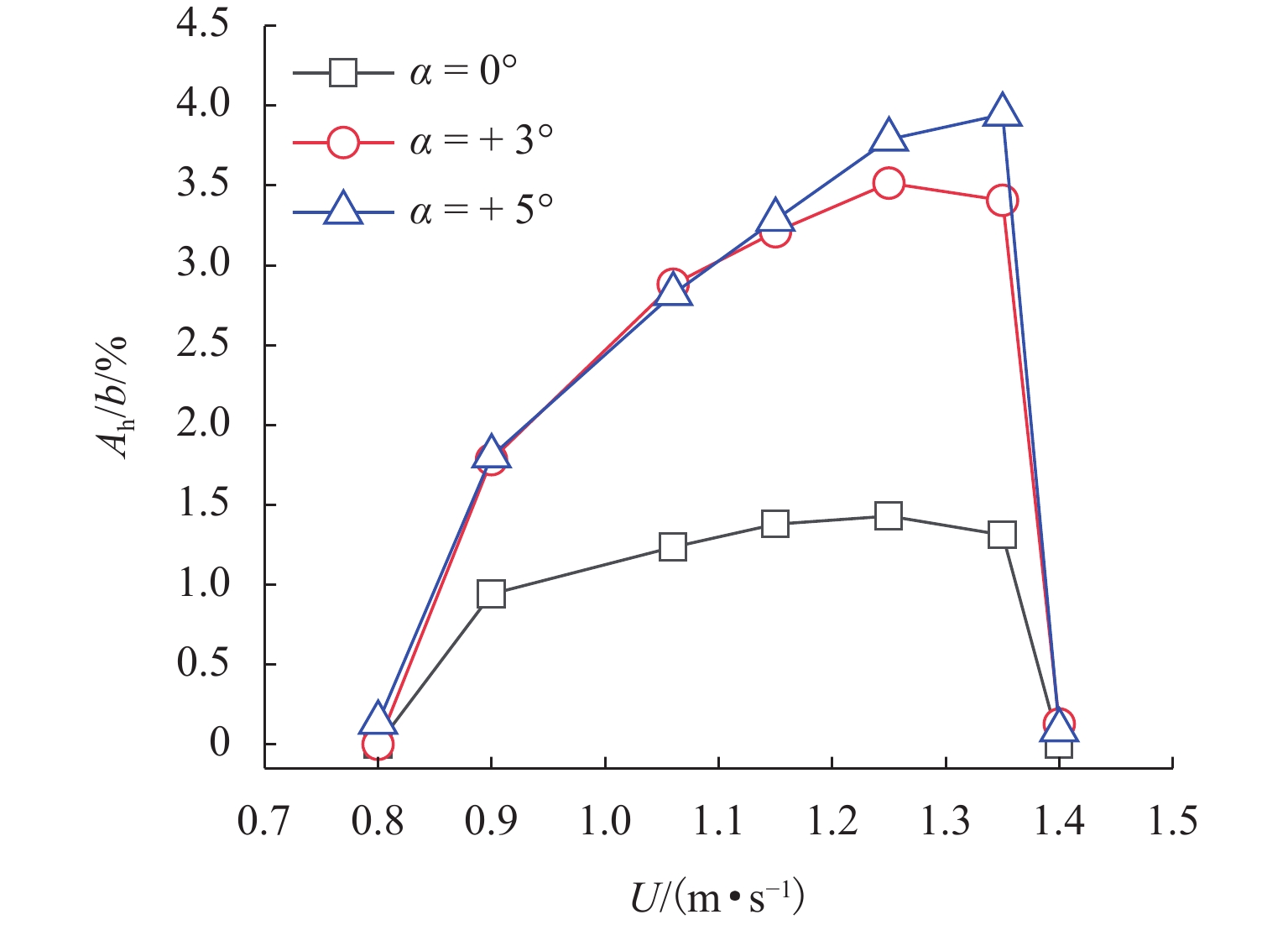
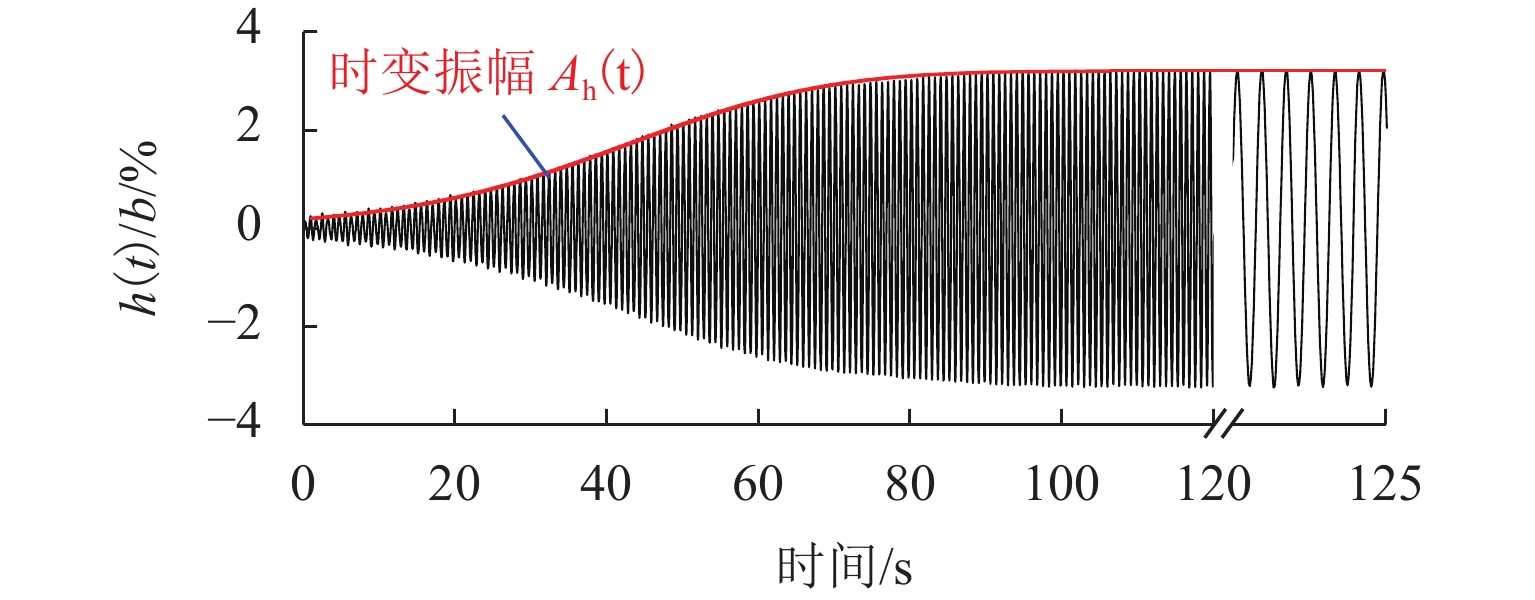
2100 mm. 涡振实验在西南交通大学XNJD-1号风洞实验室进行,如图2,模型采用两自由度自由振动弹簧悬挂系统,实验在均匀流下进行,共测试得到了箱梁模型在3个风攻角下(α= 0°, + 3°, + 5°,迎风抬头为正)的竖向涡振特性. 模型单位长度的质量m= 6.524 kg/m,模型系统的竖向自振频率为 fhs= 1.294 Hz,系统结构竖向阻尼比ξhs=0.32%.在不同风攻角下,测试并采集不同竖弯涡振风速下模型从静止到稳定振幅的整个涡振位移响应时程,稳定振幅实验结果如图3所示. 可见该箱梁在α= + 3° 和α= + 5° 攻角下竖弯涡振响应最大. 图4给出了攻角α= + 3°,风速U = 1.15 m/s下完整的涡振位移时程曲线.
具有振幅依存性的非线性气动导数H∗1的识别方法参见文献[5]. 首先,通过希尔伯特变换得到涡振位移时程的发展包络线,即时变振幅Ah(t),如图4所示;接着,将时变振幅拟合为数学解析函数,通过求导等运算得到振动系统随振幅变化的总阻尼比ξh(A),用总阻尼中减去结构阻尼即可得到竖向气动阻尼比ξha(A);最后,通过式(5)即求得H∗1,并将其拟合为振幅的二次多项式(式(6))便于后续分析使用.
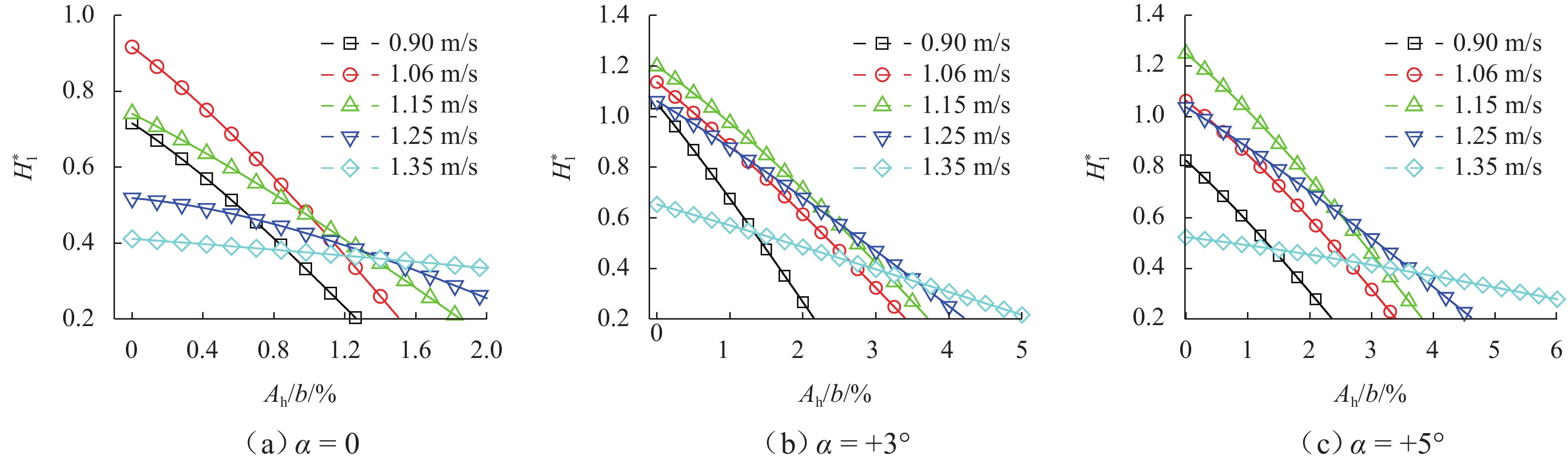
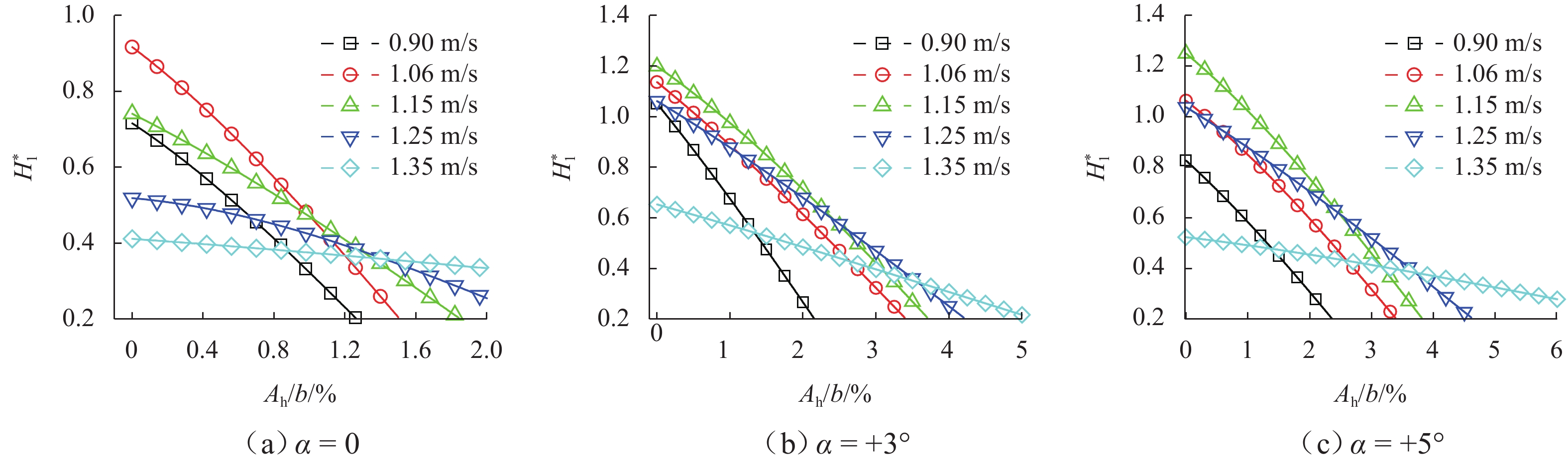
图5给出了不同攻角下,识别的非线性气动导数H∗1随风速和无量纲竖向振幅的变化. 由结果可知,H∗1随振幅的增加而减小,其值在涡振风速区间内随风速先增加后降低,在风速U=1.15 m/s左右达到最大.
2.2 主跨
1700 m悬索桥三维竖向涡振响应分析根据本文建立的三维涡振振幅响应分析方法,结合2.1节风洞实验得到的箱梁断面非线性气动力参数,对一主跨为
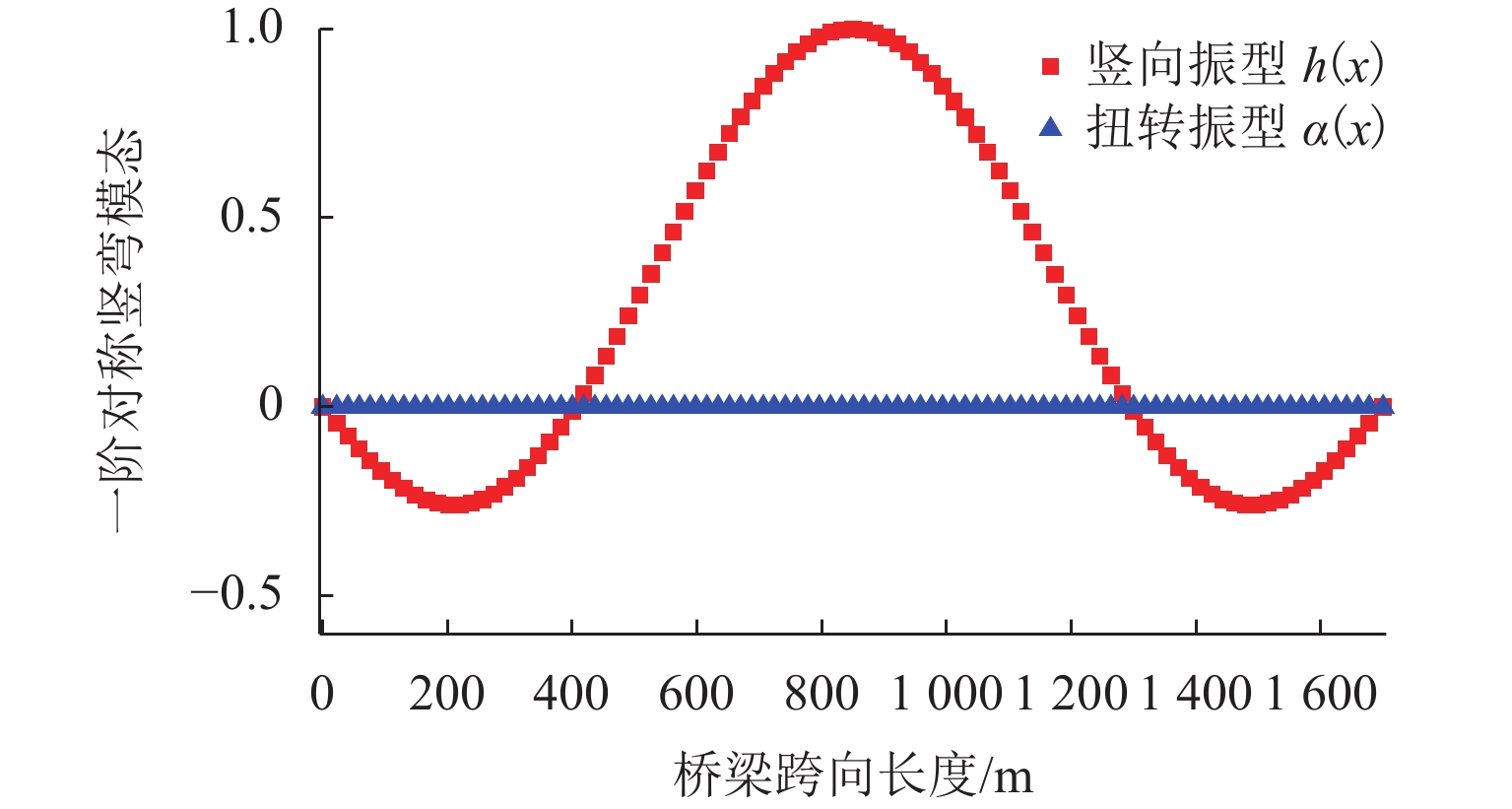
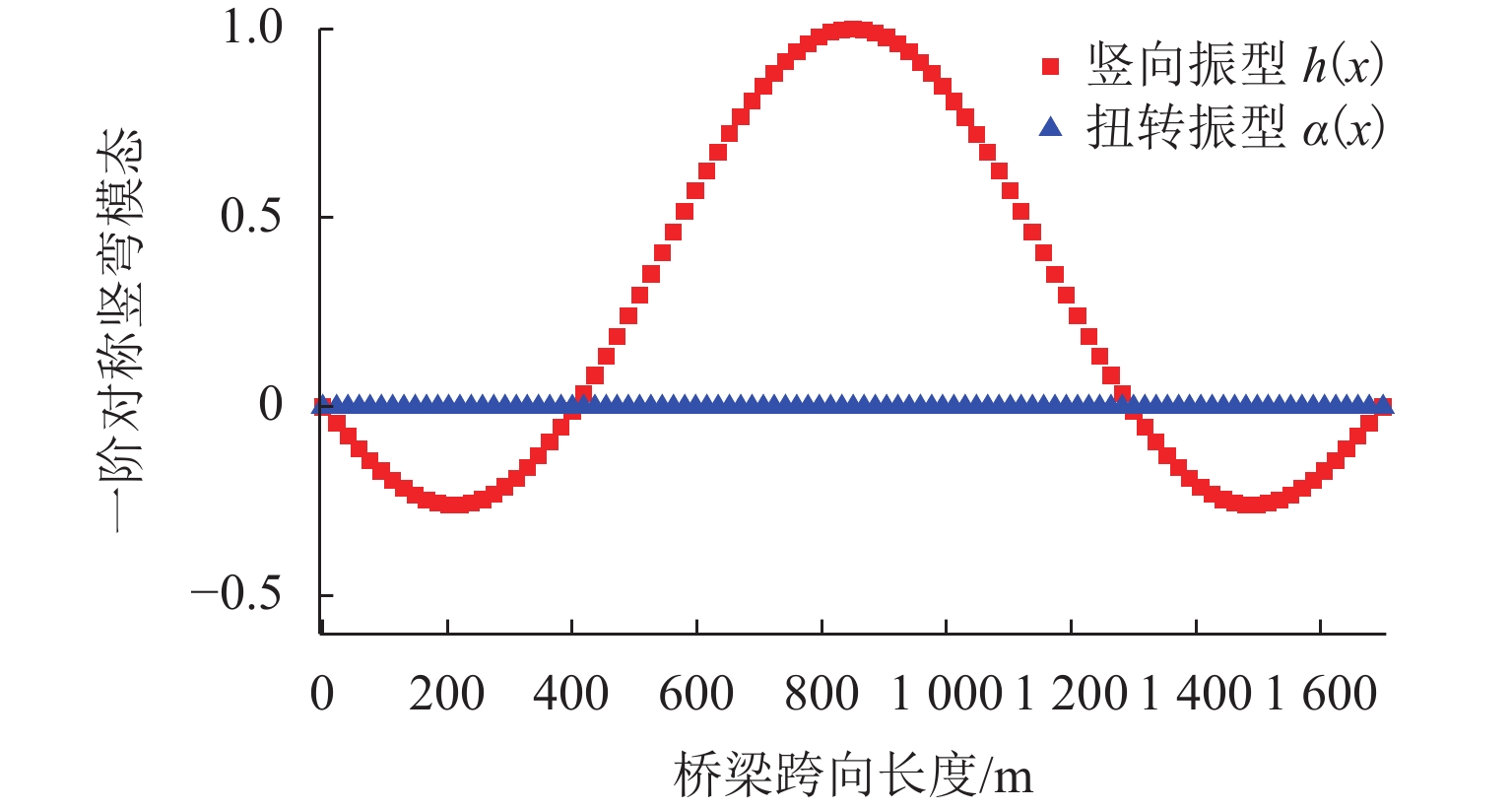
1700 m的大跨度悬索桥进行三维涡振分析计算. 图6为该桥标准化的一阶正对称竖弯模态,桥梁宽B = 31.4 m,单位长度质量比μ=0.0189 ,相对风洞节段模型的缩尺比为50/1. 根据图6和式(10)计算得:桥梁一阶竖弯模态的积分算子Gh1h1= 440.8,fhs=0.1244 Hz,ξhs= 0.35%,气动力跨向相关函数衰减系数假设为cH∗1 = 5.根据本文方法计算悬索桥第j阶竖弯模态下涡振稳态振幅响应的具体步骤如下:
步骤1 选择最大振型位移位置处的位移 (对一阶正对称竖弯模态为跨中位置) 作为参考点,首先,预设足够大的振幅区间和较小步长,给定某一振幅下,根据振型计算跨向不同位置的振幅;接着,利用风洞试验得到的用振幅依存性表达的非线性气动导数H∗1,计算桥梁跨向不同位置处的H∗1;继而,由式(10)、(13)计算得到考虑颤振导数沿跨向变化以及相关性的积分算子GcH∗1hjhj和GH∗1hjhj,得到折减因子λH∗1;最后,根据式(14)计算得到大跨度桥梁在该预设振幅下的等效气动阻尼ξhaj.
步骤2 在不同预设振幅下重复步骤1的计算,可以得到大跨度桥梁随振幅变化的等效非线性气动阻尼.
步骤3 利用系统总阻尼比为0 (ξhsj+ξhaj=0)时对应的振幅,即为所求大跨度桥梁在该阶模态下的涡振稳态振幅响应.
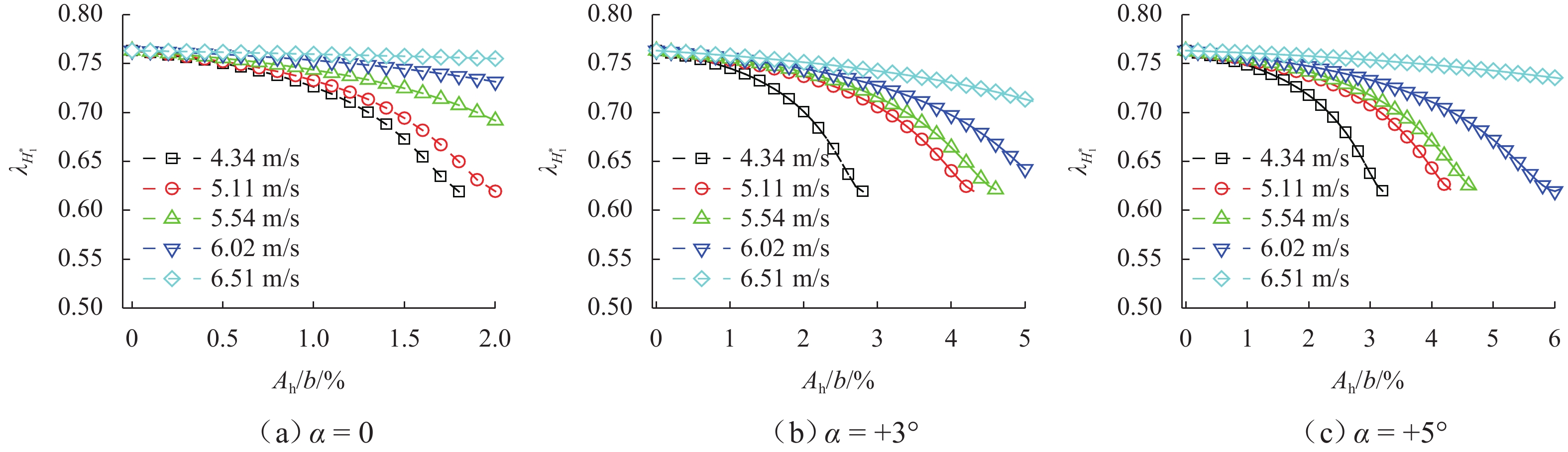
图7所示为计算过程中得到的不同风攻角和风速下,考虑气动力不完全相关性时的折减因子λH∗1随振幅的变化. 由图7可知,当考虑涡激力跨向不完全相关性时,不同工况下折减因子λH∗1均明显小于1,且值随着振幅的增加而减小. 折减因子λH∗1的大小直观地反映了不完全相关性的影响.
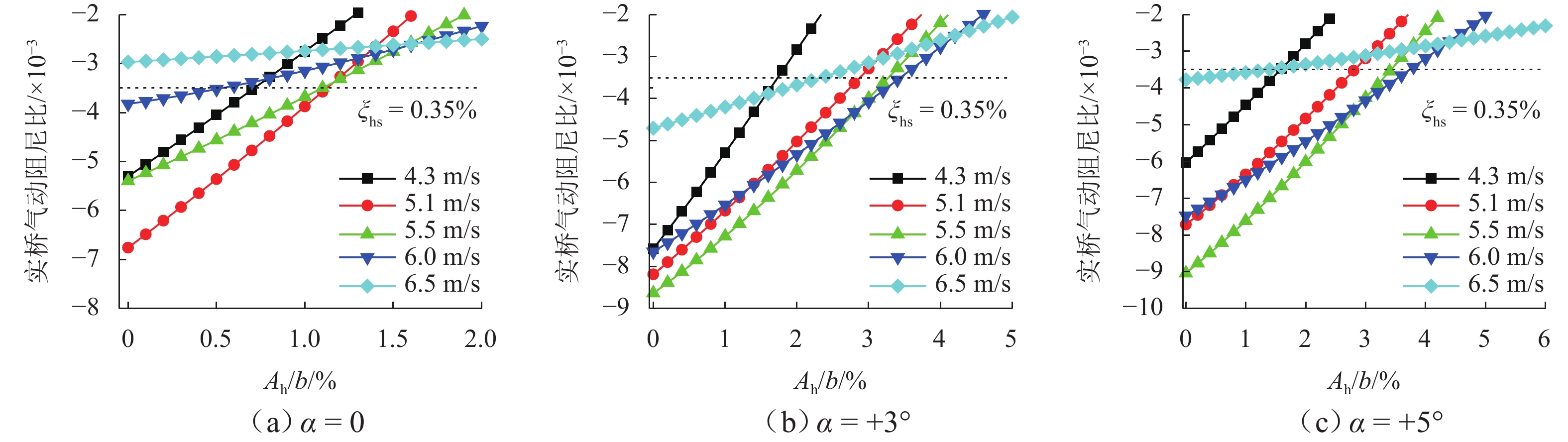
图8给出了考虑气动力不完全相关性时,该大跨度桥梁不同工况下的实桥非线性气动阻尼比的结果(式(14 )),图中同时给出了桥梁结构竖向阻尼比ξhs= 0.35%的位置. 由上述方法可知,各风速下气动阻尼比和结构阻尼比交点对应的总阻尼比为0,即ξhs+ξha=0,故其交点对应的横坐标振幅即为各风速下悬索桥在该结构阻尼下的涡振稳态振幅结果.
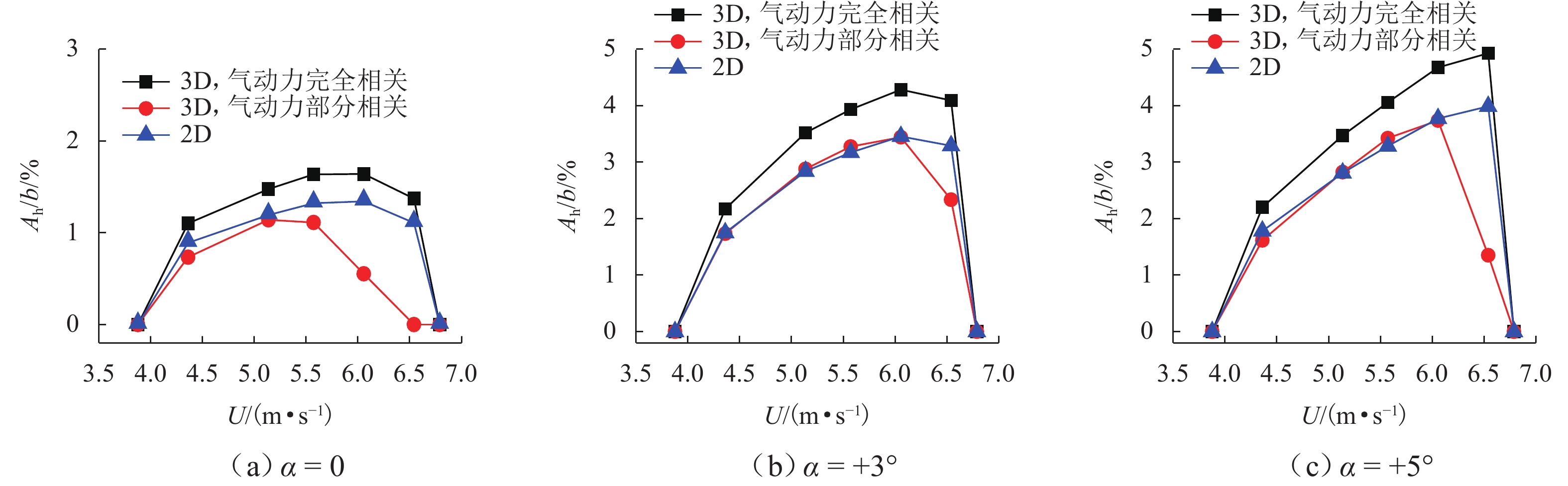
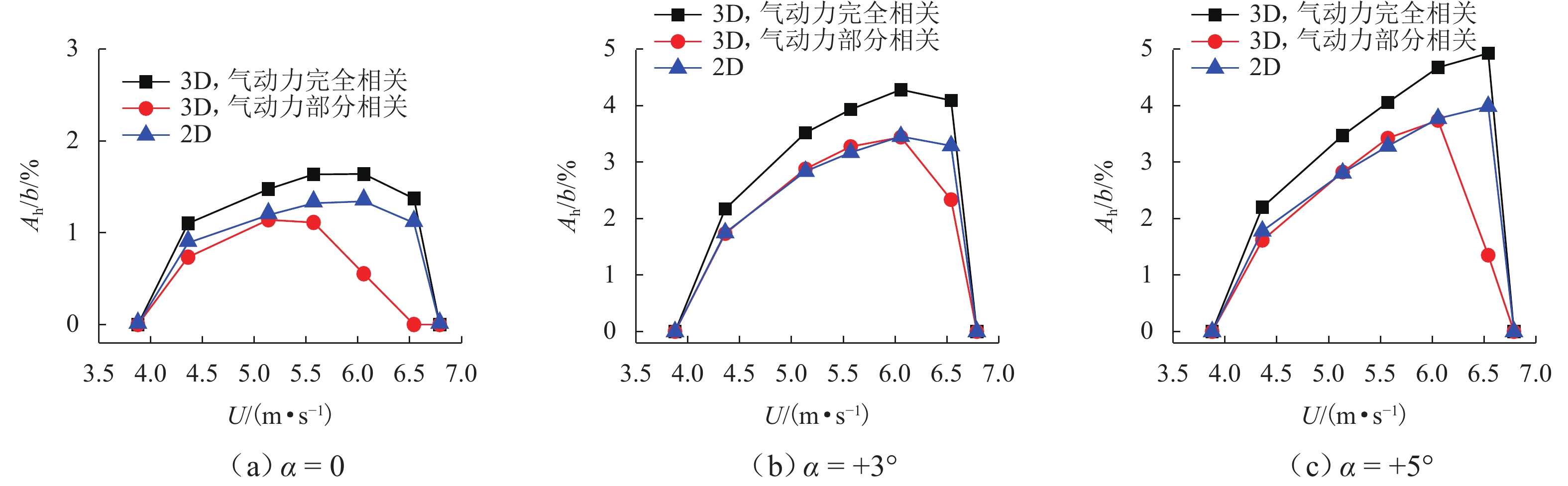
相同地,可以计算气动力跨向完全相关 (即λH∗1=1或cH∗1 = 0) 时的实桥非线性气动阻尼及涡振振幅响应. 同时,利用图8得到的实桥非线性气动阻尼比,可以预测任意结构阻尼比下的涡振振幅响应. 图9所示为根据上述过程计算的不同风攻角下,悬索桥在一阶正对称竖弯模态下跨中位置的竖向涡振稳态振幅响应. 作为对比,图中同时给出了利用二维分析方法(不考虑三维模态效应)计算的振幅响应. 结果表明:当假定气动力完全相关时(即不考虑气动力的跨向相关性,λH∗1=1),采用三维分析方法计算的各风速涡振响应要比利用二维分析方法计算的结果大19%. 但当考虑气动力的跨向不完全相关时,三维分析方法计算的涡振响应比不考虑相关性时降低明显;其中大部分风速下的降低范围在16%~30%,个别约风速下降低70%. 最大和最小涡振预测响应分别出现在风攻角α= + 5° 和α= 0°.
当不考虑气动力的跨向相关性时(即λH∗1=1),三维分析计算的涡振响应大于二维分析,其原因在于:在三维分析时受实桥模态效应影响,桥跨不同位置处的振幅沿着桥梁跨度方向是变化的,且小于最大振幅(一阶正对称竖弯模态时最大振幅为跨中位置);而由于气动负阻尼的大小随着振幅的增加是减小的(图8所示),导致跨向其他各位置处的气动负阻尼均大于最大振幅位置处. 因此,在给定一个相同振幅下,三维分析得到的全桥总的气动负阻尼要大于利用二维分析得到的气动负阻尼的大小,从式(5)和式(14)来看,也即GH∗1h1h1/Gh1h1>H∗1.
以上仅给出了大跨度悬索桥在一阶正对称竖弯模态下的涡振响应计算结果,利用上述方法,可以方便地计算其他任意高阶模态下的涡振振幅响应,同时也可以分析预测不同结构阻尼及跨向相关性影响下的大跨度桥梁涡振振幅响应,本文不再赘述.
3. 结 论
本文通过理论分析和风洞实验相结合,建立了一种可以同时考虑非线性气动力跨向相关性和振幅依存性的大跨度桥梁涡振振幅响应分析方法. 通过风洞实验识别得到了一典型流线型箱梁在不同风攻角下的气动力参数,并以跨径为
1700 m悬索桥为例,计算了其在不同工况下的涡振振幅响应,通过分析可得出如下结论:1) 本文建立的大跨度桥梁三维涡振响应分析方法简便且更具物理意义,可以方便地考虑非线性气动力的振幅依存性及跨向相关性的影响,同时适用于不同模态下的单自由度涡振响应分析.
2) 不同攻角下,本文流线型箱梁风洞实验识别的非线性气动导数H∗1随振幅的增加而减小,其值在涡振风速区间内随风速先增加后降低,在风洞实验风速U=1.15 m/s左右达到最大.
3) 当考虑悬索桥涡振气动力跨向不完全相关性时,不同工况下相关性折减因子λH∗1均明显小于1,且值随着振幅的增加而减小,折减因子λH∗1的大小直观地反映了气动力跨向不完全相关性的影响.
4) 当假定气动力完全相关时(即不考虑气动力的跨向相关性,λH∗1=1),采用三维分析方法计算的各风速涡振响应明显要大于二维分析方法计算的结果(约大19%). 其原因是气动阻尼随振幅的增加而减小,而在振型影响下跨向各位置的振幅均小于跨中振幅,因此,在给定相同振幅下,三维分析得到的实桥气动阻尼要大于二维分析.
5) 本文实桥算例最大和最小涡振预测响应分别出现在风攻角α= + 5° 和α= 0处,当考虑气动力的跨向不完全相关时,三维分析方法计算的振幅响应比不考虑相关性时降低明显,其中大部分风速下的降低范围在16%~30%,个别风速下约降低70%. 表明考虑气动力跨向不完全相关性对准确预测大跨度桥梁涡振响应非常重要.
-
-
[1] 李加武,方成,侯利明,等. 大跨径桥梁静风稳定参数的敏感性分析[J]. 振动与冲击,2014,33(4): 124-130.LI Jiawu, FANG Cheng, HOU Liming, et al. Sensitivity analysis for aerostatic stability parameter of a long-span bridge[J]. Journal of Vibration and Shock, 2014, 33(4): 124-130. [2] WU B, CHEN X Z, WANG Q, et al. Characterization of vibration amplitude of nonlinear bridge flutter from section model test to full bridge estimation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 197: 104048.1-104048.14. doi: 10.1016/j.jweia.2019.104048 [3] 朱金,黄旭,熊籽跞,等. 大跨度悬索桥竖弯涡振条件下驾驶员行车视线研究[J]. 西南交通大学学报,2023,58(1): 191-201.ZHU Jin, HUANG Xu, XIONG Ziluo, et al. Study on driver’s sight line under vertical vortex-induced vibration of long span suspension bridges[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 191-201. [4] CHEN X Z. Estimation of stochastic crosswind response of wind-excited tall buildings with nonlinear aerodynamic damping[J]. Engineering Structures, 2013, 56: 766-778. doi: 10.1016/j.engstruct.2013.05.044 [5] WANG Y F, CHEN X Z, LI Y L. Nonlinear self-excited forces and aerodynamic damping associated with vortex-induced vibration and flutter of long span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 204: 104207.1-104207.21. [6] 李永乐,侯光阳,向活跃,等. 大跨度悬索桥钢箱主梁涡振性能优化风洞试验研究[J]. 空气动力学学报,2011,29(6): 702-708. doi: 10.3969/j.issn.0258-1825.2011.06.004LI Yongle, HOU Guangyang, XIANG Huoyue, et al. Optimization of the vortex induced vibration for steel box girder of long span suspension bridges by wind tunnel test[J]. Acta Aerodynamica Sinica, 2011, 29(6): 702-708. doi: 10.3969/j.issn.0258-1825.2011.06.004 [7] 马存明,王俊鑫,罗楠,等. 宽幅分体箱梁涡振性能及其抑振措施[J]. 西南交通大学学报,2019,54(4): 724-730.MA Cunming, WANG Junxin, LUO Nan, et al. Vortex-induced vibration performance and control measures of wide twin-box girder[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 724-730. [8] 张天翼,孙延国,李明水,等. 宽幅双箱叠合梁涡振性能及抑振措施试验研究[J]. 中国公路学报,2019,32(10): 107-114,168.ZHANG Tianyi, SUN Yanguo, LI Mingshui, et al. Experimental study on vortex-induced vibration performance and aerodynamic countermeasures for a wide-width double-box composite beam[J]. China Journal of Highway and Transport, 2019, 32(10): 107-114,168. [9] 李明,孙延国,李明水,等. 宽幅流线型箱梁涡振性能及制振措施研究[J]. 西南交通大学学报,2018,53(4): 712-719.LI Ming, SUN Yanguo, LI Mingshui, et al. Vortex-induced vibration performance of wide streamlined box girder and aerodynamic countermeasure research[J]. Journal of Southwest Jiaotong University, 2018, 53(4): 712-719. [10] 葛耀君,赵林,许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报,2019,32(10): 1-18.GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 1-18. [11] EHSAN F, SCANLAN R H. Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics, 1990, 116(6): 1392-1411. doi: 10.1061/(ASCE)0733-9399(1990)116:6(1392) [12] LARSEN A. A generalized model for assessment of vortex-induced vibrations of flexible structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 281-294. [13] ZHU L D, MENG X L, GUO Z S. Nonlinear mathematical model of vortex-induced vertical force on a flat closed-box bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122: 69-82. doi: 10.1016/j.jweia.2013.07.008 [14] SUN Y G, LI M S, LIAO H L. Nonlinear approach of vortex-induced vibration for line-like structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 124: 1-6. doi: 10.1016/j.jweia.2013.10.011 [15] LI M S, LI S P, LIAO H L, et al. Spanwise correlation of aerodynamic forces on oscillating rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 154: 47-57. doi: 10.1016/j.jweia.2016.04.003 [16] ZHOU S, HUA X G, CHEN Z Q, et al. Experimental investigation of correction factor for VIV amplitude of flexible bridges from an aeroelastic model and its 1∶1 section model[J]. Engineering Structures, 2017, 141: 263-271. doi: 10.1016/j.engstruct.2017.03.023 [17] SCANLAN R H. The action of flexible bridges under wind, I: Flutter theory[J]. Journal of Sound and Vibration, 1978, 60(2): 187-199. doi: 10.1016/S0022-460X(78)80028-5 [18] MASHNAD M, JONES N P. A model for vortex-induced vibration analysis of long-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134: 96-108. doi: 10.1016/j.jweia.2014.09.002 [19] SIMIU E, SCANLAN R. Wind effects on structures: an introduction to wind engineering[M]. New York: John Wiley, 1986. 期刊类型引用(1)
1. 梅瀚雨, 廖海黎, 王昌将. 基于自编码器的非线性气动力辨识及非线性颤振分析. 西南交通大学学报. 2025(03)  本站查看
本站查看其他类型引用(0)
-






 下载:
下载:








 下载:
下载: