Formation Mechanism of Metro Wheel Polygonal Based on Vehicle-Track Coupling
-
摘要:
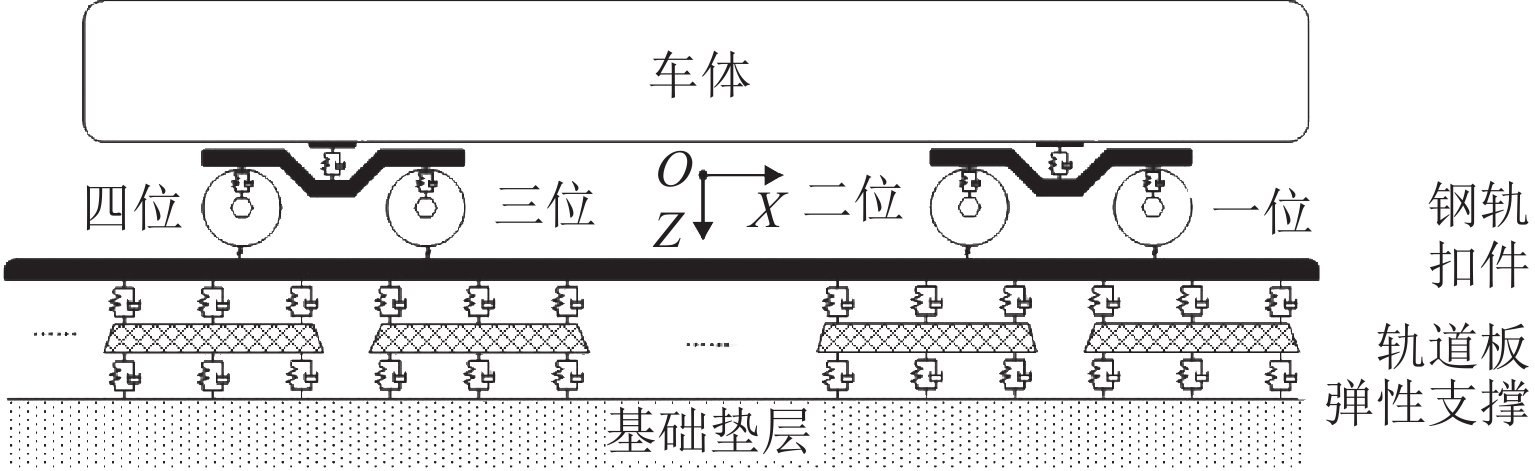
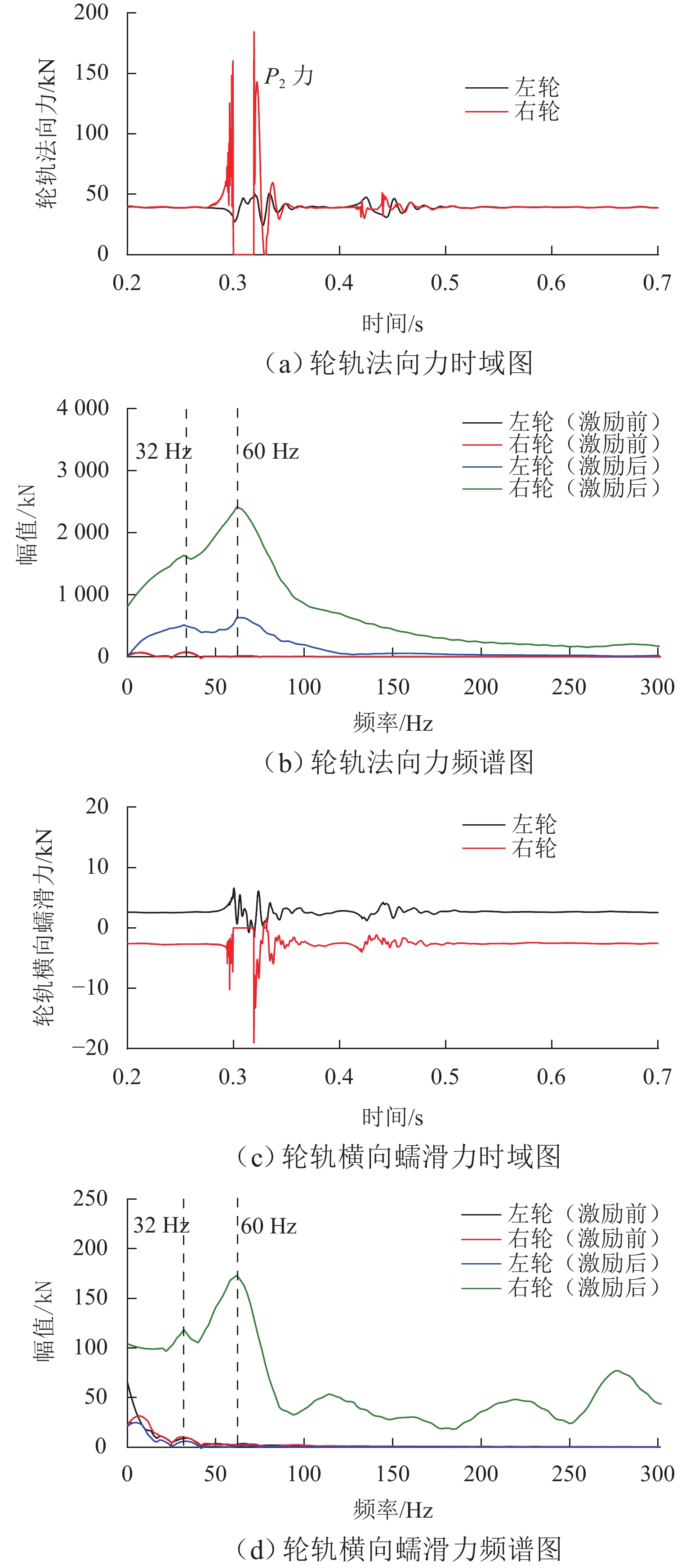
车轮多边形磨耗会恶化轨道车辆振动环境,导致结构部件的共振疲劳失效,严重威胁行车安全. 为研究地铁车辆车轮多边形磨耗的形成机理,开展线路动态跟踪试验研究,建立车轨垂向耦合有限元模型和动力学模型,并进行轮轨长期磨耗迭代仿真分析. 研究结果表明:实测车辆发生了明显的7~9阶的车轮多边形磨耗,导致车辆出现50~70 Hz的强迫振动,频率与轮轨系统耦合振动
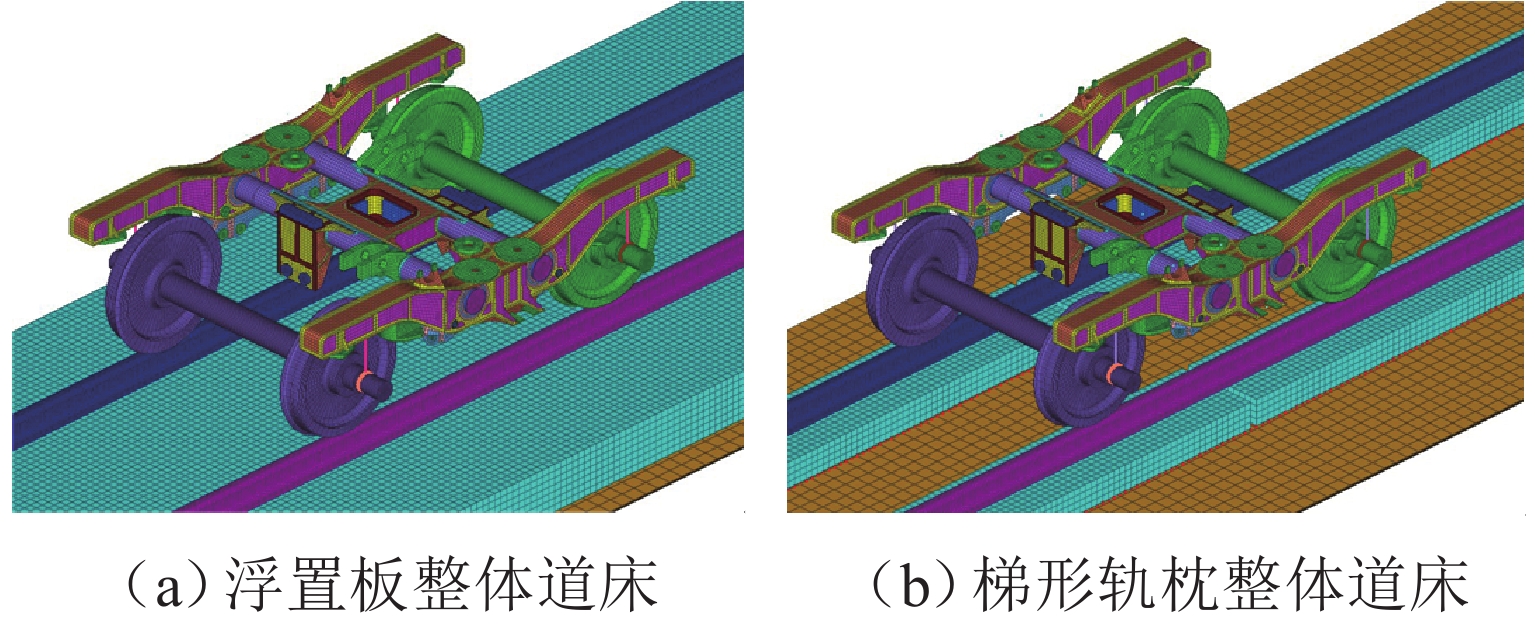
P 2力频率接近;通过车轮磨耗迭代仿真分析,确定了钢轨周期性接头焊缝不平顺引起的轮轨系统P 2力共振是导致车轮7~9阶多边形磨耗的根本原因;对钢弹簧浮置板道床和梯形轨枕道床而言,长期轮轨P 2力作用会分别引起8阶和15阶车轮多边形磨耗.Abstract:Wheel polygonal wear will deteriorate the vibration environment of rail vehicles, lead to resonance fatigue failure of structural components, and seriously threaten driving safety. To study the formation mechanism of wheel polygonal wear of metro vehicles, the dynamic line tracking test was carried out, and the vertical coupling finite element model and dynamics model of the track were established. In addition, the iterative simulation analysis of long-term wheel-track wear was carried out. The results show that the wheel polygonal wear of 7–9th order occurs in the measured vehicle, which leads to the forced vibration of 50–70 Hz, and the frequency is close to that of the
P 2 force during the coupling vibration of the wheel-track system. Through the iterative simulation analysis of wheel wear, it is determined thatP 2 force resonance of the wheel-rail system caused by periodic irregular rail joint weld is the root cause of the 7th–9th order wheel polygonal wear. Under the long-term action ofP 2 force, the floating slab track bed and the ladder sleeper track bed of steel spring will cause 8th and 15th order wheel polygonal wear, respectively.-
Key words:
- metro vehicle /
- wheel polygon /
- vehicle-track coupling /
- wear model /
- vehicle dynamics
-
磁悬浮技术具有无摩擦、微振动、长寿命及高精度等优点,被广泛地应用于高速机械领域. 磁轴承作为核心部件,一般与高速旋转电机配合用于高速旋转机械,如磁悬浮飞轮、磁悬浮控制力矩陀螺及磁悬浮电机等[1-3]. 对于直线运动,通常采用能够实现悬浮及导向功能的电磁铁与直线电机的组合,如磁浮列车、磁浮电梯等. 目前为止,世界很多国家已经对磁浮列车技术研究了较长时间,而且部分实现了商业运行,如中国、德国、日本、韩国等[4-6]. 磁浮列车由电磁铁与轨道功能件之间产生的电磁力支撑,从而实现无接触运行. 电磁铁为悬浮系统的核心执行部件,其电磁力特性决定了列车的承载能力,并与控制器、传感器相互配合实现列车的稳定悬浮. 尤其对于高速运行的磁浮列车,运行载荷更加复杂、苛刻,对承载能力及稳定性要求更高. 因此,电磁力特性分析作为基础研究,对悬浮系统的设计及优化起至关重要作用[7-9].
目前,电磁力建模分析方法主要包含等效磁路法(EMC)及有限元法(FEM),其中,FEM计算精度较高,但效率较低,很难与控制模型联合用于分析系统实时特性. EMC计算速度较高,能够与控制模型联合用于系统实时动态特性分析,但其计算精度较低. 因此,在传统EMC模型中通常会考虑加入补偿系数,通过调整系数校正电磁力结果,使其与FEM结果接近[10-11]. 然而,传统EMC模型仅考虑线性工作区,导磁材料采用恒定的相对磁导率,忽略磁饱和影响,甚至忽略导磁材料磁阻. 这样会导致EMC模型结果在小电流区间内较准确,而在大电流区间就会出现较大偏差[12-13]. 本文在搭建高速磁浮悬浮电磁铁EMC模型时,考虑了导磁材料的磁阻及其非线性. 通过导磁材料B-H (B为磁感应强度;H为磁场强度)曲线的拟合及引入,求解电磁力的准确性大幅度提高,适用范围增加.
高速磁浮列车的悬浮电磁铁共有12个磁极,极性为NS交替,相邻磁极之间通过磁轭连接,磁场经过长定子铁芯形成回路,磁极与长定子之间的磁场产生电磁吸力,实现悬浮功能. 12个磁极分为左、右两组,分别由两个悬浮控制器单独控制,从而形成两个控制回路,每个回路对应两个间隙传感器. 传感器实时监测电磁铁与长定子之间的间隙,并反馈给悬浮控制器,经过控制策略计算,悬浮控制器输出相应电压给悬浮电磁铁,实现动态稳定悬浮.
1. 电磁铁模型搭建
1.1 等效磁路
悬浮电磁铁与长定子的物理模型如图1所示. 其中电磁铁分为左、右两个回路单独控制,为简化计算模型,仅对半个电磁铁进行建模,并忽略两个回路间磁场的影响. 搭建的等效磁路模型如图2所示,磁路中包含了气隙磁阻、漏磁磁阻及导磁材料磁阻. 图中:Raj为磁极与长定子间的气隙磁阻;Rsi为长定子铁芯磁阻;Rei为磁极铁芯及磁轭磁阻;Rli为相邻磁极之间的漏磁磁阻;ϕaj、ϕsi、ϕei及ϕli分别为磁阻Raj、Rsi、Rei及Rli对应的磁通;ϕpj 为磁极磁通;θj为磁极磁动势nI,n为磁极匝数,I为控制回路电流;i=1,2,…,5,j=1,2,…,6.
根据建模需求,定义磁通、磁动势向量为
\left\{ \begin{array}{l} \boldsymbol{\phi}=\left({{\phi_{1}},{\phi_{\text{l1}}},{\phi_{2}},{\phi_{\text{l2}}}, \cdots ,{\phi_{5}},{\phi_{\text{l5}}}} \right)^\text{T}\text{,}\\ \boldsymbol{\phi}_\text{s} =\left({{\phi_{1}},{\phi_{2}},\cdots ,{\phi_{5}}} \right)^\text{T}\text{,}\\ \boldsymbol{\phi}_\text{a}=\left({{\phi_{1}},{\phi_{1}}+{\phi_{2}},\cdots ,{\phi_{4}}+{\phi_{5}}},{\phi_{5}} \right)^\text{T}\text{,}\\ \boldsymbol{\phi}_\text{e}=\left({{\phi_{1}}+{\phi_{\text{l1}}},{\phi_{2}}+{\phi_{\text{l2}}},\cdots ,{\phi_{5}}+{\phi_{\text{l5}}}} \right)^\text{T}\text{,}\\ \boldsymbol{\phi}_\text{p} = ({\phi_{1}} + {\phi_{\text{l1}}},{\phi_{1}} + {\phi_{\text{l1}}} + {\phi_{2}} + {\phi_{\text{l2}}},\cdots,{\phi_{4}} + {\phi_{\text{l4}}}+\\ \quad {\phi_{5}}+{\phi_{\text{l5}}} ,{\phi_{5}}+{\phi_{\text{l5}}})^\text{T}\text{,} \\ \boldsymbol{\theta} =\left( {{\theta_{1}},{\theta_{2}},\cdots ,{\theta_{6}}} \right)^\text{T}\text{.} \end{array} \right. (1) 磁极磁通向量ϕp与磁通向量ϕ的转换关系为
ϕp =Tϕ,
式中:
{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\text{1}}&{\text{1}}&{}&{}&{}&{}&{}&{}&{}&{} \\ {\text{1}}&{\text{1}}&{\text{1}}&{\text{1}}&{}&{}&{}&{}&{}&{} \\ {}&{}&{\text{1}}&{\text{1}}&{\text{1}}&{\text{1}}&{}&{}&{}&{} \\ {}&{}&{}&{}&{\text{1}}&{\text{1}}&{\text{1}}&{\text{1}}&{}&{} \\ {}&{}&{}&{}&{}&{}&{\text{1}}&{\text{1}}&{\text{1}}&{\text{1}} \\ {}&{}&{}&{}&{}&{}&{}&{}&{\text{1}}&{\text{1}} \end{array}} \right] \text{.} 在等效磁路中,根据基尔霍夫电压定律,建立关于磁通的方程组,如式(3).
\left\{\begin{array}{l} R_{\text{a}{ (j-1)}} \phi_{\text{a}{(j-1)}} + R_{\text{s} i} \phi_{\text{s} i} + R_{\text{a}{j}} \phi_{\text{a}{j}} + R_{\text{e} i} \phi_{\text{e} i}=\theta_{j-1} + \theta_j, \\ R_{\text{l} i} \phi_{\text{l} i} + R_{\text{e} i} \phi_{\text{e} i}=\theta_{j-1} + \theta_j, \end{array}\right. (3) 式中:{{j}}=2,3,\cdots,6.
将式(1)表达为矩阵及向量形式为
{\boldsymbol{A}}{\boldsymbol{\phi}} ={\boldsymbol{T}}^{\text{T}}{\boldsymbol{\theta}}={\boldsymbol{T}}^{\text{T}}{\boldsymbol{n}}I \text{,} (4) 式中:向量n=(n, n, n, n, n, n)T;A为磁阻矩阵,\boldsymbol{A} \in {R^{10 \times 10}},
\qquad\qquad\quad{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { {R_{\text{a1}}} + {R_{\text{a2}}} + {R_{\text{s1}}} + {R_{\text{e1}}}}& {{R_{\text{e1}}}}& {{R_{\text{a2}}}}& 0& 0& \cdots \\ {{R_{\text{e1}}}}&{{R_{\text{l1}}} + {R_{\text{e1}}}}&0&0&0& \cdots \\ {{R_{\text{a2}}}}&0&{{R_{\text{a2}}} + {R_{\text{a3}}} + {R_{\text{s2}}} + {R_{\text{e2}}}}&{{R_{\text{e2}}}}&{{R_{\text{a3}}}}& \cdots \\ 0&0&{{R_{\text{e2}}}}&{{R_{\text{l2}}} + {R_{\text{e2}}}}&0& \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \end{array}} \right]. 1.2 磁阻计算
1) 磁极与长定子间气隙磁阻
受磁极直线发电机(linear generator, LIG)槽与长定子齿槽结构的影响,磁极与长定子之间的气隙磁通分布较为复杂,如图3所示. 因此,将气隙磁通等效分为主磁通、槽磁通及LIG磁通,分别对应3种磁阻.
气隙磁阻为3种磁阻并联,即
\frac{1}{R_{\text{a} j}}=\frac{1}{R_{\text{a}, \text{m} j}} + \frac{1}{R_{\text{a}, \text{n} j}} + \frac{1}{R_{\text{a}, \text{L} j}}\text{,} (5) 式中:Ra,mj为主磁通对应的磁阻;Ra,nj为槽磁通对应的磁阻;Ra,Lj为LIG磁通对应的磁阻.
每种磁阻可由式(6)计算.
R_{{\rm{a}}, o j}=\frac{s_j + h_{o j}}{\mu_0 A_{a, o j}}, \quad o \in[\text{m}, \text{n}, \text{L}] \text{,} (6) 式中:sj为磁极与长定子齿之间的间隙;μ0为空气磁导率;Aa,oj为相应气隙面积;hoj为额外气隙长度;m、n、L分别对应主磁通、槽磁通和LIG磁通.
2) 相邻磁极间漏磁磁阻
磁极磁通大部分经过长定子回到相邻磁极,小部分未经过长定子而直接回到相邻磁极,该部分磁通为相邻磁极之间的漏磁,对应的磁阻称为漏磁磁阻,可由式(7)计算.
R_{\text{l} i}=\frac{h_{\text{l} i}}{\mu_0 A_{\text{l} i}}\text{,} (7) 式中:Ali为等效气隙面积;hli为相邻磁极间的等效气隙长度.
3) 导磁材料磁阻
对于长定子铁芯、磁极铁芯及磁轭的磁阻,采用分段方式进行求解,且尽可能保证每段的截面积相同. 具体分段如图4所示,其中,磁极及磁轭共分为5段(1~5),长定子分为3段(6~8). 该部分磁阻计算时考虑导磁材料的非线性.
磁极铁芯及磁轭磁阻为
R_{\text{e} i}=\displaystyle\sum\limits_{k=1}^5 \frac{l_{\text{e} i, k}}{\mu_0 \mu_\text{r}\left(\phi_{\text{e} i, k}\right) A_{\text{e} i, k}} \text{;} (8) 长定子铁芯磁阻为
R_{\text{s} i}=\displaystyle\sum\limits_{k=6}^8 \frac{l_{\text{s} i, k}}{\mu_0 \mu_\text{r}\left(\phi_{\text{s} i, k}\right) A_{\text{s} i, k}} \text{,} (9) 式(8)、(9)中:lei,k, lsi,k分别为悬浮电磁铁侧、长定子侧每段铁芯的长度;Aei,k, Asi,k分别
为悬浮电磁铁侧、长定子侧每段铁芯的截面积;μr为每段铁芯的相对磁导率;ϕsi,k为第i个磁回路中第k段长定子内的磁通量;ϕei,k为第i个回路中第k段磁极铁芯或磁轭内的磁通量. 为在EMC模型中引入导磁材料的非线性,不再将μr简单地设置为恒定值,而是根据每段铁芯的磁通进行计算. 磁极铁芯、磁轭及长定子铁芯均采用硅钢片,牌号为M530-50A,导磁材料的非线性可通过B-H曲线体现,如图5所示.
根据文献[14],B-H曲线可采用式(10)函数进行拟合.
H=\alpha_1 B + \alpha_2 B^{\alpha_3} , (10) 式中:α1、α2及α3为拟合函数自变量B的系数,可通过对图5中B-H曲线的拟合确定.
长定子铁芯的相对磁导率可表示为
\mu_{{\rm{r1}}}=\frac{B}{\mu_0 H}=\frac{1}{\mu_0\left(\alpha_1 + \alpha_2 B^{\alpha_3-1}\right)}\text{.} (11) 根据磁密、面积及磁通的关系,式(11)可表达为
\mu_{{\rm{r1}}} =\frac{1}{\mu_0\left(\alpha_1 + \alpha_2\left(\dfrac{\phi_{{\rm{s}}i}}{A_{\text{s} i, k}}\right)^{\alpha_3-1}\right)} \text{.} (12) 同理可求解磁极铁芯及磁轭的相对磁导率为
\mu_{{\rm{r2}}}=\frac{1}{\mu_0\left(\alpha_1 + \alpha_2\left(\dfrac{\phi_{\text{e} i}}{A_{\text{e} i, k}}\right)^{\alpha_3-1}\right)} \text{.} (13) 将式(12)、(13)代入式(8)、(9)求解磁极铁芯、磁轭及长定子铁芯磁阻. 通过式(5)~(9)可知,磁阻矩阵A与间隙s及磁通ϕ相关,因此,将其记为A(s,ϕ).
1.3 电路模型
悬浮电磁铁分为两个控制回路,分别由一个控制器进行供电. 控制器的输出为电压,根据控制回路的负载特性转变为相应的负载电流. 在进行电磁力模型与控制模型联合分析时,需要搭建电磁铁的电路模型,其功能是将控制模型的输入电压转变为负载电流,再结合EMC模型计算电磁力. 与EMC模型类似,仅搭建一个回路的模型,6个磁极串联实际可等效为6个电阻与6个电感的串联,如图6所示. 图中:RMj为单个磁极电阻;LMj为单个磁极电感;ULj为单个磁极电感电压;UM为单个控制回路的输入电压.
根据电路模型,单个控制回路的输入电压为
{U_\text{M}} = {R_\text{M}}I + \sum\limits_{j = 1}^6 {{U_{\text{L}j}}} = {R_\text{M}}I + {\boldsymbol{n}^\text{T}}\mathop {{\boldsymbol{\phi} _\text{p}}}\limits^ \bullet \text{,} (14) 式中:RM为单个控制回路的总电阻.
整理式(14),控制回路电流可表达为
I = ({U_\text{M}} - {\boldsymbol{n}^\text{T}}\mathop {{\boldsymbol{\phi} _\text{p}}}\limits^ \bullet )/{R_\text{M}} \text{.} (15) 1.4 磁力模型
式(4)给出了磁通与电流关系,式(15)给出了磁通、电流与电压关系. 将式(15)代入式(4),可得磁通与电压的关系为
{\boldsymbol{A}}(s,\phi )\boldsymbol{\phi} = {\boldsymbol{T}^\text{T}}\boldsymbol{n}({U_\text{M}} - {\boldsymbol{n}^\text{T}}\mathop {{\boldsymbol{\phi} _\text{p}}}\limits^ \bullet )/{R_\text{M}} \text{.} (16) 根据磁通关系{\boldsymbol{\phi}}_\text{p}={\boldsymbol{T}}{\boldsymbol{\phi}},式(16)整理为
{\boldsymbol{T}^\text{T}}{\boldsymbol{n}}{\boldsymbol{n}^\text{T}}\boldsymbol{T}\mathop {\boldsymbol{\phi}} \limits^ \bullet {\text{ = }}{\boldsymbol{T}^\text{T}}\boldsymbol{n}{U_\text{M}} - {R_\text{M}}\boldsymbol{A}({{s}},\phi )\boldsymbol{\phi} \text{.} (17) 经过计算发现,矩阵TTnnTT为奇异矩阵,常微分式(17)很难进行求解. 因此,为便于求解方程,采用中间变量替换原变量.
根据磁通关系ϕp=Tϕ,将式(16)整理成变量为ϕp的方程,如式(18)
\boldsymbol{A}({s},{\phi}){\boldsymbol{T}^{{ - 1}}}{\boldsymbol{\phi}_{\rm{p}}} = {\boldsymbol{T}^\text{T}}\boldsymbol{n}({U_\text{M}} - {\boldsymbol{n}^\text{T}}\mathop {{\boldsymbol{\phi} _\text{p}}}\limits^ \bullet )/{R_\text{M}}\text{.} (18) 进一步整理为
{\boldsymbol{n}^\text{T}}{\boldsymbol{\phi} _\text{p}} = {\boldsymbol{n}^\text{T}}\boldsymbol{T}{\boldsymbol{A}^{{ - 1}}}({s},\phi){\boldsymbol{T}^\text{T}}\boldsymbol{n}({U_\text{M}} - {\boldsymbol{n}^\text{T}}\mathop {{\boldsymbol{\phi} _\text{p}}}\limits^ \bullet )/{R_\text{M}}\text{.} (19) 将6个磁极的磁通之和β作为中间变量,则β可表示为
\beta=\displaystyle\sum\limits_{j=1}^6 \phi_{\text{p} j}\text{.} (20) 将式(20)代入式(19),得到关于β的常微分方程为
n\beta = {\boldsymbol{n}^\text{T}}\boldsymbol{T}{\boldsymbol{A}^{{ - 1}}}(s,\phi ){\boldsymbol{T}^\text{T}}\boldsymbol{n}({U_\text{M}} - n\mathop \beta \limits^ \bullet )/{R_\text{M}}\text{,} (21) 式中:nTTA−1(s,ϕ)TTn不再是一个矩阵或向量,而是一个关于s、ϕ的变量,记为1/M (s,ϕ).
对式(21)进行整理得
\dot{\beta}=U_\text{M} / n-R_\text{M} {M}({{s}},\phi ) \text{.} (22) 依据式(15)、(22),可得I与β间的关系为
I=n M({s},\phi ) \beta \text{.} (23) 依据式(19)、(22)及磁通关系ϕp=Tϕ,得到ϕ与β间的关系为
\boldsymbol{\phi} = {\boldsymbol{A}^{{ - 1}}}({s},\phi ){\boldsymbol{T}^\text{T}}\boldsymbol{n}M({s},\phi )n\beta \text{.} (24) 通过式(22)~(24)计算出悬浮电磁铁电流以及电磁力求解所需的磁通.
根据式(5),计算各部分气隙的磁通为
\phi_{\text{a}, o j}=\frac{\phi_{\text{a} j} R_{\text{a} j}}{R_{\text{a}, o j}}\text{.} (25) 基于虚功原理,各部分气隙对应的电磁力为
F_{\text{m} \text{a} \text{g}, o j}=\frac{\phi_{\text{a}, o j}^2}{2 \mu_0 A_{\text{a}, o j}}\text{.} (26) 单个磁极电磁力为式(26)中各部分电磁力之和,即
F_{\text{m} \text{a} \text{g}, j}=F_{\text{m} \text{a} \text{g}, \text{m} j} + F_{\text{m} \text{a} \text{g}, \text{n} j} + F_{\text{m} \text{a} \text{g}, \text{L} j}\text{.} 最后,求解半个悬浮电磁铁的电磁力为
F_{\text{m} \text{a} \text{g}}=\displaystyle\sum\limits_{j=1}^6 F_{\text{m} \text{a} \text{g}, j} \text{.} 根据电磁力解析过程,EMC模型可简化为图7所示的结构框图,输入为电压及间隙,输出为电流及电磁力. 首先进行磁阻计算,并组建磁阻矩阵,而导磁材料磁阻的计算需要将磁通作为输入. 采用磁阻矩阵A进行电流及磁通计算,磁通需通过常微分方程及代数方程求解,磁通求解结果一方面用于电磁力计算,一方面反馈给导磁材料磁阻计算.
2. 模型分析及试验验证
2.1 与传统EMC模型对比
根据悬浮电磁铁及长定子的尺寸及参数(如表1所示),对本文EMC模型进行量化. 此外,将导磁材料的相对磁导率设为恒定值,搭建基于线性导磁材料的传统EMC模型. 对两个模型电磁力的计算结果进行对比分析,如图8所示.
表 1 悬浮电磁铁及长定子参数Table 1. Parameters of maglev electromagnet and long stator项点 取值 项点 取值 定子极距/mm 258.0 铁芯厚度/mm 170.0 电磁铁极距/mm 266.5 磁极匝数 300 定子齿宽度/mm 43.0 额定磁间隙/mm 12.5 定子槽宽度/mm 43.0 恒定相对磁导率 7 000 磁间隙为12.5 mm,电流在0~35 A内,两个模型的电磁力结果非常接近;当电流超过35 A时,随着电流增加,计算结果偏差增大. 原因是实际工作状态下,随着电流增大,导磁部件的磁密增大;当达到材料饱和磁密时,磁密随电流的增加率大幅降低,电磁力也相应地出现饱和现象,而传统EMC模型并未考虑材料的磁饱和. 因此,传统EMC模型适用于小电流区间,一般应用在工作点附近的线性区间20~30 A. 而大电流区间与实际工作情况不符,例如在故障、起浮、降落等特殊工况时,模型精度大幅降低,无法用于电磁力计算及系统特性分析.
2.2 与有限元模型对比
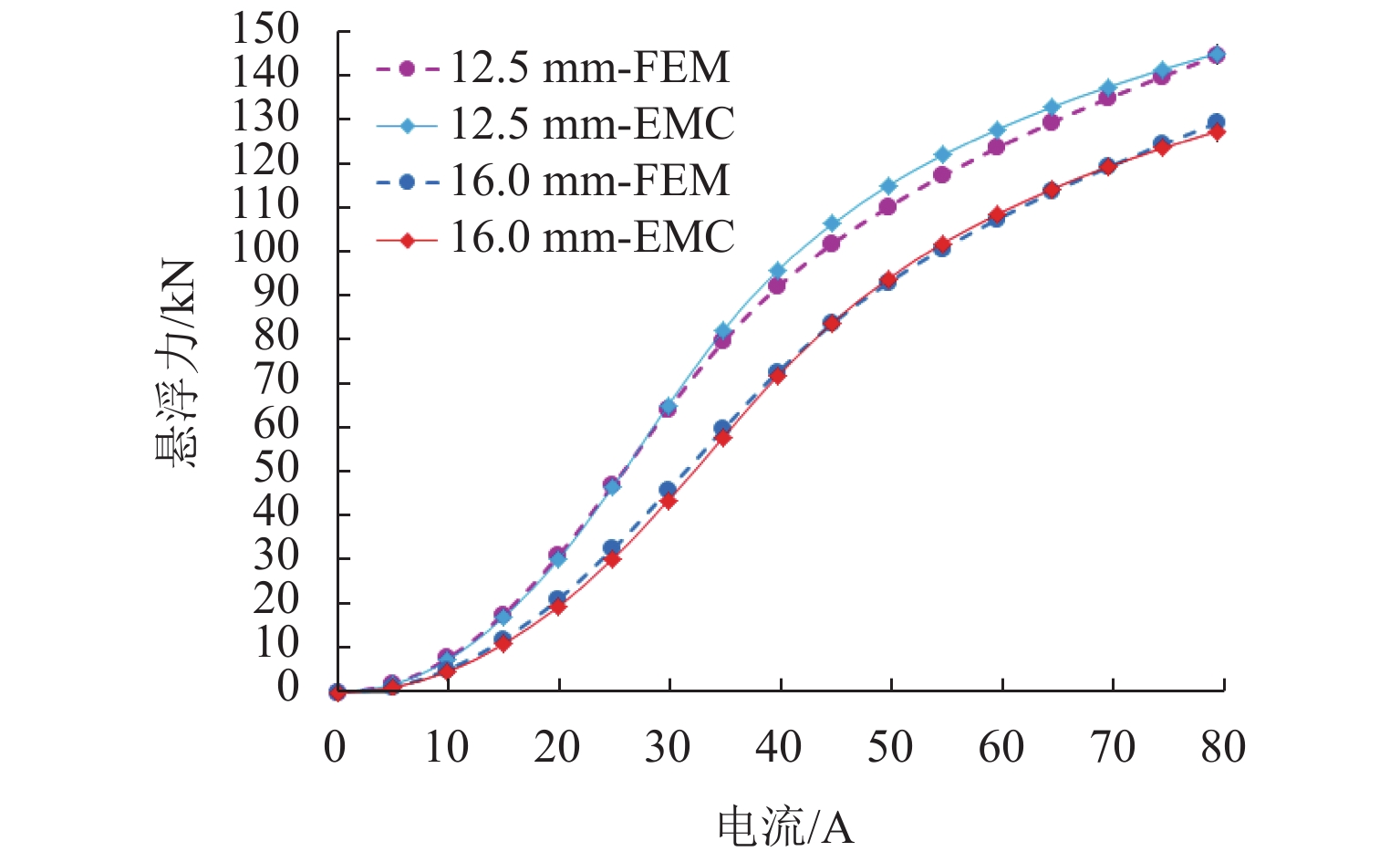
为验证本文提出的EMC模型准确性,搭建了悬浮电磁铁与长定子FEM模型,如图9所示,两者电磁力的计算结果如图10所示. 磁间隙12.5 mm与16.0 mm,电流0~80 A内,两者电磁力的计算结果具备非常高的一致性,均存在饱和现象;磁间隙12.5 mm,电流50 A时,电磁力偏差最大,EMC计算结果为115 kN,FEM计算结果为110 kN,偏差仅为4.5%,这表明了基于非线性材料的EMC模型具有较高的准确性.
2.3 试验验证
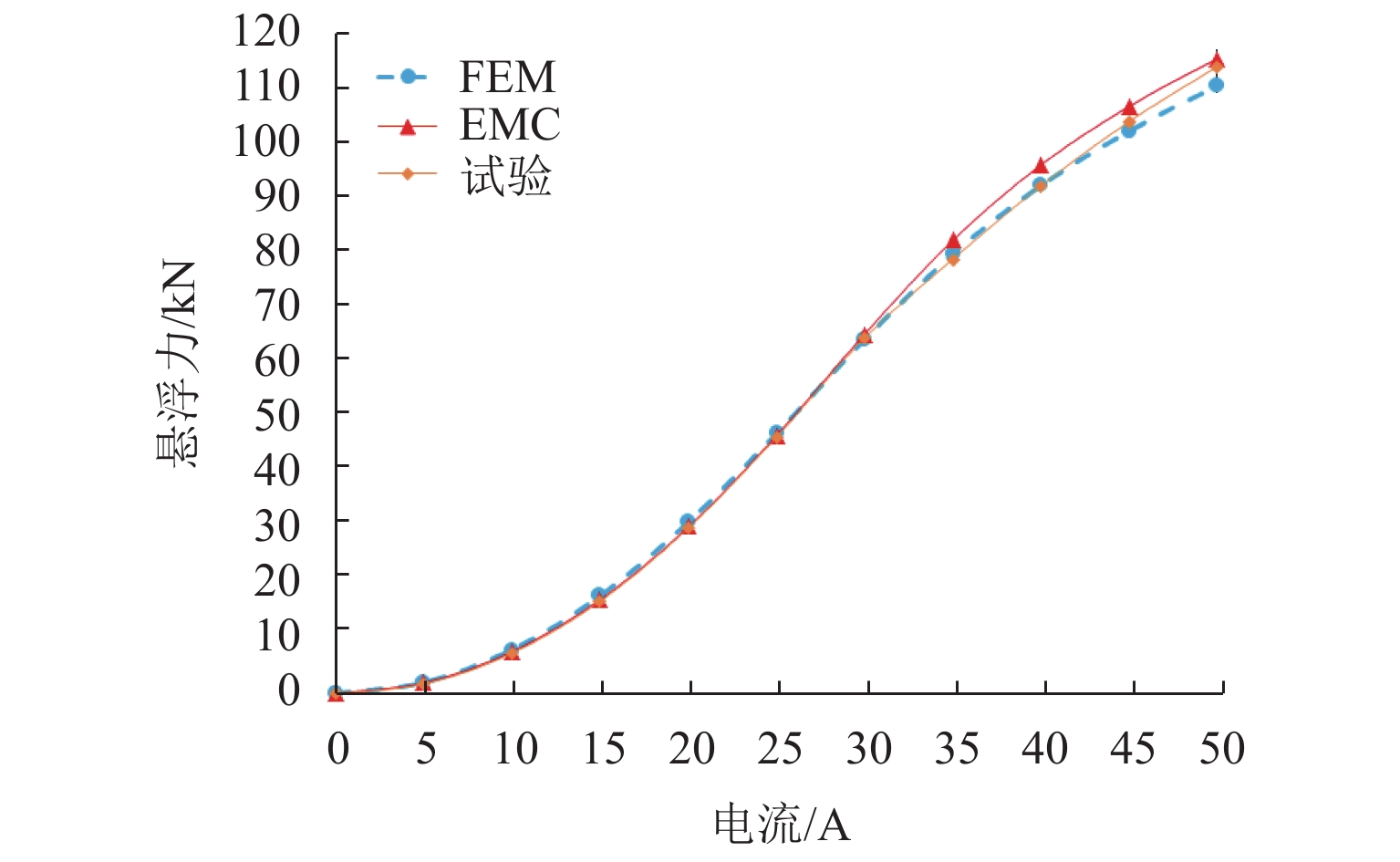
针对高速磁浮电磁铁特性研究,搭建了地面试验平台,对悬浮电磁铁的静态电磁力进行测试,如图11所示. 试验台通过液压系统调整长定子与悬浮电磁铁的间隙;采用两路电源供电,但受最大输出电流限制,仅对0~50 A电流进行测试,步长为5 A;通过力传感器检测电磁铁与长定子间的电磁力. 磁间隙12.5 mm下电磁力的测试结果与EMC及FEM的计算结果对比如图12所示.
额定工况下,悬浮电磁铁的工作点:磁间隙为12.5 mm,电流为25 A,电磁力约为46 kN. 在工作点处,EMC、FEM及试验测试的电磁力结果几乎相同,在其他电流值下,电磁力结果偏差也极小,从而进一步验证了本文EMC模型以及所搭建FEM模型的准确性.
3. 结 论
本文基于非线性材料搭建了高速磁浮悬浮电磁铁的磁路、电路及磁力模型,将计算结果与传统EMC模型进行对比分析,并通过有限元及试验验证,通过对模型研究分析,得到以下结论:
1) 搭建悬浮电磁铁EMC模型时,采用了非线性导磁材料,通过引入B-H曲线的拟合函数,将导磁材料的非线性及饱和特性体现在模型中.
2) 无论小电流区,还是大电流区,本文EMC模型求解的电磁力均与实际情况接近,相比传统EMC模型,结果更加准确,适用范围更广.
3) 本文EMC模型能够快速、准确地求解电磁力,且通过电路模型实现与控制模型的良好匹配,因此,可通过联合仿真对悬浮系统动态特性进行深入分析,为悬浮系统设计及参数优化提供了依据.
-
表 1 地铁车辆和轨道的主要参数
Table 1. Main parameters of metro vehicles and tracks
参数 符号 数值 定距之半/m lc 7.85 轴距之半/m lw 1.25 车体质量/kg Mc 24937 构架质量/kg Mf 1830 轮对质量/kg Mw 1231 一系悬挂垂向刚度/(MN·m−1) Kps 1.5 一系悬挂垂向阻尼/(kN·s·m−1) Cps 2 浮置板道床扣件垂向刚度/(MN·m−1) Ka 50 浮置板支撑刚度/(kN·s·m−1) Ca 20 梯形轨枕扣件垂向刚度(MN·m−1) Kb 60 梯形轨枕纵梁支撑刚度/(kN·s·m−1) Cb 20 普通道床扣件垂向刚度/(MN·m−1) Kc 20 浮置板长度/m La 24 梯形轨枕纵梁长度/m Lb 6 -
[1] 刘维宁,马蒙,刘卫丰,等. 我国城市轨道交通环境振动影响的研究现况[J]. 中国科学:技术科学,2016,46(6): 547-559. doi: 10.1360/N092015-00334LIU Weining, MA Meng, LIU Weifeng, et al. Overview on current research of environmental vibration influence induced by urban mass transit in China[J]. SCIENTIA SINICA Technologica, 2016, 46(6): 547-559. doi: 10.1360/N092015-00334 [2] 魏鹏勃. 城市轨道交通引起的环境振动预测与评估[D]. 北京: 北京交通大学, 2009. [3] KANG X, CHEN G X, ZHU Q, et al. Study on wheel polygonal wear of metro trains caused by frictional self-excited oscillation[J]. Tribology Transactions, 2021, 64(6): 1108-1117. doi: 10.1080/10402004.2021.1970868 [4] ZHOU C, CHI M R, WEN Z F, et al. An investigation of abnormal vibration-induced coil spring failure in metro vehicles[J]. Engineering Failure Analysis, 2020, 108: 104238.1-104238.13. doi: 10.1016/j.engfailanal.2019.104238 [5] JOHANSSON A, ANDERSSON C. Out-of-round railway wheels—a study of wheel polygonalization through simulation of three-dimensional wheel-rail interaction and wear[J]. Vehicle System Dynamics, 2005, 43(8): 539-559. doi: 10.1080/00423110500184649 [6] TAO G Q, WEN Z F, LIANG X R, et al. An investigation into the mechanism of the out-of-round wheels of metro train and its mitigation measures[J]. Vehicle System Dynamics, 2019, 57(1): 1-16. doi: 10.1080/00423114.2018.1445269 [7] SHI Y X, DAI H Y, WANG Q S, et al. Research on low-frequency swaying mechanism of metro vehicles based on wheel-rail relationship[J]. Shock and Vibration, 2020, 2020: 8878020.1-8878020.15. [8] CAI W B, CHI M R, WU X W, et al. Experimental and numerical analysis of the polygonal wear of high-speed trains[J]. Wear, 2019, 440/441: 203079.1-203079.12. doi: 10.1016/j.wear.2019.203079 [9] MA C Z, GAO L, CUI R X, et al. The initiation mechanism and distribution rule of wheel high-order polygonal wear on high-speed railway[J]. Engineering Failure Analysis, 2021, 119: 104937.1-104937.14. [10] YANG X X, TAO G Q, LI W, et al. On the formation mechanism of high-order polygonal wear of metro train wheels: experiment and simulation[J]. Engineering Failure Analysis, 2021, 127: 105512.1-105512.14. [11] QU S, ZHU B, ZENG J, et al. Experimental investigation for wheel polygonisation of high-speed trains[J]. Vehicle System Dynamics, 2021, 59(10): 1573-1586. doi: 10.1080/00423114.2020.1772984 [12] 董雅宏,曹树谦. 车轮高阶多边形磨耗发生与演化特征分析[J]. 西南交通大学学报,2023,58(3): 665-676.DONG Yahong, CAO Shuqian. Analysis of occurrence and evolution characteristics of wheel high-order polygonal wear[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 665-676. [13] 胡晓依,任海星,成棣,等. 动车组车轮多边形磨耗形成与发展过程仿真研究[J]. 中国铁道科学,2021,42(2): 107-115.HU Xiaoyi, REN Haixing, CHENG Di, et al. Numerical simulation on the formation and development of polygonal wear of EMU wheels[J]. China Railway Science, 2021, 42(2): 107-115. [14] The International Organization for Standardization. Railway applications—acoustics measurement of noise emitted by railbound vehicles: ISO 3095:2013[S]. [S.l.]: ISO Copyright Office, 2013. [15] 罗仁, 石怀龙. 铁道车辆系统动力学及应用[M]. 成都: 西南交通大学出版社, 2018. [16] ZHAI W M, WANG K Y, CAI C B. Fundamentals of vehicle−track coupled dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1349-1376. doi: 10.1080/00423110802621561 [17] KORO K, ABE K, ISHIDA M, et al. Timoshenko beam finite element for vehicle—track vibration analysis and its application to jointed railway track[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(2): 159-172. doi: 10.1243/0954409041319687 [18] 林国进. 轮对弹性及参数对轮轨接触关系影响研究[D]. 北京: 北京交通大学, 2015. [19] WU T X, THOMPSON D J. Behaviour of the normal contact force under multiple wheel/rail interaction[J]. Vehicle System Dynamics, 2002, 37(3): 157-174. doi: 10.1076/vesd.37.3.157.3533 [20] 关庆华,周业明,李伟,等. 车辆轨道系统的P2共振频率研究[J]. 机械工程学报,2019,55(8): 118-127. doi: 10.3901/JME.2019.08.118GUAN Qinghua, ZHOU Yeming, LI Wei, et al. Study on the P2 resonance frequency of vehicle track system[J]. Journal of Mechanical Engineering, 2019, 55(8): 118-127. doi: 10.3901/JME.2019.08.118 [21] 陈小平,王平,陈嵘. 弹性支承块式无砟轨道的减振机理[J]. 铁道学报,2007,29(5): 69-72. doi: 10.3321/j.issn:1001-8360.2007.05.013CHEN Xiaoping, WANG Ping, CHEN Rong. Damping vibration mechanism of the elastic bearing block track[J]. Journal of the China Railway Society, 2007, 29(5): 69-72. doi: 10.3321/j.issn:1001-8360.2007.05.013 [22] 赵晓男,陈光雄,康熙,等. 兰新客运专线动车组车轮多边形磨耗的机理[J]. 西南交通大学学报,2020,55(2): 364-371. doi: 10.3969/j.issn.0258-2724.20190027ZHAO Xiaonan, CHEN Guangxiong, KANG Xi, et al. Mechanism of polygonal wear on wheels of electric multiple units on lanzhou-Xinjiang passenger dedicated line[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 364-371. doi: 10.3969/j.issn.0258-2724.20190027 [23] QI Y Y, DAI H Y, GAN F, et al. Optimization of rail profile design for high-speed lines based on Gaussian function correction method[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2023: 095440972311525.1-095440972311525.13. [24] 王鹏,陶功权,杨晓璇,等. 中国高速列车车轮多边形磨耗特征分析[J]. 西南交通大学学报,2023,58(6): 1357-1365. doi: 10.3969/j.issn.0258-2724.20210777WANG Peng, TAO Gongquan, YANG Xiaoxuan, et al. Analysis of polygonal wear characteristics of Chinese high-speed train wheels[J]. Journal of Southwest Jiaotong University, 2023, 58(6): 1357-1365. doi: 10.3969/j.issn.0258-2724.20210777 -






 下载:
下载:












 下载:
下载: