二自由度磁浮列车悬浮系统时滞控制研究

王美琪; 曾思恒; 李源; 刘鹏飞

doi:10.3969/j.issn.0258-2724.20230282

二自由度磁浮列车悬浮系统时滞控制研究

doi: 10.3969/j.issn.0258-2724.20230282

王美琪^{1, 2,},
曾思恒²,
李源²,
刘鹏飞^{1, 2, ,}

1.
石家庄铁道大学交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043
2.
石家庄铁道大学机械工程学院，河北石家庄 050043

基金项目: 国家自然科学基金（12102273）

详细信息

作者简介:
王美琪（1987—），男，副教授，博士，研究方向为非线性动力学、磁悬浮列车动力学与控制，E-mail：wangmeiqi@stdu.edu.cn

通讯作者:
刘鹏飞（1985—），男，副教授，博士，研究方向为列车-轨道耦合动力学、磁悬浮列车动力学与控制，E-mail：lpfswjtu@163.com

中图分类号: O324
计量
- 文章访问数: 482
- HTML全文浏览量: 124
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-11
- 修回日期: 2023-09-12
- 网络出版日期: 2024-04-29
- 刊出日期: 2023-10-07

Research on Time Lag Control of Levitation System of Two-Degree-of-Freedom Magnetic Levitation Train

WANG Meiqi^{1, 2
,},
ZENG Siheng²,
LI Yuan²,
LIU Pengfei^{1, 2
, ,}

1.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

摘要

摘要:
为研究控制器时滞对磁浮列车悬浮系统稳定性的影响，首先，以位移-速度为反馈控制参数，建立考虑控制器时滞的二自由度磁浮列车悬浮系统模型；其次，通过Routh-Hurwitz稳定性判据得到无时滞系统的稳定性区域，同时，依据特征根穿越虚轴边界条件，获得系统发生Hopf分岔的控制器时滞临界值；最后，分析反馈控制参数及系统参数与控制器时滞临界值的关系. 研究结果表明：当系统参数一定时，控制器时滞临界值随位移控制增益的增大而减小，随速度控制增益的增大先增大后减小；当反馈控制参数一定时，控制器时滞临界值随二系刚度的增大而减小，随二系阻尼的增大而增大；当系统时滞以10⁻⁶数量级在时滞临界值附近渐渐增大时，系统会从稳定—周期运动—不稳定逐渐变化，期间发生超临界Hopf分岔.
- 磁浮系统 /
- 稳定性 /
- 时滞 /
- 反馈控制 /
- Hopf分岔
Abstract:
In order to study the influence of controller time lag on the stability of the levitation system of the magnetic levitation train, firstly, the two-degree-of-freedom magnetic levitation train levitation system model is established by taking displacement-velocity as the feedback control parameter, and the controller time lag is taken into account; secondly, the stability region of the time lag-free system is obtained by the stability criterion of Routh-Hurwitz, meanwhile, based on the characteristic root crossing the imaginary axis boundary condition, we obtain the critical value of the time lag of the controller when the system undergoes Hopf bifurcation; finally, we analyze the relationship between the feedback control parameters and the system parameters and the critical value of the controller time lag. The results show that: when the system parameters are certain, the critical value of the controller time lag decreases with the increase of the displacement control gain, and increases and then decreases with the increase of the velocity control gain; when the feedback control parameters are certain, the critical value of the controller time lag decreases with the increase of the secondary suspension stiffness, and increases with the increase of the secondary suspension damping; as the time lag of the system increases asymptotically by an order of magnitude 10⁻⁶ around the critical value of time lag, the system will gradually change from stable-periodic motion-unstable, during which the supercritical Hopf bifurcation occurs.
- magnetic levitation system /
- stability /
- time lag /
- feedback control /
- Hopf bifurcation

HTML全文

现行城市轨道交通工程造价测算通常采用定额计价模式，或根据历史工程造价数据建立如多元线性回归（MLR）等线性分析模型进行预测^[1]. 城市轨道交通工程造价与其影响因素间多为非线性映射关系^[2]，由于定额的滞后性、静态性以及线性回归的欠精确性，难以准确拟合各因素与造价间的高度非线性机理，导致超预算、调预算现象屡见不鲜. 城市轨道交通工程的经济费用是进行方案比选与投资决策的重要考量，从已批复概算可知，我国城市轨道交通工程造价为（7～13）亿元/km，其中，土建工程造价占比最大，约为40%^[3]，土建工程造价是城市轨道交通的投资控制重点，实现土建工程造价的快速预测与反演分析可为城市轨道交通线路方案的优化决策提供重要依据.

2020年，住房和城乡建设部宣布了未来我国工程造价的改革方向，即逐步停止发布预算定额，鼓励使用大数据和人工智能等技术作为造价测算的基础^[4]. 因此，利用以机器学习为背景的智能预测方法建立城市轨道交通土建工程造价非线性预测模型，在实现高效准确预测的同时，不仅是对我国工程造价管理改革的及时响应，也为城市轨道交通设计单位智慧选线与方案优化和政府投资决策提供一种有效的决策辅助. 已有研究中，段晓晨等^[5-6]采用BP神经网络（BPNN）结合因素筛选，预测城市轨道交通工程造价. 陈进杰等^[7-8]以多条已建城市轨道交通工程为研究对象，采用支持向量机（SVM）探究因素与造价间的非线性关系，实现了有效的造价预测. 现有研究重点关注提升模型的预测精度，城市轨道交通工程超高额的造价水平说明在造价预测过程中，看似很小的预测误差都会引起实际投资额的巨大变化. 因此，对于城市轨道交通工程造价预测模型的研究，精度要求越高越好^[9]. 但上述方法存在一定的局限性，如BPNN存在训练速度慢、易陷入局部极值和学习速率难以控制的问题^[10-11]；SVM因其固有缺陷，即使结合其他优化算法，预测精度的提高也受到限制^[12]. 极限学习机（ELM）相比于其他智能预测模型具有参数简洁、运算速率快、预测精度高、泛化性能强等优势^[13]，更适用于城市轨道交通土建工程造价的非线性预测. 张飞涟等^[1]采用ELM模型预测城市轨道交通工程投资，并针对模型权阈值随机性问题利用遗传算法（GA）实现参数优化，取得了较好的预测效果. Karaca等^[14]指出采用上述智能算法虽有助于捕获存在于数据样本中的复杂关联规则，建立具有更高精度性能的早期造价预测模型，但此类模型存在内部潜在因果关系不够透明的弊端，“黑箱”效应突出，难以获得决策信服力，影响了模型在实际工程中的应用. 引入Sobol’ 全局敏感性分析方法有助于解决这一问题，通过分析各因素敏感度，明确对模型预测结果真正高影响的因素，并结合Curve Fitting方法量化探究各因素对造价的影响机理，能够有效实现对模型内部影响机理解释反演的目的^[15].

基于此，本研究以历史工程案例为基础，选用优化效果更佳的灰狼优化算法（GWO）对ELM参数优化，建立城市轨道交通土建工程造价GWO-ELM预测模型，提升预测准确性；引入Sobol’ 全局敏感性分析方法，剖析因素敏感性；同时，为弥补GWO-ELM模型无法得到工程造价与影响因素解析关系的不足，采用Curve Fitting方法分析工程造价与其影响因素间的显性作用形式，增强模型可解释性. 为城市轨道交通工程造价的测算、分析与调控提供一种新思路.

1. 影响因素分析与案例数据库构建

1.1 影响因素初步分析

城市轨道交通土建工程造价包括土建工程费、工程建设其他费、预备费和建设期贷款利息四部分. 依据概预算编制办法，仅土建工程费中的直接工程费是形成工程实体本身的费用，其余均可以其为基础求得. 因此，确定城市轨道交通土建工程造价的关键在于确定直接工程费. 直接工程费的多少取决于工程量的大小，所以，对城市轨道交通土建工程造价影响因素的分析首先从影响工程量的角度考虑^[6]. 已有研究认为，总里程越长、车站总数越多，则工程量越大，对应造价越高^[7]；编组、平均站距和设计时速又对车站规模、车站数量和线位要求有直接影响^[16-17]，最终在造价上得以体现.

土建工程造价与工程环境及地质条件和线路敷设方式关联紧密，不同的工程环境及地质条件下采取不同的敷设方式则造价相差甚远，因此，对城市轨道交通土建工程造价影响因素的分析还应参考《城市轨道交通岩土工程勘察规范》^[18]，从工程环境及地质条件和线路敷设方式的角度考虑^[19]. 通过对城市轨道交通土建工程项目结构分解（PBS）可知，城市轨道交通土建工程主要包括线路区间土建工程和车站土建工程，根据《地铁设计规范》^[20]，线路区间土建工程涵盖地下、地面和高架3类具体敷设方式，车站又可分为地下车站和地上车站. 可知，工程环境及地质条件、地下线长度、地面线长度、高架线长度、地下车站数和地上车站数对城市轨道交通土建工程造价有影响作用^[16-17,19].

除以上对工程特征因素的考虑外，宏观经济因素的波动，如CPI （居民消费价格指数）、PPI （生产者物价指数）和GDP （国内生产总值）会引起建筑材料、劳动力和设备价格变化^[1,7,21]，影响工程造价，且难以预测，在传统的城市轨道交通工程造价预测中往往被忽略.

基于此，本研究综合考虑工程特征因素和宏观经济因素，初步识别包括总里程、车站总数、编组、平均站距、设计时速、工程环境及地质条件、地下线长度、地面线长度、高架线长度、地下车站数、地上车站数和CPI、PPI、GDP在内的14个因素作为城市轨道交通土建工程造价的初始影响因素.

1.2 数据获取与统计分析

本研究通过工程项目参与（课题组参与的城市轨道交通科研项目）、工程专项调研（城市轨道交通工程建设单位与施工单位）、政府公开资料（国家统计局、省发改委、市人民政府网等）和已有文献，共收集城市轨道交通工程造价案例118个. 基于初始影响因素，对信息不完整的案例通过查阅城市轨道交通企业官网（各地城市轨道交通集团官网）和第三方文献作针对性补充采集，最终整理得到70个完整工程案例土建造价数据.

1.2.1 数据统计与量化

最终选定的70个完整工程案例时间跨度为2009年至2019年，土建工程总费用最低为6.2亿元，最高为187.3亿元，总里程介于3.15～69.50 km，涵盖地下、地面和高架3种敷设方式，平均站距为1.12～7.66 km，设计速度最低为80 km/h，最高为160 km/h，编组类型包括8D、8A、8B、6D、6A、6B、6C、6L、5B、4A、4B和4C，按照相对体型大小量化，分别对应12、11、…、2和1. 工程环境及地质条件参考《城市轨道交通岩土工程勘察规范》，按等级可分为复杂、较复杂和一般3类，对应量化为3、2和1. 考虑宏观经济因素的时滞性^[21]，造价数据通过膨胀系数进行调整，以消除不同历史阶段工程造价计价水平的影响.

1.2.2 数据特征分析

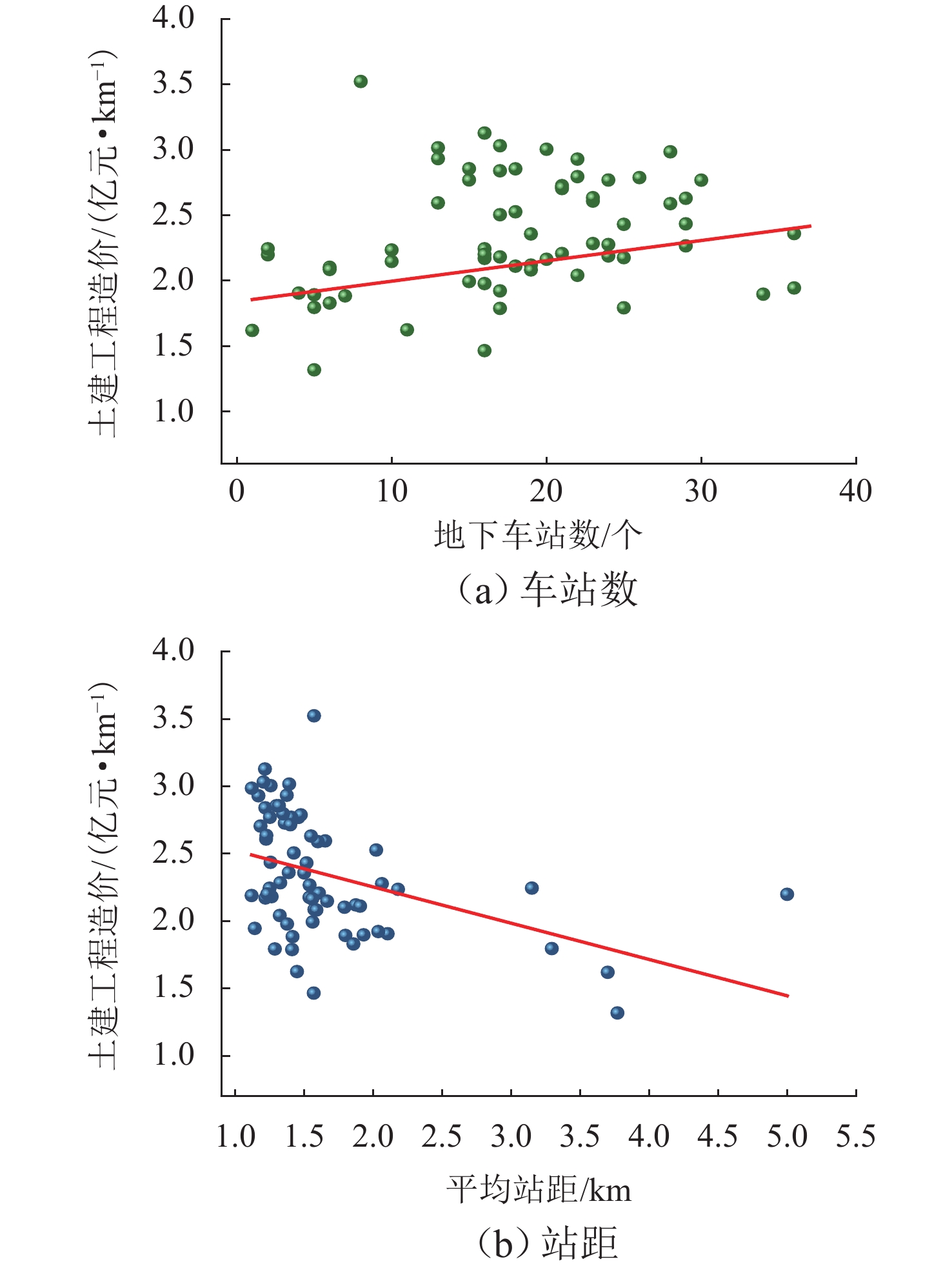
各类科学方法都有其适用性，对于城市轨道交通土建工程造价预测而言，掌握数据样本的核心特征是建立科学方法模型和开展进一步研究的基础. 本文基于所获案例数据样本，分析不同因素下实际数据与工程造价因变量间的作用机理与趋势. 限于篇幅，列举两项代表性因素与土建工程造价间的拟合关系，如图1所示.

图 1 因素自变量与造价因变量间的拟合关系

Figure 1. Fitting relationship between independent variable of factor and dependent variable of cost

下载: 全尺寸图片幻灯片

由图1可知：1）城市轨道交通土建工程造价影响因素与造价因变量间的样本点离散型较大，体现了因素自变量与造价因变量间存在直观的随机性、不确定性和复杂性等典型非线性特点；2）计算图1因素自变量与造价因变量间的线性拟合残差平方和（RSS），分别为12.20和10.91，表明线性拟合精度极低，不具有代表性. 由此，通过直观呈现和数据计算分别明确了城市轨道交通土建工程造价影响因素与造价因变量间存在典型的非线性特征. 相较于传统的定额测算和线性预测模型，非线性智能预测模型能更好地处理此类问题，有利于实现更为准确的造价预测.

1.3 影响因素优化筛选

影响因素的确定要秉持“全”和“精”的理念，既要全面识别能够体现城市轨道交通土建工程造价特殊性和差异性的因素，又要优化精选，尽可能避免对因素的重复考虑. 各因素对造价的影响大小参差，若统统纳入，则所建模型将失去实际意义^[6].

1.3.1 基于数据的影响因素定量筛选

ReliefF是一种因素过滤式定量选择方法，借助相关统计量度量因素重要性，实现对影响因素定量筛选的目的^[22]. ReliefF因素筛选更新见式（1）.

${W}_{h,s}={W}_{h,s-1}^{}-\frac{{\varDelta }_{h}\left({t}_{{\mathrm{a}}},{t}_{{\mathrm{e}}}\right)}{j} {d}_{{\mathrm{ae}}},$

(1)

式中： ${W}_{h,s}$ 为第 $h$ 个因素在第 $s$ 次计算时的权重， ${\varDelta }_{h}\left({t}_{{\mathrm{a}}},{t}_{{\mathrm{e}}}\right)$ 为样本 ${t}_{{\mathrm{a}}}$ 和 ${t}_{{\mathrm{e}}}$ 在第 $h$ 个因素上的归一化差值， ${d}_{{\mathrm{ae}}}$ 为样本 ${t}_{{\mathrm{a}}}$ 和 ${t}_{{\mathrm{e}}}$ 的距离函数， $j$ 为样本数.

基于整理得到的70个完整工程案例土建造价数据，使用ReliefF方法对城市轨道交通土建工程造价14个初始影响因素定量筛选，设定影响因素ReliefF筛选阈值为0.01，低于此阈值的因素不具有代表性. 通过MATLAB编程计算，得到包括地下线长度、高架线长度、车站总数、地下车站数、地上车站数、平均站距、编组、工程环境及地质条件、GDP和CPI在内10个因素的ReliefF值均大于0.01，其余4个因素ReliefF值均小于0.01. 由此，初步提取以上10个因素为城市轨道交通土建工程造价备选关键影响因素.

1.3.2 基于知识的影响因素定性检验

原始资料是未经加工的数据，信息是加工处理后有逻辑的数据，而知识则是用于生产的有意义信息，三者逐层递进. 就城市轨道交通土建工程造价关键影响因素优化筛选而言，基于原始数据的定量筛选可作为基础凭据，但必须结合基于实践知识的定性检验才能确保所选关键影响因素的科学合理性.

针对初步提取的10个备选关键影响因素，结合专家咨询定性分析可知，包括地下线长度、高架线长度、地下车站数、地上车站数、平均站距、编组、工程环境及地质条件、GDP和CPI在内的9个因素均与工程实践知识相符，在实际工程中对城市轨道交通土建工程造价影响效应明显. 而车站总数与地下车站数、地上车站数之间存在重复考虑现象，因此，有必要将其剔除.

综上，采用定量、定性相结合的因素优化筛选方式，最终确定包括地下线长度、高架线长度、地下车站数、地上车站数、平均站距、编组、工程环境及地质条件、GDP和CPI在内的9个因素为城市轨道交通土建工程造价关键影响因素，用于后续研究.

1.4 数据存储

根据土建工程造价关键影响因素分类并量化归纳已获数据，利用案例数据库汇总存储案例资料和造价信息. 在数据存储工具的选择上，Access数据库具备强大的动态数据交换（DDE）和对象联接及嵌入（OLE）特性，可在同一数据表中嵌入位图、音频与Excel文档，并与网络动态数据相联接，建立动态的数据库报表与窗体. 因此，以Microsoft Access平台作为数据库载体，实现城市轨道交通土建工程造价案例数据的科学存储、动态更新与高效分析.

2. 城市轨道交通土建工程造价预测与反演模型

2.1 基于PSO-GWO-ELM的土建工程造价非线性预测

2.1.1 PSO聚类相似案例

粒子群优化（PSO）算法是一种模仿鸟类捕食以求解优化问题的智能算法，特点是通过粒子扰动聚类中心，避免产生局部极值，直到多次扰动后聚类划分不再变动时得到最佳聚类. 由于传统K-means聚类方法对起始阈值有较高依赖且易陷入局部极值，为提高城市轨道交通土建工程造价预测模型的运算准确性，采用PSO算法优化聚类过程. 粒子根据式（2）与式（3）迭代寻优^[23].

${v}_{k,q + 1}=u{v}_{k,q} + {c}_{1}{r}_{1}\left({p}_{k,q}-{{\textit{z}}}_{k,q}\right) + {c}_{2}{r}_{2}\left({\delta _q}-{{\textit{z}}}_{k,q}\right)，$

(2)

${{\textit{z}}}_{k,q + 1}={{\textit{z}}}_{k,q} + {v}_{k,q + 1}，$

(3)

式中： ${v}_{k,q + 1}$ 、 ${{\textit{z}}}_{k,q + 1}$ 分别为第 $q + 1$ 次迭代运算时第 $k$ 个粒子的速度与位置， $u$ 为原速度下的权值系数， ${c}_{1}$ 、 ${c}_{2}$ 分别为个体学习因子和群体学习因子， ${r}_{1}$ 、 ${r}_{2}$ 为区间[0, 1]内的随机数， ${p}_{k,q}$ 为经过 $q$ 次迭代后第 $k$ 个粒子的最佳位置， ${\delta _q}$ 为群体在经过 $q$ 次迭代后的历史最佳位置.

2.1.2 极限学习机

极限学习机是一种非线性单隐含层前馈神经网络算法. 已有研究表明，ELM在学习速率和泛化能力上通常表现出明显优于SVM模型与BPNN模型的性能效果. 将ELM用于城市轨道交通土建工程造价预测的核心原理如下：

对于样本（ $\boldsymbol{x}_e,\boldsymbol{y}_e$ ），其中：特征 $\boldsymbol{x}_e=\left(x_{e1},x_{e2},\cdots, x_{en}\right)^{\mathrm{T}}\in\mathbf{R}^n$ ，标签 $\boldsymbol{y}_e=\left(y_{e1},y_{e2},\cdots,y_{em}\right)^{\mathrm{T}}\in\mathbf{R}^m$ ， $n$ 和 $m$ 分别为网络输入和输出层节点数， ${\mathbf{R}}^{n}$ 和 ${\mathbf{R}}^{m}$ 分别为 $n$ 维实数集和 $m$ 维实数集. 网络输出如式（4）所示.

${f}_{L}\left({\boldsymbol{x}}_{e}\right)=\sum\nolimits _{i=1}^{L}{\boldsymbol{\beta }}_{i}g\left({\boldsymbol{w}}_{i}{\text{•}} {\boldsymbol{x}}_{e} + {{b}}_{i}\right),$

(4)

式中： $L$ 为隐含层节点数； $g$ (·)为激励函数； ${\boldsymbol{w}}_{i}= {\left({w}_{i1},{w}_{i2}, \cdots ,{w}_{in}\right)}^{{\mathrm{T}}}$ ，为输入层到第i个隐含层节点的输入权重矩阵； ${{b}}_{i}$ 为第 $i$ 个隐含层节点阈值； $\;{\boldsymbol{\beta }}_{i}= {\left({\beta }_{i1},{\beta }_{i2}, \cdots ,{\beta }_{im}\right)}^{{\mathrm{T}}}$ ，为第i个隐含层节点输出权值.

训练样本数等于隐含层神经元数时， $\;{\boldsymbol{\beta }}_{i}$ 、 ${\boldsymbol{w}}_{i}$ 和 ${{b}}_{i}$ 间关系见式（5）.

${f}_{L}\left({\boldsymbol{x}}_{e}\right)=\sum\nolimits _{i=1}^{L}{\boldsymbol{\beta }}_{i}g\left({\boldsymbol{w}}_{i}{\text{•}} {\boldsymbol{x}}_{e} + {{b}}_{i}\right){=\boldsymbol{y}}_{e}.$

(5)

由式（5）简化得式（6）.

$\boldsymbol{H}\boldsymbol{\beta }=\boldsymbol{Y},$

(6)

式中： $\boldsymbol{H}$ 为隐含层输出矩阵， $\;\boldsymbol{\beta }$ 为节点输出权值， $\boldsymbol{Y}$ 为目标值期望输出矩阵.

将式（6）转化为损失函数，为逼近目标值，即求解损失函数最小化问题，得式（7）.

${\mathrm{min}}\|\boldsymbol{H}\boldsymbol{\beta }-\boldsymbol{Y}\|.$

(7)

通过求解最优初始权值（w）、阈值（b）和 $\;\boldsymbol{\beta }$ ，使得损失函数最小，由于 $\boldsymbol{w}$ 、 ${b}$ 为随机给定，而目标值 $\boldsymbol{Y}$ 已知，因此 $\; \boldsymbol{\beta }$ 也被唯一确定，见式（8）.

$\widetilde{\boldsymbol{\beta }}={\boldsymbol{H}}^{ + }\boldsymbol{Y},$

(8)

式中： $\; \widetilde{\boldsymbol{\beta }}$ 为 $\; \boldsymbol{\beta }$ 的唯一确定解， ${\boldsymbol{H}}^{ + }$ 为隐含层输出矩阵 $\boldsymbol{H}$ 的摩尔−彭洛斯广义逆.

2.1.3 改进ELM造价预测模型

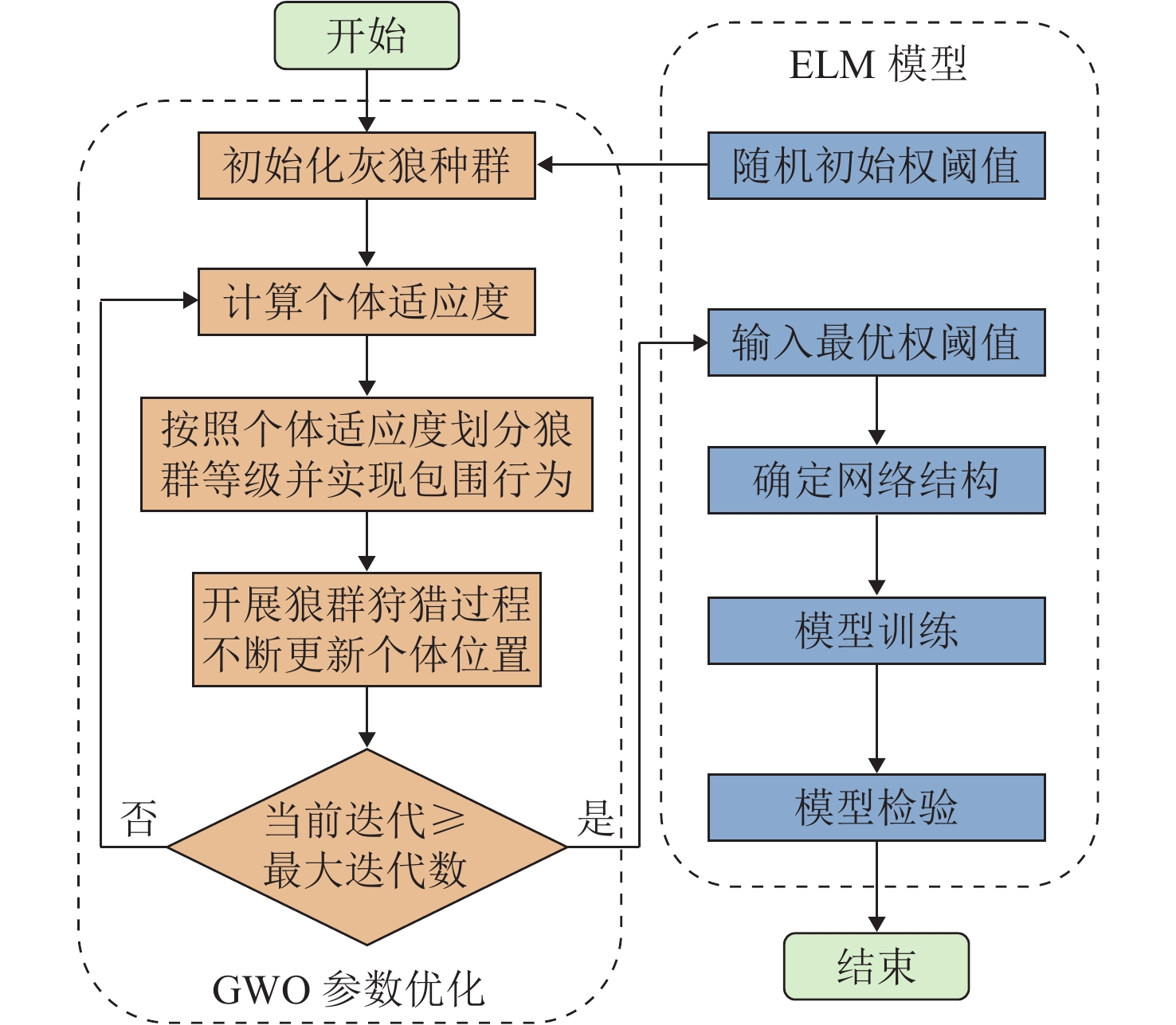
尽管ELM用于城市轨道交通土建工程造价预测训练用时短、预测精度高，但其综合性能取决于w和b，由于w、b具有随机性，使得单一ELM模型的稳定性及精度方面都存在较大影响，在实际应用中易陷入局部最优或出现过拟合现象. 因此，引入GWO算法对ELM模型的初始权阈值寻优，实现最佳收敛，以达到获得全局最优解的效果，提升预测精确性. GWO-ELM造价预测模型的建构和优化流程如图2所示.

图 2 模型建构与优化流程

Figure 2. Model construction and optimization process

下载: 全尺寸图片幻灯片

2.1.4 模型性能评判

采用平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE） 3项参数评判城市轨道交通土建工程造价预测模型的预测效果^[24]. 当综合3项评判参数难以直观得出模型误差比较结果时，以MAPE作为主要评判标准，当MAPE<10%时，可被归类为优秀的预测；在 [10%, 20%）时，可提供良好的预测；在 [20%, 50%）时，为可接受的预测；超过50%，则为不准确的预测^[9].

2.2 基于Sobol’ 与Curve Fitting的土建工程造价解释性反演

2.2.1 Sobol’ 全局敏感性分析

Sobol’ 是一种基于方差的蒙特卡罗法，采用蒙特卡罗抽样技术和模型分解思想，通过计算模型各输入对输出方差的影响，评估因素全局敏感性，从而确定模型的重点调节因素^[15]. 采用Sobol’ 全局敏感性分析方法可计算各影响因素的总敏感度. 根据总敏感度排序，找出对土建工程造价影响最大的因素，在方案优化过程中优先考虑调节该因素，有助于提高方案的经济效果.

2.2.2 影响因素与工程造价作用关系探索性拟合分析

工程造价影响因素的总敏感度反映了不同因素对造价直接影响程度的大小，但无法量化说明各因素在造价预测模型中的作用机理. 为深入探究工程造价影响因素与造价预测值的定量映射关系，得到更为明晰的因素与造价间直观作用形式，采用Curve Fitting方法对工程造价预测值与其影响因素间的关系进行具象化探索，根据系数（R²）判定拟合效果，R²∈[0, 1]，且R²值越大说明函数拟合效果越优，即自变量通过此函数作用形式对基于机器学习智能算法的造价预测模型所得因变量的解释能力越强，越有助于探究人工智能模型的“黑箱”作用机制，提升决策信服力^[25].

3. 实例分析

3.1 工程概况

成都市轨道交通10号线是成都市重要的枢纽连接线，一期工程全长10.94 km，全地下敷设，设站6座，平均站距2.19 km，6A编组，工程所处环境与地质条件复杂. 将本文提出的造价预测与反演模型用于对该工程土建造价的预测与反分析.

3.2 土建工程造价非线性预测

3.2.1 样本选取与参数设置

根据待建工程土建造价影响因素信息，基于案例数据库，以9个关键影响因素作为输入，通过MATLAB编程实现PSO聚类. 根据样本数量确定聚类数目为2，聚类过程中待建工程被归为第Ⅱ类，得到与待建工程具有较高相似度的案例38个. 随机选取32个样本组成训练集，其余作为检验集.

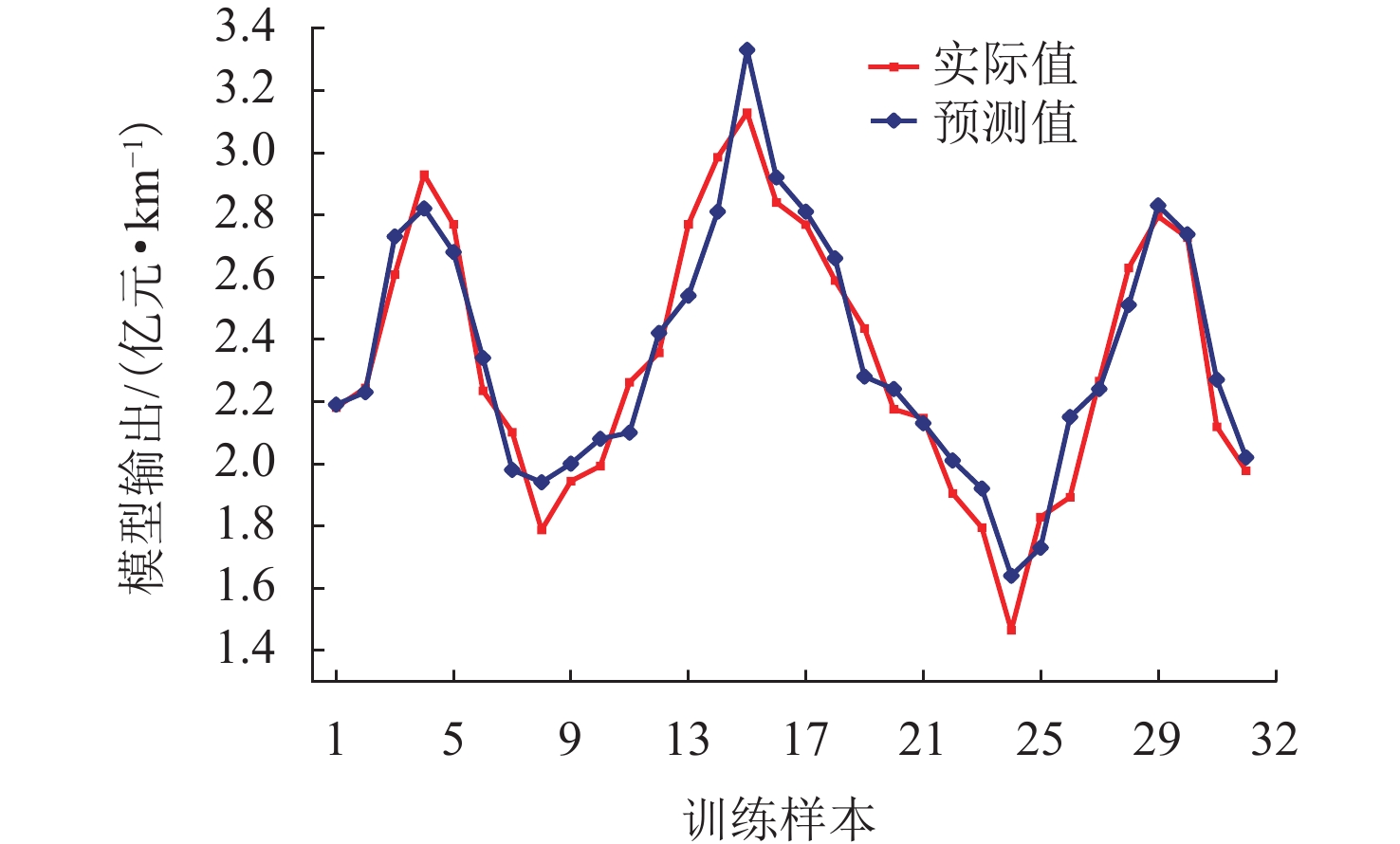
设置ELM模型输入节点数为9个；输出节点数为1个；隐含层节点数为32个；GWO算法初始种群数为10个；最大迭代次数为100次. GWO-ELM造价预测模型训练集预测值与实际值对比如图3.

图 3 训练集对比

Figure 3. Comparison of training sets

下载: 全尺寸图片幻灯片

3.2.2 GWO-ELM模型预测效果

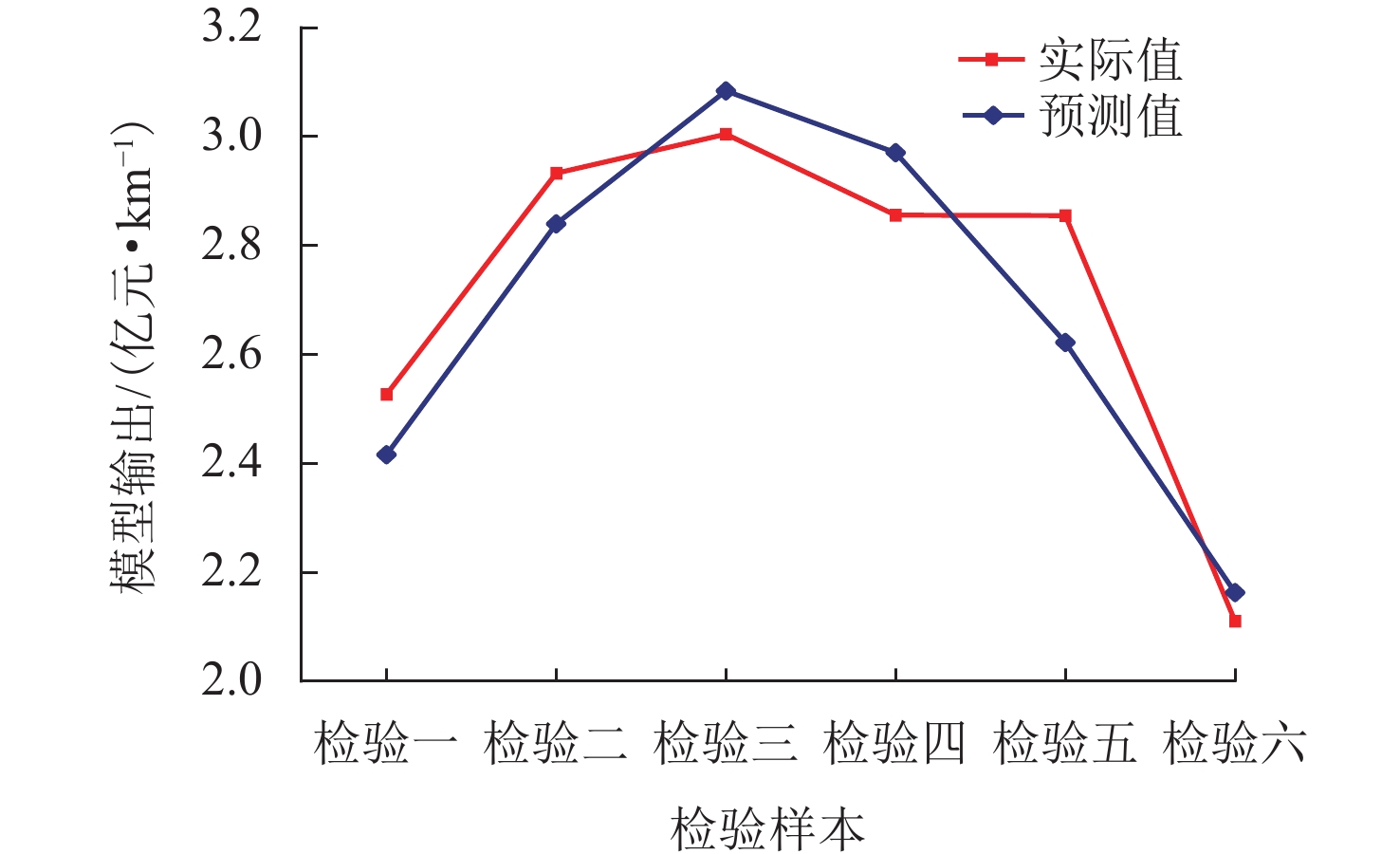
训练完成后，以6个检验样本检验GWO-ELM造价预测模型的预测效果. 检验样本不参与原模型训练，对于预测模型是全新的数据，能更好地验证模型的预测效果和泛化能力. GWO-ELM造价预测模型检验集预测值与实际值对比如图4所示.

图 4 检验集对比

Figure 4. Comparison of test sets

下载: 全尺寸图片幻灯片

由图4可知：模型检验集预测值与实际值对比曲线拟合趋势相近，说明检验效果较好；就模型性能评判参数而言，模型检验集预测值与实际值对比的MAE为0.113 9，RMSE为0.127 4，MAPE为4.14%，可被归类为优秀的预测^[9]，且满足实际工程精度要求.

3.2.3 模型预测效果控制变量分析讨论

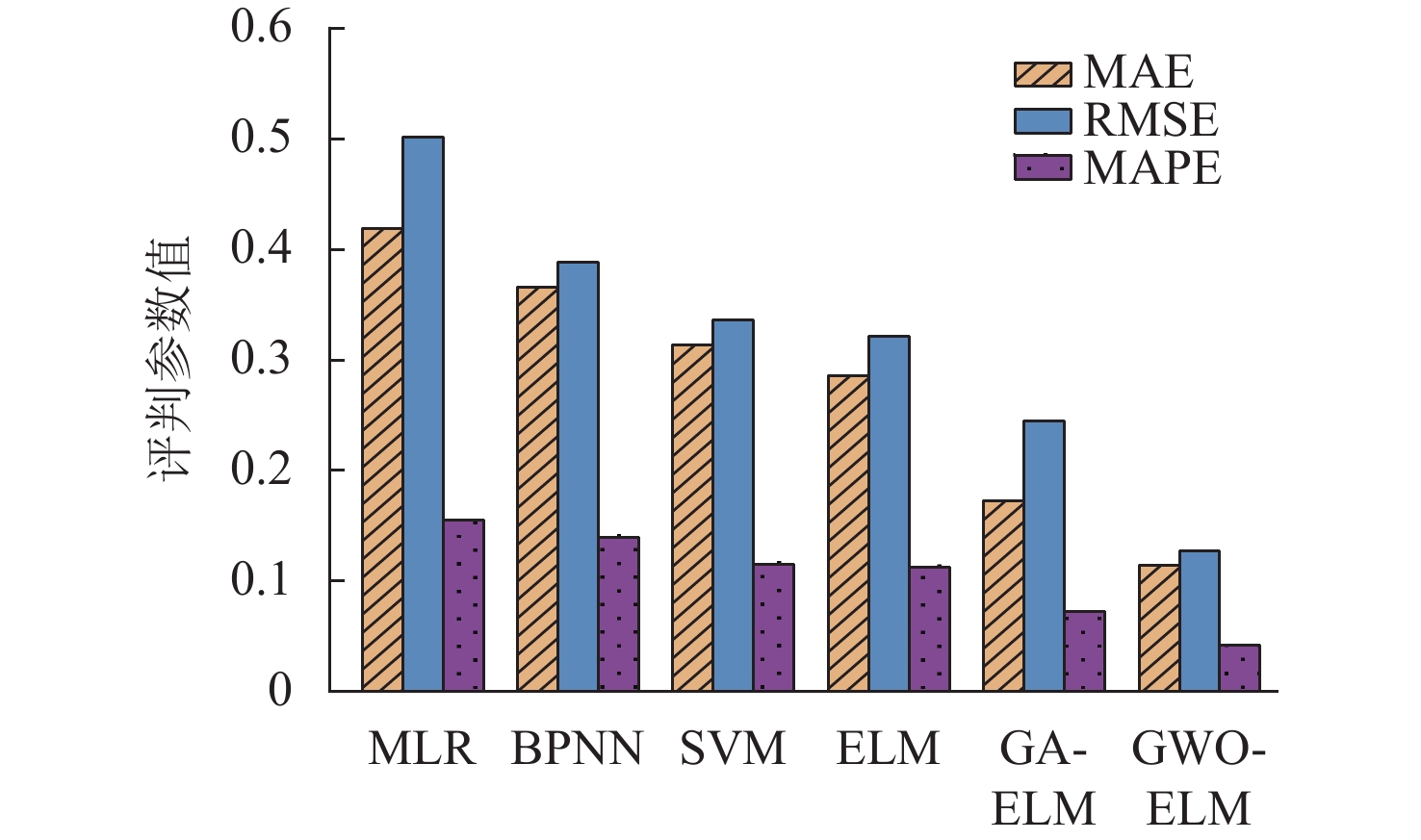
为进一步对比分析城市轨道交通土建工程造价GWO-ELM预测模型性能，在相同因素指标与数据样本下，按相同比例分别训练MLR模型、BPNN模型、SVM模型、ELM模型、GA-ELM模型和GWO-ELM模型，在相同检验样本下对比不同模型性能，如图5所示.

图 5 不同模型相同环境下性能对比

Figure 5. Performance comparison of different models in the same environment

下载: 全尺寸图片幻灯片

由图5可知，在相同因素指标与数据样本下，对于不同模型存在：非线性预测模型预测效果优于线性预测模型；建立的GWO-ELM造价预测模型预测效果优于已有的GA-ELM模型，优于单一的ELM模型、SVM模型和BPNN预测模型.

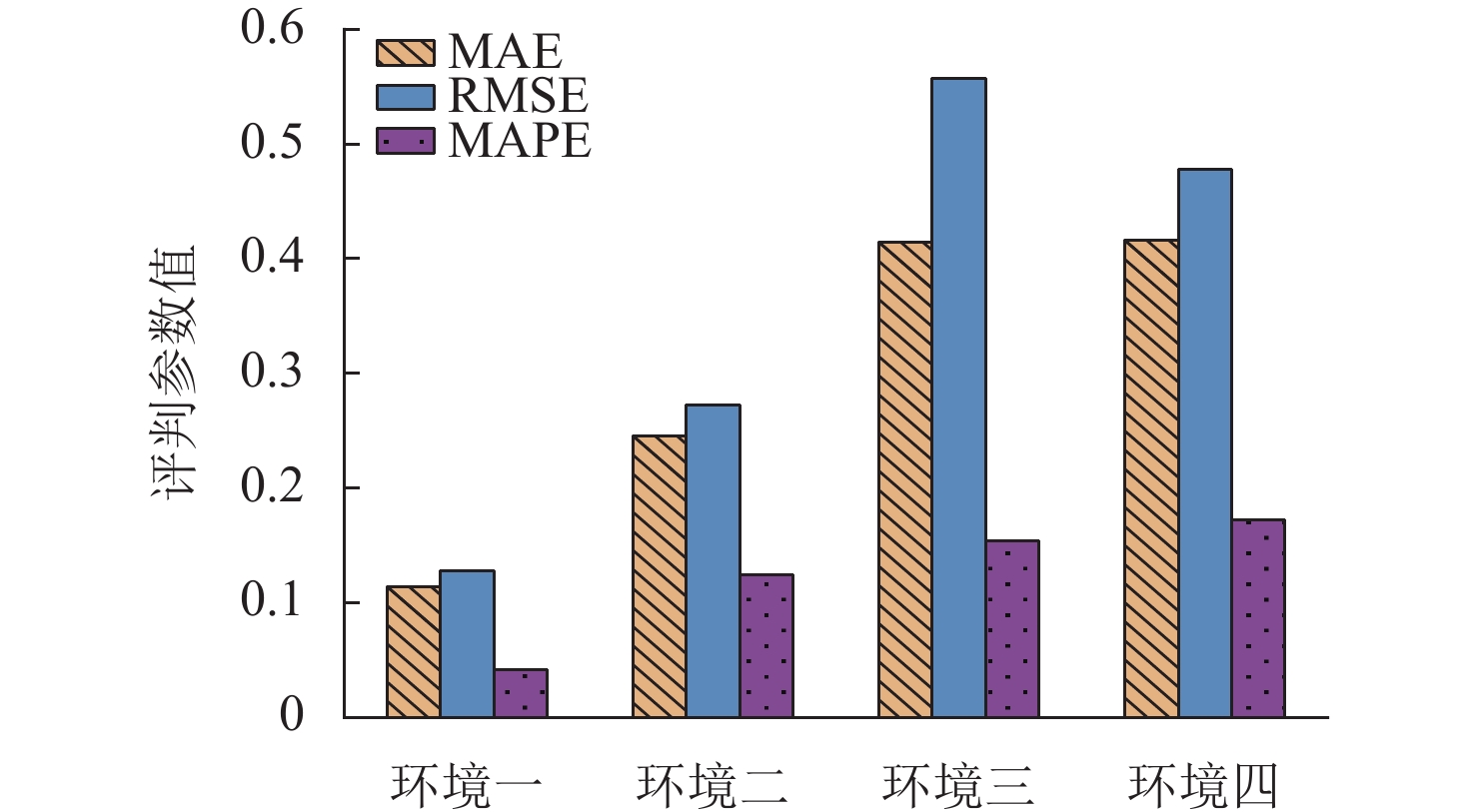
对于相同模型下不同集成环境展开对比讨论，包括相同模型下因素优化筛选与否和相似案例聚类与否4种环境（环境一，优化因素且案例聚类；环境二，优化因素无案例聚类；环境三，原始因素且案例聚类；环境四，原始因素无案例聚类），评判参数计算结果见图6.

图 6 相同模型不同环境下性能对比

Figure 6. Performance comparison of same model in different environments

下载: 全尺寸图片幻灯片

由图6可知：在相同模型下，本文优化后的9个影响因素结合相似案例聚类后的GWO-ELM模型预测效果优于仅采用优化后的9个影响因素模型预测效果，此2类集成模式优于仅采用相似案例聚类的模型预测效果，且共同优于完全不采用因素优化和相似案例聚类的模型预测效果. 有效证明了优化因素指标与聚类相似案例对于开展更为准确的造价预测研究的必要性.

综上认为，本文建立的GWO-ELM造价预测模型与对比实验中其他模型相比预测性能更佳的根本原因在于：剔除了多余或干扰的影响因素，聚类得到了高相似度历史案例且采用了更为科学合理的优化方法. 将已通过初始训练和检验评判的城市轨道交通土建工程造价GWO-ELM预测模型用于待建工程土建造价预测，得到成都市轨道交通10号线1期土建工程造价预测结果为1.874 9亿元/km.

项目完工时，该城市轨道交通项目土建工程分项实际造价额为1.919 2亿元/km，本文采用GWO-ELM方法预测得到的土建工程造价与之相比，误差<5%，模型可信度得到了实际验证.

3.3 城市轨道交通土建工程造价影响因素全局敏感性分析

基于GWO-ELM造价预测模型，进行Sobol’ 全局敏感性分析. 选取模型输入的影响因素地下线长度、高架线长度、地下车站数、地上车站数、平均站距、编组、工程环境及地质条件、GDP和CPI作为自变量，模型输出的土建工程造价作为因变量，采用Sobol’ 法求解各因素总敏感度.

根据影响因素统计分布限定采样范围，运用Python编程实现Sobol’ 全局敏感性分析，分析结果如表1所示.

表 1 全局敏感性分析结果

Table 1. Global sensitivity analysis results

影响因素	地下线长度	高架线长度	地下车站数	地上车站数	平均站距	编组	工程环境及地质条件	国内生产总值	居民消费价格指数
总敏感度	0.653 6	0.060 3	0.223 6	0.012 4	0.008 3	0.019 3	0.000 8	0.003 1	0.018 2

下载: 导出CSV

| 显示表格

城市轨道交通土建工程造价影响因素的总敏感度从大到小排序为地下线长度、地下车站数、高架线长度、编组、居民消费价格指数、地上车站数、平均站距、国内生产总值、工程环境及地质条件. 其中：地下线长度、地下车站数的总敏感度明显高于其他因素. 当开展城市轨道交通建设项目方案优化时，优先考虑调节此2项因素指标，能更好地提升城市轨道交通建设方案的经济效果.

对于工程环境及地质条件总敏感度最低的情况，经分析可知：就城市轨道交通而言，各项因素对土建造价的影响路径各异，既存在直接作用（如地下线长度、高架线长度、地下车站数等），又存在间接作用（如工程环境及地质条件等）. 在实际工程中，工程环境及地质条件是确定线路敷设方式、选择车站类型等的前提，但由于工程环境及地质条件是通过影响各类敷设长度、各类车站数等因素再在造价上得以体现的. 因此，在基于数据的全局敏感性分析中所得该因素敏感性程度更低，但整体影响程度已通过直接影响因素作用于造价，使得最终的土建工程造价预测结果准确性不受影响.

3.4 影响因素与土建造价作用关系分析

为探究城市轨道交通土建工程造价影响因素与土建造价的相关性，首先采用线性拟合方法，拟合土建造价模型预测值与因素间的作用关系. 考虑到智能模型数据驱动的特点，计算原始数据中土建造价与影响因素间的Pearson相关性，并同线性拟合函数式中影响因素与土建造价预测值之间的相关性进行对比，拟合与对比结果见表2.

表 2 线性拟合函数式及其对比

Table 2. Linear fitting functions and their comparison

影响因素	拟合函数式	拟合函数式影响因素与土建造价相关性	原始数据中影响因素与土建造价相关性	对比结果
地下线长度	f(x)=0.007 1x + 2.179 0	正相关	0.203 1 （正相关）	一致
高架线长度	f(x)=−0.059 2x + 2.467 0	负相关	−0.498 8 （负相关）	一致
地下车站数	f(x)=0.014 0x + 2.114 0	正相关	0.255 4 （正相关）	一致
地上车站数	f(x)=−0.101 4x + 2.455 0	负相关	−0.443 6 （负相关）	一致
平均站距	f(x)=−0.073 3x + 2.491 0	负相关	−0.167 1 （负相关）	一致
编组	f(x)=0.080 2x + 1.781 0	正相关	0.266 0 （正相关）	一致
工程环境及地质条件	f(x)=0.065 4x + 2.205 0	正相关	0.127 0 （正相关）	一致
国内生产总值	f(x)=0.000 1x + 2.202 0	正相关	0.253 5 （正相关）	一致
居民消费价格指数	f(x)=0.039 1x − 1.636 0	正相关	0.138 8 （正相关）	一致

下载: 导出CSV

| 显示表格

采用线性拟合的主要目的是探究影响因素与土建造价间的相关性及其在预测模型和原始数据中的异同，但影响因素与土建造价间多为非线性映射^[2]. 为改善拟合效果，得到影响因素与土建造价间更为准确的作用关系，采用多种拟合形式对土建造价预测值与影响因素间的关系进行表征，并通过对比不同拟合形式下最佳方法的可决系数得到各因素具体最优反演拟合函数式，见表3.

表 3 各因素最优拟合函数式

Table 3. Optimal fitting functions of different factors

影响因素	拟合函数式	R²
地下线长度	f(x)=2.317 0 − 0.216 0cos 0.142 6x − 0.113 9sin 0.142 6x + 0.153 4cos 0.285 2x + 0.048 5 × sin 0.285 2x + 0.247 2cos 0.427 8x + 0.125 4sin 0.427 8x + 0.007 9cos 0.570 4x − 0.085 2 × sin 0.570 4x + 0.214 8cos 0.713 0x + 0.007 5sin 0.713 0x − 0.042 0cos 0.855 6x + 0.009 1 × sin 0.855 6x + 0.025 3cos 0.998 2x − 0.164 8sin 0.998 2x − 0.089 6cos 1.140 8x + 0.066 4sin 1.140 8x	0.645 2
高架线长度	f(x)=− 6 409 + 10⁴cos 0.998 9x + 8 473sin 0.998 9x − 2 120cos 1.997 8x − 12 500sin 1.997 8x − 5 779cos 2.996 7x + 8 477sin 2.996 7x + 7 112cos 3.995 6x − 720.100 0sin 3.995 6x − 3 340cos 4.994 5x − 2 932sin 4.994 5x + 463.200 0cos 5.993 4x + 1 899sin 5.993 4x + 74.800 0cos 6.992 3x − 395.100 0sin 6.992 3x	0.488 5
地下车站数	f(x)=− 3.368 0 10⁹ + 5.946 0 10⁹cos 0.046 2x + 2.665 0 10⁹sin 0.046 2x − 3.327 0 10⁹cos 0.092 4x − 4.480 0 10⁹sin 0.092 4x + 1.306 0 10⁸cos 0.138 6x + 3.879 0 10⁹sin 0.138 6x + 1.234 0 10⁹cos 0.184 8x − 1.667 0 10⁹sin 0.184 8x − 7.959 0 10⁸cos 0.231 0x + 1.796 0 10⁸sin 0.231 0x + 1.940 0 10⁸cos 0.277 2x + 1.099 0 10⁸sin 0.277 2x − 1.126 0 10⁷cos 0.323 4x − 3.620 0 10⁷sin 0.323 4x − 1.356 0 10⁶cos 0.369 6x + 2.710 0 10⁶sin 0.369 6x	0.486 8
地上车站数	f(x)=0.007 9x⁵ − 0.139 2x⁴ + 0.823 5x³ − 1.875 0x² + 1.143 0x + 2.530 0	0.337 0
平均站距	f(x)=3.088 0 10¹¹ + 1.954 0 10¹⁰cos 0.811 8x − 5.568 0 10¹¹sin 0.811 8x − 4.067 0 10¹¹cos 1.623 6x − 2.742 0 10¹⁰sin 1.623 6x − 2.242 0 10¹⁰cos 2.435 4x + 2.381 0 10¹¹sin 2.435 4x + 1.096 0 10¹¹cos 3.247 2x + 1.231 0 10¹⁰sin 3.247 2x + 4.558 0 10⁹cos 4.059 0x − 3.827 0 10¹⁰sin 4.059 0x − 9.559 0 10⁹cos 4.870 8x − 1.067 0 10⁹sin 4.870 8x − 1.333 0 10⁸cos 5.682 6x + 1.521 0 10⁹sin 5.682 6x + 1.157 0 10⁸cos 6.494 4x + 5.302 0 10⁶sin 6.494 4x	0.579 1
编组	f(x)=− 0.008 9x⁴ + 0.226 1x³ − 2.071 0x² + 8.206 0x-9.692 0	0.089 3
工程环境及地质条件	f(x)=2.320 0 − 0.266 6cos 1.571 0x − 0.118 8sin 1.571 0x	0.068 9
国内生产总值	f(x)=1.751 0 + 0.189 1cos 2.361 0x − 1.345 0sin 2.361 0x + 1.109 0cos 4.722 0x + 0.535 3sin 4.722 0x − 1.252 0cos 7.083 0x + 0.429 1sin 7.083 0x + 1.131 0cos 9.444 0x − 0.997 2sin 9.444 0x − 0.349 1cos 11.805 0x + 1.747 0sin 11.805 0x − 0.817 2cos 14.166 0x − 1.829 0sin 14.166 0x + 1.257 0cos 16.527 0x + 0.705 4sin 16.527 0x − 0.434 9cos 18.888 0x + 0.305 6sin 18.888 0x	0.526 1
居民消费价格指数	f(x)=2.185 0 + 0.058 3cos 5.835 0x − 0.145 6sin 5.835 0x − 0.203 1cos 11.670 0x + 0.237 2sin 11.670 0x + 0.050 6cos 17.505 0x + 0.138 8sin 17.505 0x + 0.106 0cos 23.340 0x − 0.051 0sin 23.340 0x + 0.179 2cos 29.175 0x − 0.239 2sin 29.175 0x − 0.027 0cos 35.010 0x + 0.246 6sin 35.010 0x + 0.021 3cos 40.845 0x − 0.346 3sin 40.845 0x + 0.231 5cos 46.680 0x − 0.089 9sin 46.680 0x	0.486 7

下载: 导出CSV

| 显示表格

对比线性拟合函数式与原始数据发现：预测模型中影响因素与土建造价间的相关性同原始数据中相关性一致，高架线长度、地上车站数和平均站距与土建造价间为负相关，其余均为正相关. 对于城市轨道交通项目而言，在同等条件下，高架线造价远低于地下线、地上车站造价远低于地下车站. 如南京地铁造价数据显示：以高架线为主的城市轨道交通建设项目平均造价为2.23亿元/km，以地下线为主的城市轨道交通建设项目平均造价达6.38亿元/km；地上车站造价约为2 000万元/座，而标准两层明挖地下车站造价则高达9 000万元/座^[17]. 由此可知：在总里程或总设站不变的情况下，合理扩大高架线长度对地下线长度或地上车站数对地下车站数的比例，有助于降低整体造价；此外，平均站距小是工程造价高的重要原因之一，同等条件下平均站距越大则所需建造的车站数量越少，对应造价额越低. 因此，设计单位优化设计方案时，在满足其他条件的情况下，优先考虑采用高架线路长或地上车站多且平均站距大的线路方案，有助于实现控制造价的目的.

对比非线性拟合函数式与可决系数发现：编组和工程环境及地质条件两因素最优拟合函数式的可决系数小于0.10，机理解释能力不强. 结合数据处理方式分析其原因可知：在原始案例中此2项因素均为分类变量，其余为连续变量，连续函数对于分类变量的拟合效果难以控制，因此导致R²值低于预期. 为解决这一问题，后续可采用分段函数拟合或因素值标准化变换的方法开展深入研究. 对于其余因素，本文采用Curve Fitting方法提高了城市轨道交通土建工程造价机器学习智能预测模型作用机理“黑箱”效应33.70%～64.52%的解释性，提升了决策信服力. 为后续开展更为精确的城市轨道交通土建工程造价人工智能预测模型的可解释性研究提供了一种思路借鉴.

4. 结　论

城市轨道交通土建工程造价与其影响因素之间具有典型的非线性特征，而对城市轨道交通土建工程造价的解释性预测是一项复杂问题. 本文构建了基于特征选择与知识判断方法、粒子群优化聚类、灰狼优化算法、极限学习机、Sobol’ 全局敏感性分析和Curve Fitting分析的城市轨道交通土建工程造价预测与反演模型，并结合实际工程开展了实例分析，得出以下结论：

1）通过案例分析与文献编码初步得出影响城市轨道交通土建工程造价的14个因素，采用ReliefF与知识判断方法剔除了多余或干扰项，优化提取得到9个关键影响因素，建立了城市轨道交通工程案例数据库. 在保证模型预测精度的同时减少了冗余数据处理. 对知识体系的另一个贡献是，在城市轨道交通土建工程造价预测中考虑了宏观经济因素和经济因素影响的时滞性. 可为同类研究提供因素建议与数据支持.

2）构建了土建工程造价GWO-ELM非线性预测模型. 通过GWO算法优化ELM得到最优权阈值，有效克服ELM易陷入局部极值的问题，结合PSO聚类算法提取相似案例，提升预测准确度. 设计了“相同环境下的不同模型”和“不同环境下的相同模型”对比实验. 一方面，证明了本文所建模型的优越性；另一方面，得到了非线性造价预测模型预测效果优于线性测算模型和同时采用因素优化与案例聚类方法所得预测效果更佳的对比规律.

3）将Sobol’ 全局敏感性分析和Curve Fitting分析用于城市轨道交通土建工程造价的解释性反演. 全局敏感性分析结果表明：地下线长度和地下车站数的总敏感度明显高于其他因素，可作为方案优化的重点调节因素；采用Curve Fitting分析得到了不同因素与土建造价间的显性作用关系，实现了机器学习智能预测模型的作用机理解构.

4）后续可在此研究基础上，深入挖掘城市轨道交通土建工程造价各级各类影响因素间的复杂效应与作用机理；探究解释能力更强的城市轨道交通土建工程造价智能预测方法，提升城市轨道交通土建工程造价智能预测模型的可解释性和决策信服力.

致谢：河北省教育厅在读研究生创新能力培养资助项目(CXZZBS2024147)、中铁建昆仑地铁投资建设管理有限公司开发项目(KLTZ-KX01-2020)、河北大地园林有限公司开发项目(横20220209).

图 1 磁浮时滞模型

Figure 1. Time lag model of magnetic levitation

下载: 全尺寸图片幻灯片

图 2 Routh-Hurwitz稳定性范围

Figure 2. Routh-Hurwitz stability region

下载: 全尺寸图片幻灯片

图 3 无时滞稳定性验证

Figure 3. Stability verification without time lag

下载: 全尺寸图片幻灯片

图 4 控制器时滞临界值与反馈控制参数的关系

Figure 4. Relationships between critical value of controller time lag and feedback control parameters

下载: 全尺寸图片幻灯片

图 5 固有频率与反馈控制参数的关系

Figure 5. Relationships between natural frequency and feedback control parameters

下载: 全尺寸图片幻灯片

图 6 控制器时滞临界值与系统参数的关系

Figure 6. Relationships between critical value of controller time lag and system parameters

下载: 全尺寸图片幻灯片

图 7 固有频率与系统控制参数的关系

Figure 7. Relationships between natural frequency and system parameters

下载: 全尺寸图片幻灯片

图 8 τ=0.000 900 s，τ<τ₀时的系统响应

Figure 8. System response with time lag τ=0.000 900 s, τ<τ₀

下载: 全尺寸图片幻灯片

图 9 τ=0.001 000 s，τ>τ₀时的系统响应

Figure 9. System response with time lag τ=0.001 000 s, τ>τ₀

下载: 全尺寸图片幻灯片

图 10 τ=0.000 986 s，τ>τ₀时的系统响应

Figure 10. System response with time lag τ=0.000 986 s, τ>τ₀

下载: 全尺寸图片幻灯片

图 11 UM模型建立示意

Figure 11. UM model establishment

下载: 全尺寸图片幻灯片

图 12 内部控制模块示意

Figure 12. Internal control module

下载: 全尺寸图片幻灯片

图 13 τ=0.000 900 s，τ <τ₀时的系统响应

Figure 13. System response with time lag τ=0.000 900 s, τ<τ₀

下载: 全尺寸图片幻灯片

图 14 τ=0.001 000 s，τ>τ₀时的系统响应

Figure 14. System response with time lag τ=0.001 000 s, τ>τ₀

下载: 全尺寸图片幻灯片

参考文献(39)

[1]	张舒,徐鉴. 时滞耦合系统非线性动力学的研究进展[J]. 力学学报,2017,49(3): 565-587. ZHANG Shu, XU Jian. Review on nonlinear dynamics in systems with coulpling delays[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 565-587.
[2]	李帅,周继磊,任传波,等. 时变参数时滞减振控制研究[J]. 力学学报,2018,50(1): 99-108. LI Shuai, ZHOU Jilei, REN Chuanbo, et al. The research of time delay vibration control with time-varying parameters[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(1): 99-108.
[3]	王在华,胡海岩. 时滞动力系统的稳定性与分岔:从理论走向应用[J]. 力学进展,2013,43(1): 3-20. WANG Zaihua, HU Haiyan. Stability and bifurcation of delayed dynamic systems: from theory to application[J]. Advances in Mechanics, 2013, 43(1): 3-20.
[4]	公徐路,许鹏飞. 含时滞反馈与涨落质量的记忆阻尼系统的随机共振[J]. 力学学报,2018,50(4): 880-889. GONG Xulu, XU Pengfei. Stochastic resonance of a memorial-damped system with time delay feedback and fluctuating mass[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(4): 880-889.
[5]	TAFFO G I K, SIEWE M S, TCHAWOUA C. Stability switches and bifurcation in a two-degrees-of-freedom nonlinear quarter-car with small time-delayed feedback control[J]. Chaos, Solitons & Fractals, 2016, 87(1): 226-239.
[6]	马卫华,胡俊雄,李铁,等. EMS型中低速磁浮列车悬浮架技术研究综述[J]. 西南交通大学学报,2023,58(4): 20-733. MA Weihua, HU Junxiong, LI Tie, et al. Technologies research review of electro-magnetic suspension medium-low-speed maglev train levitation frame[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 20-733.
[7]	LEE H W, KIM K C, LEE J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925. doi: 10.1109/TMAG.2006.875842
[8]	刘士苋,王磊,王路忠,等. 电动悬浮列车及车载超导磁体研究综述[J]. 西南交通大学学报,2023,58(4): 734-753. LIU Shixian, WANG Lei, WANG Luzhong, et al. Review on electrodynamic suspension trains and on-board superconducting magnets[J]. Journal of Southwest Jiaotong University, 2023, 58(4): 734-753.
[9]	ZHANG L L, HUANG L H, ZHANG Z Z. Stability and Hopf bifurcation of the maglev system with delayed position and speed feedback control[J]. Nonlinear Dynamics, 2009, 57(1): 197-207.
[10]	YAU J D. Response of a maglev vehicle moving on a two-span flexible guideway[J]. Journal of Mechanics, 2010, 26(1): 95-103. doi: 10.1017/S1727719100003762
[11]	ZHANG Z Z, ZHANG L L. Hopf bifurcation of time-delayed feedback control for maglev system with flexible guideway[J]. Applied Mathematics and Computation, 2013, 219(11): 6106-6112. doi: 10.1016/j.amc.2012.12.045
[12]	王洪坡. EMS型低速磁浮列车/轨道系统的动力相互作用问题研究[D]. 长沙:国防科学技术大学,2007.
[13]	翟婉明,赵春发. 磁浮车辆/轨道系统动力学(Ⅰ)——磁/轨相互作用及稳定性[J]. 机械工程学报,2005,41(7): 1-10. doi: 10.3901/JME.2005.07.001 ZHAI Wanming, ZHAO Chunfa. Dynamics of maglev vehicle/ guideway systems(I)—Magnet/rail interaction and system stability[J]. Journal of Mechanical Engineering, 2005, 41(7): 1-10. doi: 10.3901/JME.2005.07.001
[14]	DONG H, ZENG J, XIE J H, et al. Bifurcation\instability forms of high speed railway vehicles[J]. Science China Technological Sciences, 2013, 56(7): 1685-1696. doi: 10.1007/s11431-013-5254-x
[15]	苏红建. 基于车路耦合磁悬浮列车非线性振动控制研究[D]. 淄博:山东理工大学,2022.
[16]	XU J Q, CHEN C, GAO D G, et al. Nonlinear dynamic analysis on maglev train system with flexible guideway and double time-delay feedback control[J]. Journal of Vibroengineering, 2017, 19(8): 6346-6362. doi: 10.21595/jve.2017.18970
[17]	陈晓昊,马卫华. 控制器时滞对磁浮系统稳定性影响分析[J]. 机车电传动,2019(2): 139-143,147. CHEN Xiaohao, MA Weihua. Analysis on the effect of controller time delay on the stability of maglev system[J]. Electric Drive for Locomotives, 2019(2): 139-143,147.
[18]	LI J H, LI J, ZHOU D F, et al. Self-excited vibration problems of maglev vehicle-bridge interaction system[J]. Journal of Central South University, 2014, 21(11): 4184-4192. doi: 10.1007/s11771-014-2414-5
[19]	王洪坡,李杰. 一类非自治位置时滞反馈控制系统的亚谐共振响应[J]. 物理学报,2007,56(5): 2504-2516. doi: 10.7498/aps.56.2504 WANG Hongpo, LI Jie. Sub-harmonic resonances of the non-autonomous system with delayed position feedback control[J]. Acta Physica Sinica, 2007, 56(5): 2504-2516. doi: 10.7498/aps.56.2504
[20]	WANG H P, LI J, ZHANG K. Stability and Hopf bifurcation of the maglev system with delayed speed feedback control[J]. Acta Automatica Sinica, 2007, 33(8): 829-834. doi: 10.1360/aas-007-0829
[21]	WANG H P, LI J, ZHANG K. Non-resonant response, bifurcation and oscillation suppression of a non-autonomous system with delayed position feedback control[J]. Nonlinear Dynamics, 2008, 51(3): 447-464.
[22]	WANG H P, LI J, ZHANG K. Sup-resonant response of a nonautonomous maglev system with delayed acceleration feedback control[J]. IEEE Transactions on Magnetics, 2008, 44(10): 2338-2350.
[23]	吴晗,曾晓辉,史禾慕. 考虑间隙反馈控制时滞的磁浮车辆稳定性研究[J]. 力学学报,2019,51(2): 550-557. WU Han, ZENG Xiaohui, SHI Hemu. Stability analysis of maglev vehicle with delayed position feedback control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 550-557.
[24]	沈飞,武建军. 时滞反馈磁浮控制系统的周期运动稳定性分析[J]. 兰州大学学报(自然科学版),2008,44(5): 131-136. SHEN Fei, WU Jianjun. Stability analysis of periodic motion of the maglev system with delayed velocity feedback control[J]. Journal of Lanzhou University (Natural Sciences), 2008, 44(5): 131-136.
[25]	SUN Y G, XU J Q, CHEN C, et al. Reinforcement learning-based optimal tracking control for levitation system of maglev vehicle with input time delay[J]. IEEE Transactions on Instrumentation Measurement, 2022, 71(8): 3142059.1-3142059.13.
[26]	ZHANG L L, HUANG L H, ZHANG Z Z. Hopf bifurcation of the maglev time-delay feedback system via pseudo-oscillator analysis[J]. Mathematical and Computer Modelling, 2010, 52(5/6): 667-673.
[27]	CUI X K, LI H L, ZHANG L, et al. Complete synchronization for discrete-time fractional-order coupled neural networks with time delays[J]. Chaos, Solitons & Fractals, 2023, 174:113772.1-113772.8.
[28]	FENG Y H, HU L J. On the quasi-controllability of continuous-time dynamic fuzzy control systems[J]. Chaos, Solitons & Fractals, 2006, 30(1): 177-188.
[29]	DE OLIVEIRA EVALD P J D, HOLLWEG G V, TAMBARA R V, et al. Lyapunov stability analysis of a robust model reference adaptive PI controller for systems with matched and unmatched dynamics[J]. Journal of the Franklin Institute, 2022, 359(13): 6659-6689. doi: 10.1016/j.jfranklin.2022.07.014
[30]	SOLGI Y, FATEHI A, NIKOOFARD A, et al. Design of optimal PID controller for multivariable time-varying delay discrete-time systems using non-monotonic Lyapunov-Krasovskii approach[J]. Journal of the Franklin Institute, 2021, 358(13): 6634-6665. doi: 10.1016/j.jfranklin.2021.06.026
[31]	BORASE R P, MAGHADE D K, SONDKAR S Y, et al. A review of PID control, tuning methods and applications[J]. International Journal of Dynamics and Control, 2021, 9(2): 818-827. doi: 10.1007/s40435-020-00665-4
[32]	陈志贤,李忠继,杨吉忠,等. 常导高速电磁悬浮车辆二系悬挂结构对比优化[J]. 机械工程学报,2022,58(10): 160-168,179. doi: 10.3901/JME.2022.10.160 CHEN Zhixian, LI Zhongji, YANG Jizhong, et al. Comparison and optimization of secondary suspension structure of high speed EMS vehicle[J]. Journal of Mechanical Engineering, 2022, 58(10): 160-168,179. doi: 10.3901/JME.2022.10.160
[33]	WU H, ZENG X H, GAO D G, et al. Dynamic stability of an electromagnetic suspension maglev vehicle under steady aerodynamic load[J]. Applied Mathematical Modelling, 2021, 97: 483-500. doi: 10.1016/j.apm.2021.04.008
[34]	黎松奇,张昆仑,陈殷,等. 弹性轨道上磁浮车辆动力稳定性判断方法[J]. 交通运输工程学报,2015,15(1): 43-49. LI Songqi, ZHANG Kunlun, CHEN Yin, et al. Judgment method of maglev vehicle dynamic stability on flexible track[J]. Journal of Traffic and Transportation Engineering, 2015, 15(1): 43-49.
[35]	吴晗,曾晓辉. 气动升力下磁浮车辆非线性响应研究[J]. 机械工程学报,2021,57(14): 223-231. doi: 10.3901/JME.2021.14.223 WU Han, ZENG Xiaohui. Nonlinear dynamics of maglev vehicle under aerodynamic lift[J]. Journal of Mechanical Engineering, 2021, 57(14): 223-231. doi: 10.3901/JME.2021.14.223
[36]	张继业,杨翊仁,曾京. Hopf分岔的代数判据及其在车辆动力学中的应用[J]. 力学学报,2000,32(5): 596-605. ZHANG Jiye, YANG Yiren, ZENG Jing. An algorithm crterion for Hopf bifurcation and its applications in vehicle dynamics[J]. Acta Mechanica Sinica, 2000, 32(5): 596-605.
[37]	CHEN X H, MA W H, LUO S H. Study on stability and bifurcation of electromagnet-track beam coupling system for EMS maglev vehicle[J]. Nonlinear Dynamics, 2020, 101(4): 2181-2193. doi: 10.1007/s11071-020-05917-8
[38]	张玲玲. 磁浮列车悬浮系统的Hopf分岔及滑模控制研究[D]. 长沙:湖南大学,2010.
[39]	梁鑫. 磁浮列车车轨耦合振动分析及试验研究[D]. 成都:西南交通大学,2015.

施引文献

附加材料(0)

访问统计

点击查看大图

图(14)

计量

文章访问数: 482
HTML全文浏览量: 124
PDF下载量: 68
被引次数: 0

1. 影响因素分析与案例数据库构建
1.1 影响因素初步分析
1.2 数据获取与统计分析
1.3 影响因素优化筛选
1.4 数据存储
2. 城市轨道交通土建工程造价预测与反演模型
2.1 基于PSO-GWO-ELM的土建工程造价非线性预测
2.2 基于Sobol’ 与Curve Fitting的土建工程造价解释性反演
3. 实例分析
3.1 工程概况
3.2 土建工程造价非线性预测
3.3 城市轨道交通土建工程造价影响因素全局敏感性分析
3.4 影响因素与土建造价作用关系分析
4. 结　论

1. 影响因素分析与案例数据库构建
1.1 影响因素初步分析
1.2 数据获取与统计分析
1.3 影响因素优化筛选
1.4 数据存储
2. 城市轨道交通土建工程造价预测与反演模型
2.1 基于PSO-GWO-ELM的土建工程造价非线性预测
2.2 基于Sobol’ 与Curve Fitting的土建工程造价解释性反演
3. 实例分析
3.1 工程概况
3.2 土建工程造价非线性预测
3.3 城市轨道交通土建工程造价影响因素全局敏感性分析
3.4 影响因素与土建造价作用关系分析
4. 结　论

参考文献(39)

施引文献

附加材料(0)

访问统计

二自由度磁浮列车悬浮系统时滞控制研究

doi: 10.3969/j.issn.0258-2724.20230282

作者简介: 王美琪（1987—），男，副教授，博士，研究方向为非线性动力学、磁悬浮列车动力学与控制，E-mail：wangmeiqi@stdu.edu.cn

通讯作者: 刘鹏飞（1985—），男，副教授，博士，研究方向为列车-轨道耦合动力学、磁悬浮列车动力学与控制，E-mail：lpfswjtu@163.com

计量

出版历程