磁浮交通以其无机械接触、爬坡能力强、维护成本低、运营噪声小等优点成为新型轨道交通的重要发展方向^[1-2]. 常导电磁悬浮型、超导电动悬浮型、永磁电动悬浮型和高温超导钉扎悬浮型磁浮交通作为大运能轨道交通系统，在国内外已得到广泛研究和发展^[3-4]，近年来我国提出并发展了永磁悬浮型悬挂式轨道交通系统^[5]，2022年在江西省兴国县建成世界首条永磁磁浮交通试验线. 悬挂式永磁磁浮交通利用车载Halbach永磁阵列与铺设在轨道梁上的Halbach永磁轨道之间的磁斥力实现悬浮，依靠永磁直线电机驱动列车前进，兼具悬挂式单轨交通和磁悬浮交通的技术特点，适用于观光旅游、区域接驳、城乡连接、港口物流等小运量运输场景^[6].

永磁磁浮交通具有许多优点，但当车载永磁体相对永磁轨道发生横向偏移时，永磁悬浮系统将产生横向排斥力，使得系统不具备横向自复位能力，通常需要设置机械导向系统^[7]. 为科学合理地设计机械导向系统，需要研究不同位姿条件下车载永磁体与永磁轨道之间的磁力特性. 目前，国内外已有研究主要关注Halbach永磁阵列的磁场分布特性^[8-11]，部分学者开展了永磁体与永磁体之间磁力特性的研究：杨杰等^[7]采用有限元方法，详细分析了车载永磁体悬浮力和横向力随悬浮间隙、横向偏移量的变化趋势；Jiang等^[12]分析了不同尺寸Halbach永磁阵列的磁力特性，为车载永磁体和永磁轨道结构优化提供参考；Tang等^[13]基于磁荷理论建立Halbach永磁阵列之间的磁场解析模型，利用虚功法推导了悬浮力的二维和三维解析模型，为永磁阵列参数优化提供基础. 然而，上述已有Halbach永磁阵列磁力特性研究中仅考虑了永磁体平动参数（悬浮间隙和横移量），忽略了转动参数（点头角、侧滚角、摇头角）对永磁体磁力的影响. 但是，工程实际中车载永磁体与永磁轨道之间难免发生相对转动，在复杂空间位姿条件下两者之间的磁力特性如何，对永磁磁浮车辆动力学性能有何影响，目前尚不清楚.

为更全面地掌握车载永磁体与永磁轨道之间的磁力特性，需建立准确的磁力计算模型. 现有方法中，理论解析方法主要适用于计算车载永磁体和永磁轨道无相对转角时的磁力，当考虑三方向上平动、转动后的复杂空间位置关系时，即使得到多维高阶解析公式，也很难得到解析解. 有限元方法遵循了麦克斯韦方程这一物理学定律，建模时可考虑车载永磁体与永磁轨道的复杂空间相对位置，能够较准确地计算复杂空间姿态下的磁力^[7,12]. 因此，本文采用有限元方法，参考兴国县永磁磁浮交通系统，通过Ansoft Maxwell软件建立永磁悬浮系统的三维磁场有限元模型，定量分析车载永磁体磁力在悬浮间隙、横移量、点头角、摇头角和侧滚角共5个空间位姿参数影响下的变化规律，以期为永磁磁浮车辆悬浮导向系统设计提供理论指导和应用参考.

1.   永磁悬浮系统磁场有限元模型

由于永磁体的电导率远小于普通铁磁性材料，永磁体轨道的磁场沿纵向分布均匀性好，行车速度导致的永磁体涡流效应非常小，理论上稳态和瞬态条件下的磁力差别小. 所以，本文将主要计算稳态条件下的磁力，建立的有限元模型也均为稳态磁场模型.

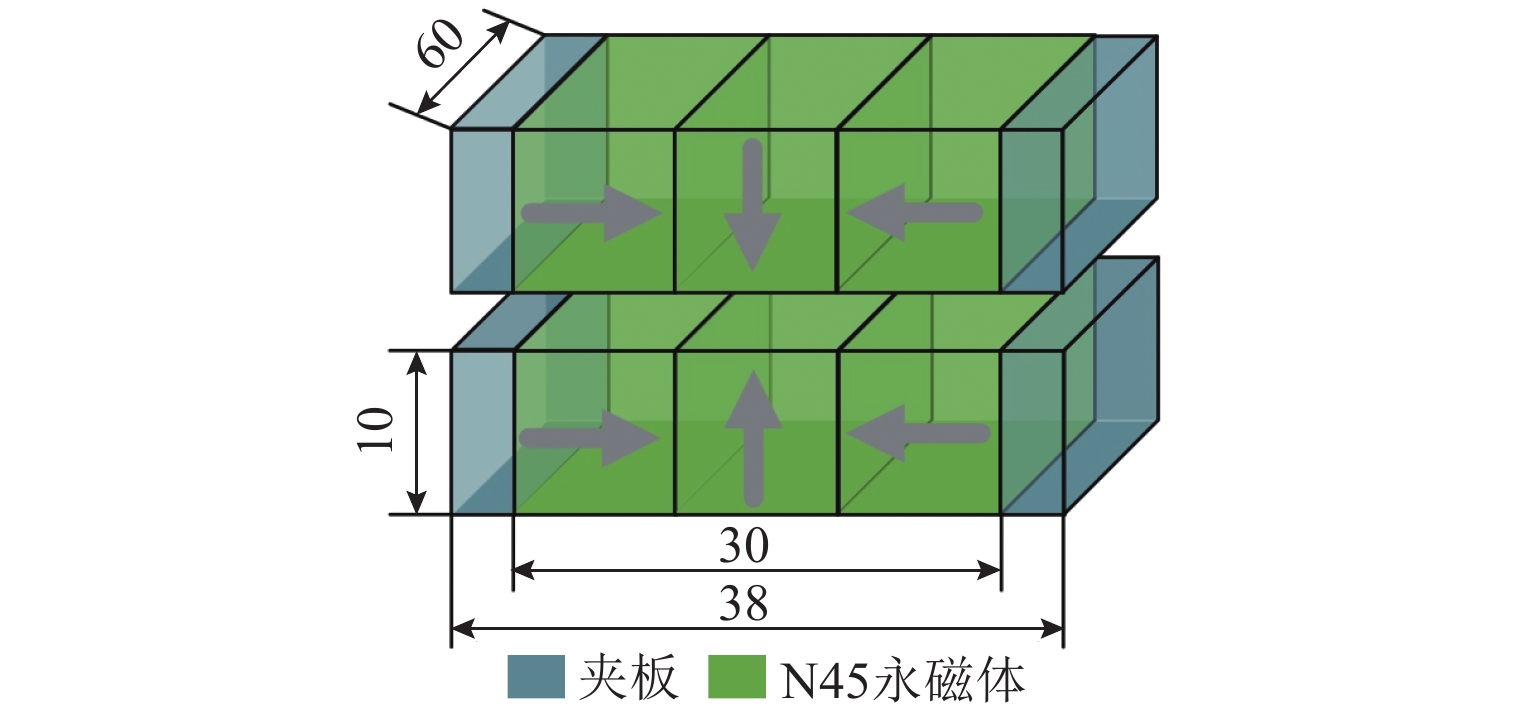
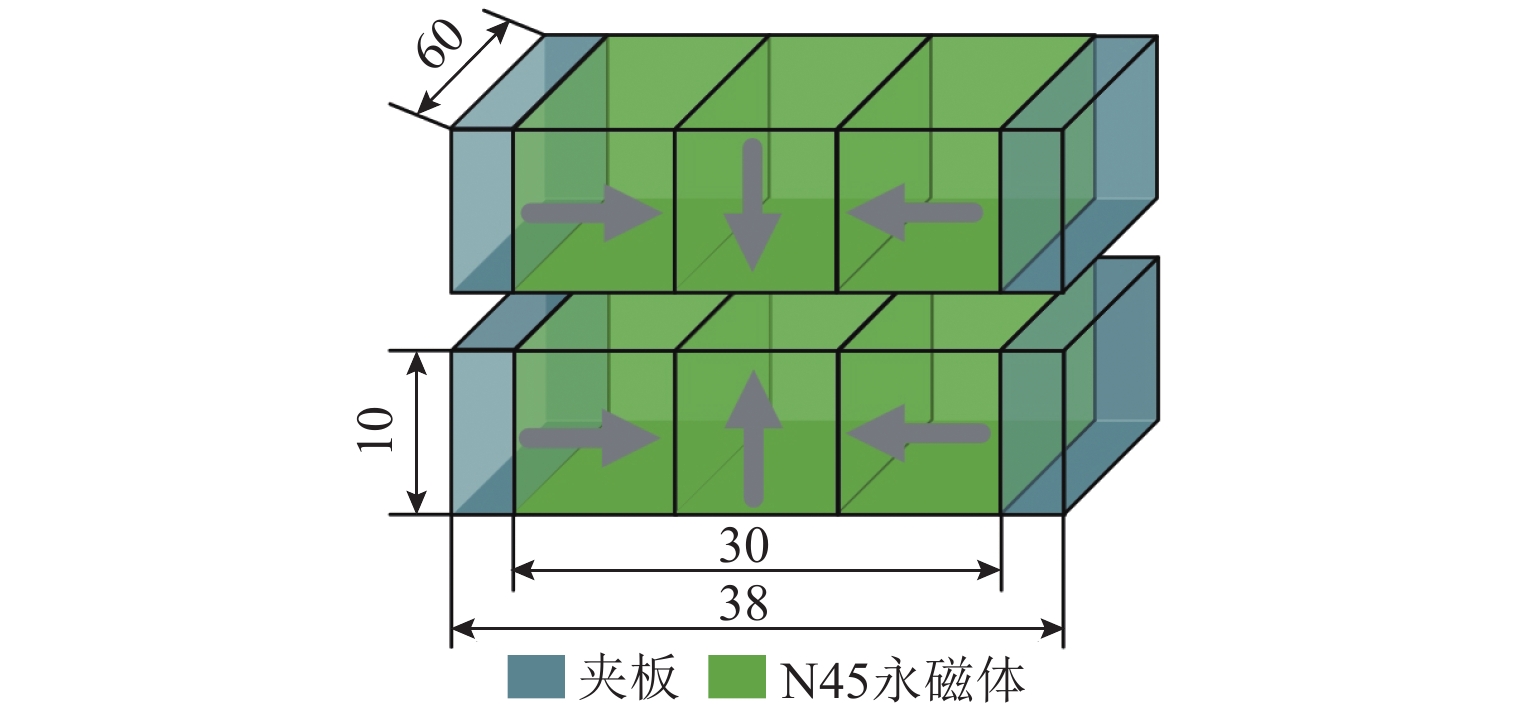
永磁磁浮交通系统中车载永磁体和永磁轨道均使用了由钕铁硼N45材料制作Halbach永磁阵列，如图1所示，图中：箭头方向表示永磁块的磁化方向. 3块永磁块沿横向布置组成Halbach阵列. 永磁阵列的两侧安装了夹板，厚度4 mm，材质为45号钢. 表1给出了钕铁硼N45永磁材料的参数.

图  1  原理实验装置的Halbach永磁阵列结构

Figure  1.  Structure of Halbach permanent magnet array of principle experimental device

下载: 全尺寸图片 幻灯片

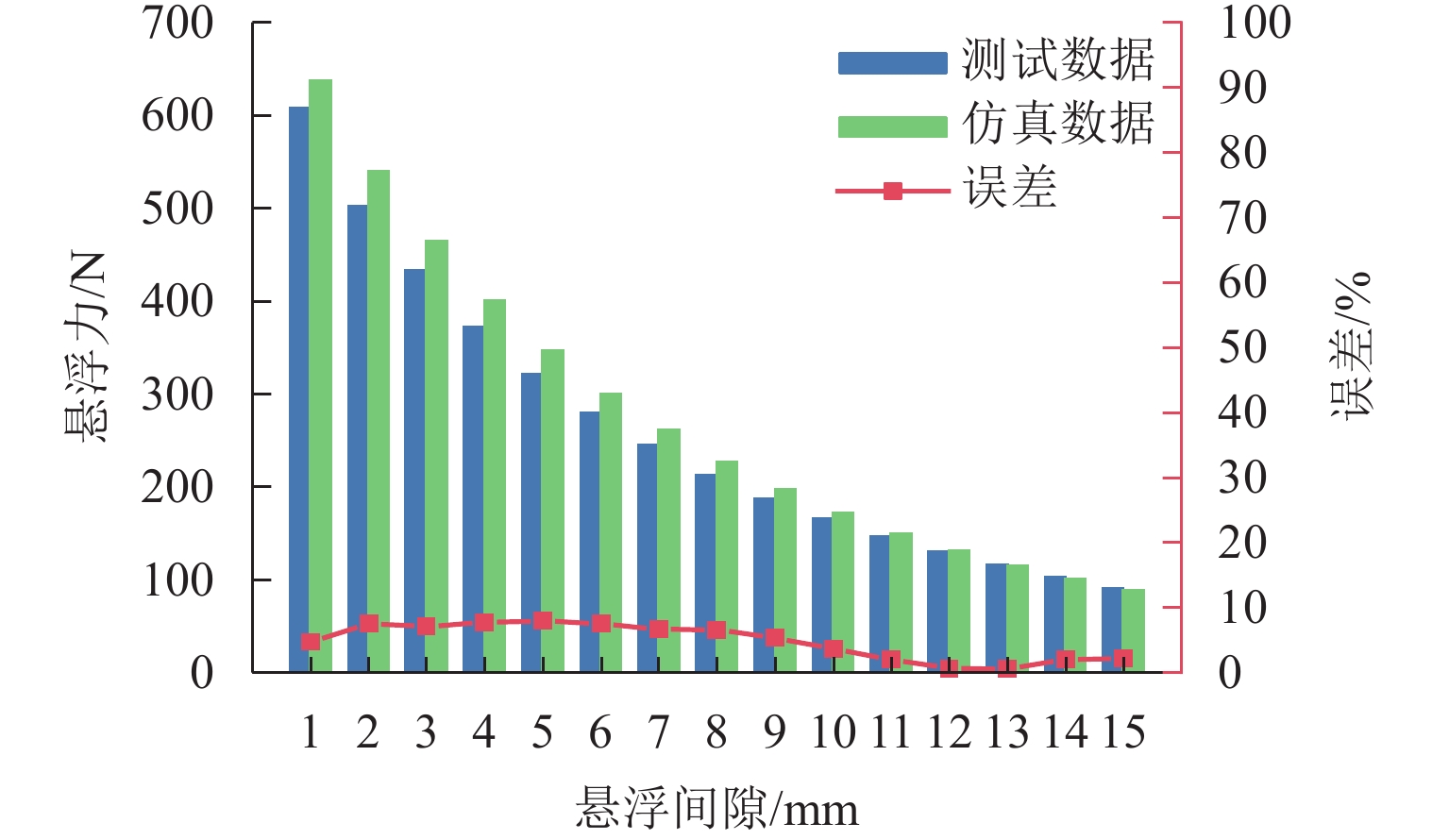
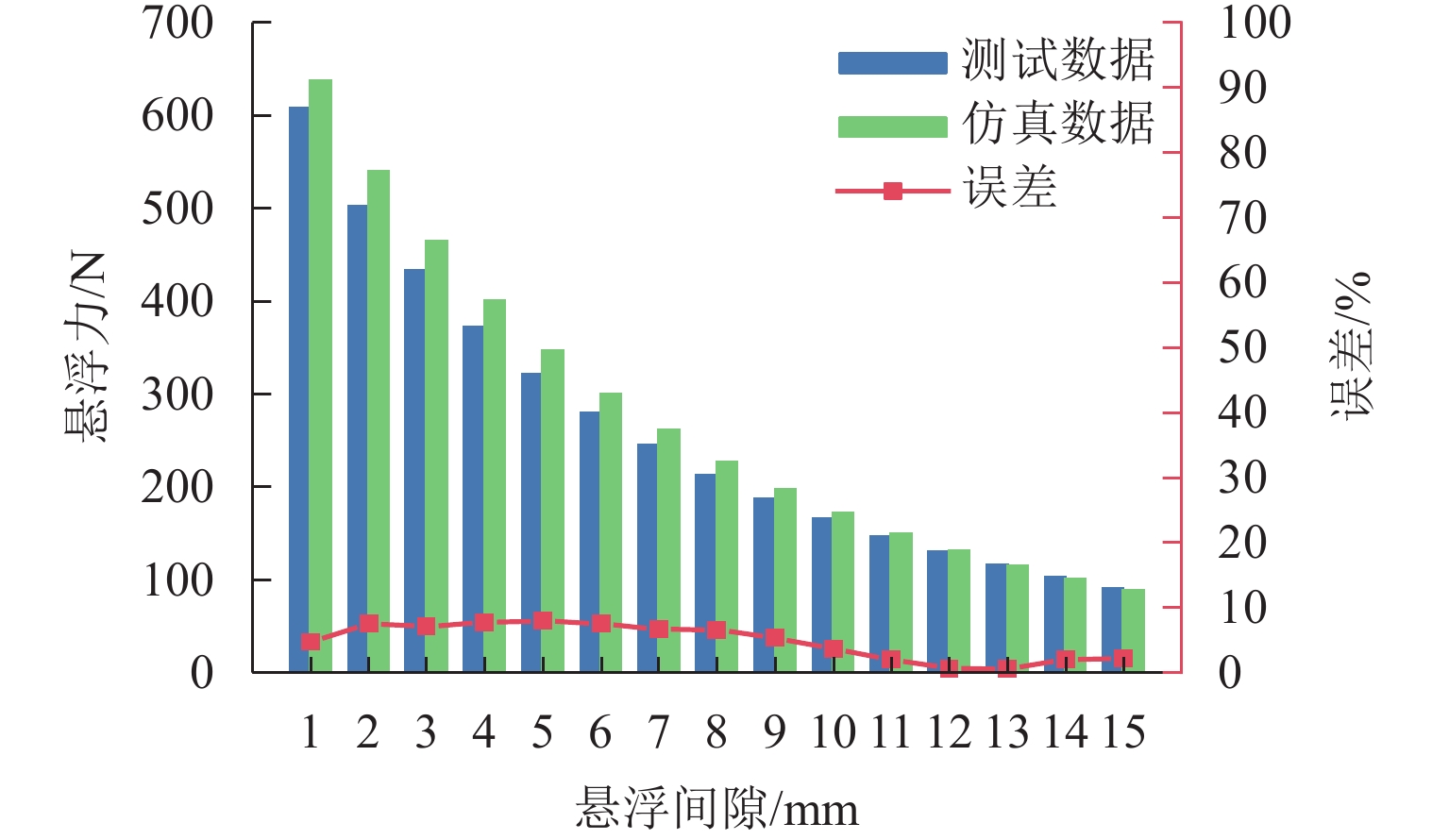
表  1  钕铁硼N45永磁材料参数

Table  1.  Parameters of NdFeB N45 permanent magnet materials

材料参数	数值
剩余磁感应强度/T	1.32
矫顽力/（kA·m−1）	890
磁化强度/（kA·m−1）	978.8
相对磁导率	1.22

下载: 导出CSV 

| 显示表格

使用Ansoft Maxwell软件建立了永磁悬浮原理实验系统的磁场有限元模型，计算了悬浮间隙1～15 mm的悬浮力大小，与文献[12]中测试结果进行对比，如图2所示. 可以发现：仿真结果与测试结果吻合良好，最大误差不超过8%，说明本文的永磁磁场有限元分析方法适当，磁力计算精度能满足工程研究需求.

图  2  永磁悬浮力有限元计算结果与测试结果^[12]比较

Figure  2.  Comparison between finite element calculation results and test results^[12] of PMS force

下载: 全尺寸图片 幻灯片

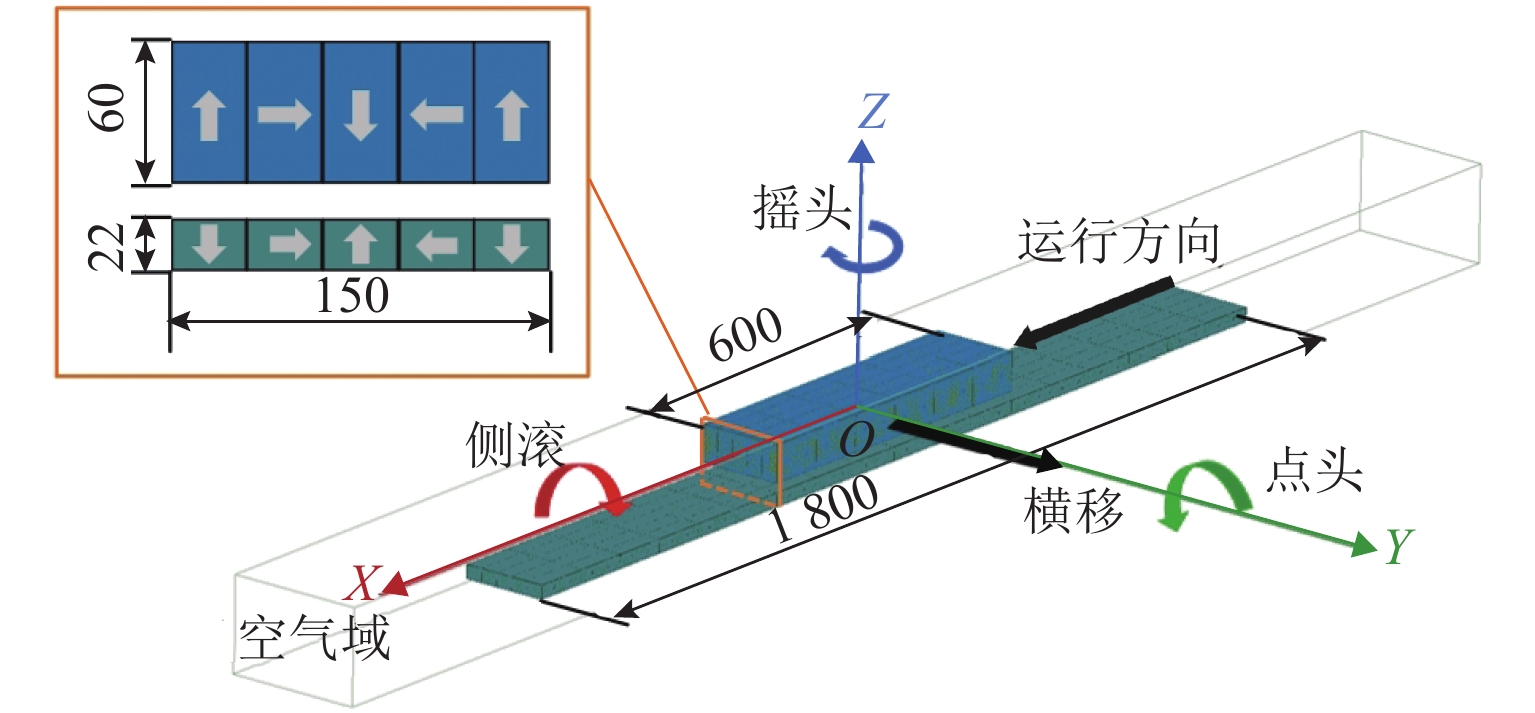
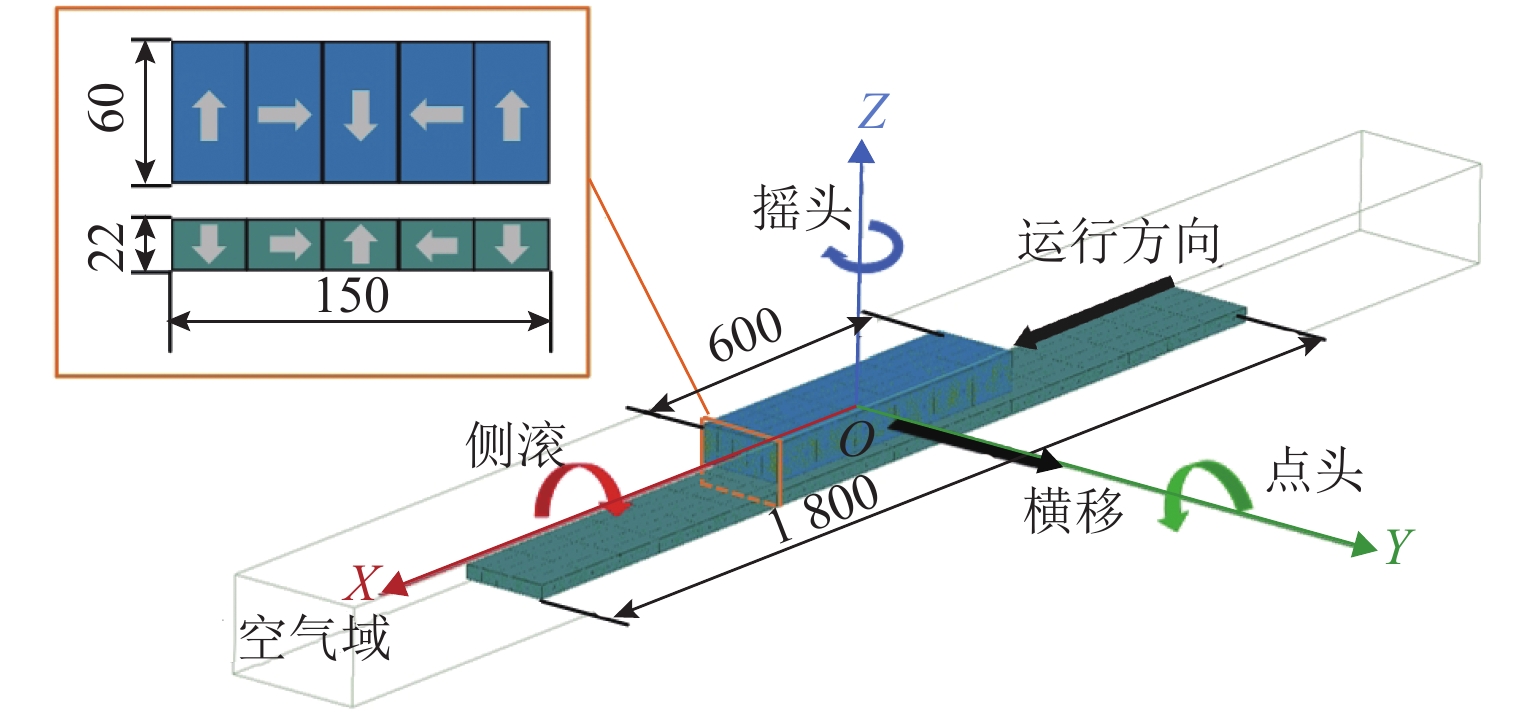
采用同样的永磁磁场有限元建模方法，参考兴国县永磁磁浮交通系统车载永磁体和永磁轨道结构参数，建立图3所示的永磁磁浮系统三维磁场有限元模型. 图中，永磁轨道单个永磁块的宽度为30 mm，厚度22 mm，5块永磁块沿横向布置，组成长度为100 mm的Halbach阵列. 纵向拼接Halbach阵列，形成永磁轨道. 车载永磁体单个永磁块的宽度和长度与永磁轨道单个永磁块的尺寸一致，但厚度增加到了60 mm. 同样采用5块永磁块横向布置，形成了一个Halbach阵列. 在有限元模型中，永磁轨道的长度为1800 mm，车载永磁体由6个Halbach阵列纵向拼接而成，长度为600 mm. 有限元模型计算域的尺寸为7200 mm（长度）×600 mm（宽度）×388 mm（高度）. 车载永磁体网格长度不超过25 mm，永磁轨道网格长度不超过20 mm，空气域采用自适应网格，共使用775923个网格.

图  3  永磁磁浮系统三维磁场有限元模型

Figure  3.  Three-dimensional magnetic field finite element model of PMS system

下载: 全尺寸图片 幻灯片

2.   纯平动和纯转动条件下磁力分析

使用图3建立的磁场有限元模型，改变车载永磁体相对于永磁轨道的垂向间隙、横向偏移量以及相对点头角、摇头角和侧滚角，计算分析了不同位姿参数下车载永磁体质心处的合力和合力矩. 由于上述5个位姿参数对永磁体磁力的影响是相互耦合的，本节将首先开展纯平动、纯转动参数对磁力的影响分析.

2.1   平动参数对磁力的影响

假定车载永磁体与永磁轨道之间不存在相对转动（悬浮间隙和横向偏移量沿线路方向均匀分布），本小节计算分析了不同悬浮间隙和横向偏移条件下车载永磁体的悬浮力和横向力. 考虑到永磁磁浮车辆的额定悬浮间隙为15 mm，设定悬浮间隙为12～18 mm，车载永磁体的横移量不超过8 mm，两者的计算步长均设置为1 mm，共设置了63个纯平动计算工况.

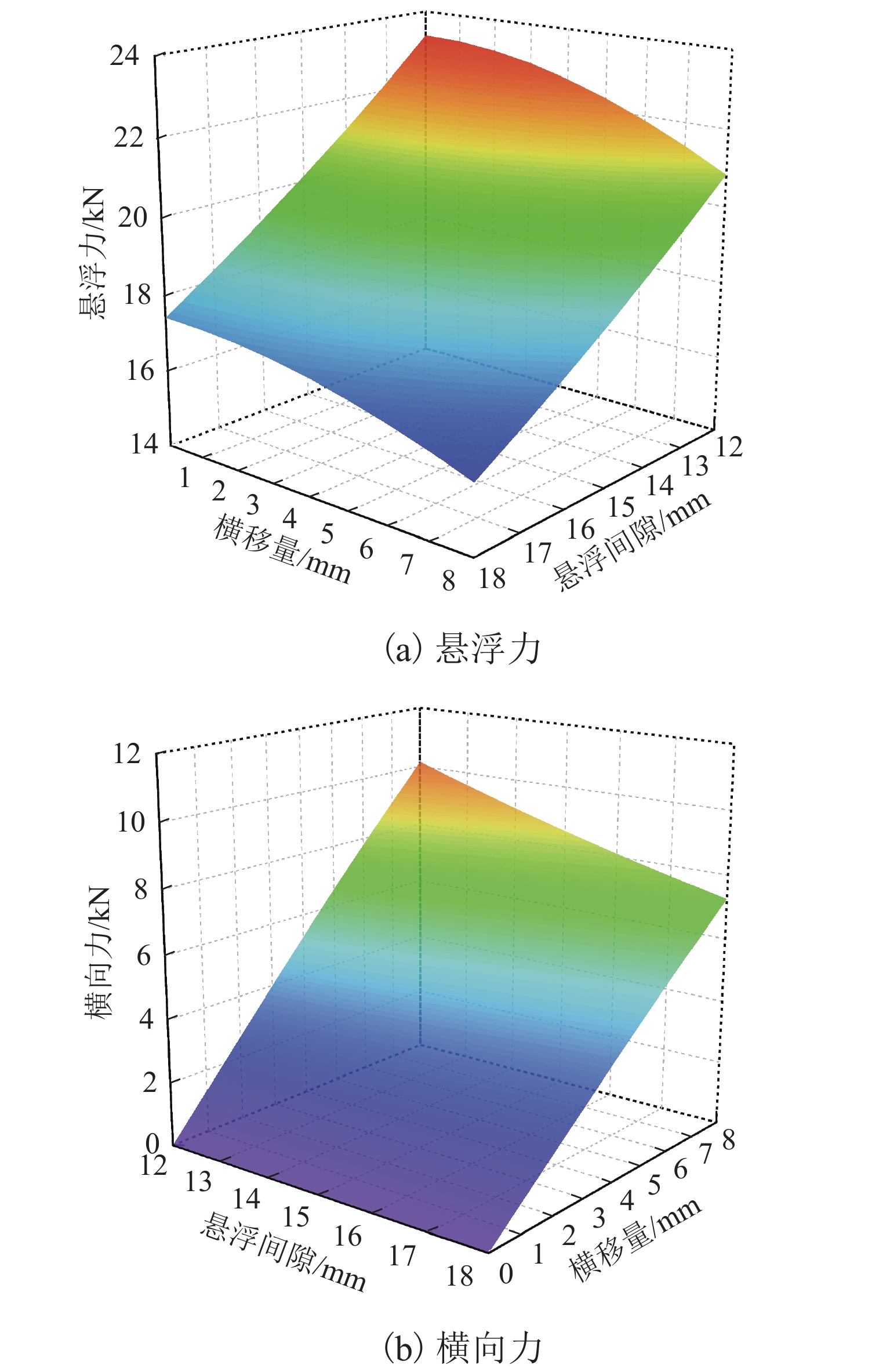
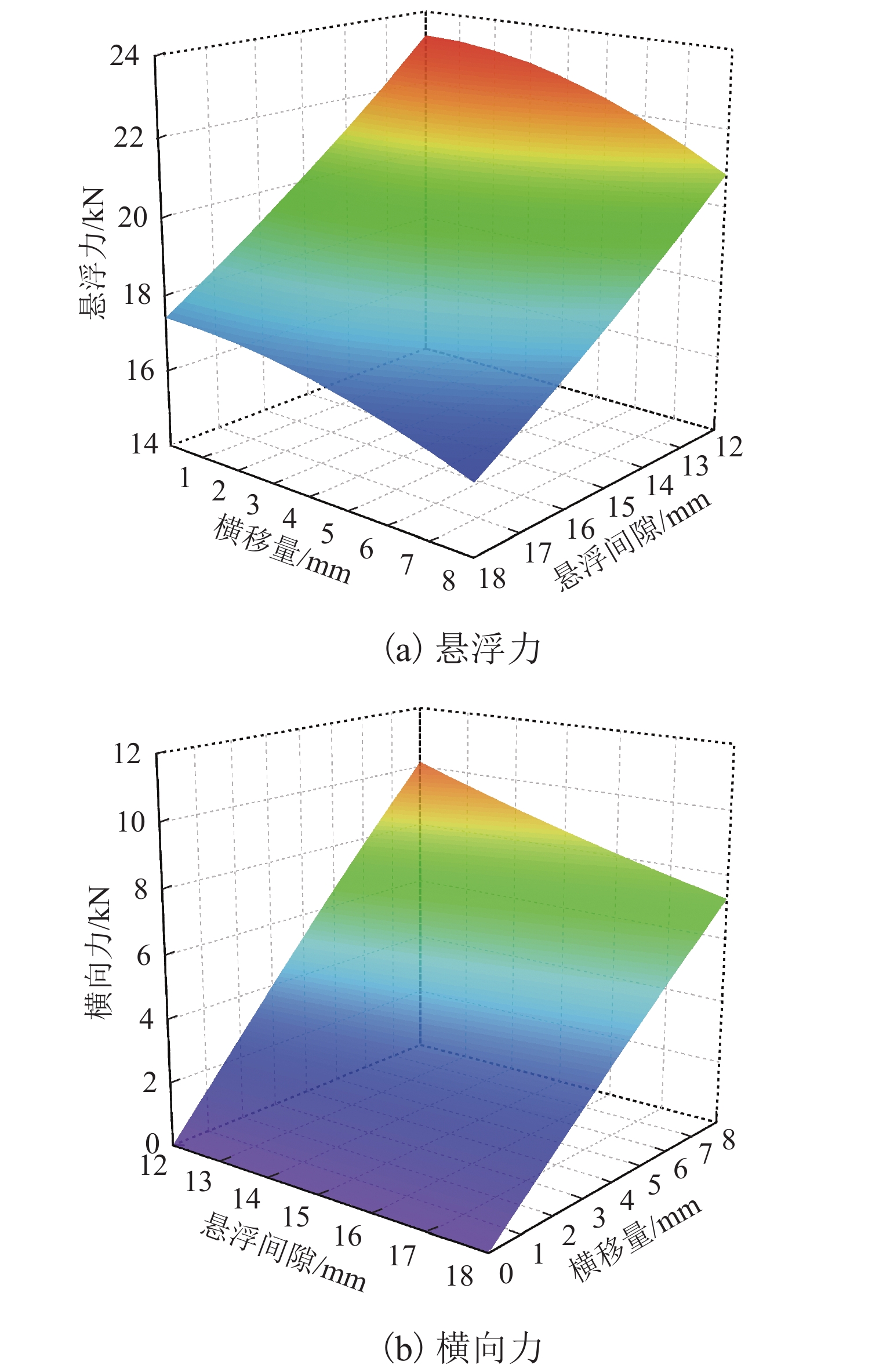
图4（a）给出了车载永磁体悬浮力随悬浮间隙和横移量的变化. 由图可知：悬浮力随悬浮间隙和横移量增大而减小，当横移量恒为0、悬浮间隙从15 mm逐渐增大至18 mm时，悬浮力由20.15 kN逐渐衰减至17.42 kN，衰减速率0.91 kN/mm（相当于悬浮刚度）；当悬浮间隙恒为15 mm、横移量从0增大到8 mm时，悬浮力由20.15 kN逐渐减小至18.13 kN，减小了10.02%. 在所有纯平动计算工况中，悬浮力最大值为23.33 kN，相对于额定悬浮力20.15 kN增加了15.78%；悬浮力最小值为15.78 kN，较额定悬浮力减小了21.69%.

图  4  无相对转动时悬浮力、横向力随悬浮间隙和横移量的变化

Figure  4.  Variation of levitation force and lateral force with levitation gap and lateral offsets in the absence of relative rotation

下载: 全尺寸图片 幻灯片

图4（b）显示了横向力随悬浮间隙和横移量的变化情况. 可以发现：当悬浮间隙恒定时，横向力随横移量增大而近似线性增大，当悬浮间隙为15 mm、横移量从0增大至8 mm时，横向力由0增大至8.56 kN，增长速率约为1.07 kN/mm （相当于负导向刚度）；当横移量恒定且不为0时，横向力随悬浮间隙的增大而减小，横移量越大，横向力随悬浮间隙增大而衰减的速度越快. 在所有纯平动计算工况中，横向力最大值为10.16 kN（悬浮间隙12 mm，横移量8 mm），与额定悬浮力之比高达50.42%.

车载永磁体所受横向力的方向与其偏移方向一致. 因此，如果车载永磁体不受横向机械约束，那么横向力将促使车载永磁体发生更大的横向偏移，而横移量的增大将导致悬浮力减小；进一步地，减小的悬浮力使得车载永磁体呈向下运动趋势，迫使悬浮间隙变小以增大悬浮力，而悬浮间隙的减小将增大横向力，促使车载永磁体继续横向偏移，从而形成横向偏移量增大—悬浮间隙减小—横向偏移继续增大的恶性循环，最终导致永磁悬浮失效. 上述分析表明：必须设置导向系统阻止永磁悬浮体发生横向偏移，否则永磁悬浮系统不能稳定悬浮. 如果永磁磁浮车辆设置了非常接触的导向胶轮，由于永磁悬浮系统具有负导向特性，永磁磁浮车辆在横向激扰作用下必然会发生横向晃动，将诱发车辆垂向振动，此类问题需要开展导向技术创新加以解决.

2.2   转动参数对磁力的影响

假定车载永磁体底面中心处的悬浮间隙恒为15 mm且横向偏移量为0，计算了车载永磁体与永磁轨道存在相对点头角、摇头角和侧滚角时的悬浮力和横向力，其中，转角参数范围参考了永磁磁浮列车试验运行情况. 当车载永磁体端部的悬浮间隙在（15±3） mm之间变化时，估算点头角最大值约为0.5°. 当车载永磁体端部的横向偏移量不超过8 mm时，摇头角最大值约为1.5°. 当车载永磁体内、外侧边缘的悬浮间隙之差不超过6 mm时，计算得到侧滚角最大值约2.3°. 由于车载永磁体和永磁轨道的几何结构及磁场分布是对称的，摇头角和点头角为正角度或负角度时，悬浮力和横向力的结果及其变化规律是一致的. 因此，本文仅计算了摇头角和点头角为正角度时的磁力，未考虑其负角度范围.

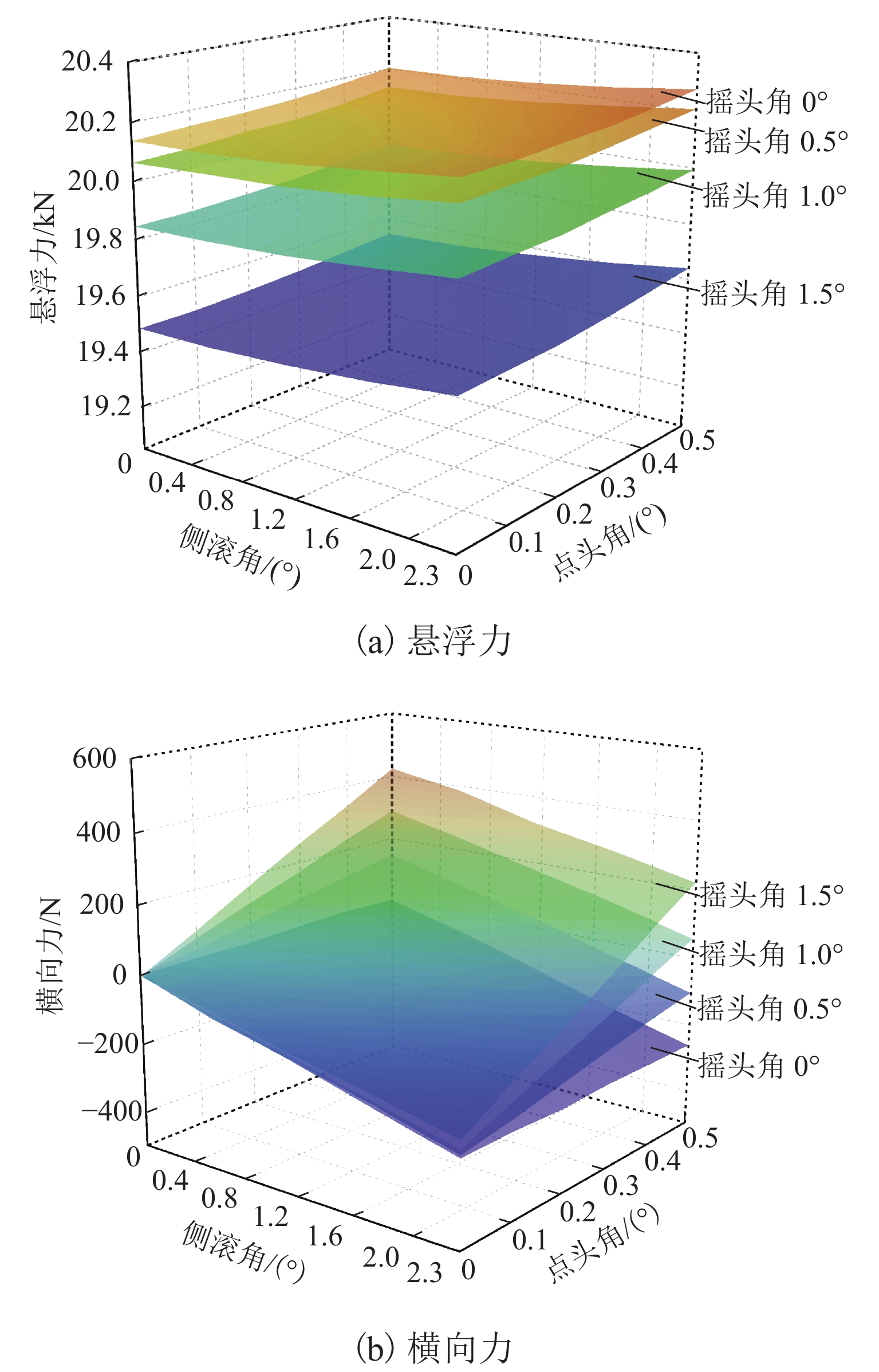
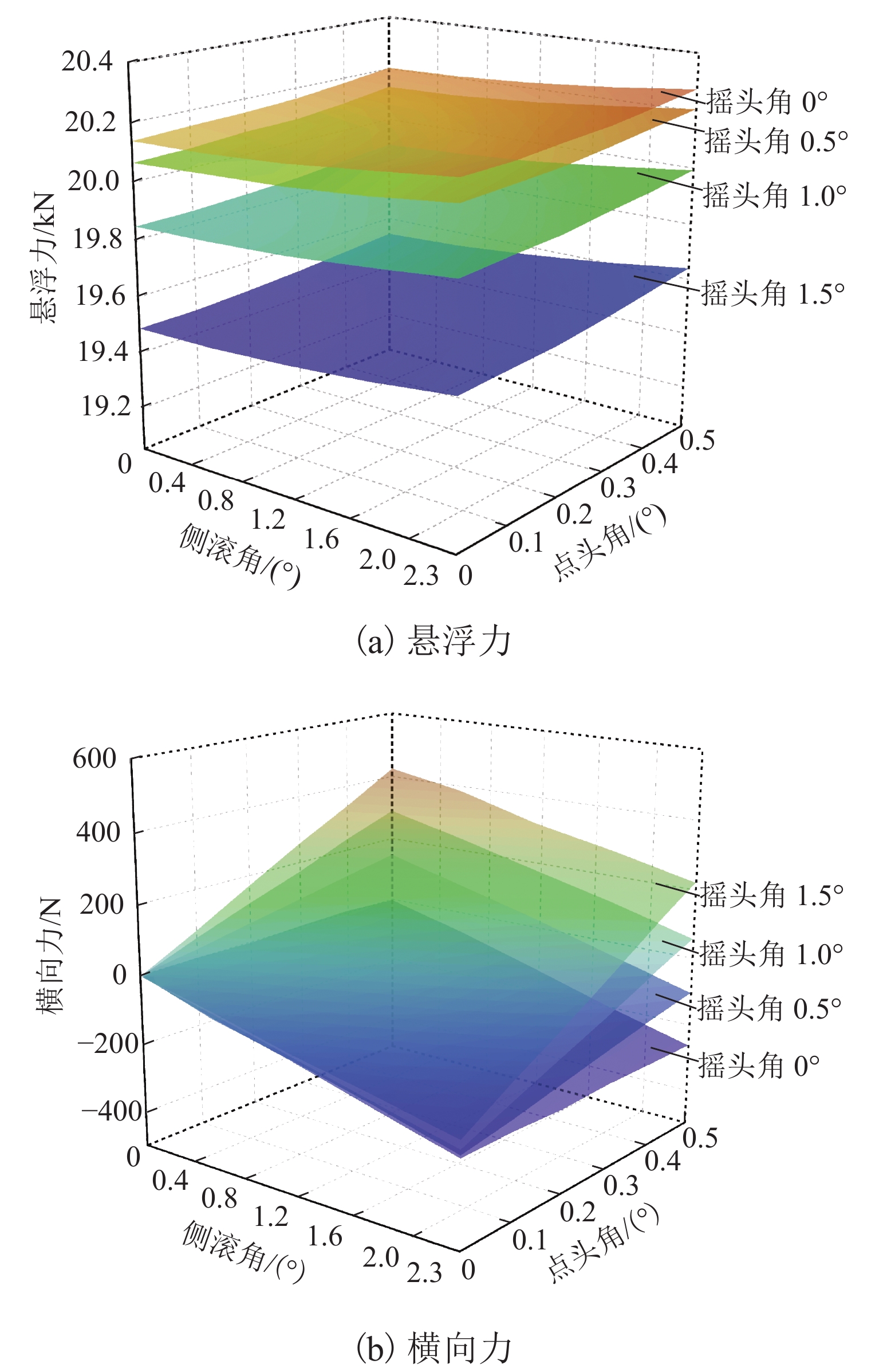
图5（a）给出了4种摇头角条件下车载永磁体悬浮力随点头角和侧滚角的变化. 可以发现：当摇头角恒定时，悬浮力随点头角和侧滚角的增大仅略微增大；在相同的点头角和侧滚角情况下，悬浮力随摇头角的增大而略有减小；当摇头角从0增大到1.5°时，悬浮力减小量不超过0.80 kN. 在所有纯转动计算工况中，悬浮力最大值为20.28 kN，最小值为19.49 kN，分别为额定悬浮力的100.65%和96.72%，说明3个方向上的纯转动对车载永磁体悬浮力的影响很小.

图  5  无横向偏移时悬浮力、横向力随转角的变化

Figure  5.  Variation of levitation force and lateral force with angle of rotation in the absence of lateral offset

下载: 全尺寸图片 幻灯片

图5（b）给出了4种摇头角条件下车载永磁体横向力随着点头角和侧滚角的变化情况. 可以发现：当只存在相对侧滚角时，横向力不为0，且恒为负值，其幅值随侧滚角增大而略有增大，但横向力绝对值不大；当仅存在点头角时，横向力为0，这是因为单纯的点头运动不会使车载永磁体横向偏离轨道，也就不会产生横向力；当仅存在摇头角时，横向力也为0，原因是单纯的摇头运动使车载永磁体前、后部分产生了大小相等、方向相反的横向力.

从图5（b）中结果还可以看出：当同时存在点头角和摇头角时，即使侧滚角为0，车载永磁体质心处仍会产生一定的横向力，其原因是车载永磁体前、后部的间隙磁场强度发生了非线性增减，导致车载永磁体质心处的横向合力不为0. 特别地，当车载永磁体相对永磁轨道发生了三方向转动时，不仅横向力大小发生变化，其方向也会发生变化. 例如，当点头角和摇头角保持恒定时，侧滚角的增大会使得横向力由正值逐渐减小，减小至0以后变为负值并反向增大；同样，当侧滚角和摇头角保持恒定时，横向力随点头角增大呈现出类似的变化规律. 在所有的纯转动计算工况中，横向力最大值为0.43 kN，约为额定悬浮力的2.13%，说明车载永磁体纯转动运动引起的横向力较小.

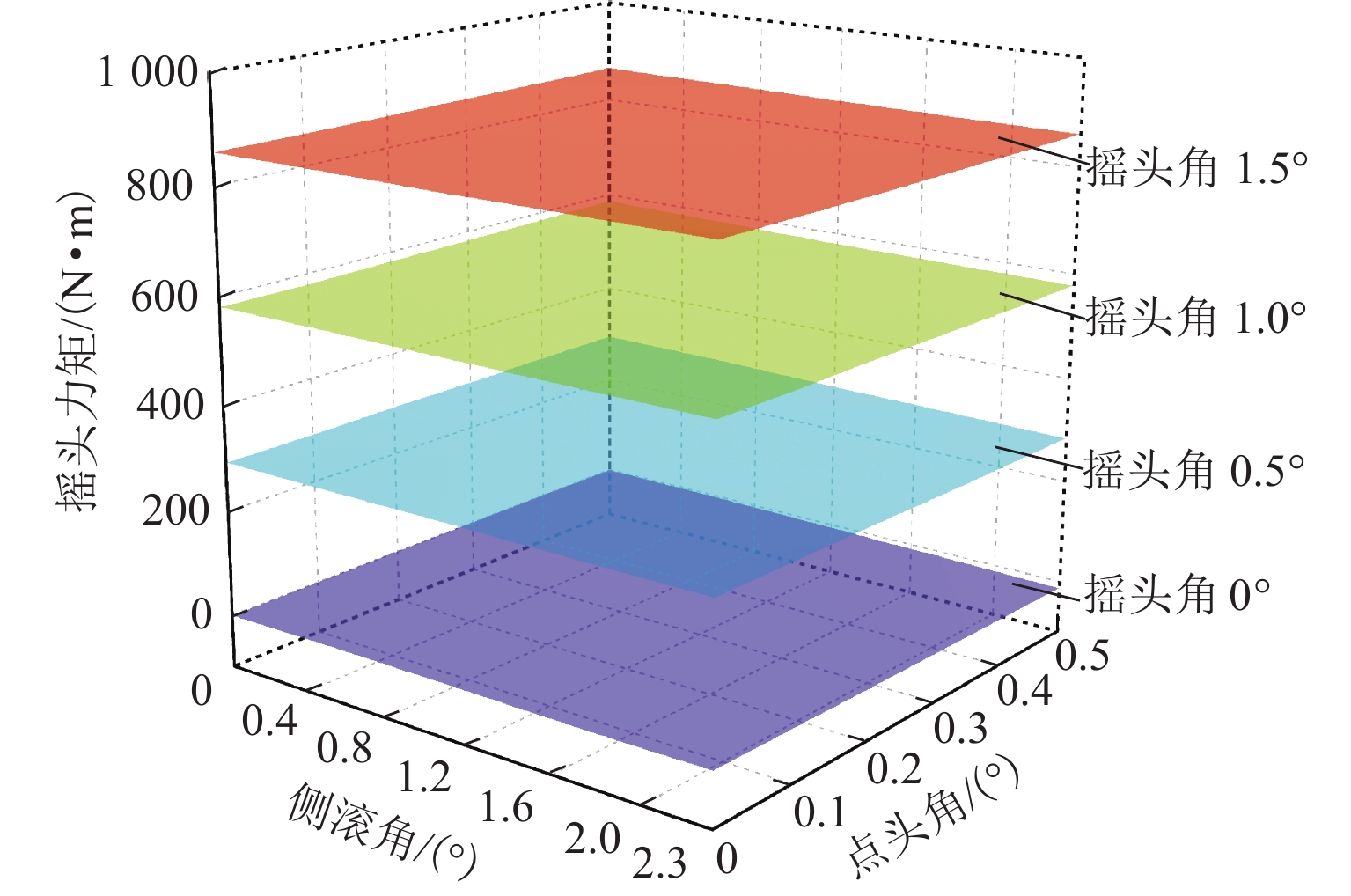
需要指出的是，当车载永磁体与永磁轨道存在相对转角时，磁力的不均分布还会带来力矩. 其中，点头力矩和侧滚力矩的方向与其转角方向相反，表现出自回复的特性，故本文不做细致分析. 但是，摇头力矩的方向与摇头角方向相同，有必要分析摇头力矩随位姿变化而变化的规律. 图6给出了悬浮间隙为15 mm、横向偏移为0时车载永磁体的摇头力矩随点头角、侧滚角和摇头角的变化规律. 可以看出：车载永磁体的摇头力矩随摇头角增大而增大，但几乎不受侧滚角和点头角的影响；摇头角从0变化到1.5° 时，摇头力矩从0增加到860 N·m.

图  6  无横向偏移时摇头力矩随转角的变化

Figure  6.  Variation of yawing torque with angle of rotation in the absence of lateral offset

下载: 全尺寸图片 幻灯片

3.   平动和转动复合条件下磁力分析

为分析平动和转动复合运动对车载永磁体磁力的影响，设置2组复合运动工况. 第一组工况中车载永磁体底面中心处的悬浮间隙设定为额定间隙值15 mm，第二组工况中悬浮间隙取为其最大允许值18 mm. 2组工况中车载磁体底面中心处的横向偏移量均设定为其最大可能值8 mm，转角参数范围与前文保持一致.

3.1   额定悬浮间隙及最大横向偏移条件下磁力分析

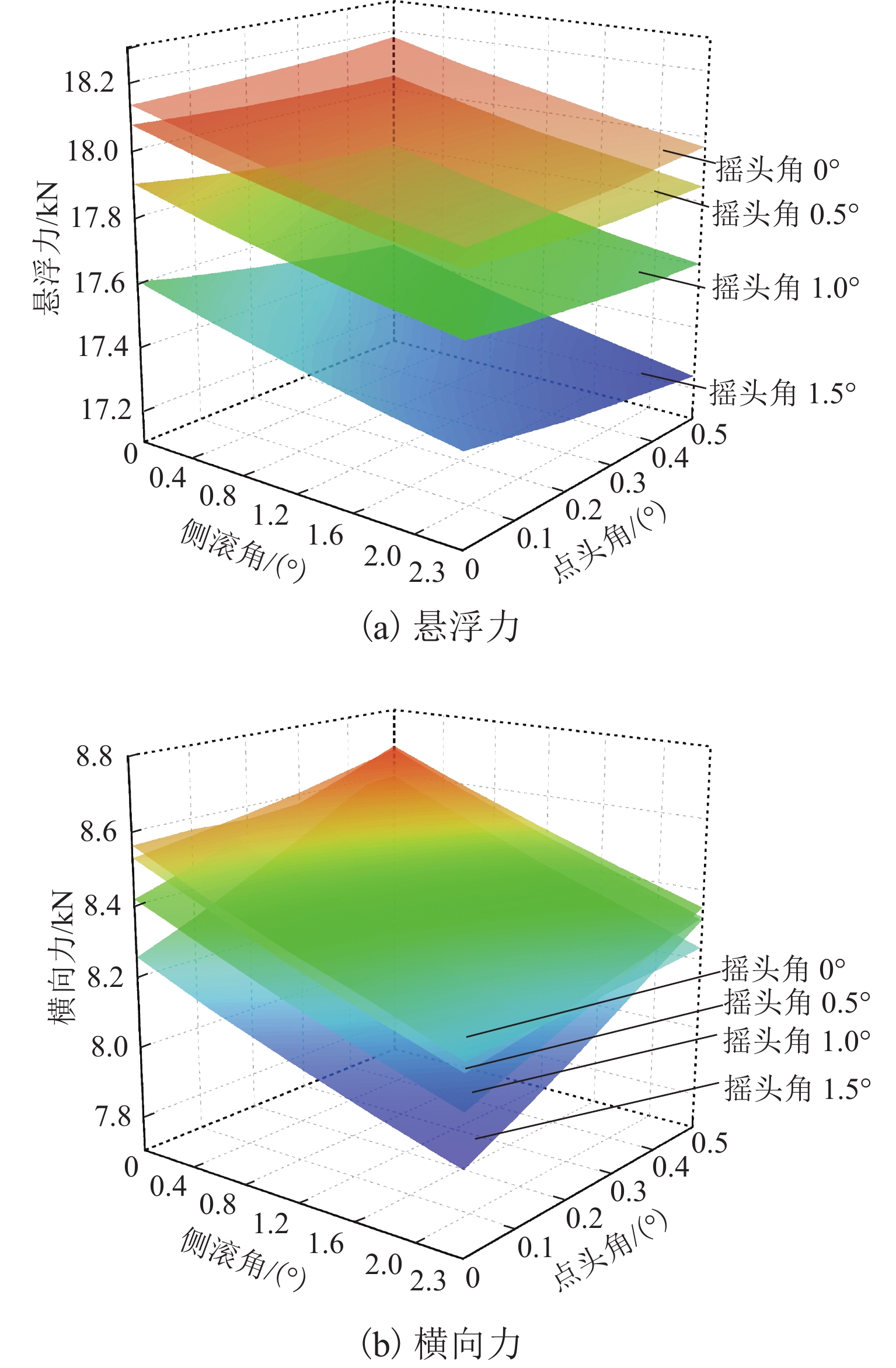
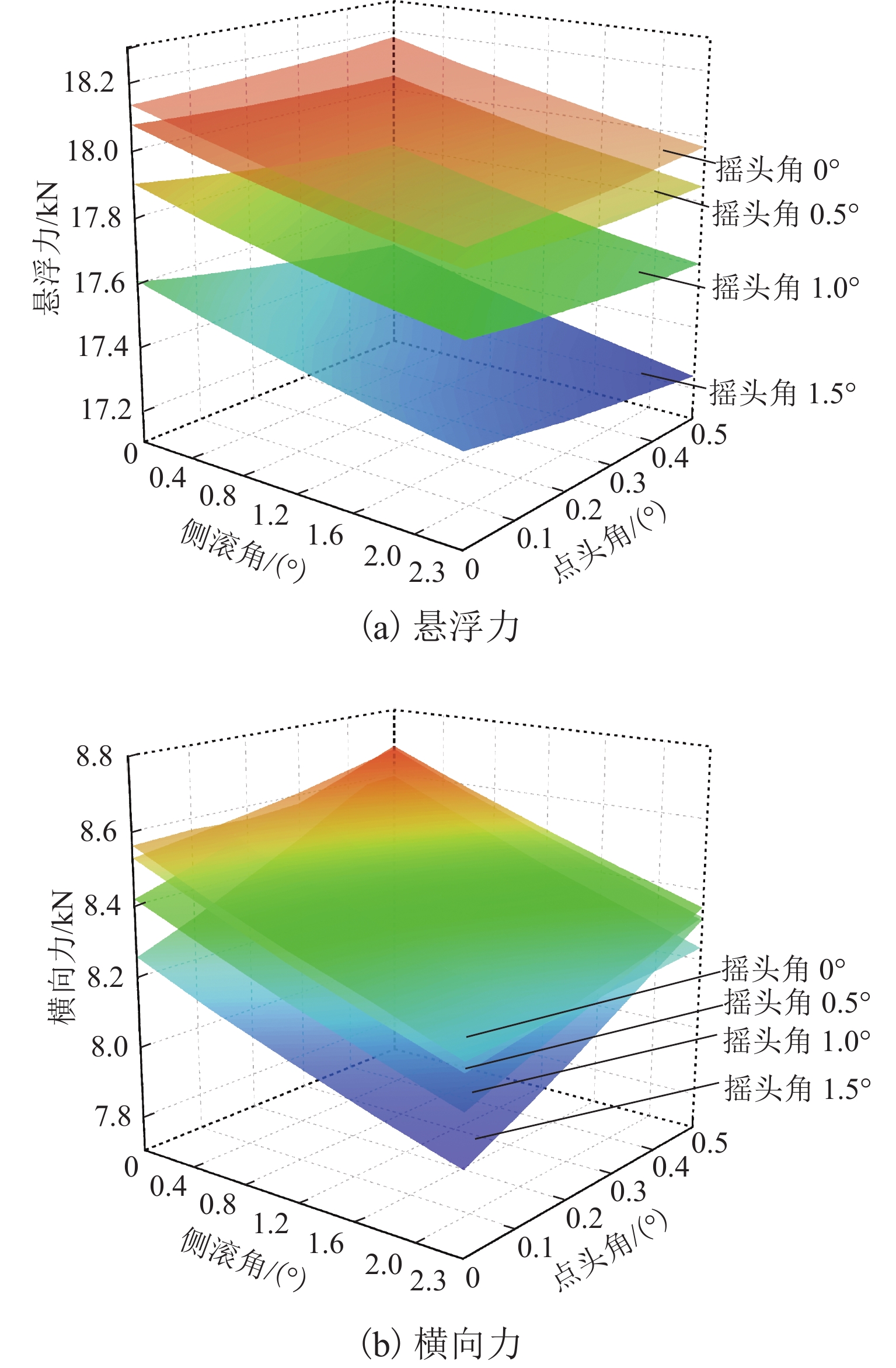
图7（a）给出了第一组复合工况下车载永磁体的悬浮力变化情况. 从图中可以看出：当车载永磁体底面中心处的悬浮间隙为15 mm、横向偏移量为8 mm时，点头、侧滚和摇头运动总体上使得悬浮力略有减小，其中，摇头角对悬浮力的影响相对较大；在第一组复合工况中，悬浮力最小值为17.24 kN，较额定悬浮力降低了14.44%；悬浮力最大值为18.18 kN，由3个转角参数变化带来的悬浮力波动量为0.94 kN，波动量约占额定悬浮力的4.67%. 进一步比较图7（a）和图5（a）（悬浮间隙为15 mm，无横向偏移）计算结果可知：8 mm的横向偏移使得悬浮力整体降低约2.00 kN，此降幅约占额定悬浮力的10.00%.

图  7  悬浮间隙15 mm和横向偏移8 mm时悬浮力、横向力变化

Figure  7.  Variation of levitation force and lateral force with 15 mm levitation gap and 8 mm lateral offset

下载: 全尺寸图片 幻灯片

图7（b）是第一组复合工况下车载永磁体横向力的变化情况. 可以发现：当悬浮间隙为15 mm、横向偏移量为8 mm时，横向力随摇头角和侧滚角增大呈减小趋势，随点头角增大呈增大趋势；横向力最大值和最小值分别为8.69 kN和7.93 kN，分别为额定悬浮力的43.13%和39.35%；3个转角参数变化带来的横向力波动量为0.76 kN，约占额定悬浮力的3.77%，约为横向力平均值8.30 kN的9.16%，说明绝大部分横向力来自于8 mm横向偏移量.

3.2   最大悬浮间隙及最大横向偏移条件下磁力分析

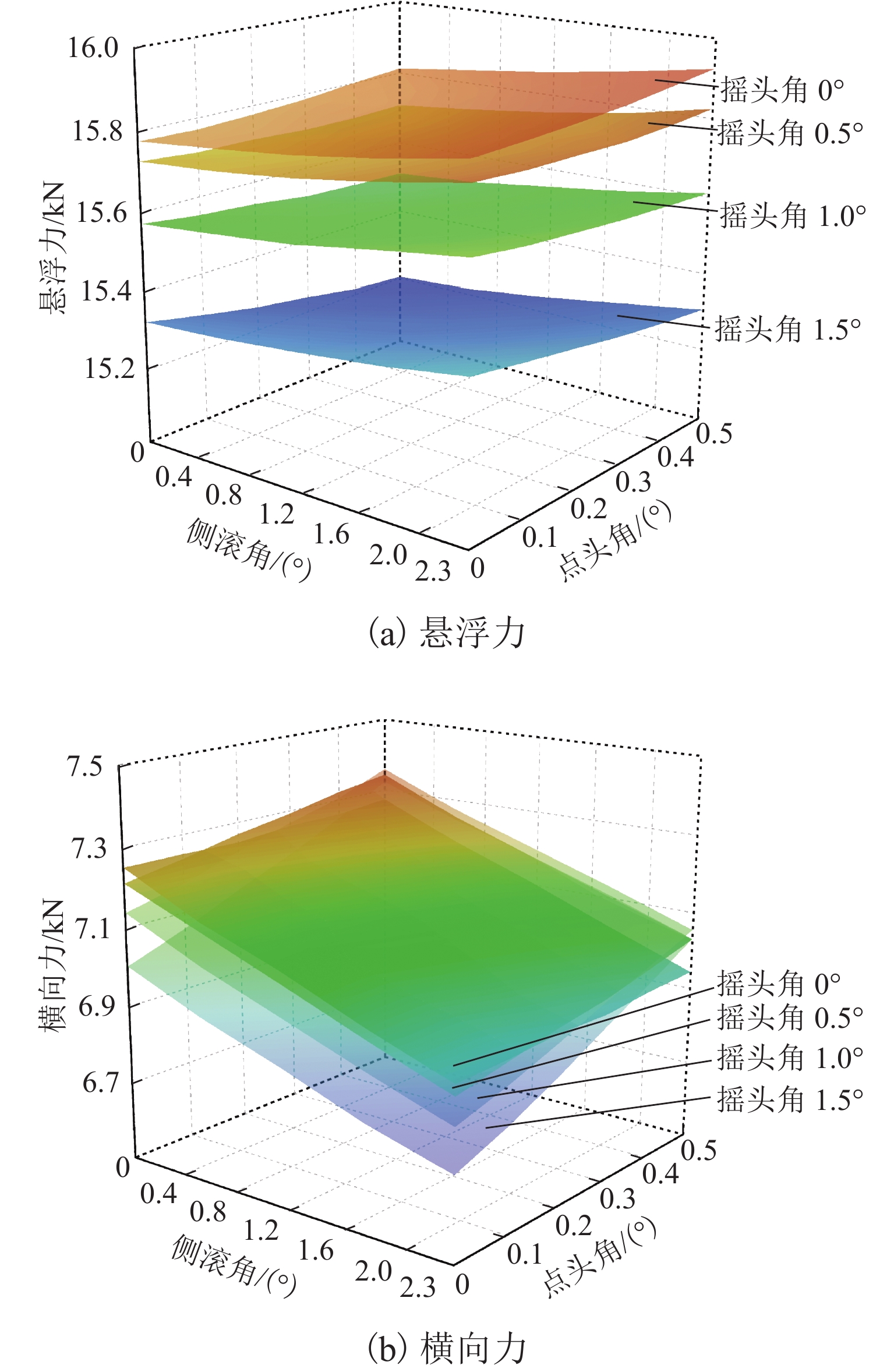
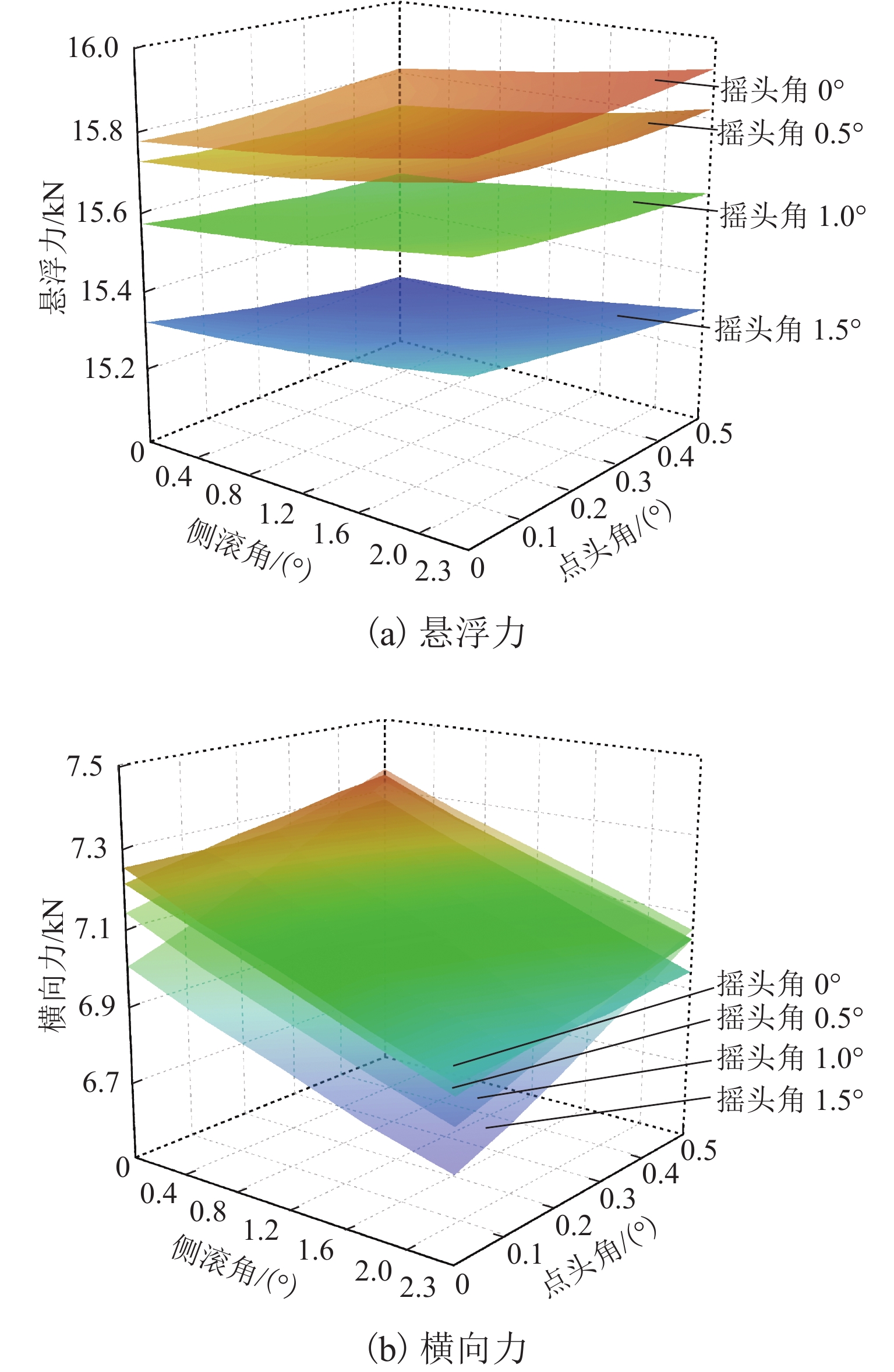
图8（a）给出了第二组复合工况下车载永磁体悬浮力的变化情况. 相比第一组复合工况（图7（a）），第二组复合工况下悬浮力随摇头角增大而减小的趋势不变，但是，随点头角和侧滚角增大不再呈减小趋势，而是略微增大. 在第二组复合工况中，悬浮力最小值为15.21 kN，较额定悬浮力减小了24.52%；悬浮力最大值为15.92 kN，3个转角参数变化导致的悬浮力波动幅值为0.71 kN，占额定悬浮力的3.52%. 比较图8（a）和图7（a）可知，由于悬浮间隙增大了3 mm，第二组复合工况的悬浮力平均值较第一组复合工况降低了2.10 kN，此降幅约占额定悬浮力的10.00%.

图  8  悬浮间隙18 mm、横向偏移8 mm时悬浮力、横向力变化

Figure  8.  Variation of levitation force and lateral force with 18 mm levitation gap and 8 mm lateral offset

下载: 全尺寸图片 幻灯片

图8（b）为第二组复合工况下车载永磁体的横向力变化情况. 可以看出，横向力随摇头角、侧滚角和点头角的变化规律与第一组复合工况相似. 横向力最大值和最小值分别为7.36 kN和6.71 kN，分别为额定悬浮力的36.53%和33.30%. 3个转角参数变化带来的横向力波动量为0.65 kN，占横向力平均值7.10 kN的9.15%，约为额定悬浮力的3.23%. 比较图8（b）和图7（b）可以发现，由于悬浮间隙增加了3 mm，第二组复合工况下横向力的平均值较第一组复合工况降低了1.20 kN，降幅达15.00%.

4.   永磁磁力的参数相关性分析

前文分析表明：车载永磁体的磁力随5个空间位姿参数的变化较为复杂，为了定量化分析各空间位姿参数对磁力的影响，利用获得的539种工况计算结果，采用Spearman相关系数法^[14] 开展了磁力与位姿参数的相关性分析.

通过计算Spearman相关性系数，可以得到一个定量的指标，用于衡量五位姿参数影响下的磁力与单一位姿参数之间的相关性强度，其值为−1～1. 相关性系数为1时表示变量之间完全正相关，为−1时表示变量之间完全负相关，为0时表示变量之间没有相关性，系数绝对值越大则表明变量之间的相关性越强. Spearman相关性系数为

式中：${x_i}$和${y_i}$为第$i$组样本对应的变量值，$i$取值为1～539；$\bar x$和$\bar y$为变量均值.

表2给出了车载永磁体磁力与五位姿参数的Spearman相关性系数. 就悬浮力而言，悬浮间隙与悬浮力的相关性系数为−0.884，是影响悬浮力的主导因素；横移量、摇头角与悬浮力的相关系数分别为−0.333和−0.282，两者对悬浮力有不可忽视的影响；点头角、侧滚角与悬浮力之间的相关性系数分别为−0.073和−0.058，说明其对悬浮力的影响很小；由于悬浮力与5个位姿参数的相关性系数均小于0，说明悬浮力将随5个位姿参数的增大而减小.

表  2  磁力与位姿参数的Spearman相关性系数

Table  2.  Spearman’s correlation coefficients for magnetic force and pose parameters

位姿参数	悬浮力	横向力
悬浮间隙	−0.884	−0.522
横移量	−0.333	0.806
点头角	−0.073	0.190
侧滚角	−0.058	−0.018
摇头角	−0.282	0.074

下载: 导出CSV 

| 显示表格

表2计算结果还表明：横移量和悬浮间隙是影响车载永磁体横向力的主要因素，相应的相关性系数分别为0.806和−0.522；点头角对横向力有一定影响，两者的相关性系数为0.190；侧滚角、摇头角与横向力之间的相关性系数很小，说明侧滚角和摇头角对横向力的影响小.

5.   结　论

以兴国县永磁磁浮交通系统为对象，采用有限元方法计算了不同位姿条件下车载永磁体与永磁体轨道之间的磁力，重点分析了悬浮力和横向力随位姿参数的变化规律，得到以下研究结论：

1） 对于车载永磁体悬浮力，悬浮间隙的影响最大，其次是横向偏移量和摇头角，点头角和侧滚角的影响很小. 悬浮力随悬浮间隙和横向偏移量增大而减小，在本文设定的五位姿参数范围内，悬浮力最大值较额定悬浮力20.15 kN增大了15.78%，原因是悬浮间隙相对于额定值15 mm减小了3 mm；悬浮力最小值较额定悬浮力减小了24.52%，其中3 mm的悬浮间隙增加量使得悬浮力降低了约10.00%，8 mm的横移量使得悬浮力降低了约10.00%.

2） 对于车载永磁体横向力，横向偏移量的影响最大，其次是悬浮间隙，3个转角参数的影响较小；横向力随横向偏移量增大而增大，随悬浮间隙增大而减小. 在本文设定的五位姿参数范围内，横向力最大值和最小值分别为10.16 kN和6.71 kN，分别为额定悬浮力的50.42%和33.30%. 特别地，车载永磁体横向力的方向与其横向偏移方向一致，在没有外部横向约束的情况下，将形成横移量增大—悬浮间隙减小—横向量继续增大的恶性循环，因此，必须为永磁悬浮系统设置主动或被动导向装置，以获得稳定的悬浮.

3） 车载永磁体的摇头运动不仅明显降低了悬浮力，还带来了促使摇头角继续增大的摇头力矩. 当悬浮间隙为15 mm、横向偏移为0、摇头角为1.5°时，摇头力矩为860 N·m. 尽管摇头力矩不大，仍有必要对其进行约束，预防车载永磁体偏航运行.

致谢：国家资助博士后研究人员计划课题（GZB20230612）.