Modeling and Dynamics Analysis of High-Temperature Magnetic Bearing-Rotor System
-
摘要:
在多电航空发动机中,主动磁悬浮轴承因其耐高温、非接触等特性可以突破温度对支承部位的限制,使支承部位能够更靠近燃烧室. 为探究温度对磁悬浮轴承转子系统动态特性的影响规律,提出一种高温磁悬浮轴承转子系统动力学建模方法. 通过仿真得到转子在不同温度下的温度分布,并使用多项式拟合转子轴向温度分布;基于有限元方法推导柔性转子单元的动力学模型,引入温度影响,建立考虑温度影响的磁悬浮轴承转子系统整体动力学模型,并通过模态试验验证模型的准确性;基于理论动力学模型分析系统的动态特性. 结果表明:温度升高会导致转子的前三阶支承模态频率下降,增大各阶幅频响应幅值;当温度从常温升至450 ℃时,转子的前三阶弯曲支承模态频率分别降低了3.818%、5.670%、3.183%,前三阶弯曲模态幅频响应幅值分别升高了83.4%、34.4%、24.1%.
Abstract:In the multi-electric aircraft engine, an active magnetic bearing can break through the limitation of temperature on the support part due to its high temperature resistance and non-contact characteristics, which enables its support part to be closer to the combustion chamber. In order to investigate the influence of temperature on the dynamic characteristics of the magnetic bearing-rotor system, a dynamics modeling method for a high-temperature magnetic bearing-rotor system was proposed. The temperature distributions of the rotor at different temperatures were obtained through simulation, and the axial temperature distribution of the rotor was fitted using polynomials. Based on the finite element method, the dynamics model of the flexible rotor unit was derived. The temperature influence was introduced, and the overall dynamics model of the magnetic bearing- rotor system considering the temperature influence was established. The accuracy of the model was verified by a modal test. The dynamic characteristics of the system were analyzed based on the theoretical dynamics model, and the results show that an increase in temperature leads to a decrease in the first three orders of the support modal frequency of the rotor and an increase in the amplitude of the amplitude frequency response of each order. When the temperature increases from room temperature to 450 ℃, the first three orders of the bending support modal frequency of the rotor decrease by 3.818%, 5.670%, and 3.183%, respectively, and the amplitudes of the first three orders of the bending modal amplitude frequency response increase by 83.4%, 34.4%, and 24.1%, respectively.
-
自20世纪90年代起,欧美相继推出各类研发计划,旨在探究磁悬浮轴承在航空发动机上应用的可能性,利用磁悬浮轴承取代机械轴承支承的“多电航空发动机”概念被提出[1]. 航空发动机转子系统中的支承轴承一般为滚动轴承,其耐热温度通常在180~260 ℃,支承位置需要远离燃烧室,同时,需要配备润滑冷却系统以避免燃烧室高温带来的影响. 主动磁悬浮轴承与转子之间无摩擦、无润滑,避免机械轴承所带来的功耗,其工作温度最高能够达到550~600 ℃[2-3]. 使得磁悬浮轴承的设置位置更加靠近燃烧室或者涡轮室,从而缩短发动机的轴向尺寸. 然而,结构紧凑的同时,磁悬浮转子系统也会受到燃烧室或者涡轮室所带来的高温温度场的影响. 因此,构建合理准确的高效转子动力学计算模型是开展高温磁悬浮转子系统动力学设计和控制的关键.
在考虑温度对转子动力学模型的影响方面:Ziaei-rad等[4]开展了考虑转子轴摩擦响应的热弹性建模方面的相关研究,将热效应等效为热弯矩,对转子的动力学特性进行相关的分析;朱向哲等[5]使用有限元软件对转子振动特性进行分析,考虑了稳态温度场对转子系统振动特性的影响,但并未给出理论的动力学模型;何鹏等[6]开展了考虑杨氏模量随轴向温度变化转子有限元建模方法研究,但温度在轴向上仅呈线性分布,与实际温度分布有所差距;Gou等[7]在对齿轮转子系统进行建模研究时,考虑了非线性齿轮接触面的瞬时温度,分析齿轮接触面瞬时温度对齿轮转子系统稳定性的影响;Xiang等[8]考虑热载荷以及气动载荷对航空发动机的影响,对转子进行建模研究,分析温度对转子刚体模态的影响,但是缺少进一步对转子弯曲模态的研究. 上述研究将温度引入系统动力学模型中,考虑温度场所带来的系统刚度、系统阻尼、接触面条件等因素对模型的影响,进一步完善了考虑温度场的转子动力学模型. 但是,磁悬浮轴承与机械轴承有着较大的区别,目前,仍缺少温度场对磁悬浮转子系统相关动力学的影响研究.
在磁悬浮转子系统建模方面:Du等[9]分析了基于滑模控制的磁悬浮转子系统动力学,对磁悬浮轴承工作点附近的磁场进行线性化,建立四自由度刚性转子-轴承系统模型;Mushi等[10]研究了应用于小型离心压缩机上的磁悬浮转子系统,建立柔性磁悬浮转子系统模型,同时使用状态空间方程将电控系统引入到模型中;Xu等[11]在磁悬浮柔性转子模型基础上,进一步对主动磁悬浮轴承的等效刚度和阻尼进行辨识,从而使得模型更加准确;沈权等[12]研究了基础激励下磁悬浮转子系统动力学,将基础激励引入到有限元模型中,建立考虑基础激励的磁悬浮转子系统机电一体化模型;Wu等[13]对汽轮机使用的多盘磁悬浮转子系统进行建模研究,利用欧拉-伯努利梁单元建立柔性轴模型,试验验证了模型的准确性. 上述研究为磁悬浮转子系统建模做出了系统的贡献,但是仍然未将温度引入磁悬浮转子系统中,缺少对高温磁悬浮转子系统建模相关方面的研究.
在高温磁悬浮轴承研究方面,中国燃气涡轮研究院与南京航空航天大学合作,在一台小型航空发动机上进行磁轴承的试验研究,试验样机实现了450 ℃的工作运行[14]. 洛桑联邦理工学院(EPFL)建立了有利于高温磁悬浮轴承优化设计的热模型,分析不同电流下磁悬浮轴承温度上升及分布情况. 基于该模型完成高温磁悬浮轴承的设计,同时,分析550 ℃ 下的转子振型[15]. 美国航空航天局(NASA)也进行了高温磁悬浮轴承的相关研究,分析磁悬浮轴承的动态特性在高机动载荷上的优点[16]. 上述研究进行了一定数量的高温磁悬浮轴承样机研制工作,并进行悬浮试验. 但并未建立对应的理论数学模型,从而在理论上解释系统的动力学现象.
针对上述问题,本文首先介绍模拟转子试验台,通过温度场仿真获取转子系统的温度分布,并使用高次多项式来拟合轴向温度场数学模型;然后,基于有限元法给出柔性转子单元动力学模型,考虑温度对材料杨氏模量和泊松比的影响,重构系统模型矩阵,构建考虑温度影响的转子机械系统整体动力学模型,推导考虑温度的系统等效刚度,分析温度对系统等效刚度的影响;再次,对比模态试验和理论模型计算的结果来验证模型的有效性. 最后,根据系统理论动力学模型对转子系统进行了动力学分析.
1. 温度场分析
1.1 试验台结构介绍
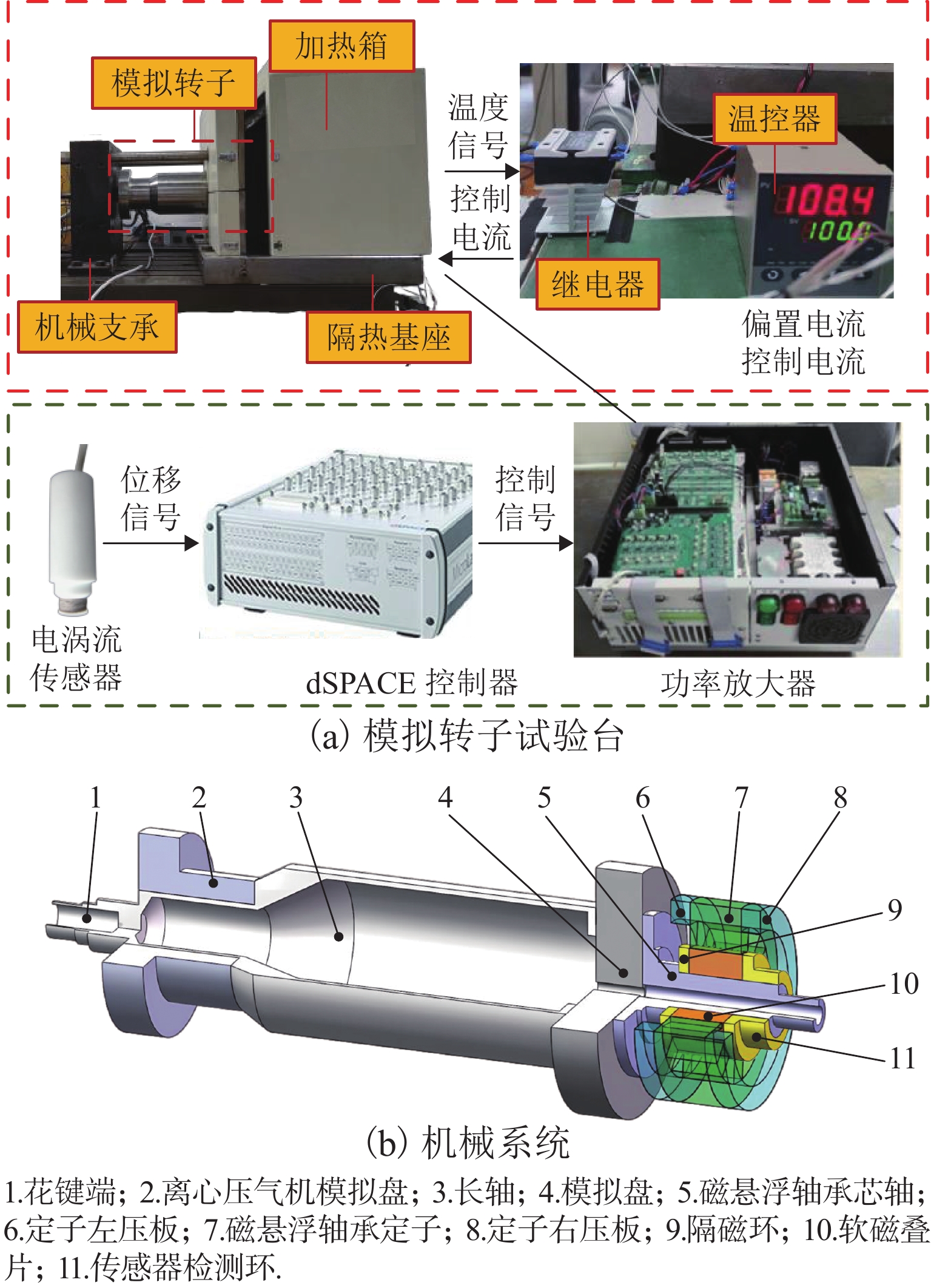
高温磁悬浮轴承模拟转子试验台结构如图1所示,其中,机械系统主要分为11个部分,所用材料如表1所示. 转子的左侧通过花键与联轴器进行连接,使用机械轴承作为支承. 离心压气机叶轮和高压压气机叶轮使用转动惯量和质量相同的圆盘来进行等效,热套在长轴上. 中间的长轴采用中空结构来模拟实际转子,转子的最右侧使用磁悬浮轴承作为支承. 电控系统中,电涡流传感器用来检测转子位移,dSPACE控制器用来输出控制信号,功率放大器用来输出偏置电流和控制电流. 温度控制系统中,温控器用来输出温度控制信号,继电器用来输出控制电流,加热烘箱用来加热高温磁悬浮轴承.
表 1 机械系统所使用的材料Table 1. Materials used in mechanical systems序号 所用材料 1,2,3,4,6,8 1Cr11Ni2W2MoV 5 GH4169 7,10 高温软磁合金(1J22) 9,11 38 黄铜 1.2 温度场数学模型拟合
由于烘箱热源位于转子系统一侧,加热时为转子单侧加热,转子轴向温度分布为非线性,传统传热方程难以准确表示出轴向温度的分布情况. 为准确表征温度场的轴向分布,本文使用有限元分析软件ANSYS Workbench进行转子系统的传热仿真.
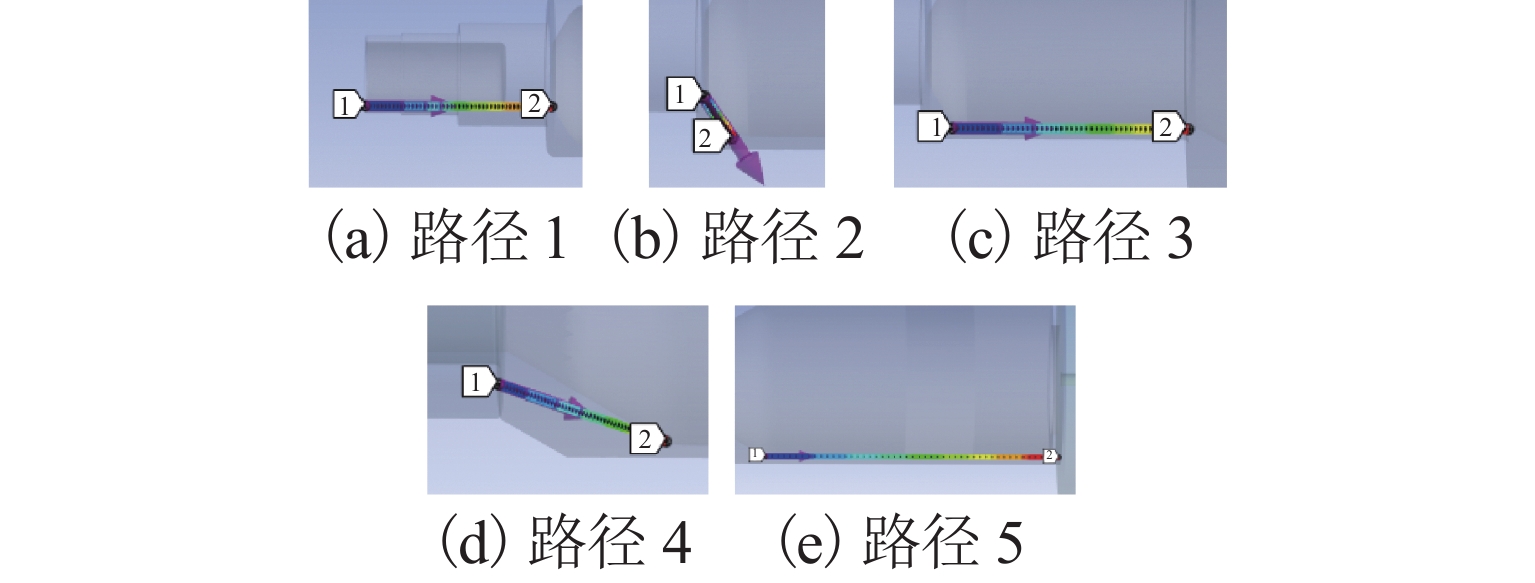
基于图1所示的模拟转子试验台,进行机械系统温度场划分,外部传热条件以及转子轴向温度数据的采样点如图2所示. 磁悬浮轴承支承部位侧设置为仿真时的热源,此区域内温度恒定,模拟实际的烘箱加热条件,其余部位根据加热工况设置不同的传热条件. 3个热对流与热传导区域外部分别设置不同的热通量值来模拟转子与外界的换热情况,热通量值需要根据加热工况不断调整,以使仿真得到的转子表面温度更贴合实际试验时转子的表面温度.
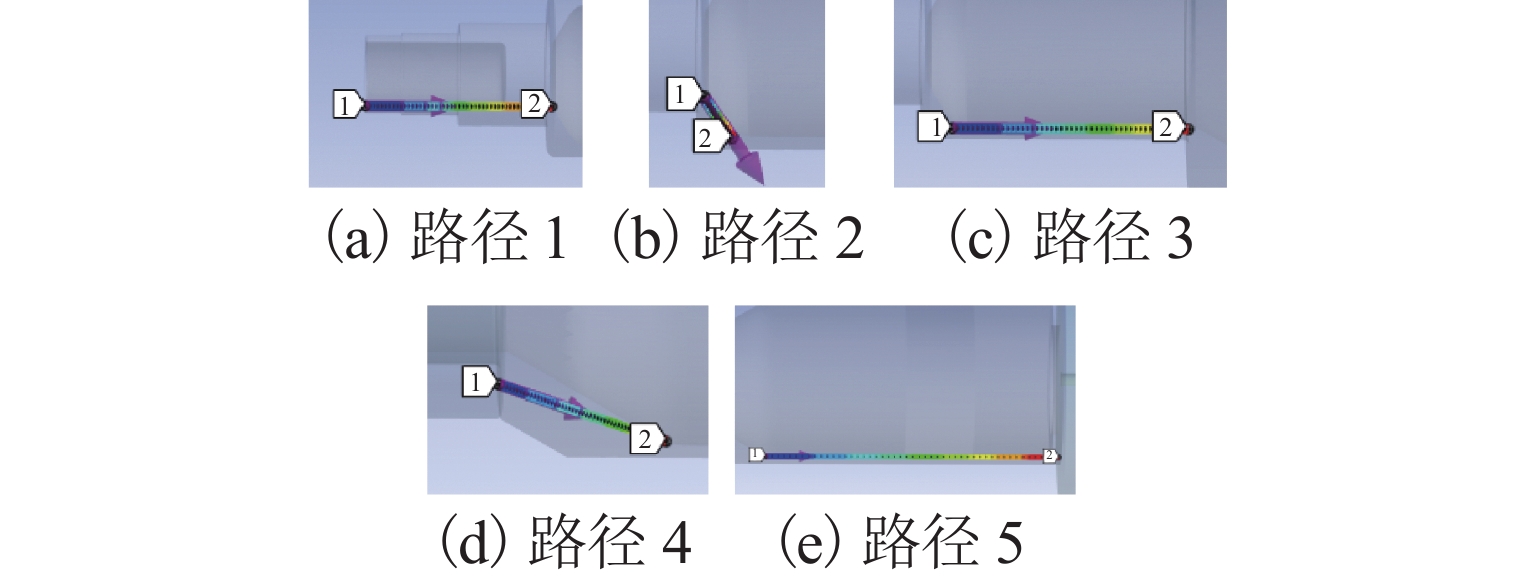
由于仿真得到的转子温度为离散的点数据,因此,在转子实体部分设置温度导出路径以及温度数据采样点. 由于热源部分温度恒定,故只需要在非恒温区设置温度数据导出点. 将转子轴向温度场的数据导出,使用多项式拟合为连续的温度场数学模型,作为后续系统建模的基础.
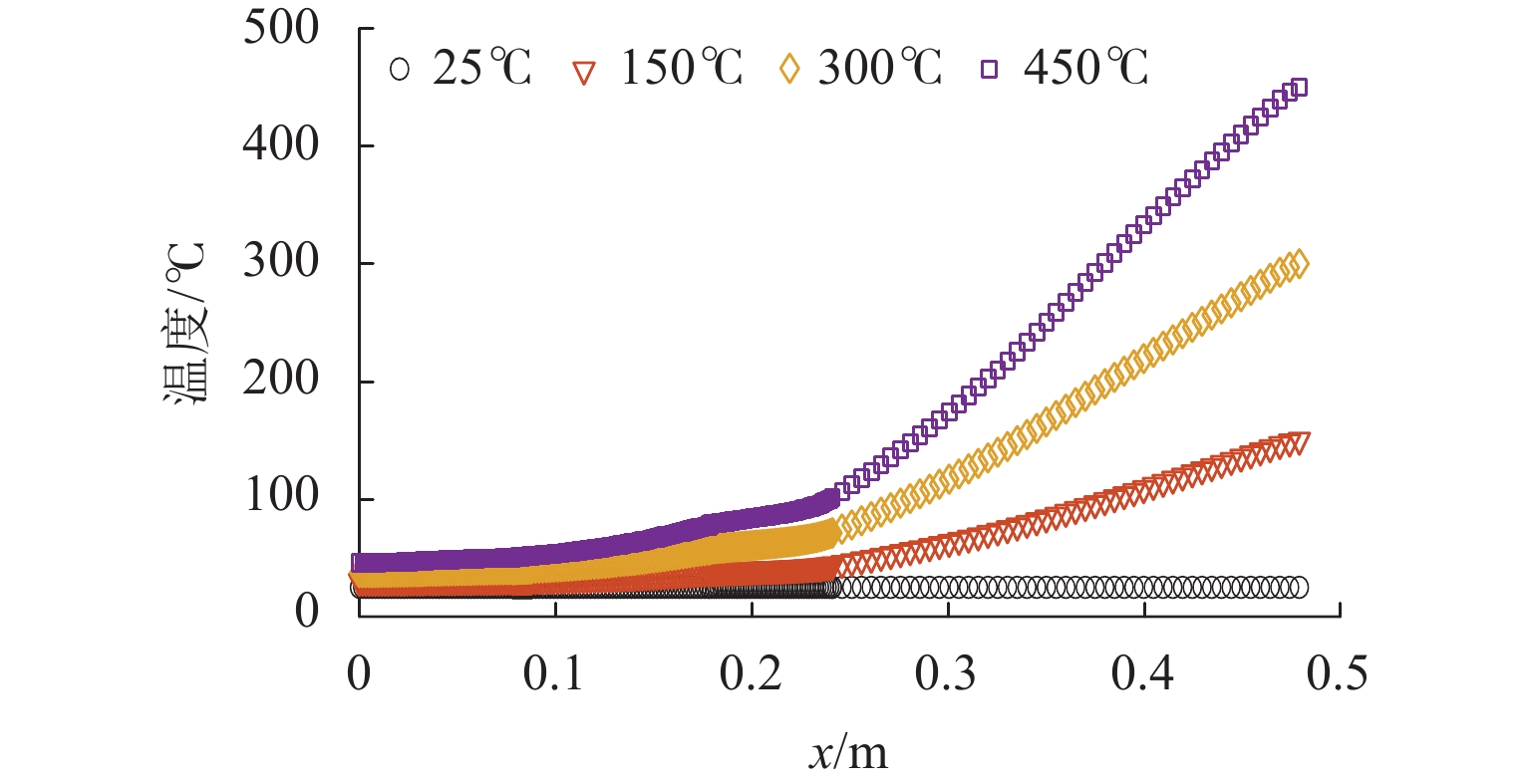
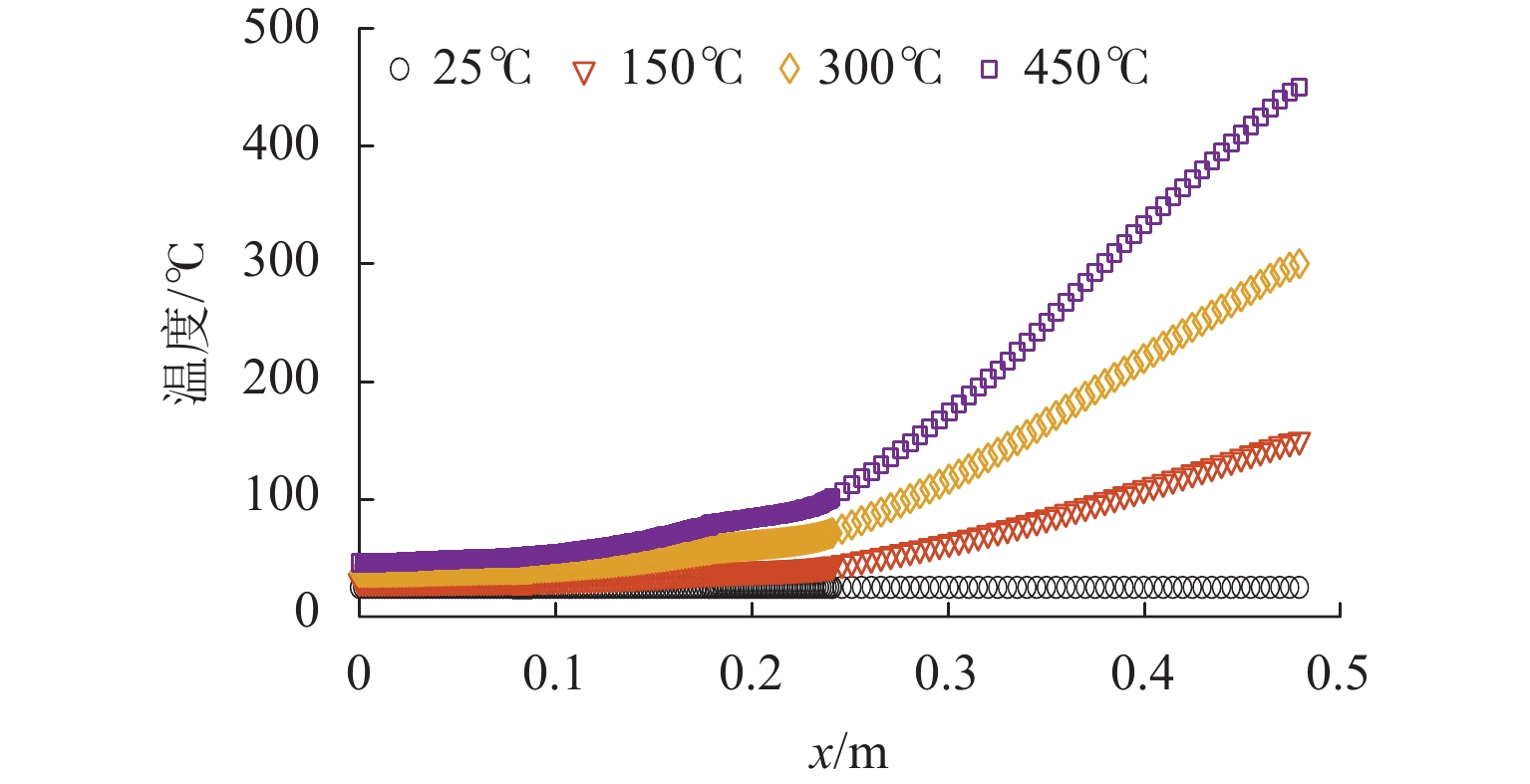
实际仿真模型如图3所示. 通过设置不同热源温度(25、150、300、450 ℃)来模拟不同温度下转子的温度分布. 将图4所示的温度场路径上采样点的温度数值导出,结果显示在图5中. 图中:x为转子上点的绝对轴向位置.
为将导出的离散点数据拟合为曲线,使用式(1)所展示多项式对离散点进行拟合,得到连续的转子轴向温度场数学模型.
T(x)=T0(m∑j=1τjxj+η), (1) 式中:T(x)为转子上轴向距离为x的点的温度值,T0为热源温度,j为拟合阶次,m为拟合的最高阶次,τj为多项式系数,η为多项式常数项.
使用最小二乘法进行拟合,得到不同拟合阶次下的多项式拟合模型. 其中,多项式的阶次会影响拟合精度,但是过高的阶次同样也会增加公式的复杂性. 因此,使用相关系数R2来评价多项式的综合性能,如式(2)所示.
R2=n∑k=1(ˆek−ˉe)2/n∑k=1(ek−ˉe)2, (2) 式中:n为样本数量(在本文中为温度采样点的总个数),ek为温度采样点k的温度数值,ˆek为拟合程序计算出的采样点的拟合数值,ˉe为采样点温度的平均值.
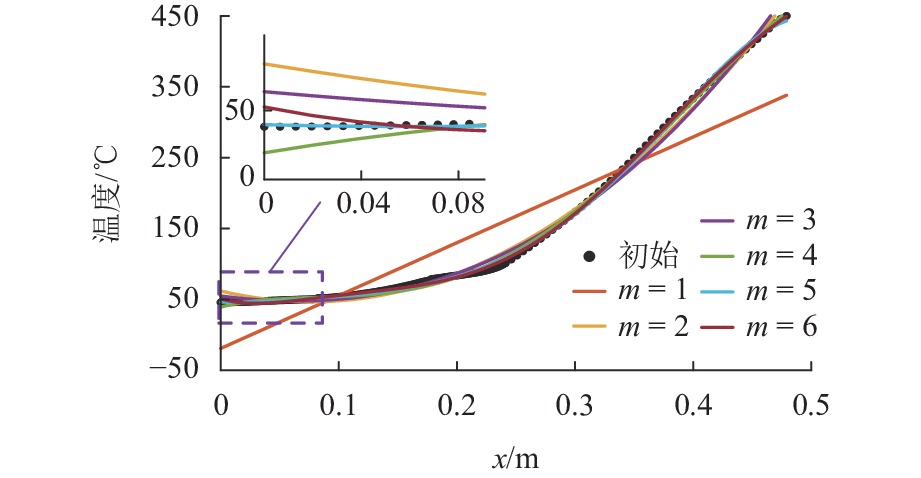
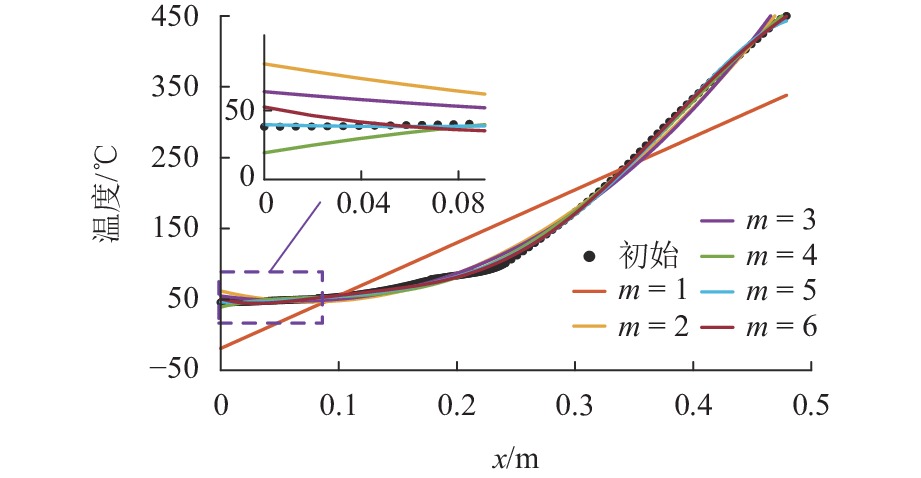
图6展示了450 ℃温度工况下,不同最高阶次的多项式模型结果. R2越大表示多项式与原数据点的拟合度越高,通常情况下R2 > 0.900000可以认为拟合的精度较高[17].
不同温度工况下,不同多项式最高拟合阶次的R2值如表2所示. 从表中可以看出,对本文所研究的转子轴向温度场所拟合的曲线,随着拟合阶次的增加,R2值也随之增加,表示拟合的精度越高,但是从图6的放大部分可以看出,在低温区域,部分拟合曲线与原始数据点的重合度不高,出现了过拟合的情况. 综合R2值的大小、低温区域拟合程度以及计算量大小,选择5次多项式来拟合轴向温度场. 最终,不同温度工况下的转子轴向温度场数学模型可以表示为
表 2 数学模型拟合的R2值Table 2. R2 by mathematical model fittingm 150 ℃ 300 ℃ 450 ℃ 1 0.799 123 0.815 718 0.824 486 2 0.993 046 0.993 757 0.993 782 3 0.996 804 0.995 234 0.994 565 4 0.998 708 0.998 45 0.998 344 5 0.999 406 0.999 188 0.999 120 6 0.999 495 0.999 374 0.999 328 {T(x)=T0(m∑j=1τjxj+η), x⩽475mm,T(x)=T0, x>475mm. (3) 2. 考虑温度的有限元建模
2.1 考虑温度影响的转子系统模型
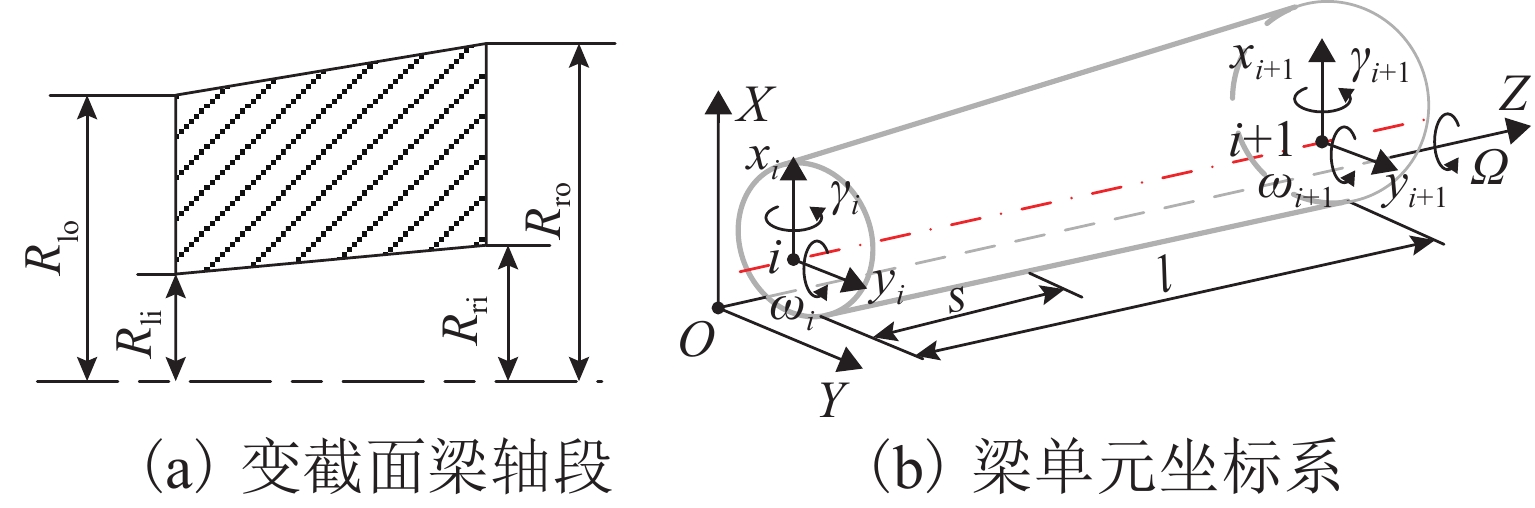
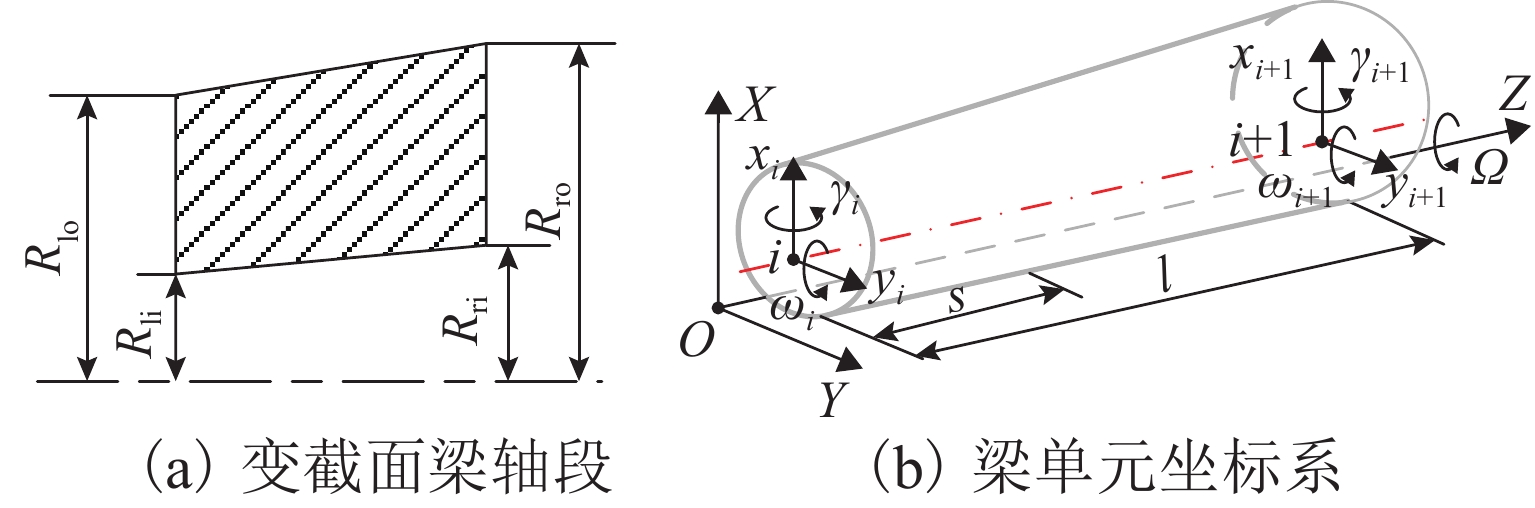
通过有限元法对试验台转子进行建模,转子单元基于8自由度的尼尔森-铁木辛柯梁单元. 图7(a)、图7(b)分别显示了厚度线性变化的锥形梁单元和梁单元坐标系. 图中:Rlo、Rli、Rro、Rri分别为单元左侧截面的外径和内径以及单元右侧截面的外径和内径;i为单元的节点位置序号(截面序号),单元两端的节点位移向量q=[xi yi γi ωi xi+1 yi+1 γi+1 ωi+1]T,xi、yi分别为单元节点i在X和Y方向上的位移,γi、ωi分别为单元节点i在X和Y方向上的角度变化;Ω为转子的转速.
单元面积A、径向惯性矩It和极惯性矩Ip如下:
A=Al(1+α1ξ+α2ξ), (4) Al=π(R2lo−R2li), (5) It=Iti(1+β1ξ+β2ξ2+β3ξ3+β4ξ4), (6) Iti=π(R2ro−R2ri)/4, (7) Ip=2It, (8) 式(4)~(8)中:ξ为无量纲位置坐标,如式(9);α1、α2、β1、β2、β3、β4的定义如式(10).
ξ=s/l, (9) 式中:s为梁单元的轴向位置坐标,l为单元的轴向长度.
{α1=2π(RloΔRo−RliΔRi)/Al,α2=π(ΔR2o−ΔR2i)/Al, β1=π(R3loΔRo−R3liΔRi)/Iti,β2=3π(R2loΔR2o−R3liΔR2i)/(2Iti), β3=π(RloΔR3o−R3liΔR3i)/Iti,β4=π(ΔR4o−ΔR4i)/4Iti, (10) 式中:ΔRo=Rro−Rlo,ΔRi=Rri−Rli.
对于一个两节点八自由度的铁木辛柯梁轴段单元,假设形函数为
\left\{ \begin{gathered} \left[ \begin{gathered} X(s) \\ Y(s) \\ \end{gathered} \right] = \psi (s){\boldsymbol{q}},\\ \left[ \begin{gathered} \gamma (s) \\ w (s) \\ \end{gathered} \right] = \phi (s){\boldsymbol{q}} \text{,} \end{gathered}\right. (11) 式中:ψ(s)和ϕ(s)均为构造的形函数,X(s)、Y(s)和γ(s)、w(s)分别为X、Y方向的位移函数和角度函数.
轴段包含扭转运动的动能和势能,分别如式(12)、(13).
\qquad T=\frac{1}{2}{\displaystyle {\int }_{ 0}^{l}\left\{\rho A\left[{\left(\frac{\partial X}{\partial s}\right)}^{2}+{\left(\frac{\partial Y}{\partial s}\right)}^{2}\right]+{I}_{{\mathrm{t}}}\left[{\left(\frac{\partial \gamma }{\partial s}\right)}^{2}+{\left(\frac{\partial w }{\partial s}\right)}^{2}\right]\right\}}{\mathrm{d}}s- \frac{1}{2}{\displaystyle {\int }_{ 0}^{l}\left[{I}_{{\mathrm{p}}}\varOmega\left(\gamma \frac{\partial w }{\partial s}-w \frac{\partial \gamma }{\partial s}\right)-{I}_{{\mathrm{p}}}\varOmega\right]}{\mathrm{d}}s, \\ (12) \qquad\qquad\quad U=\frac{1}{2}{\displaystyle {\int }_{0}^{l}E{I}_{{\mathrm{p}}}\left[{\left(\frac{\partial \gamma }{\partial s}\right)}^{2}+{\left(\frac{\partial w }{\partial s}\right)}^{2}\right]}{\mathrm{d}}s+ \text{ }\frac{1}{2}{\displaystyle {\int }_{0}^{l}K_{1}GA\left[{\left(\frac{\partial X}{\partial s}-w \right)}^{2}+{\left(\frac{\partial Y}{\partial s}+\gamma \right)}^{2}\right]}{\mathrm{d}}s, (13) 式(12)、(13)中:ρ为单元材料的密度,E为单元材料的杨氏模量, G为剪切模量,K1为剪切矫正因子,如式(14).
\begin{gathered}K_1=\frac{6(1+\nu)(1+m^2)^2}{(7+6\nu)(1+m^2)^2+(20+12\nu)m^2}, \\ \end{gathered} (14) 式中: \nu 为单元材料的泊松比, m=\sqrt{\dfrac{R_{{\mathrm{li}}}^2+R_{{\mathrm{Ri}}}^2}{R_{{\mathrm{lo}}}^2+R_{{\mathrm{Ro}}}^2}} .
将式(12)、(13)代入拉格朗日能量方程中,可以得到轴段的动力学微分方程为
\boldsymbol{M\ddot{q}}+(\boldsymbol{C}_{\mathrm{s}}+\varOmega\boldsymbol{G}){\dot{q}}+\boldsymbol{Kq}=\boldsymbol{f}_{\rm{s}}, (15) 式中:M为单元质量矩阵,Cs为单元结构阻尼矩阵,G为单元陀螺矩阵,K为单元刚度矩阵,fs为弹性轴单元所受外加力向量.
以K为例,每个单元节点包含4个自由度,含两节点的单元刚度矩阵K的大小为8 × 8,可以进一步表示为4个4 × 4大小的子矩阵k11、k12、k21、k22的组集,如式(16)所示.
{\boldsymbol{K}}=\left[\begin{array}{*{20}{c}}{\boldsymbol{k}}_{\text{11}} & {\boldsymbol{k}}_{\text{12}} \\ {\boldsymbol{k}}_{\text{21}} & {\boldsymbol{k}}_{\text{22}}\end{array}\right]. (16) 对含有n个单元的转子,两两单元共用的节点仅被视为一个节点,转子轴段共有n+1个节点. 转子系统整体的广义坐标可以表示为
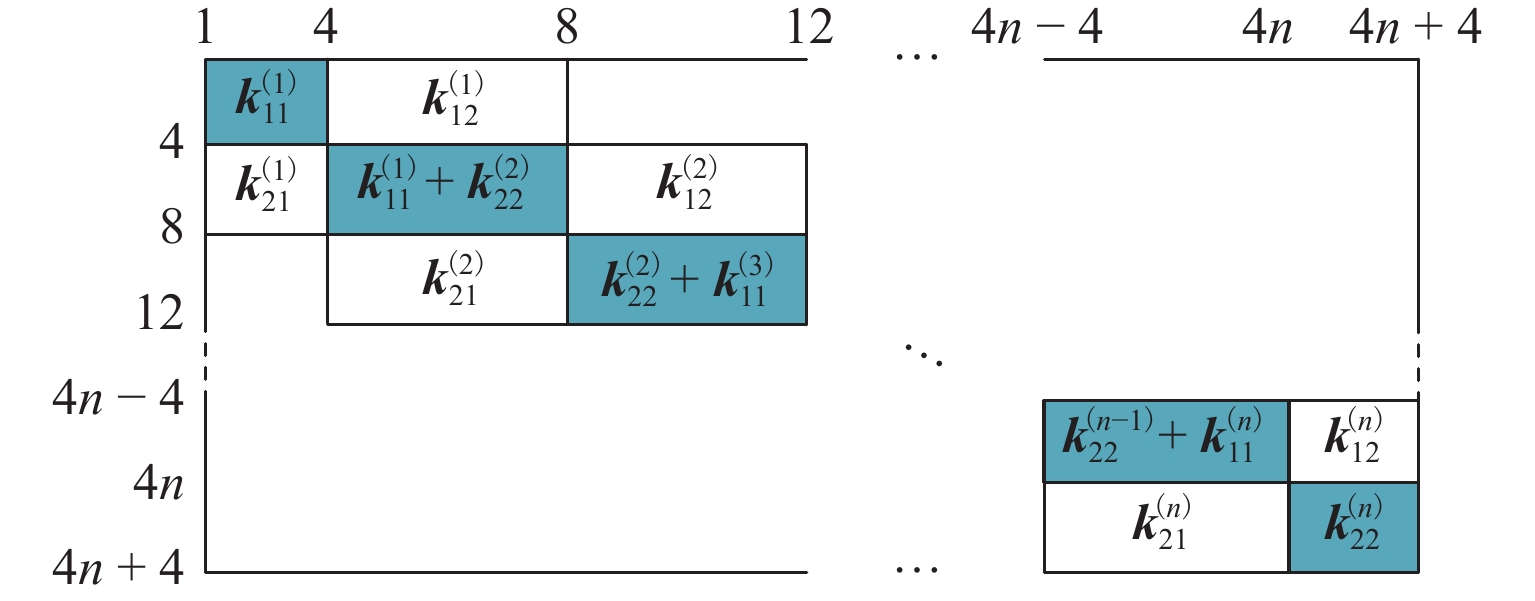
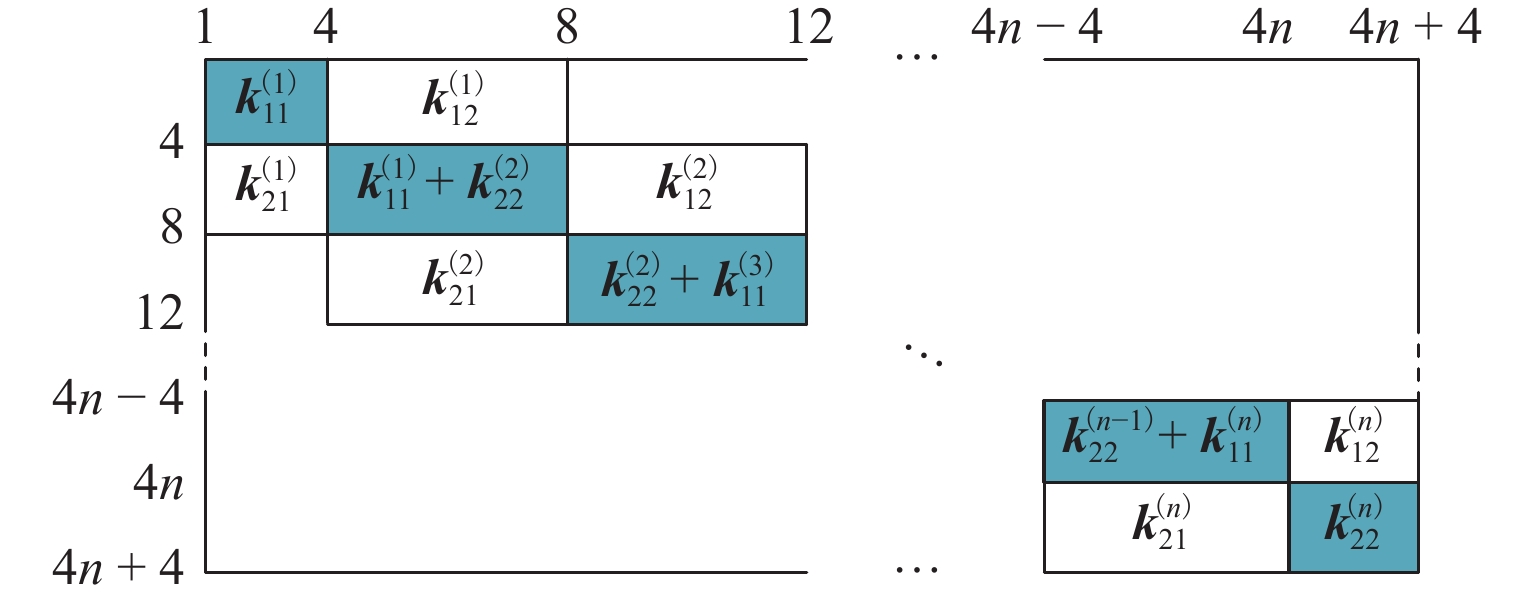
\begin{split} &{{\boldsymbol{q}}_{\mathrm{w}}} = [{x_1}{\text{ }}{y_1}{\text{ }}{\gamma _1}{\text{ }}{w _1}{\text{ }}{x_2}{\text{ }}{y_2}{\text{ }}{\gamma _2}{\text{ }}{w _2}\;\cdots\;\\ &\quad {x_{n + 1}}{\text{ }}{y_{n + 1}}{\text{ }}{\gamma _{n + 1}}{\text{ }}{w _{n + 1}}] . \end{split} (17) 对转子所含有的全部单元所具有的刚度矩阵、质量矩阵、陀螺矩阵进行组装. 组装过程如图8所示. 图中:上标(1)表示第1个单元的子矩阵,以此类推.
转子系统整体的广义坐标包含转子的所有自由度,因此其集总矩阵组成部分为(4n + 4) × (4n + 4)矩阵. 此时,转子系统整体动力学模型可以表示为
{\boldsymbol{M}}_{\mathrm{w}}\ddot{{\boldsymbol{q}}}_{\mathrm{w}}+({\boldsymbol{C}}_{{\mathrm{sw}}}+\varOmega {\boldsymbol{G}}_{\mathrm{w}})\dot{{\boldsymbol{q}}}_{\mathrm{w}}+{\boldsymbol{K}}_{\mathrm{w}}{\boldsymbol{q}}_{\mathrm{w}}={\boldsymbol{f}}_{{\mathrm{sw}}}, (18) 式中:K加下标w表示将全部单元的刚度矩阵组集在一起后的转子整体刚度矩阵,其余变量类推.
在考虑温度对材料属性的影响时,本文主要研究温度对材料的杨氏模量和泊松比的影响. 轴向的不均匀温度分布会导致材料的相关参数发生变化,如弹性模量、泊松比、密度和线膨胀系数等[17],从而对整个转子系统产生一系列的影响. 机械系统所采用的材料均为金属材料,金属材料的杨氏模量和泊松比会随着温度的升高而下降. 可以使用二次多项式较为准确的拟合材料的杨氏模量和泊松比随温度变化的情况[13]. 当热源温度为T0时第λ个单元的杨氏模量和泊松比如式(19)所示.
\left\{\begin{gathered}E_{ \lambda }=E_{\text{0}}\text{(}a_{\text{1}}T_{ \lambda }^2+b_{\text{1}}T_{ \lambda }+c_{\text{1}}\text{),} \\ \nu_{ \lambda }=\nu_{\text{0}}\text{(}a_{\text{2}}T_{ \lambda }^2+b_{\text{2}}T_{ \lambda }+c_{\text{2}}\text{),} \\ \end{gathered}\right. \\ (19) T_{ \lambda }=\left\{\begin{gathered}T_0\left(\sum\limits_{j=1}^5\tau_jx_{ \lambda }^j+\eta\right),\quad x_{ \lambda }\leqslant475\text{ mm}, \\ T_0, \quad x_{ \lambda } > 475\text{ mm}, \\ \end{gathered}\right. \\ 式中:E0和ν0分别为常温状态下材料的杨氏模量和泊松比,Tλ为第λ个单元的单元中心温度,xλ为第λ个单元中心的绝对轴向距离,a1、b1、c1、a2、b2、c2分别表示拟合二次项公式的系数和常数,不同材料的系数和常数由实际材料属性确定.
将温度对杨氏模量和泊松比的影响考虑到动力学模型式(15)当中,并对系统的各个矩阵进行重新组集以形成考虑温度的转子系统整体模型.
以转子单元刚度矩阵为例. 对转子有限元模型的第λ个单元,将xλ代入式(19)得到新单元的Eλ和νλ值,将其代入到刚度矩阵中替换E0和ν0,整个过程如图9所示. 图中:{\boldsymbol{k}}_{11}^{(\lambda )} 、{\boldsymbol{k}}_{12}^{(\lambda )} 、{\boldsymbol{k}}_{21}^{(\lambda )} 、{\boldsymbol{k}}_{22}^{(\lambda )} 为根据有限元法推导的常温状态下大小为4 × 4的子矩阵,{\boldsymbol{k}}_{{\mathrm{t}}11}^{(\lambda )} 、{\boldsymbol{k}}_{{\mathrm{t}}12}^{(\lambda )} 、{\boldsymbol{k}}_{{\mathrm{t}}21}^{(\lambda )} 、{\boldsymbol{k}}_{{\mathrm{t}}22}^{(\lambda )} 为将转子材料属性数值替换为对应温度下的数值后得到的新的子矩阵.
引入刚度矩阵,构建考虑温度的系统刚度矩阵. 将系统质量矩阵和陀螺矩阵按照此方式重构,最终可以得到考虑温度的转子机械系统动力学模型为
\boldsymbol M_{{\mathrm{wT}}}\ddot{{\boldsymbol{q}}}_{\mathrm{w}}+({\boldsymbol{C}}_{{\mathrm{swT}}}+\varOmega {\boldsymbol{G}}_{{\mathrm{wT}}})\dot{{\boldsymbol{q}}}_{\mathrm{w}}+{\boldsymbol{K}}_{{\mathrm{wT}}}{\boldsymbol{q}}_{\mathrm{w}}={\boldsymbol{f}}_{{\mathrm{swT}}}\text{,} (20) 式中:各变量加下标T表示对应的该变量考虑了温度影响后的结果,后文同.
2.2 温度场对等效刚度的影响
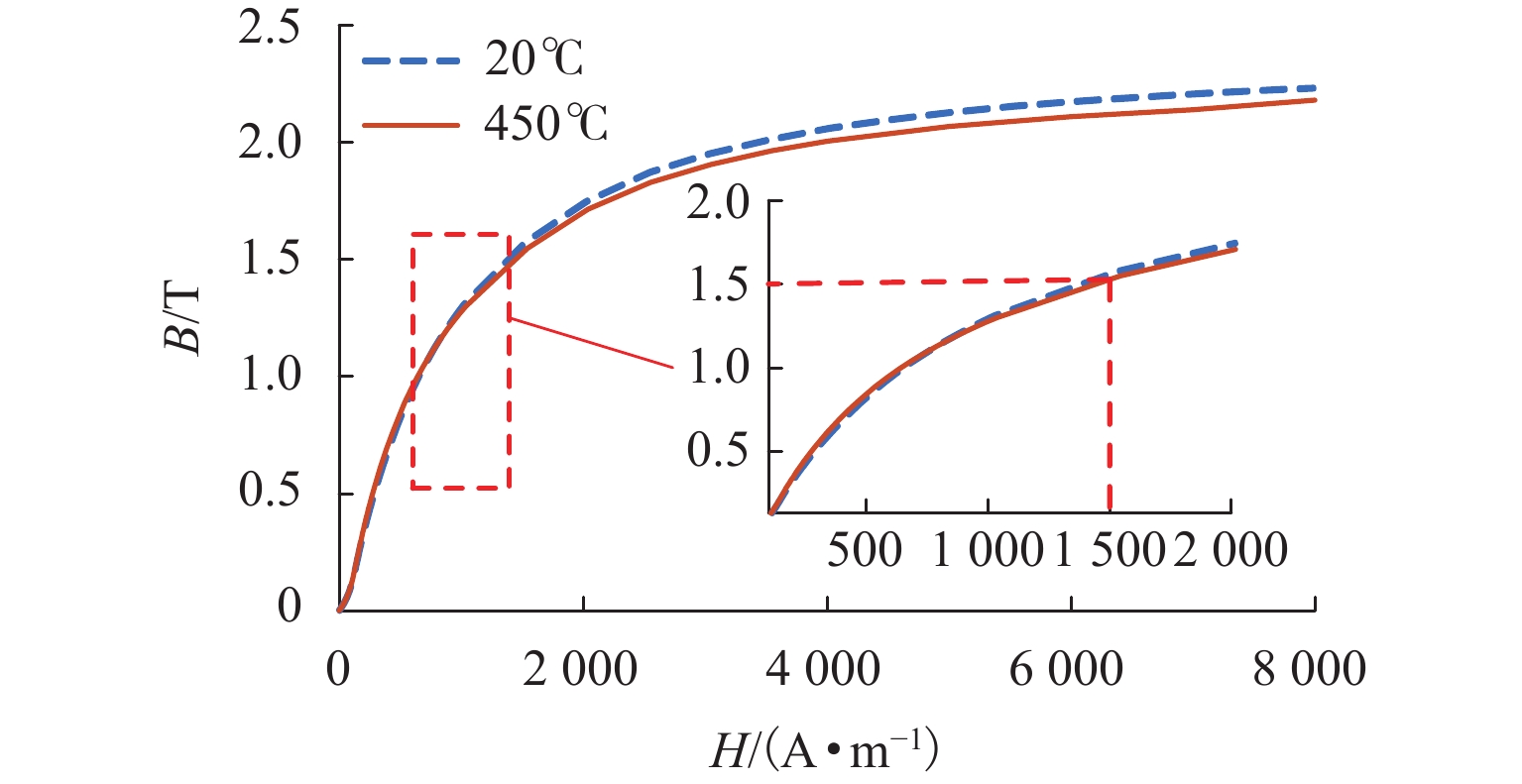
由于热胀冷缩的特性,温度升高会使定子软磁合金叠片和转子部分产生热膨胀现象. 同时,温度还会对软磁合金叠片的导磁能力产生一定影响,最终影响系统的等效刚度. 本文所采用的磁悬浮轴承在偏置电流为2 A时,定子齿部平均磁密可达1.5 T;在线圈达到最大电流4 A时,定子齿部的平均磁密可达到2.1 T. 对软磁合金叠片样品进行升温B-H曲线测试试验(B为磁感应强度,H为磁场强度),在常温和450 ℃下得到的结果如图10所示.
从图10中可以看出,即便是在偏置电流激励下,软磁合金导磁能力在2种温度工况下也会有所差异,温度升高会在一定程度上降低材料的导磁能力. 因此,计算磁悬浮轴承的电磁力时需要考虑温度对软磁合金叠片导磁性能的影响. 影响磁悬浮轴承电磁力大小的主要结构参数包括磁悬浮轴承的几何结构、气隙、线圈匝数、偏置电流、磁极夹角等. 本文所采用的高温磁悬浮轴承为八磁级C型结构,几何参数和电控参数如表3所示.
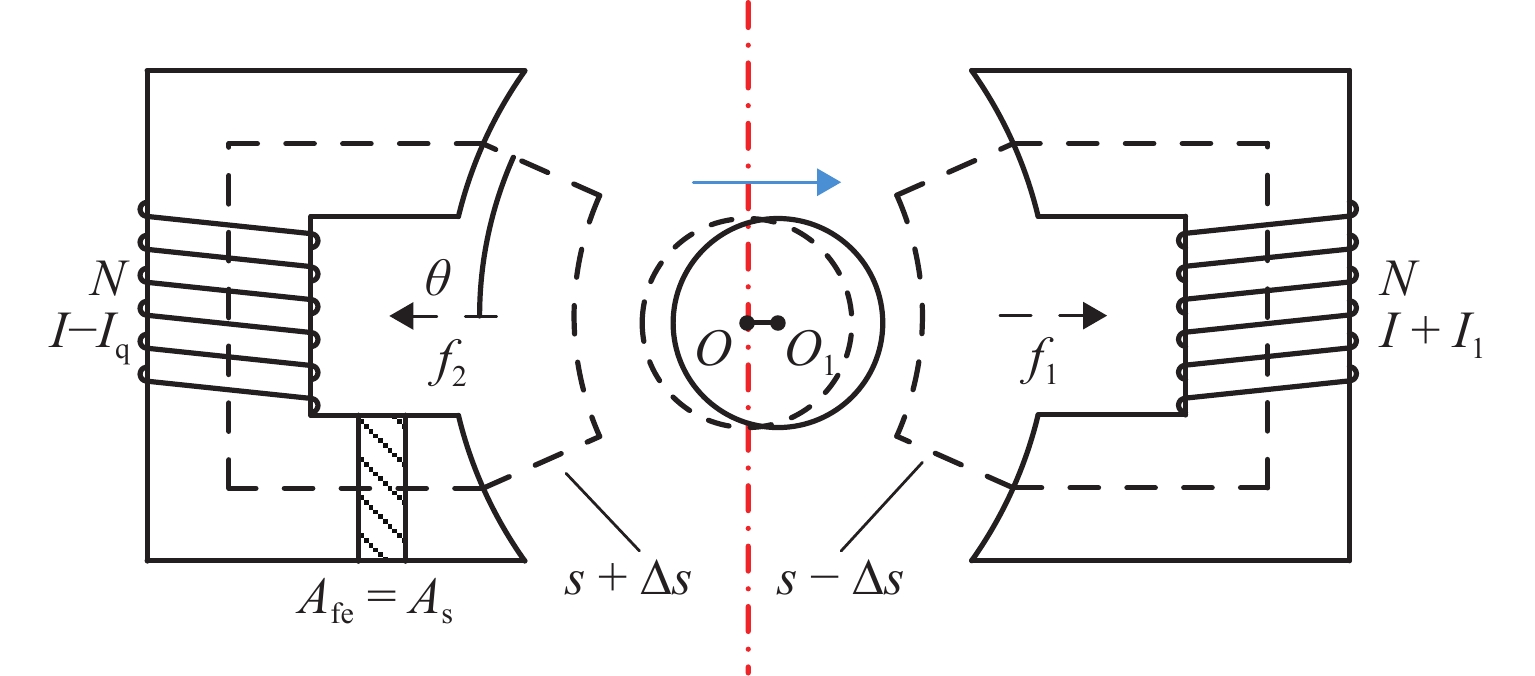
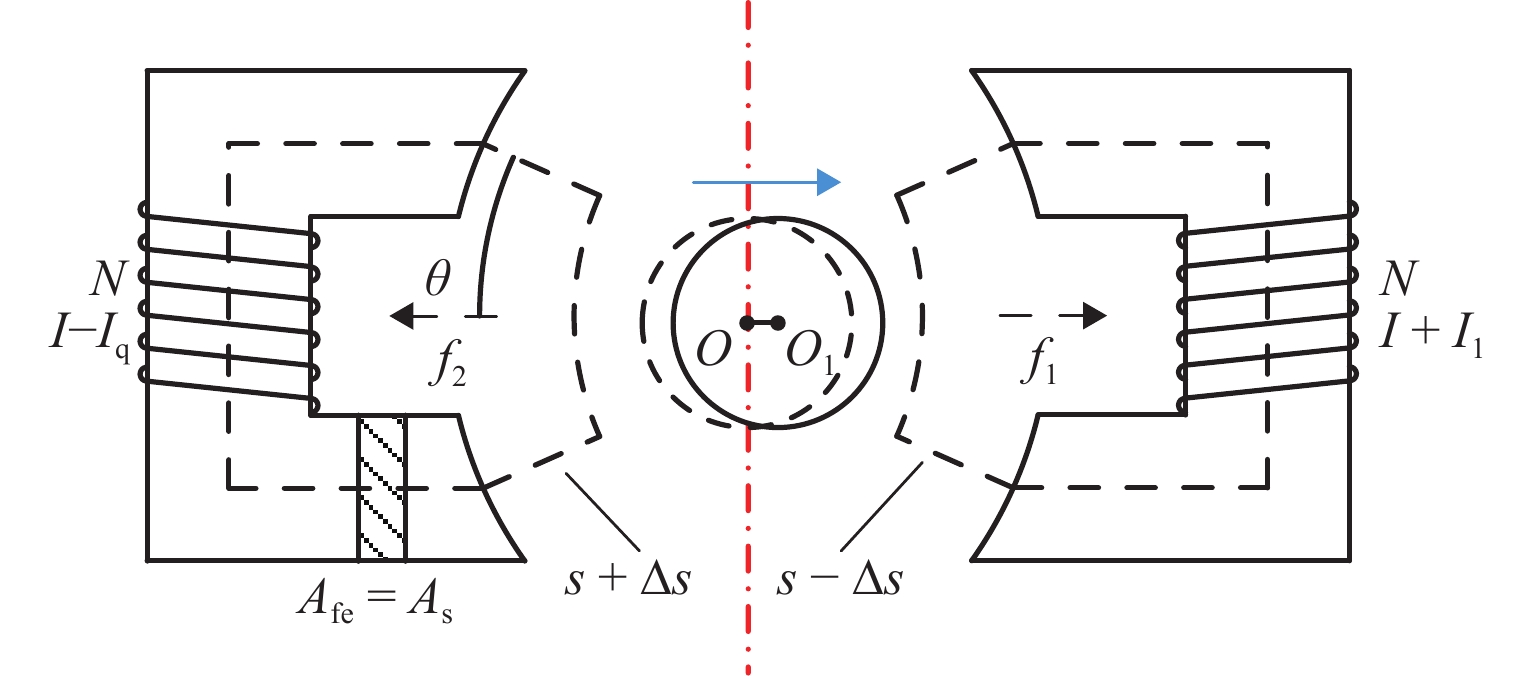
表 3 磁悬浮轴承的结构参数和电控参数Table 3. Structural parameters and electrical control parameters of magnetic bearing参数 取值 参数 取值 转子半径/mm 89.4 比例系数 kp 1 磁极面积 As/mm2 200 积分系数 ki 1 磁极夹角 θ/(°) 22.5 微分系数 kd 0.0 005 单边气隙 sa/mm 0.3 偏置电流 I/A 2 定子齿数 8 线圈匝数 N/匝 240 为分析出温度对转子等效刚度的影响. 在理想状态下,忽略漏磁和磁饱和,并且分析磁路时假设定子齿的磁极面积As和定子齿正对转子软磁合金叠片的面积Afe相等. 由于转子软磁合金叠片两侧受到强约束,因此,仅考虑径向的热膨胀. 单自由度差动布置磁悬浮轴承示意如图11所示,图中:I1为控制电流,f1、f2分别为两对磁极产生的电磁力,O、O1分别为转子移动前后的中心点,∆s为气隙变化. 常温下气隙磁感应强度Bs和电磁力f可分别表示为
{l_{{\mathrm{fe}}}}\frac{{{B_{\mathrm{s}}}}}{{{\mu _0}{\mu _{\mathrm{r}}}}} + 2s_{\mathrm{a}}\frac{{{B_{\mathrm{s}}}}}{{{\mu _0}}} = NI, (21) f = \frac{{B_{\mathrm{s}}^2{A_{\mathrm{s}}}}}{{{\mu _0}}} , (22) 式中:lfe为一对磁极磁路的长度,μ0为真空磁导率,μr为软磁合金叠片的相对磁导率.
考虑热膨胀时的磁路长度lfeT、气隙sT、软磁合金叠片相对磁导率μrT分别如式(23)所示.
\left\{\begin{array}{l}{l}_{{\mathrm{feT}}}={l}_{{\mathrm{fe}}}(1 + {\alpha }_{{\mathrm{T}}}\Delta T),\\ {s}_{{\mathrm{T}}}=s(1 + {\alpha }_{{\mathrm{T}}}\Delta T),\\ {\mu }_{{\mathrm{rT}}}={\mu }_{{\mathrm{r}}}(1-{\beta }_{{\mathrm{T}}}\Delta T),\end{array} \right. (23) 式中:αT为热膨胀系数,βT为根据试验数据计算出来的软磁合金叠片相对磁导率下降系数,ΔT为温度变化量.
联立式(21)~(23),得考虑热膨胀时电磁力为
{f_{\mathrm{T}}} = \frac{{B_{{\mathrm{sT}}}^2{A_{\mathrm{s}}}}}{{{\mu _0}}} = \frac{{{\mu _0}{N^2}{A_{\mathrm{s}}}}}{{{{(1 + \alpha \Delta T)}^2}}}\frac{{{I^2}}}{{{{({l_{{\mathrm{fe}}}}/{\mu _{{\mathrm{rT}}}} + 2s_{\mathrm{a}})}^2}}} . (24) 在气隙变化 ∆s时,差动电磁力F可以表示为
\begin{split} &F = \frac{{{\mu _0}{N^2}{A_{\mathrm{s}}}\cos {\text{ }}\theta }}{{{{(1 + {\alpha _{\mathrm{T}}}\Delta T)}^2}}}\frac{{{{(I + {I_1})}^2}}}{{{{\left[ {{{{l_{{\mathrm{fe}}}}}}/{{{\mu _{{\mathrm{rT}}}}}} + 2(s_{\mathrm{a}} - \Delta s)} \right]}^2}}} -\\ &\quad \frac{{{{(I - {I_1})}^2}}}{{{{\left[ {{{{l_{{\mathrm{fe}}}}}}/{{{\mu _{{\mathrm{rT}}}}}} + 2(s_{\mathrm{a}} + \Delta s)} \right]}^2}}}. \end{split} (25) 对电磁力线性化处理,将式(25)在I1=0和x=0处进行泰勒展开,可以得到
F = F(0,0) + \frac{{\partial F}}{{\partial x}}x + \frac{{\partial F}}{{\partial {I_1}}}{I_1} + \cdots (26) 忽略二阶以上高阶小量可得
\begin{split}F=&\dfrac{{\mu }_{0}{N}^{2}{A}_{{\mathrm{s}}}\mathrm{cos}\text{ }\theta }{4{(1 + {\alpha }_{{\mathrm{T}}}\Delta T)}^{2}}\left[\dfrac{8{I}^{2}}{{({{l}_{{\mathrm{fe}}}}/{{\mu }_{{\mathrm{rT}}}} + 2s_{\mathrm{a}})}^{3}} gx + \right.\\ &\left. \dfrac{4I}{({{l}_{{\mathrm{fe}}}}/{{\mu }_{{\mathrm{rT}}}} +2s_{\mathrm{a}})^{2}}g{I}_{1}\right] ={k}_{1}{I}_{1}-{k}_{2}x,\end{split} (27) 式中:k1和k2分别为磁悬浮轴承系统的电流刚度和位移刚度,如式(28)所示.
\left\{\begin{array}{l}{k}_{1}=\dfrac{{\mu }_{0}{N}^{2}{A}_{{\mathrm{s}}}\mathrm{cos}\text{ }\theta }{4{(1 + \alpha \Delta T)}^{2}}{{}}\dfrac{4I}{{({l}_{{\mathrm{fe}}}/{\mu }_{{\mathrm{rT}}} + 2s_{\mathrm{a}})}^{2}},\\ {k}_{2}=-\dfrac{{\mu }_{0}{N}^{2}{A}_{{\mathrm{s}}}\mathrm{cos}\text{ }\theta }{4{(1 + \alpha \Delta T)}^{2}}{{}}\dfrac{8{I}^{2}}{{({l}_{{\mathrm{fe}}}/{\mu }_{{\mathrm{rT}}} + 2s_{\mathrm{a}})}^{3}}.\end{array}\right. (28) 对转子系统来说,支承刚度的大小会影响转子的模态频率. 磁悬浮轴承支承刚度的定义有别于传统机械轴承,其大小不仅取决于整体的结构参数,还取决于控制算法、电控系统、传感器、电磁损耗等因素[18]. 多自由度磁悬浮转子系统的等效刚度[19]可表示为
{k_{\mathrm{e}}} = {k_2} + {k_1}{{\mathrm{Re}}} ( {G_{\mathrm{s}}}({\mathrm{j}}w ){G_{\mathrm{a}}}({\mathrm{j}}w ){G_{\mathrm{c}}}({\mathrm{j}}w )) , (29) 式中:Gs(jw)、Ga(jw)和Gc(jw)分别为位移传感器、功率放大器和控制器在频域的传递函数.
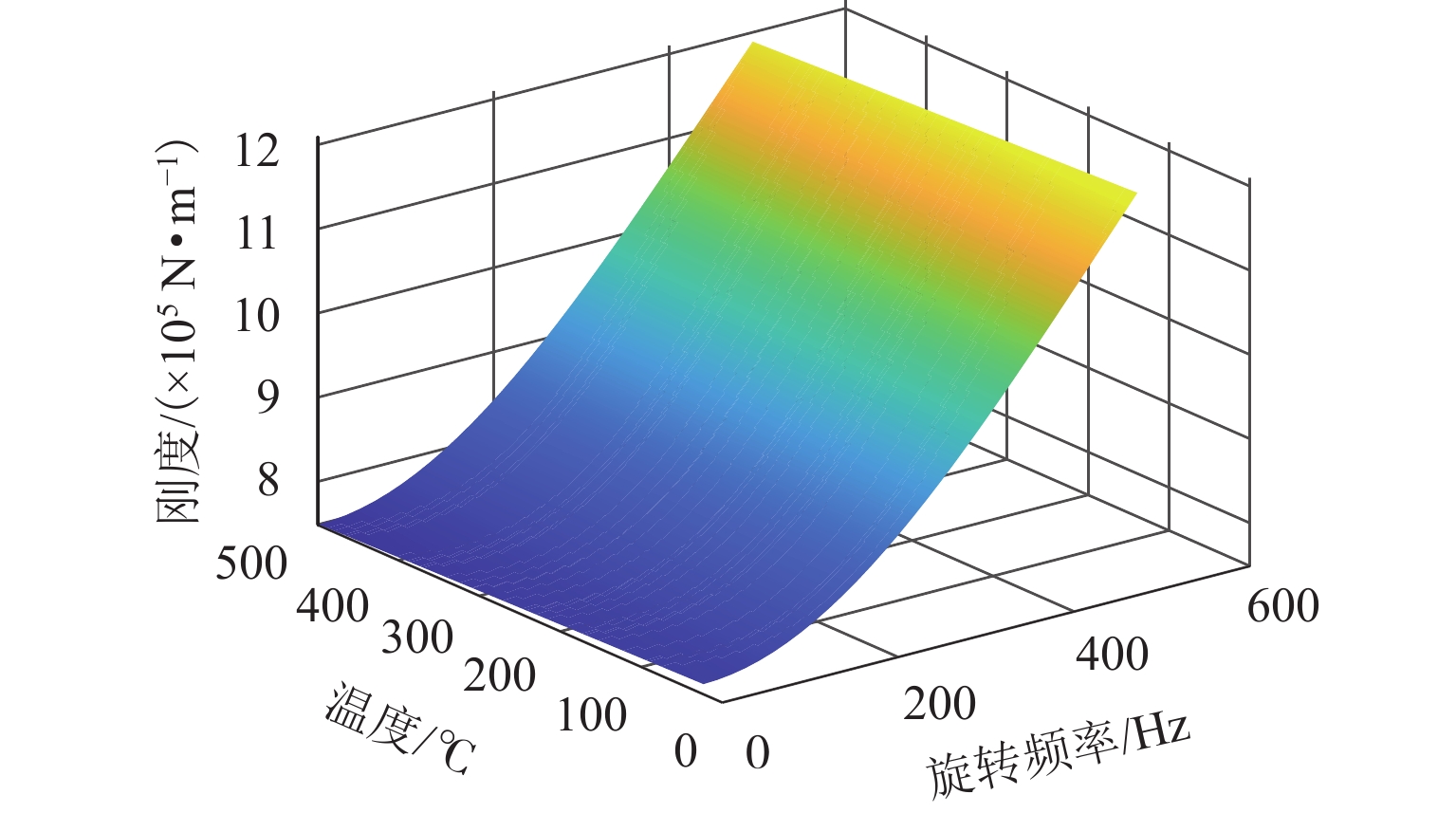
计算磁悬浮轴承的等效刚度随温度变化的数值,结果如图12所示. 功率放大器和控制器温度为室温,功率放大器采用恒电流激励,温度对二者的传递函数影响较小;位移传感器受温度影响会产生温漂. 在使用电涡流位移传感器时,温度升高会降低传感器输出,但是热胀冷缩导致的转子热膨胀会在一定程度上弥补温漂带来的影响. 同时,本文所使用的高温电涡流传感器处理电路在设计时加入了温漂补偿算法,以此来保证位移传感器传递函数维持稳定.
从图12中可以看出,磁悬浮轴承等效刚度随温度增加呈现减小趋势. 一方面是因为温度升高所带来的热膨胀使得磁悬浮轴承气隙增大;另一方面温度升高降低了材料的导磁能力,使得相同电流下磁悬浮轴承产生的电磁力减小. 在零旋转频率,温度从25 ℃上升到450 ℃时,等效刚度下降了4.684 × 103 N/m;在旋转频率为500 Hz,温度从25 ℃上升到450 ℃时,等效刚度下降了1.529 × 104 N/m.
3. 动力学分析结果与验证
3.1 温度变化对转子系统模态频率的影响
为验证整体动力学模型的有效性,加热箱的温度分别设置为25、150、300、450 ℃,采用模态试验得到转子系统在不同温度工况下的支承模态频率. 同时,根据本文第2节中所建立的高温磁悬浮转子系统整体动力学模型,计算不考虑刚体模态的前三阶支承弯曲模态频率,并与模态试验得到的结果进行对比,如表4所示. 从表中可以看出,不同温度工况下,理论模型的模态频率计算结果和试验结果误差均不超过3%,验证了理论有限元模型的准确性.
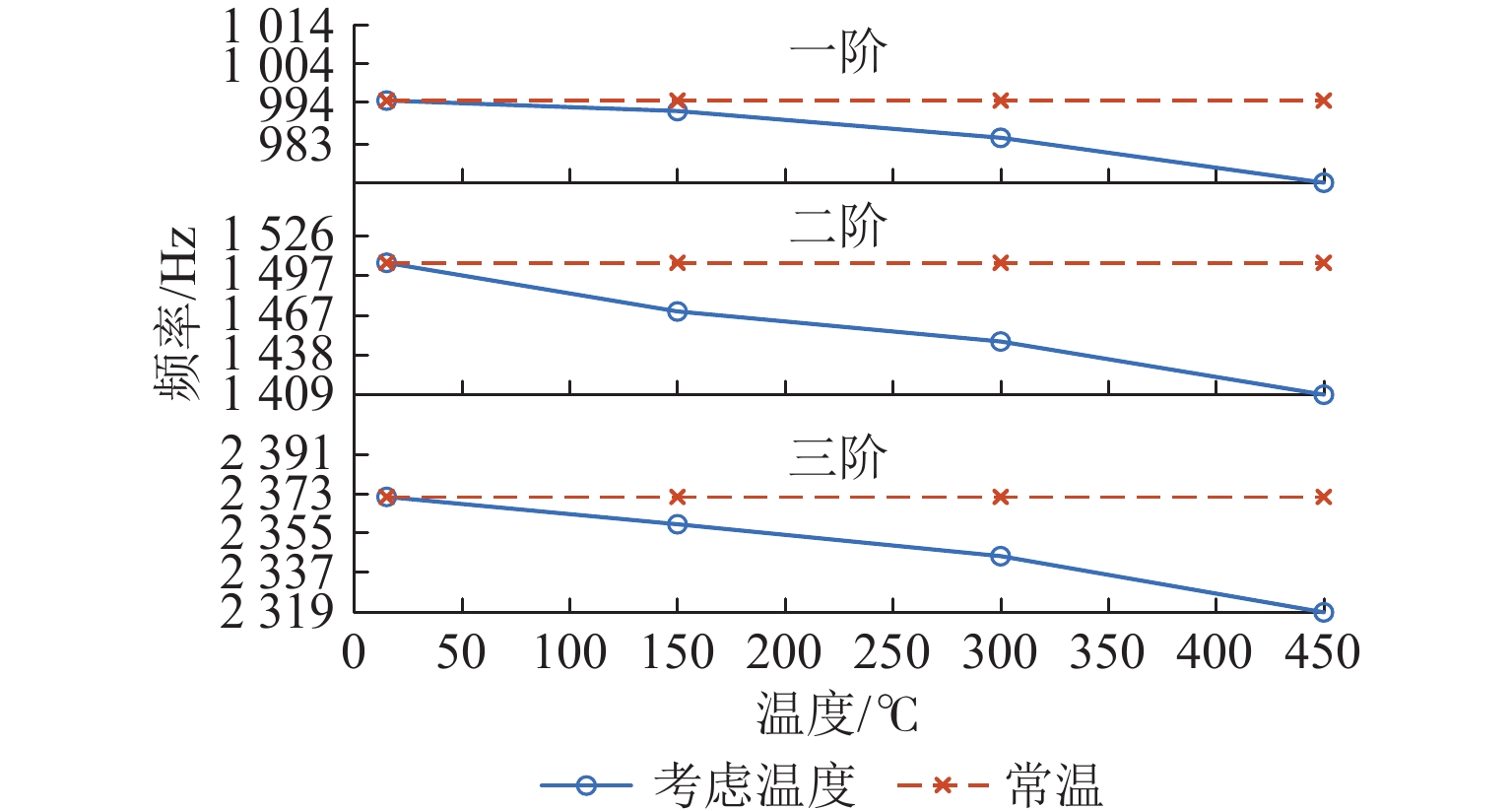
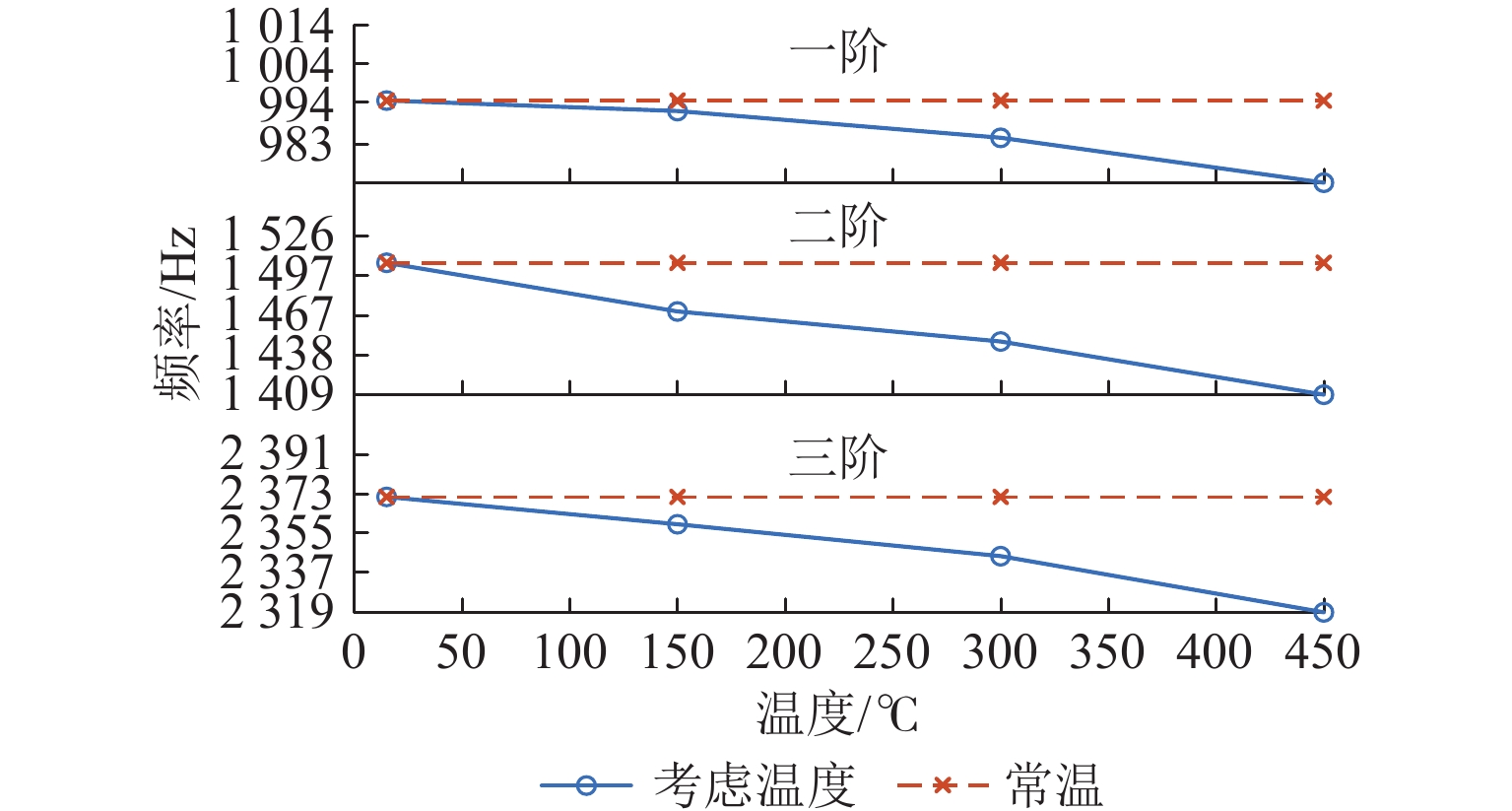
表 4 支承模态频率对比Table 4. Comparison of support modal frequency温度/℃ 阶次 计算频率/Hz 试验频率/Hz 误差/% 25 1 994.490 994.375 0.0 115 2 1506.200 1506.250 0.0 033 3 2437.090 2494.380 2.2 960 150 1 990.606 983.750 0.6 900 2 1471.570 1496.880 0.0 169 3 2421.910 2477.610 2.3 000 300 1 982.417 976.250 0.6 300 2 1450.280 1450.990 0.0 493 3 2404.800 2460.590 2.2 320 450 1 968.743 958.750 1.0 000 2 1412.160 1413.460 0.0 922 3 2374.860 2391.080 2.6 830 将温度变化时的转子支承模态频率和常温下的支承模态频率对比,结果如图13所示. 从图中可以看出:1) 转子系统前三阶支承模态频率随温度的升高而降低;温度从常温升高至450 ℃时,理论计算的转子系统前三阶支承模态频率的绝对值分别下降了21.377、97.490、53.040 Hz,相对值分别下降了2.149%、6.472%、2.237%. 2) 对转子系统弯曲模态频率有着明显的影响;随着温度的升高,转子前三阶模态频率均呈现下降趋势,二阶弯曲模态频率下降的态势较为明显,说明转子系统二阶支承模态频率受温度影响最大.
3.2 温度变化对转子系统幅频响应的影响
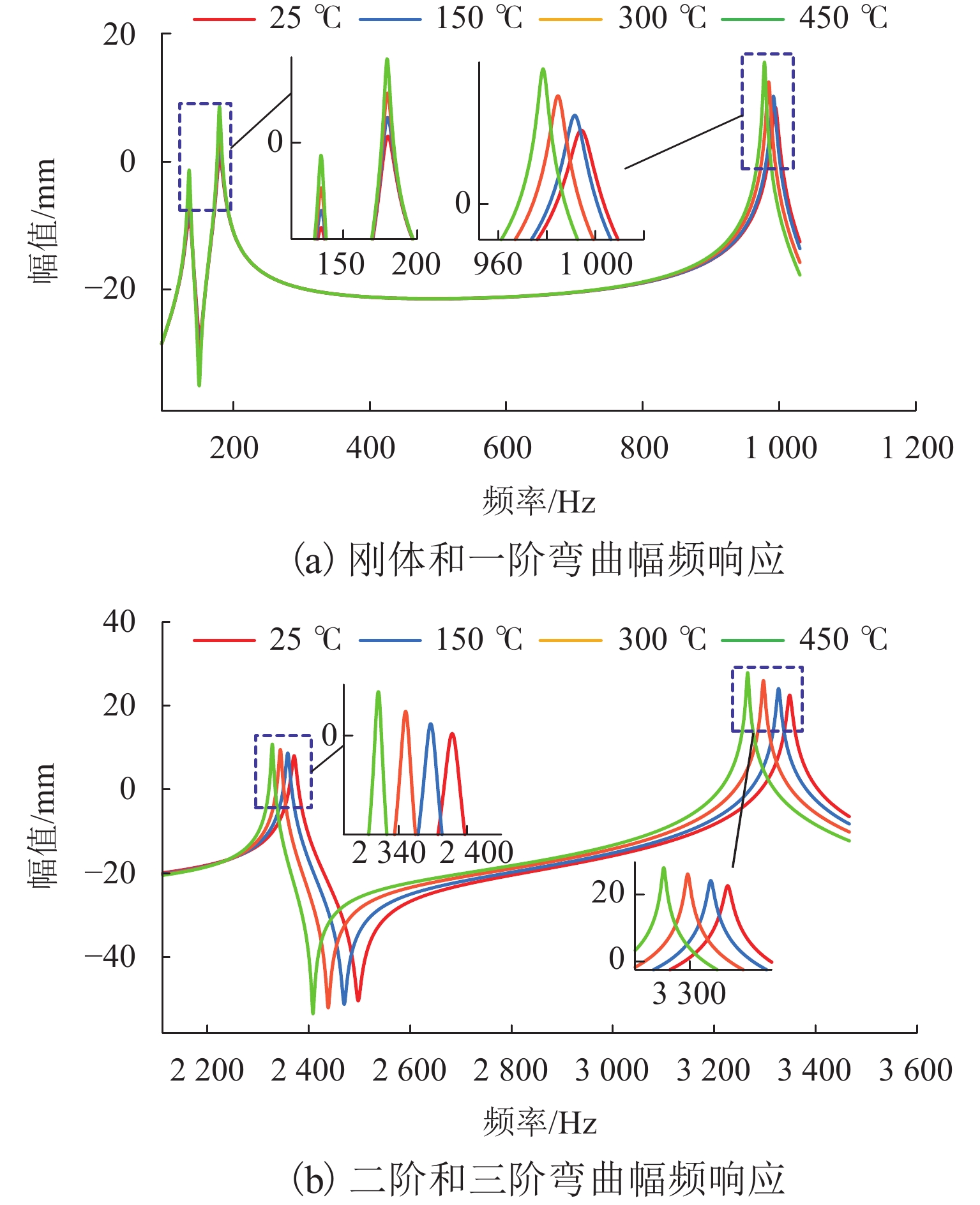
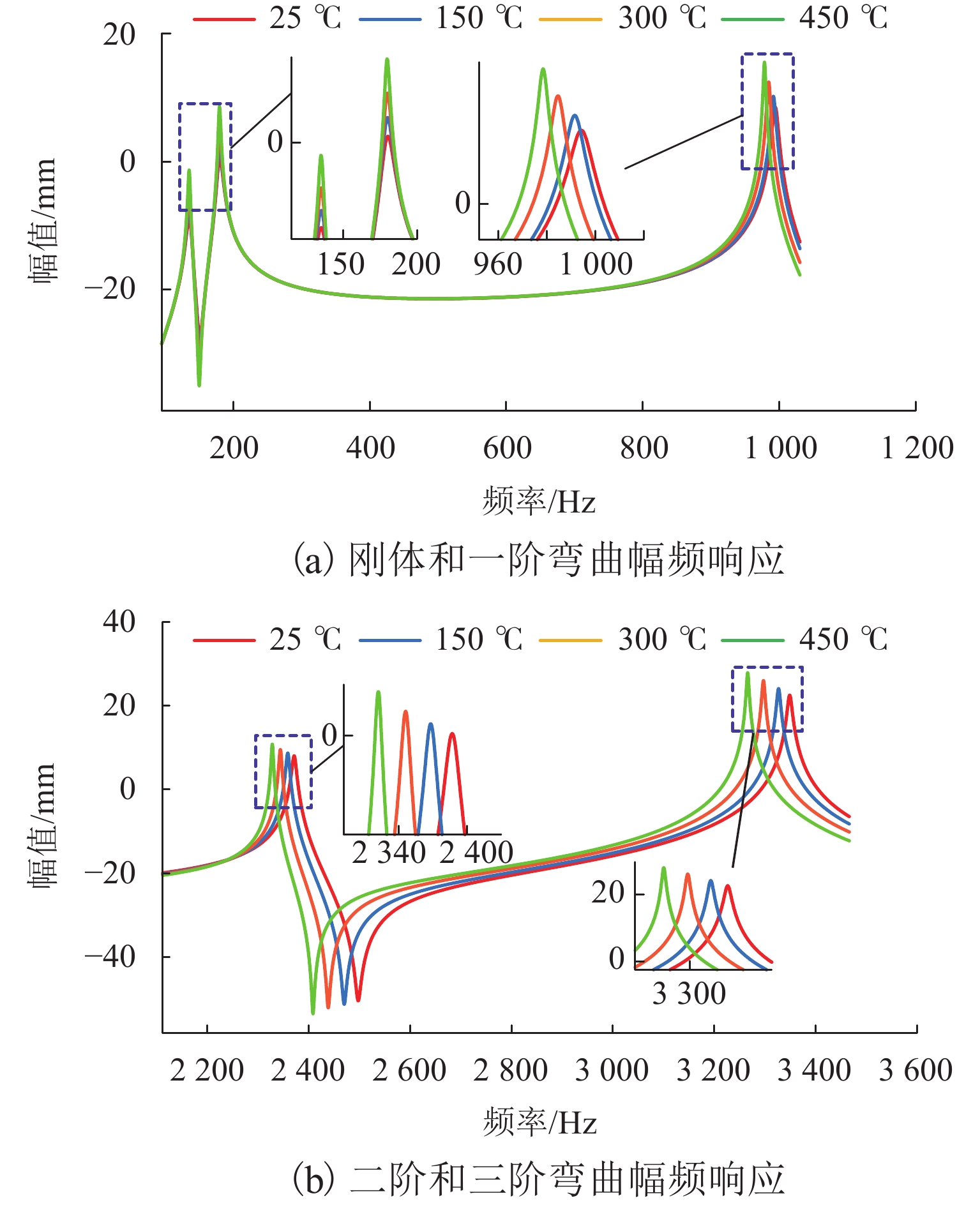
构建系统加速度动力学幅频响应分析程序. 分别设置转子系统加热工况为25、150、300、450 ℃,转子系统的动力学幅频响应结果如图14所示. 从图中可以看出,随着温度的升高,转子各阶响应的幅值呈递增趋势. 以一阶、二阶、三阶模态的稳态响应为例,当温度由常温升高至450 ℃时,其幅值分别上升了83.4%、34.4%、24.1%. 这是由于温度升高使得机械系统发生热变形,同时影响了系统的杨氏模量和泊松比等物理属性,降低系统的刚度所导致的.
4. 讨 论
使用有限元法来构建柔性转子单元的动力学模型,分析温度对转子系统产生的相关影响,重构系统动力学模型所包含的各个矩阵. 考虑温度对磁悬浮轴承的影响重新推导了系统等效刚度模型. 建立考虑温度的高温磁悬浮转子系统的整体动力学模型. 根据理论模型分析了转子模态频率和幅频响应随温度的变化规律,主要结论如下:
1) 温度会影响软磁合金叠片的相对导磁率,温度的升高使软磁合金叠片的相对磁导率下降,同时,温升带来的热膨胀会改变磁路的长度和气隙的宽度,从而降低磁悬浮轴承的等效刚度. 当温度从25 ℃上升到450 ℃时,在零旋转频率时,等效刚度下降了4.684 × 103 N/m;在500 Hz转速下,等效刚度下降了1.529 × 104 N/m.
2) 在进行温度场仿真时,基于实际加热工况设置了对应区域的热通量,但是仍然无法做到对实际工况的全真模拟. 同时,温度的升高还可能会给系统带来多源扰动. 因此,通过理论计算得到的转子模态频率和通过试验得到的转子模态频率有所差异.
3) 温度对转子系统弯曲模态频率影响较大,随着温度的升高,转子前三阶模态频率呈下降趋势. 温度从常温升高至450 ℃时,理论计算的转子系统前三阶支承模态频率的绝对值分别下降了21.377、97.490、53.040 Hz,相对值分别下降了2.149%、6.472%、2.237%.
4) 温度会对转子的动力学响应产生影响. 在响应的幅值方面,温度升高会使得转子系统幅频响应的幅值增大. 当温度由常温升高至450 ℃时,一阶、二阶、三阶模态的稳态响应幅值分别上升了83.4%、34.4%、24.1%.
-
表 1 机械系统所使用的材料
Table 1. Materials used in mechanical systems
序号 所用材料 1,2,3,4,6,8 1Cr11Ni2W2MoV 5 GH4169 7,10 高温软磁合金(1J22) 9,11 38 黄铜 表 2 数学模型拟合的R2值
Table 2. R2 by mathematical model fitting
m 150 ℃ 300 ℃ 450 ℃ 1 0.799 123 0.815 718 0.824 486 2 0.993 046 0.993 757 0.993 782 3 0.996 804 0.995 234 0.994 565 4 0.998 708 0.998 45 0.998 344 5 0.999 406 0.999 188 0.999 120 6 0.999 495 0.999 374 0.999 328 表 3 磁悬浮轴承的结构参数和电控参数
Table 3. Structural parameters and electrical control parameters of magnetic bearing
参数 取值 参数 取值 转子半径/mm 89.4 比例系数 kp 1 磁极面积 As/mm2 200 积分系数 ki 1 磁极夹角 θ/(°) 22.5 微分系数 kd 0.0 005 单边气隙 sa/mm 0.3 偏置电流 I/A 2 定子齿数 8 线圈匝数 N/匝 240 表 4 支承模态频率对比
Table 4. Comparison of support modal frequency
温度/℃ 阶次 计算频率/Hz 试验频率/Hz 误差/% 25 1 994.490 994.375 0.0 115 2 1506.200 1506.250 0.0 033 3 2437.090 2494.380 2.2 960 150 1 990.606 983.750 0.6 900 2 1471.570 1496.880 0.0 169 3 2421.910 2477.610 2.3 000 300 1 982.417 976.250 0.6 300 2 1450.280 1450.990 0.0 493 3 2404.800 2460.590 2.2 320 450 1 968.743 958.750 1.0 000 2 1412.160 1413.460 0.0 922 3 2374.860 2391.080 2.6 830 -
[1] 吴志琨,李军,时瑞军. 多电航空发动机研究现况及关键技术[J]. 航空工程进展,2012,3(4): 463-467. doi: 10.3969/j.issn.1674-8190.2012.04.015WU Zhikun, LI Jun, SHI Ruijun. Current research status and key technologies of more-electric aeroengine[J]. Advances in Aeronautical Science and Engineering, 2012, 3(4): 463-467. doi: 10.3969/j.issn.1674-8190.2012.04.015 [2] 刘程子,湛江,杨艳,等. 主动磁悬浮轴承–柔性转子的研究和发展综述[J]. 中国电机工程学报,2020,40(14): 4602-4614,4739.LIU Chengzi, ZHAN Jiang, YANG Yan, et al. Review of research status and development of flexible rotor-magnetic bearing[J]. Proceedings of the CSEE, 2020, 40(14): 4602-4614,4739. [3] 金超武. 高温磁悬浮轴承若干关键技术研究[D]. 南京:南京航空航天大学,2011. [4] ZIAEI-RAD S, KOUCHAKI E, IMREGUN M. Thermoelastic mdeling of rotor response with shaft rub[J]. Journal of Applied Mechanics, 2010, 77(6): 061010.1-061010.1. [5] 朱向哲,贺威,袁惠群. 稳态温度场对转子系统振动特性的影响[J]. 东北大学学报(自然科学版),2008,29(1): 113-116.ZHU Xiangzhe, HE Wei, YUAN Huiqun. Effects of steady temperature field on vibrational characteristics of a rotor system[J]. Journal of Northeastern University (Natural Science), 2008, 29(1): 113-116. [6] 何鹏,刘占生,刘镇星. 考虑杨氏模量随轴向温度分布变化的转子有限元建模方法研究[J]. 振动与冲击,2012,31(14): 22-26,55. doi: 10.3969/j.issn.1000-3835.2012.14.005HE Peng, LIU Zhansheng, LIU Zhenxing. Finite element modelling of rotor considering the variation of Yang’s modulus with axial temperature distribution[J]. Journal of Vibration and Shock, 2012, 31(14): 22-26,55. doi: 10.3969/j.issn.1000-3835.2012.14.005 [7] GOU X F, ZHU L Y, QI C J. Nonlinear dynamic model of a gear-rotor-bearing system considering the flash temperature[J]. Journal of Sound and Vibration, 2017, 410: 187-208. [8] XIANG F G, CHEN X, ZHANG B, et al. Simulation method of rotor dynamic characteristics considering temperature distribution and aerodynamic load[C]//Proceedings of ASME Turbo Expo 2022:Turbomachinery Technical Conference and Exposition. Rotterdam:ASME, 2022:13-17. [9] DU T C, SUN Y H, GENG H P, et al. Dynamic Analysis on Rotor System Supported by Active Magnetic Bearings based on Sliding Mode Control[C]//2018 IEEE International Conference on Mechatronics and Automation (ICMA). Changchun:IEEE, 2018:1960-1965. [10] MUSHI S E, LIN Z L, ALLAIRE P E. Design, construction, and modeling of a flexible rotor active magnetic bearing test rig[J]. ASME Transactions on Mechatronics, 2012, 17(6): 1170-1182. [11] XU Y P, ZHOU J, LIN Z L, et al. Identification of dynamic parameters of active magnetic bearings in a flexible rotor system considering residual unbalances[J]. Mechatronics, 2018, 49: 46-55. [12] 沈权,周瑾,马彦超,等. 基础激励下磁悬浮转子系统动力学建模与分析[J]. 振动与冲击,2022,41(17): 35-47,72.SHEN Quan, ZHOU Jin, MA Yanchao, et al. Dynamic modeling and analysis of maglev rotor system under base excitation[J]. Journal of Vibration and Shock, 2022, 41(17): 35-47,72. [13] WU C, SU Z Z, WANG D, et al. Dynamic modeling method for active magnetic bearings-rotor system of steam turbines[J]. Journal of Mechanical Science and Technology, 2023, 37(4): 1665-1673. [14] 王戈一. 磁悬浮多电发动机的研究[J]. 燃气涡轮试验与研究,2007,20(4): 15-18,35. doi: 10.3969/j.issn.1672-2620.2007.04.003WANG Geyi. Study of a more-electric engine with active magnetic bearings[J]. Gas Turbine Experiment and Research, 2007, 20(4): 15-18,35. doi: 10.3969/j.issn.1672-2620.2007.04.003 [15] BURDET L. Active magnetic bearing design and characterization for high temperature applications[R]. Swiss:Federal Institute of Technology in Lausanne, 2006. [16] MONTAGUE G T, JANSEN M J, PROVENZA A, et al. Experimental high temperature characterization of a magnetic bearing for turbomachinery[C]//59th Annual Forum and Technology Display. Phoenix:Vertical Flight Society, 2003:1-18. [17] SHI Z, SUN X D, LEI G, et al. Multiobjective optimization of a five-phase bearingless permanent magnet motor considering winding area[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(5): 2657-2666. [18] 周扬,周瑾,张越,等. 基于RBF近似模型的磁悬浮轴承结构优化设计[J]. 西南交通大学学报,2022,57(3): 682-692. doi: 10.3969/j.issn.0258-2724.20210766ZHOU Yang, ZHOU Jin, ZHANG Yue, et al. Optimum structural design of active magnetic bearing based on RBF approximation model[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 682-692. doi: 10.3969/j.issn.0258-2724.20210766 [19] 徐园平. 柔性转子磁悬浮轴承支承特性辨识[D]. 南京:南京航空航天大学,2018. -






 下载:
下载:













 下载:
下载: