Construction Optimization Method for Cable Domes with Alternately Lifting and Tensioning
-
摘要:
为确保索穹顶结构施工成型前索杆内力的平稳变化，提出了交替提升内拉环与张拉最外圈斜索的施工优化方法. 首先，以施工过程中的平均结构应变能最小为优化目标，对内拉环的逐级提升高度进行优化；其次，通过仿真分析得到施工过程中的索杆内力和节点位移，并与仅张拉最外圈斜索的施工方法进行对比. 结果表明：交替提升内拉环与张拉最外圈斜索的施工优化方法可有效减小施工过程中的索杆内力，降幅最大达61.83%，避免了施工成型前索杆内力的大幅波动，且结构位形变化较平缓，相邻施工步的竖向位移差最大为1.43 m，平均结构应变能较低，仅为55.03%，优化效果显著，验证了该优化方法对索穹顶结构施工模拟的适用性.
Abstract:In order to ensure the smooth change of cable-strut internal forces before molding cable domes, a construction optimization method is proposed, focusing on alternately lifting the inner ring and tensioning the outermost diagonal cables. The lifting height of the inner ring is first optimized for minimizing average structural strain energy in the construction process. The cable-strut internal forces and nodal displacements from simulation are compared with those from the construction method with the tensioned outermost diagonal cables. The results show that, alternately lifting the inner ring and tensioning the outermost diagonal cables can effectively reduce the cable-strut internal forces by 61.83%, avoiding sharp fluctuation of cable-strut internal forces before molding. It causes more gentle change of structural configuration with 1.43 m maximum vertical displacement difference between adjacent construction steps, and low average structural strain energy of only 55.03%, which demonstrates its remarkable optimization effect. Thus, the proposed method is applicable to the construction simulation of cable domes.
-
实现稳定高效行走是仿人机器人研究中的首要关键任务. 20世纪90年代，McGeer[1]首次提出了被动行走原理，由于充分利用了机器人自身的动力学特性，其能量利用率极高[2]. 与传统仿人机器人相比，被动行走机器人步态与人类更为相似[3-4]. 然而，由于模型过于简化，被动行走存在着稳定性差，行走速度低等问题[5-6].
为改善被动行走的步态特性，学者们将机器人各部分均视为理想刚体，并在此基础上通过添加脚板[7-8]、躯干[9-11]、关节弹簧[12-13]等方式，设计了稳定性更高或行走速度更快的被动行走机器人. 而生物学研究表明，人体腿部骨骼上通常还附着有肌肉、胫腱等柔性较大的软组织[14]，这些软组织在人类行走过程中通常会发生弹性变形，类似于带质量的弹簧阻尼器[15].
受此启发，学者们在机器人结构设计中添加弹性振动质量，并研究弹性振动质量对机器人步态特性的影响[16-17]. Tanaka等[18]采用2个关联的无边轮辐模型，通过在两轮辐中间添加振动质量，发现能提高被动行走速度；Asano等[19-20]在无边轮辐上添加弹性伸缩腿，提高被动行走稳定性；Akutsu等[21]设计了同时具有刚性和柔性的腿结构，发现适当的腿柔性可以提高被动行走机器人步行速度. 以上研究表明，物理结构的刚性和柔性均会影响被动行走的步态特性. 但现有文献在研究柔性元件对被动行走机器人的影响时，主要集中在腿结构的柔性研究上.
而从仿生学角度看，对于人类和鸵鸟等能够进行二足行走的动物，其躯干都有大量肌肉、脂肪和内脏等软组织[22-23]. 在行走过程中，这些软组织会随着身体的运动而发生被动的变形，从而使得躯干具有一定的柔性；此外，Hanazawa等[24]研究表明，行走过程中手臂的来回摆动，也可看作是在躯干上的柔性元件. 因此，能否利用躯干柔性这一生物特征来改善被动行走机器人的步态，是一个值得研究的问题. 为此，本文首次提出兼具刚性和柔性的仿生躯干被动行走机器人，并主要研究仿生躯干对被动行走机器人动力学特性的影响规律，以期改善被动行走机器人的行走步长、步行速度等步态特性.
将仿生躯干分为刚性部分和柔性部分，刚性部分等效为理想刚体，柔性部分等效为带质量块的悬臂梁，建立带仿生躯干的被动行走机器人动力学模型，并重点讨论仿生躯干柔性部分对被动行走机器的人行走步长及步行速度的影响.
1. 带仿生躯干的被动行走机器人建模
1.1 物理模型
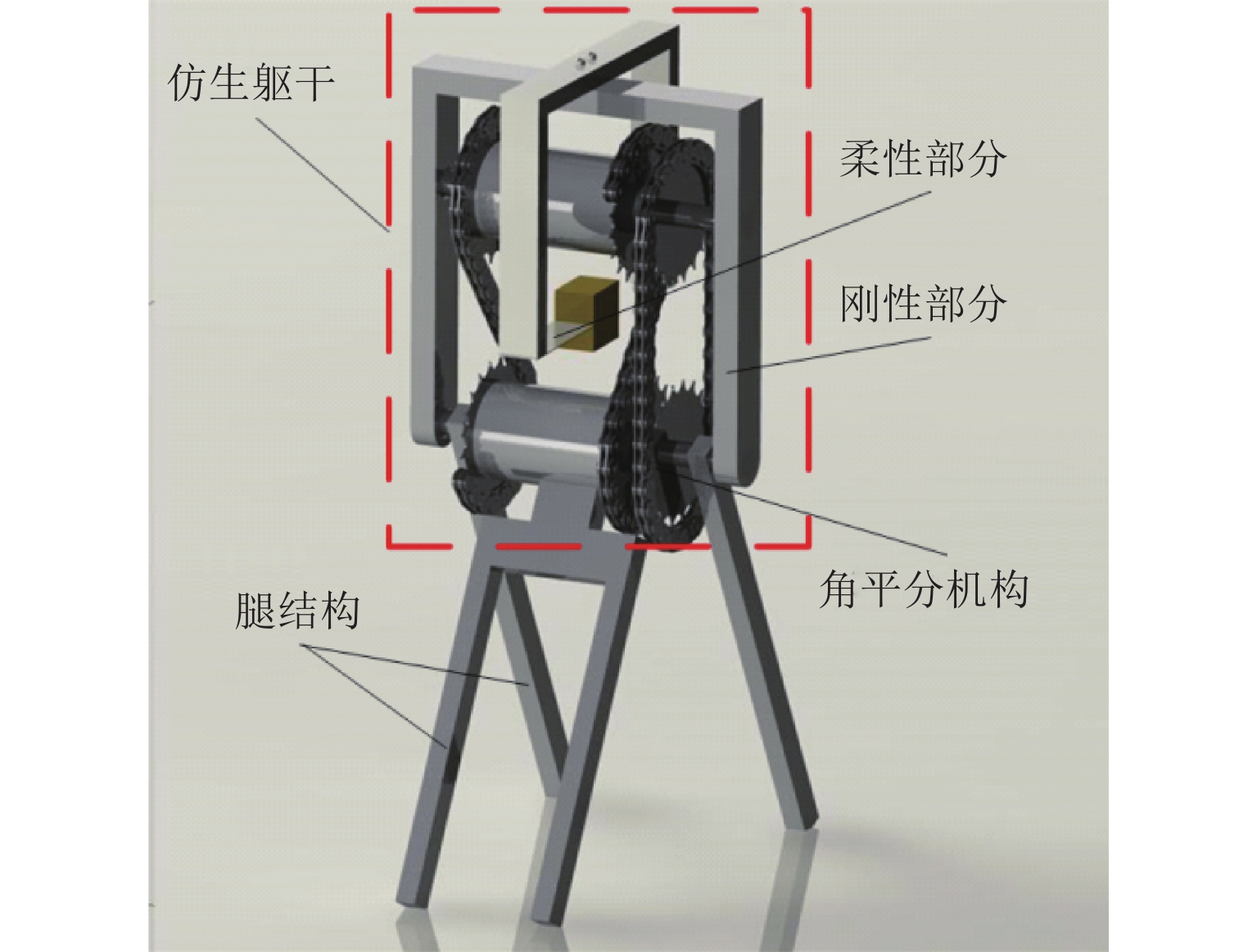
带有仿生躯干的被动行走机器人系统的三维模型如图1所示. 其中，仿生躯干的柔性部分被等效为带质量块的悬臂梁，悬臂梁的安装末端与被动行走机器人躯干的刚性部分相固连，且悬臂梁的初始位置与躯干刚性部分方向垂直. 机器人的仿生躯干通过角平分机构[11]与双腿连接.
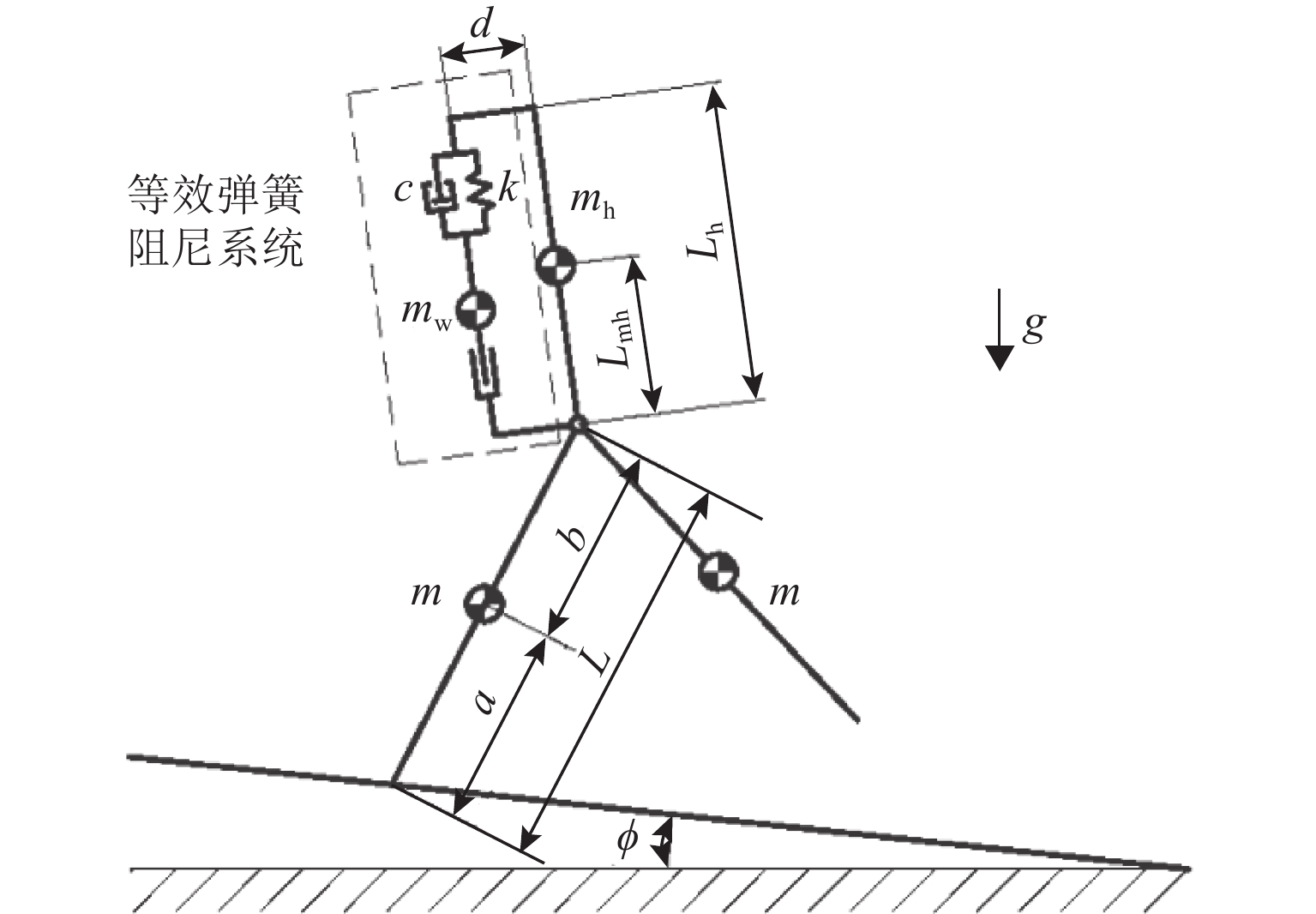
图 1 带有仿生躯干的被动行走机器人三维模型Figure 1. 3D model of passive walking robot with a bionic torso为简化建模，忽略梁的扭转与剪切变形[25-26]，使用集中参数模型[27]描述仿生躯干柔性部分的运动，图1的悬臂梁可简化为单自由度的“质量块—弹簧—阻尼”振动系统，从而建立仿生躯干被动行走机器人的物理模型，如图2所示. 图2中：k为躯干柔性部分的等效弹性系数，c为躯干柔性部分的等效阻尼系数，mw为躯干柔性部分的等效质量，mh为机器人躯干刚性部分质量，Lh为躯干长度，Lmh为髋关节到躯干质心的距离，m为腿的质量，a为腿质心到足底距离，b为腿质心到髋关节距离，L为腿长度，L=a+b，d为躯干柔性部分的等效质量块质心到躯干的安装偏置距离，本文假设d=0.
1.2 系统动力学方程
为方便叙述，将机器人与斜坡接触的腿称为支撑腿，未与斜坡接触的腿称为摆动腿. 由于机器人的腿为直腿结构，行走过程可分为单腿支撑的摆动阶段与发生碰撞的碰撞阶段[1].
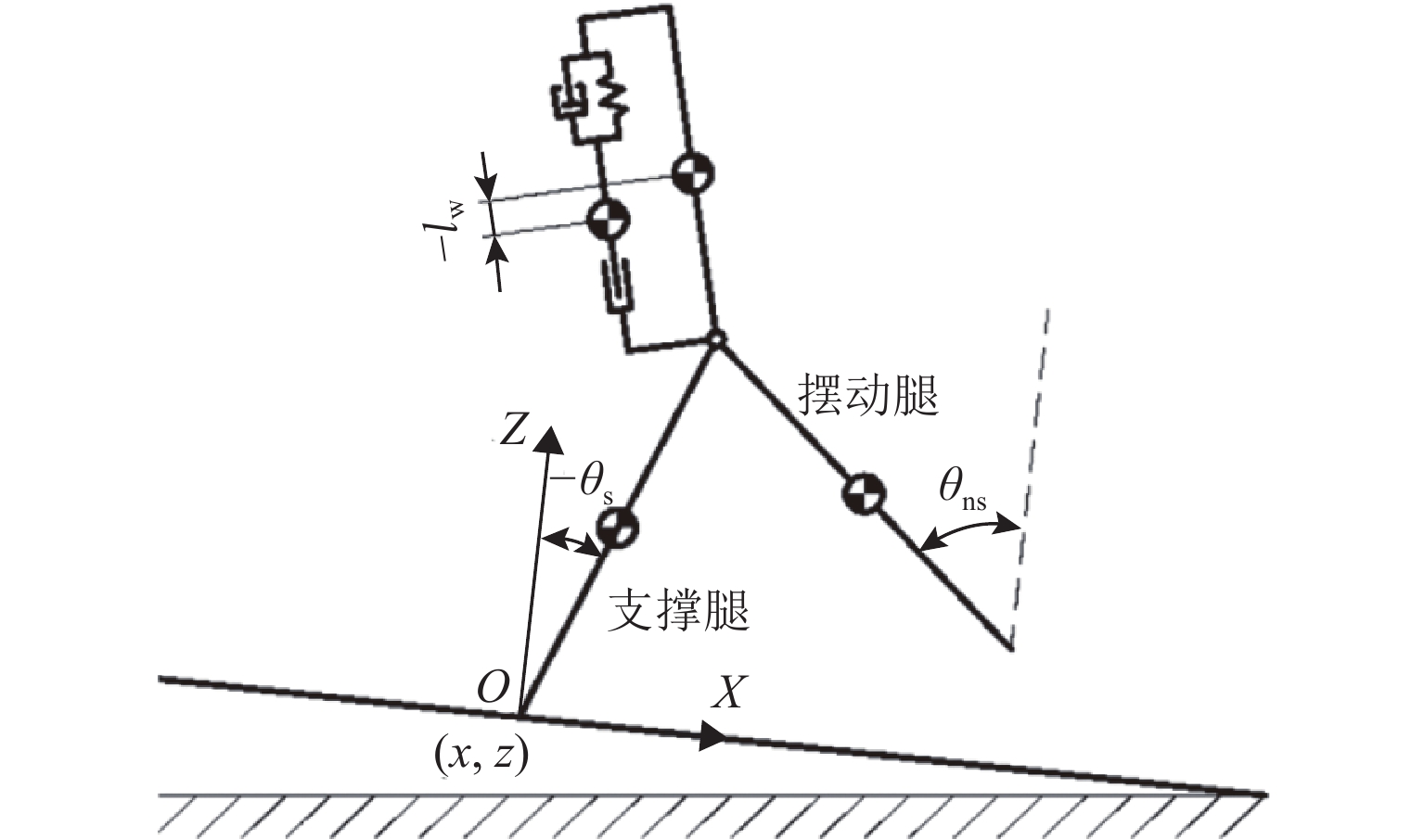
对图2系统建立坐标系，如图3所示，坐标系原点位于支撑腿的足底，X轴正方向为沿斜坡向下，Z轴正方向为垂直斜坡向上，并规定由Z轴正方向起逆时针方向转动角度为正. 用x和z分别为支撑腿足底沿X轴方向和沿Z轴方向的位移，lw为躯干柔性部分等效质心相对躯干质心位移，θs为支撑腿与Z轴方向之间的夹角，θns为摆动腿与Z轴方向之间的夹角.
图 3 带有仿生躯干的被动行走机器人广义坐标Figure 3. Generalized coordinates of passive walking robot with a bionic torso1.2.1 摆动阶段动力学方程
由图3可知，在摆动阶段，带有仿生躯干的被动行走机器人系统具有3个自由度：支撑腿转动的角度θs、摆动腿转动的角度θns和躯干柔性部分振动的位移lw.
机器人受到躯干柔性部分对躯干的作用力u以及斜坡对支撑腿足底的约束力λ作用. u的大小u包括躯干柔性部分重力mwg与等效弹簧阻尼力$ k{l_{\rm{w}}} + c{\dot l_{\rm{w}}} $两部分，即$ u = {m_{\rm{w}}}g - (k{l_{\rm{w}}} + c{\dot l_{\rm{w}}}) $；λ包含X轴方向的约束力$\lambda _1 $和Z轴方向的约束力$\lambda _2 $，即λ=[$\lambda _1 $ $\lambda _2 $]T. 由于斜坡对机器人足底只能提供支撑力，所以，$\lambda _2 $必须保持大于0，否则，支撑腿将脱离斜面. 由图3坐标原点的确定方法可知
{x=0,z=0. (1) 取广义坐标${\boldsymbol{ q}}{\mathbf{ = }}{[x\;\;{\textit{z}}\;\;{\theta _{{\rm{ns}}}}\;\;{\theta _{\rm{s}}}\;\;{l_{\rm{w}}}]^{\rm{T}}} $，利用Lagrange方法，可以得到系统的动力学方程为
M(q)¨q+h(q,˙q)=Su+JT(q)λ， (2) f(q)=0, (3) 式中：$ {\boldsymbol{M}}({\boldsymbol{q}}) \in {\mathbb{R}^{5 \times 5}} $为机器人的广义质量矩阵；$ \ddot {\boldsymbol{q}} $为广义加速度；$ {\boldsymbol{h}}({\boldsymbol{q}},\dot {\boldsymbol{q}}) $为机器人的非线性矩阵，其中，$ \dot {\boldsymbol{q}} $为广义速度；$ {\boldsymbol{M}}({\boldsymbol{q}}) $、$ {\boldsymbol{h}}({\boldsymbol{q}},\dot {\boldsymbol{q}}) $的表达式过于冗长，限于篇幅原因，在此略去；$ {\boldsymbol{S}} $为躯干柔性部分对机器人的作用力矢u的系数矩阵，由于u只作用于广义坐标lw，$ {\boldsymbol{S}} = {\left[ {{{\boldsymbol{0}}_{1 \times 4}}\;1} \right]^{\rm{T}}} $；$ {\boldsymbol{f}}({\boldsymbol{q}}) $为机器人支撑腿足底关于变量x和 z的约束条件，其表达如式（1）所示；${\boldsymbol{ J}}({\boldsymbol{q}}) $是约束方程（3）的雅可比矩阵，如式（4）所示.
J(q)=∂f∂q=[1000001000]. (4) 1.2.2 碰撞阶段动力学方程
由图3可知，当摆动腿的角度与支撑腿的角度满足关系θs + θns = 0时，被动行走机器人的摆动腿与斜坡发生碰撞；碰撞结束后，支撑腿与摆动腿立刻互换.
由于设定坐标系原点始终位于支撑腿足底，所以在碰撞结束后，必须变换系统的坐标系原点. 对此，利用文献[22]的处理方法，在摆动腿与斜坡发生碰撞的前一瞬间，先重置系统的广义坐标和广义速度.
在碰撞前一瞬间，重置后系统的广义坐标$ {{\boldsymbol{q}}_{{\rm{reset}}}} $和广义速度$ {\dot {\boldsymbol{q}}_{{\rm{reset}}}} $分别为
qreset=[00θ−nsθ−sl−w]T, (5) ˙qreset=[˙xreset˙zreset˙θ−ns˙θ−s˙l−w]T, (6) 式中：$ \theta _{{\rm{ns}}}^ - $、$ \dot \theta _{{\rm{ns}}}^ - $分别为碰撞前一瞬间摆动腿的角度、角速度；$ \theta _{\rm{s}}^ - $、$ \dot \theta _{\rm{s}}^ - $分别为碰撞前一瞬间支撑腿的角度、角速度；$ l_{\rm{w}}^ - $、$ \dot l_{\rm{w}}^ - $分别为碰撞前一瞬间躯干柔性部分等效质心的相对位移、速度；$ {\dot x_{{\rm{reset}}}} $、${\dot {\textit{z}}_{{\rm{reset}}}}$分别为重置坐标系后支撑腿足底的X轴方向速度、Z轴方向速度，${\dot x_{{\rm{reset}}}} = {\dot x^ - } + \dot \theta _{{\rm{ns}}}^ - L\cos \;\theta _{{\rm{ns}}}^ - -\; \dot \theta _{\rm{s}}^ - \;L\cos \;{\theta _{\rm{s}}}^ -$，${\dot {\textit{z}}_{{\rm{reset}}}} = {\dot {\textit{z}}^ - } + \dot \theta _{{\rm{ns}}}^ - L\times \sin \; \theta _{{\rm{ns}}}^ - - {\dot \theta _{\rm{s}}}^ - L\sin \;{\theta _{\rm{s}}}^ -$，$ {\dot x^ - } $和${\dot {\textit{z}}^ - }$分别为碰撞前一瞬间支撑腿足底的X轴方向速度、Z轴方向速度.
根据角动量守恒定律，利用Lagrange方程的冲量形式，得到摆动腿与斜坡碰撞时的系统动力学方程为
M(qreset)˙q+−M(qreset)˙qreset=JTI(qreset)λI, (7) JI(qreset)˙q+=0, (8) 式中：$ {\boldsymbol{M}}({{\boldsymbol{q}}_{{\rm{reset}}}}) $为重置后的广义质量矩阵；$ {{\boldsymbol{J}}_{\rm{I}}}({{\boldsymbol{q}}_{{\rm{reset}}}}) $为碰撞时约束方程的雅可比矩阵；$ {\lambda _{\rm{I}}} $为碰撞时的足底支撑力；$ {\dot {\boldsymbol{q}}^ + } $为碰撞后的广义速度，如式（9）所示.
˙q+=[I5−M−1(qreset)HI(qreset)]˙q−, (9) 式中：I5为5阶单位矩阵，$ {{\boldsymbol{H}}_{\rm{I}}}({{\boldsymbol{q}}_{{\rm{reset}}}}) = {\boldsymbol{J}}_{\rm{I}}^{\rm{T}}({{\boldsymbol{q}}_{{\rm{reset}}}}) \times {{\boldsymbol{X}}_{\rm{I}}^{ - 1}}({{\boldsymbol{q}}_{{\rm{reset}}}}){{\boldsymbol{J}}_{\rm{I}}}({{\boldsymbol{q}}_{{\rm{reset}}}}) $，${{\boldsymbol{X}}_{\rm{I}}} = {{\boldsymbol{J}}_{\rm{I}}}({{\boldsymbol{q}}_{{\rm{reset}}}}){{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{q}}_{{\rm{reset}}}}){\boldsymbol{J}}_{\rm{I}}^{\rm{T}}({{\boldsymbol{q}}_{{\rm{reset}}}}). $
由于重置了广义坐标，$ {\boldsymbol{M}}({{\boldsymbol{q}}_{{\rm{reset}}}}) $与$ {\boldsymbol{M}}({{\boldsymbol{q}}^ - }) $在数值上相同，并且碰撞过程中约束方程式（3）仍然成立，$ {{\boldsymbol{J}}_{\rm{I}}}({{\boldsymbol{q}}_{{\rm{reset}}}}) $的表达式与式（4）相同.
由于碰撞过程中系统的位形没有发生变化，式（5）的重置广义坐标$ {{\boldsymbol{q}}_{{\rm{reset}}}} $即为碰撞结束后的广义坐标$ {{\boldsymbol{q}}^ + } $，即$ {{\boldsymbol{q}}^ + } = {{\boldsymbol{q}}_{{\rm{reset}}}} $.
2. 仿生躯干参数对被动行走的步长及速度影响分析
利用第1节得到的动力学方程，使用MATLAB软件对式（2）、（3）、（7）、（8）所示的仿生躯干被动行走机器人进行仿真.
仿真中，若出现sgn λ2<0或 |lw|>Lh，说明支撑腿脱离了斜面或出现了不应出现的状况，则停止仿真；若机器人能够连续走200步，则认为该被动行走能够一直稳定下去. 为避免运动初始值带来的影响，只记录机器人最后20步的数据用以分析. 定义仿生躯干被动行走机器人的平均步行速度v为机器人的行走总距离与行走总时间的比值，即
v=20∑i=1ΔLi/20∑i=1Ti, (10) 式中：ΔLi为第i步的步长，Ti为第i步所用的时间.
本节主要研究仿生躯干柔性部分的参数对被动行走机器人的行走步长及步行速度的影响. 为了进行对比和分析，首先对刚性躯干的被动行走机器进行仿真，即令 mw=0， k =0， c =0，刚性躯干机器人的其他物理参数见表1所示. 对不带有躯干柔性部分（即刚性躯干）的被动行走机器人（mw=k=c=0）进行仿真，结果表明：被动行走机器人存在一个稳定的单周期步态，平均步长ΔL=0.5039 m，步行周期T=0.8232 s，平均步行速度v=0.6121 m/s.
表 1 刚性躯干机器人仿真参数及其取值Table 1. Simulation parameters and values for rigid torso robot参数 m
/kgmh
/kgLmh
/mLh
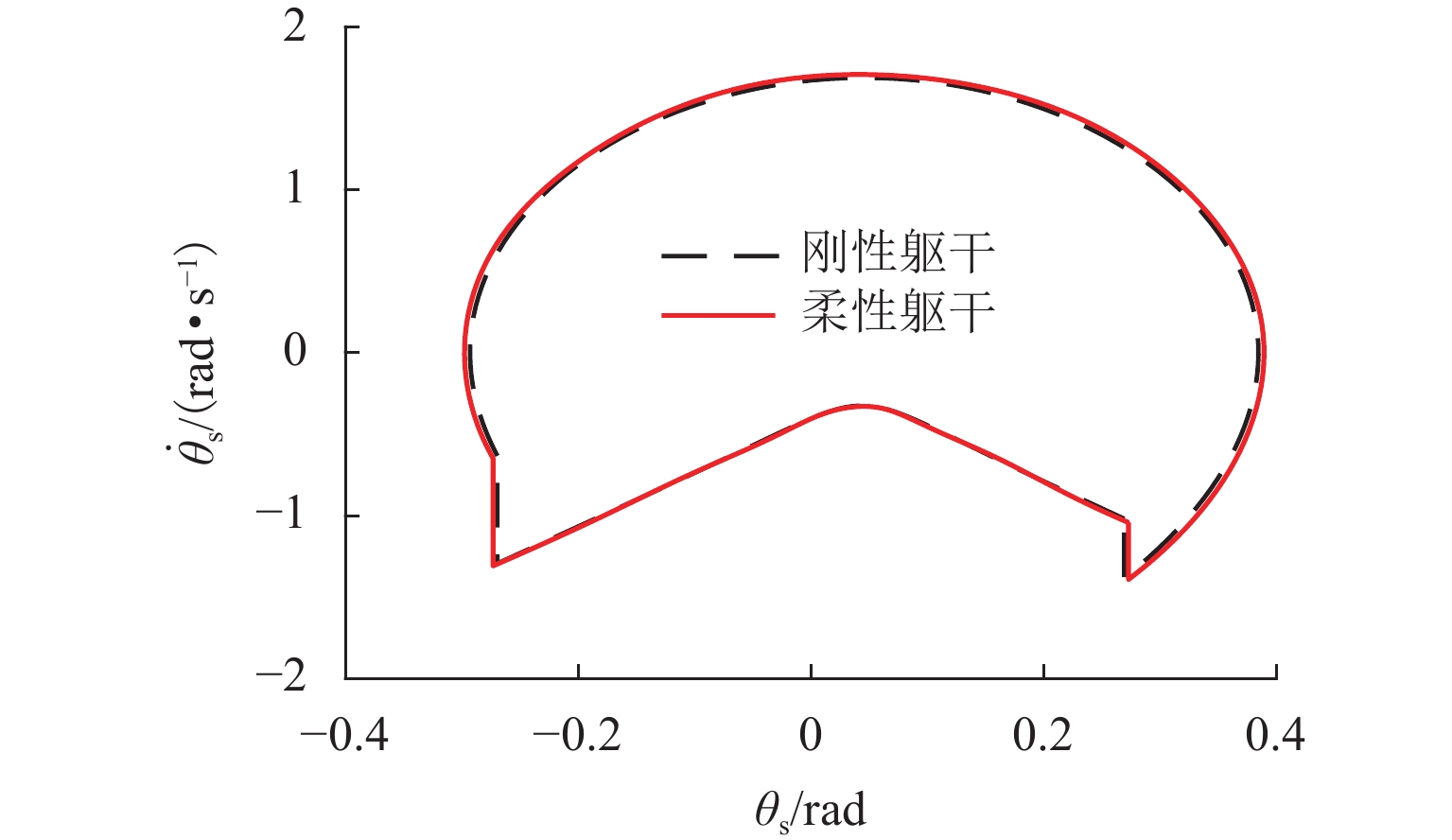
/ma，b
/mg/（m·s−2） ϕ/rad 取值 5.0 3.5 0.25 0.5 0.5 9.81 0.04 当k=700 N/m，c=2 N·s/m，mw=1 kg时，仿生躯干被动行走机器人的行走极限环如图4所示. 可以看出：在这组参数下，仿生躯干的被动行走极限环是单周期极限环，且比刚性躯干的极限环略大；仿生躯干被动行走机器人表现为单周期步态，且步行速度比刚性躯干更快.
2.1 等效弹性系数k的影响
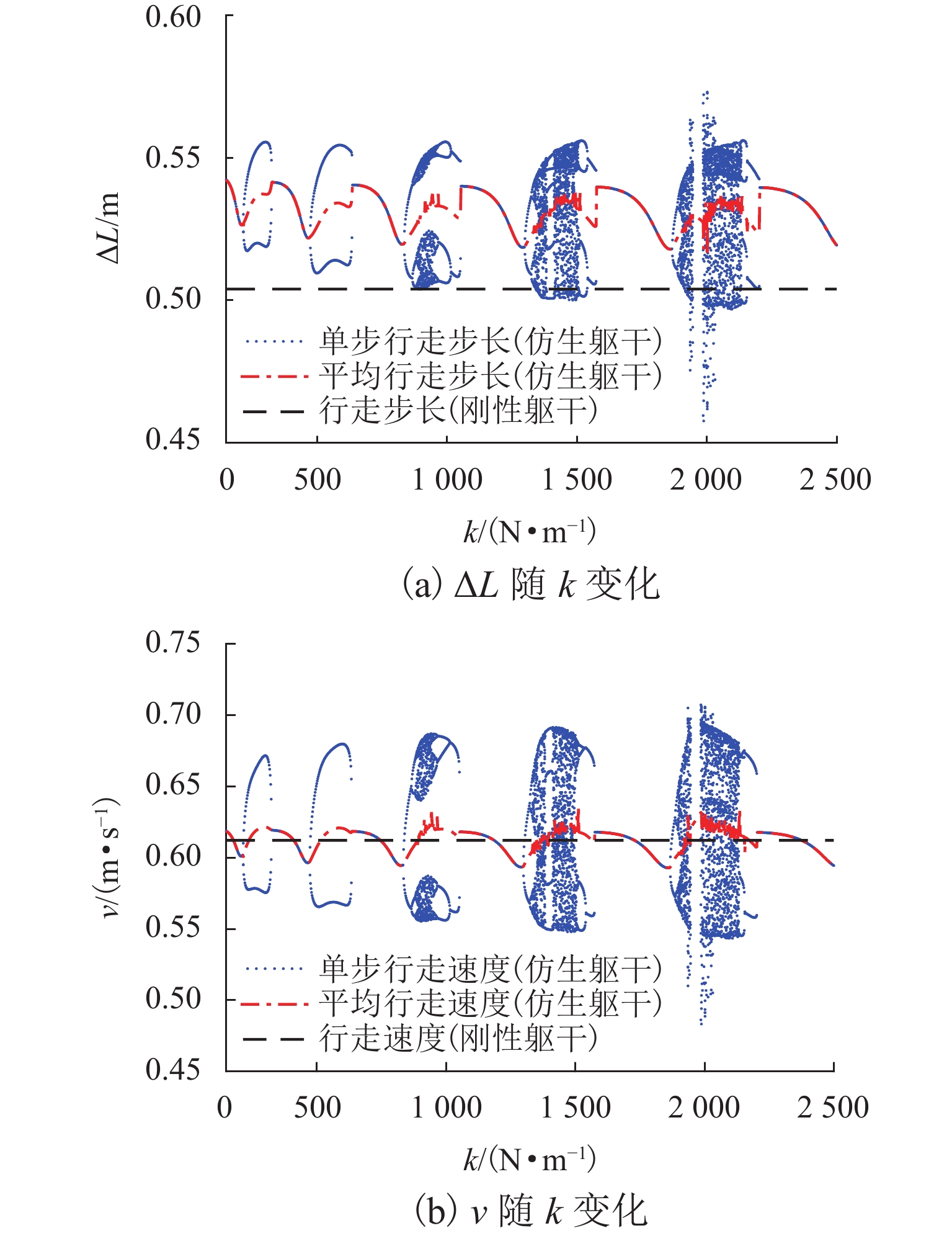
为研究等效弹性系数k对被动行走的影响，保持图4的c与mw不变，图5给出k在 [0,2500] N/m变化时，ΔL、v随k的变化规律.
图 5 等效弹性系数k与机器人步态的关系Figure 5. Relationship between equivalent elasticity coefficient k and robot gait从图5 （a）可知：整体上看，仿生躯干被动步行机器人的平均步长随着等效弹性系数的增大呈现类似于周期性的“减小—增大—减小—$ \cdots \cdots $”循环变化过程；并且在k的整个取值范围内，仿生躯干平均步长都大于刚性躯干的0.5039 m，说明仿生躯干柔性可以增大被动行走机器人的步长.
此外，随着k的变化，ΔL值也出现了类似于周期性的分岔和混沌现象. 当k<800 N/m时，随着k增加，ΔL值经历了2次“单周期—二周期—单周期”的分岔变化. 在此区间内，机器人运动不会出现混沌或失稳的现象，机器人步态行为具有良好的可预测性. 而当k>800 N/m时，ΔL值出现了3次经由倍周期分叉到混沌再回归至单周期的变化. 以k∈[1600,1985] N/m为例：k∈[1600,1866] N/m时，ΔL为单周期值；k∈(1866,1906] N/m时，ΔL为多周期值；k∈(1906,1945] N/m时，ΔL为混沌值；k∈(1945,1985] N/m时，出现了机器人无法形成稳定步态的情况.
图5 （a）结果说明，改变刚度系数可以调整别动行走机器人的步态行为. 因此，在设计仿生躯干被动行走机器人时，可以通过选择仿生躯干刚度系数来调整机器人的步长，同时，要避免使用可能会破坏机器人的稳定步态的特定等效弹性系数.
ΔL变化产生的直接影响是改变机器人的行走速度. 从图5 （b）中可以看出，与平均步长的变化趋势类似，被动步行机器人的平均速度随等效弹性系数的变化也呈现出类似周期性的“减小—增大—减小—$\cdots \cdots$”变化过程. 当k在{(0,93] , (142,436] , (558,803], $\cdots $} N/m范围内时，仿生躯干被动行走机器人的平均步行速度v>0.6121 m/s，说明一定的仿生躯干柔性可以提高机器人步行速度.
以 图5 （b）中k∈[1600,1945] N/m为例：当k∈[1600,1866] N/m时， v随着k的增大而减小，且在k=1730 N/m时，v=0.6121 m/s；当k∈(1866,1906] N/m时，v随着k的增大而增大，但都小于0.6121 m/s；当k∈(1906,1945] N/m时，v与k的整体上是呈现正相关关系. 但由于机器人在此区间内是混沌步态，v随k的增加并非是光滑的，而是呈现震荡增长的趋势. 图5 （b）结果说明，与刚性躯干相比，合适的等效弹性系数可以提高被动行走的步行速度.
对比图5 （a）和图5 （b）可以发现，平均步长增大并不意味着步行速度也一定增大. 这是由于平均步行速度不仅取决于步长的大小，还取决于步行周期的大小. 例如，当k=1600 N/m时，v>0.6121 m/s；当k=1800 N/m时，v<0.6121 m/s. 对于这2组k值，仿生躯干机器人的平均步长与步行周期如表2所示. 表中，增幅是与刚性躯干机器人相比较的结果.
表 2 k=1 600 N/m与k=1800 N/m时平均步长与步行周期的变化Table 2. Change of average step length and walking period when k=1 600 N/m and k=1800 N/mk /（N·m−1） ΔL T 数值/m 增幅/% 数值/s 增幅/% 1600 0.5396 7 0.8735 6 1800 0.5252 4 0.8740 6 由表2可知：与刚性躯干相比，当k=1600 N/m时，仿生躯干机器人步行周期的增长幅度小于步长的增长幅度，所以其平均步行速度更快；而当k=1800 N/m时，仿生躯干机器人步行周期的增长幅度大于步长的增长幅度，所以其平均步行速度更慢. 然而，对比图5（a）和图5（b）可以看到，步长增加但速度减小的区间是较为稀少的.
总而言之，仿生躯干等效刚度系数的改变会使得被动行走机器人的平均行走步长及平均行走速度发生类似于周期性的变化. 当刚度系数在合适范围内，仿生躯干对被动步行机器人具有积极的影响. 躯干柔性不仅能增加机器人的步长，以提高其跨越沟壑的能力，同时也能够提高行走速度.
2.2 等效阻尼系数c的影响
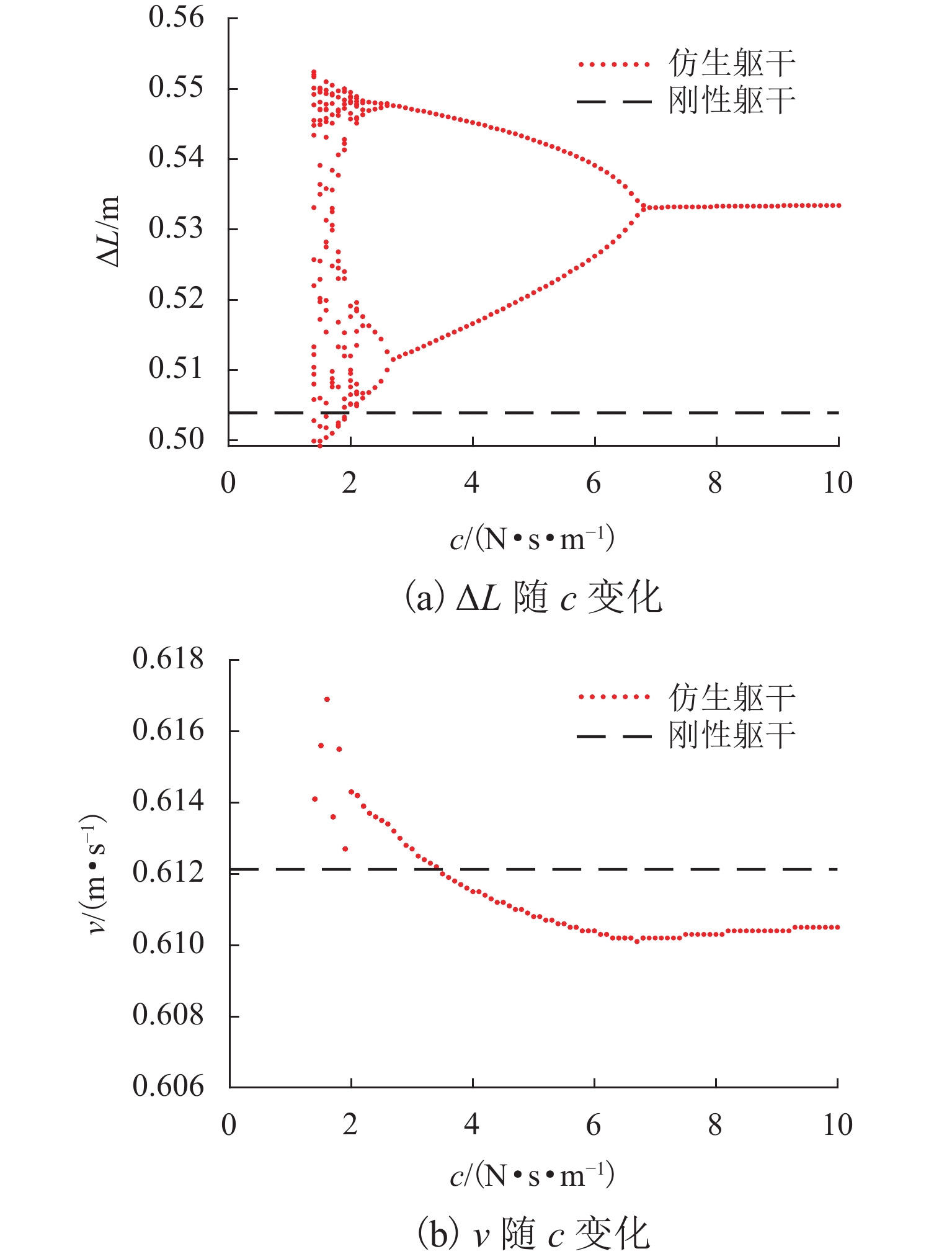
为研究等效阻尼系数c对被动行走的影响，以图5中k=904 N/m这组参数为例，由图5可知，此时被动行走机器人表现为混沌步态. 保持mw不变，将c的范围扩大至 [0,10] N·s/m，随着c的变化，ΔL及v的变化规律如图6所示.
图 6 等效阻尼系数c与机器人步态的关系Figure 6. Relationship between equivalent damping coefficient c and robot gait从图6（a）可以看出，当 c<1.4 N·s/m时，被动行走机器人无法形成稳定的步态；当 c>1.4 N·s/m时，绝大部分的c所对应的步长ΔL都大于不带有躯干柔性部分时的步长值0.5039 m. 也就是说，躯干柔性部分的等效阻尼可以使机器人的步长增大. 其中，当1.4<c<1.8 N·s/m时，ΔL的变化呈现出混沌状态；当1.8<c<6.8 N·s/m时，ΔL变为多周期值；当c>6.8 N·s/m时，ΔL变为单周期值. 仿生躯干柔性部分等效阻尼系数变化时，会使得被动行走机器人出现周期和混沌步态；并且等效阻尼系数取较小值时，不利于被动行走机器人形成稳定步态，而较大的等效阻尼系数有利于机器人形成稳定步态.
从图6（b）可以看出，当1.4<c<1.8N·s/m时， v>0.6121 m/s；当1.8<c<6.8 N·s/m时，v值随着c的增大而减小，并在 c=3.4 N·s/m时， v=0.6121 m/s；当c>6.8 N·s/m时，v随着c的增大而逐渐增大，但仍然小于0.6121 m/s. 适当的躯干柔性部分等效阻尼系数会提高被动行走机器人的速度，而较大的等效阻尼系数会降低机器人行走速度.
图6结果表明：躯干柔性部分较大的等效阻尼系数有助于被动行走机器人形成稳定的周期步态，但会降低机器人的步行速度.
2.3 等效质量mw的影响
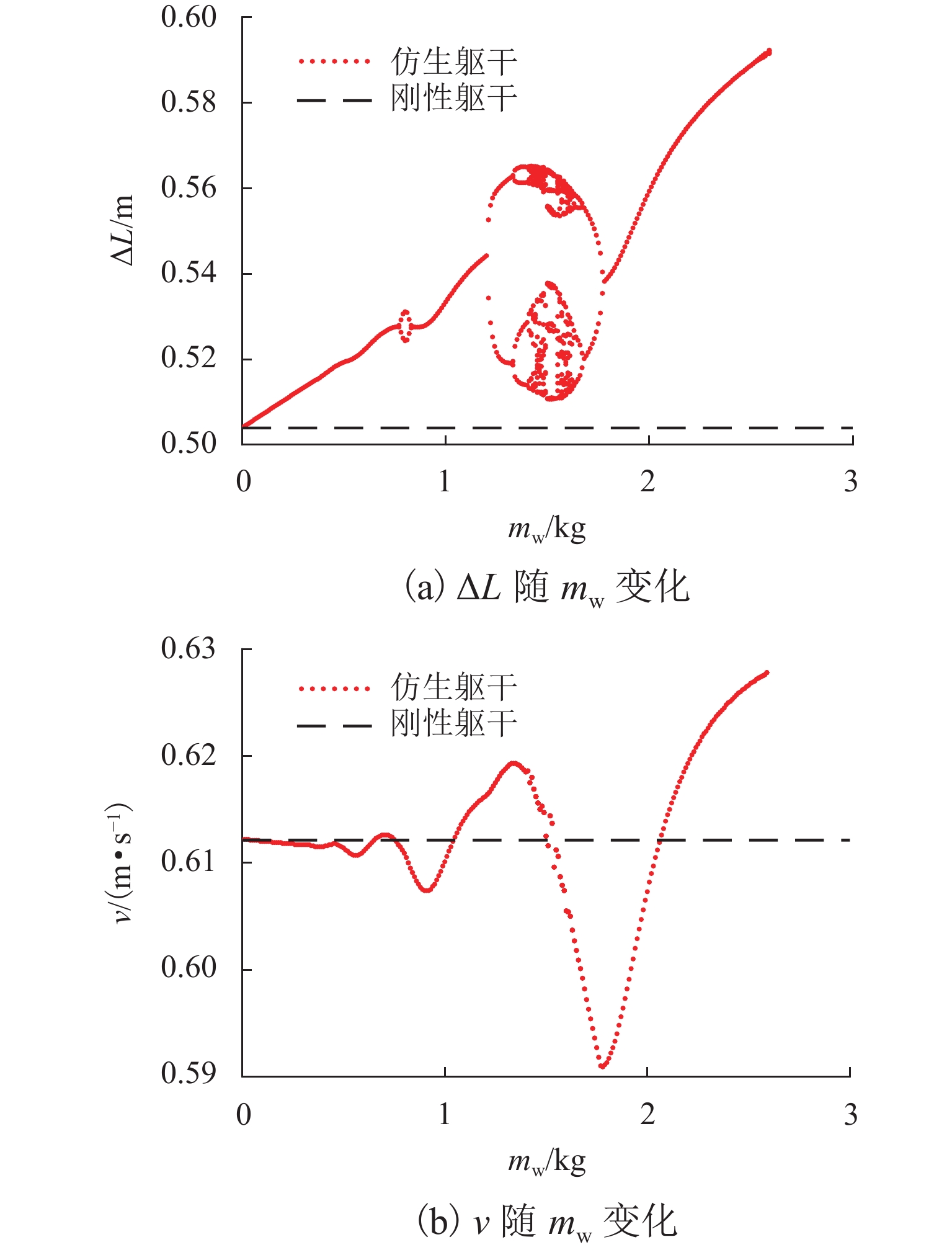
为研究躯干柔性部分的等效质量mw变化对被动行走的影响，以图5的k=750 N/m为例，并将阻尼增加至c=4 N·s/m，以提高机器人稳定性，图7给出了ΔL以及v随mw的变化规律.
由图7 （a）可以看出：当mw≤0.77 kg时，ΔL为单周期值；当0.77 kg<mw≤0.83 kg时，ΔL为双周期值；当0.83 kg< mw≤1.20 kg时，ΔL又表现为单周期值；当1.20 kg< mw≤1.78 kg时，ΔL先是由双周期通过倍周期分岔进入混沌，然后再通过倍周期分岔变为双周期值；当1.78 kg<mw≤2.59 kg时，ΔL为单周期值；当2.59 kg<mw<3.00 kg时，被动行走机器人无法形成稳定的步态. 此外，在mw<2.59 kg时，仿生躯干平均步长ΔL均大于刚性躯干的ΔL值0.5039 m.
从整体上看，除去非单周期区间，被动行走机器人步长与躯干柔性部分质量呈现正相关关系. 质量取特定值时，被动行走机器人会出现混沌步态. 但较大或者较小的柔性部分质量都会使机器人呈现单周期步态，这使机器人的运动具有较好的可预测性. 而过大的质量则会破坏被动行走机器人的稳定步态.
与3.1节所分析的刚度系数对机器人平均速度影响不同，尽管机器人步长与躯干柔性部分质量大体上呈现正相关关系，但图7 （b）却显示了机器人平均步行速度随躯干柔性部分质量呈现发散式的波动变化. 当mw<0.77 kg时，v在0.6121 m/s附近波动，说明此时机器人的平均步行速度与不带躯干柔性部分时的平均步行速度相近；当0.77 kg<mw≤1.78 kg时， v既有小于0.6121 m/s的值，又有大于0.6121 m/s的值，其中在mw=1.04，1.51 kg时，v=0.6121 m/s；当1.78 kg<mw≤2.59 kg时，v随着mw的增大而逐渐增大，mw =2.59 kg时，v=0.6280 m/s，达到最大值.
图7 （b）结果说明，躯干柔性部分的质量较小时，对被动行走机器人的平均步行速度影响不大；随着躯干柔性部分质量的增大，其对平均步行速度的影响越来越明显.
结合图7 （a）和图7 （b）的结果可以看出，为使机器人在具有较大步长的同时，又有较高的平均步行速度，可选取较大的柔性部分质量，但柔性部分质量不能过大，否则将导致机器人失稳.
为进一步说明对于不同的被动行走机器人都可利用仿生躯干来改善其步态特性，保持表1中除mh外的其他参数不变，对mh=2, 3, 4 kg这3个不同的被动行走机器人分别采用刚性躯干和仿生躯干，其行走步长与步行速度的仿真结果如表3～5所示. 可以看出，相比于刚性躯干，仿生躯干的行走步长和速度均有一定程度的提升. 这说明选择合适的躯干柔性参数，使用仿生躯干都可以有效改善被动行走机器人的步态特性，增加行走步长，提高步行速度.
表 3 mh=2 kg的行走步长与步行速度（k=100 N/m, c=2 N·s/m, mw=1.0 kg）Table 3. Walking step length and walking speed when mh=2 kg （k=100 N/m, c=2 N·s/m, mw=1.0 kg）躯干类型 ΔL/m v/（m·s−1） 刚性躯干 0.4453 0.6135 仿生躯干 0.4984 0.6238 增幅/% 12 2 表 4 mh =3 kg的行走步长与步行速度 （k=100 N/m, c=2 N·s/m, mw =1.2 kg）Table 4. Walking step length and walking speed when mh=3 kg （k=100 N/m, c=2 N·s/m, mw =1.2 kg）躯干类型 ΔL/m v/（m·s−1） 刚性躯干 0.4871 0.6130 仿生躯干 0.5375 0.6225 增幅/% 10 2 表 5 mh =4 kg的行走步长与步行速度（k=380 N/m, c=2 N·s/m, mw=1.2 kg）Table 5. Walking step length and walking speed when mh=4 kg （k=380 N/m, c=2 N·s/m, mw=1.2 kg）躯干类型 ΔL/m v/（m·s−1） 刚性躯干 0.5189 0.6110 仿生躯干 0.5600 0.6185 增幅/% 8 1 3. 结 论
本文提出带刚柔仿生躯干的被动行走机器人模型，通过建立模型动力学方程，采用数值仿真的方法研究了仿生躯干对机器人行走步长及步行速度的影响. 研究结果表明：
1） 仿生躯干柔性部分的等效弹簧系数、等效阻尼系数和等效质量对于机器人的行走步长和平均步行速度均有明显影响. 其中，等效弹性系数的改变会使被动行走机器人出现单周期步态、多周期步态以及混沌步态；较大的等效阻尼系数虽然会降低被动行走机器人的步行速度，但有助于被动行走机器人形成稳定的周期步态；过大的柔性躯干质量会导致被动行走机器人无法形成稳定步态.
2） 只要能选择合适的仿生躯干柔性部分的等效弹簧系数、等效阻尼系数和等效质量，与刚性躯干相比，仿生躯干能够使得被动行走机器人在保持稳定周期步态的同时，提高被动行走机器人的行走步长及步行速度.
本文的研究结果为利用仿生躯干来改善双足被动行走机器人的步态特性提供了相应的理论基础.
-
图 4 施工过程中撑杆上端节点的竖向位移
Figure 4. Vertical displacements of upper nodes on struts during construction
图 5 施工过程中的最外圈索杆内力
Figure 5. Internal forces of outermost ring members during construction
表 1 构件截面面积及初始预应力
Table 1. Section areas and initial prestresses of members
杆件
编号截面面
积/mm2初始预应
力/kN杆件
编号截面面
积/mm2初始预应
力/kNJS1 7260 1551.73 XS3B 9310 1636.83 JS2A 8370 521.39 HS1 10050 1294.26 JS2B 8370 1134.31 HS2 15080 3005.37 JS3A 9310 1829.04 SLH 9896 1551.55 JS3B 9310 1962.96 XLH 8262 171.97 XS1 7260 174.38 NCG 7383 −29.02 XS2A 8370 455.77 CG1 8262 −307.07 XS2B 8370 786.26 CG2A 9896 −509.03 XS3A 9310 1636.76 CG2B 9896 −509.05 
下载: 导出CSV
表 2 不同方案的施工步骤
Table 2. Construction procedures of different schemes
施工
步骤方案一
（交替提升与张拉）方案二
（仅张拉最外圈斜索）1 XS3 预留3% 张拉长度安装，内拉环与设计标高间距为h1+ h2 + h3 XS3 预留 3% 张拉长度安装 2 内拉环提升 h1 3 张拉 1% 索长 张拉 1% 索长 4 内拉环提升 h2 5 张拉 1% 索长 张拉 1% 索长 6 内拉环提升 h3，达到设计标高 7 XS3 张拉至设计长度 XS3 张拉至设计长度
下载: 导出CSV
表 3 不同方案的结果对比
Table 3. Comparison of results between different schemes
方案 μ/% 平均结构
应变能/（kN·m）脊索 斜索 环索 撑杆 一 16.47 38.04 37.88 15.99 230.66 二 43.15 64.29 48.01 35.80 419.18
下载: 导出CSV
-
[1] GEIGER D, STEFANIUK A, CHEN D. The design and construction of two cable domes for the Korean Olympics[C]//Proceedings of the IASS Symposium. Osaka: [s.n.], 1986: 265-272. [2] YAN X Y, YANG Y, CHEN Z H, et al. Mechanical properties of a hybrid cable dome under non-uniform snow distribution[J]. Journal of Constructional Steel Research, 2019, 153: 519-532. doi: 10.1016/j.jcsr.2018.10.022 [3] 冯远,向新岸,董石麟,等. 雅安天全体育馆金属屋面索穹顶设计研究[J]. 空间结构,2019,25(1): 3-13.FENG Yuan, XIANG Xinan, DONG Shilin, et al. Design and research on tensegrity type cable dome with metal roof of Ya’an Tianquan Gymnasium[J]. Spatial Structures, 2019, 25(1): 3-13. [4] 冯远,王立维,张彦,等. 成都凤凰山专业足球场结构设计[J]. 建筑结构,2020,50(19): 15-21,14.FENG Yuan, WANG Liwei, ZHANG Yan, et al. Structural design of Chengdu Fenghuangshan professional football field[J]. Building Structure, 2020, 50(19): 15-21,14. [5] XUE S D, GAO Z Y, LI X Y. Research status and prospects of cable domes[J]. Applied Mechanics and Materials, 2011, 94/95/96: 1424-1432. [6] 陈联盟,董石麟,袁行飞. 索穹顶结构施工成形理论分析和试验研究[J]. 土木工程学报,2006,39(11): 33-36,113. doi: 10.3321/j.issn:1000-131X.2006.11.006CHEN Lianmeng, DONG Shilin, YUAN Xingfei. Theoretical and experimental study on the construction of cable domes[J]. China Civil Engineering Journal, 2006, 39(11): 33-36,113. doi: 10.3321/j.issn:1000-131X.2006.11.006 [7] 董石麟,袁行飞,赵宝军,等. 索穹顶结构多种预应力张拉施工方法的全过程分析[J]. 空间结构,2007,13(1): 3-14,25.DONG Shilin, YUAN Xingfei, ZHAO Baojun, et al. Constrution analysis of cable-dome structures pretensioned by different schemes[J]. Spatial Structures, 2007, 13(1): 3-14,25. [8] LIU Z S, WANG Z Q, YOU D Q. Integral hoisting and tension-shaping techniques of Ordos cable dome[J]. Applied Mechanics and Materials, 2012, 170/171/172/173: 3208-3211. [9] 王泽强,程书华,尤德清,等. 索穹顶结构施工技术研究[J]. 建筑结构学报,2012,33(4): 67-76.WANG Zeqiang, CHENG Shuhua, YOU Deqing, et al. Research on construction techniques of cable dome roof[J]. Journal of Building Structures, 2012, 33(4): 67-76. [10] ZHANG A L, SUN C, JIANG Z Q. Experimental study on the construction shape-forming process and static behaviour of a double strut cable dome[J]. Journal of Zhejiang University: Science A, 2018, 19(3): 225-239. doi: 10.1631/jzus.A1700071 [11] 宗钟凌. 刚性屋面索穹顶结构建造技术及试验研究[D]. 南京: 东南大学,2009. [12] 罗斌,郭正兴,高峰. 索穹顶无支架提升牵引施工技术及全过程分析[J]. 建筑结构学报,2012,33(5): 16-22.LUO Bin, GUO Zhengxing, GAO Feng. Research on non-bracket tow-lifting construction technology and complete process analysis of cable dome[J]. Journal of Building Structures, 2012, 33(5): 16-22. [13] DING M M, LUO B, GUO Z X, et al. Integral tow-lifting construction technology of a tensile beam-cable dome[J]. Journal of Zhejiang University: Science A, 2015, 16(12): 935-950. [14] 蒋丰,王晓丽,刘火明,等. 大开口索穹顶巨型桁架带索整体提升技术[J]. 施工技术,2020,49(20): 46-48,75.JIANG Feng, WANG Xiaoli, LIU Huoming, et al. Integral lifting technology of cable dome large truss with large opening[J]. Construction Technology, 2020, 49(20): 46-48,75. [15] 刘小伟. 大跨度索穹顶结构的若干问题研究[D]. 广州: 华南理工大学,2017. [16] 苏延. 复合型索穹顶结构的找力优化及施工仿真分析 [D]. 广州: 华南理工大学,2021. [17] 唐承,郭书祥,莫延彧,等. 应用粒子群-序列二次规划算法的结构可靠性优化[J]. 空军工程大学学报(自然科学版),2016,17(2): 107-111.TANG Cheng, GUO Shuxiang, MO Yanyu, et al. An optimal design of structural reliability based on particle swarm optimization-sequential quadratic programming algorithm[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(2): 107-111. [18] 姜正荣,刘小伟,石开荣,等. 基于比值更新的索穹顶结构找力分析方法[J]. 西南交通大学学报,2020,55(1): 150-157. doi: 10.3969/j.issn.0258-2724.20180201JIANG Zhengrong, LIU Xiaowei, SHI Kairong, et al. Method of force-finding analysis based on ratio updating for cable domes[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 150-157. doi: 10.3969/j.issn.0258-2724.20180201 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 242
- HTML全文浏览量: 99
- PDF下载量: 58
- 被引次数: 0