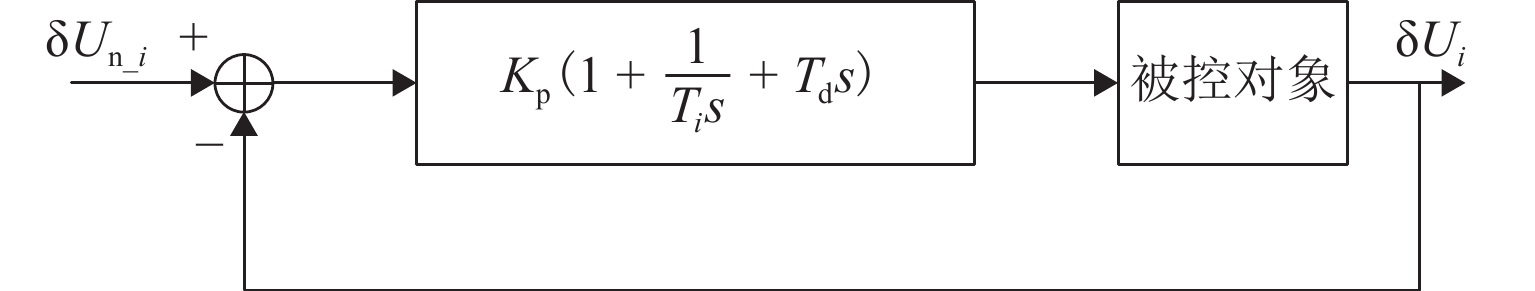电-氢混合储能型多微电网系统有功功率均衡控制方法

李奇; 李蕊睿; 李朔; 蒲雨辰; 孙彩; 陈维荣

doi:10.3969/j.issn.0258-2724.20210506

电-氢混合储能型多微电网系统有功功率均衡控制方法

doi: 10.3969/j.issn.0258-2724.20210506

西南交通大学电气工程学院，四川成都 610031

基金项目: 国家自然科学基金（51977181，52077180）；霍英东教育基金会高等院校青年教师基金（171104）

详细信息

作者简介:
李奇（1984—），男，教授，博士生导师，研究方向为轨道交通新能源技术、综合能源系统运行与控制等，E-mail：liqi0800@163.com

中图分类号: TM732
计量
- 文章访问数: 281
- HTML全文浏览量: 171
- PDF下载量: 65
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-22
- 修回日期: 2022-01-22
- 网络出版日期: 2024-03-13
- 刊出日期: 2022-03-31

Control Method for Active Power in Electric-Hydrogen Hybrid Energy-Storage Microgrids

School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
在多电-氢微电网并联运行的交流系统中，采用传统控制方法的逆变器会受到输出线路阻抗差异所产生的影响产生较大环流，甚至无法实现有功功率的合理分配，考虑到系统中电压偏差与有功功率间的关系，对多微电网的有功功率分配问题进行分析研究. 首先，构建含光伏、燃料电池、电解槽、蓄电池的电-氢混合储能微电网交流系统模型；其次，根据反下垂控制中有功功率与电压间的关系，构造考虑电压偏差的反下垂控制，并为使额定有功功率自适应调节，提出基于功率跟随控制的反下垂控制方法；最后，在多电-氢微电网并联运行的系统中，对本文所提方法进行RT-LAB半实物实验验证及与其他方法的对比验证. 实验结果显示：基于本文所提控制方法的系统稳定后功率分配的准确度达97.50%，母线电压的精准度达99.86%，环流大小的范围约为[−3.0, 3.0] A，均优于其余方法.
- 电-氢微电网 /
- 混合储能 /
- 功率控制
Abstract:
In an AC system with parallel operation of electricity-hydrogen micro-grids, when adopting traditional control methods, the difference in output line impedance will affect inverters, and large circulating currents occurs such that a reasonable distribution of active power become inaccessible. Given the relationship between the voltage deviation and the active power, the active power distribution between multiple micro-grids is analyzed. Firstly, the AC system model of the electric-hydrogen hybrid energy-storage micro-grid is constructed, including photovoltaic, battery, fuel cell, and electrolyzer. Secondly, following the relationship between the active power and the voltage in the reverse droop control, a reverse droop control based on power following control is proposed to work out voltage deviation and auto-adjust the rated active power. Finally, within a parallel operation of electric-hydrogen micro-grids, the proposed method is compared with other methods and is verified by hardware-in-the-loop experiments on the platform of RT-LAB. The experimental results show that the proposed method outperforms other methods: the accuracy of power distribution after stabilization is 97.50%, the accuracy of the bus voltage is 99.86%, and the circulating current mostly ranges in [−3.0, 3.0] A.
- electric-hydrogen microgrid /
- hybrid energy storage /
- power control

HTML全文

环境污染和能源短缺问题成为近些年来的热点问题，分布式电源（DG）应运而生，并且得到了广泛研究和应用. 目前，微电网系统作为一种较为灵活的能源利用形式，由DG、储能单元、电力负载及控制器等几部分组成，为用户端供能，较大程度地发挥DG的能效，规模较小，与大电网的兼容交互性强，更适合并入大电网中^[1-3]. 微网在离网运行时，由内部DG实现母线的功率平衡；并网运行时，大电网和微电网进行能量交换，由于传统大电网往往是交流形式，微电网并网时通常需要通过并网逆变器进行变换^[4]. 在多微电网并联运行系统中，采用对等控制模式时，通过本地控制各并网逆变器为负载供能，且各逆变器独立运行^[5-6].

对于线路阻抗差异对系统产生的影响，很多学者通过改进逆变器控制方法对该问题进行了研究与改进：文献[7]考虑到微电网中线阻差异对蓄电池荷电状态的影响，提出一种基于虚拟额定电流的策略，使荷电状态快速均衡；文献[8]分析了系统的稳定性，提出一种串联虚拟阻抗的方法，改善附加虚拟惯性系数降低系统阻尼的情况. 对于系统中的功率均衡问题，很多学者也考虑了不同方面，以更加合理地分配功率：文献[9]引入变化系数的改进互联通信荷电状态下垂控制，限制各储能模块的最大输出功率，实现功率合理分配；文献[10]和文献[11]在下垂控制中分别用增加无功功率反馈和改进传统虚拟阻抗的方法来改善功率分配的准确度；文献[12]基于虚拟感抗改变等效线路阻抗为感性，并自适应调节无功功率，实现功率均衡分配的目的. 上述有些方法虽然能实现合理分配功率，但在电压的降落大小、达到稳定的速度和不能适用于变化参数的系统等方面仍有改进空间.

本文搭建含有光伏、蓄电池、燃料电池、电解槽的多微电网系统，针对低压微电网系统中，逆变器输出有功功率分配受线路阻抗差异影响的问题进行分析，并在RT-LAB半实物平台上验证本文所提的基于功率跟随控制的反下垂控制方法，并与传统下垂控制方法等进行对比，验证本文所提方法的可行性及在改善功率分配合理度、降低电压偏差和减小环流大小方面的有效性.

1. 系统结构

1.1 多微电网并联运行结构

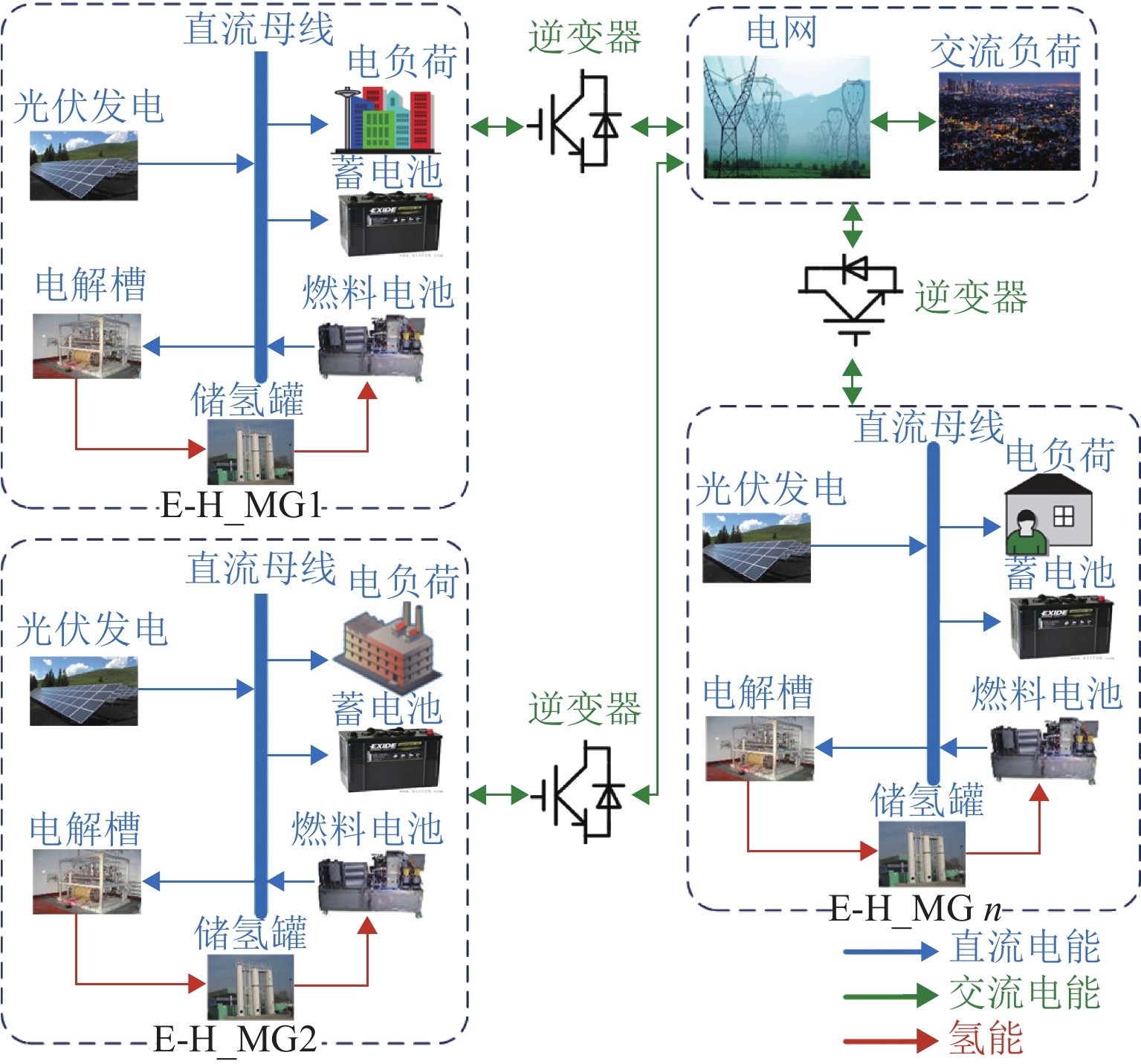
一个微电网是由DG、储能装置、电力负载等共同组成的系统，以电-氢储能直流微电网为例，光伏阵列作为DG，对蓄电池、燃料电池、储氢罐、电解槽及负载供能，多直流微电网并联运行示意如图1所示.

图 1 多微电网并联运行结构示意

Figure 1. Schematic of micro-grid parallel operation

下载: 全尺寸图片幻灯片

1.2 模型搭建

本文所搭建的直流微电网系统中，光伏电池所用的数学模型^[13]为

，

$I = {I_{{\text{sc}}}}\left\{ {{\text{1}} - {C_1}\left[ {\exp \left(\frac{U}{{{C_2}{U_{{\text{oc}}}}}}\right) - 1} \right]} \right\} \text{，}$

(1)

式中：I和I_sc分别为光伏电池的输出电流和短路电流，U和U_oc分别为光伏电池的输出电压和开路电压，C₁、C₂分别为与峰值电压、电流的相关函数.

蓄电池的数学模型可由可变电压源和内部电阻^[14]表示为

$\begin{split} & U_{\text{bat}}=E-R_{\text{bat}}i_{\text{bat}}\text{ = }E_0-kf(i_{\text{bat}},t)i_{\text{n}}- \\ &\quad k\frac{Q_{\text{b}}}{Q_{\text{b}}-Q_{\text{a}}}i_{\text{bat}}t+A\exp(-Bi_{\text{bat}}t)-R_{\text{bat}}i_{\text{bat}}, \end{split}$

(2)

式中：U_bat为蓄电池端电压，E为蓄电池开路电压，R_bat为蓄电池内阻，i_bat为蓄电池电流，E₀为蓄电池电压常数，k为极化常数，i_n为蓄电池滤波电流，Q_a为蓄电池释放的容量，Q_b为蓄电池额定容量，A为蓄电池指数电压，B为指数容量，t为时间.

质子交换膜燃料电池的输出电压^[15]为

${U_{{\text{cell}}}} = {E_{\text{N}}} - {U_{{\text{act}}}} - {U_{{\text{om}}}} - {U_{{\text{con}}}},$

(3)

式中：E_N为热力学电动势，U_act为活化过电压，U_om为欧姆过电压，U_con为浓差过电压.

电解槽电解水为氢气和氧气，制氢速度^[16]为

${V_{{\text{el}}}} = {\eta _{\text{F}}}{n_{\text{c}}}{i_{{\text{el}}}}/\left( {2F} \right) \text{，}$

(4)

式中：η_F为法拉第效率，n_c为电解槽串联个数，i_el为电解槽输出电流，F为法拉第常数.

储氢罐的储氢量^[13]为

${W_{{\text{el}}}} = \int_{{t_1}}^{{t_2}} {{V_{{\text{el}}}}} {{{\mathrm{d}}{{t}}}} ,$

(5)

式中：t₁、t₂分别为储氢罐存储氢气的开始时间和结束时间.

2. 多微电网并联运行功率分配机制

2.1 直流微电网各DG功率分配

如图1所示，各直流微电网与交流负荷之间通过逆变器对电能进行转换，而直流微电网运行时，为保证系统的正常运行，直流母线处也应保持功率平衡. 为提高光伏的利用率，光伏发电系统始终由最大功率点跟踪控制（MPPT）进行控制. 通过系统管理层控制^[6]计算得出功率参考值，与实时输出功率相比得到占空比，并通过PI （proportional integral）控制得到电、氢储能系统的占空比，改变占空比来调节各DG换流器的出力. 光伏系统输出不能满足负载需求时，由储能系统补足负载缺额；在光伏系统对负载的供应有富余时，储能系统将富余电能转化为化学能和氢能进行储备.

2.2 功率分配机制

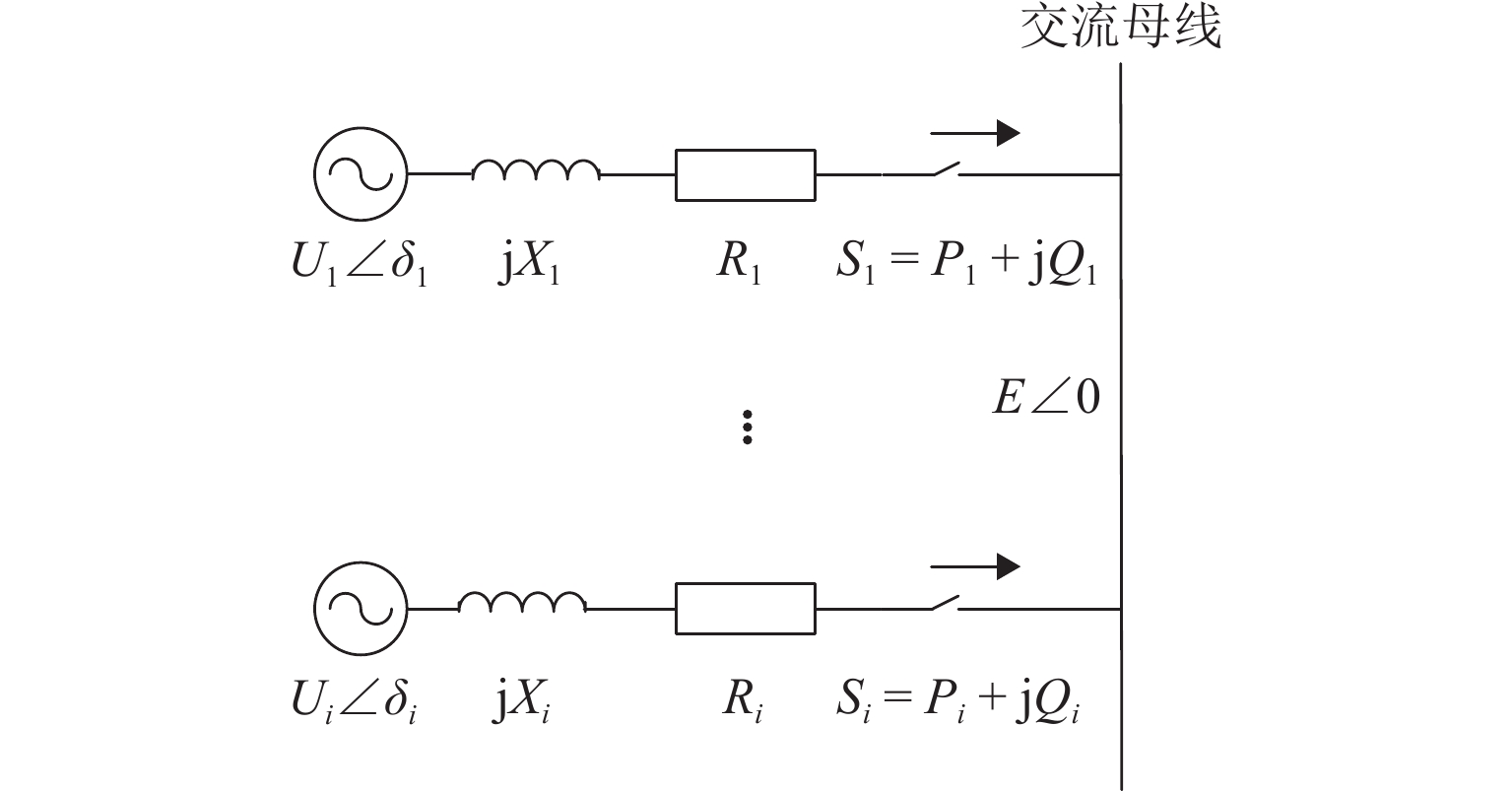
为方便分析，多微电网的并联运行可以简化为如图2所示的等效电路形式. E∠0为母线电压；U_i为第i个逆变器目标电压的相电压幅值，δ_i为第i个逆变器的电压相角， Z_i=R_i + jX_i为系统阻抗，R_i为逆变器电阻，i=1，2. 从逆变器注入母线的功率S_i=P_i + jQ_i，则有

图 2 多微网并联运行等效电路

Figure 2. Equivalent circuit of micro-grid parallel operation

下载: 全尺寸图片幻灯片

$\left\{ \begin{gathered} {P_{{i}}} = \left(\frac{{E{U_{{i}}}}}{{{Z_{{i}}}}}\cos \; {\delta _{{i}}} - \frac{{{E^2}}}{{{Z_{{i}}}}}\right)\cos \;{\theta _{{i}}} + \frac{{E{U_{{i}}}}}{{{Z_{{i}}}}}\sin \;{\delta _{{i}}}\sin \; {\theta _{{i}}}, \\ {Q_{{i}}} = \left(\frac{{E{U_{{i}}}}}{{{Z_{{i}}}}}\cos \; {\delta _{{i}}} - \frac{{{E^2}}}{{{Z_{{i}}}}}\right)\sin \; {\theta _{{i}}} - \frac{{E{U_{{i}}}}}{{{Z_{{i}}}}}\sin \;{\delta _{{i}}}\cos \;{\theta _{{i}}}, \\ \end{gathered} \right.$

(6)

式中：P_i和Q_i为两逆变器注入母线的有功、无功功率，θ_i为阻抗角.

由于δ_i很小，再令sin δ_i≈δ_i，cos δ_i≈1，且低压微电网中线路阻抗的电阻远大于电抗，使得系统阻抗整体呈阻性，令Z_i≈R_i，δ_i≈0. 则式（6）可简化为

$\left\{ \begin{gathered} {P_{{i}}} \approx \frac{{E({U_{{i}}} - E)}}{{{R_{{i}}}}}, \\ {Q_{{i}}} \approx - \frac{{E{U_{{i}}}}}{{{R_{{i}}}}}{\delta _{{i}}}. \\ \end{gathered} \right.$

(7)

由式（7）可知：P_i取决于电压降U_i−E， Q_i取决于电压相角δ_i，且角速度ω、电压相角δ_i和系统频率f关系如式（8）.

$f=\frac{\omega}{2\text{π }}=\frac{\text{d}\delta_i}{\text{d}t}.$

(8)

由式（8）可知，Q_i的大小与f密切相关，可以通过调节f来调节Q_i. 因此，在低压系统中，逆变器所采用的传统下垂控制策略为P-U、Q-f反下垂控制，方程为

$\left\{ \begin{gathered} {\omega _{{i}}} = \omega _{{{\text{n}\_i}}}^{} + {n_i}\left( {Q_{{{\text{n}\_i}}}^{} - {Q_i}} \right) ,\\ {U_{{i}}}{\text{ = }}U_{{{\text{n}\_i}}}^{} - {m_i}\left( {P_{{{\text{n}\_i}}}^{} - {P_i}} \right) ,\\ \end{gathered} \right.$

(9)

式中： U_{n_i}为额定相电压幅值，ω_i为目标角速度，ω_{n_i}为额定角速度，m_i为电压调节下垂系数，n_i为频率调节下垂系数，P_{n_i}、Q_{n_i}分别为逆变器额定有功、无功功率.

多微电网并联运行的系统中，由于逆变器的额定容量和所供应的负荷功率按比例匹配是很难实现的，下面对两微网并联运行系统进行简化分析，功率分配情况如式（10）所示.

$\left\{ \begin{gathered} \Delta P = {P_1} - c{P_2} = E\left( {\frac{{{U_1} - E}}{{{R_1}}} - c\frac{{{U_2} - E}}{{{R_2}}}} \right) ,\\ \Delta Q = {Q_1} - c{Q_2} = - E\left( {\frac{{{U_1}}}{{{R_1}}}{\delta _1} - c\frac{{{U_2}}}{{{R_2}}}{\delta _2}} \right) , \\ \end{gathered} \right.$

(10)

式中：ΔP、ΔQ分别为两台逆变器的有功、无功功率环流，c为逆变器的额定容量比例.

联立式（9）、（10）可知，当系统处于下垂控制的稳态运行状态时，若想按容量比例合理分配功率，即ΔP=ΔQ=0，需满足式（11）条件.

$\frac{{{m_1}}}{{{m_2}}} = \frac{{{n_1}}}{{{n_2}}} = \frac{{{R_1}}}{{{R_2}}} = \frac{1}{c} .$

(11)

由于系统频率是全局变量，使得线路阻抗的差异对无功功率的分配影响较小. 显然，由于各逆变器的输出电压幅值是局部变量，在线路阻抗不能满足合理分配的条件时，传统反下垂控制下合理分配有功功率是很难实现的.

3. 基于功率跟随控制的反下垂控制

3.1 考虑电压偏差的反下垂控制

在系统运行中，输出线路阻抗显然很难满足式（11）所示条件，因此，对P-U下垂控制器进行分析，电压偏差与有功功率关系为

$\left\{ \begin{gathered} {\text{δ}}{U_{{i}}} = {m_{{i}}}\left( {P_{{{\text{n}\_i}}}^{} - {P_{{i}}}} \right) \\ {U_{{{\text{d}i}}}} = \frac{{{\text{d}}\left( {{\text{δ}}U} \right)}}{{{{\text{d}t}}}} = {m_{i}}\frac{{{\text{d}}\left( {P_{{{\text{n}\_i}}}^{} - {P_i}} \right)}}{{{{\text{d}t}}}} , \\ \end{gathered} \right.$

(12)

式中：δU_i为额定电压与输出电压的偏差，U_di为电压偏差δU_i的变化率.

由式（12）可知：P_i的大小与δU_i有直接关系，若输出电压与额定电压存在偏差，P_i也与P_{n_i}存在偏差；而有功功率的稳定与δU_i的变化率U_di有直接关系，电压若持续变化，有功功率将无法稳定. 根据上述关系，构造反下垂控制器为

$\left\{ \begin{gathered} {U_{{i}}} = U_{{{\text{n}\_i}}}^{} - {\text{δ}}{U_{{i}}}, \\ {U_{{{\text{d}i}}}} = U_{{{\text{dn}\_i}}}^{} - {m_{{i}}}\left( {P_{{{\text{n}\_i}}}^{} - {P_{{i}}}} \right), \\ \end{gathered} \right.$

(13)

式中：U_{dn_i}为额定电压偏差变化率，取值为0.

由式（13）可知：在考虑电压偏差的反下垂控制（RDVD）运行过程中，电压偏差变化率为0时，即电压稳定时，有功功率就会稳定.

将式（13）中的U_{dn_i}取值为0，同样以两逆变器并联运行为例，则有

$\left\{ \begin{gathered} {U_{{\text{d1}}}} = - {m_{\text{1}}}P_{{\text{n\_1}}}^{} + {m_1}{P_1} , \\ {U_{{\text{d2}}}} = - {m_2}P_{{\text{n\_2}}}^{} + {m_2}{P_2} .\\ \end{gathered} \right.$

(14)

结合式（13）和式（14），得到两逆变器的输出电压为

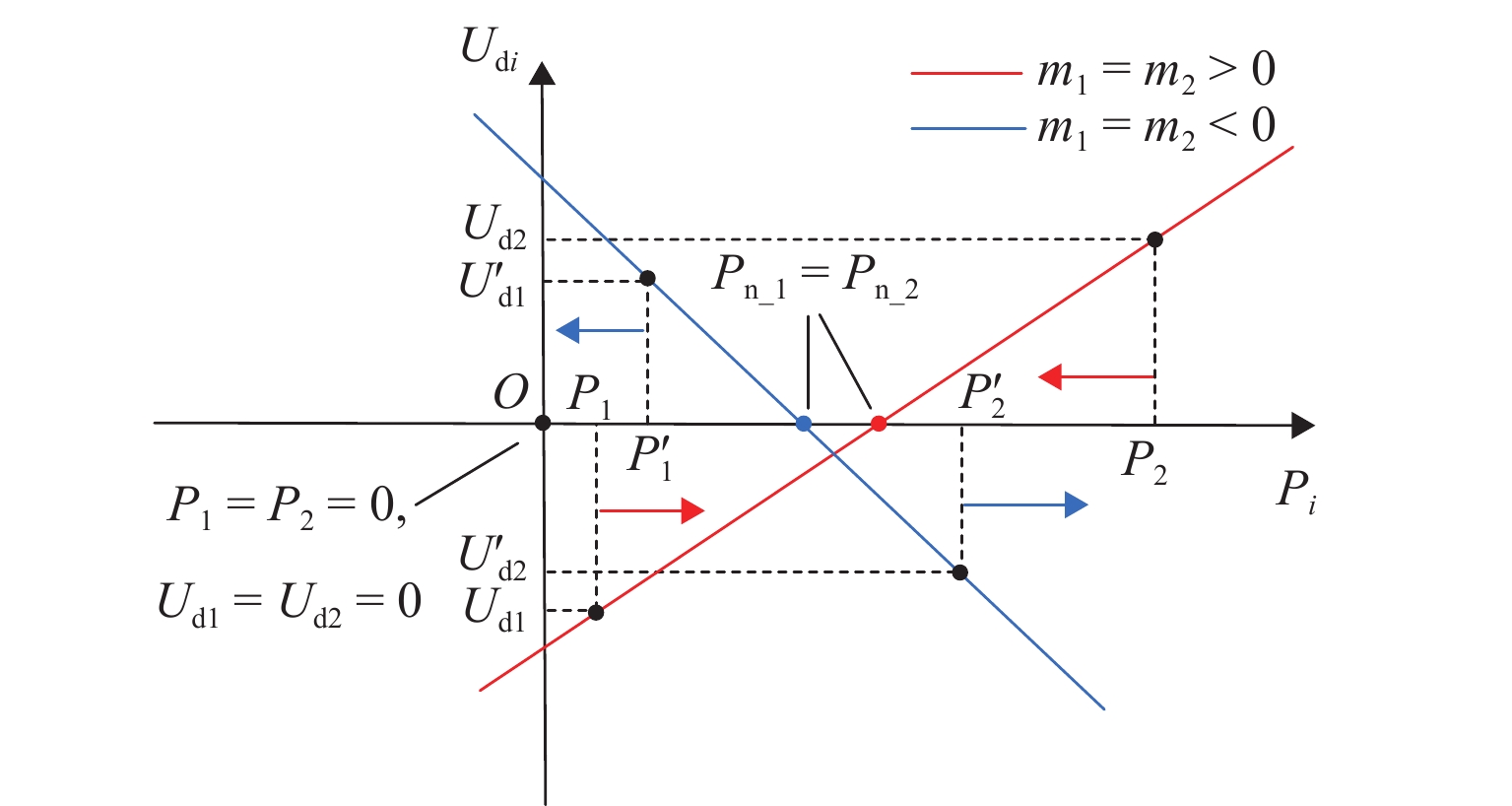
$\left\{ \begin{gathered} {U_1} = U_{{\text{n\_1}}}^{} - \int {{U_{{\text{d1}}}}{{\mathrm{d}}t} } , \\ {U_2} = U_{{\text{n\_2}}}^{} - \int {{U_{{\text{d2}}}}{{\mathrm{d}}t} } . \\ \end{gathered} \right.$

(15)

假设P_{n_1}=P_{n_2}，令m₁=m₂>0和m₁=m₂<0，在反下垂控制下，可以得到系统在2种情况下运行时两逆变器有功功率的趋势. 由于在一种情况下两逆变器的趋势相同，两种情况下的逆变器运行趋势将分别重合为2条曲线，如图3所示. 图中，变量加一撇为各变量变化后的值.

图 3 系统运行示意

Figure 3. Schematic of system operation

下载: 全尺寸图片幻灯片

又由于两逆变器带公共负荷，则有功功率有如下关系：

$P_1+P_2=P_{\text{sum}} ,$

(16)

式中：P_sum为系统的公共负荷.

由式（16）可知，负荷固定的情况下，若P₁<P₂，则必为P₁<P_{n_1}<P₂. 从图3中的红色曲线可以看出，所对应的U_di关系为U_d1<0<U_d2. 联合式（15）可知，输出电压U₁会增大，输出电压U₂则减小；有功功率会随电压而变化，P₁会相应增大，P₂会随之减小，最终实现P₁=P₂=P_{n_1}=P_{n_2}，功率分配在参考值下.

同理，从图3中的蓝色曲线可以看出：所对应的U_di关系为U_d1>0>U_d2，即输出电压U₁会减小，输出电压U₂则增大；P₁会相应减小，P₂会随之增大，最终系统失稳. 从图3中也可以看出，下垂控制系数的选择对系统运行也是至关重要的.

3.2 功率跟随控制

由3.1可知，若P_{n_i}是一个固定值，系统投切负荷时，P_i随系统变化，而P_{n_i}不随之变化，有功功率将一直存在偏差，进而反馈到电压上，电压会持续降低或增加，而电压的变化也会再影响到有功功率，有功功率会持续降低或增加，最后系统失稳. 且系统负荷变化时，所期望的母线电压幅值是不变的，由式（13）可知，电压幅值的稳定可以带动有功功率的稳定，最终系统稳定.

因此，用电压差反馈来自动调节P_{n_i}，如式（17）.

$P_{{{\text{n}\_{i}}}}^{} = {\text{δ}}U_{{{\text{n}\_{i}}}}^{} - {\text{δ}}{U_{{{i}}}},$

(17)

式中：δU_{n_i}为额定电压偏差，取值为0.

显然，该控制器下的控制效果远远不够，为电压偏差δU_i引入PID （proportional integral derivative）控制器，构造后的功率跟随控制框图如图4所示. 图中：K_p为比例系数，T_d为微分系数，T_i为积分系数，s为复频域变量.

图 4 功率跟随控制框图

Figure 4. Block diagram of power following control

下载: 全尺寸图片幻灯片

通过RDVD控制对功率跟随控制中PID控制器的输出量进行控制，构造出基于功率跟随控制的反下垂控制方法，控制框图如图5所示.

图 5 基于功率跟随控制的反下垂控制框图

Figure 5. Block diagram of reverse droop control based on power following control

下载: 全尺寸图片幻灯片

对于式（17）所示控制器来说，图4中的被控对象对应为图5中的P_i，电压偏差反馈所得为被控对象的参考值，最终控制目标为P_i与U_i达到共同稳定，且U_i与U_{n_i}偏差小，功率分配合理. 如图5所示，令电压偏差率U_di取值为0，且m_i取值为负，当负荷增大时，输出功率P_i增大，则P_{n_i}－P_i和U_di将减小，即δU_{n_i}－δU_i随之增大，P_{n_i}增大，最终使输出电压和功率趋于共同稳定.

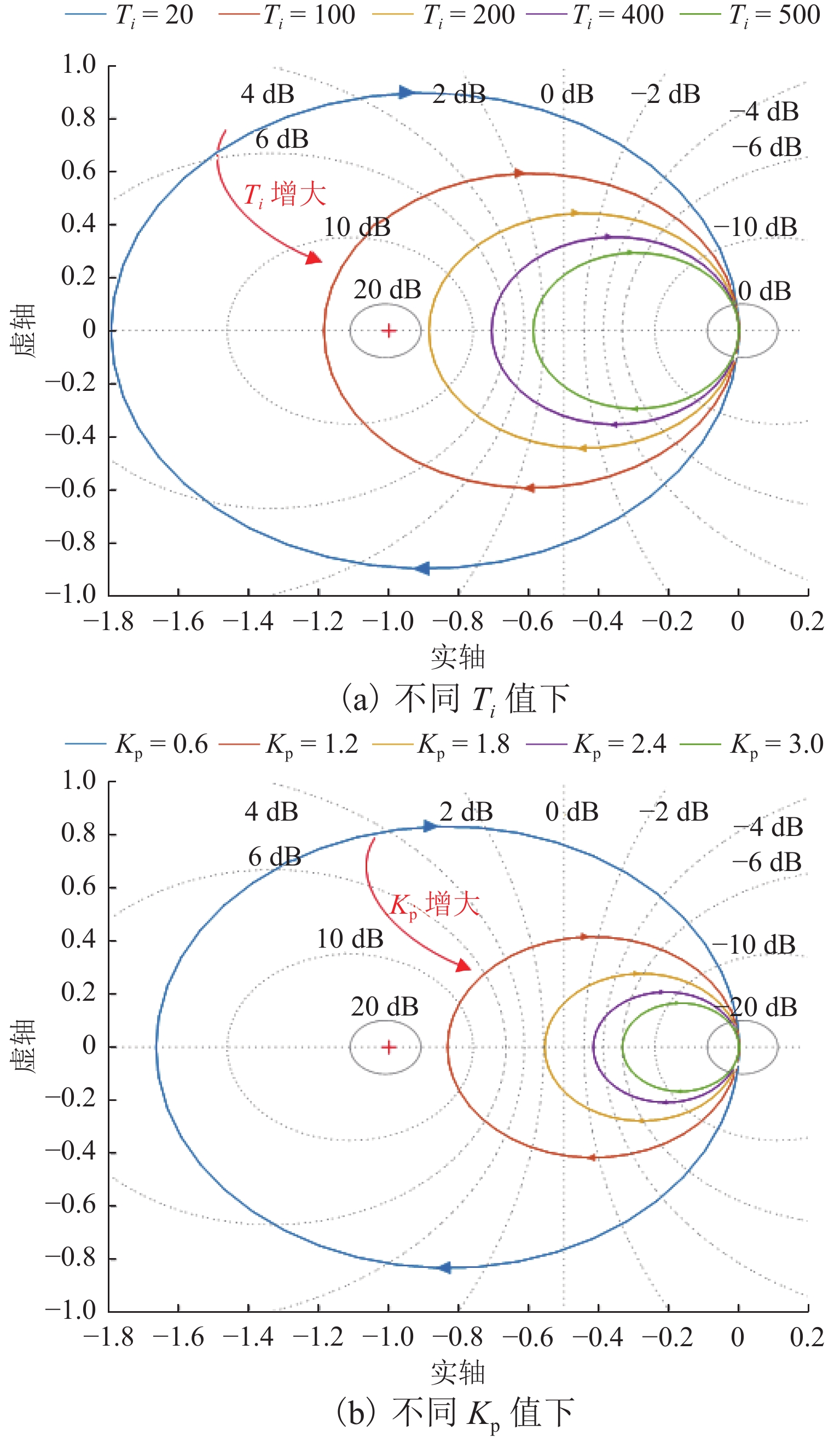
由3.1分析可知：m_i的取值会影响到系统的稳定性；由于PID控制器自身3个参数对被控对象的调节作用各不相同，该部分取值同样对系统响应速度、电压质量和系统稳定性有很大影响. 由图5可推出基于功率跟随控制的反下垂控制器所对应的闭环传递函数，进而可绘制出奈奎斯特曲线来反映控制系数取值对系统稳定性的影响. 如图6（a）所示：当T_i=20时，根据奈奎斯特稳定判据可知，此时系统不稳定；当T_i=200及更大时，系统能稳定运行. 如图6（b）所示：K_p=0.6时，根据奈奎斯特稳定判据可知，此时系统不稳定；K_p=1.2及更大时，系统能稳定运行.

图 6 基于功率跟随控制的反下垂控制频谱响应特性

Figure 6. Spectrum response characteristics of reverse droop control based on power following control

下载: 全尺寸图片幻灯片

4. 实验验证

4.1 实验平台及参数设置

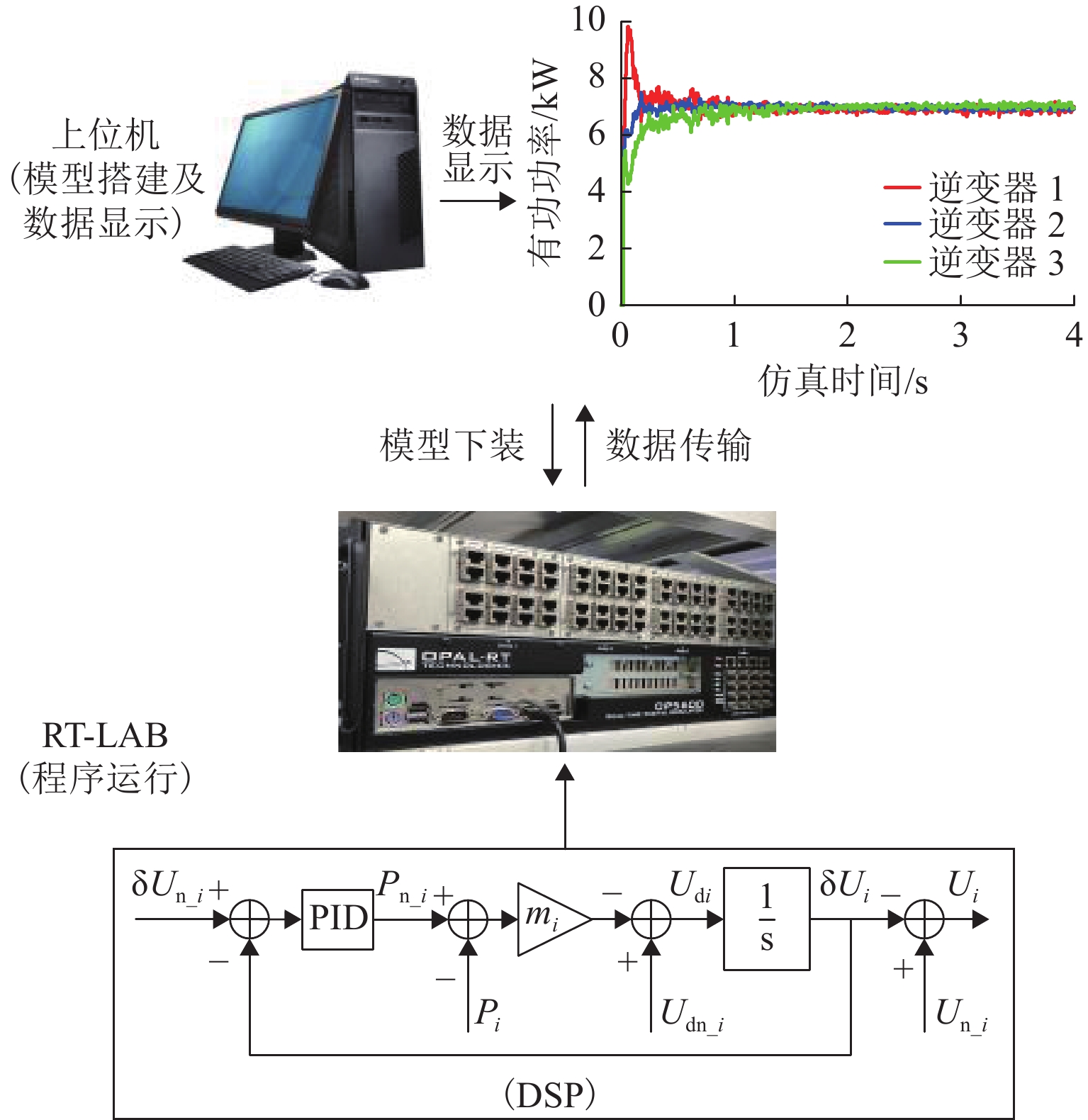
为验证本文所提方法的可行性，使用RT-LAB半实物仿真平台，通过系统的实时仿真运行来进行测试. 搭建的实验平台系统如图7所示，该仿真平台的型号为OP5600，并使用DSP TMS28335控制器对模型进行控制.

图 7 RT-LAB实时仿真平台

Figure 7. Real-time simulation platform RT-LAB

下载: 全尺寸图片幻灯片

本文实验以3个电-氢储能直流微电网并联运行在低压微电网系统下为例. 各逆变器对无功功率始终采用传统Q-f反下垂控制，对有功功率采用传统反下垂控制、基于电压恢复机制的反下垂控制^[11]、RDVD反下垂控制和本文所提控制方法分别进行实验验证，并将实验结果（输出有功功率、输出电压和逆变器1、2间的A相环流）进行对比分析，微电网系统参数和元件参数设置如表1、2所示.

表 1 系统参数

Table 1. System parameters

参数	取值
逆变器 1 线路阻抗 Z_{line_1}/Ω	0.642 + j0.083
逆变器 2 线路阻抗 Z_{line_2}/Ω	0.963 + j0.124 5
逆变器 3 线路阻抗 Z_{line_3}/Ω	1.284 + j0.166
滤波电感/MH	5
滤波电容/MF	0.5
额定电压/V	220
额定无功功率/kvar	5
逆变器容量比例	1∶1∶1

下载: 导出CSV

| 显示表格

表 2 元件参数

Table 2. Component parameters

元件	参数	数值
光伏阵列	环境温度/℃	25
燃料电池	额定功率/W	2000
燃料电池	额定电压/V	24
电解槽	额定功率/W	2000
储氢罐	最大容许压强/MPa	35
	体积/L	1
	初始容量/%	50
蓄电池	最大充放电功率/W	4000
	容量/（A·h）	40
	额定电压/V	500
	初始荷电状态/%	50

下载: 导出CSV

| 显示表格

4.2 方法验证

4.2.1 传统反下垂控制

令P_sum=20.00 kW，P_{n_i}=5.00 kW，用传统反下垂控制方法对各逆变器控制.

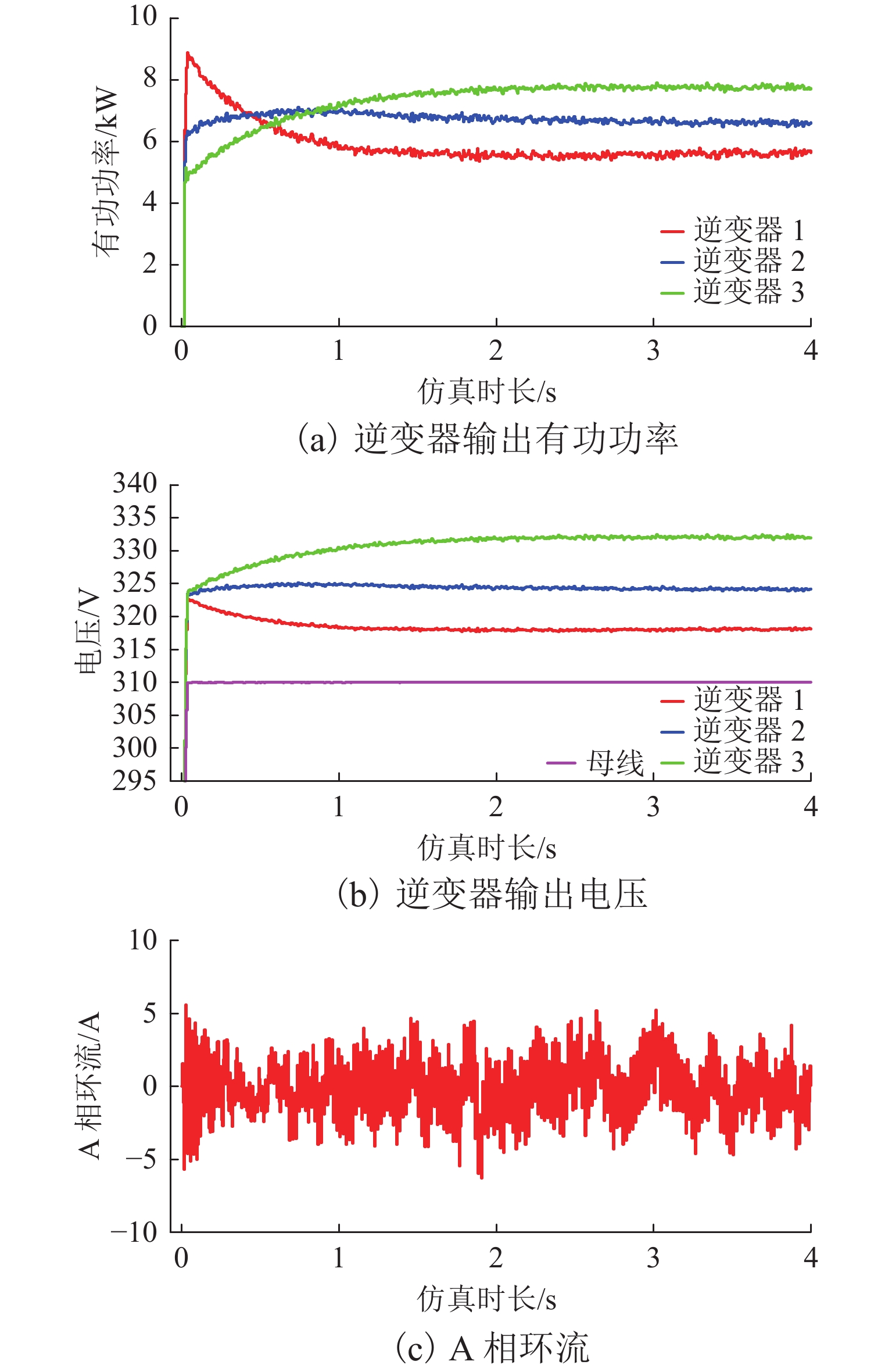
如图8（a）所示，各逆变器输出有功功率相差较大，功率分配精度较低. 如图8（b）所示，母线电压很快稳定在310 V下，与额定母线电压幅值310.27 V相差较小. 如图8（c）所示，逆变器1、2间的A相环流大小基本在[−5.0,5.0] A波动.

图 8 传统下垂控制方法实验结果

Figure 8. Experimental results of traditional droop control

下载: 全尺寸图片幻灯片

4.2.2 基于电压恢复机制的反下垂控制

令P_sum=20 kW不变，用基于电压恢复机制的反下垂控制方法^[11]对各逆变器进行控制.

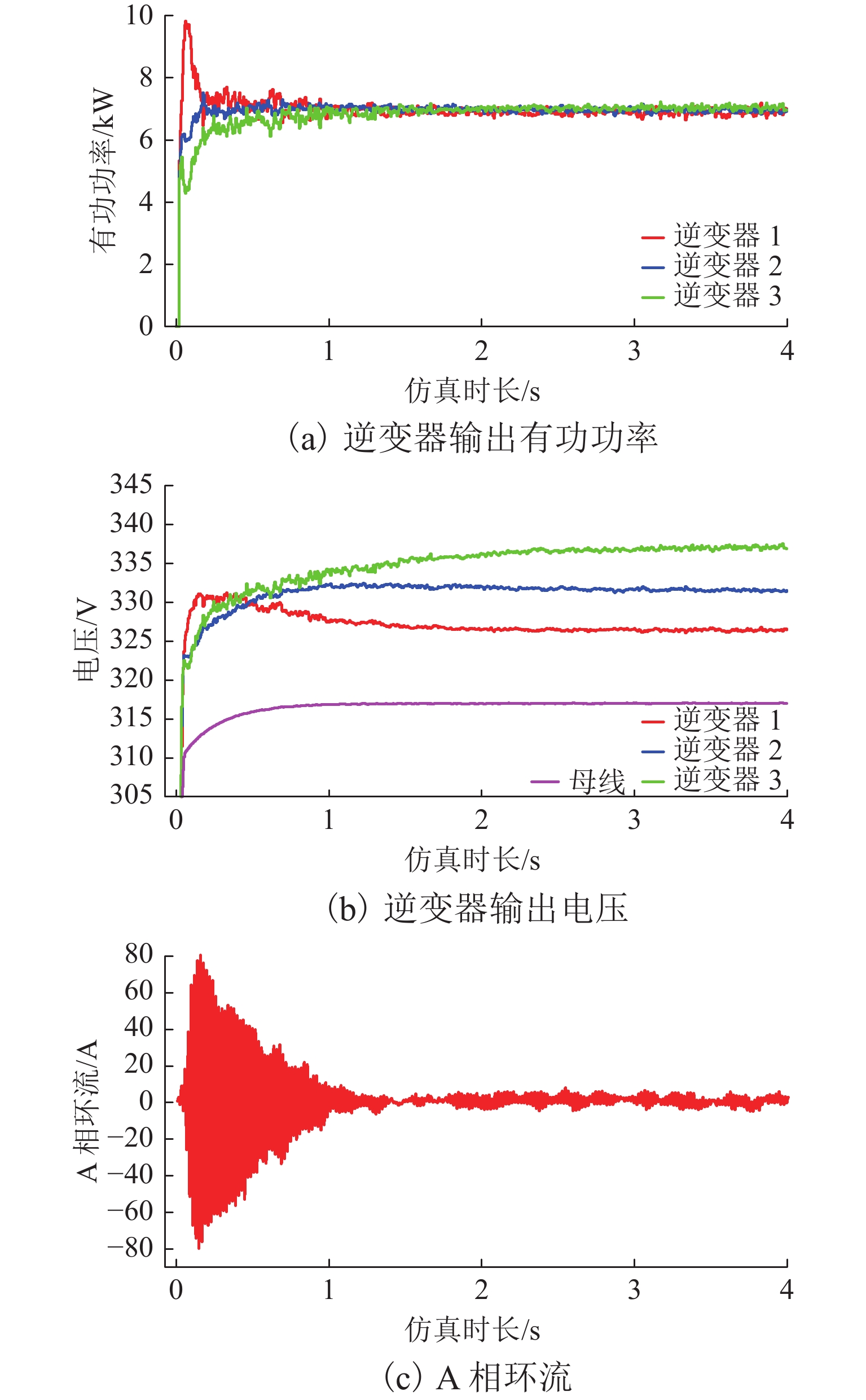
如图9（a）所示，逆变器输出有功功率响应速度慢，并在1.50 s后基本稳定在7.00 kW，功率分配精度较高，但略高于额定值. 如图9（b）所示，母线电压在1.00 s后稳定在317.00 V下，与额定母线电压幅值310.27 V相差较大. 如图9（c）所示，启动时逆变器1、2间的A相环流峰值达到81.5 A，随后逐渐减小，1.50 s后，环流大小基本在[−8.0,8.0] A波动.

图 9 基于电压恢复机制的反下垂控制方法实验结果

Figure 9. Experimental results of reverse droop control based on voltage recovery mechanism

下载: 全尺寸图片幻灯片

4.2.3 RDVD控制

令P_sum=20.00 kW不变，启动时设定额定P_{n_i}=6.67 kW，2.00 s时设定P_{n_i}=5.00 kW，用RDVD控制方法对各逆变器进行控制.

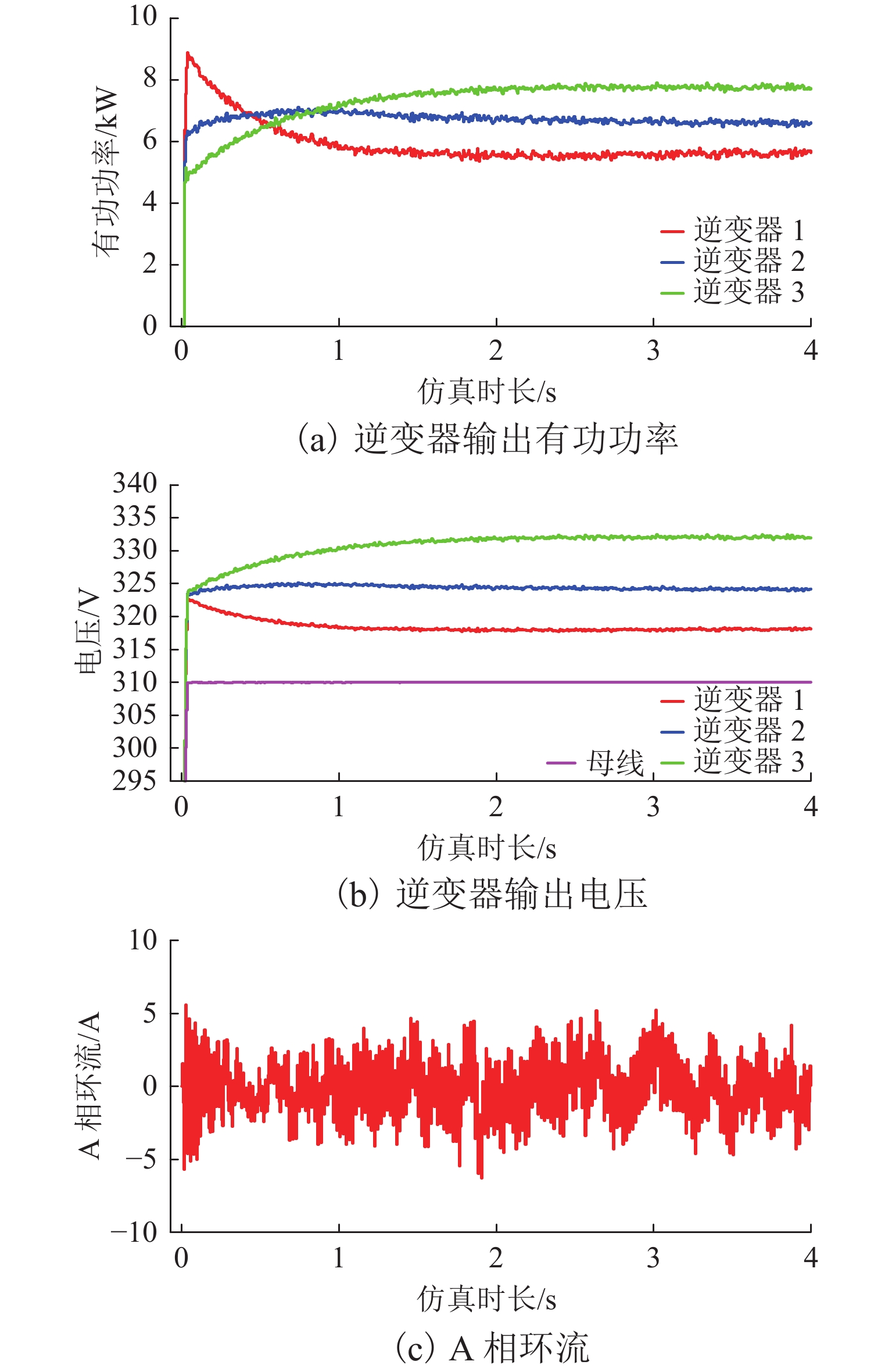
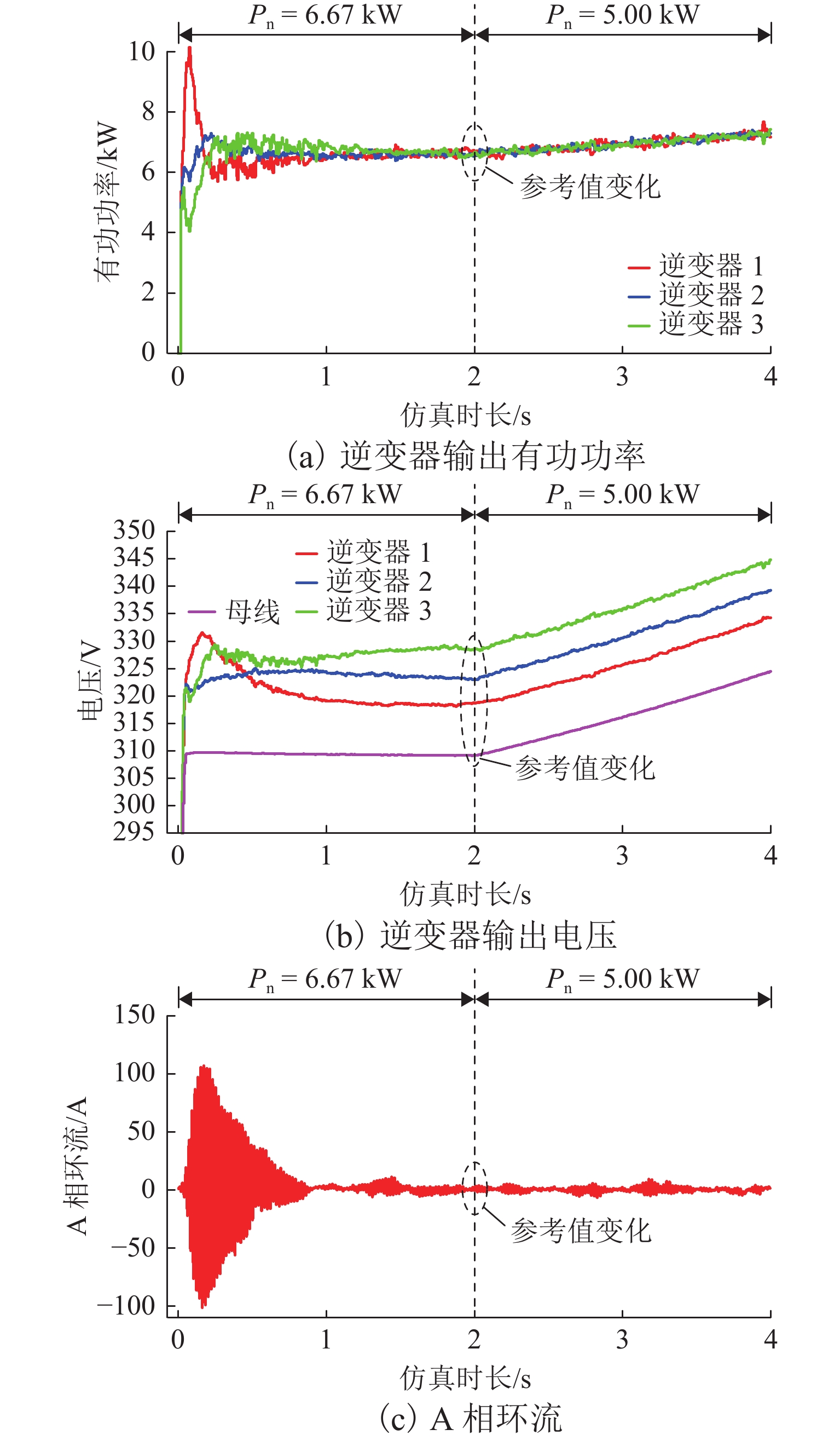
如图10（a）所示：各逆变器输出有功功率响应速度慢，并在1.00 s后基本稳定在6.67 kW，功率分配精度较高；但在参考值变化后，各逆变器输出功率均提高，并在4.00 s时达到7.30 kW，高于系统均分功率. 如图10（b）所示，母线电压在1.00 s后稳定在309.20 V下，并于参考值变化后急剧上升，并在4.00 s时达到324.50 V，与额定母线电压幅值310.27 V相差较大. 如图10（c）所示，启动时逆变器1、2间的A相环流较大，峰值达到108 A， 0.80 s后，环流大小基本在[−10.0,10.0] A波动.

图 10 RDVD控制方法实验结果

Figure 10. Experimental results of RDVD control method

下载: 全尺寸图片幻灯片

4.2.4 本文所提方法

启动时，令P_sum=20.00 kW，t=4.00 s时令P_sum=25.00 kW，用本文所提方法对各逆变器进行控制，其他参数不变.

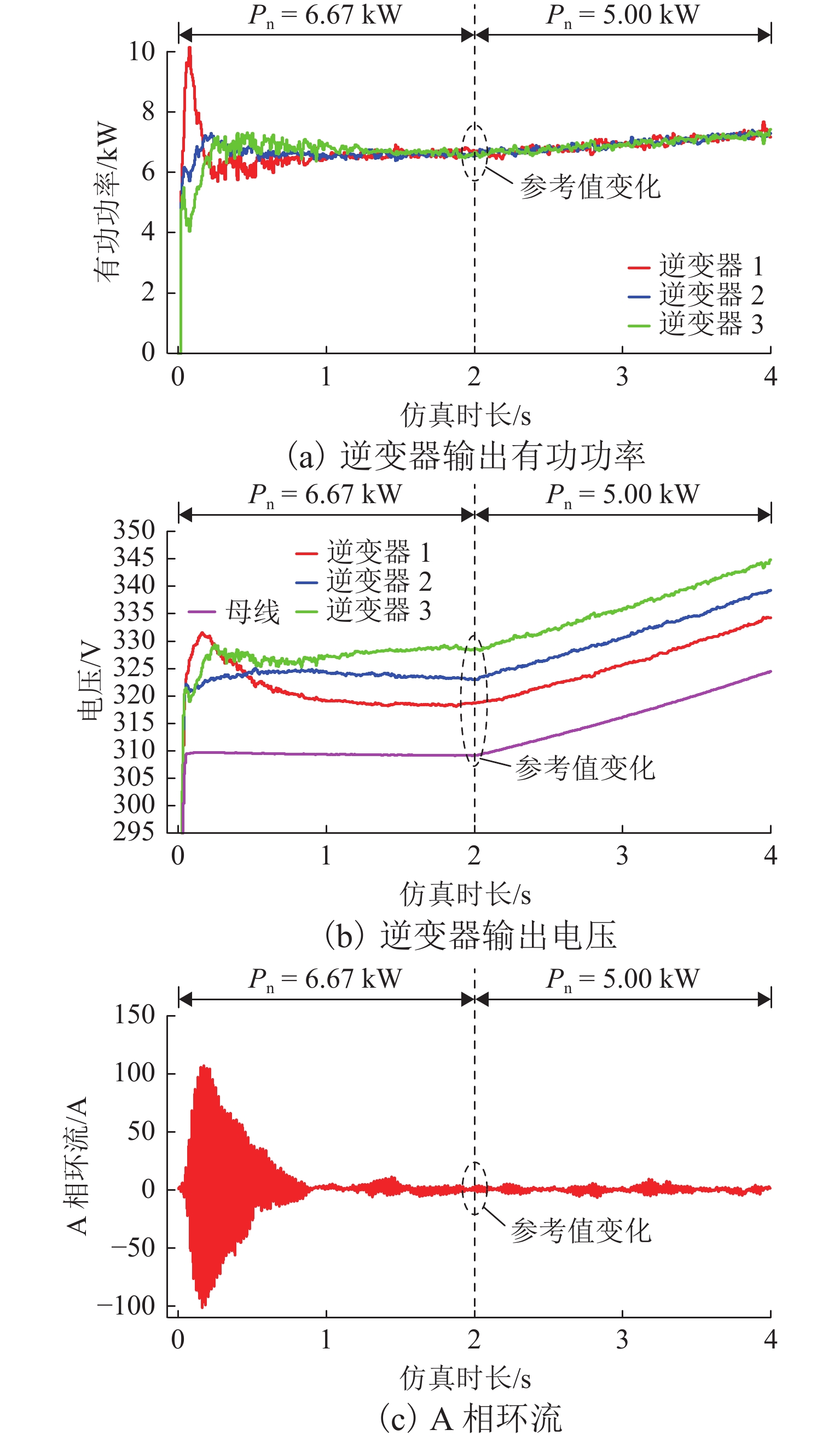
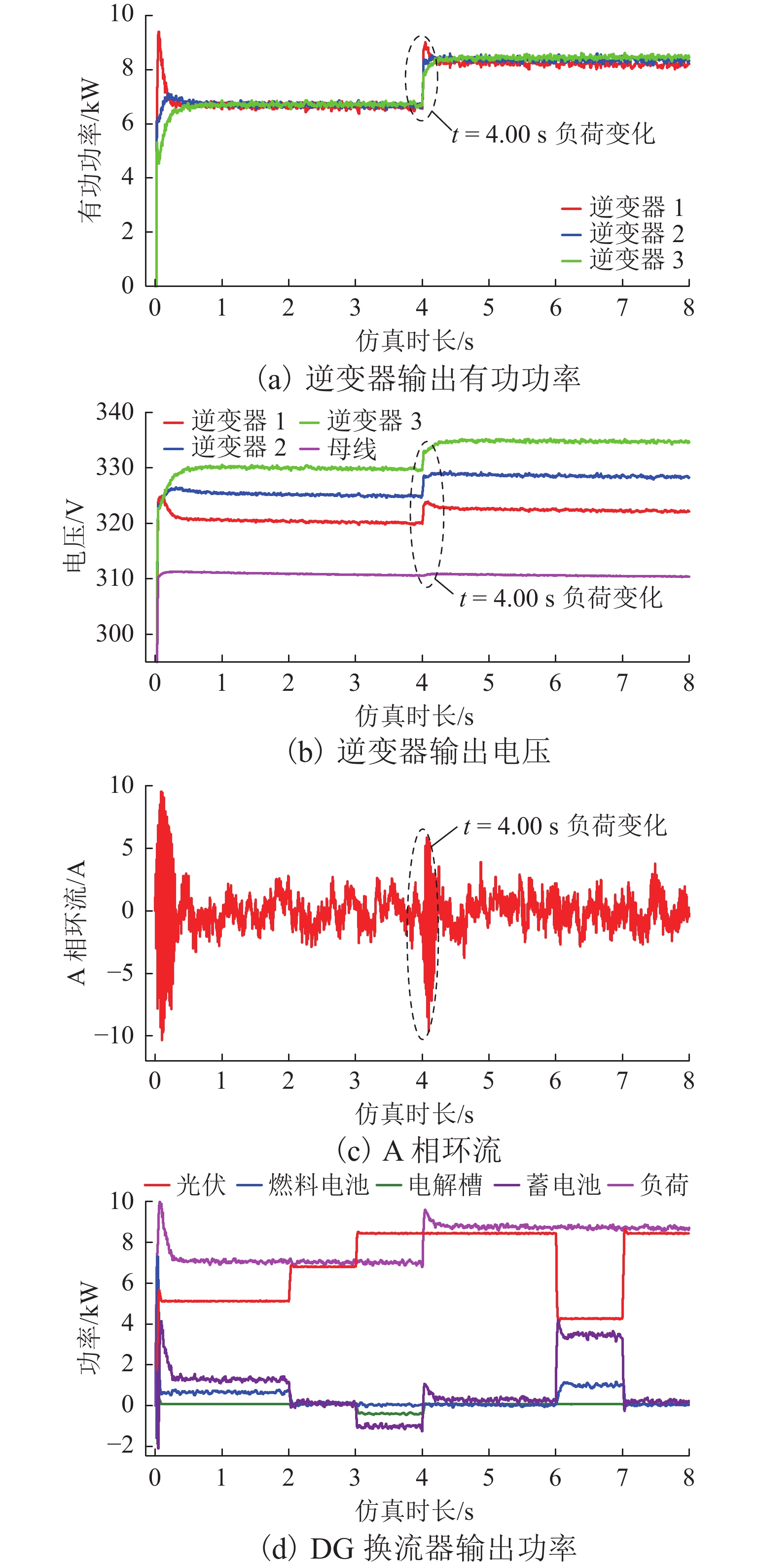
如图11（a）所示：各逆变器输出有功功率在启动后0.50 s时达到功率稳定，响应速度较快且功率分配精度高，准确度达97.50%；在t=4.00 s，负荷变化时，功率在0.15 s内稳定并均分. 如图11（b）所示，母线电压很快稳定在310.70 V下，并于4.00 s时重新稳定在310.60 V，与额定值310.27 V相差较小，准确度达99.86%. 如图11（c）所示，启动时及负荷变化后A相环流的峰值达到−10.3A，随后逐渐减小并基本在[−3.0,3.0] A间波动. 如图11（d）所示，在负荷和辐射度变化时，微电网1中各DG换流器的输出功率均能迅速合理分配.

图 11 本文所提控制方法实验结果

Figure 11. Experimental results of proposed control method

下载: 全尺寸图片幻灯片

5. 结　论

本文提出一种适用于逆变器控制的反下垂控制方法，并通过RT-LAB半实物仿真平台，在多电-氢微电网并联运行的交流系统中进行方法验证和对比验证，现有结论如下.

1）本文所提方法实现了负荷变化时逆变器的额定有功功率的自适应调节.

2）在所搭建系统中，对传统反下垂控制方法、基于电压恢复机制的反下垂控制方法、RDVD控制方法及本文所提方法进行对比验证，本文所提方法在响应速度、功率分配合理性、母线电压偏差及环流大小方面均优于其他方法.

3）本文所提方法的各换流器的输出有功功率、母线电压等在0.50 s后快速达到基本稳定；输出有功功率分配合理，准确度达97.50%；母线电压与额定电压偏差小，准确度达99.86%；环流大小稳定在[−3.0,3.0] A；各DG在环境变化时均可随之改变输出.

图 1 多微电网并联运行结构示意

Figure 1. Schematic of micro-grid parallel operation

下载: 全尺寸图片幻灯片

图 2 多微网并联运行等效电路

Figure 2. Equivalent circuit of micro-grid parallel operation

下载: 全尺寸图片幻灯片

图 3 系统运行示意

Figure 3. Schematic of system operation

下载: 全尺寸图片幻灯片

图 4 功率跟随控制框图

Figure 4. Block diagram of power following control

下载: 全尺寸图片幻灯片

图 5 基于功率跟随控制的反下垂控制框图

Figure 5. Block diagram of reverse droop control based on power following control

下载: 全尺寸图片幻灯片

图 6 基于功率跟随控制的反下垂控制频谱响应特性

Figure 6. Spectrum response characteristics of reverse droop control based on power following control

下载: 全尺寸图片幻灯片

图 7 RT-LAB实时仿真平台

Figure 7. Real-time simulation platform RT-LAB

下载: 全尺寸图片幻灯片

图 8 传统下垂控制方法实验结果

Figure 8. Experimental results of traditional droop control

下载: 全尺寸图片幻灯片

图 9 基于电压恢复机制的反下垂控制方法实验结果

Figure 9. Experimental results of reverse droop control based on voltage recovery mechanism

下载: 全尺寸图片幻灯片

图 10 RDVD控制方法实验结果

Figure 10. Experimental results of RDVD control method

下载: 全尺寸图片幻灯片

图 11 本文所提控制方法实验结果

Figure 11. Experimental results of proposed control method

下载: 全尺寸图片幻灯片

表 1 系统参数

Table 1. System parameters

参数	取值
逆变器 1 线路阻抗 Z_{line_1}/Ω	0.642 + j0.083
逆变器 2 线路阻抗 Z_{line_2}/Ω	0.963 + j0.124 5
逆变器 3 线路阻抗 Z_{line_3}/Ω	1.284 + j0.166
滤波电感/MH	5
滤波电容/MF	0.5
额定电压/V	220
额定无功功率/kvar	5
逆变器容量比例	1∶1∶1

下载: 导出CSV

表 2 元件参数

Table 2. Component parameters

元件	参数	数值
光伏阵列	环境温度/℃	25
燃料电池	额定功率/W	2000
燃料电池	额定电压/V	24
电解槽	额定功率/W	2000
储氢罐	最大容许压强/MPa	35
	体积/L	1
	初始容量/%	50
蓄电池	最大充放电功率/W	4000
	容量/（A·h）	40
	额定电压/V	500
	初始荷电状态/%	50

下载: 导出CSV

参考文献(16)

[1]	李霞林,郭力,王成山,等. 直流微电网关键技术研究综述[J]. 中国电机工程学报,2016,36(1): 2-17. LI Xialin, GUO Li, WANG Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.
[2]	LI Q, QIU Y, YANG H, et al. Stability-constrained two-stage robust optimization for integrated hydrogen hybrid energy system[J]. CSEE Journal of Power and Energy Systems, 2021, 7(1): 162-171.
[3]	刘欣博,刘宁,宋晓通,等. 基于交流恒功率负载特性的交直流混合微电网系统大信号稳定性判据[J]. 高电压技术,2021,47(10): 3441-3451. LIU Xinbo, LIU Ning, SONG Xiaotong, et al. Large-signal stability criteria of AC/DC hybrid microgrid based on AC constant power loads[J]. High Voltage Engineering, 2021, 47(10): 3441-3451.
[4]	蔡国伟,孔令国,薛宇,等. 风氢耦合发电技术研究综述[J]. 电力系统自动化,2014,38(21): 127-135. doi: 10.7500/AEPS20131231004 CAI Guowei, KONG Lingguo, XUE Yu, et al. Overview of research on wind power coupled with hydrogen production technology[J]. Automation of Electric Power Systems, 2014, 38(21): 127-135. doi: 10.7500/AEPS20131231004
[5]	EHSAN A, YANG Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: a review of analytical techniques[J]. Applied Energy, 2018, 210: 44-59. doi: 10.1016/j.apenergy.2017.10.106
[6]	李奇,蒲雨辰,韩莹,等. 电-氢孤岛直流微电网的分层能量管理[J]. 西南交通大学学报,2020,55(5): 912-919. LI Qi, PU Yuchen, HAN Ying, et al. Hierarchical energy management for electric-hydrogen island direct current micro-grid[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 912-919.
[7]	米阳,陈鑫,季亮,等. 基于虚拟额定电流的直流微电网分布式储能单元精确电流分配研究[J]. 电网技术,2020,44(3): 823-835. MI Yang, CHEN Xin, JI Liang, et al. Accurate current sharing of distributed energy storage units in DC microgrid based on virtual rated current[J]. Power System Technology, 2020, 44(3): 823-835.
[8]	朱晓荣,韩丹慧,孟凡奇,等. 提高直流微电网稳定性的并网换流器串联虚拟阻抗方法[J]. 电网技术,2019,43(12): 4523-4531. ZHU Xiaorong, HAN Danhui, MENG Fanqi, et al. Grid converter series virtual impedance method for improving DC microgrid stability[J]. Power System Technology, 2019, 43(12): 4523-4531.
[9]	柴秀慧,张纯江,柴建国,等. 改进互联通信荷电状态下垂控制及功率均衡优化[J]. 电工技术学报,2021,36(16): 3365-3374. CHAI Xiuhui, ZHANG Chunjiang, CHAI Jianguo, et al. Improved interconnected communication state of charge droop control and power balance optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3365-3374.
[10]	王晓寰,王书光,刘聪哲,等. 下垂控制并联系统中功率精确分配的控制策略[J]. 电力电子技术,2019,53(8): 4-7. WANG Xiaohuan, WANG Shuguang, LIU Congzhe, et al. Accurate power sharing strategy for parallel system based on droop control[J]. Power Electronics, 2019, 53(8): 4-7.
[11]	麦倩屏,陈鸣. 用于多微源低压微电网的虚拟阻抗反下垂控制[J]. 电力系统保护与控制,2018,46(1): 96-102. doi: 10.7667/PSPC162039 MAI Qianping, CHEN Ming. P-V/Q-f droop control strategy with virtual impedance for low-voltage microgrid with multiple micro sources[J]. Power System Protection and Control, 2018, 46(1): 96-102. doi: 10.7667/PSPC162039
[12]	白小丹,苗虹,曾成碧,等. 适用于低压微网中逆变器无功均分的改进下垂控制策略[J]. 高电压技术,2020,46(4): 1310-1318. BAI Xiaodan, MIAO Hong, ZENG Chengbi, et al. Improved droop control strategy for reactive power sharing of inverters in low-voltage microgrids[J]. High Voltage Engineering, 2020, 46(4): 1310-1318.
[13]	PU Y C, LI Q, CHEN W R, et al. Hierarchical energy management control for islanding DC microgrid with electric-hydrogen hybrid storage system[J]. International Journal of Hydrogen Energy, 2019, 44(11): 5153-5161. doi: 10.1016/j.ijhydene.2018.10.043
[14]	LI L Y, CHEN W R, HAN Y, et al. A stability enhancement method based on adaptive virtual resistor for electric-hydrogen hybrid DC microgrid grid-connected inverter under weak grid[J]. Electric Power Systems Research, 2021, 191: 106882.1-106882.
[15]	LI Q, WANG T H, DAI C H, et al. Power management strategy based on adaptive droop control for a fuel cell-battery-supercapacitor hybrid tramway[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5658-5670. doi: 10.1109/TVT.2017.2715178
[16]	IPSAKIS D, VOUTETAKIS S, SEFERLIS P, et al. Power management strategies for a stand-alone power system using renewable energy sources and hydrogen storage[J]. International Journal of Hydrogen Energy, 2009, 34(16): 7081-7095. doi: 10.1016/j.ijhydene.2008.06.051