Analysis of Internal forces and Damage of Broad-Narrow Joint of CRTSⅡ Slab Track Under Temperature Rise
-
摘要:
为研究宽窄接缝在温升作用下的受力和损伤,根据混凝土塑性损伤理论和内聚力理论,建立考虑新旧混凝土界面的宽窄接缝细部的有限元模型;计算不同温升条件下的宽窄接缝应力和损伤因子,并分析宽窄接缝强度和窄接缝宽度的影响. 研究结果表明:窄接缝挤碎是一种渐变受压损伤,宽、窄接缝交界处断裂是一种脆性受拉损伤;与宽、窄接缝交界处断裂相比,窄接缝挤碎对结构受力影响更大;宽窄接缝尺寸不均匀导致宽、窄接缝交界处垂向受拉,这是宽窄接缝产生损伤的主要原因;提高宽窄接缝的混凝土强度可有效降低垂向拉应力和受拉损伤,但对纵向应力和受压损伤影响较小;为改善受力并降低损伤,建议宽窄接缝混凝土与轨道板等强,并且宽窄接缝上下等宽.
-
关键词:
- 无砟轨道 /
- CRTSⅡ型板式轨道 /
- 宽窄接缝
Abstract:In order to study the internal forces and the damage of broad-narrow joint under a temperature rise, a detailed finite element model with the interface between old and new concrete is established on the basis of concrete damaged plasticity model and cohesive zone model. The damage parameters and stress under different temperature rises are calculated, and the effects of the concrete strength at broad-narrow joint and the narrow joint width are analyzed. The results show that the fracture at the junction between broad and narrow joints is a brittle tension failure, and the breakage of narrow joint is a gradual compression failure. Compared with the fracture at the junction between broad and narrow joints, the breakage of narrow joint has a greater impact on the structural stress. The vertical tension stress arising from the uneven geometry at the junction between broad and narrow joints is the main cause for the damaged broad-narrow joint. Increasing the broad-narrow joint strength reduces the longitudinal compression stress and the compression damage, but contribute less to the vertical tension stress and the tension damage. To reduce damage and improve strength, it is recommended to equate the widths for the broad and narrow joints and the strengths for the concrete at the broad-narrow joint and the slab.
-
Key words:
- ballastless track /
- CRTS Ⅱ slab track /
- broad-narrow joint
-
近年来,高速铁路快速发展,在中国建成的3.8万公里高速铁路中无砟轨道占2/3以上,其高平顺性、高稳定性、高可靠性和少维修等优点得到了充分体现[1-3]. CRTSⅡ型板式轨道是其中应用较广的一种,其结构从上到下分别为钢轨、扣件系统、轨道板、砂浆层和混凝土支承层,相邻的预制轨道板之间设置宽窄接缝,实现轨道结构纵向连续,宽窄接缝是一个后浇带,该处混凝土等级为C35,而轨道板为C55,内有张拉锁件将相邻板中预留的6根纵筋连接. 宽窄接缝是上宽下窄的结构,接缝宽上部21 cm,下部仅5 cm. 运营实践中,宽窄接缝是CRTSⅡ型板式轨道病害较为严重的部位,尤其是窄接缝损坏严重,威胁轨道结构稳定性和行车安全性,主要表现为窄接缝部位挤碎和宽、窄接缝交界处断裂.
无砟轨道的受力和损伤问题引起了科研工作者的广泛关注. 钟阳龙等[4]基于内聚力模型研究了不同植筋方案下轨道板与砂浆层间的抗剪性能,认为植筋可以明显提高轨道层间的抗剪能力,层间开裂温度可提高20 ℃左右. 许玉德等[5]提出了与Ⅰ型、Ⅱ型断裂模式更符合的混合内聚力模型,并通过反演文献和试验对其进行了改进和验证,建议在17:00—次日00:00进行砂浆层灌注施工并尽快完成纵连作业. 闫斌等[6]对快速冻融循环作用下混凝土和砂浆试件开展了轴心受压和劈裂破坏试验,建立了无砟轨道-路基冻胀冻融有限元模型,研究了冻融损伤后轨道的静力特性,研究表明,与未冻融工况相比,300次冻融循环后,试件峰值抗压强度降幅达30%左右. 目前,关于无砟轨道的研究通常将轨道结构考虑成完好的整体,并没有考虑宽窄接缝以及混凝土界面等薄弱带,具有一定的局限性,本文针对宽窄接缝的细部模型,分析其受力和损伤的特点.
1. 力学模型
1.1 混凝土塑性损伤模型
混凝土的本构模型采用塑性损伤模型[7-9],假定材料总应变ε包括弹性εel和塑性εpl,结构应力-应变关系为
σ=(1−d)E0ε−εpl, (1) 式中:σ为应力;d为损伤因子,取1时表示完全失效,取0时表示无损伤;E0为初始刚度.
单轴有效应力为
σE=σ1−d=E0(ε−εpl). (2) 屈服准则采用Lubliner屈服准则,用有效应力表达的屈服函数为
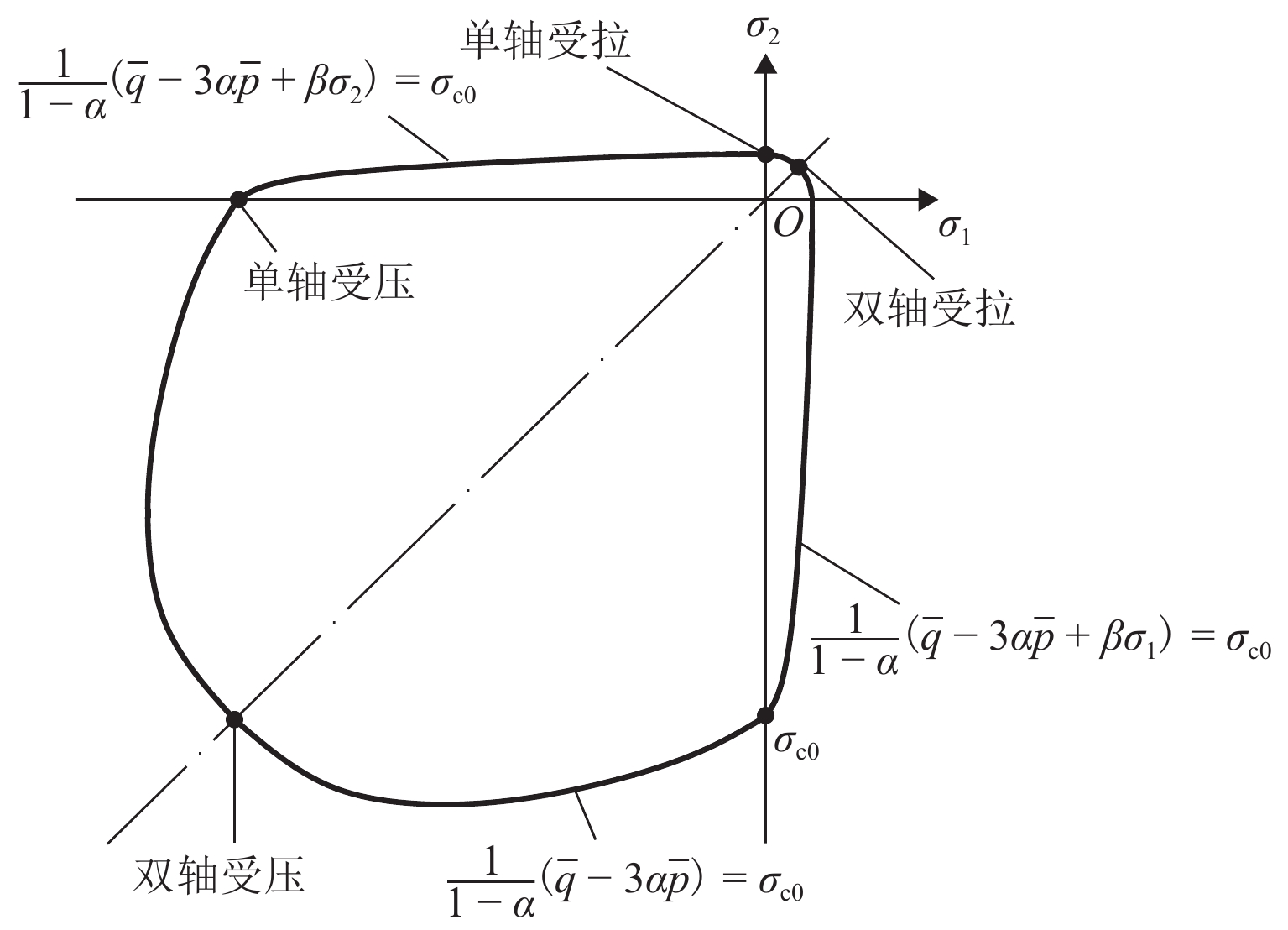
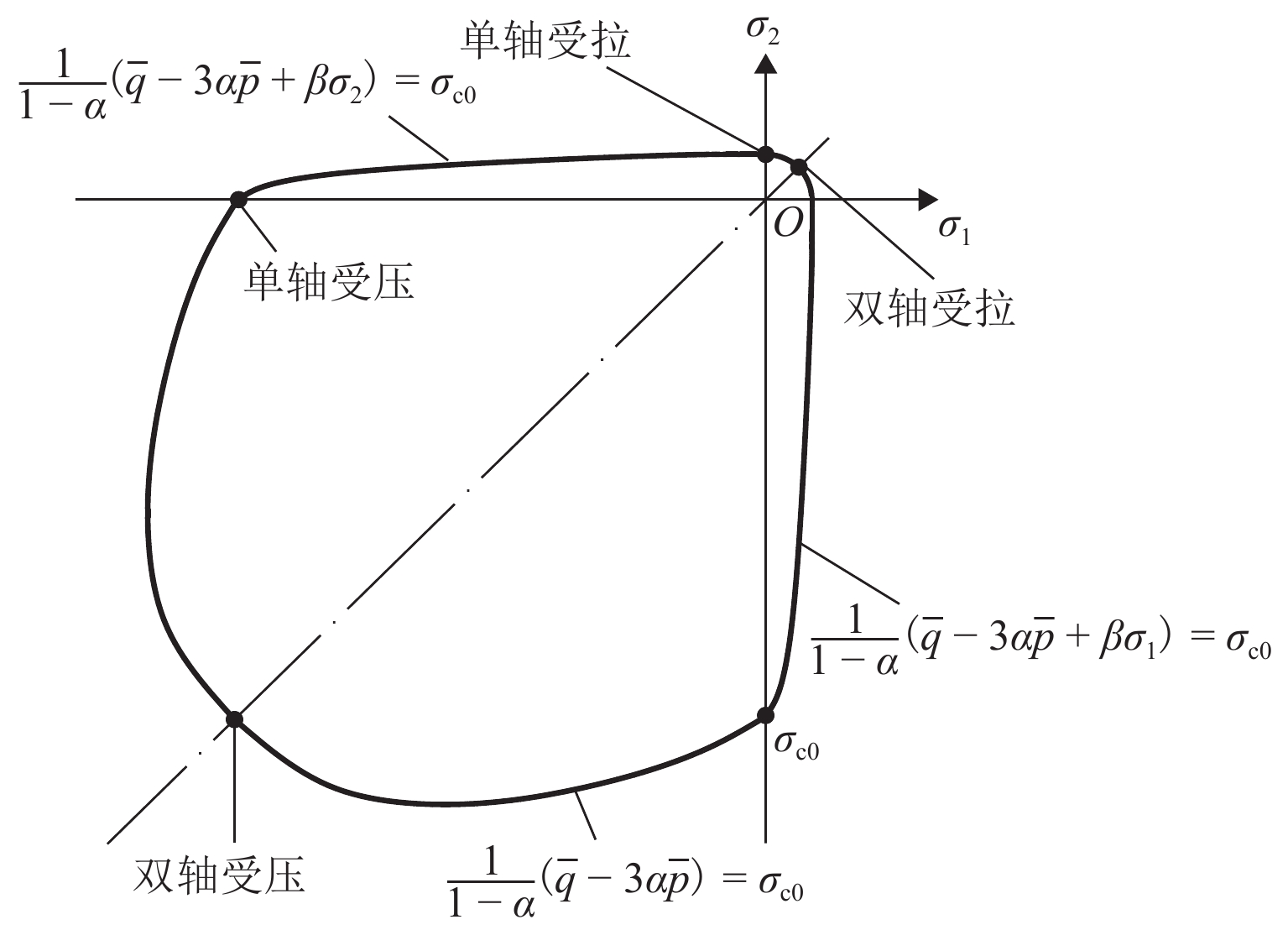
F=11−α{¯q−3α¯p+[σEcεpl,cσEtεpl,t(1−α)−(1+α)]×⟨σmax⟩−γ⟨−σmax⟩}=0, (3) 式中:α和γ为无量纲材料参数,¯q为Mises等效应力,¯p为有效静水压力,σmax为σE的代数最大值,σEt和σEc分别为有效拉、压应力,εpl,t和εpl,c分别为塑性拉、压应变.
平面应力状态下的屈服面见图1. 图中:σ1和σ2分别为平面2个方向的应力,σc0为单轴抗压强度.
1.2 内聚力理论
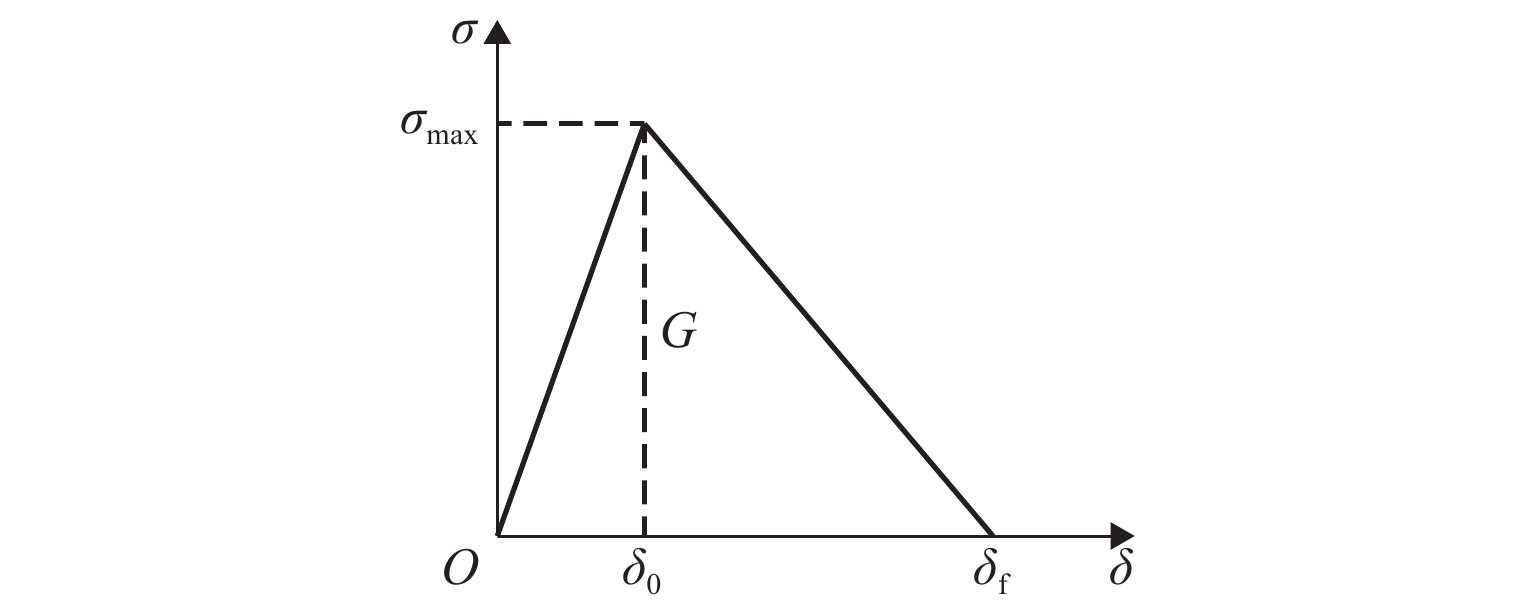
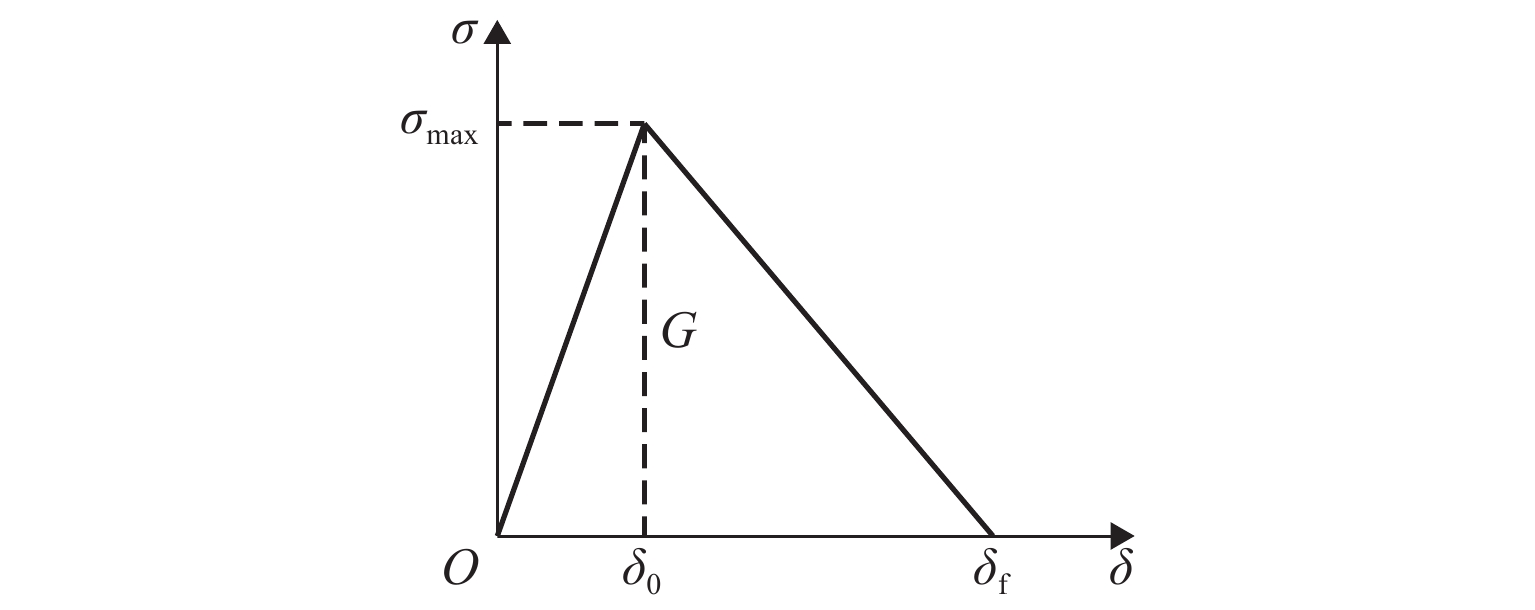
内聚力理论是一种广泛用于模拟新旧混凝土界面拉伸、剪切分离行为的力学模型[10-12]. 内聚力单元的应力σ-位移δ关系(式(4))如图2所示,σmax反映材料的强度,δ0为σmax对应位移,δf为最大开裂宽度,G为断裂能(式(5)).
σ={σmaxδ0δ,δ<δ0,σmaxδf−δδf−δ0,δ>δ0. (4) G=12σmaxδf. (5) 采用最大主应力准则作为材料初始损伤的判据,由式(6)加以描述.
max{σnσn,max,σt1σt1,max,σt2σt2,max}=1, (6) 式中:σn和σt1、σt2分别为内聚力单元法向正应力和2个切向应力,σn,max和σt1,max、σt2,max分别为垂向强度和2个切向强度.
1.3 有限元模型
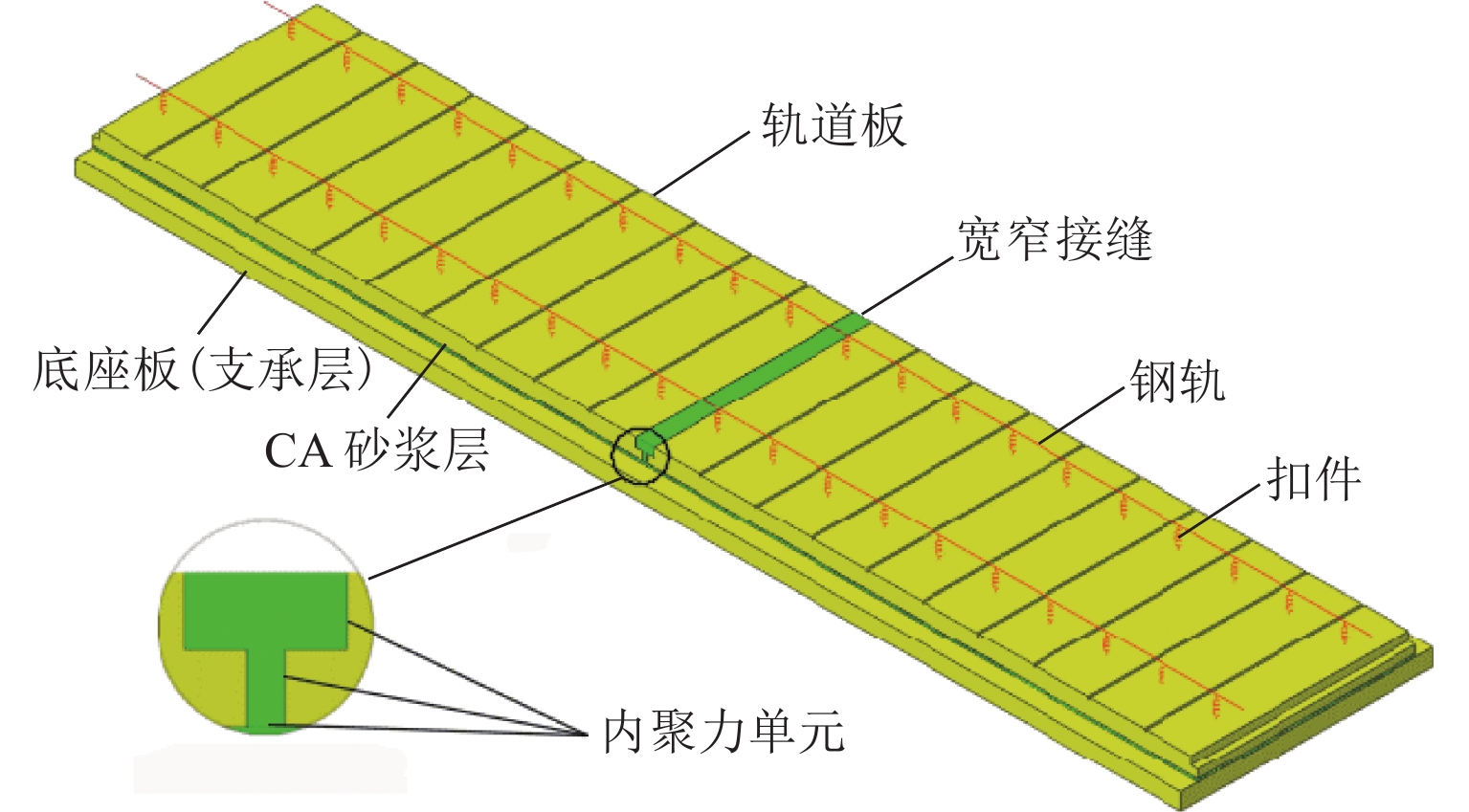
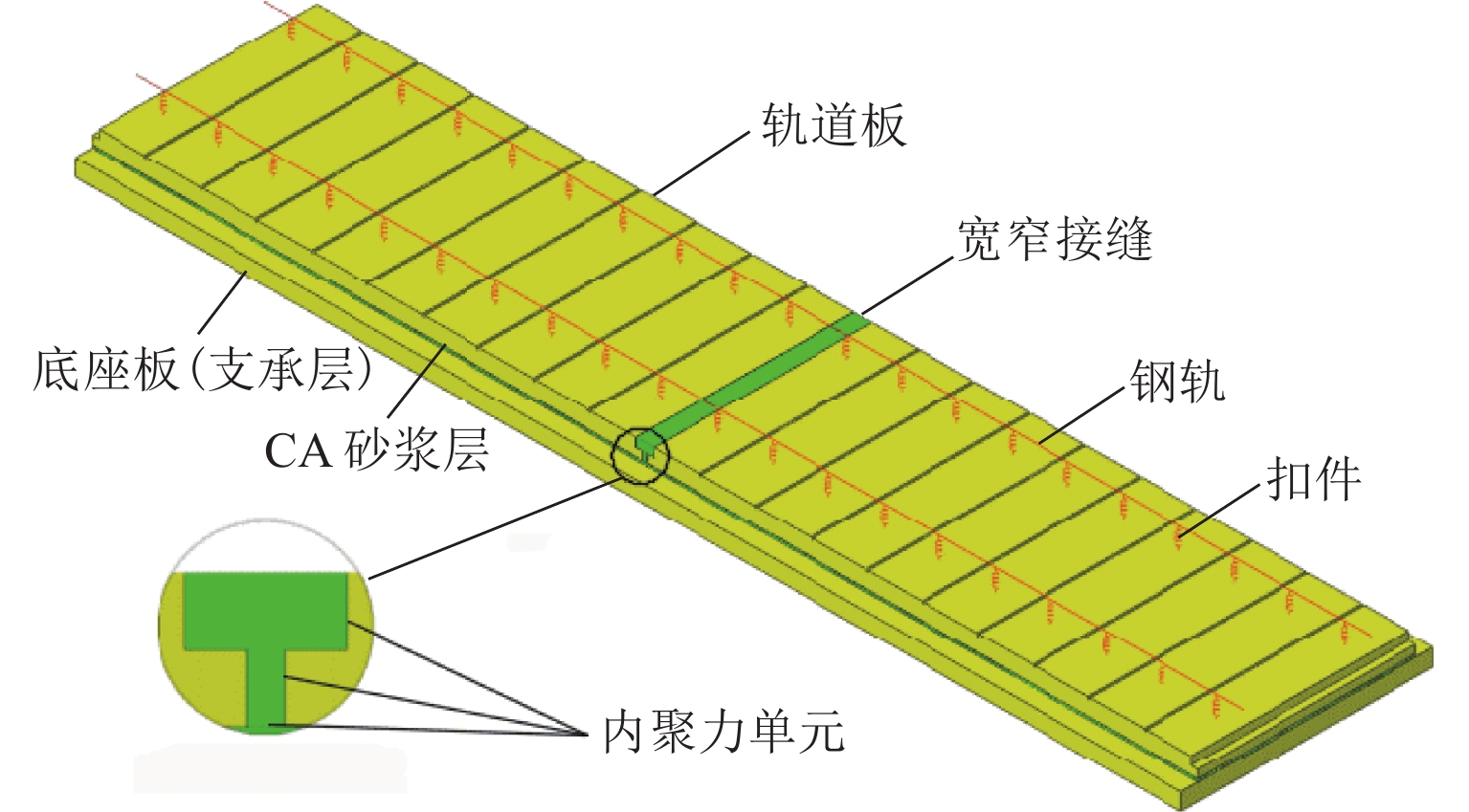
依据CRTSⅡ型板式轨道的结构特点,建立长度为2块轨道板(13 m)的模型,如图3所示. 钢轨和扣件分别采用欧拉梁单元和垂向弹簧单元模拟. 轨道板、宽窄接缝、CA砂浆层和支承层均采用一阶实体单元,为避免剪力锁闭,宽窄接缝采用一阶线性缩减积分单元. 宽窄接缝与轨道板、CA砂浆与轨道板的界面区由内聚力单元模拟. 为提高计算效率,仅在宽窄接缝处定义混凝土的塑性损伤模型,其他部位简化为线弹性材料. 宽窄接缝处网格尺寸最大为12.5 mm,模型其他位置网格最大为300.0 mm,支承层底部和端部以及轨道板的端部采用固定约束. 宽窄接缝细部模型如图4所示.
2. 参数取值
宽窄接缝处混凝土的应力-应变关系参考《混凝土结构设计规范》(GB 50010—2010)[13]. 损伤因子[14]为
dt,c=(1−β)εinE0αt,c+(1−β)εinE0, (7) 式中:β为塑性应变与非弹性应变之比,受压时取0.4,受拉时取0.7;εin为非弹性应变;αt,c为无量纲参数.
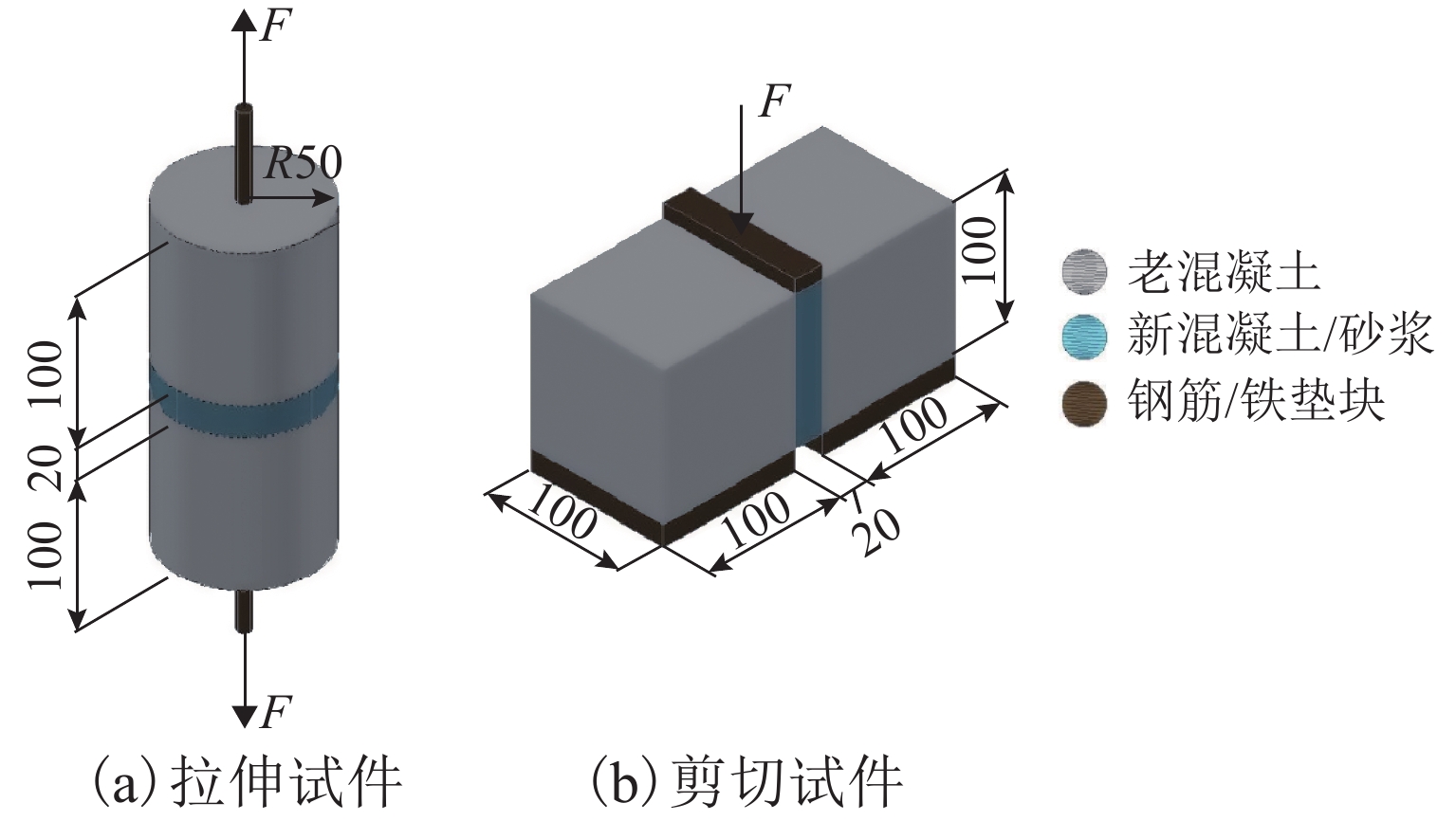
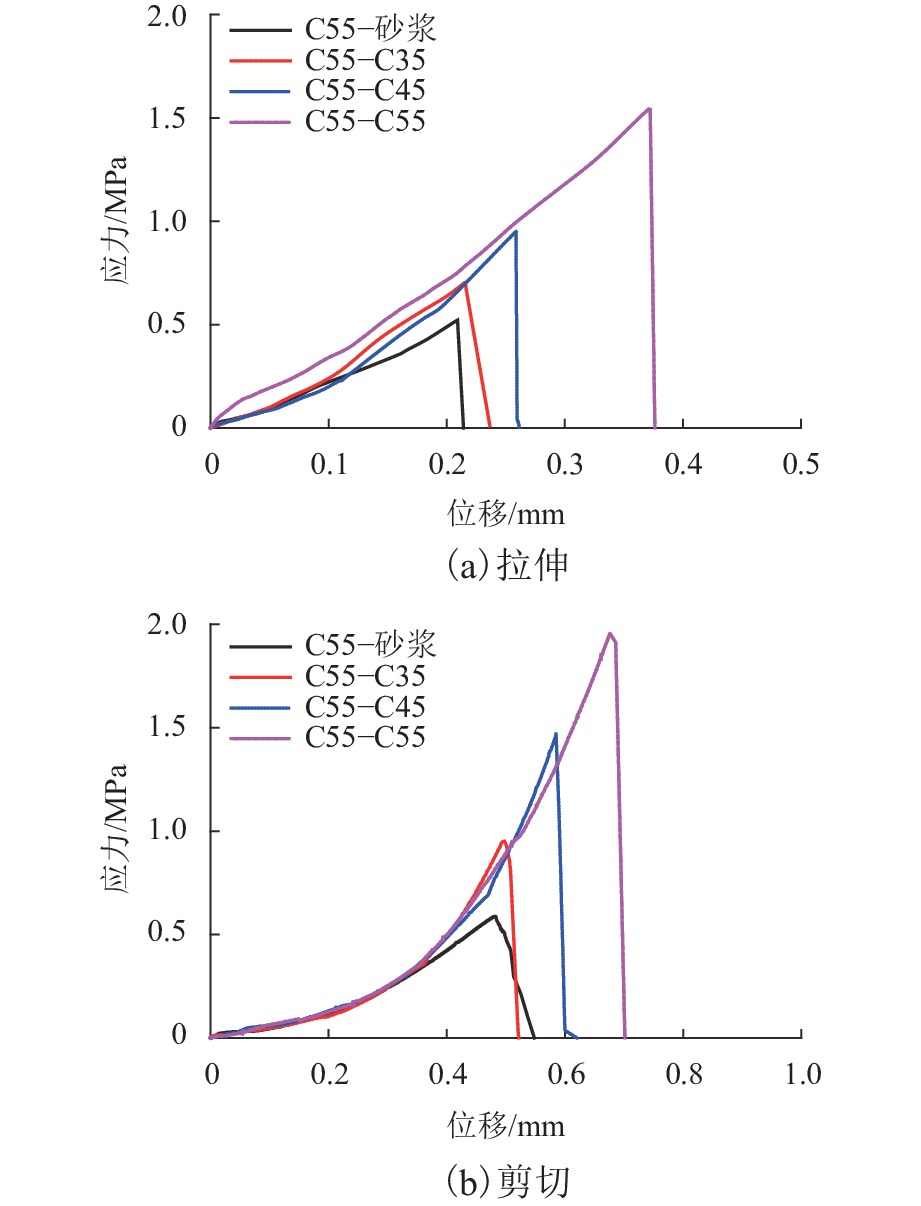
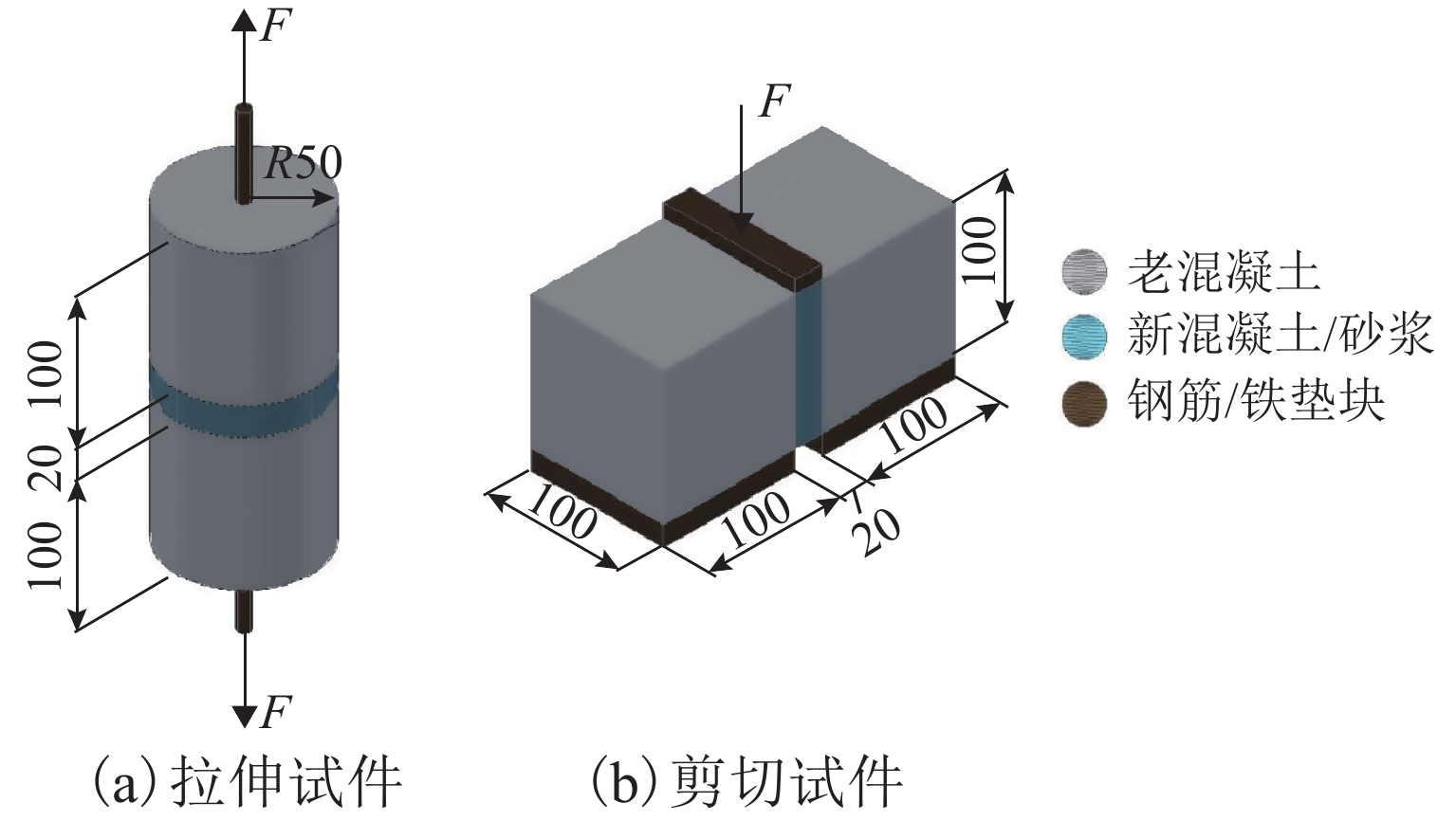
内聚力单元参数取值对界面的强度和刚度有重要影响,进而影响整个结构的受力和变形以及宽窄接缝的受力和损伤,故内聚力单元参数是整个模型计算的关键,为确定相关参数,参照相关文献[15]设计并开展材料试验. 试件如图5所示,拉伸试件为直径10 cm的圆柱形试件,剪切试件为长方体试件,断面为边长10 cm的正方形. 通过万能试验机施加荷载F,可得力-位移曲线(见图6).
根据试验数据,可计算得到内聚层单元的刚度、强度和断裂能,如表1所示,其他主要计算参数见表2[16-18].
表 1 界面参数Table 1. Interface parameters编号 拉伸刚度/
(GPa·m−1)拉伸强度/MPa 拉伸断裂能/
(N·m−1)剪切刚度/
(GPa·m−1)剪切强度/MPa 剪切断裂能/
(N·m−1)C55−砂浆 2.50 0.522 50.5 1.22 0.587 123.5 C55−C35 3.27 0.704 73.7 1.92 0.952 146.3 C55−C45 3.67 0.950 95.6 2.52 1.470 241.1 C55−C55 4.16 1.548 267.5 2.89 1.960 424.7 表 2 主要计算参数Table 2. Main calculation parameters部件 弹性模量/GPa 泊松比 热膨胀系数/℃ 密度/(kg·m−3) 宽度/m 厚度/m 轨道板 36.0 0.20 1.0 × 10−5 2500 2.55 0.20 CA 砂浆 10.0 0.20 1.0 × 10−5 2000 2.55 0.03 宽窄接缝 31.5 0.20 1.0 × 10−5 2500 3. 计算结果及分析
3.1 宽窄接缝的损伤和力学特性
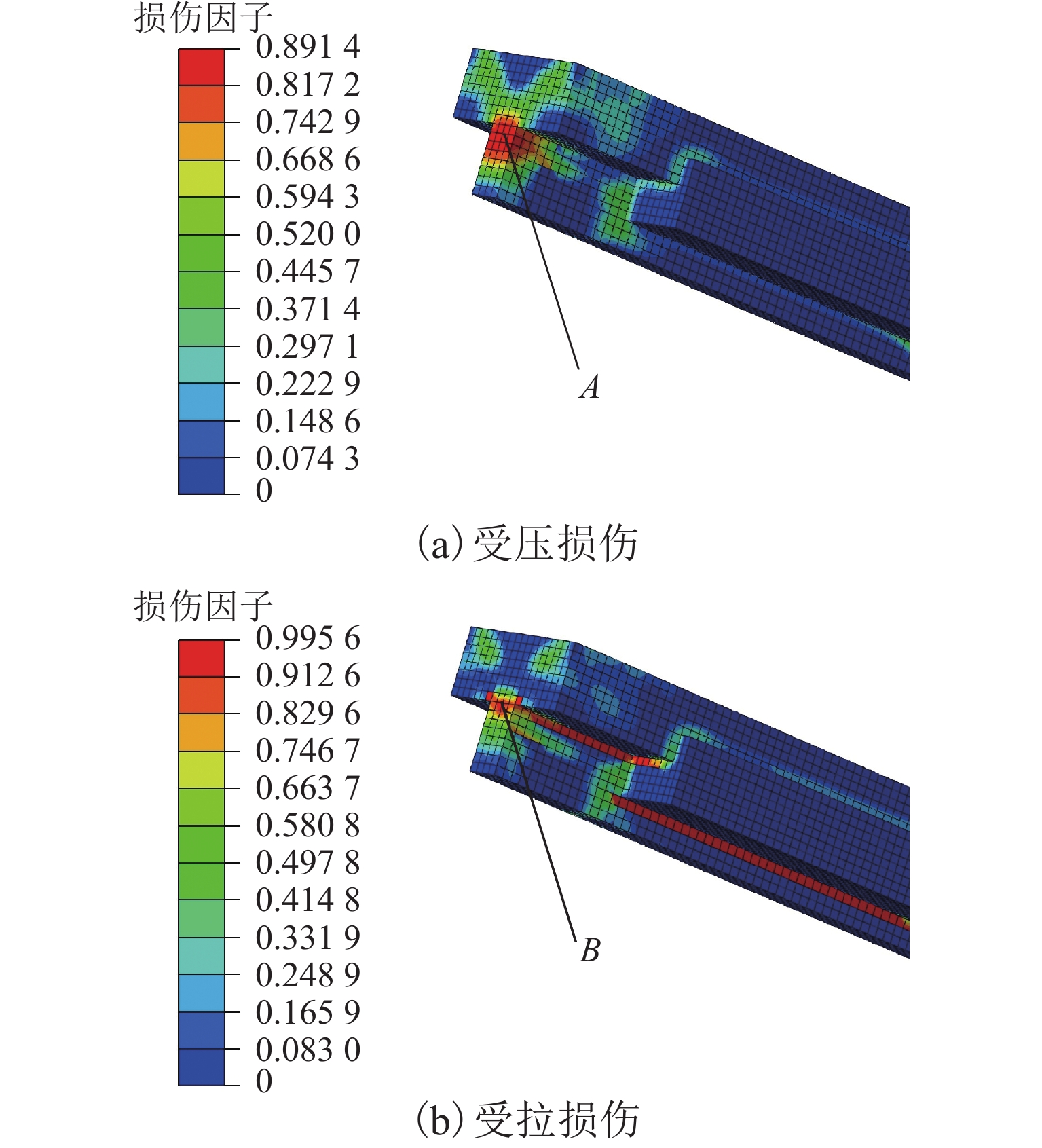
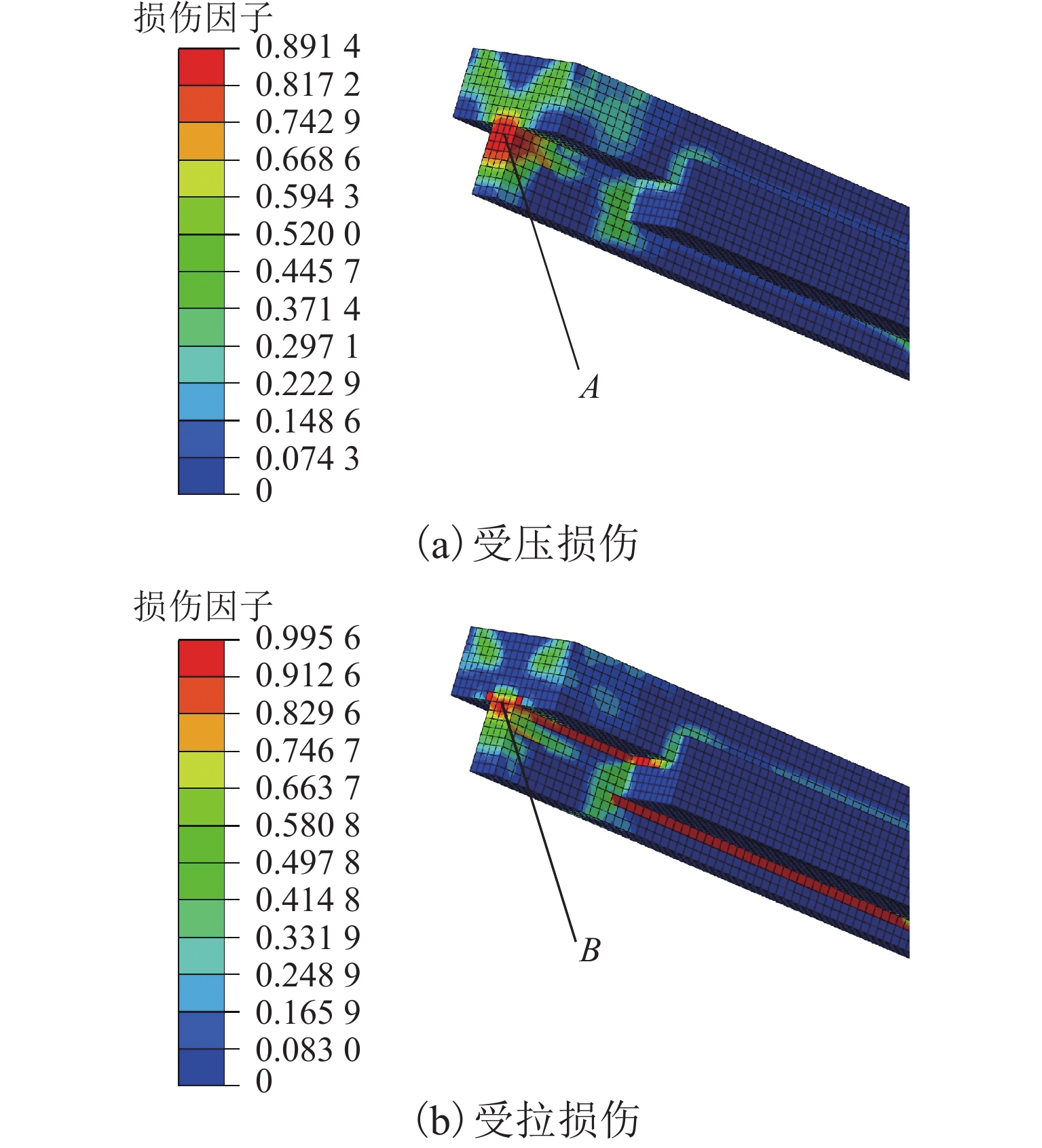
文献[19]表明,无砟轨道内部的最高温度约50 ℃,轨道板温升小于50 ℃,计算时取轨道板的最大温升40 ℃. 在实际尺寸和强度条件下,宽窄接缝在温升40 ℃时的受压损伤和受拉损伤因子云图如图7所示.
图7(a)表明,受压损伤主要分布在窄接缝两端靠近宽接缝处,损伤范围较大,最大伤损出现于点A,其值为0.891,接近于完全破坏,损伤形式与现场窄接缝挤碎类似,这表明窄接缝挤碎属于受压损伤. 图7 (b)表明,受拉损伤主要分布于宽、窄接缝交界处及尺寸突变处,损伤范围较小,但完全贯通,最大损伤出现在点B,其值为0.996,已完全破坏,损伤形式与现场宽、窄接缝交界处断裂类似,这表明宽、窄接缝交界处断裂属于受拉损伤. 宽接缝的拉、压损伤均较小,这与现场一致.
图8表明温升为40℃时,宽窄接缝在不考虑损伤和考虑损伤时的受力. 考虑损伤即将宽窄接缝定义为塑性损伤模型,不考虑损伤即将其视为线弹性材料. 由图可见,宽窄接缝的纵向主要受压. 出现受压损伤的区域(窄接缝处)附近的纵向压应力为9.9~16.0 MPa,小于其抗压强度(23.4 MPa),损伤后降低至0.3~10.2 MPa. 宽窄接缝垂向受拉,而对于理想的均匀结构而言,在温升作用下,其垂向应力应为0. 损伤前,最大垂向拉应力出现在受拉损伤区域(宽、窄接缝交界处)附近,最大垂向拉应力高达19.4 MPa,远超其抗拉强度(2.2 MPa),损伤后垂向拉应力释放,最大仅为0.6 MPa. 综上,在温升荷载的作用下,宽窄接缝垂向受拉、纵向受压,宽窄接缝处的断裂是由垂向受拉导致的受拉损伤,由于其垂向受拉,宽窄接缝处于不利的受力状态,在纵向压力远小于其强度的情况下便出现了明显受压损伤.
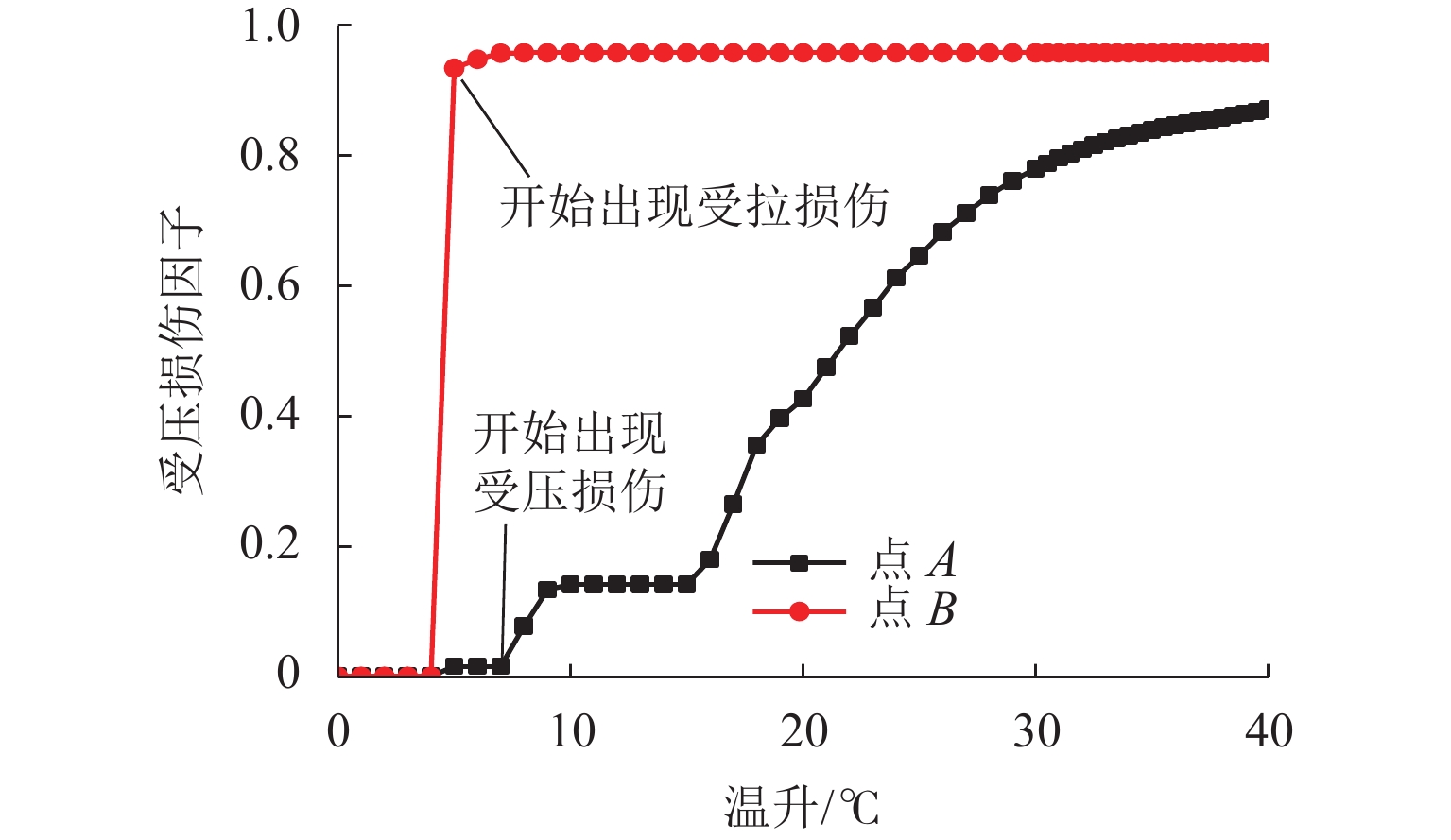
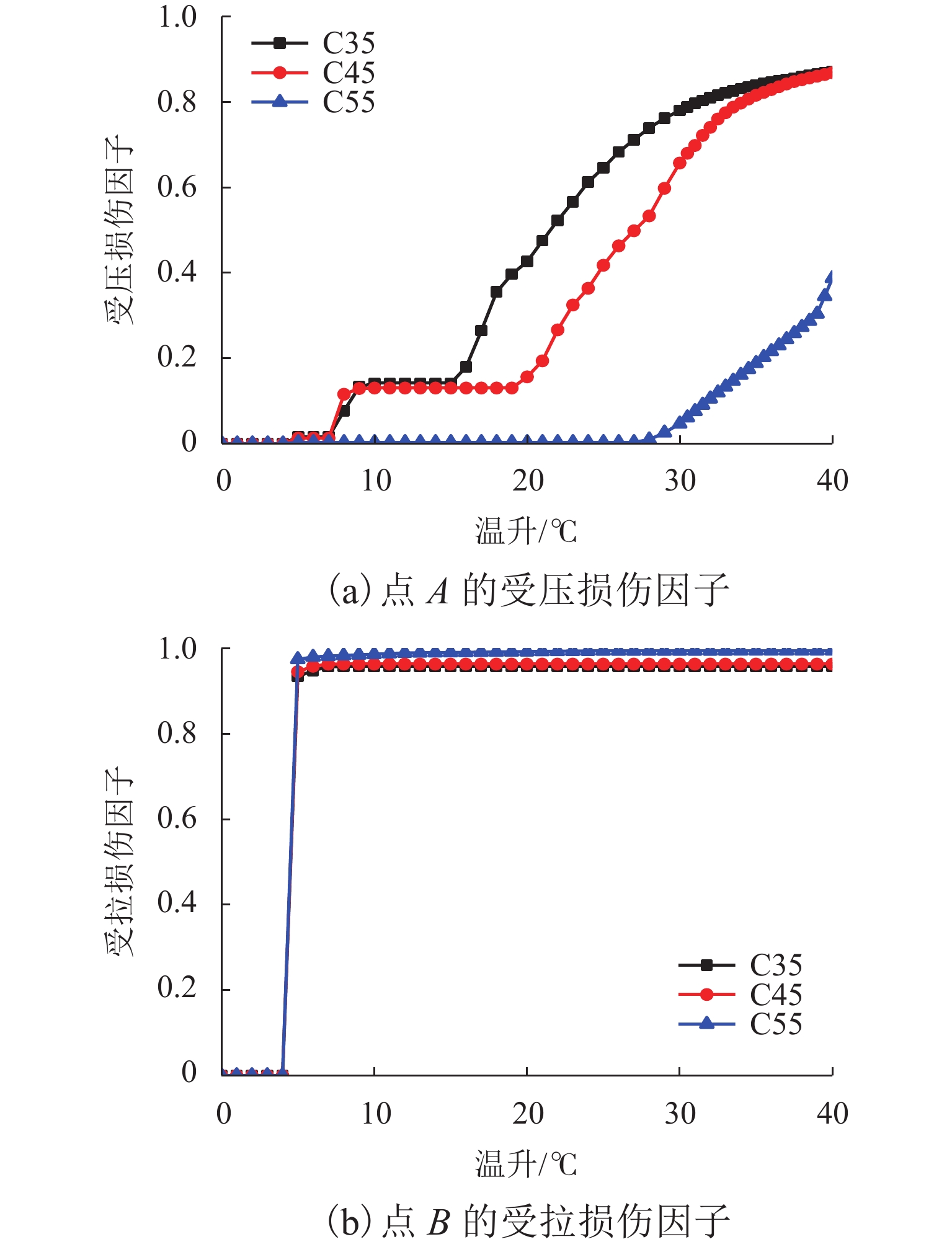
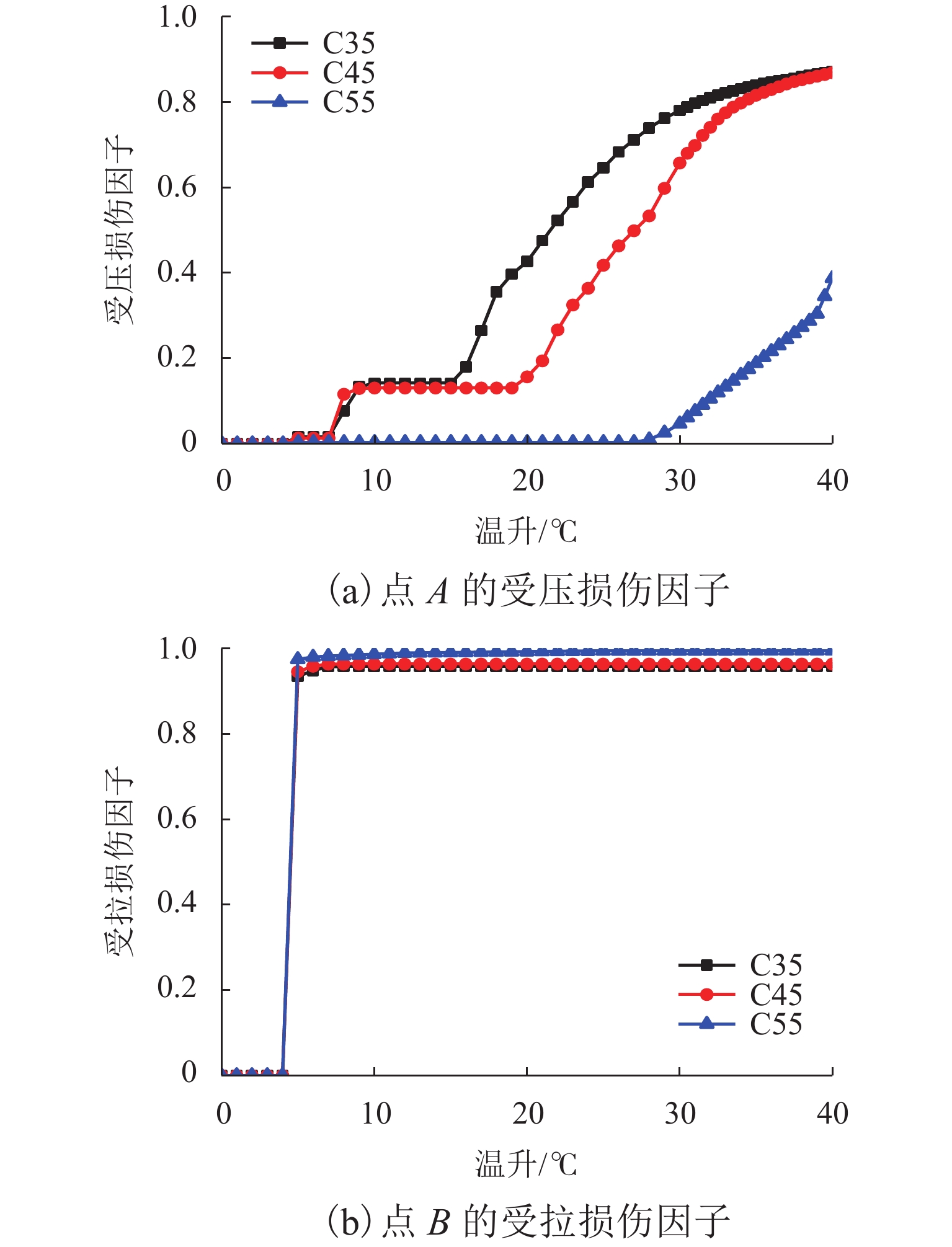
点A的受压损伤因子和点B的受拉损伤因子随温升的变化如图9所示. 结果表明:宽窄接缝的受压损伤随着温升增加而增大,是一个渐变过程;温升达到7 ℃左右时,窄接缝开始出现受压损伤;当温升达到30 ℃左右时,接近于完全破坏;宽窄接缝受拉损伤随着温升的增加而增大,温升为5 ℃时,宽、窄接缝交界处的受拉损伤因子由0突增至接近于1.00,该损伤是脆性破坏,且由于其出现较早,故难以避免,现场大量的宽、窄接缝交界处断裂也证明了这一点.
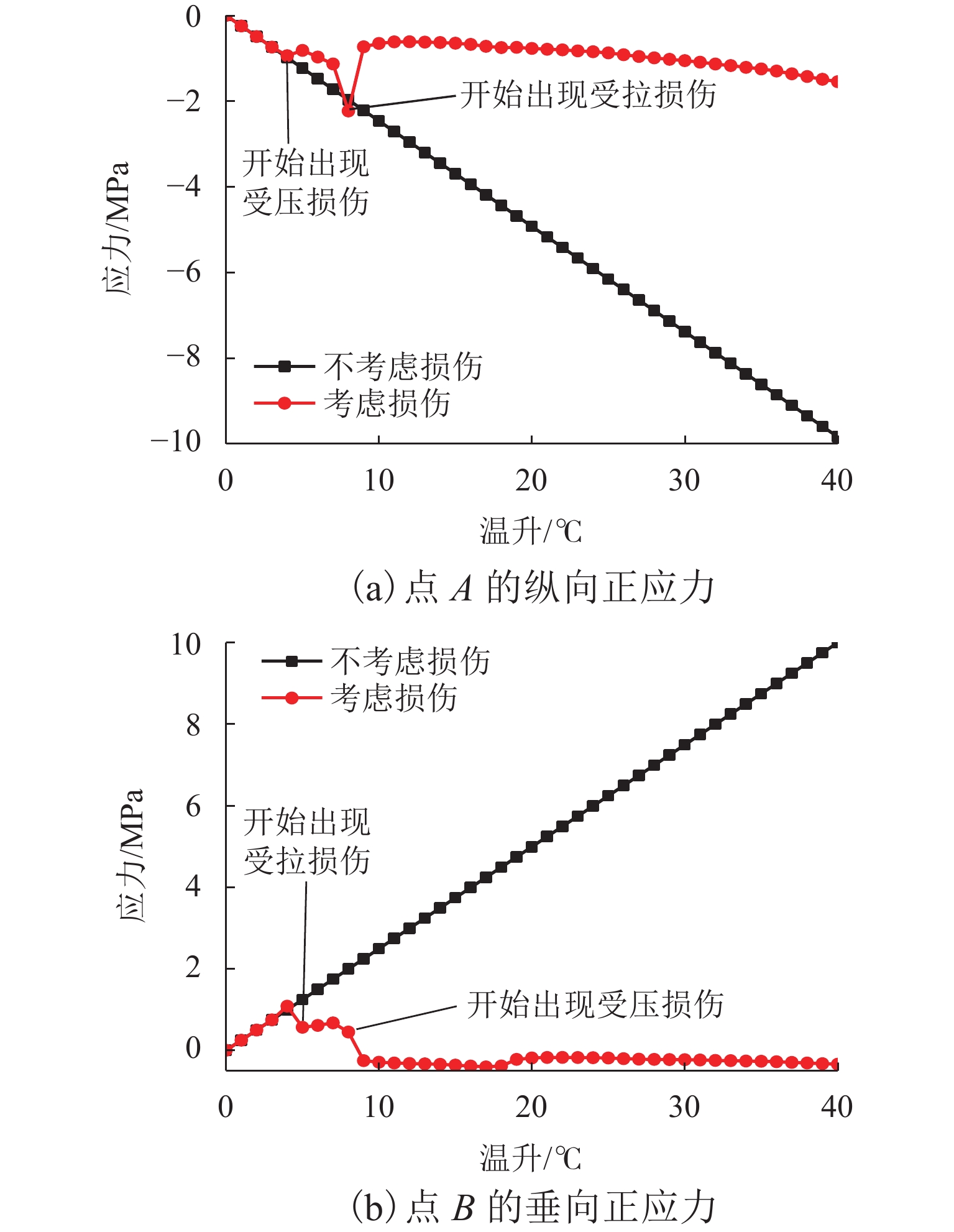
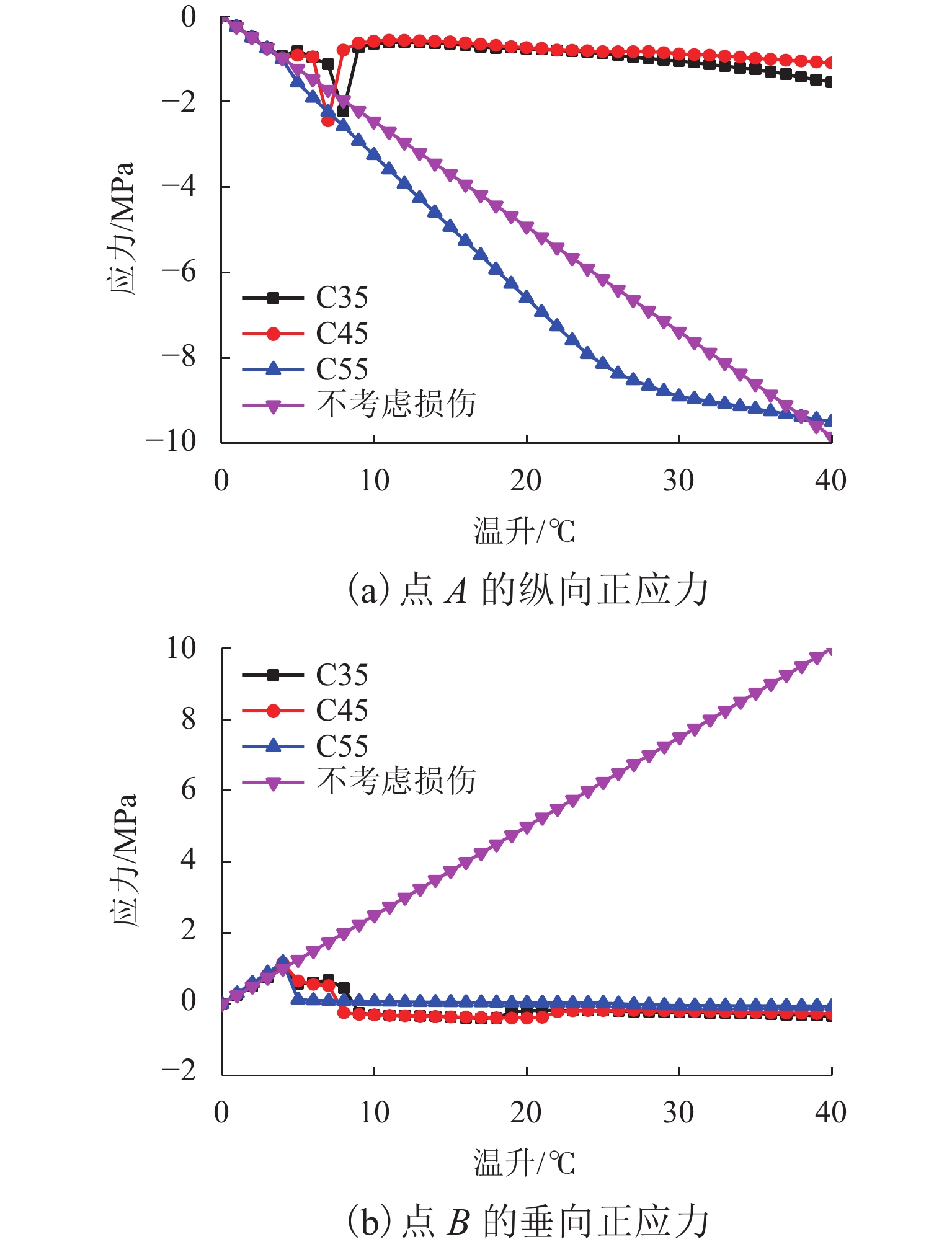
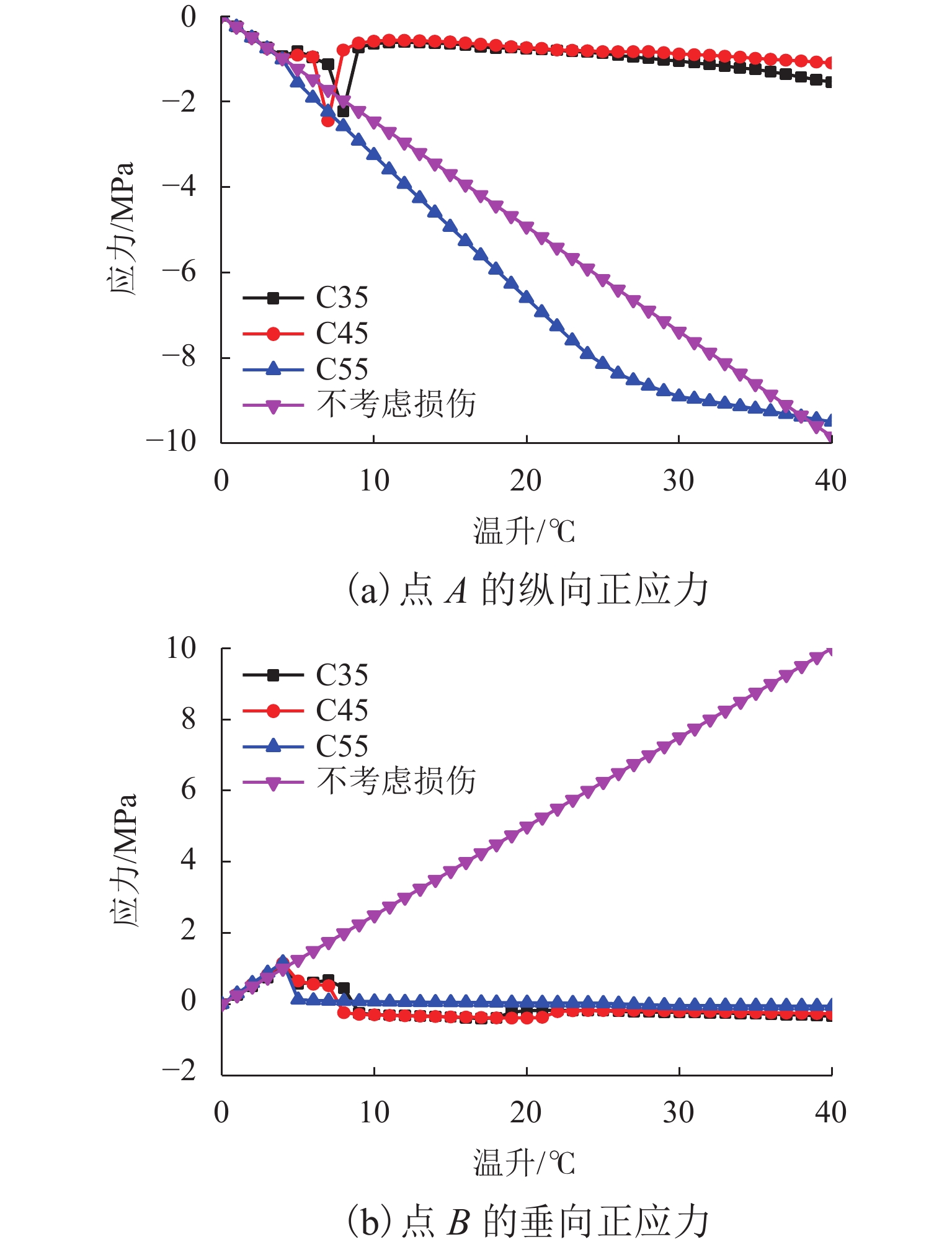
图10(a)反映点A的纵向正应力随温升的变化,负值表示受压. 考虑损伤后,点A的纵向压应力小于不考虑损伤时. 未出现受拉损伤(温升小于5 ℃)时,考虑损伤和不考虑损伤2种条件下,点A的纵向应力相等,出现受拉损伤后,点A纵向压力出现小幅的降低,但仍可以继续承受压力,出现受压损伤后(温升大于7 ℃),点A的纵向压力迅速释放,几乎不能继续承受压力. 图10(b)反映点B垂向正应力随温升的变化,正值表示受拉. 考虑损伤时,点B的垂向拉应力小于不考虑损伤时. 未出现受拉损伤时,2种条件下点B的垂向应力相等,出现受拉损伤后,点B垂向拉力出现小幅的降低,但仍可以继续承受拉力,出现受压损伤后,点B的垂向拉力迅速释放,直至受压.
3.2 影响因素分析
3.2.1 宽窄接缝混凝土强度的影响
宽窄接缝混凝土强度等级分别取C35 (设计强度)、C45和C55 (与轨道板等强),窄接缝宽度按照实际尺寸(5 cm)取值. 不同强度条件下,宽窄接缝的损伤因子和受力分别如图11和图12所示.
图11(a)表明:宽窄接缝的混凝土强度越高,受压损伤越小,并可延迟受压损伤的出现;当混凝土为C55时,点A在温升为28 ℃时才开始出现损伤,在温升为40 ℃时,其受压损伤因子仅为0.38;混凝土为C35和C45时,其值均接近于1.00. 这表明提高宽窄接缝的强度可以降低其受压损伤,尤其是宽窄接缝与轨道板等强时. 图11(b)表明,不同条件下点B受拉损伤基本相同,温升为40 ℃时,点B的受拉损伤因子均接近于1.00,这表明宽窄接缝强度对其受拉损伤影响较小.
由图12(a)可知:宽窄接缝混凝土强度等级为C35和C45时,点A纵向压应力有较大的释放;混凝土强度等级为C55时,由于受压损伤较小,点A的压应力几乎没有释放,甚至较不考虑损伤时更大,这表明宽窄接缝混凝土强度与轨道板等强可使其保持承受压力的能力,同时减少受压损伤. 由图12(b)可知,不同强度下点B的垂向应力变化趋势大致相同,出现损伤后,点B垂向均处于受压状态,这表明提高宽窄接缝混凝土的强度并不能改善其垂向的受力并减小其受拉损伤.
3.2.2 窄接缝宽度的影响
窄接缝宽度分别取5 cm (设计尺寸)、13 cm、21 cm(与宽接缝等宽),不同窄接缝宽度条件下宽窄接缝的损伤因子和受力分别如图13和图14所示,其中,宽窄接缝的混凝土强度等级为C55.
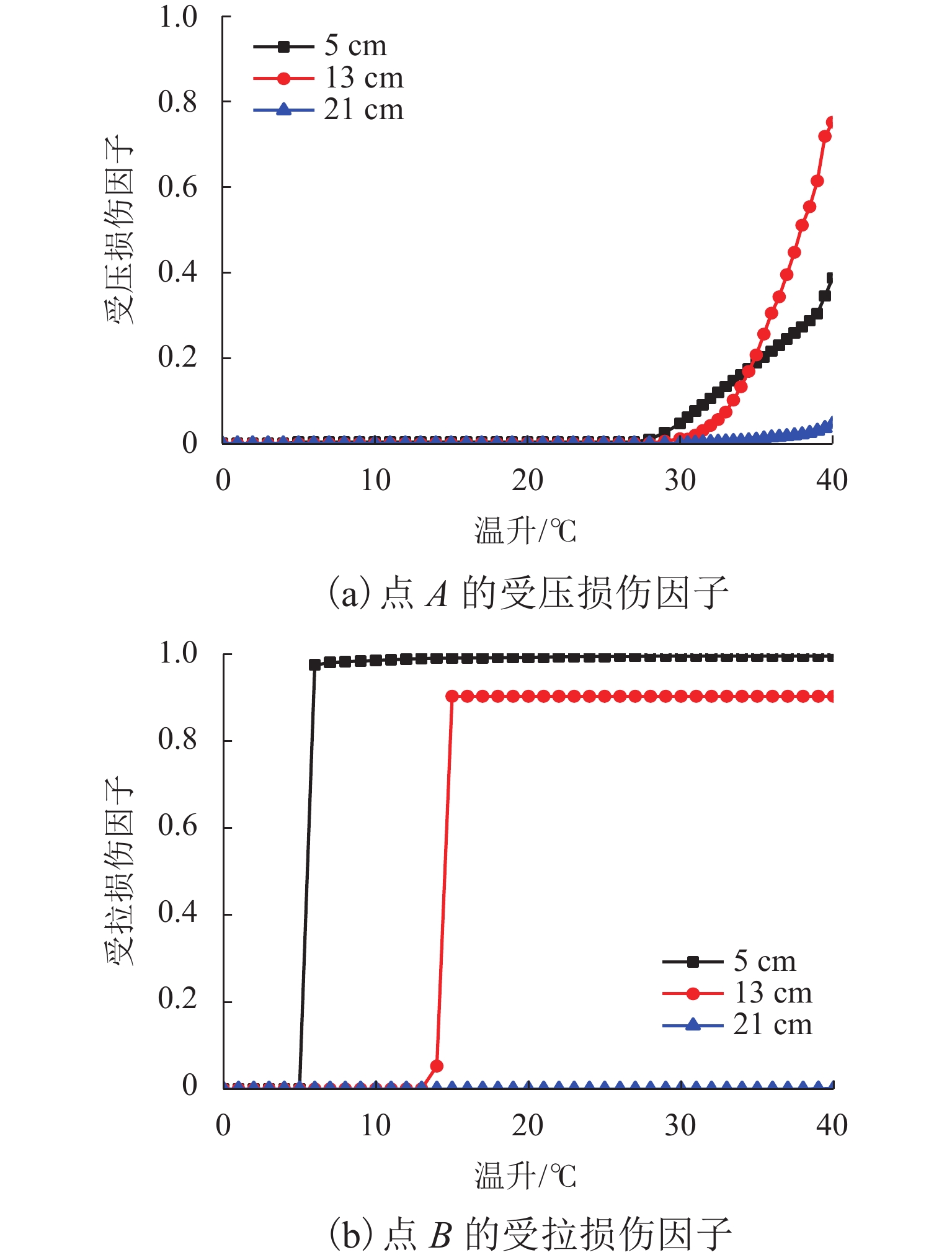
由图13(a)可知,温升为40 ℃时,窄接缝宽度为5、13、21 cm条件下,点A的受压损伤因子分别为0.39、0.75和0.05,这表明只有宽、窄接缝等宽才可有效减小宽窄接缝的受压损伤. 由图13(b)可知,随着窄接缝宽度的增加,点B的受拉损伤逐渐减小,温升为40 ℃,窄接缝宽度为5、13、21 cm条件下,点B的受拉损伤因子分别为0.99、0.90、0.01,这表明增加窄接缝宽度可有效避免其受拉损伤.
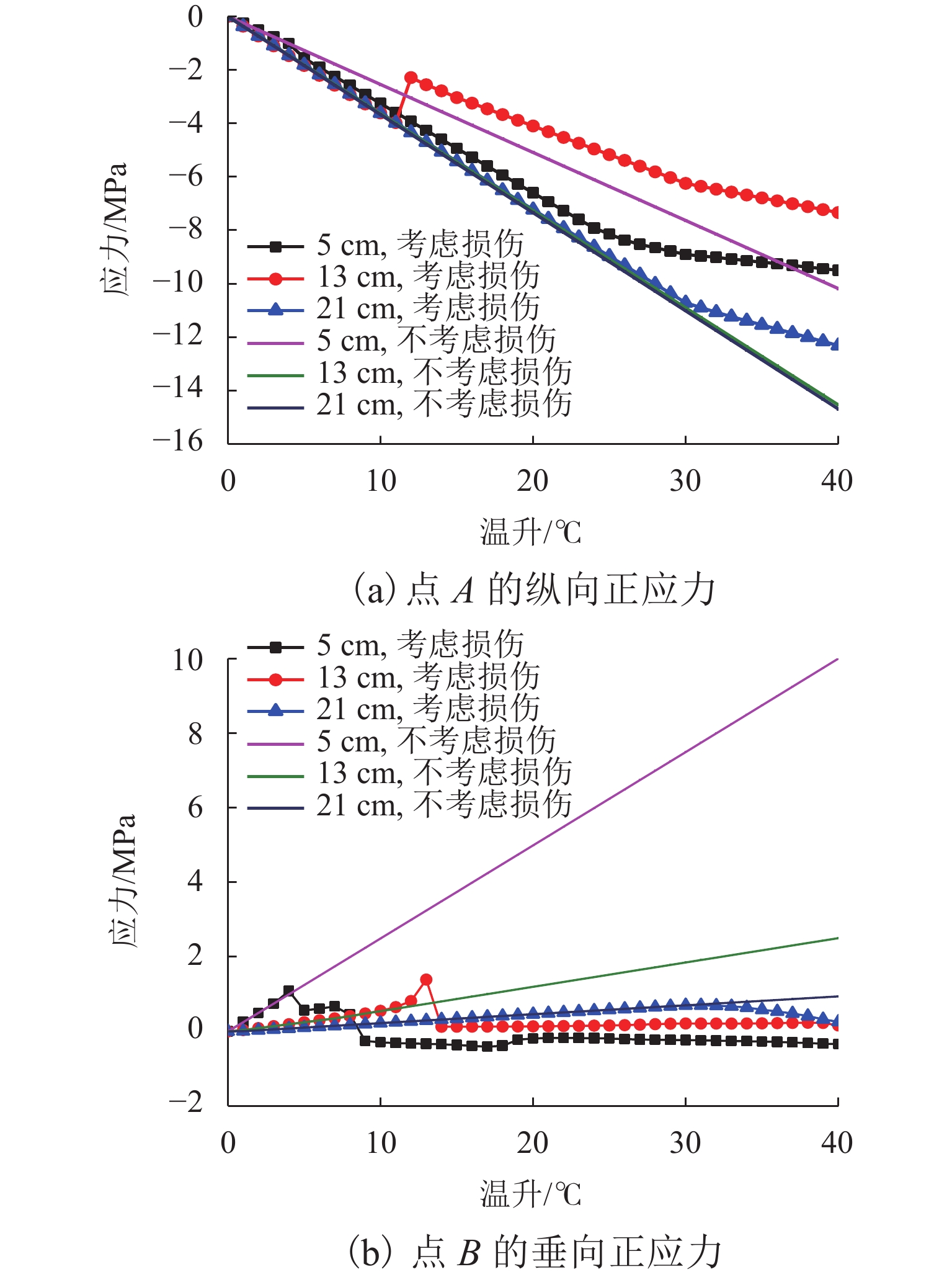
图14(a)表明,窄接缝越宽,温度力释放越少,温升为40 ℃时,纵向压应力分别为1.55、7.33、 12.31 MPa,这说明增加窄接缝的宽度可有效改善宽窄接缝的纵向受力. 图14(b)表明,当窄接缝宽度取13、21 cm时,点B均处于受拉状态,温升为40 ℃时,窄接缝宽度为5、13、21 cm条件下,点B垂向应力分别 −0.34、0.16、0.26 MPa,这说明窄接缝越宽,垂向拉应力释放越小.
4. 结 论
1) 宽窄接缝尺寸不均匀导致其在温升作用下垂向受拉纵向受压,这是宽窄接缝损伤的主要原因.
2) 宽、窄接缝交界面断裂是一种脆性受拉损伤,对轨道结构的受力影响较小. 窄接缝挤碎是一种渐变受压损伤,对轨道结构的受力影响较大.
3) 提高宽窄接缝的强度一定程度上可减小纵向压应力的释放(尤其是混凝标号为 C55 时),但不能有效降低垂向拉应力的释放,因此,可有效减小受压损伤,无法减小受拉损伤.
4) 增加窄接缝的宽度可从根本上减小偏心作用,这对结构的受力十分有利,尤其是宽、窄接缝等宽时. 宽、窄接缝等宽可降低纵向压力的释放和垂向拉力的大小,尤其是后者,且对宽窄接缝的受拉和受压损伤均能有效减小.
5) 为减小宽窄接缝的损伤并改善其受力,建议宽、窄接缝等宽,且宽窄接缝与轨道板等强.
-
表 1 界面参数
Table 1. Interface parameters
编号 拉伸刚度/
(GPa·m−1)拉伸强度/MPa 拉伸断裂能/
(N·m−1)剪切刚度/
(GPa·m−1)剪切强度/MPa 剪切断裂能/
(N·m−1)C55−砂浆 2.50 0.522 50.5 1.22 0.587 123.5 C55−C35 3.27 0.704 73.7 1.92 0.952 146.3 C55−C45 3.67 0.950 95.6 2.52 1.470 241.1 C55−C55 4.16 1.548 267.5 2.89 1.960 424.7 表 2 主要计算参数
Table 2. Main calculation parameters
部件 弹性模量/GPa 泊松比 热膨胀系数/℃ 密度/(kg·m−3) 宽度/m 厚度/m 轨道板 36.0 0.20 1.0 × 10−5 2500 2.55 0.20 CA 砂浆 10.0 0.20 1.0 × 10−5 2000 2.55 0.03 宽窄接缝 31.5 0.20 1.0 × 10−5 2500 -
[1] 戴公连,葛浩. 桥上纵连板式无砟轨道初始状态特征统计分析[J]. 铁道工程学报,2020,37(9): 1-6. doi: 10.3969/j.issn.1006-2106.2020.09.001DAI Gonglian, GE Hao. Statistical analysis of the initial state characteristics of the longitudinally connected ballastless track on bridge[J]. Journal of Railway Engineering Society, 2020, 37(9): 1-6. doi: 10.3969/j.issn.1006-2106.2020.09.001 [2] 刘笑凯,刘学毅,肖杰灵,等. 温度作用下纵连式无砟轨道垂向稳定性研究[J]. 西南交通大学学报,2018,53(5): 921-927,944. doi: 10.3969/j.issn.0258-2724.2018.05.007LIU Xiaokai, LIU Xueyi, XIAO Jieling, et al. Vertical stability of longitudinal continuous ballastless track under temperature variation[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 921-927,944. doi: 10.3969/j.issn.0258-2724.2018.05.007 [3] FENG Q S, CHAO H Y, LEI X Y. Influence of the seam between slab and CA mortar of CRTSⅡ ballastless track on vibration characteristics of vehicle-track system[J]. Procedia Engineering, 2017, 199: 2543-2548. doi: 10.1016/j.proeng.2017.09.259 [4] 钟阳龙,高亮,侯博文. 不同植筋方案纵连板轨道砂浆层抗剪性能分析[J]. 西南交通大学学报,2018,53(1): 38-45,63. doi: 10.3969/j.issn.0258-2724.2018.01.005ZHONG Yanglong, GAO Liang, HOU Bowen. Shear behavior of mortar layer in continuous slab track with different arrangement schemes of embedded steel bars[J]. Journal of Southwest Jiaotong University, 2018, 53(1): 38-45,63. doi: 10.3969/j.issn.0258-2724.2018.01.005 [5] 许玉德,缪雯颖,严道斌,等. 基于改进混合模式内聚力模型的无砟轨道层间损伤分析[J]. 铁道学报,2021,43(4): 125-135. doi: 10.3969/j.issn.1001-8360.2021.04.016XU Yude, MIAO Wenying, YAN Daobin, et al. Analysis of interlayer interface damage in ballastless track based on improved mixed-mode cohesive zone model[J]. Journal of the China Railway Society, 2021, 43(4): 125-135. doi: 10.3969/j.issn.1001-8360.2021.04.016 [6] 闫斌,娄徐瑞利,谢浩然,等. 冻胀冻融作用下材料劣化对板式无砟轨道性能的影响[J]. 交通运输工程学报,2021,21(5): 62-73. doi: 10.19818/j.cnki.1671-1637.2021.05.005YAN Bin, LOU Xuruili, XIE Haoran, et al. Effect of material deterioration on slab ballastless track performance under frost heaving and freezing-thawing[J]. Journal of Traffic and Transportation Engineering, 2021, 21(5): 62-73. doi: 10.19818/j.cnki.1671-1637.2021.05.005 [7] LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299-326. doi: 10.1016/0020-7683(89)90050-4 [8] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900. doi: 10.1061/(ASCE)0733-9399(1998)124:8(892) [9] SARIKAYA A, ERKMEN R E. A plastic-damage model for concrete under compression[J]. International Journal of Mechanical Sciences, 2019, 150: 584-593. doi: 10.1016/j.ijmecsci.2018.10.042 [10] PARK K, PAULINO G H. Cohesive zone models: a critical review of traction-separation relationships across fracture surfaces[J]. Applied Mechanics Reviews, 2011, 64(6): 060802.1-060802.20. [11] LÓPEZ-PUENTE J, ARIAS A, ZAERA R, et al. The effect of the thickness of the adhesive layer on the ballistic limit of ceramic/metal armours: an experimental and numerical study[J]. International Journal of Impact Engineering, 2005, 32(1/2/3/4): 321-336. [12] YANG J F, LIAN H J, NGUYEN V P. Study of mixed mode Ⅰ/Ⅱ cohesive zone models of different rank coals[J]. Engineering Fracture Mechanics, 2021, 246: 107611.1-107611.16. [13] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. [14] 张劲,王庆扬,胡守营,等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构,2008,38(8): 127-130. doi: 10.19701/j.jzjg.2008.08.036ZHANG Jin, WANG Qingyang, HU Shouying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130. doi: 10.19701/j.jzjg.2008.08.036 [15] 李培刚. CRTSⅡ型板式轨道层间损伤及其影响研究[D]. 成都: 西南交通大学, 2015. [16] 李再帏,吴刚,朱文发,等. 基于Lamb波的CRTSⅡ型板式无砟轨道层间损伤检测方法[J]. 铁道学报,2020,42(12): 120-126. doi: 10.3969/j.issn.1001-8360.2020.12.016LI Zaiwei, WU Gang, ZHU Wenfa, et al. CRTSⅡ slab ballastless track interlayer damage detection method based on Lamb wave[J]. Journal of the China Railway Society, 2020, 42(12): 120-126. doi: 10.3969/j.issn.1001-8360.2020.12.016 [17] 赵国堂,刘钰. CRTSⅡ型板式无砟轨道结构层间离缝机理研究[J]. 铁道学报,2020,42(7): 117-126.ZHAO Guotang, LIU Yu. Mechanism analysis of delamination of CRTS Ⅱ slab ballastless track structure[J]. Journal of the China Railway Society, 2020, 42(7): 117-126. [18] 张鹏飞,涂建,桂昊,等. 温梯荷载下桥上CRTSⅡ型板式无砟轨道的力学特性[J]. 西南交通大学学报,2021,56(5): 945-952.ZHANG Pengfei, TU Jian, GUI Hao, et al. Mechanical properties of CRTS Ⅱ slab ballastless track on bridge under temperature gradient loads[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 945-952. [19] 欧祖敏,孙璐,程群群. 基于气象资料的无砟轨道温度场计算与分析[J]. 铁道学报,2014,36(11): 106-112. doi: 10.3969/j.issn.1001-8360.2014.11.021OU Zumin, SUN Lu, CHENG Qunqun. Analysis on temperature field of ballastless track structure based on meteorological data[J]. Journal of the China Railway Society, 2014, 36(11): 106-112. doi: 10.3969/j.issn.1001-8360.2014.11.021 期刊类型引用(2)
1. 杨绍楠. 长钢轨轨道板上拱换板施工技术研究. 建筑机械. 2025(01): 141-146+6 .  百度学术
百度学术2. 任西冲. 纵连板式无砟轨道温度力释放关键参数研究. 中国铁路. 2025(02): 54-63 .  百度学术
百度学术其他类型引用(3)
-






 下载:
下载:













 下载:
下载:







 百度学术
百度学术