Compound Fault Diagnosis Method Guided by Variational Mode Decomposition for Wheelsets and Bearings
-
摘要:
针对列车轮对轴承系统复合故障难以辨识与诊断问题,提出一种变分模态分解(variational mode decomposition, VMD)引导的多故障特征提取匹配方法. 首先,为避免预定义模式数在运行过程中对先验知识依赖从而对诊断结果造成影响,对原始轴箱振动数据进行逐阶VMD分解,模式数为2~
N ;其次,对VMD分解获取的本征模态函数(VMD intrinsic mode functions, VIMF)进行相关峭度计算,提取相关峭度最大的VIMF;然后,将相关峭度最大的VIMF进行平方包络分析,提取故障特征频率;最后,将所提方法与快速峭度谱、相关峭度谱方法进行对比. 仿真信号和试验数据分析表明:所提方法完全规避了VMD模型中关键参数K 的选择问题,可以准确、有效地分别提取出轮对和轴承的故障特征;与快速谱峭度与相关谱峭度方法相比,获取的故障特征谐波分量在数量和信噪比上均具有明显优势.Abstract:A multi-fault feature extraction and matching method guided by variational mode decomposition (VMD) was proposed to address the difficulty in identifying and diagnosing composite faults in train wheelset bearing systems. Firstly, in order to avoid the pre-defined mode number relying on prior knowledge during operation and thus affecting the diagnosis results, the original axle-box vibration data are directly decomposed by VMD step by step, and the number of modes is 2–
N . Secondly, the VMD intrinsic mode functions (VIMF) obtained by VMD are calculated to extract the VIMF with the largest correlation kurtosis; then, the determined VIMF is analyzed by square envelope analysis to extract the fault feature frequency. Finally, the proposed method is compared with the fast spectral Kurtogram method and the correlation Kurtogram method. The analysis of simulation signals and experimental data shows that the proposed method can completely avoids the problem of selecting the key parameterK in the VMD model, and can accurately and effectively extract the fault characteristics of wheelsets and bearings, respectively. Compared with the fast spectral Kurtogram method and the correlation Kurtogram method the proposed method can diagnose compound faults effectively, and the obtained fault feature harmonic components are more advantageous in quantity and signal-to-noise ratio. -
轮对轴承系统是轨道车辆的基础走行机构之一,包括轮对与轴承两大核心部件. 在列车实际运行过程中,由于受到轨道不平顺激励、轮轨耦合作用及其他部件的复杂激扰,轮对轴承系统故障多发、频发[1-2],成为轨道车辆重要的安全风险源和维保对象. 轮对轴承系统复合故障主要包括轴承滚柱、外圈、内圈故障以及轮对踏面上的扁疤、凹陷、裂纹、剥落、点蚀等局部损伤. 由于轮对和轴承都做旋转运动,损伤或缺陷一旦产生,都会形成一系列冲击[1,3]. 随着轮对和轴承的旋转,系统的共振激励会产生重复脉冲响应. 安装在轴箱上的振动传感器可收集周期性的冲击信号,但由于冲击信号常受到强背景噪声的干扰,很难直接从信号中探测到故障特征频率. 此外,测量的加速度信号通常包含两种循环脉冲分量:一种是轴承故障相关信号;另一种是轮对踏面缺陷相关信号. 尽管由缺陷导致的重复瞬态冲击与缺陷的位置、设备转速和几何形状相关,但在轴箱振动响应信号中两个部件故障产生的脉冲性和振动特征极其相似,因此,从采集的信号中提取不同的故障相关脉冲是一个挑战. 传统的信号处理方法通常旨在提高信号的脉冲性,但缺乏两种脉冲的分辨能力[4]. 包络谱分析作为实现旋转机械故障诊断的有效方法得到了广泛的应用. 在共振频带附近进行滤波,能有效提高故障特征频率的检测能力,因此,许多先进的方法都聚焦于共振频带的选取. 由于轮对和轴承振动传递路径不同,两个部件的共振频带也不同,因此,可以通过提取相应的故障特征频率实现复合故障的诊断[5].
针对共振带探测问题,目前应用较为广泛的自适应共振频带提取算法主要包括经验模态分解 (empirical mode decomposition, EMD)、局部均值分解(local mean decomposition, LMD)、经验小波变换(empirical wavelet transform, EWT)和变分模态分解(variational mode decomposition, VMD). 这些算法能够自适应地将分析信号分解为多个互相独立的子信号,在理想的结果中这些子信号各自包含不同的共振频带,从而为下一步的分析提供更高信噪比的振动信号. EMD模态混叠、端点效应和筛选停止准则等一直是方法改进的重点;LMD算法在抑制端点和保留信号信息方面优于EMD,但仍存在模态混叠问题;与EMD相比,EWT不仅有坚实的数学基础,而且避免了模式混叠,具有很强的鲁棒性,然而,如何将傅里叶谱分割成适当的模式数和频率边界一直是EWT算法性能的瓶颈[6]. EMD可以递归地将信号分解为不同的模式,但分解结果与极值点的选择和插值方法密切相关. 因此,基于EMD和EWT,Dragomiretskiy等[7]在2014 年研究了一种非递归自适应信号分解方法,即VMD. 在VMD算法中,假设信号的傅里叶谱是紧支撑的,然后构造一个维纳滤波器组来同时提取所有模式,每个模式主要围绕其中心频率进行压缩. 由于维纳滤波器的最优滤波特性,VMD在分解频率接近的频带和减少模式混淆方面都具有良好的性能,在多分量信号分析中优于EMD和EWT. 因此,VMD也被广泛用于机械故障诊断[8]. 然而,与不依赖先验知识的EMD相比,VMD算法的实现需要预定义模式数. 近年来关于提高VMD适应性的研究较多,但大多需要先对VMD进行处理后通过大量递归计算来优化参数或合并模态分量(IMFs),这类方法非常依赖优化指标的选择. 快速谱峭度(fast kurtogram, FK)在一系列固定划分的1/3二叉树滤波器组中探索具有最大峭度的共振带,已被称为故障诊断领域的基准技术[9]. 由其原理可知,决定FK性能的两个因素分别是滤波器组的设计和刻画指标的选择. 本文基于FK算法框架,提出一种无需预定义模式数的自适应VMD方法,同时避免了IMF合并带来的指标选择问题.
为克服峭度对时域异常脉冲敏感的缺点,许多更具鲁棒性的优良指标相继提出. Miao等[10]创新地使用基尼系数Gini index作为频带选择指标,提高了评估指标的鲁棒性. Bozchalooi等[11]提出的平滑指数Smoothness已被认为是另一个极具应用价值和重要的统计参数,用于描述信号的重复瞬变. Wang[12]利用L2/L1范数来表征轴承故障信号. 虽然这类指标比峭度指标更鲁棒,但是这些指标只关注故障信号的脉冲性而忽略了故障信号脉冲的周期性. Mcdonald等[13]提出使用相关峭度(correlation kurtosis, CK)刻画故障共振带,利用故障的周期性消除随机脉冲的影响,提高了峭度指标的鲁棒性. 相关峭度中人为地引入周期信息,不仅提高了指标的刻画性能还具备了多发故障的检测能力. 因此,相关峭度被本文用来提取轮对和轴承故障激发的共振频带.
1. VMD基础理论
VMD可以将输入信号f(t)分解为K个离散的模态 uk(t)(k=1,2,…,K),uk(t)在频率中的带宽都具有特定的稀疏属性,是一种以经典维纳滤波、希尔伯特变换和频率混合3个概念为基础的变分问题求解方法,其中,t为时间.
维纳滤波用于信号去噪,希尔伯特变换用于构造分析信号以获得单边带频谱,而频率混合用来将频谱移到基带. 为了获得具有紧凑带宽的模态,并要求所有模态总和能重构输入信号f,构造了以下约束变分问题[7]:
min{uk},{ωk}{∑Kk=1‖(∂(t)+jπt)uk(t)ejωkt‖22}, (1) ∑Kk=1uk(t)=f, (2) 式中:δ(t)为狄拉克分布,ωk为各个模态的中心频率.
为了在高斯白噪声存在的情况下将输入信号完全分解为uk(t)模态,引入二次惩罚因子α和拉格朗日因子λ,将约束问题转化为无约束优化问题,用交替方向乘子法(alternate direction method of multipliers, ADMM)进行优化求解. 二次惩罚项保证信号的重构精度,而拉格朗日乘子保持约束条件的严格性.
VMD的算法流程如下:
1) 初始化u(1)k、ω(1)k、λ(1)和n为0;
2) n=n+1,开始整个算法的循环;
3) 根据式(3)、(4)更新uk和ωk(加^表示对应各变量的傅里叶变换,余同).
ˆu(n+1)k(ω)=ˆf(ω)−∑i≠kˆu(n)k(ω)+ˆλ(n)(ω)21+2α(ω−ω(n)k)2, (3) ω(n+1)k=∫∞0ω|ˆu(n+1)k(ω)|2dω∫∞0|ˆu(n+1)k(ω)|2dω; (4) 4) 更新λ,如式(5)
λ(n+1)=λ(n)+τ(f−∑Kk=1ˆu(n+1)k(ω)), (5) 式中:τ为拉格朗日乘子的更新因子.
5) 给定判定精度ε>0,若满足判定表达式:
∑kk=1‖ˆu(n+1)k−ˆu(n)k‖22/‖ˆu(n)k‖22<ε, (6) 则迭代终止,否则返回流程第2步.
基于以上流程可看出,VMD是在频域内实现不断迭代,最终通过傅里叶逆变换转化到时域. 与EMD相比,VMD有严格的数学模型,其实质是多个自适应维纳滤波组,表现出更好的噪声鲁棒性. VMD可以精确地分解各种谐波,无需考虑谐波之间的相对幅值和各自中心频率的距离.
2. VMD引导的相关峭度谱
根据VMD分解原理,实现算法需要预先确定一个重要参数(K),这是实现VMD自适应分解的关键,K的大小对信号分解有较大影响. K值太小,信号将不能完全分解;K值过大,信号会被过度分解,导致高频模态过多. 对于K值的确定,现有研究通常是基于经验或中心频率观测的方法来确定,以及运用预测测试法、皮尔逊相关系数法、空间尺度法、多指标评价法、粒子群优化算法和灰狼算法等[14]. 这些方法逻辑严密且通常具有较好的自适应性,但在VMD前端增加额外的算法来确定K值,通常都存在初始参数确定依据先验、收敛速度慢和易陷入局部最优等问题. 另外,VMD将信号分解为频率由低到高的一系列固有模态分量(设为VIMF),传统的方法是选取有效分量进行重构从而实现信号降噪,重构的过程相当于在VMD后端增加额外的算法来实现应用. 为有效避免上述两方面问题,结合轮对轴承系统故障特点,一种基于VMD构成相关峭度谱的故障诊断方法被提出,该方法的实现步骤如下:
步骤1 采集轮对轴承系统振动信号,截取适当长度进行后续分析.
步骤2 对分析信号进行VMD分解,其中K的取值为2~N,即对信号进行N−1次分解,得到的VIMF表示为{u(N−1)k(t)},其中,uk=u1,u2,⋯,uK;
步骤3 计算每一个VIMF的相关峭度,得到相关峭度指标的集合{V(N−1)k};
步骤4 为了更直观地观测共振频带,将相关峭度集合根据指标大小铺成一个二维谱图,计算出最大的相关峭度值,并定位到相应的VIMF;
步骤5 对具有最大相关峭度指标的VIMF进行平方包络分析,提取轮对轴承系统的故障特征.
关于上述方法,有3个关键点需要讨论:
1) 分析信号长度. 由于轮对轴承系统高速旋转,特别是高速列车,轮对轴承系统振动信号的采样频率一般为10 kHz,信号长度过长导致计算成本剧增. 另外,考虑列车运行条件下轴箱振动信号始终处于波动状态,根据轮对和轴承故障周期,1 s的数据长度足以提取到故障特征频率及其多次谐波.
2) 分解次数N的确定. 根据VMD算法原理,VMD的性能对K值非常敏感. 本文方法将输入信号分解2~N次,从而避免了K值最优选择问题,这里N应足够大,确保信号能够完全分解,但N值太大,可能造成过度分解,频带太窄有可能丢失故障相关信息. 同时,随着分解次数的增加,计算成本也不可避免地增加. 本文所提方法是在FK方法的框架下提出的,借鉴了FK最大分层数的设置原则,因此,N=[log2N(f)]+1,其中,N(f)为原始信号的数据长度. 由于不涉及FK中分叉树结构,因此,并不建议其他保持比例.
3)相关峭度指标的计算. 如上所述,采集到的列车轴箱振动信号一般包含2个脉冲分量,分别是轮对踏面缺陷和轴承故障激发的周期性脉冲. 因此,故障诊断方法要同时考虑脉冲特性和周期特性. 相关峭度用于指示具有指定周期T的周期脉冲频带. 周期T的第一个移位相关峭度为
V1(T)=∑Ll=1(ylyl−T)2(∑Ll=1y2l)2, (7) 式中:yl为被测信号的复包络,L为被测信号的长度.
为了提高对周期脉冲的敏感性,周期T的第M个移位相关峭度CKM(T)定义为
CKM(T)=∑Ll=1(∏Mm=0yl−mT)2(∑Ll=1y2l)M+1. (8) 随着M的增加,故障周期T会得到更好的估计. 当信号包含多个周期性脉冲时,传统的峭度和包络谱峭度等指标可能失效,而相关峭度指标对人工设定的周期T的重复瞬态具有强表征力,特别适用于轮对轴承系统这类多源振动信号.
3. 仿真信号对比验证
为验证本文所提的VMD引导的相关峭度谱方法在轮对轴承系统故障诊断中的有效性,现构建一轮对轴承振动信号:
y(t)=yb(t)+yw(t)+yr(t)+N(t), (9) 式中:yb(t) 为轴承外圈故障引起的脉冲响应信号,具有故障特征频率fBPFO,如式(10);yw(t)为旋转频率为fr的轮对踏面缺陷所引起的脉冲响应信号,如式(11);yr(t)为随机脉冲响应信号,如式(12);N(t)为具有−5 dB噪声比的高斯白噪声.
yb(t)=∑Nbn=1Abe−βb(t−nTb)cos(2πωb(t−nTb−τb))u(t−nTb−τb), (10) yw(t)=∑Nwn=1Awe−βw(t−nTw)cos(2πωw(t−nTw−τw))u(t−nTw−τw), (11) yr(t)=Are−βrtcosωrt, (12) 式(10)~(12)中:Nb和Nw分别为轴承和轮对的故障脉冲个数;Ab、Aw和Ar分别为轴承、轮对故障和随机冲击响应的振幅;ωb、ωw和ωr为轴承、轮对故障和随机冲击响应的激振;u为阶跃响应函数共振频率;βb、βw和βr为轴承、轮对故障和随机冲击响应的结构阻尼系数;Tb=f−1BPFO和Tw=fr−1分别是轴承和轮对故障周期;τb、τw为采用小范围内的随机数,分别反映了滚子和轮对转动中发生的随机滑移现象.
设置的信号采用频率为10 kHz,信号长度为1 s,详细参数见表1.
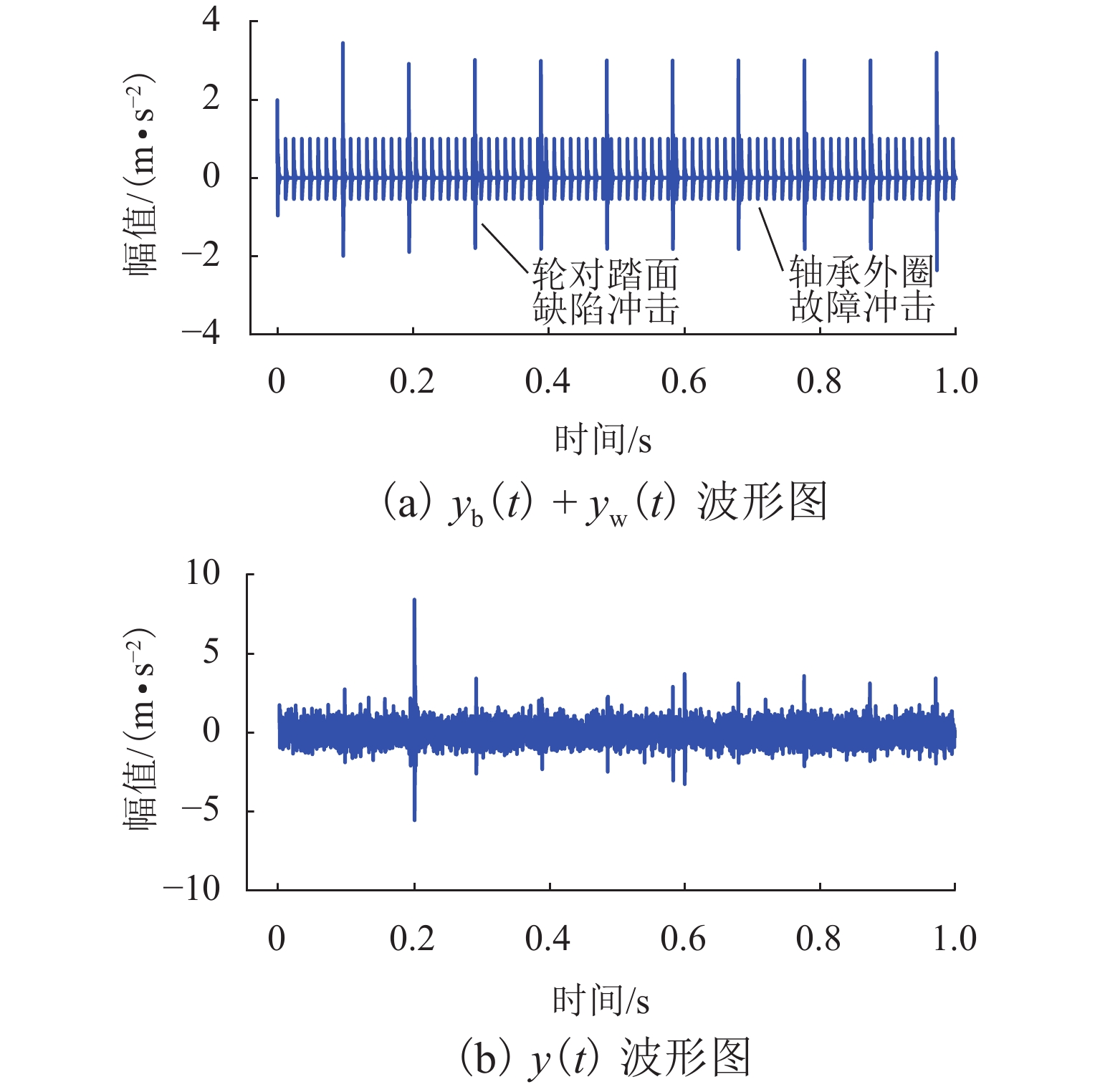
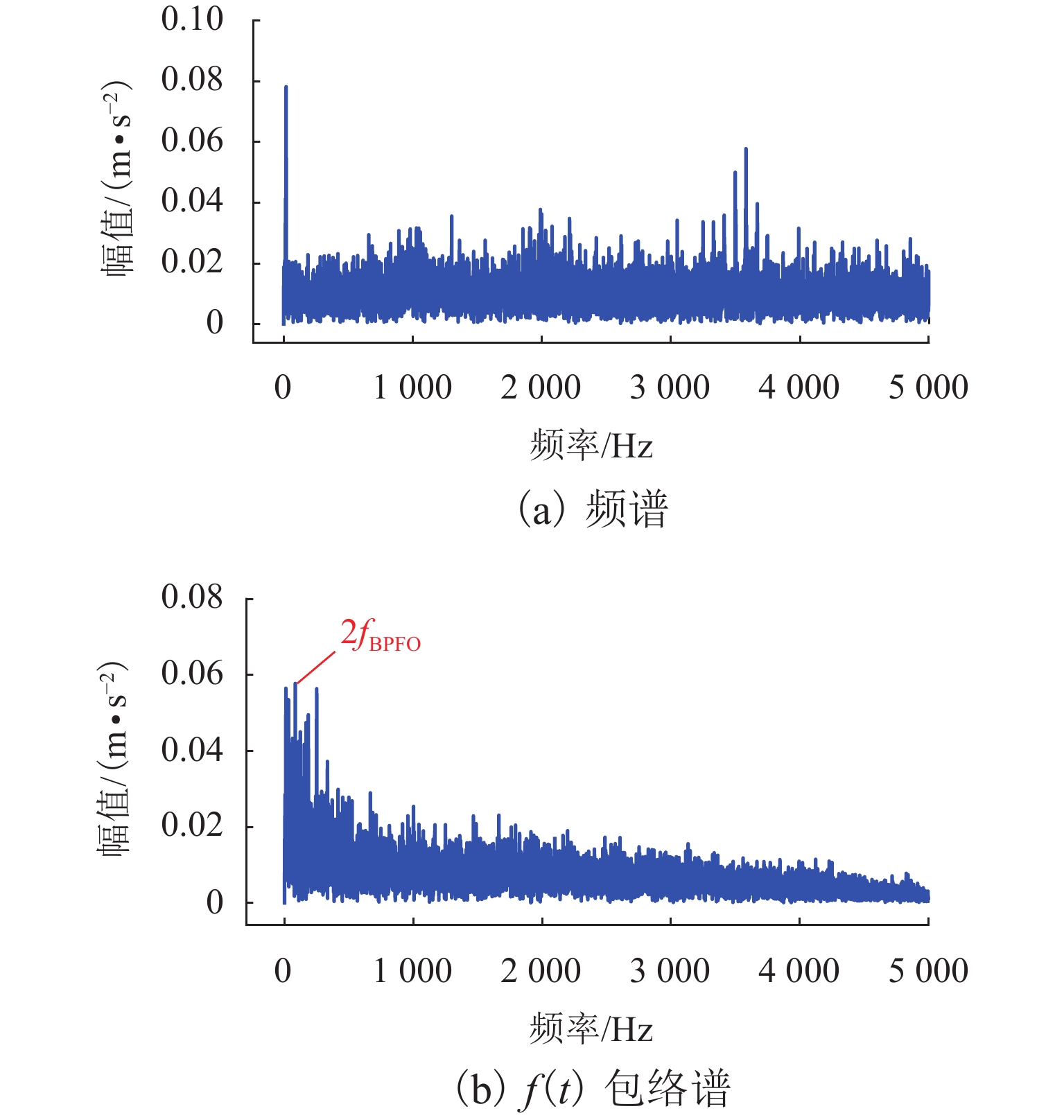
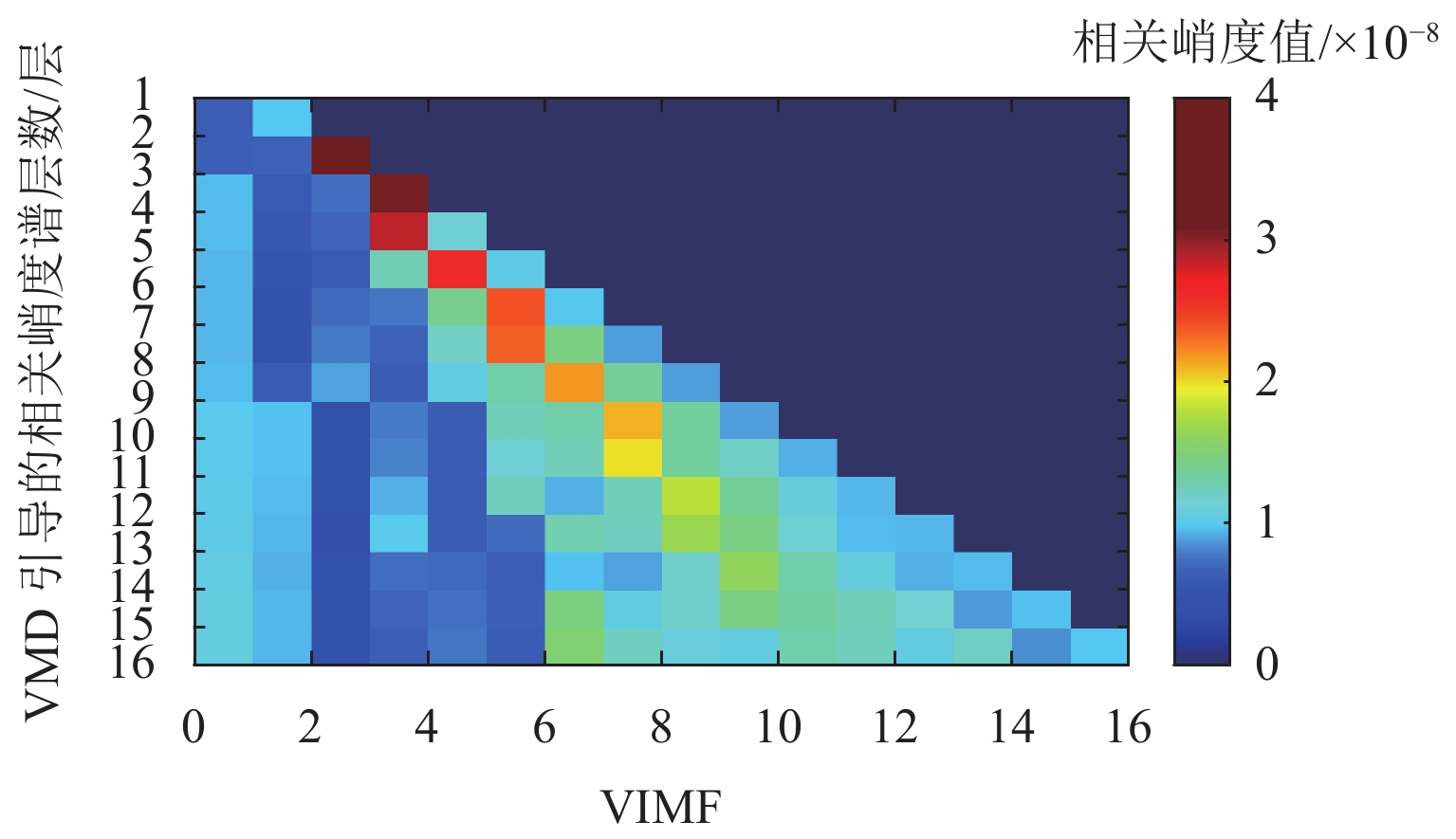
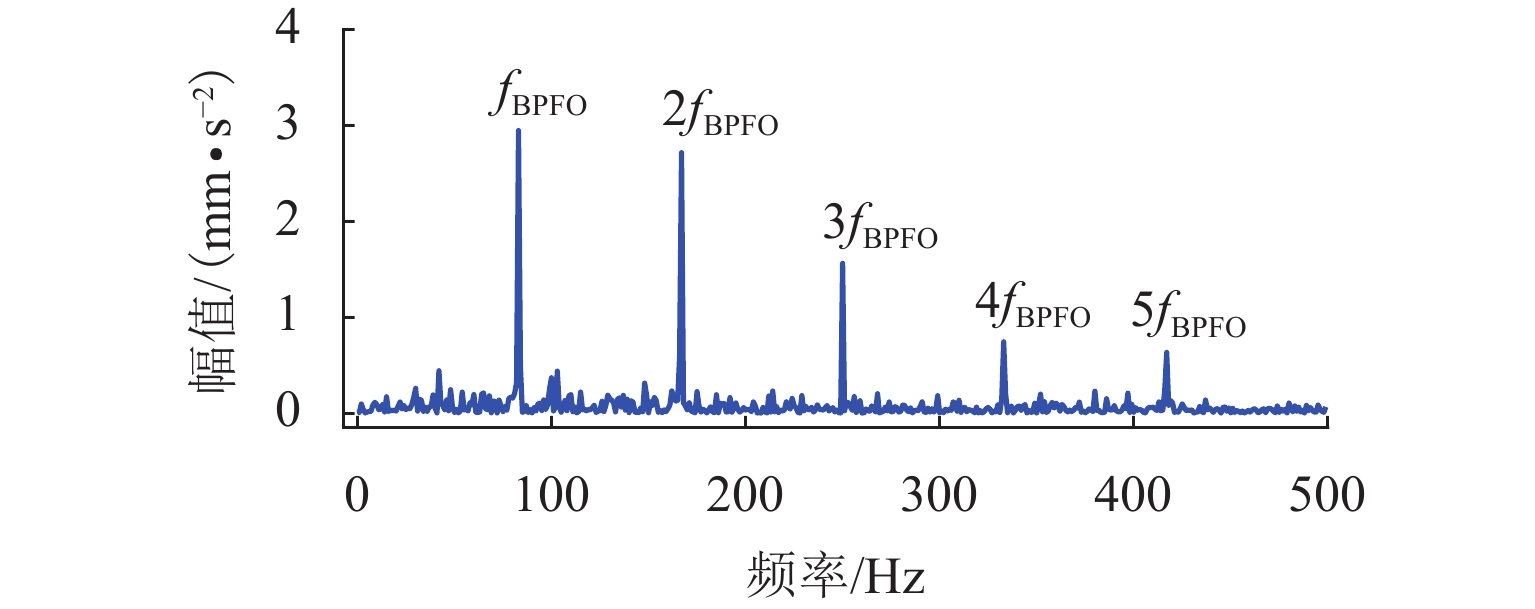
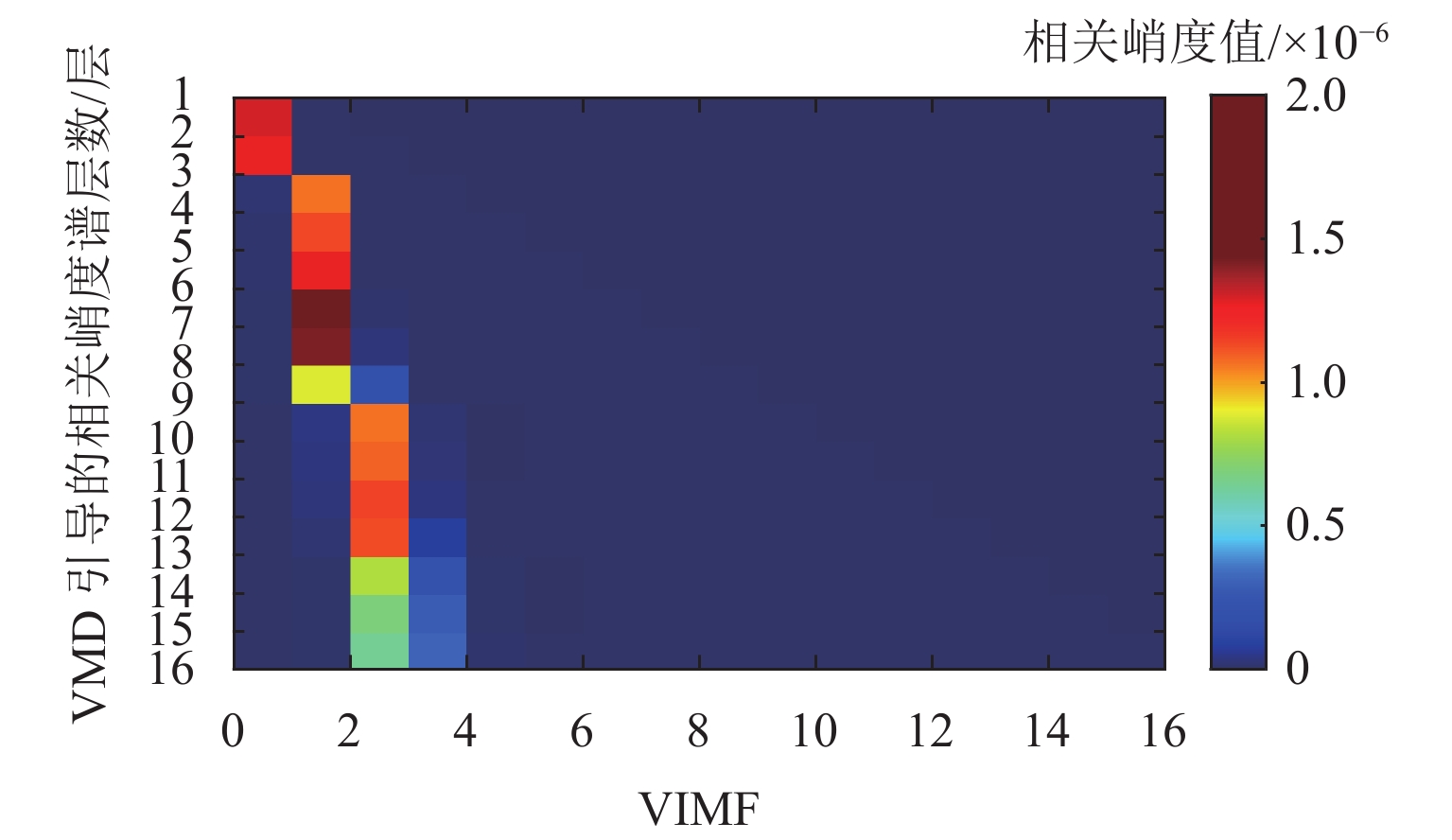
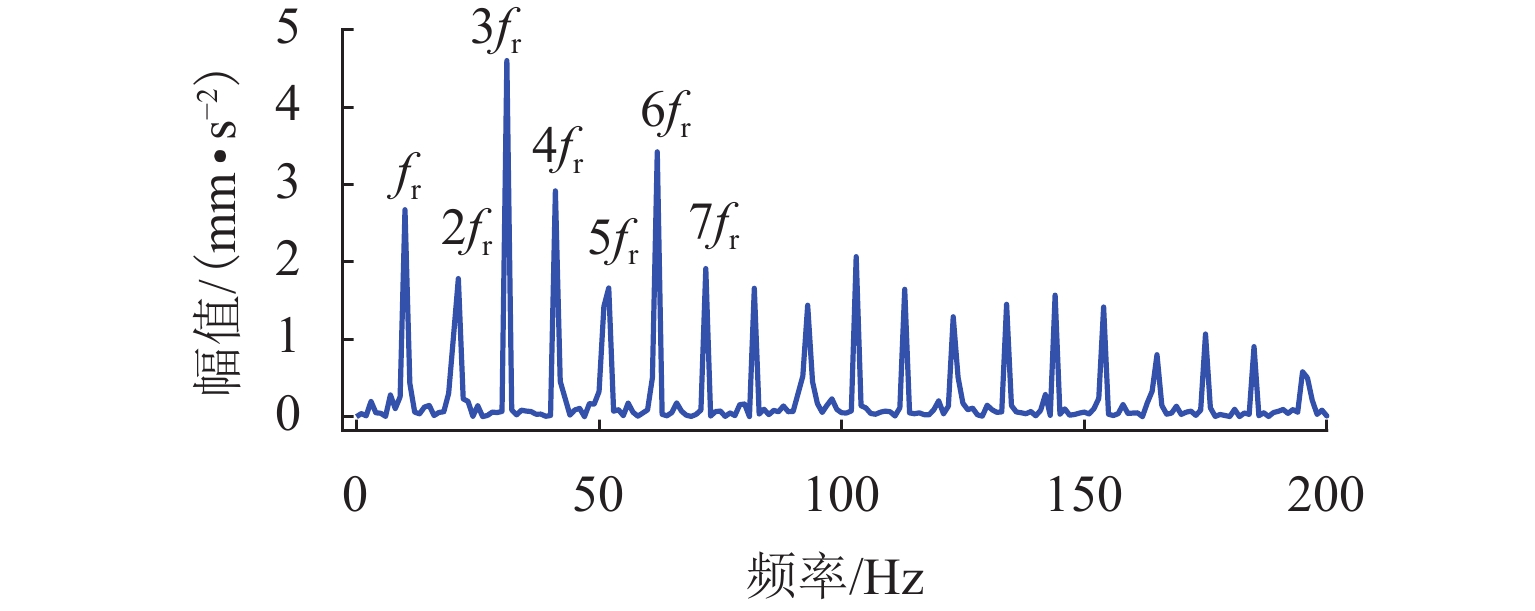
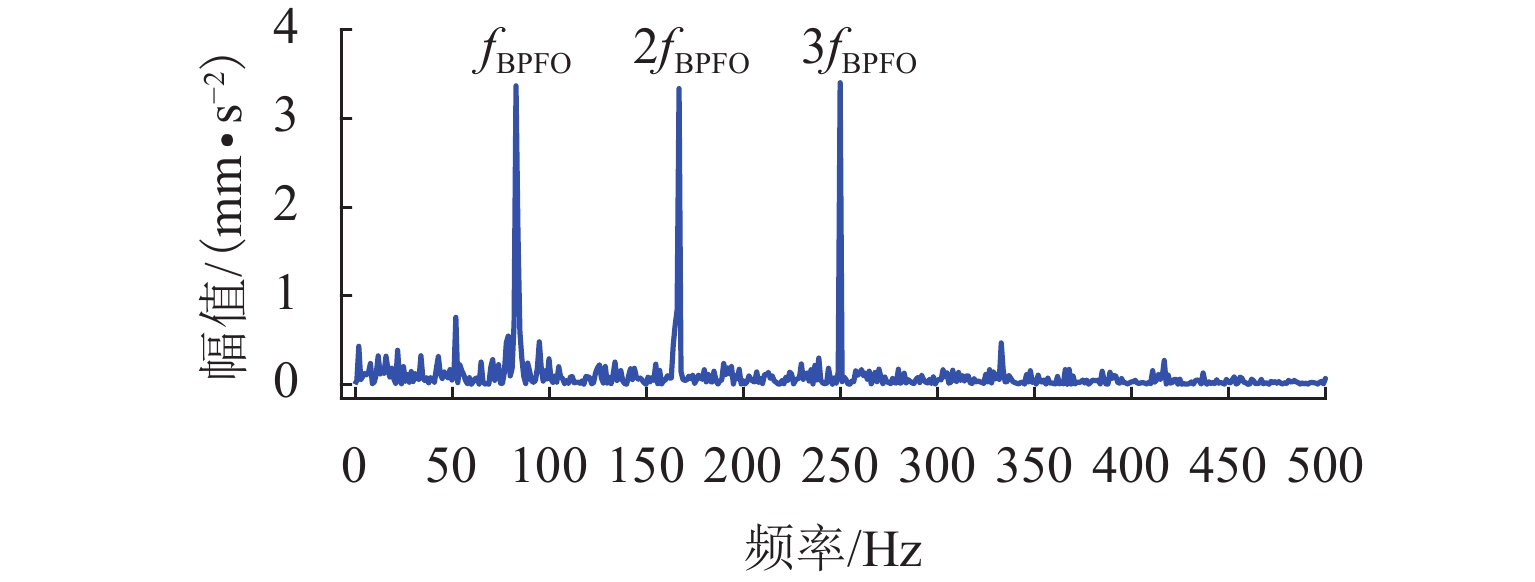
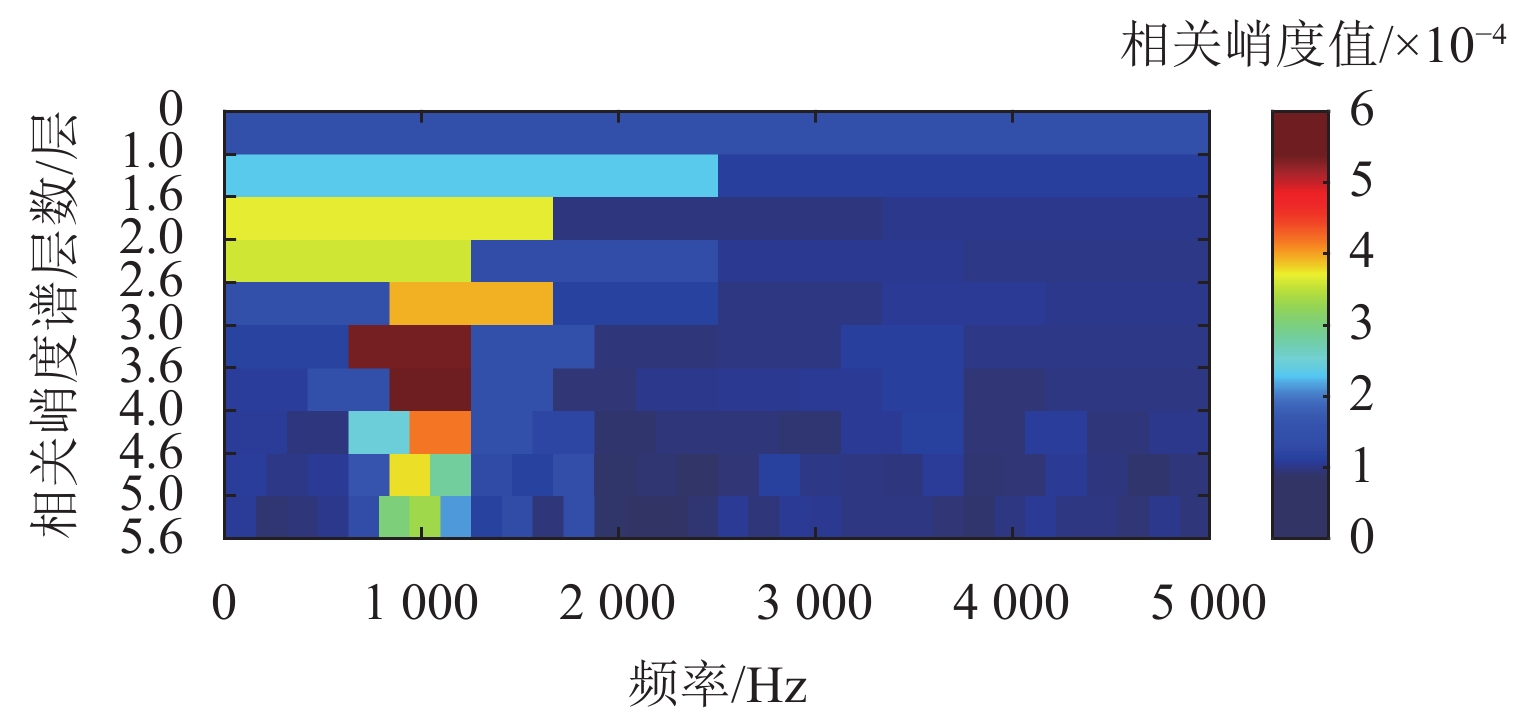
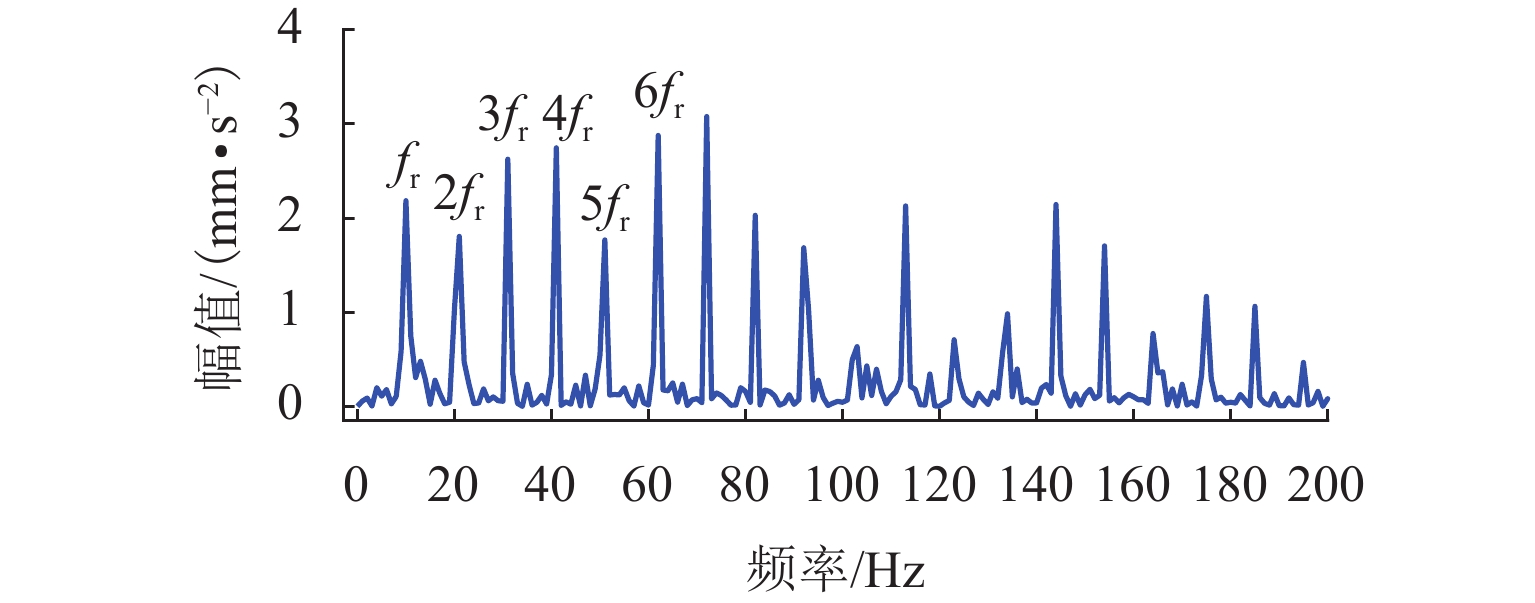
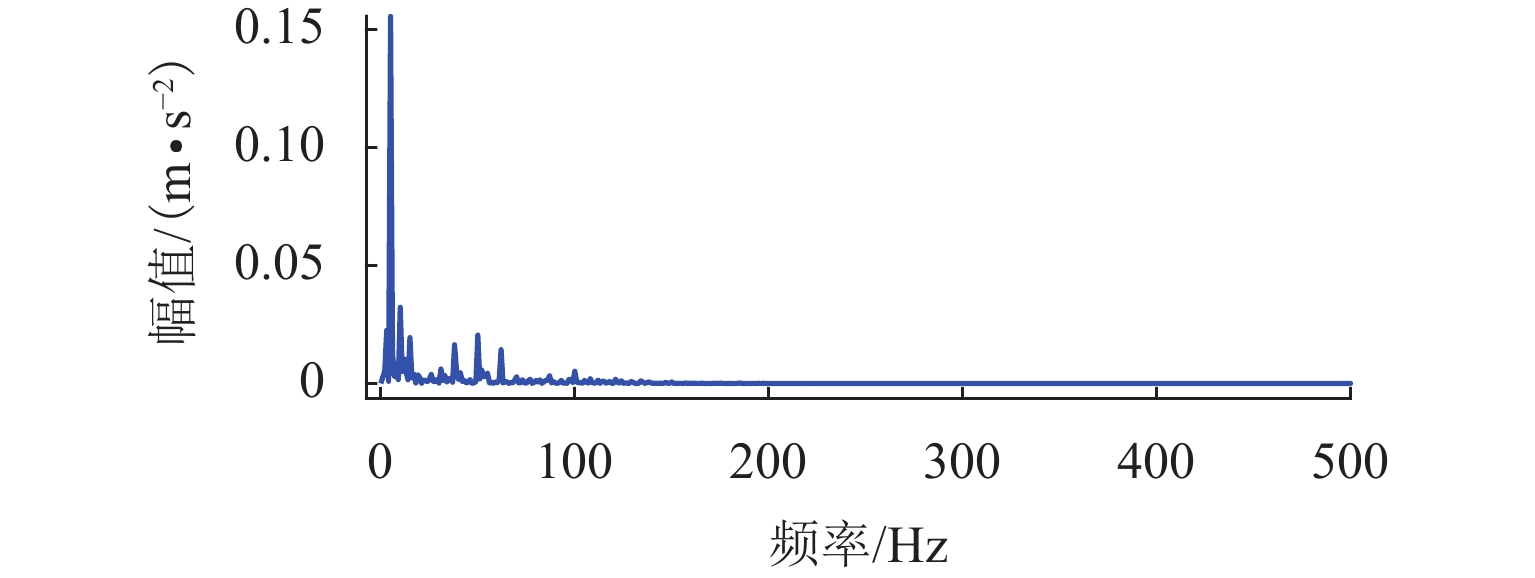
表 1 仿真信号参数设置Table 1. Parameter description of simulation signals类型 振幅 结构阻尼系数 激振 周期 随机系数 轴承 1 1000 3500 1/83.3 0.01Tb 轮对故障 8 2000 1000 1/10.29 0.01Tw 随机冲击响应 10 1000 2000 仿真信号波形如图1所示,其频谱和包络谱如图2所示. 从图2可发现,常规的包络谱中能找到轴承外圈故障的2倍频,其他外圈故障特征频率谐波以及轮对踏面缺陷引起的故障特征频率都淹没在干扰冲击中. 根据最大分层原则,对该振动信号进行13次VMD分解,其中K=2~14. 首先,依据轴承外圈故障的周期,计算每次分解得到的VIMF的相关峭度指标,根据指标大小铺成的谱图如图3所示. 将相关峭度指标最大的VIMF进行平方包络分析,结果如图4所示,外圈故障特征频率及其2倍~5倍频能清晰地被提取出来. 依据轮对踏面缺陷的周期,重新计算每次分解得到的VIMF的相关峭度指标,重复上述步骤,轮对踏面缺陷相关峭度谱如图5所示,相关峭度指标最大的VIMF的平方包络谱如图6所示,图6中,轮对踏面缺陷的冲击频率及其多倍频非常显著.
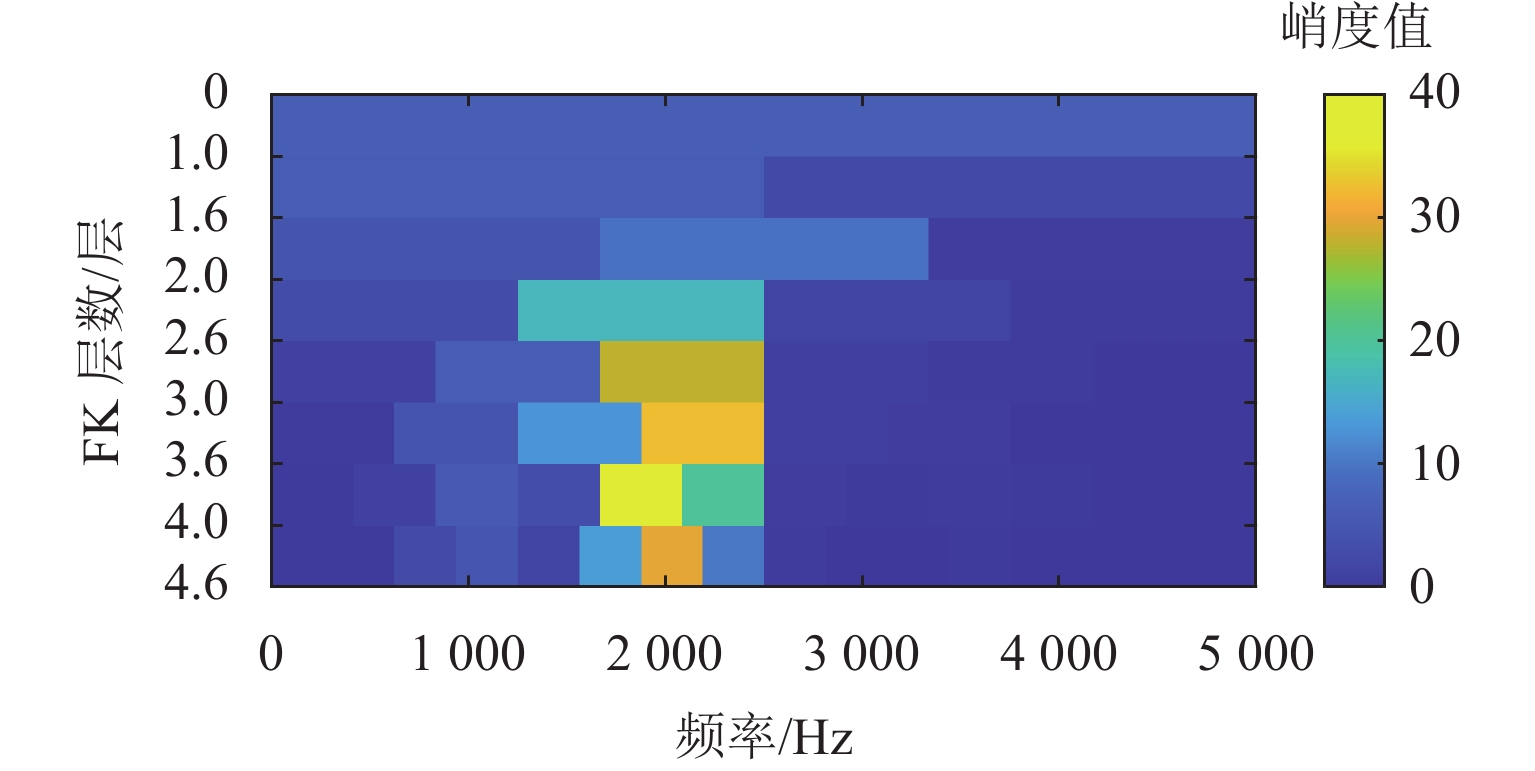
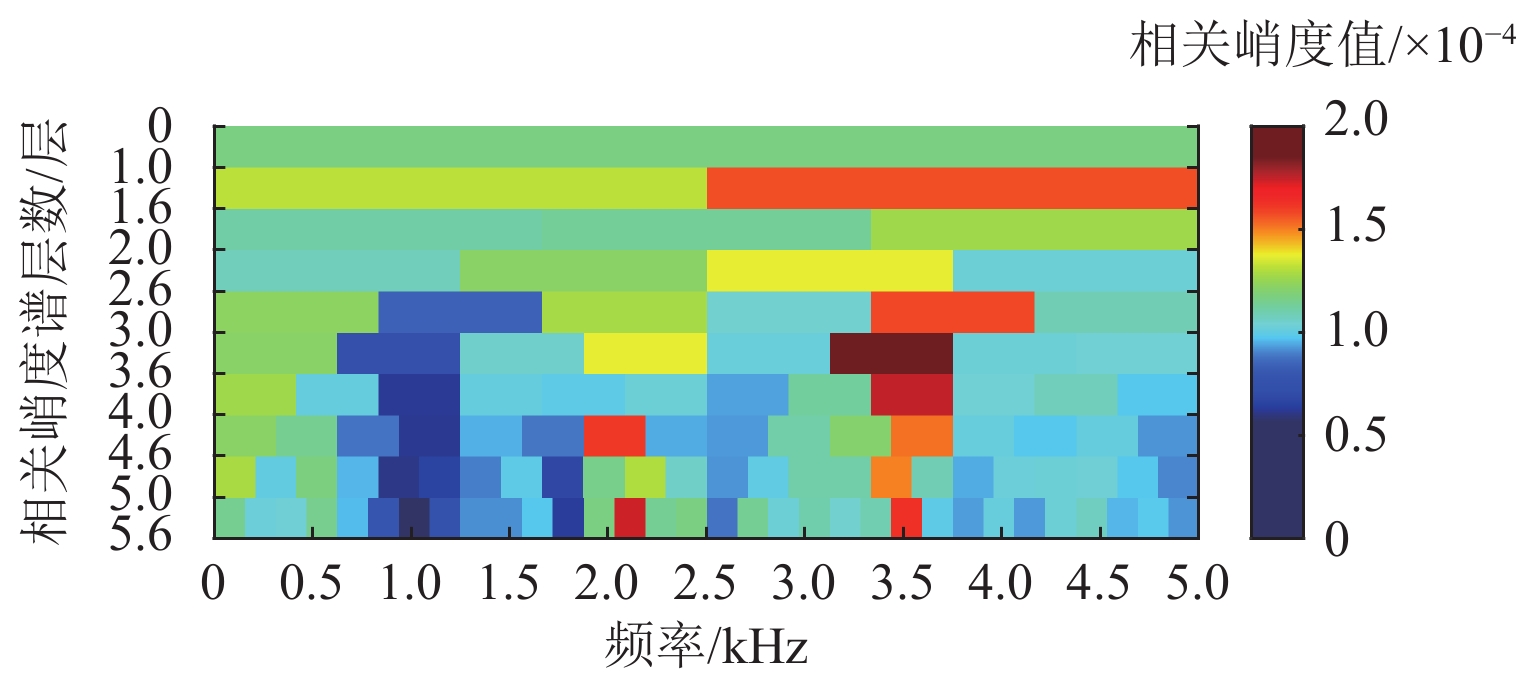
为了验证所提方法的优越性,将上述仿真信号进行快速峭度谱计算,得到的峭度谱如图7所示,将最大峭度的分量信号提取出来进行包络分析,提取信号的平方包络谱如图8所示,图中能有效提取轮对踏面缺陷引起的脉冲响应信号. 但由于受冲击干扰频率的影响,无法获取轮对踏面缺陷冲击的谐波信号以及轴承外圈故障引起的脉冲信号. 在快速谱峭度的框架下,依据轴承外圈故障的周期,计算相关峭度,得到相关峭度谱如图9所示,将轴承外圈故障信号引导下的最大峭度的频带信号提取出来做平方包络分析,结果如图10所示,外圈故障特征频率及其2倍~3倍频能被清晰地提取出来,但和图4相比,VMD引导的相关峭度谱方法能提取到轴承外圈故障1~5阶谐波,且能量逐阶递减,说明VMD引导的相关峭度谱方法提取的轴承外圈故障频带覆盖了更完整的共振频带. 依据轮对踏面缺陷的故障周期信息,计算相关峭度,得到的相关峭度谱及最大峭度频带信号的平方包络分析结果分别如图11、12所示,从图12可看出,对该组仿真信号,相关峭度谱能较好地提取到轮对踏面缺陷故障频率.
4. 试验信号对比验证
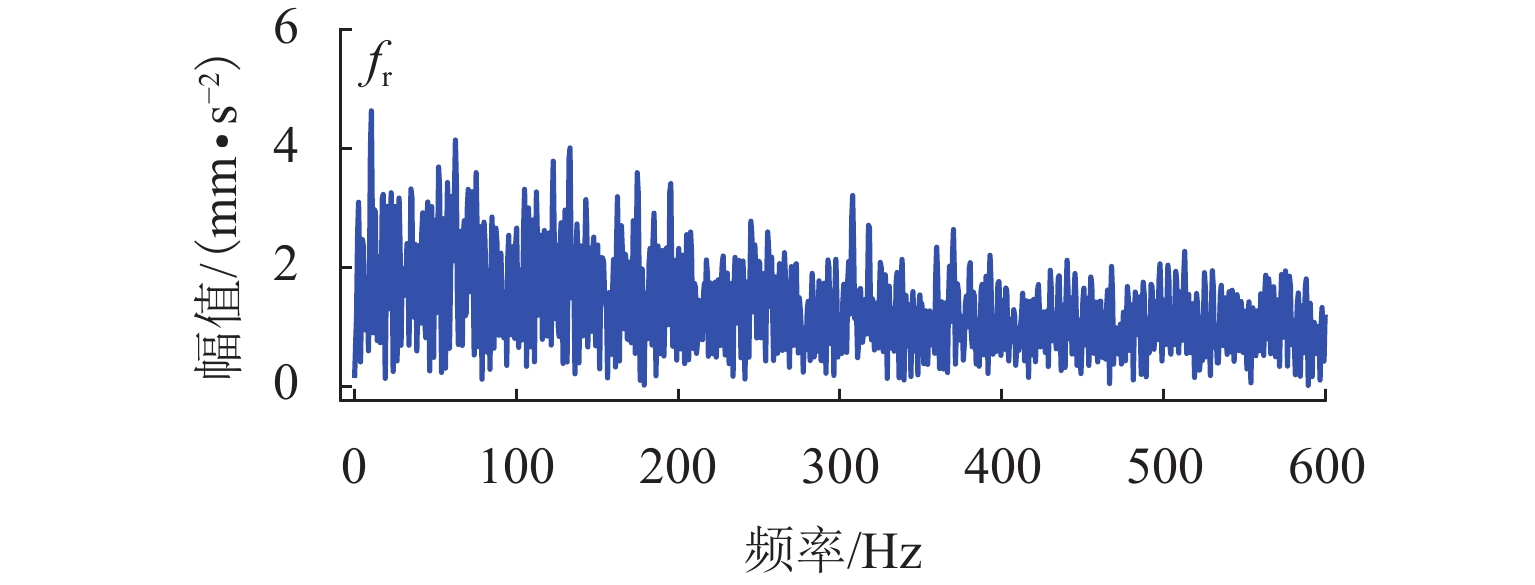
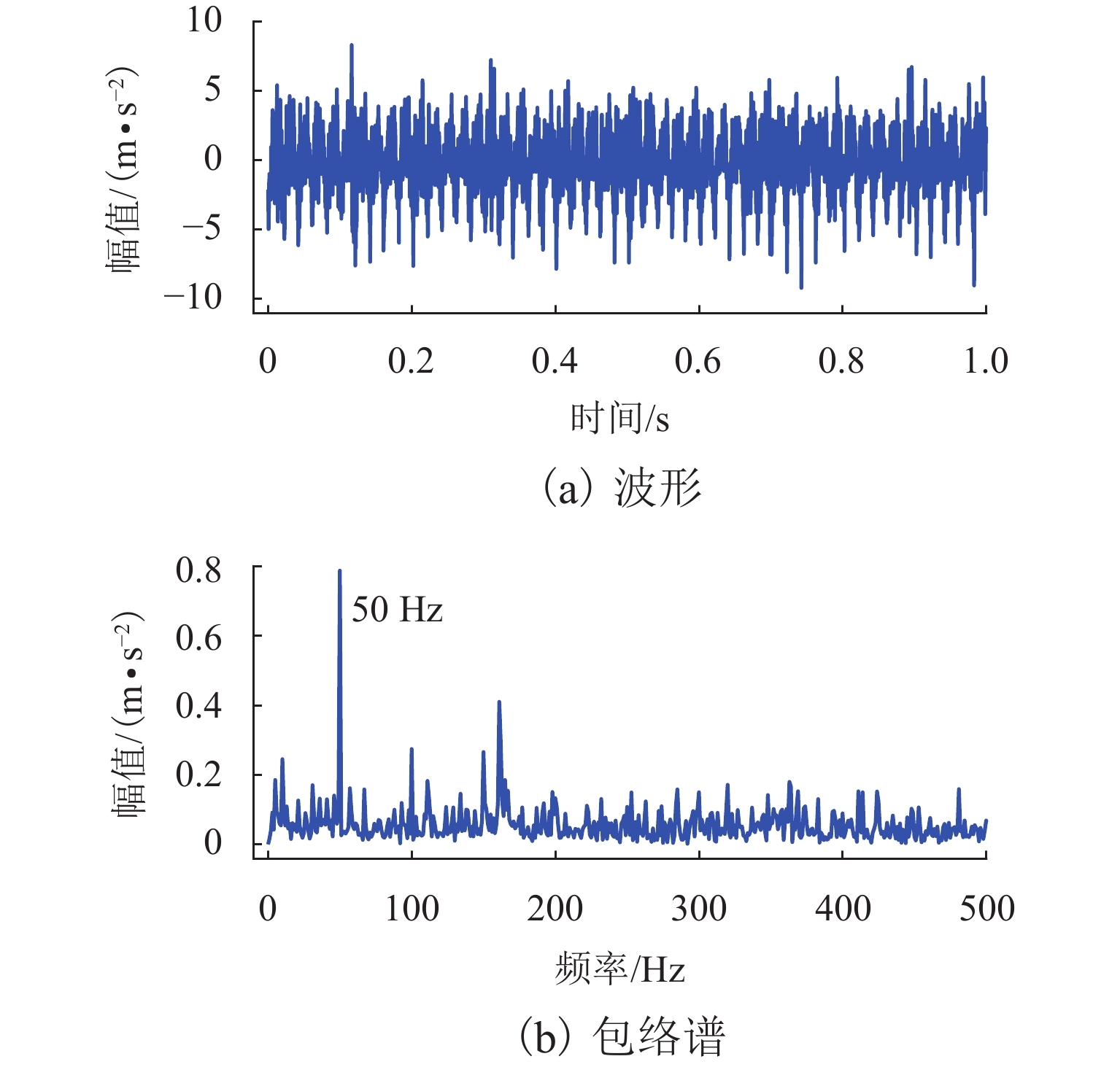
本节采用试验台实测数据对所提方法进行验证. 轮对跑合试验台及加速度传感器安装位置如图13所示. 图中传感器安装位置所在的车轮有轻微踏面损伤,相同位置的轴承存在外圈故障,车轮踏面和轴承外圈损伤如图14所示. 试验速度为50 km/h,其中,车轮转速为2.46 rad/s,轴承转速为147 r/s,相应的fr=5.14 Hz,fBPFO=41.65 Hz. 数据采样频率为10 kHz,截取1 s内的数据进行方法的验证计算. 实测数据的波形图和包络谱如图15所示,从包络谱中可发现,50 Hz的试验台激振频率(驱动轮对跑合试验台正常运转的电机工频)为包络谱的主要频率,轮对踏面缺陷的脉冲响应频率和轴承外圈故障特征频率被淹没在干扰频率中,难以提取.
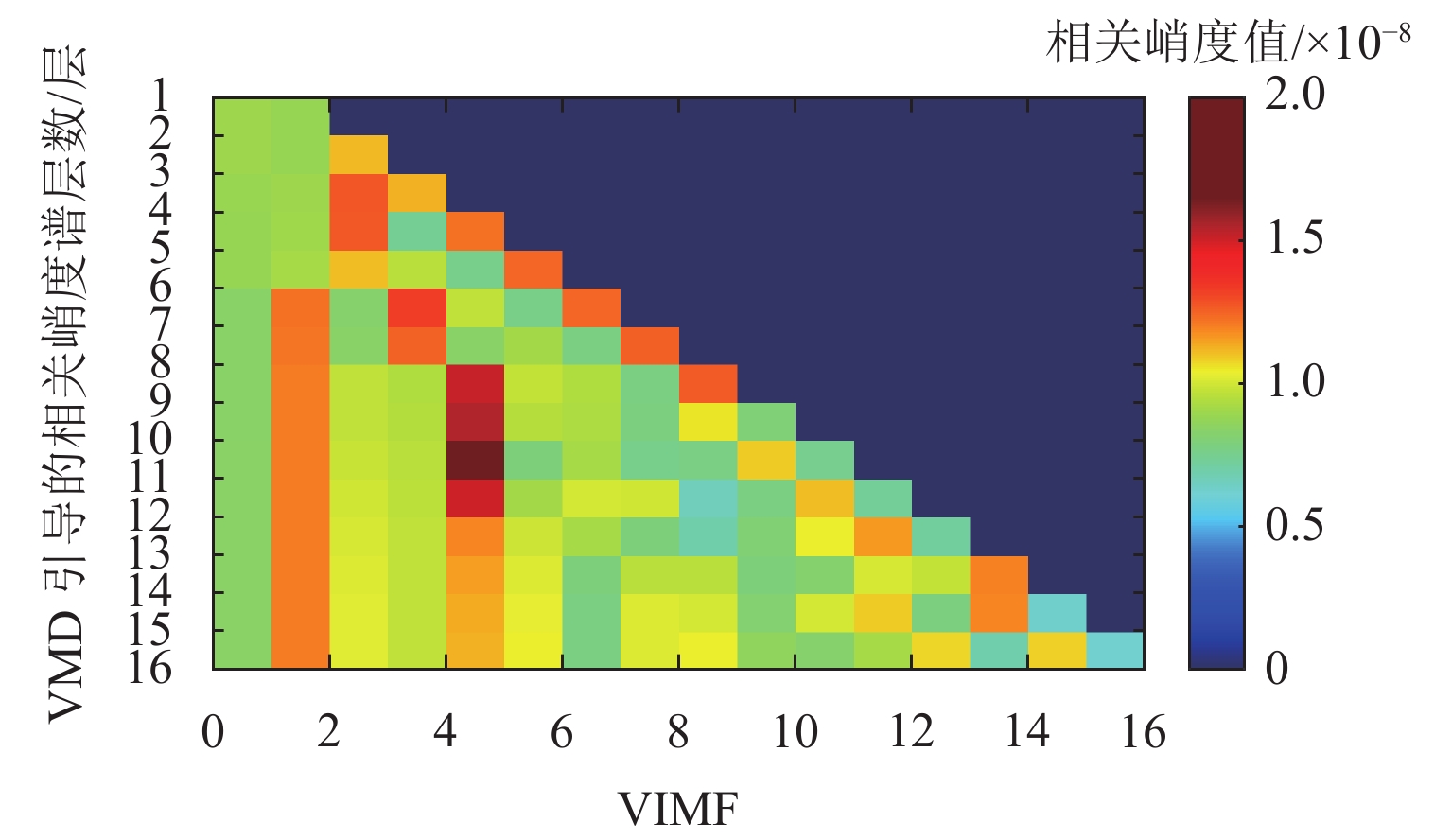
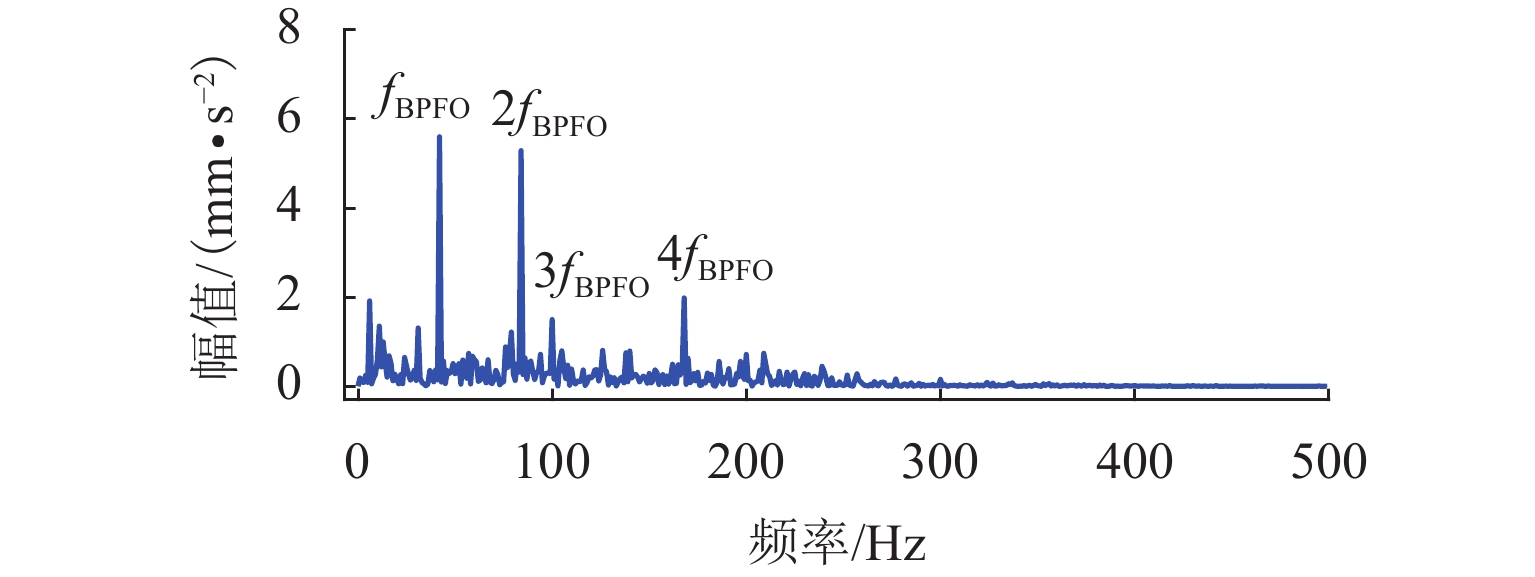
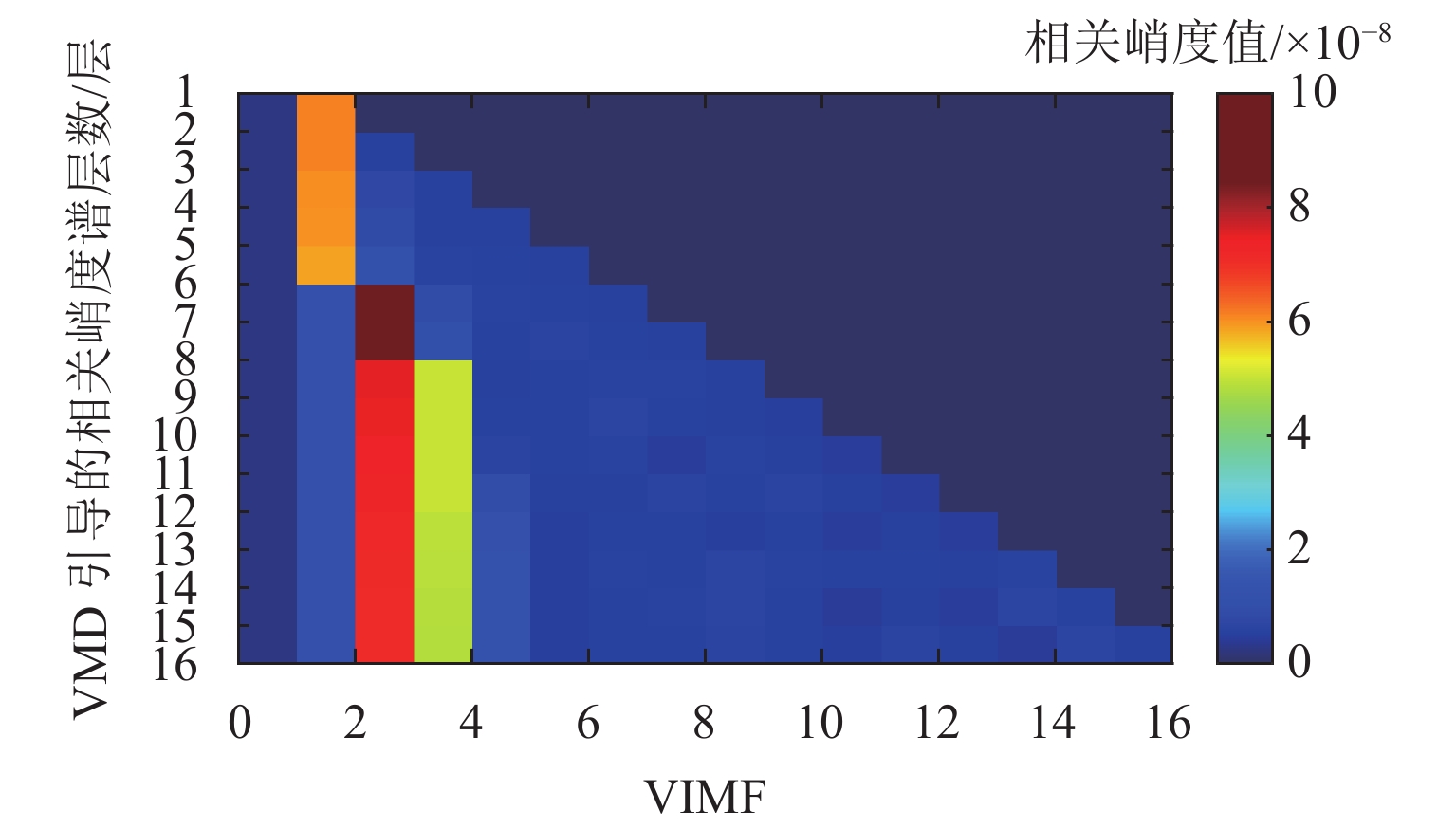
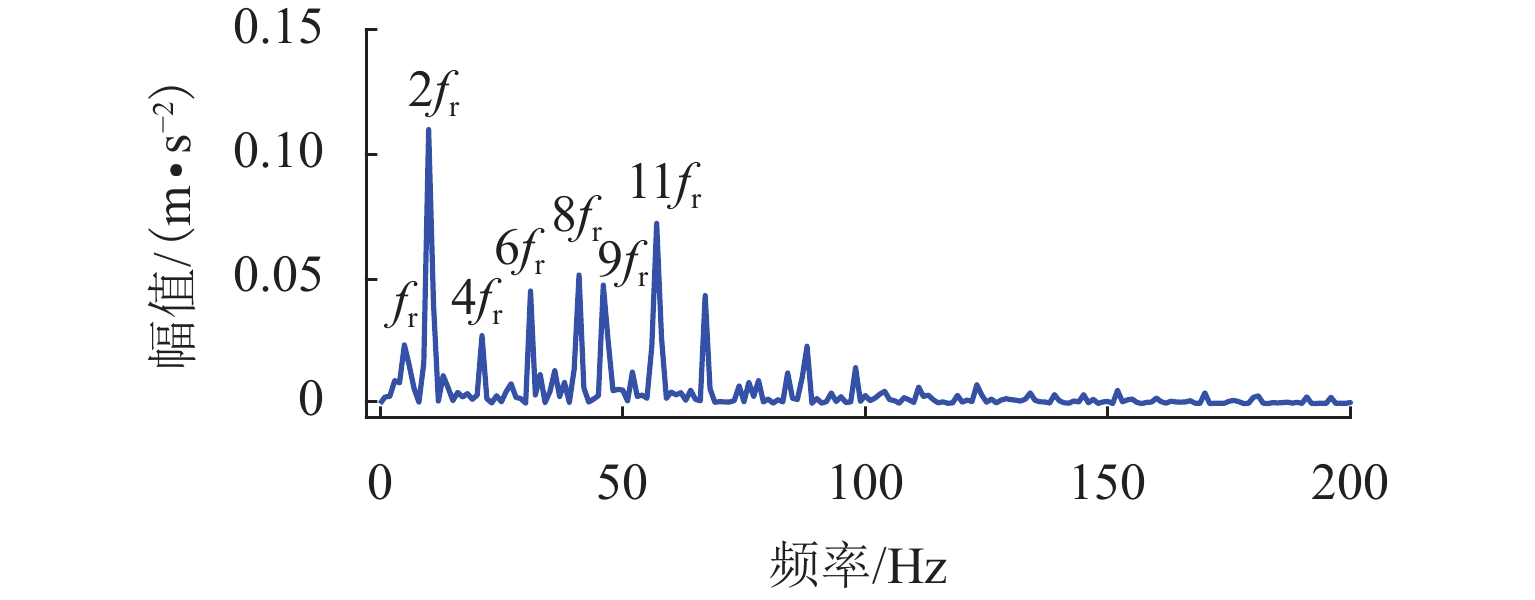
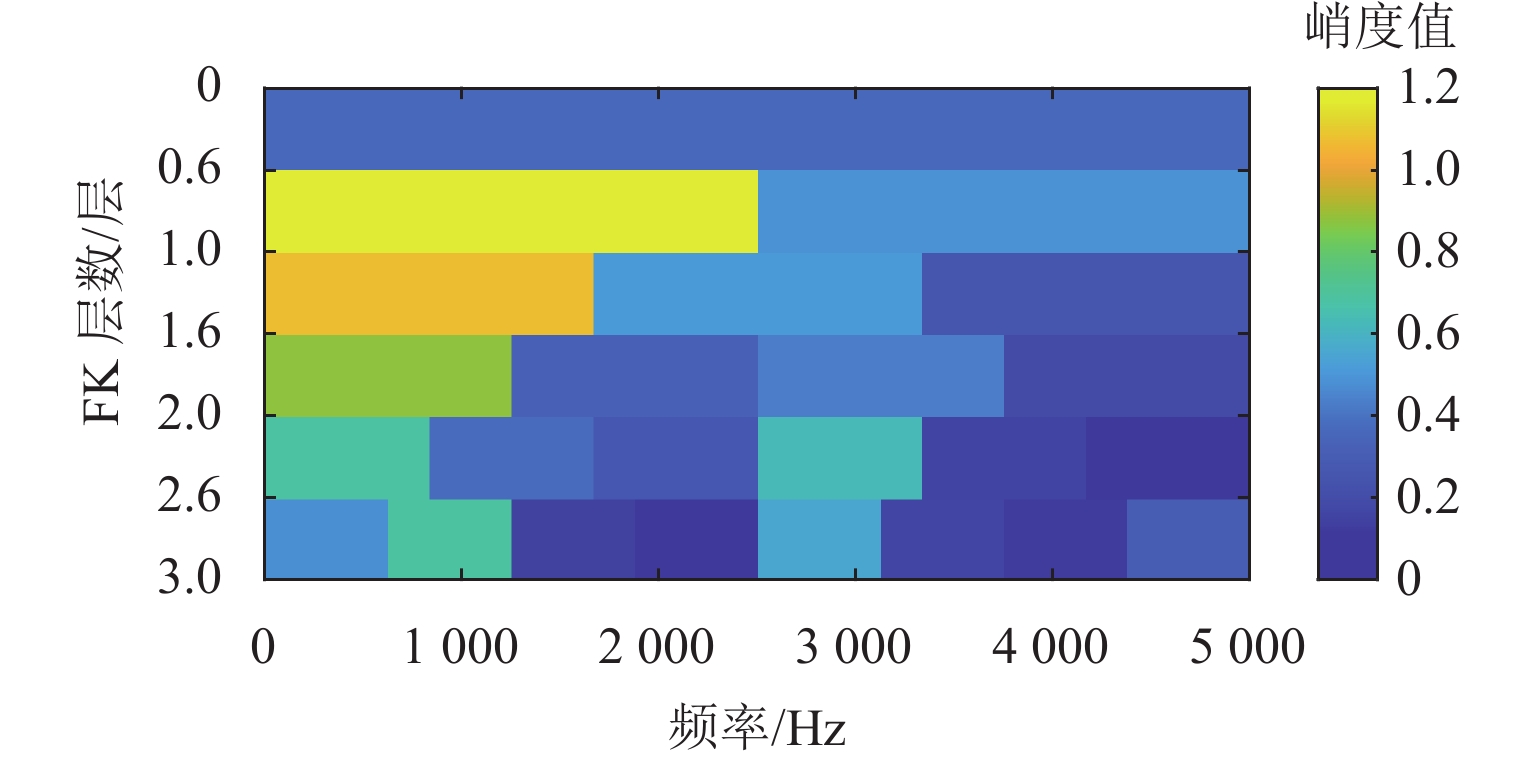
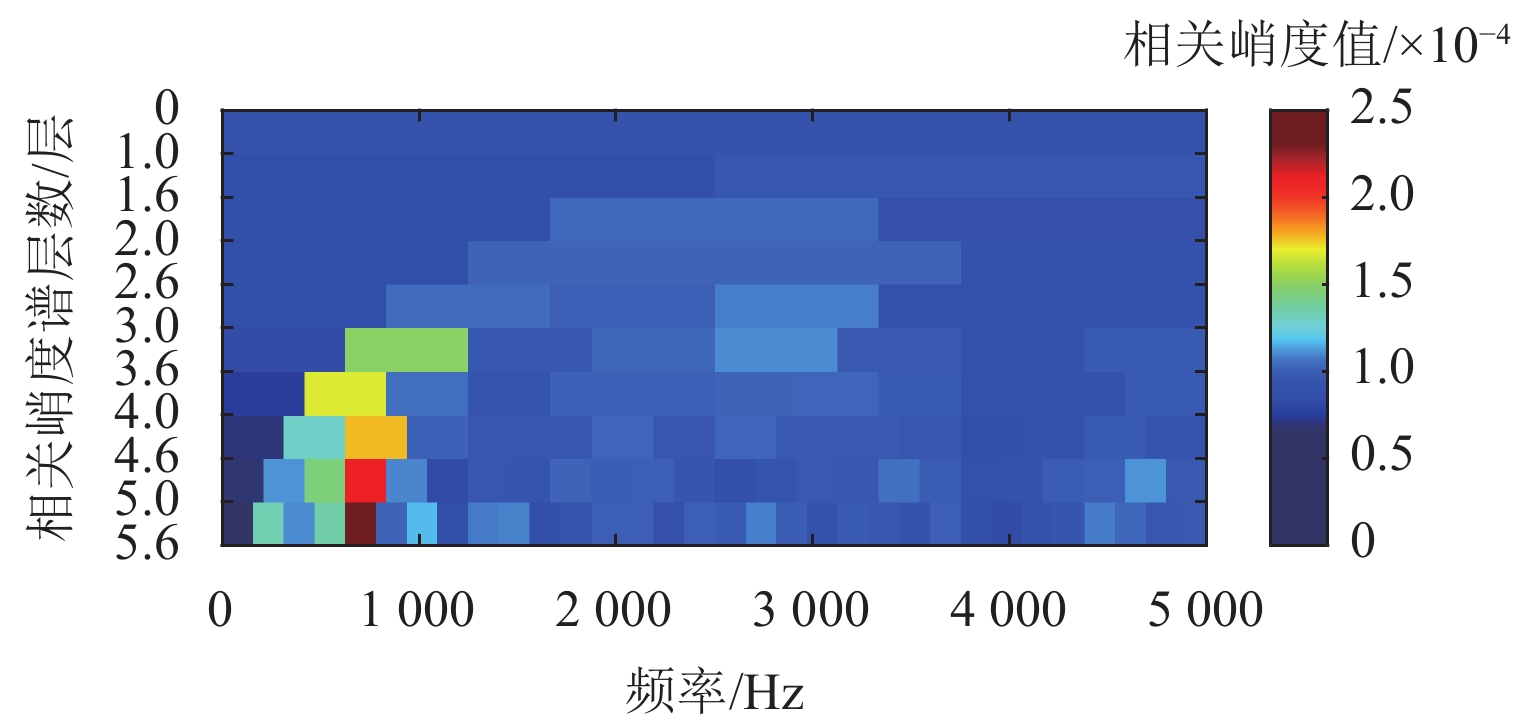
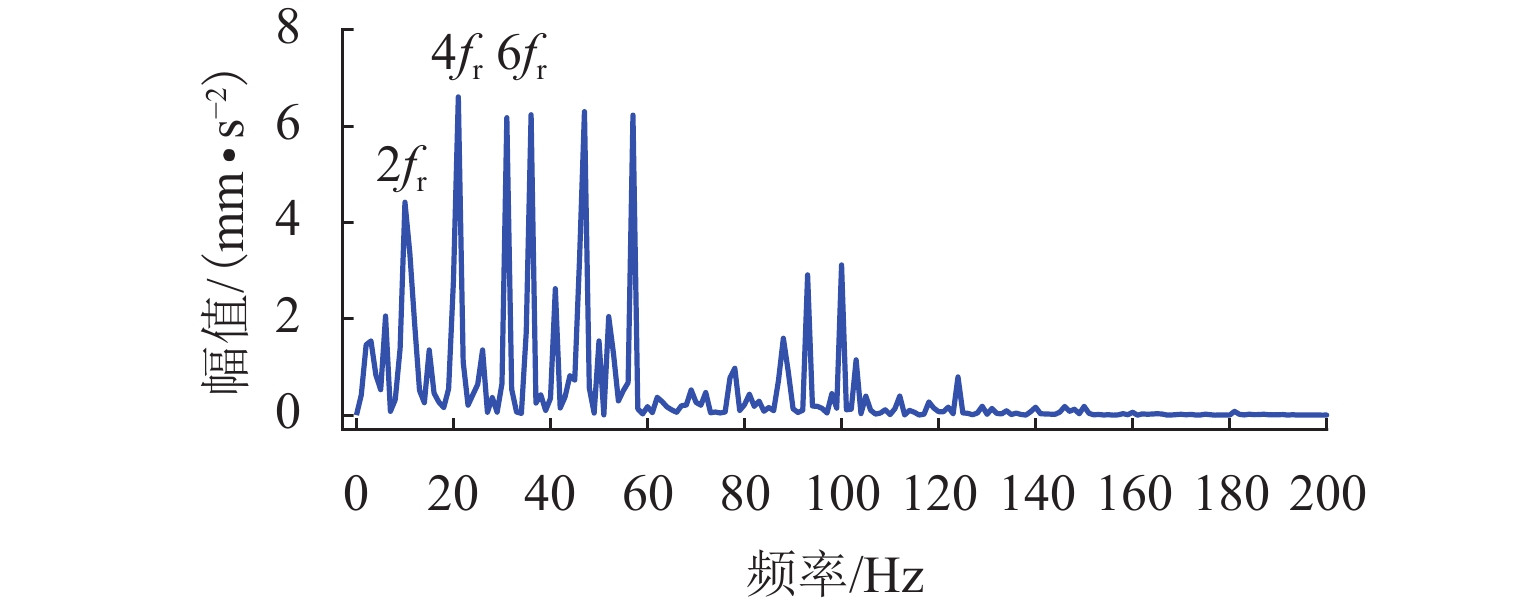
将图15中的试验数据进行VMD分解,根据最大分层原则,对该振动信号同样进行13次VMD分解. 首先依据轴承外圈故障的周期1/fBPFO,计算K=2~14过程中每次分解得到的所有VIMF的相关峭度指标,根据指标大小铺成的谱图如图16所示. 将相关峭度指标最大的VIMF进行平方包络分析,结果如图17所示,外圈故障特征频率及其2倍~4倍频能清晰地被提取出来. 依据轮对踏面缺陷的周期1/fr,重新计算每次分解得到的VIMF的相关峭度指标,重复上述步骤,轮对踏面缺陷相关峭度谱如图18所示,相关峭度指标最大的VIMF的平方包络谱如图19所示,图19中,轮对踏面缺陷的冲击频率及其多倍频非常显著. 可见,本文所提方法能有效诊断轮对和轴承的复合故障.
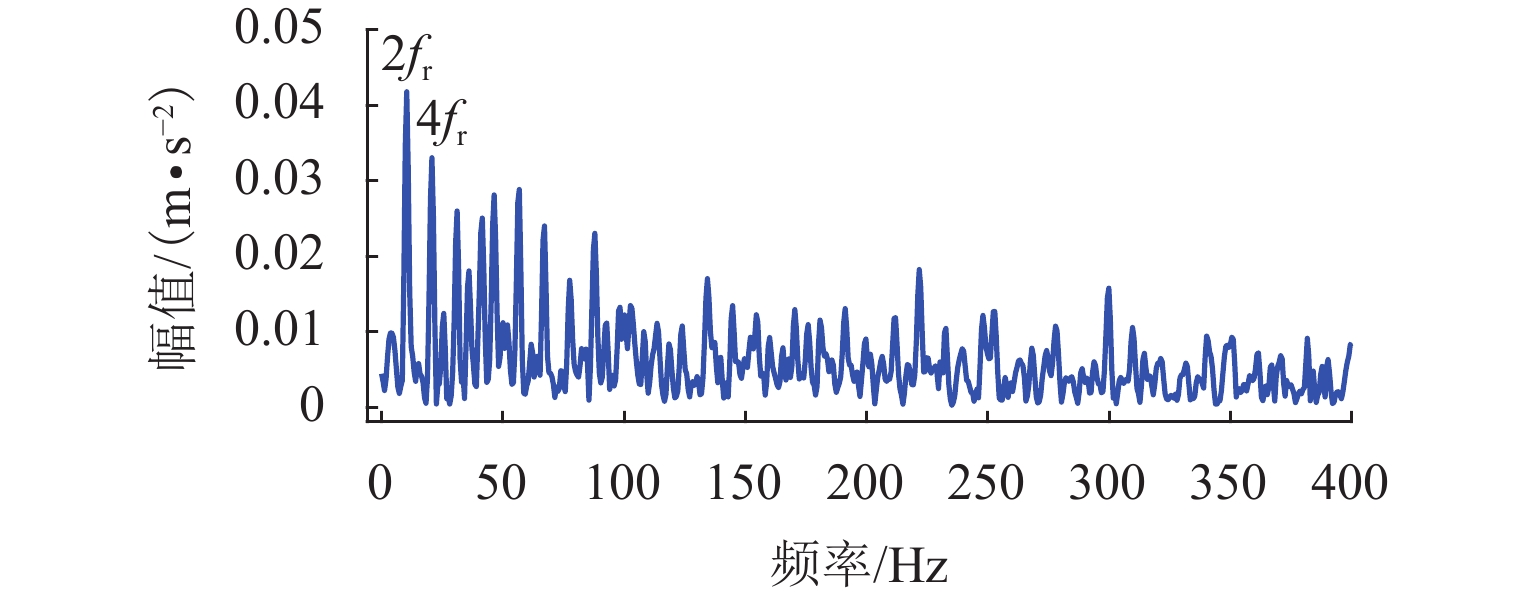
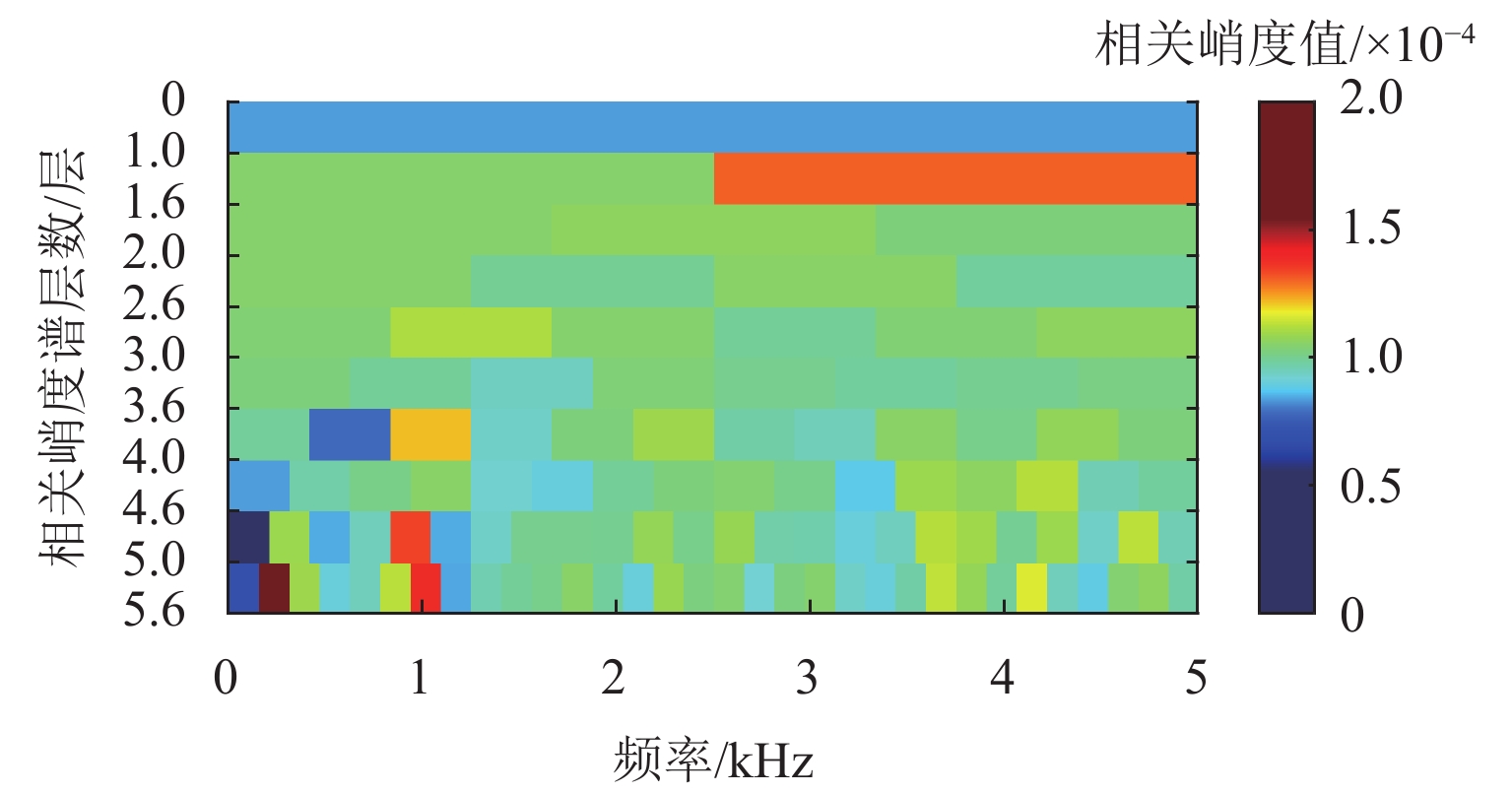
同样,将上述实测故障信号进行快速峭度谱计算,得到的峭度谱如图20所示,将最大峭度的分量信号提取出来进行包络分析,时域信号的包络曲线和傅里叶平方包络谱如图21所示,从平方包络谱中能有效提取轮对踏面缺陷引起的脉冲响应信号,但无法获取轴承外圈故障引起的脉冲信号. 可见,快速谱峭度方法难以实现复合故障的诊断,特别是针对轮对轴承系统,由于轮对踏面缺陷随车轮转动引发脉冲响应,其能量在该系统中占据主导地位,因此,轴承的故障特征频率很容易淹没在轮对踏面缺陷的脉冲响应和强大的背景噪声干扰频率中(图21),在轮对踏面和轴承同时发生故障情况下,轴承故障容易发生漏检. 进一步地,在快速谱峭度的框架下,依据轴承外圈故障的周期计算相关峭度,得到相关峭度谱如图22所示,将轴承外圈故障信号引导下的最大峭度的频带信号提取出来做平方包络分析,结果如图23所示,从图中无法提取到外圈故障特征频率. 依据轮对踏面缺陷的故障周期信息,计算相关峭度,得到的相关峭度谱及最大峭度频带信号的平方包络分析结果分别如图24和图25所示,从图25可看出,相关峭度谱能有效提取到轮对踏面缺陷故障频率. 可见,相关峭度谱由于固定频带划分,难以准确提取到旋转机械故障引起的共振频带,容易造成漏检.
5. 结 论
本文提出了一种基于VMD引导的轮对与轴承复合故障诊断方法,该方法有以下特点:
1) 变分模态分解模型中模态数目K的最优辨识一直是影响该方法理论研究与应用的关键,本文方法规避了参数K的最优选择问题,实现了不依赖先验知识的VMD自适应分解.
2) 相较于峭度指标,相关峭度能准确、有效地提取复杂机电系统中的复合故障特征,不会造成故障漏检.
3) 基于VMD引导建立相关峭度谱,实际上是一个提取共振频带的过程,结果表明,该方法具有良好的噪声鲁棒性.
致谢:西南交通大学牵引动力国家重点实验室自主课题(2020TPL-T14)对本文试验的资助.
-
表 1 仿真信号参数设置
Table 1. Parameter description of simulation signals
类型 振幅 结构阻尼系数 激振 周期 随机系数 轴承 1 1000 3500 1/83.3 0.01Tb 轮对故障 8 2000 1000 1/10.29 0.01Tw 随机冲击响应 10 1000 2000 -
[1] 刘志亮,潘登,左明健,等. 轨道车辆故障诊断研究进展[J]. 机械工程学报,2016,52(14): 134-146. doi: 10.3901/JME.2016.14.134LIU Zhiliang, PAN Deng, ZUO Mingjian, et al. A review on fault diagnosis for rail vehicles[J]. Journal of Mechanical Engineering, 2016, 52(14): 134-146. doi: 10.3901/JME.2016.14.134 [2] 赵聪聪,刘玉梅,赵颖慧,等. 基于物元-阴性选择算法的轴箱轴承故障检测[J]. 西南交通大学学报,2021,56(5): 973-980.ZHAO Congcong, LIU Yumei, ZHAO Yinghui, et al. Fault detection of axle box bearing based on matter-element and negative selection algorithm[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 973-980. [3] 刘国云,曾京,罗仁,等. 轴箱轴承缺陷状态下的高速车辆振动特性分析[J]. 振动与冲击,2016,35(9): 37-42,51. doi: 10.13465/j.cnki.jvs.2016.09.007LIU Guoyun, ZENG Jing, LUO Ren, et al. Vibration performance of high-speed vehicles with axle box bearing defects[J]. Journal of Vibration and Shock, 2016, 35(9): 37-42,51. doi: 10.13465/j.cnki.jvs.2016.09.007 [4] LIU Z C, YANG S P, LIU Y Q, et al. Adaptive correlated Kurtogram and its applications in wheelset-bearing system fault diagnosis[J]. Mechanical Systems and Signal Processing, 2021, 154: 107511.1-107511.21. [5] XING Z, YI C, LIN J H, et al. Multi-component fault diagnosis of wheelset-bearing using shift-invariant impulsive dictionary matching pursuit and sparrow search algorithm[J]. Measurement, 2021, 178: 109375.1-109375.17. [6] WANG D, ZHAO Y, YI C, et al. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2018, 101: 292-308. doi: 10.1016/j.ymssp.2017.08.038 [7] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. doi: 10.1109/TSP.2013.2288675 [8] 黄衍,林建辉,刘泽潮,等. 基于自适应VMD的高速列车轴箱轴承故障诊断[J]. 振动与冲击,2021,40(3): 240-245. doi: 10.13465/j.cnki.jvs.2021.03.032HUANG Yan, LIN Jianhui, LIU Zechao, et al. Fault diagnosis of axle box bearing of high-speed train based on adaptive VMD[J]. Journal of Vibration and Shock, 2021, 40(3): 240-245. doi: 10.13465/j.cnki.jvs.2021.03.032 [9] YI C, LI Y Q, HUO X M, et al. A promising new tool for fault diagnosis of railway wheelset bearings: SSO-based Kurtogram[J]. ISA Transactions, 2021, 128: 498-512. [10] MIAO Y H, ZHAO M, LIN J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification[J]. Measurement Science and Technology, 2017, 28(12): 125001.1-125001.14. [11] BOZCHALOOI I S, LIANG M. A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection[J]. Journal of Sound and Vibration, 2007, 308(1/2): 246-267. [12] WANG D. Spectral L2/L1 norm: a new perspective for spectral kurtosis for characterizing non-stationary signals[J]. Mechanical Systems and Signal Processing, 2018, 104: 290-293. doi: 10.1016/j.ymssp.2017.11.013 [13] MCDONALD G L, ZHAO Q, ZUO M J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing, 2012, 33: 237-255. doi: 10.1016/j.ymssp.2012.06.010 [14] 夏茂森,江玲玲. 变分模态分解模型中关键参数K的辨识研究: 基于加权最大信息系数法[J]. 统计与信息论坛,2021,36(2): 23-35.XIA Maosen, JIANG Lingling. Research on identification of key parameter K in variational mode decomposition model: based on weighted maximum information coefficient method[J]. Journal of Statistics and Information, 2021, 36(2): 23-35. 期刊类型引用(1)
1. 刘文朋,杨绍普,刘永强,顾晓辉,王久健. 轮轨激励下高速列车轴箱轴承故障诊断方法研究. 机械工程学报. 2025(06): 249-259 .  百度学术
百度学术其他类型引用(3)
-





 下载:
下载:


























 下载:
下载:
























 百度学术
百度学术