Geometric Contour of Slip Surfaces and Loosening Earth Pressure in Sand Under Soil-Arching Effect
-
摘要:
土拱效应本质上是由于土体内部松动引起的应力转移现象，土体松动过程伴随着滑移面的形成和延展，但目前针对滑移面几何轮廓、松动影响范围以及考虑松动区动态演变对松动土压力的影响等方面的研究尤待深入. 利用Trapdoor试验对砂土拱效应滑移面轮廓及演变开展研究，获得滑移面几何轮廓及其演变模式在不同填土高度、活动门下移和宽度以及砂料密度下的表征区别. 通过界定滑移面影响范围内松动核心区域，提出基于核心区几何形状的松动应力计算方法. 分析松动应力-活动门下移曲线特征，以揭示最大、最小拱状态条件下的曲线特征随填土高度、活动门下移和宽度以及砂密度的变化规律. 研究结果表明：1） 滑移面轮廓随活动门下移的演化过程为三角形—子弹头形—椭圆形，填土高度越高，活动门宽度越小，初始和次级滑移面轮廓越尖锐；2） 初始、次级滑移面高度随活动门下移递增，第Ⅲ级滑移面拐点高度随活动门下移递减， 初始、次级滑移面夹角随活动门下移先增后减，第Ⅲ级滑移面上半夹角与下半夹角均随活动门下移递增；3） 随着填土高度的增加，松动核心区形状演化过程为三角形—梯形—矩形，核心区高度为填土高度的0.5倍～0.8倍，核心区夹角与核心区面积均随内摩擦角的增加近似线性递减；4） 基于核心区面积的松动应力计算方法相比，Terzaghi等方法更具适用性，且其适用于计算低填土试验组的临界应力和高填土试验组的极限应力. 研究成果为更精确地描述砂土松动区的位移破坏模式及其界定标准以及松动区稳定性评价提供参考.
-
关键词:
- 土拱效应 /
- Trapdoor试验 /
- 滑移面轮廓 /
- 松动区 /
- 松动土压力
Abstract:The soil-arching effect, in essence, is a stress transfer phenomenon triggered by the loosening of the internal structure of the soil. The loosening process is accompanied by the formation and expansion of slip surfaces. At present, research on the geometric contour of slip surfaces, loosening-affected areas, and influence of the dynamic evolution of loosening zones on the loosening earth pressure remains sparse. Therefore, Trapdoor tests were conducted to investigate the contour of slip surfaces and their evolution in sand under the soil-arching effect. In this way, differences in the characterization of the geometric contour of slip surfaces and their evolution modes under different filling heights, downward movements and widths of trapdoors, and sand densities were obtained. By defining a core loosening zone in the area affected by slip surfaces, a calculation method for the loosening stress based on the geometric contour of the core loosening zone was proposed. In addition, the curve characteristics of the loosening stress and downward movement of the trapdoor were analyzed to reveal the changes in curve characteristics with the filling height, downward movement and width of the trapdoor, and sand density under maximum and minimum arch states. The research results show that: 1) the contour of slip surfaces evolves from a triangle, to a bullet shape, and finally to an ellipse with the downward movement of the trapdoor. As the filling height gets greater, and the trapdoor becomes narrower, the contour of primary and secondary slip surfaces is sharper. 2) with the downward movement of the trapdoor, the height of the primary and secondary slip surfaces increases, while that of inflection points of the level-Ⅲ slip surface decreases. In addition, as the trapdoor moves downward, the angles of the primary and secondary slip surfaces both increase first and then decrease, while the upper and lower half-angles of the level-Ⅲ slip surface both increase. 3) the contour of the core loosening zone changes from a triangle, to a trapezoid, and finally to a rectangle with increasing filling height. The height of the core loosening zone is 0.5–0.8 times the filling height, and the angle and area of the zone both decrease in a quasi-linear manner with increasing internal friction angle. 4) the calculation method for the loosening stress based on the area of the core zone is more applicable than Terzaghi’s method, and it is suggested that it be used to calculate the critical stress of test groups with a low and a high filling height respectively. The research results provide more accurate descriptions and judgment criteria for the displacement and failure modes of the loosening zone in sand. They also provide a reference for evaluating the stability of the loosening zone.
-
土拱效应是广泛存在的自然现象，是由于土颗粒介质的不均匀位移而导致在土体中表现出的一种应力重分布效应. 土拱效应普遍存在于桩承式路堤、山体抗滑桩、隧道与基坑开挖以及挡土构筑物等岩土及地下工程领域. Terzaghi[1]在1943年通过Trapdoor试验揭示了这一现象的存在，观测到了土体内部出现的滑裂面，并提出了作用在活动门上的松动土压力计算方法. 此后迄今，Trapdoor试验作为经典且实用的力学试验，一直备受国内外土拱效应研究的广泛应用和密切关注.
国内外学者基于Trapdoor试验或其改进装置，针对填料内部的滑移面形态与活动门上土压力的分布及变化等特征开展了丰富研究. 滑移面形态的发展与土体破坏模式是拱效应的宏观表现，结合先进测试手段，国内外众多模型试验对其开展了全面的观测和分析. Costa等[2-3]通过离心机Trapdoor试验研究滑移面形态在不同重力场和砂密度条件下的变化发现：随着活动门下移，滑移面形态经历弧形—三角形—竖直面的演变过程；离心加速度越高，砂密度越小，滑移面水平夹角越大；随着X射线、CT扫描及PIV （粒子图像测速）等观测技术的发展，滑移面形态被更精确地采集. Rui等[4]自制多沉陷门试验装置，利用PIV技术观测砂土中滑移面的演变过程，发现在低填土中滑移面由三角形演变为竖直面，高填土中滑移面由三角形变为烟囱形再变为竖直面. Eskisar等[5]利用CT扫描技术对三维模型试验中“拱结构”形态进行观测，发现“拱结构”形态近似为楔形体，且楔形体高度随填料内摩擦角的增加而减小. 土拱效应在砂土等细粒料中直观表现为滑移面，而在粗粒料中通常形成塌落拱结构，为此，不少学者选用球珠颗粒替代土以探明自承拱结构的形态及稳定特性. Hong等[6]和Ahmadi等[7]分别研究砾石和球珠材料在活动门下移过程中“稳定拱”的形成及演化发现，“稳定拱”形状为半圆环形（2D）或穹顶形（3D），稳定拱跨为0.75倍～1.15倍活动门宽度，且砾石填料的拱跨远大于球珠填料的拱跨. 目前，关于滑移面形态及演化规律等研究结论虽存在相似[2,4,6,8-11]，但由于试验装置、观测手段和填料种类有所差别，造成滑移面高度、宽度和夹角等具体几何轮廓存在较大的区别[2,5,12-17]，尚未形成一致性示例以准确描述滑移面的延展路径，同时缺乏适用的几何特征参数以全面掌握滑移面的几何轮廓信息.
活动门上的松动土压力直接反映应力转移的多少，体现土拱效应的发挥程度. 国内外学者同样基于Trapdoor试验对松动土压力开展了一系列研究. Chevalier等[11]和Dewoolkar等[12]均对活动门上的松动应力随活动门下移的变化规律进行研究发现，松动应力-活动门下移曲线可分为衰减、恢复与稳定3段，并且恢复段应力-位移曲线呈线性. Iglesia等[3]针对曲线的衰减段进行研究发现，填土越高，活动门宽度越小，应力衰减越多. Han等[13]将该曲线近似简化为三段直线，并提出简化曲线由最大、最小拱来确定. 通过对比试验结果及国内外研究结论，验证了简化曲线的可靠性. 目前研究所得的松动应力-活动门下移曲线特征类似 [3,12,15,17-22]，但对该曲线的衰减、恢复段斜率、稳定段长度以及最大、最小拱状态下的松动应力和活动门下移等曲线特征的变化规律犹未可知.
本文基于Trapdoor试验深入研究滑移面几何轮廓特征以及松动应力-活动门下移曲线特征. 通过指定滑移面轮廓特征参数获得轮廓特征在土层中的分布以及随活动门下移的变化规律，利用滑移面几何轮廓信息界定土体内部松动区范围及松动区形态演变模式，并提出考虑松动区形态演变的松动土压力计算方法. 通过指定松动应力-活动门下移曲线特征参数获得最大、最小拱状态下的松动应力随填土高度和内摩擦角的变化规律. 将松动土压力改进算法与试验结果以及国内外研究成果进行对比，验证了本文改进方法的可靠性和实用性.
1. Trapdoor模型试验
1.1 试验装置
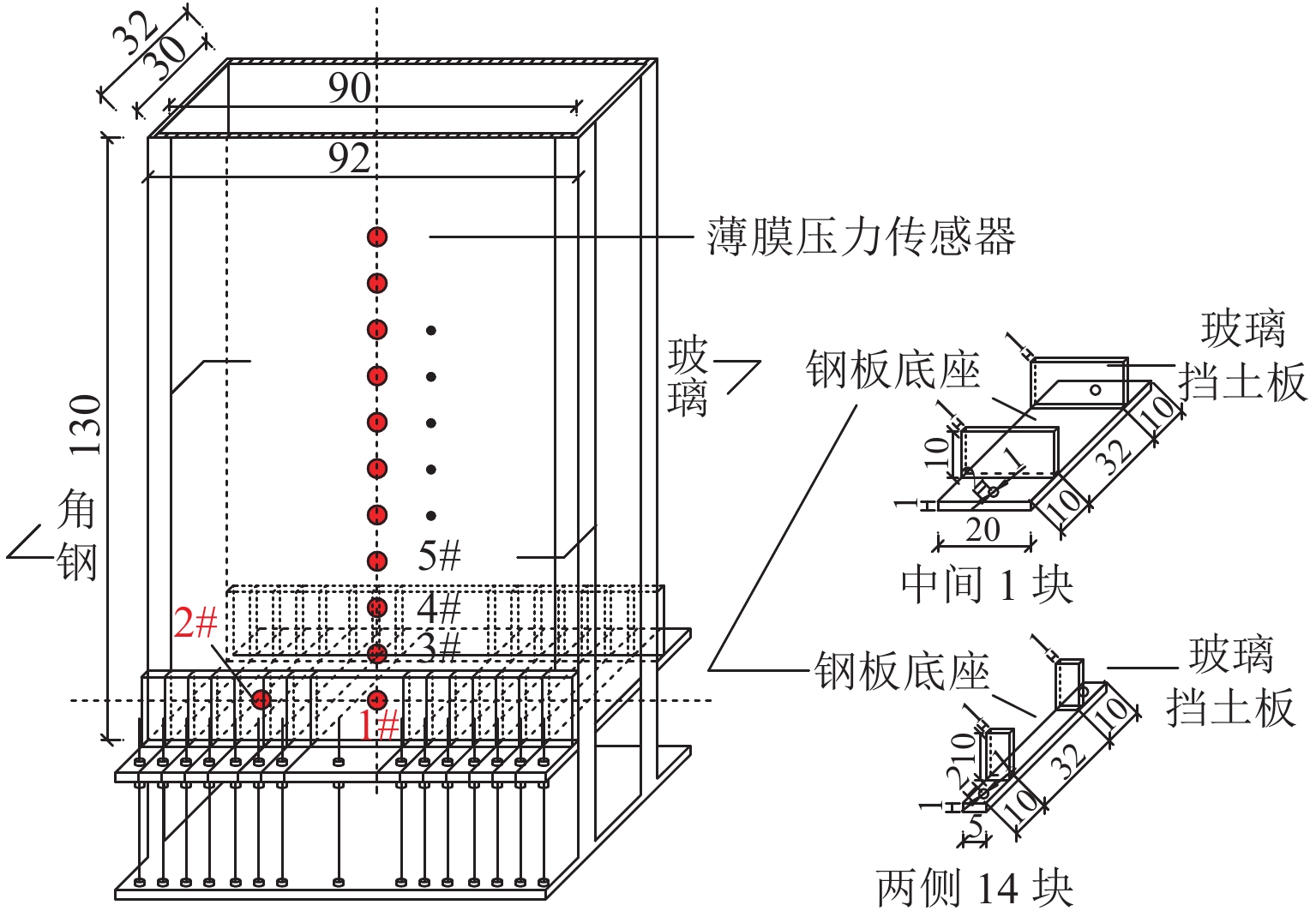
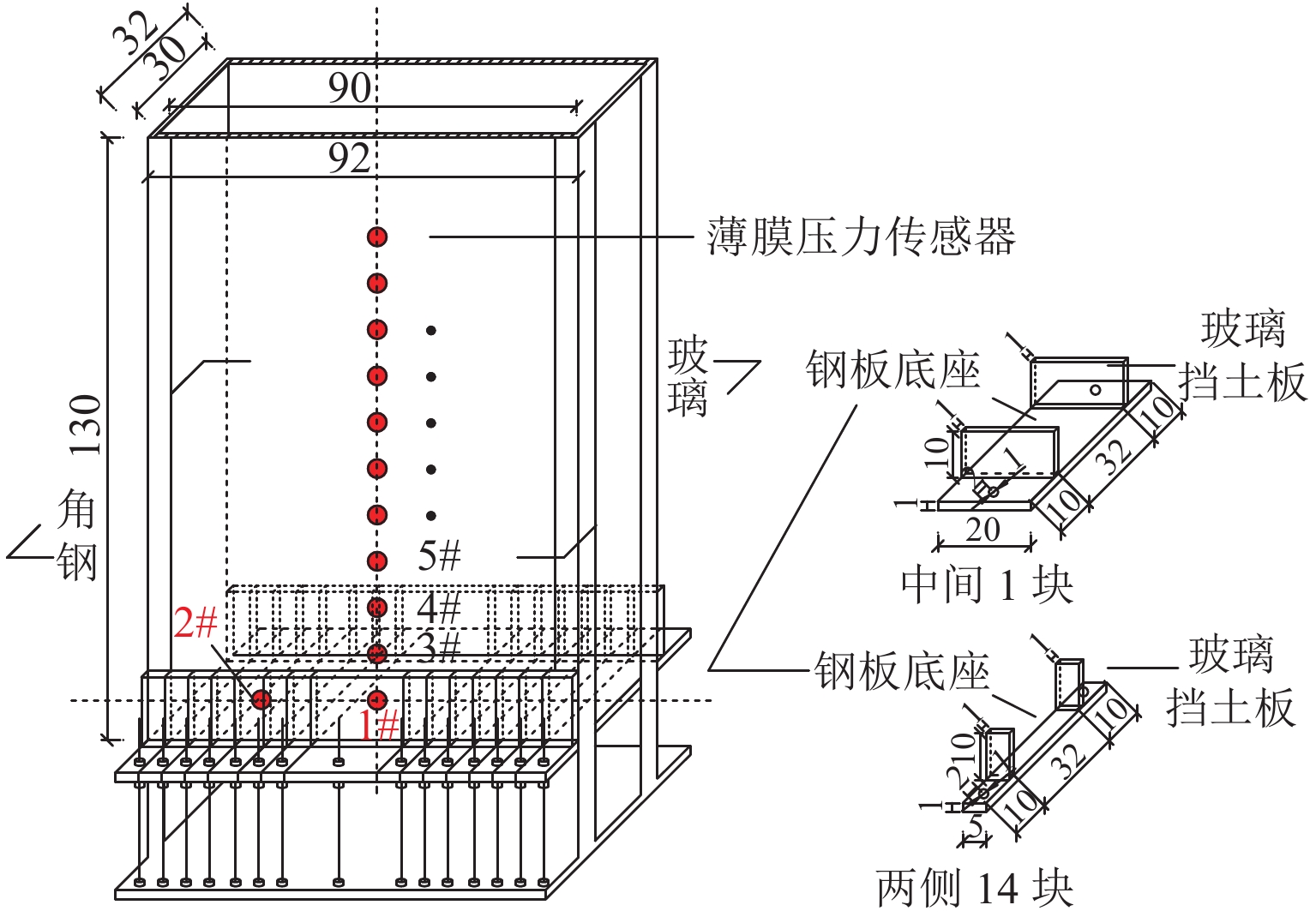
Trapdoor试验模型箱如图1所示，模型箱由上部箱体和下部底座构成. 上部箱体为上、下两端开口的长方体，箱体外框主骨架由角钢焊接而成，箱体四周侧面为1 cm厚有机玻璃. 下部底座由15块钢板拼接组成，包括中心钢板（宽200 mm）与两侧条形钢板（宽50 mm），可灵活调节改变活动门与其两侧不动底座的宽度. 每块钢板前、后两侧均采用螺栓与底板的前、后两端固定连接，通过螺杆控制任意一块钢板的下移，最大下移高度达100 mm. 同时为确保平面应变条件，在每块条形钢板的前、后两侧均固定有高100 mm的玻璃挡土板，挡土板内壁紧贴箱体外壁，从而在活动门下移过程中对箱内填料的位移方向加以约束.
在活动门与其一侧底座的中心以及活动门上方沿填料中心线等间距布置多点式薄膜（MFF）压力传感器（如图1所示），以测试作用在活动门、不动底座上的应力以及填料各层的竖向应力. 薄膜压力传感器长、宽 、 厚分别为51、14、 0.2 mm，受力感应区为圆形，直径9.52 mm，量程10 N，精度1.2%满量程，根据标定系数由输出电压E获得压应力σ （由感应区面积转换为kPa）. 采用百分表测量活动门下移量，百分表量程100 mm，分度值0.01 mm，在下移钢板的前后两端各安装1个. 将光源、摄像头、支架等固定在试验箱正面，试验中同步拍摄填料变形，并获得土层位变信息.
1.2 测试方法
对试验拍摄填料变形图像进行处理分析，以获取图像中目标测试点的位置变化信息[23-25]. OpenPIV是基于MATLAB和C++ 语言的开源程序，在物体瞬态位移及运动轨迹追踪等摄影测量技术领域得到了广泛应用[23]. 其基本原理：通过将一系列连续拍摄的瞬时图像依次导入程序，根据图像中色彩纹理及光散射率特性的不同，采集图像中目标测试点的坐标并识别相邻图像测试点坐标的变化；通过图像区块相关性匹配输出全场速度和位移矢量；根据图像与原型之间的比例转换得到实际的速度和位移，从而实现图像中任意点位置变化的实时监测.
测试过程中，将图像导入OpenPIV[23]后设置界面图幅大小，图幅像素范围4～256 像素，为满足数据采集鲁棒性的同时确保较高的分辨率，本试验选取32 像素 × 32 像素. 同时，利用OpenPIV界面的局部图像分析模块（ROI）加密布置分析区域内的测点，以实现局部范围内数据的重点采集分析. 程序运行后得到各测点的水平和竖向速度矢量，单位像素/s，与相邻图像拍摄的时间间隔t（s）及比例尺（m/像素）相乘即可得到位移矢量.
1.3 试验方案
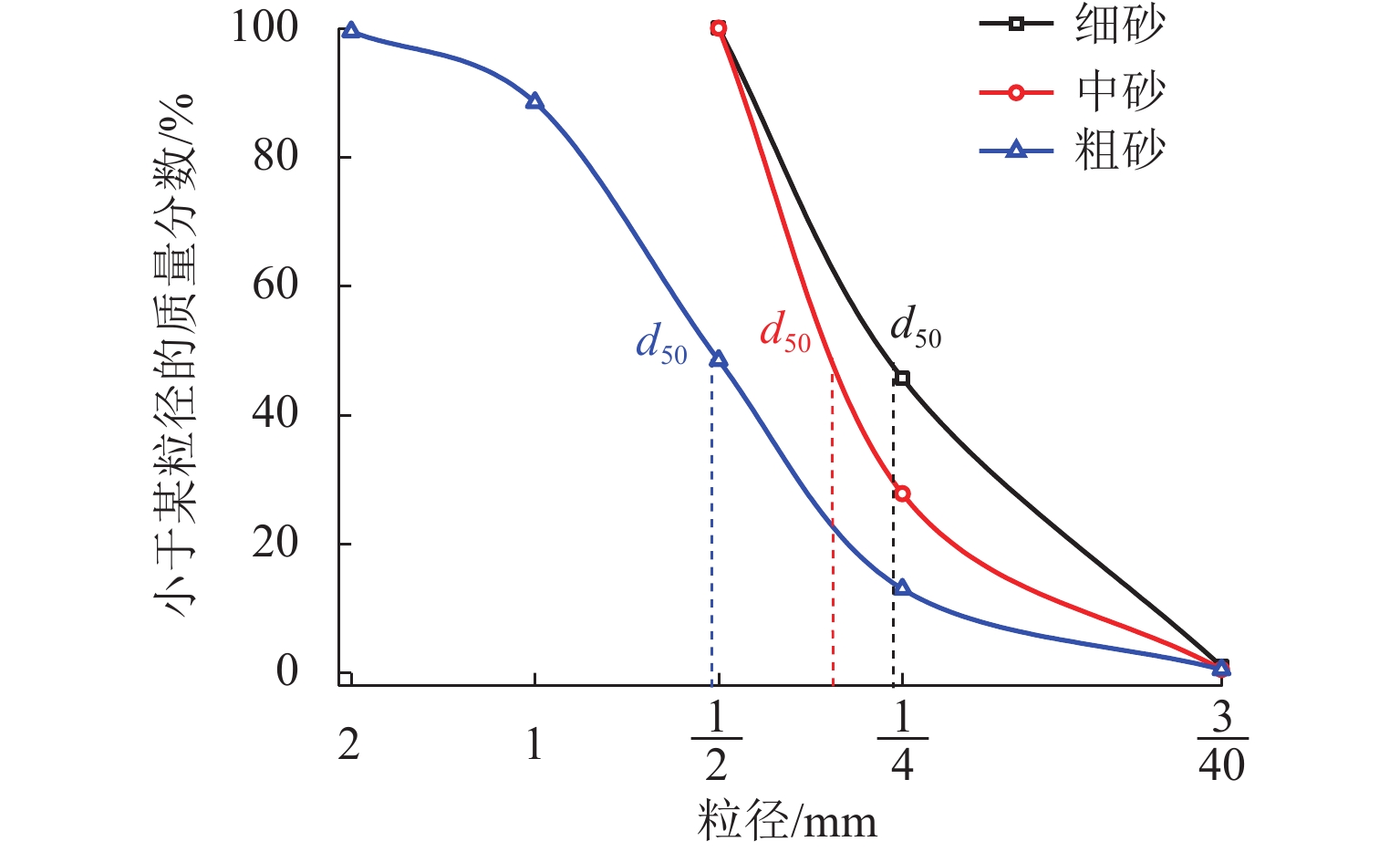
Trapdoor试验是一种基于理想二维条件下开展的平面应变和平面应力试验. Trapdoor试验箱长宽比通常取4～8[10-16]，在这种狭长空间内试验填料与箱体内壁的摩擦将会破坏理想平面状态，显著影响试验结果. 因此，需测定和严格要求填料的黏聚力、相对密度、内摩擦角等物力指标，通常选用黏聚力低、配位数小、流动性强的材料作为试验填料[4,7,10,17,21,22]，并严格保证试验箱内壁光滑. 本文选用 中值粒径d50为0.25～0.55 mm，相对密度Dr为0.200～0.850 的粗、中、细3种洁净干砂开展Trapdoor试验，3种干砂的颗粒级配曲线如图2所示，经测试获得3种砂的系列物理力学参数如表1所示. 针对3种砂分别开展不同填土高度h和活动门宽度w的Trapdoor试验，试验组工况如表2所示.
表 1 砂物理力学参数Table 1. Physical and mechanical parameters of sand种类 d50/mm 不均匀
系数 cu曲率系数 cc 最大干密度
ρdmax/（kg·m−3）最小干密度
ρdmin/（kg·m−3）Dr 内摩擦角 φ/（°） 细砂 0.27 2.67 0.95 1719 1318 0.208 31.4 中砂 0.32 2.57 1.34 1616 1354 0.607 34.5 粗砂 0.53 2.92 0.84 1703 1439 0.860 38.4 表 2 Trapdoor试验组工况Table 2. Trapdoor test conditions试验组工况 种类 h/m w/m 传感器埋设间距/m A1 细砂 0.4 0.2 0.1 A2 0.6 0.3 0.1 A3 0.8 0.4 0.2 A4 0.6 0.2 0.1 A5 0.9 0.3 0.2 A6 1.2 0.4 0.2 B1 中砂 0.4 0.2 0.1 B2 0.6 0.3 0.1 B3 0.8 0.4 0.2 B4 0.6 0.2 0.1 B5 0.9 0.3 0.2 B6 1.2 0.4 0.2 C1 粗砂 0.4 0.2 0.1 C2 0.6 0.3 0.1 C3 0.8 0.4 0.2 C4 0.6 0.2 0.1 C5 0.9 0.3 0.2 C6 1.2 0.4 0.2 试验中对砂料内滑移面的形成和延展过程进行观测，获得上述试验组各级滑移面的几何轮廓及其典型演变模式，在此基础上提出全面描述滑移面几何轮廓信息的特征参数，并获得砂料种类以及试验条件对几何特征参数的影响规律. 试验结果为滑移面几何轮廓及其延展路径分类提供典型示例与指标. 具体试验步骤如下：
步骤1 按每层50 mm分层填砂，层间均匀铺撒一层10 mm厚的天然彩砂，并在预设位置埋设薄膜式压力传感器（如图1所示）；
步骤2 填至预定高度后，静置待压力传感器读数稳定，记录读数并拍摄砂料照片；
步骤3 缓慢下移活动门，每下移1 mm，待变形和传感器读数稳定后同步完成数据采集和拍摄. 利用OpenPIV对拍摄的砂料变形瞬时图像进行粒子图像测速 （PIV）分析，依次对比活动门每下移1 mm前、后的颗粒位置、输出颗粒速度和位移矢量；
步骤4 重复步骤1～3，直至彩砂条带破坏或箱体底部出现坍砂时结束试验.
2. 试验结果分析
2.1 滑移面几何轮廓特征
将各层彩砂变形曲线的拐点自下而上依次连接，得到从活动门两侧边缘向砂内部延伸的滑移面. 为研究不同砂料种类和试验条件下典型滑移面轮廓及其一般性的演变模式，选取高宽比h/w=3的粗砂与高宽比h/w=2的细砂试验组进行对比观测，如图3所示，ΔS为滑移面轮廓随活动门下移位移.
由图3可知：ΔS/w的演变过程为三角形—子弹头形—椭圆形，与Rui等[4]“初始三角拱”及“烟囱形滑移面”结论相似；对于高宽比h/w=2的细砂试验组，初始三角形滑移面随活动门下移表现为“顶部上升、两侧扩展”的演变特征，同Rui等[4]的“三角扩展型滑移面”结论相合；对于高宽比h/w=3的粗砂试验组，初始滑移面形成后即保持稳定，随活动门下移基本不再变化.
将各组最终形成的完整滑移面进行比较，通过OpenPIV中的局部图像布点功能（ROI），按照砂料分层厚度将图像分解为若干层，分别采集获得各层彩砂测点的颗粒位移场，如图4所示. 由图4可得：初始、次级滑移面均随填土高度的增加和活动门宽度的减小而愈发尖锐，当填土高度足够高时，“子弹头”下部近似呈竖直面（如图4（d）所示）.
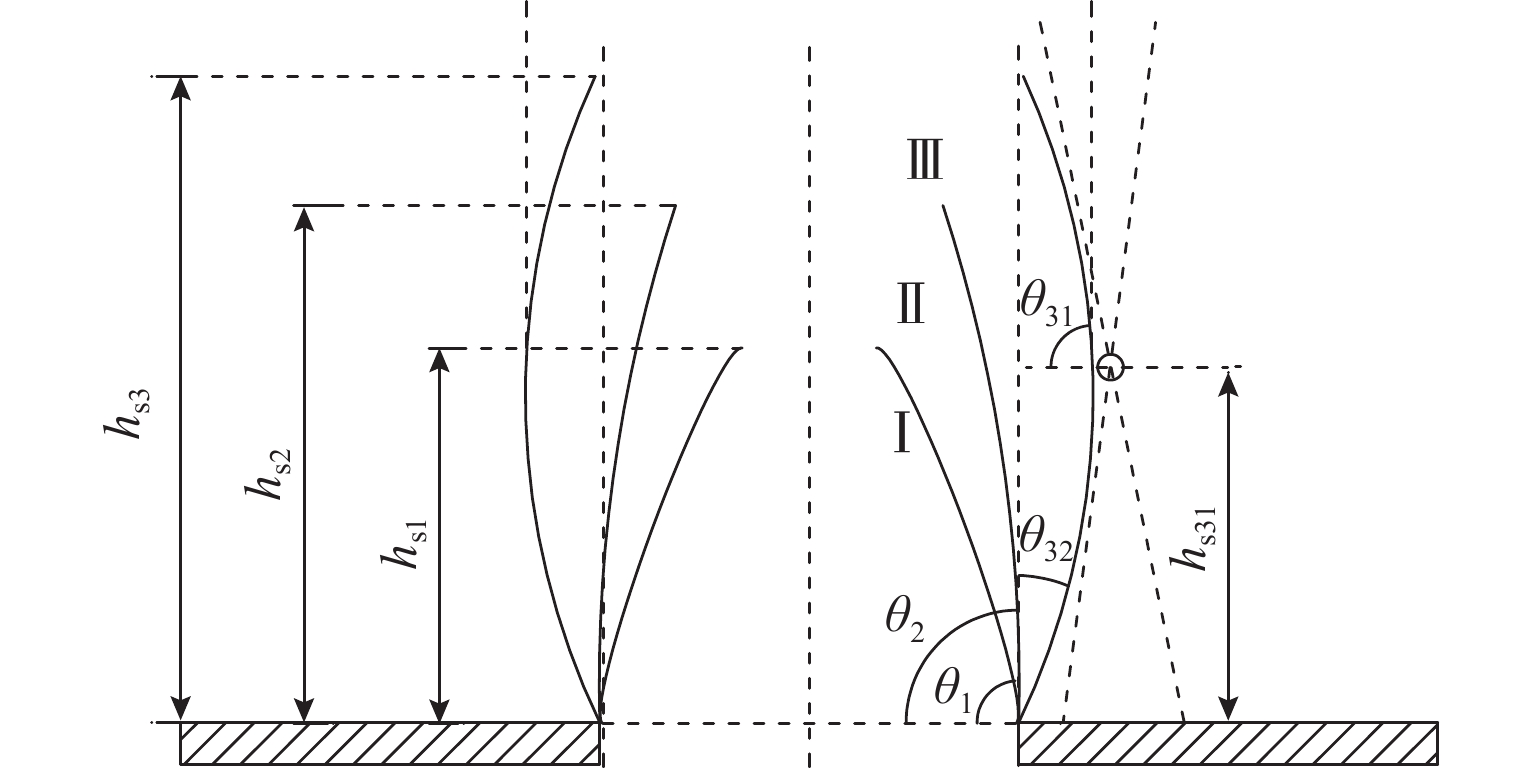
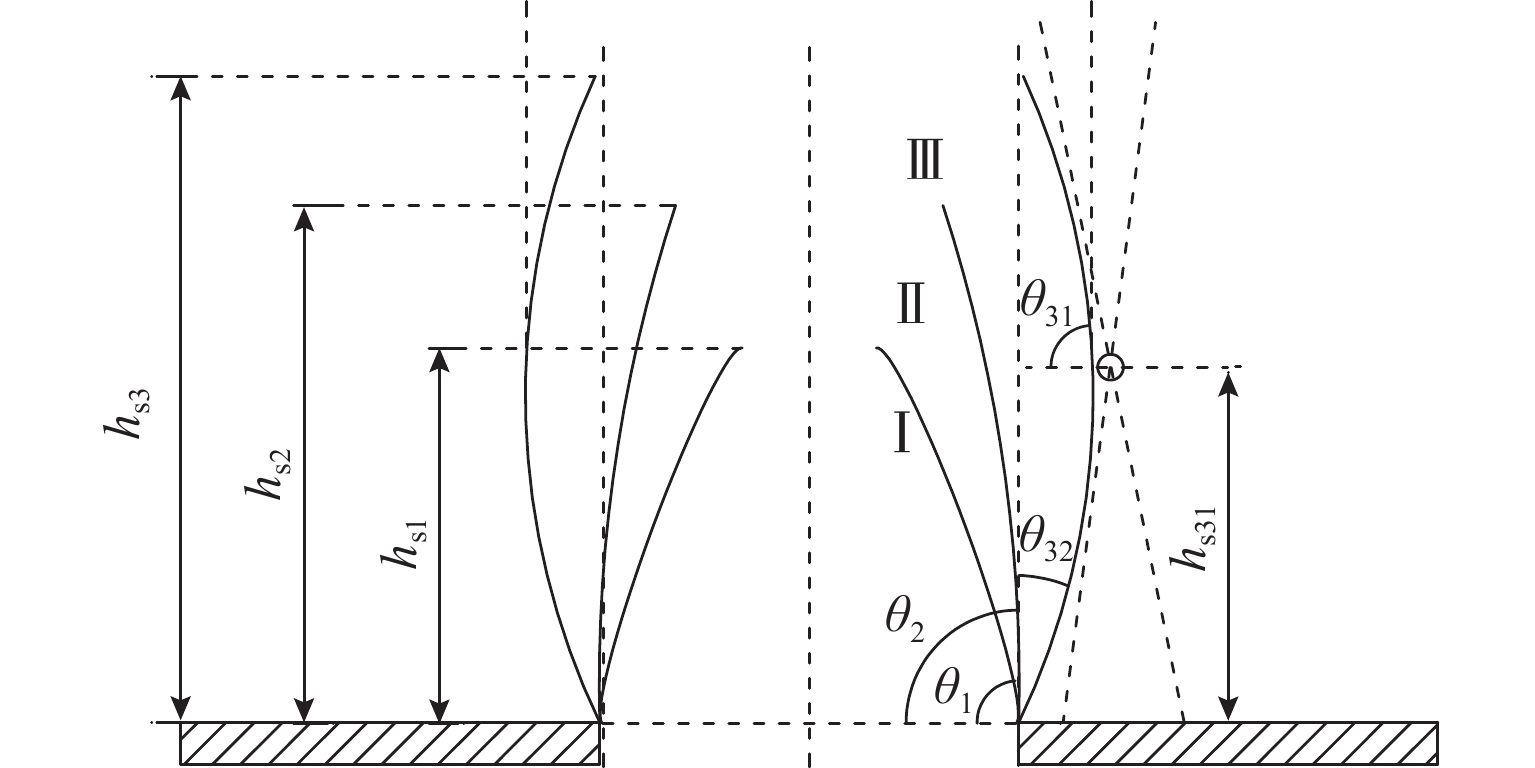
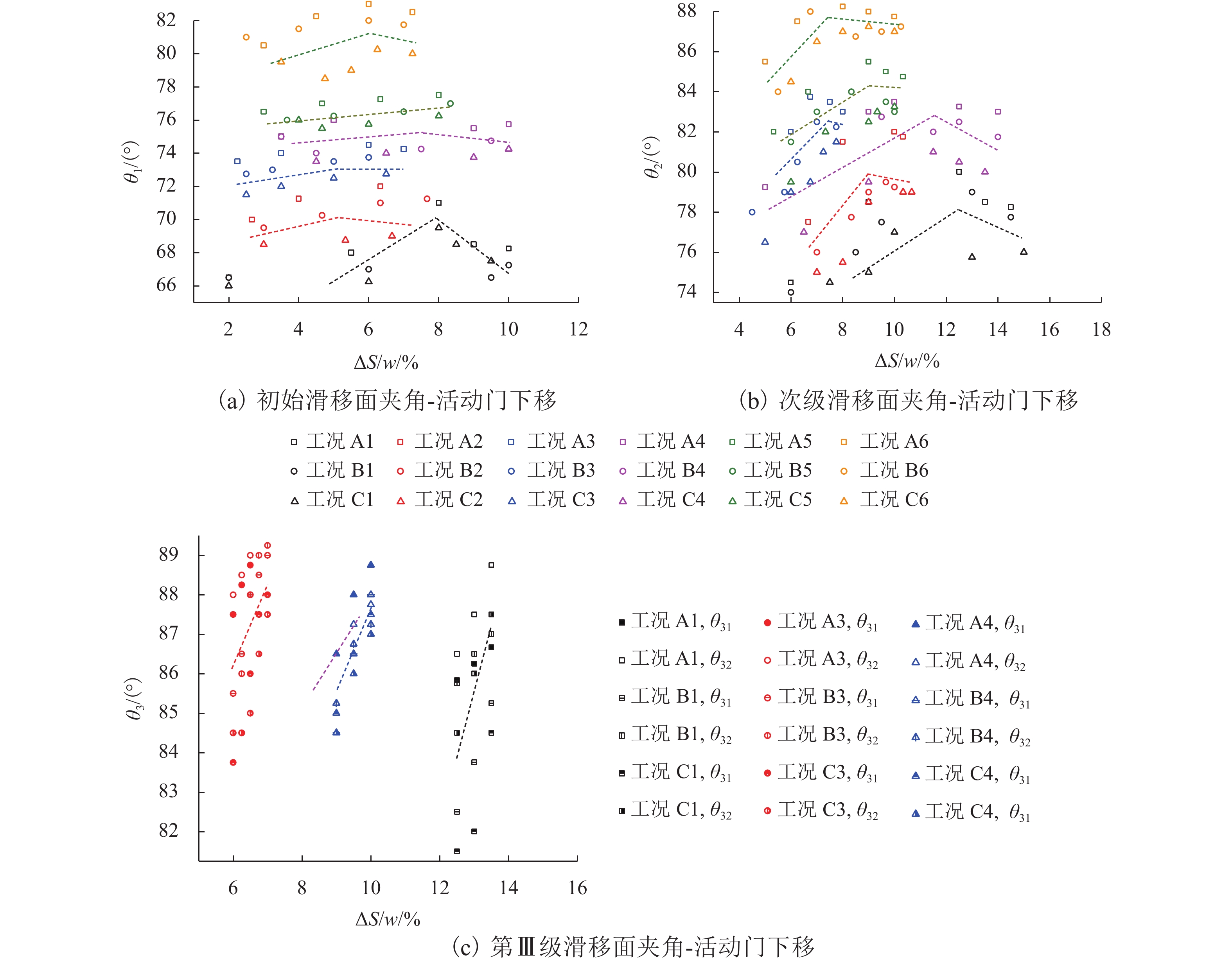
图 4 滑移面典型轮廓及其等值线（粗砂， Dr=0.860）Figure 4. Typical contours of slip surface and its contour line （coarse sand， Dr = 0.860）第Ⅲ级滑移面随活动门下移不断向上延伸，在低填土试验组中延伸至顶面并交于表面沉陷槽两侧边缘，在高填土内则形成完整椭圆形闭合圈，且活动门越宽，闭合圈面积越大，如图5所示，图中： hs1、hs2、hs3和hs31 分别为初始、次级、第Ⅲ级滑移面高度和第Ⅲ级滑移面拐点高度；θ1、θ2、θ31和θ32分别为初始、次级滑移面夹角和第Ⅲ级滑移面上半夹角、下半夹角.
图 5 滑移面几何轮廓特征参数释义Figure 5. Interpretation of geometric contour parameters of slip surface2.1.1 滑移面高度hs
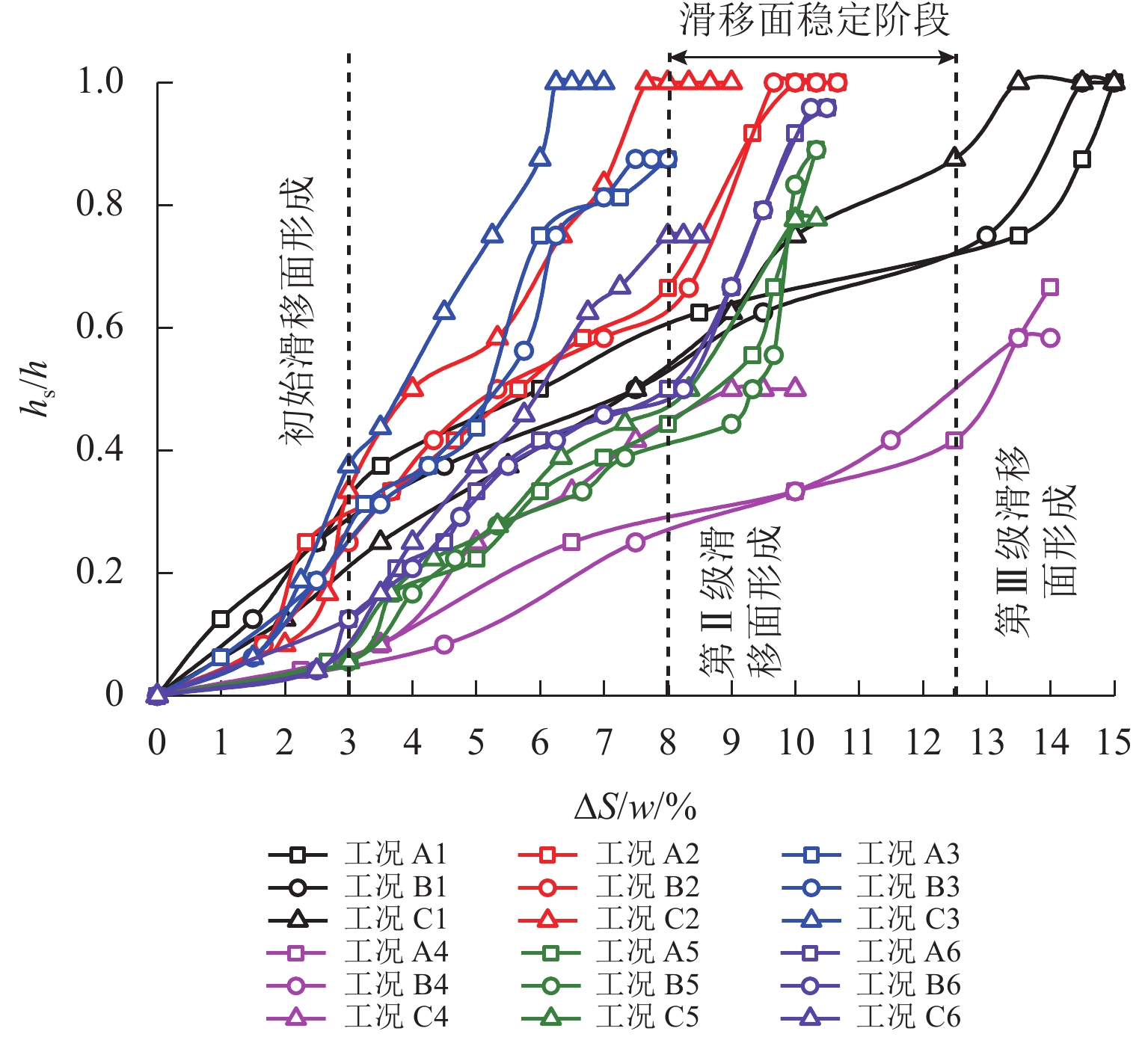
滑移面高度hs随活动门下移的变化如图6所示. 由图可知：各试验组变化规律类似，hs随活动门下移递增；当活动门下移较小时，hs增长较缓慢，随着活动门下移的增加，hs增长速率先增大，后减小，再增大，最终趋缓，分别对应于初始滑移面形成、次级滑移面形成、滑移面稳定阶段、第Ⅲ级滑移面形成以及滑移面破坏阶段；高宽比和密度越大，曲线第一阶段增长越缓慢，第二、三阶段增长越显著，反映初始滑移面形成过程较长，次级、第Ⅲ级滑移面随活动门下移的演化程度相对更高.
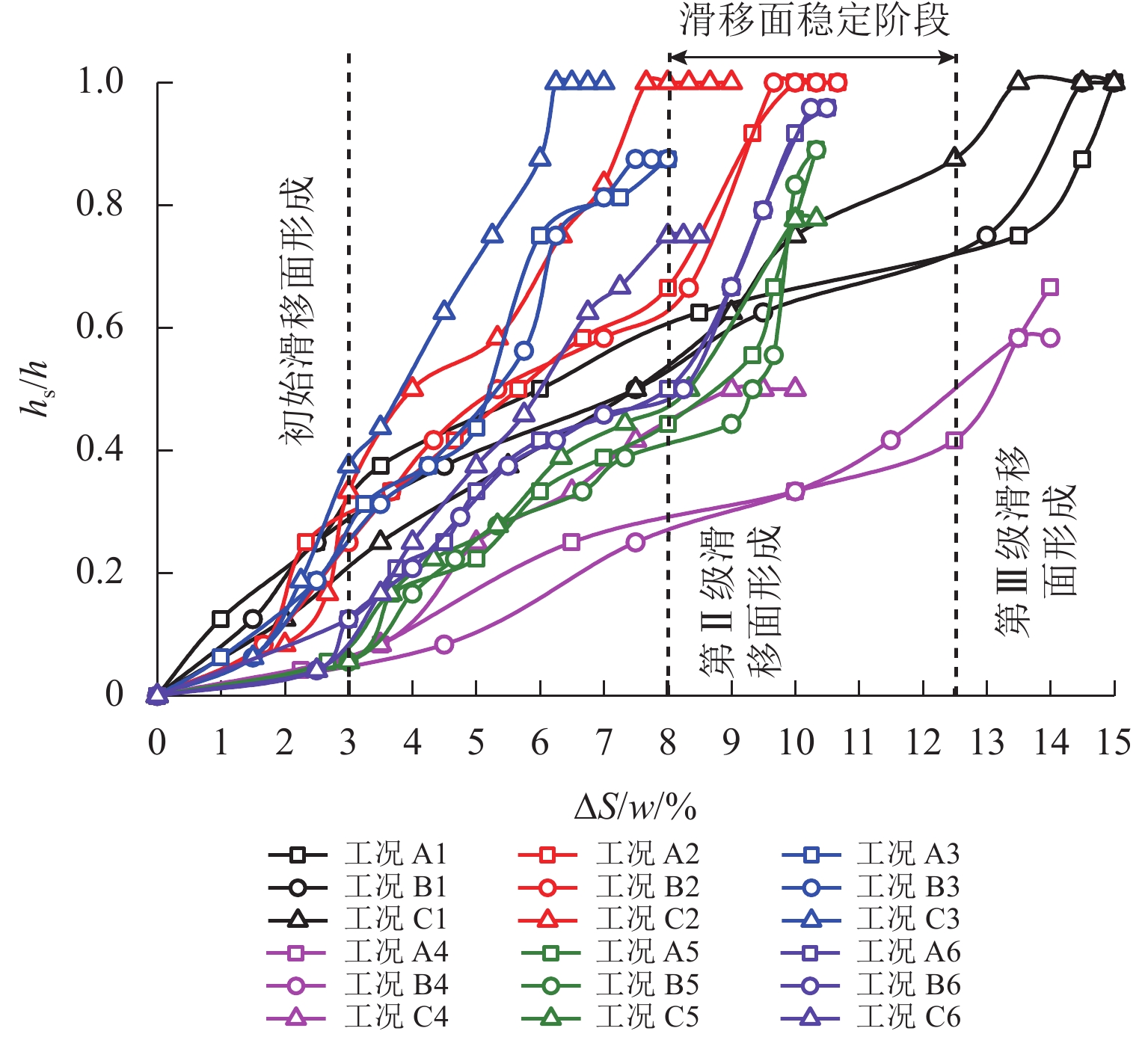
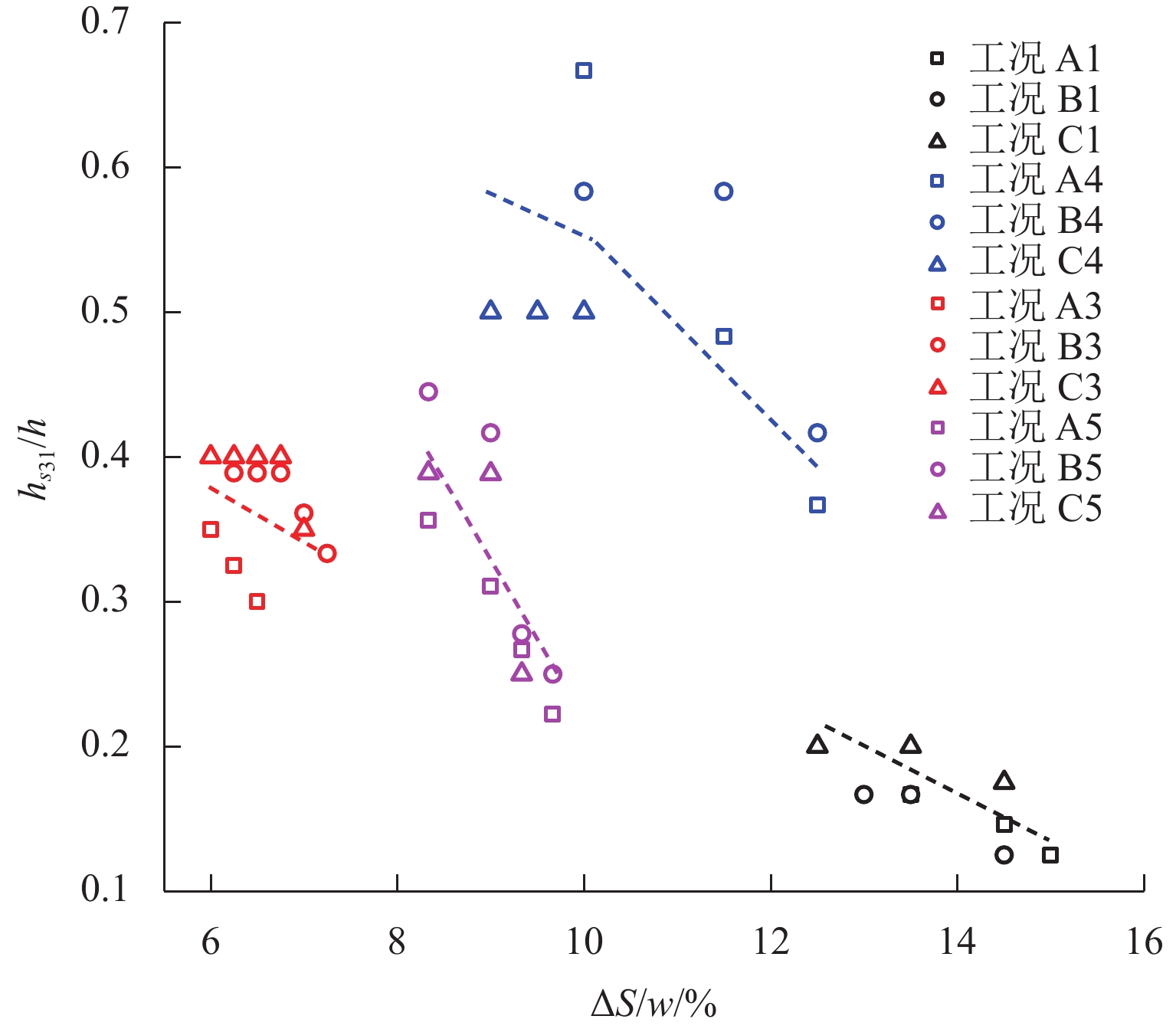
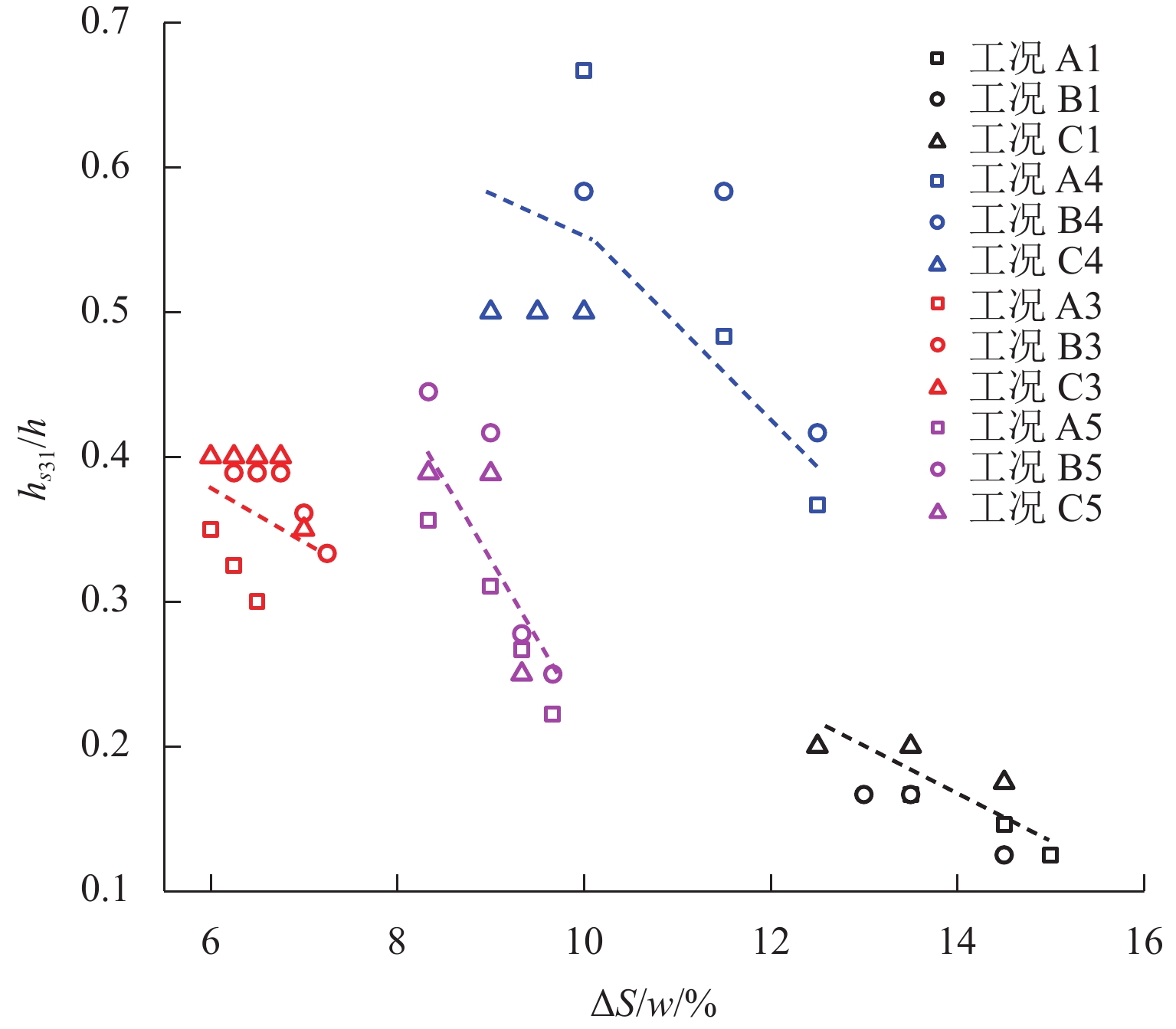
图 6 滑移面高度随活动门下移变化Figure 6. Change of slip surface height with downward movement of trapdoor第Ⅲ级滑移面椭圆拐点处填土高度随活动门下移的变化如图7所示. 由图7可知：hs31为填土高度的0.1倍～0.7倍；hs31随活动门下移递减，填土越高，密度越小，hs31变化幅度越大.
图 7 第Ⅲ级滑移面拐点高度随活动门下移变化Figure 7. Change of inflection point height of level-Ⅲ slip surface with downward movement of trapdoor各试验组（h=0.4 m与h=0.6 m）完全形成的初始、次级、第Ⅲ级滑移面高度，如表3所示. 由表可知：各试验组变化规律类似，初始滑移面高度hs1在填土高度的0.2倍范围内变化，填土高度越高，活动门越宽，hs1越大；次级滑移面高度hs2为填土高度的0.3倍～1.0倍，hs2随高宽比与内摩擦角的增加而增大；试验组中，第Ⅲ级滑移面延至填土表面，故hs3稳定在填土高度保持不变，对于未延至表面的试验组，hs3为0.5倍～1.0倍填土高度；hs3与填土高度呈正相关，与内摩擦角呈负相关；第Ⅲ级滑移面拐点高度hs31为填土高度的0.1倍～0.5倍，hs31随内摩擦角近似线性递增.
表 3 稳定滑移面高度-内摩擦角Table 3. Stable slip surface height-internal friction anglem φ/（°） h=0.4 m, w=0.2 m h=0.8 m, w=0.4 m h=0.6 m, w=0.2 m h=0.9 m, w=0.3 m hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 31.4 0.225 0.250 0.400 — 0.625 0.750 — — 0.363 0.425 — — 0.275 0.523 0.875 0.675 34.5 0.238 — — — 0.625 0.788 0.725 0.352 0.338 0.463 0.600 0.425 0.312 — — — 38.4 0.225 0.263 — — 0.688 0.763 — — 0.413 0.488 0.525 0.450 0.337 0.575 0.900 0.708 注：部分试验未形成次级或第Ⅲ级滑移面，以“—”表示. 2.1.2 滑移面夹角θi
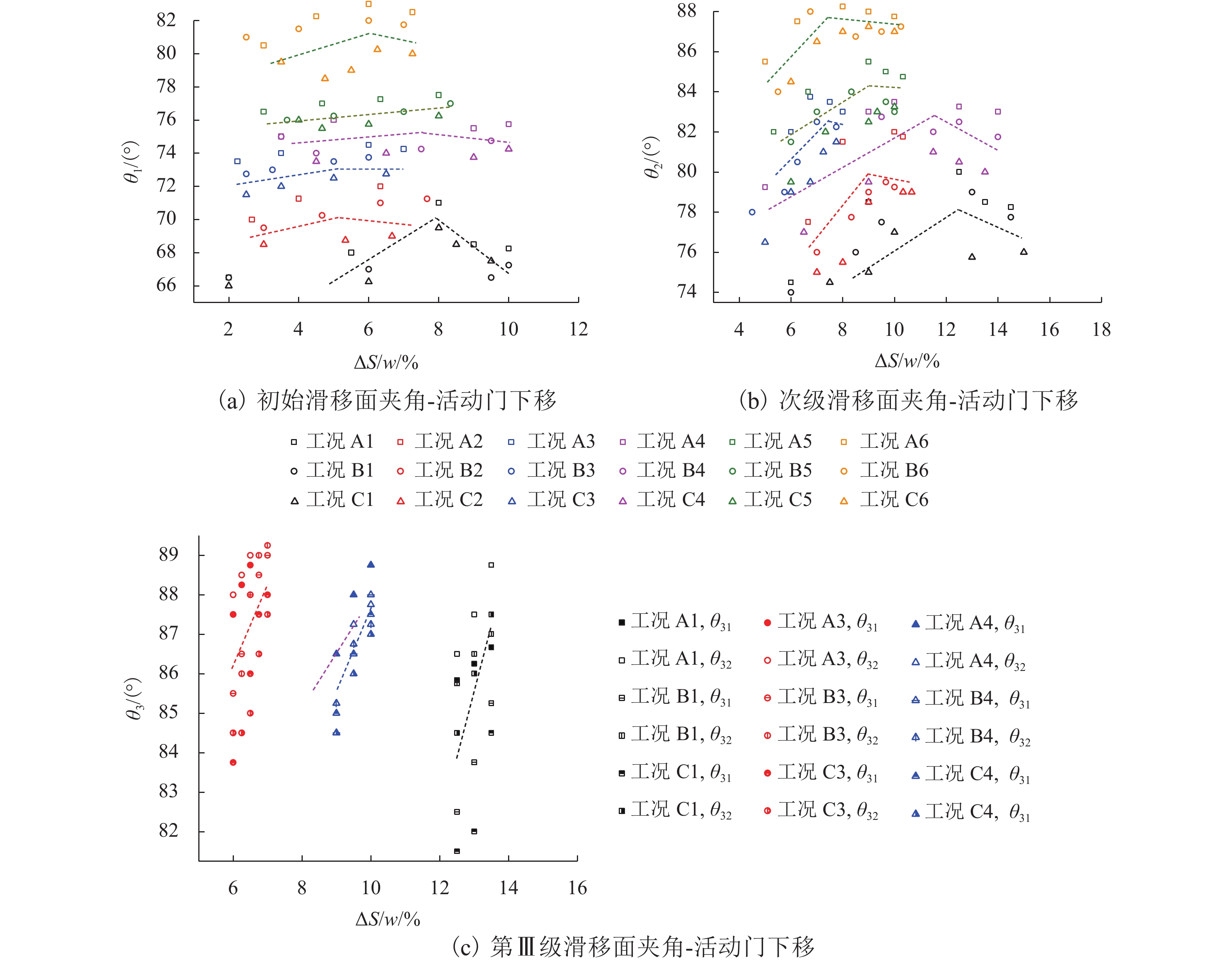
滑移面夹角随活动门下移的变化曲线如图8所示. 由于各级滑移面左右两侧夹角相近，故取平均值进行统计和分析. 由图可得：初始、次级滑移面夹角随活动门下移均先增后减，其中，初始滑移面夹角θ1在65°～83° 内变化，次级滑移面夹角θ2为74°～90°，两者均介于（45° + φ/2）～90° ，同Costa等[2]75°～85° 以及Rui等[4]67°～78° 试验结果相符；θ1的变化幅值小于θ2，且在θ2的变化过程中θ1基本不变，表明初始滑移面稳定性更高，θ1、θ2均同填土高度呈正相关，同活动门宽度及内摩擦角呈负相关；填土高度的影响更显著，当h=0.4 m增至1.2 m，θ1、θ2分别增长了21.56%、14.47%，内摩擦角对θ2的影响较大，对θ1影响相对较小；θ31、θ32大小相近，均在80°～90° 内变化，且均随活动门下移而增大，高宽比越大，θ31、θ32越小，砂密度对θ31的影响较大，对θ32的影响较小.
图 8 滑移面夹角随活动门下移的变化Figure 8. Change of angles of slip surface with downward movement of trapdoor2.1.3 松动核心区形态
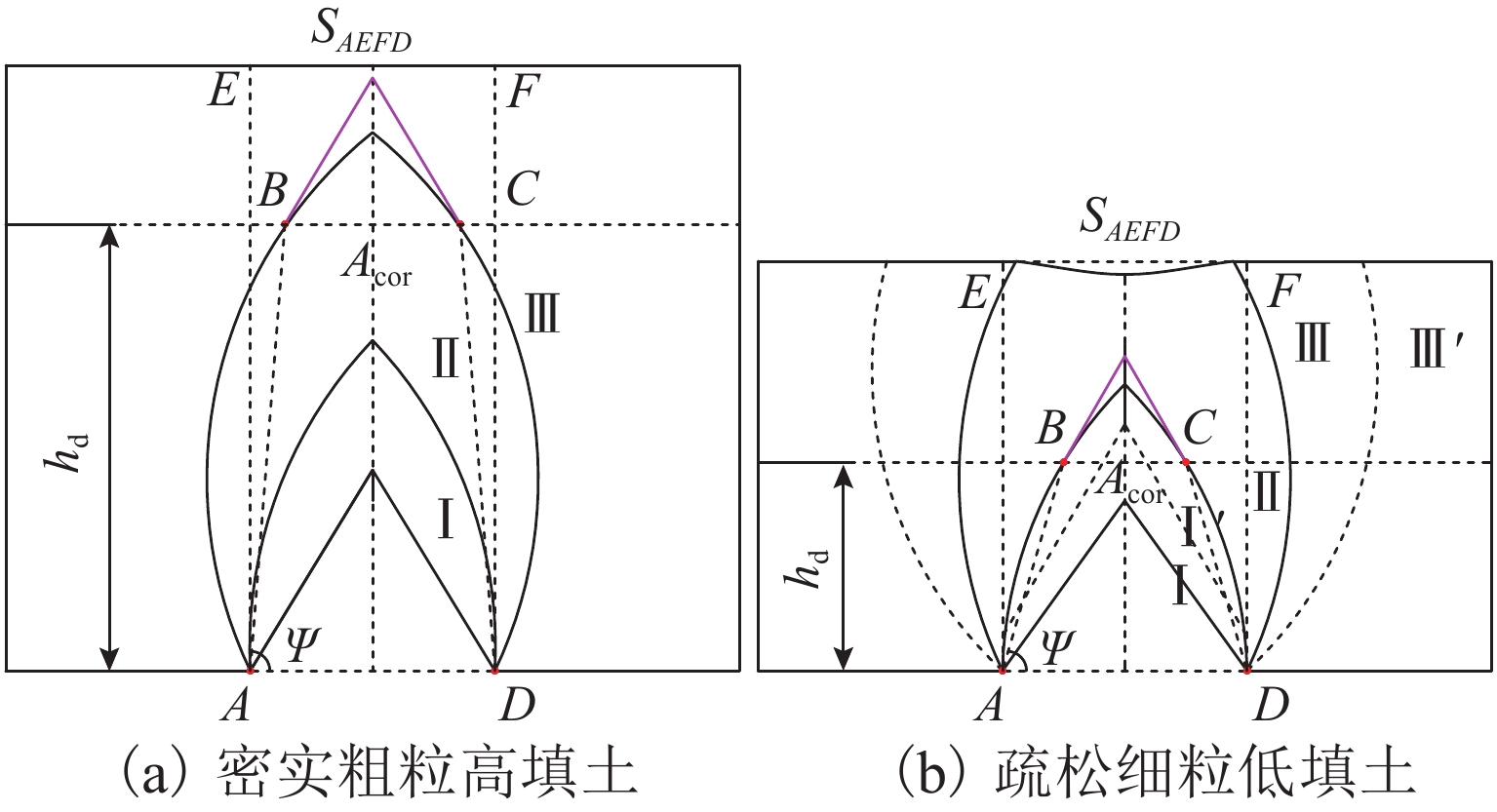
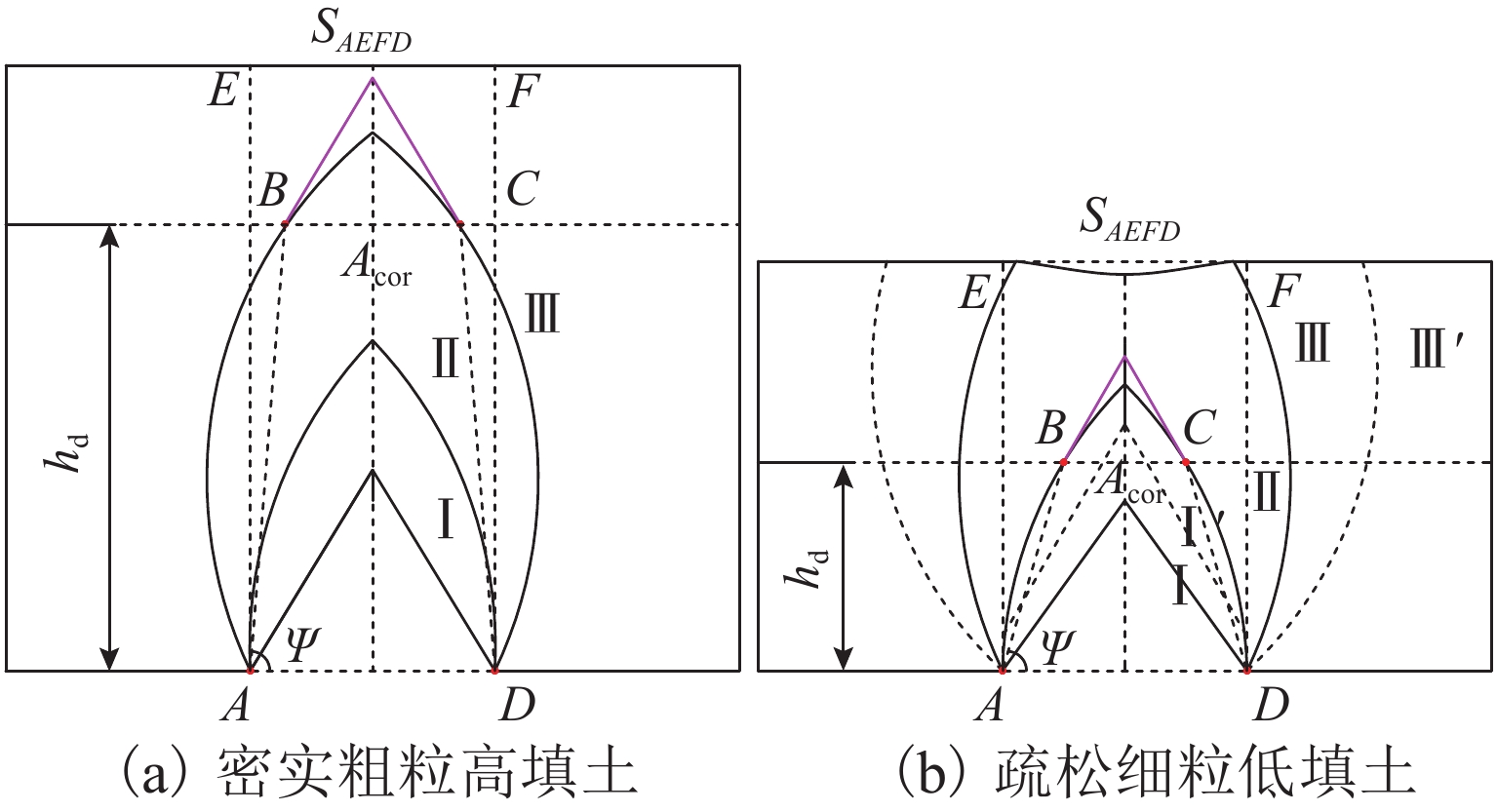
θ2与θ31沿土层自下而上逐渐减小，减小至θ1时对应的填土高度定义为等斜率填土高度hd. 将连接活动门两侧边缘与hd同次级或第Ⅲ级滑移面两侧交点构成的四边形作为活动门上方松动核心区域，如图9中区域ABCD所示. 图9中：ψ （区域ABCD两侧底角）为松动核心区水平夹角；SAEFD为竖直面松动区面积； Acor （区域ABCD面积）为松动核心区面积.
图 9 2类典型试验组中松动核心区形态Figure 9. Morphology of core loosening zones in two types of typical test groups统计各试验组中上述几何参数随内摩擦角的变化，如表4. 由表4可知： hd为填土高度的0.5倍～0.8倍，填土高度越高，hd越大；内摩擦角越大，hd越小，ψ随内摩擦角的增加而减小，低填土试验组（h=0.4 m，h=0.6 m）中ψ为80.0°～85.0°，高填土试验组（h=0.8 m，h=1.2 m）中ψ为87.5°～90.0°，随着填土高度的增加，核心区形态由三角形演变为梯形或矩形； Acor/SAEFD同内摩擦角近似呈线性负相关.
表 4 松动核心区几何特征Table 4. Geometric characteristics of core loosening areaφ/（°） h/m w/m hd/m ψ/（°） Acor/m2 Acor/SAEFD 31.4 0.4 0.2 0.40 81.5 0.036 0.45 1.2 0.4 0.85 88.5 0.385 0.80 34.5 0.8 0.4 0.75 88.5 0.231 0.72 0.6 0.2 0.55 85.0 0.057 0.48 38.4 0.6 0.2 0.60 83.5 0.056 0.47 1.2 0.4 0.80 89.0 0.375 0.78 2.2 松动应力-活动门下移曲线特征
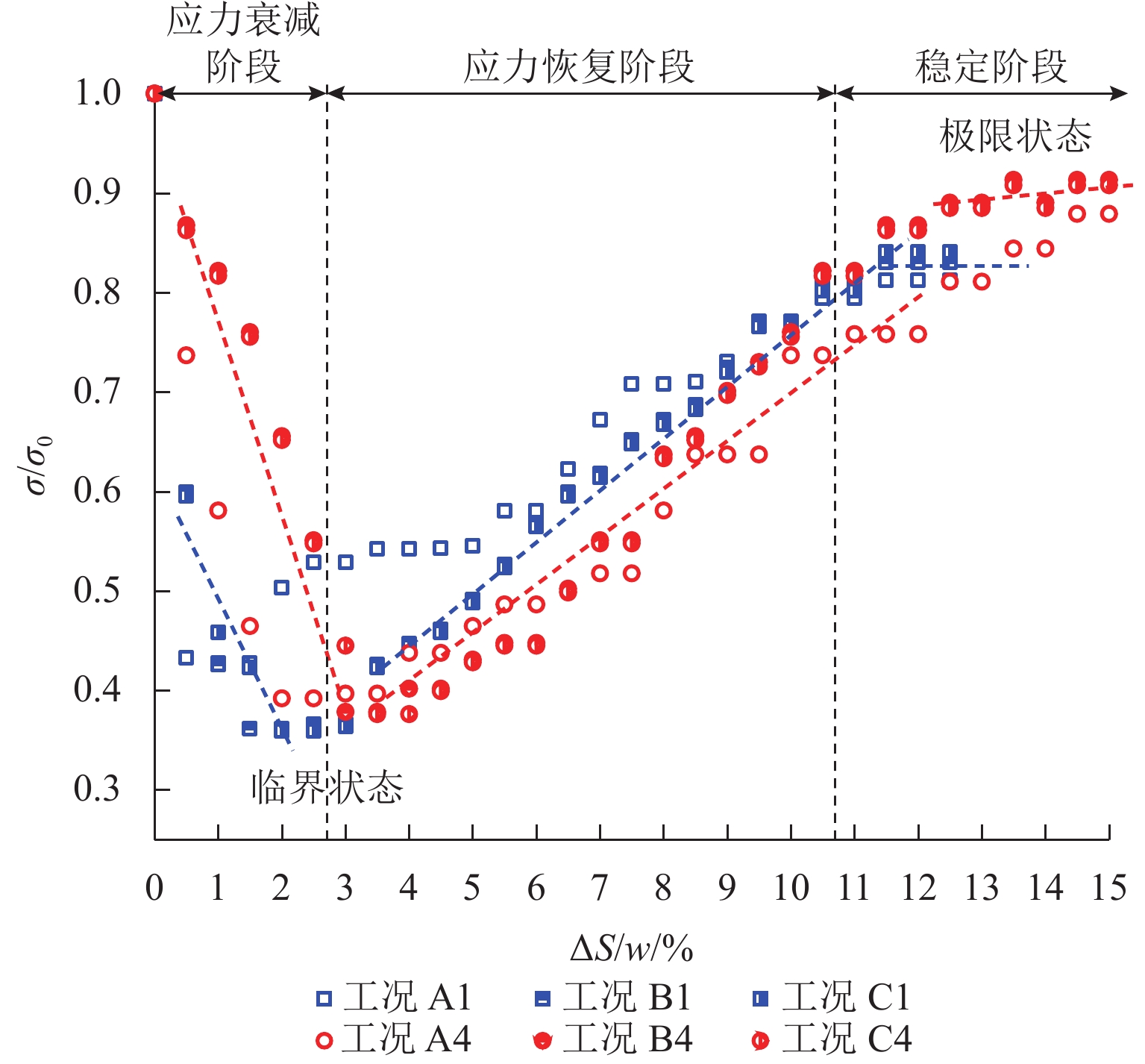
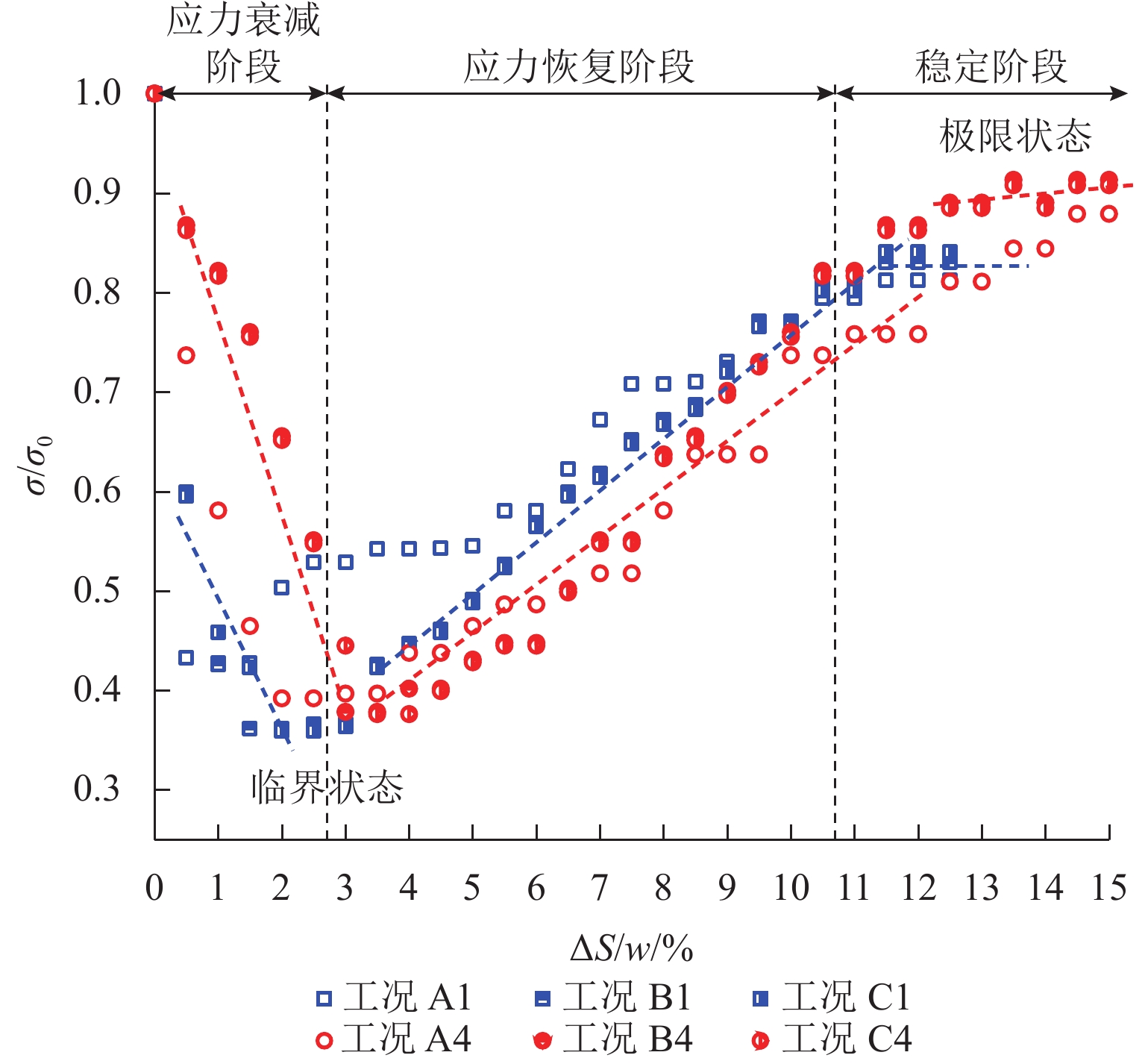
采集活动门上的应力（传感器1# 读数）随活动门下移的变化，如图10所示，图中，σ0为初始应力. 经分析可知，各试验组变化规律类似，随着活动门下移，应力变化过程可分为衰减、恢复和稳定3阶段：衰减阶段对应于初始滑移面的形成，土拱效应的发展将上覆填土荷载由活动门上方向两侧转移，导致活动门上土应力降低；恢复阶段对应次级滑移面的形成和演化，滑移面区域的扩张使得越来越多的填土荷载作用于活动门上，造成活动门应力的增长；稳定阶段对应于第Ⅲ级滑移面的形成及稳定后，活动门应力基本保持不变. 试验结果同Chevalier等[11]、Dewoolkar等[12]所得结论相合.
图 10 松动应力-活动门下移归一化曲线Figure 10. Normalization curves of loosening stress-downward movement of trapdoor统计各试验组曲线中临界状态（应力谷值点）、极限状态（应力稳定段起点）的应力和活动门下移量，如表5所示，表中：σcri为临界应力；ΔScri为临界位移；σult为极限应力；ΔSult为极限位移. 结果表明：σcri/σ0在0.30～0.45内变化，高于Dewoolkar 等[12]20%的结论；高宽比和内摩擦角越大，σcri/σ0越小；ΔScri占活动门宽度的0.5%～3.5%，与Dewoolkar等[12]1.5%的试验结果相符，高宽比和内摩擦角越大，ΔScri/w越大；σult/σ0为0.8～1.0，σult/σ0与填土高度、内摩擦角呈正相关；ΔSult/w为5.0%～15.0%，ΔSult/w随活动门宽度和内摩擦角的增加而减小，随填土高度的增加而增大.
表 5 临界、极限状态特征Table 5. Characteristics of critical and ultimate statesφ/
（°）h=0.4 m, w=0.2 m h=0.8 m, w=0.4 m h=0.6 m, w=0.2 m h=1.2 m, w=0.4 m σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
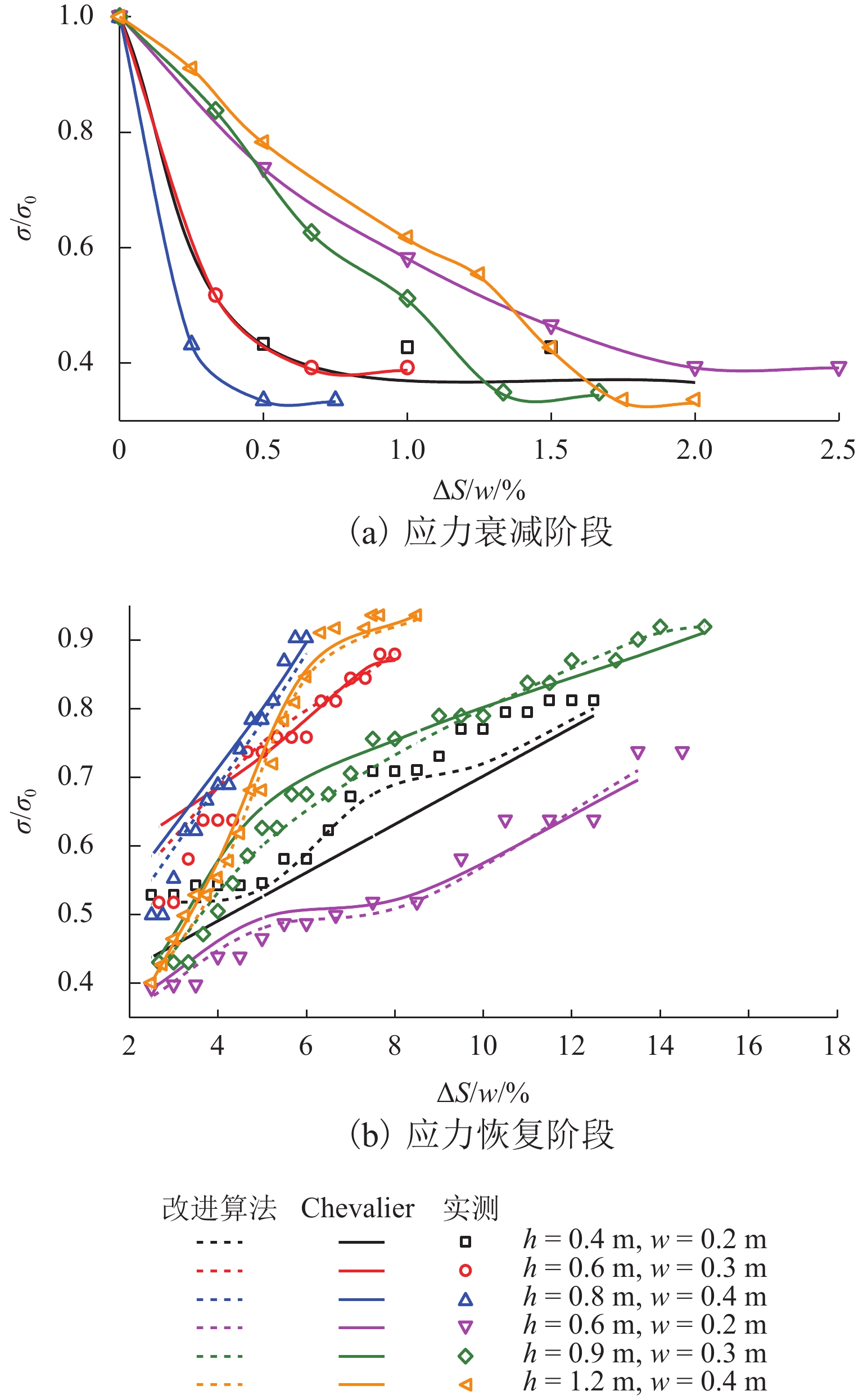
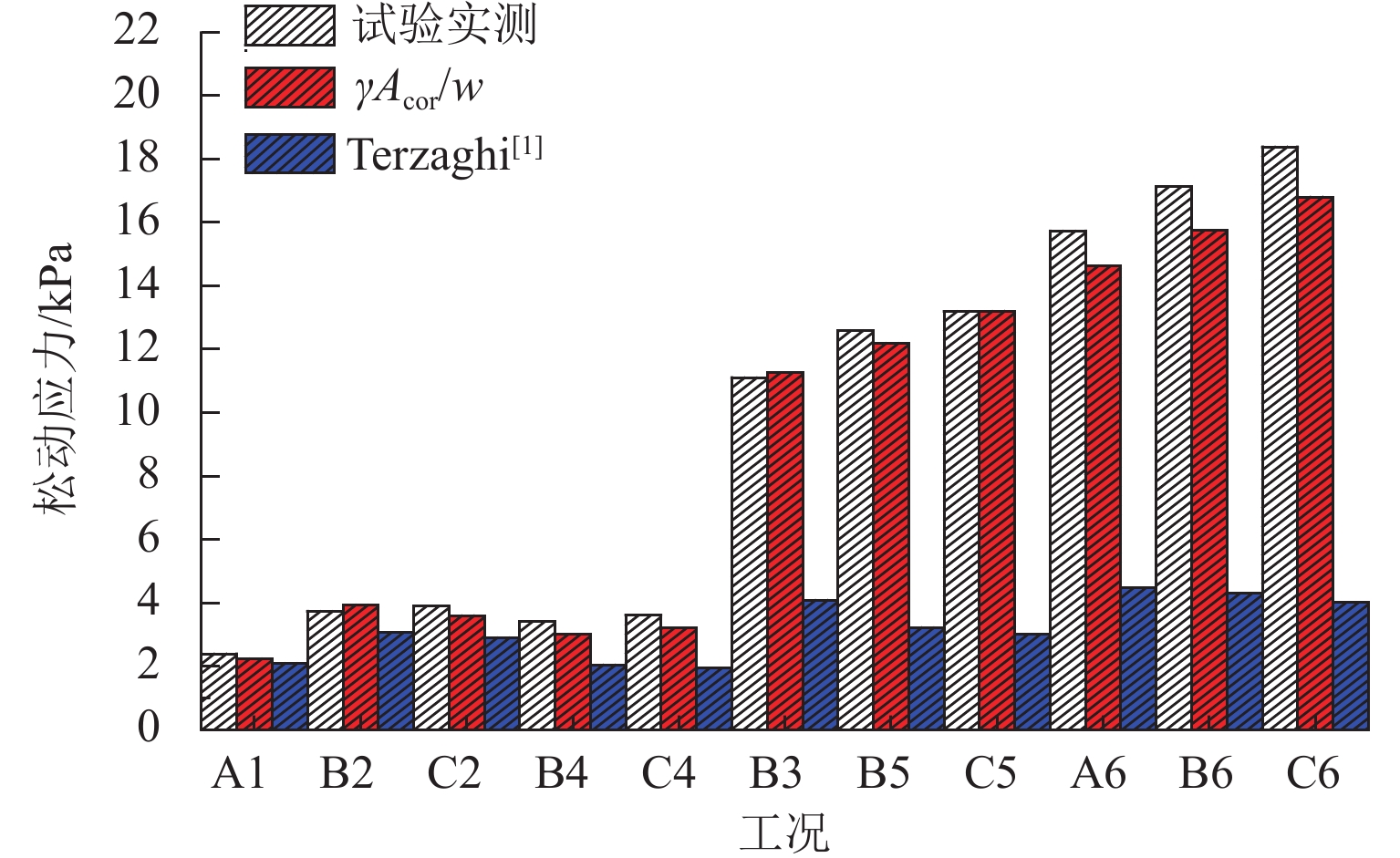
%31.4 0.43 0.81 1.2 11 0.33 0.90 0.5 5.7 0.39 0.89 2.0 14 0.34 0.93 1.8 7.2 34.5 0.36 0.83 1.5 10 0.34 0.92 1.0 5.5 0.38 0.90 3.2 12 0.32 0.95 1.8 6.5 38.4 0.35 0.84 2.0 9 0.33 0.93 1.3 5.2 0.37 0.90 3.3 11 0.31 0.96 2.3 5.8 将活动门上应力大小近似为松动核心区域内土重，通过Acor计算松动土压力（γAcor/w），同试验结果以及Terzaghi[1]松动土压力计算结果进行对比，如图11. 由图可知：低填土试验组（h=0.4 m，h=0.6 m）中，核心区Acor计算结果与Terzaghi[1]计算方法所得应力大小同试验实测临界应力大小相近；高填土试验组（h=0.8 m，h=1.2 m）中Acor计算结果同实测极限应力大小相近，Terzaghi[1]计算误差相对较大. 利用Acor计算松动应力的改进算法相比Terzaghi[1]基于竖直破坏面的应力计算方法具有更好的适用性. 当填土高度较低时，核心区形态近似三角形，改进算法适用于计算临界应力；当填土高度较高时，核心区形态为四边形，改进算法适用于计算极限应力.
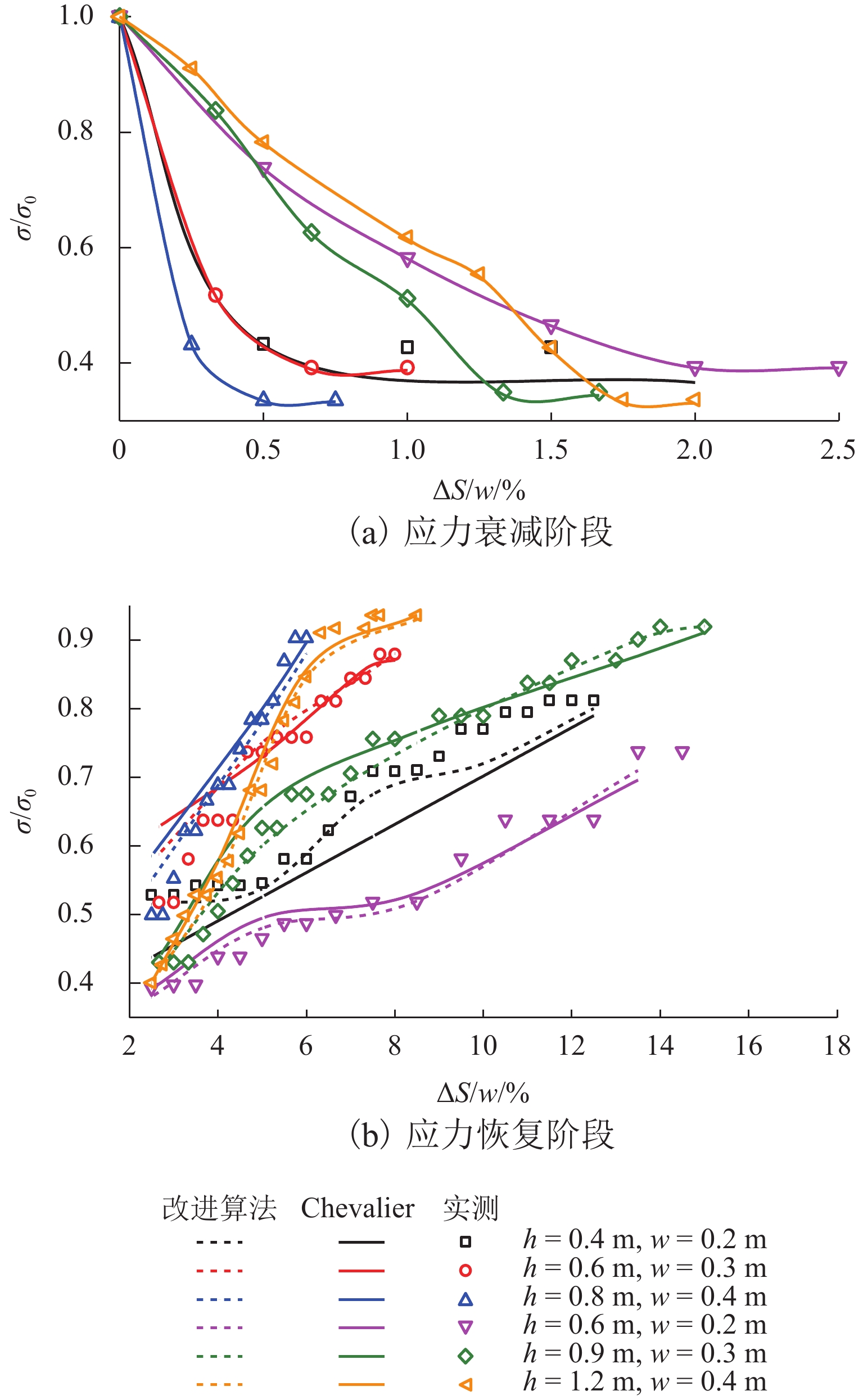
将试验结果与Chevalier等[11]松动应力-活动门下移近似计算结果进行比较，如图12所示. 由图可知，应力衰减阶段与恢复阶段，Chevalier等[11]计算结果均与试验结果接近. Chevalier等[11]采用三角形滑移面区域面积SΔ计算恢复阶段应力（σ=γ(SΔ/w × ΔS))，利用表4中Acor替代SΔ计算出的所得应力与实测结果具有更高的吻合程度（如图12（b）），进一步验证了本文计算方法的实用性.
图 12 松动应力-活动门下移近似计算Figure 12. Approximate calculation of loosening stress-downward movement of trapdoor3. 结 论
通过Trapdoor试验对砂土拱效应滑移面几何轮廓特征以及松动应力-活动门下移曲线特征开展了较为系统的研究. 获得了填土高度、活动门下移和宽度以及砂土密度对上述特征量的影响规律. 通过对松动核心区几何形态的研究，提出了考虑松动区形态演变的松动土压力计算方法. 主要结论如下：
1） 随着活动门下移，滑移面轮廓的演化过程为三角形—子弹头形—椭圆形. 随着填土高度的增加，松动核心区形状演变过程为三角形—梯形—矩形.
2） 初始、次级滑移面高度随活动门下移递增，与内摩擦角呈正相关. 第Ⅲ级滑移面高度与内摩擦角呈负相关，第Ⅲ级滑移面拐点高度随活动门下移递减. 大小顺序为hs31<hs1<hs2<hs3. 初始、次级滑移面夹角随活动门下移先增后减，第Ⅲ级滑移面夹角随活动门下移递增，大小顺序为θ1<θ2<θ31≈θ32.
3） σcri/σ0∈（0.3，0.45）；ΔScri/w∈（0.5%，3.5%）；σult/σ0∈（0.8，1.0）；ΔScri/w∈（5.0%，15.0%）. 填土高度越高，内摩擦角越大，临界应力越小，临界位移越大. 极限应力与极限位移同填土高度呈正相关，同活动门宽度呈负相关.
4） 松动核心区高度为填土高度的0.5倍～0.8倍，松动核心区夹角与松动核心区面积随内摩擦角的增加近似线性递减. 相比Terzaghi土柱理论和Chevalier等近似计算，利用Acor的松动土压力计算方法与试验结果更吻合.
-
图 4 滑移面典型轮廓及其等值线（粗砂， Dr=0.860）
Figure 4. Typical contours of slip surface and its contour line （coarse sand， Dr = 0.860）
图 5 滑移面几何轮廓特征参数释义
Figure 5. Interpretation of geometric contour parameters of slip surface
图 6 滑移面高度随活动门下移变化
Figure 6. Change of slip surface height with downward movement of trapdoor
图 7 第Ⅲ级滑移面拐点高度随活动门下移变化
Figure 7. Change of inflection point height of level-Ⅲ slip surface with downward movement of trapdoor
图 8 滑移面夹角随活动门下移的变化
Figure 8. Change of angles of slip surface with downward movement of trapdoor
图 9 2类典型试验组中松动核心区形态
Figure 9. Morphology of core loosening zones in two types of typical test groups
图 10 松动应力-活动门下移归一化曲线
Figure 10. Normalization curves of loosening stress-downward movement of trapdoor
图 12 松动应力-活动门下移近似计算
Figure 12. Approximate calculation of loosening stress-downward movement of trapdoor
表 1 砂物理力学参数
Table 1. Physical and mechanical parameters of sand
种类 d50/mm 不均匀
系数 cu曲率系数 cc 最大干密度
ρdmax/（kg·m−3）最小干密度
ρdmin/（kg·m−3）Dr 内摩擦角 φ/（°） 细砂 0.27 2.67 0.95 1719 1318 0.208 31.4 中砂 0.32 2.57 1.34 1616 1354 0.607 34.5 粗砂 0.53 2.92 0.84 1703 1439 0.860 38.4 
下载: 导出CSV
表 2 Trapdoor试验组工况
Table 2. Trapdoor test conditions
试验组工况 种类 h/m w/m 传感器埋设间距/m A1 细砂 0.4 0.2 0.1 A2 0.6 0.3 0.1 A3 0.8 0.4 0.2 A4 0.6 0.2 0.1 A5 0.9 0.3 0.2 A6 1.2 0.4 0.2 B1 中砂 0.4 0.2 0.1 B2 0.6 0.3 0.1 B3 0.8 0.4 0.2 B4 0.6 0.2 0.1 B5 0.9 0.3 0.2 B6 1.2 0.4 0.2 C1 粗砂 0.4 0.2 0.1 C2 0.6 0.3 0.1 C3 0.8 0.4 0.2 C4 0.6 0.2 0.1 C5 0.9 0.3 0.2 C6 1.2 0.4 0.2
下载: 导出CSV
表 3 稳定滑移面高度-内摩擦角
Table 3. Stable slip surface height-internal friction angle
m φ/（°） h=0.4 m, w=0.2 m h=0.8 m, w=0.4 m h=0.6 m, w=0.2 m h=0.9 m, w=0.3 m hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 hs1 hs2 hs3 hs31 31.4 0.225 0.250 0.400 — 0.625 0.750 — — 0.363 0.425 — — 0.275 0.523 0.875 0.675 34.5 0.238 — — — 0.625 0.788 0.725 0.352 0.338 0.463 0.600 0.425 0.312 — — — 38.4 0.225 0.263 — — 0.688 0.763 — — 0.413 0.488 0.525 0.450 0.337 0.575 0.900 0.708 注：部分试验未形成次级或第Ⅲ级滑移面，以“—”表示.
下载: 导出CSV
表 4 松动核心区几何特征
Table 4. Geometric characteristics of core loosening area
φ/（°） h/m w/m hd/m ψ/（°） Acor/m2 Acor/SAEFD 31.4 0.4 0.2 0.40 81.5 0.036 0.45 1.2 0.4 0.85 88.5 0.385 0.80 34.5 0.8 0.4 0.75 88.5 0.231 0.72 0.6 0.2 0.55 85.0 0.057 0.48 38.4 0.6 0.2 0.60 83.5 0.056 0.47 1.2 0.4 0.80 89.0 0.375 0.78
下载: 导出CSV
表 5 临界、极限状态特征
Table 5. Characteristics of critical and ultimate states
φ/
（°）h=0.4 m, w=0.2 m h=0.8 m, w=0.4 m h=0.6 m, w=0.2 m h=1.2 m, w=0.4 m σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%σcri/
σ0σult/
σ0ΔScri/w/
%ΔSult/w/
%31.4 0.43 0.81 1.2 11 0.33 0.90 0.5 5.7 0.39 0.89 2.0 14 0.34 0.93 1.8 7.2 34.5 0.36 0.83 1.5 10 0.34 0.92 1.0 5.5 0.38 0.90 3.2 12 0.32 0.95 1.8 6.5 38.4 0.35 0.84 2.0 9 0.33 0.93 1.3 5.2 0.37 0.90 3.3 11 0.31 0.96 2.3 5.8
下载: 导出CSV
-
[1] TERZAGHI K. Theoretical soil mechanics[M]. Hoboken: John Wiley & Sons, Inc. , 1943. [2] COSTA Y D, ZORNBERG J G, BUENO B S, et al. Failure mechanisms in sand over a deep active trapdoor[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(11): 1741-1753. doi: 10.1061/(ASCE)GT.1943-5606.0000134 [3] IGLESIA G R, EINSTEIN H H, WHITMAN R V. Investigation of soil arching with centrifuge tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(2): 04013005.1-04013005.13. [4] RUI R, VAN TOL A F, XIA Y Y, et al. Investigation of soil-arching development in dense sand by 2D model tests[J]. Geotechnical Testing Journal, 2016, 39(3): 20150130.1-20150130.16. [5] ESKIŞAR T, OTANI J, HIRONAKA J. Visualization of soil arching on reinforced embankment with rigid pile foundation using X-ray CT[J]. Geotextiles and Geomembranes, 2012, 32: 44-54. doi: 10.1016/j.geotexmem.2011.12.002 [6] HONG W P, LEE J H, LEE K W. Load transfer by soil arching in pile-supported embankments[J]. Soils and Foundations, 2007, 47(5): 833-843. doi: 10.3208/sandf.47.833 [7] AHMADI A, SEYEDI HOSSEININIA E. An experimental investigation on stable arch formation in cohesionless granular materials using developed trapdoor test[J]. Powder Technology, 2018, 330: 137-146. doi: 10.1016/j.powtec.2018.02.011 [8] LAI H J, ZHENG J J, ZHANG R J, et al. Classification and characteristics of soil arching structures in pile-supported embankments[J]. Computers and Geotechnics, 2018, 98: 153-171. doi: 10.1016/j.compgeo.2018.02.007 [9] SANTICHAIANAINT K. Centrifuge modeling and analysis of active trapdoor in sand[D]. Boulder: University of Colorado at Boulder. [10] GUO P J, ZHOU S H. Arch in granular materials as a free surface problem[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(9): 1048-1065. doi: 10.1002/nag.1137 [11] CHEVALIER B, COMBE G, VILLARD P. Experimental and discrete element modeling studies of the trapdoor problem: influence of the macro-mechanical frictional parameters[J]. Acta Geotechnica, 2012, 7(1): 15-39. doi: 10.1007/s11440-011-0152-5 [12] DEWOOLKAR M M, SANTICHAIANANT K, KO H Y. Centrifuge modeling of granular soil response over active circular trapdoors[J]. Soils and Foundations, 2007, 47(5): 931-945. doi: 10.3208/sandf.47.931 [13] HAN J, WANG F, AL-NADDAF M, et al. Progressive development of two-dimensional soil arching with displacement[J]. International Journal of Geomechanics, 2017, 17(12): 04017112.1-04017112.12. [14] IGLESIA G R, EINSTEIN H H, WHITMAN R V. Validation of centrifuge model scaling for soil systems via trapdoor tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1075-1089. doi: 10.1061/(ASCE)GT.1943-5606.0000517 [15] KEAWSAWASVONG S, UKRITCHON B. Undrained stability of an active planar trapdoor in non-homogeneous clays with a linear increase of strength with depth[J]. Computers and Geotechnics, 2017, 81: 284-293. doi: 10.1016/j.compgeo.2016.08.027 [16] PARDO G S, SÁEZ E. Experimental and numerical study of arching soil effect in coarse sand[J]. Computers and Geotechnics, 2014, 57: 75-84. doi: 10.1016/j.compgeo.2014.01.005 [17] HAN G X, GONG Q M, ZHOU S H. Soil arching in a piled embankment under dynamic load[J]. International Journal of Geomechanics, 2015, 15(6): 4014094.1-4014094.11. [18] SADREKARIMI J, ABBASNEJAD A. Arching effect in fine sand due to base yielding[J]. Canadian Geotechnical Journal, 2010, 47(3): 366-374. doi: 10.1139/T09-107 [19] KHOSRAVI M H, PIPATPONGSA T, TAKEMURA J. Theoretical analysis of earth pressure against rigid retaining walls under translation mode[J]. Soils and Foundations, 2016, 56(4): 664-675. doi: 10.1016/j.sandf.2016.07.007 [20] YAO Q Y, DI H G, JI C, et al. Ground collapse caused by shield tunneling in sandy cobble stratum and its control measures[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(10): 5599-5614. doi: 10.1007/s10064-020-01878-9 [21] 陈强,董桂城,王超,等. 基于透明土技术的桩后土拱效应特征分析[J]. 西南交通大学学报,2020,55(3): 509-522.CHEN Qiang, DONG Guicheng, WANG Chao, et al. Characteristics analysis of soil arching effect behind pile based on transparent soil technology[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 509-522. [22] 周思危. 砂土平面土拱形状及沉降特性研究[D]. 长沙: 中南大学, 2019. [23] TAYLOR Z J, GURKA R, KOPP G A, et al. Long-duration time-resolved PIV to study unsteady aerodynamics[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(12): 3262-3269. doi: 10.1109/TIM.2010.2047149 [24] HADAD T, GURKA R. Effects of particle size, concentration and surface coating on turbulent flow properties obtained using PIV/PTV[J]. Experimental Thermal and Fluid Science, 2013, 45: 203-212. doi: 10.1016/j.expthermflusci.2012.11.006 [25] 郑云,刘志祥,余志祥,等. 基于PIV试验的积雪平屋面风场特性研究[J]. 西南交通大学学报,2023,58(2): 430-437,461.ZHENG Yun, LIU Zhixiang, YU Zhixiang, et al. Wind field characteristics of snow-covered low-rise building roof based on PIV experiments[J]. Journal of Southwest Jiaotong University, 2023, 58(2): 430-437,461. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 388
- HTML全文浏览量: 177
- PDF下载量: 56
- 被引次数: 0