Passenger Flow Assignment Method for Urban Rail Transit Networks Based on Inference of Spatiotemporal Path
-
摘要:
针对城市轨道交通客流分布推算问题,根据自动客票采集系统(AFC)数据和列车时刻表数据,提出基于乘客出行时空路径推算的网络客流分配方法. 首先,利用前述两类数据估算乘客出行时间参数;其次,使用基于插点法的可行路径搜索算法得到全网各OD (origin–destination)对的可行路径集合;再次,基于乘客进出站刷卡信息、列车时刻表数据及匹配的可行路径集合,构建乘客有效出行路径集和列车集的推算模型,获得有效出行结果集;进一步,结合所得有效结果集合与列车载客量限制,并根据列车时刻表完成列车运行推演,确定唯一的有效出行路径和所乘列车;最后,设计开发基于C# 语言的城市轨道交通网络客流推算系统,对某城市轨道交通工作日客流数据进行案例研究. 结果表明:客流推算系统所得的断面客流推算值与运营参照值的平均差异上、下行分别为2.03%、3.90%;列车满载率变化趋势符合线路路由特点;早晚高峰时段换乘站的换乘客流来源站点固定,但早高峰来源量比例较晚高峰稳定.
Abstract:To calculate passenger flow distribution in urban rail transits, a passenger flow assignment method based on inference of passenger spatiotemporal path is proposed with the data collected from the automatic fare collection (AFC) and train timetables. Firstly, the passenger travel time parameters are estimated with the above two types of data. The feasible path set of each origin–destination (OD) in the whole network is then obtained by using the feasible path search algorithm based on the node-inserting method. Subsequently, according to the inbound and outbound information from passenger smart cards, train timetable and matched feasible path set, an inference model of passenger effective travel path and train set is built to obtain the effective travel result set. Finally, a train operation is developed with the obtained effective result set, train load capacity, and train timetable to determine the sole effective travel path and riding train. A calculation system for the passenger flow in urban rail transit networks is designed and developed, and a case study is conducted on weekday passenger flow data of urban rail transit. The results show that the average difference of section passenger flow between the calculated results and operation reference data of upstream and downstream is 2.03% and 3.90%, respectively, and the trend of train load rate confirms to the line routing. Moreover, the source of transfer passenger flow at transfer station is stable in the morning and evening peaks, but the proportion of sources in the morning peak is more stable that in the evening peak.
-
城市轨道交通网络客流分配的关键在于确定乘客的有效出行路径及所乘列车,现有乘客刷卡数据仅记录进、出站点和时刻信息,无法准确获知客流在线网中的分布情况. 既有客流分配研究主要集中于基于路径的集计分配和乘客出行时空路径推算.
基于路径的集计分配方法需首先构建包含多效用因素的广义费用函数[1-2],随后使用线性规划[1]求解路径配流结果或Logit 衍生模型[2-3]刻画乘客出行路径选择行为,以得到客流分配结果. 基于路径的集计分配方法无法保证所分配路径上存在有效出行服务,易导致乘客出行结果估计的偏差. 为保证客流分配的有效性,需进行针对乘客-路径-列车匹配的时空路径推算. 乘客出行时空路径推算使用自动客票采集系统(AFC)数据和列车时刻表数据[4-5],估计乘客出行路径及所乘列车,流程为网络出行时间参数估计、乘客出行前后路径选择[6]、采用列车运行仿真[7]或匹配概率模型[8]确定所乘列车,以得到乘客的有效出行结果.
综上,有效合理的客流推算依赖于准确推算乘客的出行时空路径,需完成可行物理路径集的确定和乘客与列车的匹配,以确保出行路径的物理可达性和动态服务的有效性. 本文基于AFC 数据和列车时刻表数据,以乘客时空路径推算方法研究城市轨道交通网络客流分配问题. 在此基础上,设计开发基于C# 语言的客流推算系统.
1. 网络客流推算方法
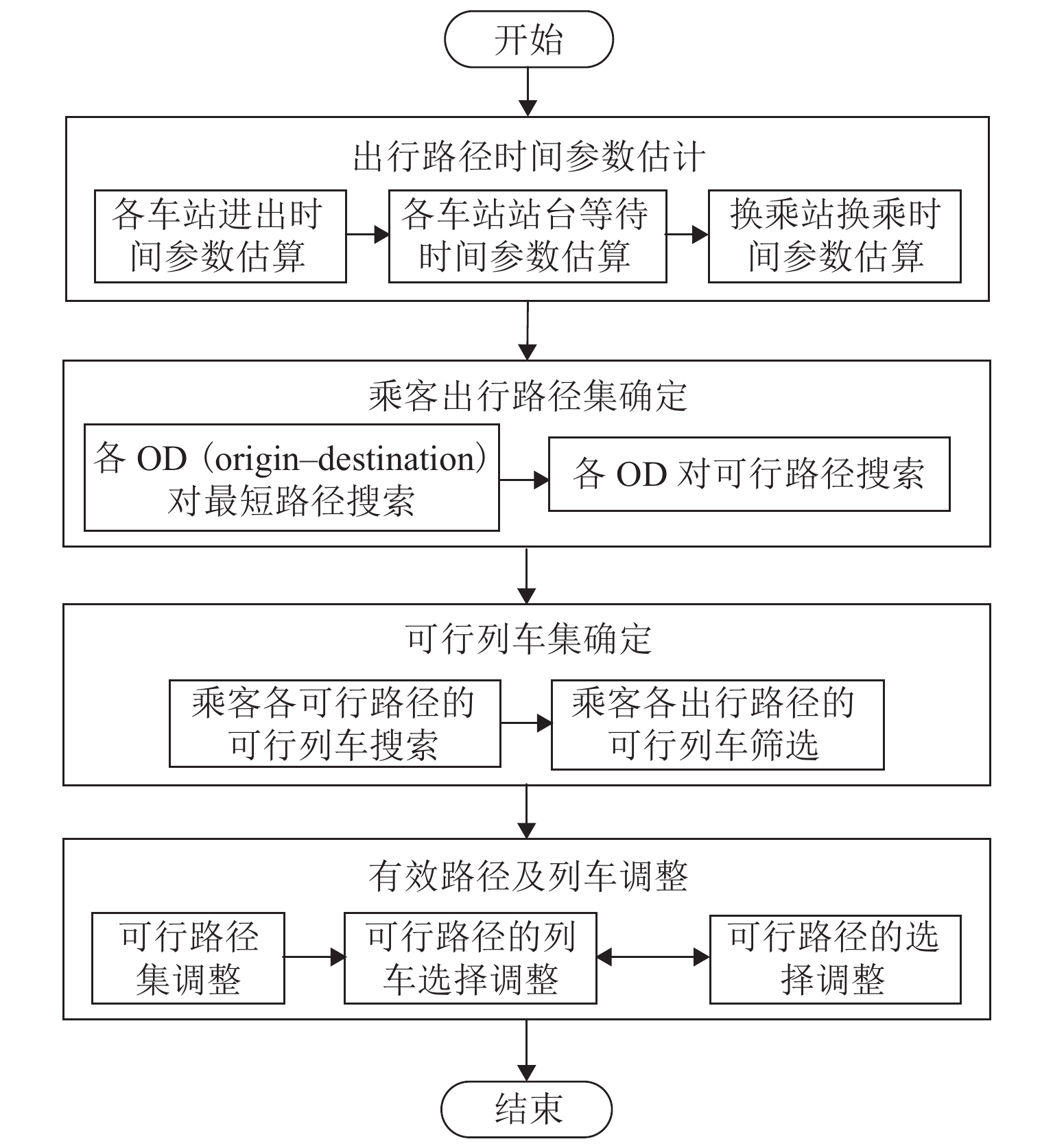
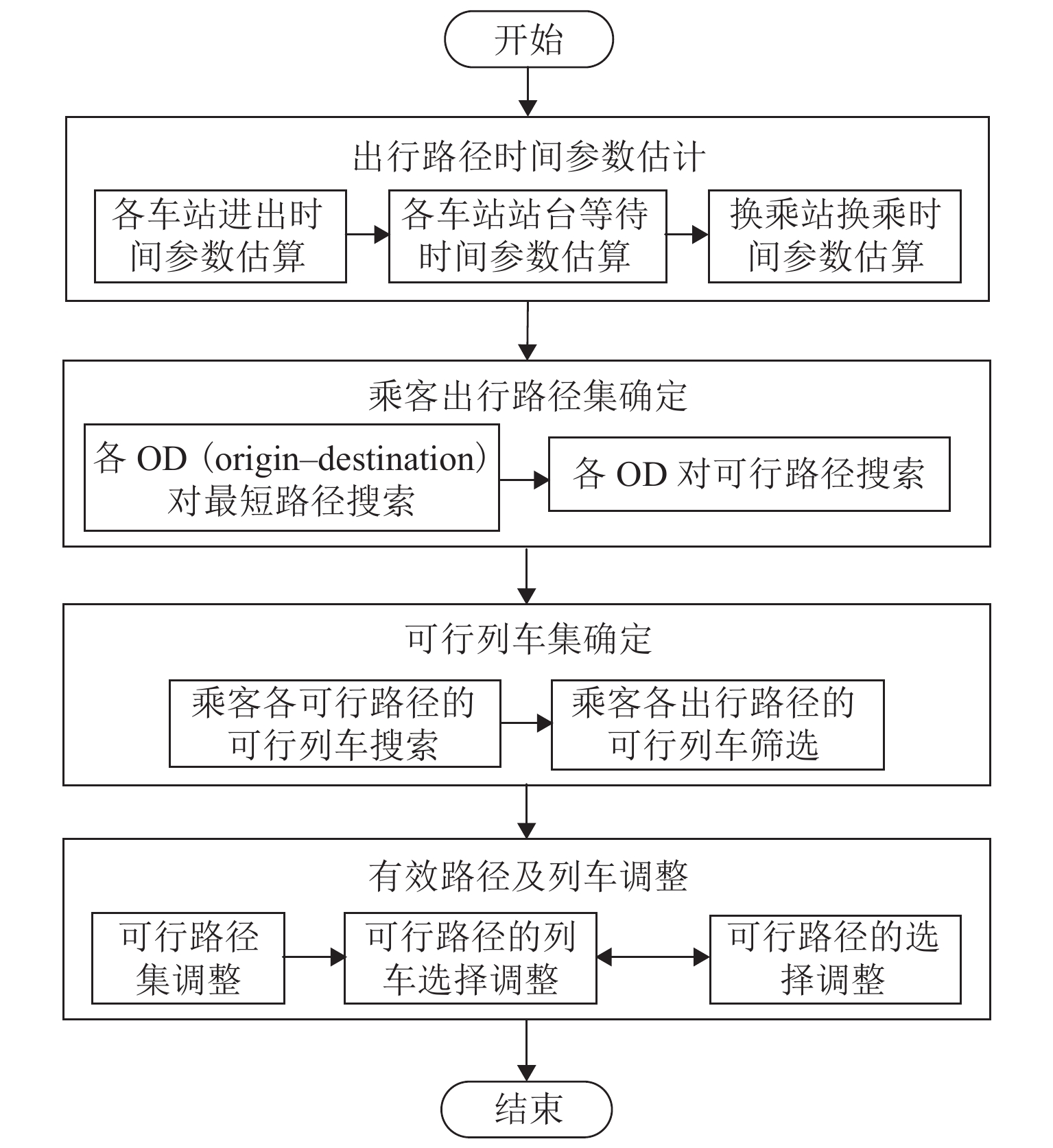
网络客流推算方法包括乘客出行路径的生成和基于乘客出行路径的可行列车搜索与匹配2部分:第1部分包括出行时间参数的估计和可行路径集的确定;第2部分首先进行乘客与出行路径集的匹配,随后在相应出行路径上完成可行列车集的搜索与确定.
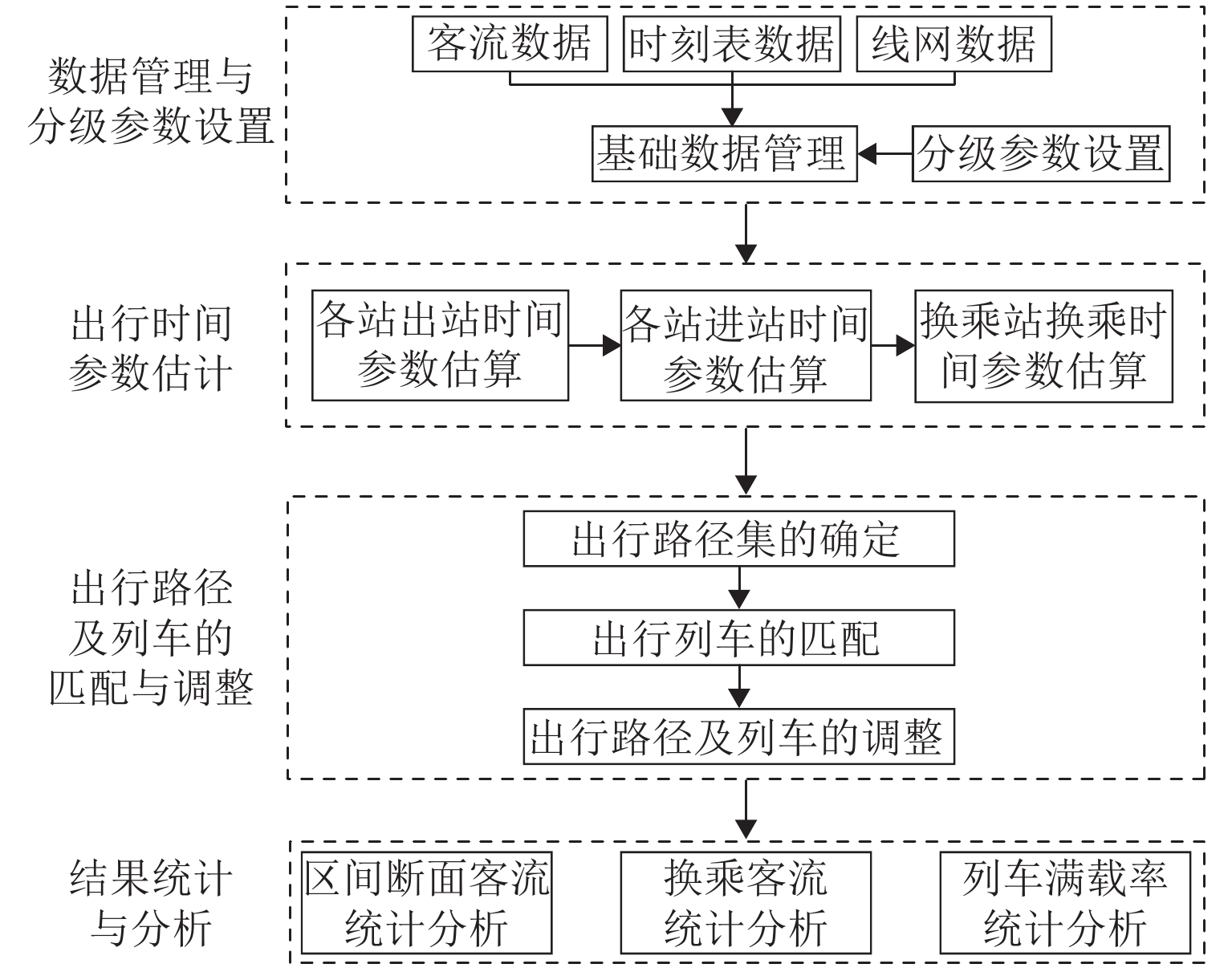
此外,乘客有效出行结果中可能存在可行路径或可行列车不唯一的情况. 此时,需要先完成有效路径的选择优先级排序,然后,确定可行列车的检验次序,最后,以路径优先级及路径所含各可行列车的检验次序完成列车运行过程推演,从而获得各个乘客唯一的有效出行路径及列车,即进行“有效路径及列车调整”. 客流推算流程如图1所示.
本文所使用的单个乘客f 的AFC 数据包括进站站点Of、出站站点Df、进站刷卡时刻tf,et、出站刷卡时刻tf,ex,时刻表数据内容包括各列车途经站点及到发时刻. 为便于推算,提出以下假设:
1) 网络中出行的乘客按路径换乘次数和出行时间的综合排序选择可行路径.
2) 忽略乘客在车站中的微观行为,乘客以刷卡进站时刻的先后顺序上车,并受到列车载客容量的限制.
3) 各线均开行站站停的单一交路列车.
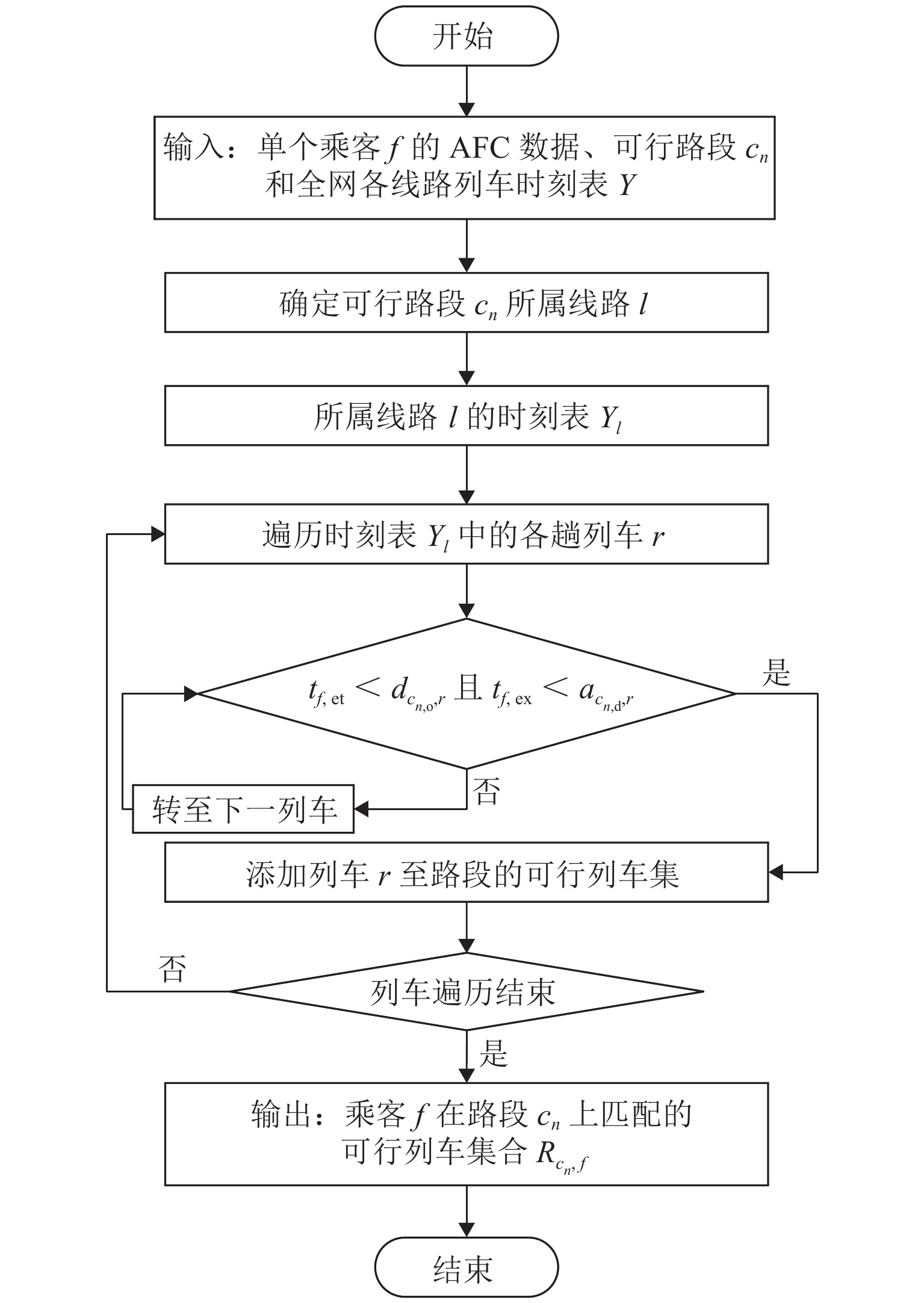
为便于后续描述,统一将可行路径p以换乘站拆分为路段集Cp(非换乘路径不拆分). 网络客流推算的核心在于生成单个乘客f 在其第n个可行路段cn∈Cp的可行列车集Rcn,f. 其匹配条件为:所匹配的可行列车r在cn起点cn,o的出站时刻dcn,o,r应晚于乘客f 进站时刻tf,et,且在终点cn,d的到达时刻acn,d,r应早于乘客出站时刻tf,ex(算法1),如图2所示.
1.1 乘客出行时间参数估计
城市轨道交通系统中乘客出行时间包括起点站的进站时间、起点站的站台等待时间、在车时间、换乘站的换乘时间、换乘站的站台等待时间和终点站的出站时间[9]. 其中,在车时间可以由列车时刻表数据直接得到,其余时间无法直接从AFC数据中得到,需用可行路径单一的本线进出的和换乘方向明确的一次换乘的乘客样本进行估计. 在给定AFC数据、列车时刻表数据及线网数据后,依次估算各车站在高峰时段(t=1)和平峰时段(t=0)的进站时间均值μac,t和方差σ2ac,t、换乘站换乘时间均值μtr,t和方差σ2tr,t、出站时间均值μeg,t和方差σ2eg,t. 结合列车时刻表可得全网各OD的出行时间均值μod,t,用于生成可行路径集.
1.1.1 进出站时间参数估计
对于本线进、出乘客,在进、出站刷卡时间范围内仅有唯一可行列车的情况下,可以准确计算乘客的进、出站时间. 本线进、出乘客f在起点站的进站时间、终点站的出站时间可由其本线出行路径pb上唯一可行列车的出站时刻、到站时刻及乘客的进、出站刷卡时刻计算得到,如式(1)、(2)所示. 对所得进、出站时间样本集去除极端异常值后,计算样本均值及方差,以此分别作为对应时段t在相应起点站O的进站时间和终点站D的出站时间均值μac,t,O与μeg,t,D.
tac,f,Of=dOf,r−tf,et,|Rpb,f|=1, (1) teg,f,Df=tf,ex−aDf,r,|Rpb,f|=1, (2) 式中:tac,f,Of、teg,f,Df为本线进出乘客f分别在站点Of的进站时间、站点Df的出站时间;dOf,r和aDf,r分别为列车r在站点Of和站点Df的发车时刻和到站时刻;|Rpb,f|=1表示在本线路径pb上的可行列车唯一.
1.1.2 换乘时间参数估计
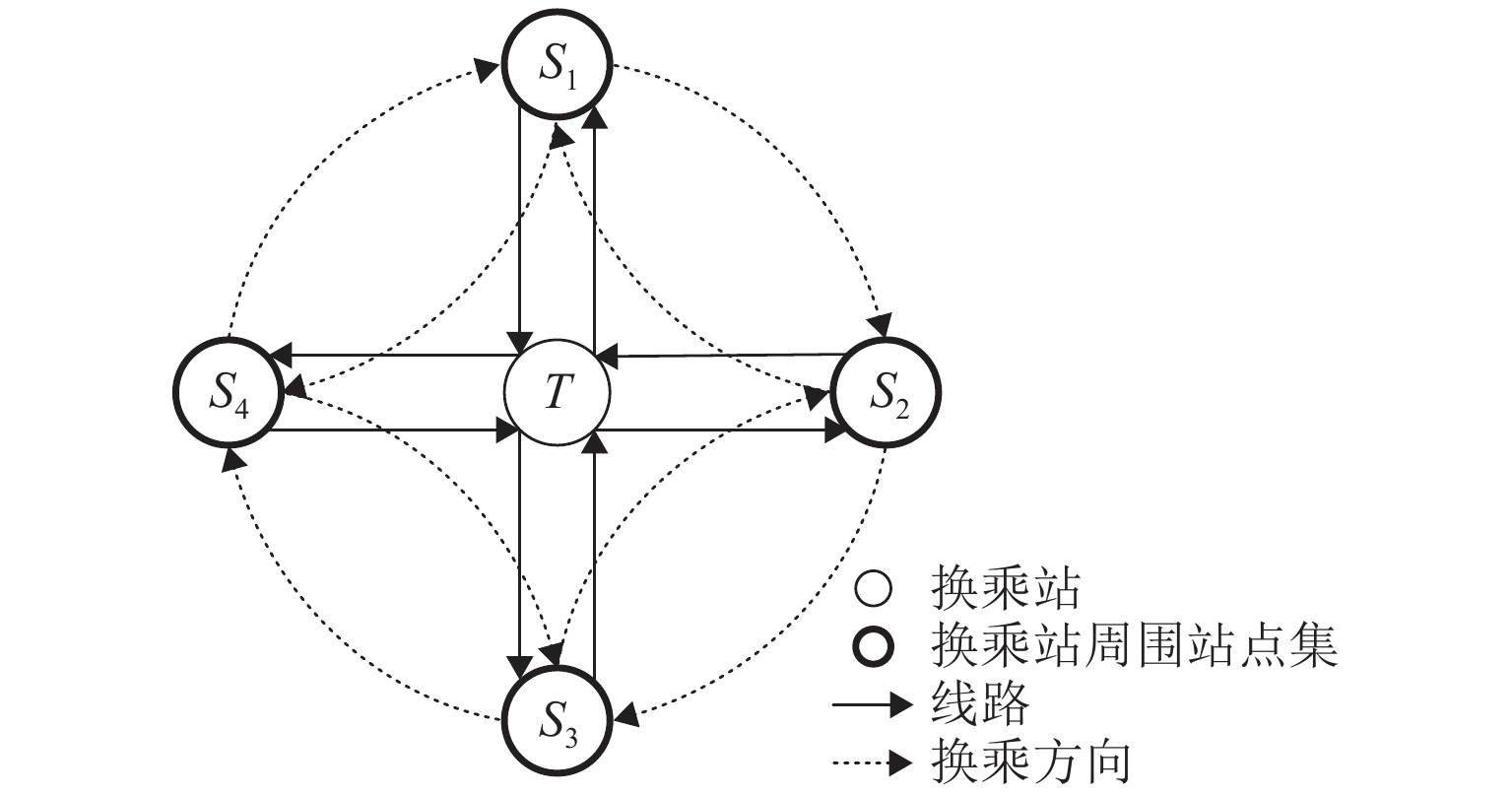
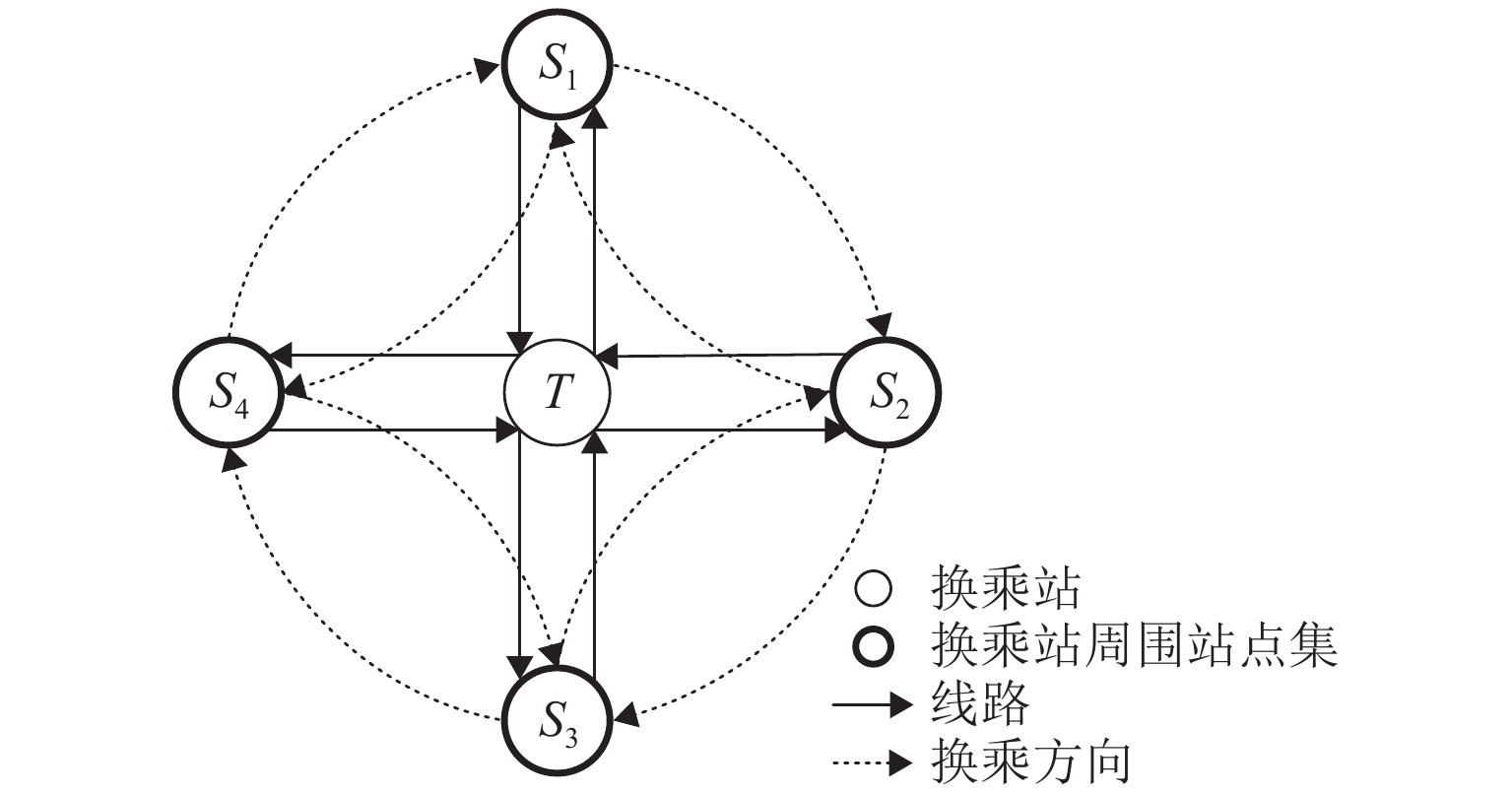
该时间参数可由一次换乘乘客进行估计. 对此,可以换乘站T为中心,整合其周围车站集(S1~S4),如图3所示,构建一次换乘乘客的筛选OD表,并以该表筛选得到在换乘站的换乘时间未确定的一次换乘乘客. 因此,其换乘时间tT,f可由对应时段进站站点的进站时间均值μac,t,Of、出站站点的出站时间均值μeg,t,Df、行程时间tf和首路段n = 1至末路段n = 2列车运行时间和∑2n=1ˉtcn得到,如式(3)所示,其中,ˉtcn为路段cn上列车运行时间均值. 对所得换乘站T在换乘方向di的换乘时间样本集去除极端异常值后,计算样本均值μT,t,di,即为该时段换乘站T在换乘方向di的换乘时间参数估计值.
tT,f=tf−∑2n=1ˉtcn−μac,t,Of−μeg,t,Df, (3) 式中:tT,f为乘客f在换乘站T的换乘时间.
1.2 乘客可行物理路径集生成
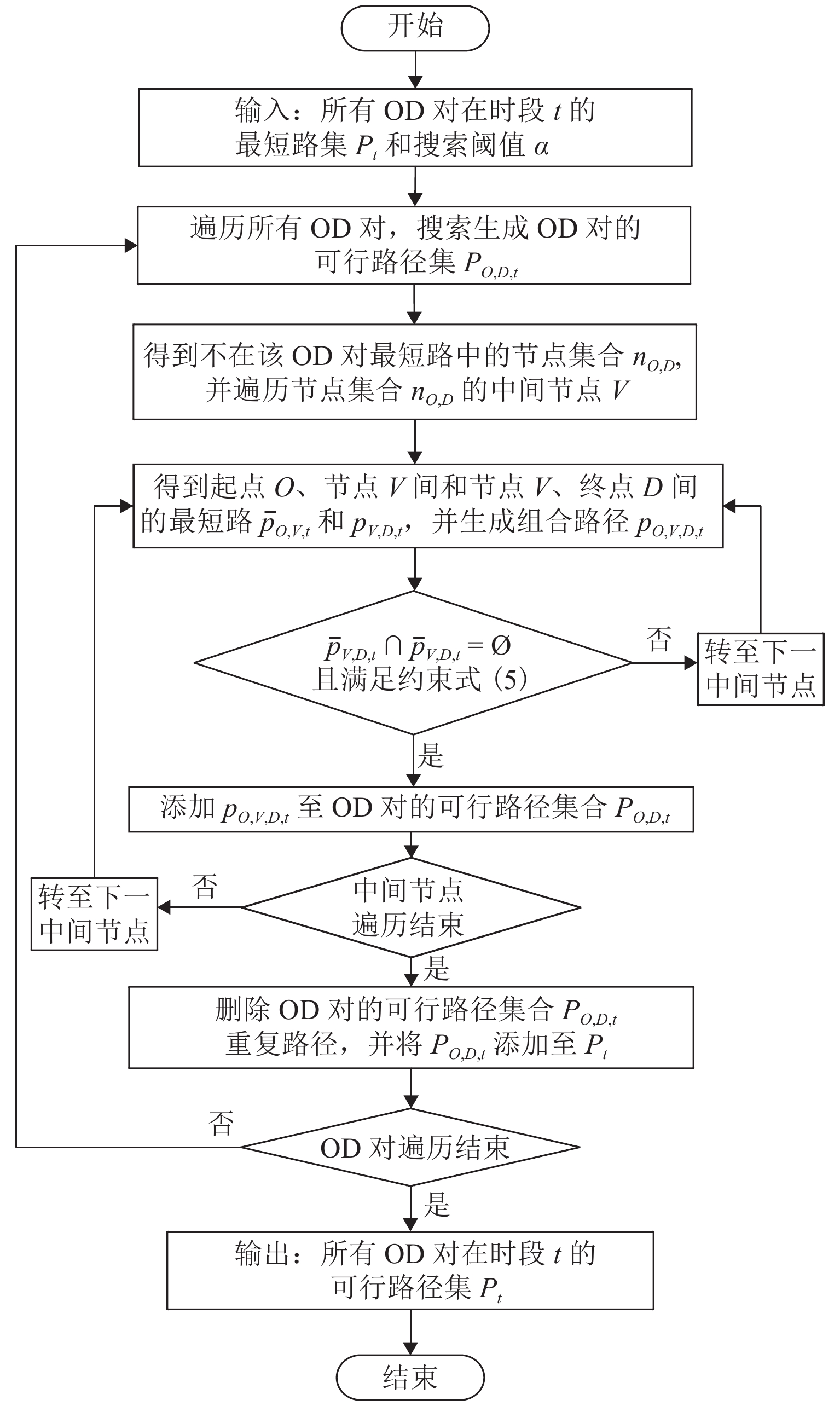
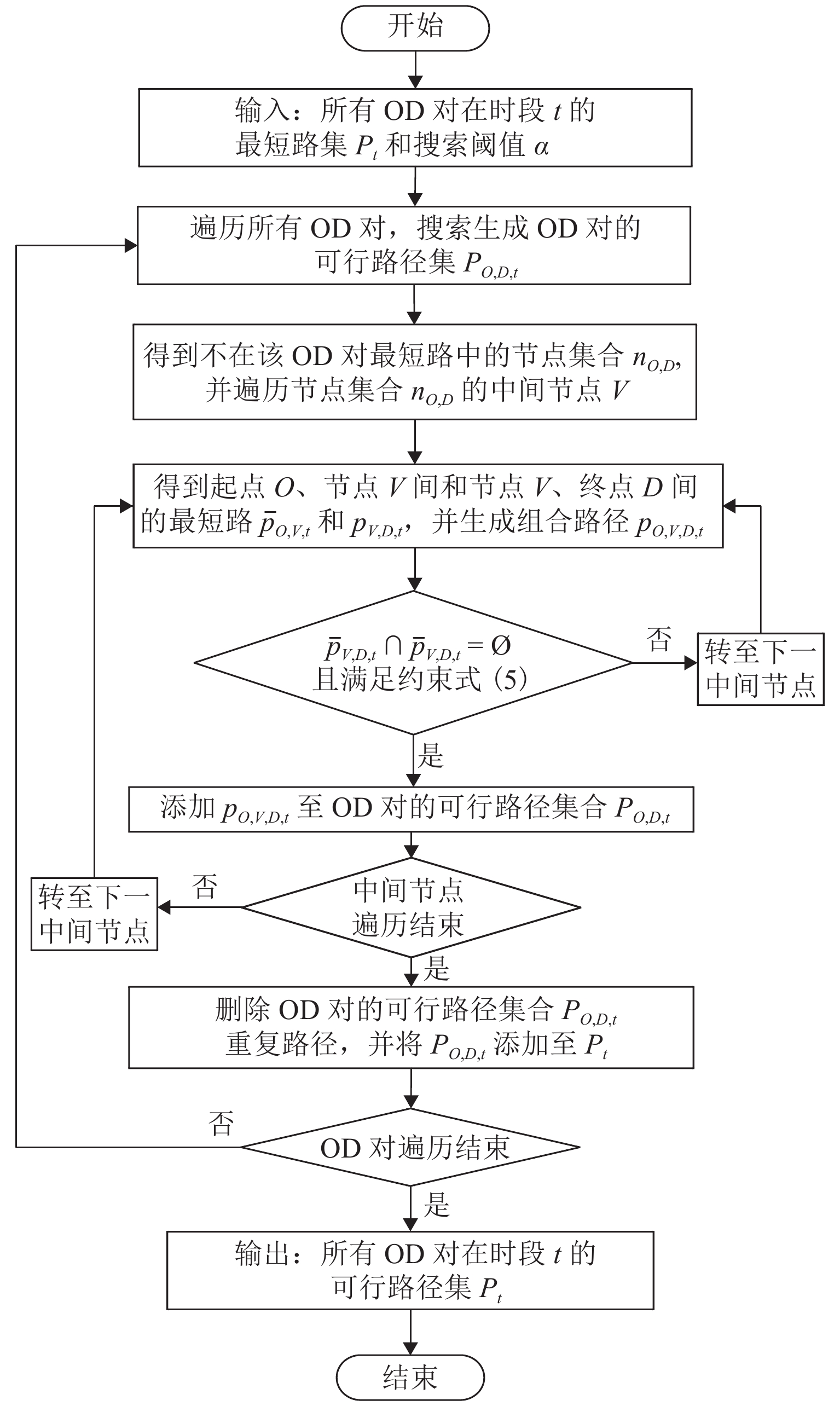
根据所估计的出行时间参数,乘客可行路径集生成的目标为获得各OD对满足时间阈值约束的可行物理路径集P,如式(4)~(6)所示. 先使用Dijkstra算法得到全网各OD对在高峰时段和平峰时段的最短路径集ˉP,随后,使用图4所示的基于插点的可行路径搜索算法(算法2)得到所有OD对的可行路径集合P,其包含了不超过各OD对最短路出行时间 α 倍的所有可行路径,如式(7)所示约束.
P={Pt|t∈{0,1}}, (4) Pt={PO,D,t|O,D∈S}, (5) PO,D,t={pO,D,t,1,pO,D,t,2,⋯,pO,D,t,j,⋯}, (6) x(pO,D,t,j)⩽ (7) 式中:Pt为时段t各OD对的可行路径集;S为线网车站集; {P_{O,D,t}} 为时段t单个OD对的可行路径集; {p_{O,D,t,j}} 为时段t单个OD对的第j条可行路径; x(·)为路径的出行时间.
算法2的原理为:对于单个OD对而言,其次短路中存在不属于该OD对最短路的节点,因而可对不在该OD对最短路径上的节点集 {n_{OD}} 进行遍历,并将起点O到节点V ( V \in {n_{OD}} )的最短路 {\bar p_{O,V,t}} 与节点V到终点D的最短路 {\bar p_{V,D,t}} 进行组合,若 {\bar p_{O,V,t}} 与 {\bar p_{V,D,t}} 无回头路关系,即 {\bar p_{O,V,t}} 与 {\bar p_{V,D,t}} 上的车站序列不存在重叠( {\bar p_{O,V,t}} \cap {\bar p_{V,D,t}} = Ø),且满足时间阈值约束,则生成组合路径 {p_{O,V,D,t}} ,最后删除重复路径,从而得到该OD对的可行路径集.
1.3 乘客可行列车集确定
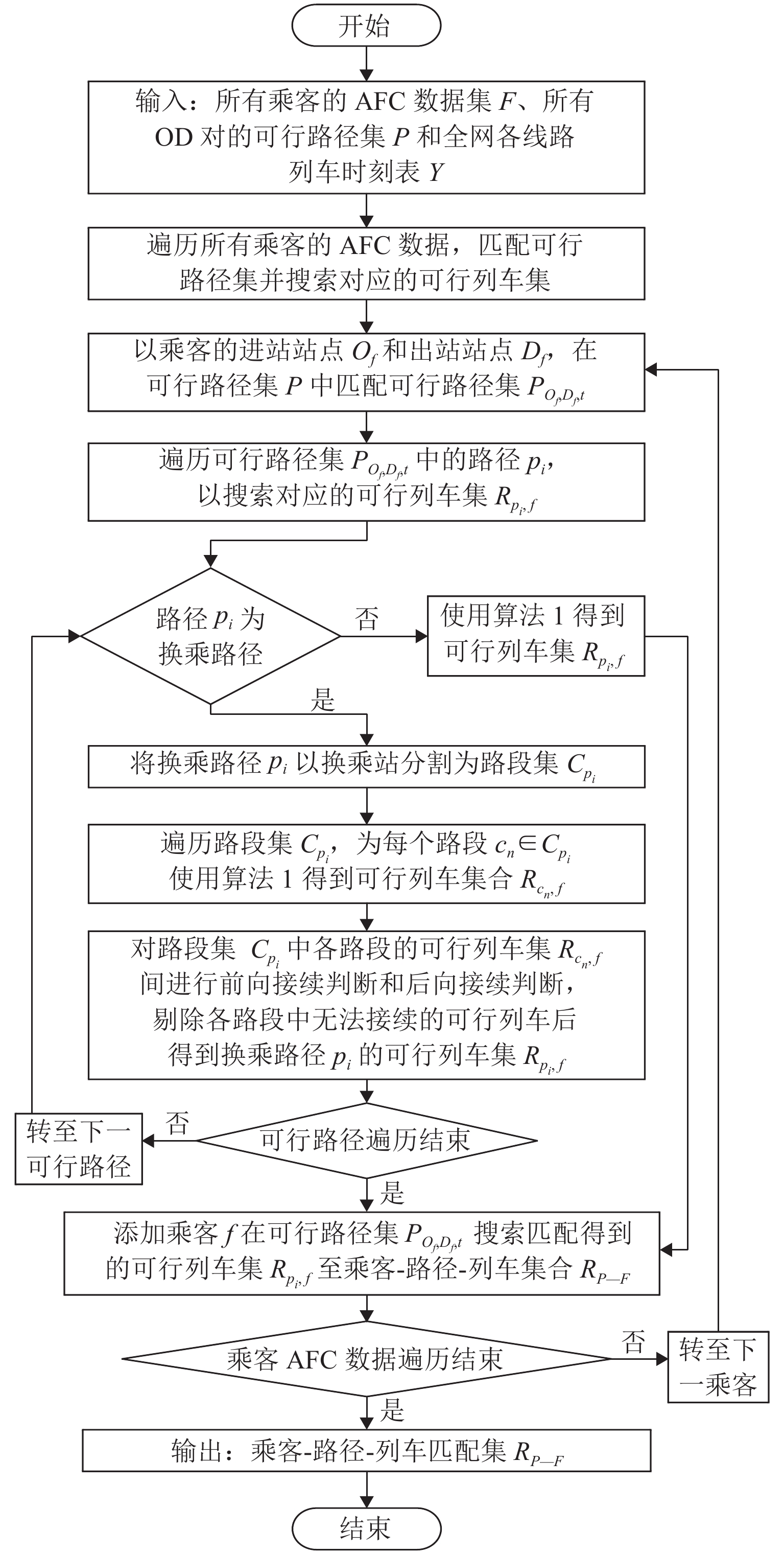
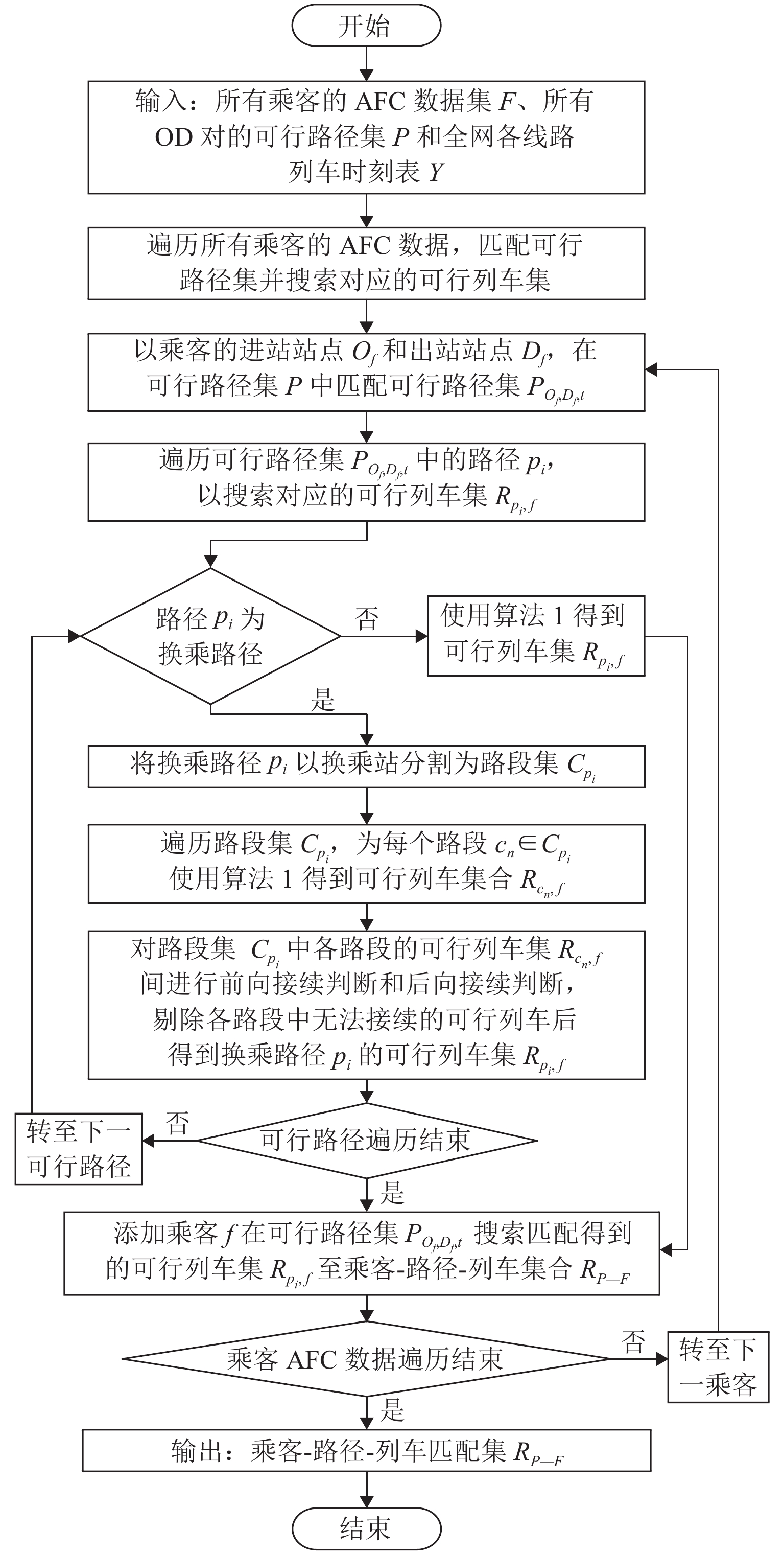
乘客可行列车集确定即进行乘客与列车的匹配,生成乘客f在相应可行路径集 {P_{{O_f},{D_f},t}} 中各路径pi上的可行列车集 {R_{{p_i},f}} ,如式(8). 基于所定义的变量及相关参数,乘客可行列车集匹配算法(算法3)如图5所示. 其原理为:1) 根据单个乘客f的进、出站站点匹配可行路径集 {P_{{O_f},{D_f},t}} . 2) 对于单条可行路径 {p_i} \in {P_{{O_f},{D_f},t}} ,若为非换乘路径,则直接使用算法1得到路径pi上的可行列车集 {R_{{p_i},f}} ;若为换乘路径,则对pi进行分割,生成路段集 {C_{{p_i}}} . 3) 对各个路段 {c_n} \in {C_{{p_i}}} 使用算法1得到该路段的可行列车集 {R_{{c_n},f}} . 4) 对路径上各路段的可行列车集 {R_{{p_i},f}} = \left\{ {{R_{{c_n},f}}|{c_n} \in {C_{{p_i}}}} \right\} 间进行前向和后向列车接续判断,即得到换乘路径的可行列车集.
式(9)和式(10)表示乘客f 在路径pi上第 \omega 个可行列车集 {R_{{p_i},f,\omega }} 中的列车在路径起点站发车,并到达路径终点. 式(11)和式(12)表示可行列车集 {R_{{p_i},f,\omega }} 中的列车在乘客进站站点的发车时刻晚于乘客的进站时刻,且在乘客出站站点的到站时刻早于乘客的出站时刻. 式(13)表示路径换乘次数大于0时,可行列车集 {R_{{p_i},f,\omega }} 中前序路段 {c_n} 上的列车在路径上换乘站T的到达时刻{a}_{{T,{\rm{pre}}}}( {{r_{{c_n},f,y}}})要早于后序路段 {c_{n + 1}} 上的列车在换乘站的发车时刻{d_{T,{\rm{pos}}}}\left( {{r_{{c_{n + 1}},f,{\textit{z}}}}} \right).
{R_{{p_i},f}} = \left\{ {{R_{{p_i},f,1}},{R_{{p_i},f,2}}, \ldots ,{R_{{p_i},f,\omega }}|{p_i} \in {P_{{O_f},{D_f},t}}} \right\} , (8) {s_{{O_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right) = {O_f},\quad{r_{{p_i},f,\omega ,u}} \in {R_{{p_i},f,\omega }} , (9) {s_{{D_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right) = {D_f},\quad{r_{{p_i},f,\omega ,u}} \in {R_{{p_i},f,\omega }} , (10) {d_{{O_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right) > {t_{f,{\text{et}}}},\quad{r_{{p_i},f,\omega ,u}} \in {R_{{p_i},f,\omega }} , (11) {a_{{D_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right) < {t_{f,{\text{ex}}}},\quad{r_{{p_i},f,\omega ,u}} \in {R_{{p_i},f,\omega }} , (12) \begin{split} & {a_{{{T,{\rm{pre}}}}}}\left( {{r_{{c_n},f,y}}} \right) < {d_{{{T,{\rm{pos}}}}}}\left( {{r_{{c_{n + 1}},f,{\textit{z}}}}} \right),\quad\;\;\;{r_{{c_n},f,y}} \in {R_{{c_n},f}},\; \\ &\quad {r_{{c_{n + 1}},f,{\textit{z}}}} \in {R_{{c_{n + 1}},f}},\;\;\;{R_{{c_n},f}},{R_{{c_{n + 1}},f}} \in {R_{{p_i},f,\omega }},\quad q\left( {{p_i}} \right) > 0, \end{split} (13) 式中: {R_{{p_i},f}} 为乘客f在路径pi的可行列车集; {r_{{p_i},f,\omega ,u}} 为可行列车集 {R_{{p_i},f,\omega }} 中的第u趟可行列车; {r_{{c_n},f,y}} 和 {r_{{c_{n + 1}},f,{\textit{z}}}} 分别为可行列车集 {R_{{c_n},f}} 和 {R_{{c_{n + 1}},f}} 中的第y和z趟可行列车,其中,cn+1为cn的后续路段;{s}_{{O}_{f}}({{r_{{p_i},f,\omega ,u}}})、{s}_{{D}_{f}}({{r_{{p_i},f,\omega ,u}}})分别为可行列车在乘客f进、出站点的到、发情况;{d_{{O_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right)、{a_{{D_f}}}\left( {{r_{{p_i},f,\omega ,u}}} \right)分别为可行列车在乘客f进、出站点的发、到时刻; q\left( {{p_i}} \right) 为路径pi的换乘次数.
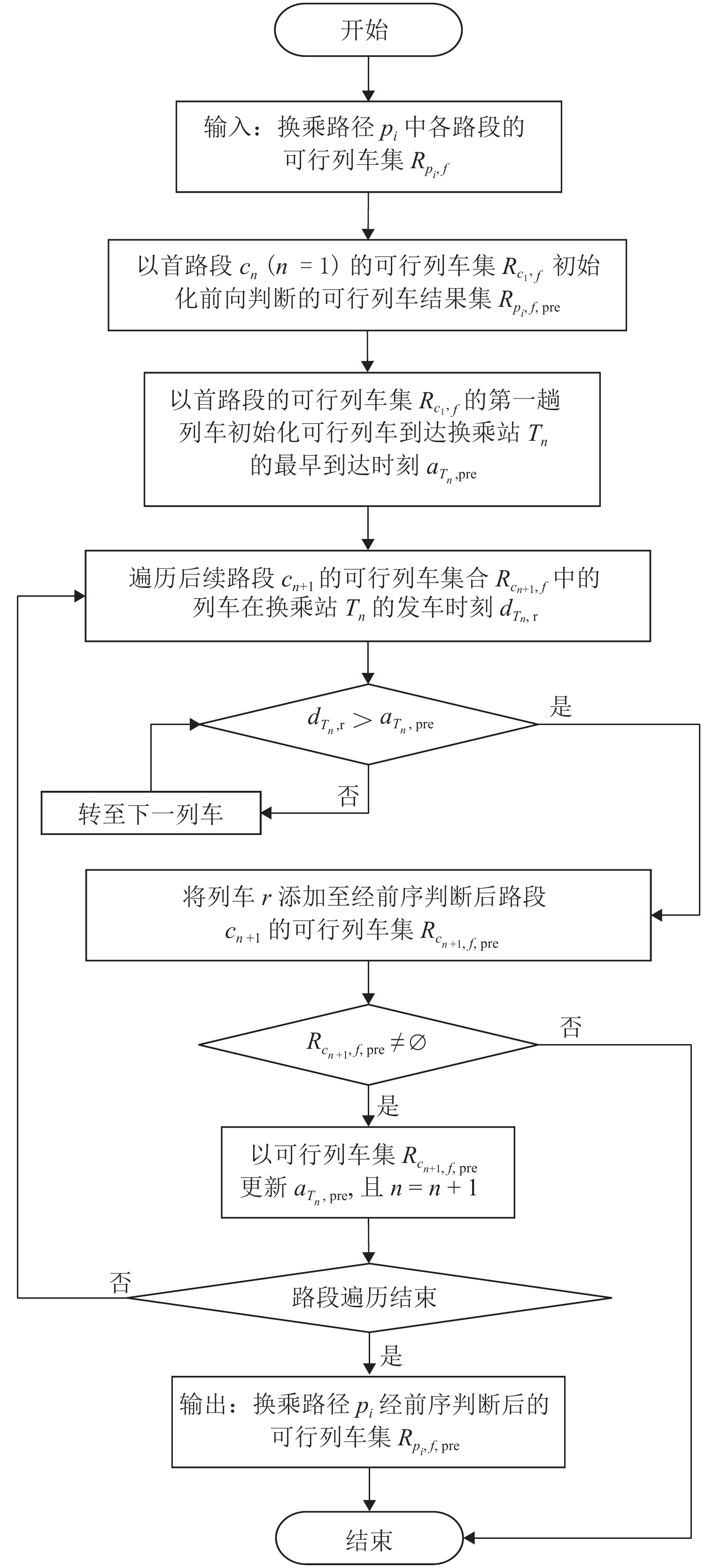
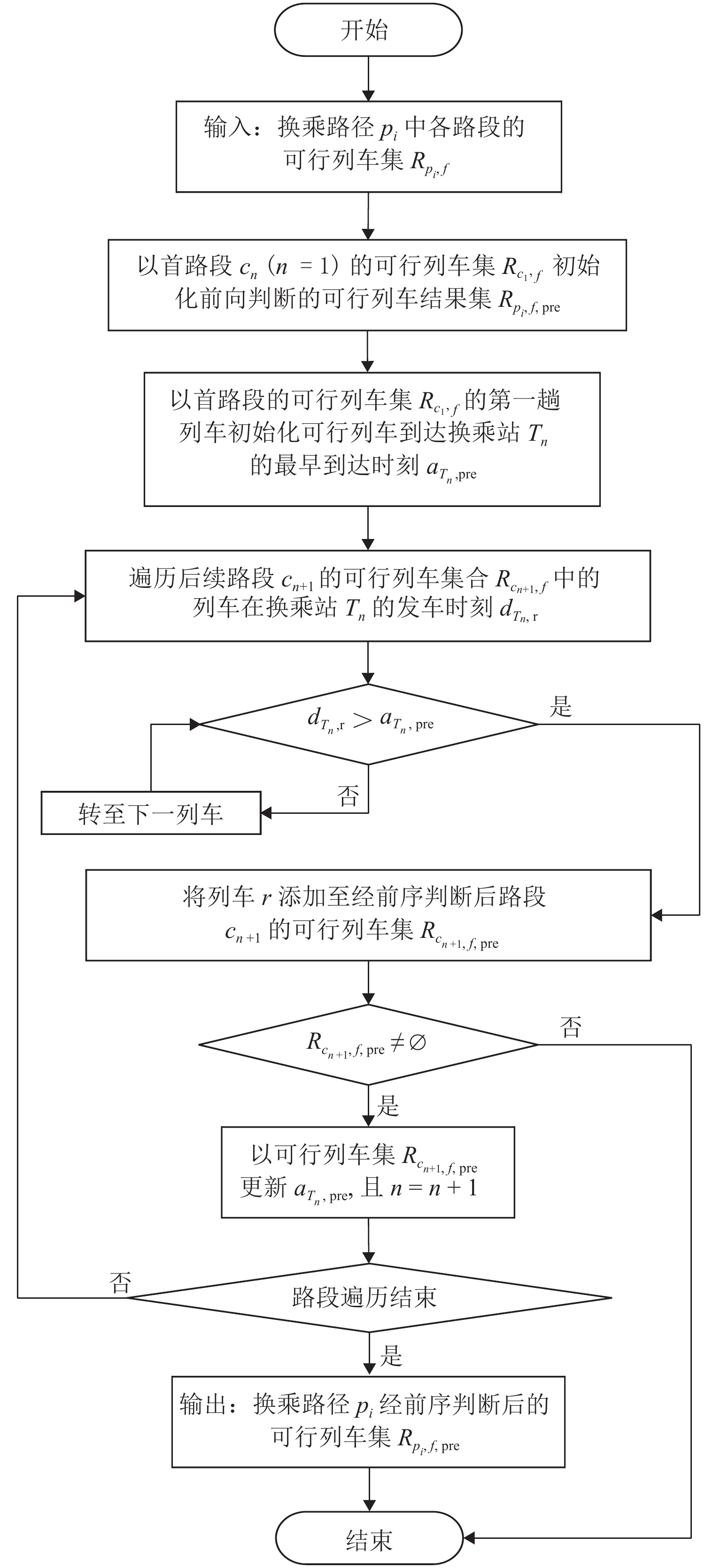
换乘路径上可行列车集的前向和后向列车接续判断过程分别是:乘客在后序路段的可行列车在换乘站 {{T}} 的发车时刻 {d_{{{T,{\rm{pos}}}}}} 需晚于前序路段的最早一趟列车在换乘站的到达时刻 {a_{{{T,{\rm{pre,hd}}}}}} ;并且在前序路段的可行列车在换乘站的到达时刻 {a_{{{T,{\rm{pre}}}}}} 需早于后序路段最后一趟可行列车在换乘站的发车时刻 {d_{{{T,{\rm{pos,tl}}}}}} . 前向判断算法(算法4)如图6所示,后向判断与其类似.
1.4 有效出行结果确定
确定乘客可行路径集和可行列车集后,根据表1所列的唯一性条件将乘客-路径-列车匹配结果分为4类,其中,类型2、3、4的乘客可行路径或可行路径中的可行列车数量不唯一,因而需要对其可行路径或可行列车进行进一步调整,最终得到乘客出行的唯一有效路径和列车.
表 1 乘客-路径-列车初始匹配结果类型Table 1. Result types of matching initial passenger–route–train类型 可行路径
情况可行列车
情况处理方式 类型 1 唯一 唯一 直接确定 类型 2 唯一 不唯一 算法 5 类型 3 不唯一 所有路径
均唯一算法 5 类型 4 不唯一 存在路径
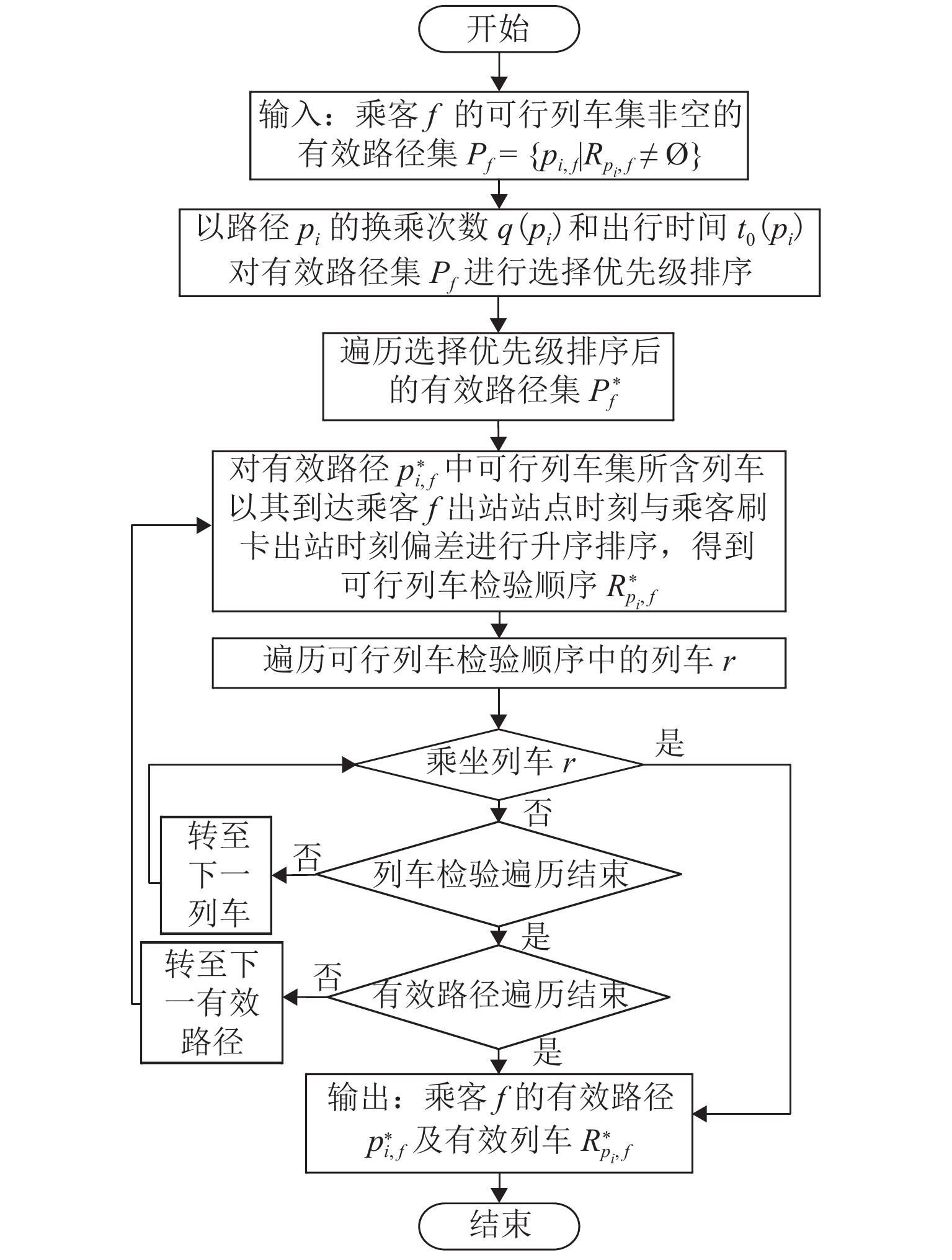
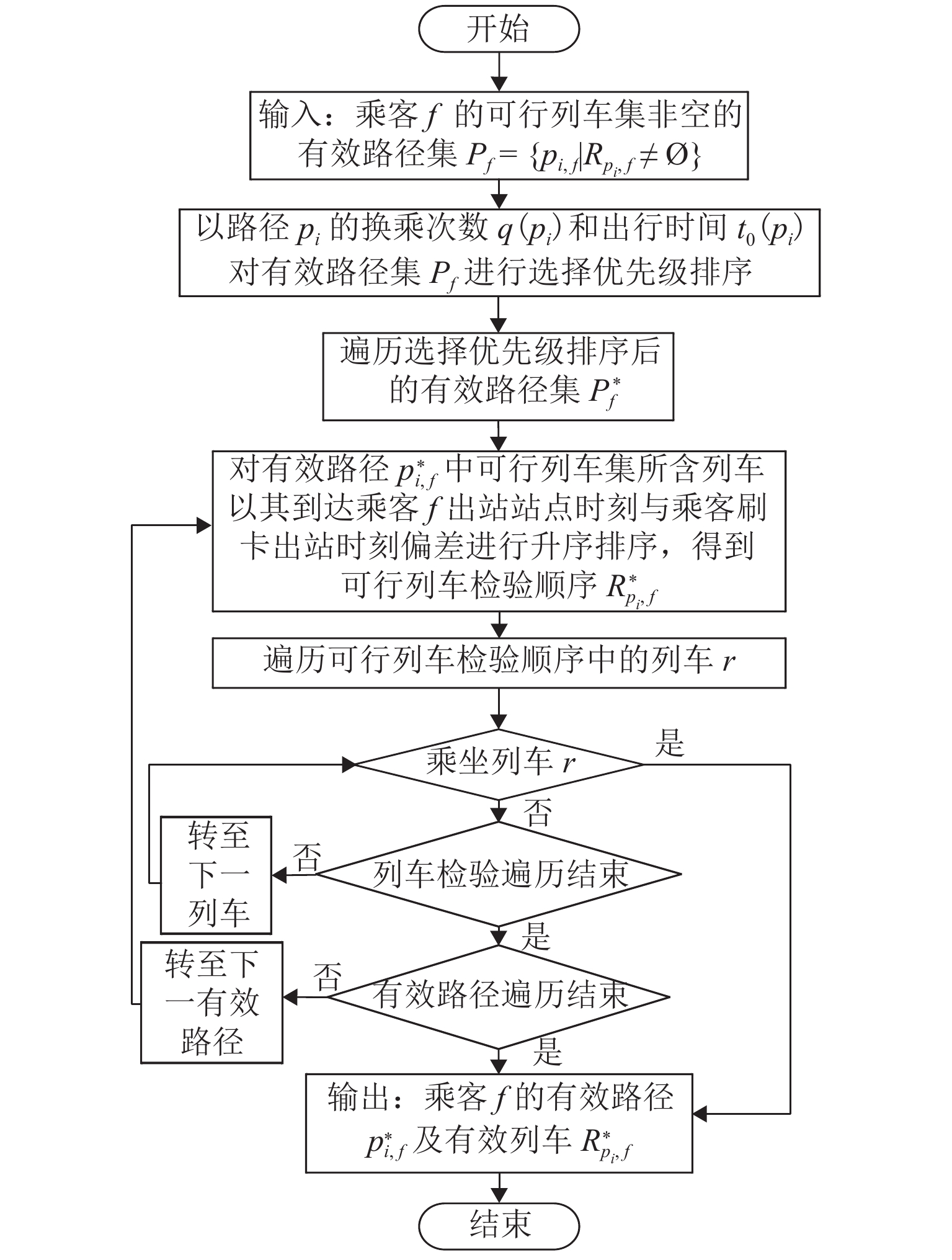
不唯一算法 5 针对类型2、3、4类乘客采用乘客出行的有效路径及有效列车确定方法,得到其有效出行结果. 如图7所示(算法5),输入单个乘客的有效结果集 {P_f} 后,首先,结合路径pi的换乘次数 q(p_i) 和出行时间 t_0(p_i) ,使用有效路径排序算法,生成路径选择优先级排序 P_f^* . 因乘客通常会尽快出站,所以对各有效路径中的各可行列车 {R_{{p_i},f}} 到达乘客出站站点时刻与乘客出站时刻 {t_{f,{\text{ex}}}} 的偏差进行升序排序,以确定有效路径中各可行列车的检验顺序R_{{{{p_i},f}}}^*. 随后以列车时刻表完成列车运行推演,依据路径优先级排序和对应各可行列车的检验顺序,结合乘客进站时刻 {t_{f,{\text{et}}}} 和站点 {O_f} 与列车载客量限制 {C_{\max }} ,使用乘车判断算法确定乘客能否乘坐列车. 最终得到3种待定类型乘客的唯一有效路径及列车.
有效路径排序流程为:首先,对有效路径集中的路径依据换乘次数q进行非降序的分层排序,得到分层排序集 {P_f}\left( q \right) ;随后,对于单个分层有效路径集 {p_{i,f}} \in {P_f}\left( q \right) ,若只有一条路径,则直接添加至综合排序集 P _f^{\;\;*} ,若含有多条路径,则以路径的出行时间t对该层的路径进行升序排序,再添加至 P _f^{\;\;*} . 乘车判断流程为:以乘客进站时刻 {t_{f,{\text{et}}}} 和站点 {O_f} 得到列车r的当前载客量 {C_r} ;若 {C_r} < {C_{\max }} ,则可乘坐列车r,否则无法乘坐列车 r .
2. 推算系统的架构与功能
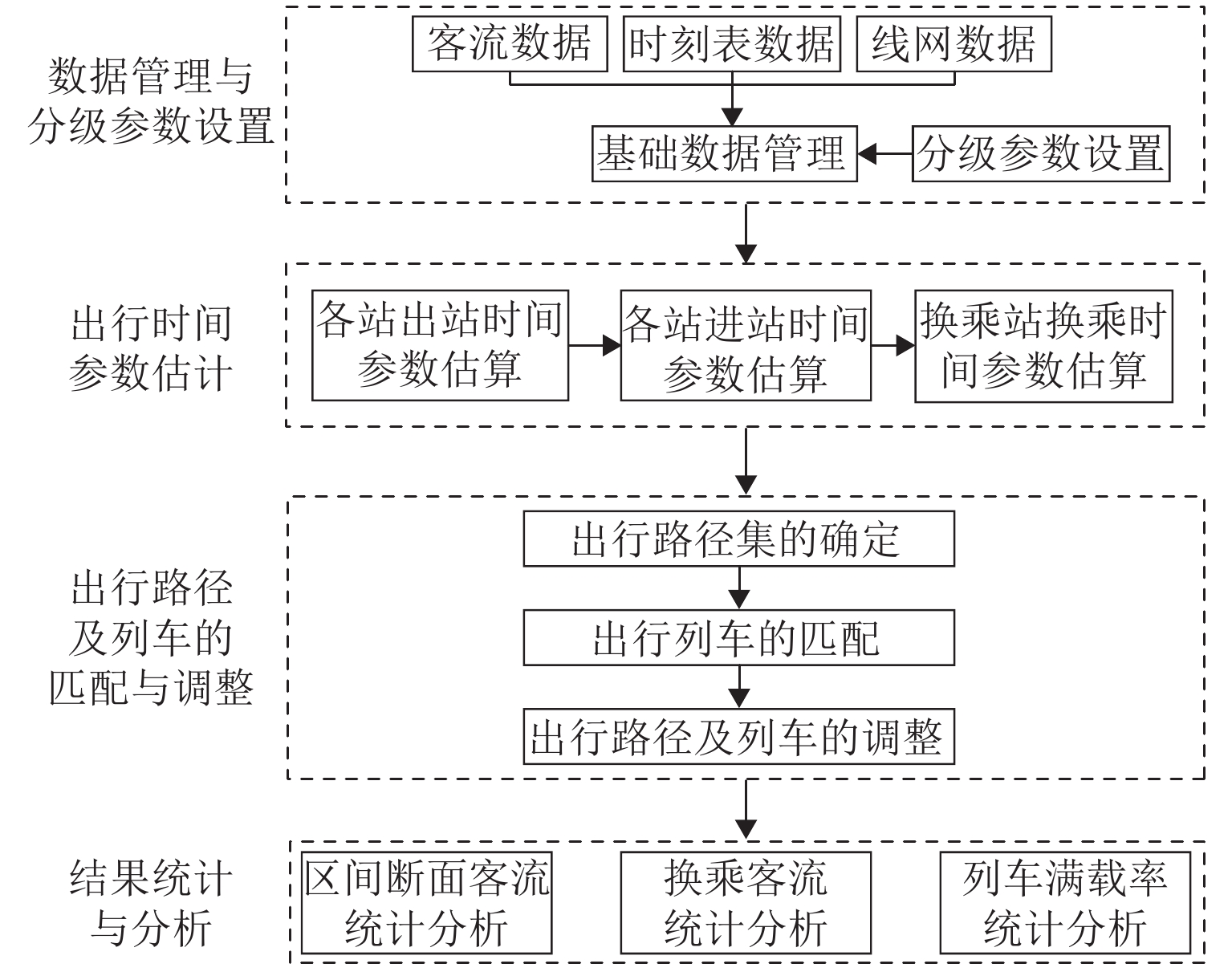
基于C# 语言开发的系统包括数据管理与分级参数设置、出行时间参数估算、出行路径及列车的匹配与调整和结果统计与分析4个模块. 系统架构如图8所示. 其中,数据管理与分级参数设置用于输入表2所列数据;出行时间参数估计模块完成进出站时间和换乘站各换乘方向换乘时间参数估计;出行路径及列车的匹配与调整模块首先以乘客OD信息匹配可行路径集,随后对各条可行路径完成可行列车集推算,最后,进行列车运行推演,调整并确定所有乘客的有效出行结果,完成客流分配;匹配结果统计可进行各线路断面客流、列车满载率和换乘站各方向换乘客流的统计与分析.
表 2 输入的数据名称及内容Table 2. Name and content of input data数据名称 数据内容 乘客行程信息 进站时间、进站车站名、出站时间、出站车站名 时刻表信息 所属线路名、车次号、车站名、到站时刻、发车时刻 线路属性 线路名称、线路类型、是否开通、线路颜色(RGB) 车站属性 车站编号、车站名、是否为换乘站、衔接线路、衔接线路车站 满载率分级参数 分级数量、各线各区间分级标准 车站客流分级参数 线路名称、分级数量、全线分级标准、全线各站分级标准 3. 推算结果分析
系统界面包含线网显示区,分时段各车站进、出站量及换乘站各换乘方向换乘量的统计区和由数据管理、客流匹配、客流管理及结果统计构成的菜单栏区. 以下针对某市城市轨道交通部分线网2021年5月12日的数据进行网络客流推算结果进行分析.
3.1 区间断面客流对比
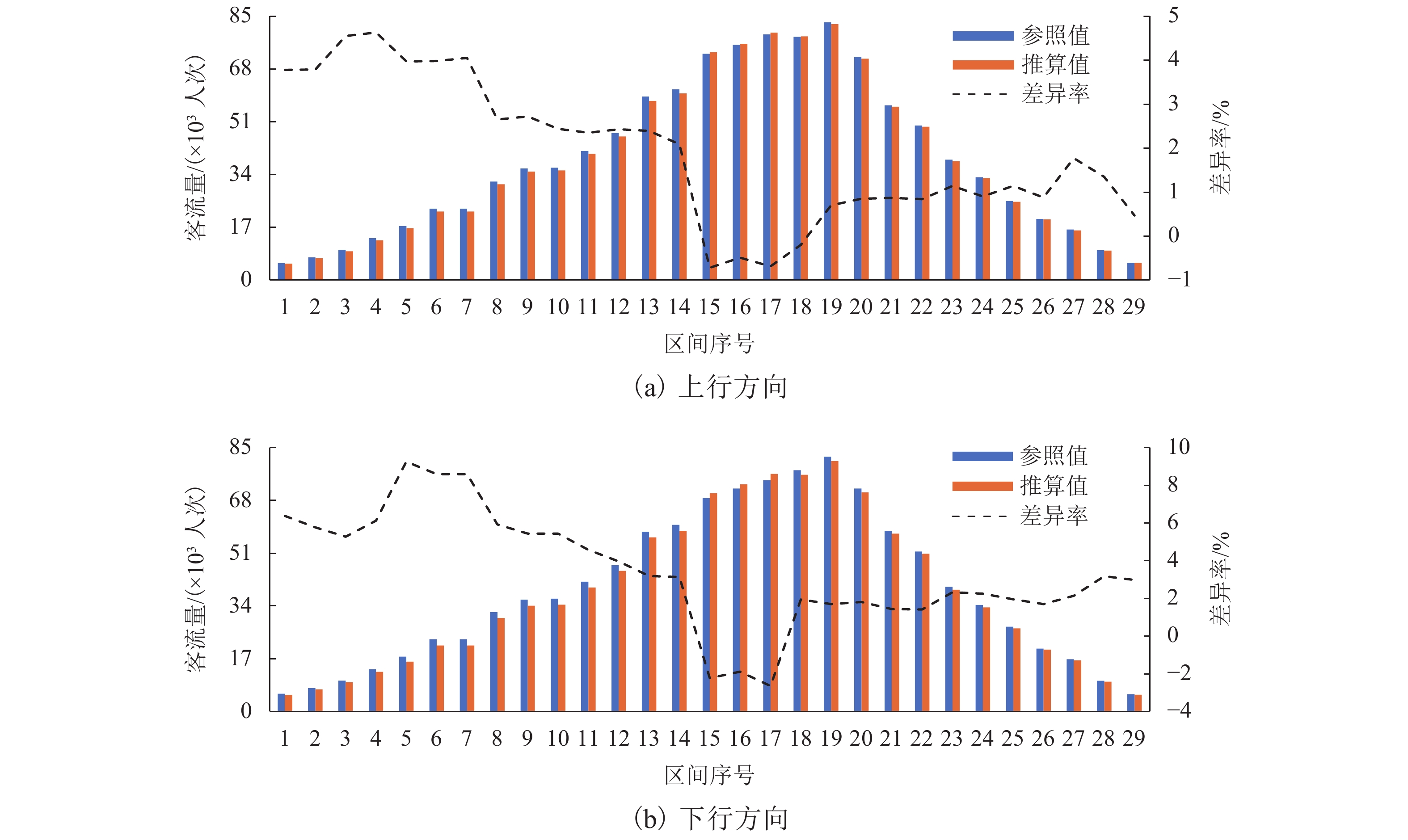
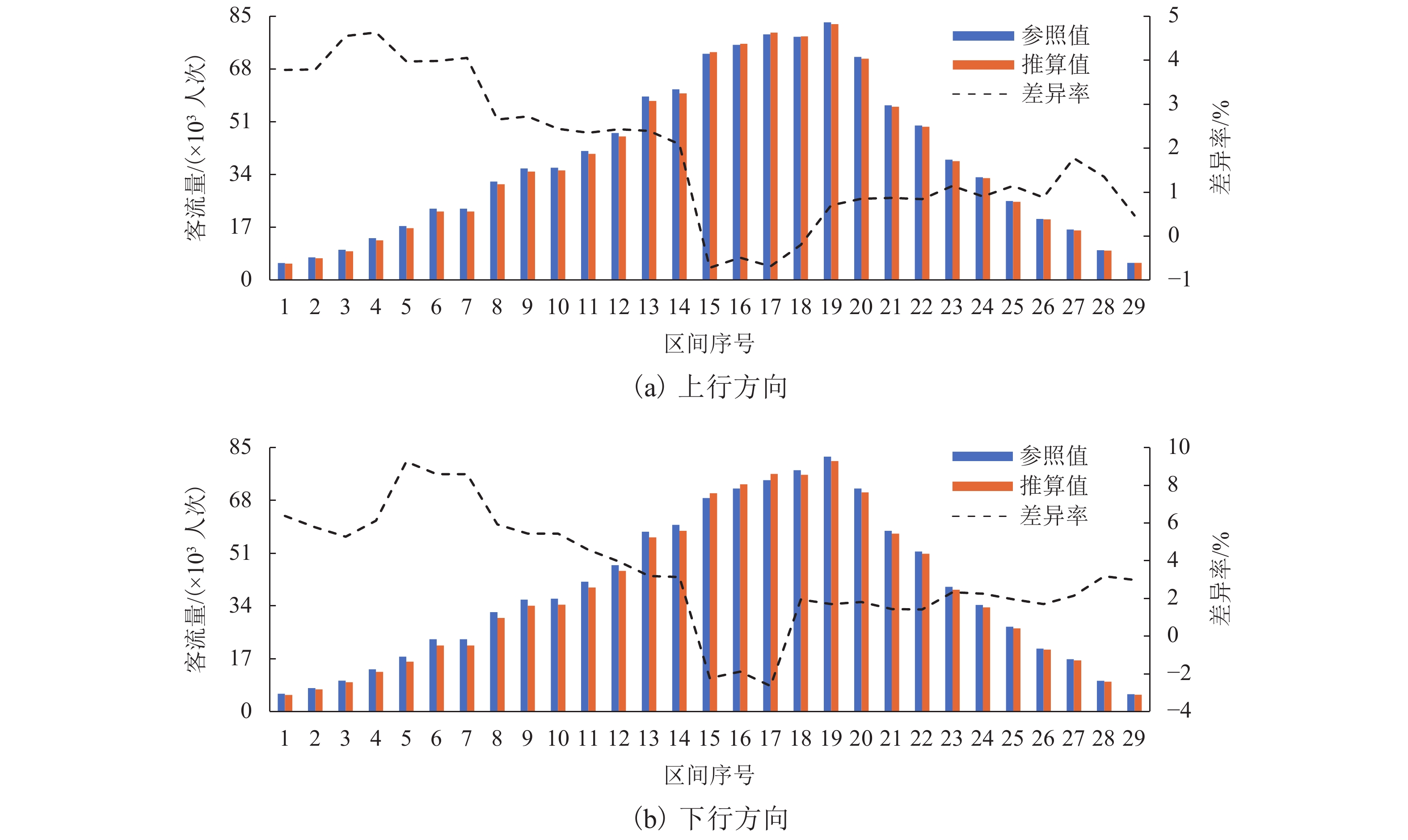
以该市YH线的29个区间断面客流参照值和推算系统推算值的变化趋势和差异率进行比较,如图9所示. 由图可知:参照值和推算值随区间的变化趋势相同,表明二者结果存在相似性;上行方向区间断面客流差异率为 −0.72%~4.63%,下行方向区间断面客流差异率为 −2.66%~9.25%;总体而言,上行方向绝对差异率小于5.00%,平均差异率为2.03%,下行方向绝对差异率小于10.00%,平均差异率为3.90%,表明推算系统的推算结果较稳定且贴近于参照值;此外,上下行方向断面客流差异值均较小,线路的断面客流因端部区间较小,而中部区间较大,造成差异率在端部较高,中部较低.
3.2 换乘客流统计分析
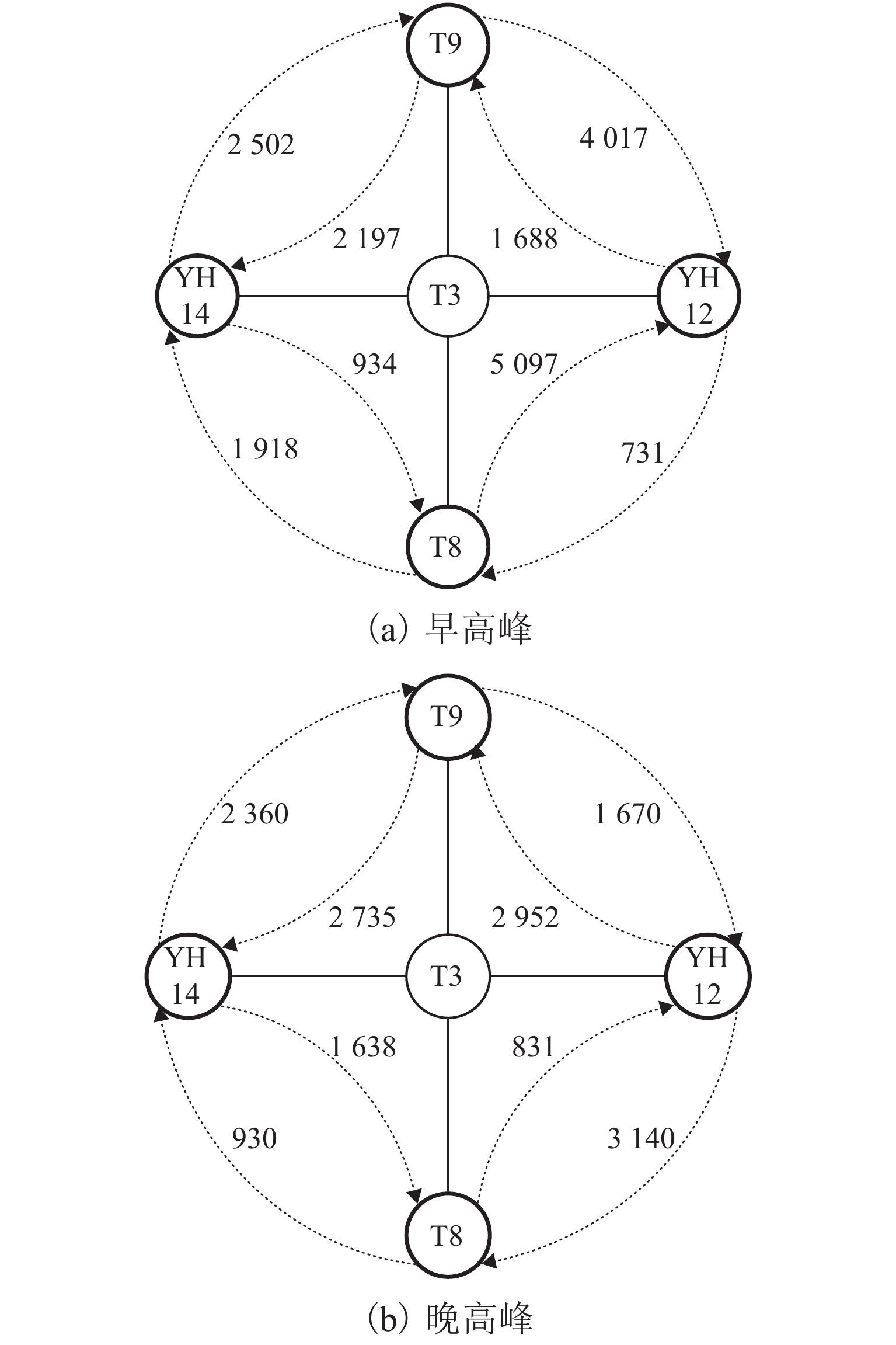
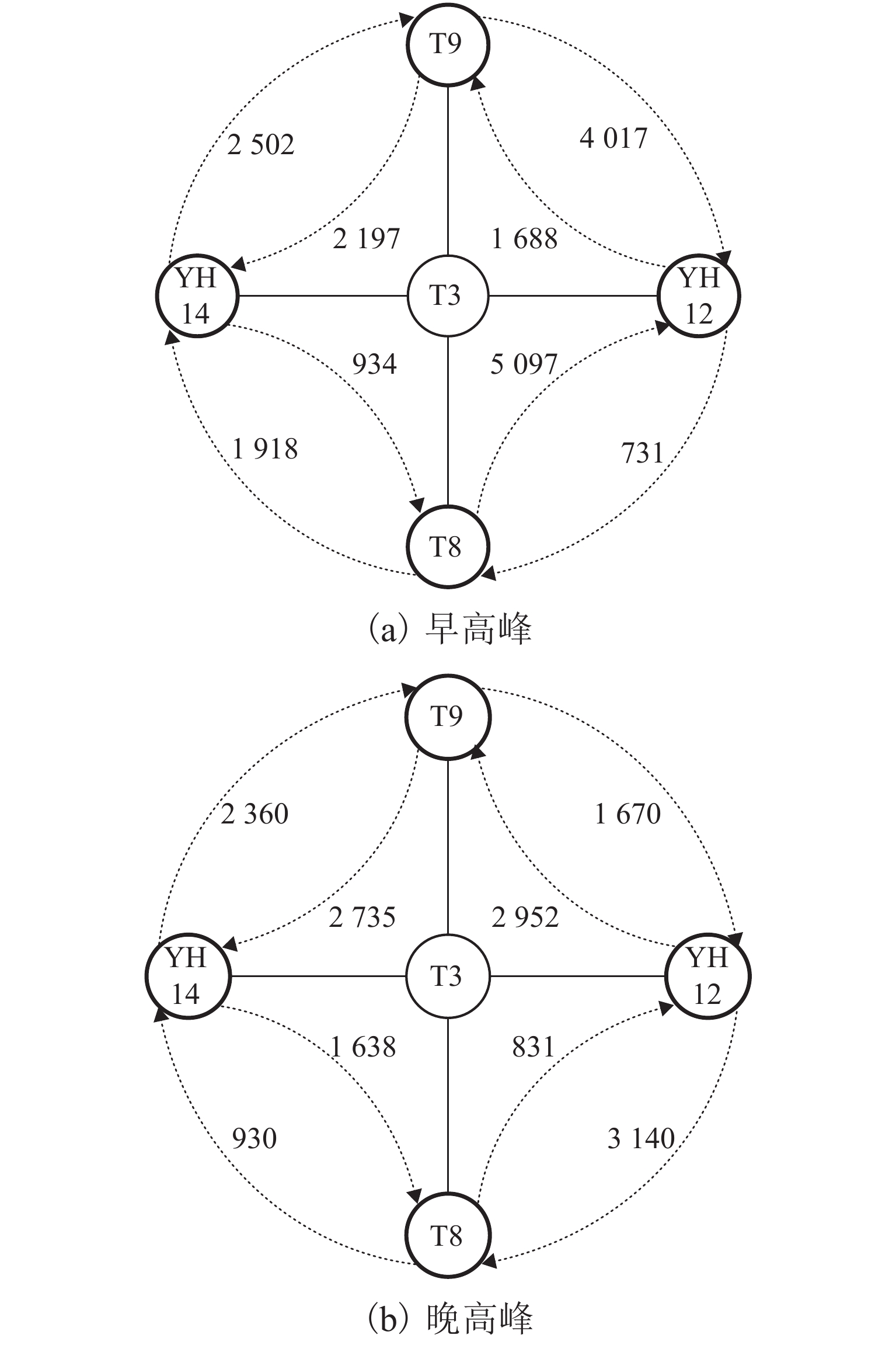
车站T3为YH线和EH线的两线换乘站,各换乘方向的早高峰(7:00—9:00)和晚高峰(17:00—19:00)换乘量如图10所示. 图中,T8、T9、YH12和YH14均为车站名. 对该换乘站直接关联的YH线和EH线早晚高峰时段换乘客流来源量前5的车站进行统计,结果如表3和表4所列. 由表可知:YH线早晚高峰时段换乘客流来源站较EH线的固定,但来源量比例的波动均较EH线大;YH线和EH线早高峰换乘客流来源量比例的标准差均小于晚高峰的,表明早高峰换乘客流来源量较稳定.
表 3 YH线早晚高峰换乘客流来源统计Table 3. Statistics on source of transfer passenger flow for YH line in morning and evening peaks% 来源
站名早高峰来源
量比例来源
站名晚高峰来源
量比例RML 22.6 BSG 22.3 ZZHCZ 21.3 LCGC 21.6 LCGC 19.7 RML 20.1 BSG 19.6 ZZHCZ 19.7 YXY 16.9 QLL 16.3 标准差 1.91 标准差 2.08 表 4 EH线早晚高峰换乘客流来源统计Table 4. Statistics on source of transfer passenger flow for EH line in morning and evening peaks% 来源
站名早高峰来源
量比例来源
站名晚高峰来源
量比例NSH 22.0 LHDL 21.8 JW 20.8 JW 21.1 SWL 20.1 LZ 20.6 LZ 18.9 LL 18.4 HNC 18.2 HHYBG 18.0 标准差 1.35 标准差 1.51 3.3 列车满载率统计分析
根据文献 [10] 所确定的列车区间满载率等级如表5所列. 以此对EH线早高峰(7:00—9:00)和晚高峰(17:00—19:00)的列车满载率进行统计分析. 结果表明,早高峰时段线路中段区间(GHT—NSH)在7:40—8:40内上行方向列车满载率高,多处于等级3和4,持续时间短且区间集中;晚高峰时段,线路中段区间(DFL—ZMT)在17:30—19:30内下行列车满载率较高,多处于等级2,持续时间长且区间分散;早高峰时段区间满载率高的列车数量多于晚高峰的. 这与线路中段位于市区,两端位于郊区,且早高峰上班时间集中、晚高峰下班时间分散的情况相对应.
表 5 列车区间满载率分级Table 5. Classification of train-section load rate% 等级 满载率范围 等级 满载率范围 等级 1 (0,50] 等级 4 (100,120] 等级 2 (50,80] 等级 5 (120,130] 等级 3 (80,100] 等级 6 (130,∞) 4. 结 论
本文以乘客时空路径推算方法对城市轨道交通网络客流分配问题进行了研究,并以实际AFC 数据和列车时刻表数据使用所开发的客流推算系统开展了案例研究. 具体结论如下:
1) 系统推算的断面客流结果稳定且与参照值差异较小,上、下行方向的平均差异率分别为2.03%和3.90%.
2) 换乘站的换乘客流主要来源为直接关联线路车站,并且早高峰时段来源量比例较晚高峰更稳定.
3) 从郊区贯穿市区的线路早高峰时段列车满载率高于晚高峰时段,持续时间较短且区间更集中.
-
表 1 乘客-路径-列车初始匹配结果类型
Table 1. Result types of matching initial passenger–route–train
类型 可行路径
情况可行列车
情况处理方式 类型 1 唯一 唯一 直接确定 类型 2 唯一 不唯一 算法 5 类型 3 不唯一 所有路径
均唯一算法 5 类型 4 不唯一 存在路径
不唯一算法 5 表 2 输入的数据名称及内容
Table 2. Name and content of input data
数据名称 数据内容 乘客行程信息 进站时间、进站车站名、出站时间、出站车站名 时刻表信息 所属线路名、车次号、车站名、到站时刻、发车时刻 线路属性 线路名称、线路类型、是否开通、线路颜色(RGB) 车站属性 车站编号、车站名、是否为换乘站、衔接线路、衔接线路车站 满载率分级参数 分级数量、各线各区间分级标准 车站客流分级参数 线路名称、分级数量、全线分级标准、全线各站分级标准 表 3 YH线早晚高峰换乘客流来源统计
Table 3. Statistics on source of transfer passenger flow for YH line in morning and evening peaks
% 来源
站名早高峰来源
量比例来源
站名晚高峰来源
量比例RML 22.6 BSG 22.3 ZZHCZ 21.3 LCGC 21.6 LCGC 19.7 RML 20.1 BSG 19.6 ZZHCZ 19.7 YXY 16.9 QLL 16.3 标准差 1.91 标准差 2.08 表 4 EH线早晚高峰换乘客流来源统计
Table 4. Statistics on source of transfer passenger flow for EH line in morning and evening peaks
% 来源
站名早高峰来源
量比例来源
站名晚高峰来源
量比例NSH 22.0 LHDL 21.8 JW 20.8 JW 21.1 SWL 20.1 LZ 20.6 LZ 18.9 LL 18.4 HNC 18.2 HHYBG 18.0 标准差 1.35 标准差 1.51 表 5 列车区间满载率分级
Table 5. Classification of train-section load rate
% 等级 满载率范围 等级 满载率范围 等级 1 (0,50] 等级 4 (100,120] 等级 2 (50,80] 等级 5 (120,130] 等级 3 (80,100] 等级 6 (130,∞) -
[1] 曾鸣凯,黄鉴,彭其渊. 客运专线旅客列车开行方案的客流分配方法[J]. 西南交通大学学报,2006,41(5): 571-574. doi: 10.3969/j.issn.0258-2724.2006.05.006ZENG Mingkai, HUANG Jian, PENG Qiyuan. Research on assignment of passenger train plan for dedicated passenger train line[J]. Journal of Southwest Jiaotong University, 2006, 41(5): 571-574. doi: 10.3969/j.issn.0258-2724.2006.05.006 [2] 张思佳,贾顺平,毛保华,等. 乘客出行距离分布对轨道线网内公交竞争力的影响[J]. 浙江大学学报(工学版),2019,53(2): 292-298. doi: 10.3785/j.issn.1008-973X.2019.02.012ZHANG Sijia, JIA Shunping, MAO Baohua, et al. Influence of passenger trip distance distribution on competitiveness of bus lines in urban rail transit network[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(2): 292-298. doi: 10.3785/j.issn.1008-973X.2019.02.012 [3] 许得杰,巩亮,朱宁,等. 城市轨道交通多交路共线运营客流分配方法[J]. 交通运输系统工程与信息,2021,21(5): 206-213. doi: 10.16097/j.cnki.1009-6744.2021.05.021XU Dejie, GONG Liang, ZHU Ning, et al. Passenger flow assignment method for common-line operation with multi-routing of urban rail transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(5): 206-213. doi: 10.16097/j.cnki.1009-6744.2021.05.021 [4] ASAKURA Y, IRYO T, NAKAJIMA Y, et al. Estimation of behavioural change of railway passengers using smart card data[J]. Public Transport, 2012, 4(1): 1-16. doi: 10.1007/s12469-011-0050-0 [5] KUSAKABE T, IRYO T, ASAKURA Y. Estimation method for railway passengers’ train choice behavior with smart card transaction data[J]. Transportation, 2010, 37: 731-749. [6] YAO X M, HAN B M, YU D D, et al. Simulation-based dynamic passenger flow assignment modelling for a schedule-based transit network[J]. Discrete Dynamics in Nature and Society, 2017, 2017: 1-15. [7] 刘峰博,周庭梁,王小敏. 城市轨道交通故障下客流分布计算及评估方法[J]. 西南交通大学学报,2021,56(5): 921-927,966.LIU Fengbo, ZHOU Tingliang, WANG Xiaomin. Calculation and evaluation method of passenger flow distribution under urban rail transit failure[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 921-927,966. [8] ZHU Y W, KOUTSOPOULOS H N, WILSON N H M. A probabilistic passenger-to-train assignment model based on automated data[J]. Transportation Research Part B: Methodological, 2017, 104: 522-542. [9] 陈钱飞. 城市轨道交通网络乘客时空路径估计与瓶颈识别方法研究[D]. 北京: 北京交通大学, 2021. [10] 中华人民共和国建设部, 中华人民共和国国家发展和改革委员会. 城市轨道交通工程项目建设标准: 建标 104—2008[S]. 北京: 中国计划出版社, 2008. 期刊类型引用(3)
1. 茧敏,陈绍宽,王卓,李昊. 城市轨道交通网络跨线列车开行方案优化模型研究. 交通运输系统工程与信息. 2024(05): 116-127 .  百度学术
百度学术2. 杨陶源,郑宣传,孟海超. 城市轨道交通网络动态客流分配方法研究. 交通工程. 2024(12): 15-21 .  百度学术
百度学术3. 许得杰,潘星,巩亮,胡晨皓,王雪鑫. 基于列车开行方案的城市轨道交通多交路客流分配方法. 交通运输系统工程与信息. 2023(05): 238-246+289 .  百度学术
百度学术其他类型引用(7)
-






 下载:
下载:









 下载:
下载:
 百度学术
百度学术