一种高静-低动刚度磁弹簧的建模与特性分析

张明; 谢延松; 李洪涛; 孙凤; 徐方超; 张磊

doi:10.3969/j.issn.0258-2724.20220821

一种高静-低动刚度磁弹簧的建模与特性分析

doi: 10.3969/j.issn.0258-2724.20220821

张明^1, ,,
谢延松¹,
李洪涛¹,
孙凤¹,
徐方超¹,
张磊²

1.
沈阳工业大学机械工程学院，辽宁沈阳 110870
2.
辽宁科技学院机械工程学院，辽宁本溪 117004

基金项目: 国家自然科学基金（52005344，52005345）；国家重点研发计划（2020YFC2006701）；辽宁省自然科学基金（2022-MS-271）；辽宁省教育厅青年项目（LJKQZ2021044）；辽宁省教育厅科学研究经费（202007141）

详细信息

通讯作者:
张明（1988—），男，副教授，研究方向为磁力减震与柔性机器人技术，E-mail：mingzhang@sut.edu.cn

中图分类号: TH135；TB535.1
计量
- 文章访问数: 383
- HTML全文浏览量: 663
- PDF下载量: 63
- 被引次数: 1
出版历程
- 收稿日期: 2022-11-24
- 修回日期: 2023-03-17
- 网络出版日期: 2023-06-16
- 刊出日期: 2023-03-30

Modeling and Characteristic Analysis of a Magnetic Spring with High Static Stiffness and Low Dynamic Stiffness

1.
School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China
2.
School of Mechanical Engineering, Liaoning Institute of Science and Technology, Benxi 117004, China

摘要

摘要:
为解决低频隔振领域存在的低固有频率和高承载力之间的矛盾，设计了一种新型高静-低动刚度磁弹簧元件. 首先，基于电磁场理论和分子电流法建立磁弹簧的弹簧力和刚度模型；其次，建立系统的动力学模型，同时分析线圈通入不同电流时对位移传递率的影响，并与等效线性弹簧进行比较；最后，研制实验样机并进行实验研究. 仿真与实验结果表明：磁弹簧气隙-刚度曲线呈先平缓后急剧的非线性关系，具有明显的高静-低动刚度特性；其刚度与电流近似线性关系，磁弹簧可通过改变电流实现较大范围的刚度调整，且刚度响应迅速；在未通入电流时，相对于等效线性弹簧，起始隔振频率和传递率峰值降低26%，在通入负向额定电流时，起始隔振频率和传递率峰值降低了41%.
- 低频隔振 /
- 高静-低动 /
- 磁弹簧 /
- 电流 /
- 非线性
Abstract:
A novel magnetic spring element with high static stiffness and low dynamic stiffness was designed to address the conflict between low natural frequency and high bearing capacity in the field of low-frequency vibration isolation. First, the spring force and stiffness models of the magnetic spring were built based on electromagnetic field theory and molecular current method; secondly, the dynamics model of the system was established, and the influence of coils with different currents on displacement transmissibility was analyzed and compared with the equivalent linear spring; finally, an experimental prototype was developed, and an experimental study was carried out. The simulation and experimental results show that the air-gap stiffness curve of the magnetic spring presents a nonlinear relationship of being initially flat and then sharp, which indicates obvious characteristics of high static stiffness and low dynamic stiffness. The stiffness is approximately linear with the current. The magnetic spring can achieve a wide range of stiffness adjustment by changing the current, and the stiffness response is rapid; when no current is applied, the starting vibration isolation frequency and peak transmissibility are decreased by 26% compared with the equivalent linear spring. When a negative rated current is applied, the starting vibration isolation frequency and peak transmissibility are reduced by 41%.
- low-frequency vibration isolation /
- high static stiffness and low dynamic stiffness /
- magnetic spring /
- current /
- nonlinear

HTML全文

精密仪器设备的故障多与特殊工作环境中因膨胀、旋转、推进等运动所引起的低频范围0.5～70.0 Hz内的往复振动相关，会严重降低仪器设备的精度和使用寿命^[1-3].

在隔振系统中，只有当外部振动频率高于系统固有频率的 $\sqrt 2$ 倍时，系统才能获得隔振效果^[4]. 这意味着若要提高隔振性能，则需要降低系统的固有频率，降低振动对精密仪器带来的危害，但获得更低的固有频率和更宽的隔振频带的代价是系统刚度的降低，这会导致系统承载能力下降，并引发系统静态变形加剧等问题，因此，高承载能力和低固有频率之间的矛盾成为制约低频隔振技术发展的瓶颈. 研究表明，具备高静-低动刚度特性的非线性隔振系统能够很好地解决上述矛盾^[5]，被许多学者视为抑制低频振动的重要方向. Carrella等^[6]运用永磁铁组合和机械弹簧联立设计了一种高静-低动刚度隔振器，工作原理是由永磁体提供的负刚度抵消弹簧的正刚度；Zhang等^[7]开发了一款由可变磁力的负刚度磁弹簧和机械弹簧并联而成的高静-低动刚度隔振器，通过有限元分析了磁弹簧的可调磁力特性，用实验证明其有效性，且通过改善共振区内系统的阻尼降低共振峰值；Zhou等^[8]提出一种由一对电磁铁和永磁体构成的磁弹簧与金属板簧联立而成的新型隔振器，并通过实验验证了隔振器可以通过改变固有频率改善其隔振性能；王迎春等^[9]设计了一种双永磁环型隔振器和三磁体型隔振器并联的组合式被动隔振装置，并搭建实验系统验证其能够通过永磁体间的负刚度降低系统的固有频率，降低系统的传递率峰值.

但上述学者多是利用永磁体间或永磁体与电磁铁间的吸力作为负刚度，与线性或非线性机械弹簧联立构成高静-低动刚度隔振器，这种与机械弹簧联立构成的结构一旦确定结构尺寸，起始隔振频率也就确定，而当需要改变起始隔振频率时，只能重新确定结构的尺寸参数. 本文利用3个永磁体间的斥力，并结合空心电磁线圈构成一种高静-低动刚度隔振装置，由于加入了电磁线圈，可以通过改变电磁线圈中的电流来改变结构中的电磁磁通，从而达到改变起始隔振频率的目的. 通过电磁场理论和等效磁荷法建立装置回复力和刚度的理论计算模型，研究系统参数对装置特性的影响和系统振动传递率等.

1. 磁弹簧结构与工作原理

本文设计的高静-低动刚度磁弹簧的三维模型如图1所示. 磁弹簧包括：两侧的空心线圈和内置于线圈的环形永磁体Ⅰ、Ⅲ组成系统的定子；可轴向滑动的环形永磁体Ⅱ和铝制输出轴组成系统的动子. 3个永磁体沿轴向，同极相对布置，输出轴前后穿过两侧的直线轴承，磁弹簧动子沿轴线方向往复运动.

图 1 高静-低动刚度磁弹簧示意

Figure 1. Magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

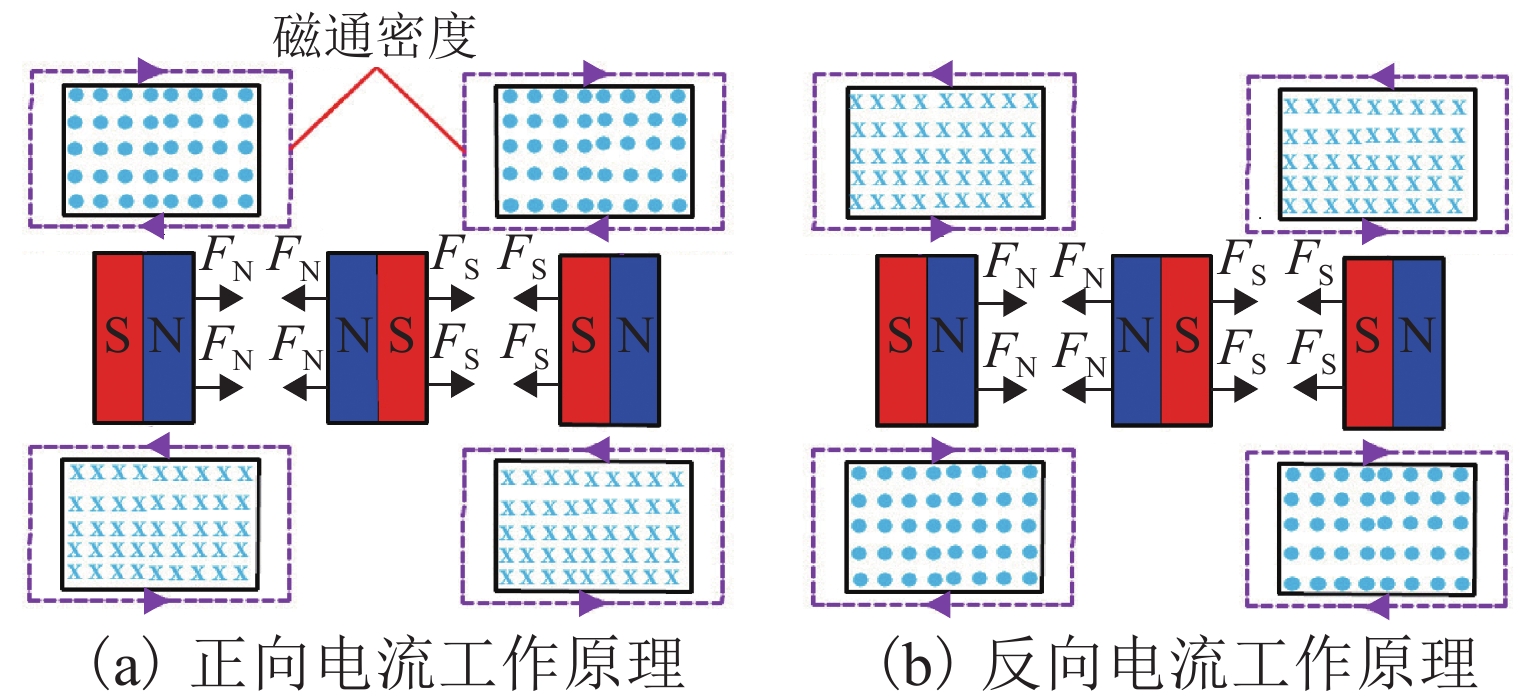
如图2所示，永磁体Ⅰ、Ⅲ分别给永磁体Ⅱ等大反向的轴向斥力F_N、F_S，使磁弹簧动子保持在机构的平衡位置. 未加载电流时，依靠永磁铁间的斥力可以实现被动隔振；当线圈加载正向或者反向的激励电流I时，产生稳定且可控的电磁磁通，调节永磁体间的轴向斥力，实现磁弹簧自身刚度调节. 通过永磁体间正负刚度的耦合作用，使磁弹簧获得高静-低动刚度特性，通过调整空心线圈中的电流可以对磁弹簧刚度特性进行调整，且响应迅速.

图 2 高静-低动刚度磁弹簧工作原理

Figure 2. Working principle of magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

由于永磁体能在无接触的情况下产生磁力，这样就能减小摩擦所带来的损耗，刚度调整速度快. 同时，还减小了隔振器体积，结构变得紧凑.

磁弹簧拥有“被动”和“半主动”两种工作模式：被动模式下，磁弹簧视作被动隔振器，可实现定频段隔振；半主动模式下，通过调整线圈中电流的大小和方向，可以改变起始隔振频率，以达到更宽泛的刚度调整范围的目的. 两种工作模式共同作用，使磁弹簧拥有更宽的隔振频段.

2. 磁弹簧力和刚度模型建立

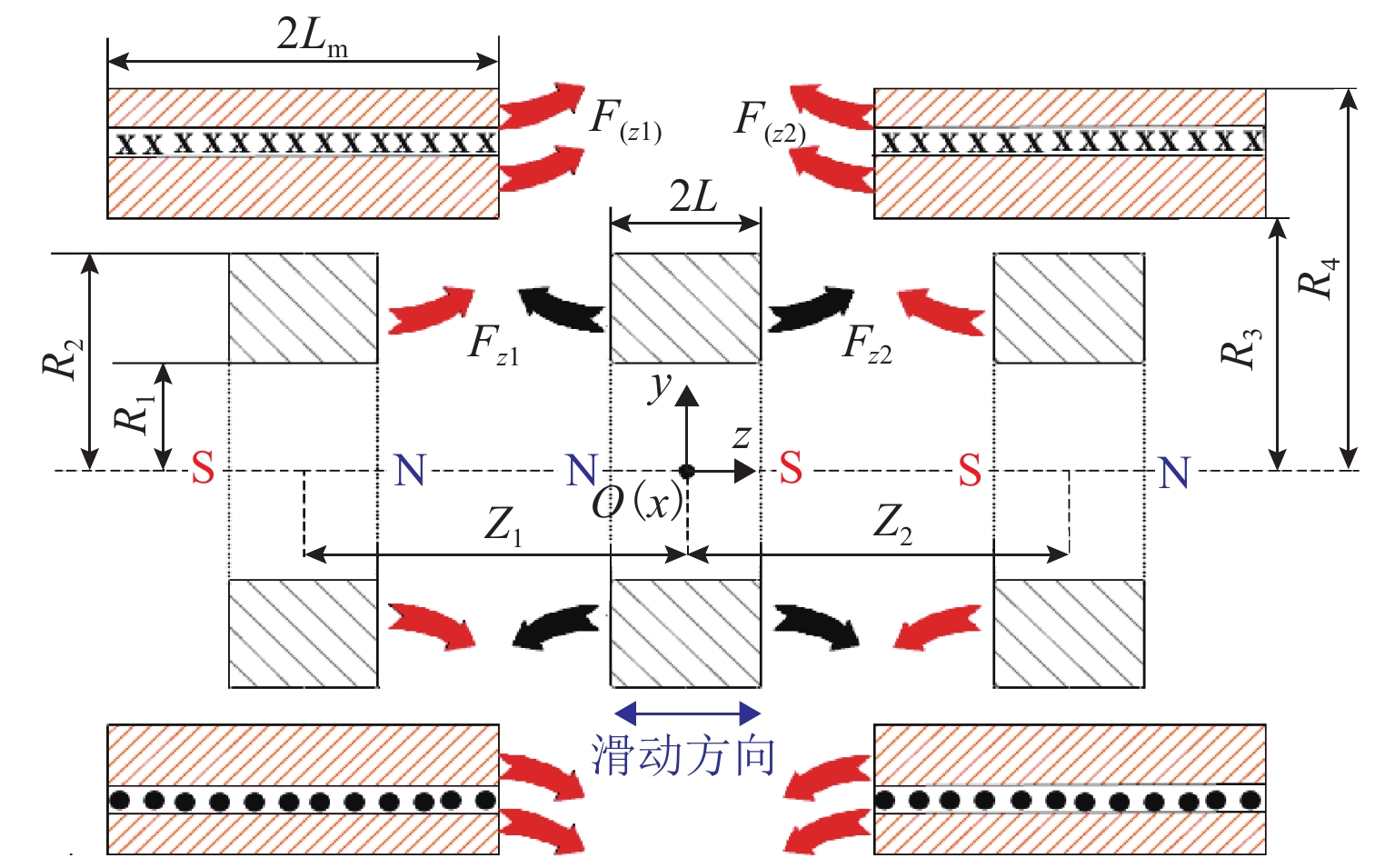
磁弹簧的磁场分布如图3所示. 图中：z轴为滑动方向；燕尾箭头表示磁场方向；L_m为线圈轴向长度的一半；L为环形永磁体长度的一半；R₁、R₂分别为环形永磁体内径、外径；R₃、R₄分别为线圈内、外半径；Z_i为环形永磁体间气隙，i=1，2；F_zi为永磁体Ⅰ、Ⅲ与永磁体Ⅱ之间的轴向磁力；F_(zi)为空心线圈对永磁体Ⅱ的电磁力. 磁弹簧各部件间的相互作用简化为磁力F_(zi)和F_zi.

图 3 磁弹簧磁场分布

Figure 3. Magnetic field distribution of magnetic spring

下载: 全尺寸图片幻灯片

2.1 电磁线圈与永磁体间的交互作用

运用分子电流法，并结合电磁场理论计算空心线圈对于永磁体Ⅱ的电磁力F_(zi).

假设环形永磁体与线圈的磁通密度在轴向截面均匀分布，单层圆环线圈的轴向磁通密度^[10-12]为

$B_{({\textit{z}})} = \frac{{{\mu _0}{I_{\rm{c}}}}}{2}\left[ {\frac{{Z + {L_{\text{m}}}}}{{\sqrt {{{{r}}^2} + {{\left( {Z + {L_{\text{m}}}} \right)}^2}} }} - \frac{{Z - {L_{\text{m}}}}}{{\sqrt {{{{r}}^2} + {{\left( {Z - {L_{\text{m}}}} \right)}^2}} }}} \right],$

(1)

式中：I_c为线圈的输入电流；μ₀为真空磁导率；Z为永磁体Ⅱ相对于线圈中心平面的轴向距离；r为线圈的半径.

将圆环线圈沿径向和轴向叠加，可得空心线圈的轴向磁通密度为

$\begin{split} & {B_{({\textit{z}})}} = \dfrac{{{\mu _0}N{I_{\rm{c}}}}}{{4{L_{\rm{m}}}({R_4} - {R_3})}}\left[ {(Z + {L_{\rm{m}}})\ln \dfrac{{{R_4} + \sqrt {R_4^2 + (Z + {L_{\rm{m}}})} }}{{{R_3} + \sqrt {R_3^2 + (Z + {L_{\rm{m}}})} }} - } \right.\\& \left. {(Z - {L_{\rm{m}}})\ln \dfrac{{{R_4} + \sqrt {R_4^2 + (Z - {L_{\rm{m}}})} }}{{{R_3} + \sqrt {R_3^2 + (Z - {L_{\rm{m}}})} }}} \right] , \end{split}$

(2)

式中：N为线圈的匝数.

如图3所示，线圈磁场的分布内强外弱，且沿中心轴线向两侧逐渐减弱，由磁场强度公式可计算出磁场强度H. 在磁弹簧动子向一侧偏移的过程中，线圈对永磁体Ⅱ两侧轴向充磁面存在一个磁场强度差，单侧线圈施加在永磁体Ⅱ上的电磁力为

$\begin{split} &{{F}}_{\left( {{\text{Z}}i} \right) }= \frac{{B_{\text{r}}SN{I_{\rm{c}}}}}{{4{L_{\text{m}}}\left( {{R_4} - {R_3}} \right)}}\left[ {{{a}}_i}{\text{ln(}}\varphi ({a_i}{\text{))}} - {b_i}{\text{ln(}}\varphi ({b_i}{\text{))}} {{ - }}\right. \\ &\quad \left.{c_i}{\text{ln(}}\varphi ({c_i}{\text{))}} + {d_i}{\text{ln(}}\varphi ({d_i}{\text{))}} \right] ,\\[-12pt] \end{split}$

(3)

式中：S为永磁体的充磁极面积；B_r为永磁体的剩磁； ${a_i} = {Z_i} - L + {L_{\rm{m}}}$ ； ${b_i} = {Z_i} - L - {L_{\rm{m}}}$ ； ${c_i} = {Z_i} + L + {L_{\rm{m}}}$ ； ${d_i} = {Z_i} + L - {L_{\rm{m}}}$ ； $\varphi (x_i) = \dfrac{{R}_{4} + \sqrt{{R}_{4}^{2} + {x}_{i}{}^{2}}}{{R}_{3} + \sqrt{{{R}}_{\text{3}}^{\text{2}} + {x}_{i}{}^{2}}} ,$ $x_i \in \left\{ {{a_i},{b_i},{c_i},{d_i}} \right\}$ .

2.2 永磁体间的交互作用

运用分子环流模型，计算轴向磁力F_Zi. 将均匀材料，均匀充磁的永磁体Ⅰ ～ Ⅲ等效为通电多重螺线管，如图4所示. 图中：Z_d1、Z_d2为永磁体之间的轴向气隙；I₁～I₃为永磁体Ⅰ ～ Ⅲ表面电流；dl₁、dl₃和dl₂为载流环路上假想微电流元长度；R₂₁、R₂₃分别为永磁体Ⅰ、Ⅲ和永磁体Ⅱ之间的距离向量. 等效表面电流I_m为

图 4 永磁体磁场分布

Figure 4. Magnetic field distribution of permanent magnet

下载: 全尺寸图片幻灯片

${I_{\rm{m}}} = 2L{B_{\rm{r}}}/({N_{\rm{m}}}{\mu _0}),$

(4)

式中：N_m为永磁体等效成的薄线圈的匝数.

根据安培力定律，可推导出载流环路上电流元dl₁和dl₃对dl₂施加的磁力^[11]分别为

$\begin{array}{l}\text{d}{\boldsymbol{F}}_{21}=\dfrac{{\mu }_{0}{I}_{{\rm{m}}1}{I}_{{\rm{m}}2}}{4{\text{π}} {{\boldsymbol{R}}}_{21}^{3}}·\left[\text{d}{{\boldsymbol{l}}}_{1}\times {\boldsymbol{R}}_{21}\right]·\text{d}{{\boldsymbol{l}}}_{2},\\ \text{d}{\boldsymbol{F}}_{23}=\dfrac{{\mu }_{0}{I}_{{\rm{m}}2}{I}_{{\rm{m}}3}}{4{\text{π}} {{\boldsymbol{R}}}_{23}^{3}}·\left[\text{d}{{\boldsymbol{l}}}_{3}\times {\boldsymbol{R}}_{23}\right]·\text{d}{{\boldsymbol{l}}}_{2},\end{array}$

(5)

式中：I_m1、I_m2和I_m3分别为永磁体Ⅰ、Ⅱ、Ⅲ上的等效表面电流，且I_m2和I_m1、I_m3的极性相反.

载流回路之间的作用力F₂₁和F₂₃的轴向分量 $F_{({\textit{z}}_{\rm{d1}})}$ 和 $F_{({\textit{z}}_{\rm{d2}})}$ 分别为

$\left\{ \begin{array}{l} F_{({\textit{z}}_{{\rm{d}}1})}=\dfrac{{\mu }_{0}{I}_{{\rm{m}}1}{I}_{{\rm{m}}2}{\left(R_2-R_1\right)}^{2}}{4\text{π} }{\displaystyle {\int }_{{}^{}0}^{2\text{π} }}{\displaystyle {\int }_{{}^{}0}^{2\text{π} }}\left[ \begin{array}{l}\dfrac{-Z_{\text{d1}}{\rm{cos}}({\theta }_{2}-{\theta }_{1})}{(2{R}_{1}^{2} + 2{R}_{1}^{2}\text{cos}({\theta }_{2}-{\theta }_{1}) + {Z_{{\rm{d1}}}^2}{)}^{3/2}} + \dfrac{Z_{\text{d1}}{\rm{cos}}({\theta }_{2}-{\theta }_{1})}{(2{R}_{2}^{2} + 2{R}_{2}^{2}\text{cos}({\theta }_{2}-{\theta }_{1}) + {Z_{{\rm{d1}}}^2}{)}^{3/2}}\end{array} \right]\text{d}{\theta }_{1}\text{d}{\theta }_{2},\\ F_{({\textit{z}}_{{\rm{d}}2})}=\dfrac{{\mu }_{0}{I}_{{\rm{m}}3}{I}_{{\rm{m}}2}{\left(R_2-R_1\right)}^{2}}{4\text{π} }{\displaystyle {\int }_{{}^{}0}^{2\text{π} }}{\displaystyle {\int }_{{}^{}0}^{2\text{π} }}\left[ \begin{array}{l}\dfrac{-Z_{\text{d2}}{\rm{cos}}({\theta }_{2}-{\theta }_{3})}{(2{R}_{3}^{2} + 2{R}_{3}^{2}\text{cos}({\theta }_{2}-\theta_ 3) + {Z_{{\rm{d2}}}^2}{)}^{3/2}} + \dfrac{Z_{\text{d2}}{\rm{cos}}({\theta }_{2}-{\theta }_{3})}{(2{R}_{2}^{2} + 2{R}_{2}^{2}\text{cos}({\theta }_{2}-{\theta }_{3}) + {Z_{{\rm{d2}}}^2}{)}^{3/2}}\end{array} \right]\text{d}{\theta }_{3}\text{d}{\theta }_{2}. \end{array}\right.$

(6)

将式（6）沿永磁体长度积分，得到永磁体Ⅰ、Ⅲ和永磁体Ⅱ间斥力的轴向分量F_z1、F_z2分别为

$\left\{ \begin{array}{l} {F}_{{\textit{z}}1} = \dfrac{\mu_ 0{I}_{{\rm{m}}1}{I}_{{\rm{m}}2}{\left(R_2-R_1\right)}^{2}}{4\text{π} {(2L)}^{2}} {\displaystyle {\int }_{{}^{}0}^{2L} {\displaystyle {\int }_{ -2L}^{{}^{}0} {\displaystyle {\int }_{{}^{}0}^{2\text{π} } {\displaystyle {\int }_{{}^{}0}^{2\text{π} } \left[ \begin{array}{l}\dfrac{-{Z}_{{\rm{R}}1}\text{cos}(\theta _2-\theta_1)}{(2{R}_{1}^{2} + 2{R}_{1}^{2}\text{cos}(\theta_2-\theta_1) + {{Z}_{{\rm{R}}1}^{2}}{)}^{3/2}} + \dfrac{{\text{Z}}_{{\rm{R}}1}\text{cos}(\theta_2 - \theta_1)}{(2{R}_{2}^{2} + 2{R}_{2}^{2}\text{cos}(\theta_2-\theta_1) + {{Z}_{{\rm{R}}1}^{2}}{)}^{3/2}}\end{array} \right] \text{d}{\theta }_{1}\text{d}{\theta }_{2}\text{d}{{\boldsymbol{l}}}_{1}\text{d}{{\boldsymbol{l}}}_{2}}}}},\\ {F}_{{\textit{z}}2} = \dfrac{\mu_ 0{I}_{{\rm{m}}3}{I}_{{\rm{m}}2}{\left(R_2-{R}_{3}\right)}^{2}}{4\text{π} {(2L)}^{2}} {\displaystyle {\int }_{0}^{2L} {\displaystyle {\int }_{ -2L}^{{}^{}0} {\displaystyle {\int }_{0}^{2\text{π} } {\displaystyle {\int }_{{}^{}0}^{2\text{π} } \left[ \begin{array}{l}\dfrac{-{Z}_{{\rm{R}}2}\text{cos}(\theta_2-\theta_3)}{(2{R}_{3}^{2} + 2{R}_{3}^{2}\text{cos}(\theta_2-\theta_3) + {Z}_{{\rm{R}}2}{)}^{3/2}} + \dfrac{{\text{Z}}_{{\rm{R}}2}\text{cos}(\theta_2 - \theta_3)}{(2{R}_{2}^{2} + 2{R}_{2}^{2}\text{cos}(\theta_2 - \theta_3) + {{Z}_{{\rm{R}}2}^{2}}{)}^{3/2}}\end{array} \right] \text{d}\theta_3\text{d}\theta_2\text{d}{{\boldsymbol{l}}}_{3}\text{d}{{\boldsymbol{l}}}_{2}}}}},\end{array} \right.$

(7)

式中： ${Z_{{\rm{R}}1}} = {Z_{{\rm{d}}1}} - {L_1} + {L_2}$ ； ${Z_{{\rm{R}}2}} = {Z_{{\rm{d}}2}} - {L_3} + {L_2}$ ； ${L_1}$ ～ ${L_3}$ 分别为永磁体Ⅰ ～Ⅲ的长度.

磁弹簧的轴向磁力F_z为

$F_{\textit{z}}=F_{{\textit{z}}1} + F_{{\textit{z}}2} + F_{({\textit{z}}1)} + F_{({\textit{z}}2)} .$

(8)

磁弹簧的刚度K_z为

${K_{\textit{z}}} = \frac{{{\text{d}}F_{\textit{z}}}}{{{\text{d}}Z}} .$

(9)

3. 弹簧参数特性分析

高静-低动刚度磁弹簧结构参数如表1所示，磁弹簧永磁体材料为N35H.

表 1 高静-低动刚度磁弹簧结构参数

Table 1. Structural parameters of magnetic spring with high static stiffness and low dynamic stiffness mm

参数	R₁	R₂	Z_d1	Z_d2	2L	R₃	R₄	2L_m
数值	15	30	15	15	20	35	52	52

下载: 导出CSV

| 显示表格

根据式（3）、（8）、（9）以及表1中的参数，可以计算出高静-低动刚度磁弹簧的轴向磁力F_z. 根据理论模型分析电流、工作气隙对磁弹簧的力学和刚度的影响规律.

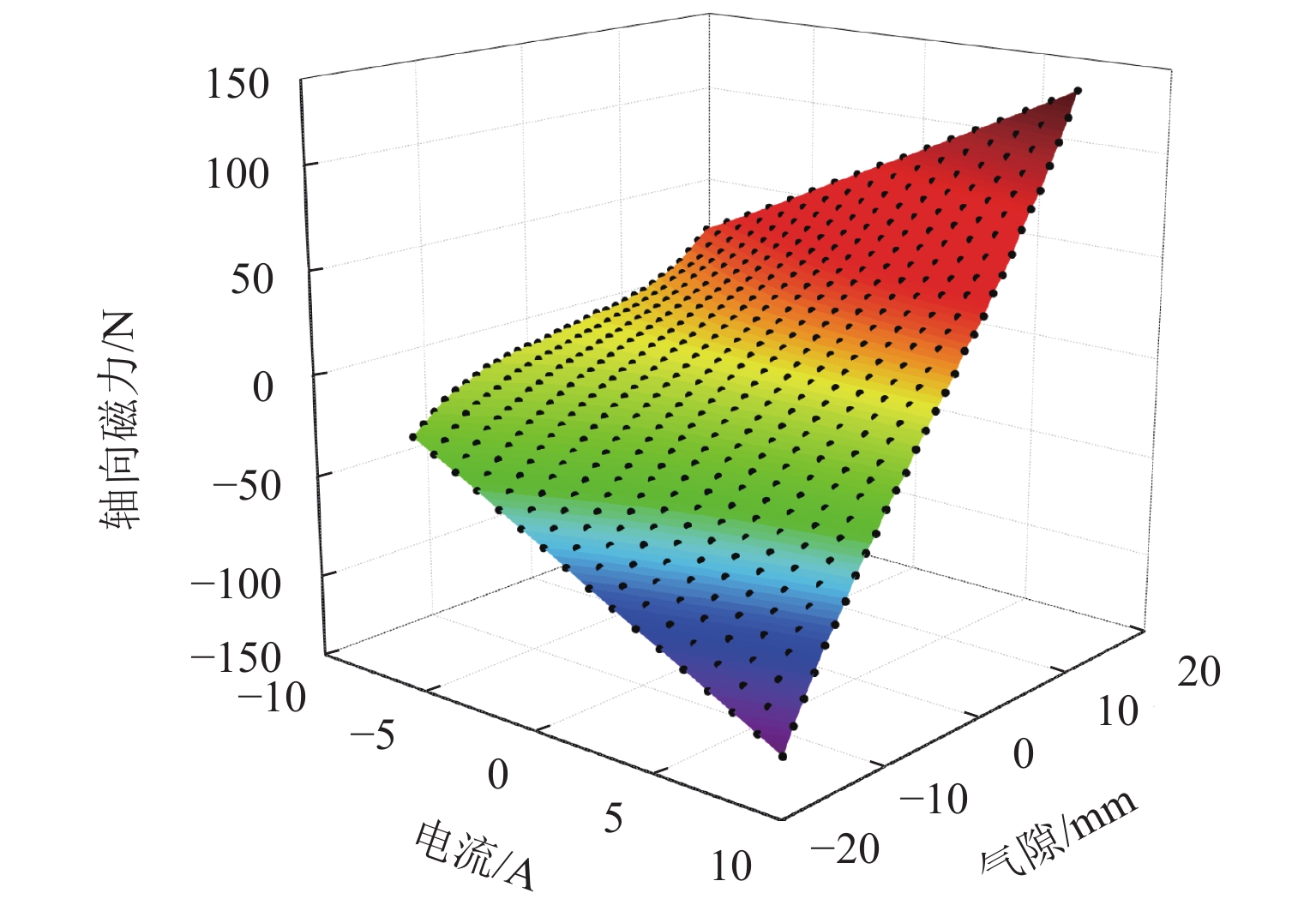
电磁线圈由直径1 mm的铜线绕制而成，从安全角度考虑：短时间内直径为1 mm线圈最多加载8 A的电流. 当永磁体间的工作气隙从 −15 mm变化至 +15 mm，电流从 −8 A变化至 +8 A时，磁弹簧轴向磁力的解析计算结果如图5所示. 图中：曲面为理论计算值，实心点为实验测量值. 由理论计算和实验测量可知：随着磁弹簧动子向一侧偏置，永磁体Ⅱ和永磁体Ⅰ、Ⅲ间的气隙一侧减小，一侧增加. 永磁体Ⅱ两侧充磁面的磁场强度H之差增大，磁弹簧的轴向磁力F_z随着永磁体Ⅱ偏离平衡位置先平缓变化，后急剧变化的非线性关系；轴向磁力和正向电流呈正相关，和反向电流呈负相关，且呈现良好的线性关系特性. 轴向刚度K_z为轴向磁力曲线的斜率，所以K_z的变化规律与轴向磁力大致相同. 通过上述结果可以发现，调节线圈电流的大小和方向，可以增大或减小磁弹簧的轴向磁力F_z和刚度K_z，改变系统的承载能力.

图 5 磁力理论计算与实验测量对比

Figure 5. Comparison of theoretically calculated magnetic force and experimentally measured magnetic force

下载: 全尺寸图片幻灯片

4. 动力学建模与传递率分析

高静-低动刚度磁弹簧在接收地面振动信号时，可以近似看作一种单自由度振动系统，对其进行动力学分析.

系统接收的简谐位移激励 $X_{\text{d}} = A{\text{cos}}\;\omega {{t}}$ ，负载位移为X_L，则负载的相对位移X=X_L−X_d，如图6所示，图中：M为负载的质量；K为系统刚度；C为系统阻尼.

图 6 磁弹簧动力学模型

Figure 6. Dynamics model of magnetic spring

下载: 全尺寸图片幻灯片

系统的动力学模型表示为

$M\ddot {{X_{\rm{L}}}} + C\dot X + KX = 0,$

(10)

$M\ddot {{X_{\rm{L}}}} + C(\dot {{X_{\text{d}}}} - \dot {{X_{\text{L}}}} ) + K({X_{\text{d}}} - {X_{\rm{L}}}) = 0.$

(11)

在激励幅值较小的情况下，计算振动传递率非线性算法与线性算法具有较好的近似性，采用线性化传递率算法，经傅里叶变换后，地面输入位移与输出位移的传递率^[13]为

$T = \sqrt {\frac{{1 + {{\left( {2\xi \omega /{\omega _{\text{n}}}} \right)}^2}}}{{{{\left[ {1 - {{\left( {\omega /{\omega _{\text{n}}}} \right)}^2}} \right]}^2} + {{\left( {2\xi \omega /{\omega _{\text{n}}}} \right)}^2}}}} ,$

(12)

式中： ${\omega _{\text{n}}} = \sqrt {K/M}$ ，为系统频率； $\xi = C/(2M{\omega _{\text{n}}})$ ，为系统阻尼比.

系统的固有频率为

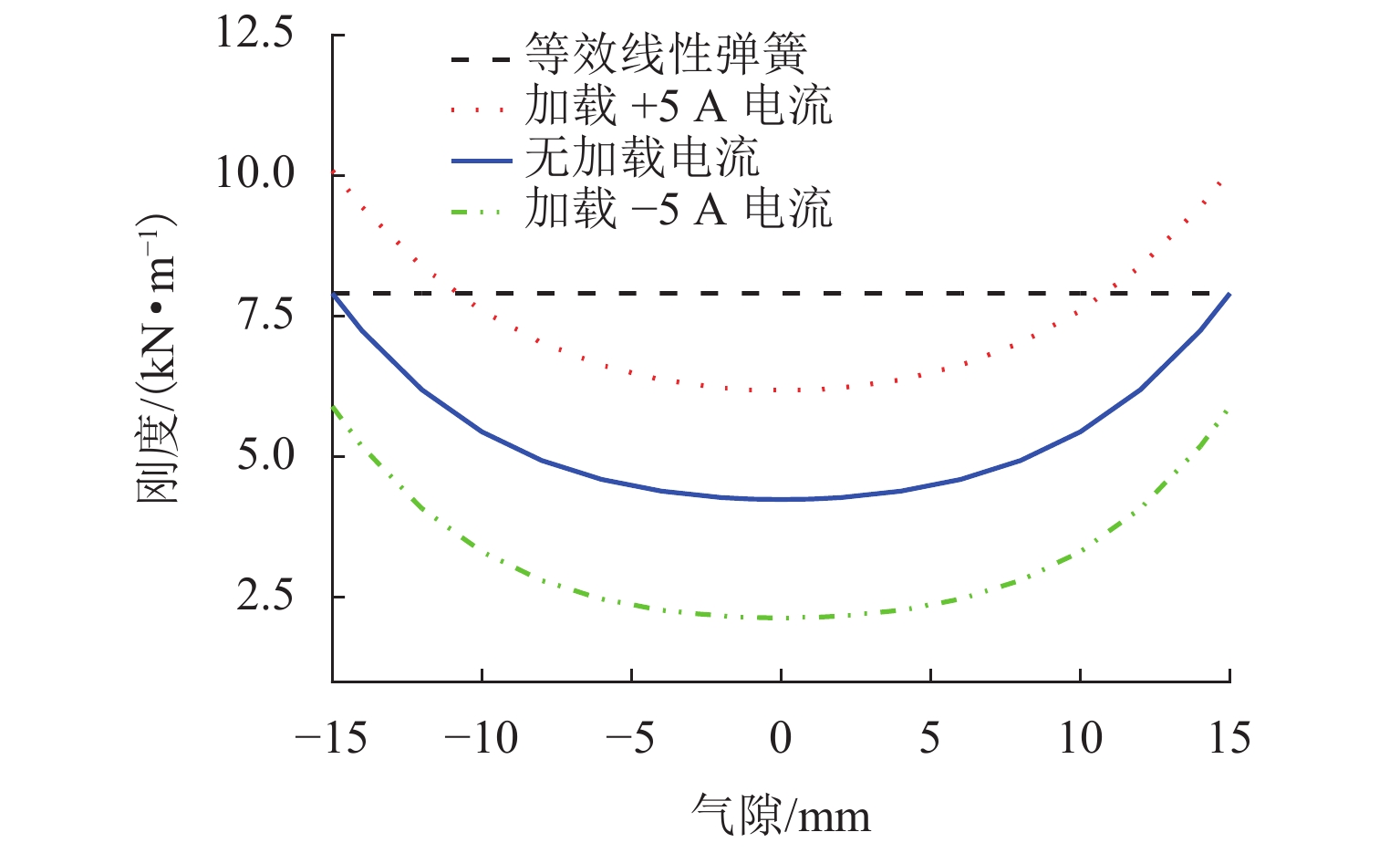
${{f}} = \frac{1}{{2\text{π} }}\sqrt {\frac{K}{M}}.$

(13)

根据磁弹簧工作原理和刚度计算模型并结合表1中磁弹簧的物理参数，得到磁弹簧的刚度变化曲线如图7所示. 在无加载电流时，磁弹簧的等效线性刚度为7905 N/m，磁弹簧的工作刚度为4236 N/m. 在M=10 kg，C=0.5 N/（m·s⁻¹）的情况下，传递率仿真计算结果如图8所示. 由图3可知：无加载电流时，系统固有频率从4.47 Hz降到3.27 Hz，系统的固有频率相对于等效线性弹簧降低了26%，起始隔振频率从6.32 Hz降到4.62 Hz，有效隔振频带增加了26%；线圈中的额定电流从 +5 A变换到 −5 A时，系统固有频率从3.95 Hz变化为2.32 Hz，通入 +5 A电流时，系统的固有频率相对于通入 −5 A电流时降低了41%，起始隔振频率从5.59 Hz变化为3.28 Hz，有效隔振频带增加了41%；传递率峰值从37.86 dB变化为30.59 dB. 图8验证了所提出的磁弹簧可以有效降低系统的起始隔振频率，同时，通过调整线圈中的电流可以拓宽隔振频带，随着电流的减小，可以大幅降低传递率峰值.

图 7 磁弹簧理论刚度

Figure 7. Theoretical stiffness of magnetic spring

下载: 全尺寸图片幻灯片

图 8 振动传递率仿真对比

Figure 8. Simulation comparison of vibration transmissibility

下载: 全尺寸图片幻灯片

5. 样机研制和特性分析

搭建实验测量平台对磁弹簧的轴向输出力和刚度特性进行实验研究. 实验平台如图9所示，磁弹簧固定在龙门框架内，轴向位移平台通过测力传感器与输出轴的一端相连，另外一端对准激光位移传感器. 通过转动位移平台上的螺柱，使磁弹簧动子向一侧偏置，工作气隙Z随之改变，气隙变化量可通过激光位移传感器读取，测力传感器可检测出机构间轴向磁力F_z. 通过模拟量电压信号控制电磁线圈驱动器产生电流变化，电流变化范围为 [−5，5] A.

图 9 轴向磁力测量实验平台

Figure 9. Experimental platform formeasuring axial magnetic force

下载: 全尺寸图片幻灯片

5.1 轴向磁力与气隙位移变化关系分析

未加载激励电流时，将永磁体Ⅱ的静力平衡位置x₀定义为坐标零点，通过位移平台推动磁弹簧动子轴向偏置，当气隙在 [−15，15] mm内，以1 mm为间隔均匀变化时，力值显示仪记录下气隙变化时所对应的轴向磁力的测量结果，如图10所示. 由图可知：轴向磁力与气隙间的关系曲线呈先平缓增加后急剧增加的非线性变化；当线圈未通电时，轴向磁力最大值为81.5 N；当线圈加载正向激励电流 +5 A时，轴向磁力可增加至112.3 N；当加载反向激励电流 −5 A时，轴向磁力可减弱至49.9 N，可实现约76.6%的输出力范围调节.

图 10 轴向磁力与轴向气隙的关系

Figure 10. Relationship between axial magnetic force and axial air gap

下载: 全尺寸图片幻灯片

5.2 轴向磁力F_z和线圈电流I变化关系分析

将磁弹簧动子定位在 −15、−10、−5、0、+5、+10、+15 mm 7个位置，调节线圈电流，使线圈在 [−5，5] A内以1 A为间隔变化，轴向磁力随电流的变化关系，如图11所示. 结果表明，轴向磁力与正向电流呈正相关，与反向电流呈负相关，且均呈现良好的线性关系变化. 而且当加载电流相同时，可以发现系统动子轴向偏置量越大，轴向磁力越大. 实验分析表明，磁弹簧可以通过控制激励电流实现输出力的线性化调节，与磁弹簧的设计理念高度吻合，具有很高的可靠性和有效性.

图 11 轴向磁力与电流的关系

Figure 11. Relationship between axial magnetic force and current

下载: 全尺寸图片幻灯片

5.3 输出刚度与气隙位移变化关系分析

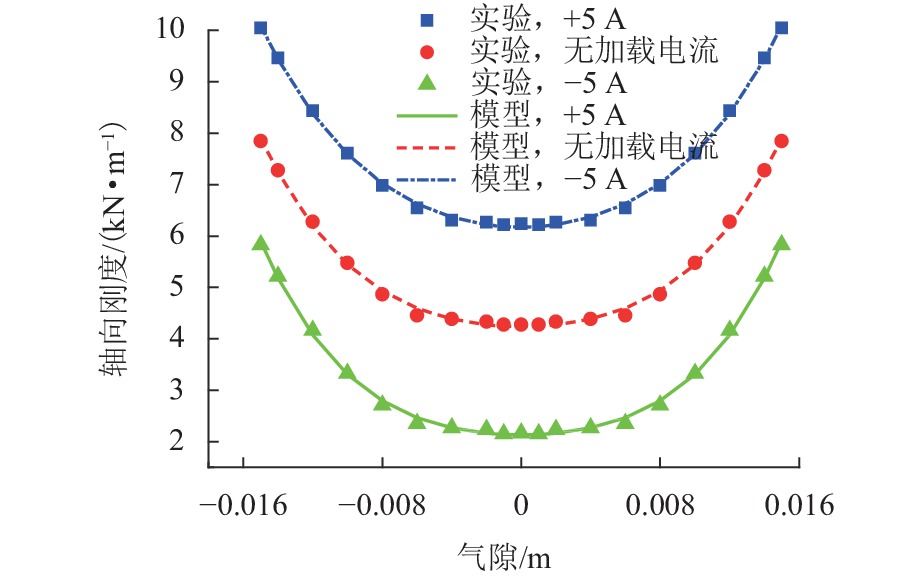
磁弹簧动子从 −15 mm变化至 +15 mm的过程中，分别给线圈加载 +5 A正向激励电流、无加载电流和 −5 A反向激励电流. 磁弹簧的输出刚度随气隙变化的关系如图12所示. 由图可知：磁弹簧刚度与气隙变化近似呈抛物线规律变化；磁弹簧的工作刚度要远低于等效线性刚度，因此表明本文设计磁弹簧具有高静-低动刚度特性；调整线圈中的电流并不会改变刚度曲线的变化趋势，只是改变了系统的刚度变化范围；未加载电流时，输出刚度调整范围为 [3901.28，8503.59] N/m；加载 +5 A激励电流时，刚度调整范围为 [5818.39，10395.75] N/m；加载 −5 A激励电流时，刚度调整范围为 [1733.37，6349.35] N/m；在激励电流 [−5，5] A内，磁弹簧的刚度调节范围比未通电时增加约188.2%.

图 12 轴向刚度与气隙的关系

Figure 12. Relationship between axial stiffness and air gap

下载: 全尺寸图片幻灯片

5.4 输出刚度与线圈电流变化关系分析

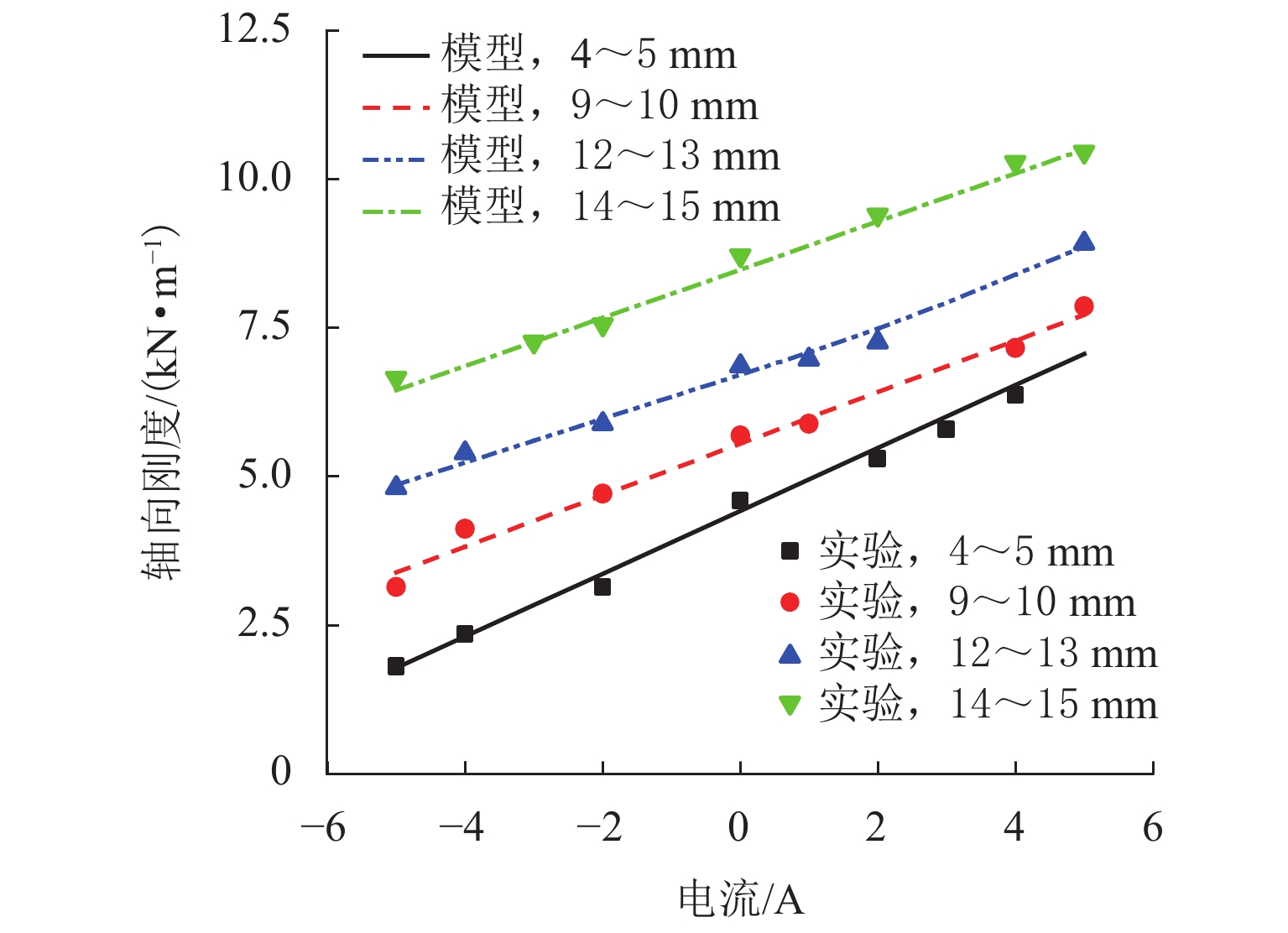
调节线圈电流，使其以1 A为间隔在 [−5，5] A内均匀变化，当系统动子从4、9、12、14 mm 4个位置轴向偏置至5、10、13、15 mm，计算当偏置1 mm时随电流变化所对应的系统刚度值，如图13所示. 结果表明，磁弹簧刚度与正向激励电流呈正相关，与反向激励电流呈负相关，且均为线性变化关系，可以通过调节激励电流，改变系统刚度，使磁弹簧拥有不同的起始隔振频率，适应不同的工程需求.

图 13 轴向刚度与电流的关系

Figure 13. Relationship between axial stiffness and current

下载: 全尺寸图片幻灯片

5.5 系统刚度调节响应速度分析

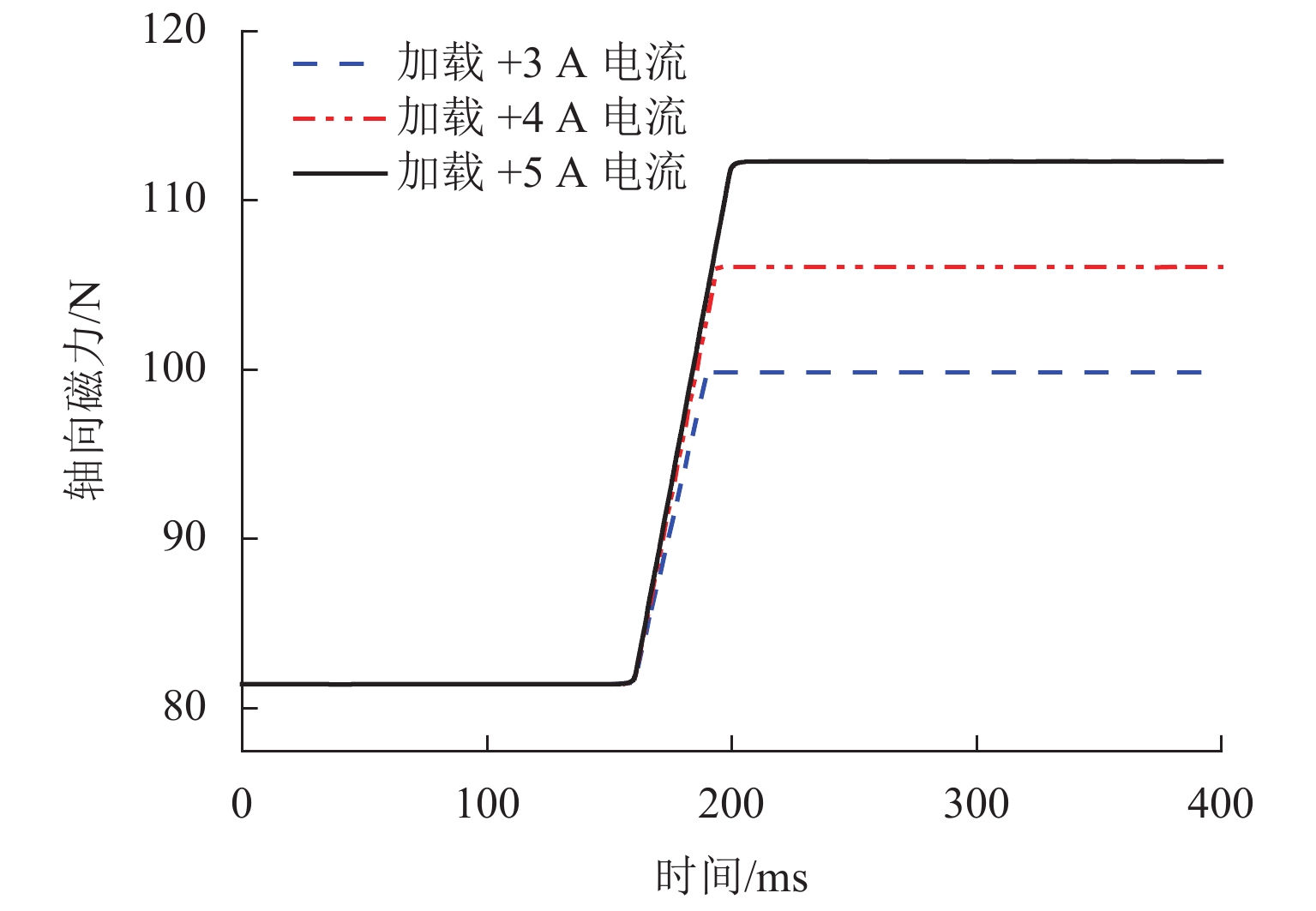
快速的刚度调整可以迅速地调整系统的起始隔振频率，这将有益于系统隔振的主动控制. 为此，对磁弹簧的刚度响应速度进行了测试. 鉴于磁弹簧刚度调节速度难以测量，所以将磁弹簧产生一定偏置量时，轴向磁力的变化量视为磁弹簧的输出刚度. 首先，使磁弹簧动子在“无电流”的情况下轴向偏置15 mm，而后瞬间分别给线圈加载 +3、+4、+5 A电流，加载电流将会使磁弹簧的输出刚度迅速增大. 在通电瞬间，测力传感器能够检测到磁弹簧的轴向磁力的变化情况，并记录变化时间，如图14所示，轴向磁力从81.53 N分别变化到98.20、106.05、112.30 N，刚度从8503.59 N/m分别变化到9407.99、9804.19、10395.75 N/m，用时分别为30、34、40 ms. 由于磁弹簧的结构相较于机械结构更简单，没有复杂的刚度调整机构，因此，磁弹簧的采用电流控制实现刚度调整的速度要比通过机械结构调整方式迅速是可以理解的，并且观察到随着刚度的增加调整速度略有降低.

图 14 刚度阶跃响应

Figure 14. Stiffness step response

下载: 全尺寸图片幻灯片

6. 结　论

本文提出一种新型的高静-低动刚度磁弹簧. 利用电磁场理论建立了磁弹簧的力学和刚度模型. 通过仿真对磁弹簧参数进行优化设计，并明确气隙和电流对系统输出力和刚度的影响规律；理论计算和实验测量共同表明，其输出力和刚度曲线与气隙呈先平缓后急剧的非线性关系，且具有高静-低动刚度特性；输出力和刚度与电流近似线性关系，磁弹簧可通过改变电流实现较大范围的刚度调整，且刚度阶跃响应迅速. 磁弹簧可有效调节刚度，在未通入电流时，系统的固有频率相对于等效线性弹簧降低了26%，有效隔振频带增加了26%. 在通入电流时，通入 +5 A电流时系统的固有频率相对于通入 −5 A电流时降低了41%，有效隔振频带增加了41%. 该磁弹簧有效降低了系统的固有频率，拓宽了有效隔振频带.

研究中也发现了一些问题，比如，磁弹簧中的电磁线圈的作用是调整线圈中的电流，以此实现更宽泛的刚度调整范围，但在长时间通入电流的同时，电磁线圈会由于本身的特性从而发热，因此，在后续研究中应考虑散热装置.

图 1 高静-低动刚度磁弹簧示意

Figure 1. Magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

图 2 高静-低动刚度磁弹簧工作原理

Figure 2. Working principle of magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

图 3 磁弹簧磁场分布

Figure 3. Magnetic field distribution of magnetic spring

下载: 全尺寸图片幻灯片

图 4 永磁体磁场分布

Figure 4. Magnetic field distribution of permanent magnet

下载: 全尺寸图片幻灯片

图 5 磁力理论计算与实验测量对比

Figure 5. Comparison of theoretically calculated magnetic force and experimentally measured magnetic force

下载: 全尺寸图片幻灯片

图 6 磁弹簧动力学模型

Figure 6. Dynamics model of magnetic spring

下载: 全尺寸图片幻灯片

图 7 磁弹簧理论刚度

Figure 7. Theoretical stiffness of magnetic spring

下载: 全尺寸图片幻灯片

图 8 振动传递率仿真对比

Figure 8. Simulation comparison of vibration transmissibility

下载: 全尺寸图片幻灯片

图 9 轴向磁力测量实验平台

Figure 9. Experimental platform formeasuring axial magnetic force

下载: 全尺寸图片幻灯片

图 10 轴向磁力与轴向气隙的关系

Figure 10. Relationship between axial magnetic force and axial air gap

下载: 全尺寸图片幻灯片

图 11 轴向磁力与电流的关系

Figure 11. Relationship between axial magnetic force and current

下载: 全尺寸图片幻灯片

图 12 轴向刚度与气隙的关系

Figure 12. Relationship between axial stiffness and air gap

下载: 全尺寸图片幻灯片

图 13 轴向刚度与电流的关系

Figure 13. Relationship between axial stiffness and current

下载: 全尺寸图片幻灯片

图 14 刚度阶跃响应

Figure 14. Stiffness step response

下载: 全尺寸图片幻灯片

表 1 高静-低动刚度磁弹簧结构参数

Table 1. Structural parameters of magnetic spring with high static stiffness and low dynamic stiffness mm

参数 R₁ R₂ Z_d1 Z_d2 2L R₃ R₄ 2L_m
数值 15 30 15 15 20 35 52 52

下载: 导出CSV

参考文献(13)

[1]	刘尚举,晏巨,陈虬. 电磁永磁混合悬浮隔振系统控制研究[J]. 西南交通大学学报,1999,34(3): 279-283. doi: 10.3969/j.issn.0258-2724.1999.03.006 LIU Shangju, YAN Ju, CHEN Qiu. Study of controlling of an electromagnet and permanent magnet suspension isolation system[J]. Journal of Southwest Jiaotong University, 1999, 34(3): 279-283. doi: 10.3969/j.issn.0258-2724.1999.03.006
[2]	韩俊淑,孙景工,孟令帅. 一种曲面-弹簧-滚子机构的非线性隔振器特性分析[J]. 振动与冲击,2019,38(3): 170-178. doi: 10.13465/j.cnki.jvs.2019.03.024 HAN Junshu, SUN Jinggong, MENG Lingshuai. Design and characteristics analysis of a nonlinear vibration isolator using a curved surface-spring-roller mechanism as negative stiffness element[J]. Journal of Vibration and Shock, 2019, 38(3): 170-178. doi: 10.13465/j.cnki.jvs.2019.03.024
[3]	赵川,孙凤,裴文哲,等. 永磁悬浮平台的分散串级控制方法[J]. 西南交通大学学报,2022,57(3): 618-626. ZHAO Chuan, SUN Feng, PEI Wenzhe, et al. Independent cascade control method for permanent magnetic levitation platform[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 618-626.
[4]	李爽,楼京俊,杨庆超,等. 双环永磁体型高静低动刚度隔振器设计、建模与试验研究[J]. 振动工程学报,2019,32(4): 675-684. doi: 10.16385/j.cnki.issn.1004-4523.2019.04.015 LI Shuang, LOU Jingjun, YANG Qingchao, et al. Design and experiment of a vibration isolator using double-ring permanent magnets springs with negative stiffness[J]. Journal of Vibration Engineering, 2019, 32(4): 675-684. doi: 10.16385/j.cnki.issn.1004-4523.2019.04.015
[5]	高双,朱翔,谌宗琦,等. 基于欧拉梁的准零刚度隔振系统动力特性分析[J]. 中国机械工程,2016,27(21): 2869-2876. doi: 10.3969/j.issn.1004-132X.2016.21.006 GAO Shuang, ZHU Xiang, SHEN Zongqi, et al. Analyses on dynamics characteristics of a quasi-zero-stiffness vibration isolation system based on Euler beam[J]. China Mechanical Engineering, 2016, 27(21): 2869-2876. doi: 10.3969/j.issn.1004-132X.2016.21.006
[6]	CARRELLA A, BRENNAN M J, WATERS T P, et al. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J]. Journal of Sound and Vibration, 2008, 315(3): 712-720. doi: 10.1016/j.jsv.2008.01.046
[7]	ZHANG F, XU M L, SHAO S B, et al. A new high-static-low-dynamic stiffness vibration isolator based on magnetic negative stiffness mechanism employing variable reluctance stress[J]. Journal of Sound and Vibration, 2020, 476: 115322.1-115322.17
[8]	ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001
[9]	王迎春,柴凯,刘树勇,等. 永磁体型高静低动刚度隔振器试验研究[J]. 噪声与振动控制,2019,39(5): 223-230. doi: 10.3969/j.issn.1006-1355.2019.05.042 WANG Yingchun, CHAI Kai, LIU Shuyong, et al. Experimental study on the permanent magnets vibration isolators with high-static and low-dynamic stiffness[J]. Noise and Vibration Control, 2019, 39(5): 223-230. doi: 10.3969/j.issn.1006-1355.2019.05.042
[10]	ZHAO Y, YU J, WANG H, et al. Design of an electromagnetic prismatic joint with variable stiffness[J]. Industrial Robot, 2017, 44(2): 222-230. doi: 10.1108/IR-09-2016-0249
[11]	EBRAHIMI B, KHAMESEE M B, GOLNARAGHI M F. Design and modeling of a magnetic shock absorber based on eddy current damping effect[J]. Journal of Sound and Vibration, 2008, 315(4/5): 875-889.
[12]	曹琪,王皓,余觉. 基于电磁变刚度的力控制装置研究[J]. 机械设计与研究,2020,36(3): 170-175,181. doi: 10.13952/j.cnki.jofmdr.2020.0124 CAO Qi, WANG Hao, YU Jue. Research on the force control device based on electromagnetic variable stiffness principle[J]. Machine Design & Research, 2020, 36(3): 170-175,181. doi: 10.13952/j.cnki.jofmdr.2020.0124
[13]	孟凯,顾勇,刘豫喜,等. 基于可控电磁负刚度的半主动隔振器传递率特性研究[J]. 振动与冲击,2022,41(7): 228-234. doi: 10.13465/j.cnki.jvs.2022.07.030 MENG Kai, GU Yong, LIU Yuxi, et al. Transmissibility characteristics of semi-active vibration isolator based on controllable electro-magnetic negative stiffness[J]. Journal of Vibration and Shock, 2022, 41(7): 228-234. doi: 10.13465/j.cnki.jvs.2022.07.030