改进型悬浮架系统的动力学特性和性能评估

张明亮; 杨新梦; 张连朋; 李明远; 刘丽茹

doi:10.3969/j.issn.0258-2724.20220885

改进型悬浮架系统的动力学特性和性能评估

doi: 10.3969/j.issn.0258-2724.20220885

张明亮^{1, 2, 3,},
杨新梦¹,
张连朋¹,
李明远¹,
刘丽茹¹

1.
石家庄铁道大学机械工程学院，河北石家庄 050043
2.
西南交通大学轨道交通运载系统全国重点实验室，四川成都 610031
3.
兰州交通大学光电技术与智能控制教育部重点实验室，甘肃兰州 730070

基金项目: 国家自然科学基金（52205064）；河北省高等学校科学技术研究项目（ZD2022064）

详细信息

作者简介:
张明亮（1984—），男，副教授，博士，研究方向为磁悬浮技术和车辆动力学，E-mail：zmlhit@126.com

中图分类号: U266.4
计量
- 文章访问数: 503
- HTML全文浏览量: 234
- PDF下载量: 29
- 被引次数: 1
出版历程
- 收稿日期: 2022-12-27
- 修回日期: 2023-05-10
- 网络出版日期: 2023-06-19
- 刊出日期: 2023-05-12

Dynamic Characteristics and Performance Assessment of Improved Suspension Frame System

1.
School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 610031, China
3.
Key Lab of Opt-Electronic Technology and Intelligent Control of Ministry of Education, Lanzhou Jiaotong University, Lanzhou 730070, China

摘要

摘要:
为了增大高温超导钉扎磁悬浮列车的悬浮力和提升安全性，提出了抱轨式改进型悬浮架系统，首先，采用等效处理方法计算了高温超导块材阵列和永磁轨道之间的悬浮力，并利用悬浮力实验装置测量两者的悬浮力，实验验证了等效处理方法的正确性；其次，基于等效处理方法得到改进型悬浮架系统的悬浮力，利用悬浮力和悬浮间隙的关系建立了单个改进型悬浮架本体在轨道不平顺简谐激励下的动力学模型，进一步基于线性微分方程理论推导得到简谐激励下的幅频方程；最后，研究了运行速度和阻尼对稳态振幅的影响，得到阻尼在最高运行速度下应取的范围. 研究结果表明：在质量、刚度、轨道不平顺波长和幅值一定的情况下，稳态振幅的大小取决于运行速度和阻尼，且稳态振幅随着运行速度的增大而增大，随着阻尼的减小而增大；以磁悬浮安全性指标为约束，在最高运行速度600 km/h情况下阻尼应大于6905 Ns/m.
- 改进型悬浮架系统 /
- 悬浮力 /
- 轨道不平顺 /
- 稳态振幅 /
- 阻尼
Abstract:
In order to improve the levitation force and enhance the safety of high-temperature superconducting pinned maglev trains, an improved rail-holding suspension frame system was proposed. Firstly, the levitation force between high-temperature superconductor arrays and permanent magnet guideways was calculated based on the equivalent processing method. The levitation forces of high-temperature superconductor arrays and permanent magnet guideways were also measured by the levitation force test device, which validated the equivalent processing method experimentally. Then, the levitation force of the improved suspension frame system was obtained based on the equivalent processing method. According to the relationship between levitation force and levitation gap, the dynamic model of a single improved suspension frame was set up under track irregularity harmonic excitation. The amplitude-frequency equation was derived by linear differential equation theory. Lastly, the influence of running velocity and damping on the steady-state amplitude was investigated. The feasible domain of damping under the maximum running velocity was obtained. The results show that the steady-state amplitude is dependent on the running velocity and damping under a certain mass, stiffness, and track irregularity wave length and amplitude. In addition, the steady-state amplitude increases as the running velocity improves, or as the damping decreases. With the maglev safety index as the constraint, the damping should be more than 6 905 Ns/m under the maximum running velocity of 600 km/h.
- improved suspension frame system /
- levitation force /
- track irregularity /
- steady-state amplitude /
- damping

HTML全文

自从西南交通大学提出了利用高温超导体的磁通钉扎效应设计磁悬浮列车方案之后，众多科研单位研制出相应的实验样车和工程样车. 2000年，西南交通大学率先研制出世界首辆高温超导钉扎磁悬浮实验列车“世纪号”^[1]，通过实验验证了高温超导体应用于磁悬浮列车的可行性. 悬浮架系统是高温超导钉扎磁悬浮列车的重要组成部分，且悬浮架系统的悬浮力由高温超导块材阵列和永磁轨道之间的相互作用力产生，直接影响着列车的安全性和运行性能，是高温超导钉扎磁悬浮列车重要的力学性能指标. 肖玲等^[2]研究得到了最大悬浮力与表磁强度的平方成正比的结论； Liu等^[3]研究表明高温超导体捕获磁场越大，悬浮力也越大；闫兆盈等^[4]采用Kim模型和考虑超导块材的“鱼尾效应”模型两种方法计算超导块材在不同磁场强度（2～3 T的高强磁场）下的悬浮性能. 除磁场对悬浮力影响外，高温超导体和磁体的尺寸及其配对尺寸同样是影响悬浮力的重要因素. 肖玲等^[2]研究表明最大悬浮力随着永磁铁直径的增大先增大后减小，当永磁铁直径和超导块直径相同时达到最大；吴爽等^[5]研究表明当高温超导体直径固定为40 mm时，永磁铁直径由20 mm增大到60 mm时悬浮力先增大后减小，直径接近40 mm，悬浮力达到最大. 除研究悬浮力影响因素外，悬浮力的计算方法也是研究的热点之一. 伊建辉等^[6]提出了一种基于临界态Bean模型计算悬浮力的方法，研究了悬浮力的变化规律. 张明亮等^[7]基于冻结镜像模型提出了等效处理高温超导体的方法（等效处理方法），利用该方法计算了悬浮力.

高温超导钉扎磁悬浮列车的动态特性主要取决于刚度和阻尼. Deng等^[8]研究得到了高温超导钉扎磁悬浮列车的刚度随着场冷高度的增大而减小，而阻尼系数和场冷高度的关系比较复杂的结论；赵宪锋等^[9]研究得到了高温超导系统刚度和悬浮高度的关系具有明显滞回特性的结论. 除刚度和阻尼研究外，杨文姣等^[10]基于三维电磁-热-力多物理场强耦合模型提出了研究高温超导钉扎磁悬浮系统动态特性的模拟方法；邓斌等^[11]基于新型高温超导磁浮转向架研究了车辆通过曲线线路时的动态响应规律；Zhang等^[12]利用多体动力学软件仿真分析了高温超导钉扎磁悬浮列车在直线运行的动态性能.

在受轨道不平顺、磁场不均匀等因素影响时，列车在运行中会产生振动，若产生异常振动必将影响列车的安全性，因此需对振动行为进行研究. Weinberger等^[13]研究发现，当外界激励频率约为系统固有频率的2倍时，磁悬浮系统会发生共振的现象；Zhuo等^[14-15]通过改进的悬浮力模型，研究发现了系统存在从倍周期分岔和阵发性通往混沌的两条路径，测试了高温超导体与Halbach永磁轨道之间的悬浮力，提出了悬浮力的指数模型；Li等^[16-17]分别研究了高温超导钉扎磁悬浮系统的垂向和横向运动稳定性问题，给出了稳定性的条件；Li等^[18]基于悬浮力指数模型研究了高温超导钉扎磁悬浮系统受谐波激励时的振动特性，确定了系统发生次共振的激励范围. 除此之外，邓自刚等^[19]为了实现转弯提出了电磁道岔方案.

尽管上述文献对高温超导钉扎磁悬浮系统进行研究，并取得了较好的研究成果，但是目前仍存在如下的问题：由于永磁轨道和高温超导块材阵列为单层面面相对布置，较容易出现脱轨的风险；高温超导钉扎磁悬浮列车振动特性研究偏少. 本文首先提出用于高温超导钉扎磁悬浮列车的抱轨式改进型悬浮架系统（改进型悬浮架系统）；采用等效处理方法计算改进型悬浮架系统的悬浮力；建立单个改进型悬浮架本体在轨道不平顺简谐激励下的动力学模型；利用线性微分方程理论求解幅频响应，研究不同阻尼对稳态振幅的影响，在给定的最高运行速度下得到了阻尼的推荐范围.

1. 改进型悬浮架系统的提出

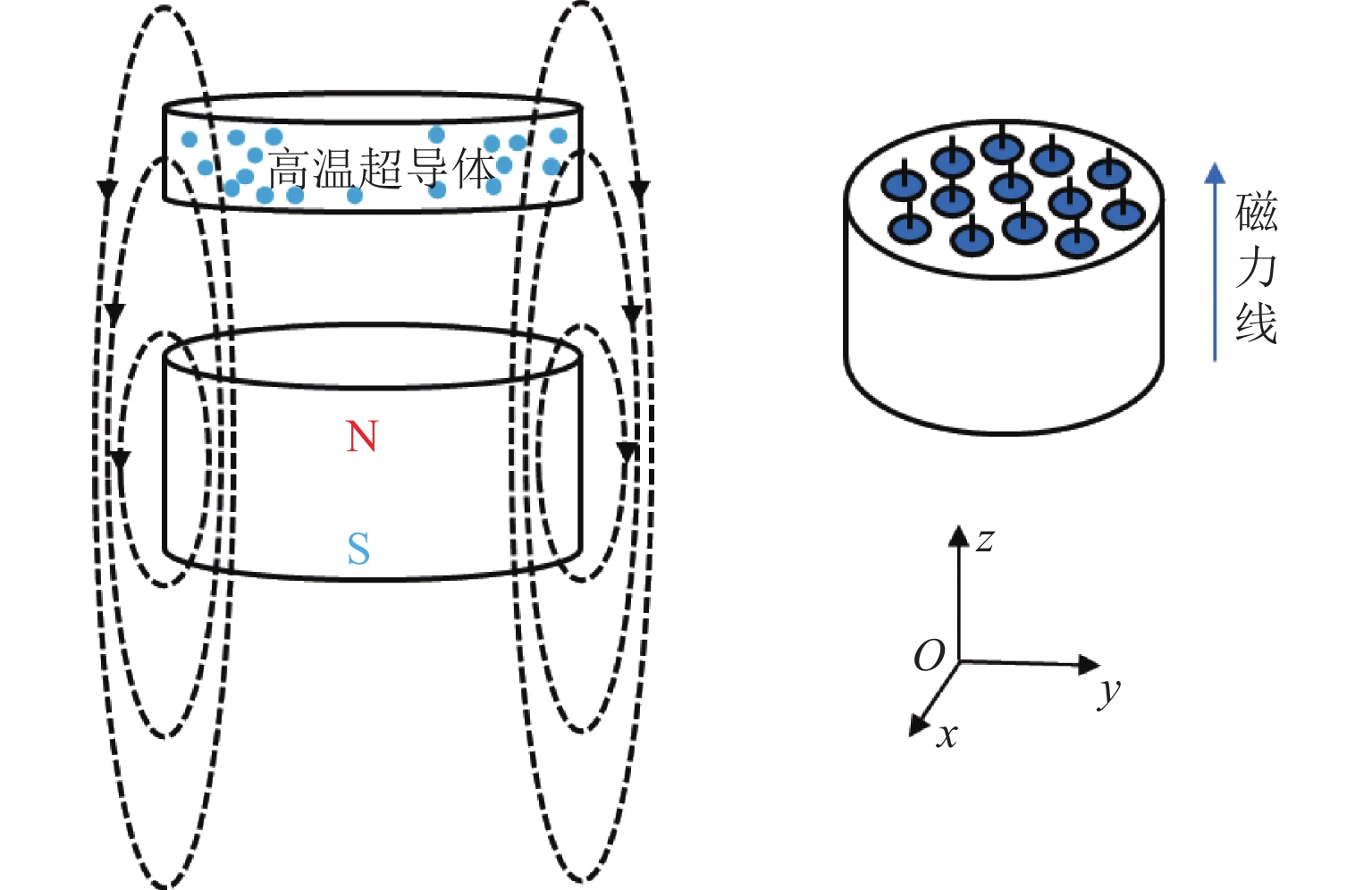
高温超导体在磁体磁场中冷却进入超导态的过程称为场冷. 高温超导体场冷进入超导态后，由于钉扎中心的影响，部分量子磁通线被高温超导体的缺陷或其他各种势阱所束缚，部分磁通线因抗磁性很难穿过高温超导体，形成“磁通钉扎”效应，如图1所示. 此时，高温超导体和磁铁之间既可以产生宏观的吸引力（因势阱捕获钉扎）又可以产生宏观的排斥力（因抗磁性），两者的合力为悬浮力，该悬浮力决定了无须主动控制就能维持高温超导体稳定悬浮在磁体上方.

图 1 高温超导磁通钉扎效应示意

Figure 1. High-temperature superconducting flux pinned effect

下载: 全尺寸图片幻灯片

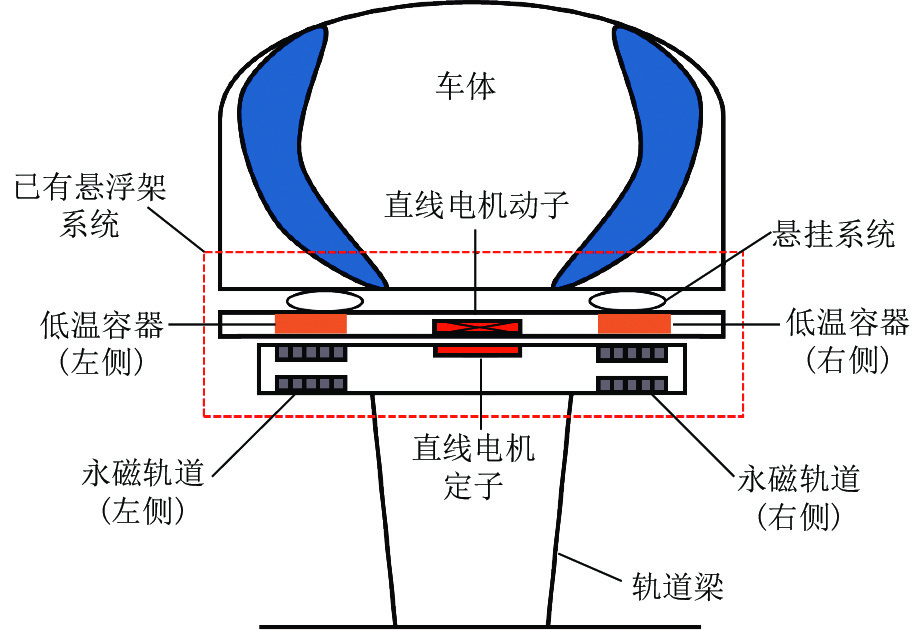
为了增大悬浮力和提升列车运行安全性，本文改高温超导体和永磁轨道的单层面面相对布置（图2）为多层抱轨式结构，提出用于列车的改进型悬浮架系统，磁悬浮列车的主要组成如图3所示.

图 2 包含已有悬浮架系统的高温超导钉扎磁悬浮列车主要组成

Figure 2. Components of high-temperature superconducting pinned maglev train with current suspension frame system

下载: 全尺寸图片幻灯片

图 3 包含改进型悬浮架系统的高温超导钉扎磁悬浮列车主要组成

Figure 3. Components of high-temperature superconducting pinned maglev train with improved suspension frame system

下载: 全尺寸图片幻灯片

由图3可以观察到，磁悬浮列车主要由改进型悬浮架系统、悬挂系统、车体、直线电机和轨道梁组成. 改进型悬浮架系统通过悬挂系统与车体相连，主要由悬浮架骨架、左右两侧的上下层低温容器（含高温超导块材阵列）和上下层永磁轨道（固定在轨道梁上）组成. 为描述和分析方便，将悬浮架骨架、左右两侧的上下层低温容器、直线电机动子一起称为悬浮架本体，下文所指的悬浮间隙为上悬浮间隙.

2. 磁轨关系分析及讨论

2.1 实验装置和测试原理

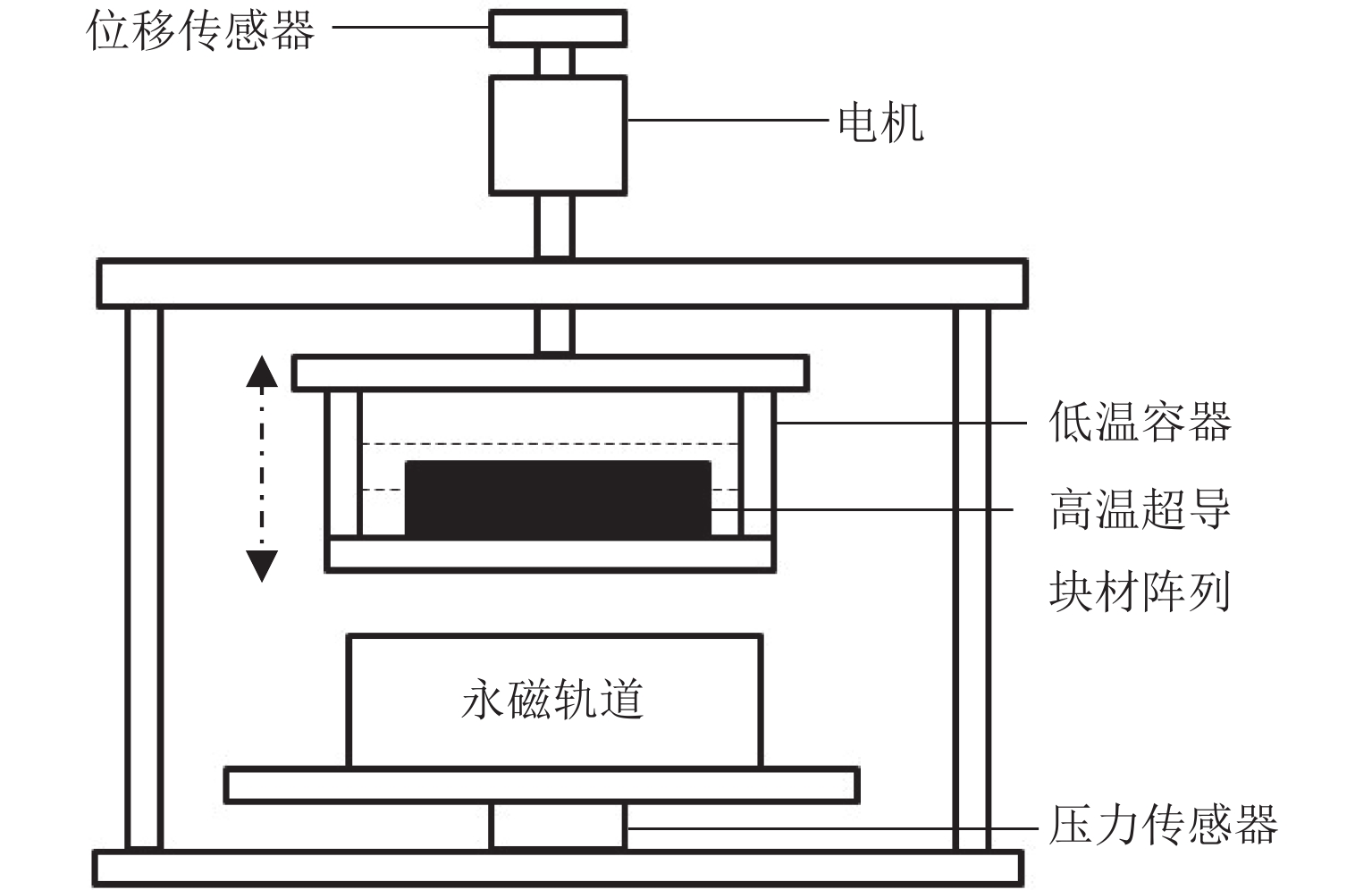
本文利用实验装置测试得到高温超导块材阵列和永磁轨道的悬浮力，悬浮力实验装置实物如图4，测试原理如图5所示.

图 4 悬浮力实验装置

Figure 4. Test device of levitation force

下载: 全尺寸图片幻灯片

图 5 悬浮力实验装置测试原理示意

Figure 5. Principle of levitation force test device

下载: 全尺寸图片幻灯片

实验装置主要由位移传感器、压力传感器、电机、低温容器、高温超导块材阵列和永磁轨道组成. 其中位移传感器安装在电机上，通过电机转过的转数和丝杆的螺距可以计算得到上下移动的距离；低温容器固定连接在电机转轴的端部，可以通过电机带动下上下运动（见虚线双向箭头）；高温超导块材阵列固定在低温容器中；压力传感器安装在永磁轨道固定板和机座底板之间，通过永磁轨道受到的压力反映悬浮力的大小.

实验测试的基本步骤为

步骤1　利用电机旋转丝杆螺母机构产生的运动移动低温容器，使高温超导块材阵列接近永磁轨道，保持两者的距离不变，即设定场冷高度d；

步骤2　然后将液氮倒入到低温容器中，使高温超导块材阵列在永磁轨道的磁场下冷却进入超导态（即场冷）；

步骤3　高温超导块材阵列在电机的带动下上下移动，位移传感器获得上下移动的悬浮间隙，压力传感器获得悬浮力.

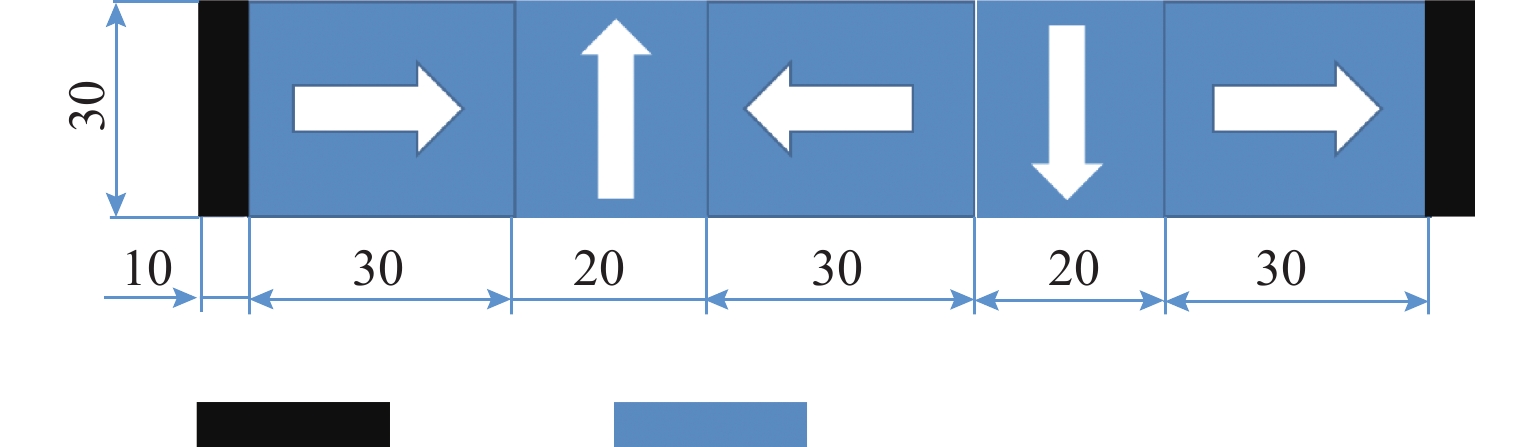
永磁轨道采用Halbach构型，其材料为钕铁硼，轨道长度为800 mm，实物如图6所示，具体尺寸参数和磁化方向如图7所示，其中充磁方向为箭头方向，黑色两边采用纯铁，起着聚磁作用. 本实验中的高温超导块材阵列由10块YBaCuO（钇钡铜氧）高温超导块材拼装组合构成，单块尺寸为ϕ30 mm × 14 mm，按5 × 2的方式排列.

图 6 永磁轨道实物

Figure 6. Permanent magnet guideway

下载: 全尺寸图片幻灯片

图 7 永磁轨道尺寸和磁化方向

Figure 7. Size and magnetization direction of permanent magnet guideway

下载: 全尺寸图片幻灯片

2.2 等效处理方法提出和验证

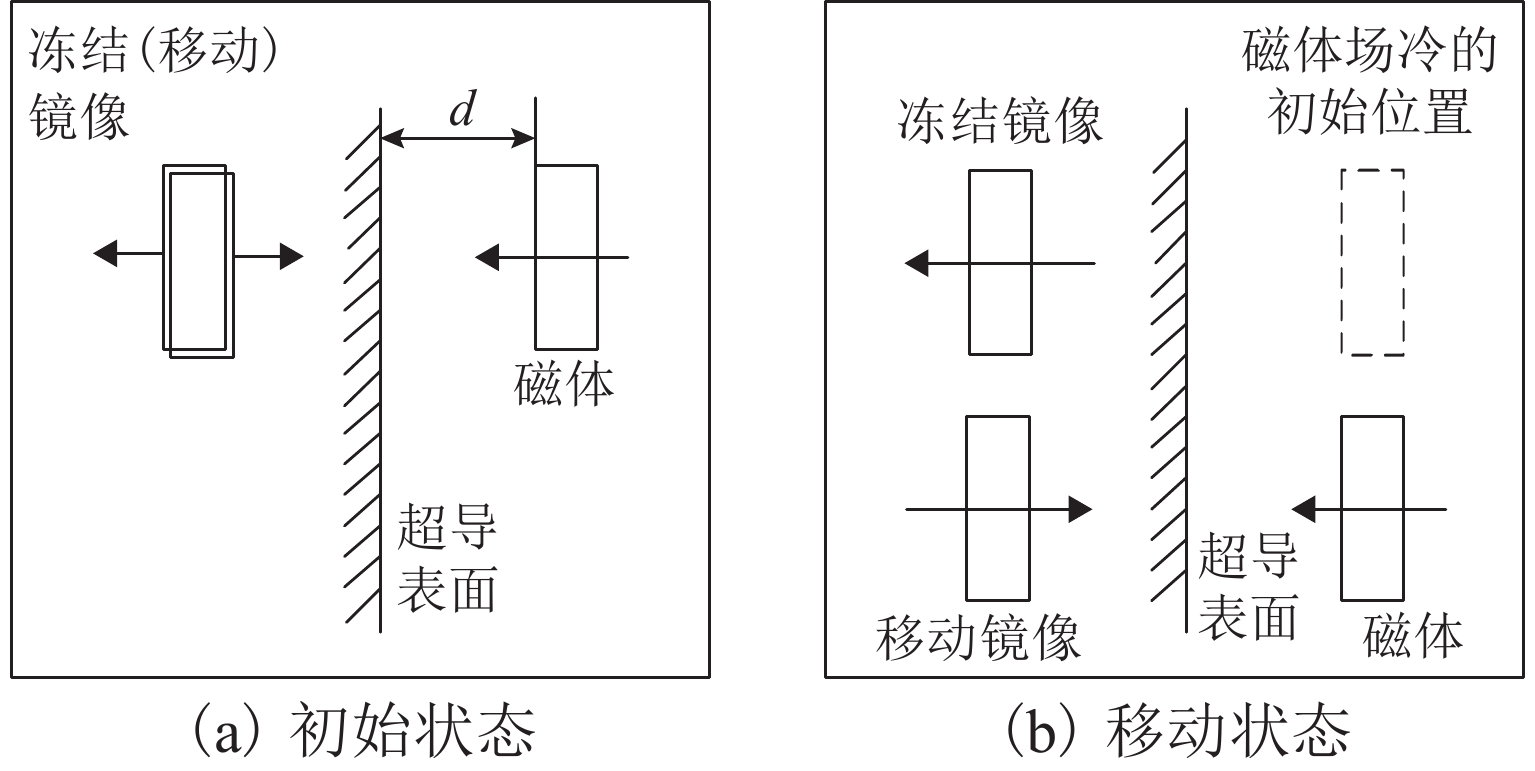
针对高温超导体处在超导态（浸泡在液氮中）时具有捕获磁场和抗磁性的混合特性，本团队基于冻结镜像模型^[7,20]提出了等效处理方法，冻结镜像模型原理如图8所示.

图 8 冻结镜像模型示意

Figure 8. Frozen-image model

下载: 全尺寸图片幻灯片

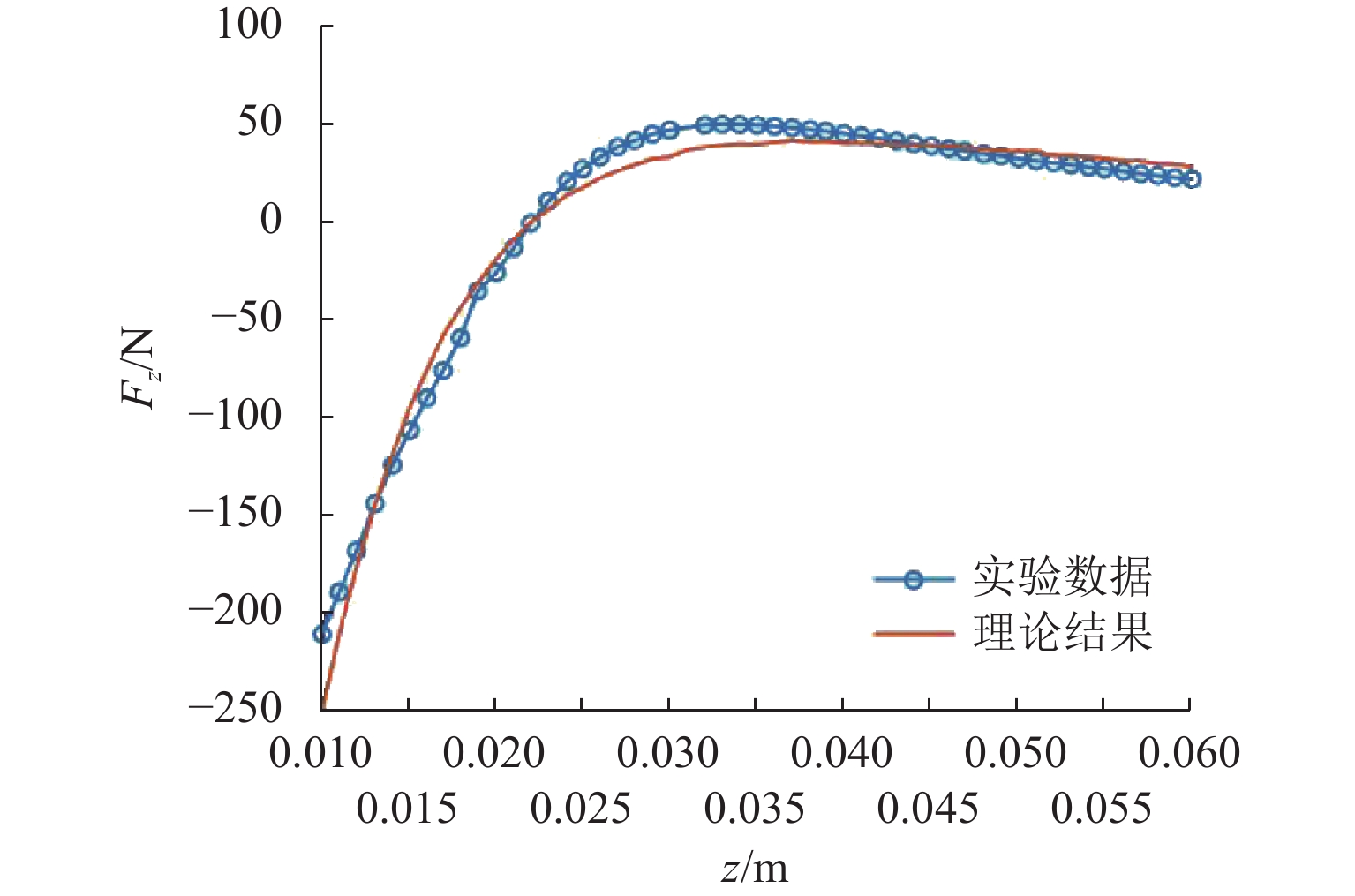
由图8可以观察到，高温超导体场冷时在超导表面内部同时产生冻结镜像和移动镜像. 当高温超导体移动时，冻结镜像保持不动，而移动镜像随高温超导体的移动而呈镜向关系移动. 冻结镜像相当于高温超导体的捕获磁场；移动镜像相当于高温超导体的抗磁性. 具体处理方式为：基于冻结镜像将高温超导块材阵列等效处理成磁化的磁体，模拟捕获磁性特性，此时高温超导块材阵列和永磁轨道产生引力；基于移动镜像将高温超导块材阵列处理成小的相对导磁率，模拟抗磁性，此时高温超导块材阵列和永磁轨道产生斥力；然后将引力和斥力矢量求和即可得到高温超导块材阵列和永磁轨道之间的宏观悬浮力. 该悬浮力类似非线性的弹簧，基于等效处理方法得到在场冷高度为0.022 m情况下不同悬浮间隙（z）下的悬浮力（F_z）理论数据，将利用实验装置测得的实验数据和理论数据进行对比，如图9所示.

图 9 悬浮力和悬浮间隙的关系

Figure 9. Relationship between levitation force and levitation gap

下载: 全尺寸图片幻灯片

由图9可观察到：实验测量和理论计算的悬浮力都随着悬浮间隙增大先快速增大后缓慢增大至最大值然后缓慢减小最终趋近于0；且在场冷高度处悬浮力为0，即此位置为不受重力影响下的平衡点；在悬浮间隙大于场冷高度情况下，悬浮力大于0，表明悬浮力为引力，该力使高温超导块材阵列和永磁轨道之间处于相互吸引的状态，阻碍两者远离平衡位置；在悬浮间隙小于场冷高度情况下，悬浮力小于0，表明悬浮力为斥力，该力使高温超导块材阵列和永磁轨道之间处于相互排斥的状态，阻碍两者靠近平衡位置. 更为重要的是，理论结果和实验数据吻合得较好，验证等效处理方法的正确性.

2.3 悬浮力经验公式

为了增大悬浮力，需要增大永磁轨道的尺寸（大永磁轨道）和增加高温超导块的块数，以100块高温超导块材阵列（10 × 10排列）为一个标准高温超导块材阵列. 基于等效处理方法得到大永磁轨道和标准高温超导块材阵列之间的悬浮力，如图10所示.

图 10 大永磁轨道和标准高温超导块材阵列的悬浮力

Figure 10. Levitation force between large permanent magnet guideway and standard high-temperature superconductor array

下载: 全尺寸图片幻灯片

由图10可以观察到：悬浮力随着悬浮间隙的增大先增大后减小；改变永磁轨道和高温超导块材阵列配合参数后的悬浮力比实验参数下的悬浮力要大许多，且悬浮力与悬浮间隙表现为明显的非线性关系.

为了受力均匀，假定改进型悬浮架本体左右两侧各安装5个标准高温超导块材阵列. 为了设计和安装方便，改进型悬浮架本体上下安装的标准高温超导块材阵列与大永磁轨道的场冷高度都设定为0.022 m. 假定双面布置的标准高温超导块材阵列与大永磁轨道完全相同，且永磁轨道处于抱轨式悬浮架骨架的中间位置，则基于等效处理方法计算单侧标准高温超导块材阵列和大永磁轨道之间的作用力，减小上方间隙距离为下方间隙增大距离，如上方间隙减小0.001 m，则下方间隙增大0.001 m，则基于尺寸约束条件可以将两者的作用力矢量求和，即可得到改进型悬浮架系统的悬浮力和悬浮间隙的关系，改进型悬浮架系统和已有悬浮架系统悬浮力的对比关系如图11所示.

图 11 改进型悬浮架系统和已有悬浮架系统的悬浮力对比关系

Figure 11. Comparison between levitation forces of improved suspension frame system and current suspension frame system

下载: 全尺寸图片幻灯片

由图11可以观察到，改进型悬浮架系统的悬浮力和悬浮间隙呈线性关系，与已有悬浮架系统的悬浮力和悬浮间隙呈非线性关系不同，且改进型悬浮架系统的悬浮力比已有悬浮架系统的悬浮力大. 根据线性规律，改进型悬浮架系统的悬浮力拟合公式可表示为

${F_{\textit{z}}} = 1.6 \times {10^6}\left( {{\textit{z}} - 0.022} \right) .$

(1)

改进型悬浮架系统在垂向上除受悬浮力作用外，还受重力作用，悬浮力和重力的合力为系统总作用力. 由于平衡原点不为0，需要根据坐标平移原理将平衡点移动到原点0. 假定原平衡点为z_eq，则需平移z_eq，可得

${\textit{z}} = u + {{\textit{z}}_{{\rm{eq}}}} \text{，}$

(2)

式中：u为距离z_eq的偏移间距.

整理得到合力F_sum与偏移间距的关系为

${F_{{\rm{sum}}}} = ku \text{，}$

(3)

式中：k为线性刚度.

3. 垂向动力学建模和解析求解

文献[21]研究表明，高温超导块材阵列和永磁轨道之间存在阻尼，且该悬浮架系统的阻尼可以通过在高温超导块材阵列下方增加导电材料，如铜，当悬浮架本体振动时铜片上产生涡流阻尼力，阻尼力大小和系数可通过铜的结构和尺寸改变. 考虑轨道不平顺简谐激励的影响，基于悬浮力经验公式得到改进型悬浮架系统的垂向力学模型，如图12所示. 图中：z₀、z₁分别为轨道不平顺激励位移以及悬浮架本体垂向位移.

图 12 改进型悬浮架系统的垂向力学模型

Figure 12. Vertical force model of improved suspension frame system

下载: 全尺寸图片幻灯片

根据平移原理（式（3）），以z_eq为坐标原点，向上为正方向. 基于达朗贝尔原理建立改进型悬浮架本体振动的垂向动力学模型，整理变形可得微分方程为

$m\ddot u + ku + c\dot u = 4mF{\text{π} ^2}{f^2}\cos (2\text{π} ft) ,$

(4)

式中：m为改进型悬浮架本体的质量；c为阻尼系数；F为激励幅值；f为激励频率；t为时间.

由轨道不平顺的周期性可得波长 $\lambda$ 和运行速度 $v_x$ 的关系为

$f = \frac{{{v_x}}}{\lambda } \text{.}$

(5)

由式（4）和式（5）可得

$\ddot u + \frac{c}{m}\dot u + \frac{k}{m}u = \frac{{4F{\text{π} ^2}{v_x}^2}}{{{\lambda ^2}}}\cos \left(\frac{{2\text{π} {v_x}}}{\lambda }t\right).$

(6)

由于本文关注的是振动稳态解，根据线性微分方程求解理论得到非自治系统的特解u_soluspe，整理得到

$\qquad {u_{{\rm{soluspe}}}} = \left\{ {\begin{array}{*{20}{l}} \dfrac{{4{\text{π} ^2}Fm}}{{k\sqrt {{{\left( {\dfrac{{{\lambda ^2}}}{{{v_x^2}}} - \dfrac{{2{{\text{π}} ^2}}}{{{k^2}}}\left( {2km - {c^2}} \right)} \right)}^2} + \dfrac{{16{\text{π} ^4}{m^2}}}{{{k^2}}} - \dfrac{{4{\text{π} ^4}}}{{{k^4}}}{{\left( {2km - {c^2}} \right)}^2}} }} \times \cos \left( {\dfrac{{2\text{π} {v_x}}}{\lambda }t - \varphi } \right), &{{v_x} \ne 0},\\ 0,\quad {{v_x} = 0}, \end{array}} \right.$

(7)

式中：φ为相角，

$\varphi = \arccos \left( {\dfrac{{k - \dfrac{{4{\text{π} ^2}m{v_x}^2}}{{{\lambda ^2}}}}}{{\sqrt {4{\text{π} ^2}{c^2}{v_x^2}{\lambda ^2} + {{\left( {k{\lambda ^2} - 4{\text{π} ^2}m{v_x}^2} \right)}^2}} }}} \right).$

4. 系统参数对振动的影响和性能评估

当速度等于0时稳态振幅等于0，故不再讨论. 当速度不等于0时，由式（7）易得稳态振幅u_a为

$\qquad\qquad\qquad\qquad {u_{\rm{a}}} = \dfrac{{4{\text{π} ^2}Fm}}{{k\sqrt {{{\left( {\dfrac{{{\lambda ^2}}}{{{v_x^2}}} - \dfrac{{2{\text{π} ^2}}}{{{k^2}}}\left( {2km - {c^2}} \right)} \right)}^2} + \dfrac{{16{\text{π} ^4}{m^2}}}{{{k^2}}} - \dfrac{{4{\text{π} ^4}}}{{{k^4}}}{{\left( {2km - {c^2}} \right)}^2}} }}.$

(8)

由式（6）可以得到强迫激励下幅频响应的数值解，由式（8）可以得到幅频响应的解析解，两者的对比关系，如图13所示.

图 13 数值解和解析解的幅频响应对比结果

Figure 13. Comparison of numerical and analytical amplitude-frequency responses

下载: 全尺寸图片幻灯片

由图13可以观察到，改进型悬浮架本体的主共振是唯一的，且数值解和解析解在较宽的频率范围内吻合很好，从而验证解析解的正确性，故可以利用式（8）对振动特性进行分析.

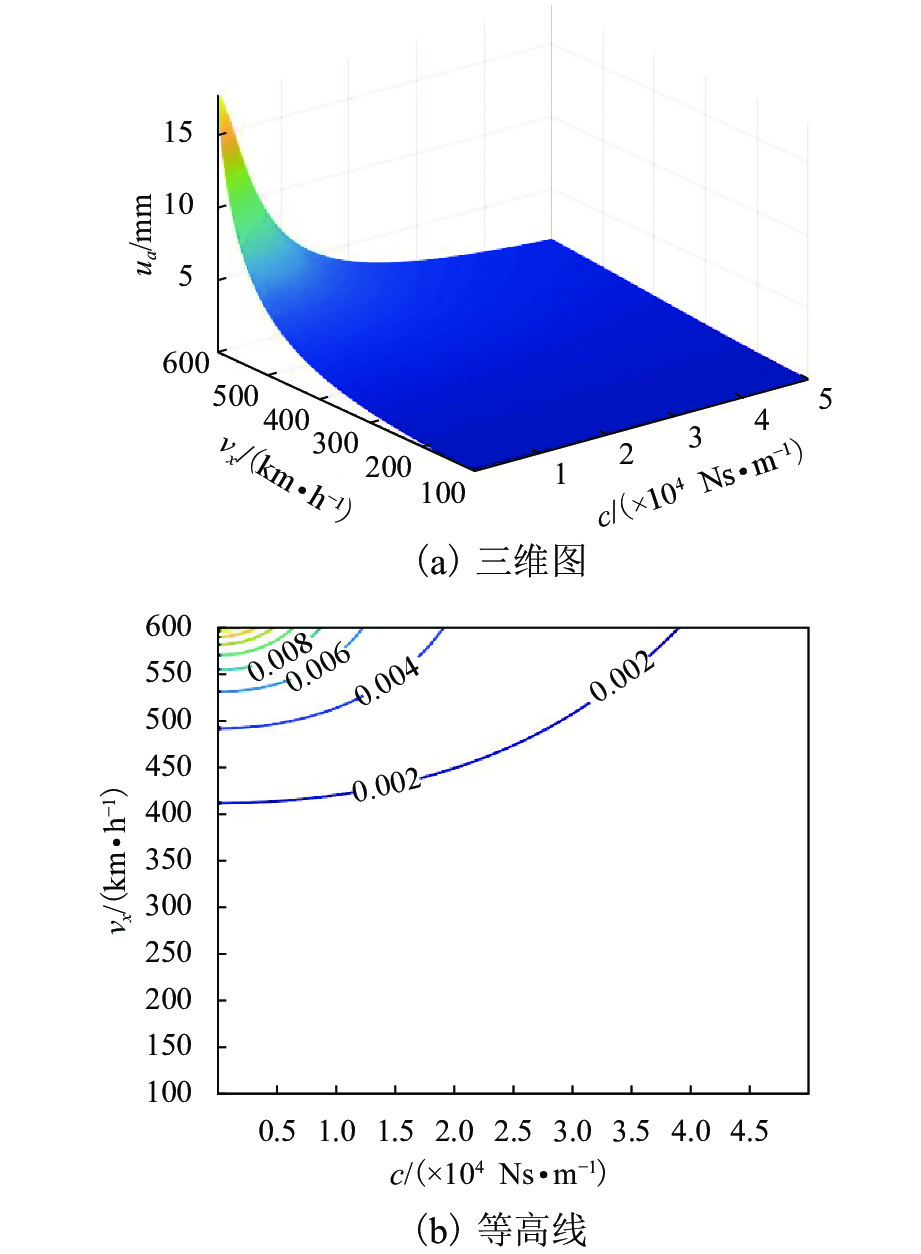
由式（8）可以观察到，在质量和刚度一定的情况下，稳态振幅与阻尼、运行速度、轨道不平顺波长和幅值有关，其中与轨道不平顺幅值成正比. 因EMS磁悬浮列车的悬浮架本体和铁轨之间的悬浮高度约为0.01 m，故两者间的距离偏离平衡位置的安全限值为0.005 m；而高温超导钉扎磁悬浮列车的悬浮高度约为0.02 m，根据同样比例限值规定，后者距离偏离平衡的安全限值为0.01 m. 根据上海磁悬浮轨道不平顺的数据，确定不平顺波长为20 m，幅值为0.003 m. 由式（8）得到阻尼和运行速度对稳态振幅的影响规律，如图14所示.

图 14 稳态振幅与阻尼和运行速度的关系

Figure 14. Relationship between steady-state amplitude and damping and running velocity

下载: 全尺寸图片幻灯片

由图14可以观察到，稳态振幅随着速度的增大而增大，随着阻尼的减小而增大. 当速度较高，阻尼偏小时，会出现稳态振幅超过安全限值0.01 m的要求，故在高速运行情况时需要设置合适的阻尼.

4.1 小阻尼运行情况

由式（8）可以得到 $2km - {c^2} > 0$ 的情况下，当速度等于临界速度v_xcri（式（9））时

${v_{x{\rm{cri}}}} = \frac{{\lambda k}}{{\text{π} \sqrt {2\left( {2km - {c^2}} \right)} }} ,$

(9)

稳态振幅达到最大，其最大值为

${u_{{\rm{amax}} }} = \frac{{4{\text{π} ^2}Fm}}{{k\sqrt {\dfrac{{16{\text{π} ^4}{m^2}}}{{{k^2}}} - \dfrac{{4{\text{π} ^4}}}{{{k^4}}}{{\left( {2km - {c^2}} \right)}^2}} }} \text{.}$

采用上述参数可得临界速度和阻尼系数的关系，如图15所示.

图 15 临界速度和阻尼系数的关系

Figure 15. Relationship between critical velocity and damping coefficient

下载: 全尺寸图片幻灯片

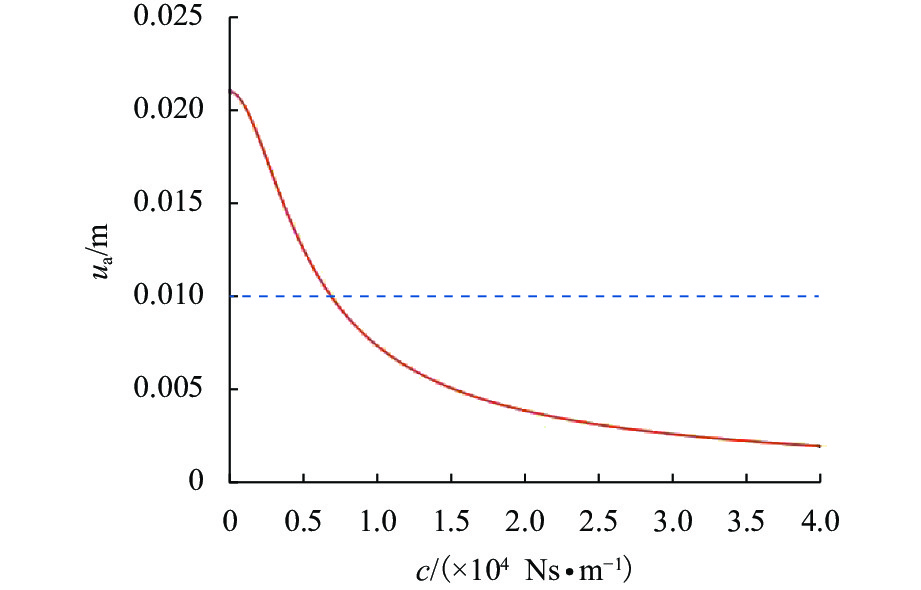
由图15可以观察到，临界速度随着阻尼系数的增大而增大，阻尼系数等于0时，最小的临界速度为648 km/h，目前设计的运行速度600 km/h为最高运行速度，该值小于最小的v_xcri. 由式（8）可知，当速度小于临界速度时，振幅随着运行速度的增大而增大. 由此得到在最高运行速度时阻尼对稳态振幅的影响如图16所示.

图 16 稳态振幅在小阻尼下的变化规律

Figure 16. Steady-state amplitude under small damping

下载: 全尺寸图片幻灯片

由图16可以观察到，稳态振幅随着阻尼系数的增大先快速减小之后缓慢减小，且阻尼较小时振幅会超过安全限值.

4.2 大阻尼运行情况

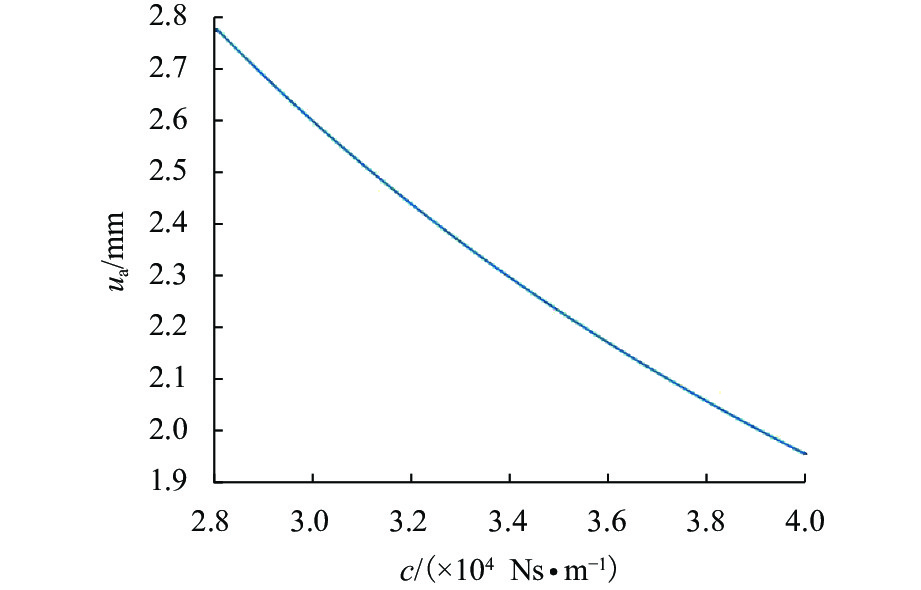
由式（8）可以得到，当 $2km - {c^2} \leqslant 0$ 时，稳态振幅随运行速度的增大而增大. 由此得到最高运行速度情况下阻尼不同时稳态振幅的变化规律，如图17所示.

图 17 稳态振幅在大阻尼下的变化规律

Figure 17. Steady-state amplitude under large damping

下载: 全尺寸图片幻灯片

由图17可以观察到，稳态振幅随着阻尼系数的增大近似线性减小，在限定阻尼参数下振幅不会超过安全限值.

4.3 综合分析

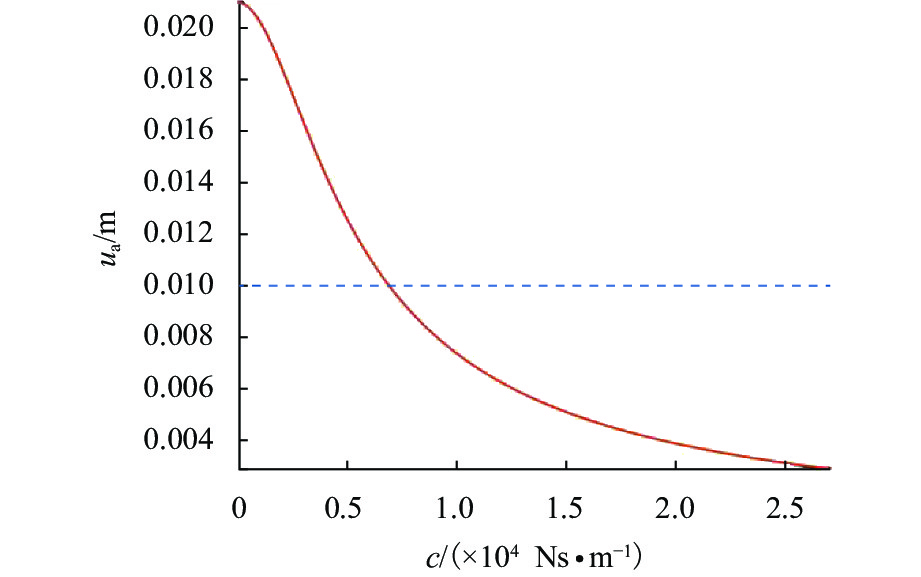
根据小阻尼和大阻尼的分析，由式（8）得到在最高速度时全阻尼阶段下稳态振幅的变化规律，如图18所示.

图 18 稳态振幅在全阻尼下的变化规律

Figure 18. Steady-state amplitude under panoramic damping

下载: 全尺寸图片幻灯片

由图18可以观察到：稳态振幅随着阻尼系数的增大先快速减小后缓慢减小，在阻尼等于6905 Ns/m时稳态振幅等于安全限值0.01 m，阻尼小于6905 Ns/m时振幅将大于0.01 m；阻尼大于6905 Ns/m时振幅将小于0.01 m. 因此为了保证高温超导钉扎磁悬浮列车运行速度能够达到600 km/h，改进型悬浮架系统具有的阻尼系数应大于6905 Ns/m.

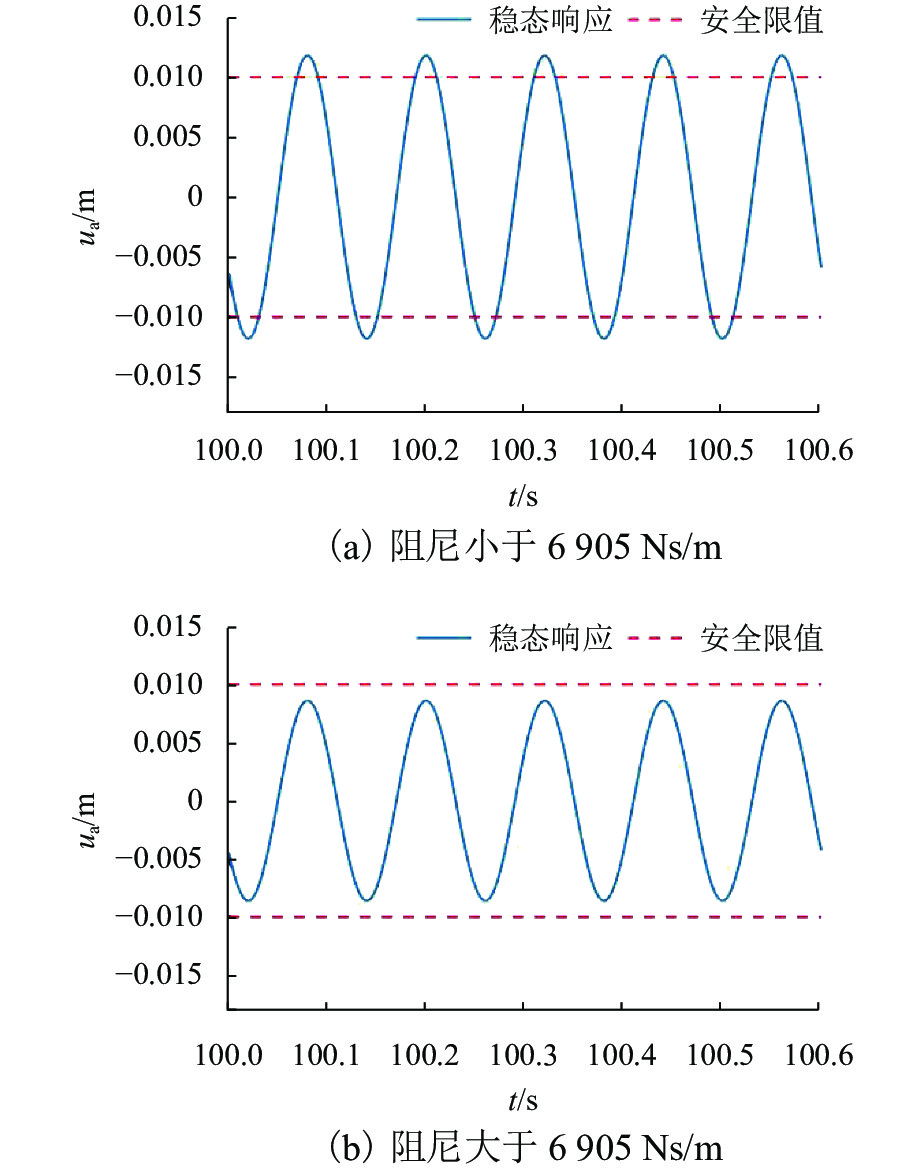
根据上述分析得到，在速度600 km/h时不同阻尼下的稳态振动响应，如图19所示.

图 19 高速时不同阻尼下稳态响应

Figure 19. Steady-state responses under different damping at high velocity

下载: 全尺寸图片幻灯片

由图19可以观察到，阻尼小于推荐值时，稳态振动幅值超过了安全限值，而阻尼大于推荐值时，稳态振动幅值不会超过安全限值，进一步说明分析结果的正确性.

5. 结　论

本文通过改变高温超导体和永磁轨道的相对布置关系提出了抱轨式改进型悬浮架系统，建立改进型悬浮架本体在轨道不平顺简谐激励下的动力学模型，推导得到了幅频特性，主要结论如下：

1）基于冻结镜像模型提出了等效处理方法，通过实验验证该方法的正确性，基于该方法得到改进型悬浮架系统的悬浮力，结果表明悬浮力在小范围内为线性作用力；

2）基于线性微分方程理论得到改进型悬浮架本体振动时的幅频响应方程，研究了运行速度和阻尼对稳态振幅的影响，稳态振幅随着速度的增大而增大，随着阻尼的减小而增大；

3）基于磁悬浮安全性指标，得到了阻尼过小时稳态振幅会超过安全限值，且设计最高运行速度为600 km/h时，阻尼需要大于6905 Ns/m.

致谢：本文得到了牵引动力国家重点实验室（西南交通大学）开放课题（TPL2010）、光电技术与智能控制教育部重点实验室（兰州交通大学）开放课题（KFKT2020-7）的支持，对此表示感谢！

图 1 高温超导磁通钉扎效应示意

Figure 1. High-temperature superconducting flux pinned effect

下载: 全尺寸图片幻灯片

图 2 包含已有悬浮架系统的高温超导钉扎磁悬浮列车主要组成

Figure 2. Components of high-temperature superconducting pinned maglev train with current suspension frame system

下载: 全尺寸图片幻灯片

图 3 包含改进型悬浮架系统的高温超导钉扎磁悬浮列车主要组成

Figure 3. Components of high-temperature superconducting pinned maglev train with improved suspension frame system

下载: 全尺寸图片幻灯片

图 4 悬浮力实验装置

Figure 4. Test device of levitation force

下载: 全尺寸图片幻灯片

图 5 悬浮力实验装置测试原理示意

Figure 5. Principle of levitation force test device

下载: 全尺寸图片幻灯片

图 6 永磁轨道实物

Figure 6. Permanent magnet guideway

下载: 全尺寸图片幻灯片

图 7 永磁轨道尺寸和磁化方向

Figure 7. Size and magnetization direction of permanent magnet guideway

下载: 全尺寸图片幻灯片

图 8 冻结镜像模型示意

Figure 8. Frozen-image model

下载: 全尺寸图片幻灯片

图 9 悬浮力和悬浮间隙的关系

Figure 9. Relationship between levitation force and levitation gap

下载: 全尺寸图片幻灯片

图 10 大永磁轨道和标准高温超导块材阵列的悬浮力

Figure 10. Levitation force between large permanent magnet guideway and standard high-temperature superconductor array

下载: 全尺寸图片幻灯片

图 11 改进型悬浮架系统和已有悬浮架系统的悬浮力对比关系

Figure 11. Comparison between levitation forces of improved suspension frame system and current suspension frame system

下载: 全尺寸图片幻灯片

图 12 改进型悬浮架系统的垂向力学模型

Figure 12. Vertical force model of improved suspension frame system

下载: 全尺寸图片幻灯片

图 13 数值解和解析解的幅频响应对比结果

Figure 13. Comparison of numerical and analytical amplitude-frequency responses

下载: 全尺寸图片幻灯片

图 14 稳态振幅与阻尼和运行速度的关系

Figure 14. Relationship between steady-state amplitude and damping and running velocity

下载: 全尺寸图片幻灯片

图 15 临界速度和阻尼系数的关系

Figure 15. Relationship between critical velocity and damping coefficient

下载: 全尺寸图片幻灯片

图 16 稳态振幅在小阻尼下的变化规律

Figure 16. Steady-state amplitude under small damping

下载: 全尺寸图片幻灯片

图 17 稳态振幅在大阻尼下的变化规律

Figure 17. Steady-state amplitude under large damping

下载: 全尺寸图片幻灯片

图 18 稳态振幅在全阻尼下的变化规律

Figure 18. Steady-state amplitude under panoramic damping

下载: 全尺寸图片幻灯片

图 19 高速时不同阻尼下稳态响应

Figure 19. Steady-state responses under different damping at high velocity

下载: 全尺寸图片幻灯片

参考文献(21)

[1]	WANG J S, WANG S Y, ZENG Y W, et al. The first man-loading high temperature superconducting Maglev test vehicle in the world[J]. Physica C: Superconductivity, 2002, 378/379/380/381: 809-814.
[2]	肖玲,任洪涛,焦玉磊,等. YBCO超导体的磁悬浮力及其测量[J]. 低温物理学报,1999,21(4): 317-320. XIAO Ling, REN Hongtao, JIAO Yulei, et al. Magnetic levitation force of YBCO superconductor and its measurement[J]. Low Temperature Physical Letters, 1999, 21(4): 317-320.
[3]	LIU W, WANG J S, LIAO X L, et al. Influence of the trapped field on the levitation performance of the magnetized bulk high-T_c superconductor[J]. Journal of Superconductivity and Novel Magnetism, 2011, 24(5): 1563-1569. doi: 10.1007/s10948-010-1058-4
[4]	闫兆盈,刘坤,杨文姣,等. 高温超导体在强磁外场下的磁悬浮性能仿真研究[J]. 低温物理学报,2018,40(4): 46-50. YAN Zhaoying, LIU Kun, YANG Wenjiao, et al. Numerical studies of magnetic levitation performance of high temperature superconductor in strong magnetic field[J]. Low Temperature Physical Letters, 2018, 40(4): 46-50.
[5]	吴爽,方进. 永磁体尺寸对高温超导磁悬浮力的影响分析[J]. 低温与超导,2018,46(7): 38-42. WU Shuang, FANG Jin. Analysis of the influence of permanent magnet size on high temperature superconducting magnetic suspension force[J]. Cryogenics & Superconductivity, 2018, 46(7): 38-42.
[6]	伊建辉,孟范鹏,姜衍猛,等. 高温超导磁悬浮列车静态悬浮特性研究[J]. 低温工程,2019(6): 56-61. YI Jianhui, MENG Fanpeng, JIANG Yanmeng, et al. Study on static suspension characteristics of high temperature superconducting maglev train[J]. Cryogenics, 2019(6): 56-61.
[7]	张明亮,李明远,刘鹏飞,等. 面向高温超导钉扎磁悬浮列车悬浮特性研究[J]. 中国机械工程,2022,33(22): 2764-2771. ZHANG Mingliang, LI Mingyuan, LIU Pengfei, et al. Study on levitation characteristics of high temperature superconducting pinned maglev train[J]. China Mechanical Engineering, 2022, 33(22): 2764-2771.
[8]	DENG Z G, ZHENG J, SONG H H, et al. Free vibration of the high temperature superconducting maglev vehicle model[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 2071-2074. doi: 10.1109/TASC.2007.899247
[9]	赵宪锋,周又和. 高温超导悬浮系统的磁刚度研究[J]. 兰州大学学报(自然科学版),2015,51(4): 577-582. ZHAO Xianfeng, ZHOU Youhe. Magnetic stiffness of a high-temperature superconducting levitation system[J]. Journal of Lanzhou University (Natural Sciences), 2015, 51(4): 577-582.
[10]	杨文姣,马光同,Loic Queval,等. 基于三维多物理场强耦合模型的超导磁悬浮振动特性[J]. 科学通报,2019,64(31): 3255-3266. YANG Wenjiao, MA Guangtong, QUEVAL L, et al. Vibration characteristics research on HTS magnetic levitation system based on a strong-coupled multi-physics model[J]. Chinese Science Bulletin, 2019, 64(31): 3255-3266.
[11]	邓斌,陈武,邓自刚,等. 新型高温超导磁浮车辆通过曲线时的运动学规律[J]. 城市轨道交通研究,2019,22(5): 34-38. DENG Bin, CHEN Wu, DENG Zigang, et al. Kinematics law of high temperature superconducting maglev train in curve passing[J]. Urban Mass Transit, 2019, 22(5): 34-38.
[12]	ZHANG M L, SUN G X, LIU P F, et al. Research on force characteristics and running performance of novel type high-temperature superconductor magnetic levitation vehicle[J]. Journal of Superconductivity and Novel Magnetism, 2022, 35(3): 635-646. doi: 10.1007/s10948-021-06075-7
[13]	WEINBERGER B R, LYNDS L, HULL J R. Magnetic bearings using high-temperature superconductors: some practical considerations[J]. Superconductor Science and Technology, 1990, 3(7): 381-388. doi: 10.1088/0953-2048/3/7/010
[14]	ZHUO P J, ZHANG Z X, GOU X F. Chaotic motion of a magnet levitated over a superconductor[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(2): 1-6.
[15]	LI J P, LI H T, ZHENG J, et al. Nonlinear vibration behaviors of high-T_c superconducting bulks in an applied permanent magnetic array field[J]. Journal of Applied Physics, 2017, 121: 243901.1-243901.6.
[16]	LI J P, ZHENG J, HUANG H A, et al. Motion stability of the magnetic levitation and suspension with YBa₂Cu₃O_{7- x} high-T_c superconducting bulks and NdFeB magnets[J]. Journal of Applied Physics, 2017, 122: 153902.1-153902.8.
[17]	LI H T, DENG Z G, JIN L A, et al. Lateral motion stability of high-temperature superconducting maglev systems derived from a nonlinear guidance force hysteretic model[J]. Superconductor Science and Technology, 2018, 31: 075010.1-075010.8.
[18]	LI J P, DENG Z G, XIA C C, et al. Subharmonic resonance in magnetic levitation of the high-temperature superconducting bulks YBa₂Cu₃O_7-_x under harmonic excitation[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(4): 1-8.
[19]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530.
[20]	ZHANG M L, HAN Y J, GUO X, et al. The connection characteristics of flux pinned docking interface[J]. Journal of Applied Physics, 2017, 121: 113907.1-113907.10.
[21]	LI J P, DENG Z G, XIA C C, et al. Subharmonic resonance in magnetic levitation of the high-temperature superconducting bulks YBa₂Cu₃O_7-_x under harmonic excitation[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(4): 3600908.1-3600908.8.