交通便利性对地区经济发展起到至关重要的作用，随着桥位资源越来越紧张，背负多种交通功能的超大跨度桥梁逐渐变为设计首选的方案之一. 公铁合建大跨度斜拉桥近十年间发展迅速，2009年天兴洲长江大桥建成，形成了一整套公铁斜拉桥建造技术，成为铁路桥梁的一个里程碑工程^[1]. 2020年沪苏通长江大桥建成，实现了公铁两用斜拉桥跨越能力突破千米级，更显其里程碑工程风采^[2]. 目前，已建成的公铁合建桥梁均采用横桥向对称布置方案，即公路对称布置于铁路两侧. 但有时受到两岸接线场地的限制，也会采用公路与铁路分别独立布置于主梁上、下游的非对称布置^[3]. 这种非对称的布置方案会导致结构横桥向的恒载不对称，使得大跨度斜拉桥在恒载作用下横桥向的变形和受力均不一致，具体表现为：主梁、主塔发生扭转和横桥向变形，上、下游主桁、塔肢受力不一致.

在结构力学行为方面，秦顺全等^[4-7]通过引入单元无应力状态量，用能量法建立了分阶段成形结构力学平衡方程和线形控制方程，从理论上严密地阐述了成桥内力和位移与成形过程之间的关系，解决了分阶段施工桥梁的安装计算问题，实现了施工中多工序并行作业. 许磊平等^[8-9]建立了基于Timoshenko梁及平面薄壳单元的分阶段成形结构力学平衡方程，为二维分阶段施工桥梁的计算分析提供了理论基础. 苑仁安等^[10-11]以平面杆单元和平面梁单元为研究对象，建立了考虑几何非线性效应的分阶段成形结构力学平衡方程，为几何非线性效应的分阶段成形结构计算提供了理论依据. 苑仁安等^[12]基于斜拉桥成桥力学特征，为精准高效地确定斜拉桥目标状态，提出一种新型快速精准调索方法. 张清华等^[13]为了研究大跨度钢斜拉桥关键构件制造误差在桥梁施工过程中的形成机理和传播特性，建立了误差效应传播方程，并以苏通大桥为研究对象，阐明了主梁节段无应力角度误差、主梁节段长度制造误差和斜拉索长度制造误差对施工过程中主梁线形、斜拉索索力的影响. 谢明志等^[14]基于双目标几何控制法建立了施工监控体系，研究了大跨度斜拉桥初始无应力状态量的确定方法、关键构件制造控制、关键构件安装控制等一系列施工控制的关键问题. 上述研究均是在横桥向恒载对称的前提条件下开展的，横桥向非对称恒载作用下桥梁受力分析和施工控制技术方面的研究较为少见.

本文以常泰长江大桥为工程背景，对常泰长江大桥在横桥向非对称恒载作用下的结构力学行为进行分析，并依据分析结果提出相应的控制措施，保证结构成桥状态的内力、线形满足设计规范的要求.

1.   工程背景

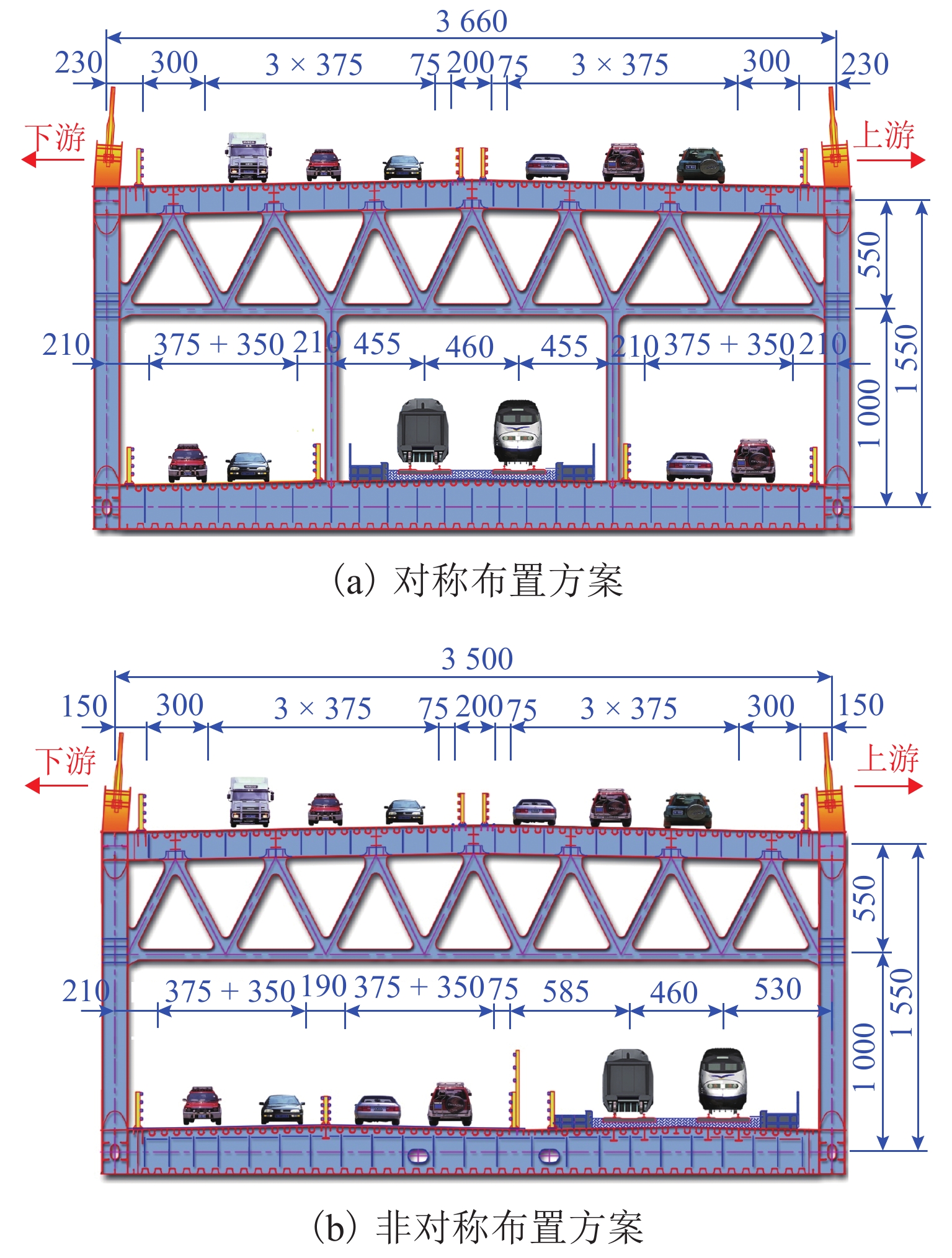
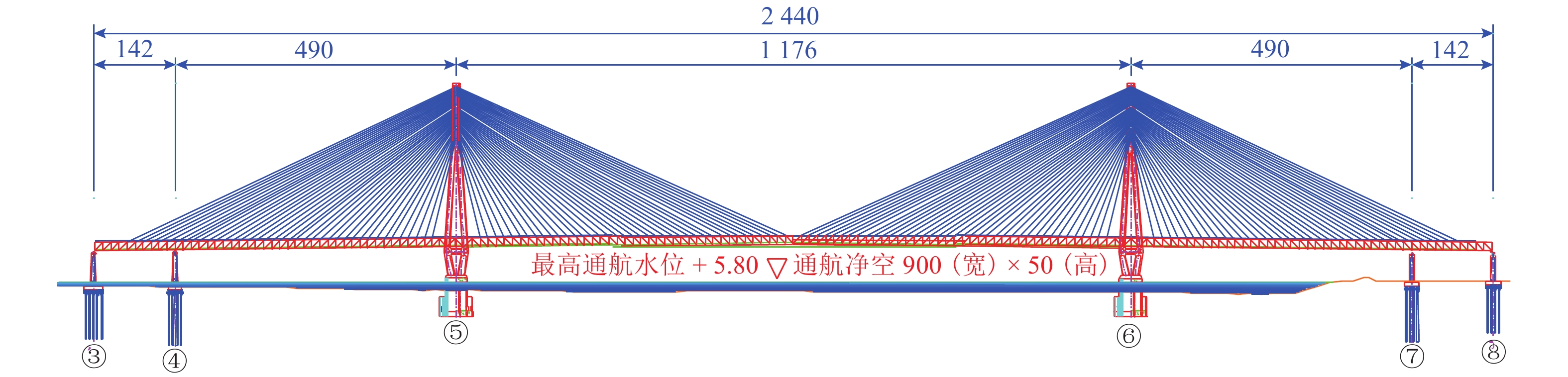
如图1所示，常泰长江大桥采用双塔斜拉桥方案，主跨跨度1 176 m，孔跨布置为：（142 + 490 + 1 176 + 490 + 142）=2 440 m，结构体系采用“温度自适应塔梁纵向约束体系”. 主梁采用两片主桁的钢桁梁结构，桁高为15.5 m，桁宽35.0 m，桁式采用N形桁. 主塔采用“钢-混”混合结构空间钻石形桥塔，主塔设计总高354.0 m.

图  1  主航道桥布置图（单位：m）

Figure  1.  Overall arrangement of main bridge （unit： m）

下载: 全尺寸图片 幻灯片

主梁上层布置六车道高速公路，下层布置双线城际铁路和四车道普通公路. 针对下层交通功能的布置形式，提出了如图2所示的两种主梁横桥向布置方案. 1） 对称布置方案：该方案上、下游主桁力学行为一致，受力简单，设计和施工控制难度小，但接线复杂，两岸土地占用多，且公路行车条件差. 2） 非对称布置方案：该方案下层公路、铁路分幅布置，接线简单，节约了两岸土地资源，提高了公路行车条件，基于此该桥采用非对称布置的主梁方案.

图  2  主梁横桥向布置方案（单位：cm）

Figure  2.  Configuration schemes of main girder cross section （unit：cm）

下载: 全尺寸图片 幻灯片

主梁横桥向非对称布置方案会使得主梁的恒载在横桥向不对称，具体体现在两个方面. 在一期恒载方面：主梁结构上、下游主桁规格相同，下层桥面铁路下方布设4道倒T型纵梁结构，造成上游侧一期恒载比下游侧一期恒载大5 kN/m；初步方案中，上、下游斜拉索采用不同规格、相同强度级别的平行钢丝，上游侧斜拉索较下游侧斜拉索恒载差值为10 kN/m. 在二期恒载方面：双线城际铁路速度标准为250 km/h，线间距4.6 m. 初步方案中，铁路道床采用宽9 m，道砟为35 cm的常规道床结构，防水结构采用6 cm厚UHPC结构，计入轨枕、钢轨、员工走道、风水管线等，上游侧铁路二期恒载为150 kN/m. 下游侧普通公路铺装、护栏等二期恒载为40 kN/m，二期恒载上、下游差值110 kN/m. 综上，上游侧比下游侧恒载大125 kN/m.

2.   成桥状态力学行为分析

斜拉桥设计的核心是确定出结构的合理成桥状态，即结构在确定的荷载下，通过调整斜拉索索力，实现结构线形和结构内力满足设计要求，且结构状态达到最优的成桥状态. 对于横桥向恒载非对称布置的斜拉桥，若是采用上、下游索力一致的设计方案，主梁势必会发生扭转变形，经计算：主梁扭转角为0.02 rad，上、下游主桁竖向线形差值达750 mm，主塔塔偏4 mm. 该设计方案利于主塔结构，但对主梁线形影响很大，经计算不能满足铁路运营要求.

为了使得上、下游恒载相同，提出配重方案. 在下层桥面下游侧钢箱内进行配重，经分析，配重方案增加了主塔、主梁、斜拉索及基础用量，工程造价增加约2亿元，该方案不可取. 需要对结构力学行为进行研究，解决横桥向恒载非对称布置对结构线形的影响.

2.1   合理成桥状态确定

对于恒载非对称布置的斜拉桥结构，如何确定其满足运营要求的合理成桥状态至关重要，包括成桥应力和成桥线形. 由横桥向恒载差引起的结构内力差异可通过采用不同断面的结构构件或不同强度等级的材料解决，最大的挑战是如何使成桥状态的桥梁线形在横桥向没有高差，符合铁路运营要求. 为实现合理的成桥线形，提出以下两种方案.

1） 方案1：通过构件单元无应力长度控制主梁线形. 上、下游成桥状态索力相同，依据主梁成桥线形和成桥内力确定出上、下游主桁杆件不同无应力构形，实现主梁平直状态. 该方案上、下游主桁无应力构形存在竖向高差，桥面板需要做成梯形结构，且主梁各板件单元在拼装时很难控制单元之间的连接，基于此，不考虑该方案.

2） 方案2：通过调整上、下游侧斜拉索索力控制主梁线形，解决主梁扭转. 该方案需要确定上、下游斜拉索合理的索力比值，其值与主梁的扭心和荷载有关. 对于钢桁梁扭心的确定，可将其等效为箱梁结构.

2.1.1   上、下游斜拉索索力比确定

空间桁架结构扭转时，假设其截面几何形状不变，设想将其等效成闭合箱梁截面，在相同的扭矩作用下，所产生的扭转变形与空间桁架相同. 因此，等效模式如下所述：

1） 上、下层桥面板考虑U形加劲肋作用. 根据闭口薄壁截面扭转公式（式（1）），U肋厚度可直接加至桥面板厚度.

式中：I_t为闭口薄壁截面的抗扭惯性矩；Ω为闭口截面所围面积的两倍；s为闭口截面的弧长；∆t为微段长度的厚度.

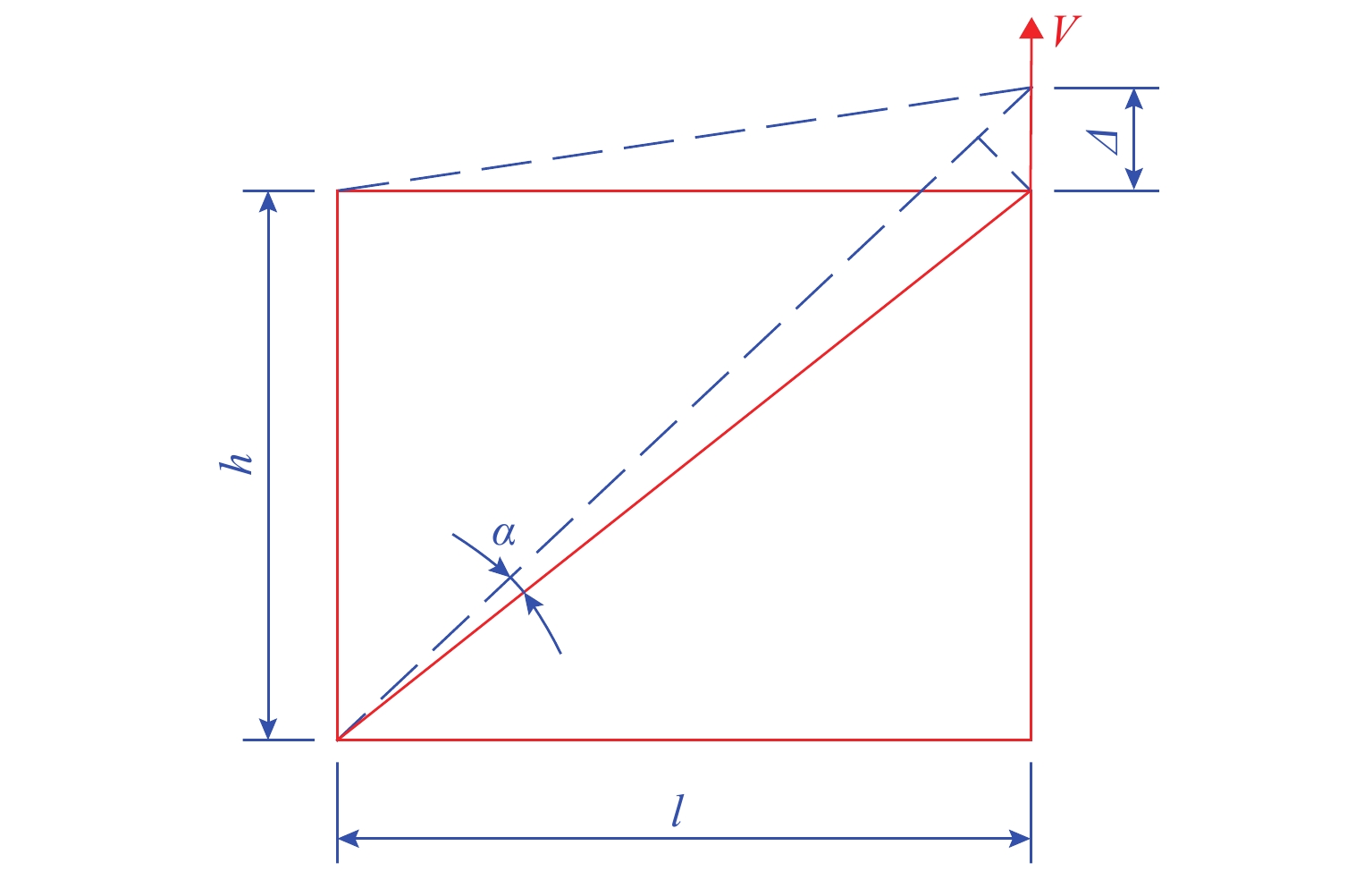
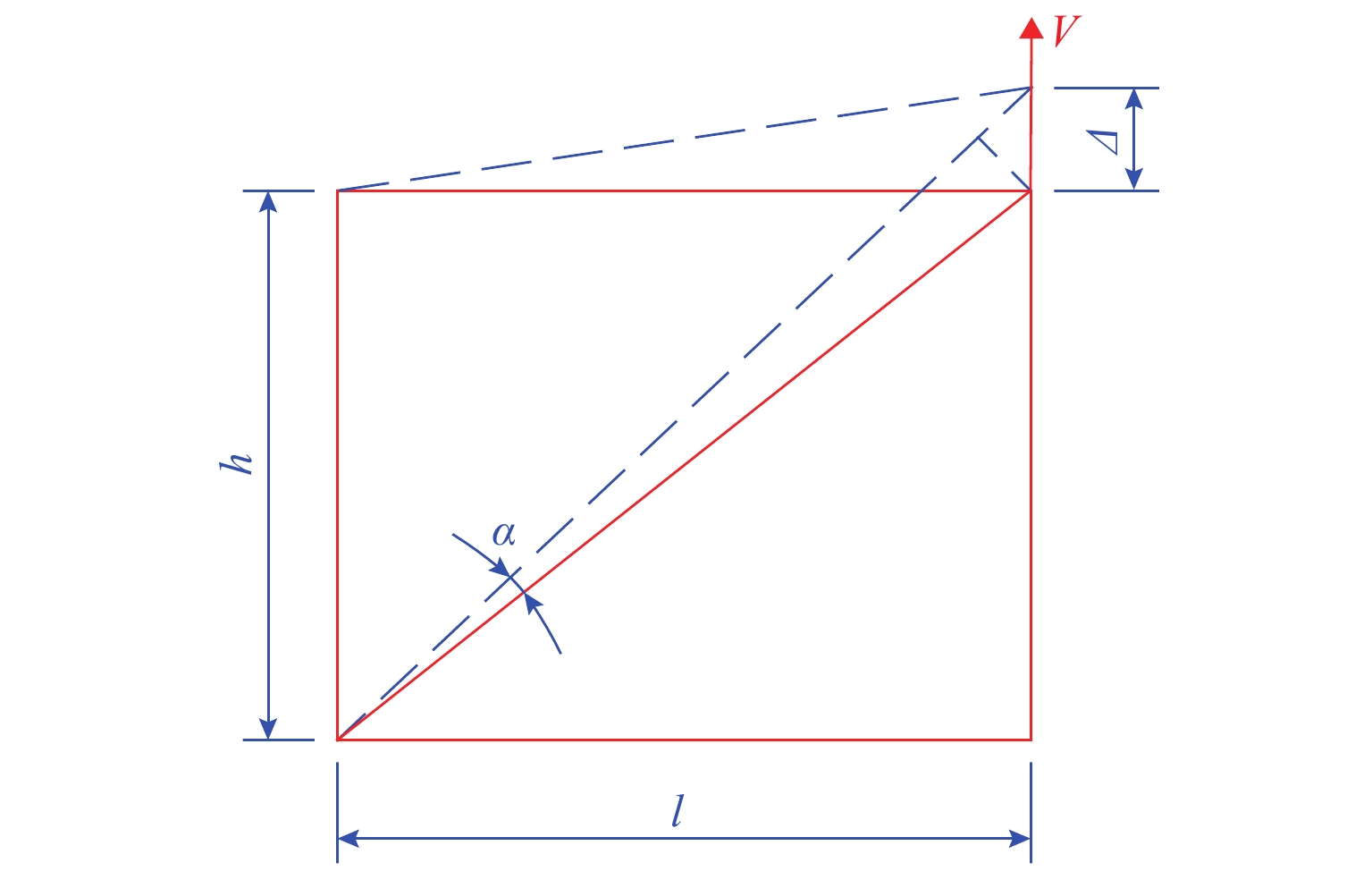
2） 主桁桁片依据扭转变形等效为薄壁厚度δ. 对于桁架扭转，竖杆上方作用竖向剪力V时产生变形Δ，斜杆为轴向变形，上、下弦杆为弯曲变形，如图3所示. 图中：α为斜杆与下弦杆的夹角；h为竖杆的长度；l为弦杆的长度；V为剪力. 轴向变形线刚度为EA/l，A为杆件截面积，E为弹性模量；弯曲变形线刚度为3EI/l³. 可知剪力V主要由斜杆承担. 腹杆承受扭转等效剪力V，根据剪切变形相同，换算出δ为

图  3  空腹式主桁扭转变形

Figure  3.  Torsion deformation diagram of vierendeel truss

下载: 全尺寸图片 幻灯片

式中：G为剪切模量；I为截面惯性矩.

对于中跨侧钢梁斜杆截面积为0.137 m²，等效板厚为9 mm. 上、下层桥面根据实际的板肋、U肋进行等效，计算出扭心位置距横桥向中心线0.05 m，偏上游侧.

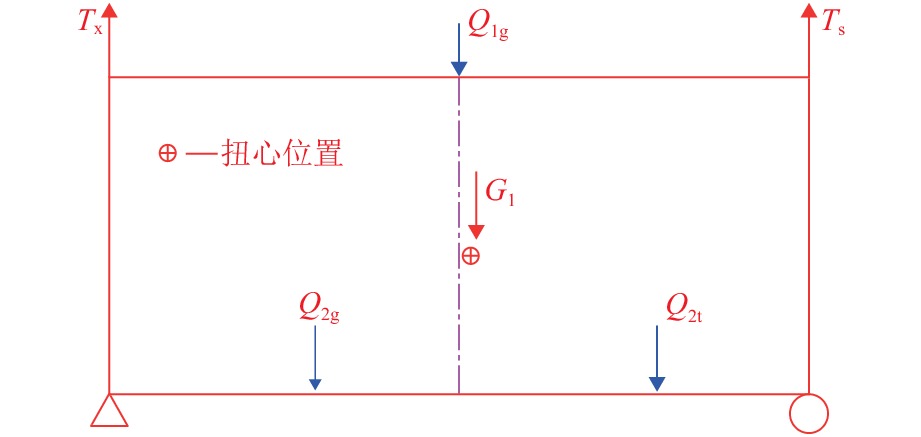
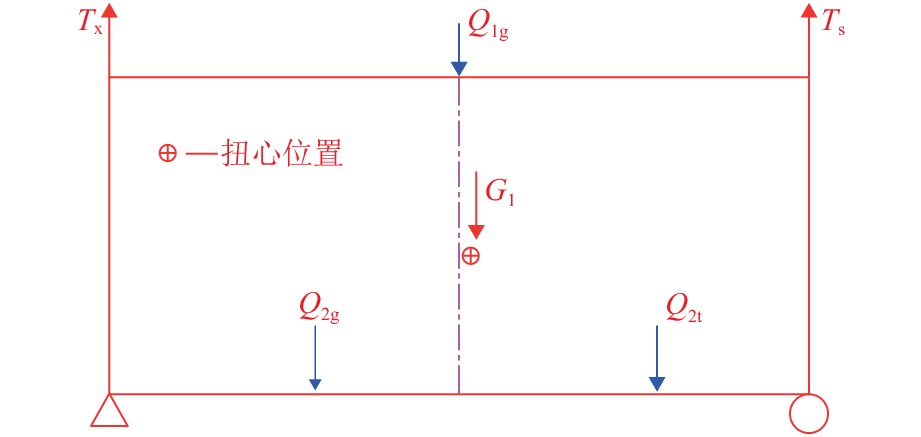
将主梁断面横桥向等效为如图4所示的简支梁结构，T_s为上游侧索力，T_x为下游侧索力，考虑主梁一期恒载G₁、上层二期恒载Q_1g、下层公路侧二期恒载Q_2g、下层铁路侧二期恒载Q_2t作用位置，依据索力之和与恒载相等，以及各个荷载至扭心的力矩之和为0，求出T_s与T_x的比值为1.19.

图  4  桁架结构横桥向力学模型

Figure  4.  Mechanical model of truss in transverse direction

下载: 全尺寸图片 幻灯片

2.1.2   合理成桥状态索力确定

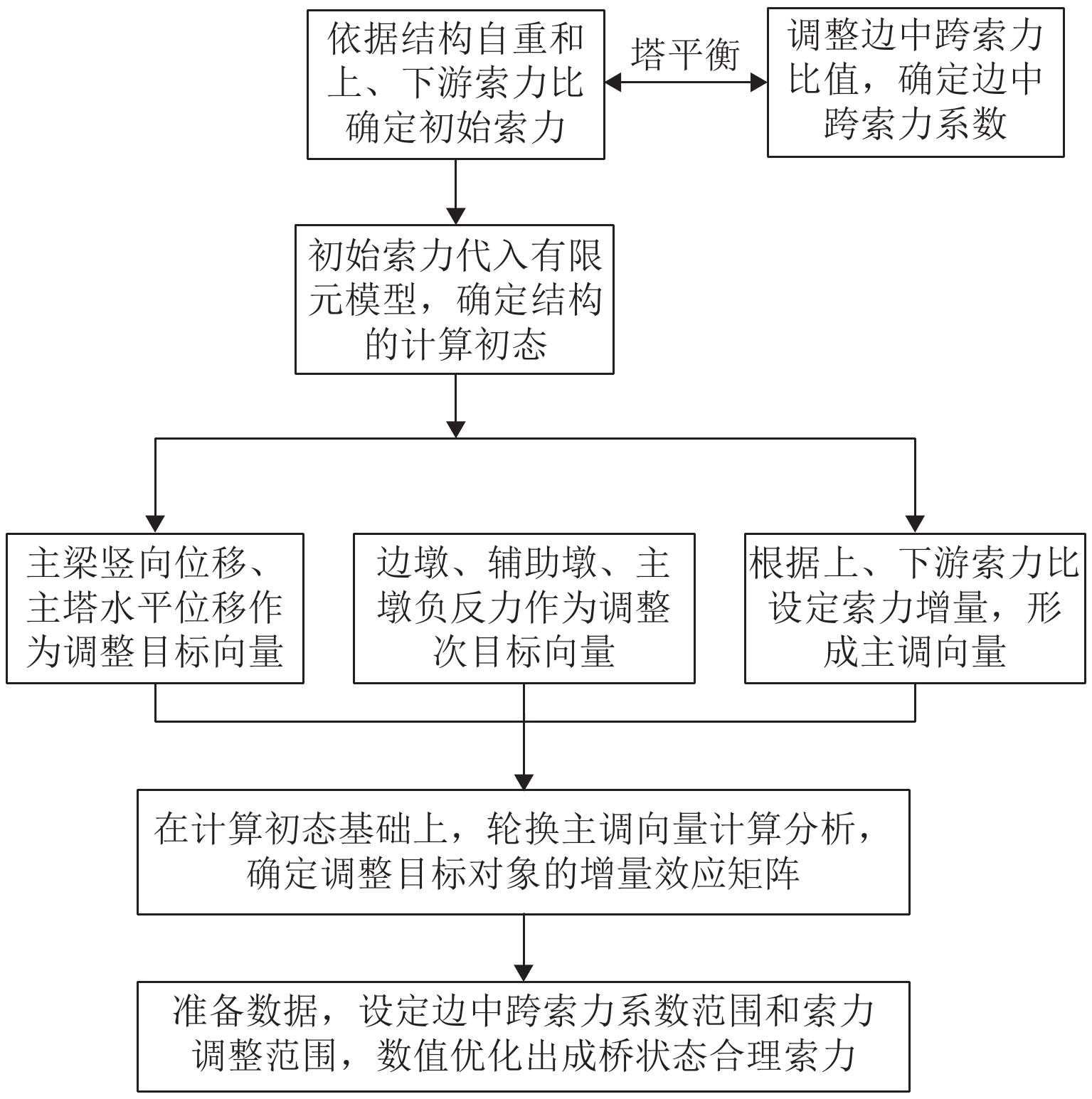
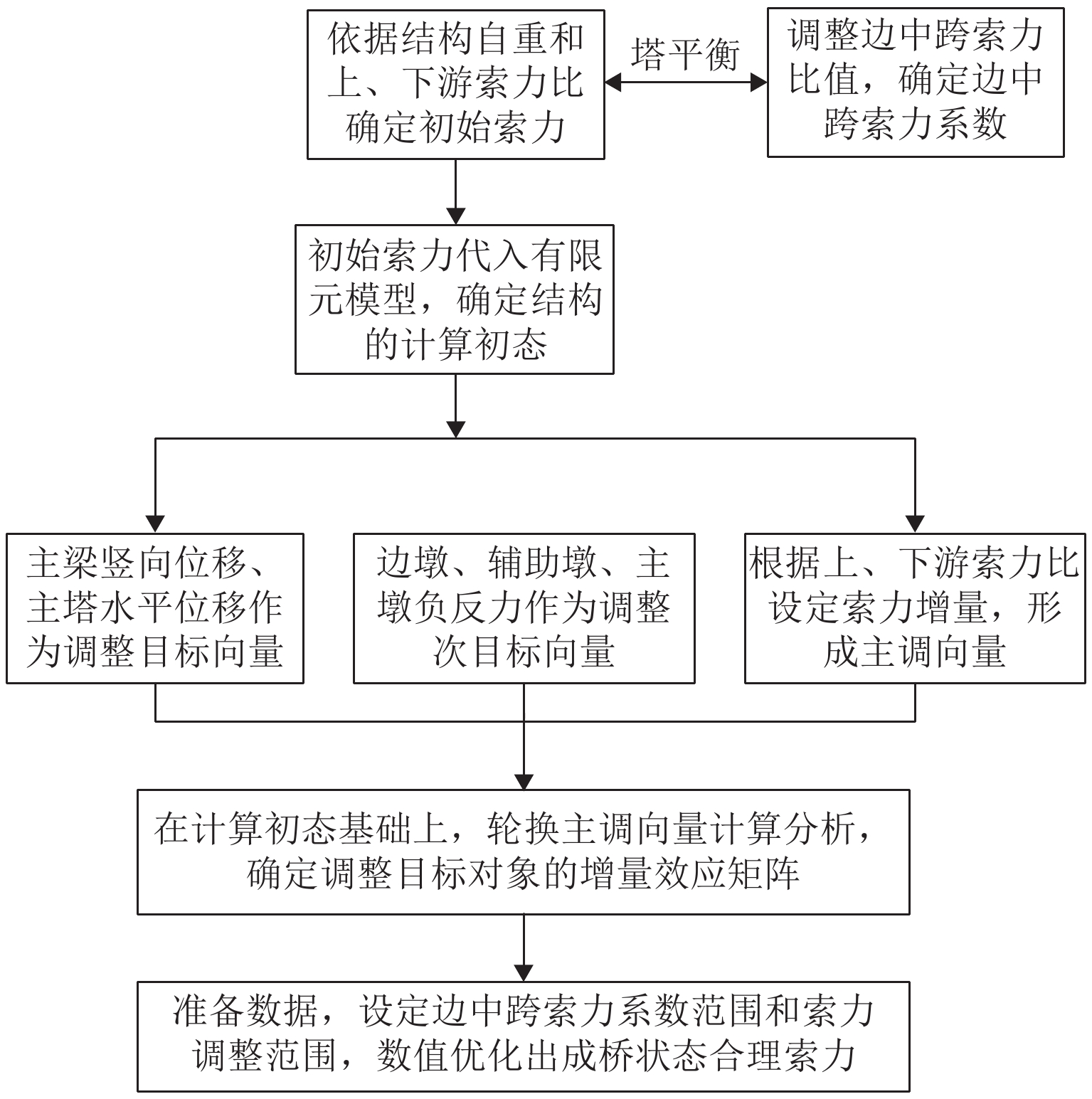
结合文献[12]快速精准调索方法，提出针对横桥向恒载非对称布置的斜拉桥结构索力确定方法. 上、下游斜拉索索力之和控制主梁竖向位移，上、下游斜拉索索力之比控制主梁扭转. 为了精准分析斜拉索的非线性效应对结构力学行为的影响，斜拉索采用悬链线单元模拟. 常泰长江大桥合理成桥状态索力确定流程如图5.

图  5  合理成桥状态索力确定流程

Figure  5.  Flowchart for determining cable forces

下载: 全尺寸图片 幻灯片

在确定斜拉桥合理成桥索力时，合理的目标值与合理的目标对象调整值关系到斜拉索索力值和分布规律，常泰长江大桥合理成桥索力求解时，主要原则如下：

1） 活载对主塔最不利加载工况为中跨加载，由于主塔为空间索塔，边跨侧塔肢为拉力，不利于结构受力. 经运营期荷载检算，成桥状态时主塔在顺桥向方向向边跨侧偏移10 cm以上，边跨侧塔肢预存一定压力，保证运营期受力合理.

2） 边中跨索力比值依据主塔受力确定，无法保证边中跨主梁同时达到梁平状态. 中跨侧主梁通过索力确定梁平状态，边跨侧主梁通过边中跨索力系数设定范围值0.99～1.01和主梁预制拱度确定边跨侧主梁处于梁平状态. 中跨侧主梁、主塔调整对象的权重系数设定为3，边跨侧主梁调整对象的权重系数为1.

3） 成桥状态下，各墩支座均为压力.

4） 初始状态依据结构自重确定斜拉索初始索力，斜拉索索力由主塔向两侧逐渐增大，索力增量调整范围设置为−300～400 kN，以此保证斜拉索索力的合理性.

5） 为保证主梁不发生扭转，上、下游斜拉索在初始索力和索力增量中的索力比值均为1.19. 且主梁竖向位移调整值取上、下游侧主桁节点平均值.

依据上述原则和索力确定方法，可以确定出合理成桥状态斜拉索索力值，代入有限元模型得到结构的成桥状态.

2.2   结果分析

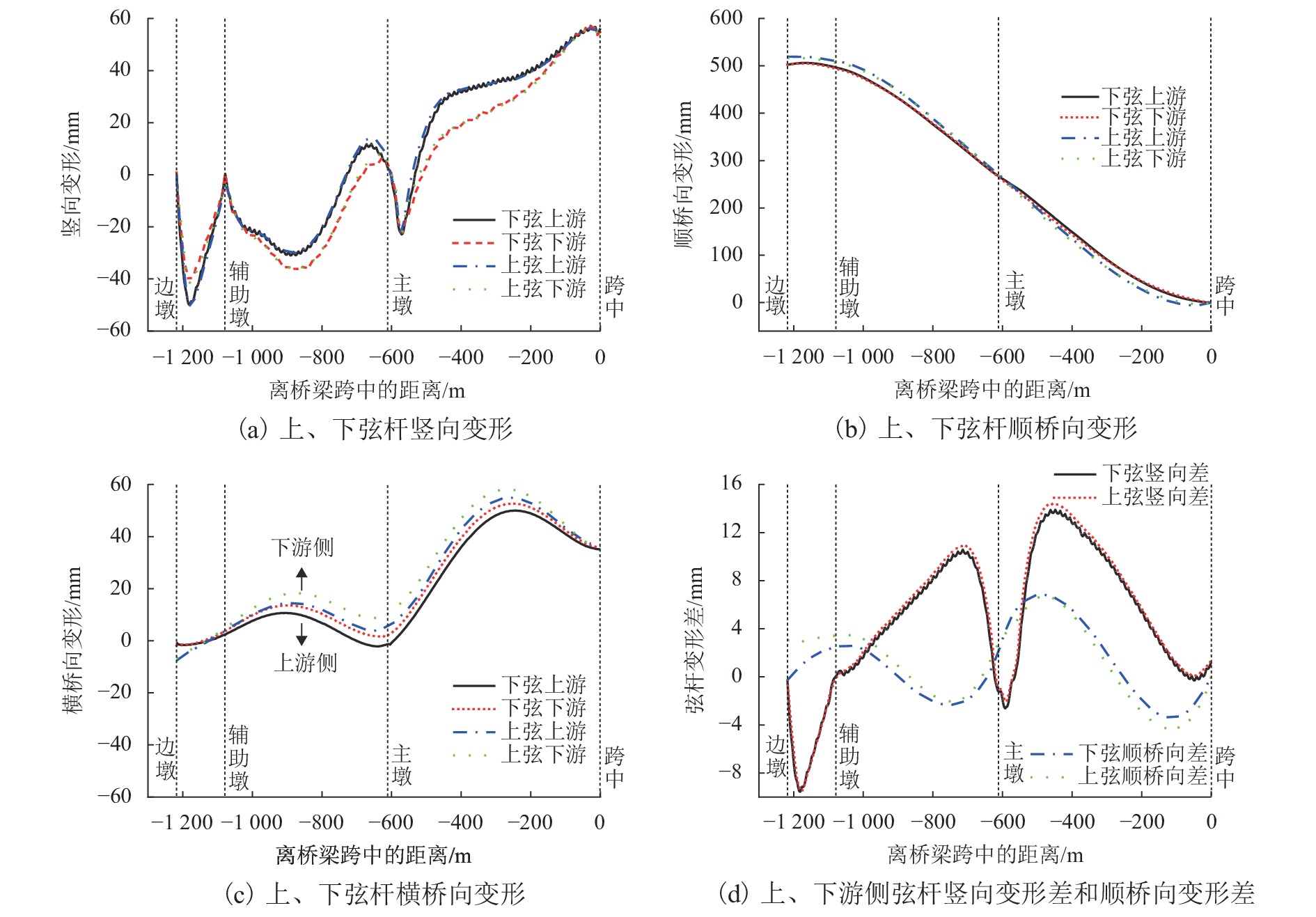
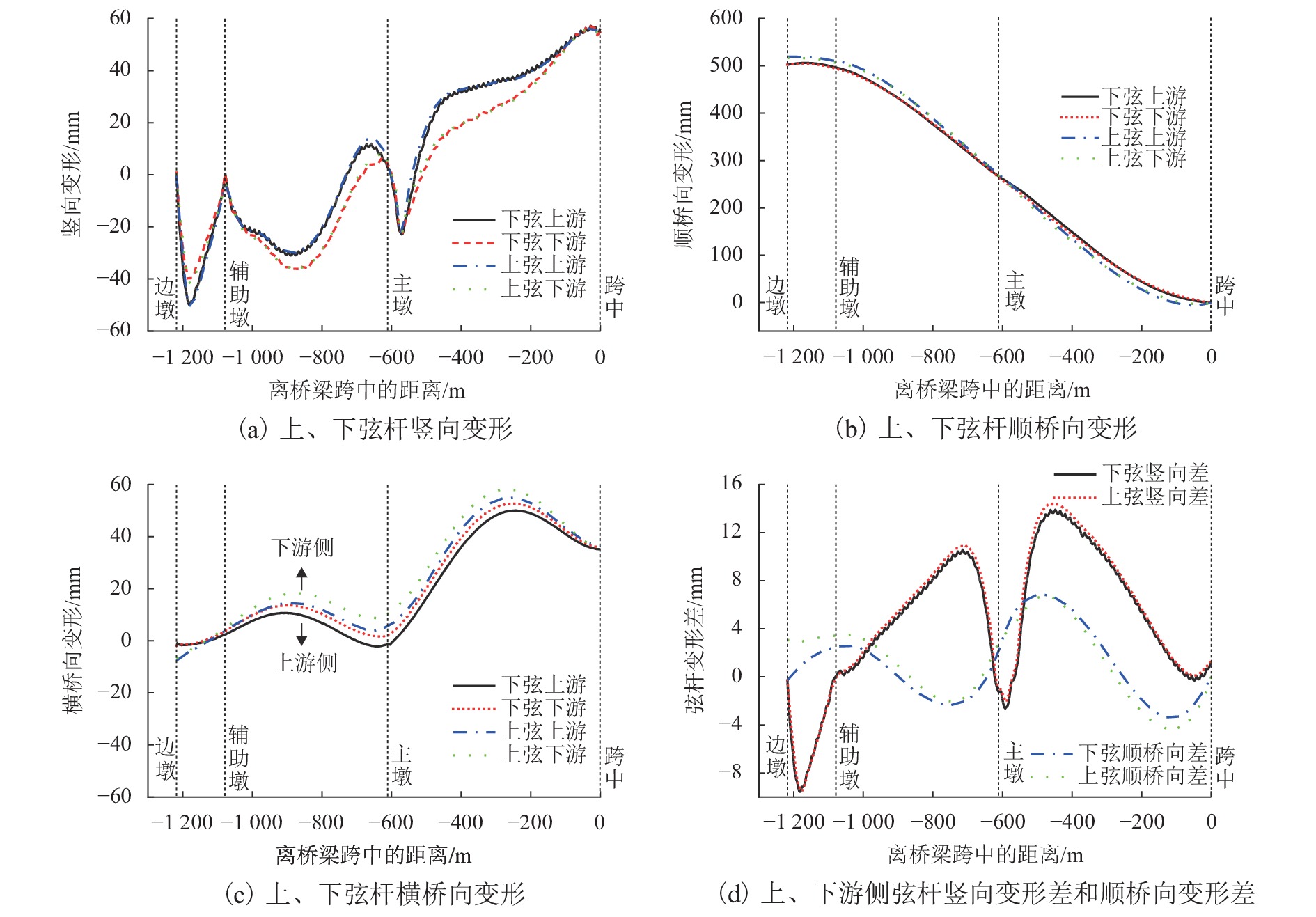
成桥状态下主梁弦杆上、下游侧变形及变形差如图6. 主塔塔顶变形列于表1中.

图  6  成桥状态主梁弦杆变形

Figure  6.  Deformations of main girder chords at completed state

下载: 全尺寸图片 幻灯片

表  1  主塔塔顶变形

Table  1.  Deformations of the top of the main tower mm

不计入收缩徐变效应			计入收缩徐变效应
顺桥向变形	横桥向变形		顺桥向变形	横桥向变形
−104.6	−88.1		−100.9	−125.2

下载: 导出CSV 

| 显示表格

从图6（a）、（d）可以看出：成桥状态上、下游主桁的竖向变形基本一致，最大竖向变形差发生在1/3边跨处和主墩两侧位置，最大值为14 mm；1/3边跨处为最外侧索位置，横桥向非对称载使得上游侧弦杆竖向变形大. 主墩两侧位置大约在6# 拉索位置，主墩处主梁杆件截面相应增大，上、下游索力比理应降低，而索力确定时采用统一索力比，使得下游侧弦杆竖向变形大. 结果表明：通过上、下游斜拉索索力的不同，可以将主梁的扭转效应消除，主梁处于梁平状态，竖向变形符合列车运营要求. 表1中主塔塔顶向边跨侧偏移10.09 cm，边跨侧塔肢预存了一定预压力. 主梁竖向位移和主塔顺桥向位移结果达到索力优化预期，表明本文提出的合理成桥状态索力确定方法合适.

从图6（b）可以看出，在边跨侧主梁上层桥面较下层桥面顺桥向变形大，在中跨侧上层桥面较下层桥面顺桥向变形小，主要是由于斜拉索作用在上弦杆，上、下层桥面轴向应变不一致产生的. 从图6（d）可以看出，上、下弦杆的上、下游顺桥向变形差值规律一致，主墩中跨侧7# 索位置上下游顺桥向变形差值最大达到6 mm左右，主要是由于主梁发生横弯引起的.

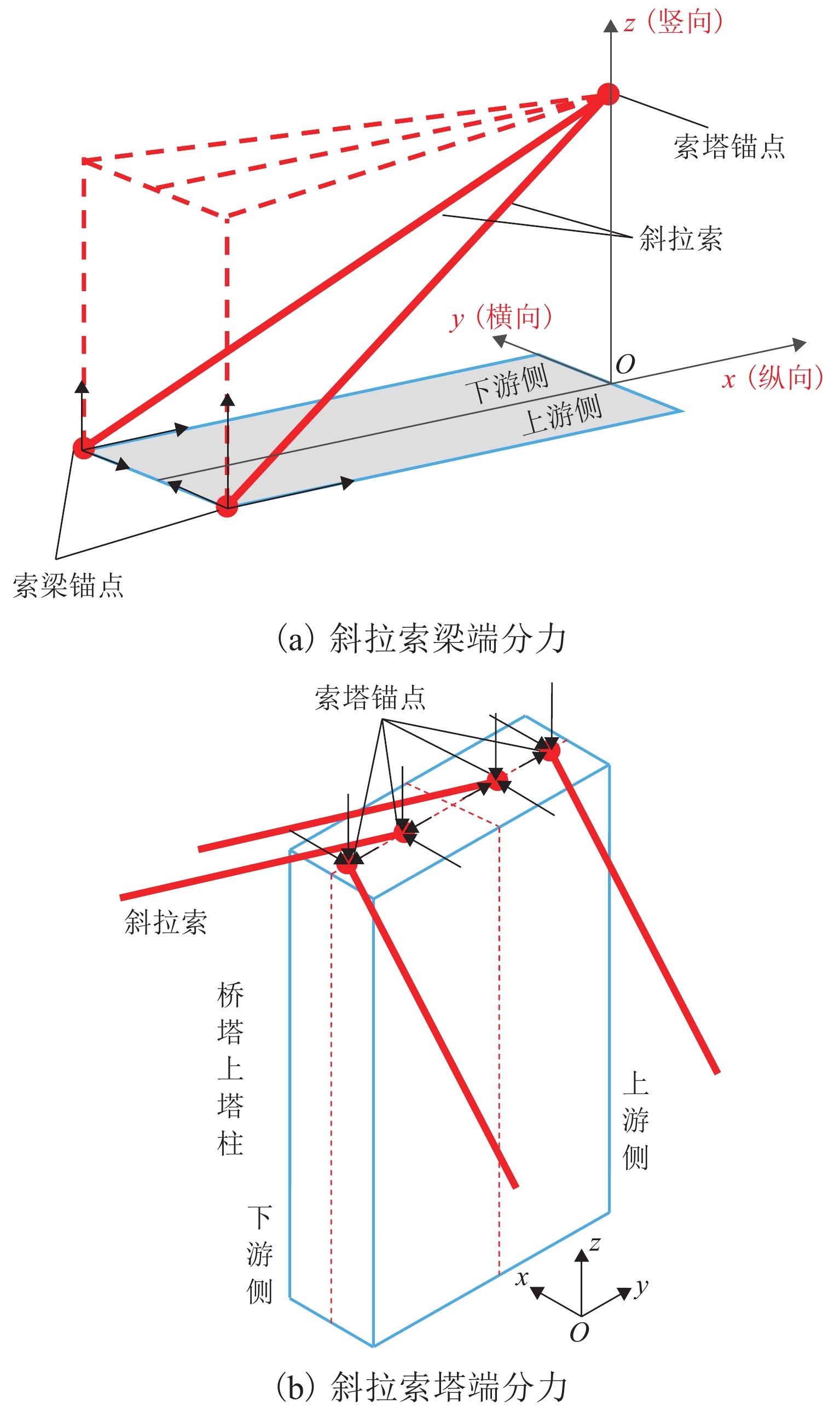
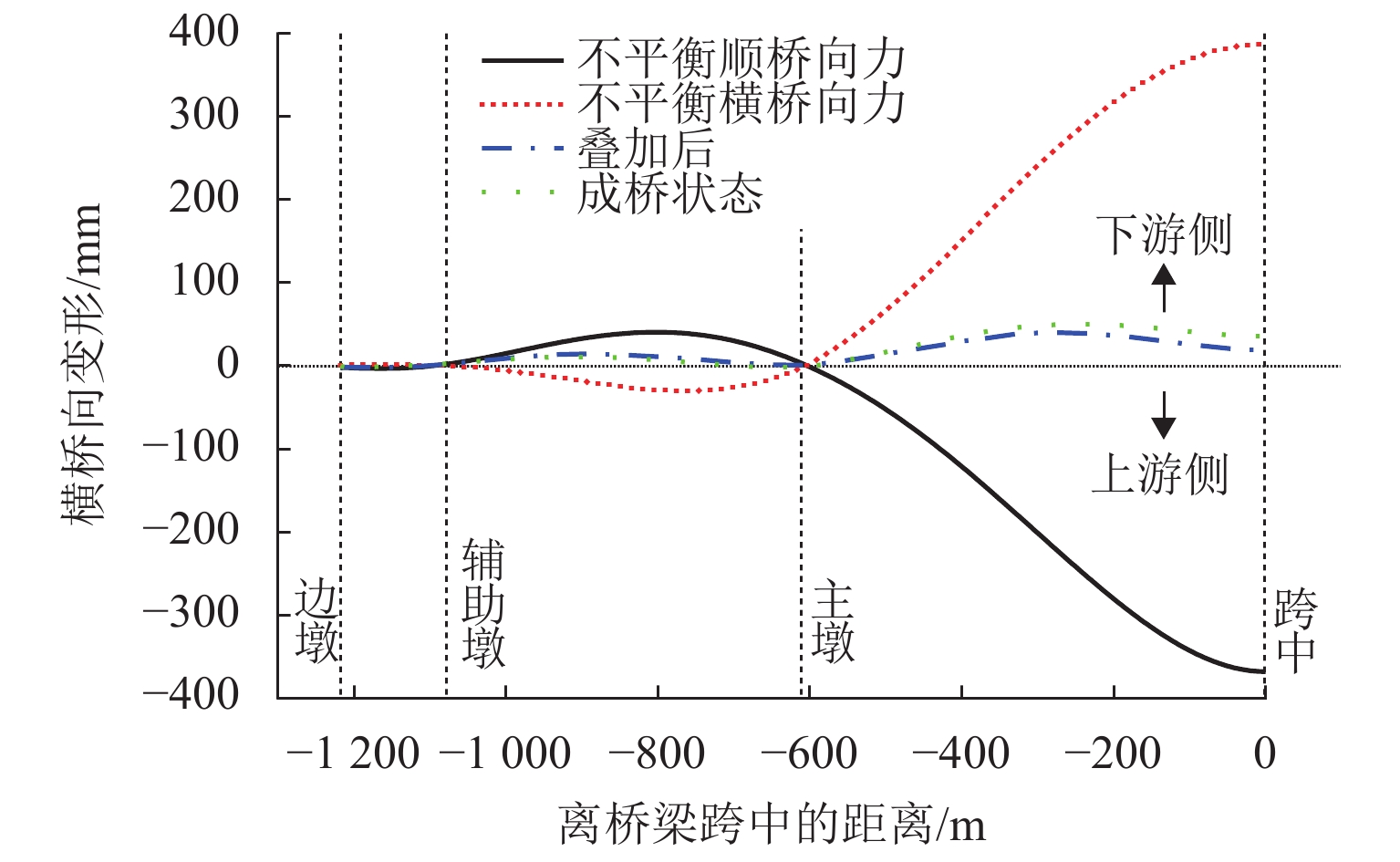
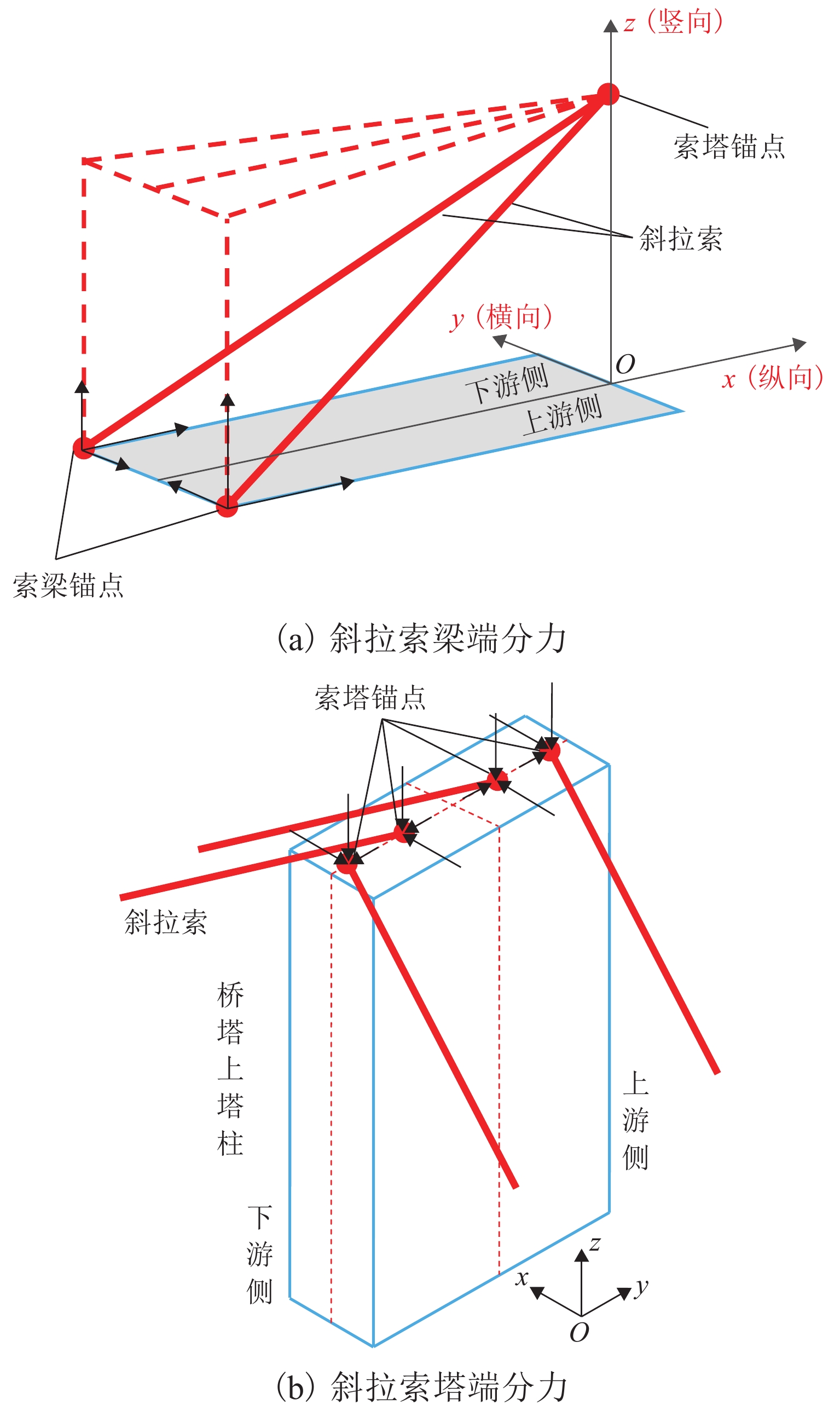
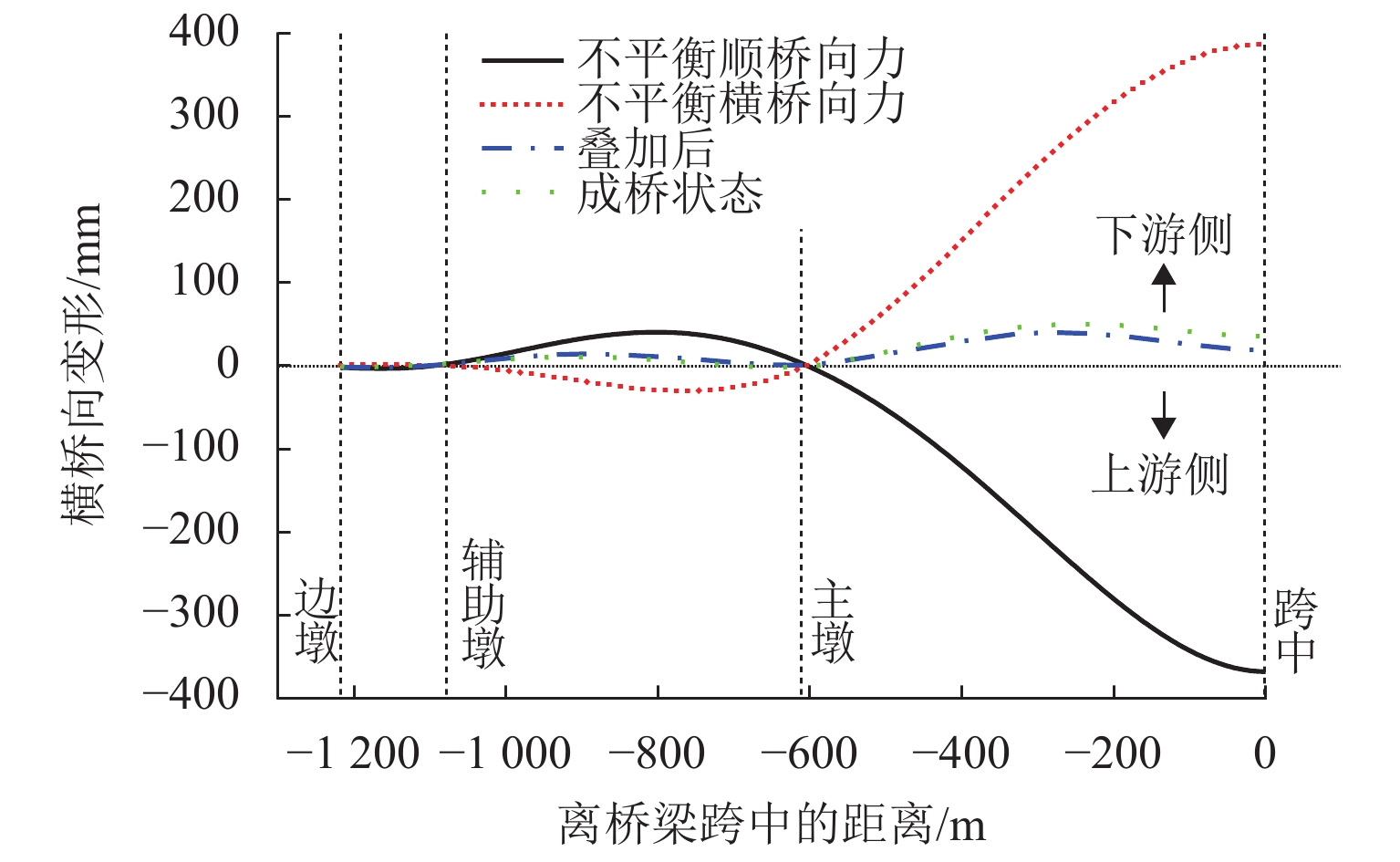
从图6（c）可以看出，主梁发生向下游侧横弯，最大横桥向变形为58 mm，位于1/4中跨. 主梁上层桥面横桥向变形较下层桥面大，最大差值为6 mm；且下游侧横桥向变形比上游侧大，最大差值为3 mm. 另外由表1可知，桥塔向上游侧横弯，塔顶横桥向变形为125 mm，向上游侧偏. 主梁、主塔均发生了由恒载非对称产生的横弯现象. 如图7所示，空间斜拉索的索力可以分解为顺桥向分力F_x、横桥向分力F_y和竖向分力F_z. 斜拉索上游侧索力比下游侧索力大19%，上、下游斜拉索空间角度基本一致，因此，斜拉索三分力的比值与索力比值一致. 主梁横弯变形主要由斜拉索顺桥向分力和横桥向分力引起：在顺桥向不平衡分力作用下，每对拉索位置处会形成一个力偶，在该力偶的作用下，主梁会发生往上游侧的横桥向弯曲变形；在横桥向不平衡分力作用下，上游侧的横桥向分力比下游侧大，主梁会发生往下游侧的横桥向弯曲变形. 顺桥向不平衡分力和横桥向不平衡分力对主梁的横桥向弯曲变形相反，将两种分力单独作用在主梁上，上游侧下弦杆横桥向弯曲变形如图8所示. 不平衡顺桥向分力会使主梁往上游侧横桥向弯曲，跨中最大偏移值为−368.5 mm；不平衡横桥向分力会使主梁往下游侧横桥向弯曲，跨中最大偏移值为387.2 mm. 可以看出，两个不平衡分力引起主梁的横桥向变形在数值上是基本一致的，但方向相反，主梁的横桥向偏位受纵向不平衡分力的影响略大.

图  7  斜拉索在梁端、塔端分力示意

Figure  7.  Cable force components at the anchor point

下载: 全尺寸图片 幻灯片

图  8  主梁横桥向变形

Figure  8.  Deformations of main girder in transverse direction

下载: 全尺寸图片 幻灯片

对于主塔，主塔横弯主要由竖向不平衡分力和横桥向不平衡分力引起的. 竖向不平衡分力使得主塔向上游侧弯曲；横桥向不平衡分力使得主塔向上游侧弯曲. 两个不平衡分力产生主塔横桥向变形方向一致，经计算，不平衡竖向分力引起塔顶的横桥向变形为34.5 mm，不平衡水平分力引起塔顶横桥向变形为90.5 mm. 桥塔横桥向弯曲主要由斜拉索不平衡横桥向分力控制.

从桥梁后期运营角度上来看，主梁58 mm的横桥向变形对应的曲线半径为60 km，满足列车运营要求. 而对于主塔塔顶横桥向变形则达到了125 mm，若不计混凝土塔的收缩徐变效应，横桥向变形仅为88 mm，可见，混凝土的收缩徐变效应对主塔的横桥向变形影响较大. 另外，主塔横桥向变形也反映了主塔、主墩基础横桥向不均匀受力，基础在长期的横桥向弯矩作用会发生相应的不均匀沉降. 基于上述两点，必须要控制主塔因恒载非对称引起的横桥向位移值. 为解决这一问题，提出了斜拉索在塔端锚固向下游侧偏移的设计方案：塔端锚点向下游侧偏，增大了竖向分力的力矩，但同时也增大了横桥向分力，两者对主塔横桥向弯曲的方向相反. 计算分析表明，需要将锚点向下游侧偏移4 m左右. 该方案不利于塔端锚固设计，且影响结构整体景观效果，不能使得主塔达到设计预定要求. 因此，必须降低上、下游侧恒载的差值.

2.3   控制措施

前已述及，配重增加工程造价，那么降低上、下游恒载的差值只有降低铁路侧恒载的大小，其中，最主要的是降低铁路二期恒载的大小. 经过调研和科研论证，提出了降低铁路侧恒载的措施，如表2所示.

表  2  降低铁路侧恒载措施

Table  2.  Measures to reduce secondary dead load of the railway

措施	优化前	优化后
降低铺砟厚度	35 cm 厚普通 道床	25 cm 厚聚氨酯固化道床
压缩道床宽度	9 m	8.2 m
调整铁路防水面板结构	6 cm 厚高性能混凝土铺装	3 mm 不锈钢与基材形成复合钢板
斜拉索	不同规格、相同 强度	同种规格、不同 强度

下载: 导出CSV 

| 显示表格

采用上述调整措施，上游侧较下游侧恒载差值由125 kN/m降低为65 kN/m. 上、下游侧斜拉索索力比为1.1.

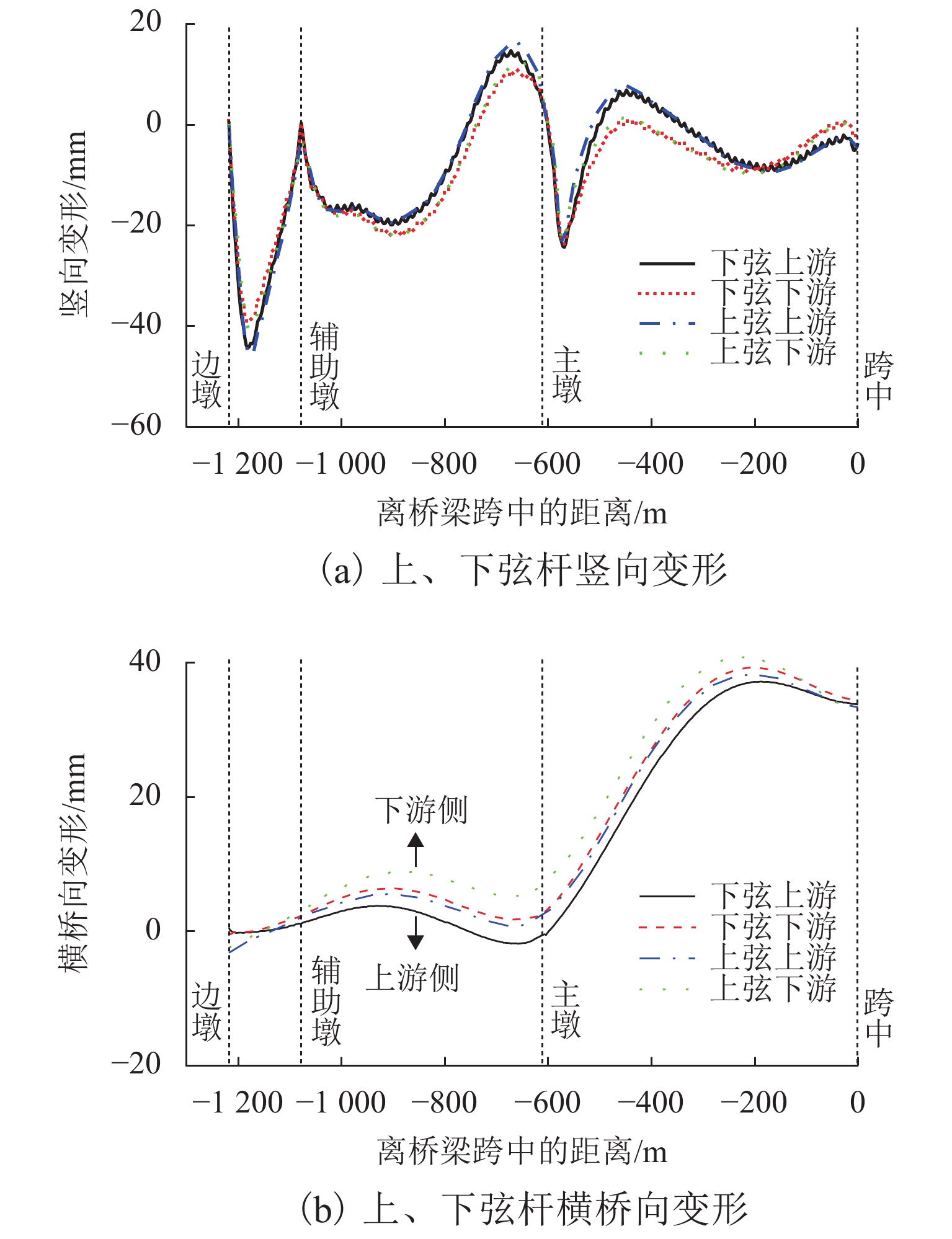
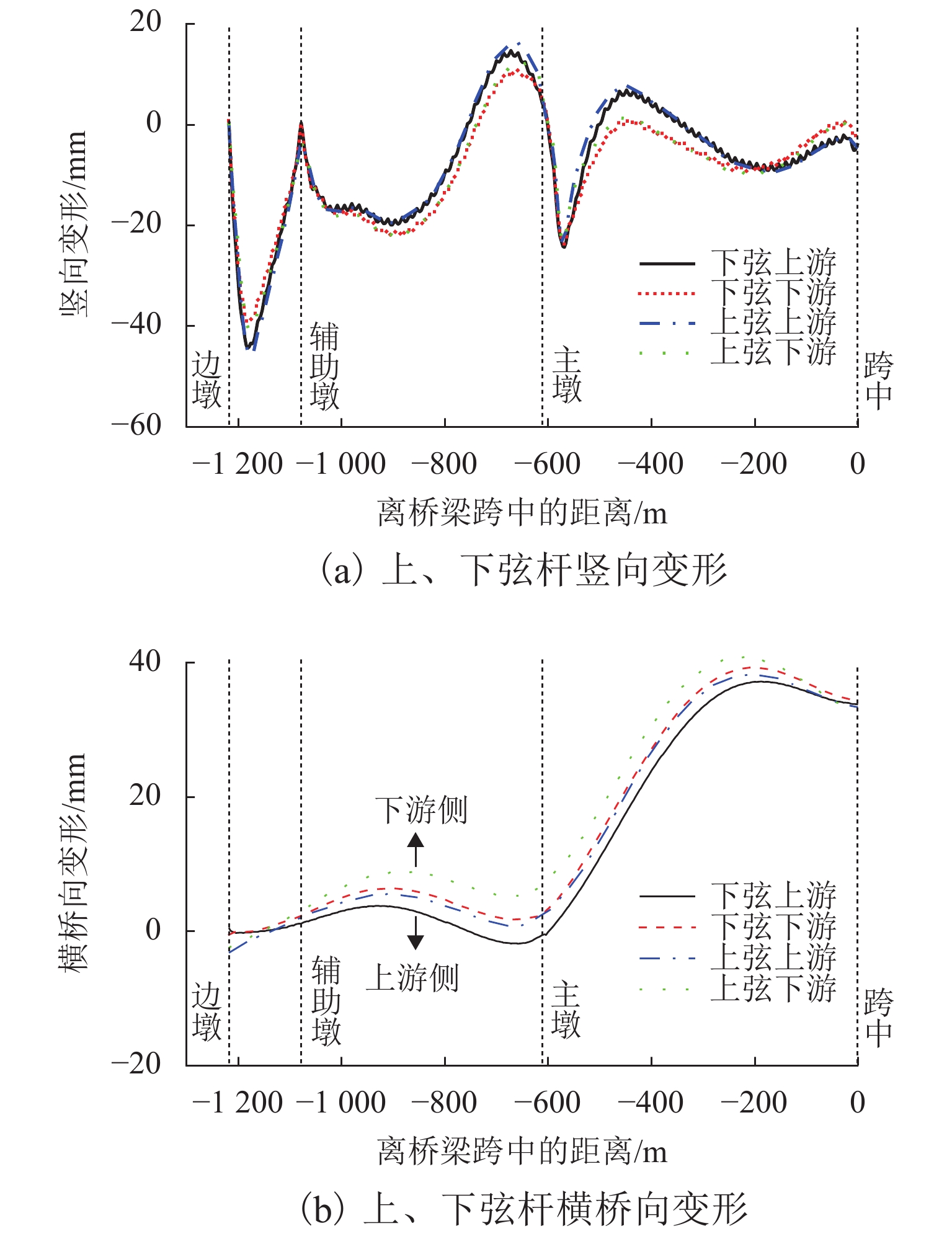
优化后的成桥状态为主梁竖向、横桥向变形，如图9所示，主梁上、下游杆件竖向变形一致，未发生扭转. 主梁最大横桥向变形仍在1/4中跨处，数值为40 mm. 主塔塔顶横桥向弯曲变形为向上游侧偏移42 mm，主塔横桥向变形改善明显. 结果表明：通过上述控制措施，可以有效控制主梁、主塔的横桥向变形.

图  9  优化后成桥状态主梁弦杆变形

Figure  9.  Deformations of main girder chords in bridge state after optimization

下载: 全尺寸图片 幻灯片

3.   结　论

本文依据提出的恒载非对称索力确定方法，对常泰长江大桥恒载非对称引起的成桥状态力学行为进行了分析，提出了相应的控制措施优化结构变形，得到如下结论：

1） 横桥向恒载非对称布置对主梁产生扭转变形，可以通过上、下游索力不同控制主梁扭转. 但同时由于空间拉索的三向不平衡分力，继而引起主梁、主塔发生横桥向弯曲变形.

2） 对于主梁，斜拉索顺桥向不平衡分力和横桥向不平衡分力产生的横桥向弯曲变形大小基本一致，方向相反，总体效果是抵消的，有利于降低主梁横桥向弯曲变形.

3） 对于主塔，斜拉索竖向不平衡分力和横桥向不平衡分力产生的横桥向弯曲变形方向相同，总体效果是叠加的，不利于控制主塔横桥向弯曲变形. 因此，为进一步控制主梁横偏和主塔横弯，提出了降低道床宽度、厚度和调整防水面板结构等设计方案，将横桥向非对称恒载降低至65 kN/m，效果明显.