Simulation Analysis on Influence of Congestion Propagation on Operation of Carsharing Systems
-
摘要:
随着共享汽车渗透率的不断增加,站点、路段层面的车辆溢出和拥挤传播现象日趋严重. 为刻画拥挤传播对汽车共享系统运行的影响机理,首先,搭建具有时变性和状态相关性的汽车共享系统排队网络;其次,基于C# 语言和O2DES离散事件仿真框架,提出并设计考虑车路交互影响和拥挤传播现象的汽车共享系统仿真模型,分析动态随机环境下站点与路段层面的拥挤传播现象对汽车共享系统运行的影响;最后,以成都市三站点的小规模汽车共享系统为例,在不同转运比例、需求和道路拥堵场景下,将该模型与引入虚拟空间的无穷排队模型进行对比分析. 研究结果表明:站点和路段层面的拥挤传播现象会导致系统服务率下降9.3%~16.9%,相比无穷排队模型,考虑拥挤传播现象的排队模型更能反映汽车共享系统的实际运营过程;当路网的道路占用率为70% (路网处于中度拥堵)时,考虑拥挤传播现象的汽车共享系统可实现最大收益;汽车共享系统的引入会为道路资源的动态分配带来新变化,当公共交通转向汽车共享系统的用户占比超过70%时,路网拥堵加剧,不利于汽车共享系统的有效运营和可持续发展.
Abstract:With the increasing penetration of carsharing, vehicle overflow and congestion propagation at the level of station and path tend to be serious. In order to describe the influence mechanism of congestion propagation on the operation of carsharing systems, firstly, a queuing network of the carsharing system is built with time-varying and state-dependence properties. Secondly, based on C# language and O2DES framework of discrete event simulation, a simulation model of the carsharing system under dynamic stochastic environment is proposed, which allows for the influence of vehicle–road interaction and congestion propagation. The influence of congestion propagation on the operation of the carsharing system is analyzed in terms of the station and path levels. Finally, a small-scale carsharing system, i.e., three stations in Chengdu, is exemplified. The proposed model and the infinite queuing model in virtual space are compared and analyzed under different transfer ratios, demands and road congestion scenarios. The results show that congestion propagation at the stations and paths will decline the system service rate by 9.3%–16.9%. Compared with the infinite queuing model, the proposed model can better reflect the actual operation of the carsharing system because of considering congestion propagation. When the occupancy rate of the road network reaches 70% (the road network is in moderate congestion), the proposed carsharing system can achieve maximum benefits. The introduction of the carsharing system will bring new changes to the dynamic allocation of road resources. When the proportion of users from public transportation to the carsharing system exceeds 70%, it will intensify the congestion of the road network, which is not conducive to the effective operation and sustainable development of the carsharing system.
-
作为缓解交通拥堵[1]和减少资源消耗[2-3]的创新型交通方式,共享汽车在全球得到了大力推广,渗透率不断增加[4]. 2019年全球汽车共享市场规模超过25亿美元,预计到2026年增长超过24%[5]. 现阶段需要更全面地对汽车共享系统展开研究,以支撑企业决策,提升行业服务水平.
为进一步揭示汽车共享系统内各因素间的相互作用关系,本文综合考虑动态性(用车需求率、服务时间随时段明显变化)、随机性(用车、停车需求的不对称性和不确定性)、车路交互影响和拥挤传播这四项重要特征. 汽车共享系统呈现明显的动态性和随机性[6-7],使得供需在时空上不匹配. 共享汽车会吸引公共交通用户 [8],若大量无车族高频率使用共享汽车,势必会加剧交通拥堵[9]. 以网约车为例:网约车因能提高车辆利用率而减缓交通拥堵被普遍看好,随着网约车大量涌入,北京、广州等城市拥挤传播现象日趋严重,拥堵延时指数同比上升11%~17%[10-11].因此,在推广汽车共享系统之际,研究系统的动态性、随机性、车路交互影响和拥挤传播现象具有迫切性和前瞻性.
在刻画汽车共享系统运营所处的动态随机环境时,Zhao等[12]构建的时空网络模型考虑了需求和用车时间的动态性;Hu等[13]构建混合排队网络模型,考虑了需求和用车时间的随机性,但尚未对两者进行结合考虑;Deng等[14-15]构建的离散事件仿真模型较好地刻画了系统的动态随机环境,但尚未对车路交互影响和拥挤传播现象加以刻画.
少量研究对车路交互影响进行了解析或仿真建模,马舒予等[16]搭建的汽车共享排队模型考虑了用户需求与道路拥堵的交互影响;蒋阳升等[17]搭建的汽车共享仿真模型考虑了道路拥堵与系统运营的交互影响. 本文借鉴上述研究[16-17],采用具有状态相关性的平均速度指数模型刻画车路交互影响.
随着共享汽车渗透率增加,拥挤传播现象日趋明显,当前研究缺乏有效方法刻画其对系统运行的影响. 站点车辆溢出时,Hu等[13]假设站点前方存在虚拟缓冲区以存储溢出车辆,Park等[18]提出系统会安排调度员将溢出车辆调往其他站点. 以上研究[13,18]均忽略了溢出车辆对系统运行的影响,而这一影响在拥挤网络和共享汽车高渗透率的条件下不容忽视.
O2DES (object-oriented discrete event simulation)仿真框架灵活且高效,被成功运用于动态随机环境下的汽车共享系统建模[17,19-20]. 排队网络拓扑结构在保证仿真质量的同时,又能有效降低仿真系统的复杂性. 因此,本文基于汽车共享系统排队网络和O2DES仿真框架搭建离散事件仿真模型,将车路交互作用机制和拥挤传播机制嵌入模块化站点和路段模型的事件中,分析其对系统运行的影响,从而获取更贴近现实和更精准的仿真结果,支撑系统决策方案的有效评估.
1. 汽车共享系统排队网络搭建
本文以单程式汽车共享系统为研究对象,用户提前预订车辆,在系统运营允许的时间窗内到达站点取车,行程结束后可在任意站点还车.
1.1 汽车共享系统排队网络描述
系统的拓扑网络由有向网络
$G\left( {N,A} \right)$ 表示,$N$ 为站点集合,$A$ 为路径集合. 系统由以下部分组成:1) 共享车辆. 共享车辆有等待预订、用户取车、道路行驶、站点还车四种状态.
2) 站点. 站点是用户借还共享车辆的场所.
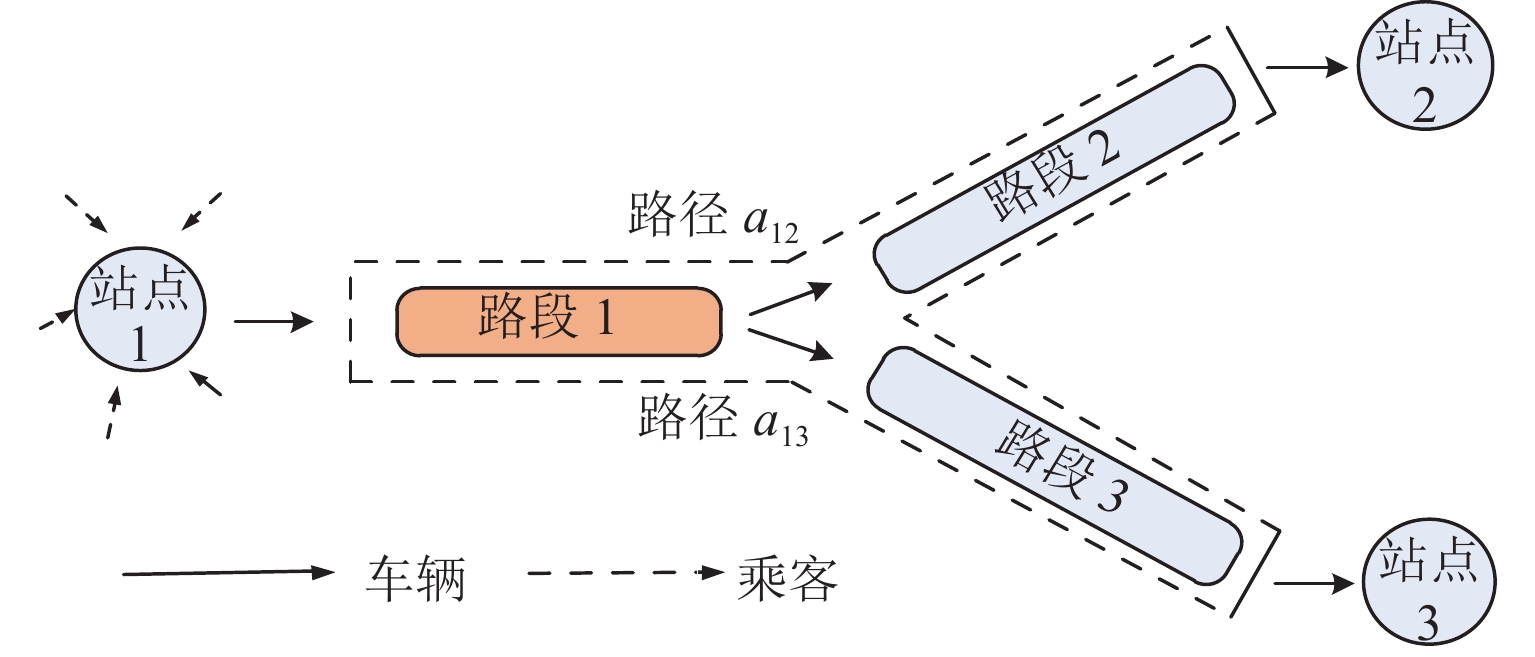
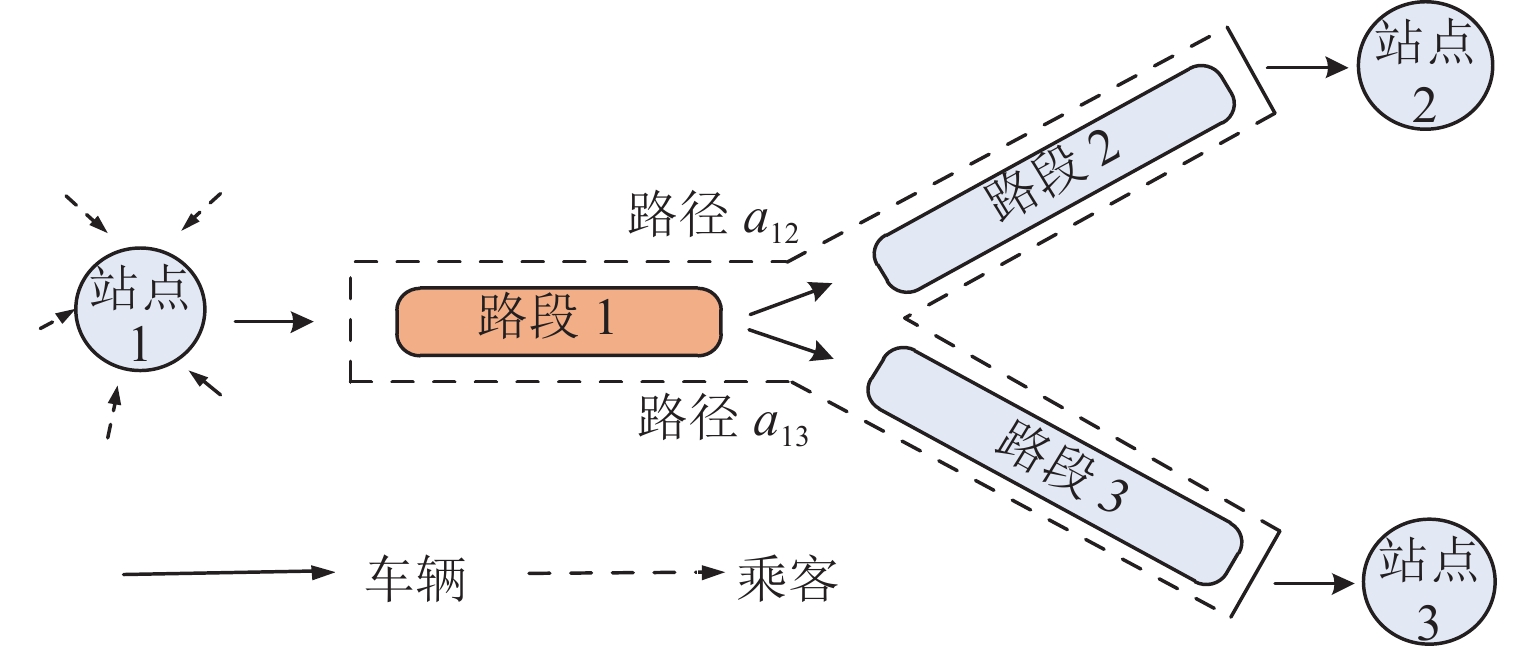
3) 路径和路段. 从站点集合
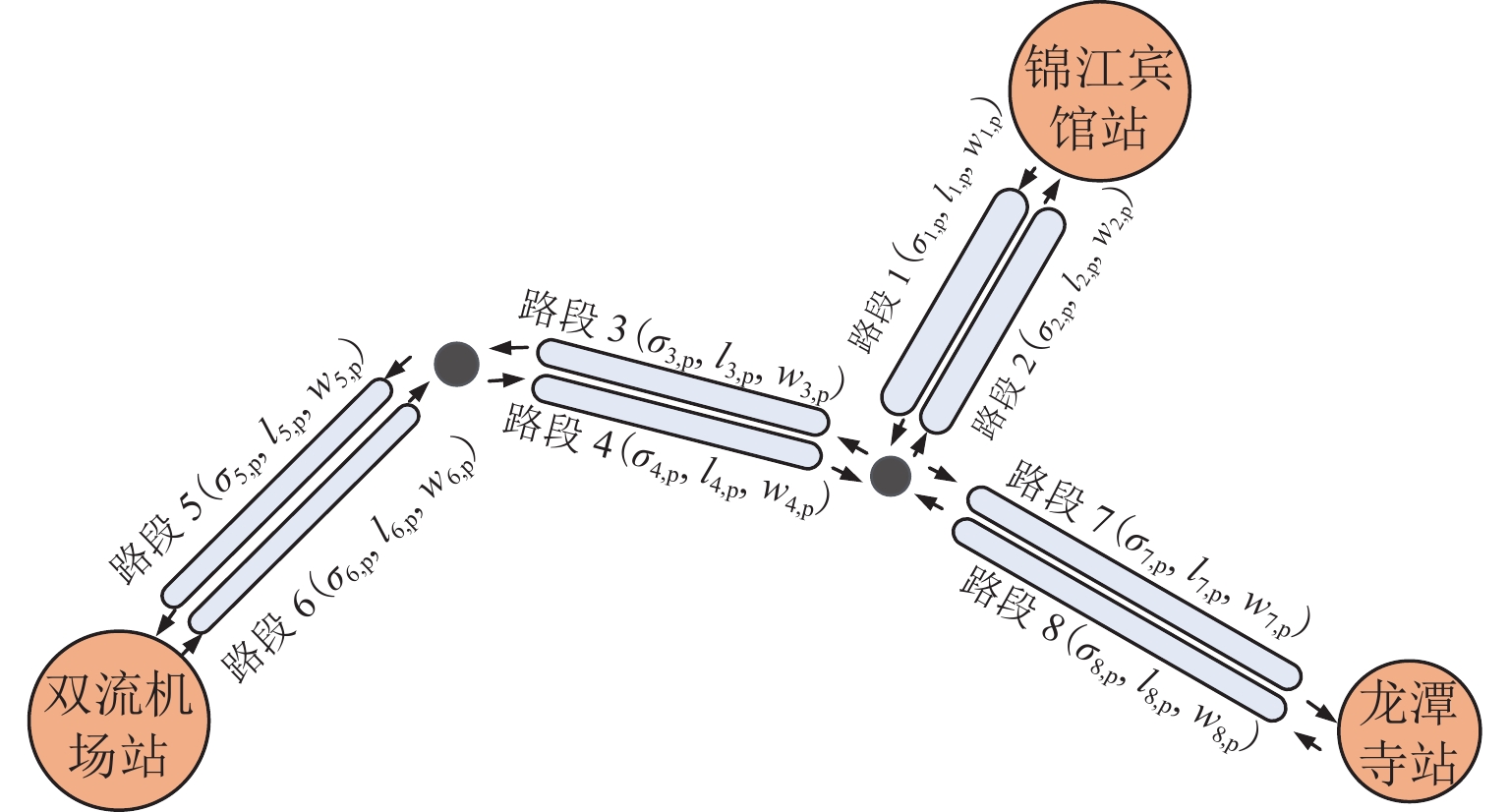
$N$ 中任取站点$i、j$ ,假定用户选择站点$i、j$ 间的最短路径$ {a_{ij}} $ 出行. 路径可划分为多条同向有序路段. 如图1所示,路段1作为路径$ {a_{12}} $ 、${a_{13}}$ 的共用路段,需要承担更多的出行需求,也更容易拥堵.1.2 汽车共享系统排队网络搭建
基于汽车共享系统拓扑结构,将站点排队系统和路段排队系统连接成排队网络. 排队网络中车辆遵循流量守恒原则:下游节点排队系统的输入车辆为上游节点排队系统输出车辆之和.
1.2.1 站点排队系统
将用户还车视为车辆到达,到站取车视为服务过程,取车离开视为服务结束. 用户的到达时间间隔服从负指数分布M[21],服务时间服从一般分布G[22]. 站点i在时段t可预订的
$ {k_{i,{\text{s}}}}(t) $ 辆共享汽车视为$ {k_{i,{\text{s}}}}(t) $ 个并联服务台,站点i的停车容量为$ {c_{i,{\text{s}}}} $ (下标中“S”表示站点(station),后同). 根据Kendall符号[23],可将站点i抽象为$ {\text{M}}/{\text{G}}/{k_{i,{\text{s}}}}(t)/{c_{i,{\text{s}}}} $ 并联排队模型. 考虑用车需求率的动态性和服务率的状态相关性(服务时间随时段t站点i的系统状态$ {x_{i,{\text{s}}}}(t) $ 而变化),本文用$ {\lambda _{i,{\text{s}}}}(t) $ 表示时段t站点i时变的到达率,$ {\mu _{i,{\text{s}}}}({x_{i,{\text{s}}}}(t)) $ 表示时段t站点i状态相关的服务率.1.2.2 路段排队系统
将车辆驶入路段视为到达,行驶过程视为服务过程,驶离路段表明服务结束. 车辆的到达时间间隔服从负指数分布M[21],且服务时间服从一般分布G[22]. 将时段t路段m的剩余道路空间
${k_{m,{\text{p}}}}(t)$ 视为混联服务台,路段m的道路容量为${c_{m,{\text{p}}}}$ (下标中 “p” 代表路段(path),后同). 根据Kendall符号[23],可将路段m抽象为${\text{M}}/{\text{G}}/{k_{m,{\text{p}}}}(t)/{c_{m,{\text{p}}}}$ 混联排队模型. 考虑到达率的时变性和服务率的状态相关性(服务时间随时段t 路段m的系统状态${x_{m,{\text{p}}}}(t)$ 而变化),本文用${\lambda _{m,{\text{p}}}}(t)$ 表示时段t路段m时变的到达率,${\mu _{m,{\text{p}}}}({x_{m,{\text{p}}}}(t))$ 表示时段t路段m状态相关的服务率.1.3 非线性弹性出行需求
根据Xu等[3]的研究,用户从站点i到站点j的实际出行需求
${r_{ij}}(t)$ 不仅随着t动态变化,还随出行价格${\text{ }}{p_{ij}}(t)$ 弹性变化,可表示为rij(t)={Rij(t)exp(−σij(t)pij(t)),0⩽pij(t)⩽pij,max(t),0, pij(t)>pij,max(t), (1) 式中:
$ {R_{ij}}(t) $ 为站点$i、j$ 间的用户潜在预订需求;$ {\sigma _{ij}}(t) $ 为价格弹性系数;$ {p_{ij,\max }}(t) $ 为价格阈值.2. 汽车共享系统仿真建模
2.1 仿真建模方法
基于C# 语言和事件驱动机制, O2DES仿真框架开发了离散事件仿真建模的新范式,通过静态属性、动态属性和事件三种组件描述模块[19]. 静态属性在仿真过程中不会改变,动态属性会随着仿真时钟的推进而更新,动态属性能有效刻画系统运行的动态特征[20]. 本文基于O2DES框架搭建仿真模型,遵循模块化概念,以保证仿真的高效性[24],将系统分为共享车辆、站点和路段三种模块进行描述.
2.2 共享车辆模块
共享车辆模块只包含动态属性集,各属性随仿真时钟的推进而动态变化. 任取一共享车辆e,下标“V”表示共享车辆(vehicle),时段t动态属性集
${D_{e,{\text{v}}}}$ 可表示为De,v={se,v(t),oe,v(t),de,v(t),Le,v(t),ne,v(t)}, (2) 式中:
${s_{e,{\text{v}}}}(t)$ 为共享车辆的状态,${s_{e,{\text{v}}}}(t) = 1$ 表示时段t用户正在使用车辆,${s_{e,{\text{v}}}}(t) = 0$ 表示车辆接受预订;${o}_{e,\text{v}}(t)、{d}_{e,\text{v}}(t)$ 分别为用户取、还车的时间戳;${L_{e,{\text{v}}}}(t)$ 为车辆e驶过的路段集合;${n_{e,{\text{v}}}}(t)$ 为时段t车辆e将进入的下游设施.2.3 站点模块
站点模块包含静态、动态属性集和模块事件.
2.3.1 站点模块静态属性集
站点i的静态属性集
$ {Q_{i,{\text{s}}}} $ 表示为Qi,s={ci,s,gi,s}, (3) 式中:
$ {g_{i,{\text{s}}}}$ 为站点允许用户预订的时间窗长度.2.3.2 站点模块动态属性集
时段t站点i的动态属性集
$ {D_{i,{\text{s}}}} $ 表示为Di,s={Ei,s(t),xi,s(t),Hi,s(t),hi,s(t),bi,s(t),ki,s(t),rij(t),λi,s(t),μi,s(xi,s(t)),ωij(t)}, (4) 式中:
$ {E_{i,{\text{s}}}}(t) $ 为时段t站点i停放的共享车辆集合,$\left| {{E_{i,{\text{s}}}}(t)} \right| = {x_{i,{\text{s}}}}(t) $ ,表示车辆数;$ {H_{i,{\text{s}}}}(t) $ 为站点i在时段t未被预订的车辆集合;$ {h_{i,{\text{s}}}}(t) = \left| {{H_{i,{\text{s}}}}(t)} \right| $ ,为站点未被预订的车辆数;$ {b_{i,{\text{s}}}}(t) $ 为共享车辆的服务率;${\omega _{ij}}(t) $ 为时段t用户在站点i、j间的选择概率,如式(5)所示;$k_{i,\text{s}}$ 、$\lambda_{i,\text{s}}$ 和$\mu_{i,\text{s}}(x_{i,\text{s}}(t))$ 如式(6)~(8)所示.ωij(t)=rij(t)/rij(t)∑∀n∈Nrin(t)∑∀n∈Nrin(t), (5) ki,s(t)=min{ci,s,∑∀n∈Nrin(t)/∑∀n∈Nrin(t)bi,s(t)bi,s(t)}, (6) λi,s(t)=∑∀n∈Nrin(t), (7) μi,s(xi,s(t))=min{xi,s(t),ki,s(t)}bi,s(t). (8) 2.3.3 站点模块事件
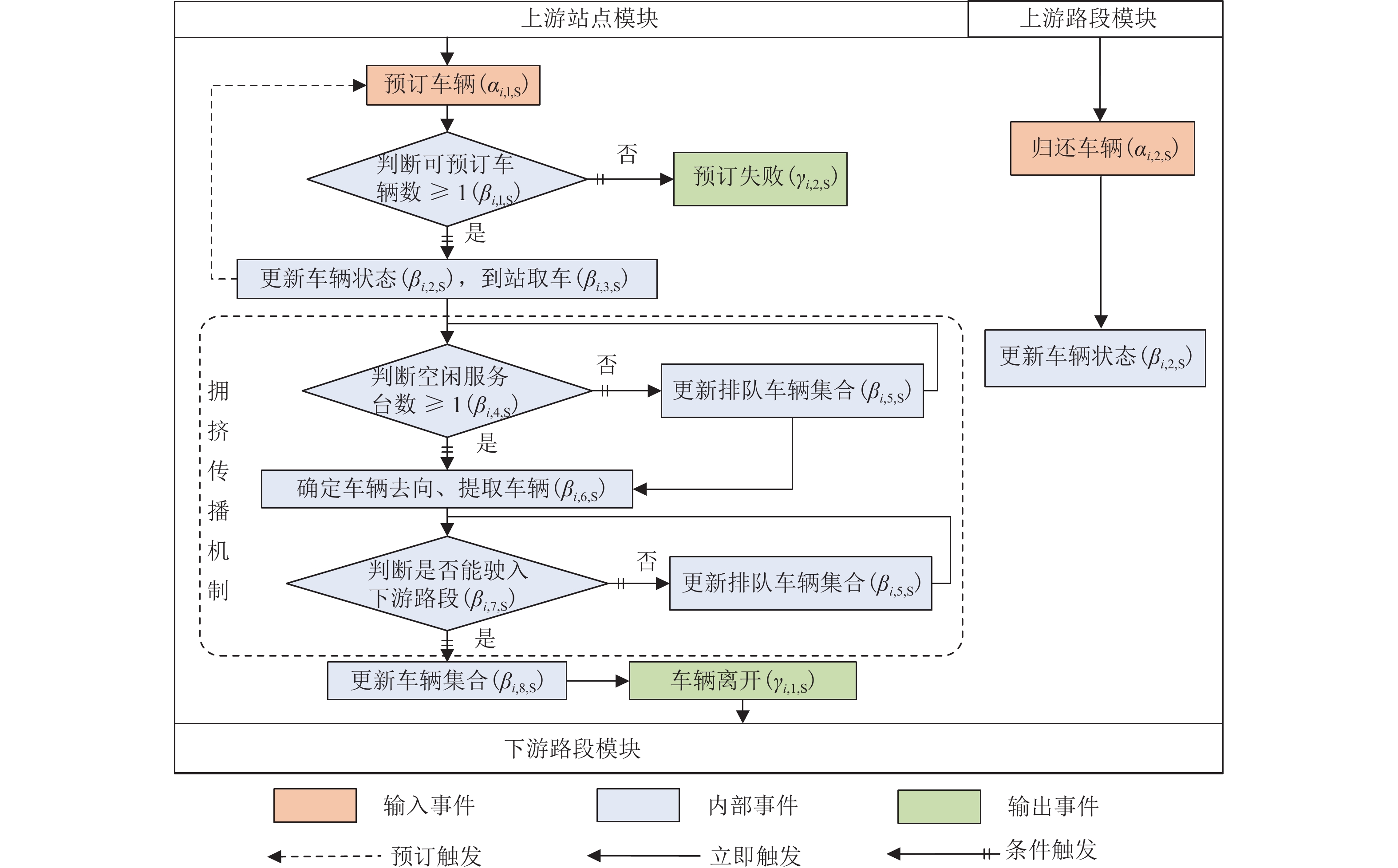
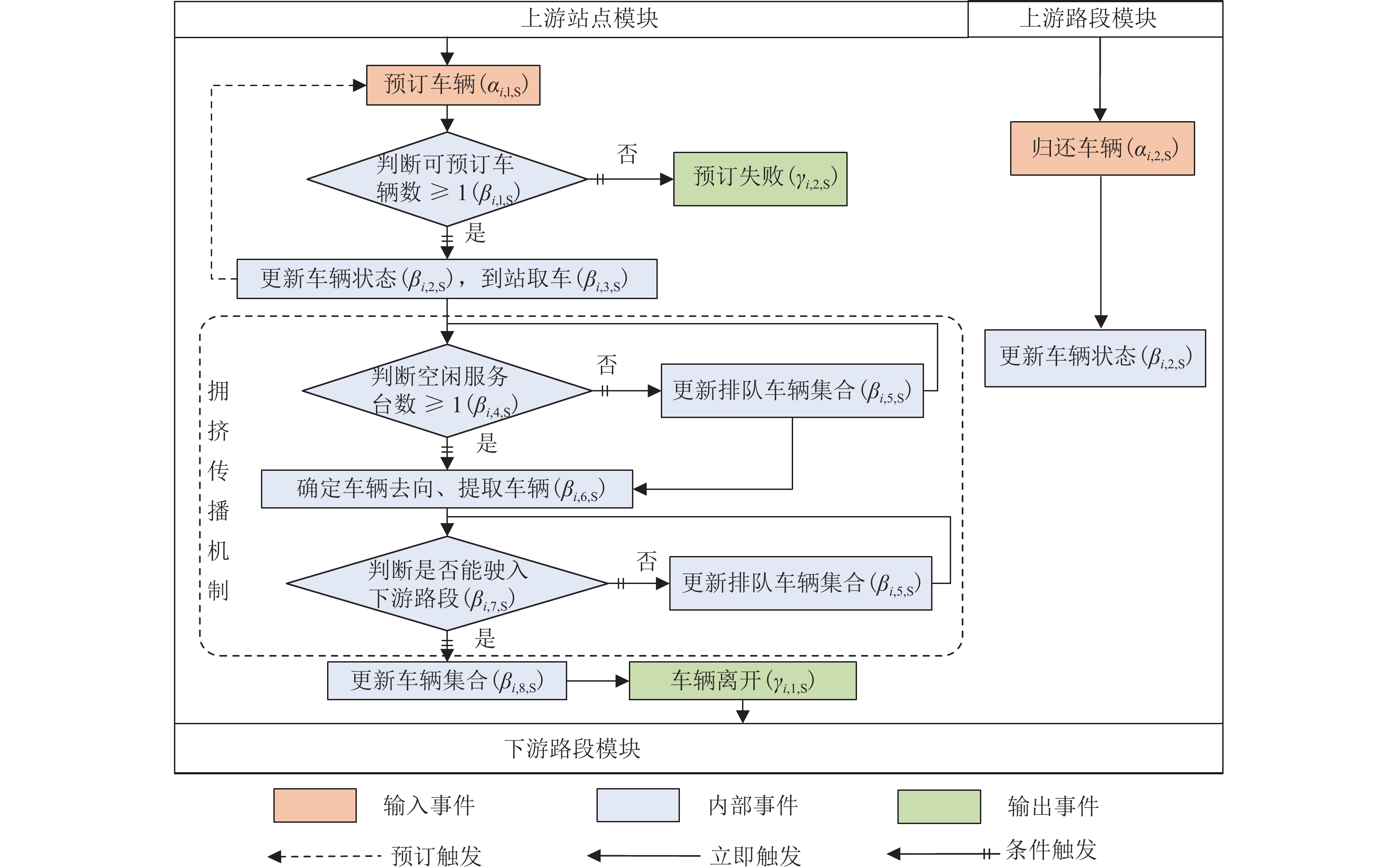
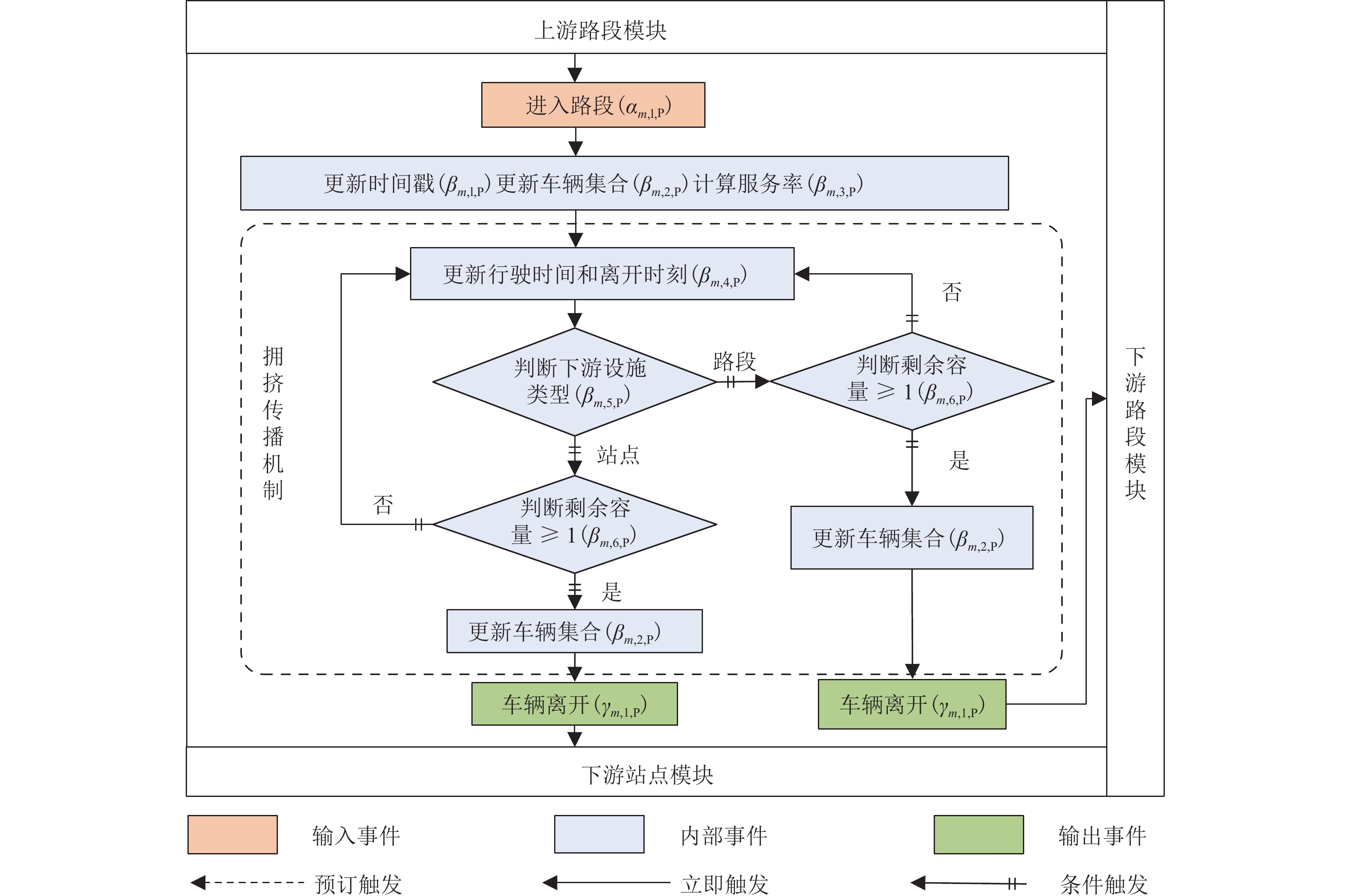
站点i模块事件触发关系如图2所示.
事件触发过程如下:
1) 预订车辆
步骤1
$\alpha _{i,1,{\text{s}}}^{}$ 触发$\beta _{i,1,{\text{s}}}^{}$ 判断可预订车辆数$ {h_{i,{\text{s}}}}(t) $ ,若$ {h_{i,{\text{s}}}}(t) \geqslant 1 $ ,执行$\beta _{i,2,{\text{s}}}^{}$ ,车辆e状态更新为“已被预订”,${H_{i,{\text{s}}}}(t)\backslash \left\{ e \right\}$ →${H_{i,{\text{s}}}}(t) $ 表示将车辆e从可预订车辆集合$ {H_{i,{\text{s}}}}(t) $ 中删除后更新$ {H_{i,{\text{s}}}}(t) $ ;步骤2 在时间窗长度
$ {g_{i,{\text{s}}}} $ 内,预订触发$\beta _{i,3,{\text{s}}}^{}$ ;步骤3 预订触发
$\alpha _{i,1,{\text{s}}}^{}$ ,下一位用户预订车辆.2) 到站取车
步骤1 触发
$\beta _{i,4,{\text{s}}}^{}$ 判断空闲服务台数,如果有空闲服务台,则执行$\beta _{i,5,{\text{s}}}^{}$ ,车辆$e$ 在站点排队等待,否则直接触发$\beta _{i,6,{\text{s}}}^{}$ ;步骤2 触发
$\beta _{i,6,{\text{s}}}^{}$ ,确定用户目的站点;步骤3 触发
$\beta _{i,7,{\text{s}}}^{}$ 判断下游设施剩余空间,没有则触发车辆排队事件$\beta _{i,5,{\text{s}}}^{}$ ,有则执行$\beta _{i,7,{\text{s}}}^{}$ 并更新站点车辆集合,${E_{i,{\text{s}}}}(t)\backslash \left\{ e \right\}$ →$ {E_{i,{\text{s}}}}(t) $ 表示将车辆从站点车辆集合中$ {E_{i,{\text{s}}}}(t) $ 删除后更新集合$ {E_{i,{\text{s}}}}(t) $ ,执行$\gamma _{i,1,{\text{s}}}^{}$ ,车辆离开站点.3) 站点还车
步骤1 用户驾驶车辆到达站点还车,触发
$\alpha _{i,2,{\text{s}}}^{}$ 和$\beta _{i,2,{\text{s}}}^{}$ ,将车辆更新为可预订状态;步骤2 车辆加入站点可预订车辆集合
$ {H_{i,{\text{s}}}}(t) $ .站点模块事件嵌入了拥挤传播机制:用户驶入路段前,需执行
$\beta _{i,7,{\text{s}}}^{}$ 判断下游路段的剩余空间,下游路段严重拥堵(道路无剩余空间)时触发$\beta _{i,5,{\text{s}}}^{}$ ,车辆排队等待并继续占用站点停车位,下游路段的拥挤现象传播至上游站点. 直至下游路段有剩余空间时触发$\beta _{i,7,{\text{s}}}^{}$ 和$\gamma _{i,1,{\text{s}}}^{}$ ,车辆遵从先到先服务的排队规则离开队列和站点车辆集合,驶入路段.2.4 路段模块
路段模块包含静态属性集、动态属性集和模块事件. 从连接站点
$i、j$ 的路段集合$ {B_{ij}} $ 中任取路段m.2.4.1 路段模块静态属性集
路段m的静态属性集
${Q_{m,{\text{p}}}}$ 可表示为式(9).Qm,p={σm,p,lm,p,wm,p,cm,p,vm,0,p,χm,p}, (9) cm,p=σm,plm,pwm,p, (10) 式中:
$ {\sigma _{m,{\text{p}}}} $ 为路段m的阻塞密度(辆/(km$\text{•}$ 车道));${l_{m,{\text{p}}}}$ 为路段长度(km);${w_{m,{\text{p}}}}$ 为路段m的单向车道数;${c_{m,{\text{p}}}}$ 为路段容量[25];${v_{m,0,{\text{p}}}}$ 为路段m中车辆的自由流速度,表示车辆相对密度为0时,路段中的车流行驶速度;${\chi _{m,{\text{p}}}}$ 为路段$m$ 下游设施类型,${\chi _{m,{\text{p}}}} = 1$ 表示下游设施仍为路段,${\chi _{m,{\text{p}}}} = 0$ 表示下游设施为站点.2.4.2 路段模块动态属性集
时段t 路段
$m$ 的动态属性集${D_{m,{\text{p}}}}$ 表示为式(11).\begin{split} & D_{m,{\rm{p}}}=\{ {E_{m,{\rm{p}}}(t),x_{m,{\rm{p}}}(t),η_{m,{\rm{p}}}(t),} {k_{m,{\rm{p}}}(t),\theta_{m,{\rm{p}}}(t),} \\ &\quad{ v_{m,{\rm{p}}}(x_{m,{\rm{p}}}(t)),\mu_{m,{\rm{p}}}(x_{m,{\rm{p}}}(t))} \},\end{split} (11) {k_{m,{\text{p}}}}(t) = {c_{m,{\text{p}}}}(t) (1 - {\eta _{m,{\text{p}}}}(t)) , (12) 式中:
${E_{m,{\text{p}}}}(t)$ 为时段t在路段m内共享车辆的集合,$ \left| {{E_{m,{\text{p}}}}(t)} \right| = {x_{m,{\text{p}}}}(t)$ ,表示共享车辆数;${\eta _{m,{\text{p}}}}(t)$ 为路段m在引入共享汽车前其他交通流的道路占用率,${\eta _{m,{\text{p}}}}(t) \in \left[ {0,1} \right]$ ;${k_{m,{\text{p}}}}(t)$ 为路段m在时段t的剩余容量;${\theta _{m,{\text{p}}}}(t)$ 为时段t来自公共交通的用户占比;${v_{m,{\text{p}}}}({x_{m,{\text{p}}}}(t))$ 为路段m内共享车辆的平均速度;$ {\mu _{m,{\text{p}}}}({x_{m,{\text{p}}}}(t)) $ 为时段t路段m的服务率.2.4.3 车路交互作用机制
汽车共享系统的引入会为道路资源分配带来新的动态演变,而道路拥堵情况也会动态影响汽车共享系统的运营. 基于Hu等[25]提出的速度指数模型,采用状态相关的速度模型刻画车路交互作用,见式(13)~(17).
{v_{m,{\text{p}}}}({x_{m,{\text{p}}}}(t)) = \left\{ \begin{aligned} &{v_{m0,{\text{p}}}} \exp \left[ { - {{\left( {{{{f_{m,{\text{p}}}}(t)} \mathord{\left/ {\vphantom {{{f_{m,{\text{p}}}}(t)} {{\beta _{m,{\text{p}}}}}}} \right. } {{\beta _{m,{\text{p}}}}}}} \right)}^{{\gamma _{m,{\text{p}}}}}}} \right],\\ &\quad{f_{m,{\text{p}}}}(t) \leqslant 1 , \\ &{v_{m0,{\text{p}}}} \exp \left[ { - {{\left( {{1 \mathord{\left/ {\vphantom {1 {{\beta _{m,{\text{p}}}}}}} \right. } {{\beta _{m,{\text{p}}}}}}} \right)}^{{\gamma _{m,{\text{p}}}}}}} \right]{\text{ }},\\ &\quad{f_{m,{\text{p}}}}(t) > 1 , \end{aligned} \right. (13) {f_{m,{\text{p}}}}(t) = {\eta _{m,{\text{p}}}}(t) + {{{x_{m,{\text{p}}}}(t) {\theta _{m,{\text{p}}}}(t)} \mathord{\left/ {\vphantom {{{x_{m,{\text{p}}}}(t) {\theta _{m,{\text{p}}}}(t)} {{c_{m,{\text{p}}}}}}} \right. } {{c_{m,{\text{p}}}}}} , (14) \begin{split} &{\gamma _{m,{\text{p}}}} = {\ln \left[ {{{\ln ({{{v_{m,1,{\text{p}}}}} / {{v_{m,0,{\text{p}}}}}})} / {\ln ({{{v_{m,2,{\text{p}}}}} / {{v_{m,0,{\text{p}}}}}})}}} \right]} /\\ &\quad{\ln ({{{b_{m,1,{\text{p}}}}} / {{b_{m,2,{\text{p}}}}}})} , \end{split} (15) {\beta _{m,{\text{p}}}} = {{{b_{m,1,{\text{p}}}}} / { {\ln {{({{{v_{m,0,{\text{p}}}}} /{{v_{m,1,{\text{p}}}}}})}^{{1 / {{\gamma _{m,{\text{p}}}}}}}}} }} , (16) {\mu _{m,{\text{p}}}}({x_{m,{\text{p}}}}(t)) = {x_{m,{\text{p}}}}(t) {{{v_{m,{\text{p}}}}({x_{m,{\text{p}}}}(t))} \mathord{\left/ {\vphantom {{{v_{m,{\text{p}}}}({x_{m,{\text{p}}}}(t))} {{l_{m,{\text{p}}}}}}} \right. } {{l_{m,{\text{p}}}}}} , (17) 式中:fm,p(t)为车辆相对密度;
$ {\gamma _{m,{\text{p}}}} $ 和$ {\beta _{m,{\text{p}}}} $ 为速度指数模型的两个标定参数;vm,1,p和vm,2,p为标准点,分别表示车辆相对密度$ {\text{ }}{f_{m,{\text{p}}}}(t) $ 取值为${b_{m,1,{\text{p}}}}$ 和${b_{m,2,{\text{p}}}}$ 时路段m中的车辆行驶速度.式(14)、(15)表明共享车辆的行驶速度取决于道路占用率,且只有来自公共交通的用户会增加道路占用率,进而加剧道路拥堵,因为来自非公共交通(私家车等)的汽车共享服务需求只是实现了交通工具的转移,并未增加道路的实际占用率.
2.4.4 路段模块事件
事件触发流程如图3所示.
路段模块中事件触发过程如下:
1) 到达路段
步骤1 车辆驶入路段,触发
${\beta _{m,1,{\text{p}}}}$ 更新时间戳;步骤2 触发
${\beta _{m,2,{\text{p}}}}$ ,${E_{m,{\text{p}}}}(t) \cup \left\{ e \right\}$ →${E_{m,{\text{p}}}}(t) $ 表示车辆e加入路段车辆集合${E_{m,{\text{p}}}}(t)$ 后更新集合${E_{m,{\text{p}}}}(t)$ .2) 接受服务
步骤1 执行
${\beta _{m,3,{\text{p}}}}$ ,计算车辆行驶速度$ {v_{m,{\text{p}}}} ({x_{m,{\text{p}}}}(t)) $ ;步骤2 在下一个时间戳预订触发
${\beta _{m,4,{\text{p}}}}$ .3) 离开路段
步骤1 执行
${\beta _{m,5,{\text{p}}}}$ ,判断下游设施类型;步骤2 触发
${\beta _{m,6,{\text{p}}}}$ ,判断下游设施是否有剩余容量,若没有剩余容量,车辆将在路段m内排队等待,若有剩余容量则触发${\beta _{m,2,{\text{P}}}}$ 更新路段内车辆集合:${E_{m,{\text{p}}}}(t)\backslash \left\{ e \right\}$ →${E_{m,{\text{p}}}}(t) $ ,表示将车辆e从站点车辆集合中${E_{m,{\text{p}}}}(t)$ 删除后更新集合${E_{m,{\text{p}}}}(t)$ .路段模块事件嵌入了拥挤传播机制:车辆驶离路段前,需触发事件
${\beta _{m,6,{\text{p}}}}$ 和${\beta _{m,7,{\text{p}}}}$ 判断下游设施类型及剩余容量. 若下游设施严重拥堵(站点无剩余停车位或道路无剩余空间),触发${\beta _{m,4,{\text{p}}}}$ ,共享车辆加入排队集合,在路段巡游并继续占用道路空间,下游设施的拥挤现象传播至上游路段. 直至下游设施有剩余空间时触发${\beta }_{m,5,\text{p}}$ 和${\gamma _{m,1,{\text{p}}}}$ ,车辆遵从先到先服务的排队规则,离开队列和路段车辆集合,进入下游设施.2.5 性能指标
本文使用5个性能指标评估汽车共享系统的服务水平和运行效率.
1) 系统服务率
系统服务率为单日完成的订单总数在用户实际出行需求总数中的占比.
2) 订单流失率
订单流失率为由于站点无车可用而流失的订单总数在用户出行需求总数中的占比.
3) 汽车共享系统单日总利润
汽车共享系统收入为运营周期
$ T $ 内的租车费用,成本$ Z $ 包括油耗、车辆固定成本和停车位成本等,如式(18)所示.Z = \sum\limits_i {\sum\limits_j {\sum\limits_{\Delta t} {\left[{p_{ij}}(t) - {C_{\rm{G}}}\right] {x_{m,{\text{P}}}}(t) \Delta t - } } } \sum\limits_i {{C_{\rm{p}}} {c_{i,{\text{s}}}} - F {C_{\rm{F}}}} , (18) 式中:
$ \Delta t $ 为时间步长,$\Delta t \in \left\{ {1,2,\cdots,T} \right\}$ ;${C_{\rm{G}}}$ 为共享车辆每分钟的油耗成本;$F$ 为汽车共享系统的车队规模;${C_{\rm{F}}}$ 为单位共享车辆的日固定成本;${C_{\rm{p}}}$ 为单个停车位的日固定成本.4) 车辆利用率
车辆利用率为用户使用车辆的总时长在所有车辆可供使用的总时长中的占比.
5) 虚拟空间存储车辆占比
虚拟空间存储车辆占比的不同反映了模型对溢出车辆处理方式的不同.
3. 案例分析
3.1 案例背景
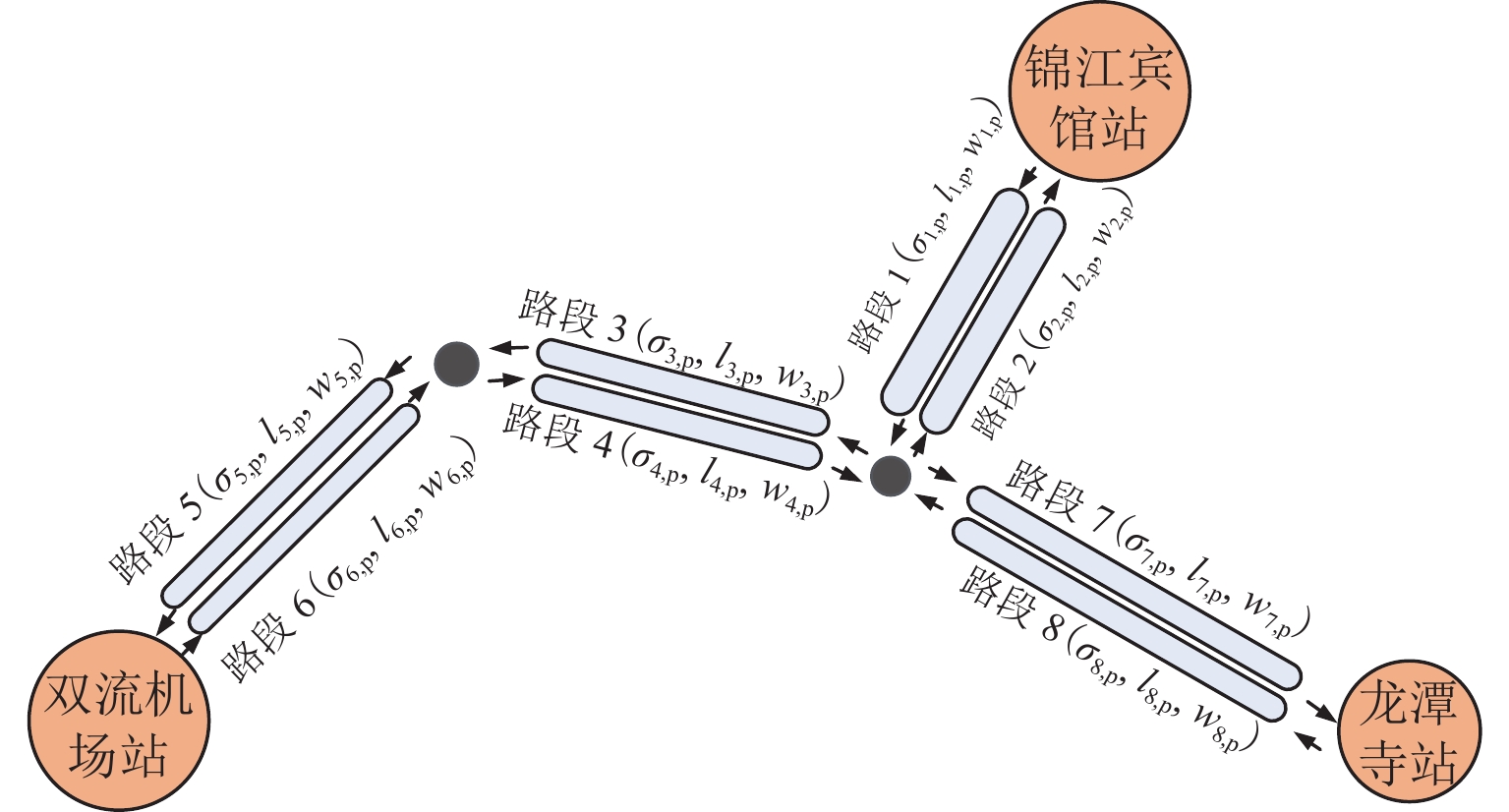
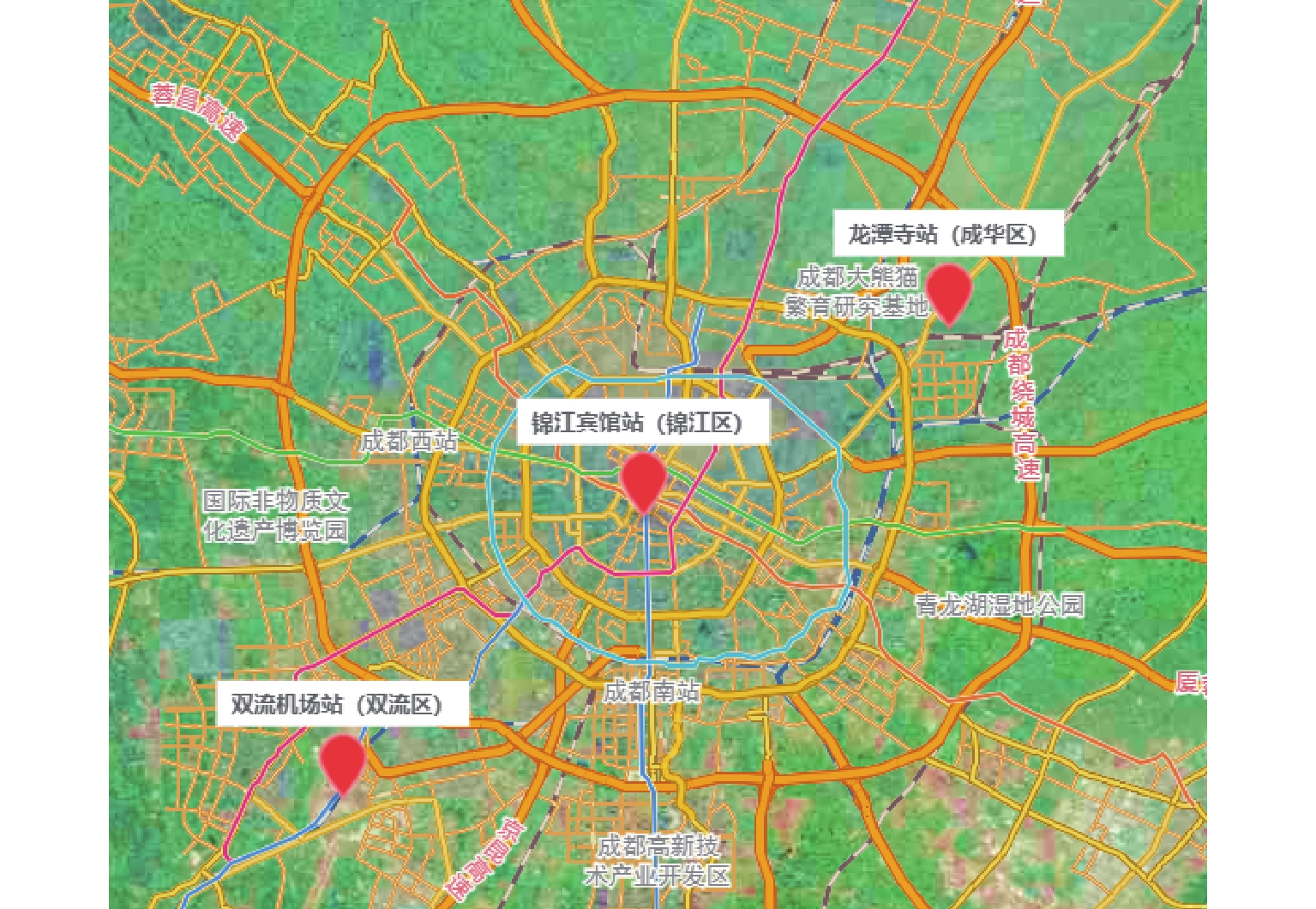
基于成都市EVCARD的用户出行OD数据对站点的小规模汽车共享系统展开仿真建模分析,设定运营时间为6 :00—24 :00. 所选取站点用车需求较大,且时空不均衡性显著,站点分布如图4所示. 锦江宾馆站位于成都的中央商务区,双流机场站和龙潭寺站位于高密度居民住宅区. 站点间出行需求以通勤为主,有明显的时变性和潮汐现象. 系统运营中站点车辆积压、部分路段拥堵现象明显.
根据Hu等[25]对道路交通流的研究,状态相关的速度模型中3个标准点取值如表1所示.
表 1 速度模型标准点取值Table 1. Representative point values of velocity model相对密度 平均行驶速度/(km•min−1) ${\text{ } }{f_{m,{\text{p} } } }(t){\text{ = } }0$ ${v_{m,0,{\text{p} } } } = 1.00$ ${f_{m,{\text{p} } } }(t) = {b_{m,1,{\text{p} } } }(t){\text{ = } }0.1$ ${v_{m,1,{\text{p} } } } = 0.55$ ${f_{m,{\text{p} } } }(t) = {b_{m,2,{\text{p} } } }(t){\text{ = } }0.2$ ${v_{m,2,{\text{p} } } } = 0.40$ 基于实际路网,将各站点间的路径划分为8条单向路段. 搭建汽车共享系统排队网络(如图5),路段m的阻塞密度
${\sigma _{m,{\text{p}}}}$ 、长度${l_{m,{\text{p}}}}$ 和车道数${w_{m,{\text{p}}}}$ 通过百度API和实际路网数据获取. 本文进行以下实验:1) 将考虑拥挤传播的排队网络模型(拥挤传播排队模型)与Hu等[13]提出的站点、路段有无限容量的混合排队网络模型(无穷排队模型)运用于本案例,对比分析两种模型的求解结果;
2) 基于不同的场景,研究拥挤传播现象对汽车共享系统实际运营的影响.
3.2 拥挤传播排队模型与无穷排队模型求解结果对比分析
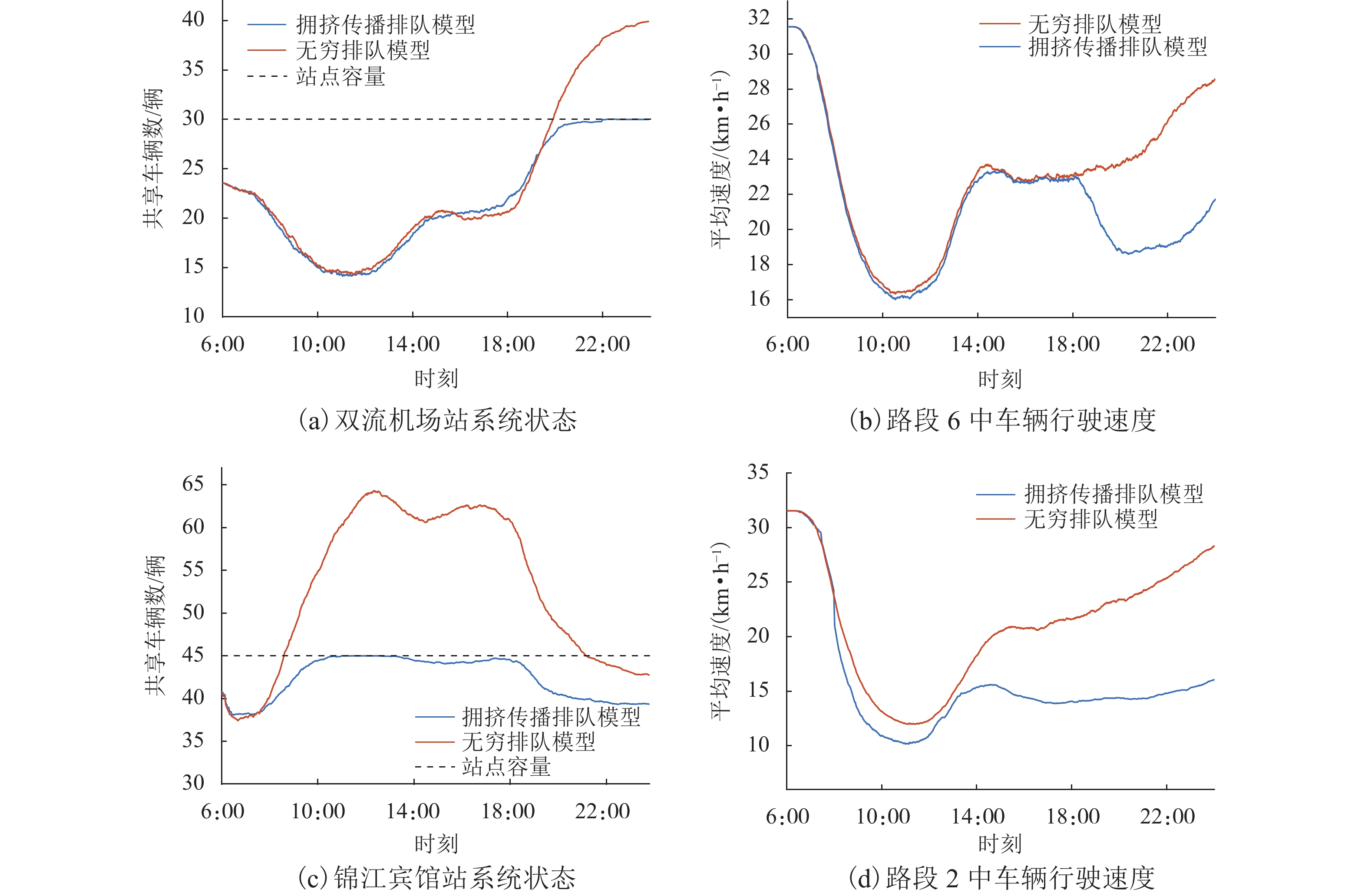
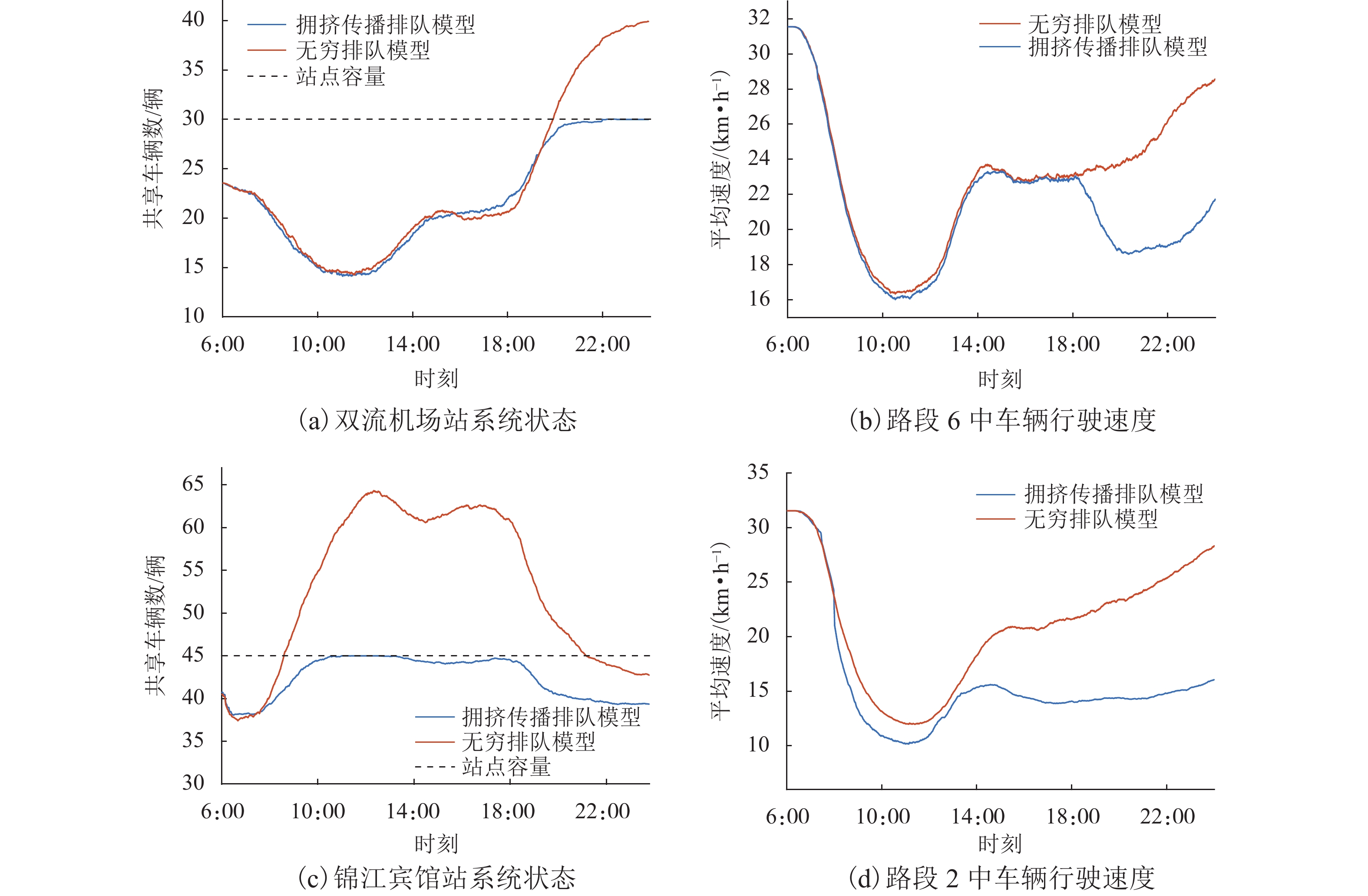
图6展示了双流机场站和锦江宾馆站在运营时段的系统状态和站点上游路段车辆的行驶速度.
由图6(a)、(b)可知:两种模型在6 :00—16 :00描述的双流机场站的运行过程基本一致,表明这一时段站点供需平衡;晚高峰时期需求和用车时间呈现明显的动态性,大量车辆向双流机场站附近的居民住宅区转移,18 :00—24 :00期间站点车辆溢出,还车困难;无穷排队模型将溢出车辆存于虚拟空间,拥挤传播排队模型的溢出车辆在上游路段巡游,溢出车辆在上游路段大量积压,导致其拥挤加剧,该时段拥挤传播排队模型的平均车速低于无穷排队模型.
由图6(c)可知:由于无穷排队模型站点车辆数为实际站点与虚拟空间车辆数之和,因此,锦江宾馆站的系统状态远超其停车泊位数;拥挤传播排队模型的溢出车辆在上游路段巡游,站点的系统状态不会超出停车容量. 由图6(d)可知:路段2为其余两个站点到锦江宾馆站的共用路段,在高峰时期通行能力十分有限;锦江宾馆站车辆溢出时,拥挤传播排队模型的巡游车辆加剧了路段2的拥堵,车辆行驶速度保持在较低水平;无穷排队模型忽略了溢出车辆对上游路段车辆平均速度的影响,路网流通性更好,车辆平均速度始终高于拥挤传播排队模型.
两种模型得到的性能指标如表2所示.
表 2 两种排队模型的性能指标求解结果Table 2. Solved performance indicators of two queuing models模型 系统服务率/% 车辆利用率/% 虚拟空间
存储车辆
占比率/%订单流失率/% 利润/
(元•d−1)拥挤传播
排队模型78.50 23.78 0 21.50 4081.50 无穷排队模型 91.33 31.09 34.28 8.67 5139.60 表2结果表明,无穷排队模型的日利润、系统服务率和车辆利用率均高于拥挤传播排队模型,订单流失率低了12.83%,但无穷排队模型的虚拟空间存储车辆占比高达34.28%,且忽略了溢出车辆对系统运行的影响,表明无穷排队模型的运营场景趋于理想化,高估了日利润和系统服务率,不符合实际运营过程.
3.3 不同场景下系统性能指标分析
保持其他参数不变,分别设定不同的场景,对比分析两种排队模型的各项性能指标.
3.3.1 不同需求场景下系统运行分析
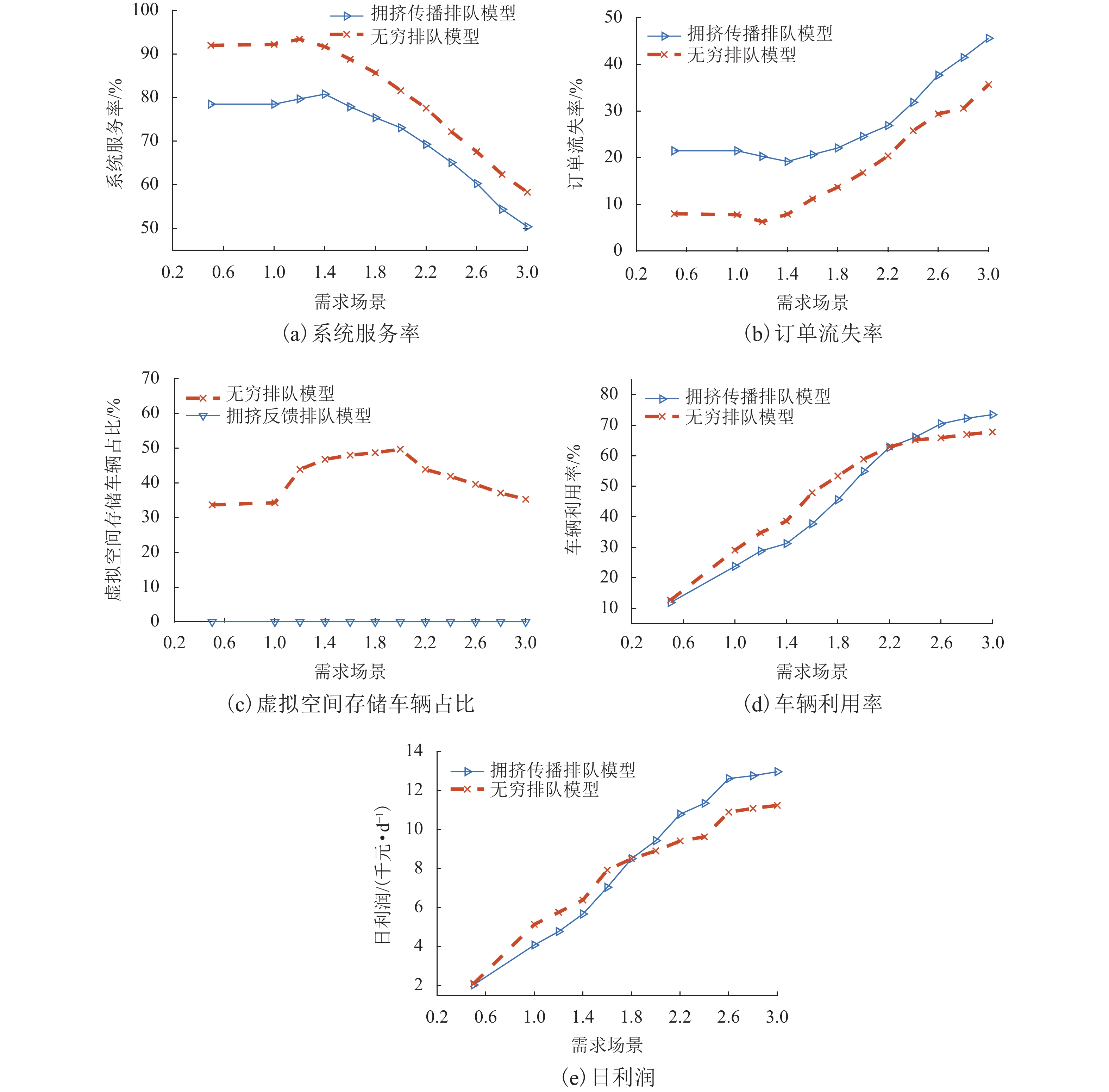
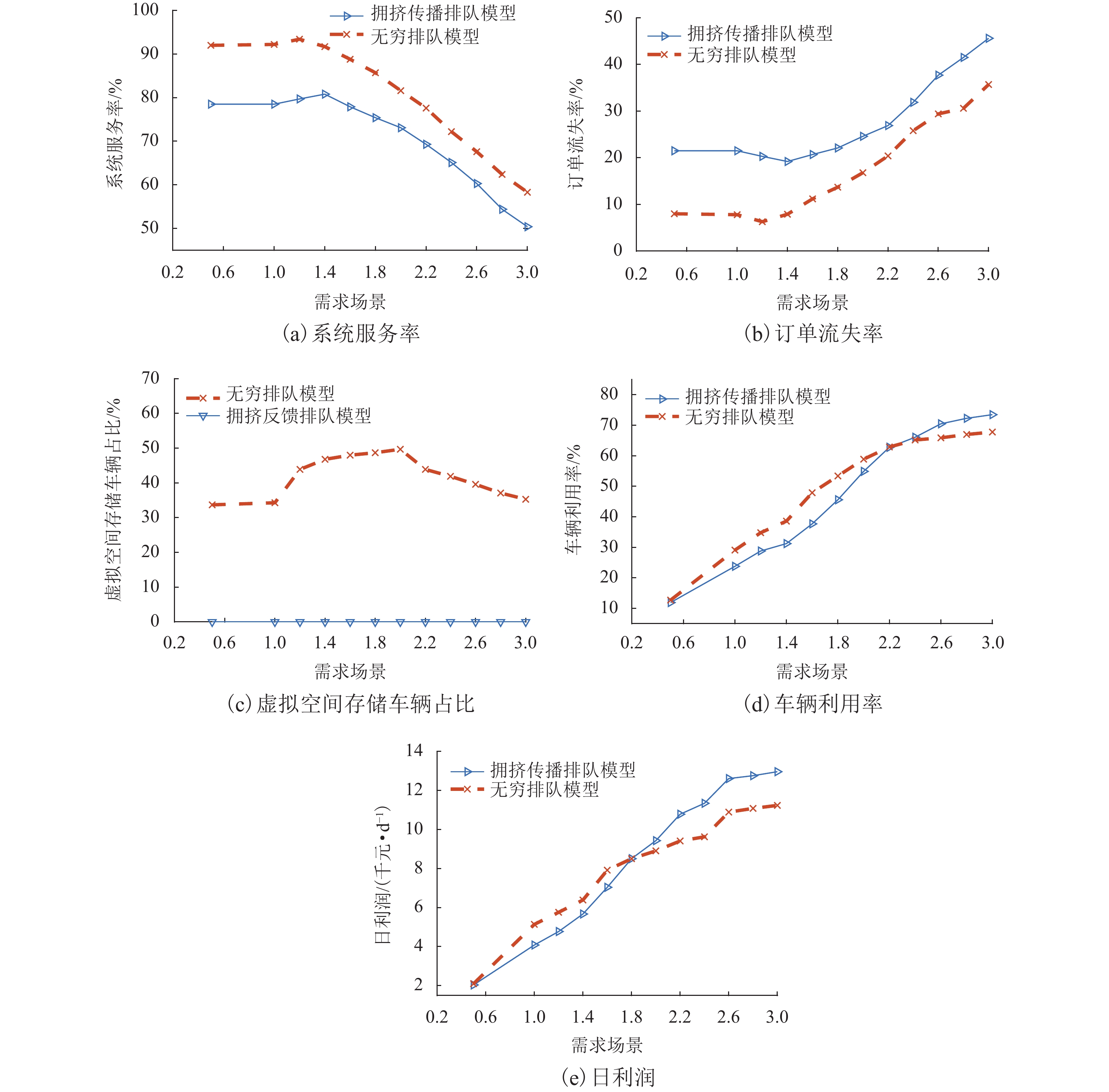
设置不同的需求场景,研究出行需求对汽车共享系统运行的影响,如图7所示. 随着出行需求增加,用户需求的时空不均衡性更加显著,拥挤传播现象使系统服务率下降9.3%~16.9%,订单流失率增加6.1%~26.8%.
由图7(a)、(b)可知:无穷排队模型忽略了溢出车辆的影响,系统流通性更好,系统服务率始终高于拥挤传播排队模型,最大差异达16.70%;拥挤传播排队模型的订单流失率始终高于无穷排队模型;当出行需求处于1.0倍~1.4倍时,系统服务率随需求的增加而升高. 需求进一步增加时,系统供不应求加剧,服务率下降,订单流失率增加,在出行需求超过2.0倍时,变化趋势更加显著.
由图7(c)可知:由于拥挤传播排队模型的溢出车辆不会进入“虚拟空间”,故虚拟空间存储车辆占比恒为0;无穷排队模型中,在需求场景为当前需求的2.0倍时,虚拟空间存储车辆占比高达49.7%.
由图7(d)可知:车辆利用率和日利润均随用户需求的增加而增加; 当需求在0.5倍~2.2倍时,无穷排队模型系统行程服务数更多,车辆利用率更高; 当需求超过2.2倍时,拥挤传播现象加剧,拥挤传播排队模型的车辆利用率高于无穷排队模型.
由图7(e)可知:当出行需求在0.5倍~1.8倍时,无穷排队模型可获更高利润;随后,行程时间的不断增加使拥挤传播排队模型产生的收益更高.
3.3.2 不同道路占用率下系统运行分析
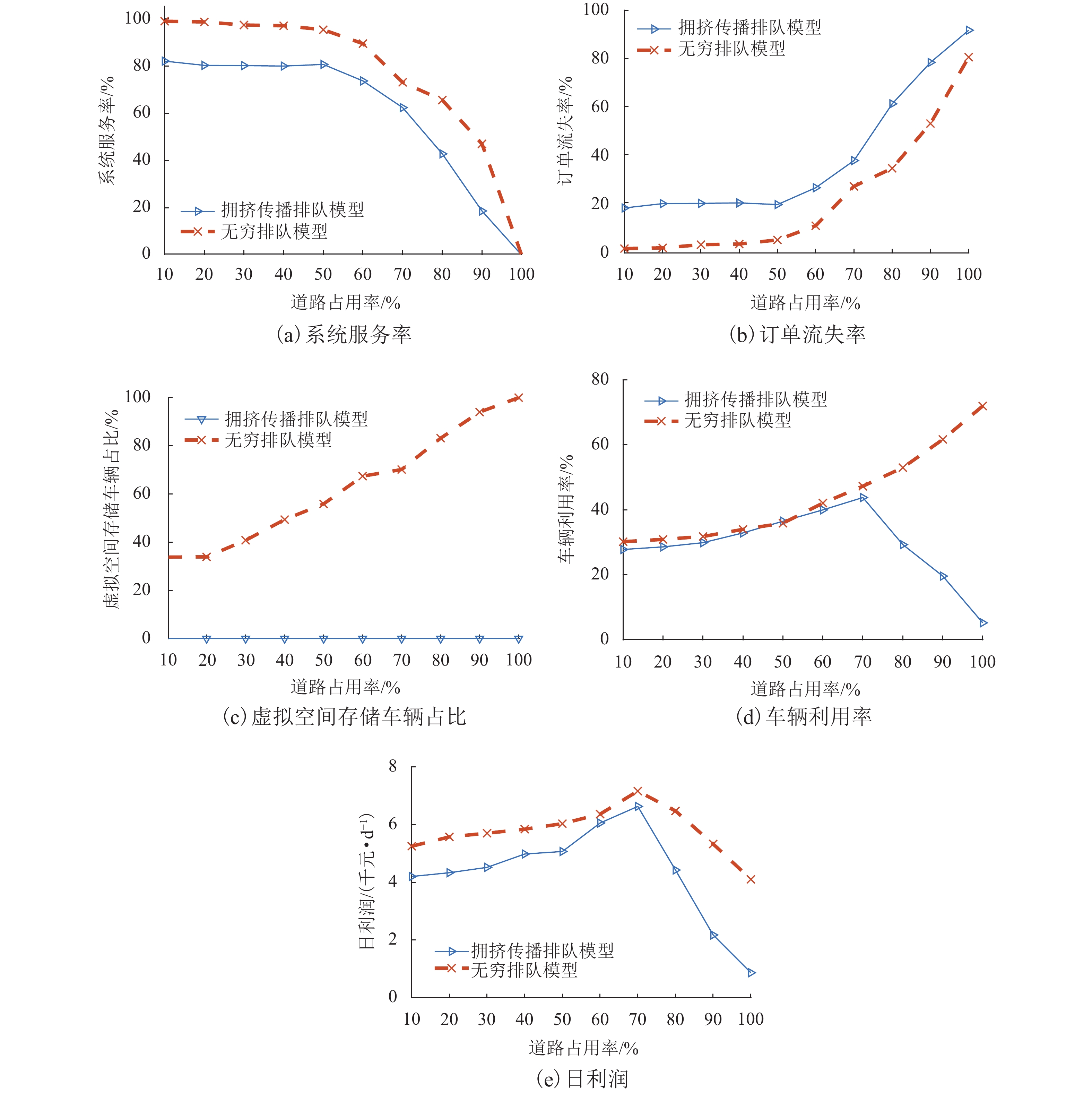
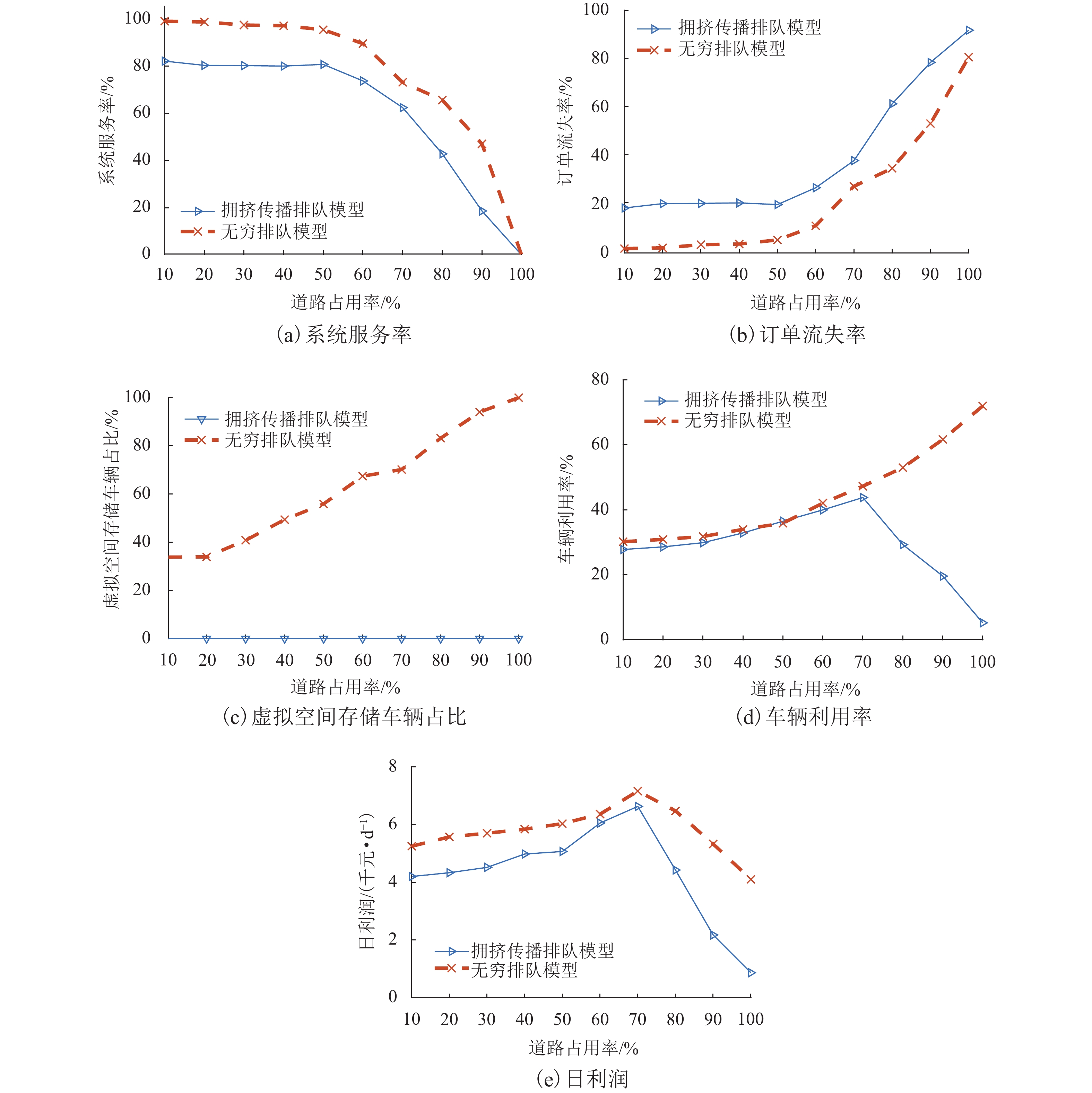
设置不同的道路拥堵场景,研究道路拥堵情况对汽车共享系统运行的影响,如图8所示.
由图8(a)、(b)可知:随着道路占用率增加,订单流失率升高,系统服务率降低;道路占用率高于60%时,变化趋势更加明显;无穷排队模型的系统服务率始终高于拥挤传播排队模型,且对应的订单流失率更低.
由图8(c)可知:无穷排队模型道路占用率较低时车辆溢出主要体现在站点层面,随着道路占用率升高,路段层面拥挤传播现象加剧,在道路占用率为90%时,虚拟空间存储车辆占比达到了94.0 %.
由图8(d)、(e)可知:道路占用率小于70%时,车辆利用率和日利润随着道路占用率的升高而升高; 道路占用率为70%时,两种模型都可实现最大收益; 道路占用率超过70%时拥挤传播排队模型产生大量的巡游车辆,系统服务率明显下降;大量订单流失导致系统日利润显著下降;无穷排队模型的车辆利用率增加,但系统利润随之降低; 在道路完全拥堵时,两种模型的系统日利润相差达3238.3元.
3.3.3 不同转运比例下系统运行分析
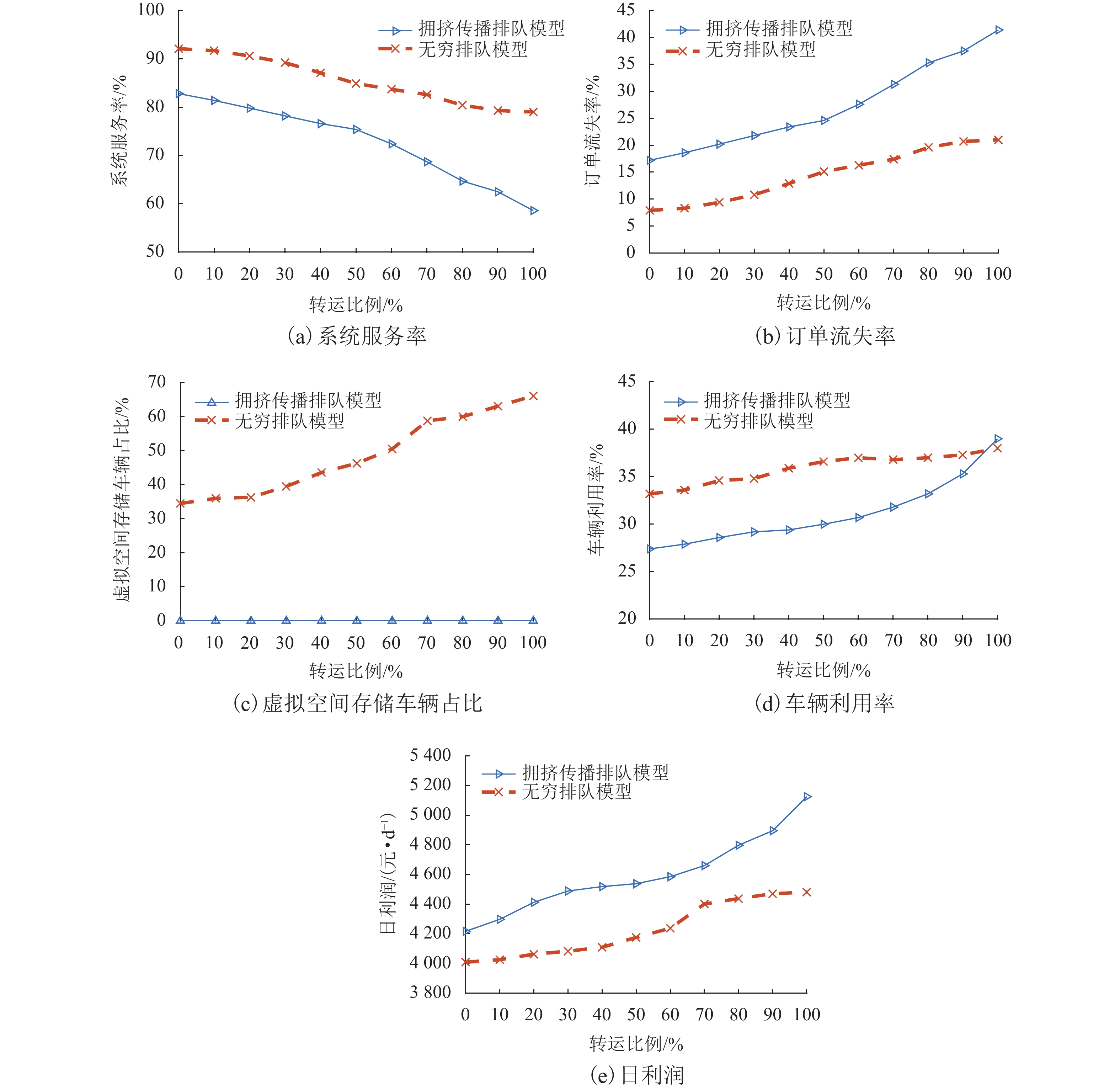
转运比例表示来自公共交通的用户占比. 图9表明车辆利用率、订单流失率和日利润均随转运比例的增加而升高,而系统服务率呈相反趋势. 转运比例对无穷排队模型各性能指标的影响小于拥挤传播排队模型.
由图9可知:两种模型的系统服务率均随转运比例的升高而降低;随着转运比例升高,车辆利用率和订单流失率会随之升高,在转运比例小于60%时,变化幅度较小; 转运比例进一步升高时,道路拥挤加剧,用户行程时间增加,拥挤传播模型的车辆利用率显著增加,订单流失率增加了13.8%;转运比例从70%升高至100%时,系统服务率会降低14.8%;系统利润会随着转运比例的增加而增加,以拥挤传播排队系统为例,系统日利润增加了907.7元,但转运比例过高会抑制系统服务率的升高,不利于汽车共享系统的可持续发展.
4. 结 论
1) 用户需求有明显时空不均衡性时,拥挤传播现象使系统服务率下降9.3%~16.9%,订单流失率增加6.1%~26.8%,无穷排队模型忽略了溢出车辆对系统运行的影响,高估了系统服务率,拥挤传播排队模型更能反映汽车共享系统的实际运营活动.
2) 用户出行需求的适当增加,可以提高车辆利用率并实现最大收益;但出行需求过大会导致订单流失率显著增加和系统服务率快速下降,不利于系统运营质量和服务水平的提升.
3) 适度提升道路占用率可增加运营收入,道路占用率为70% (路网中度拥堵)时可实现最大收益.
4) 转运比例从70%升高至100%时,系统服务率会降低14.8%;共享汽车渗透率过高会加剧路网拥堵,不利于汽车共享系统的有效运营和可持续发展.
后续研究可考虑加入实际运营决策(定价和车辆调度策略),研究拥挤传播对中大型规模汽车共享系统的影响;考虑到用户会根据实时拥堵情况更改还车站点或变更出行路径,后续可在离散事件仿真模型中嵌入多项Logit模型,研究在考虑出行时间和成本的情况下,用户在出行路径、取还车站点之间的动态随机的选择行为;此外,在获取到共享汽车更全面运营数据的前提下,可将仿真结果与实际数据进行对比分析,进一步验证该模型的有效性.
-
表 1 速度模型标准点取值
Table 1. Representative point values of velocity model
相对密度 平均行驶速度/(km•min−1) ${\text{ } }{f_{m,{\text{p} } } }(t){\text{ = } }0$ ${v_{m,0,{\text{p} } } } = 1.00$ ${f_{m,{\text{p} } } }(t) = {b_{m,1,{\text{p} } } }(t){\text{ = } }0.1$ ${v_{m,1,{\text{p} } } } = 0.55$ ${f_{m,{\text{p} } } }(t) = {b_{m,2,{\text{p} } } }(t){\text{ = } }0.2$ ${v_{m,2,{\text{p} } } } = 0.40$ 表 2 两种排队模型的性能指标求解结果
Table 2. Solved performance indicators of two queuing models
模型 系统服务率/% 车辆利用率/% 虚拟空间
存储车辆
占比率/%订单流失率/% 利润/
(元•d−1)拥挤传播
排队模型78.50 23.78 0 21.50 4081.50 无穷排队模型 91.33 31.09 34.28 8.67 5139.60 -
[1] YE J H, WANG D G, LI X, et al. Assessing one-way carsharing’s impacts on vehicle ownership: evidence from Shanghai with an international comparison[J]. Transportation Research Part A: Policy and Practice, 2021, 150: 16-32. doi: 10.1016/j.tra.2021.05.012 [2] 张淼,惠英,汪鸣泉. 汽车共享对城市温室气体排放的影响[J]. 中国人口 · 资源与环境,2012,22(9): 48-53. doi: 10.3969/j.issn.1002-2104.2012.09.008ZHANG Miao, HUI Ying, WANG Mingquan. Urban greenhouse gas emission of car sharing[J]. China Population, Resources and Environment, 2012, 22(9): 48-53. doi: 10.3969/j.issn.1002-2104.2012.09.008 [3] XU M, MENG Q, LIU ZY. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment[J]. Transportation Research Part B:Methodological, 2018, 111: 60-82. doi: 10.1016/j.trb.2018.03.001 [4] BAPTISTA P, MELO S, ROLIM C. Car sharing systems as a sustainable transport policy: a case Study from Lisbon, Portugal[M]//ATTARD M, SHIFTAN Y. Transport and Sustainability. [S.l.]: Emerald Group Publishing Limited, 2015: 205-227. [5] NANSUBUGA B, KOWALKOWSKI C. Carsharing: a systematic literature review and research agenda[J]. Journal of Service Management, 2021, 32(6): 55-91. doi: 10.1108/JOSM-10-2020-0344 [6] 曹可心,邓羽. 城市共享汽车分布的时空演变及影响因素研究:以北京市主城区为例[J]. 地理科学,2021,41(10): 1792-1801.CAO Kexin, DENG Yu. Spatial-temporal characteristics and impacting factors of carsharing in Beijing[J]. Scientia Geographica Sinica, 2021, 41(10): 1792-1801. [7] 伊二妮. 基于排队论的汽车共享服务系统车辆配置优化研究[D]. 青岛: 山东科技大学, 2018. [8] EFTHYMIOU D, ANTONIOU C, WADDELL P. Factors affecting the adoption of vehicle sharing systems by young drivers[J]. Transport Policy, 2013, 29: 64-73. doi: 10.1016/j.tranpol.2013.04.009 [9] 刘向,洪林,王宁,等. 基于时空消耗的共享汽车拥堵治理效用研究[J]. 汽车工程学报,2020,10(5): 335-341. doi: 10.3969/j.issn.2095-1469.2020.05.04LIU Xiang, HONG Lin, WANG Ning, et al. Research on the effect of car-sharing on traffic congestion management based on spatiotemporal consumption[J]. Chinese Journal of Automotive Engineering, 2020, 10(5): 335-341. doi: 10.3969/j.issn.2095-1469.2020.05.04 [10] 高永,安健,全宇翔. 网络约租车对出行方式选择及交通运行的影响[J]. 城市交通,2016,14(5): 1-8. doi: 10.13813/j.cn11-5141/u.2016.0501GAO Yong, AN Jian, QUAN Yuxiang. The impact of APP-based car sharing on travel mode shift and transportation operation performance[J]. Urban Transport of China, 2016, 14(5): 1-8. doi: 10.13813/j.cn11-5141/u.2016.0501 [11] 张三省,苏倩,张俊青. 基于系统动力学的网约车政策对城市交通的影响研究[J]. 天津大学学报(社会科学版),2019,21(6): 494-502.ZHANG Sanxing, SU Qian, ZHANG Junqing. Analysis of the influence of ride-hailing policy on urban traffic based on system dynamics[J]. Journal of Tianjin University (Social Sciences), 2019, 21(6): 494-502. [12] ZHAO M, LI X, YIN J, et al. An integrated framework for electric vehicle rebalancing and staff relocation in one-way carsharing systems: model formulation and Lagrangian relaxation-based solution approach[J]. Transportation Research Part B: Methodological, 2018, 117: 542-572. doi: 10.1016/j.trb.2018.09.014 [13] HU L, LIU Y. Joint design of parking capacities and fleet size for one-way station-based carsharing systems with road congestion constraints[J]. Transportation Research Part B: Methodological, 2016, 93: 268-299. doi: 10.1016/j.trb.2016.07.021 [14] DENG Y H, CARDIN M A. Integrating operational decisions into the planning of one-way vehicle-sharing systems under uncertainty[J]. Transportation Research Part C: Emerging Technologies, 2018, 86: 407-424. doi: 10.1016/j.trc.2017.11.018 [15] KASPI M, RAVIV T, TZUR M. Parking reservation policies in one-way vehicle sharing systems[J]. Transportation Research Part B: Methodological, 2014, 62: 35-50. doi: 10.1016/j.trb.2014.01.006 [16] 马舒予,胡路,吴佳媛,等. 共享电动汽车系统车队规模与停车泊位数优化[J]. 交通运输工程与信息学报,2022,20(3): 31-42.MA Shuyu, HU Lu, WU Jiayuan, et al. Fleet size and parking capacity optimization of electric carsharing system[J]. Journal of Transportation Engineering and Information, 2022, 20(3): 31-42. [17] 蒋阳升,李衍,李皓,等. 基于模块化仿真的共享汽车联合调度优化[J]. 西南交通大学学报,2023,58(1): 74-82. doi: 10.3969/j.issn.0258-2724.20210083JIANG Yangsheng, LI Yan, LI Hao, et al. Optimization for joint relocation of carsharing based on modular simulation[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 74-82. doi: 10.3969/j.issn.0258-2724.20210083 [18] PARK S, YU W. Analysis of system parameters for one-way carsharing systems[J]. Transportation Letters: the International Journal of Transportation Research, 2021,14(3): 1-11. [19] LI H B, ZHU Y C, CHEN Y X, et al. The object-oriented discrete event simulation modeling: a case study on aircraft spare part management[C]//2015 Winter Simulation Conference (WSC). Huntington Beach: IEEE, 2015: 3514-3525. [20] LI H B, ZHOU C H, LEE B K, et al. Capacity planning for mega container terminals with multi-objective and multi-fidelity simulation optimization[J]. IISE Transactions, 2017, 49(9): 849-862. doi: 10.1080/24725854.2017.1318229 [21] 张维戈,陈连福,黄彧,等. M/G/K排队模型在电动出租汽车充电站排队系统中的应用[J]. 电网技术,2015,39(3): 724-729. doi: 10.13335/j.1000-3673.pst.2015.03.021ZHANG Weige, CHEN Lianfu, HUANG Yu, et al. Application of M/G/K queuing model in queuing system of electric taxi charging station[J]. Power System Technology, 2015, 39(3): 724-729. doi: 10.13335/j.1000-3673.pst.2015.03.021 [22] 李仕鹏. 基于排队论的汽车共享优化设计[D]. 杭州: 杭州电子科技大学, 2013. [23] KENDALL D G. Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain[J]. The Annals of Mathematical Statistics, 1953, 24(3): 338-354 [24] ZEIGLER B P, PRAEHOFER H, KIM T G. Theory of modeling and simulation: integrating discrete event and continuous complex dynamic systems[M]. 2nd edition. Pittsburgh: Academic Press, 2000: 4-5. [25] HU L, ZHAO B, ZHU J X, et al. Two time-varying and state-dependent fluid queuing models for traffic circulation systems[J]. European Journal of Operational Research, 2019, 275(3): 997-1019. doi: 10.1016/j.ejor.2019.01.020 期刊类型引用(2)
1. 王世鹏,高姗,董现垒. 考虑共享单车接驳的共享汽车站点选址模型构建及应用研究. 经济问题. 2024(06): 108-114 .  百度学术
百度学术2. 侯博宇,刘洪汛,胡路. 自动驾驶电动共享车系统自适应集中调度优化. 交通运输工程与信息学报. 2024(04): 25-36 .  百度学术
百度学术其他类型引用(1)
-















 下载:
下载:




























































































































































 下载:
下载:
 百度学术
百度学术