Heat-Mass Transfer Test and Coupling Model of Sulfate Saline Soil
-
摘要:
为研究西部寒旱区盐渍土传热传质行为,首先,在无压补给条件下进行非饱和硫酸盐渍土的单向冻结试验;其次,考虑结晶潜热、结晶阻抗及结晶消耗等因素,建立非饱和硫酸盐渍土水-热-盐三场耦合模型;最后,采用COMSOL Multi-physics对耦合模型进行数值模拟,将模拟结果与试验数据进行对比分析. 研究结果表明:盐渍土内温度随冻结时长呈三阶段发展,逐步形成上冷下暖的温度梯度;在温度梯度和基质吸力双重驱动下,水、盐向冻结锋位置迁移,冻结锋位置水、盐含量出现峰值,峰值含水率、含盐量相较初始值分别增加2.16%和0.28%;冻结锋沿冻结温度线移动,形成冻结锋面;土柱最大冻结深度约为15.5 cm.
Abstract:In order to study the heat and mass transfer behavior of saline soil in western cold-arid regions, firstly unsaturated sulfate saline soil experienced unidirectional freezing tests with no pressure recharge. In addition, while the latent heat of crystallization, crystallization impedance and crystallization consumption are considered, a three-field coupling model of water-heat-salt for unsaturated sulfate saline soil is established. Finally, COMSOL Multi-physics is used to simulate the coupling model, the simulation results of which are then compared with the experimental data for analysis. The results show that the internal temperature of saline soils develops in three stages with the freezing time, gradually forming a temperature gradient of cold at the top and warm at the bottom. Driven by both temperature gradient and matrix suction, water and salt migrate to the freezing front position, and the water and salt contents reach peaks at the freezing front position, and compared with the initial values, the peak water content and salt content increase by 2.16% and 0.28%, respectively. The freezing front moves along the frozen temperature line, and forms a freezing front. The maximum freezing depth of soil column is about 15.5 cm.
-
盐渍土作为特殊土广泛分布于我国西部寒旱地区[1]. 在西部大幅温差条件下,盐渍土内水分、盐分会发生迁移、结晶及相变行为,不仅会引发土壤盐渍化、荒漠化等一系列环境问题[2-3],还会造成土体盐胀、冻胀等工程病害[4-7]. 因此,研究盐渍土水-盐迁移机制对解决西部生态问题和工程病害问题具有重要意义. 然而,盐渍土内部水盐迁移机制是一个复杂的热-水-盐耦合问题,水、盐结晶潜热对温度场均有较大影响,盐晶体的生成对液态水有消耗,相变作用下的负孔隙水压力是水盐迁移的主要驱动力,冰晶、盐晶体填充土体孔隙后对水盐迁移产生阻抗作用.
目前,土壤热-质迁移机制试验及耦合模型方面的研究取得了一定成果. 试验方面,罗金明等[8]通过野外定位观测,揭示了温度是土体水盐迁移的驱动力;周凤玺等[9]在封闭系统中研究正温梯度下非饱和盐渍土水盐迁移规律,结果表明,水分由高温端向低温端迁移,盐分由低温端向高温端迁移;Xu等[10]在封闭系统中对盐渍黄土进行的单向冻结试验表明,冻结区水盐含量均增大,峰值出现在冻结缘附近;Zhang等[11] 对饱和硫酸钠盐渍土在开放系统进行单向冻结试验,发现水、盐不断向冻结锋面迁移. 耦合模型方面,Richards[12]首次提出了多孔介质中水流运动的基本方程,标志着土壤水分定量研究的开始;Hansson等[13]基于Richards方程提出了一种求解非饱和冻土水-热耦合的新方法;Younes[14]建立了水-热-盐耦合模型,但没有考虑结晶潜热对耦合模型的影响;田亚护等[15]认为结晶潜热对模型传热影响较大;Xu等[16]考虑冰晶阻抗作用,建立了水-热-盐迁移模型,但忽略了芒硝结晶对水分场及温度场的影响; Wang等[17-19]研究显示,盐渍冻土中盐分结晶会消耗土壤液态水含量. 因此,建立模型时不可忽略结晶潜热、结晶阻抗及结晶消耗等因素.
综上所述,在冻结非饱和硫酸盐渍土热-质迁移机制方面的研究尚不完善. 多数研究未考虑结晶潜热及结晶消耗对传热传质的影响,并且很少考虑盐结晶累积而引起的阻抗效应;此外,多数研究在封闭系统中进行,然而地下水对土体中的热-质迁移影响较大,封闭系统并不能模拟地下水的影响. 鉴于此,本文采用无压补给下的单向冻结试验,探究非饱和硫酸盐渍土水盐迁移规律,并采用COMSOL Multi-physics对多物理场耦合模型进行数值模拟,比较模拟结果与试验数据,揭示非饱和盐渍冻土热-质迁移规律,以期为西部地区土壤盐渍化治理及工程建设提供参考.
1. 试验概况
1.1 试验土样力学指标测试
试验用土取自河西走廊张掖市郊区. 试验前对土壤进行脱盐,脱盐过程:将土壤碾碎装桶,加入纯净水,搅拌均匀,静置24 h后抽出上部清水,重复上述操作3~4次,最后将土壤进行摊铺风干. 对脱盐后土壤严格依据《公路土工试验规程》(JTG 3430—2020)[20]进行室内土工试验,得到物理力学指标值,见表1. 表中:Gs为土粒比重;ρmax为最大干密度;ωopt 为最优含水率;wL为液限;wP为塑限;Cu为不均匀系数;Cc为曲率系数.
表 1 脱盐后土壤物理力学指标Table 1. Physical and mechanical indexes of soil samples after desalination参数 Gs ρmax/(g·cm−3) ωopt/% wL/% wP/% Cu Cc 取值 2.70 1.78 13.7 25.35 12.62 5.29 0.59 1.2 水-热-盐迁移试验
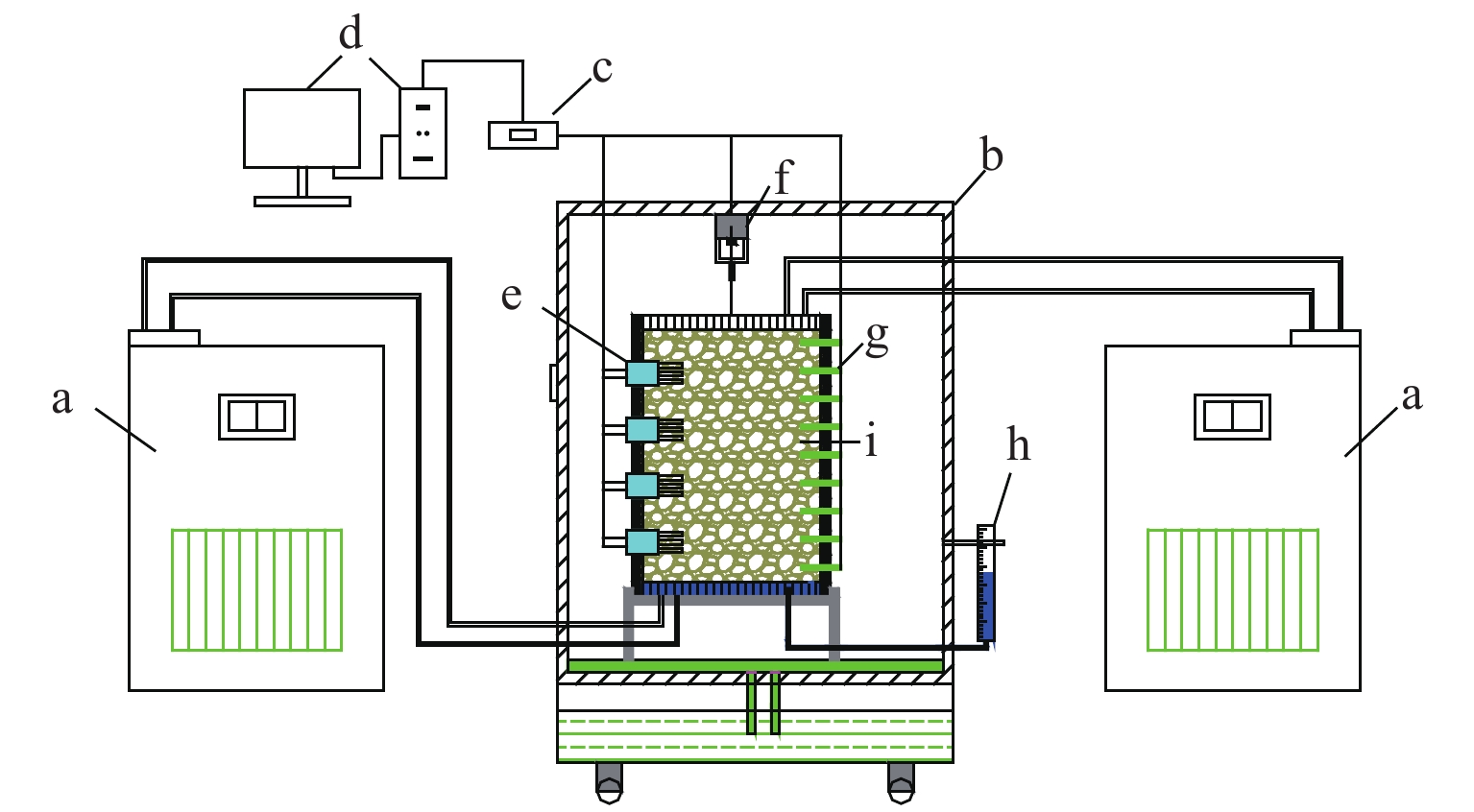
1) 测试系统:热-质迁移试验在TMS9018环境冻融循环系统中进行,包括温控箱、无压补水监测装置、传感器和数据采集装置三大部件. 其中,温控箱可控制顶板、底板及箱内温度,有效温控为−50~60 ℃;温度传感器间距2.5 cm,探针长度4.5 cm,入土深度2.5 cm,精度为 ±0.01℃;5TE水盐传感器间距2.5 cm,入土深度5.0 cm,体积含水率(VWC)精度为 ±1%,电导率精度为 ±0.01 S/m;采集仪为CR1000,每10 min记录一次,设备连接见图1.
2) 试验方案:盐渍土饱和度为72.5%,浓度为0.345 mol/kg,压实度为90%,试样尺寸直径15 cm、高24 cm,补给溶液浓度为0.345 mol/kg,盐渍土柱初试温度为22 ℃,设顶板温度为−14 ℃,底板温度为4 ℃,环境箱内温度为4 ℃. 冻结时长设为96 h[1,11],结果分析时取盐渍土柱底端为坐标原点.
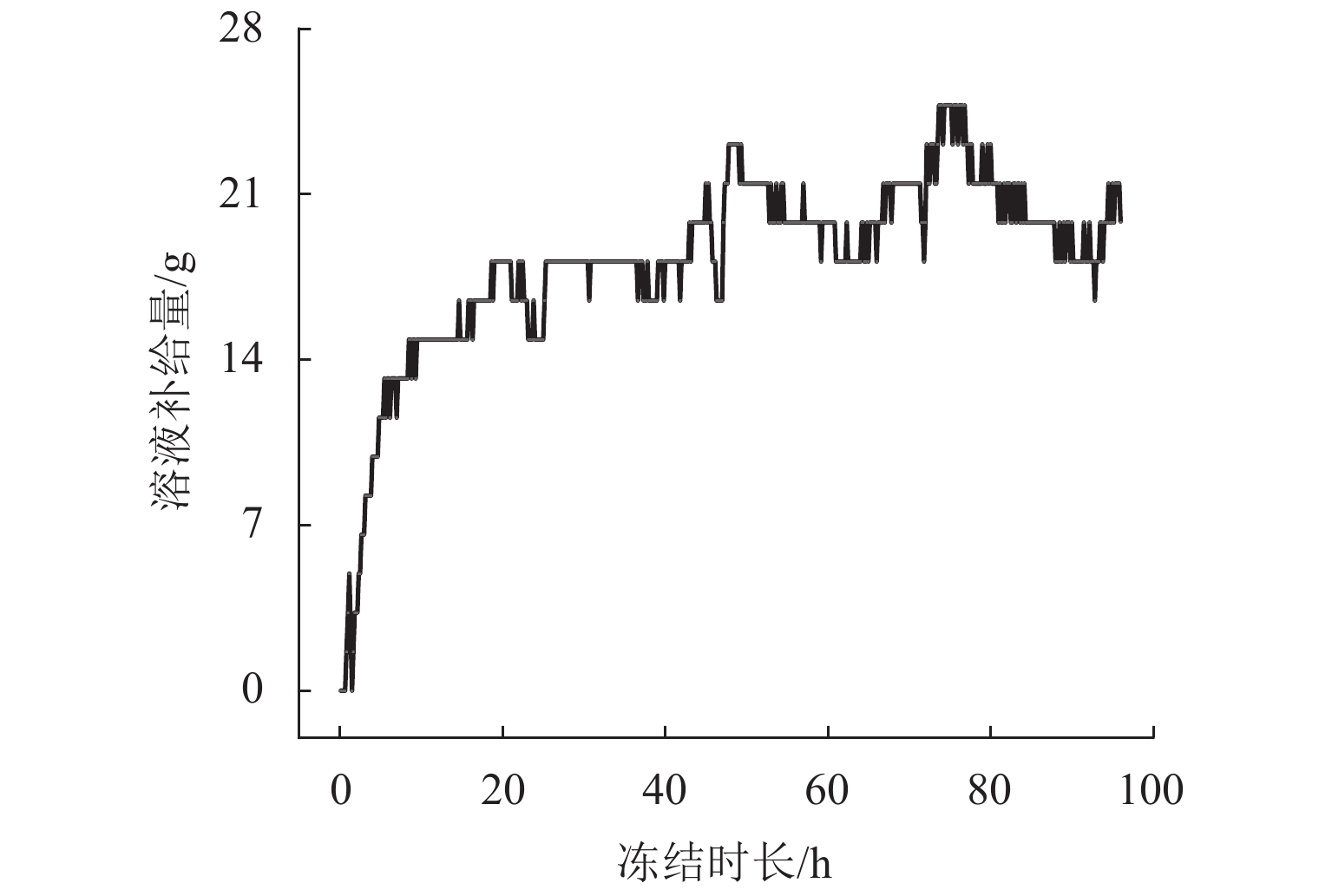
3) 试验过程:① 制样,将配置好的盐渍土装入密封袋48 h,采用静压法在钢化玻璃容器中分层压实. ② 安装,将装有样品的钢化玻璃模具安装在保温箱底座(底板)上,再在样品顶层覆盖一层塑料薄膜,然后盖上顶板,插入传感器设备. ③ 保温,在钢化玻璃桶周围包裹2.0 cm厚的保温材料三层. 单向冻结试验全程实时监测土柱内不同位置温度、液态水含量、孔隙溶液电导率及无压补给量等数据. 试验结束后取出5TE传感器,分别在5TE接孔位置、试样顶部、底端掏取适量盐渍土,烘干后按土水比1∶5配置成盐渍土溶液,采用5TE测量电导率,计算出含盐量. 土柱不同高度的总含水率采用烘干法测量. 溶液补给曲线如图2所示.
2. 试验结果分析
2.1 盐渍土传热分析
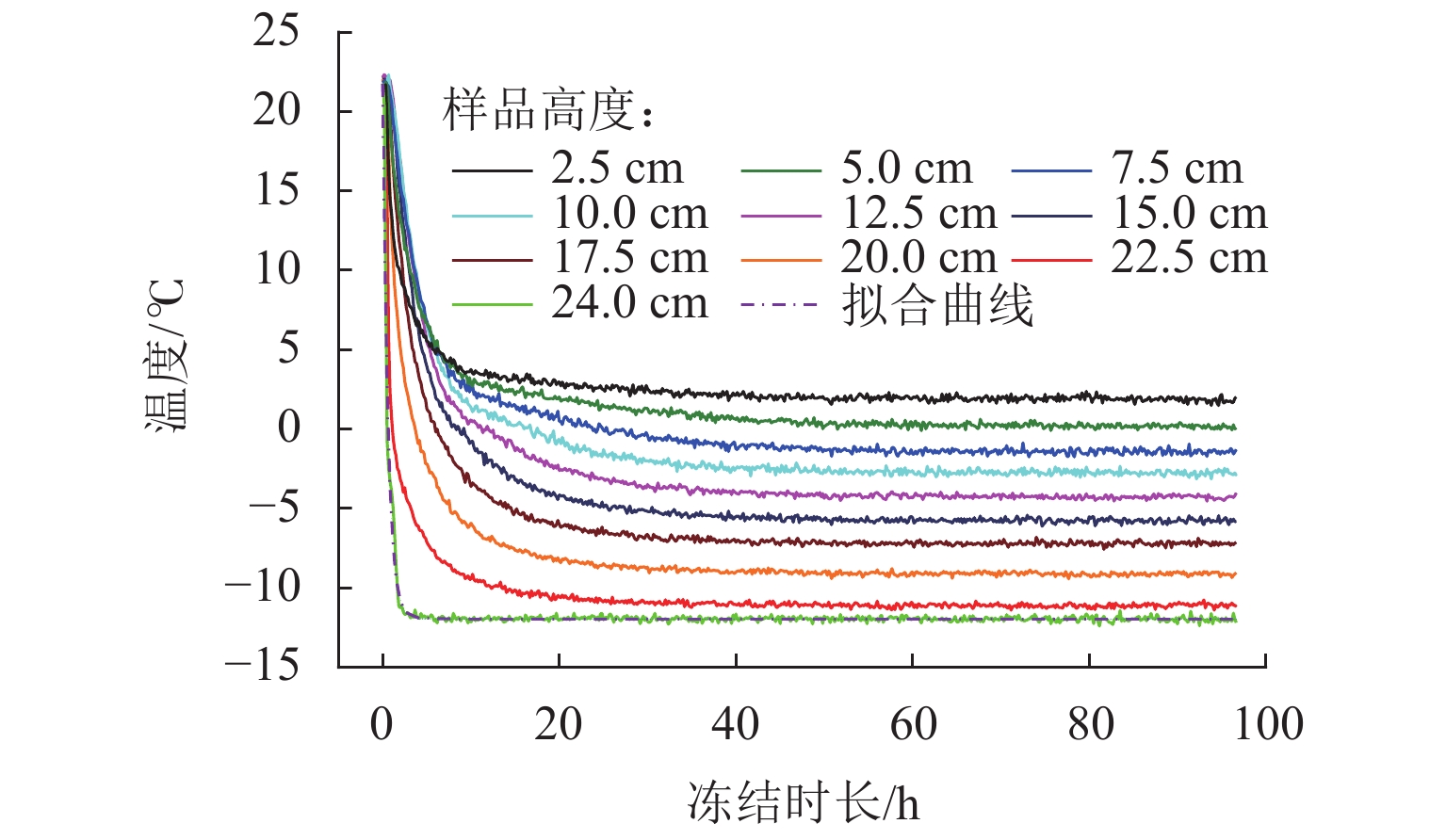
单向冻结作用下盐渍土柱温度随时间变化如图3所示. 曲线呈三阶段发展:速冻阶段(0~8 h),温度骤降;过渡阶段(8~48 h),温度缓降;平稳阶段(48 h以后),温度平稳. 冷端实测温度T0拟合函数为T0=32.29 exp(−t/0.594)−11.95 ℃,t为时间.
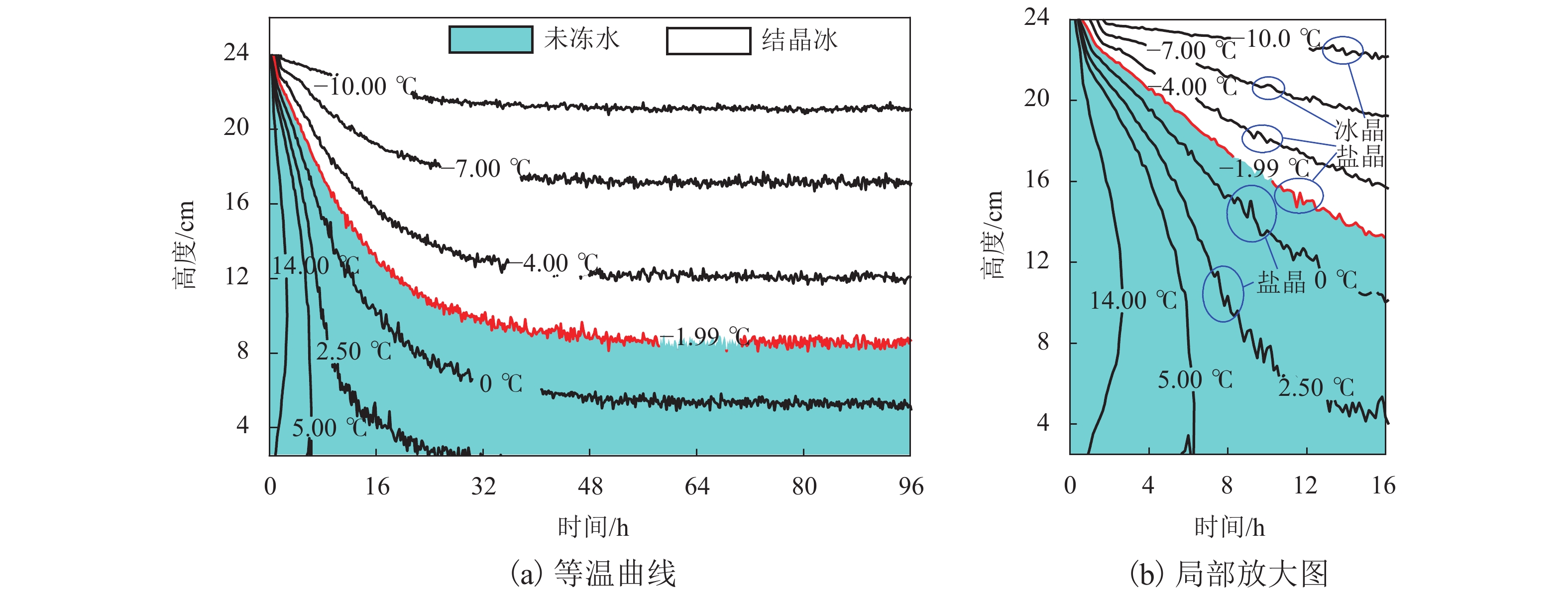
图4为盐渍土柱等温线分布状况. 盐渍土冻结温度Tf (图中红色曲线)实测值为−1.99 ℃,Tf线将土柱分为冻结区和非冻结区. 盐渍土内温度曲线有明显的波动现象. 温度波动是由降温引起的结晶(冰晶、盐晶)潜热所致. 冻结区温度低于Tf值,既有冰晶体也有盐晶体产生;非冻结区温度高于Tf值,因此只析出盐晶体.
2.2 盐渍土水分迁移分析
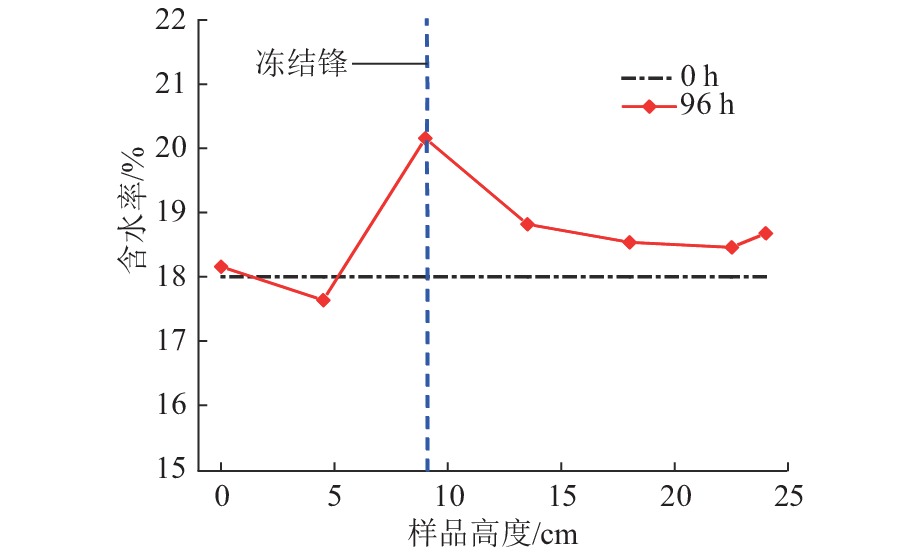
图5为土柱含水率分布状况. 在无压补给条件下冻结96 h,土柱的含水率相较初始含水率变化明显,冻结区含水率增大,冻结锋位置含水率出现峰值,峰值相较初始值增加了2.16%;在非冻结区含水率骤降形成拐点. 研究表明,平稳阶段持续时间较长,孔隙中未冻水有充足时间向冻结锋面迁移,致使冻结区域含水率增加,冻结锋面附近的含水率达到峰值.
2.3 盐渍土盐分迁移分析
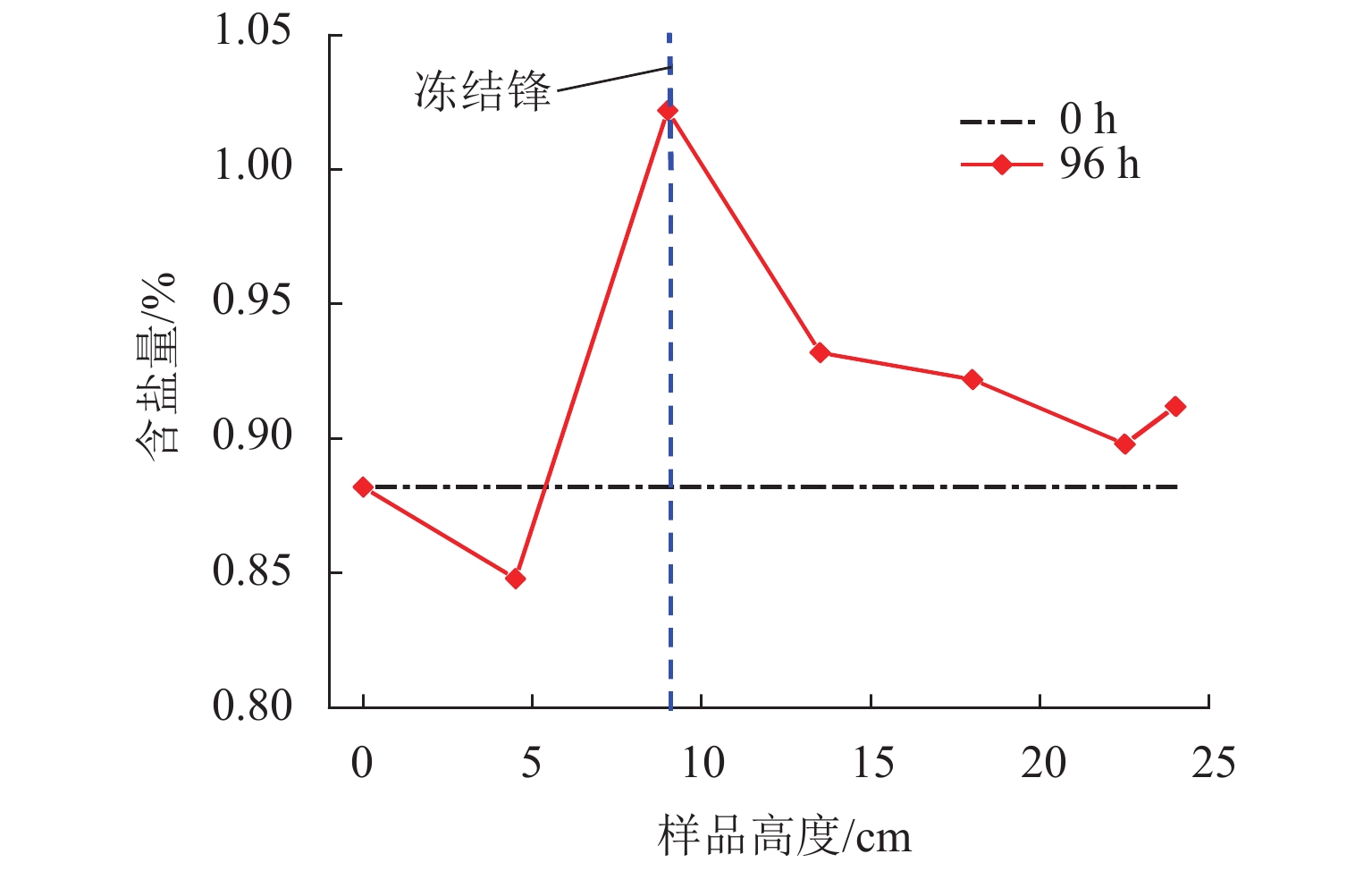
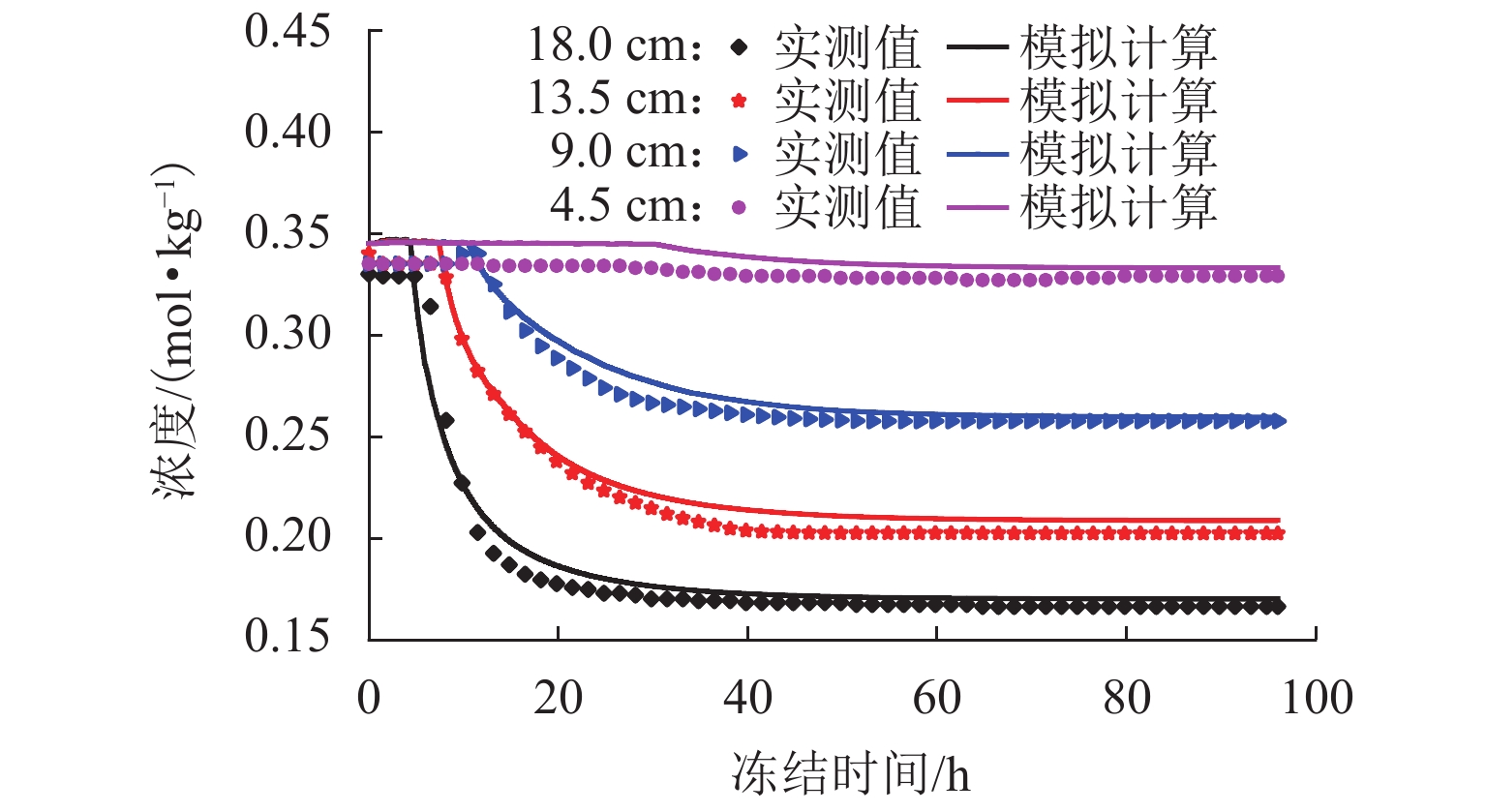
图6为土柱含盐量分布状况. 相较初始状态,冻结区含盐量增加,在冻结锋位置达到峰值,峰值相较初始值增加了0.28%;非冻结区含盐量骤降,形成拐点,这与图5含水率分布状况较为相似. 分析可知,盐分迁移以水分为载体通过对流和水动力弥散作用进行,对流导致冻结区含盐量的增加,弥散效应加剧了冻结锋面处的盐分累积.
3. 理论模型
3.1 水分场控制方程
本文基于Richards方程[12],水分迁移遵循非饱和土Darcy定律,忽略水分在水平向的迁移. 考虑芒硝结晶过程对液态水的消耗及冰晶、盐晶对水分迁移的阻滞作用. 基于此,修正后的非饱和盐渍冻土中水分迁移控制方程为
∂θu∂t+ρiρw∂θi∂t+ρcMwρwMc∂θc∂t−∂∂z[D(θu)∂θu∂z+k(θu)]=0, (1) 式中:
θu 为液态水的体积含量;θi 为结晶冰的体积含量;ρi 为冰的密度;ρw 为水的密度;ρc 为结晶盐的密度;θc 为结晶盐的体积含量;Mw 为结晶水的摩尔质量;Mc 为结晶盐的摩尔质量;D(θu) 为土体的水分扩散率,如式(2)所示[21];z 为纵向高度;k(θu) 为非饱和冻土的渗透系数.D(θu)=k(θu)P(θu)I, (2) 式中:
P(θu) 为比水容量,表示基质势对含水率的影响;I=10−10(θi+θc) ,为阻抗因子,冻土中表示冰对液态水迁移的阻滞作用,在盐渍冻土中,液态水迁移不仅受到孔隙中冰晶的阻碍,还受到盐晶体的阻碍[10].基于V-G模型 [22],考虑阻抗效应,得出非饱和盐渍冻土
P(θu) 、k(θu) 分别为P(θu)=a0mS1/m(1−S1/m)mI/(1−m), (3) k(θu) = ksSl[1−(1−S1/m)m]2I, (4) 式中:
a0 、m 和l 为土壤本构系数;ks 为饱和土渗透系数;相对饱和度S=(θu−θr)/(θs−θr) ,θr 为残余体积含水率,θs 为饱和体积含水率.3.2 温度场控制方程
依据能量守恒定律和Fourier传热定律,考虑冰水相变、芒硝结晶潜热影响,将冰水相变和芒硝结晶相变的潜热作为热源处理,得出非饱和盐渍土传热微分方程为
ϕS∂T∂t−∂∂z(λ∂T∂z)=Liρi∂θi∂t+Lcρc∂θc∂t, (5) 式中:
ϕS 为盐渍土有效比热容;T 为温度;λ 为盐渍土导热系数;Li 为冰水相变潜热;Lc 为芒硝结晶析出潜热.土壤有效比热容用各种物质成分的体积加权平均值来表示,而导热系数具有指数加权性质[11]. 因此,盐渍土的有效比热容和导热系数分别为
ϕS=Cwρwθu+Ciρiθi+Ccρcθc+Csρs(1−θs), (6) λ=λθuwλiθiλθccλ(1−θs)s, (7) 式中:
Cw 、Ci 、Cc 、Cs 分别为液态水、冰、芒硝结晶及土颗粒的体积比热容;λw 、λi 、λc 、λs 分别为液态水、冰、芒硝结晶及土颗粒的热导率.3.3 盐分场控制方程
溶质运移方式主要有对流运动、分子扩散和机械弥散三种形式,其中,分子扩散和机械弥散被统称为溶质的水动力弥散运动. 本文以质量守恒[19]为依据,考虑盐分结晶引起的溶质变化,忽略水平向的溶质迁移,得出盐分场控制方程如式(8)所示.
∂mc∂t+ρcρwMc∂θc∂t=−∂∂z(Jc+Js+Jh), (8) {Jc=qc,Js=−Ds∂c∂z,Jh=−Dh∂c∂z, (9) q=−k∂∂z(ψm+z), (10) ψm={−4.47θu−3.71,θu<0.31,−12.84θu−2.83,θu⩾0.31, (11) 式中:
mc=θuc ,为溶质摩尔质量;c为溶质摩尔浓度;Jc 、Js 、Jh 分别为溶质的对流、扩散和机械弥散通量; q为土体中水分对流速度;ψm 为非饱和盐渍土的基质势[23],cm;Ds=D0aebθu ,为溶质有效的扩散系数;Dh=α|v| ,为机械弥散系数,v=q/θu [23];D0 、a 、b 、α 为与土体性质有关的系数.将式(9)代入式(8)得出盐分场控制方程为
∂(θuc)∂t+ρcMcρw∂θc∂t+∂∂z[−(Ds+Dh)∂c∂z+qc]=0. (12) 3.4 相变结晶动态平衡关系
盐渍土中液态水含量是关于温度的函数,引入固液比
Bi 计算冰晶含量[16,21],如式(13)所示.θi={Biθu,Biθu<ρwρiθs,ρwρiθs,Biθu⩾ρwρiθs, (13) Bi={ρwρi(TTf)B−1,T<Tf,0,T⩾Tf, (14) 式中:
B 为土体的经验参数.硫酸钠的溶解度函数对芒硝晶体含量的计算非常重要,Zhang等[11]基于Frezchem模型计算得出硫酸钠溶解度函数为
nNa2SO4(T)=0.3223e0.0717T. (15) 盐渍土孔隙中硫酸钠的摩尔浓度为
cj={nNa2SO4(T),c⩾nNa2SO4(T),c,c<nNa2SO4(T). (16) 冻结时温度降低导致硫酸钠溶解度减小,当溶解度降至盐渍土孔隙溶液浓度时,开始盐分结晶. 随着温度降至Tf值,盐渍土孔隙溶液中水分子开始结晶,由于冰的自净作用,溶质分子被排除在冰晶外形成盐晶体[23-24].
降温导致孔隙溶液浓度大于硫酸钠溶解度,溶质分子析出,形成芒硝体积 [10]为
θc1=(c−cj)ρwθuMcρc. (17) 盐渍土孔隙内的未冻水相变形成冰晶,由于冰的自净作用,溶质分子被排除在冰晶外,形成自净芒硝体积为
θc2 = cjρiθiMc/ρc. (18) 盐渍冻土孔隙中结晶盐体积含量为
θc=θc1+θc2. (19) 4. 数值结果对比分析
4.1 基于COMSOL盐渍土水-热-盐耦合数值模型
非饱和硫酸盐渍土水-热-盐耦合数学模型由式(1)、(5)、(12)组成,方程中的主要变量及参数是随时间和空间变化而变化,具有高度非线性特点. COMSOL Multi-physics有限元仿真软件具有强大的多物理场耦合能力和强非线性微分方程组求解能力. 因此,本文利用其中的PDE模块进行二次开发,求解非饱和硫酸盐渍土的水-热-盐耦合数学模型. PDE模块中的偏微分方程为
ea∂2u∂t2+da∂u∂t∂∂z(−η∂u∂z−κu+γ)+β∂u∂z+ξu=f, u∈Ω, (20) 式中:
Ω 为计算区域;u∈{S,T,c};ea为质量系数;da为阻滞系数;η为扩散系数;κ 为通量对流系数;γ 为通量源项;β为对流系数;ξ 为吸收系数.4.2 几何模型与参数确定
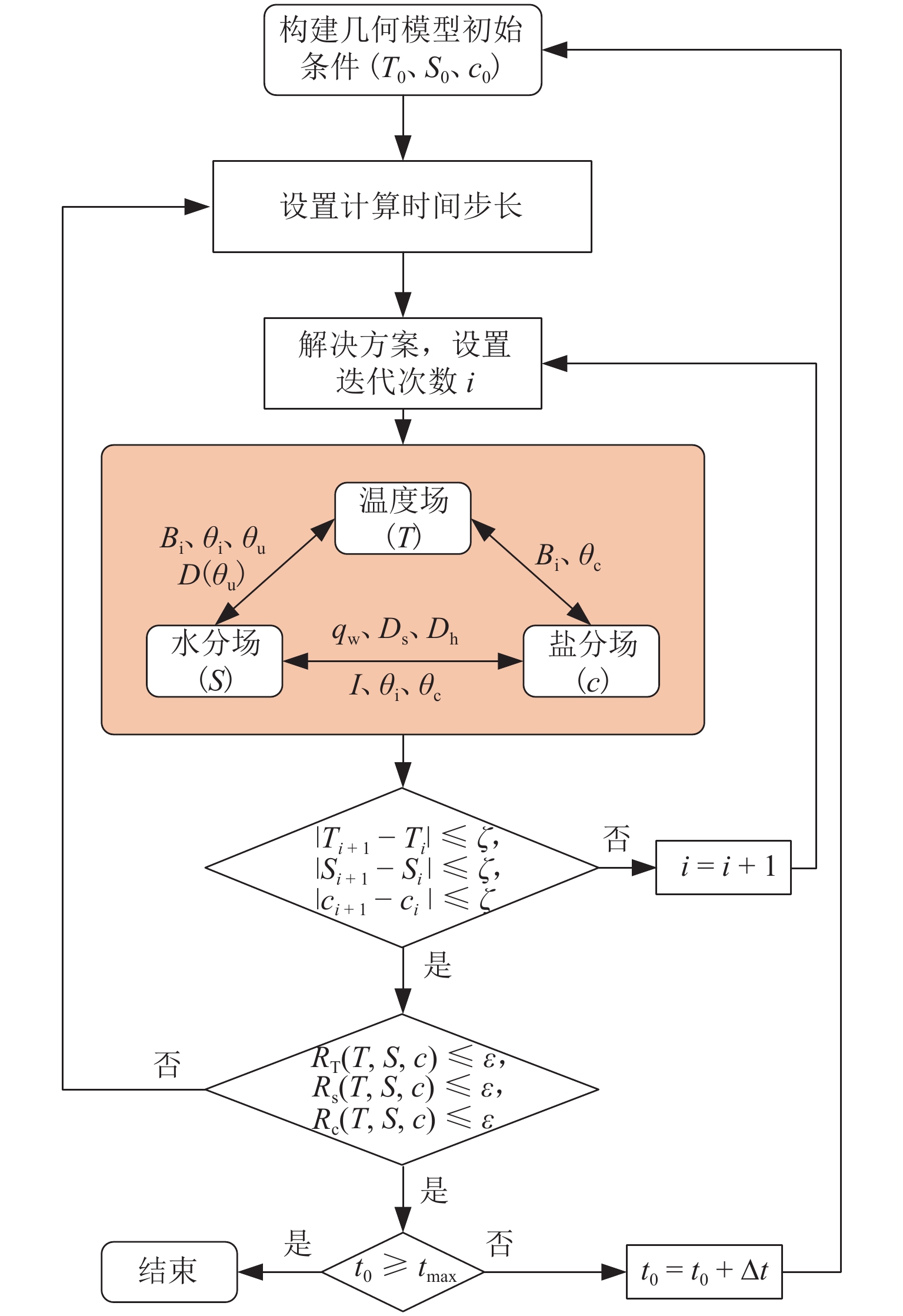
模型尺寸为高24 cm、宽15 cm的矩形. 模拟初试温度为22 ℃,暖端温度为4 ℃,冷端温度设为图3中的温度拟合函数. 初始含水率为18%,可换算为初始饱和度S0为0.725,初始含盐量为0.88%,对应初始浓度c0为0.345 mol/kg. 计算步长Δt设为0.1 h,总时长tmax为96 h. 数值模拟计算流程如图7 所示. 图中:Ti、Si、ci分别为第i次迭代的温度、相对饱和度、溶质摩尔浓度;t0为计算时间,初始值为0;ζ为收敛标准;RT、RS、Rc分别为温度、饱和度及溶质浓度的误差项;ε为数值计算误差,取0.001.
耦合模型参数见表2,其中,饱和盐渍土渗透系数ks、饱和体积含水率ɵs、干密度ρd、土颗粒密度ρs等参数通过室内试验获取.
表 2 模型参数Table 2. Model parameters参数 数值 参数 数值 a0 2 Li/(kJ·kg−1) 334.6 m 0.15 Lc/(kJ·kg−1) 210 l 0.5 Cw/(J·(kg·℃) −1) 4180 ɵr 0.002 Ci/(J·(kg·℃) −1) 2090 ɵs 0.397 Cc/(J·(kg·℃) −1) 1090 ks/(m·s−1) 10−6 Cs/(J·(kg·℃) −1) 850 B 0.61 λw/(W·(m·K) −1) 0.58 ρw/(kg·m−3) 1000 λi/(W·(m·K) −1) 2.22 ρi/(kg·m−3) 918 λc/(W·(m·K) −1) 0.14 ρc/(kg·m−3) 1460 λs/(W·(m·K) −1) 1.50 ρs/(kg·m−3) 2700 D0/(m2·h−1) 1.098 × 10−5 ρd/(kg·m−3) 1600 a 0.00261 Mw/(g·mol−1) 180 b 10 Mc/(g·mol−1) 322 α/mm 7.021 4.3 结果对比分析
4.3.1 温度场
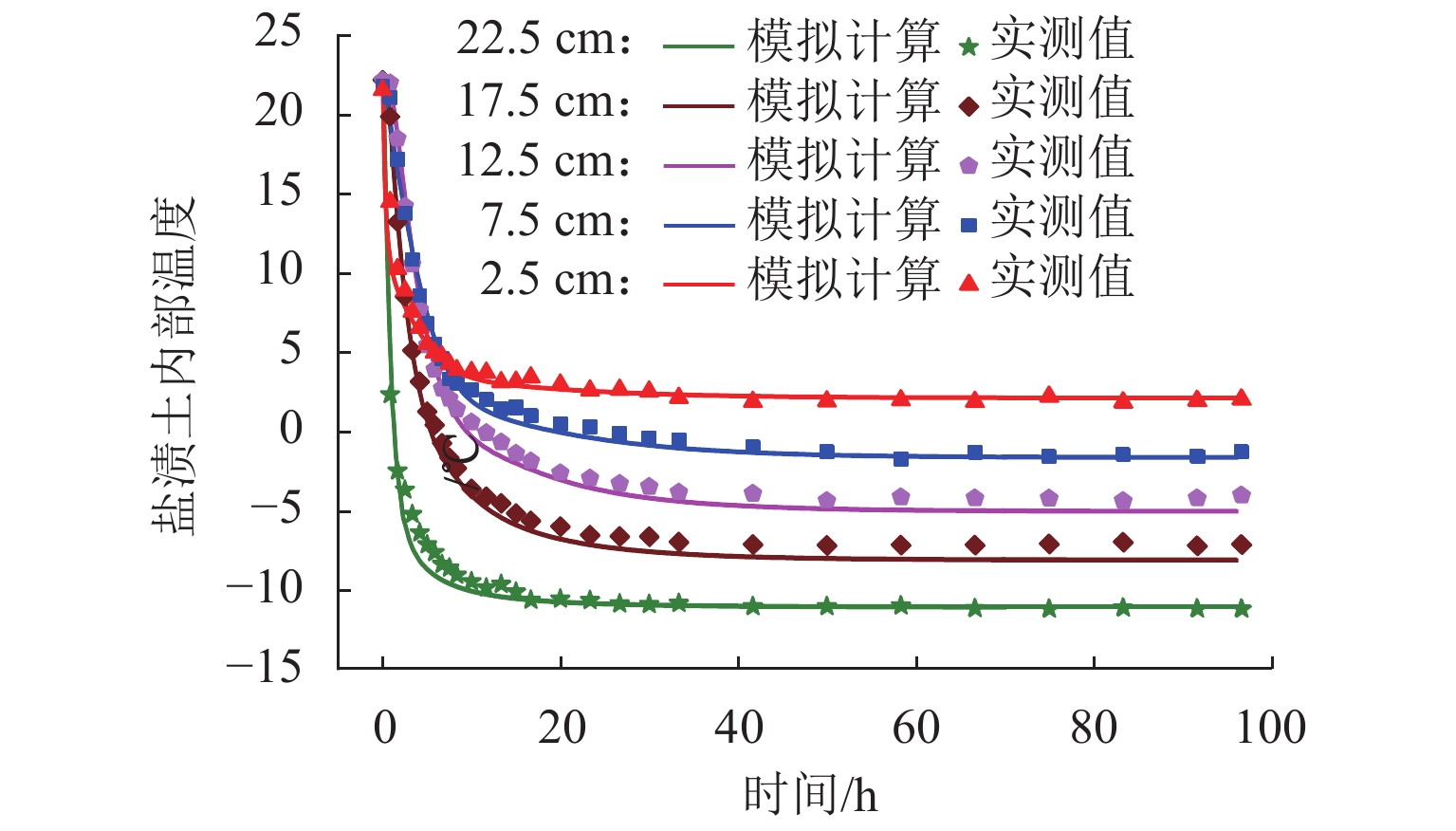
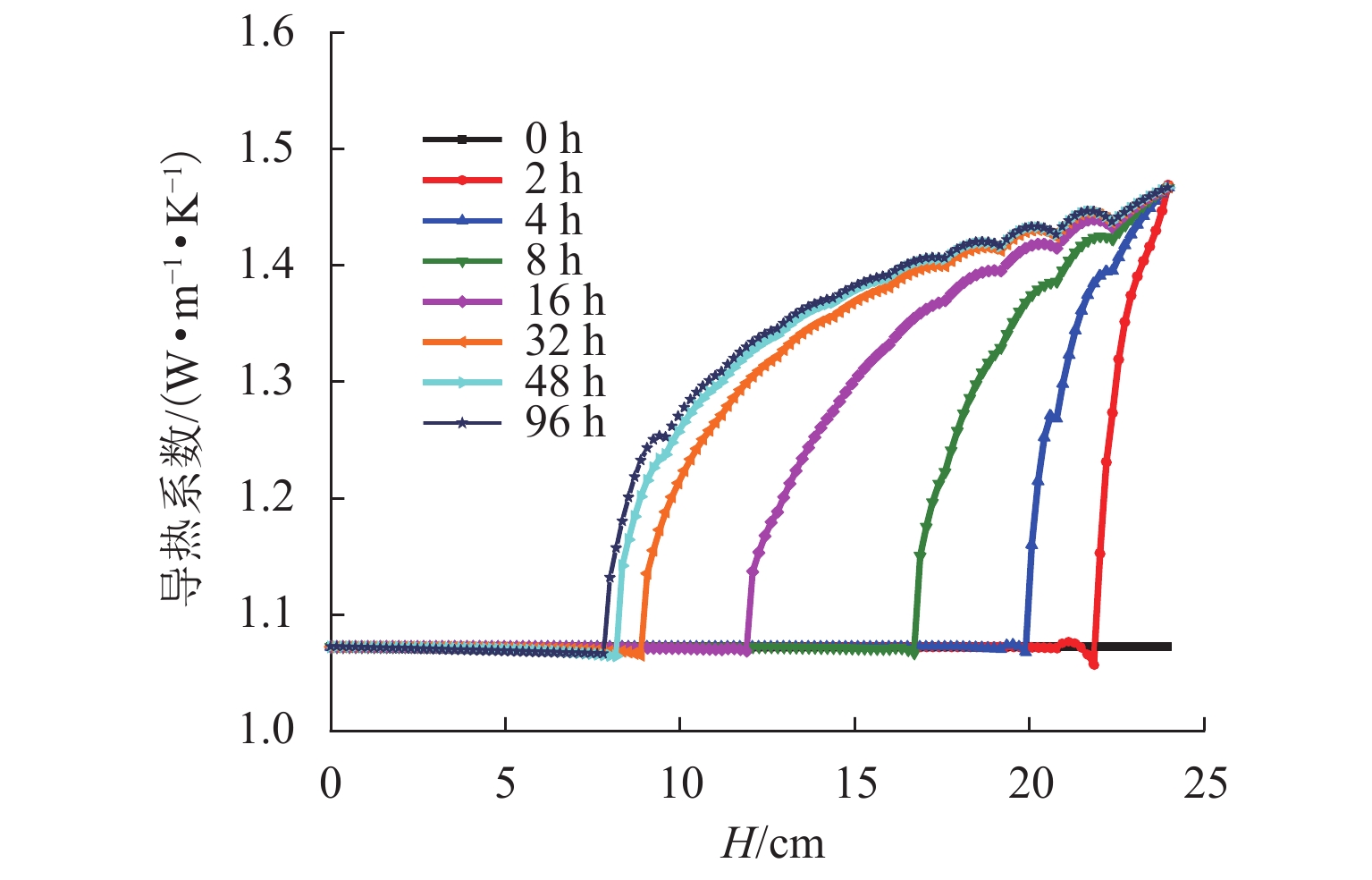
土柱不同高度H的瞬时温度模拟结果与实测值对比如图8所示,模型计算结果与实测数据吻合度较好. 盐渍土内温度分布受土体热物理学性质影响,其中,导热系数越大,温度下降速率越快. 盐渍土导热系数大小取决于各组分(土颗粒、未冻水、冰晶、盐晶)的含量,冰晶的导热系数远高于水、盐及土颗粒,因此,冰晶的相对含量对盐渍冻土导热系数影响最大. 图9为不同冻结时长盐渍土导热系数分布,随着冻结时长增加,冻结区不断扩大,冻结区冰晶相对含量逐渐增大,导热系数也随之增大. 非冻结区无冰晶析出,各组分含量相对稳定,导热系数接近初始值. 本文提出的耦合模型能够较好地预测硫酸盐渍土的传热机制。
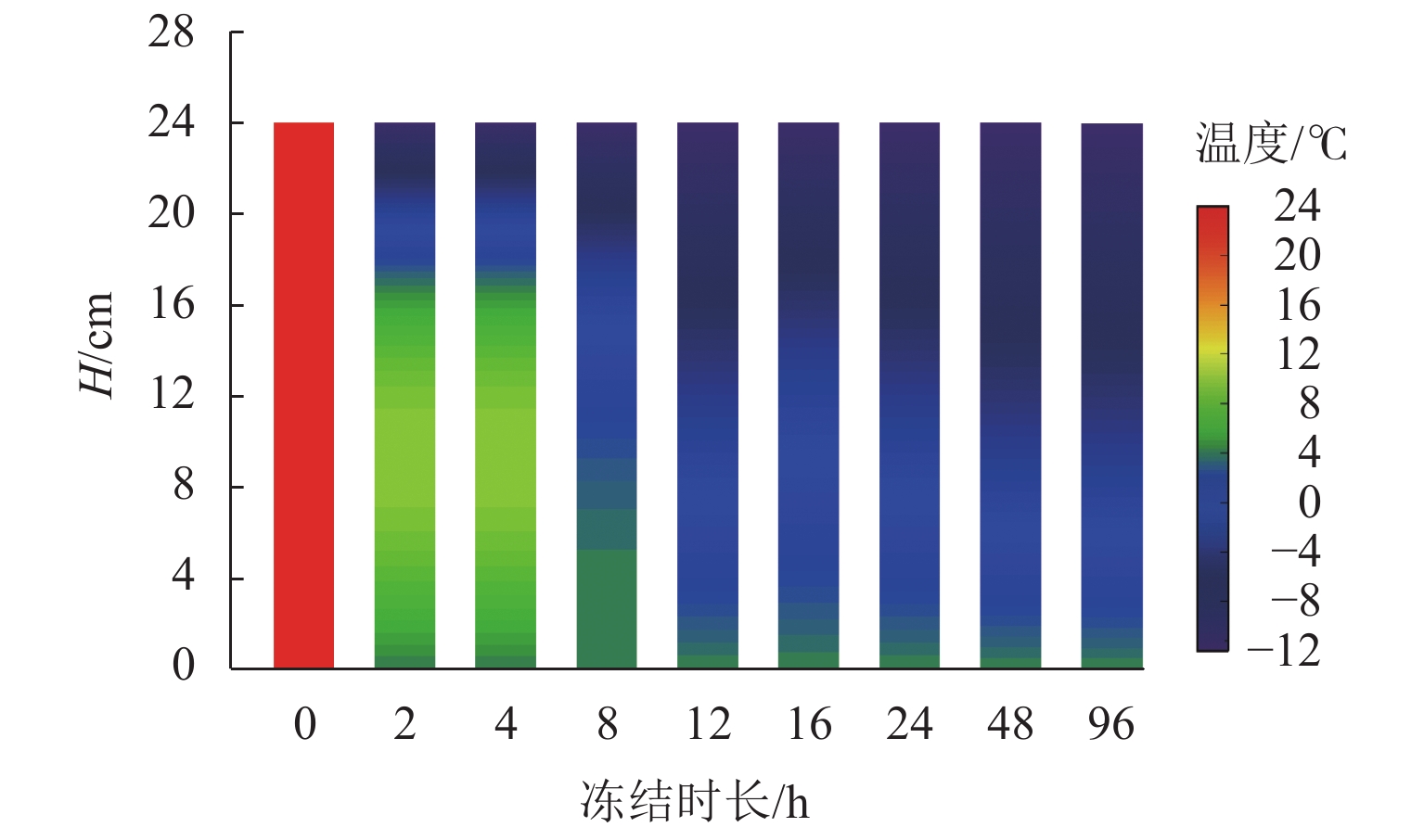
单向冻结作用下土柱模型温度分布如图10所示. 样品初始状态温度为22 ℃,冻结开始后,模型中降温由两端趋向中间,最终形成了上冷下暖的温度梯度.
4.3.2 水分场
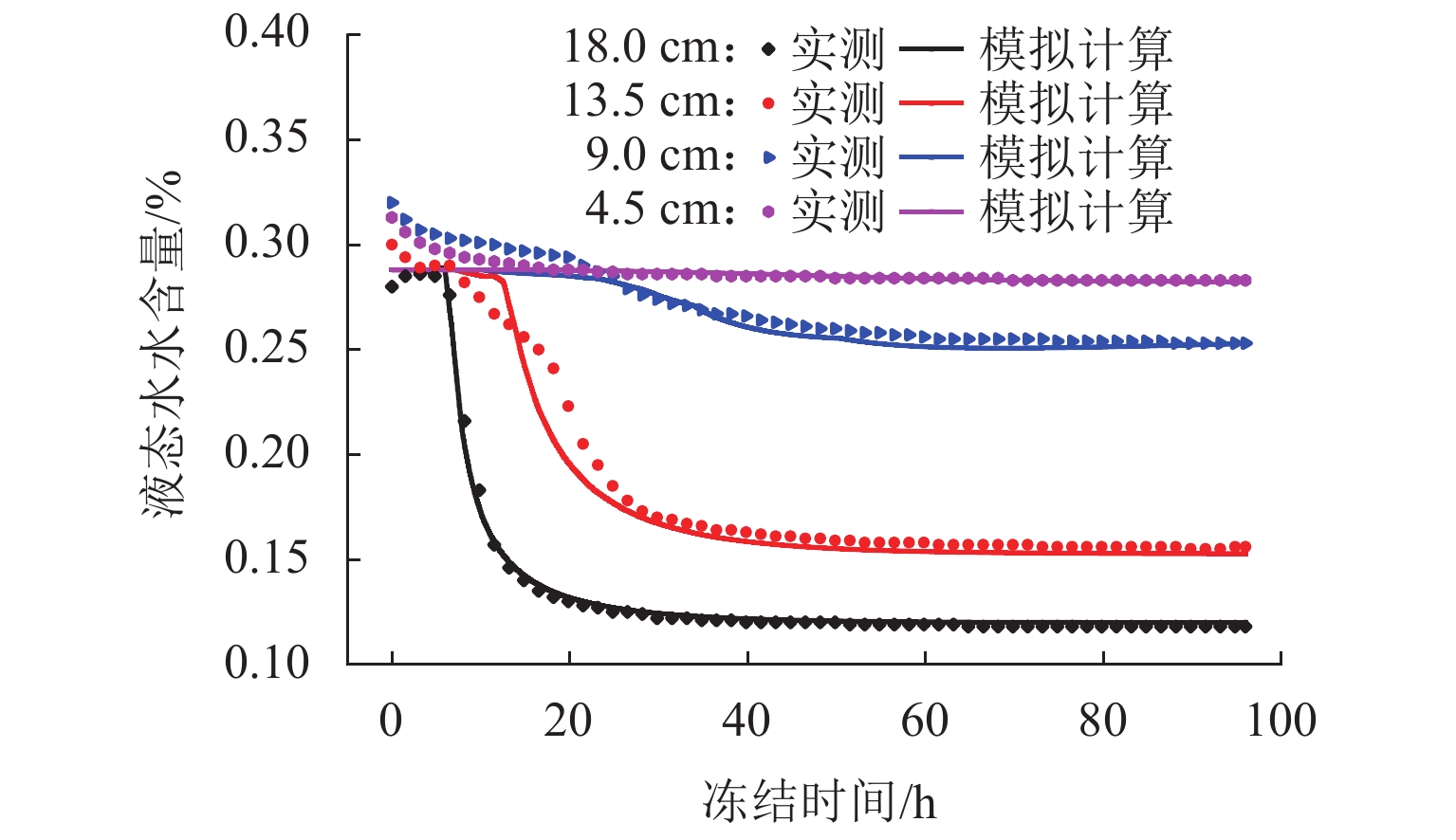
图11为土柱不同高度位置液态水含量时程曲线. 冻结区温度低于Tf值,孔隙中部分液态水冻结为冰晶,导致水含量减小,距离冷端越近,液态水含量越小. 非冻结区在温度梯度和基质吸力双重作用下水分发生迁移,液态水含量略有减小. 不同高度处液态水含量数值计算结果与实测结果吻合度较好,因此,本文提出的水-热-盐耦合模型能够较好地描述盐渍冻土液态水动态变化状况.
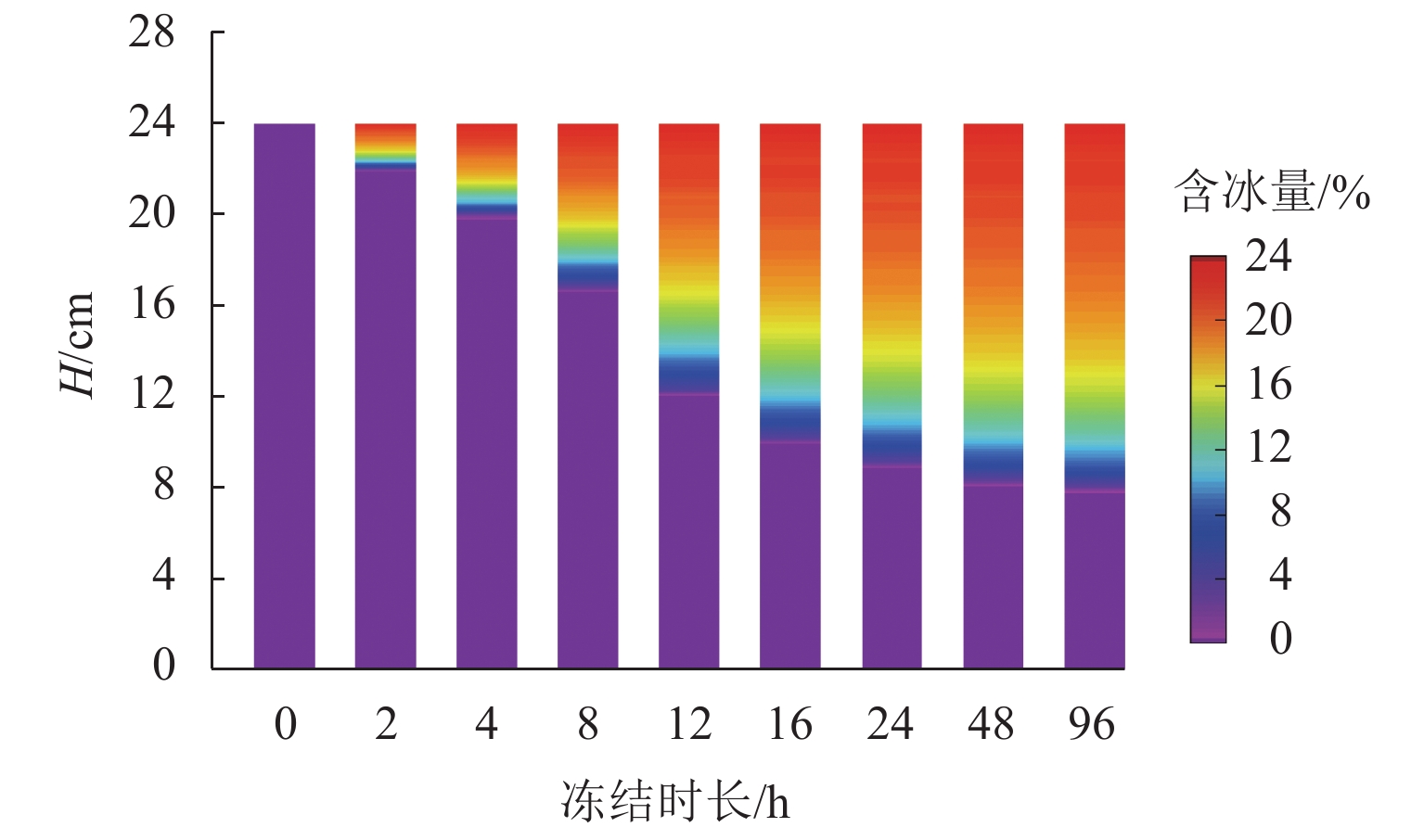
图12为样品中结晶冰含量分布特征. 随着冻结时长0增加,样品内液态水逐渐被冻结为冰晶,冰晶含量不断增加. 图中冻结锋清晰可见(冻结区与非冻结区交界处),随着冻结时长递增,冻结锋不断地向下移动,冻结区不断扩大(图中红色部分),而未冻区不断缩减(图中紫色部分).
4.3.3 盐分场
盐渍土孔隙溶液浓度受温度、液态水含量的双重影响. 速冻阶段温度急速下降,靠近冷端的孔隙溶液首先达到过饱和状态,溶质分子结晶,溶液浓度减小. 当温度降至Tf值,液态水开始结晶,此时浓度降低的速率被反向抑制而减缓. 最后进入平稳阶段,温度、液态水含量趋于稳定,浓度平稳发展. 如图13所示. 分析发现,盐渍冻土孔隙溶液浓度降低主要与盐分结晶聚集和温度梯度导致的真空吸力有关.
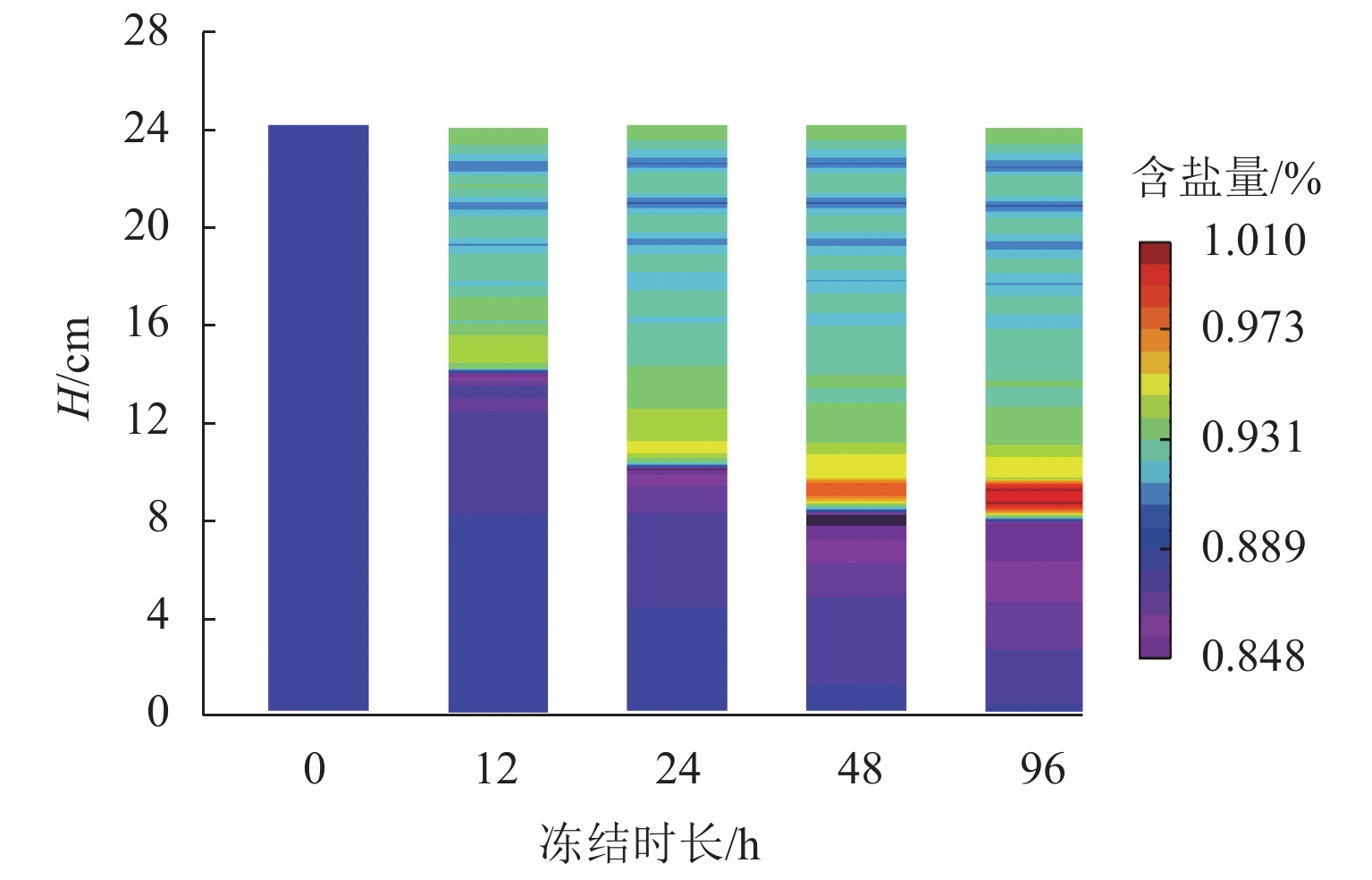
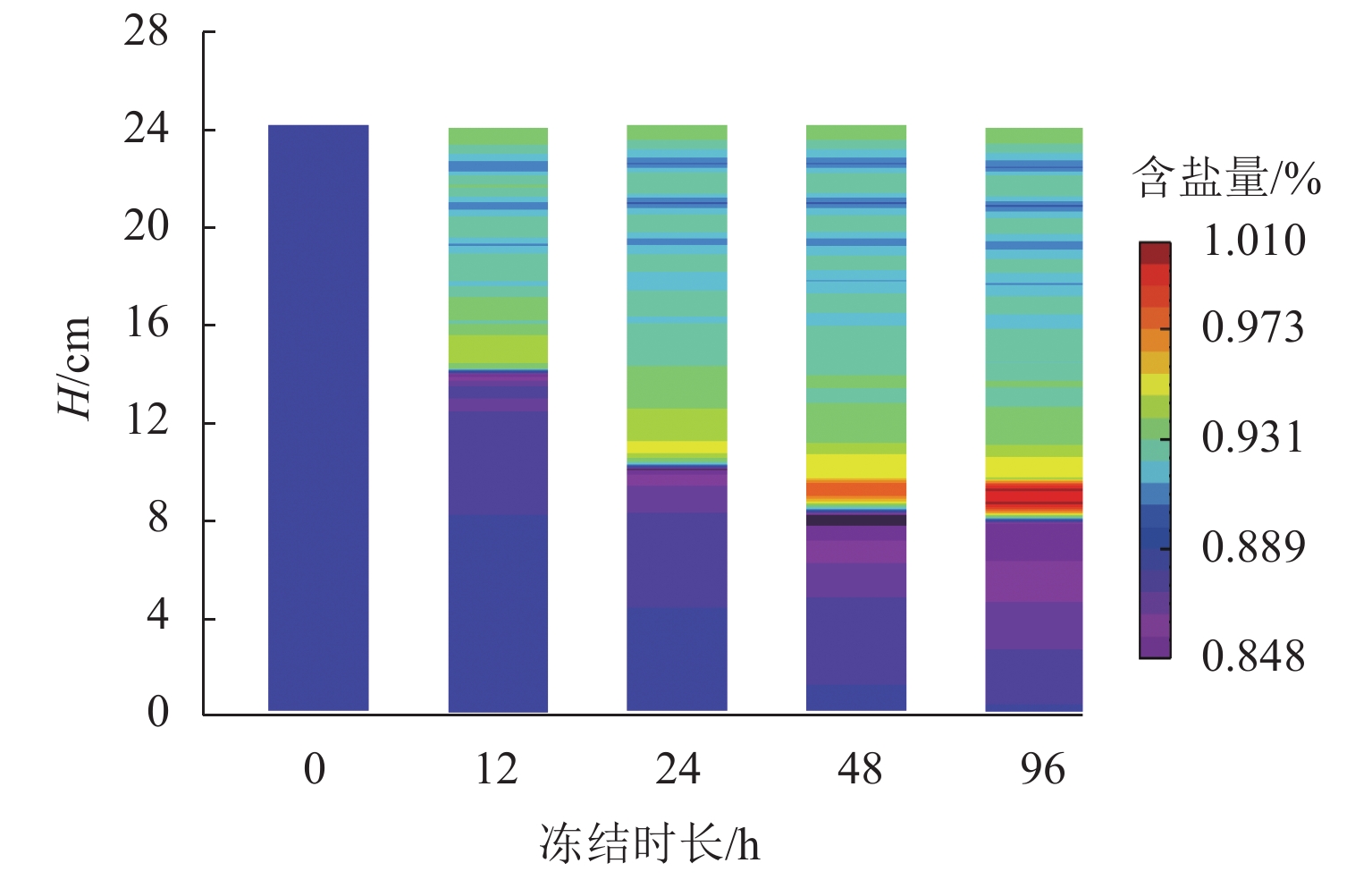
图14为不同时刻样品含盐量分布云图. 图中冻结锋清晰可见,冻结时长由12 h增至24、48 h,冻结锋由14.0 cm降至10.0、8.5 cm,冻结锋的下移速率逐步减缓;冻结锋将土柱分割为冻结区和非冻结区,冻结区含盐量大于非冻结区,冻结锋面处含盐量达到最大值. 研究表明,降温会引起盐渍土内盐分重分布现象,盐分在温度梯度作用下由暖端向冷端迁移;盐分结晶引起的孔隙填充效应,阻碍盐分的迁移通道,导致冻结锋面位置盐分的聚集现象.
4.3.4 冻结深度
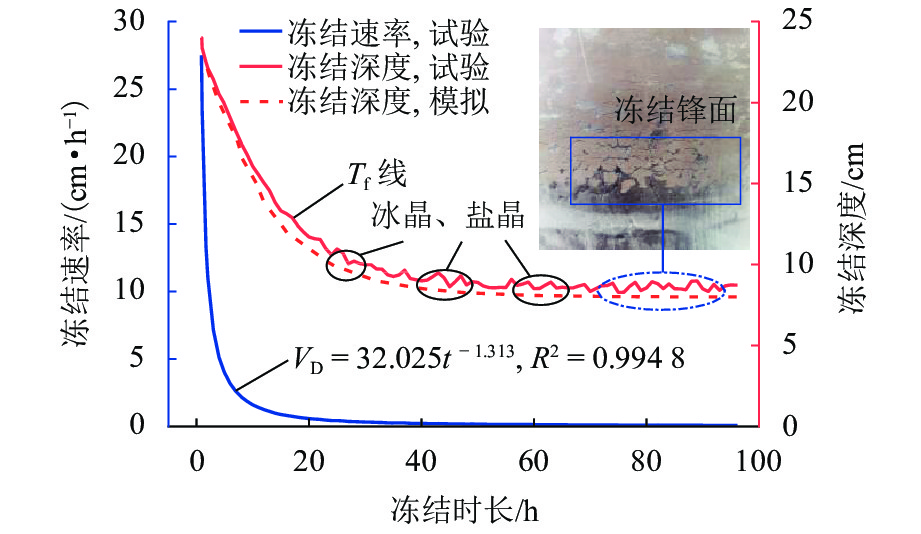
图15为冻结速率VD和冻结深度时程曲线. 冻结速率从峰值到0快速下降,可用幂函数描述,其相关系数R2=0.9948. 冻结深度随冻结时长增加逐渐趋于平稳波动,波动现象由结晶潜热所致. 图中数值模拟结果与试验值基本吻合,最大冻结深度约为15.5 cm. 鉴于冻结锋形成于冻结温度Tf位置,因此,冻结锋的移动轨迹沿Tf曲线发展,最终趋于平稳形成冻结锋面.
5. 结 论
1) 单向冻结作用下非饱和盐渍土内温度随冻结时长变化呈三阶段发展,温度传递受土壤导热系数的影响,结晶潜热会引起温度波动现象.
2) Tf曲线将盐渍土柱划分为冻结区和非冻结区;冻结96 h土柱含水率和含盐量峰值出现在冻结锋位置,冻结区含水率和含盐量均增大,非冻结区含水率和含盐量均减小.
3) 降温使盐渍土内部发生了复杂的物理化学过程,热-质迁移导致盐渍土内水、盐重分布;结晶相变导致盐渍土液态水含量和孔隙溶液浓度均减小. 随冻结时长增加,冻结深度逐渐趋于平稳,冻结速率呈幂函数.
4) 本文建立的水-热-盐耦合模型能够较好地模拟补给条件下非饱和硫酸盐渍土温度场、水分场、盐分场的动态变化规律,可动态描述冻结锋的移动轨迹及冻结锋面的形成过程.
-
表 1 脱盐后土壤物理力学指标
Table 1. Physical and mechanical indexes of soil samples after desalination
参数 Gs ρmax/(g·cm−3) ωopt/% wL/% wP/% Cu Cc 取值 2.70 1.78 13.7 25.35 12.62 5.29 0.59 表 2 模型参数
Table 2. Model parameters
参数 数值 参数 数值 a0 2 Li/(kJ·kg−1) 334.6 m 0.15 Lc/(kJ·kg−1) 210 l 0.5 Cw/(J·(kg·℃) −1) 4180 ɵr 0.002 Ci/(J·(kg·℃) −1) 2090 ɵs 0.397 Cc/(J·(kg·℃) −1) 1090 ks/(m·s−1) 10−6 Cs/(J·(kg·℃) −1) 850 B 0.61 λw/(W·(m·K) −1) 0.58 ρw/(kg·m−3) 1000 λi/(W·(m·K) −1) 2.22 ρi/(kg·m−3) 918 λc/(W·(m·K) −1) 0.14 ρc/(kg·m−3) 1460 λs/(W·(m·K) −1) 1.50 ρs/(kg·m−3) 2700 D0/(m2·h−1) 1.098 × 10−5 ρd/(kg·m−3) 1600 a 0.00261 Mw/(g·mol−1) 180 b 10 Mc/(g·mol−1) 322 α/mm 7.021 -
[1] ZHANG J, LAI Y M, ZHAO Y H, et al. Study on the mechanism of crystallization deformation of sulfate saline soil during the unidirectional freezing process[J]. Permafrost and Periglacial Processes, 2021, 32(1): 102-118. doi: 10.1002/ppp.2080 [2] WEISBROD N, NIEMET M R, ROCKHOLD M L, et al. Migration of saline solutions in variably saturated porous media[J]. Journal of Contaminant Hydrology, 2004, 72(1/2/3/4): 109-133. [3] 肖泽岸,朱霖泽,侯振荣,等. 盐渍土二次相变温度变化规律[J]. 农业工程学报,2022,38(8): 64-71. doi: 10.11975/j.issn.1002-6819.2022.08.008XIAO Zean, ZHU Linze, HOU Zhenrong, et al. Temporal variation in eutectic temperature of pore solution in saline soil[J]. Transactions of the Chinese Society of Agricultural Engineering, 2022, 38(8): 64-71. doi: 10.11975/j.issn.1002-6819.2022.08.008 [4] 路建国,万旭升,刘力,等. 降温过程硫酸钠盐渍土水-热-盐相互作用过程[J]. 哈尔滨工业大学学报,2022,54(2): 126-134. doi: 10.11918/202102029LU Jianguo, WAN Xusheng, LIU Li, et al. Water-heat-salt interaction of sodium sulfate saline soil during a cooling process[J]. Journal of Harbin Institute of Technology, 2022, 54(2): 126-134. doi: 10.11918/202102029 [5] 张树明,蒋关鲁,杜登峰,等. 新型桩板结构路基在季节冻土区的适用性[J]. 西南交通大学学报,2021,56(3): 541-549.ZHANG Shuming, JIANG Guanlu, DU Dengfeng, et al. Applicability of novel pile-plank embankment in seasonally frozen regions[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 541-549. [6] 张文,罗艳珍,刘昕,等. 青海盐湖区路基结构层级配及其阻盐效果[J]. 西南交通大学学报,2020,55(6): 1264-1271,1296. doi: 10.3969/j.issn.0258-2724.20190056ZHANG Wen, LUO Yanzhen, LIU Xin, et al. Gradation of subgrade soil and its salt-resistance effect in salt lake area in Qinghai[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1264-1271,1296. doi: 10.3969/j.issn.0258-2724.20190056 [7] XIE Y L, YU Q H, YOU Y H, et al. The changing process and trend of ground temperature around tower foundations of Qinghai−Tibet power transmission line[J]. Sciences in Cold and Arid Regions, 2019, 11(1): 13-20. [8] 罗金明,许林书,邓伟,等. 盐渍土的热力构型对水盐运移的影响研究[J]. 干旱区资源与环境,2008,22(9): 118-123. doi: 10.3969/j.issn.1003-7578.2008.09.023LUO Jinming, XU Linshu, DENG Wei, et al. The influence of thermal dynamic structure of saline soil on water and salinity transportation[J]. Journal of Arid Land Resources and Environment, 2008, 22(9): 118-123. doi: 10.3969/j.issn.1003-7578.2008.09.023 [9] 周凤玺,周立增,王立业,等. 温度梯度作用下非饱和盐渍土水盐迁移及变形特性研究[J]. 岩石力学与工程学报,2020,39(10): 2115-2130.ZHOU Fengxi, ZHOU Lizeng, WANG Liye, et al. Study on water and salt migration and deformation properties of unsaturated saline soil under temperature gradient[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2115-2130. [10] XU J, LAN W, REN C, et al. Modeling of coupled transfer of water, heat and solute in saline loess considering sodium sulfate crystallization[J]. Cold Regions Science and Technology, 2021, 189: 103335.1-103335.13. [11] ZHANG J, LAI Y M, LI J F, et al. Study on the influence of hydro-thermal-salt-mechanical interaction in saturated frozen sulfate saline soil based on crystallization kinetics[J]. International Journal of Heat and Mass Transfer, 2020, 146: 118868.1-118868.14. [12] RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318-333. doi: 10.1063/1.1745010 [13] HANSSON K, ŠIMUNEK J, MIZOGUCHI M, et al. Water flow and heat transport in frozen soil[J]. Vadose Zone Journal, 2004, 3(2): 693-704. [14] YOUNES A. On modelling the multidimensional coupled fluid flow and heat or mass transport in porous media[J]. International Journal of Heat and Mass Transfer, 2003, 46(2): 367-379. doi: 10.1016/S0017-9310(02)00264-8 [15] 田亚护,刘建坤,钱征宇,等. 多年冻土区含保温夹层路基温度场的数值模拟[J]. 中国铁道科学,2002(2): 59-64. doi: 10.3321/j.issn:1001-4632.2002.02.009TIAN Yahu, LIU Jiankun, QIAN Zhengyu, et al. Numerical simulation for temperature field of roadlbed on permafrost with insulation[J]. China Railway Science, 2002(2): 59-64. doi: 10.3321/j.issn:1001-4632.2002.02.009 [16] XU J, LAN W, LI Y F, et al. Heat, water and solute transfer in saline loess under uniaxial freezing condition[J]. Computers and Geotechnics, 2020, 118: 103319.1-103319.20. [17] WANG D Y, LIU J K, LI X. Numerical simulation of coupled water and salt transfer in soil and a case study of the expansion of subgrade composed by saline soil[J]. Procedia Engineering, 2016, 143: 315-322. doi: 10.1016/j.proeng.2016.06.040 [18] 马敏,邴慧,李国玉. 硫酸钠盐渍土未冻水含量的实验研究[J]. 冰川冻土,2016,38(4): 963-969. doi: 10.7522/j.issn.1000-0240.2016.0110MA Min, BING Hui, LI Guoyu. Experimental research on unfrozen water content of sodium sulphate saline soil[J]. Journal of Glaciology and Geocryology, 2016, 38(4): 963-969. doi: 10.7522/j.issn.1000-0240.2016.0110 [19] 张莎莎,叶素纤,张林,等. 粗粒盐渍土路基水热盐力耦合方程修正及试验验证[J]. 公路交通科技,2020,37(3): 31-40.ZHANG Shasha, YE Suqian, ZHANG Lin, et al. Correction of hydrothermal salt force coupled equations for coarse-grained sulphate saline soil roadbed and its experimental verification[J]. Journal of Highway and Transportation Research and Development, 2020, 37(3): 31-40. [20] 中华人民共和国交通运输部. 公路土工试验规程: JTG 3430—2020[S]. 北京: 人民交通出版社, 2020. [21] 白青波,李旭,田亚护,等. 冻土水热耦合方程及数值模拟研究[J]. 岩土工程学报,2015,37(增2): 131-136. doi: 10.11779/CJGE2015S2026BAI Qingbo, LI Xu, TIAN Yahu, et al. Equations and numerical simulation for coupled water and heat transfer in frozen soil[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 131-136. doi: 10.11779/CJGE2015S2026 [22] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x [23] 牛玺荣. 硫酸盐渍土地区路基水、热、盐、力四场耦合机理及数值模拟研究[D]. 西安: 长安大学, 2006. [24] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001. 期刊类型引用(3)
1. 罗玚,周凤玺,罗崇亮. 单向冻结条件下非饱和铅污染黄土热-质迁移研究. 长江科学院院报. 2025(05): 174-183 .  百度学术
百度学术2. 周志雄,周凤玺,张明礼,马强. 降雨作用下硫酸盐渍土水–热–盐迁移及变形特性试验研究. 岩石力学与工程学报. 2024(08): 2056-2068 .  百度学术
百度学术3. 钟华锹,赵嘉进,姚传芹,张得煊,李希. 石窟寺表面泛盐病害热学响应的离散元模拟. 重庆大学学报. 2024(10): 110-119 .  百度学术
百度学术其他类型引用(3)
-





 下载:
下载:






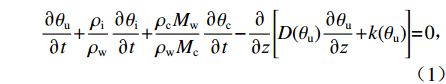
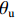
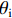
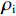
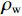
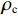
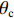
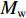
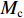
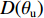

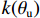

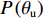
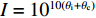
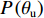
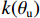
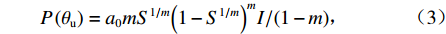
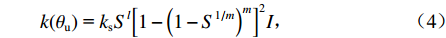
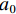
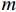
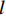
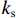
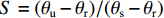
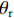
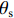
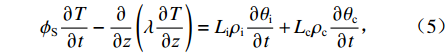
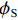
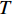
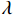
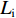
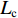
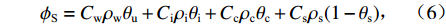

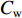
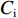
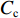
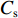
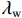
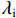
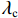
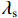
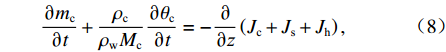


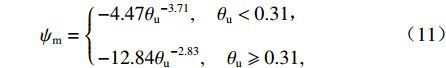
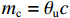
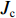
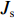
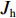
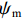
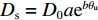
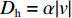
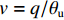
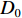
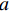
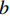
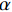
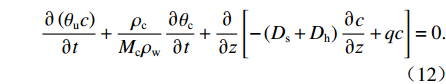
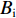
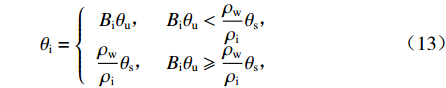
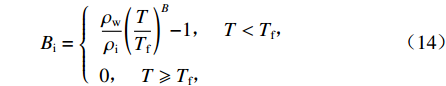
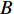
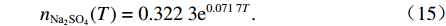
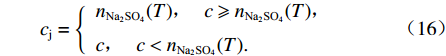
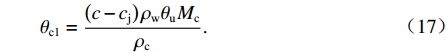


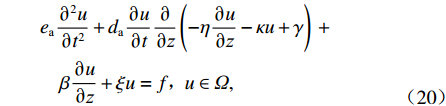

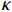
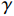
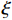










 下载:
下载:













 百度学术
百度学术