Numerical Simulation of In-plane Tensile Properties of High-Strength Steel Wire Mesh
-
摘要:
采用高强钢丝编织的格栅网在边坡浅层地质灾害和军事工程防护领域均有着广泛的应用. 由于影响格栅网面内力学性能的参数较多,精细化的数值分析可为优化格栅网的制备工艺充分发挥其力学性能提供依据. 为此,基于ANSYS Mechanical模块,在格栅网力学性能理论研究基础上,考虑钢丝材料的非线性应力强化效应、格栅网几何构造形成的各向异性以及连接节点处编织工艺造成的接触和状态非线性等因素,开展了格栅网面内拉伸力学性能的非线性数值分析. 结果表明:数值计算与试验获得的格栅网应力应变变化趋势基本一致;与试验结果相比,数值计算获得的格栅网等效弹性模型(刚度)在
Y 方向误差为10.6%,X 方向误差为18.5%;数值计算获得的格栅网极限应力应变在Y 方向误差分别为10.0%和12.8%,在X 方向误差分别为0.7%和18.3%.Abstract:The mesh woven with high-strength steel wires are widely used in fields of shallow geological disasters of slope and military engineering protection. As there are many weaving process parameters that affect the in-plane mechanical properties of the mesh, a refined numerical analysis can provide a basis for optimizing the mesh preparation process to give full play to its mechanical properties. Based on ANSYS Mechanical module and theoretical study of the mechanical properties of the mesh, a nonlinear numerical analysis of the mechanical properties of the wire mesh in plane tension was carried out taking into consideration the nonlinear stress strengthening effect of the steel wire material, the anisotropy formed by the geometric structure of the mesh, and the contact and state nonlinearity caused by the weaving process at the connection nodes of the mesh. Results show that the variation trend of stress and strain of the mesh obtained by numerical calculation is basically consistent with that obtained by experiment. Compared with the experimental results, the error of the equivalent elastic model (stiffness) of the mesh obtained by numerical calculation is 10.6% in the
Y direction and is 18.5% in theX direction. The errors of ultimate stress and ultimate strain obtained by the numerical calculation are 10.0% and 12.8% in theY direction and are 0.7% and 18.3% in theX direction, respectively.-
Key words:
- high-strength steel wire /
- wire mesh /
- equivalent elastic modulus /
- non-linearity /
- numerical simulation
-
高强钢丝是指强度在1770 MPa以上,反复弯曲性能达到或超过22次,单向扭转次数达到或超过25次的一种低应变、高强度圆形钢丝[1]. 由于这种钢丝具有优良的强度和韧性,将其编织成格栅网在边坡浅层地质灾害防治和军事工程防护领域具有广泛的应用.
在边坡浅层地质灾害防治中,格栅网作为柔性防护系统的主要构件,应用在浅层坡面地质灾害主动加固或坡面落石的被动拦截中 [2-4];在军事工程防护领域,格栅网主要应用在RPG (rifle propelled grenade)火箭弹、迫击炮弹的主动拦截中 [5-6].
由于受此类钢丝化学组成成分、力学性能要求等相关因素影响,在成型格栅网时,钢丝交叉位置采用焊接或机械连接实施难度较大,为此采用编织组装的方法形成网格,同时在两根编织钢丝的端部,采用扭结的方式进行连接,因此,高强钢丝编织的格栅网属于松散结构. 此外,由于制作工艺的原因,在采用钢丝编织成型格栅网时,钢丝在折弯处通过压扭成型,在空间上具有一定的厚度,因此,格栅网属于三维空间结构[7].
由于高强钢丝编织网型(格栅网或环形网)在连接部位处于拉伸、弯曲、剪切和滑移等复杂受力状态,且在受外荷载作用下的力学行为涉及几何非线性、材料非线性和状态非线性,建立此类编织网型的数值模型难度较大,国内外学者在环形网的数值建模方面开展了较多研究工作,提出了分区等代模型[8-9]、类似弹簧单元的离散模型[10]或简化的等效刚度模型[11-12]等建模方法,同时,采用各种商用软件(YADE、ABAQUS和ASNYS等)或自编程软件FARO等开展了数值分析验证[13]. 由于格栅网的组网方式与环形网存在区别,基于环形网的建模方法无法解决格栅网的建模问题. 为此,Del Cozdíaz等[14]基于格栅网的编织参数和ANSYS Mechanical 模块,采用耦合节点的方式考虑格栅网中钢丝交叉部位的连接,提出了三维格栅网的数值模型建立方法,但这种处理钢丝交叉部位连接的方法无法考虑钢丝之间在拉伸过程中状态的改变,计算结果与实际差距较大. Escallón等[15]基于格栅网的试验结果和ABAQUS Explicit模块,对格栅网中钢丝连接部位进行力学等效处理,但这种处理方法无法分析格栅网厚度、成型时弯曲半径等变化带来的影响,在预测格栅网编织工艺参数对其性能影响上还有一定的差距.
由于格栅网的编织工艺参数,尤其是钢丝交叉连接部位的工艺参数对其力学性能影响很大,因此,从格栅网力学特性及工艺参数着手,利用ANSYS Mechanical模块建立符合实际的数值模型,开展格栅网在面内拉伸荷载作用下的数值分析,并与试验结果进行了对比,验证了数值计算结果的可靠性,研究成果可为后续格栅网的工艺设计和拓展工程应用奠定良好的基础.
1. 高强钢丝编织格栅网试验
1.1 高强钢丝单轴拉伸力学试验
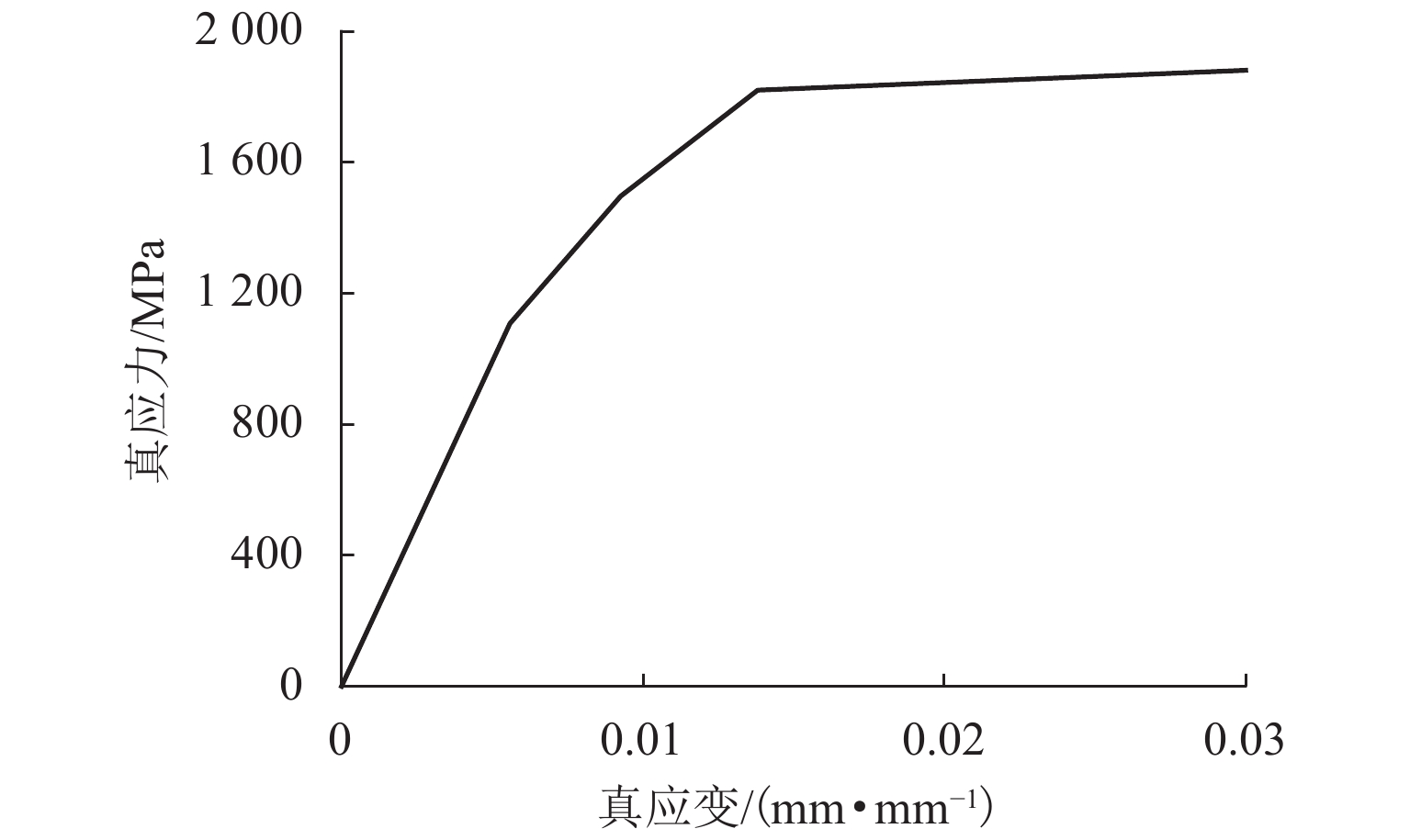
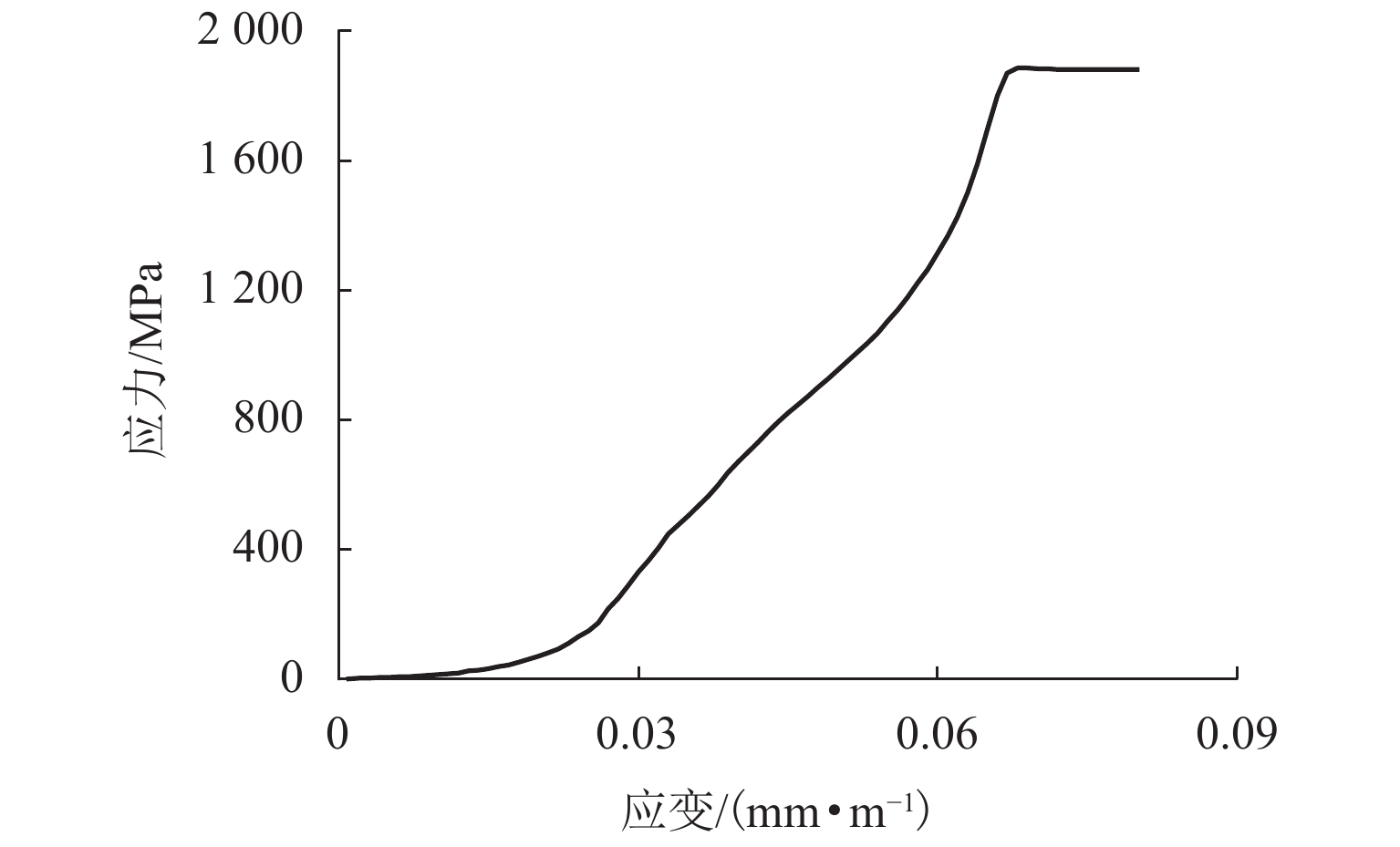
对直径为3 mm高强钢丝进行了静力拉伸试验,如图1,单轴拉伸试验按照GB/T 36915—2019[16]相关要求进行,参考Del Cozdíaz等[14]对此类钢丝的测试结果和西南交通大学柔性防护系统研究团队的测试结果[17],确定了钢丝的工程应力-应变关系. 由于在后续非线性分析计算中,均采用真应力-应变关系曲线,因此,根据工程应力-应变关系换算得到了高强钢丝的真应力-真应变关系曲线,如图2,从图中可以看出,高强钢丝在后期具有典型的应力强化现象,属于低应变高强度钢丝.
1.2 高强钢丝编织格栅网面内拉伸试验
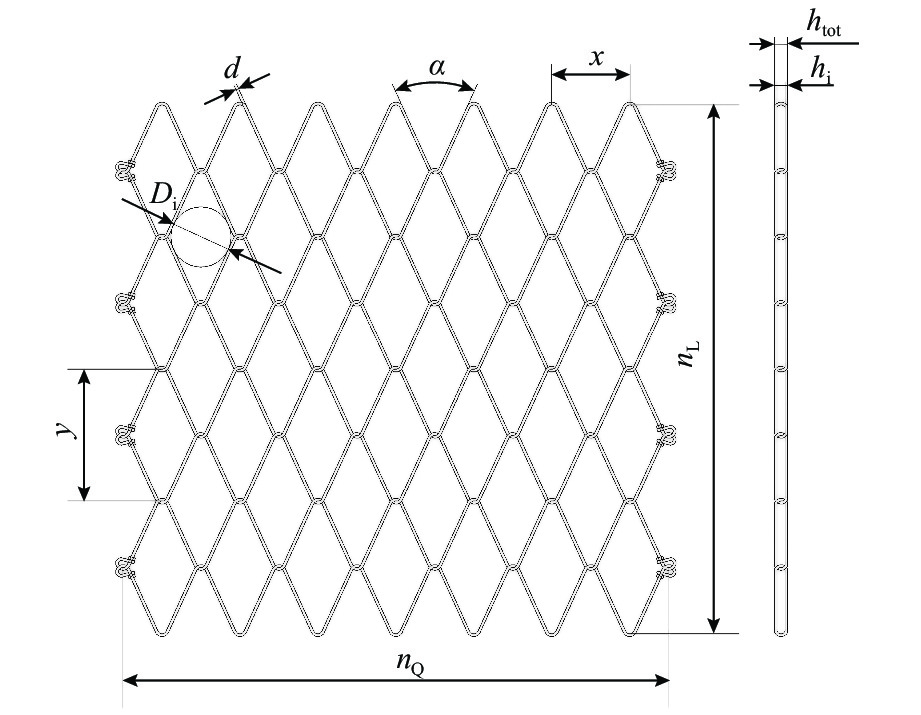
根据用途的不用,高强钢丝编织的格栅网规格尺寸也不一样,目前应用较多的网型为G65,详细布置及尺寸如图3所示. 图中:d为编网钢丝直径,d=3 mm;沿水平方向,菱形网孔短边尺寸x=83 mm,每延米(nQ=1 m)共12个菱形网格;沿竖直方向,菱形网孔长边尺寸y=143 mm,每延米(nL=1 m)共有7个菱形网格;菱形网孔锐角α=49°;网孔内切圆直径为Di=65 mm;沿平面外法线方向,外边界厚度htot=12.5 mm,内净厚度hi=6.5 mm.
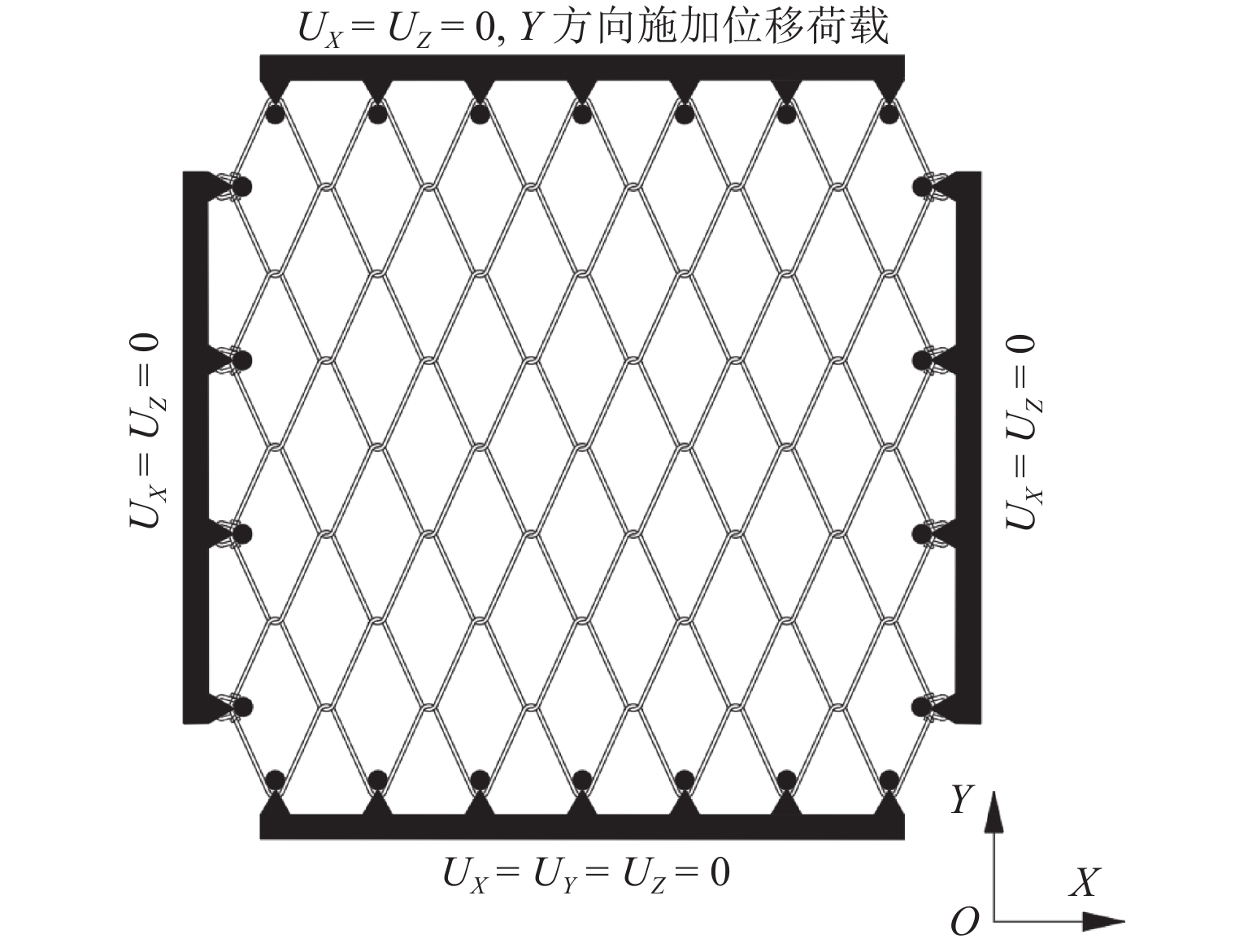
Sasiharan等[18]和Escallón等[15]均开展了G65格栅网平面内拉伸试验,获得了格栅网在两个方向(X方向和Y方向)拉伸荷载作用下的应力-应变关系曲线(应力为格栅网拉伸方向的荷载与横向宽度的比值,应变为拉伸方向的位移与拉伸方向的长度的比值),为此类格栅网的应用提供了基础试验数据. 拉伸试验简图及边界条件设置如图4所示. 图中:UX、UY、UZ 分别为沿X、Y、Z方向的位移. 沿Y方向进行试验过程中,格栅网一端固定,限制平面内X、Y、Z方向的移动;两侧面限制X、Z方向移动,Y方向自由移动;荷载施加端限制X、Z方向不发生移动,Y方向施加位移荷载. 同理,可以进行设置X方向拉伸的边界条件,并沿X方向试验.
2. 数值建模及求解方法研究
2.1 高强钢丝编织格栅网面内拉伸力学特性分析
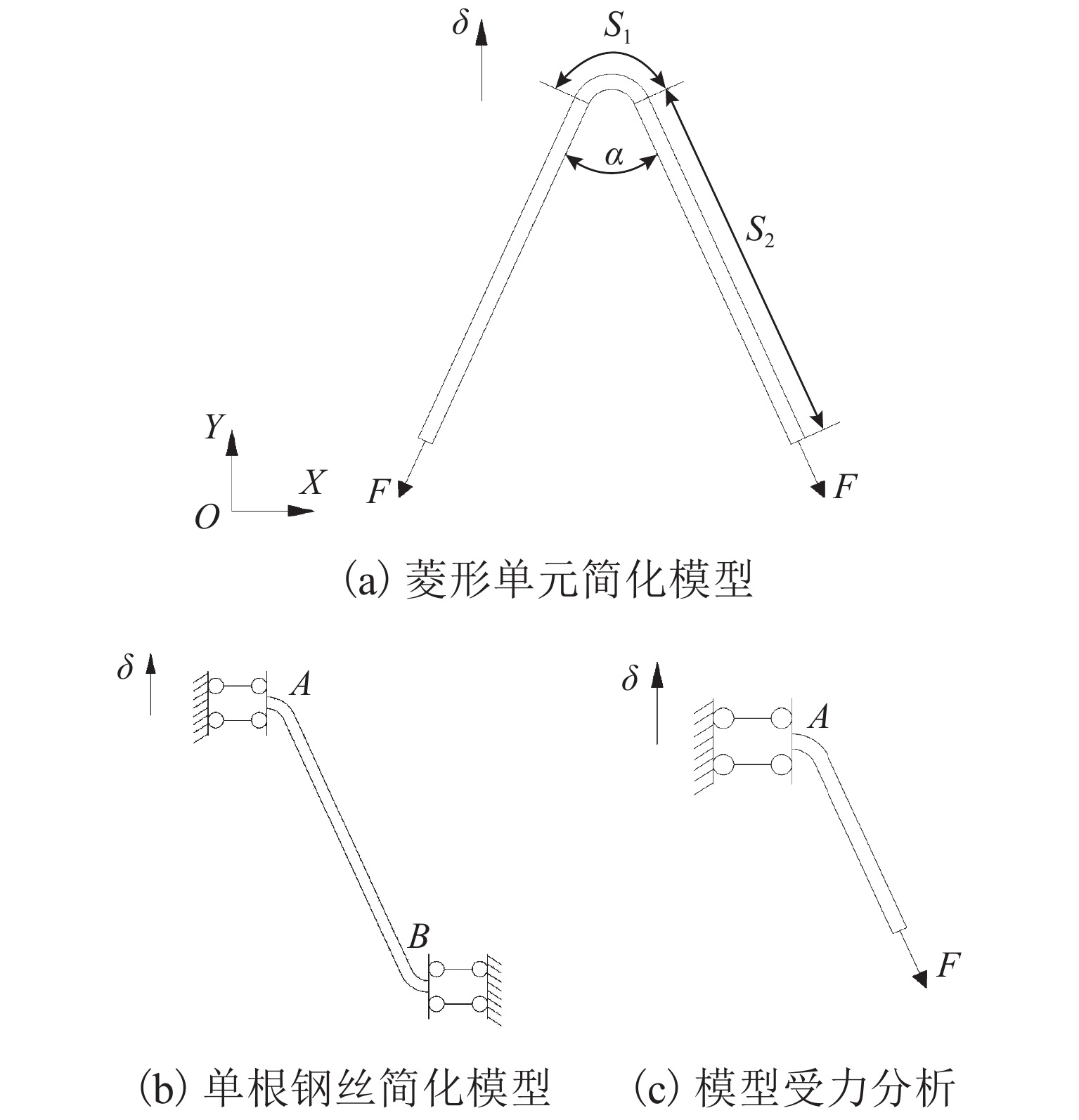
以Y方向拉伸试验进行分析,从图3中选取由单根钢丝组成的半个菱形单元,投影到XOY平面,如图5(a). 图中:S1为圆弧段投影长度;S2为菱形边长;按图4的试验边界条件,δ为钢丝的顶点沿Y方向的位移;F为两侧钢丝受力. 选取图5(a)的一半钢丝,忽略空间扭转的影响,按平面情况进行分析,可近似简化为图5(b)的计算模型[1],对图5(b)进行内力分析,可按图5(c)的受力图进行. 对截面A,存在弯矩
M 、轴力N 和剪力V ,分别如式(1)~(4).M=Fcosα2(S2+λS1)sinα2, (1) N=Fsinα2, (2) V=Fcosα2, (3) F=sfy, (4) 式(1)~(4)中:
λ 为考虑钢丝初始弯曲的修正系数;s 为截面面积;fy 为钢丝屈服应力.截面上的复合正应力为
σ=MWz+NS, (5) 式中:S为截面面积.
截面上的剪应力为
τ=VSzIzd, (6) 式(5)、(6)中:
Wz 为抗弯截面系数;Sz 为截面静矩;Iz 为截面惯性矩.当格栅网沿Y方向发生位移δ时,S1、α均发生变化,材料也将由弹性进入塑性,因此,联立式(1)~(6),基于Von.Mises屈服准则,通过不断地迭代近似求得格栅网破断时的极限荷载. 同理,也可对X方向进行类似求解.
2.2 格栅网的数值计算方法和数值模型的建立
格栅网平面内拉伸问题的数值求解主要涉及以下几个方面的内容:高强钢丝单轴拉伸的性能属性为材料非线性;格栅网在平面内拉伸下存在大变形,属于几何非线性;格栅网交叉点位置,随着拉伸变形的发展,接触状态会发生改变,属于状态非线性.
综合初步理论分析和数值求解涉及的非线性问题,采用ANSYS Mechanics 模块建立数值模型时,进行如下定义:
1) 几何建模:按Castro[19]的试验条件,格栅网在交叉连接的初始接触,沿Y方向尺寸约为0.972 m;沿X方向尺寸约为1.010 m;其余几何尺寸满足图3的参数要求;
2) 单元选择:由于格栅网中钢丝在交叉部位受轴向拉伸、弯曲和剪切作用,因此,选用BEAM189单元(3D二次有限应变梁单元),该单元基于Timoshenko理论,包括剪切变形的影响,可以考虑梁单元在轴力、弯矩和剪力耦合效应的影响. 为了节省计算时间,同时考虑到编织钢丝属于小应变材料,因此,计算中不考虑材料的塑形流动,使横截面面积保持不变.
3) 材料属性:在材料非线性方面,考虑塑形强化,基于图2的真应力-应变关系曲线进行计算,基于Von.Mises屈服准则判断材料的失效.
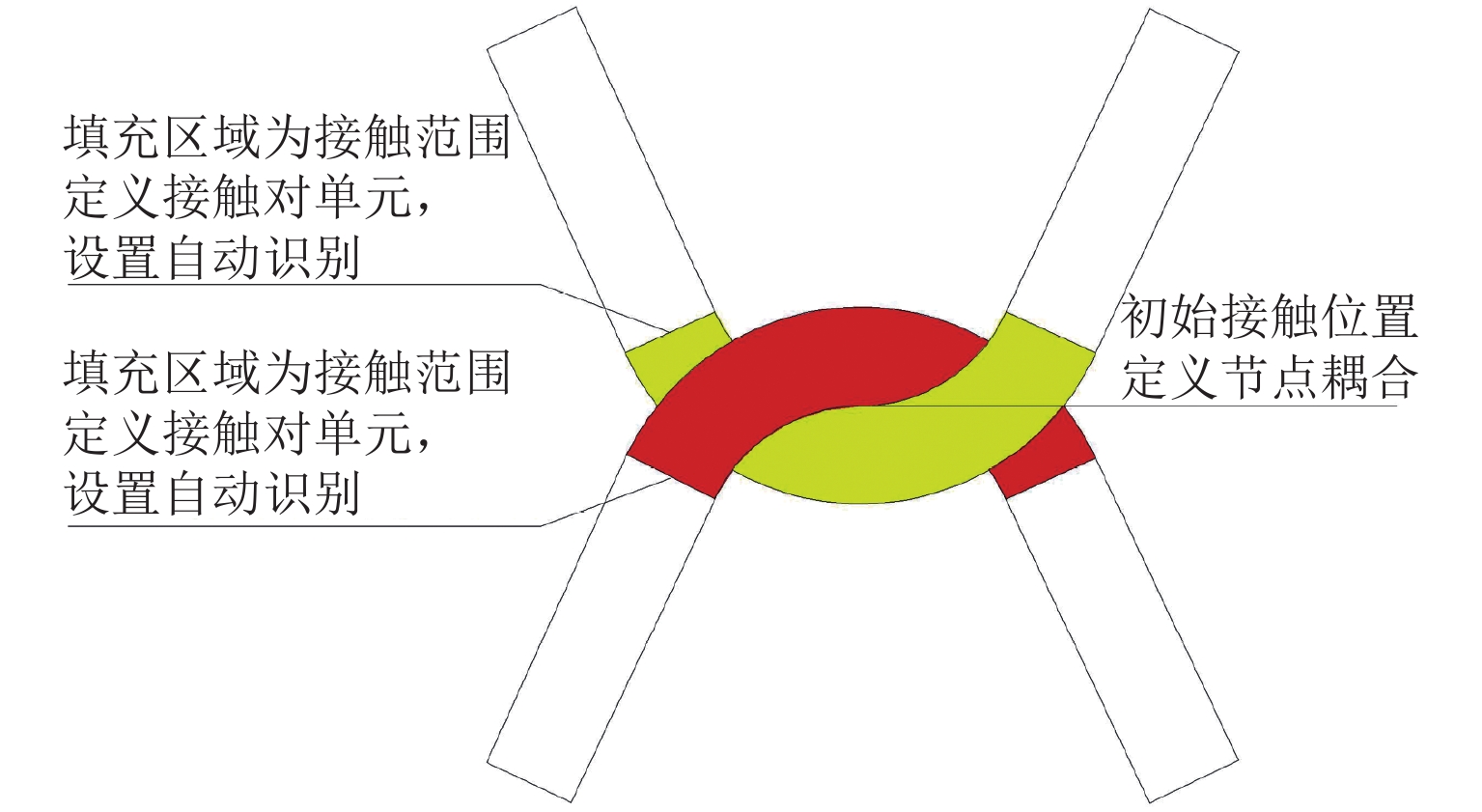
4) 状态非线性:当格栅网受到平面内荷载作用发生变形时,钢丝交叉部位由开始的线接触逐步过渡到面接触. 为此,定义接触类型为柔体-柔体接触,接触方式为梁单元接触,定义CONTA177和TARGE170为接触对单元,强制接触协调的计算方法采用罚函数法,设置接触自动识别,根据钢丝弯曲状态,自动探测接触范围. 由于钢丝连接部位的接触刚度非常大,仅定义接触计算收敛异常困难,需要很小荷载步和较大的计算时长,计算效率较低. 因此,这里假设在初始接触位置两者不产生滑移,在初始接触部位补充定义节点耦合(图6).
在边界条件及单元划分上:
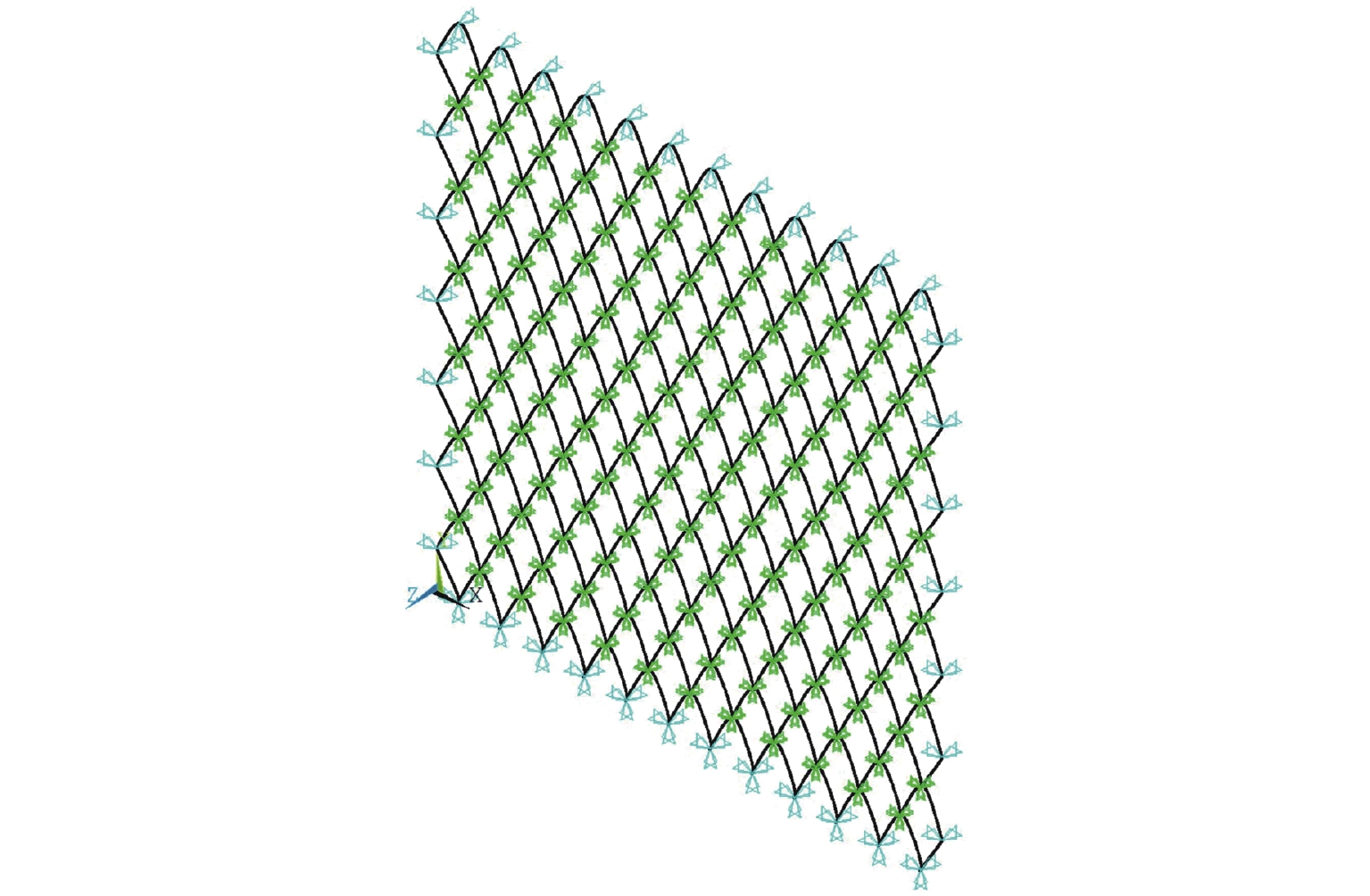
1) 当进行Y方向拉伸计算时,沿Y方向的一侧,对所有节点固定约束,即UX=UY=UZ=0;沿X方向的两个侧边,施加UX=UZ=0,UY方向可以自由移动;沿Y方向的另一侧,施加位移荷载,施加的最大位移为80 mm,建立的Y方向拉伸数值模型如图7所示.
2) 当进行X方向拉伸计算时,沿X方向的一侧,对所有节点固定约束,即UX=UY=UZ=0;沿Y方向的两个侧边,施加UY=UZ=0,UX方向可以自由移动;沿X方向的另一侧,施加位移荷载,施加的最大位移为300 mm.
3) 格栅网在拉伸过程中,S1圆弧段将发生急剧弯曲,同时承受轴力和剪力作用,且控制格栅网的破断,因此,对S1圆弧段进行细分,每个单元划分的长度尺寸为1 mm;对S2直线段,考虑到这部分不作为控制破断荷载,为平衡计算精度和效率,这部分单元划分的尺寸适当放宽.
4) 求解中,激活程序的线性搜索和大变形选项,基于力和位移共同控制的收敛准则和收敛容差,施加位移荷载步,每个荷载步施加1 mm的位移.
3. 数值计算与试验结果的对比
3.1 格栅网失效破坏判断
基于Von.Mises应力可以确定出金属韧性材料产生失效的准则,即结构中的Von.Mises应力
σVM (式(7))应当不大于材料的极限应力σY .σVM=1√2√(σ1−σ2)2 + (σ2−σ3)2 + (σ3−σ1)2, (7) 式中:
σ1 为最大主应力;σ2 为中间主应力;σ3 为最小主应力.由于采用ANSYS Mechanical 模块计算无法自动判断失效,需要通过后处理程序获得单元平均等效Von.Mises应力,并应用式(7)来判断单元是否失效.
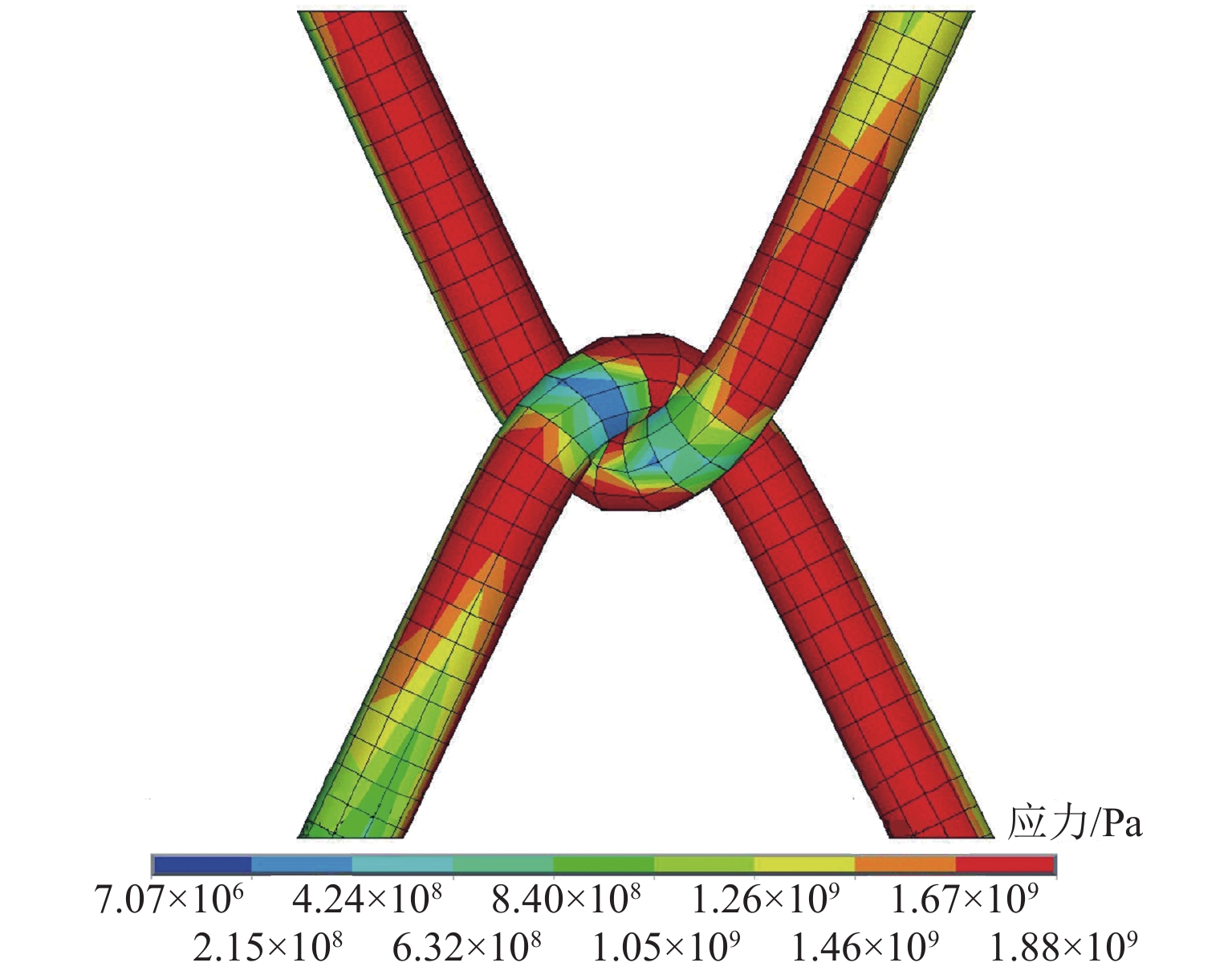
数值计算中,钢丝的失效均发生在交叉连接节点部位,这与试验和理论分析结果相吻合. 图8给出了格栅网中交叉连接部位失效单元在Y方向拉伸过程中的平均等效Von. Mises应力随拉伸应变的变化关系,数值计算中当拉伸应变达到0.068时,单元应力
σVM 超过极限应力σY ,此时格栅网发生破坏,破坏部位的等效应力云图见图9所示,由此可以确定格栅网Y方向拉伸应变极限为0.067. 采用相同的方法同样可以获得格栅网在X方向拉伸的极限应力.3.2 格栅网应力应变关系和等效弹性模量
在格栅网失效破坏判断的基础上,利用ANSYS后处理程序获得了数值计算得到的Y、X方向平面内拉伸荷载作用下的应力-应变关系曲线,并与试验获得的应力-应变关系曲线[19]进行对比分析,见图10所示.
从图10中可以看出:
1) 数值计算获得的格栅网Y方向应力-应变关系曲线开始时位于试验结果曲线下方,而后慢慢接近试验结果曲线,最终状态时位于试验结果曲线的上方;
2) 数值计算获得的格栅网X方向应力-应变关系曲线开始时位于试验结果曲线下方,经历较小的变形以后,迅速接近试验结果曲线,之后数值计算结果曲线位于试验结果曲线上方,且误差逐渐偏大.
采用线性拟合方法对图10中数值计算和试验的应力-应变关系曲线进行拟合(不考虑截距拟合),得到两个方向近似的等效弹性模量(刚度)见表1所示,从表中可以看出:数值计算数据拟合获得的格栅网等效弹性模量(刚度)与试验值较接近,Y方向误差为10.6%,X方向误差为18.5%.
表 1 应力-应变拟合的等效弹性模量(刚度)Table 1. Equivalent elastic modulus obtained by stress-strain curve fitting项目 Y 向 X 向 试验[19] 1929.7 178.6 数值计算 2133.3 145.5 误差/% 10.6 18.5 此外,从图10中可以获得格栅网面内拉伸荷载作用下的极限应力、应变,并与试验获得的极限应力、应变列于表2. 从表中可以看出:试验和数值计算获得的格栅网极限应变、应力值比较接近,Y方向极限应力的误差为10.0%,极限应变误差为12.8%;X方向极限应力的误差为0.7%,极限应变误差为18.3%.
3.3 数值模型和数值计算方法的误差分析
对比数值计算和试验获得的格栅网应力应变-关系曲线、极限应力、应变和等效弹性模量,从数值模型和数值计算方法方面作如下分析:
1) 数值计算格栅网X、Y方向面内拉伸过程中,初期的应力较试验结果偏小,而后期的应力均较试验结果偏大. 主要原因在于非线性数值计算中,没有考虑在变形过程中材料的塑形流动,而材料采用的应力-应变关系为真应力-真应变关系曲线,造成钢丝截面的承载力大于实际承载力,同等应变下越到后期数值计算的应力值应比试验值偏大越多. 但钢丝为低应变材料,因此,这一方面的影响对计算结果不会产生太大影响,从Y方向的拉伸曲线对比情况看,结果吻合度能达到工程应用要求.
2) 数值计算Y方向的应力-应变关系曲线与试验结果吻合较好,而X方向的应力-应变关系曲线较试验结果偏差较大. 主要原因在于数值建模过程中,钢丝交叉部位为保证计算效率和精确,采用了“节点耦合 + 接触”的方式处理,对Y方向的拉伸而言,拉伸方向与可能滑移方向垂直,钢丝交叉部位产生滑移的可能性较小,因此,数值计算结果与试验结果吻合度高;对X方向的拉伸而言,拉伸方向与可能滑移方向平行,滑移对数值计算结果影响较大,忽略滑移会造成一定的偏差.
3) 数值计算中X、Y方向的极限应力与试验结果吻合较好,而极限应变均与试验结果有较大偏差. 主要有3个方面原因:滑移对极限应力计算结果影响不大,节点部位的破断主要由拉伸过程中钢丝内部的弯矩、剪力和轴力控制,钢丝间因滑移而产生的内力不占主要部分;滑移对极限应变存在一定的影响,忽略滑移会造成极限应变计算结果偏小,对Y方向拉伸影响小,对X方向拉伸影响大;采用beam189单元进行计算,无法考虑弯扭耦合作用,因此对数值计算结果偏差也造成了影响.
4. 结 论
高强钢丝编织的格栅网在面内拉伸荷载作用下的数值分析涉及到材料非线性、几何非线性和状态非线性,交叉连接位置处于复杂应力状态,数值计算难度较大. 为此,基于ANSYS Mechanical模块,开展了格栅网平面内拉伸力学性能的数值分析,获得了如下结论:
1) 格栅网钢丝交叉点受力状态复杂,采用单独的定义节点耦合或定义接触,均无法较好地解决接触状态非线性或计算收敛问题,因此,提出了采用“节点耦合 + 接触”的方法来考虑此类松散结构的连接,计算效率和精度均达到了较好的效果;
2) 提出的数值模型和计算方法在预测格栅网平面内拉伸荷载作用下的应力-应变变化趋势、极限应力-应变和等效弹性模量方面均具有较好的精度,可作为后续对不同编织参数格栅网力学性能分析的有效计算手段.
-
表 1 应力-应变拟合的等效弹性模量(刚度)
Table 1. Equivalent elastic modulus obtained by stress-strain curve fitting
项目 Y 向 X 向 试验[19] 1929.7 178.6 数值计算 2133.3 145.5 误差/% 10.6 18.5 -
[1] 汪敏. 柔性防护技术和柔性棚洞的设计及工程应用研究[D]. 重庆: 后勤工程学院, 2011. [2] 汪敏,石少卿,崔廉明,等. 三开间单跨柔性棚洞在落石冲击作用下的试验研究[J]. 土木工程学报,2018,51(5): 37-47.WANG Min, SHI Shaoqing, CUI Lianming, et al. Experimental investigation on three-bay and single-span flexible rock-shed under impact of rockfall[J]. China Civil Engineering Journal, 2018, 51(5): 37-47. [3] 赵世春,余志祥,赵雷,等. 被动防护网系统强冲击作用下的传力破坏机制[J]. 工程力学,2016,33(10): 24-34. doi: 10.6052/j.issn.1000-4750.2016.06.ST08ZHAO Shichun, YU Zhixiang, ZHAO Lei, et al. Damage mechanism of rockfall barriers under strong impact loading[J]. Engineering Mechanics, 2016, 33(10): 24-34. doi: 10.6052/j.issn.1000-4750.2016.06.ST08 [4] 余志祥,张丽君,骆丽茹,等. 韧性挑篷防护网系统抗冲击性能研究[J]. 岩石力学与工程学报,2020,39(12): 2505-2516.YU Zhixiang, ZHANG Lijun, LUO Liru, et al. Study on impact resistance of a resilient steel canopy protection system[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(12): 2505-2516. [5] 俞棠荣. 金属网对弹体主动诱爆拦截的作用机理研究[D]. 重庆: 陆军勤务学院, 2019. [6] 刘一鸣,熊自明,王德荣,等. 飞网弹主动防护拦截系统初探[J]. 防护工程,2018,40(6): 30-35.LIU Yiming, XIONG Ziming, WANG Derong, et al. Preliminary research on active protection interception system of flying net projectile[J]. Protective Engineering, 2018, 40(6): 30-35. [7] 崔廉明,石少卿,汪敏,等. 多位置分布配重下引导式落石缓冲系统冲击防护性能研究[J]. 岩石力学与工程学报,2019,38(2): 332-342. doi: 10.13722/j.cnki.jrme.2018.1052CUI Lianming, SHI Shaoqing, WANG Min, et al. Research on the impact protection performance of the rockfall attenuator system under multiposition distributed counterweights conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(2): 332-342. doi: 10.13722/j.cnki.jrme.2018.1052 [8] 郭立平,余志祥,骆丽茹,等. 基于力流等效的环形网顶破力学行为解析方法[J]. 工程力学,2020,37(5): 129-139.GUO Liping, YU Zhixiang, LUO Liru, et al. An analytical method of puncture mechanical behavior of ring nets based on the load path equivalence[J]. Engineering Mechanics, 2020, 37(5): 129-139. [9] 余志祥,严绍伟,许浒,等. 活塞杆点支式柔性缓冲系统冲击力学行为[J]. 土木工程学报,2018,51(11): 61-69,112.YU Zhixiang, YAN Shaowei, XU Hu, et al. Mechanical behavior of piston rod point-supported flexible buffer system[J]. China Civil Engineering Journal, 2018, 51(11): 61-69,112. [10] ALBABA A, LAMBERT S, KNEIB F, et al. DEM modeling of a flexible barrier impacted by a dry granular flow[J]. Rock Mechanics and Rock Engineering, 2017, 50(11): 3029-3048. doi: 10.1007/s00603-017-1286-z [11] ESCALLON J P, WENDELER C, CHATZI E, et al. Parameter identification of rockfall protection barrier components through an inverse formulation[J]. Engineering Structure, 2014, 77: 1-16. [12] 汪敏,石少卿,刘盈丰,等. 防落石柔性棚洞的耗能性能分析及优化设计[J]. 振动与冲击,2018,37(1): 216-222.WANG Min, SHI Shaoqing, LIU Yingfeng, et al. Eneigy dissipation analysis and optimum design on a flexible rock-shed for rockfall protection[J]. Journal of Vibration and Shock, 2018, 37(1): 216-222. [13] VON BOETTICHER A, VOLKWEIN A. Numerical modelling of chain-link steel wire nets with discrete elements[J]. Canadian Geotechnical Journal, 2019, 56(3): 398-419. doi: 10.1139/cgj-2017-0540 [14] DEL COZDÍAZ J J, NIETO P J G, FRESNO D C, et al. Non-linear analysis of cable networks by FEM and experimental validation[J]. International Journal of Computer Mathematics, 2009, 86(2): 301-313. doi: 10.1080/00207160801965339 [15] ESCALLÓN J P, BOETTICHER V, WENDELER C, et al. Mechanics of chain-link wire nets with loose connections[J]. Engineering Structures, 2015, 101: 68-87. doi: 10.1016/j.engstruct.2015.07.005 [16] 全国钢标准化技术委员会. 钢丝及钢丝制品(通用试验方法): GB/T 36915—2019[S]. 北京: 中国标准化出版社, 2019. [17] 齐欣,余志祥,张丽君,等. 被动柔性防护系统对落石冲击作用的传播效应[J]. 西南交通大学学报,2020,55(5): 1085-1093. doi: 10.3969/j.issn.0258-2724.20180442QI Xin, YU Zhixiang, ZHANG Lijun, et al. Propagation effect of passive flexible protection system on rockfall impact[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 1085-1093. doi: 10.3969/j.issn.0258-2724.20180442 [18] SASIHARAN N, MUHUNTHAN B, BADGER T C, et al. Numerical analysis of the performance of wire mesh and cable net rockfall protection systems[J]. Engineering Geology, 2006, 88(1/2): 121-132. [19] CASTRO D F. Study and analysis of flexible membranes as support elements for the stabilization of land-fill slopes[D]. Spain: University of Cantabria, 2000 期刊类型引用(1)
1. 汪敏,黄祺临,周帅,崔廉明. 刚性弹体冲击金属网网孔的试验和数值分析. 振动与冲击. 2023(23): 55-64 .  百度学术
百度学术其他类型引用(0)
-






 下载:
下载:



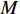





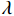
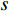
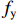


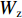
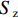



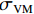
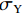
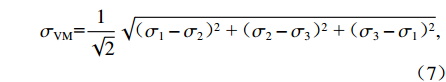
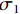
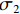
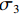
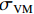
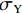




 下载:
下载:









 百度学术
百度学术