Day-Ahead Optimal Scheduling of Co-phase Traction Power Supply System with Photovoltaic and Hybrid Energy Storage
-
摘要:
既有牵引供电系统中以负序为主的电能质量问题以及电分相环节严重制约了其安全、高效运行，目前理想的解决方案是基于对称补偿理论的同相供电技术. 通过同相补偿装置中的直流母线接入光伏发电系统以及混合储能装置，进一步实现再生回馈能量利用和牵引负荷削峰填谷，提高光伏渗透率. 因此，建立了一种同相牵引供电系统优化运行模型，该模型以同相牵引变电所日运行成本最低为目标，以混合储能装置充放电策略、光伏出力以及潮流控制器功率为决策变量，尤其考虑了电网侧三相电压不平衡度约束；进一步将原始优化模型中非线性约束进行线性化处理，得到混合整数线性规划模型，并利用商业规划求解器CPLEX进行求解. 算例分析结果表明：接入光伏与混合储能装置后日运行成本可节省36.45%，且三相电压不平衡度满足国标上限2%的要求.
Abstract:Power quality issues represented by voltage unbalance and the electrical sectioning issues have severely restricted the safe and efficient operation of the traction power supply system. At present, the ideal solution is the co-phase power supply technology based on symmetrical compensation theory. By integrating the photovoltaic power generation system and the hybrid energy storage system with the DC bus of power flow controller, the utilization of regenerative braking energy, and peak-shaving and valley-filling of traction load can be further achieved to improve photovoltaic penetration rate. For this purpose, the optimal operation model of co-phase traction power supply system is established, which sets the minimum daily operation cost of traction substation as the objective, and takes the charging and discharging strategy of hybrid energy storage, photovoltaic output and power flow controller power as decision variables, and also takes into account the three-phase voltage unbalance constraint. The nonlinear constraints are linearized to formulate the mixed-integer linear programming model, which can be solved by programming solver CPLEX. The case study results show that the integration of photovoltaic and hybrid energy storage can effectively reduce 36.45% of daily operating cost, while the three-phase voltage unbalance meets the upper limit of 2% in the national standard.
-
工频单相交流制牵引供电系统不仅是高速铁路和重载铁路的最主要动力来源，还推动了城市轨道交通以及市域铁路的发展. 未来，我国牵引供电系统将朝着“安全、高质、高效”的目标进一步发展.
然而，既有牵引供电系统不可避免存在着以三相电压不平衡为主的电能质量问题以及电力机车过分相问题[1]. 李群湛[2]提出的基于对称补偿理论的同相供电技术方案可以有效解决上述问题，即在牵引所采用三相-单相对称变换的潮流控制器（power flow controller，PFC），彻底解决负序问题，同时牵引侧电压统一，取消电分相环节.
另一方面，我国可再生能源近年来发展迅速，其中光伏发电具有无污染、无噪音和地域限制小等优点. 同时，电气化铁路具有地域分布广、铁路网与可再生能源网存在地理交集多的特点，如兰新、川藏铁路穿越光伏资源丰富的西南和西北地区[3]. 此外，牵引负荷需求较大，具有很高的消纳潜力，尤其是在外部电源薄弱地区，可再生能源接入亦可起重要支撑作用. 以光伏为主的可再生能源接入牵引供电系统不仅可以提高可再生能源渗透率，还可以结合储能装置，促进再生制动能量利用，实现牵引负荷削峰填谷，有效降低电费成本[4-5].
为推动铁路能量管理智能化，欧盟在第七框架方案下开展了MERLIN项目[6]. 基于该项目，文献[7]引入智能电网理念以及架构体系，提出了一种“集中-分散”式架构的铁路能量管理系统（railway energy management system, REM-S），以实现多时间尺度下能量优化利用. 在REM-S框架基础上，文献[8]开发了REM-S软件套件，并进行了离线和在线试验，验证了软件套件的有效性和可靠性. 文献[9]考虑了光伏/风电以及混合储能装置接入的牵引供电系统，建立了计及牵引网阻抗的牵引供电系统最优运行模型. 然而，该模型为混合整数非线性规划模型，计算复杂度极大. 文献[10]针对光伏和储能装置接入铁路车站的场景，提出了基于混合整数线性规划模型的智能车站能量管理策略. 文献[11]基于接入光伏和混合储能的柔性牵引供电系统，建立了基于模型预测控制的多时间尺度优化调度模型.
组合式同相牵引供电系统具有独特的网络拓扑结构、潮流分布规律以及运行组织方式，如何揭示系统内部“源-车-储”互动特性，准确描述系统稳态数学模型，同时计及以电压不平衡为主的电能质量约束，并通过合理的模型转化实现快速、准确求解，需要进一步研究.
本文面向集成光伏和混合储能装置的同相牵引供电系统优化调度场景，建立了以同相牵引变电所日内运行成本最低为目标，以光伏出力、混合储能装置充放电策略以及潮流控制器为决策变量的同相牵引供电系统优化运行模型，尤其考虑了电网侧电压不平衡度约束. 通过将原始模型中非线性元素进行线性化处理，得到混合整数线性规划模型（mixed integer linear program，MILP）并利用商业规划求解器CPLEX进行求解. 最后通过算例分析验证上述优化模型的正确性和有效性.
1. 系统结构与问题描述
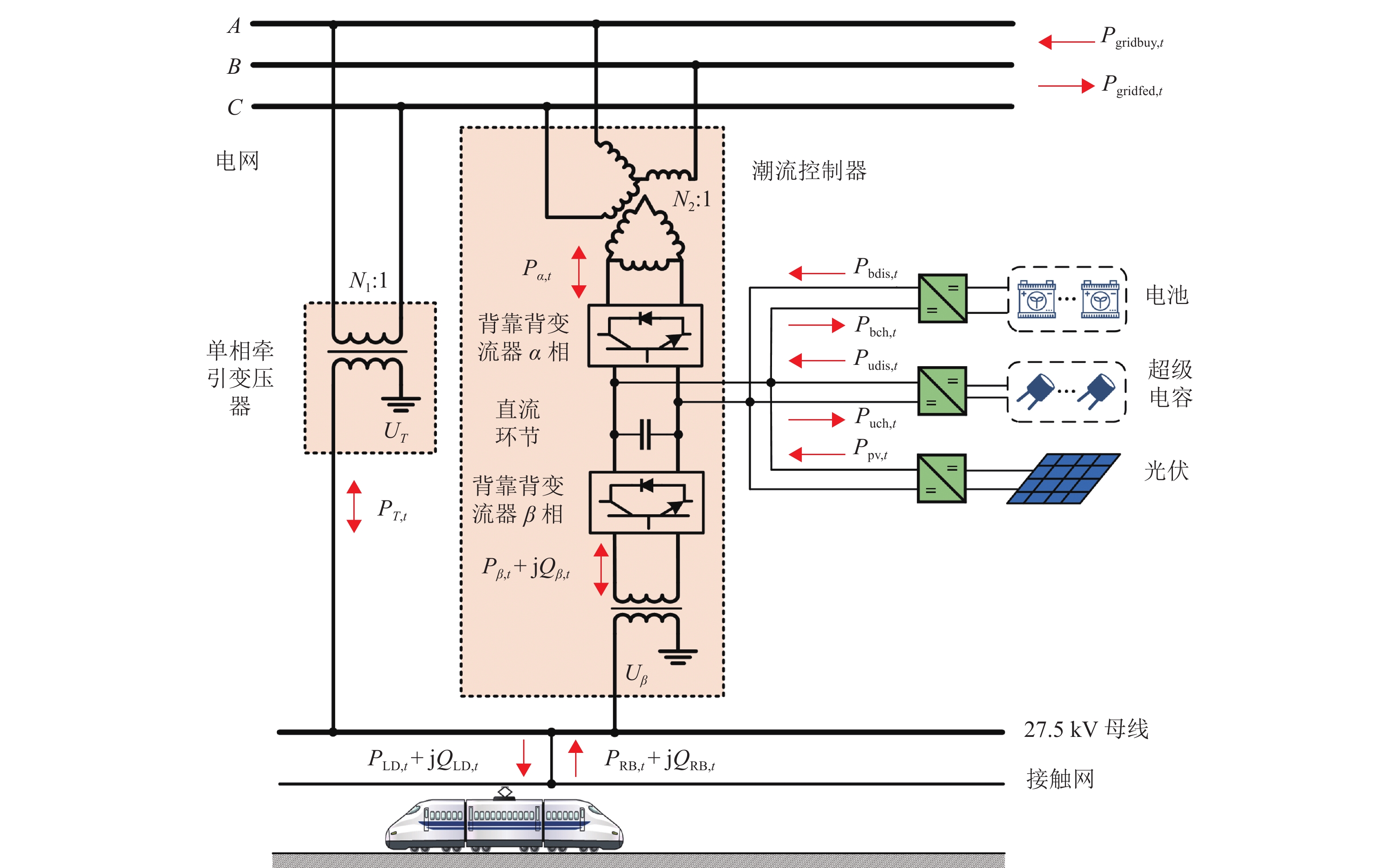
同相牵引供电系统中潮流控制器的直流环节为混合储能装置以及光伏的接入提供了有利条件，避免了额外的交直流变流器，以单三相组合式同相牵引供电方案为例，其系统结构如图1所示. 图中：Pgridbuy,t和Pgridfed,t分别为同相牵引变电所从电网购得的电能功率和反馈回电网的功率，t为时刻；Ppv,t为光伏出力功率；Pbdis,t、Pbch,t和Pudis,t、Puch,t分别为电池和超级电容的放电、充电功率；PT,t、Pα,t、Pβ,t和Qβ,t分别为牵引变压器、PFC中背靠背变流器α相、β相有功潮流功率和β相无功潮流功率；PLD,t和QLD,t分别为有功和无功牵引负荷功率；PRB,t和QRB,t分别为再生制动功率的有功和无功分量；UT和Uβ分别为单相牵引变压器在牵引侧的输出电压和β相变流器在电网侧的输入电压；N1和N2分别为单相牵引变压器和YNd11接线匹配变压器的变比.
图1中，单相牵引变压器与潮流控制器组成电网侧与牵引侧间的有功潮流传递通道，而无功补偿则由潮流控制器中的背靠背变流器完成. 更具体地，β相变流器负责牵引侧的无功补偿，而α相变流器参与电网侧与直流环节有功传递以及电网侧无功补偿. 此外，电网侧负序电流包含牵引变压器电流和α相变流器电流两个元素，通过潮流控制器中背靠背变流器使得两部分电流方向相反，则可以实现负序电流的部分补偿甚至完全补偿.
通过背靠背变流器直流环节接入的混合储能装置是实现同相牵引供电系统能量平衡以及经济运行的重要基础，其作用主要体现在：1） 平抑可再生能源出力的波动性，减小可再生能源并网对牵引供电系统的冲击性，保持系统稳定，提高可再生能源渗透率；2） 通过合理控制其充放电，实现牵引负荷的时空转移，继而实现牵引负荷削峰填谷，大幅减小两部制电价政策下的需量电费成本以及电度电费成本. 面向同相牵引供电系统的应用场景，考虑到牵引负荷较大且具有剧烈波动特性，高容量密度的电池与高功率密度的超级电容相组合的混合储能系统较为适合[9].
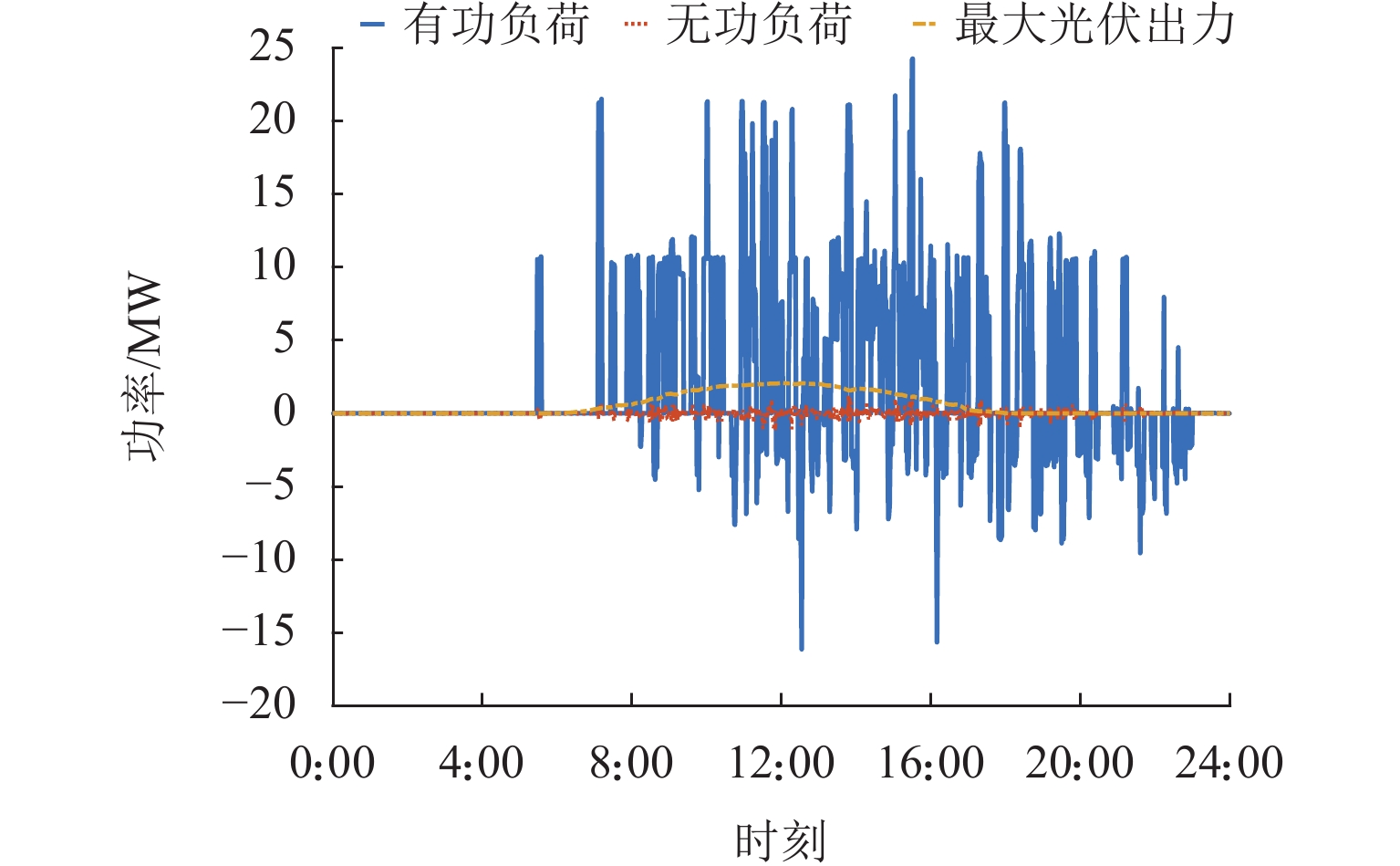
同相牵引供电系统优化调度模型中，对于优化调度单位时间尺度 ∆t的选择，电力系统以及微电网相关文献以15 min或者1 h为主[12-13]. 考虑到牵引供电系统应用场景中牵引负荷的波动特性，本文取∆t =1 min作为模型精度与计算复杂度的折衷[10].
2. 优化模型的建立
2.1 目标函数
目标函数旨在最小化同相牵引变电所日运行成本f0，包括电度电费成本Cgrid、需量电费成本Cdem、光伏运行维护成本CPV以及混合储能装置运行维护成本CHESS. 需要注意的是，此处日前优化调度阶段没有考虑电池老化及更换成本.
$$ \min \;{f_0} = {C_{{\text{grid}}}} + {C_{{\text{PV}}}} + {C_{{\text{HESS}}}} + {C_{{\text{dem}}}}, $$ (1) $$ {C_{{\text{grid}}}} = \sum\limits_{t = 1}^{{N_{\text{T}}}} {\left( {{c_{{\text{buy,}}t}}{P_{{\text{gridbuy,}}t}}{\text{ + }}{c_{{\text{fed,}}t}}{P_{{\text{gridfed,}}t}}} \right)} \Delta t , $$ (2) $$ {C_{{\text{PV}}}} = \sum\limits_{t = 1}^{{N_{\text{T}}}} {{c_{{\text{pv,}}t}}{P_{{\text{pv,}}t}}} \Delta t , $$ (3) $$ {C_{{\text{HESS}}}} = \sum\limits_{t = 1}^{{N_{\text{T}}}} {\left[ {{c_{{\text{b,}}t}}\left( {{P_{{\text{bdis,}}t}} + {P_{{\text{b}},{\text{ch,}}t}}} \right) + {c_{{\text{u,}}t}}\left( {{P_{{\text{udis,}}t}} + {P_{{\text{uch,}}t}}} \right)} \right]\Delta t}, $$ (4) $$ {C_{{\text{dem}}}} = {{\left(\max \; {{P_{{\text{dem,}}t}}} \right) {c_{{\text{dem}}}}} / {{N_{{\text{day}}}}}}, $$ (5) $$ {P_{{\text{dem,}}t}} = \sum\limits_t^{t + 14} {{{{P_{{\text{gridbuy,}}t}}} \mathord{\left/ {\vphantom {{{P_{{\text{gridbuy,}}t}}} {15}}} \right. } {15}}} ,\quad \forall t = 1,2,\cdots,{N_{\text{T}}} - 14 , $$ (6) 式中： Pdem,t为需量大小；cpv,t、cb,t、cu,t、cdem分别为光伏、电池、超级电容运行维护成本价格、需量电费价格；Nday为系统月运行天数，一般取30 d；cbuy,t和cfed,t分别为购电价格和反馈回电网电能的征收费用价格，需要注意的是根据不同的反馈电能电费征收标准，cfed,t的取值也有所区别，可能的取值有正值、负值或0；NT为每日总时间段数，NT=1440.
实际运营中，最大需量由月内每15 min牵引负荷均值的最大值决定，即定义1个时刻为15 min. 假定月内列车时刻表固定情况下同相牵引变电所日内运行具有重复性，故计算最大需量值的时间尺度可以取为一天. 此处最大需量由滑动法求得，且由于∆t取1 min，故式（6）中t的取值为1～(NT−14).
2.2 约束条件
2.2.1 功率平衡约束
根据图1所示的潮流分布规律，得到系统功率平衡约束. 需要注意的是，考虑到变流器运行效率高，其功率损耗与系统潮流相比影响较小，故可不考虑变流器损耗[14].
$$ {P_{{\text{gridbuy,}}t}} - {P_{{\text{gridfed,}}t}} = {P_{{\text{T,}}t}} + {P_{\alpha ,t}} , $$ (7) $$ {P_{\alpha ,t}} + {P_{{\text{bdis,}}t}} + {P_{{\text{udis,}}t}} + {P_{{\text{pv,}}t}} = {P_{\beta {\text{,}}t}} + {P_{{\text{bch,}}t}} + {P_{{\text{uch,}}t}} ,$$ (8) $$ {P_{{\text{T,}}t}} + {P_{\beta {\text{,}}t}} = {P_{{\text{LD,}}t}} - {P_{{\text{RB,}}t}}, $$ (9) $$ {Q_{\beta {\text{,}}t}} = {Q_{{\text{LD,}}t}} - {Q_{{\text{RB,}}t}}, $$ (10) $$ 0 \leqslant {P_{{\text{gridbuy,}}t}} \leqslant {v_{{\text{grid,}}t}}{{\overline P_{{\text{grid}}}}} ,$$ (11) $$ 0 \leqslant {P_{{\text{gridfed,}}t}} \leqslant \left( {1 - {v_{{\text{grid,}}t}}} \right){P_{{\text{gridbuy,}}t}}, $$ (12) 式中：
${{\overline P_{{\text{grid}}}}}$ 为同相牵引变电所与电网交互功率的最大限值；vgrid,t为同相牵引变电所与电网交互功率方向的二进制变量，vgrid,t =1表示交互功率由电网流向同相牵引变电所，vgrid,t =0表示交互功率由同相牵引变电所反馈至电网.2.2.2 混合储能系统约束
1） 前后时刻充放电功率与存储能量约束
时刻t +1储能元件存储电能与时刻t剩余电能以及充放电功率相关，同时计及充放电效率，如式（13）所示.
$$ \left\{ {\begin{aligned} {{E_{{\text{b}},t + 1}} = \left( {1 - {\varepsilon _{\text{b}}}} \right){E_{{\text{b}},t}} - {{{P_{{\text{bdis,}}t}}\Delta t} \mathord{\left/ {\vphantom {{{P_{{\text{bdis,}}t}}\Delta t} {{\eta _{{\text{bdis}}}}}}} \right. } {{\eta _{{\text{bdis}}}}}} + {\eta _{{\text{bch}}}}{P_{{\text{bch,}}t}}\Delta t} ,\\ {{E_{{\text{u}},t + 1}} = \left( {1 - {\varepsilon _{\text{u}}}} \right){E_{{\text{u}},t}} - {{{P_{{\text{udis,}}t}}\Delta t} \mathord{\left/ {\vphantom {{{P_{{\text{udis,}}t}}\Delta t} {{\eta _{{\text{udis}}}}}}} \right. } {{\eta _{{\text{udis}}}}}} + {\eta _{{\text{uch}}}}{P_{{\text{uch,}}t}}\Delta t},\\ \end{aligned}} \right. $$ (13) 式中：Eb,t、Eu,t分别为时刻t电池、超级电容存储的能量；ηbch、ηbdis和ηuch、ηudis分别为电池和超级电容的充电、放电效率；εb、εu分别为电池、超级电容的自放电率.
2） 充电功率与存储容量约束
为避免储能元件过充过放，其荷电状态（state of charge，SOC）需要始终处于设定的上下限范围内. 此外，储能元件充放电功率也受其变流器容量大小限制，故约束为
$$ \left\{ {\begin{aligned} &{{{{\underline {S }}\; _{{\text{ocb}}}}} {E_{{\text{b,rate}}}} \leqslant {E_{{\text{b,}}t}} \leqslant {{{\overline {S }}_{{\text{ocb}}}}} {E_{{\text{b,rate}}}}} ,\\ & {{{{\underline {S }}\; _{{\text{ocu}}}}} {E_{{\text{u,rate}}}} \leqslant {E_{{\text{u,}}t}} \leqslant {{{\overline {S }}_{{\text{ocu}}}}} {E_{{\text{u,rate}}}}}, \\ & 0 \leqslant {P_{{\text{bdis,}}t}} \leqslant {v_{{\text{b,}}t}}{P_{{\text{b,rate}}}}, \\ & 0 \leqslant {P_{{\text{bch,}}t}} \leqslant \left( {1 - {v_{{\text{b,}}t}}} \right){P_{{\text{b,rate}}}}, \\ &0 \leqslant {P_{{\text{udis,}}t}} \leqslant {v_{{\text{u,}}t}}{P_{{\text{u,rate}}}}, \\ &0 \leqslant {P_{{\text{uch,}}t}} \leqslant \left( {1 - {v_{{\text{u,}}t}}} \right){P_{{\text{u,rate}},}} \end{aligned}}\right. $$ (14) 式中：
$ {{ \overline {S }_{{\text{ocb}}}}} $ 、$ {{\underline {S }\; _{{\text{ocb}}}}} $ 和$ {{\overline {S }_{{\text{ocu}}}}} $ 、$ {{\underline {S }\; _{{\text{ocu}}}}} $ 分别为电池荷电状态和超级电容荷电状态的上、下限值；Pb,rate、Pu,rate分别为电池、超级电容额定功率；vb,t、vu,t分别为电池、超级电容充、放电状态的二进制变量，如值为1表示放电，值为0表示充电，以保证充电和放电状态不会同时存在.3） 始末荷电状态约束
为便于牵引变电所的每日运行调度，令电池和超级电容每日初始时刻的荷电状态与结束时刻荷电状态相等.
$$ \left\{ {\begin{aligned} {{E_{{\text{b,}}t}|_{t{\text{ = }}1}} = {E_{{\text{b,}}t}|_{t = {N_{\text{T}}}}} = {S _{{\text{ocb}},t}|_{t = 0}}{E_{{\text{b,rate}}}}} ,\\ {{E_{{\text{u,}}t}|_{t{\text{ = }}1}} = {E_{{\text{u,}}t}|_{t = {N_{\text{T}}}}} = {S _{{\text{ocu}},t}|_{t = 0}}{E_{{\text{u,rate}}}}} , \end{aligned}} \right. $$ (15) 式中：Socb,t|t=0、Socu,t|t=0分别为蓄电池、超级电容的初始荷电状态值.
4） 电池的充放电次数约束
为了避免日内电池频繁充放电，基于电池的充放电状态二进制变量vb,t，进行如下约束：
$$ \left\{ {\begin{aligned} &{{v_{{\text{b}},t{\text{ + }}1}} - {v_{{\text{b}},t}} \leqslant {v_{{\text{switch,}}t}}} ,\\ &{{v_{{\text{b}},t}} - {v_{{\text{b}},t{\text{ + }}1}} \leqslant {v_{{\text{switch,}}t}}} ,\\ &{\displaystyle\sum\limits_{t = 1}^{{N_{\text{T}}}} {{v_{{\text{switch,}}t}}} \leqslant 2{N_{{\text{cycle}}}} - 1} , \end{aligned}} \right. $$ (16) 式中：vswitch,t为电池充电和放电状态发生切换的二进制变量，vswitch,t =1表示电池由充电状态变为放电状态或放电状态变为充电状态，vswitch,t =0表示状态不变；Ncycle为日内电池充放电循环次数的上限.
为了便于线性化建模，认为连续两次电池充放电状态切换等效于一次充放电循环，且忽略最后一次状态的切换，故要求日内vswitch,t之和应不大于2Ncycle−1.
2.2.3 光伏出力约束
在同相牵引供电系统的日前调度阶段，光伏出力为非负且受其预测值上界的约束. 在日内运行时，光伏变流器可以实时控制光伏输出，因而光伏出力约束为
$$ 0 \leqslant {P_{{\text{pv}},t}} \leqslant {{\overline P_{{\text{pv}},t}}} ,$$ (17) 式中：
$ {{\overline P_{{\text{pv}},t}}} $ 为光伏出力功率上界值.2.2.4 潮流控制器约束
潮流控制器中流过α和β相变流器的有功及无功功率受其额定容量约束，即：
$$ \left\{ {\begin{aligned} {{{ {{P^2_{\alpha ,t}}} }} + {{ {{Q^2_{\alpha ,t}}} }} \leqslant {{ {{S ^2_{\alpha ,{\rm{cap}}}}} }}}, \\ {{{ {{P^2_{\beta ,t}}} }} + {{ {{Q^2_{\beta ,t}}} }} \leqslant {{ {{S ^2_{\beta ,{\rm{cap}}}}} }}} , \end{aligned}} \right. $$ (18) 式中：Pα,t、Qα,t和Pβ,t、Qβ,t分别为流过α和β相变流器的有功、无功功率；Sα,cap和Sβ,cap分别为α和β相变流器额定容量.
假定α相变流器只参与电网侧与牵引侧的有功功率传递，不参与电网侧无功补偿，则约束式（18）中α相变流器容量约束等效为
$$ - {S _{\alpha ,{\rm{cap}}}} \leqslant {P_{\alpha ,t}} \leqslant {S _{\alpha ,{\rm{cap}}}}. $$ (19) 2.2.5 电压不平衡约束
针对目前高速铁路牵引供电系统中最突出的电能质量问题，本文中考虑由负序引起的三相电压不平衡约束. 通常情况下，电力部门以牵引供电系统在公共连接点（point common connection，PCC）处的三相电压不平衡度评估其负序影响. 根据我国电能质量标准[15]，三相电压不平衡度表达式为
$$ {\varepsilon _{\text{U}}} = \sqrt 3 \frac{{{U_{\text{S}}}\left| {{{I}_{{\text{neg}}}}} \right|}}{{{S _{{\text{cap}}}}}} \leqslant {{\overline \varepsilon _{\text{U}}}} ,$$ (20) 式中：|·|为电流相量幅值；US、Scap分别为三相侧额定线电压（kV）、电网短路容量（MV·A）；
${{\overline \varepsilon _{\text{U}}}}$ 为三相电压不平衡度上限值. 这些参数的数值在同相牵引供电系统日前调度阶段均已经确定.根据文献[16]，电网侧负序电流表达式为
$$ \begin{split}&{{I}}_{\text{neg}}=\frac{1-a}{3{N}_{1}}{{I}}_{\text{T}} + \frac{{a}^{2}}{3{N}_{2}}{{I}}_{\alpha }={\frac{1}{\sqrt{3}{N}_{1}}\frac{{P}_{\text{T,}t}}{{U}_{\text{T}}}\text{e}^{-\text{j(}{60}^{\circ } + {\varphi }_{\text{T}})}} + \\[-4pt] & \quad {\frac{1}{3{N}_{2}}\frac{{P}_{\alpha \text{,}t}}{{U}_{\alpha }}\text{e}^{-\text{j(}{120}^{\circ }-{\varphi }_{\alpha }\text{)}}}\,, \\[-24pt]\end{split}$$ (21) 式中：a = ej120°；
$\varphi_{\rm{T}} $ 和$\varphi_{\rm{\alpha}} $ 分别为单相牵引变压器和α相变流器的电压电流相位差；Uα为α相变流器在电网侧的输入电压；IT和Iα分别为单相牵引变压器和α相变流器的电流.式（21）所示的负序电流表达式由两部分组成，第一部分为单相牵引变压器有功功率，第二部分为PFC中α相变流器有功功率. 需要注意的是本文中单相牵引变压器不参与电网侧与牵引侧间无功功率传递，且此处不考虑α相变流器参与电网侧无功功率补偿，因此，有
$\varphi_{\rm{T}}=\varphi_{\rm{\alpha}} $ = 0°. 负序电流幅值为$$ \left| {{{I}_{{\text{neg}}}}} \right| = \left| {\frac{1}{{\sqrt 3 {U_{\text{T}}}{N_1}}}{P_{{\text{T,}}t}} - \frac{1}{{3{U_\alpha }{N_2}}}{P_{\alpha {\text{,}}t}}} \right|, $$ (22) 因此，电压不平衡约束表达式为
$$ \left| {\frac{1}{{\sqrt 3 {U_{\text{T}}}{N_1}}}{P_{{\text{T,}}t}} - \frac{1}{{3{U_\alpha }{N_2}}}{P_{\alpha {\text{,}}t}}} \right| \leqslant \frac{{{{\overline \varepsilon _{\text{U}}}} {S_{{\text{cap}}}}}}{{\sqrt 3 {U_{\text{S}}}}}. $$ (23) 3. 模型线性化
值得注意的是，上文建立的同相牵引供电系统日前优化调度模型为非凸非线性模型，现有的优化求解器很难求解. 为降低模型求解复杂度，本节将上述模型中的非线性元素进行线性化处理，以建立混合整数线性规划模型.
3.1 目标函数需量电费线性化
式（5）所示的需量电费成本含有max函数，可以通过引入辅助变量进行线性化.
$$ \left\{\begin{aligned} &\mathrm{max}\;{P}_{\text{dem,}t}\text={{\overline P}_{\text{dem}}}, \\ &{{\overline P}_{\text{dem}}}\geqslant {P}_{\text{dem,}t}, \quad \forall t=1,2,\cdots ,{N}_{\text{T}}-14, \end{aligned}\right. $$ (24) 式中：
${{\overline P_{{\text{dem}}}}}$ 为一天中最大需量值的辅助变量.3.2 目标函数需量电费线性化
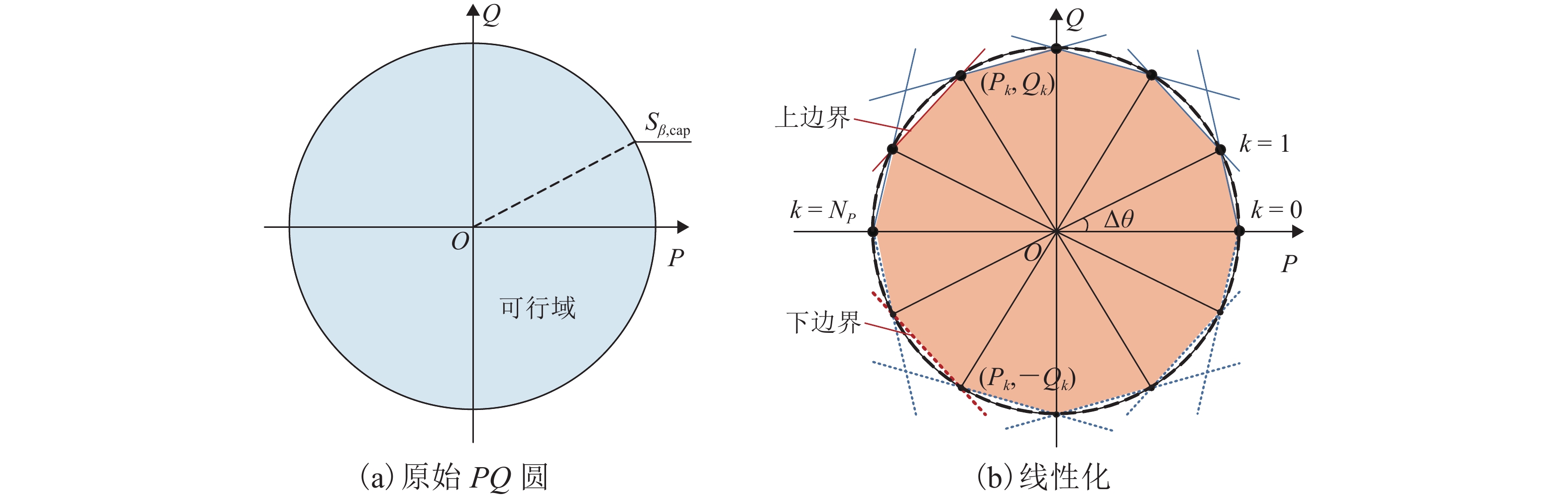
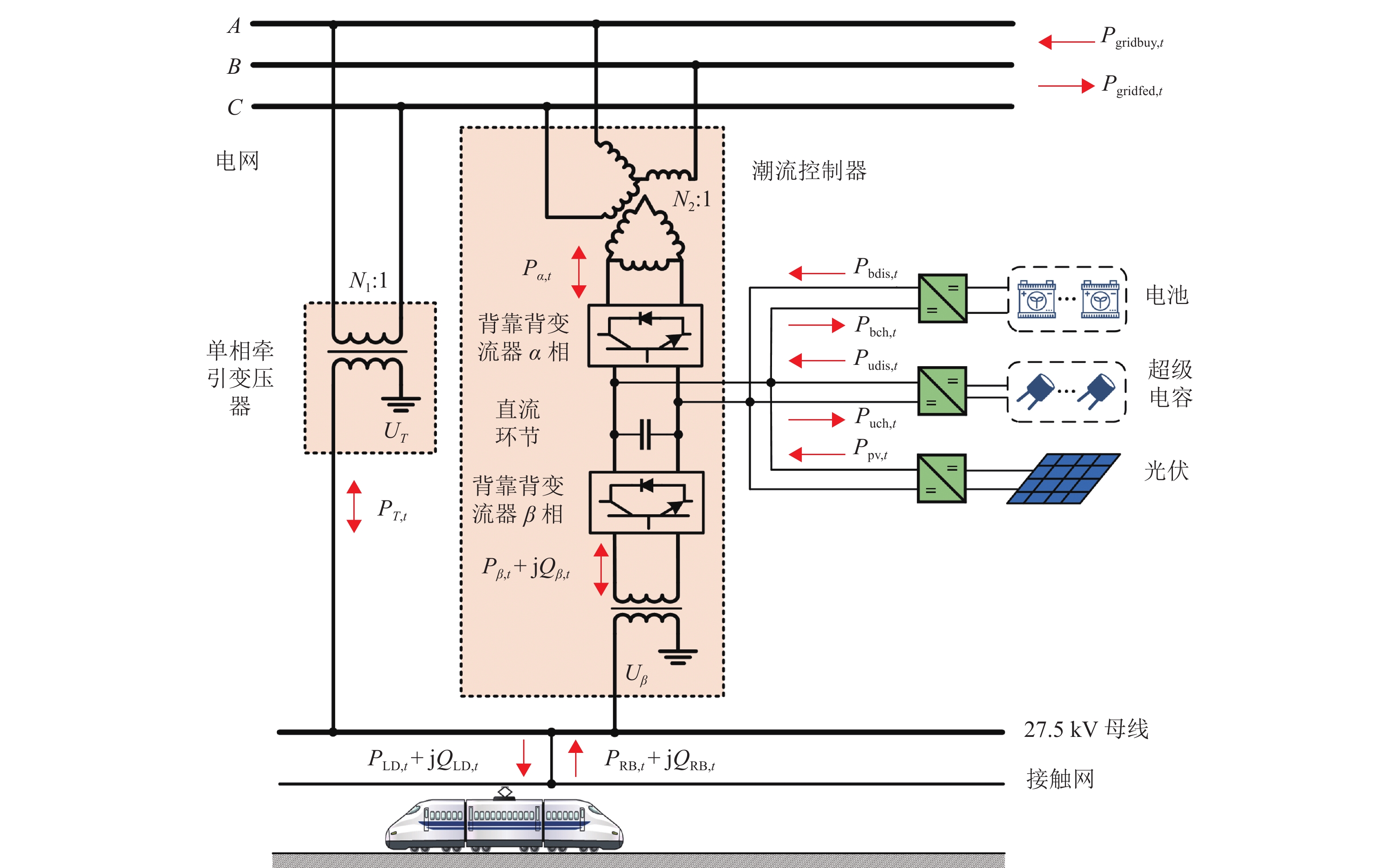
对于式（18）所示的变流器视在功率约束，文献[17]提出了一种基于梯形的线性化方法，通过将PQ圆近似为一系列梯形从而实现线性化，然而需要引入二进制辅助变量. 本文采用了更简单和快速的线性化方法，即利用一系列直线切割该PQ圆，继而近似视在功率约束，如图2所示.
在图2所示的PQ坐标系中，满足Q≥0的PQ半圆被等分成了NP个扇形，每个扇形夹角为∆θ，即 ∆θNP = π. 扇形与PQ半圆的分割点(Pk, Qk)包含在集合ΩPQ中. 基于集合ΩPQ中的坐标点以及其关于P轴的对称点，通过相邻坐标点间的连线可以构建2NP个线性约束来近似该约束. 线性化表达式为
$$ \left\{ \begin{aligned} &{P}_{k}={S }_{\beta ,\text{cap}}\mathrm{sin}(k\Delta \theta ),\\ &{Q}_{k}={S }_{\beta ,\text{cap}}\mathrm{cos}(k\Delta \theta ), \quad -{S }_{\beta ,\text{cap}}\leqslant {P}_{\beta ,t}\leqslant {S }_{\beta ,\text{cap}}, \\ &-{Q}_{k}-\dfrac{{Q}_{k}-{Q}_{k + 1}}{{P}_{k}-{P}_{k + 1}}\left({P}_{\beta ,t}-{P}_{k}\right)\leqslant {Q}_{\beta ,t}, \\ &{Q}_{k} + \dfrac{{Q}_{k}-{Q}_{k + 1}}{{P}_{k}-{P}_{k + 1}}\left({P}_{\beta ,t}-{P}_{k}\right)\geqslant {Q}_{\beta ,t}, \\ &\left({P}_{k},{Q}_{k}\right)\in {\varOmega }_{PQ}, \quad \forall k=0,1,\cdots ,{N}_{{P}}. \end{aligned} \right. $$ (25) 3.3 电压不平衡约束线性化
式（23）中的绝对值函数可以通过引入非负辅助变量ρT,t和ρα,t，二进制变量vα,t，并基于big-M法进行线性化，如式（26）.
$$ \left\{\begin{array}{l} \left|\dfrac{1}{\sqrt{3}{U}_{\text{T}}{N}_{1}}{P}_{\text{T,}t}-\dfrac{1}{3{U}_{\alpha }{N}_{2}}{P}_{\alpha \text{,}t}\right|={\rho }_{\text{T},t}\text{ + }{\rho }_{\alpha ,t}\leqslant \dfrac{\overline{{\varepsilon }}_{\text{U}}{S }_{\text{cap}}}{\sqrt{3}{U}_{\text{S}}}, \\ \quad 0\leqslant {\rho }_{\text{T},t}\leqslant {v}_{\rho ,t}M, \;\;0\leqslant {\rho }_{\alpha ,t}\leqslant \left(1-{v}_{\rho ,t}\right)M , \\ \dfrac{1}{\sqrt{3}{U}_{\text{T}}{N}_{1}}{P}_{\text{T},t}-\dfrac{1}{3{U}_{\alpha }{N}_{2}}{P}_{\alpha ,t}={\rho }_{\text{T},t}-{\rho }_{\alpha ,t}, \end{array}\right. $$ (26) 式中：M为一任意大（而非无穷大）的正数.
4. 算例分析
为验证所提模型和方法的有效性，以国内某高速铁路为例进行算例分析. 硬件平台为AMD Ryzen 5 2500U CPU @ 2.0 GHz和8 GB RAM. 软件平台为MATAB R2016b，集成优化工具箱YALMIP （版本20190425）和求解器IBM ILOG CPLEX （版本12.9）.
4.1 输入参数
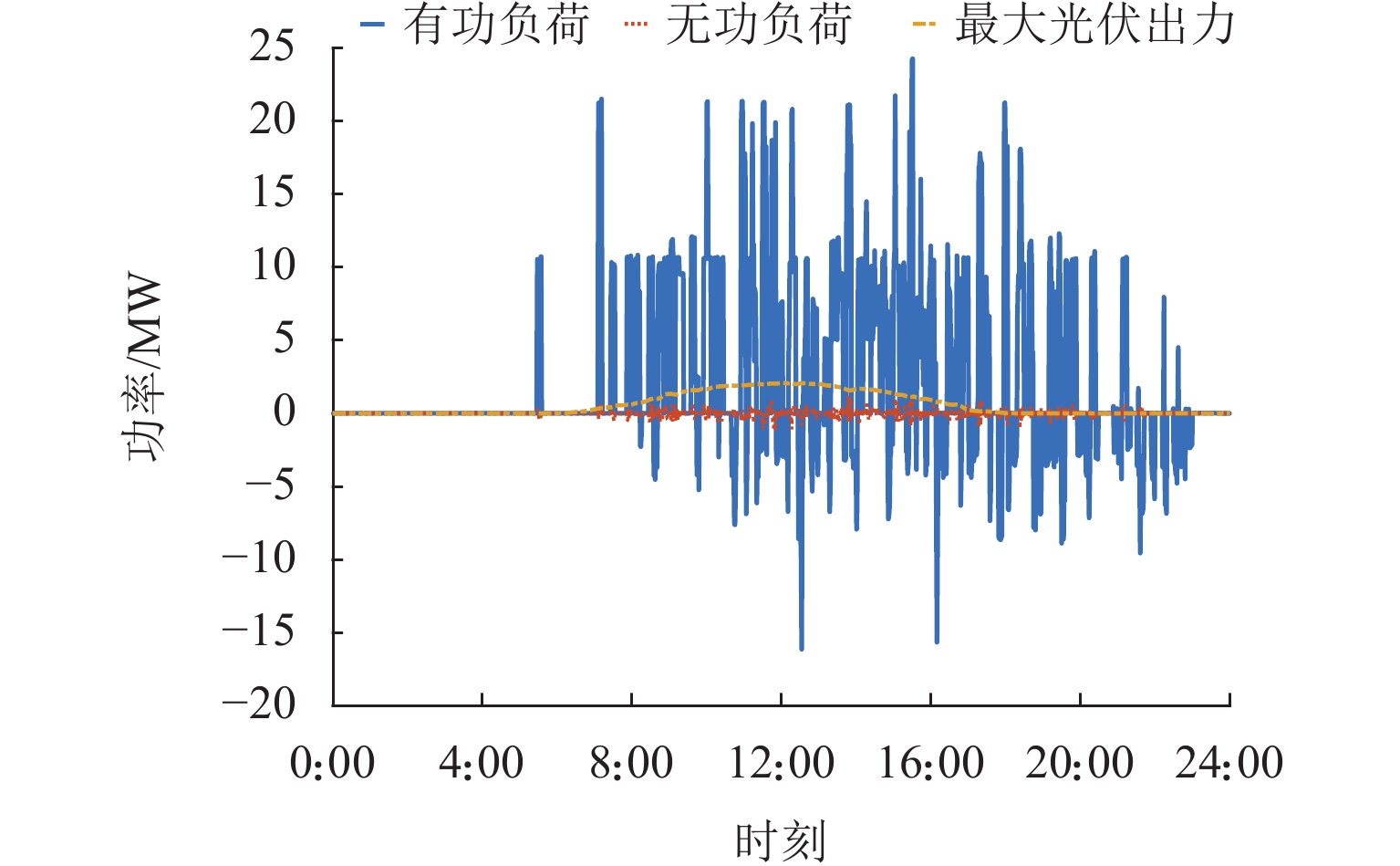
所提模型的输入参数如表1所示，其中，cbuy和cfed分别为购电价格和反馈回电网电能的收费价格. 需要注意的是：表1中收费方案a对应“反送不计”；方案b对应“反送正计”；方案c对应“反送反计”，即未来铁路部门与电力部门实现市场化交易后的售电价格，故取负值. 此外，由于税率因素，在目前微电网中售电价格低于购电价格，故此处同相牵引变电所售电价格系数取0.8. 光伏、电池以及超级电容运行维护费用价格均取0.1元/kW. 实测牵引负荷数据以及最大光伏出力日前预测见图3. 此外，PFC变流器线性化中扇形角 ∆θ = 30°.
表 1 模型输入参数Table 1. Input parameters of model项目 参数 参数取值 电网 US/kV 220.0 Scap/（MV·A） 750 $ {{\overline \varepsilon _{\text{U}}}} $/% 2 牵引变压器 N1 4 N2 4$/ {\sqrt 3 }$ UT/kV 27.5 潮流控制器 Uα/kV 27.5 Uβ/kV 27.5 Sα,cap/（MV·A） 10 Sβ,cap/ （MV·A） 10 混合储能装置 电池 超级电容 SOC 范围 [0.20, 0.80] [0.05, 0.95] 初始 SOC 0.5 0.5 效率（充/放电） 0.80/0.80 0.95/0.95 额定容量/（MW·h） 5.00 0.25 额定功率/MW 2 10 日最大循环数/次 15 不限 电价 峰时 平时 谷时 电度/ （元·（kW·h）−1） 1.252 0.782 0.370 需量/
（元·（kW·月−1）−1）42.000 42.000 42.000 时间段 8：00—11：00,
18：00—21：007：00—8：00,
12：00—17：000：00—6：00,
22：00—0：00反馈电能
计费方案方案 a cfed = 0 方案 b cfed = cbuy 方案 c cfed = −0.8cbuy 
图 3 牵引负荷及最大光伏出力日前预测数据Figure 3. Day-ahead forecast values of traction load and maximum photovoltaic output4.2 光伏及储能接入的影响分析
为了分析光伏与混合储能接入及供电方式对优化结果的影响，考虑以下两种方案，两者均采用反馈电能收计费方案b. 方案Ⅰ：不含光伏和混合储能装置的既有牵引供电系统；方案Ⅱ：集成光伏和混合储能的同相牵引供电系统.
4.2.1 日前优化调度结果
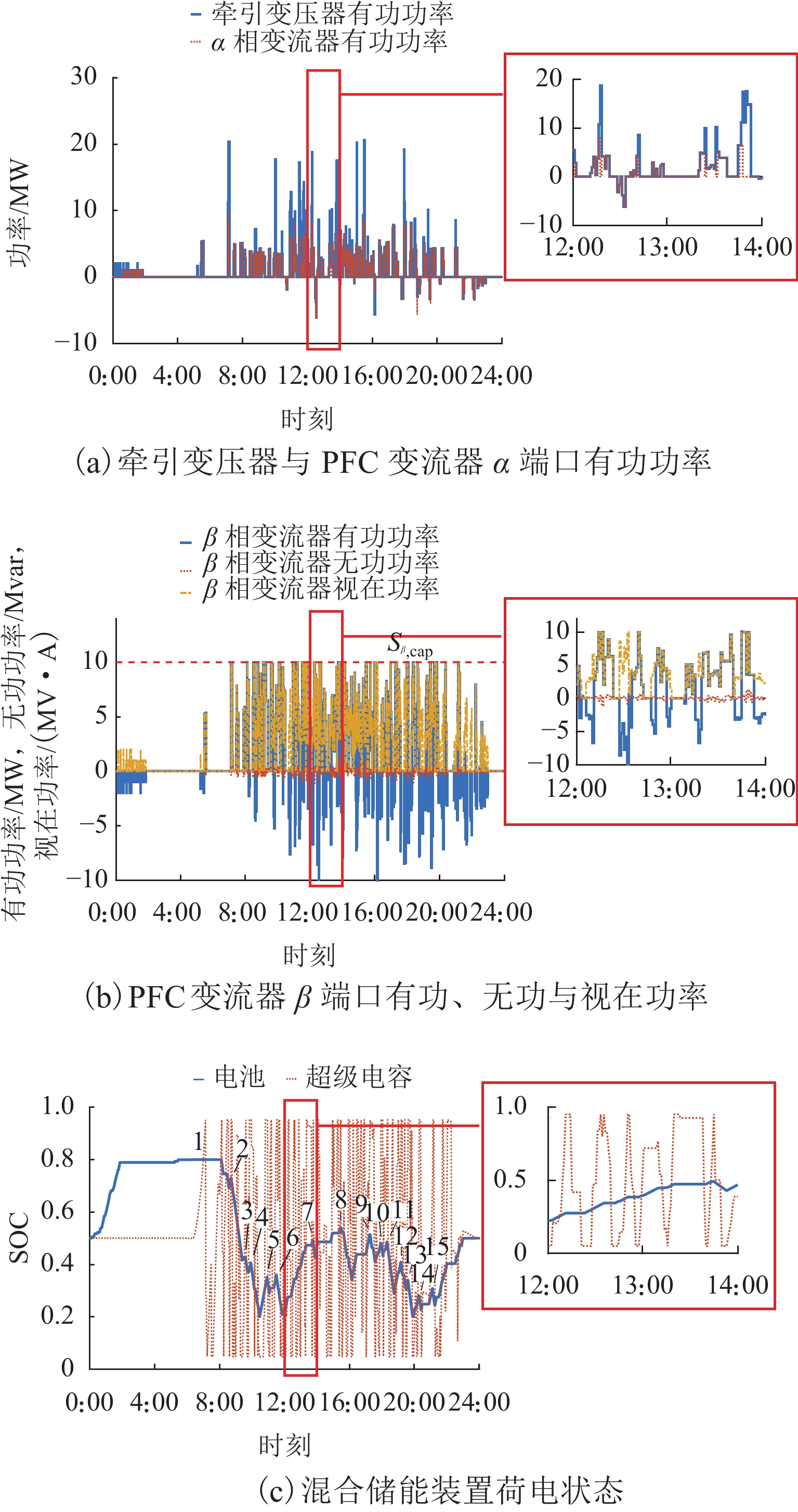
图4（a）、（b）分别为牵引变压器和变流器α相端口、变流器β相端口功率，其中正值表示潮流功率方向为电网侧至牵引侧，负值表示牵引侧至电网侧. 由于混合储能的充放电，变流器β相端口吸收来自变流器α相端口以及混合储能的功率或者反方向释放功率，因此，可以观察到变流器β相端口有功功率明显大于变流器α相端口. 此外，变流器β相端口视在功率Sβ始终不大于其额定容量，由此验证了第3.3节中潮流控制器变流器容量约束线性化的有效性.
图4（c）为日内混合储能装置荷电状态. 电池荷电状态曲线中的循环计数验证了优化模型中的电池循环约束的正确性. 此外可以看到：超级电容的充放电频率远高于电池. 凭借着循环寿命高以及响应迅速的特点，超级电容主要承担高频的冲击性负荷响应，而电池由于能量密度高，循环寿命较短，主要负责低频的牵引负荷响应. 两者的组合可以实现功率密度和能量密度的兼顾，并且避免电池的过度充放电从而延长其使用寿命，适合于电气化铁路大功率、冲击性负荷的应用场景.
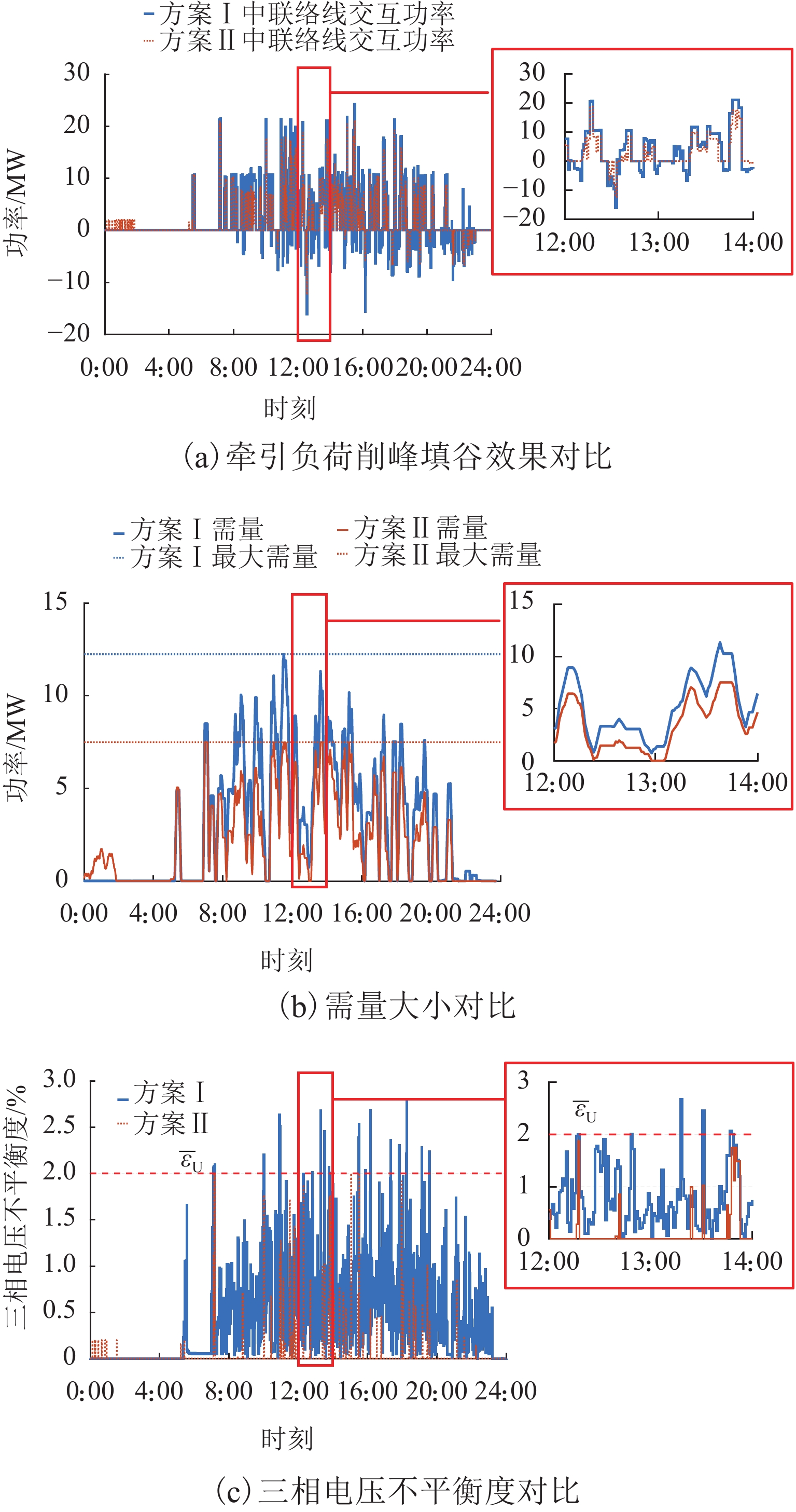
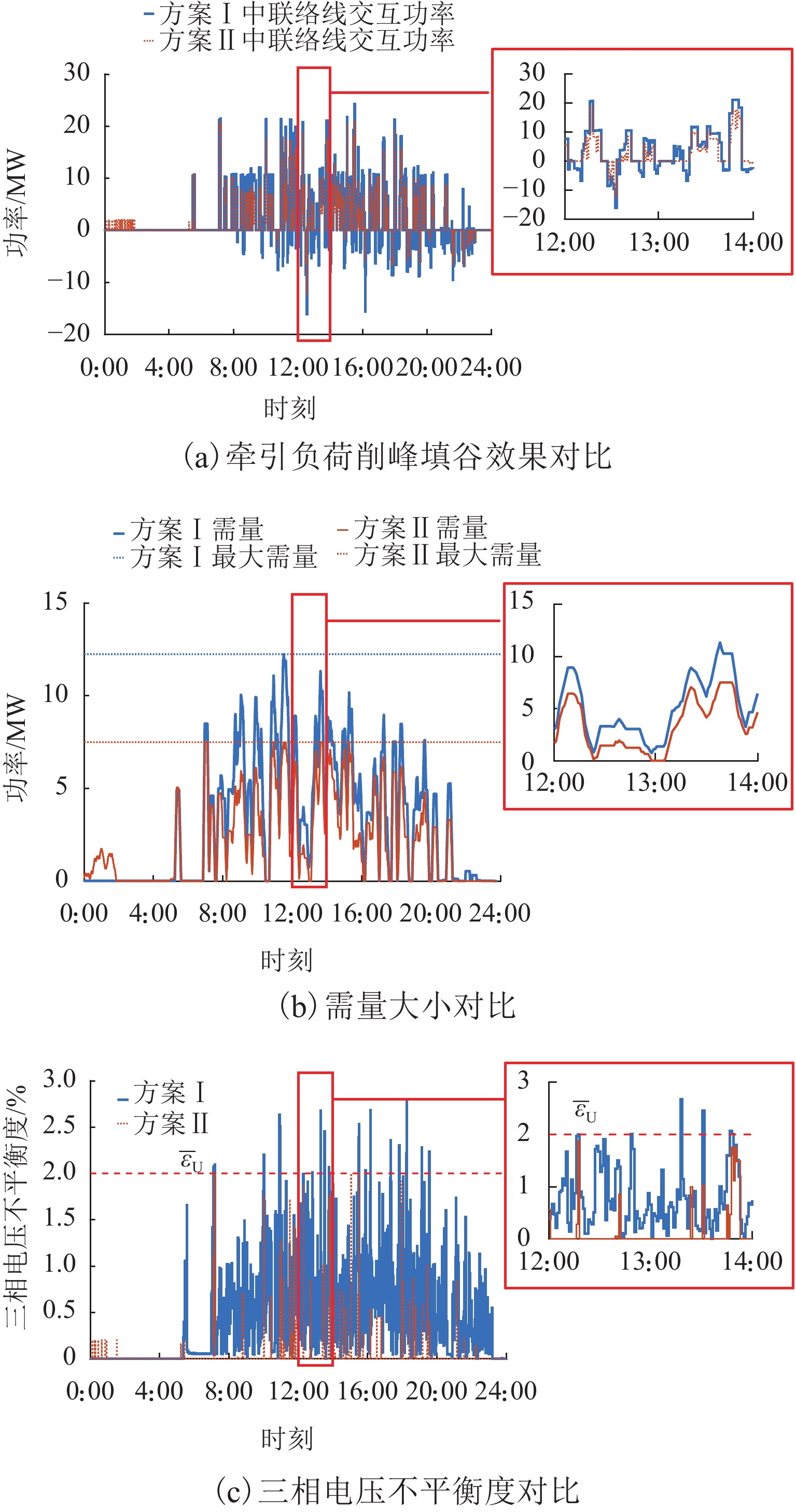
4.2.2 方案Ⅰ与方案Ⅱ对比
图5和表2为方案Ⅰ与方案Ⅱ优化结果对比. 由图5（a）、（b）可知：通过对同相牵引变电所接入光伏及混合储能的协调控制，牵引负荷削峰填谷效果明显，再生制动能量利用率提高至80.27%，电度电费由方案Ⅰ中的67077.81元减小到方案Ⅱ中44674.85元，降幅为33.40%，而最大需量值由方案Ⅰ中的12.24 MW减小到了方案Ⅱ中的7.49 MW，与之相关的需量电费则由17129.90元减小到10489.85元，降幅达38.76%. 由于混合储能吸收电能再利用，回馈至电网的反向潮流大幅降低，在“反送正计”计费方案下，回馈电能费用由14759.58元降低至2636.13元，降幅达82.14%. 尽管计及光伏与混合储能的运维费用，总运行成本依旧节省了36.48%.
表 2 方案Ⅰ与方案Ⅱ优化结果对比Table 2. Comparison of scheme Ⅰ and scheme Ⅱ指标 方案Ⅰ 方案Ⅱ 优化率/% 经济 电度电费/元 67 077.81 44 674.85 33.40 需量电费/元 17 129.90 10 489.85 38.76 回馈电能计费/元 14 759.58 26 36.13 82.14 光伏运维费用/元 0 12 56.80 储能运维费用/元 0 3 833.72 总成本/元 98 967.29 62 891.35 36.45 技术 制动能量
利用率/%0 80.27 80.27 最大电压
不平衡度/%2.79 2.00 28.32 对于三相电压不平衡情况，可以看到图5（c）方案Ⅰ中电压不平衡度值多次违反国标约束，最大值为2.79%. 由于同相牵引供电系统优化调度模型中计及该约束，因此，方案Ⅱ的电压不平衡度相较方案Ⅰ有大幅改善，上限被约束在了国标上限值2%.
4.3 反馈电能计费方案的影响分析
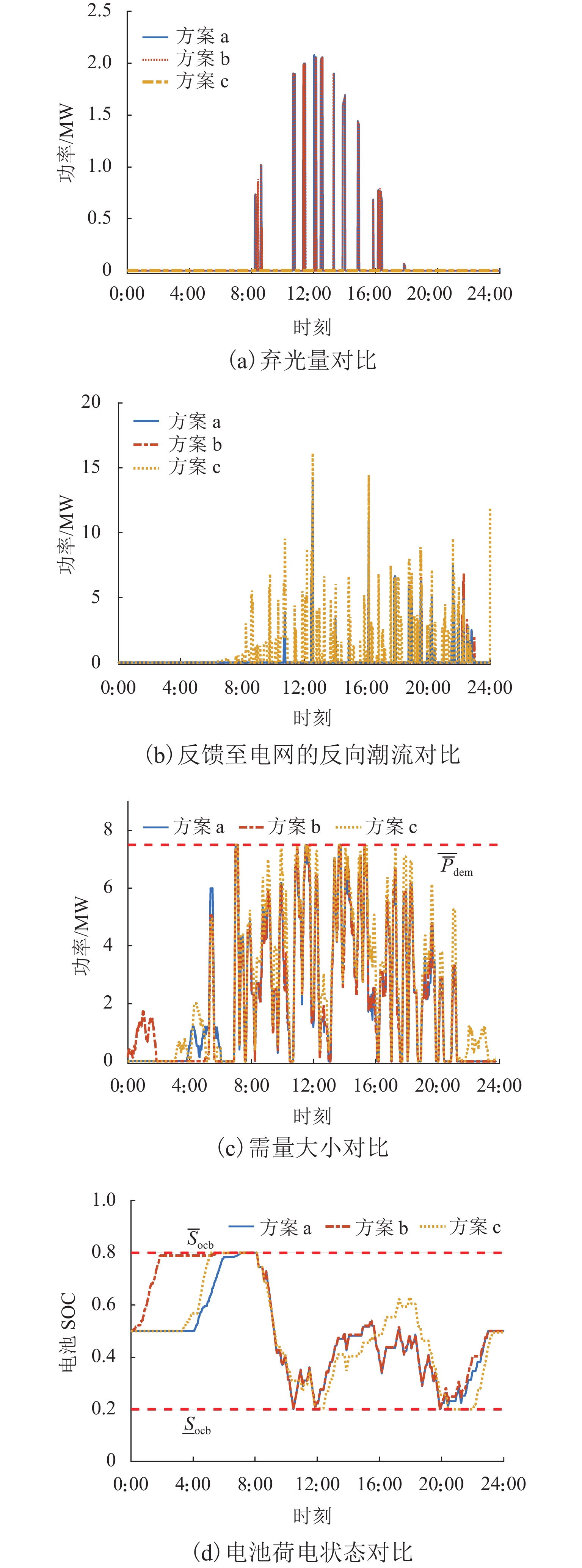
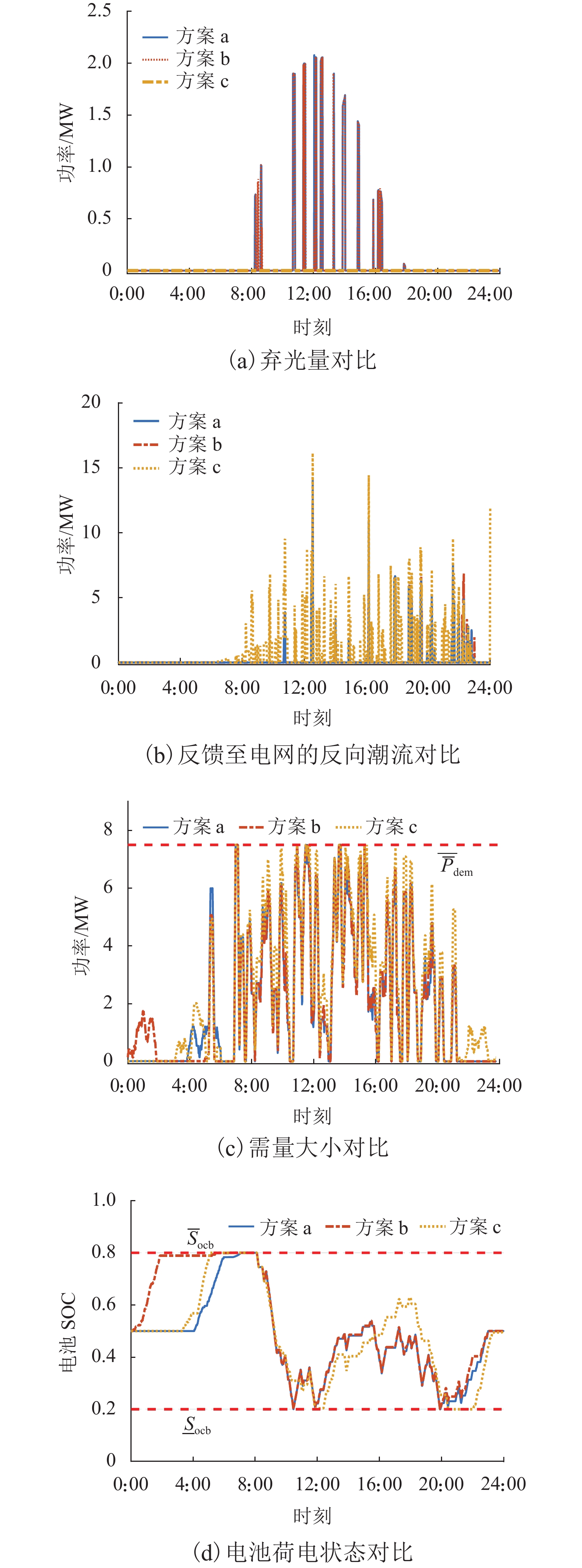
为分析回馈电能计费方案a、b和c对优化调度结果的影响，对第4.2节中的方案Ⅱ采用不同的反馈电能计费方案，优化结果如图6和表3所示.
图 6 反馈电能计费方案 a、b 和 c 结果对比Figure 6. Comparison of feedback power billing schemes a, b and c由图6（a）可知：方案a和b日弃光量大小分别为1.43 MW•h和1.47 MW•h，而方案c弃光量为0，这是由于方案a和b对反馈电能采取“反送不计”和“反送正计”政策，在牵引负荷需求以及PFC和储能容量约束下，多余的光伏电能不会被反馈回电网侧，光伏变流器实时限制光伏出力. 在方案c中，为了最大化牵引供电系统售电收入，光伏变流器不会限制光伏出力，多余的电能被反馈回电网，故弃光量为0. 图6（b）中方案c反馈电能明显大于方案a和b反映出同样的规律. 由图6（c）可知：3种反馈电能计费方案下的最大需量值相等，均为7.49 MW，这表明最大需量值受反馈电能收费方案影响不大.
从图6（d）所示的电池SOC对比可知，方案a和b的电池SOC波动程度比方案c更大，前两者电池日循环数为15次，而后者仅为6，这主要是因为反馈电能计费方案的变化，导致在方案a中优先将多余电能给储能充电，剩余的反馈至电网侧，在方案b中需要通过储能充放电限制多余电能反馈至电网侧以避免计费，而在方案c中则尽可能促进多余电能回馈至电网侧，兼顾给储能充电. 因此，方案b中电池参与能量交互的活跃度最大，方案c最小，这与表3中储能运维费用关系一致.
表 3 反馈电能计费方案a、b和c优化结果对比Table 3. Optimal result comparison of feedback power billing schemes a, b and c项目 方案 a 方案 b 方案 c 总弃光量/（MW·h） 1.43 1.47 0 电池日循环数 15 15 6 电度电费/元 44 674.85 44 674.85 53 149.54 需量电费/元 10 489.85 10 489.85 10 489.85 回馈电能收费/元 0 2 636.13 −12 704.86 光伏运维费用/元 1 261.25 1 256.80 1 409.51 储能运维费用/元 3 770.44 3 833.72 1 713.61 总成本/元 60 196.39 62 891.35 5 4057.66 总成本节省率
（相较方案Ⅰ） /%28.51 36.45 25.33 通过对比表3中三种计费方案下的优化结果，可知反馈电能计费采用方案b时，方案Ⅱ相较方案Ⅰ的总成本节省率最高，而方案c下的总成本节省率最低，这主要是因为方案b中通过再生制动能量的吸收再利用可以大大节省反馈电能的费用，而方案c下无论方案Ⅰ还是方案Ⅱ反馈电能均可带来售电收入，故电费节省效益不如前者明显.
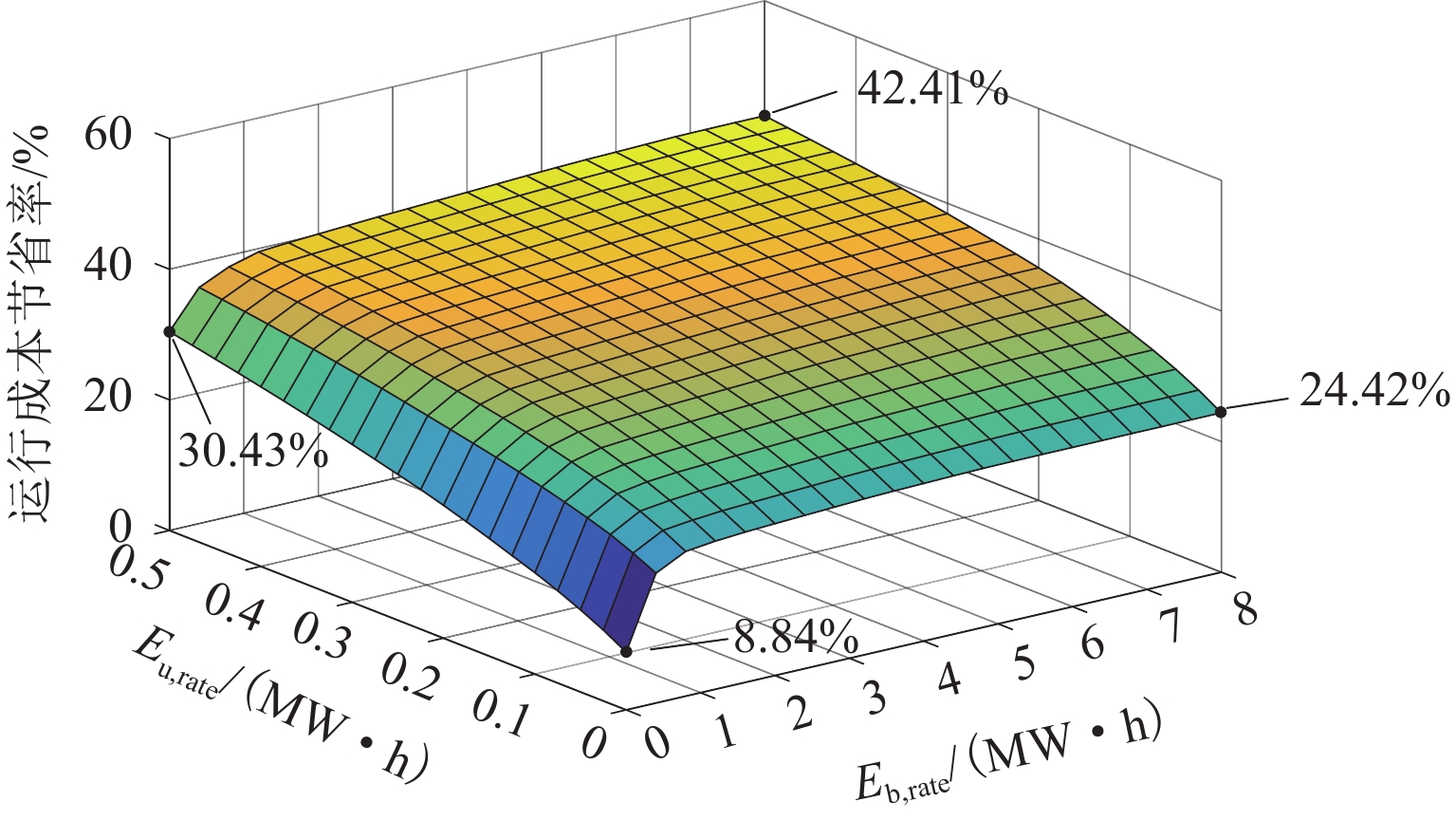
4.4 混合储能容量灵敏度分析
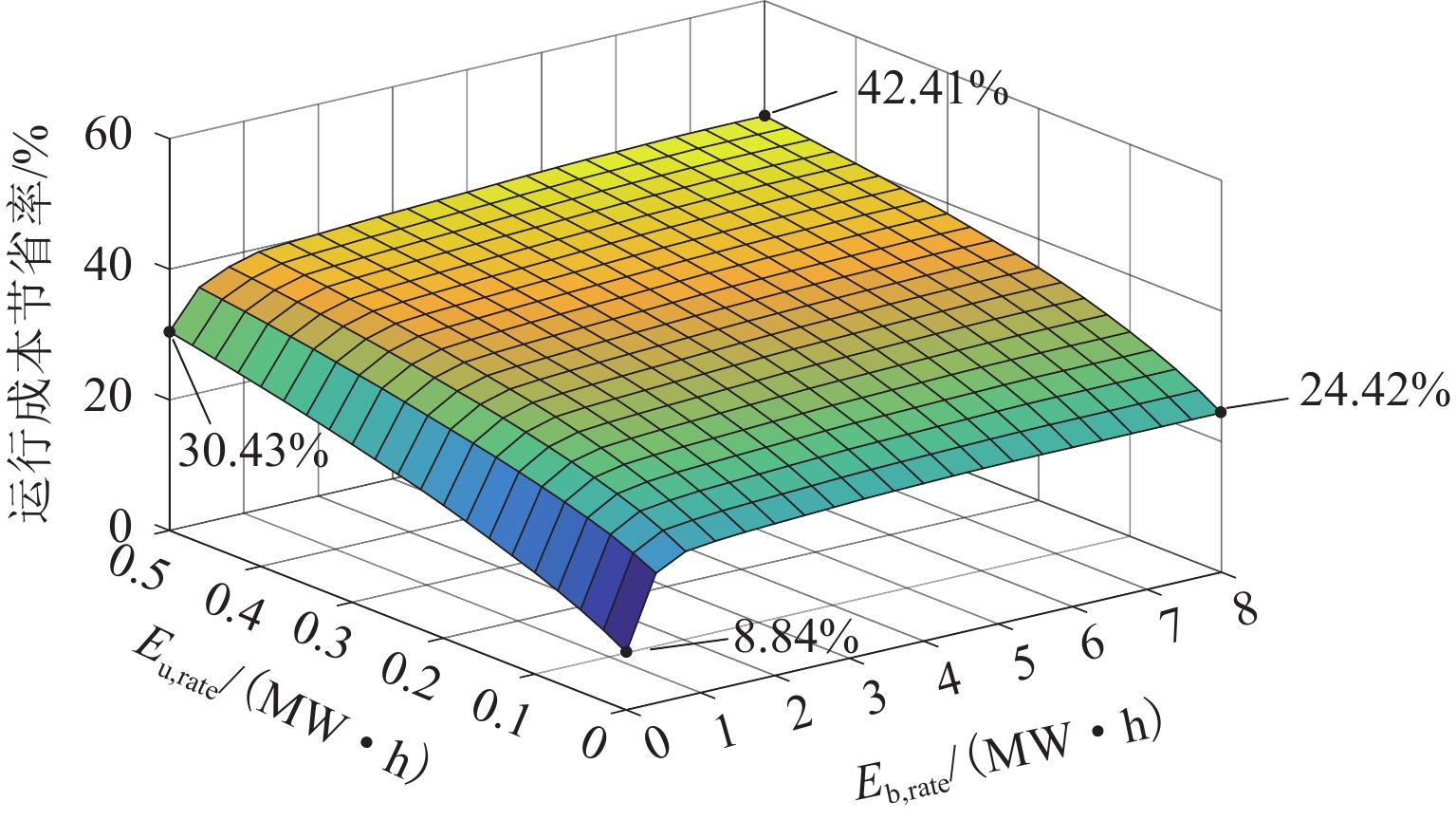
为分析电池和超级电容的不同容量配置对优化调度结果的影响，维持储能元件变流器容量（即储能元件额定功率）不变，输入一系列离散的电池和超级电容容量参数，仿真得到如图7所示的日运行成本节省率随两者容量变化的三维图.
由图7可知：当电池和超级电容容量为0时，8.84%的成本节省率主要由光伏接入所贡献. 随着电池和超级电容容量的增加，总体的成本节省率不断提高，最终达到42.41%. 若单独配置电池，可知Eb,rate∈[0,1.0] MW•h时，成本节省率上升速度较大，随后在Eb,rate∈[2.0,8.0] MW•h范围内小幅升至24.42%. 曲线斜率呈现此特征主要是因为电池功率密度低且日循环次数受限，无法充分响应高频冲击性牵引负荷，因此，超过一定范围后其容量大小影响有限. 相对应地，超级电容容量Eu,rate∈[0,0.5] MW•h范围内成本节省率的上升趋势更易感知，但考虑到超级电容极高的单位容量价格，仍需将其与电池配合实现经济效益的最大化.
5. 结 论
针对集成光伏和混合储能的同相牵引供电系统，本文建立了一种基于混合整数线性规划的优化调度模型，并利用CPLEX商业规划求解器进行求解，得到如下结论：
1） 同相牵引供电系统的潮流控制器直流环节接入光伏与混合储能，实现牵引负荷的削峰填谷，电度电费和需量电费大幅降低，文中算例条件下，总运行成本降幅达36.45%，且电网侧三相电压不平衡度满足国标2%上限要求.
2） 通过对优化模型中非线性元素进行线性化处理，建立了混合整数线性规划模型，基于商业规划求解器实现可高效和准确的快速求解.
3） 不同反馈电能计费方案中，“反送反计”方案下弃光量为0，且电池日循环次数最少，而“反送正计”方案下的运行成本节省率最高.
4） 电池与超级电容容量的增加有助于进一步降低以电费为主的牵引供电系统运行成本，但还应充分考虑两种储能元件物理特性以及成本因素，同时计及寿命损耗，实现生命周期最优综合经济效益.
下一步将着重研究计及光伏和牵引负荷不确定性的同相牵引供电系统优化调度策略，以及全寿命周期内混合储能装置功率与容量的优化配置.
-
图 3 牵引负荷及最大光伏出力日前预测数据
Figure 3. Day-ahead forecast values of traction load and maximum photovoltaic output
图 6 反馈电能计费方案 a、b 和 c 结果对比
Figure 6. Comparison of feedback power billing schemes a, b and c
表 1 模型输入参数
Table 1. Input parameters of model
项目 参数 参数取值 电网 US/kV 220.0 Scap/（MV·A） 750 $ {{\overline \varepsilon _{\text{U}}}} $/% 2 牵引变压器 N1 4 N2 4$/ {\sqrt 3 }$ UT/kV 27.5 潮流控制器 Uα/kV 27.5 Uβ/kV 27.5 Sα,cap/（MV·A） 10 Sβ,cap/ （MV·A） 10 混合储能装置 电池 超级电容 SOC 范围 [0.20, 0.80] [0.05, 0.95] 初始 SOC 0.5 0.5 效率（充/放电） 0.80/0.80 0.95/0.95 额定容量/（MW·h） 5.00 0.25 额定功率/MW 2 10 日最大循环数/次 15 不限 电价 峰时 平时 谷时 电度/ （元·（kW·h）−1） 1.252 0.782 0.370 需量/
（元·（kW·月−1）−1）42.000 42.000 42.000 时间段 8：00—11：00,
18：00—21：007：00—8：00,
12：00—17：000：00—6：00,
22：00—0：00反馈电能
计费方案方案 a cfed = 0 方案 b cfed = cbuy 方案 c cfed = −0.8cbuy 
下载: 导出CSV
表 2 方案Ⅰ与方案Ⅱ优化结果对比
Table 2. Comparison of scheme Ⅰ and scheme Ⅱ
指标 方案Ⅰ 方案Ⅱ 优化率/% 经济 电度电费/元 67 077.81 44 674.85 33.40 需量电费/元 17 129.90 10 489.85 38.76 回馈电能计费/元 14 759.58 26 36.13 82.14 光伏运维费用/元 0 12 56.80 储能运维费用/元 0 3 833.72 总成本/元 98 967.29 62 891.35 36.45 技术 制动能量
利用率/%0 80.27 80.27 最大电压
不平衡度/%2.79 2.00 28.32
下载: 导出CSV
表 3 反馈电能计费方案a、b和c优化结果对比
Table 3. Optimal result comparison of feedback power billing schemes a, b and c
项目 方案 a 方案 b 方案 c 总弃光量/（MW·h） 1.43 1.47 0 电池日循环数 15 15 6 电度电费/元 44 674.85 44 674.85 53 149.54 需量电费/元 10 489.85 10 489.85 10 489.85 回馈电能收费/元 0 2 636.13 −12 704.86 光伏运维费用/元 1 261.25 1 256.80 1 409.51 储能运维费用/元 3 770.44 3 833.72 1 713.61 总成本/元 60 196.39 62 891.35 5 4057.66 总成本节省率
（相较方案Ⅰ） /%28.51 36.45 25.33
下载: 导出CSV
-
[1] 李群湛. 我国高速铁路牵引供电发展的若干关键技术问题[J]. 铁道学报,2010,32(4): 119-124. doi: 10.3969/j.issn.1001-8360.2010.04.022LI Qunzhan. On some technical key problems in the development of traction power supply system for high-speed railway in China[J]. Journal of the China Railway Society, 2010, 32(4): 119-124. doi: 10.3969/j.issn.1001-8360.2010.04.022 [2] 李群湛. 论新一代牵引供电系统及其关键技术[J]. 西南交通大学学报,2014,49(4): 559-568. doi: 10.3969/j.issn.0258-2724.2014.04.001LI Qunzhan. On new generation traction power supply system and its key technologies for electrification railway[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 559-568. doi: 10.3969/j.issn.0258-2724.2014.04.001 [3] 邓文丽,戴朝华,陈维荣. 轨道交通能源互联网背景下光伏在交/直流牵引供电系统中的应用及关键问题分析[J]. 中国电机工程学报,2019,39(19): 5692-5702,5897. doi: 10.13334/j.0258-8013.pcsee.181848DENG Wenli, DAI Chaohua, CHEN Weirong. Application of PV generation in AC/DC traction power supply system and the key problem analysis under the background of rail transit energy Internet[J]. Proceedings of the CSEE, 2019, 39(19): 5692-5702,5897. doi: 10.13334/j.0258-8013.pcsee.181848 [4] 李群湛,王喜军,黄小红,等. 电气化铁路飞轮储能技术研究[J]. 中国电机工程学报,2019,39(7): 2025-2033. doi: 10.13334/J.0258-8013.PCSEE.180919LI Qunzhan, WANG Xijun, HUANG Xiaohong, et al. Research on flywheel energy storage technology for electrified railway[J]. Proceedings of the CSEE, 2019, 39(7): 2025-2033. doi: 10.13334/J.0258-8013.PCSEE.180919 [5] 黄小红,赵艺,李群湛,等. 电气化铁路同相储能供电技术[J]. 西南交通大学学报,2020,55(4): 856-864. doi: 10.3969/j.issn.0258-2724.20181083HUANG Xiaohong, ZHAO Yi, LI Qunzhan, et al. Co-phase traction power supply and energy storage technology for electrified railway[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 856-864. doi: 10.3969/j.issn.0258-2724.20181083 [6] MERLIN Project. Sustainable and intelligent management of energy for smarter railway systems in europe[EB/OL]. (2015-12-10)[2020-3-25]. http://www.merlin-rail.eu. [7] KHAYYAM S, PONCI F, GOIKOETXEA J, et al. Railway energy management system: centralized-decentralized automation architecture[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 1164-1175. doi: 10.1109/TSG.2015.2421644 [8] RAZIK L, BERR N, KHAYYAM S, et al. REM-S–railway energy management in real rail operation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1266-1277. doi: 10.1109/TVT.2018.2885007 [9] AGUADO J A, SÁNCHEZ RACERO A J, DE LA TORRE S. Optimal operation of electric railways with renewable energy and electric storage systems[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 993-1001. doi: 10.1109/TSG.2016.2574200 [10] ŞENGÖR İ, KILIÇKIRAN H C, AKDEMIR H, et al. Energy management of a smart railway station considering regenerative braking and stochastic behaviour of ESS and PV generation[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1041-1050. doi: 10.1109/TSTE.2017.2759105 [11] CHEN M W, CHENG Z, LIU Y L, et al. Multitime-scale optimal dispatch of railway FTPSS based on model predictive control[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 808-820. doi: 10.1109/TTE.2020.2992693 [12] 葛乐,陆文涛,袁晓冬,等. 基于多维动态规划的柔性光储参与主动配电网优化运行[J]. 电网技术,2017,41(10): 3300-3306. doi: 10.13335/j.1000-3673.pst.2016.2523GE Le, LU Wentao, YUAN Xiaodong, et al. Optimal operation of active distribution network based on photovoltaic and energy-storage system of multi-dimensional dynamic programming[J]. Power System Technology, 2017, 41(10): 3300-3306. doi: 10.13335/j.1000-3673.pst.2016.2523 [13] 周丹,孙可,张全明,等. 含多个综合能源联供型微网的配电网日前鲁棒优化调度[J]. 中国电机工程学报,2020,40(14): 4473-4485,4727. doi: 10.13334/J.0258-8013.PCSEE.190390ZHOU Dan, SUN Ke, ZHANG Quanming, et al. Day-ahead robust dispatch of distribution network with multiple integrated energy System-based Micro-grids[J]. Proceedings of the CSEE, 2020, 40(14): 4473-4485,4727. doi: 10.13334/J.0258-8013.PCSEE.190390 [14] ZHANG C, XU Y, DONG Z Y, et al. Robust operation of microgrids via two-stage coordinated energy storage and direct load control[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2858-2868. doi: 10.1109/TPWRS.2016.2627583 [15] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电能质量 三相电压不平衡: GB/T 15543—2008[S]. 北京: 中国标准出版社, 2009 [16] CHEN M W, LI Q Z, ROBERTS C, et al. Modelling and performance analysis of advanced combined co-phase traction power supply system in electrified railway[J]. IET Generation, Transmission & Distribution, 2016, 10(4): 906-916. [17] HAMIDI A, GOLSHANNAVAZ S, NAZARPOUR D. D-FACTS cooperation in renewable integrated microgrids: a linear multiobjective approach[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 355-363. doi: 10.1109/TSTE.2017.2723163 期刊类型引用(19)
1. 唐兆祥，许万涛，邓昊，卢文杰. 基于机会约束规划的含电动汽车市域铁路牵引供电系统优化运行. 储能科学与技术. 2024(02): 526-535 . 
百度学术2. 刘明亮，田忠北，董鸿志，郑俊锋，朱东坡. 考虑节能降耗的轨道牵引供电系统优化仿真模型. 自动化与仪器仪表. 2024(02): 82-86 . 百度学术3. 李光耀，袁佳歆，甘栋良，杨爱民. 高铁新能源混合储能系统低碳经济优化运行研究. 电气工程学报. 2024(01): 67-78 . 百度学术4. 赵丽颖，张灵芝，郑焕坤，龚事引. 考虑光伏和能量调度装置的电气化铁路储能运行调度. 东北电力大学学报. 2024(02): 51-57 . 百度学术5. 李俊豪，涂春鸣，王鑫，郭祺，肖凡. 基于“规则+优化”的电气化铁路站点实时能量管控策略. 电工技术学报. 2024(11): 3339-3352 . 百度学术6. 高锋阳，宋志翔，高建宁，高翾宇，杨凯文. 计及光伏和储能接入的牵引供电系统日前调度. 上海交通大学学报. 2024(05): 760-775 . 百度学术7. 周萌，于龙，王子龙. “双碳”目标下电气化铁路源网车储关键技术研究. 电力电子技术. 2024(07): 80-85 . 百度学术8. 王飞阳，陈玉新. 多维度融合发展策略下城市轨道交通碳排放测算模型. 市政技术. 2024(08): 130-135+161 . 百度学术9. 康德建，胡亮，乔美林，杨步荣. 基于运行图优化的重载牵引负荷削峰策略研究. 电气化铁道. 2024(04): 82-85 . 百度学术10. 秦浩庭，钟帆. 光伏接入铁路牵引供电系统谐振特性分析. 铁道标准设计. 2024(12): 169-175 . 百度学术11. 陈冲，贾利民，赵天宇，邵晨虎，王扬慧. 光伏和储能植入铁路牵引供电系统的拓扑架构与控制策略研究综述. 电工技术学报. 2024(24): 7874-7901 . 百度学术12. 刘继宗，张祖涛，王浩，孔苓吉，伊敏熠，朱忠尹. 城轨交通制动能量利用技术研究现状与展望. 西南交通大学学报. 2024(06): 1322-1345 . 
本站查看13. 陈民武，陈垠宇，徐烈，崔明建. 基于机会约束的贯通式同相牵引供电系统分布式优化运行策略. 中国电机工程学报. 2024(24): 9583-9594 . 百度学术14. 董文哲，杨斯泐，梁宗佑，陈垠宇. 集成混合储能及RPC的牵引供电系统优化运行. 储能科学与技术. 2023(04): 1185-1193 . 百度学术15. 周桔红，刘建委，殷杰，陈朝晖，贾沛，周海琦，冯玎，林圣. 地铁交流供电系统无功平衡策略研究——以广州地铁18号线为例. 都市快轨交通. 2023(03): 160-167 . 百度学术16. 赵宏程，李再华，赖俊宏，陈垠宇，张波琦，龚康华，曾毅. 基于RPC的混合储能接入双流制牵引供电系统协调运行方法. 储能科学与技术. 2023(09): 2862-2870 . 百度学术17. 陈垠宇，陈民武，李东阳，范家彬，梁宗佑，李波. 计及牵引负荷不确定性的同相供电系统随机优化运行策略. 中国铁道科学. 2023(05): 191-200 . 百度学术18. 刘骆川，黄大锐. 牵引供电系统光储接入方案及其控制策略. 电工技术. 2023(18): 44-48 . 百度学术19. 龚志恒，张翼扬，朱楚扬，赵鼎威，刘湘. 计及新能源接入的柔性牵引供电系统区间最优潮流研究. 电工技术. 2022(24): 48-52+57 . 百度学术其他类型引用(19)
-
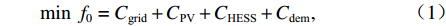
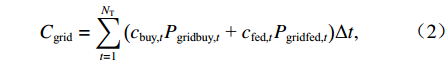
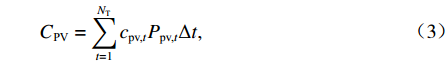
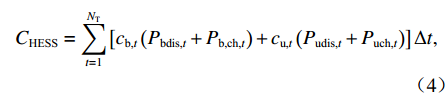
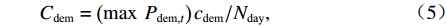
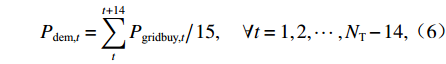
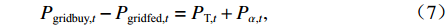
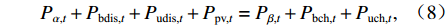
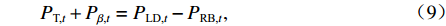
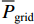
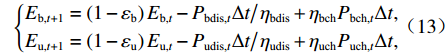
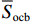
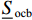
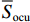
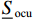
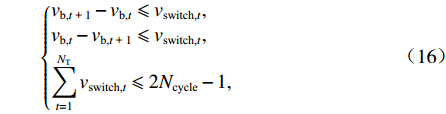
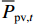
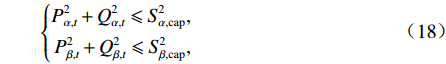
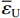
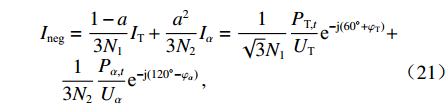
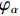
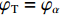
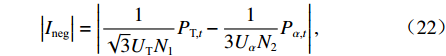
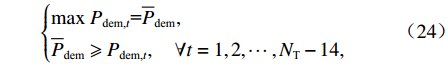
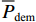
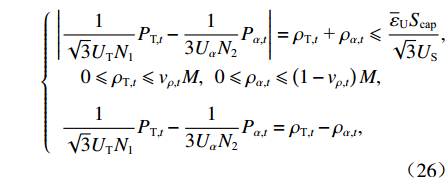
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 598
- HTML全文浏览量: 319
- PDF下载量: 50
- 被引次数: 38