Safety Design of Level Crossing Control System Based on Formal Method
-
摘要:
铁路平交道口控制系统是一种典型的安全苛求系统,为提高铁路平交道口的安全性,提出一个能适应双线双向接车的自动控制系统. 首先,分析现有铁路平交道口的作业流程,利用新的控制系统解决现有系统中常见的三个问题,即出清检查、制动距离限制、连续接车中防护门短时间开放问题;其次,基于Event-B语言以及精化策略对设计的自动控制系统建立形式化模型;最后,检查证明义务以验证需求属性是否被满足,并应用动画器Animation展示系统功能的正确性. 结果显示:相比传统的道口管理系统,本文提出的自动控制系统增加了双线连续接车功能,且使用形式化建模和验证,避免系统设计中存在的二义性,对平交道口安全管理有一定的参考意义.
Abstract:Railway level crossing (RLC) control system is a typical safety-critical system. A novel automatic control system (ACS) that responds to a two-track bi-direction operation is proposed to improve the safety of RLC. Firstly, the operational processes at traditional railway level crossings is analyzed, and the corresponding solutions are proposed in the ACS for three general problems, i.e., clearing inspection, braking distance limitation, and short-time opening of the barriers during continuous work. Secondly, a formal model based on the Event-B language and refinement strategy are developed for the proposed ACS. Finally, proof obligations are checked to verify that the required properties are satisfied, and the Animation is applied to demonstrate the correctness of the system functionality. The results reveal that, compared with the traditional level-crossing management system, the proposed ACS adds the function of two tracks of continuous work, and the use of formal modeling and verification avoids the ambiguity in the system design, all of which have reference significance for RLC safety management.
-
Key words:
- level crossing /
- control system /
- requirement specification /
- safety-critical system /
- formal method
-
铁路平交道口(railway level crossing, RLC)是铁路与道路的交叉区域,也是铁路事故发生率较高的场所,一旦发生事故,容易造成巨大的财产损失和严重的人员伤亡[1-2]. 近年来,尽管许多平交道口已整改为立交道口,但由于地理条件和高昂的工程改造成本,国内外仍有许多平交道口被保留使用.
平交道口控制系统是一个安全苛求的系统,对保证平交道口的安全起着至关重要的作用. 平交道口控制系统负责根据接收的预警信号及管理规范,对道口信号灯、防护门、列车等进行控制和监测,可信的控制系统可以有效地防止道口事故的发生,提高安全性. 本文分析了双线双向平交道口安全管理中经常遇到的3个问题:一是平交道口在短时间内需要连续接车时,易造成控制系统中各个组件作业的混乱;二是当列车接近平交道口时,交叉区域仍有行人车辆滞留;三是预留制动距离不够长,导致紧急制动时列车最终停在交叉区域. 基于形式化方法设计了一个新的自动控制系统,从而提高双线双向平交道口(简称“平交道口”)控制系统的可信性.
形式化方法具有精确的数学逻辑,有助于开发人员在设计的早期阶段发现安全苛求系统中存在的潜在错误,纠正设计规范,适用于开发复杂且安全性要求高的系统[3-4],已成功应用于航空航天、轨道交通、网络安全、医疗等安全苛求相关领域. 如Mekki等[5]使用UPPAAL建立RLC控制系统的时间自动机模型,并用模型检测完成了对系统的验证. 王恪铭等[6-7]利用形式化方法分析单线道口,发现现有规范中存在列车驶入道口时不能确保系统安全状态的缺陷. Event-B语言用于对反应式系统进行建模,其支撑平台RODIN将模型检测和定理证明方法有机结合起来[8]. 定理证明弥补了模型检测只能处理有限状态空间的缺陷[9]. 因此,本文使用Event-B对道口控制系统进行形式化建模,通过模型检测和定理证明进行验证.
本文主要贡献如下:
1) 分析目前平交道口控制系统的3个安全问题且提出了相应的解决方案.
2) 设计了一个新的平交道口自动控制系统(automatic control system,ACS),并分析系统的需求属性.
3) 基于RODIN平台,建立控制系统的Event-B模型. 使用模型检测和定理证明进行形式化验证. 根据证明结果对模型进行修正,直至证明义务全部通过.
1. 平交道口功能分析
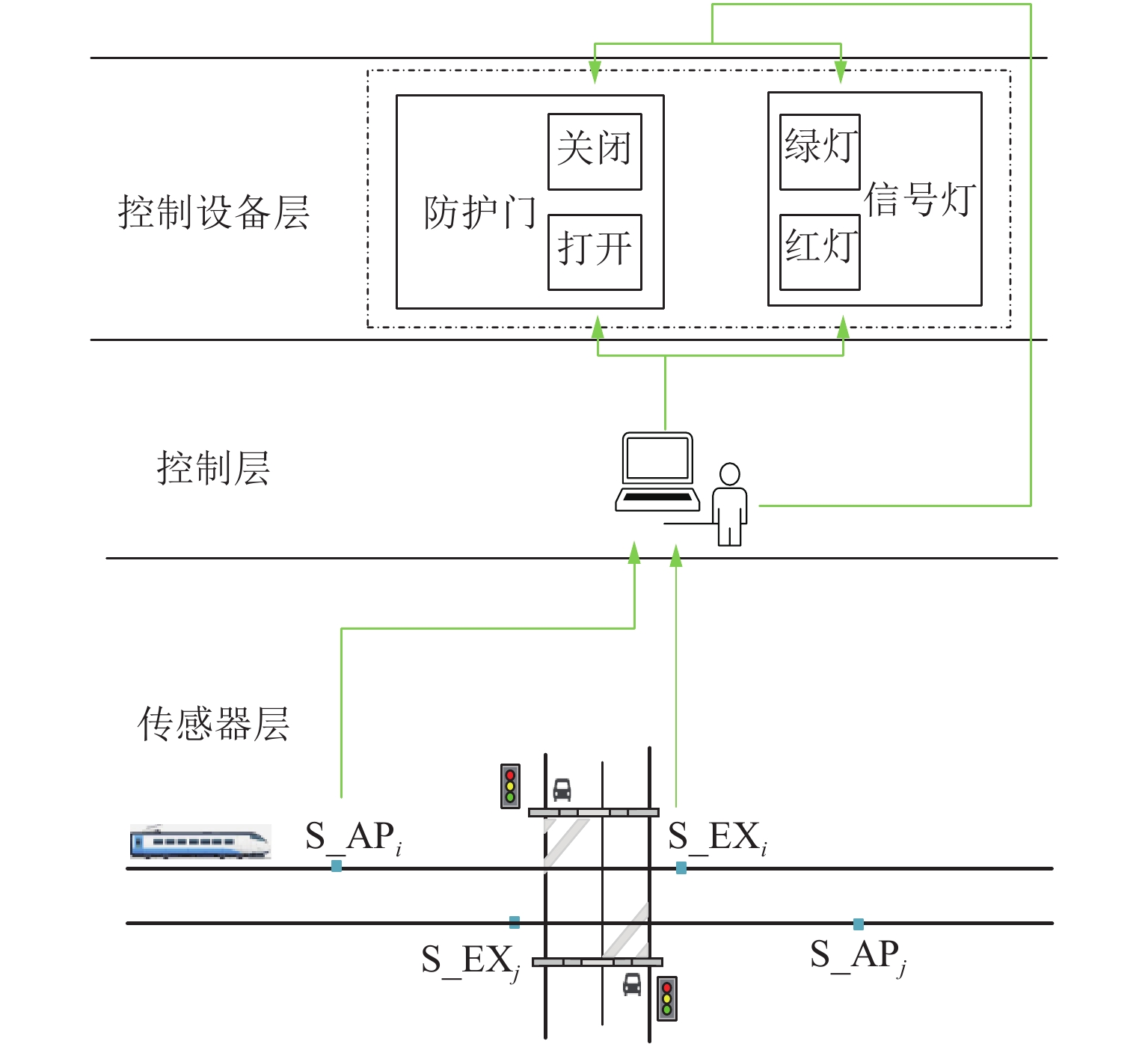
本文分析配有两条轨道可双向通行的平交道口,这类平交道口一般在轨道的两侧配置两个防护门和信号灯. 控制系统负责对所有相关设备进行控制.
传统的平交道口控制系统设置了两种传感器,分别是放置在接近道口方向的接近传感器(S_APi)和在离开道口方向的离开传感器(S_EXi),i、j表示上、下行两个不同方向. 传统平交道口控制系统的工作流程如图1所示. 信号灯有红灯和绿灯两种状态,防护门有打开和关闭两种状态,控制器控制防护门和信号灯,并与列车驾驶员保持通信. 列车司机应观察周围环境,接收控制器发送的信息,并在紧急情况下准备制动. 具体作业流程如下:
步骤1 当一列车进入铁路道口的监控区域时,接近传感器(S_APi)被激活.
步骤2 道口控制器接收到列车接近的信息,并向公路方向防护门发送关闭命令,将信号灯切换成红色.
步骤3 道口防护门关闭.
步骤4 此时控制器对道口是否出清进行判断;如果道口状态为出清(即满足列车通行条件),那么控制器向列车司机发送行车许可命令,列车缓慢通过道口交叉区段20 m后,离开传感器(S_EXi)被激活.
步骤5 控制器向防护门发送打开命令,将信号灯切换成绿色.
步骤6 所有的防护门都打开.
步骤7 平交道口回到初始状态.
2. 道口安全属性功能完善
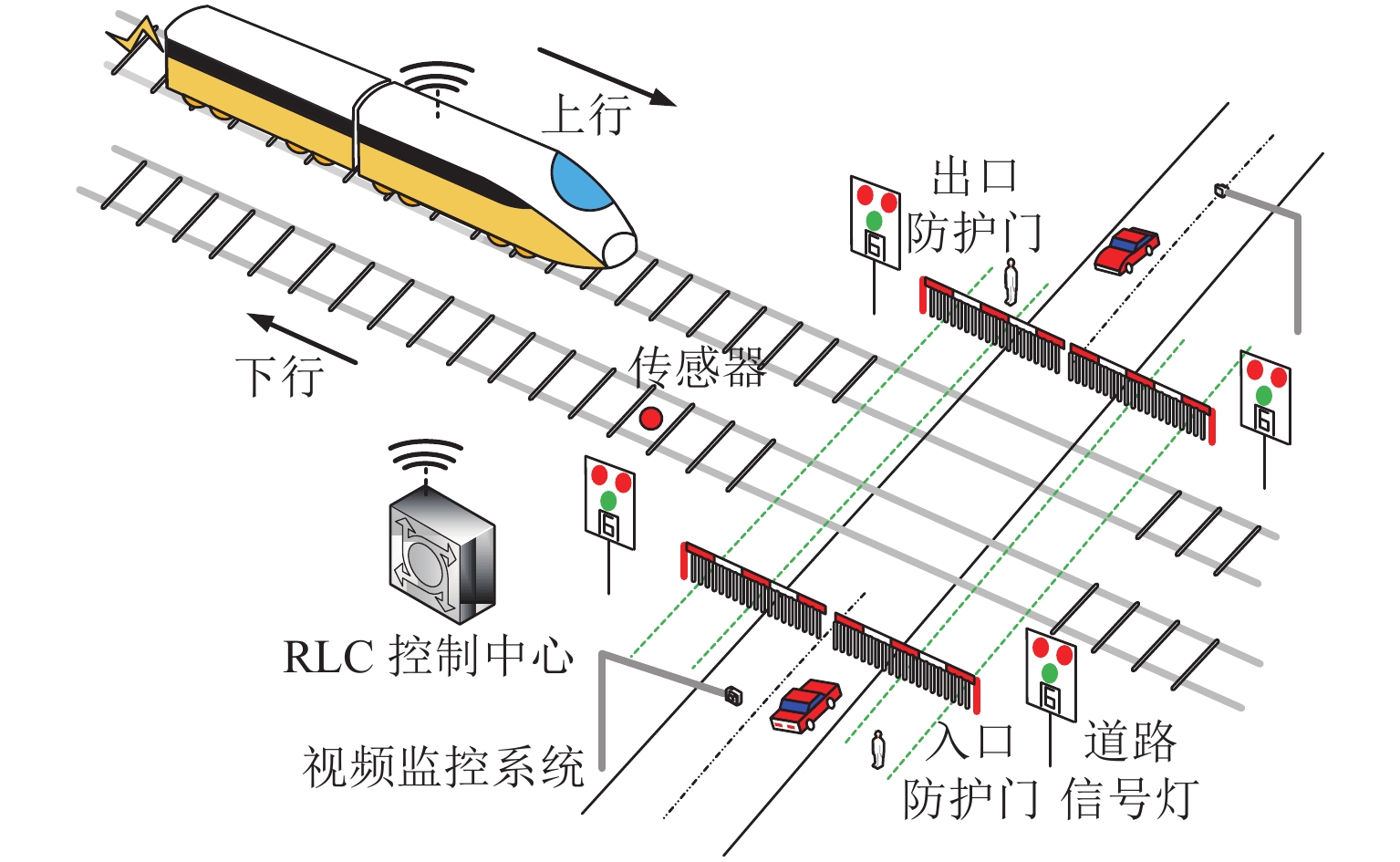
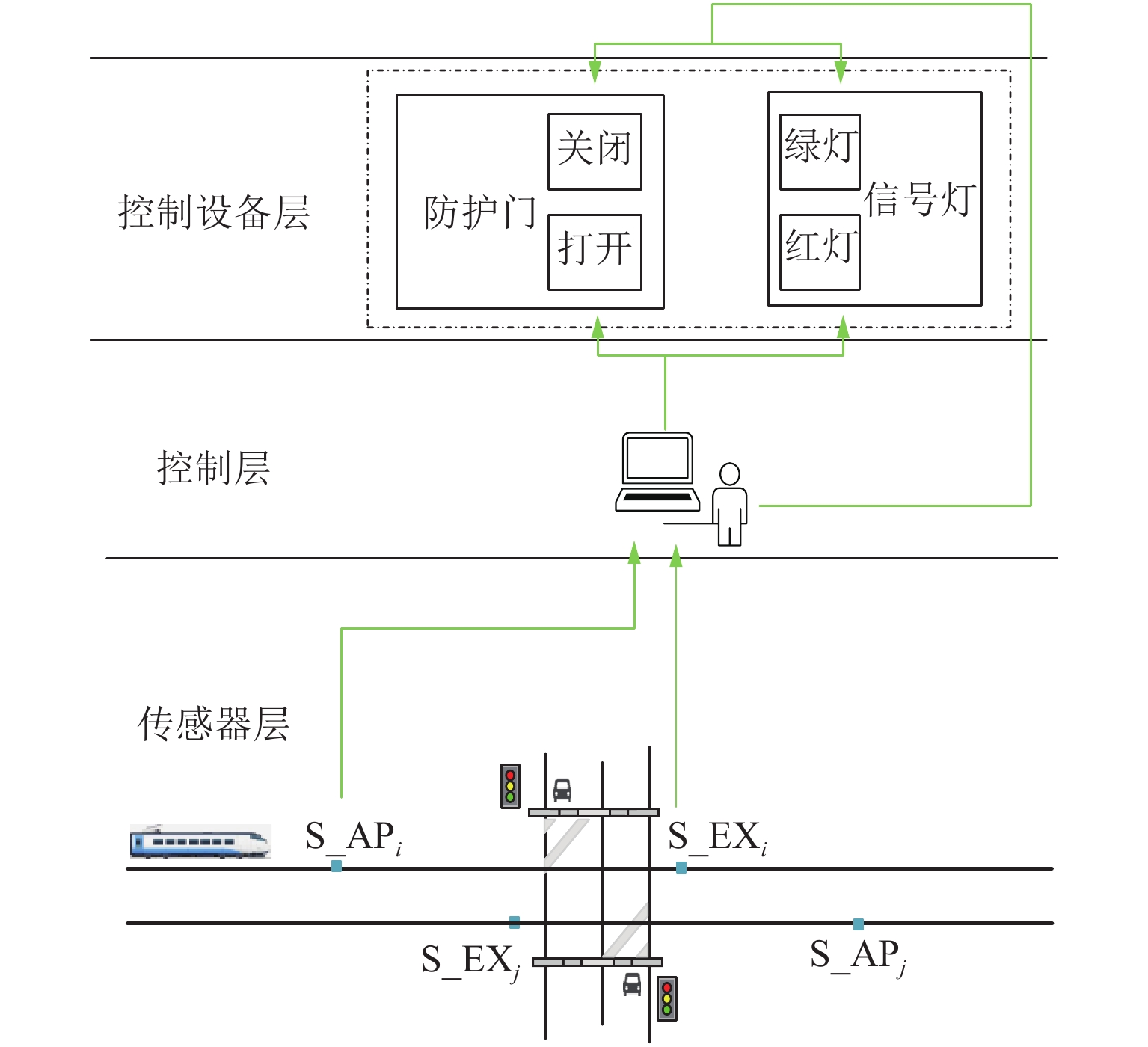
为解决平交道口易引发事故的3个问题,提高安全性,在传统控制系统的基础上设计了一个可信的ACS系统,在平交道口工作示意如图2所示.
ACS系统构成组件主要有:控制器、预告传感器、信号灯、防护门和列车. 其中,预告传感器由传统的2个增加到4个,增加了到达传感器和出清检查传感器;信号灯由2种显示增加至3种显示;防护门采用双方向双开模式.
各组成部分的需求属性包括环境属性(environment property,EVN)、功能属性(function property,FUN)和安全属性(safe property,SAF). 环境属性描述系统中建模的对象;功能属性表示系统对象应当具备的基本功能;安全属性用来表示在运行过程中保障安全应具备的条件[7].
2.1 预告传感器
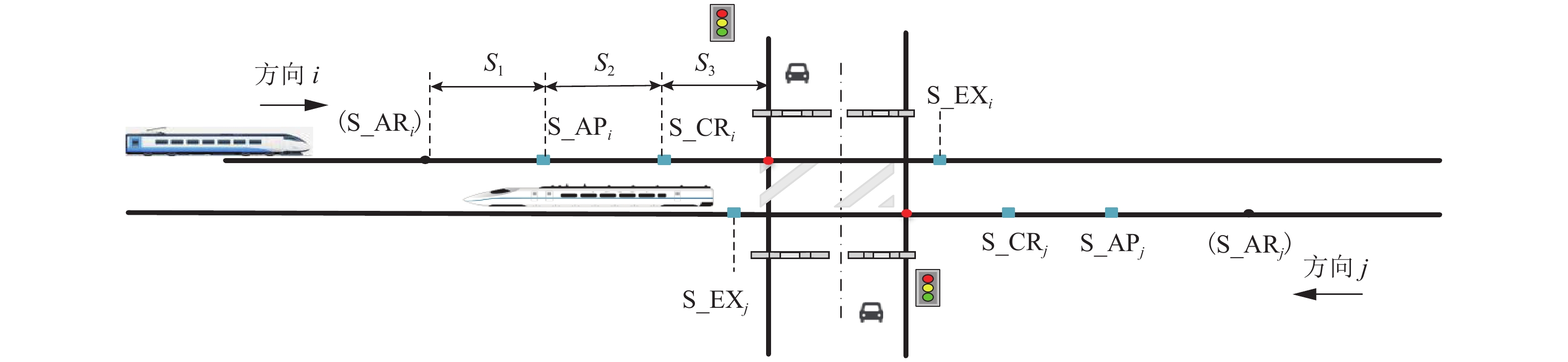
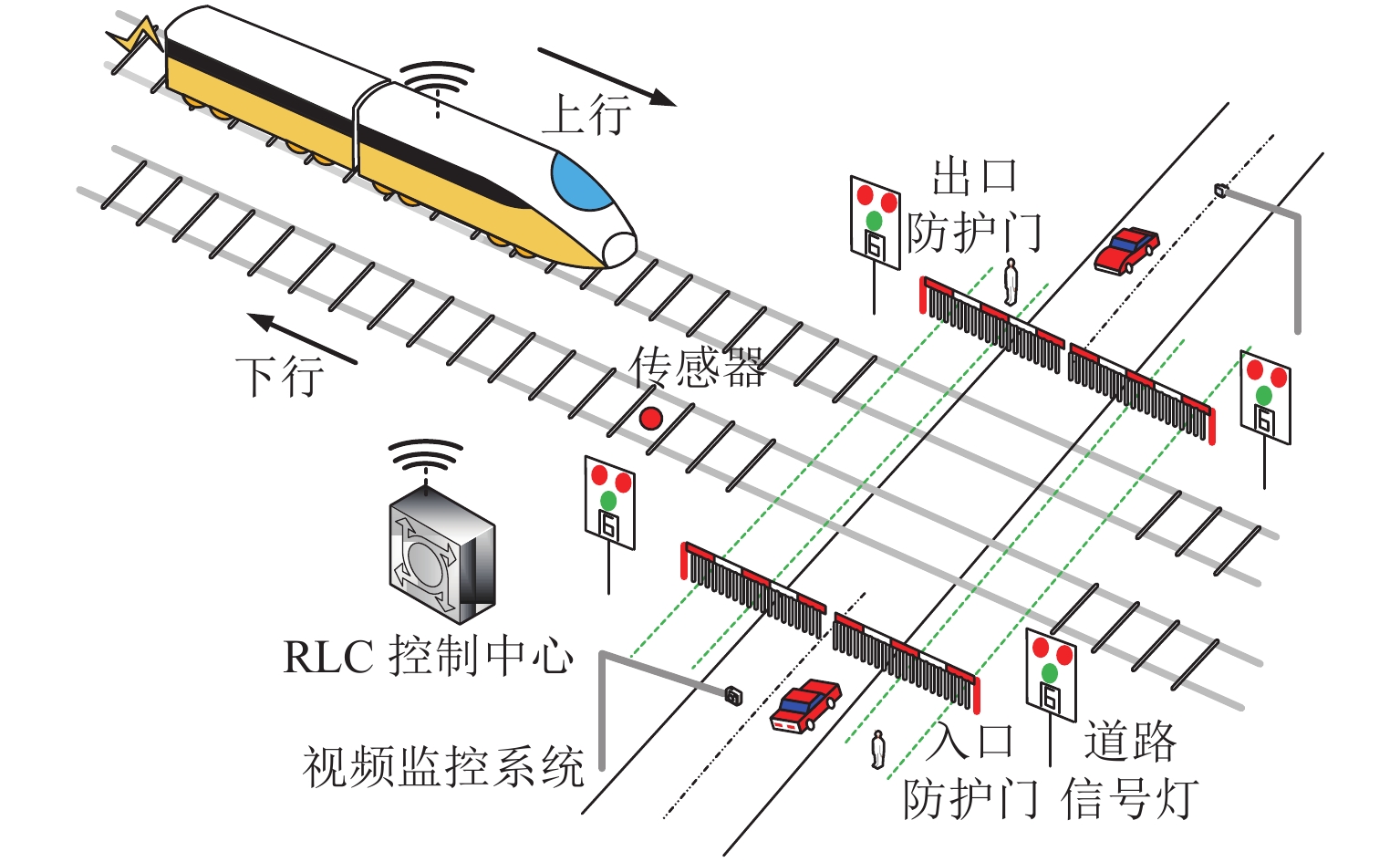
在平交道口轨道上每个方向设置4个传感器,列车到达传感器(S_ARi)、接近传感器(S_APi)、道口出清检查传感器(S_CRi)、离开传感器(S_EXi),传感器均为无线通信传感器,且假设均能正常工作. ACS系统中铁路道口的传感器布局如图3所示. 图中:S1~S3为各点之间的距离.
当一列车通过后,正常情况下,控制器应该命令防护门打开并将信号灯切换成绿色. 如果此时相反方向有列车驶近道口,那么防护门和信号灯都需要再次进行切换. 这时候可能导致防护门刚打开就要关闭,公路方向的行人车辆被滞留在交叉区域,造成危险. 本文在S_APi前设置了S_ARi,S_ARi可以在连续接车时起到关键作用. S_ARi和S_APi之间满足一定的距离要求,使得列车通过该距离的时间可以满足公路方向行人车辆一次通行所需要的时间. 这样,在一列车通过道口且激活S_EXi后,若另一方向的S_ARj被激活,则证明另一列车已进入监控区域,此时,防护门保持关闭,信号灯仍为红闪. 待下一列车通过道口后,再切换状态. 即可避免第1个问题,即避免因道口短时间开放而造成的控制系统各个组件作业混乱.
在单一接车时,当S_APi被激活发出警报,表示有列车接近平交道口. 此时,控制器应根据道口是否空闲进行判断,并向列车司机发送信息. 列车司机根据控制器发送的信息来对列车进行操控. 如果道口空闲,那么列车可以保持缓慢运行并通过道口;如果道口未及时出清,列车司机需要在到达S_CRi时或者之前采取紧急制动,以满足在到达交叉区域前停下. 即可避免发生第2个和第3个问题.
当S_EXi被激活时,表示该列车已经通过并离开道口.
为了更好解释,在ACS中对3个传感器的距离设定了约束:
1) S1为S_ARi和S_APi之间的距离. 列车通过该区域的时间应满足防护门的最小开放时间Tmin,而Tmin满足公路方向行人车辆一次通行的最大需求时间. 该距离设置是为了解决第1个问题.
2) S2为S_APi与S_CRi之间的距离. 当S_APi被激活时,此时道口交叉区域可能还有部分行人车辆正在通行,需要保持道口开放一定的时间来保证行人车辆完全离开危险区域. 而S_APi与S_CRi的距离则要满足道口出清的最大时间. 该距离设置是为了避免提出的第2个问题.
3) S3为S_CRi到交叉开始点Pi的距离. 若列车到达S_CRi时道口未能及时出清,列车司机接收到未出清的消息后,需要采取紧急制动,使得列车能在到达Pi点前停下并预留一定的安全距离. 设置该距离是为避免第3个问题,表示为
S3=Sb+ΔS, (1) 式中:
Sb 为列车制动距离,其值参考文献[10];ΔS 为安全冗余距离.预告传感器应该满足的需求属性包括:
EVN_1,一个方向只有一条轨道;
EVN_2,在每个接车方向设置了4个传感器(S_ARi、S_APi、S_CRi、S_EXi);
FUN_1,当列车到达、接近、离开道口时,传感器应该及时向控制器发送对应的信号.
2.2 控制器
控制器是ACS系统的核心组件,与参与道口工作的其他部件相互通信,主要进行以下工作:
在列车到达监控区域,即S_ARi被激活后,控制器将为接车作业做准备. 当S_APi被激活时,控制器接收列车接近的信息,关闭入口防护门,且将信号灯切换成红色,禁止防护门外的行人车辆进入. 当S_CRi被激活后,如果交叉区域空闲,控制器将关闭出口防护门,并给列车司机发送行车许可指令. 如果未完成出清,那么控制器需要及时通过S_CRi向列车司机发送“不能通过”指令,出口防护门保持开放状态,直到道口出清,列车恢复运行,通过道口且激活S_EXi为止.
控制器要满足的需求属性包括:
FUN_2,根据列车的位置来对入口防护门和出口防护门的状态进行控制;
FUN_3,控制器根据列车的位置,入口防护门和出口防护门的状态,使得信号灯显示正确的颜色.
2.3 防护门
普通平交道口只在轨道两侧分别设立一个防护门,且两个防护门的动作始终保持一致. 本文打破了常规设置,在轨道两侧分别设置了两个防护门:入口防护门和出口防护门. 当S_APi被激活后,入口防护门应该被关闭,出口防护门保持开放以供滞留在交叉区域的人群及时疏散. 当S_CRi被激活时,如果道口完成出清,关闭出口防护门;如果道口未完成出清,出口防护门应该保持开放. 当S_EXi被激活,且不进行连续接车,所有的防护门都将被打开.
这里使用S_ARj检测是否要连续接车. 如果当S_EXi被激活时,S_ARj被激活或已被激活,那么所有的防护门都应该保持关闭,直到下一列车通过道口;如果没有被激活,证明短时间内没有列车接近道口,此时所有防护门都将被打开,以便公路方向人群通行.
防护门应该满足的需求属性包括:
EVN_3,所有的防护门都具有打开和关闭两个状态;
FUN_4,控制器通过向防护门发送打开或者关闭命令来控制防护门的状态,在非连续接车的作业中,防护门的状态切换为打开→关闭→打开;
FUN_5,在连续接车作业中,防护门的状态切换为打开→关闭→保持关闭→打开;
SAF_1,在连续接车作业中,防护门应该保持关闭;
SAF_2,当无连续接车时,列车激活S_EXi传感器后,出口防护门和入口防护门应被打开;
SAF_3,在列车激活S_APi传感器时,入口防护门应被关闭.
2.4 信号灯
信号灯的作用是为了向公路方向的人群示意道口的状态,起到警示作用. 大部分道口信号灯只设置了红灯和绿灯,本文增加了红闪状态. 红灯表示有列车接近道口,禁止进入防护门;红闪表示道口有连续来车,防护门保持关闭,禁止通行;绿灯表示道口空闲,可通行.
信号灯的需求属性包括:
EVN_4,信号灯有红灯、红闪和绿灯3种状态;
FUN_6,当S_APi被激活后,信号灯将切换为红灯.
2.5 列车
列车司机在运行时应仔细观察周围的运行环境,且注意接收道口控制器发出的信息. 司机在接到异常信息时应及时制动,否则应保持正常运行且通过道口. 相应的安全需求属性为:
SAF_4,当接收到控制器发出的异常或者未出清等消息后,列车司机应该及时采取制动措施.
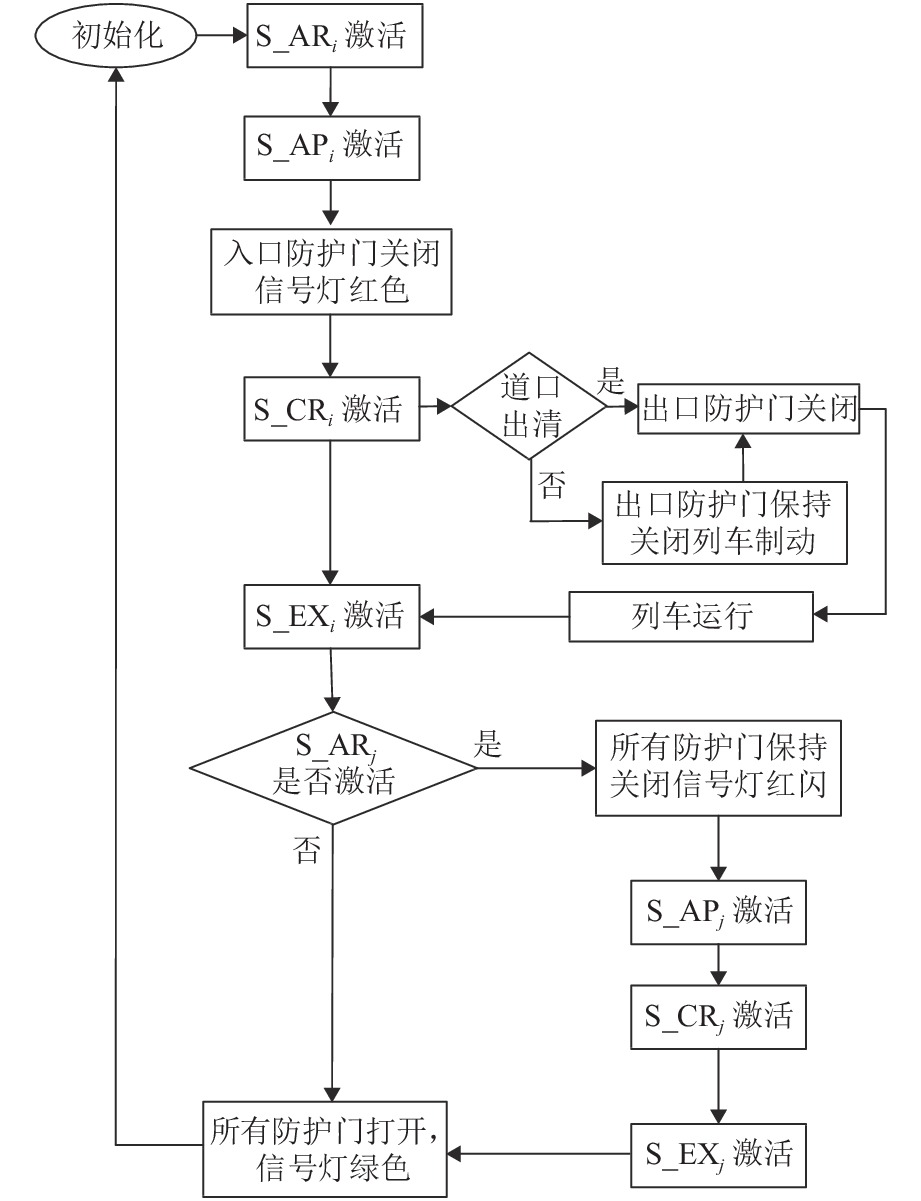
整个ACS系统的作业流程如图4所示.
3. 基于Event-B的形式化建模
Event-B模型由元组
(C,S,A,V,I,Σ,E,Init) 构成,其中:C和S分别为模型常量和集合类型;A为模型公理的集合;V 为系统变量集;I为一组不变式;Σ为由向量的所有可能值定义的模型状态空间;Init为定义初始模型状态的非空集合的谓词;E为一个模型事件集,集合中元素事件e表示为[5]e⇒anyαwhereGuardsthenActionsend 当条件Guards均成立时,可以执行Actions,α为事件参数.
RODIN[5]是Event-B建模与验证平台. 在RODIN中采用精化的建模方式,精化的过程就是将初始模型转化为更具体的模型[11]. 设计人员在建模中逐层精化,直到系统需要满足的所有功能都已包含在模型中.
本文由一个初始模型展开,经过了7层精化获得最终模型. 初始模型文件构造了在方向i的轨道和列车动态事件. 每层精化的内容如下:
第1层 在初始模型的基础上,构造了在方向j的轨道和列车动态事件.
第2层 添加了列车的位置变化信息,其中,通过不同传感器被激活的事件来表示列车所到达的位置.
第3层 添加了入口防护门和出口防护门的状态,以及状态改变事件.
第4层 添加了信号灯的状态,以及状态改变事件.
第5层 考虑到平交道口出清的检查,在这种改进中使用了几个事件呈现不同的决策. 如果道口完成出清,出口护栏门应关闭,列车将继续行驶.
第6层 添加驶近列车的多个运行状态,包括列车的制动.
第7层 增加了连续接车的相关事件.
以精化后得到的模型防护门关闭事件为例进行说明. 如前所述,本文将防护门分为入口防护门和出口防护门,在对防护门进行关闭操作时,入口防护门和出口防护门的关闭事件发生有所不同. 给入口防护门事件(EntranceBarriers_Closed)的代码如图5所示. 图中:i_train为方向i列车变量(方向j的定义相同);i_train_lc_pos(i_n)为方向i列车的位置;continue_flag用于判断是否连续接车. 当方向i (方向j)有列车激活S_APi (S_APj)传感器(grd1和grd2)且没有连续接车(grd3)时,入口防护门应该关闭. 而当列车激活S_CRi传感器,控制器发送Normal信号,且对列车发送保持前进命令后,出口防护门才可以被关闭.
4. 系统属性验证
为了保证系统满足需求属性,基于RODIN平台利用模型检测和定理证明两种方式对系统模型进行验证.
4.1 Animation
在RODIN平台上,ProB插件能够充分支持模型的仿真,并提供Animation中隐含的模型检测技术. Animation通过观察模型的执行来检查模型的行为.
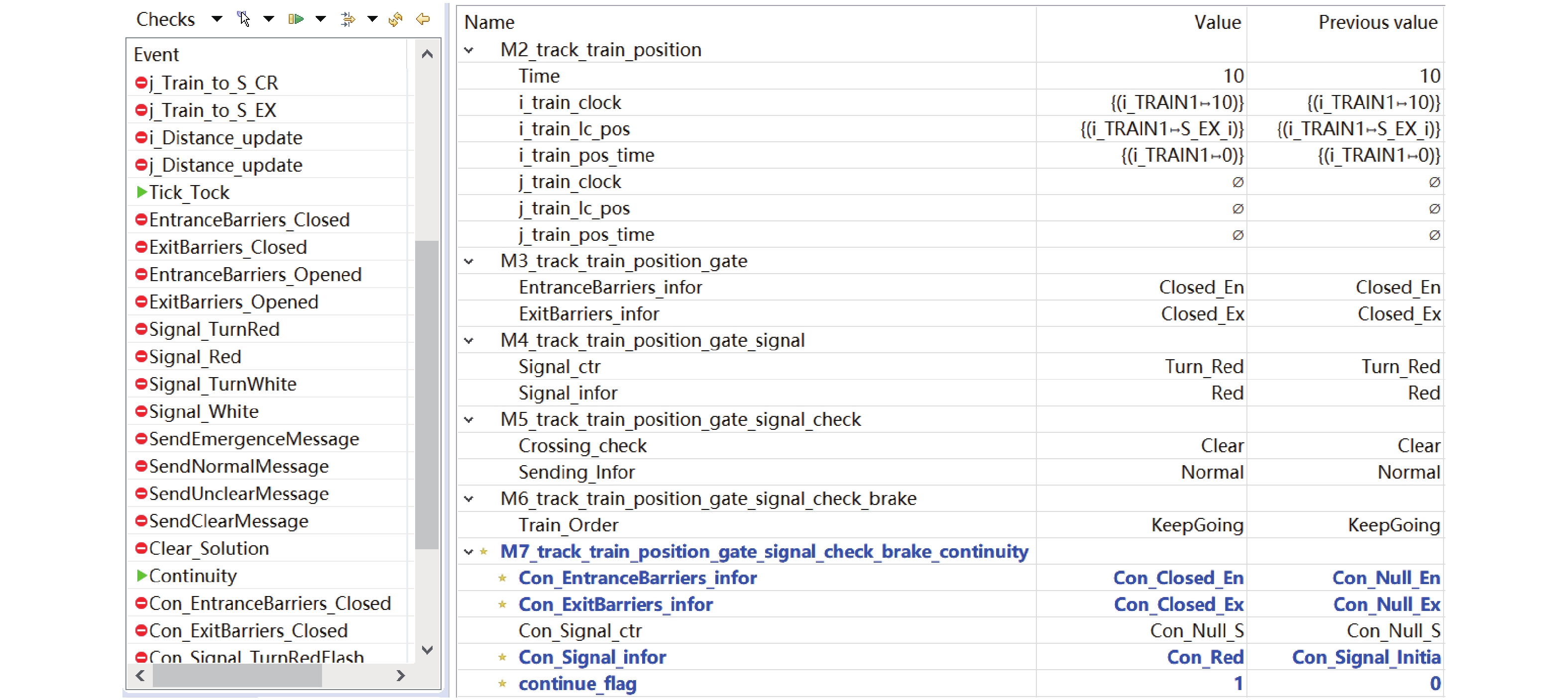
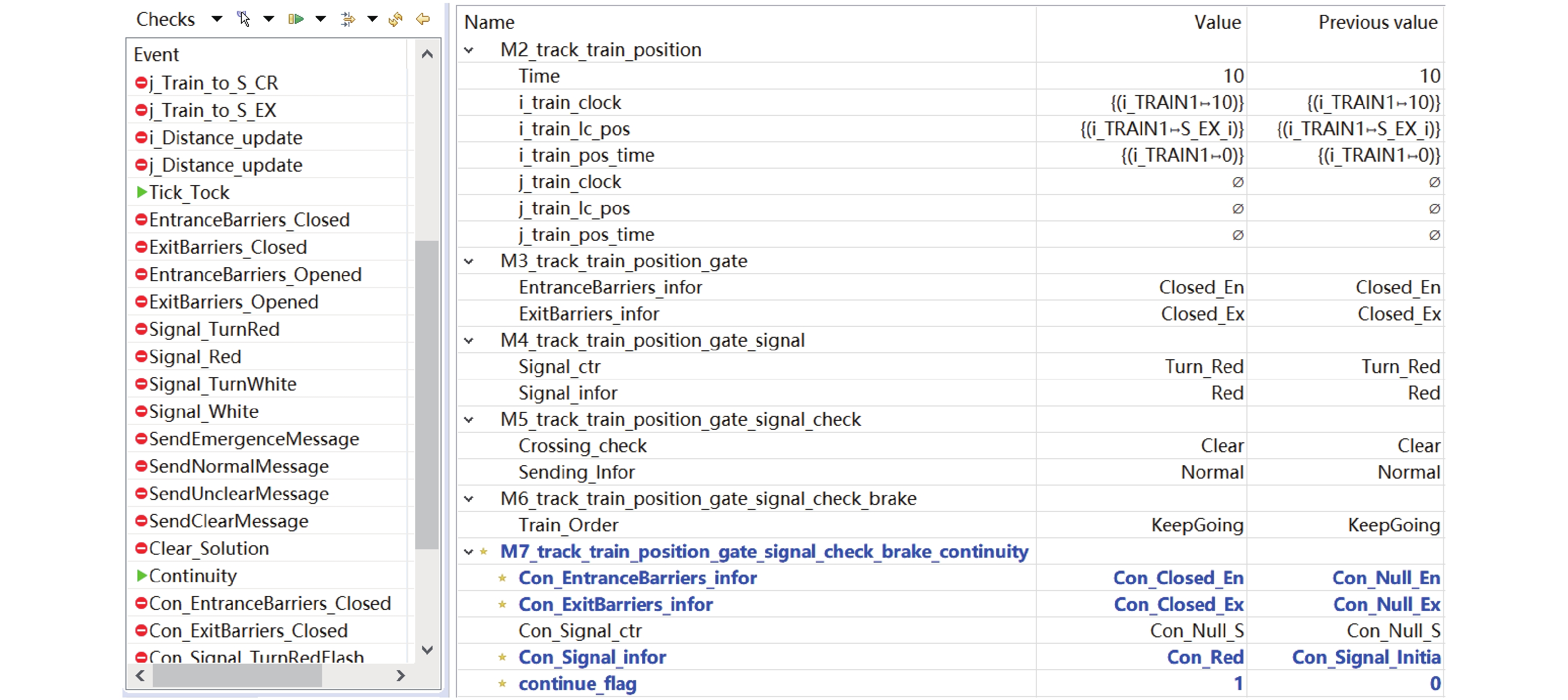
在Animation中,每个变量可以在连续的时间中进行更改. 以连续接车为例,列车激活S_EXi后,系统将满足所有的防护门均保持关闭.
由此,在第7层精化中给定不变式(Con_ExitBarriers_infor = Keep_Closed_Ex ∧ Con_EntranceBarriers_infor = Keep_Closed_En)
⇒continue_flag = 1,其中:Con_ExitBarriers_infor表示出口防护门接收的命令;Con_EntranceBarriers_infor表示入口防护门接收的命令;Keep_Closed_Ex、Keep_Closed_En分别表示出、入口防护门保持关闭. 该不变式表明在连续接车时,出口和入口防护门均保持关闭. 在Animation仿真过程中,该需求被满足. 图6显示了对应的动画状态及变量值.4.2 证明义务验证
不变式用于表示形式化模型的性质,必须在所有的初始状态被满足,并在所有给定系统可达状态的迁移中得到满足. 在该模型中,使用不变式描述安全属性如下,其含义见第2节.
SAF_1: (Con_ExitBarriers_infor = Keep_Closed_Ex∧Con_EntranceBarriers_infor = Keep_Closed_En)
⇒continue_flag = 1. 其中:Ex和En分别表示出口和入口防护门.SAF_2:(Con_ExitBarriers_infor = Con_Opened_Ex∧Con_EntranceBarriers_infor = Con_Opened_En)
⇒(((∃ i_n·i_n∈i_train∧(i_train_lc_pos(i_n) = S_EX_i)) ∧(∃ j_m · j_m∈j_train∧(j_train_lc_pos(j_m) = S_EX_j)))∨((i_train_lc_pos =Ø∧(∃ j_m·j_m ∈ j_train∧(j_train_lc_pos(j_m) = S_EX_j))) ∧(j_train_lc_pos = Ø∧(∃ i_n·i_n ∈ i_train ∧ (i_train_lc_pos(i_n) = S_EX_i))))). 其中:i_train_lc_pos(i_n)表示方向i上列车所处的位置;j_train_lc_pos(j_m)表示方向j上列车所处的位置.SAF_3:(EntranceBarriers_infor = Closed_En)
⇒ ((∃i_n · i_n∈i_train ∧ (i_train_lc_pos(i_n) =S_AP_i))∨ (∃j_m ·j_m ∈j_train∧(j_train_lc_pos(j_m) = S_AP_j)).SAF_4:Train_Order
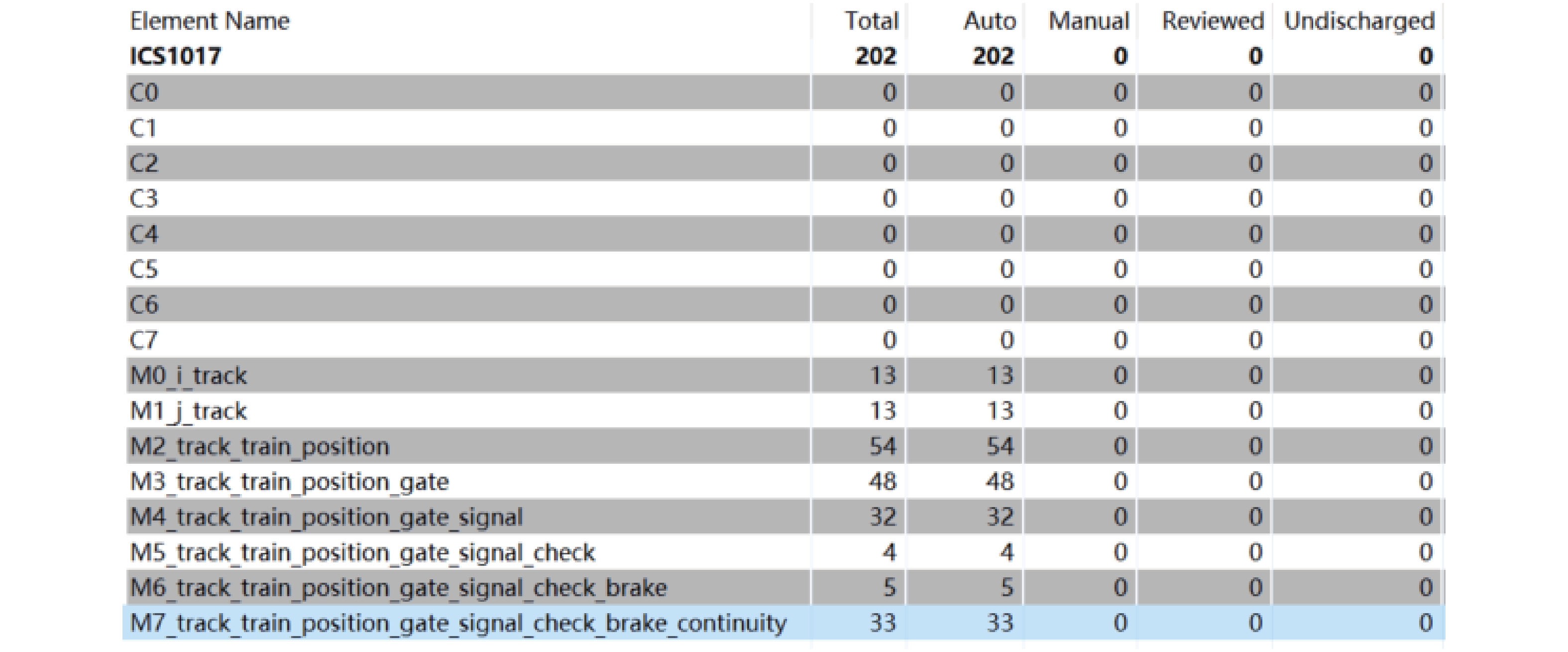
⇒Brake⇒ Sending_Infor = Abnormal. 其中:Train_Order表示列车接收的命令;Sending_Infor表示给列车发送的信息.每个不变式可以自动生成多条证明义务. 通过自动验证所有证明义务,可以判断不变式在每个事件的执行过程中是否一直正确. 本文建立的精化模型中产生的证明义务统计如图7所示. 该模型共有8个文本文件(C开头)、8个机器文件(M开头),总计产生202条证明义务,且所有证明义务均自动通过验证.
5. 结 论
为提高铁路平交道口控制系统的安全性,本文提出一个新的双线双向平交道口控制系统. 基于形式化语言Event-B对控制系统进行形式化建模. 为验证系统的有效性和正确性,对模型的证明义务进行验证,并通过ProB中的动画器对操作流程进行仿真. 结果表明,该新系统在满足平交道口双线双向接车的需求属性的同时解决了传统道口控制系统常见的3类问题:
1) 连续接车中防护门短时间开放. 增加S_ARi传感器,可以及时反馈相反方向是否有来车,并做出是否连续接车的判断. 此时,增加了信号灯双闪提示,以警示道路方向的可运行状态.
2) 出清检查. 分别设置进出口防护门状态,对及时疏散道路方向的行人车辆有着较好的效果. 在每个接车方向增加传感器S_CRi,可以满足列车在道口未完成出清条件下,及时制动.
3) 制动距离限制. 给定S_CRi的设置位置,以满足列车制动距离不会逾越安全区域.
-
[1] LIU B S, GHAZEL M, TOGUYÉNI A. Model-based diagnosis of multi-track level crossing plants[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2): 546-556. doi: 10.1109/TITS.2015.2478910 [2] JONSSON L, BJÖRKLUND G, ISACSSON G. Marginal costs for railway level crossing accidents in Sweden[J]. Transport Policy, 2019, 83: 68-79. doi: 10.1016/j.tranpol.2019.09.004 [3] GHAZEL M, EL-KOURSI E M. Two-half-barrier level crossings versus four-half-barrier level crossings: a comparative risk analysis study[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 1123-1133. doi: 10.1109/TITS.2013.2294874 [4] 曹源,唐涛,罗丹,等. 列车运行控制系统设计正确性的验证方法[J]. 西南交通大学学报,2010,45(4): 86-91. doi: 10.3969/j.issn.0258-2724.2010.04.015CAO Yuan, TANG Tao, LUO Dan, et al. Method for verifying the correctness of train control system design[J]. Journal of Southwest Jiaotong University, 2010, 45(4): 86-91. doi: 10.3969/j.issn.0258-2724.2010.04.015 [5] MEKKI A, GHAZEL M, TOGUYENI A. Validation of a new functional design of automatic protection systems at level crossings with model-checking techniques[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 714-723. doi: 10.1109/TITS.2011.2178238 [6] 王恪铭,王峥. 基于形式化方法的道口控制系统规范建模与验证[J]. 西南交通大学学报,2019,54(3): 573-578,603.WANG Keming, WANG Zheng. Modeling and verification of control system specification for railway level crossings based on formal method[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 573-578,603. [7] 王霞,刘宁,王恪铭. 道口管理系统多参数的形式化建模与验证[J]. 综合运输,2019,41(2): 65-72.WANG Xia, LIU Ning, WANG Keming. Formal modeling and verification of multi-parameter model of level crossing management system[J]. China Transportation Review, 2019, 41(2): 65-72. [8] ABRIAL J R. Modeling in Event-B: system and software engineering [M]. Cambridge: Cambridge University Press, 2010 [9] 王恪铭,王霞,程鹏,等. 车站联锁系统行为验证与数据确认的形式化方法[J]. 西南交通大学学报,2021,56(3): 587-593,613.WANG Keming, WANG Xia, CHENG Peng, et al. Formal method for behavior verification and data validation of station interlocking system[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 587-593,613. [10] 柏卓彤,柏赟,李佳杰,等. 基于制动距离表的高速铁路ATP常用制动曲线研究[J]. 铁道标准设计,2018,62(11): 139-143,149. doi: 10.13238/j.issn.1004-2954.201712310002BAI Zhuotong, BAI Yun, LI Jiajie, et al. The research on automatic train protection service braking curve based on braking distance table[J]. Railway Standard Design, 2018, 62(11): 139-143,149. doi: 10.13238/j.issn.1004-2954.201712310002 [11] BÖRGER E. The ASM refinement method[J]. Formal Aspects of Computing, 2003, 15(2/3): 237-257. 期刊类型引用(2)
1. 王萌,刘皓玮,郑泽熙,欧阳籽勃,刘宁馨. 面向匈塞铁路的道口控制系统差异性分析及结构设计研究. 铁道运输与经济. 2025(03): 95-101 .  百度学术
百度学术2. 王萌,刘皓玮,欧阳籽勃,段鹏宇. 适用于匈塞铁路的道口控制系统研究. 铁路通信信号工程技术. 2025(04): 103-108+116 .  百度学术
百度学术其他类型引用(2)
-






 下载:
下载:



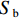
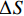

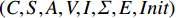
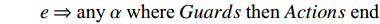


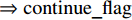




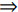
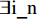
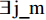
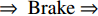

 下载:
下载:



 百度学术
百度学术