钢轨波磨预测模型验证工况的研究

陈光雄

doi:10.3969/j.issn.0258-2724.20200842

钢轨波磨预测模型验证工况的研究

doi: 10.3969/j.issn.0258-2724.20200842

陈光雄

西南交通大学机械工程学院，四川成都 610031

基金项目: 国家自然科学资金（51775461）

详细信息

作者简介:
陈光雄（1962—），男，教授，博士，研究方向为摩擦学与车辆动力学，E-mail：chen_guangx@163.com

中图分类号: V221.3
计量
- 文章访问数: 556
- HTML全文浏览量: 275
- PDF下载量: 43
- 被引次数: 13
出版历程
- 收稿日期: 2020-12-22
- 修回日期: 2021-06-09
- 网络出版日期: 2022-08-13
- 刊出日期: 2021-09-08

Study on Validation Conditions of Rail Corrugation Prediction Models

CHEN Guangxiong

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
钢轨波磨会降低乘坐舒适性，增大轨道结构伤损，甚至影响列车的安全运行. 为判断钢轨波磨预测模型的准确性，首先，基于钢轨波磨现场调研数据，统计地铁线路和干线铁路的钢轨波磨发生率；其次，针对现有钢轨波磨预测模型验证方法的局限性，同时结合钢轨波磨发生的规律性，提出预测模型验证的3种基本工况：线路曲线半径≤350 m时的内轨波磨和外轨波磨、曲线半径 ≥ 650 m时的非科隆蛋扣件曲线线路或者直线线路钢轨的波磨，并进行实例验证；最后，根据基于轮轨蠕滑力饱和情况，提出了一种快速预测钢轨波磨发生的新方法. 研究结果表明：现有的波磨预测模型验证工况缺乏一般性，大部分没有考虑线路曲线半径的影响，忽视了从新轨到波磨出现阶段的钢轨振动演变规律，造成通过验证的波磨预测模型预测准确率偏低；所提出的波磨快速预测方法准确率可达到85.00%.
- 钢轨波磨 /
- 磨损 /
- 模型验证 /
- 摩擦耦合 /
- 自激振动
Abstract:
Rail corrugation not only reduces the ride comfort of passengers, but also increases damages of tracks and vehicles, and even affects the safe operation of trains. In order to verify the correctness of rail corrugation prediction models, firstly the occurrence probability of rail corrugation was calculated based on field investigation data into a metro line and railway main-lines. Secondly, aiming to the shortcomings of the validation method of traditional rail corrugation prediction models, and based on the regularity of rail corrugation occurrence, the benchmark conditions for the verification of the rail corrugation prediction models were proposed, which include the first condition: rail corrugation on the low and high rails at a tight curved tracks whose radii are less than 350 m;the second condition: rail corrugation on the low and high rails at mild curved tracks whose radii are larger than 650 m without Colong-egg fasteners; the third condition: rail corrugation on the two rails of tangential tracks without Colong-egg fasteners. A case study on the prediction of rail corrugation on an actual metro line was performed. Finally, based on whether the creep force is saturated or not, a fast method for predicting rail corrugation was proposed. The research result shows that existing validation conditions for rail corrugation are not universal, that the traditional rail corrugation models neglect the effect of track radii; and that the rail vibration evolution from a new rail without corrugation to the rail with corrugation was ignored in the model validation procedure, which lead to a low model prediction accuracy of rail corrugation. The prediction accuracy of the proposed fast method for predicting rail corrugation reaches 85.00%.
- rail corrugation /
- wear /
- model validation /
- friction coupling /
- self-excited vibration

HTML全文

为建成交通强国，我国将推动高速磁浮列车技术研究列为交通强国战略的重要组成部分^[1]. 测速定位技术是磁浮列车高效安全运行的基础^[2-3]，精确无延时地检测出列车在每个时刻的速度和位置是确保整个列车系统安全运行的首要条件. 在运行过程中，列车通过测速定位系统获得列车的位置信息，从而实现高效牵引^[4]. 高速磁浮列车测速定位与运行控制、牵引控制、车地通信、悬浮控制等多个方面紧密相关，对精度、响应时间等指标要求较高^[5].

基于常导制式高速磁浮特有的长定子齿槽结构，齿槽检测定位技术具有精度高、可靠性高、维护相对简单、造价相对较低的特点^[6]，已应用于上海磁浮线及四方磁浮试验线. 目前，此类方法的研究主要集中在轨道接缝和磁浮间隙对定位的影响. 罗桂斌^[7]提出一种多传感器自适应加权融合算法，对传感器实际数据与随机抽样一致算法（RANSAC）预测模型的数据进行融合，解决了磁极相角信号过接缝时的畸变问题. 窦峰山等^[8]采用一种新型跟踪微分器（TD），用于解决轨道接缝导致的信号畸变问题. 吴峻等^[9]为了降低悬浮波动对相对位置检测的影响，利用悬浮间隙归一化处理相对位置检测信号的方法，使输出统一变换为8 mm悬浮间隙下的信号,达到了磁极相角精度2.8° 的检测要求.

针对多影响因素下的高速磁浮定位问题，本文提出一种基于加权融合无迹卡尔曼滤波（UKF）的常导高速磁浮列车测速定位算法，该算法以四路磁极相角信息（PRW）定位信号为输入信息，先局部处理，再全局加权融合后经无迹卡尔曼滤波算法进行隐藏状态预测，减小不确定性因素影响，获得更加准确可靠的速度位置信息.

1. 高速磁浮列车测速定位系统

1.1 基于长定子齿槽检测的测速定位方法

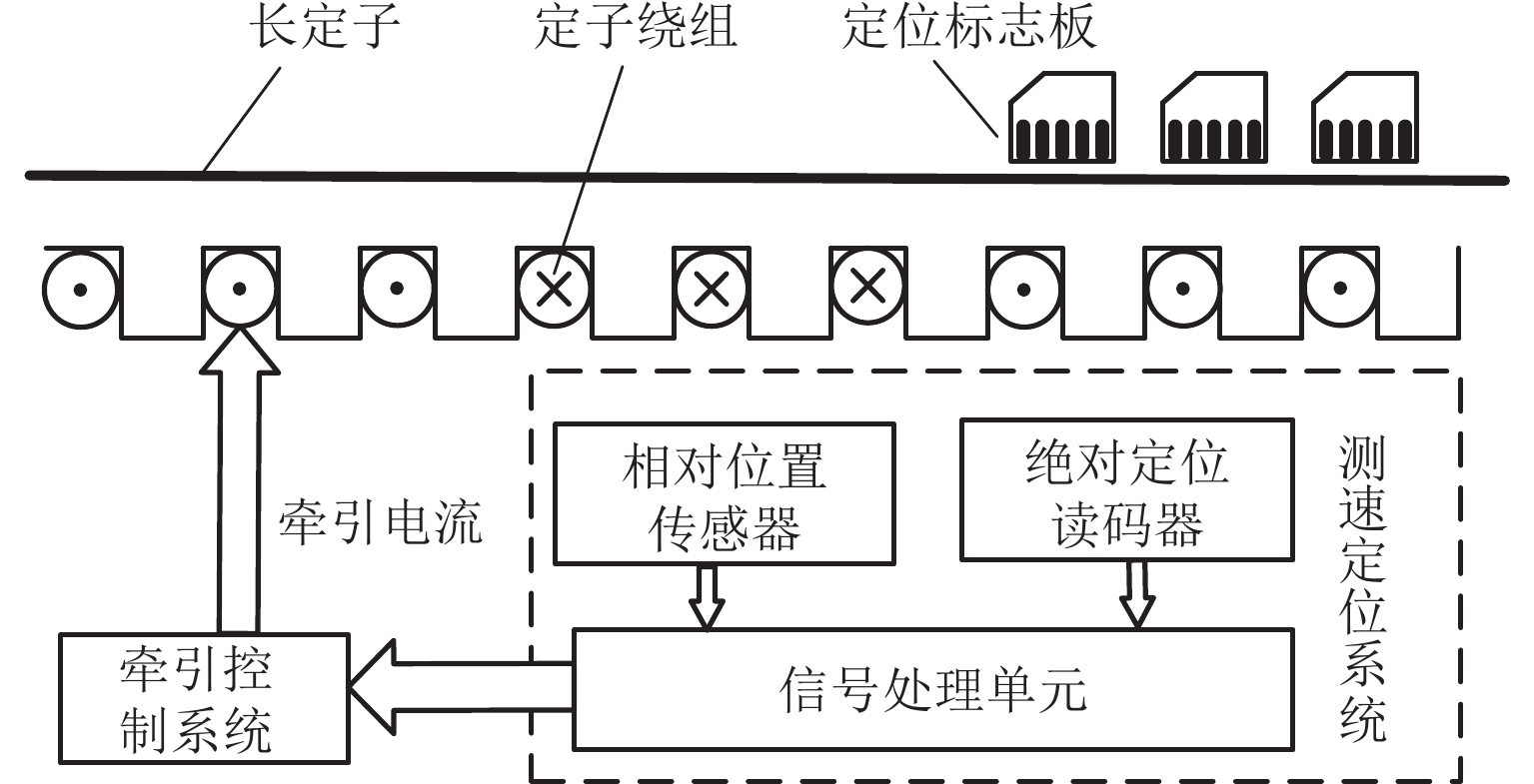
在常导制式高速磁浮列车中，采用基于长定子齿槽检测的测速定位方法，该测速定位系统包括相对位置传感器、绝对位置传感器、绝对定位标志板、长定子齿槽和信号处理单元. 长定子直线同步电机作为牵引电机置于轨道上，长定子具有齿槽结构^[5]. 当列车沿轨道运行时，位于列车转子侧的相对位置传感器感应线圈由固定频率的激励信号源和谐振电路驱动组成，检测到感应线圈自身等效电感的周期性变化，经信号处理，可以得到单位时间内线圈通过的齿槽数，经过系列处理后得到列车速度. 在列车运行过程中由于各种不定因素的影响，比如测速定位系统（ORT）工作故障、误码等现象的存在，需要每隔一段里程通过绝对位置传感器检测轨道两侧的绝对位置标志板的位置信息，对列车运行的里程位置进行校正，依此来消除运行过程中累计的误差. 综合计算得出位置速度值输出至运控牵引控制系统，系统根据目标速度控制列车牵引电流，从而控制磁浮列车运行. 此种测速定位方法具有分辨力高、可靠性好、造价低的优点. 基于长定子齿槽检测的测速定位方法示意如图1.

图 1 基于长定子齿槽检测的测速定位示意

Figure 1. Speed measurement and positioning based on tooth slot detection of long stator

下载: 全尺寸图片幻灯片

1.2 高速磁浮列车测速定位数据预处理

磁浮列车通过整合处理相对位置传感器和绝对位置传感器收集的位置信息，生成PRW报文，经解析后，得到列车速度信息.

$P = {P_{{\text{PPA}}}} + {P_{{\text{LRF}}}} + {P_{{\text{ASI}}}},$

(1)

$v(a) = \frac{{P(a + 1) - P(a)}}{{\Delta t}} = \frac{{\Delta P}}{{\Delta t}},$

(2)

式中：P为列车位置信息，m； ${P}_{\mathrm{P}\mathrm{P}\mathrm{A}}$ 为磁极相角度数PPA对应的里程信息，m； ${P}_{\mathrm{L}\mathrm{R}\mathrm{F}}$ 为储存的绝对定位标志板的里程信息，m； ${P}_{\mathrm{A}\mathrm{S}\mathrm{I}}$ 为列车的相对位置信息，m；v(a)为第a次通信时刻列车的速度，m/s；P(a)为第a次通信时刻列车的位置，m； $\Delta t$ 为取样时间， $\Delta t$ =0.02 s.

2. 高速磁浮列车定位测速算法研究

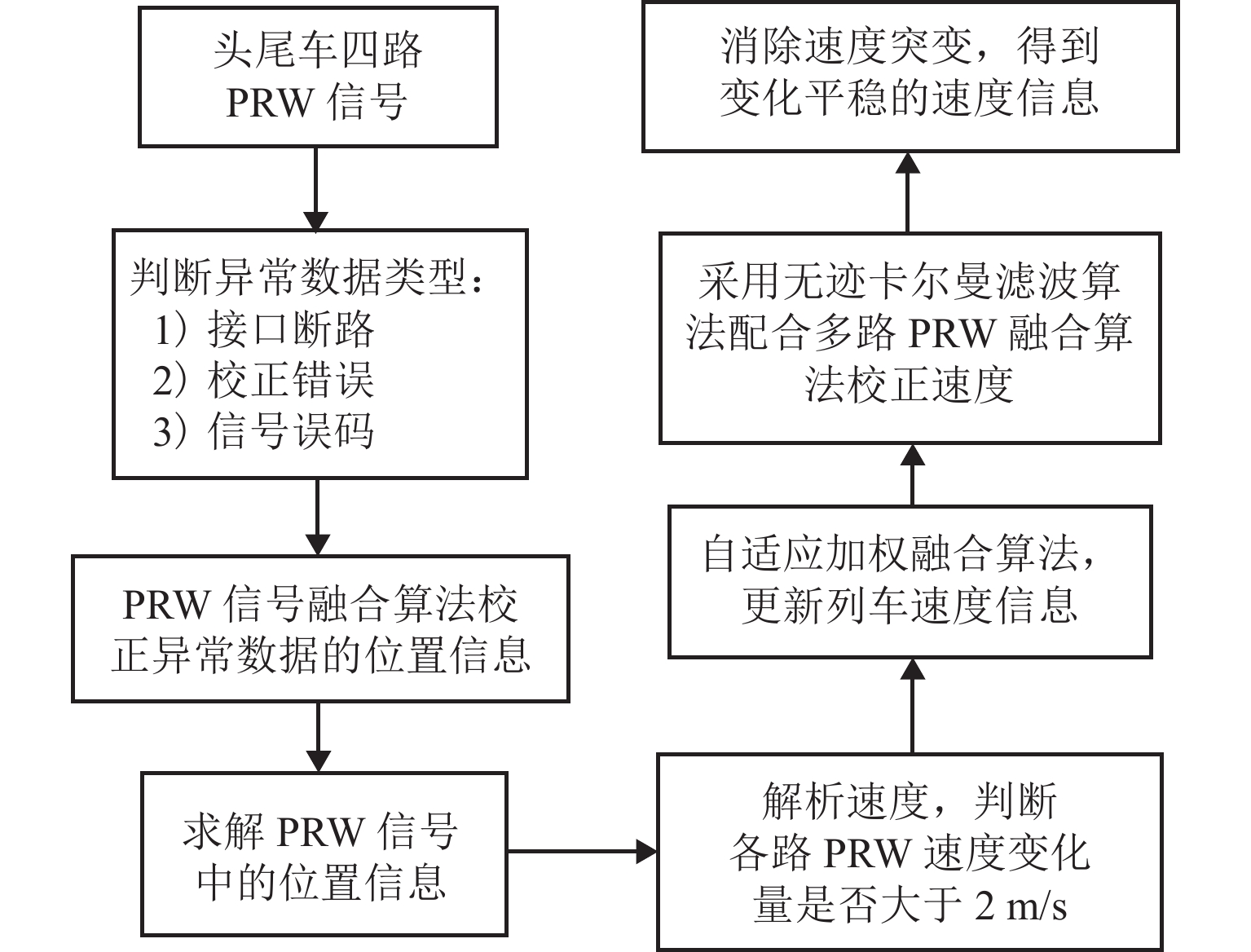
本文从自适应调整多路冗余定位信息角度出发，进行多路定位传感器信号融合，并基于无迹卡尔曼算法进行自适应滤波，以提高整个测速定位系统的滤波精度、容错性和可靠性，满足列车控制系统要求. 整个测速定位算法流程如图2所示.

图 2 多路定位信号融合算法流程

Figure 2. Flowchart of multi-channel positioning signal fusion algorithm

下载: 全尺寸图片幻灯片

2.1 高速磁浮定位信号自适应加权融合

磁悬浮列车传感器将PRW定位信号传输到车载计算机用于电机控制，车载计算机需要解析PRW信号中位置、速度信息，根据目标速度控制列车牵引力大小和列车运行速度. 列车运行过程中，牵引电机控制单元（MCU）会收到来自车头车尾共4路PRW定位信号. PRW定位信号可能会出现重发、丢包等现象，导致解析位置信息时出现误差. 因此，本文对列车运行过程中采集到的4路PRW定位信号进行研究，建立多路定位信号融合算法，采用自适应加权融合算法可得到均方误差最小的结果，以下为自适应加权融合过程.

1）通过格拉布斯准则将4路PRW定位信号中同一时刻的异常速度信息剔除，根据支持度进行速度异常值替换，如式（3）.

${L_{ij}} = \sqrt {\frac{{{x_i}{{^2}_{}} - 2{x_i}{x_j} + {x_j}^2}}{2}} = \frac{{\left| {{x_i} - {x_j}} \right|}}{{\sqrt 2 }},$

(3)

式中： ${{L}}_{{ij}}$ 为某通信时刻第i路PRW定位单元和第j路定位单元之间的测量相关性，i,j=1,2,3,4，且i≠j； ${x}_{i}$ 为第i路PRW定位单元的速度测量值.

归一化处理不同定位单元之间的测量相关性，如式（4）.

${l_{ij}} = \frac{{{L_{ij}}}}{{\mathop {\max }\limits_{i,j} \;{L_{ij}}}} = \frac{{\left| {{x_i} - {x_j}} \right|}}{{\mathop {\max }\limits_{i,j} \left| {{x_i} - {x_j}} \right|}}.$

(4)

由（4）式可知，0≤ ${l}_{ij}$ ≤1，且 ${l}_{ij}$ 越接近于1，PRW定位单元之间的相关性越低，即PRW定位单元之间的支持度越小.

若同一时刻4路PRW定位信号相同，即 $\mathrm{max}\dfrac{\left|{x}_{i}-{x}_{j}\right|}{\sqrt{2}}=$ 0，则 ${l}_{ij}$ =0. 得到支持度函数，如式（5），其中， ${S} _{ij}={S} _{ji}$ .

${S _{ij}} = 1 - {l_{ij}}.$

(5)

构造出支持度矩阵S为

${\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} 1&{{S _{12}}}&{{S _{13}}}&{{S _{14}}} \\ {{S _{21}}}&1&{{S _{23}}}&{{S _{24}}} \\ {{S _{31}}}&{{S _{32}}}&1&{{S _{34}}} \\ {{S _{41}}}&{{S _{42}}}&{{S _{43}}}&1 \end{array}} \right] .$

(6)

第i路PRW定位单元与其他PRW定位单元之间的支持度为

${S _i} = \frac{1}{4}\sum\limits_{j = 1}^4 {{S _{ji}}} .$

(7)

通过支持度计算公式，将支持度最高的数据代替异常数据.

2）在整体融合方差最小的条件下，对每个测量值进行权重分配. 四路PRW定位信息相互独立，设x为待测的速度真值，某时刻第i路PRW定位单元的速度测量方差为

$\sigma _i^2 = {{E}}{(x_i^{} - x)^2}.$

(8)

通信时刻t第i路PRW定位单元的方差估计值计算过程如式（9）.

${\sigma _i^2}{(t)} = \frac{{t - 1}}{t}{R_{xii}}(t - 1) + \frac{1}{t}{x_i^2}{(t)} - \frac{1}{3}\sum\limits_{j = 1,j \ne i}^4 {{R_{ij}}(t)},$

(9)

式中： ${R}_{xii}$ 为 ${x}_{i}$ 的自协方差函数， ${R}_{ij}$ 为 ${x}_{i}$ 和 ${x}_{j}$ 的协方差函数.

每一时刻第i路PRW定位单元的权重为

${\omega _i}(t) = \frac{1}{{{\sigma _i}{{(t)}^2}}} \frac{1}{{\displaystyle\sum\limits_{i = 1}^4 {\dfrac{1}{{{\sigma _i}{{(t)}^2}}}} }}.$

(10)

3）将每一时刻四路PRW定位单元的速度测量值与其对应权重相乘得最终加权融合结果 $\hat x$ ，如式（11）.

$\left\{ \begin{gathered} \hat x = \sum\limits_{i = 1}^4 {{x_i}{\omega _i}}, \\ \sum\limits_{i = 1}^4 {{\omega _i} = 1}, \\ {\sigma ^2} = \sum\limits_{i = 1}^4 {\omega _i^2\sigma _i^2} . \\ \end{gathered} \right.$

(11)

2.2 基于无迹卡尔曼滤波的高速磁浮列车测速方法

在列车实际运行过程中，系统噪声和量测噪声难以准确统计且系统模型为强非线性，因此，引入改进卡尔曼滤波算法，常见有扩展卡尔曼滤波（EKF）^[10]、UKF^[11]等. EKF将模型误差作为过程噪声处理，与实际不符，且当系统非线性较强时，滤波精度会降低^[12]. 而UKF不需要对非线性系统进行线性化，在处理强非线性系统问题上比EKF有更高的精度和稳定性.

UKF的核心思想是采用UT （unscented transformation）变换，利用一组Sigma采样点描述随机变量的高斯分布，然后通过非线性函数的传递，利用加权统计线性回归技术来近似非线性函数的后验均值和方差.

UKF计算过程如下^[13]：

1）初始化

$\hat {{{\boldsymbol{X}}_0}} = {{E}}\left[ {{{\boldsymbol{X}}_0}} \right],$

(12)

${{\boldsymbol{L}}_0} = {{E}}\left[ {\left( {{{\boldsymbol{X}}_0} - \hat {{{\boldsymbol{X}}_0}} } \right){{\left( {{{\boldsymbol{X}}_0} - \hat {{{\boldsymbol{X}}_0}} } \right)}^{\text{T}}}} \right],$

(13)

式中： ${\hat {\boldsymbol{X}}_0}$ 为初始时刻状态向量 ${\boldsymbol{X}}_{0}$ 的均值， ${{\boldsymbol{L}}}_{0}$ 为初始时刻状态向量 ${\boldsymbol{X}}_{0}$ 的方差.

2）计算Sigma点

采用基于Cholesky分解的对称采样策略进行Sigma点采样，计算2n + 1个Sigma点，如式（14），n为状态维数，本文中假设仅有一个速度状态变量.

$\left\{\begin{array}{l} \lambda=(n+\kappa)\alpha^2-n, \\ \boldsymbol{\chi}_{k-1}=\left[\begin{array}{c} \hat{\boldsymbol{X}}_{k-1} \\ \hat{\boldsymbol{X}}_{k-1}+\sqrt{(n+\lambda) \boldsymbol{L}_{k-1}} \\ \hat{\boldsymbol{X}}_{k-1}-\sqrt{(n+\lambda) \boldsymbol{L}_{k-1}} \end{array}\right], \end{array}\right.$

(14)

式中：λ为尺度因子；α为比例缩放因子，0≤α≤1，常取极小的正数，本文α=10⁻³；κ为比例因子，常取0或3−n，此处κ=0； ${\boldsymbol{\chi }}_{\mathit{k}-1}$ 为k−1时刻的Sigma点； ${\hat {\boldsymbol{X}} _{k - 1}}$ 为k−1时刻的状态估计值； ${\boldsymbol{L}}_{k-1}$ 为k−1时刻状态向量的方差.

对应权值为

$\left\{ \begin{gathered} {W}_{{\mathrm{a}}0,n} = \lambda /(n + \lambda ), \\ {W}_{{\mathrm{b}}0,c} = \lambda /(n + \lambda ) + (1 - {\alpha ^2} + \beta ), \\ {W}_{{\mathrm{a}}l,n} = {W_{l,c}} = 1/[2(n + \lambda )], \quad l = 1,2, \cdots ,2n , \\ \end{gathered} \right.$

(15)

式中： ${W}_{{\mathrm{a}}0,n}$ 为初始状态n维状态参数均值的权值； ${W}_{{\mathrm{b}}0,c}$ 为初始状态c维状态参数方差的权值； ${W}_{{\mathrm{a}}l,n}$ 为第l个n维状态参数均值的权值； ${W}_{{\mathrm{b}}l,c}$ 为第l个c维状态参数方差的权值；β用于融入 ${{\boldsymbol{\chi }}_l}$ 的先验信息，β≥0，本文β=2.

3）时间更新

利用非线性测量函数（式（16））计算k时刻系统状态、均值和协方差的单步预测^[13].

$\left\{\begin{array}{l} {\boldsymbol{\chi}}_{k \mid k-1}=f\left({\boldsymbol{\chi}}_{k-1}\right) ,\\ \hat{\boldsymbol{X}}=\displaystyle\sum_{l=0}^{2 n} W_{{\mathrm{a}}l, n} {\boldsymbol{\chi}}_{l, k| k-1}, \\ \boldsymbol{P}_{k \mid k-1}=\displaystyle\sum_{l=0}^{2 n} W_{{\mathrm{b}} l, c}\bigg[\left({\boldsymbol{\chi}}_{l, k \mid k-1}-\hat{\boldsymbol{X}}_{k \mid k-1}\right)\bigg. \times \\ \quad \left.\left({\boldsymbol{\chi}}_{l|k| k-1}-\hat{\boldsymbol{X}}_{k \mid k-1}\right)^{\mathrm{T}}\right]+\boldsymbol{Q}_k, \end{array}\right.$

(16)

式中： ${{\boldsymbol{\chi }}_{k|k - 1}}$ 为k−1时刻到k时刻的Sigma点， ${\hat {\boldsymbol{X}}_{k\left| {k - 1} \right.}}$ 为k−1时刻到k时刻系统状态预测估计值， ${{\boldsymbol{\chi }}_{l,k|k - 1}}$ 为 ${{\boldsymbol{\chi }}_{k|k - 1}}$ 的第l列， ${{\boldsymbol{P}}_{k|k - 1}}$ 为状态预测估计的协方差矩阵， ${{\boldsymbol{Q}}_k}$ 为过程噪声协方差矩阵.

4）测量更新

与时间更新过程相似，测量更新过程如下：

$\left\{ \begin{gathered} {{\boldsymbol{Z}}_{k|k - 1}} = g({{\boldsymbol{\chi }}_{k|k - 1}}), \\ {\hat {\boldsymbol{Z}} _k} = \sum\limits_{l = 0}^{2n} {W_{{\mathrm{a}}l,n}{{\boldsymbol{Z}}_{l,k|k - 1}}}, \\ {{\boldsymbol{P}}_{{\mathrm{zz}},k}} = \sum\limits_{l = 0}^{2n} {W_{{\mathrm{a}}l,n}({{\boldsymbol{Z}}_{l,k|k - 1}} - {{\hat {\boldsymbol{Z}} }_k}){{({{\boldsymbol{Z}}_{l,k|k - 1}} - {{\hat {\boldsymbol{Z}} }_k})^{\text{T}}}} + {{\boldsymbol{R}}_k}}, \\ \end{gathered} \right.$

(17)

式中： ${{\boldsymbol{Z}}_{k|k - 1}}$ 为k−1时刻到k时刻的预测观测值， ${\hat {\boldsymbol{Z}}_k}$ 为k时刻的观测值， ${{\boldsymbol{Z}}_{l,k|k - 1}}$ 为 ${{\boldsymbol{Z}}_{k|k - 1}}$ 的第l列， ${\boldsymbol{P}}_{{\mathrm{zz}},k}$ 为 ${\hat {\boldsymbol{Z}}_k}$ 的协方差矩阵， ${\boldsymbol{R}}_{k}$ 为k时刻测量噪声协方差矩阵.

5）滤波增益

基于时间更新和量测更新，k时刻的滤波增益矩阵、估计值和协方差矩阵计算过程如式（18）.

$\left\{ \begin{gathered} {{\boldsymbol{P}}_{{\mathrm{xz}},k}} = \sum\limits_{l = 0}^{2n} {W_{{\mathrm{b}}l,c}({{\boldsymbol{\chi }}_{l,k|k - 1}} - {{\hat {\boldsymbol{X}}}_{k|k - 1}}){{({{\boldsymbol{Z}}_{l,k|k - 1}} - {{\hat {\boldsymbol{Z}}}_k})}^{\mathrm{T}}}}, \\ {{\boldsymbol{K}}_k} = {{\boldsymbol{P}}_{{\mathrm{xz}},k}}{{\boldsymbol{P}}_{{\mathrm{zz}},k}^{ - 1}}, \\ {\hat {\boldsymbol{X}} _k} = {\hat {\boldsymbol{X}} _{k|k - 1}} + {{\boldsymbol{K}}_k}({{\boldsymbol{Z}}_k} - {\hat {\boldsymbol{Z}}_k}) , \\ {{\boldsymbol{P}}_k} = {{\boldsymbol{P}}_{k|k - 1}} - {{\boldsymbol{K}}_k}{{\boldsymbol{P}}_{{\mathrm{zz}},k}}{\boldsymbol{K}}_k^{\text{T}} , \\ \end{gathered} \right.$

(18)

式中： ${\boldsymbol{P}}_{{\mathrm{xz}},k}$ 为预测状态向量协方差矩阵， ${\boldsymbol{K}}_{k}$ 为k时刻滤波增益矩阵， ${\boldsymbol{Z}}_{\mathit{k}}$ 为k时刻观测向量， ${\boldsymbol{P}}_{k}$ 为 ${\hat {\boldsymbol{X}}_k}$ 的协方差矩阵.

将4路PRW定位信号经速度预处理和自适应加权融合算法处理后得到列车速度V(t)，如式（19）.

$V\left(t\right)=\sum _{i=1}^{4}{\omega }_{i}\left(t\right) {v}_{i}(t),\quad t=\mathrm{1,2},\cdots, 5\;695,$

(19)

式中： ${v}_{i}\left(t\right)$ 为t时刻第i路PRW速度.

将所得速度代入无迹卡尔曼滤波器中，根据观测系统本身所处数量级，系统过程噪声取值为0.01，将测量噪声设置为0.1，取样时间 $\Delta$ t=0.02 s. 通过UT变换对定位信息概率密度逼近，并通过Cholesky分解直接预测状态误差协方差，减小了噪声对计算结果的影响.

3. 测速定位算法验证分析

3.1 测速定位在环测试工况

基于青岛四方高速磁浮列车试验线，利用实时获取与交互的高速磁浮测速定位在环系统时空数据进行测速定位算法效果分析，如图3.

图 3 车载环境模拟与在环测试设备

Figure 3. Vehicle environment simulation and in-loop test equipment

下载: 全尺寸图片幻灯片

该在环测试设备针对轨道长度、弯道参数、列车运行速度曲线、运行时间等信息，可以自动生成给定列车运行状态下的ORT报文信号. 报文信号涵盖实际系统误差信息，将通信报文通过相应的信号转换传输给车载安全计算机，仿真系统与真实车载设备连接，在列车静止条件下，实现向磁浮列车安全计算机（VSC）传递列车运动状态信息的功能.

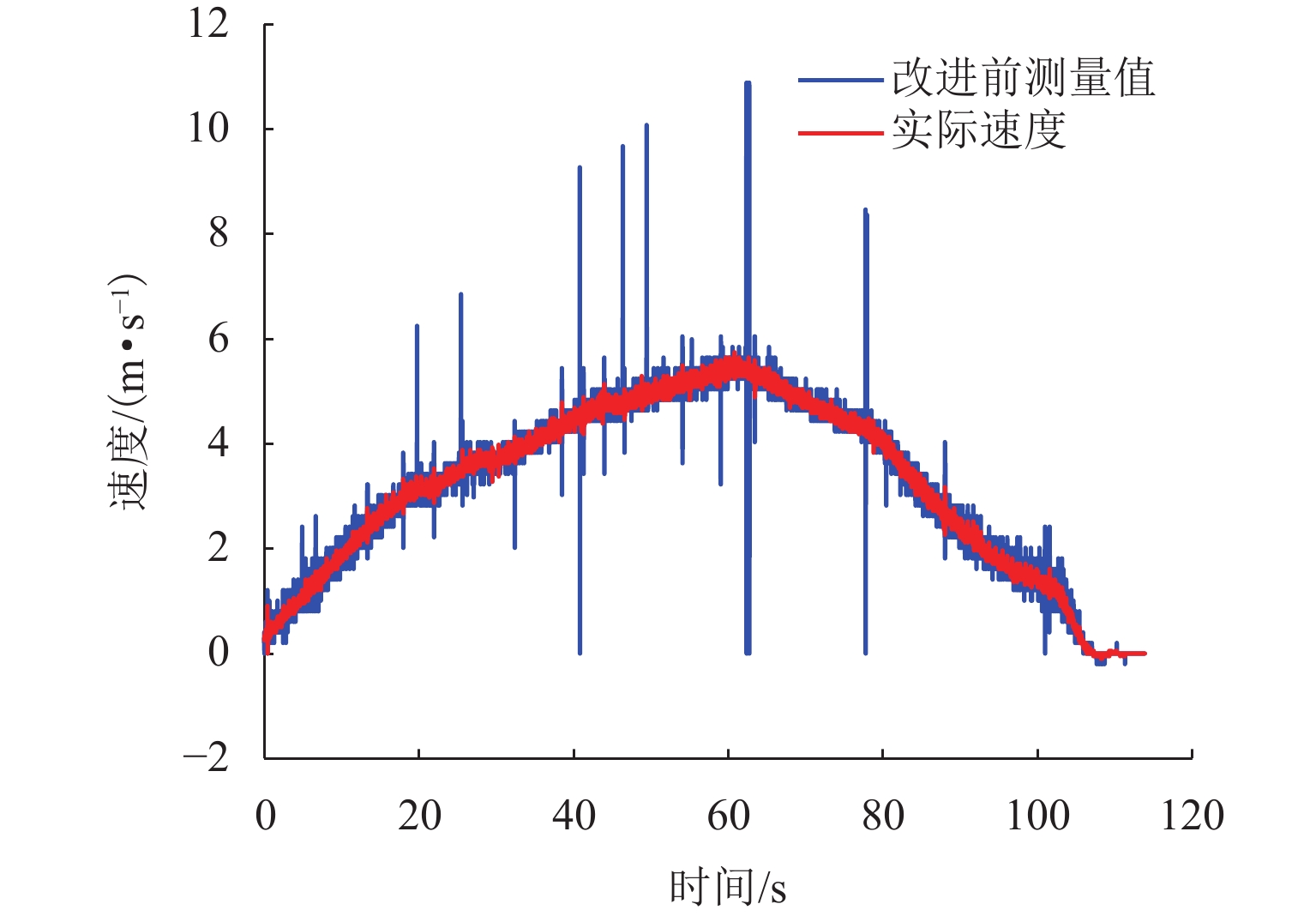
使用高速磁浮列车车载环境模拟与在环测试设备进行了测速定位系统运行工况测试，初始速度为0.2 m/s，以2.5 m/s²的加速度开始运行，达到速度5.6 m/s后，以2.5 m/s²的减速度继续行驶，最终行驶到506.4 m处速度为0，通信时间为0.02 s. 以同一时刻列车头尾四路的平均位置为列车实际位置，将相邻时刻的实际位置之差除以通信时间，得到实际速度. 由测速定位系统传感器测量值直接平均处理计算得到的车速值与实际速度对比，见图4. 由图4可知：列车速度测量值多处出现速度突变，并且在列车运行过程中出现速度为0的情况；测量值距真实值有较大误差，速度误差最大达5.6 m/s，测速定位测量值待优化，以避免运控系统由于速度突变引起牵引力的频繁调节，减少牵引电机功率损耗.

图 4 速度测量值和实际速度对比

Figure 4. Comparison of measured speed and actual speed

下载: 全尺寸图片幻灯片

3.2 测速定位效果分析

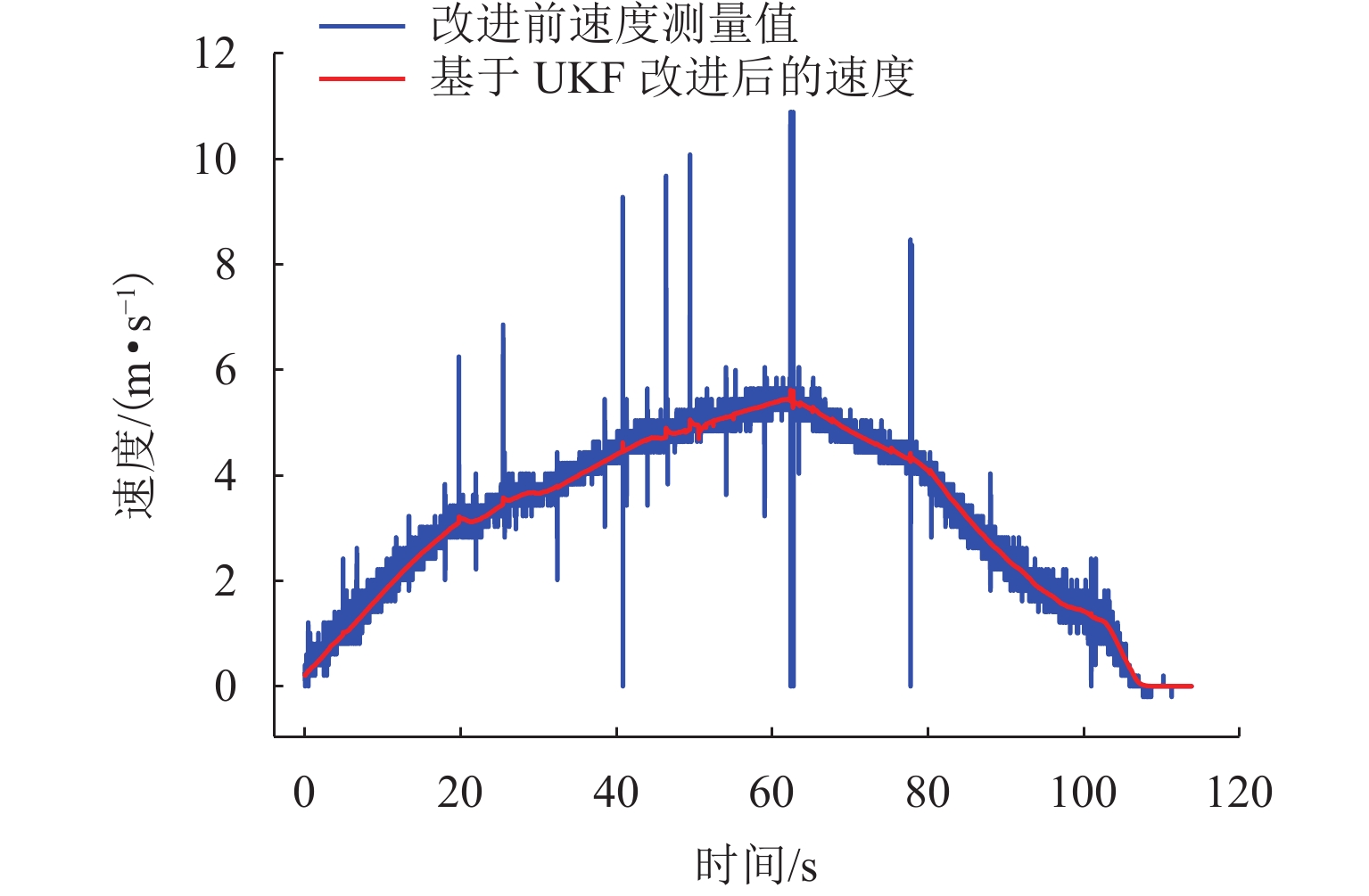
基于加权融合UKF的常导高速磁浮列车测速定位算法的定位测速结果如图5所示.

图 5 速度测量值与基于加权融合的UKF改进速度对比

Figure 5. Comparison of measured speed and speed after application of UKF based on weighted fusion

下载: 全尺寸图片幻灯片

由图5可知：经UKF改进后的测速定位曲线能较好地跟踪其真实轨迹，检测速度精度得到有效改善；改进前速度测量值极差为11.09 m/s，改进后速度极差为5.62 m/s，速度极差降低了49.3%.

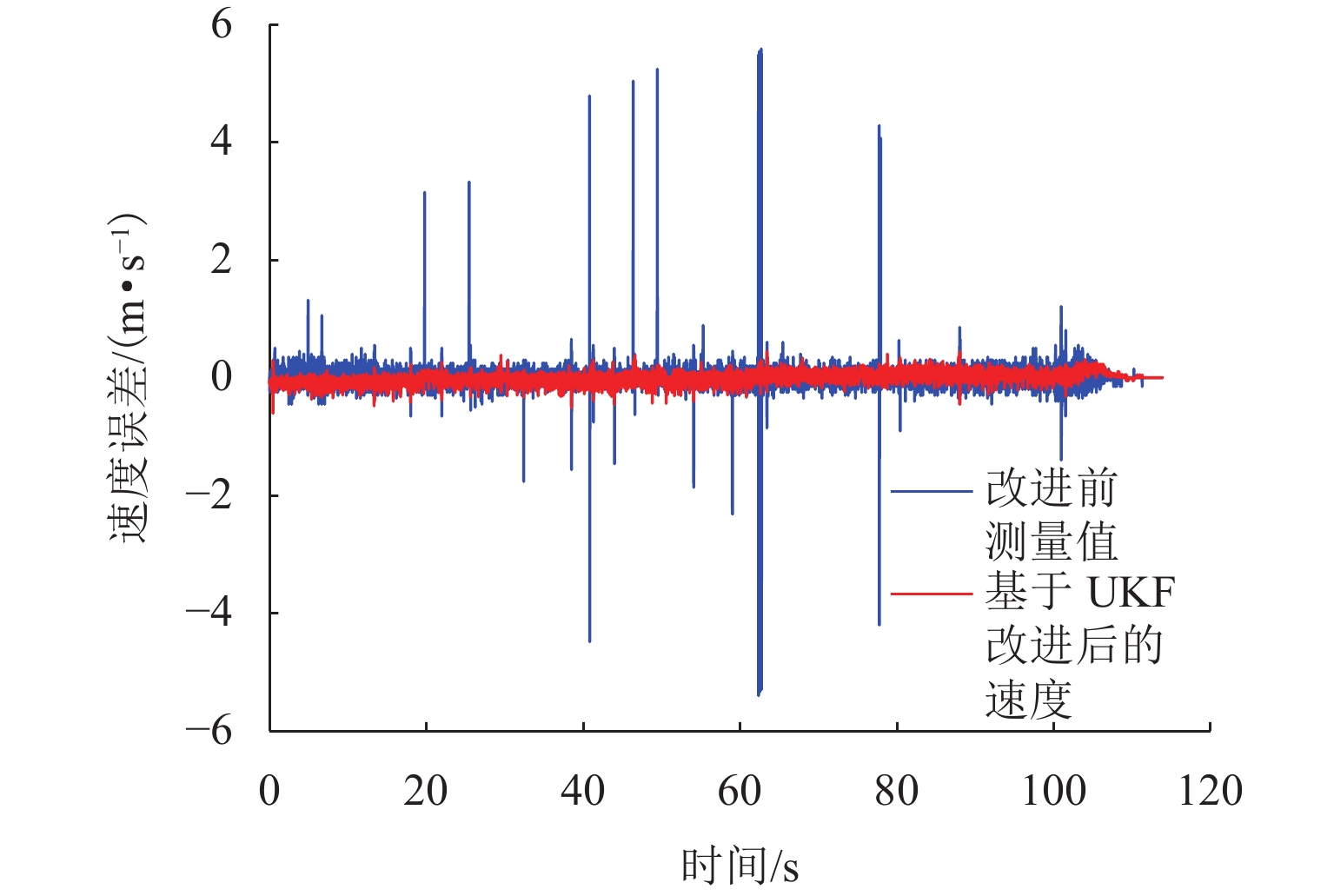
改进前后的速度误差对比如图6所示，改进前平均速度误差为0.12 m/s. 经UKF改进后，其速度误差明显减小，平均速度误差为0.08 m/s，减小了32.6%. 并且，改进后测速误差基本稳定在0.44 m/s以内，满足测速定位精度要求.

图 6 改进前后速度误差对比

Figure 6. Comparison of speed errors before and after improvement

下载: 全尺寸图片幻灯片

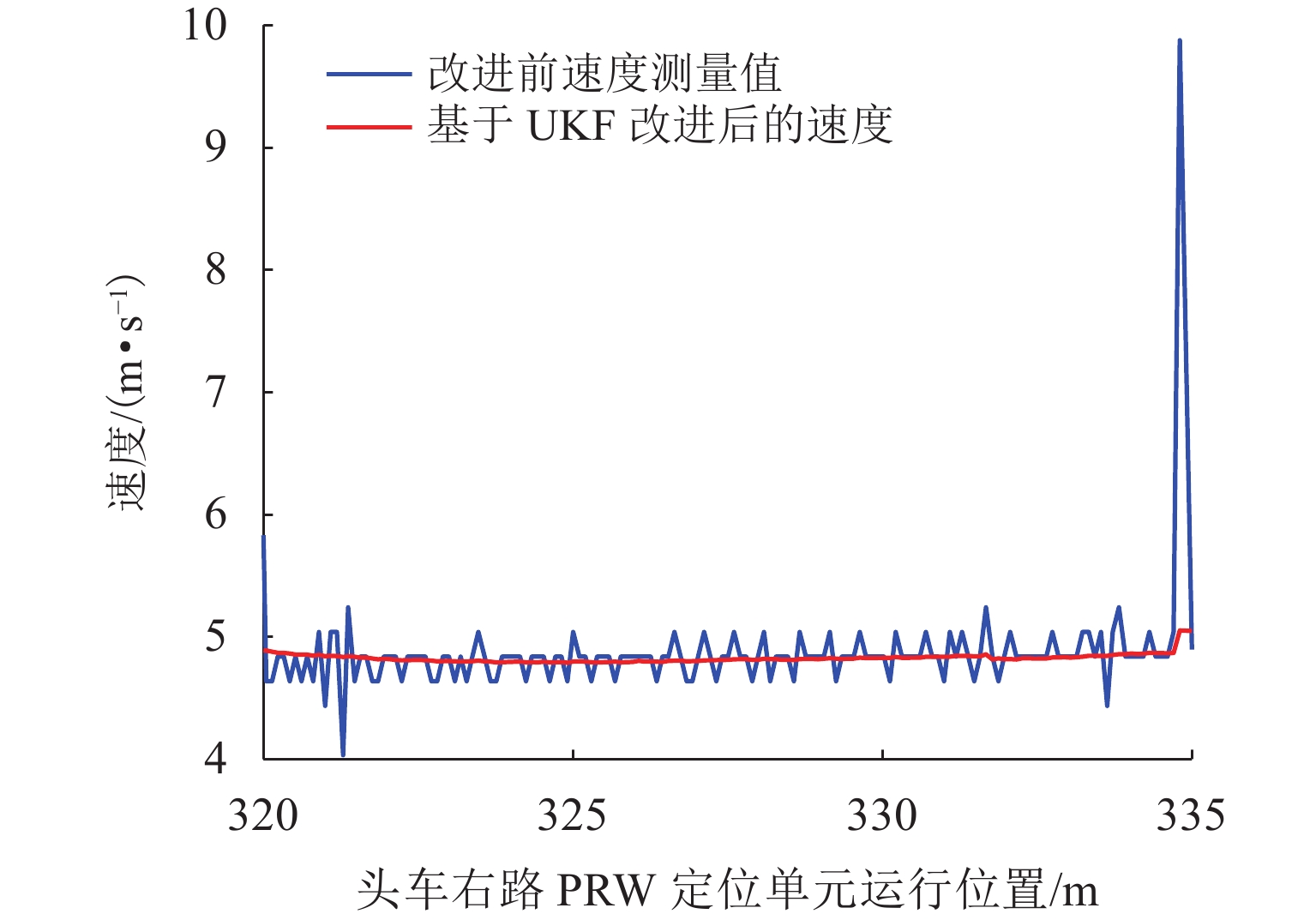
头车右路速度测量值与应用基于加权融合的UKF的速度对比如图7所示.

图 7 头车右路速度测量值与应用基于加权融合的UKF算法后的速度对比

Figure 7. Comparison of measured right-channel speeds of head train and speed after application of UKF algorithm based on weighted fusion

下载: 全尺寸图片幻灯片

由图7可知，以头车右路PRW定位单元320～335 m运行距离的速度变化为例. 经统计，速度测量值的平均速度为4.86 m/s，速度极差为5.85 m/s；改进后平均速度为4.82 m/s，速度极差为0.29 m/s. 且改进后的速度波动明显小于速度测量值，数据变化更加平滑且趋于平稳，可视为匀速运动. 说明应用基于加权融合UKF的常导高速磁浮列车测速定位算法可以使速度波动减小，有效减小信号干扰等因素的不良影响，磁浮列车定位更加准确.

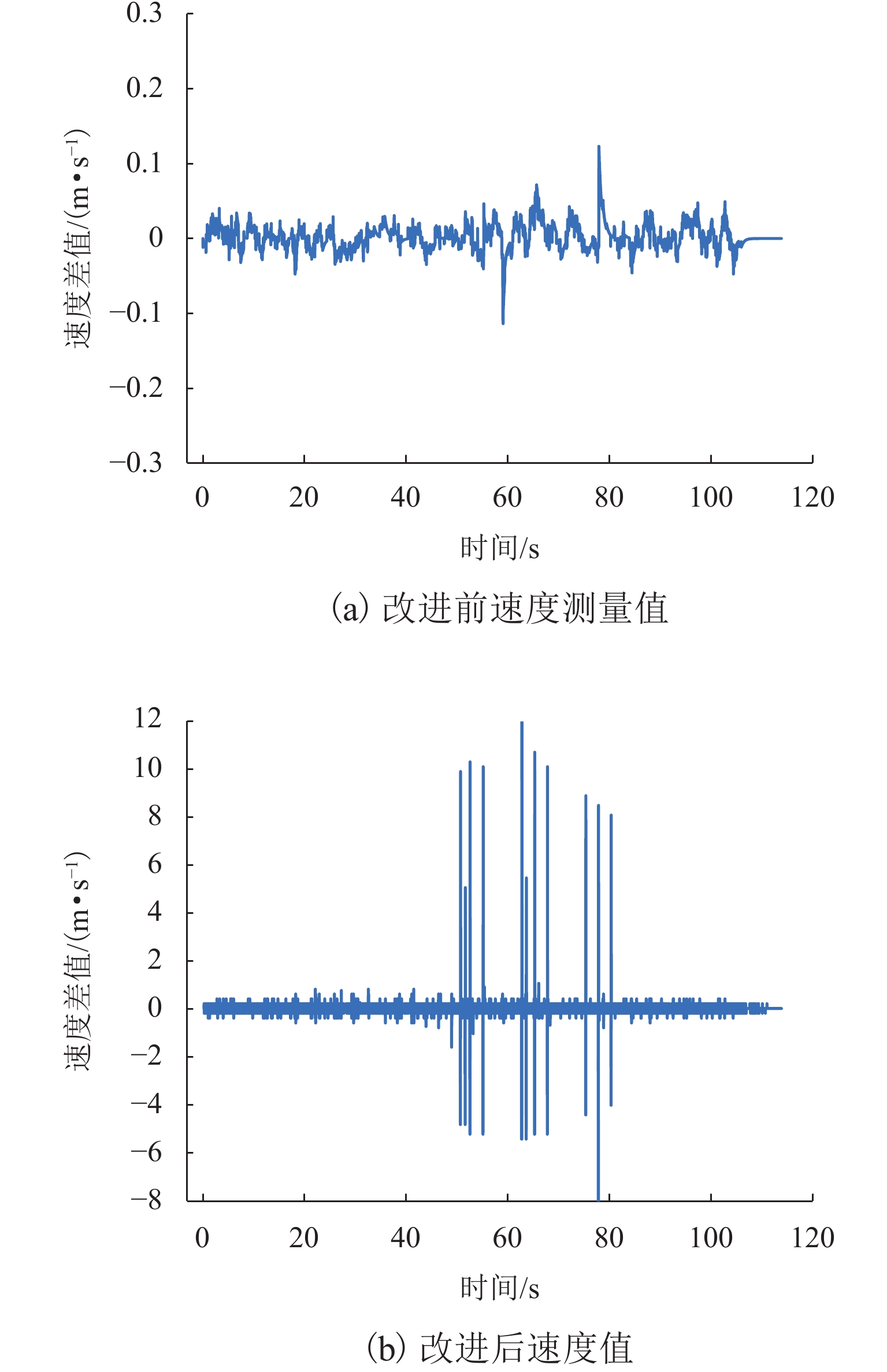
图8所示为采用基于加权融合UKF的常导高速磁浮列车测速定位算法改进前、后的头车左、右两路速度差值.

图 8 采用基于加权融合的UKF改进前、后的头车左、右两路速度差值

Figure 8. Difference between right/left-channel speeds of head train before and after application of UKF based on weighted fusion

下载: 全尺寸图片幻灯片

由图8（a）可知：同一时刻头车左右两路的速度测量值的差值最大达21.57 m/s，误差明显. 经改进后如图8（b）的头车左右路差值基本稳定在0.12 m/s内. 采用基于加权融合UKF的常导高速磁浮列车测速定位算法可以有效消除速度突变，减小相邻时刻速度变化，减小列车输出牵引力波动.

4. 结　论

基于长定子齿槽检测测速定位方法的不足，提出了加权融合的UKF对高速磁浮列车定位算法进行优化，并通过硬件在环仿真分析该算法的测速定位效果，仿真结果表明：本文所提出的方法能够有效消除定位信号采集噪声，显著提高了基于长定子齿槽检测测速定位方法的可靠性及精确性，使得车载计算机能够准确地对列车的行驶情况做出判断和估计，保证牵引系统高效工作. 为后续高速工况下的稳定可靠运行测试提供了有效的数据基础.

致谢：感谢中车青岛四方机车车辆股份有限公司高速磁浮运载技术全国重点实验室对本文工作的支持.

图 1 钢轨磨痕照片

Figure 1. Photographs of rail worn scars

下载: 全尺寸图片幻灯片

图 2 波磨预测的原理

Figure 2. Principle schematic for predicting rail corrugation

下载: 全尺寸图片幻灯片

图 3 蠕滑力饱和系数相对于曲线半径的变化

Figure 3. Variation of creep force saturation coefficient with radius of curved track

下载: 全尺寸图片幻灯片

图 4 轮轨系统摩擦耦合自激振动模型

Figure 4. Friction coupling self-excited vibration model ofwheelset-track system

下载: 全尺寸图片幻灯片

图 5 轮轨系统摩擦耦合自激振动

Figure 5. Friction coupling self-excited vibration ofwheelset-track system

下载: 全尺寸图片幻灯片

参考文献(29)

[1]	钟掘, 蔡鹤皋, 郭东明, 等. 10000个科学难题——制造科学卷[M]. 北京: 科学出版社, 2018: 1194-1197
[2]	GRASSIE S L. Rail corrugation: characteristics, causes, and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(6): 581-596. doi: 10.1243/09544097JRRT264
[3]	SATO Y, MATSUMOTO A, KNOTHE K. Review on rail corrugation studies[J]. Wear, 2002, 253(1/2): 130-139.
[4]	OOSTERMEIJER K H. Review on short pitch rail corrugation studies[J]. Wear, 2008, 265(9/10): 1231-1237.
[5]	JIN X S, WEN Z F, ZHANG W H, et al. Numerical simulation of rail corrugation on a curved track[J]. Computers & Structures, 2005, 83(25/26): 2052-2065.
[6]	WANG Y R, WU T X. The growth and mitigation of rail corrugation due to vibrational interference between moving wheels and resilient track[J]. Vehicle System Dynamics, 2020, 58(8): 1257-1284. doi: 10.1080/00423114.2019.1616099
[7]	ZHANG H G, LIU W N, LIU W F, et al. Study on the cause and treatment of rail corrugation for Beijing metro[J]. Wear, 2014, 317(1/2): 120-128.
[8]	任彤,王安斌,王志强,等. 小半径曲线段钢轨短波波磨的影响因素分析[J]. 噪声与振动控制,2018,38(6): 105-108,112. doi: 10.3969/j.issn.1006-1355.2018.06.020 REN Tong, WANG Anbin, WANG Zhiqiang, et al. Analysis of influencing factors on rail corrugation in small radius curved tracks[J]. Noise and Vibration Control, 2018, 38(6): 105-108,112. doi: 10.3969/j.issn.1006-1355.2018.06.020
[9]	CHEN G X, ZHOU Z R, OUYANG H, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset-track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011
[10]	肖宏,陈鑫,赵越. 基于摩擦自激理论的单侧钢轨波磨机理分析[J]. 西南交通大学学报,2022,57(1): 83-89,119. XIAO Hong, CHEN Xin, ZHAO Yue. Analysis of unilateral rail corrugation mechanism based on friction self-excited theory[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 83-89,119.
[11]	BESHBICHI O E, WAN C, BRUNI S, et al. Complex eigenvalue analysis and parameters analysis to investigate the formation of railhead corrugation in sharp curves[J]. Wear, 2020, 450/451: 203150.1-203150.10.
[12]	FOURIE D, FRÖHLING R, HEYNS S. Railhead corrugation resulting from mode-coupling instability in the presence of veering modes[J]. Tribology International, 2020, 152: 106499.1-106499.12.
[13]	陈光雄, 陈若茜, 闫硕, 等. 一种能够明显减少钢轨波磨的铁路车轮: 中国, CN107415575B[P]. 2020-05-15.
[14]	刘志伟,刘建新,蔡久凤. 钢轨波磨激励下重载机车振动响应分析[J]. 噪声与振动控制,2020,40(5): 119-125. doi: 10.3969/j.issn.1006-1355.2020.05.020 LIU Zhiwei, LIU Jianxin, CAI Jiufeng. Vibration response analysis of heavy haul locomotives excited by rail corrugation[J]. Noise and Vibration Control, 2020, 40(5): 119-125. doi: 10.3969/j.issn.1006-1355.2020.05.020
[15]	王平,刘奕斌,高原,等. 表面选区强化对钢轨波磨处轮轨滚动接触行为的影响[J]. 铁道学报,2020,42(5): 105-112. doi: 10.3969/j.issn.1001-8360.2020.05.014 WANG Ping, LIU Yibin, GAO Yuan, et al. A study on influence of surface strengthening on wheel-rail rolling contact behavior at rail corrugation[J]. Journal of the China Railway Society, 2020, 42(5): 105-112. doi: 10.3969/j.issn.1001-8360.2020.05.014
[16]	金锋,肖宏,赵越,等. 重载铁路小半径曲线波磨演化过程实测分析[J]. 铁道标准设计,2021,65(5): 49-54. JIN Feng, XIAO Hong, ZHAO Yue, et al. Measurement and analysis of the evolution process of small radius curve corrugation in heavy haul railway[J]. Railway Standard Design, 2021, 65(5): 49-54.
[17]	李响,任尊松,徐宁. 地铁小半径曲线段钢弹簧浮置板轨道的钢轨波磨研究[J]. 铁道学报,2017,39(8): 70-76. doi: 10.3969/j.issn.1001-8360.2017.08.010 LI Xiang, REN Zunsong, XU Ning. Study on rail corrugation of steel spring floating slab track on subway with small radius curve track[J]. Journal of the China Railway Society, 2017, 39(8): 70-76. doi: 10.3969/j.issn.1001-8360.2017.08.010
[18]	雷震宇,王志强,李莉,等. 地铁普通扣件钢轨波磨特性[J]. 同济大学学报(自然科学版),2019,47(9): 1334-1340. doi: 10.11908/j.issn.0253-374x.2019.09.014 LEI Zhenyu, WANG Zhiqiang, LI Li, et al. Rail corrugation characteristics of the common fastener track in metro[J]. Journal of Tongji University (Natural Science), 2019, 47(9): 1334-1340. doi: 10.11908/j.issn.0253-374x.2019.09.014
[19]	尧辉明,沈钢,高利君. 基于试验验证的磨耗型钢轨波磨形成机理[J]. 同济大学学报(自然科学版),2018,46(10): 1427-1432. doi: 10.11908/j.issn.0253-374x.2018.10.015 YAO Huiming, SHEN Gang, GAO Lijun. Formation mechanism of worn profile rail corrugation based on experimental verification[J]. Journal of Tongji University (Natural Science), 2018, 46(10): 1427-1432. doi: 10.11908/j.issn.0253-374x.2018.10.015
[20]	于淼. 高速铁路轨道-车辆系统高频瞬态仿真及波磨机理研究[D]. 北京: 中国铁道科学研究院, 2019.
[21]	TASSILLY E, VINCENT N. A linear model for the corrugation of rails[J]. Journal of Sound and Vibration, 1991, 150(1): 25-45. doi: 10.1016/0022-460X(91)90400-E
[22]	HEMPELMANN K, KNOTHE K. An extended linear model for the prediction of short pitch corrugation[J]. Wear, 1996, 191(1/2): 161-169.
[23]	IGELAND A, ILIAS H. Rail head corrugation growth predictions based on non-linear high frequency vehicle/track interaction[J]. Wear, 1997, 213(1/2): 90-97.
[24]	SUDA Y, HANAWA M, OKUMURA M, et al. Study on rail corrugation in sharp curves of commuter line[J]. Wear, 2002, 253(1/2): 193-198.
[25]	TORSTENSSON P T, SCHILKE M. Rail corrugation growth on small radius curves—measurements and validation of a numerical prediction model[J]. Wear, 2013, 303(1/2): 381-396.
[26]	HIENSCH M, NIELSEN J C O, VERHEIJEN E. Rail corrugation in The Netherlands—measurements and simulations[J]. Wear, 2002, 253(1/2): 140-149.
[27]	TASSILLY E, VINCENT N. Rail corrugations: analytical model and field tests[J]. Wear, 1991, 144(1/2): 163-178.
[28]	CORREA N, VADILLO E G, SANTAMARIA J, et al. A versatile method in the space domain to study short-wave rail undulatory wear caused by rail surface defects[J]. Wear, 2016, 352/353: 196-208. doi: 10.1016/j.wear.2016.02.012
[29]	陈光雄,崔晓璐,王科. 高速列车车轮踏面非圆磨耗机理[J]. 西南交通大学学报,2016,51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004 CHEN Guangxiong, CUI Xiaolu, WANG Ke. Generation mechanism for plolygonalization of wheel treads of high-speed trains[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004

施引文献

期刊类型引用(7)

1.	姚宇飞. 地铁曲线地段扣件刚度对钢轨波磨的影响实测与仿真分析. 山西建筑. 2025(01): 129-133 . 百度学术
2.	王波，罗世辉，王晨，曲天威，马卫华，雷成. 青藏线双源动车组黏着适应性研究. 西南交通大学学报. 2025(01): 214-224 . 本站查看
3.	陈清华，閤鑫，王开云. 基于SRCKF算法的轨道车辆轮轨垂向力识别. 西南交通大学学报. 2025(02): 403-410 . 本站查看
4.	冯晓航，陈光雄，梅桂明，董丙杰，赵鹏鹏，李先航. 地铁弓网系统摩擦自激振动研究. 西南交通大学学报. 2025(02): 418-424 . 本站查看
5.	黄河山，王伟华，姚宇飞，汤雪扬，王俊龙. 地铁曲线地段钢弹簧浮置板轨道钢轨波磨成因及控制方法. 铁道标准设计. 2024(07): 33-39 . 百度学术
6.	唐宇，陈光雄，冯晓航，常勇，张峻才，华浩，刘崧楠. 弹性轨道集电系统摩擦自激振动研究. 润滑与密封. 2024(12): 15-21 . 百度学术
7.	何俊华，陈光雄，康熙，李先航，宋启峰，董丙杰. 轮对-轨道系统波磨预测模型的建立及预测分析. 润滑与密封. 2023(01): 79-84 . 百度学术